1. Introduction
Equalisation, as described in [
1], is an integral part of the music production workflow, with applications in live sound engineering, recording, music production, and mastering, in which multiple frequency dependent gains are imposed upon an audio signal. Generally, the process of equalisation can be categorised under one of the following headings as described in [
2], corrective equalisation: in which problematic frequencies are often attenuated in order to prevent issues such as acoustic feedback, and creative equalisation: in which the audio spectrum is modified to achieve a desired timbral aesthetic. Whilst the former is primarily based on adapting the effect parameters to the changes in the audio signal, the latter often involves a process of translation between a perceived timbral adjective such as
bright,
flat, or
sibilant and an audio effect input space, by which a music producer must reappropriate a perceptual representation of a timbral transformation as a configuration of multiple parameters in an audio processing module. As music production is an inherently technical process, this mapping procedure is not necessarily trivial, and is made more complex by the source-dependent nature of the task.
2. Background
2.1. Semantically-Controlled Audio Effects
Engineers and producers generally use a wide variety of timbral adjectives to describe sound, each with varying levels of agreement. By modelling these adjectives, we are able to provide perceptually meaningful abstractions, which lead to a deeper understanding of musical timbre and systems that facilitate the process of audio manipulation. The extent to which timbral adjectives can be accurately modelled is defined by the level of exhibited agreement, a concept investigated in [
3], in which terms such as
bright,
resonant, and
harsh all exhibit strong agreement scores, and terms such as
open,
hard, and
heavy all show low subjective agreement scores. It is common for timbral descriptors to be represented in low-dimensional space;
brightness, for example, is shown to exhibit a strong correlation with spectral centroid [
4,
5] and has further dependency on the fundamental frequency of the signal [
6]. Similarly, studies such as [
7,
8] demonstrate the ability to reduce complex data to lower-dimensional spaces using dimensionality reduction.
Recent studies have also focused on modification of the audio signal using specific timbral adjectives, where techniques such as spectral morphing [
9] and additive synthesis [
10] have been applied. For the purposes of equalisation, timbral modification has also been implemented via psychoacoustic measurements such as loudness [
11], spectral masking [
12], and semantically-meaningful controls and intuitive parameter spaces. SocialEQ [
13], for example, collects timbral adjective data via a web interface and approximates the configuration of a graphic equaliser curve using multiple linear regression. Similarly, subjEQt [
14] provides a two-dimensional interface, created using a Self-Organising Map, in which users can navigate between presets such as
boomy,
warm, and
edgy using natural neighbour interpolation. This is a similar model to 2DEQ [
15], in which timbral descriptors are projected onto a two-dimensional space using Principal Component Analysis (PCA). The Semantic Audio Feature Extraction (SAFE) project provides a similar non-parametric interface for semantically controlling a suite of audio plug-ins, in which semantics data is collected within a given Digital Audio Workstation (DAW). Adaptive presets can then be selectively derived based on audio features, parameter data, and music production metadata.
2.2. Aims
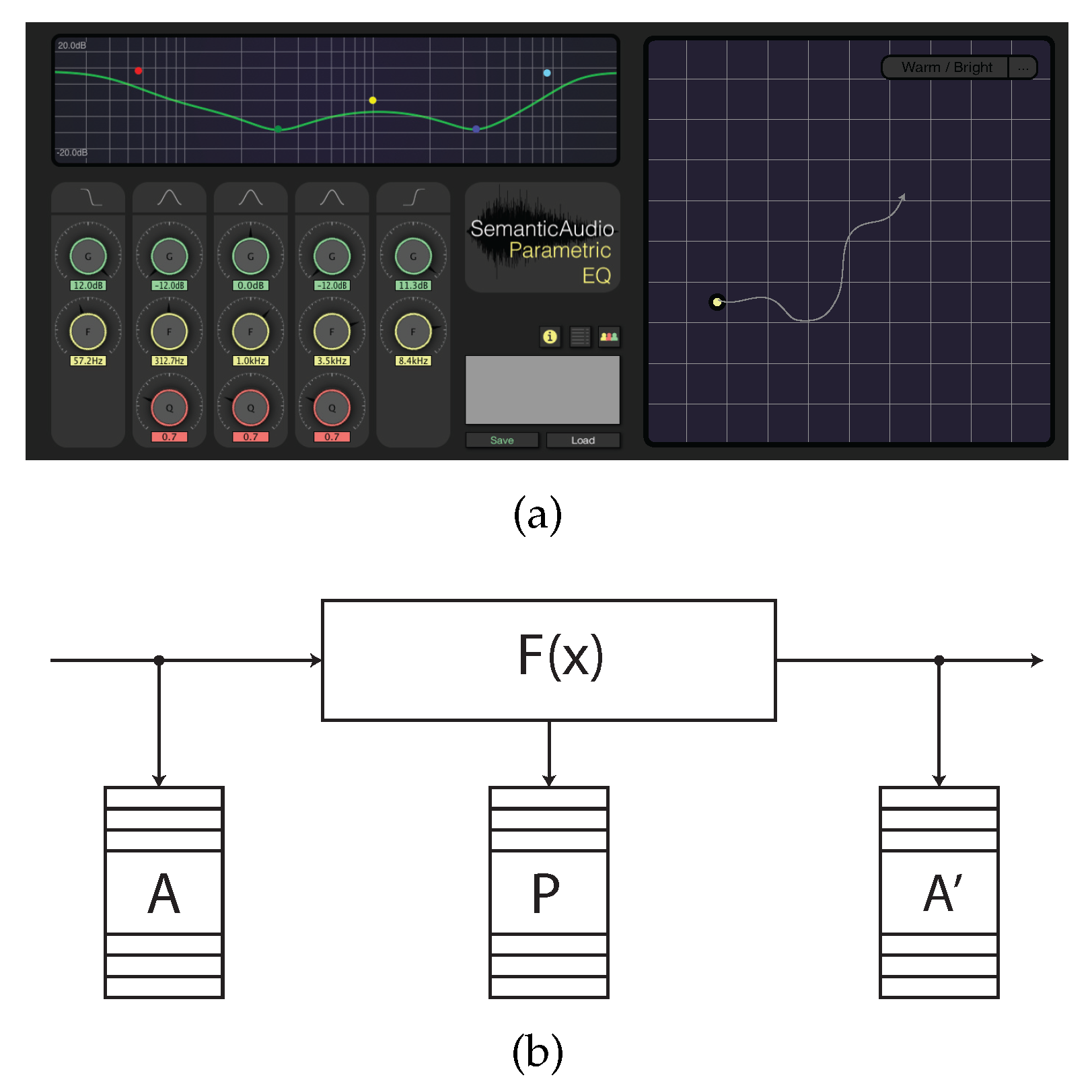
In this study, we propose a system that projects the controls of a parametric equaliser comprising five biquad filters, as detailed in [
16], arranged in series onto an editable two-dimensional space, allowing the user to manipulate the timbre of an audio signal using an intuitive interface. Whilst the axes of the two-dimensional space are somewhat arbitrary, underlying timbral characteristics are projected onto the space via a training stage using two-term musical semantics data. In addition to this, we propose a signal processing method of adapting the parameter modulation process to the incoming audio data based on feature extraction applied to the long-term average spectrum (LTAS), as detailed in [
17,
18,
19], capable of running in near-real-time. The model is implemented using the SAFE architecture (detailed in [
20]), and is provided as an extension of the current Semantic Audio Parametric Equaliser (available for download at [
21]), as shown in
Figure 1a.
3. Methodology
In order to model the desired relationship between the two parameter spaces, a number of problems must be addressed. Firstly, the data reduction process should account for maximal variance in high-dimensional space without bias towards a smaller subset of the equaliser parameters. Similarly, we should be able to map to the high-dimensional space with minimal reconstruction error, given a new set of (x, y) coordinates. This process of mapping between spaces is nontrivial, due to loss of information in the reconstruction process. Furthermore, the low-dimensional parameter space should be configured in a way that preserves an underlying timbral characteristic in the data, thus allowing a user to transform the incoming audio signal in a musically meaningful way. Finally, the process of parameter space modification should not be agnostic of the incoming audio signal, meaning that any mapping between the two-dimensional plane and the equaliser parameters should be expressed as a function of the (x, y) coordinates and some representation of the signal spectral energy. In addition to this, the system should be capable of running in near-real time, enabling its use in a DAW environment.
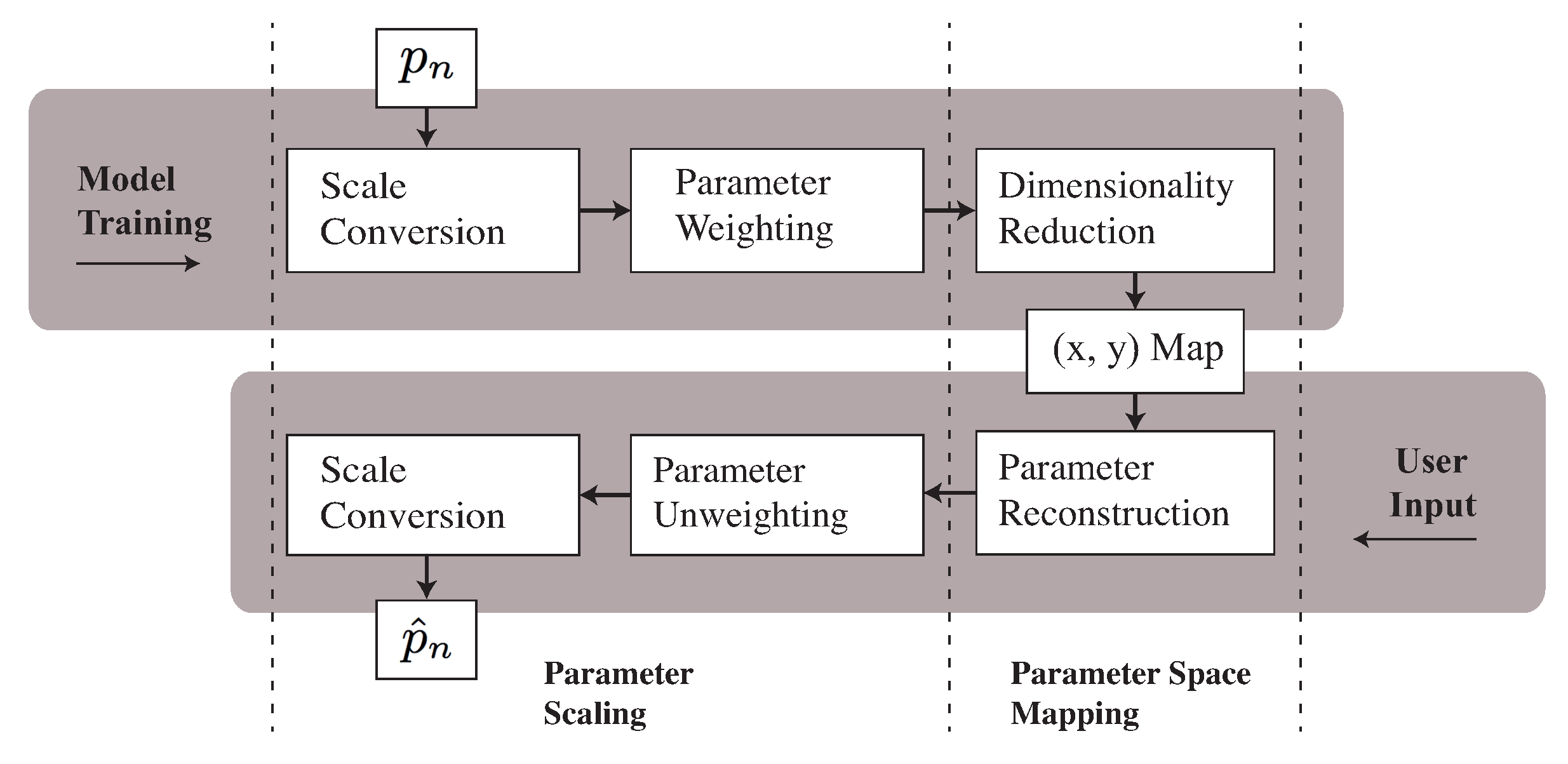
To address these problems, we develop a model that consists of two phases. The first is a training phase, in which a map is derived from a corpus of semantically-labelled parameter data, and the second is an implementation phase in which a user can present (x, y) coordinates and an audio spectrum, resulting in a 13-dimensional vector of parameter state variables. To optimise the mapping process, we experiment with a combination of 6 dimensionality reduction techniques and 5 reconstruction methods, followed by a stacked-autoencoder (sAE) model that encapsulates both the dimensionality reduction and reconstruction processes. The techniques were chosen to represent a variable range of complexity and nonlinearity, and were intended to provide a selection of possible solutions to the problem, in which the highest performing section would be used for implementation. With the intention of scaling the parameters to the incoming audio signal, we derive a series of weights based on a selection of features, extracted from the signal LTAS coefficients. To evaluate the model performance under a range of conditions, we train it with binary musical semantics data and measure both objective and subjective performance based on the reconstruction of the input space and the structural preservation in reduced dimensionality space.
3.1. Dataset
For the training of the model, we compile a dataset of 800 semantically-annotated equaliser parameter space settings, comprising 40 participants equalising 10 musical instrument samples using two descriptive terms: warm and bright. To do this, participants were presented with the musical instrument samples in a DAW and asked to use a parametric equaliser to achieve the two timbral settings. After each setting was recorded, the data were recorded and the equaliser was reset to unity gain. During the test, samples were presented to the participants in a random order across separate DAW channels. Furthermore, the musical instrument samples were all performed unaccompanied, were Root Mean Square (RMS) normalised and ranged from 20 to 30 s in length. All of the participants had normal hearing, were aged 18–40, and all had at least 3 years’ music production experience.
The descriptive terms (
warm and
bright) were selected for a number of reasons; firstly, the agreement levels exhibited by participants tend to be high (as suggested by [
3]), meaning there should be less intra-class variance when subjectively assigning parameter settings. When measured using an agreement metric, defined by [
13] as the log number of terms over the trace of the covariance matrix,
warm and
bright were the two highest ranked terms in a dataset of 210 unique adjectives. Secondly, the two terms are deemed to be sufficiently different enough to form an audible timbral variation in low dimensional space. While the two terms do not necessarily exhibit orthogonality (for example,
brightness can be modified with constant
warmth [
9]), they have relatively dissimilar timbral profiles, with
brightness widely accepted to be highly correlated with the signal’s spectral centroid, and
warmth often attributed to the ratio of the first three harmonics to the remaining harmonic partials in the magnitude spectrum [
22].
The parameter settings were collected using a modified build of the SAFE data collection architecture, in which descriptive terms, audio feature data, parameter data, and metadata can be collected remotely within the DAW environment and uploaded to a server. As illustrated in
Figure 1b, the SAFE architecture allows for the capture of audio feature data before and after processing has been applied. Similarly, the interface parameters
P are captured and stored in a linked database. For the purpose of this experiment, the architecture was modified by adding the functionality to capture LTAS coefficients, with a window size of 1024 samples and a hop size of 256.
While the SAFE project comprises a number of DAW plug-ins, we focus solely on the parametric equaliser, which utilises five biquad filters arranged in series, consisting of a low-shelving filter (LS), three peaking filters (
), and a high-shelving filter (HS), where the LS and HS filters each have two parameters and the (
) filters each have three, as described in
Table 1.
3.2. Evaluation Criteria
To evaluate the model under various conditions and to select an appropriate mapping topology, we apply objective metrics to the data during the dimensionality reduction and reconstruction processes. These allow us to evaluate the extent to which (1) the dimensionality reduction technique retains the structure of the high-dimensional data (trustworthiness, continuity, K-Nearest Neighbours (K-NN)), (2) the classes are separable in low-dimensional space (Jeffries–Matusita Distance), and (3) the system accurately reconstructs the high-dimensional parameter space (reconstruction error).
3.2.1. Trustworthiness and Continuity
To evaluate the structural preservation of each technique, the metrics
trustworthiness and
continuity [
23] are applied to the dataset. Here, the distance of point
i in high-dimensional space is measured against its
k closest neighbours using rank order, and the extent to which each rank changes in low-dimensional space is measured. For
n samples, let
be the rank in distance of sample
i to sample
j in the high-dimensional space
. Similarly, let
be the rank of the distance between sample
i and sample
j in low-dimensional space
. Using the
k-nearest neighbours, the map is considered
trustworthy if these
k neighbours are also placed close to point
i in the low-dimensional space, as shown in Equation (
1).
Similarly,
continuity (shown in Equation
2) measures the extent to which original clusters of datapoints are preserved, and can be considered the inverse to
trustworthiness, finding sample points that are close to point
i in low-dimensional space, but not in the high-dimensional plane.
In both of these equations, a normalising factor is used to bound the
trustworthiness and
continuity scores between 0 and 1. These measures evaluate the extent to which the local structure of the original dataset is preserved in a low-dimensional map; this is described in [
24], where it is shown that the local structure of the dataset needs to be retained for a successful map of the datapoints.
3.2.2. K-NN
In order to measure the similarities in inter-class structures within the high and low dimensional space, we apply a K-NN classifier with
, as described in [
25], and then measure the differences in classification accuracies. The nearest neighbours are found using Euclidean distances with 13 and 2 dimensions, respectively. The accuracies are derived using K-fold cross validation with
K = 20, where 20% of the data is partitioned for testing. This allows us to measure the extent to which the between-class structures have been preserved in the reduction process, and effectively acts as a supervised structural preservation metric.
3.2.3. Jeffries–Matusita Distance
In order to evaluate the extent to which timbral descriptors lie at opposing ends of the mapped parameter space, we can measure the extent to which the timbre classes are separable using a distance metric. Typically, this can be done by finding the divergence between class distributions using a technique such as Kullback–Leibler Divergence (KLD), as we proposed in [
26]; however, as explained in [
27], this does not satisfy the triangle inequality based on the measurement’s asymmetry. While two-sided KLD addresses this, as explained in [
28], [
29] proposes Jeffries–Matusita Distance (JMD) as a more appropriate alternative. JMD (as shown in Equation
4) is a metric derived from the Bhattacharya (BH) distance, as in Equation (
3), which bounds the output of the measure from 0 (no separability) to 2 (perfect separability).
Here m represents the mean and S represents the covariance of classes i and j, respectively.
3.2.4. Reconstruction Error
To measure the reconstruction accuracy (low-to-high-dimensionality mapping) of the model, we measure the input/output error for each pair-wise combination of dimensionality reduction and reconstruction techniques by computing the mean absolute error between predicted and actual parameter values. This is done using
K-fold cross validation with
iterations, and a test partition size of 20% (160 training examples). As some of the dimensionality reduction techniques are unable to embed new information into the reduced-dimensionality space, the first part of the test process (
i.e., the prediction of new low-dimensional values as implemented in [
26]) was omitted, and only regression and interpolation techniques were evaluated.
3.3. Subjective Evaluation
Using the metrics defined in
Section 3.2, we are able to select an appropriate model which is capable of accurately reducing the dataset while preserving the data structure and accurately reconstructing the input parameters with minimal error. To validate this, we implement subjective user tests in which participants are asked to equalise a series of audio samples using the reduced-dimensionality interface. To do this, 10 participants were asked to apply the process to 10 input sounds using only the two-dimensional interface. Each participant was asked to achieve a
warm or
bright output sound for each stimuli. During the test, samples were presented to participants in a random order across separate DAW channels, and the equaliser parameters remained hidden. No indication was given as to the underlying distribution of datapoints. The stimuli comprised unaccompanied musical instrument samples and ranged from 20 to 30 s in length. The samples were primarily taken from electric guitars and included a variety of genres, taken from the Mixing Secrets Multitrack Audio Dataset [
30]. All of the participants had normal hearing, were aged 18–35, and had varied music production experience, from 0 to 5 years.
4. Model
The proposed system maps between the equaliser parameter space, consisting of 13 filter parameters and a two-dimensional plane, while preserving the context-dependent nature of the audio effect. After an initial training phase, the user can then submit (x, y) coordinates to the system using a track-pad interface, resulting in a timbral modification via the corresponding filter parameters. To demonstrate this, we train the model with two class (bright, warm) musical semantics data taken from the SAFE equaliser database, thus resulting in an underlying transition between opposing timbral descriptors in two-dimensional space. By training the model in this manner, we intend to retain the high-dimensional structure of the dataset in the two-dimensional space while minimising the reconstruction error inherent to dimensionality reduction methods.
The model (illustrated in
Figure 2) has two key operations. The first involves weighting the parameters by computing the vector
from the input signal long-term spectral energy (
A). We can then modify the parameter vector (
P) to obtain a weighted vector (
). The second component scales the dimensionality of (
), resulting in a compact audio-dependent representation. During the model implementation phase, we apply an unweighting procedure based on the (
x,
y) coordinates and the signal modified spectrum. This is done by multiplying the estimated parameters with the inverse weight vector, resulting in an approximation of the original parameters. In addition to the weighting and dimensionality reduction stages, a scale-normalisation procedure is applied, aiming to convert the ranges of each parameter (given in
Table 1), to (
). This converts the data into a suitable format for dimensionality reduction.
4.1. Parameter Scaling
As the configuration of the filter parameters assigned to each descriptor by the user during equalisation is likely to vary based on the audio signal being processed, the first requirement of the model is to apply weights to the parameters based on knowledge of the audio data at the time of processing. To do this, we selectively extract features from the signal LTAS before and after the filter is applied. This is possible due to the configuration of the data collection architecture, highlighted in
Figure 1b. The weights (
) can then be expressed as a function of the LTAS, where the function’s definition varies based on the parameter representation (
i.e., gain, centre frequency, or bandwidth of the corresponding filter). We use the LTAS to prevent the parameters from adapting each time a new frame is read. In practice, we are able to do this by presenting users with means to store the audio data, rather than continually extracting it from the audio stream. Each weighting is defined as the ratio between a spectral feature taken from the filtered audio signal (
) and the signal filtered by an enclosing rectangular window (
). Here, the rectangular window is bounded by the minimum and maximum frequency values attainable by the observed filter
.
We can define the equaliser as an array of biquad functions arranged in series, as depicted in Equation (
5).
Here,
represents the number of filters used by the equaliser and
represents the
biquad function, which we can define by its transfer function, given in Equation (
6).
The LTAS is then modified by the filter as in Equation (
7) and the weighted parameter vector can be derived using the function expressed in Equation (
8).
where
is the
parameter in the vector
P. The weighting function is then defined by the parameter type (
m), where
represents gain,
represents centre-frequency, and
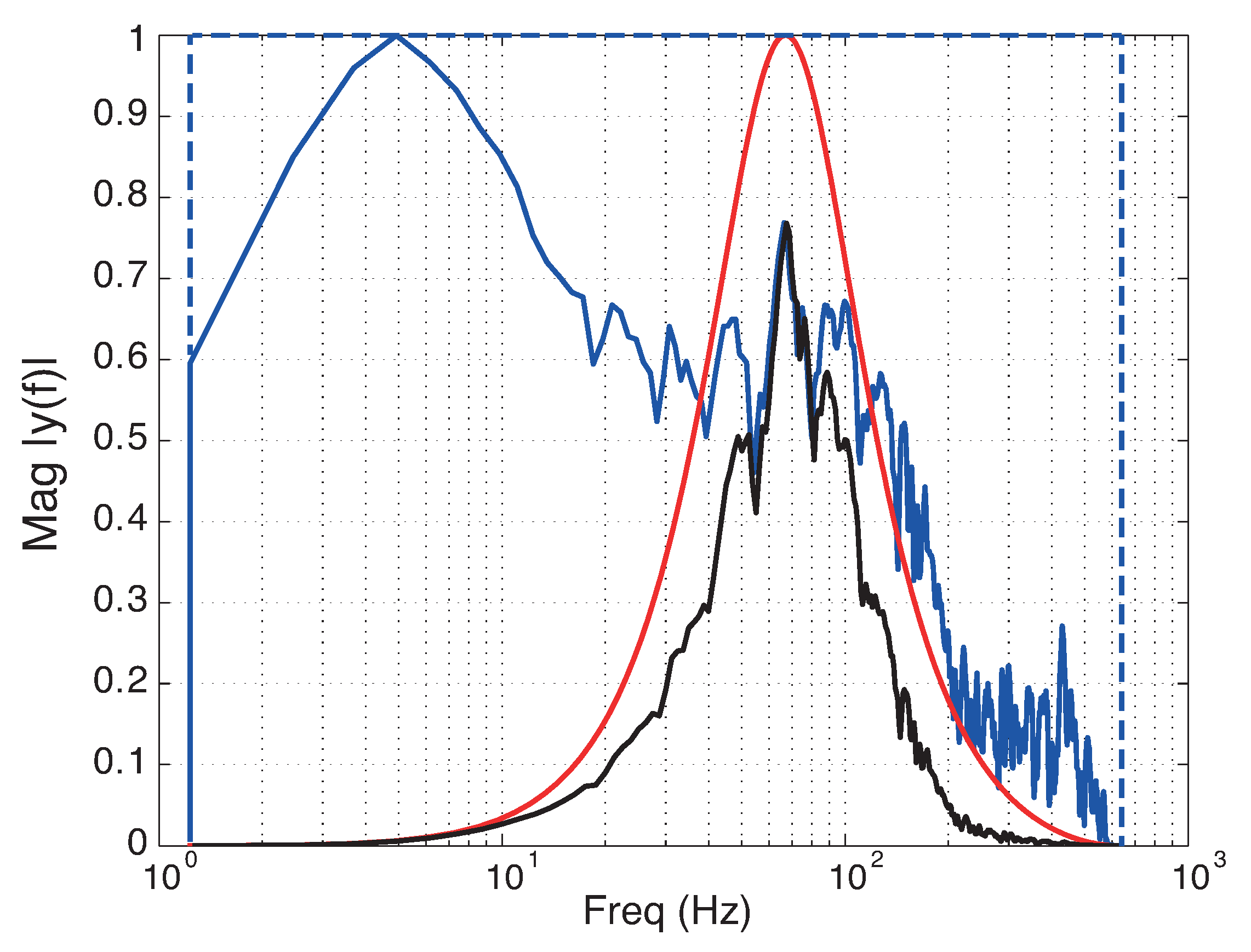
represents bandwidth. For gain parameters, the weights are expressed as a ratio of the spectral energy in the filtered spectrum (
) to the spectral energy in the enclosing rectangular window (
), derived in Equation (
9) and illustrated in
Figure 3.
For frequency parameters (
), the weights are expressed as a ratio of the respective spectral centroids of
and
, as demonstrated in Equation (
10), where
are the corresponding frequency bins.
Finally, the weights for bandwidth parameters (
) are defined as the ratio of spectral spread exhibited by both
and
. This is demonstrated in Equation (
11), where
represents the spectral centroid of
x.
During the implementation phase, retrieval of the unweighted parameters, given a weighted vector, can be achieved by simply multiplying the weighted parameters with the inverse weights vector, as in Equation (
12).
where
is a reconstructed version of
p, after dimensionality reduction has been applied.
To ensure the parameters are in a consistent format for each of the dimensionality scaling algorithms, a scale normalisation procedure is applied using Equation (
13), where during the training process, the
and
represent the minimum and maximum values for each parameter (given in
Table 1), and
and
represent 0 and 1. During the implementation process, these values are exchanged such that
and
represent the minimum and maximum values for each parameter and
and
represent 0 and 1.
Additionally, a sorting algorithm was used to place the three mid-band filters in ascending order based on their centre frequency. This prevents normalisation errors due to the frequency ranges, allowing filters to be rearranged by the user.
4.2. Parameter Space Mapping
Once the filters have been weighted by the audio signal, the mapping from 13 equaliser variables to a two-dimensional subspace can be accomplished using a range of dimensionality reduction techniques. In this study, we expand on [
26] and evaluate the performance of six dimensionality reduction techniques. Here, the algorithms that were used for the dimensionality reduction are available as part of the dimensionality reduction toolbox in [
31]. In addition to this, parameter space mapping is evaluated by measuring the quality of reduction with rank-based measures and nearest neighbour classification algorithms. In dimensionality reduction, the reconstruction process is often less common due to the nature of the task (e.g., feature optimisation, data reduction). We evaluate the efficacy of two regression-based techniques and three interpolation techniques at mapping two-dimensional interface variables to a vector of equaliser parameters. This is done by approximating functions using the weighted parameter data and measuring the reconstruction error. Finally, we evaluate an sAE model of data reduction, in which the parameter space is both reduced and reconstructed in the same algorithm; we are then able to isolate the reconstruction (decoder) stage for the implementation process.
Dimensionality reduction is implemented using the following techniques: PCA, a widely used method of embedding data into a linear subspace of reduced dimensionality by finding the eigenvectors of the covariance matrix, originally proposed by [
32];
Kernel PCA (kPCA), a non-linear manifold mapping technique in which the eigenvectors are computed from a kernel matrix as opposed to the covariance matrix, as defined by [
33];
probabilistic PCA (pPCA), a method that considers standard PCA as a latent variable model and makes use of an Expectation Maximisation (EM) algorithm, a method for finding the maximum-likelihood estimate of the parameters in an underlying distribution from a given data set, depending on unobserved latent variables [
34] as described in [
35];
Factor Analysis (FA), a statistical analysis technique that identifies the relationship between different variables of a dataset and groups those variables by the correlation of the underlying factors [
36];
Diffusion Maps (DM), a technique inspired by the field of dynamical systems, reducing the dimensionality of data by embedding the original dataset in a low-dimensional space by retrieving the eigenvectors of Markov random walks [
37];
Linear Discriminant Analysis (LDA), a supervised projection technique that maps to a linear subspace while maximising the separability between data points that belong to different classes (see [
38]). As LDA projects the data-points onto the dimensions that maximise inter-class variance for C classes, the dimensionality of the subspace is set to
. This means that in a binary classification problem such as ours, we need to reconstruct the second dimension arbitrarily. For each of the other algorithms, we select the first two variables for mapping, and for the kPCA algorithm, the feature distances are computed using a Gaussian kernel.
The parameter reconstruction process was implemented using the following techniques:
Linear Regression (LR), a process by which a linear function is used to estimate latent variables;
Natural Neighbour Interpolation (NaNI), a method for interpolating between scattered data points using Voronoi tessellation, as used by [
14] for a similar application;
Nearest Neighbour Interpolation (NeNI), an interpolation method where the query point takes the value of the nearest neighbour [
39];
Linear Interpolation (LI), an interpolation technique that assumes a linear relationship between the existing points in a dataset;
Support Vector Regression (SVR), a non-linear kernel-based regression technique (see [
40]), for which we choose a Gaussian kernel function.
An autoencoder is an Artificial Neural Network (ANN) with a topology capable of learning a compact representation of a dataset by optimising a matrix of weights, such that a loss function representing the difference between the output and input vectors is minimised. Autoencoders can then be stacked together using the output of the prior layer as the input for the next in order to construct a deep network architecture. Each autoencoder is then trained individually, learning to minimise the reconstruction error between its input and the predicted output. This approach has been used for data compression [
41], and by extension, dimensionality reduction. This type of ANN is often used in order to improve the classification accuracy of logistic regression [
42]; however, since our problem involves data reconstruction as opposed to classification, a logistic layer is not implemented.
Network Topology
The autoencoder was built using the Theano Python library [
43], where we observed an error of 0.086 using a single hidden layer with
N (in this case
) units. To reduce the error, a mirrored
architecture was selected empirically, resulting in an error measurement of 0.08. To improve reconstruction accuracy further, noise was introduced at each stage in the network, as demonstrated by [
44]. Here, the first autoencoder was corrupted with 0.6 magnitude noise, and the second with 0.5. This approach is able to further reduce the reconstruction error to 0.0784. Additionally, we replace the previously-used stochastic gradient descent algorithm with an
RMSprop method [
45] with a batch size of 10 as the pre-training and fine-tuning methods of optimization, and a learning rate of 0.01 and 0.001, respectively. This approach allows for faster optimization, as shown in [
46]. For the weighted parameters, we found that a three-layer denoising autoencoder with an architecture of
and noise of magnitude
is able to outperform our two-layer denoising autoencoder model.
5. Results
5.1. Parameter Space Evaluation
To evaluate the extent to which structures in the parameter space are preserved in the reduced dimensionality map, we report the
trustworthiness,
continuity, and class-wise similarity (
k-NN). This is applied to data shown in
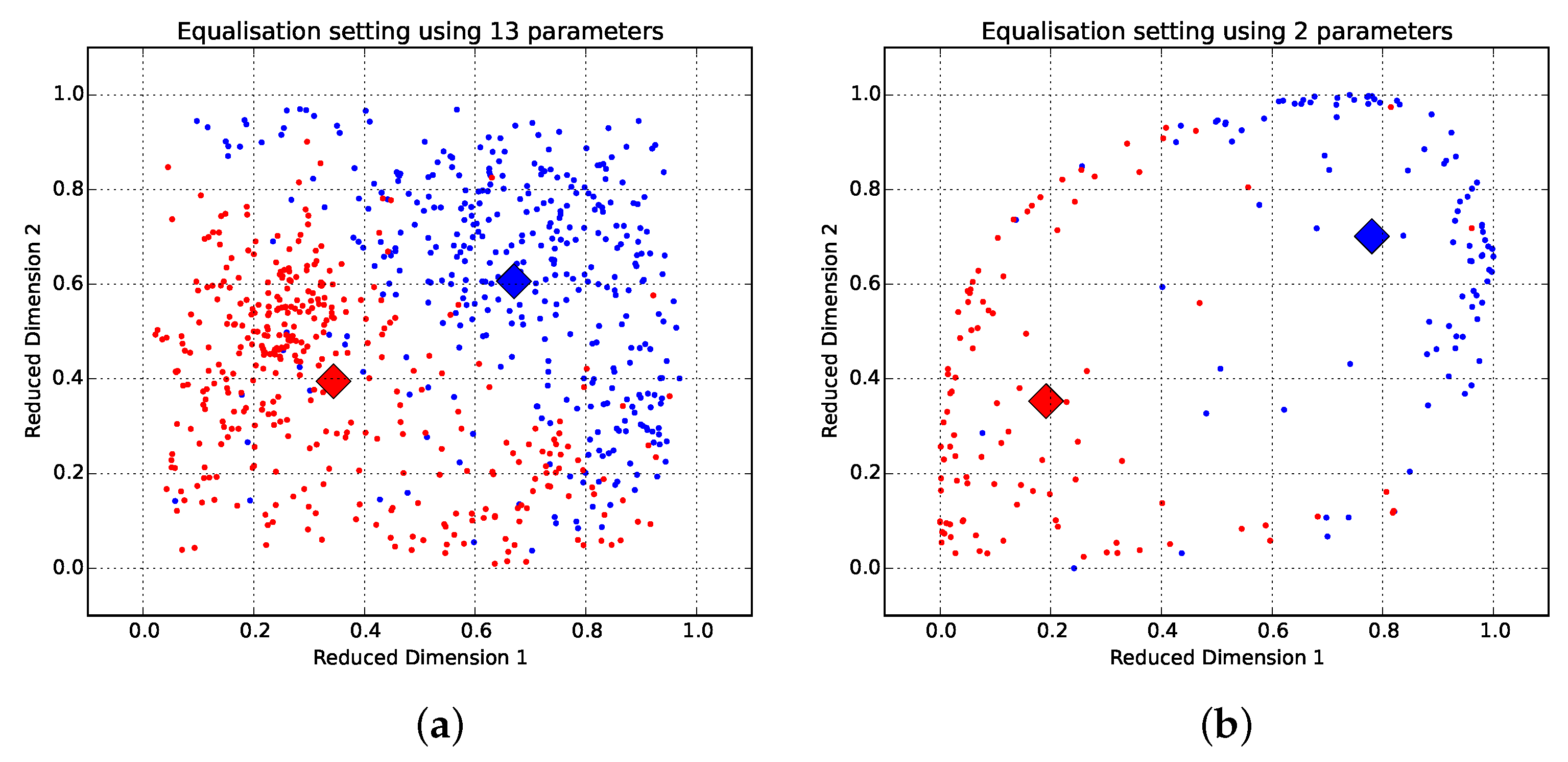
Figure 4a–g, in which a two-dimensional projection of the 13 equaliser parameters is given for both
warm and
bright samples in the dataset.
5.1.1. Low-Dimensional Mapping Accuracy
From
Table 2 we show that for
trustworthiness, pPCA achieves the highest rating (0.8426), with the sAE also performing similarly (0.842). The rest of the techniques are also able to achieve a high score, ranging from 0.81 for kPCA to 0.839 for standard PCA. The only technique that does not perform to the same standard is LDA, as the algorithm maximizes the separability of classes in the data instead of preserving the structure of the original dataset unrelated to its classes. For
continuity, we can see that the majority of the techniques perform similarly, with scores ranging from 0.943 for the sAE to 0.958 for kPCA. However, as was the case with
trustworthiness, LDA does not perform as well (0.868), due to the map reduction process.
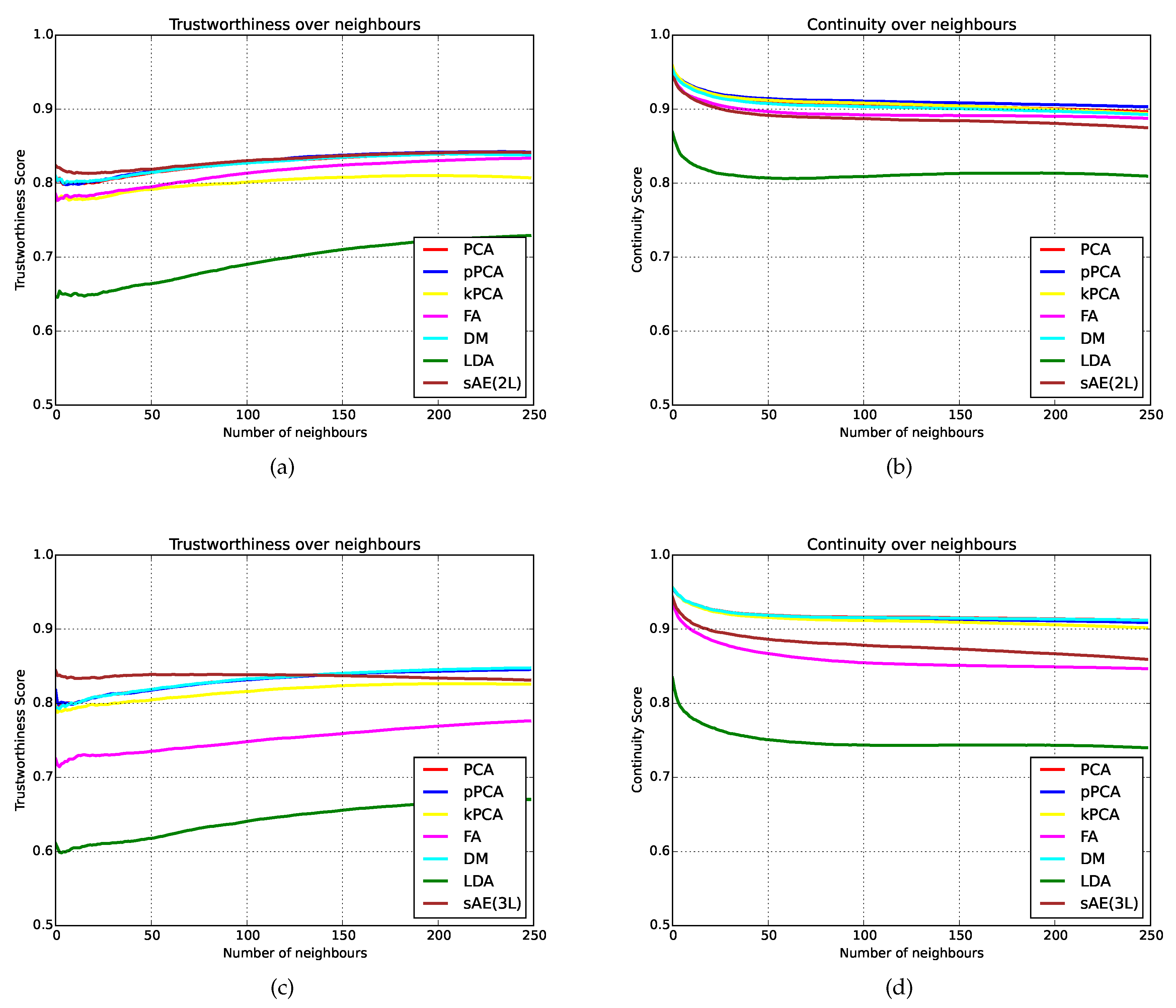
Trustworthiness and
continuity metrics were used with a varying number of neighbours, ranging from 1 to 250. Here, the sAE exhibits higher scores for a lower number of neighbours (<120), as shown in
Figure 5a—a result that suggests the system is better at retaining the local structure of the data, which is a necessary goal for a successful mapping technique. Furthermore, while the
continuity score of the autoencoder is lower than the remaining dimensionality reduction techniques (
Table 2), its error from the best performing technique in terms of
continuity (kPCA) is only 0.015, which is deemed negligible.
5.1.2. Class Preservation
The classification of 1-NN in the original dataset achieves an average of 91.21% for 100 iterations of the algorithm. None of the dimensionality reduction techniques are able to replicate this response, with pPCA achieving the highest score (87.92%), as seen in
Table 2. On the other hand, the sAE achieved an accuracy of 84.01%, the lowest among the techniques being tested, 7.2% worse than the classification accuracy of the algorithm in the high-dimensional dataset. This result reveals that sAE is not as capable as other reduction techniques in preserving the classes on the low-dimensional space; however, as sAE is able to achieve better results than the other techniques for
trustworthiness for a lower number of neighbours, and its performance in
1-NN is not drastically worse (3.91%) than the best technique in pPCA, it can be considered a minor problem.
5.1.3. Class Separation
By applying JMD (Equation
4) to the dimensionality reduction techniques, we find that kPCA outperforms the rest of the techniques used, achieving 0.607, whereas the optimised autoencoder model performs slightly less favourably with a score 0.558, as shown in
Table 3. The only technique that was excluded from this process was LDA, for two reasons: (1) it is a supervised technique that specifically maximizes the separability between the different classes in the low-dimensional space, and (2) in the context of our study, LDA has reduced the dataset to a single dimension, while all the other techniques have reduced the dimensionality to two dimensions. While class-separability is not necessarily correlated with accurate preservation of structure, high separability will allow users to effectively modulate between contrasting timbral descriptors.
5.2. Parameter Reconstruction Error
In [
26], the sAE was able to achieve the lowest reconstruction error, 0.086, while the technique that came the closest to its accuracy was kPCA with support vector regression, achieving an error of 0.09. The sAE technique still outperforms all the other combinations of techniques, as can be seen in
Table 4, achieving an overall error 0.074. It should also be noted that the sAE is able to reconstruct the most parameters of the equaliser (6) more accurately than any other combination of techniques.
5.3. Parameter Weighting
In order to evaluate the effectiveness of the signal specific weights, we measure the reconstruction accuracy of each system after the weights have been applied (see
Table 5). Overall, the systems exhibit a general improvement in the reconstruction accuracy of the gain and Q parameters. All the systems have improved accuracy measurements, with the highest performing pair being PCA with SVR, achieving an error of 0.059. Similarly, the sAE with the same architecture, with hidden layer sizes
, is able to achieve a reconstruction accuracy of 0.06—a further improvement from the 0.0748 error observed with unweighted parameters. For the weighted parameters we found that a three-layer denoising autoencoder was able to outperform our two-layer autoencoder, improving the reconstruction accuracy by 0.02.
Finally, the parameter weighting stage improves the
trustworthiness of the low-dimensional mapping when using PCA, pPCA, kPCA, DM, and sAE, whilst FA and LDA exhibited significantly lower scores, as presented in
Table 6. On the other hand, the
continuity of the systems had very little change, with pPCA, kPCA, DM, FA, and sAE showing very minor reductions, LDA showing significant reduction, and PCA showing an improvement. In this case, sAE with parameter weighting still outperforms the other techniques in terms of
trustworthiness for a lower number of neighbours, as in
Figure 5c, and the performance in terms of continuity sees the sAE performing better than FA (
Figure 5d).
5.4. User Evaluation
We evaluate the performance of the selected mode (sAE) using subjective tests in which we present the user with various samples and ask them to equalise it using the low-dimensional space (shown in
Figure 6). We then measure the class separability using the JMD metric presented in
Section 3.2. In
Table 7 we present the degree of separation between user inputs using high-dimensional and low-dimensional responses from the subjective data. From this we can deduce that the overlap between
warm and
bright descriptors has decreased, with a value of 0.8527. This is higher than the high-dimensional dataset instances (0.5581). Furthermore, we see an increase in separation between the high-dimensional classes and the opposing low-dimensional classes. For instance, the high-dimensional
warm examples and the low-dimensional
bright examples achieve a separation of 0.7719, again higher than the original separation between the high-dimensional classes. Similarly, a strong positive correlation between high-dimensional and low-dimensional equalisation is exhibited by examples in the same class, a desired effect that displays the ability of the users to choose the corresponding regions for the two descriptors.
This is reinforced by the low Euclidean distances between class centroids (shown in
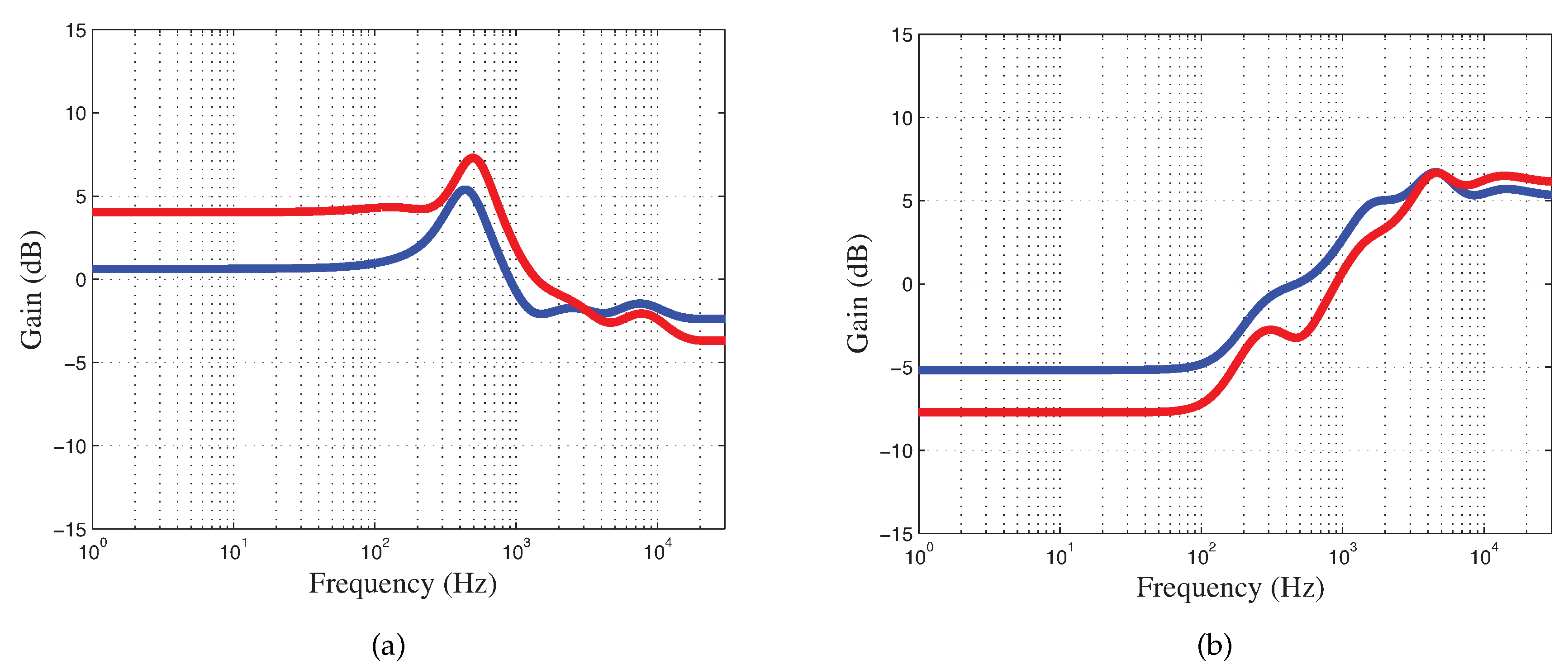
Figure 6) and strong positive coherence (spectral correlation) between the equaliser curves achieved using the 13- and 2-dimensional interfaces (shown in
Figure 7a,b). These results are provided through the Pearson correlation measures in
Table 8, revealing a positive correlation between the high-dimensional and low-dimensional datasets for the same descriptor: 0.9346 for warm and 0.9247 for bright, and a negative correlation between opposite high-dimensional and low dimensional descriptors: −0.7594 and −0.9121, respectively.
6. Discussion
For reconstruction accuracy we find that the sAE is able to outperform all pairwise combinations of dimensionality reduction and reconstruction techniques, whether the system includes parameter weighting or not (
Table 4 and
Table 5). Furthermore, the sAE is able to achieve the second highest
trustworthiness score (see
Table 2,
Figure 5a,c) in low-dimensional space, and performs to a high standard in the preservation of high-dimensional clusters (
continuity), as in
Table 2 and
Figure 5b,d. Using a sAE however, the class-separability in low-dimensional space is reduced when parameter weighting is applied. Furthermore, the system is able to reconstruct the most parameters of the equaliser accurately (six for the unweighted parameters and five for the weighted parameters), while FA with SVR is the only combination able to accurately reconstruct five parameters for the weighted reconstruction. It achieves lower results for overall reconstruction accuracy (0.065), trustworthiness (0.7761), and classification (59.52%), and marginally lower for continuity (0.9359).
Whilst the parameter reconstruction of the autoencoder is sufficiently accurate for our application, it is bound by the intrinsic dimensionality of the data, defined as the minimum number of variables required to accurately represent the variance in lower dimensional space. For the
bright/
warm parameter-space data used in this experiment, we can show that the intrinsic dimensionality requires three variables when computed using Maximum Likelihood Estimation [
47]. As our application requires a two-dimensional interface, this means the reconstruction accuracy is inherently limited.
Additionally, the user tests revealed that the two-dimensional slider using a sAE is able to accurately reconstruct the equaliser curve, retaining the characteristics associated with
warm (boost on low-mid and cut on high-end) and
bright (cut on low-end and boost on high-end), as displayed in
Figure 7a,b. Participants of the experiment also commented that the underlying two-dimensional map is easy to quickly learn and provides an intuitive tool for controlling an audio equaliser. Taking into account that the final audio effect should be incorporated alongside the equaliser, with the high-dimensional parameters also available to the users, and with indications as to where the semantic regions are placed, it can be expected that the resulting effect will feature a quick way of achieving the different descriptors (using the two-dimensional slider) and a further fine-tuning stage (via changing the high-dimensional equaliser parameters) if that is necessary.
Providing the model training is applied offline, mapping techniques such as PCA, LDA, DM, pPCA, kPCA, and FA are all capable of running in real-time given the lower degree of computational complexity, as do reconstruction methods such as the interpolation techniques (LI, NaNI, NeNI) and the sAE. Similarly, while the sAE requires iterative training, which will have variable training times based on the number of iterations, the learning rate and the number of neurons and hidden layers, it still offers a fast implementation as the user-input process is relatively lightweight.
7. Conclusions
We have presented a model for the modulation of equalisation parameters using a two-dimensional control interface. The model utilises a sAE to modify the dimensionality of the input data and a weighting process that adapts the parameters to the LTAS of the input audio signal. We train the model with semantics data in order to get the appropriate decoder weights and bias units, which can then be applied to any new input data. This data is given by a user as the position of the cursor changes in an (x,y) Cartesian space. This new information will compute high-dimensional values, which will be rescaled and unweighted, and consequently passed to the equaliser parameters. We show that the sAE model achieves better reconstruction accuracy than other regression and interpolation techniques, achieving an error as low as 0.058. Similarly, the trustworthiness and continuity of the system perform similarly to (and in some cases outperform) the rest of the dimensionality reduction techniques. Through subjective testing, we can show that the 2D equaliser provides users with an intuitive tool to recreate the high-dimensional equaliser settings extracted from the original dataset. This is demonstrated by comparing the centroids taken from the high and low-dimensional maps and by comparing the equalisation curves when applied to warm and bright samples.