Abstract
Fibre lasers are light sources that are synonymous with stability. They can give rise to highly coherent continuous-wave radiation, or a stable train of mode locked pulses with well-defined characteristics. However, they can also exhibit an exceedingly diverse range of nonlinear operational regimes spanning a multi-dimensional parameter space. The complex nature of the dynamics poses significant challenges in the theoretical and experimental studies of such systems. Here, we demonstrate how the real-time experimental methodology of spatio-temporal dynamics can be used to unambiguously identify and discern between such highly complex lasing regimes. This two-dimensional representation of laser intensity allows the identification and tracking of individual features embedded in the radiation as they make round-trip circulations inside the cavity. The salient features of this methodology are highlighted by its application to the case of Raman fibre lasers and a partially mode locked ring fibre laser operating in the normal dispersion regime.
1. Introduction
Fiber lasers are systems capable of exhibiting nonlinear dynamics over a staggering array of operational regimes spanning a multi-dimensional parameter space [1]. The complete characterization of a fibre laser over this whole space is a daunting task, especially when the regime of operation can become highly dynamic or chaotic, and the typical time scales of evolution are of the order of the laser cavity round trip time, or even less. Such dynamics can manifest themselves in the form of soliton rains [2,3] and molecules [4], soliton explosions [5,6,7], optical turbulence [8,9,10,11,12,13,14,15] and rogue waves [16,17,18,19,20,21]. An understanding of such dynamic regimes is of interest from both an academic and experimental perspective, as one would like to ensure stable operation and avoid excursions between operational regimes.
The inherent complexity of such systems do not always facilitate a direct theoretical or numerical investigation. An experimental characterization of such regimes is thus highly desirable—but herein lies the challenge. While the typical evolutionary time scales can be anywhere between a few hundred nanoseconds for metre long cavities, to microseconds for kilometre long cavities, conventionally used experimental devices like grating based optical spectrum analyzers (OSAs) or radio frequency (RF) analyzers average several times over this time scale as they have very slow acquisition rates (< Hz). Pulse characterization devices like autocorrelators or Frequency Resolved Optical Gating (FROG) [22] apparatuses operate under the apriori assumption that the laser operates in a stationary state, and thus present an averaged picture of the underlying dynamic. Single shot equivalents of the FROG devices do exist [23], but they again are limited by the data acquisition rates of the CCD sensors to kilohertz orders. The complexity is increased further, depending on the operational regime of the laser (continuous wave, quasi-continuous wave, or pulsed). Thus, recent times have seen in a growing interest in real-time measurement methodologies for the characterization of such dynamical systems [24,25,26,27]. Here, the terminology real-time is used to emphasize that the methods are capable of resolving the evolutionary behaviour of the operational regime.
In this paper, the experimental methodology of spatio-temporal dynamics is presented as a way for the unambiguous identification of lasing regimes in fibre lasers. In this method, the intensity evolution in the fibre laser is traced as it makes round trip circulations within the laser cavity. Employing state of the art, high bandwidth real-time digital storage oscilloscopes (DSOs), it is shown how long term records of one-dimensional intensity vs. time information can be used to experimentally arrive at a round-trip resolved two-dimensional intensity domain representation for laser dynamics. The strength of the technique lies in the fact that it is not limited to mode locked lasers, and can also be used for the characterization of continuous and quasi-continuous wave sources. The organization of the paper is as follows. Section 2 details the principle and experimental aspects of the spatio-temporal methodology. The methodology is then applied in the study of Raman fibre lasers (Section 3.1) and partially mode locked fibre lasers (Section 3.2), highlighting its strengths and salient features in the process.
2. Experimental Section
2.1. Principle
The availability of state of the art DSOs allow the continuous observation and record of laser intensity dynamics over time scales ranging from a few hundreds to thousands of round trips. Such long-term intensity variation records have proven to be very fruitful in the statistical studies of laser emission (see for example [13,28,29,30,31]). More importantly, the records would also reveal coherent features such as mode locked pulses, which would appear periodically at the output port of the laser after making round trip circulations inside the cavity. In this case, one can select temporal segments along the intensity dynamics centered about consecutive re-occurrences of these features, and stack them one atop another. The resulting two-dimensional representation then depicts the intensity evolution of the feature of interest as it makes successive round trips within the cavity. The temporal co-ordinate along each segment takes the notion of a temporal co-ordinate in the rest frame of the feature. Successive segments describe the evolution of the feature as it travels over a physical length along the cavity. Hence the round trip number N takes the notion of a spatial co-ordinate. Indeed, it can be rescaled into appropriate distance units (or , for a Fabry Perot configuration), where L is the physical length of the cavity. Thus, this temporally segmented and collated representation of one-dimensional intensity dynamics is called the spatio-temporal evolution of laser intensity, or simply, spatio-temporal dynamics [32,33] (also see Supplementary, [33]). In a broader context, spatio-temporal representations of intensity dynamics have been employed in describing the dynamic behaviour of semiconductor lasers [34,35] including vertical cavity surface emitting lasers [36,37], transverse pattern formation in various lasers and parametric oscillators [38,39], in the study of multimode instabilities [40,41,42], including those observed in high power fibre lasers [43,44] and in the influence of stimulated Brillouin scattering [45,46]. Spatio-temporal representations of intensity evolution have also been routinely used in the numerical modelling of various kinds of fibre-based light sources [47,48,49]. From an experimental perspective, intensity evolution has been represented in similar two dimensional forms as in the study of inter-pulse interactions in multi-soliton fibre lasers [50,51], ultraweak soliton interaction via the transverse Brillouin effect [52], and in the study of phase bits in a driven semiconductor laser [24]. Here, we extend this concept to the study of quasi-continuous wave and partially mode locked fibre lasers.
The methodology for arriving at the spatio-temporal dynamics is as follows. Say the laser radiation consists of features which move with a characteristic round trip time and survive over multiple round cavity passes (Figure 1a). These features would then appear periodically at the output of the laser at intervals of the time . Such a train of pulses can be represented mathematically as
where gives the shape of the pulse, the peak intensity, the round trip periodicity of the pulse, T is an integer indicating the round trip number, and ’⊗’ indicates a convolution operation. An estimate of the round trip time can be obtained by calculating the autocorrelation function (ACF) of :
where τ is defined as the delay coefficient, which defines the relative overlap of the function and its copy . The value of the ACF increases over an average level at the periodic intervals corresponding to the round trip time of the features, as the overlap between the functions are maximized. Particularly, the ACF would peak at a mean round trip time interval (Figure 1b). It can be shown that the ACF can be mathematically expressed as
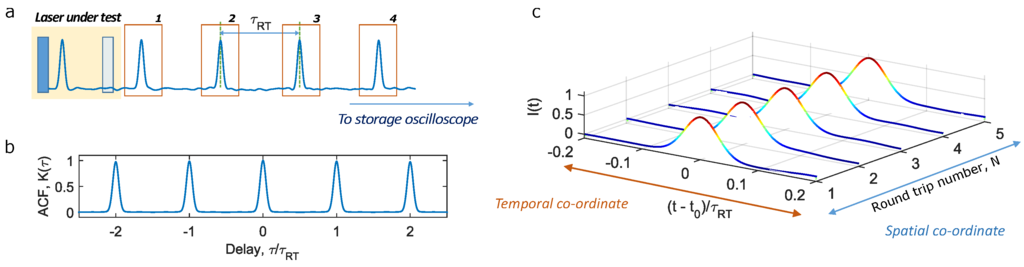
Figure 1.
Principle of spatio-temporal dynamics—(a) Intensity dynamics (simulated) depicting evolution over multiple round trips; (b) The autocorrelation of the intensity dynamics . The periodic interval between the peaks gives the round trip time ; (c) The spatio-temporal dynamics, describing evolution of the pulse features. Horizontal co-ordinate—temporal, vertical co-ordinate—spatial.
That is, the ACF periodically peaks at intervals of the round trip time , where each peak is convolved with the autocorrelation of the peak shape function . Thus, the round trip time for a coherent feature of interest can be determined by simply noting the separation between the peaks generated by it in the ACF. It is desirable to perform the autocorrelation over a large number of round trips, as this would average out any uncorrelated noise and help reveal weak periodicities.
The value of can now be used to select windows of intensity dynamics occuring at round trip intervals (Figure 1c), arriving at a two dimensional representation of intensity evolution , where T now takes the notion of an evolution co-ordinate. Figure 1c then essentially presents the intensity evolution of the pulse, as observed in its rest frame, whilst it makes round trip circulations within the cavity.
2.2. Experimental Considerations
Ideally when performing spatio-temporal measurements for fibre lasers, one would like to make real-time observations of the laser dynamics over time scales several times over the characteristic round trip time period , while simultaneously maintaining a high temporal resolution along the instantaneous temporal co-ordinate t. However, several technical aspects limit high bandwidth measurements of spatio-temporal dynamics over laboratory time scales. These can be summarized as follows.
As the output characteristics are typically measured at one point along the cavity, the temporal resolution along the evolution co-ordinate is limited to the cavity round trip time. The resolution of small scale features in the spatio-temporal dynamics depends on the combined electrical bandwidth of the photodetector-oscilloscope (PD-DSO) combination. An estimate of the requisite resolution can be obtained using the value of the transform limited pulse width corresponding to the spectral width of emission. For example, for -like pulses corresponding to a spectral emission of width , the transform limited pulse width is given via the relation
where c is the velocity of light in vacuum. Thus, the electrical bandwidth must be at least to resolve such features. The optimal temporal resolution can also be determined by performing a second harmonic generation based intensity autocorrelation measurement, which would give a statistical estimate of the scale of small features present in the radiation [53,54,55]. This bandwidth condition can be relaxed when one is more interested in the dynamics of interaction between the different components of radiation than their internal structures.
The shortest laser that can be investigated using the spatio-temporal methodology is limited by the finite time domain impulse response function of the PD-DSO combination. If the rise time of the photodetector is known, the full-width at half maximum of the impulse response can be given as
A similar expression can also be arrived at for the impulse response of the DSO, in which case the FWHM of the impulse response of the PD-DSO combination can be obtained to be
For example, if the photodetector has a cut-off frequency of 60 GHz, and the oscilloscope has a cut-off of 33 GHz, Equation (6) gives ps. For adequate resolution of the spatio-temporal features, the round trip time of the laser should be several times this width.
The longest laser that can be investigated is limited by the memory of the oscilloscope. The total number of round trips that can be observed depends on the round trip time of the cavity, the sampling resolution of the oscilloscope, and the total number of data points that can be recorded in a single sweep. These values are related via the expression
For example, the spatio-temporal evolution in a 375 km long linear cavity based laser can be investigated over round trips, using a 33 GHz oscilloscope with a memory of points and performing a time sampling ps.
3. Results
The following sections present the results of application of the spatio-temporal methodology for the case of quasi-CW Raman fibre lasers [32,56,57,58,59] (Section 3.1), and partially mode locked fibre lasers [33,54,60] (Section 3.2). It is shown how the use of the spatio-temporal methodology helps in the unambiguous identification and discernment between the staggering diversity of lasing regimes in both systems, highlighting the relevance of identification of lasing regimes on the basis of their spatio-temporal dynamics rather than one-dimensional temporal variations of intensity alone.
3.1. Spatio-Temporal Dynamics of Raman Fibre Lasers
Raman fibre lasers are wavelength versatile, high efficiency fibre lasers capable of generating watt order output powers. They find applications in the distributed amplification of optical signals for telecommunications [56,61], secure key communications [62], and even as astronomical guide stars [63]. They operate via the gain obtained via the Stimulated Raman scattering mechanism in optical fibres, doing away the need of doped fibres and simplifying device construction. However, the relatively low value of the gain in comparison to that obtained with rare earth doped gain media require the use of higher pump powers and longer lengths for achieving the lasing threshold. The length of such fibre lasers can hence be anywhere from a few hundred meters, to hundreds of kilometres [58]. The long lengths lead to extremely high mode densities, which together with the higher intracavity powers, lead to nonlinear interactions between them. These interactions can be described in the framework of weak wave turbulence [9,10], and hence Raman fibre lasers are considered to give rise to turbulent generation. The turbulent nature of interaction gives rise to a plethora of lasing regimes, which are further diversified by the available variation in dispersion, nonlinearity, and grating parameters (see for example, [64]). While such turbulent lasing regimes have been been discerned on the basis of their experimentally measured intensity probability distribution functions [15,19,31], these are ensemble-averaged representations of the underlying dynamics. The identification and classification of such lasing regimes in a Raman fibre laser is thus a challenging task, given the multi-parameter nature of the operational space.
The intensity output of Raman fibre lasers can be characterized by a mean intensity level, arising from the average contribution of all the longitudinal modes. Yet, owing to the turbulent nature of the interaction between the modes, the intensity fluctuates seemingly stochastically about this mean level. This quasi-continuous wave nature of Raman fibre lasers makes it particularly hard to discern the operational regimes from the temporal domain alone. Figure 2a shows the time domain variations in intensity from a linear cavity configuration based Raman fibre laser operating in the normal dispersion regime D = −44 ps/nm/km). The laser comprises of a 770 m long fibre span, encapsulated at both ends by highly reflecting fibre Bragg gratings (FBG), with 1 nm spectral width centred at 1550 nm. The laser is pumped with a watt-order pump source centred at 1450 nm, and lasing near 1550 nm is obtained via SRS gain. The observed time dynamics appear to be highly stochastic, characterized by a mean level over long time scales (∼μs), while exhibiting very fast fluctuations with seemingly no correlation over short time scales (∼ns), Figure 2b. An application of the spatio-temporal methodology as described in the previous section then clearly reveals the underlying turbulent dynamics, Figure 2c. The spatio-temporal dynamics are composed of intensity undulations, striated by several dark features that frequently intersect with each other. These correspond to the dips in the intensity dynamics of Figure 2a,b, and are dark solitons [32], which survive over time scales of tens of round trips. The differing inclinations of these features are indicative of the differences in their velocities. It must be mentioned that in most of the above cases, the intensity dips are just resolved by the measuring apparatus (i.e., sampled by just one data point), and it is in fact the spatio-temporal methodology that reveals the true nature of these features, which would have otherwise been misinterpreted as noise.
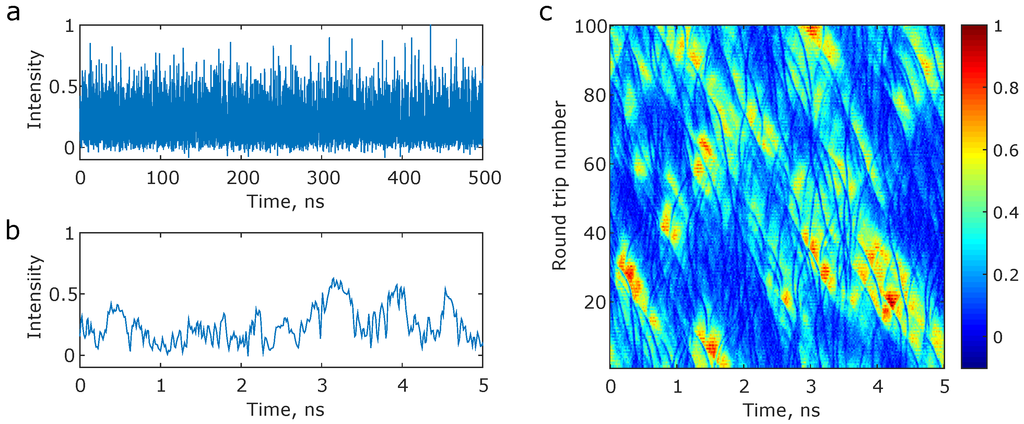
Figure 2.
Spatio-temporal dynamics of Raman fibre lasers—Typical quasi-continuous wave intensity dynamics of a Raman fibre laser over (a) long and (b) short time scales; (c) The corresponding spatio-temporal dynamics. The color scale indicates normalized intensity.
The spatio-temporal methodology offers a unique tool to identify and distinguish between the staggering diversity of operational regimes exhibited by Raman lasers [65]. For example, Figure 3 shows some of the operational regimes exhibited by a 1 km long Raman fibre laser operating in the normal dispersion in a linear cavity configuration similar as above, obtained at different pump powers. Figure 3a depicts a regime obtained for a pump power = 1.5 W. Here, the laser can be thought to be operating in a partially harmonic-mode locked regime, giving rise to a periodic train of nanosecond order pulses, with a repetition period shorter than the average round trip time. These pulses in turn are criss-crossed by dark coherent features that undergo round-trip circulations, and survive over time scales of several tens of round trips. Upon increasing the pump power to = 2.0 W, Figure 3b, the operational regime transfers to a noisy one, resulting in the generation of bright coherent features surviving over time scales of 40–50 round trips, much longer than the typical nonlinear length. Increasing the pump power to 3.0 W (Figure 3c) results in the narrowing of the above coherent features along both the temporal and spatial co-ordinates. A further increase of pump power to = 3.25 W (Figure 3d) results in a drastic transition of the operational regime to one comprising of picosecond order pulses that survive over time scales as large as 200 to 300 times the characteristic round trip time period. It is speculated that at this pump power level, the gain in the cavity becomes high enough to support the formation of parabolic pulses, and is currently being studied.
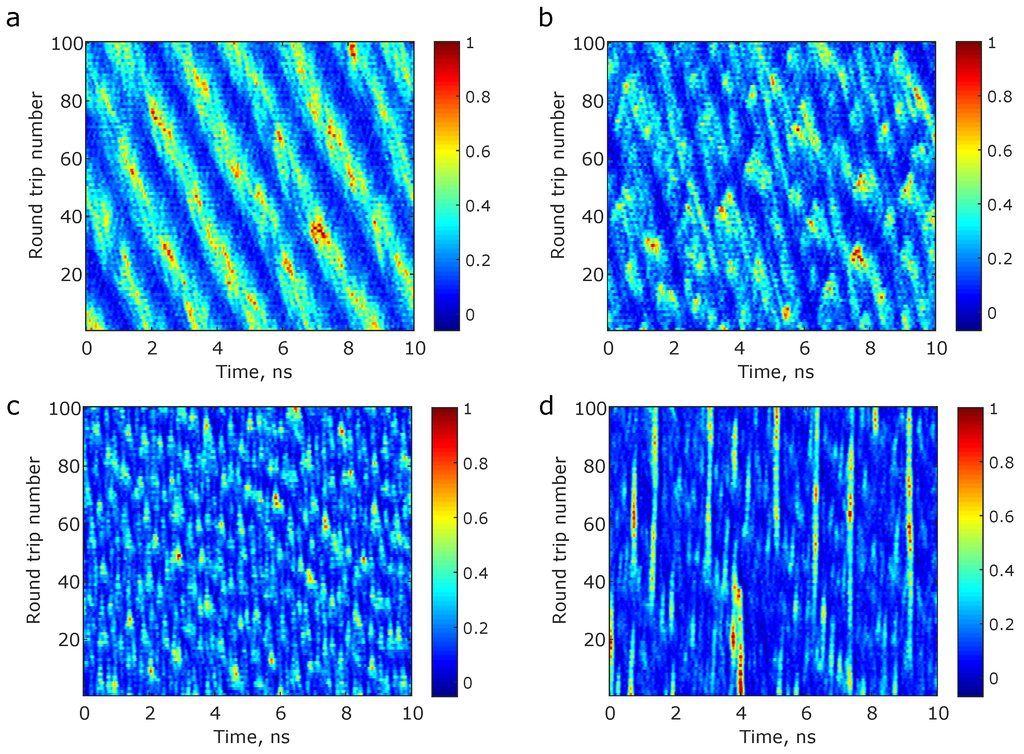
Figure 3.
Spatio-temporal regimes of the Raman fibre laser—Spatio-temporal dynamics of a Raman fibre laser operating in the normal dispersion regimes, at different pump powers ; (a) = 1.5 W; (b) = 2.0 W; (c) = 3.0 W; and (d) = 3.25 W.
As the spatio-temporal dynamics allows one to track the evolution of particular features of interest, they are particularly well suited in the study of the rogue wave formation in such system. It was shown theoretically [19,57,66] and experimentally [31] that Raman fibre lasers including random fibre lasers can exhibit such rare, short lived, high intensity events, facilitated by the underlying turbulent four wave mixing dynamics. The polarized nature of rogue events have been reported in numerical solutions of the Manakov system of Schrödinger equations [67], and in the vector Ginzburg Landau model simulations of the Raman fibre laser [68]. This aspect can be verified by obtaining polarization diverse spatio-temporal dynamics of the Raman laser. Here, the output from the Raman fibre laser is fed to a polarization beam splitter that resolves the incoming radiation along two orthogonal polarizations. The resulting outputs are then measured simultaneously using a multi-channel DSO. The differences in the lengths of the arms of the beam splitter then are compensated off-line to arrive at the time-aligned polarization spatio-temporal dynamics of the Raman fibre laser. Figure 4a shows an instance of such measurements, where the intensity has been normalized to the mean intensity level. Short lived rogue events as high as 12 times the mean level are observed. Also, these events exhibit a high degree of linear polarization, as evidenced by the extinction ratio of the signals arriving from the two arms of the beam splitter. Figure 4b and c are the corresponding polarization resolved spatio-temporal dynamics, which trace the formation and evolution of this rogue event over the time scale of tens of round trips. The striations (which are complementary in orthogonal polarizations) arise from period doubling dynamics—a phenomenon yet to be explored.
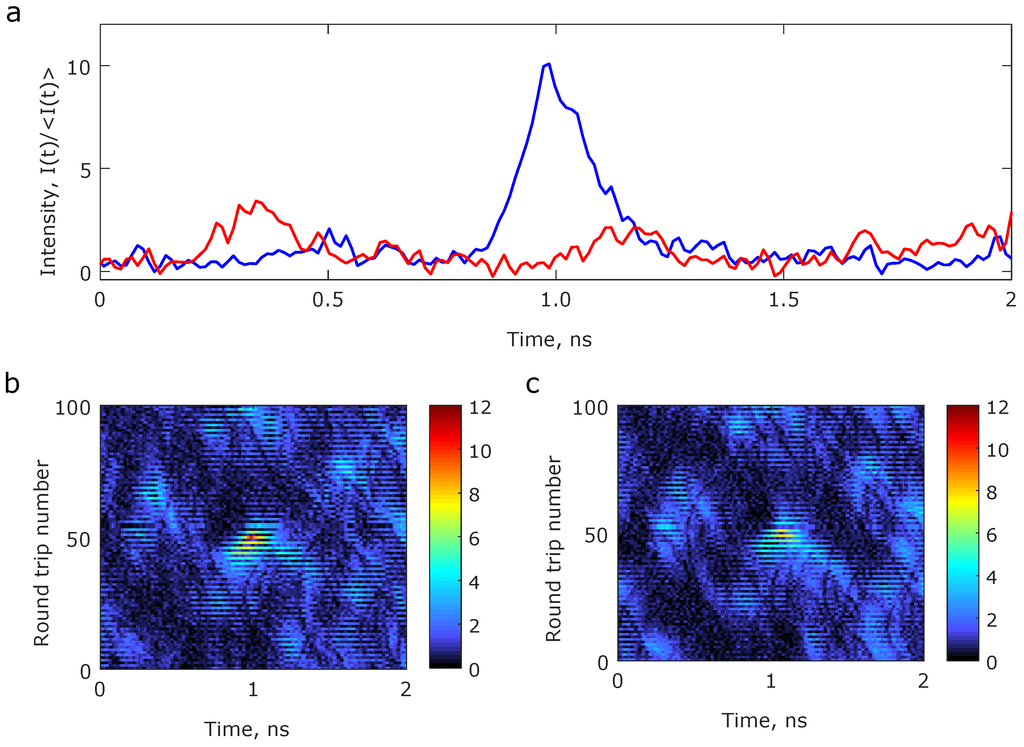
Figure 4.
Polarized rogue waves in the Raman fibre laser—(a) Experimentally measured polarization resolved intensity dynamics of the Raman fibre laser, and (b,c) corresponding polarization resolved spatio-temporal dynamics ((b)—blue curve, (c)—red curve), revealing the existence of linearly polarized rogue waves.
The spatio-temporal dynamics of Raman fibre lasers in lieu of simple one dimensional intensity variations thus reveals a lot more information about the underlying dynamics, as evidenced in the above the above experimental configuraton. The spatio-temporal dynamics clearly reveals the extent of variation exhibited by the laser, ranging from partial mode locking regimes, to purely stochastic generation of short lived features, and eventually, the probable generation of parabolic pulses. These features would have been very difficult to observe and interpret using conventional measurement methodologies, especially given the non-stationary nature of generation in all of the above cases.
3.2. Spatio-Temporal Dynamics of Partially Mode Locked Fibre Lasers
The spatio-temporal methodology is not limited to Raman fibre lasers, and can be extended to other varieties of lasers. Of particular interest is the study of long and ultralong mode locked fibre lasers. There is constant effort to construct mode locked fibre lasers that can produce shorter pulses (∼fs) at higher energies (> or more). Considerable progress has been made in this regard, particularly with the development of normal dispersion fibre lasers [69,70,71]. The stretched pulse operation, together with increased cavity length [60,72], helps in realization of pulse energies much higher than conventional soliton based mode locked lasers. However, higher pulse energies bring about additional nonlinear interactions, resulting in dispersive wave generation [73,74], pulse break up and formation of noisy pulses [75], and even generation of rogue waves [76,77,78,79]. The intrinsic variability of the mode locked regimes gives rise to further diversity of outputs [80]. Such fibre lasers, wherein mode-locked pulses co-exist with highly transient radiation components, embedded in a sea of dispersive waves are said to operate in a partially mode locked regime [33]. Here, it is shown how the spatio-temporal methodology can be applied to lasers exhibiting such complex mode locked regimes.
The laser used in the experiment is a 1 km long ring fibre laser operating in the normal dispersion regime ( ps nm km) employing Erbium gain [33]. The laser exhibits a staggering diversity of operational regimes, which can be accessed simply by adjusting the polarization controllers along its cavity. While these regimes exhibit stationary behaviour over long time scales, characterized by a well defined periodicity and without any pulse-drop outs, the pulses themselves exhibit seemingly non-stationary behaviour (Figure 5a,b), making it difficult to determine whether there is significant coherence in the pulse characteristics from shot to shot, or if the laser actually hops from one lasing regime to another. The result of the application of the spatio-temporal methodology to the time dynamics is shown in Figure 5c. Firstly, it is confirmed that the laser operates in one lasing regime, which is characterized by a well defined intensity evolution over round trips. Secondly, the spatio-temporal dynamics reveal that the noise like features observed riding the one dimensional intensity dynamics of Figure 5a,b actually correspond to bright and dark features that survive and evolve over time scales ranging from tens to several hundred round trips.
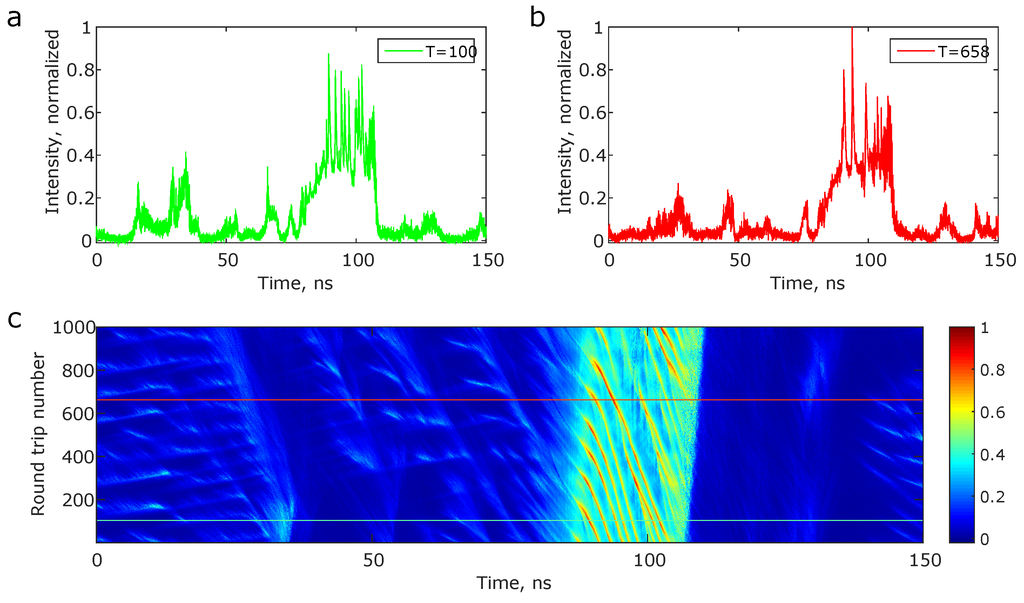
Figure 5.
Spatio-temporal dynamics of a partially mode locked fibre laser regime—(a,b) Typical intensity dynamics observed at different time instants; and (c) the spatio-temporal dynamics of the operational regime.
Figure 6 shows a small subset of the vastly diverse spatio-temporal regimes of the fibre laser. These were accessed just by controlling the polarization controllers for a fixed pump power. The regimes range from stationary ones, wherein the average pulse characteristics remain fairly constant from pulse to pulse (Figure 6a)—to those exhibiting more complex breathing dynamics, where the pulse characteristics evolve with a well defined periodicity along the evolution co-ordinate (Figure 6b). Regimes where the pulse interacts extensively with the background are also spotted (Figure 6c, and also Figure 5c). Figure 6d shows a highly chaotic spatio-temporal regime, with features much similar to puffs observed in turbulent fluid dynamics [81]. The observed diversity clearly highlights the advantage of identifying lasing regimes based on their two-dimensional spatio-temporal dynamics, rather than the simple one-dimensional intensity dynamics.
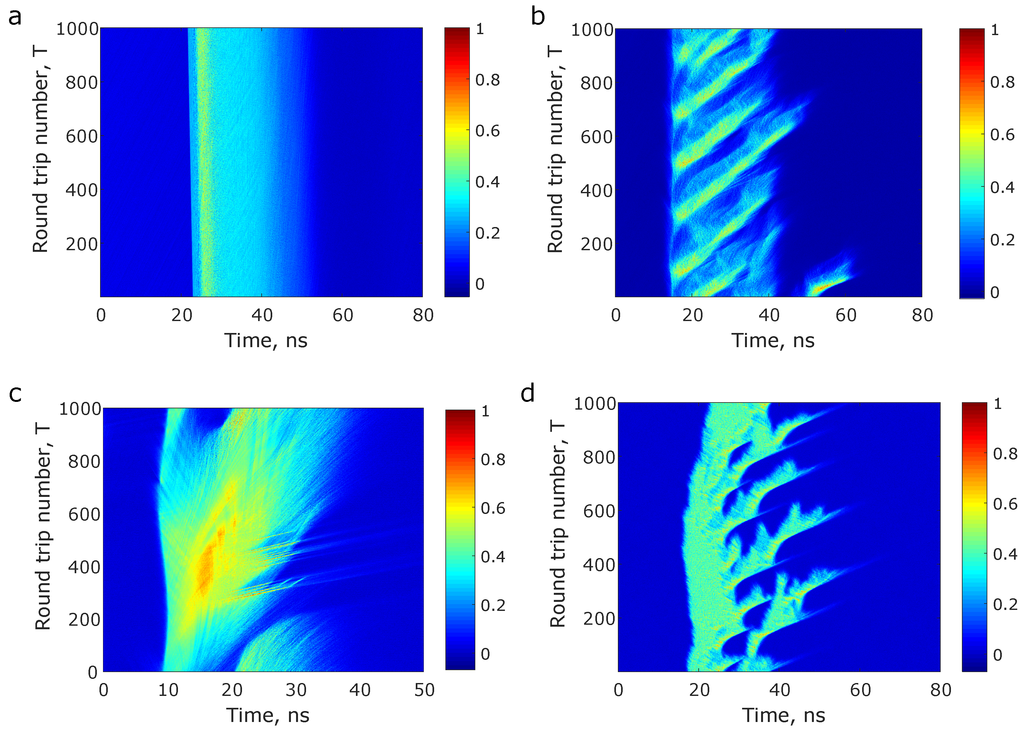
Figure 6.
Spatio-temporal diversity of the partially mode locked regimes—Different spatio-temporal regimes with varying characteristics accessed via tuning of the polarization controllers. The panels give examples of regimes exhibiting (a) stationary characteristics over evolution co-ordinate T; (b) periodicity over evolution co-ordinate T; (c) interactions between the pulse and the background; and (d) highly chaotic, turbulent generation.
As observed in Figure 5, the spatio-temporal regimes are composed of an exceeding diversity of features moving with different velocities. By choosing the right value of the round trip time , one can then arrive at the rest frame of the particular feature of interest. A background-subtracted autocorrelation based analysis was proposed in [33] for the identification of the constituents of radiation and their respective rest frames. However, the exact temporal location of the underlying features along the recorded intensity dynamics remains inaccessible in such an approach. Alternatively, one can locate a region of interest in the spatio-temporal dynamics and analyze its content. For example, Figure 7 shows the application of a cross correlation methodology to arrive at a characteristic round trip time for the background features of Figure 5c. In this approach, an arbitrary time slice centred around a feature of interest is cross correlated with another time slice . The existence of a positive correlation for then indicates the possible existence of coherent features, and the shift of the peak away from the zero-lag position, , indicates a difference in its group velocity from that used to obtain the spatio-temporal dynamics I(t,T) itself. One such instance is shown in Figure 7b, where . The difference in the round trip time can then be simply calculated as
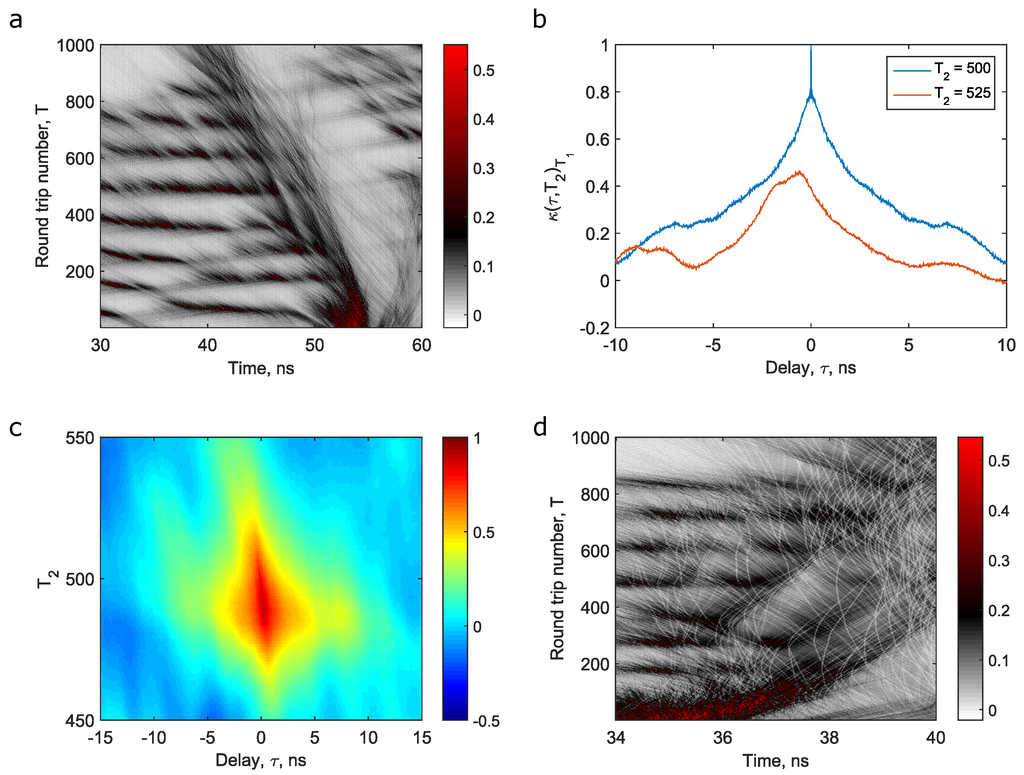
Figure 7.
Cross-correlation based analysis for revealing the constituents of radiation—(a) Spatio-temporal dynamics of the background region between the pulses for the regime of Figure 5c; (b) Cross correlation of intensity dynamics, . Here is chosen to be the 500th round trip of Figure 7(a); (c) Close up of cross correlation matrix . The peak progressively shifting with indicates the possible existence of coherent features moving with a distinct velocity; and (d) the spatio-temporal dynamics of the background corresponding to its rest frame, revealing the existence of dark solitons.
Figure 7c shows the cross correlation function carried out for a range of values of . The shift of the peak of the cross correlation function away from indicates the existence of features which have a velocity different from that of the rest frame of Figure 7a. The spatio-temporal dynamics corresponding to the rest frame of these features is shown in Figure 7d. This reveals the existence of dark features in the background, which move with their own characteristic velocity. Note that the existence of such dark coherent features have been earlier reported in numerical simulations of similar ultralong mode locked fibre lasers, and have been confirmed to be dark solitons [82]. Note that the difference in velocity between the pulse and these background dark solitons are of the order of . While the existence of with features differing in periodicity by this order of magnitude would be barely revealed by conventional RF analyzers, the spatio-temporal dynamics can confirm their existence, even if they are exceedingly intermittent, and even if they last over time scales of only a few round trips.
Figure 8 shows how the dark solitons interact with the pulse. The dark solitons move faster than the pulse, as evidenced by their relative inclinations in Figure 8a. Upon meeting up with the pulse, a signficant number of dark solitons decelerate and get trapped at the edge of the pulse for a significant duration, propagating with the same speed as that of the pulse edge, after which they seemingly accelerate away from the pulse, as seen in Figure 8b. Many dark solitons are also seen to cross over the pulse envelop and move away from the pulse. Such complex interactions between the pulse and background are impossible to infer from conventional one-dimensional intensity domain dynamics, and indeed, to the best of the knowledge of the authors, such interactions were observed directly in experiment for the first time using the spatio-temporal methodology [33].
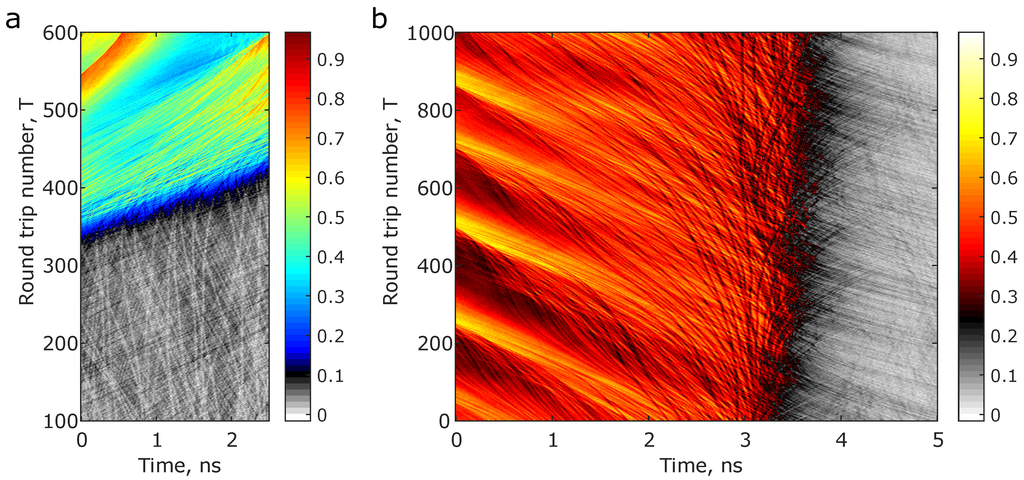
Figure 8.
Pulse-background interactions—Spatio-temporal dynamics showing the interaction of the background dark solitons and the pulse. (a) Faster moving dark solitons meet the slow moving pulse; (b) Trapped dark solitons at the pulse-background interface.
4. Discussion
In this paper, the methodology of spatio-temporal dynamics has been proposed as a way for the unambiguous identification of lasing regimes in fibre lasers. The strength of the technique lies in the fact that it is not limited to fibre lasers, and it can be used for the characterization of a wide variety of continuous and quasi-continuous wave lasers, or even passive or driven cavity systems, as has been recently demonstrated in the bunching of cavity solitons via forward Brillouin Scattering [83]. The availability of an evolution co-ordinate facilitates higher order analysis, for example in the calculation of two-dimensional autocorrelation functions for estimating the life-time of coherent features [65]. The real-time approach of acquiring very long traces allows the observation of highly transient events like rogue waves and their evolution with round-trip time accuracy, which would otherwise be missed by conventional measurement methodologies. Indeed, when used in conjunction with real-time spectral measurements like the Dispersive Fourier Transform [79,84,85], it can provide a time-aligned spatio- and spectro-temporal characterization of such transient regimes—a feat which has remained possible only in numerical simulations [20,47,86]. While technical factors currently limit temporal resolution, laser dimensions, etc., these are more a limitation of the state of the art of the back-end devices used. A diverse variety of fibre lasers have been experimentally demonstrated thus far in the literature, but most of the reported research focuses on their stable regimes. The spatio-temporal methodology proposed above would allow a deeper understanding of such highly nonlinear lasing regimes, the transition dynamics between them, and more importantly, their formation process in itself.
Acknowledgments
Authors acknowledge the support of the ERC project ULTRALASER, H2020 project CARDIALLY, Russian Ministry of Science and Education (agreement 14.584.21.0014), Russian Foundation for Basic Research (projects 16-32-60153, 15-02-07925).
Author Contributions
D.V.C. conceived the idea. N.T. performed the experimental characterization of the spatio-temporal diversity of Raman fibre lasers and analyzed its data. S.S. performed the polarization resolved measurements of the Raman fibre laser and partially mode locked fibre laser and analyzed the data. S.S. developed the cross-correlation analysis for identification of coherent features. S.S. prepared the figures. S.S. and D.V.C. wrote the manuscript. D.V.C. supervised the project.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Grelu, P.; Akhmediev, N. Dissipative solitons for mode-locked lasers. Nat. Photonics 2012, 6, 84–92. [Google Scholar] [CrossRef]
- Chouli, S.; Grelu, P. Rains of solitons in a fiber laser. Opt. Express 2009, 17, 11776–11781. [Google Scholar] [CrossRef] [PubMed]
- Chouli, S.; Grelu, P. Soliton rains in a fiber laser: An experimental study. Phys. Rev. A 2010, 81, 063829. [Google Scholar] [CrossRef]
- Stratmann, M.; Pagel, T.; Mitschke, F. Experimental observation of temporal soliton molecules. Phys. Rev. Lett. 2005, 95, 143902. [Google Scholar] [CrossRef] [PubMed]
- Cundiff, S.T.; Soto-Crespo, J.M.; Akhmediev, N. Experimental evidence for soliton explosions. Phys. Rev. Lett. 2002, 88, 073903. [Google Scholar] [CrossRef] [PubMed]
- Runge, A.F.J.; Broderick, N.G.R.; Erkintalo, M. Observation of soliton explosions in a passively mode-locked fiber laser. Optica 2015, 2, 36–39. [Google Scholar] [CrossRef]
- Runge, A.F.J.; Broderick, N.G.R.; Erkintalo, M. Dynamics of soliton explosions in passively mode-locked fiber lasers. J. Opt. Soc. Am. B 2016, 33, 46–53. [Google Scholar] [CrossRef]
- Kärtner, F.X.; Zumbühl, D.M.; Matuschek, N. Turbulence in mode-locked lasers. Phys. Rev. Lett. 1999, 82, 4428–4431. [Google Scholar] [CrossRef]
- Babin, S.A.; Churkin, D.V.; Ismagulov, A.E.; Kablukov, S.I.; Podivilov, E.V. Four-wave-mixing-induced turbulent spectral broadening in a long Raman fiber laser. J. Opt. Soc. Am. B 2007, 24, 1729–1738. [Google Scholar] [CrossRef]
- Babin, S.A.; Churkin, D.V.; Ismagulov, A.E.; Kablukov, S.I.; Podivilov, E.V. Turbulence-induced square-root broadening of the Raman fiber laser output spectrum. Opt. Lett. 2008, 33, 633–635. [Google Scholar] [CrossRef] [PubMed]
- Wabnitz, S. Optical turbulence in fiber lasers. Opt. Lett. 2014, 39, 1362–1365. [Google Scholar] [CrossRef] [PubMed]
- Picozzi, A.; Garnier, J.; Hansson, T.; Suret, P.; Randoux, S.; Millot, G.; Christodoulides, D. Optical wave turbulence: Towards a unified nonequilibrium thermodynamic formulation of statistical nonlinear optics. Phys. Rep. 2014, 542, 1–132. [Google Scholar] [CrossRef]
- Randoux, S.; Walczak, P.; Onorato, M.; Suret, P. Intermittency in integrable turbulence. Phys. Rev. Lett. 2014, 113, 113902. [Google Scholar] [CrossRef] [PubMed]
- Walczak, P.; Randoux, S.; Suret, P. Optical Rogue Waves in integrable turbulence. Phys. Rev. Lett. 2015, 114, 143903. [Google Scholar] [CrossRef] [PubMed]
- Walczak, P.; Randoux, S.; Suret, P. Statistics of a turbulent Raman fiber laser. Opt. Lett. 2015, 40, 3101–3104. [Google Scholar] [CrossRef] [PubMed]
- Lecaplain, C.; Grelu, P.; Soto-Crespo, J.M.; Akhmediev, N. Dissipative Rogue Waves generated by chaotic pulse bunching in a mode-locked laser. Phys. Rev. Lett. 2012, 108, 233901. [Google Scholar] [CrossRef] [PubMed]
- Runge, A.F.J.; Aguergaray, C.; Broderick, N.G.R.; Erkintalo, M. Raman rogue waves in a partially mode-locked fiber laser. Opt. Lett. 2014, 39, 319–322. [Google Scholar] [CrossRef] [PubMed]
- Lecaplain, C.; Grelu, P. Rogue waves among noiselike-pulse laser emission: An experimental investigation. Phys. Rev. A 2014, 90, 013805. [Google Scholar] [CrossRef]
- Churkin, D.V.; Gorbunov, O.A.; Smirnov, S.V. Extreme value statistics in Raman fiber lasers. Opt. Lett. 2011, 36, 3617–3619. [Google Scholar] [CrossRef] [PubMed]
- Dudley, J.M.; Dias, F.; Erkintalo, M.; Genty, G. Instabilities, breathers and rogue waves in optics. Nat. Photonics 2014, 8, 755–764. [Google Scholar] [CrossRef]
- Chen, S.; Baronio, F.; Soto-Crespo, J.; Grelu, P.; Conforti, M.; Wabnitz, S. Optical rogue waves in parametric three-wave mixing and coherent stimulated scattering. Phys. Rev. A 2015, 92, 033847. [Google Scholar] [CrossRef]
- Kane, D.; Trebino, R. Characterization of arbitrary femtosecond pulses using frequency-resolved optical gating. IEEE J. Quantum Electron. 1993, 29, 571–579. [Google Scholar] [CrossRef]
- Kane, D.J.; Trebino, R. Single-shot measurement of the intensity and phase of an arbitrary ultrashort pulse by using frequency-resolved optical gating. Opt. Lett. 1993, 18, 823–825. [Google Scholar] [CrossRef] [PubMed]
- Garbin, B.; Javaloyes, J.; Tissoni, G.; Barland, S. Topological solitons as addressable phase bits in a driven laser. Nat. Commun. 2015, 6, 5915. [Google Scholar] [CrossRef] [PubMed]
- Goda, K.; Jalali, B. Dispersive Fourier transformation for fast continuous single-shot measurements. Nat. Photonics 2013, 7, 102–112. [Google Scholar] [CrossRef]
- Butler, T.; Slepneva, S.; O’Shaughnessy, B.; Kelleher, B.; Goulding, D.; Hegarty, S.P.; Lyu, H.C.; Karnowski, K.; Wojtkowski, M.; Huyet, G. Single shot, time-resolved measurement of the coherence properties of OCT swept source lasers. Opt. Lett. 2015, 40, 2277–2280. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Pang, M.; Russell, P.S. Wideband-tunable soliton fiber laser mode-locked at 1.88 GHz by optoacoustic interactions in solid-core PCF. Opt. Express 2015, 23, 24945–24954. [Google Scholar] [CrossRef] [PubMed]
- Gorbunov, O.A.; Sugavanam, S.; Churkin, D. Revealing statistical properties of quasi-CW fibre lasers in bandwidth-limited measurements. Opt. Express 2014, 22, 28071–28076. [Google Scholar] [CrossRef] [PubMed]
- Gorbunov, O.A.; Sugavanam, S.; Churkin, D.V. Intensity dynamics and statistical properties of random distributed feedback fiber laser. Opt. Lett. 2015, 40, 1783–1786. [Google Scholar] [CrossRef] [PubMed]
- Solli, D.R.; Ropers, C.; Koonath, P.; Jalali, B. Optical rogue waves. Nature 2007, 450, 1054–1057. [Google Scholar] [CrossRef] [PubMed]
- Randoux, S.; Suret, P. Experimental evidence of extreme value statistics in Raman fiber lasers. Opt. Lett. 2012, 37, 500–502. [Google Scholar] [CrossRef] [PubMed]
- Turitsyna, E.G.; Smirnov, S.V.; Sugavanam, S.; Tarasov, N.; Shu, X.; Babin, S.A.; Podivilov, E.V.; Churkin, D.V.; Falkovich, G.; Turitsyn, S.K. The laminar-turbulent transition in a fibre laser. Nat. Photonics 2013, 7, 783–786. [Google Scholar] [CrossRef]
- Churkin, D.V.; Sugavanam, S.; Tarasov, N.; Khorev, S.; Smirnov, S.V.; Kobtsev, S.M.; Turitsyn, S.K. Stochasticity, periodicity and localized light structures in partially mode-locked fibre lasers. Nat. Commun. 2015, 6, 7004. [Google Scholar] [CrossRef] [PubMed]
- Hess, O.; Kuhn, T. Maxwell-Bloch equations for spatially inhomogeneous semiconductor lasers. II. Spatiotemporal dynamics. Phys. Rev. A 1996, 54, 3360–3368. [Google Scholar] [CrossRef] [PubMed]
- Fischer, I.; Hess, O.; Elsäßer, W.; Göbel, E. Complex spatio-temporal dynamics in the near-field of a broad-area semiconductor laser. Europhys. Lett. 1996, 35, 579. [Google Scholar] [CrossRef]
- Mulet, J.; Balle, S. Transverse mode dynamics in vertical-cavity surface-emitting lasers: Spatiotemporal versus modal expansion descriptions. Phys. Rev. A 2002, 66, 053802. [Google Scholar] [CrossRef]
- Paulau, P.V.; Gomila, D.; Ackemann, T.; Loiko, N.A.; Firth, W.J. Self-localized structures in vertical-cavity surface-emitting lasers with external feedback. Phys. Rev. E 2008, 78, 016212. [Google Scholar] [CrossRef] [PubMed]
- Oppo, G.L.; Brambilla, M.; Lugiato, L.A. Formation and evolution of roll patterns in optical parametric oscillators. Phys. Rev. A 1994, 49, 2028–2032. [Google Scholar] [CrossRef] [PubMed]
- Anstett, G.; Nittmann, M.; Wallenstein, R. Experimental investigation and numerical simulation of the spatio-temporal dynamics of the light-pulses in nanosecond optical parametric oscillators. Appl. Phys. B 2004, 79, 305–313. [Google Scholar] [CrossRef]
- Tredicce, J.R.; Quel, E.J.; Ghazzawi, A.M.; Green, C.; Pernigo, M.A.; Narducci, L.M.; Lugiato, L.A. Spatial and temporal instabilities in a CO2 laser. Phys. Rev. Lett. 1989, 62, 1274–1277. [Google Scholar] [CrossRef] [PubMed]
- Huyet, G.; Rica, S. Spatio-temporal instabilities in the transverse patterns of lasers. Physica D 1996, 96, 215–229. [Google Scholar] [CrossRef]
- Huyet, G.; Martinoni, M.C.; Tredicce, J.R.; Rica, S. Spatiotemporal dynamics of lasers with a large fresnel number. Phys. Rev. Lett. 1995, 75, 4027–4030. [Google Scholar] [CrossRef] [PubMed]
- Stutzki, F.; Otto, H.J.; Jansen, F.; Gaida, C.; Jauregui, C.; Limpert, J.; Tünnermann, A. High-speed modal decomposition of mode instabilities in high-power fiber lasers. Opt. Lett. 2011, 36, 4572–4574. [Google Scholar] [CrossRef] [PubMed]
- Otto, H.J.; Stutzki, F.; Jansen, F.; Eidam, T.; Jauregui, C.; Limpert, J.; Tünnermann, A. Temporal dynamics of mode instabilities in high-power fiber lasers and amplifiers. Opt. Express 2012, 20, 15710–15722. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.C.; Potter, W.N.; Thompson, J.R. Stochastic, spatiotemporal intensity dynamics of stimulated Brillouin scattering in a two-mode optical fiber. J. Opt. Soc. Am. B 2013, 30, 2676–2683. [Google Scholar] [CrossRef]
- Armstrong, C.R.; David, J.A.; Thompson, J.R. Phenomenological model of stochastic, spatiotemporal, intensity dynamics of stimulated Brillouin scattering in a two-mode optical fiber. Opt. Express 2015, 23, 17866–17882. [Google Scholar] [CrossRef] [PubMed]
- Dudley, J.M.; Genty, G.; Coen, S. Supercontinuum generation in photonic crystal fiber. Rev. Mod. Phys. 2006, 78, 1135–1184. [Google Scholar] [CrossRef]
- Zaviyalov, A.; Iliew, R.; Egorov, O.; Lederer, F. Multi-soliton complexes in mode-locked fiber lasers. Appl. Phys. B 2011, 104, 513–521. [Google Scholar] [CrossRef]
- Kibler, B.; Fatome, J.; Finot, C.; Millot, G.; Dias, F.; Genty, G.; Akhmediev, N.; Dudley, J.M. The Peregrine soliton in nonlinear fibre optics. Nat. Phys. 2010, 6, 790–795. [Google Scholar] [CrossRef]
- Olivier, M.; Roy, V.; Piché, M.; Babin, F. Pulse collisions in the stretched-pulse fiber laser. Opt. Lett. 2004, 29, 1461–1463. [Google Scholar] [CrossRef] [PubMed]
- Roy, V.; Olivier, M.; Piché, M. Pulse interactions in the stretched-pulse fiber laser. Opt. Express 2005, 13, 9217–9223. [Google Scholar] [CrossRef] [PubMed]
- Jang, J.K.; Erkintalo, M.; Murdoch, S.G.; Coen, S. Ultraweak long-range interactions of solitons observed over astronomical distances. Nat. Photonics 2013, 7, 657–663. [Google Scholar] [CrossRef]
- Kobtsev, S.; Kukarin, S.; Smirnov, S.; Turitsyn, S.; Latkin, A. Generation of double-scale femto/pico-second optical lumps in mode-locked fiber lasers. Opt. Express 2009, 17, 20707–20713. [Google Scholar] [CrossRef] [PubMed]
- Smirnov, S.; Kobtsev, S.; Kukarin, S.; Ivanenko, A. Three key regimes of single pulse generation per round trip of all-normal-dispersion fiber lasers mode-locked with nonlinear polarization rotation. Opt. Express 2012, 20, 27447–27453. [Google Scholar] [CrossRef] [PubMed]
- Rulliere, C. Femtosecond Laser Pulses; Springer: Berlin, Germany, 2005. [Google Scholar]
- Ania-Castañón, J.D. Quasi-lossless transmission using second-order Raman amplification and fibre Bragg gratings. Opt. Express 2004, 12, 4372–4377. [Google Scholar] [CrossRef] [PubMed]
- Churkin, D.; Smirnov, S. Numerical modelling of spectral, temporal and statistical properties of Raman fiber lasers. Opt. Commun. 2012, 285, 2154–2160. [Google Scholar] [CrossRef]
- Turitsyn, S.K.; Ania-Castañón, J.D.; Babin, S.A.; Karalekas, V.; Harper, P.; Churkin, D.; Kablukov, S.I.; El-Taher, A.E.; Podivilov, E.V.; Mezentsev, V.K. 270-km ultralong Raman fiber laser. Phys. Rev. Lett. 2009, 103, 133901. [Google Scholar] [CrossRef] [PubMed]
- Smirnov, S.V.; Tarasov, N.; Churkin, D.V. Radiation build-up in laminar and turbulent regimes in quasi-CW Raman fiber laser. Opt. Express 2015, 23, 27606–27611. [Google Scholar] [CrossRef] [PubMed]
- Kobtsev, S.; Kukarin, S.; Fedotov, Y. Ultra-low repetition rate mode-locked fiber laser with high-energy pulses. Opt. Express 2008, 16, 21936–21941. [Google Scholar] [CrossRef] [PubMed]
- Ania-Castañón, J.D.; Karalekas, V.; Harper, P.; Turitsyn, S.K. Simultaneous spatial and spectral transparency in ultralong fiber lasers. Phys. Rev. Lett. 2008, 101, 123903. [Google Scholar] [CrossRef] [PubMed]
- El-Taher, A.; Kotlicki, O.; Harper, P.; Turitsyn, S.; Scheuer, J. Secure key distribution over a 500 km long link using a Raman ultra-long fiber laser. Laser Photonics Rev. 2014, 8, 436–442. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, H.; Cui, S.; Hu, J.; Feng, Y. Versatile Raman fiber laser for sodium laser guide star. Laser Photonics Rev. 2014, 8, 889–895. [Google Scholar] [CrossRef]
- Turitsyna, E.G.; Turitsyn, S.K.; Mezentsev, V.K. Numerical investigation of the impact of reflectors on spectral performance of Raman fibre laser. Opt. Express 2010, 18, 4469–4477. [Google Scholar] [CrossRef] [PubMed]
- Tarasov, N.; Sugavanam, S.; Churkin, D. Spatio-temporal generation regimes in quasi-CW Raman fiber lasers. Opt. Express 2015, 23, 24189–24194. [Google Scholar] [CrossRef] [PubMed]
- Smirnov, S.V.; Churkin, D.V. Modeling of spectral and statistical properties of a random distributed feedback fiber laser. Opt. Express 2013, 21, 21236–21241. [Google Scholar] [CrossRef] [PubMed]
- Baronio, F.; Degasperis, A.; Conforti, M.; Wabnitz, S. Solutions of the vector nonlinear schrödinger equations: Evidence for deterministic rogue waves. Phys. Rev. Lett. 2012, 109, 044102. [Google Scholar] [CrossRef] [PubMed]
- Sugavanam, S.; Tarasov, N.; Wabnitz, S.; Churkin, D.V. Ginzburg-Landau turbulence in quasi-CW Raman fiber lasers. Laser Photonics Rev. 2015, 9, L35–L39. [Google Scholar] [CrossRef]
- Chong, A.; Renninger, W.H.; Wise, F.W. All-normal-dispersion femtosecond fiber laser with pulse energy above 20nJ. Opt. Lett. 2007, 32, 2408–2410. [Google Scholar] [CrossRef] [PubMed]
- Renninger, W.H.; Chong, A.; Wise, F.W. Dissipative solitons in normal-dispersion fiber lasers. Phys. Rev. A 2008, 77, 023814. [Google Scholar] [CrossRef]
- Renninger, W.H.; Chong, A.; Wise, F.W. Self-similar pulse evolution in an all-normal-dispersion laser. Phys. Rev. A 2010, 82, 021805. [Google Scholar] [CrossRef] [PubMed]
- Nyushkov, B.N.; Ivanenko, A.V.; Kobtsev, S.M.; Turitsyn, S.K.; Mou, C.; Zhang, L.; Denisov, V.I.; Pivtsov, V.S. Gamma-shaped long-cavity normal-dispersion mode-locked Er-fiber laser for sub-nanosecond high-energy pulsed generation. Laser Phys. Lett. 2012, 9, 59–67. [Google Scholar] [CrossRef]
- Erkintalo, M.; Xu, Y.Q.; Murdoch, S.G.; Dudley, J.M.; Genty, G. Cascaded phase matching and nonlinear symmetry breaking in fiber frequency combs. Phys. Rev. Lett. 2012, 109, 223904. [Google Scholar] [CrossRef] [PubMed]
- Yulin, A.V.; Driben, R.; Malomed, B.A.; Skryabin, D.V. Soliton interaction mediated by cascaded four wave mixing with dispersive waves. Opt. Express 2013, 21, 14481–14486. [Google Scholar] [CrossRef] [PubMed]
- Tang, D.; Zhao, L.; Zhao, B. Soliton collapse and bunched noise-like pulse generation in a passively mode-locked fiber ring laser. Opt. Express 2005, 13, 2289–2294. [Google Scholar] [CrossRef] [PubMed]
- Lecaplain, C.; Grelu, P.; Soto-Crespo, J.M.; Akhmediev, N. Dissipative rogue waves: Extreme pulses generated by passively mode-locked lasers. Phys. Rev. E 2011, 84, 016604. [Google Scholar]
- Zaviyalov, A.; Egorov, O.; Iliew, R.; Lederer, F. Rogue waves in mode-locked fiber lasers. Phys. Rev. A 2012, 85, 013828. [Google Scholar] [CrossRef]
- Liu, M.; Cai, Z.R.; Hu, S.; Luo, A.P.; Zhao, C.J.; Zhang, H.; Xu, W.C.; Luo, Z.C. Dissipative rogue waves induced by long-range chaotic multi-pulse interactions in a fiber laser with a topological insulator-deposited microfiber photonic device. Opt. Lett. 2015, 40, 4467–4770. [Google Scholar]
- Liu, Z.; Zhang, S.; Wise, F.W. Rogue waves in a normal-dispersion fiber laser. Opt. Lett. 2015, 40, 1366–1369. [Google Scholar] [CrossRef] [PubMed]
- Kobtsev, S.; Smirnov, S.; Kukarin, S.; Turitsyn, S. Mode-locked fiber lasers with significant variability of generation regimes. Opt. Fiber Technol. 2014, 20, 615–620. [Google Scholar] [CrossRef]
- Avila, K.; Moxey, D.; de Lozar, A.; Avila, M.; Barkley, D.; Hof, B. The Onset of turbulence in pipe flow. Science 2011, 333, 192–196. [Google Scholar] [CrossRef] [PubMed]
- Kelleher, E.J.R.; Travers, J.C. Chirped pulse formation dynamics in ultra-long mode-locked fiber lasers. Opt. Lett. 2014, 39, 1398–1401. [Google Scholar] [CrossRef] [PubMed]
- Erkintalo, M.; Luo, K.; Jang, J.K.; Coen, S.; Murdoch, S.G. Bunching of temporal cavity solitons via forward Brillouin scattering. New J. Phys. 2015, 17, 115009. [Google Scholar] [CrossRef]
- Runge, A.F.J.; Aguergaray, C.; Broderick, N.G.R.; Erkintalo, M. Coherence and shot-to-shot spectral fluctuations in noise-like ultrafast fiber lasers. Opt. Lett. 2013, 38, 4327–4330. [Google Scholar] [CrossRef] [PubMed]
- Descloux, D.; Laporte, C.; Dherbecourt, J.B.; Melkonian, J.M.; Raybaut, M.; Drag, C.; Godard, A. Spectrotemporal dynamics of a picosecond OPO based on chirped quasi-phase-matching. Opt. Lett. 2015, 40, 280–283. [Google Scholar] [CrossRef] [PubMed]
- Toenger, S.; Godin, T.; Billet, C.; Dias, F.; Erkintalo, M.; Genty, G.; Dudley, J.M. Emergent rogue wave structures and statistics in spontaneous modulation instability. Sci. Rep. 2015, 5, 10380. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).