Adaptive Control of Active Magnetic Bearing against Milling Dynamics
Abstract
:1. Introduction
1.1. Active Magnetic Bearing (AMB)
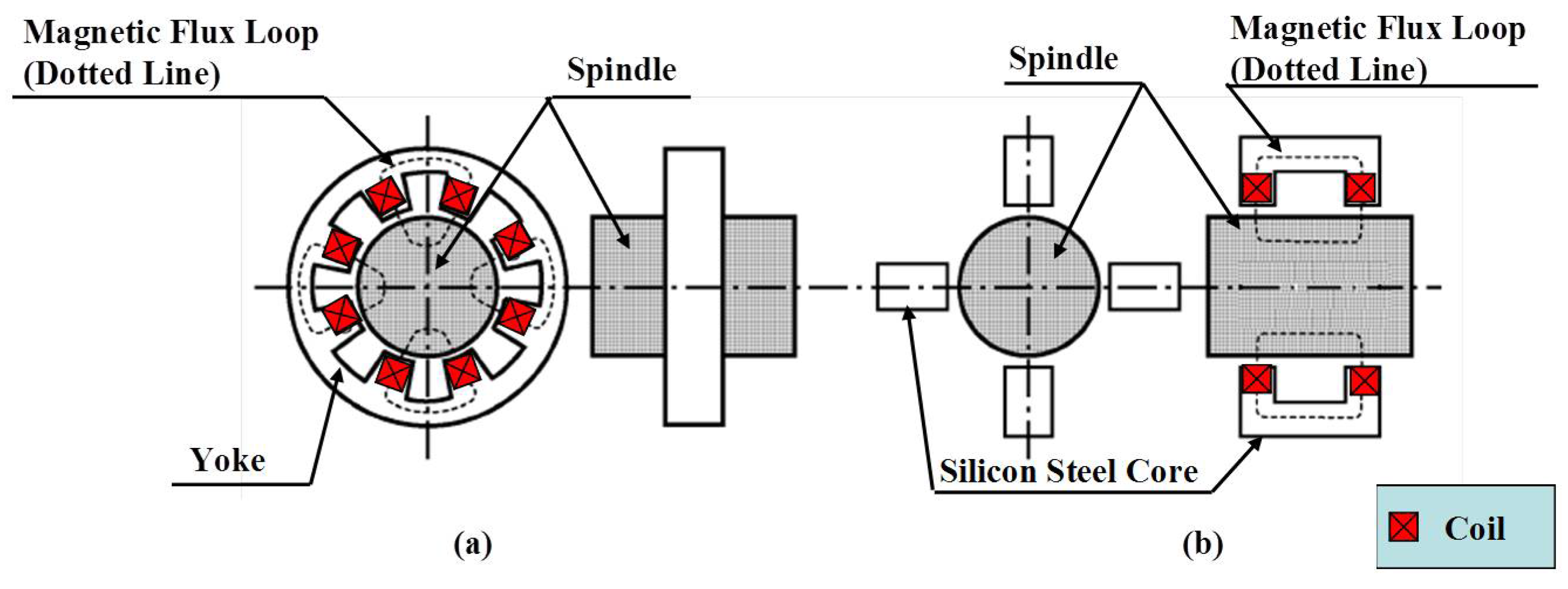
1.2. Milling Dynamics
1.3. Embedded Cylindrical-Array Magnetic Actuator (ECAMA)
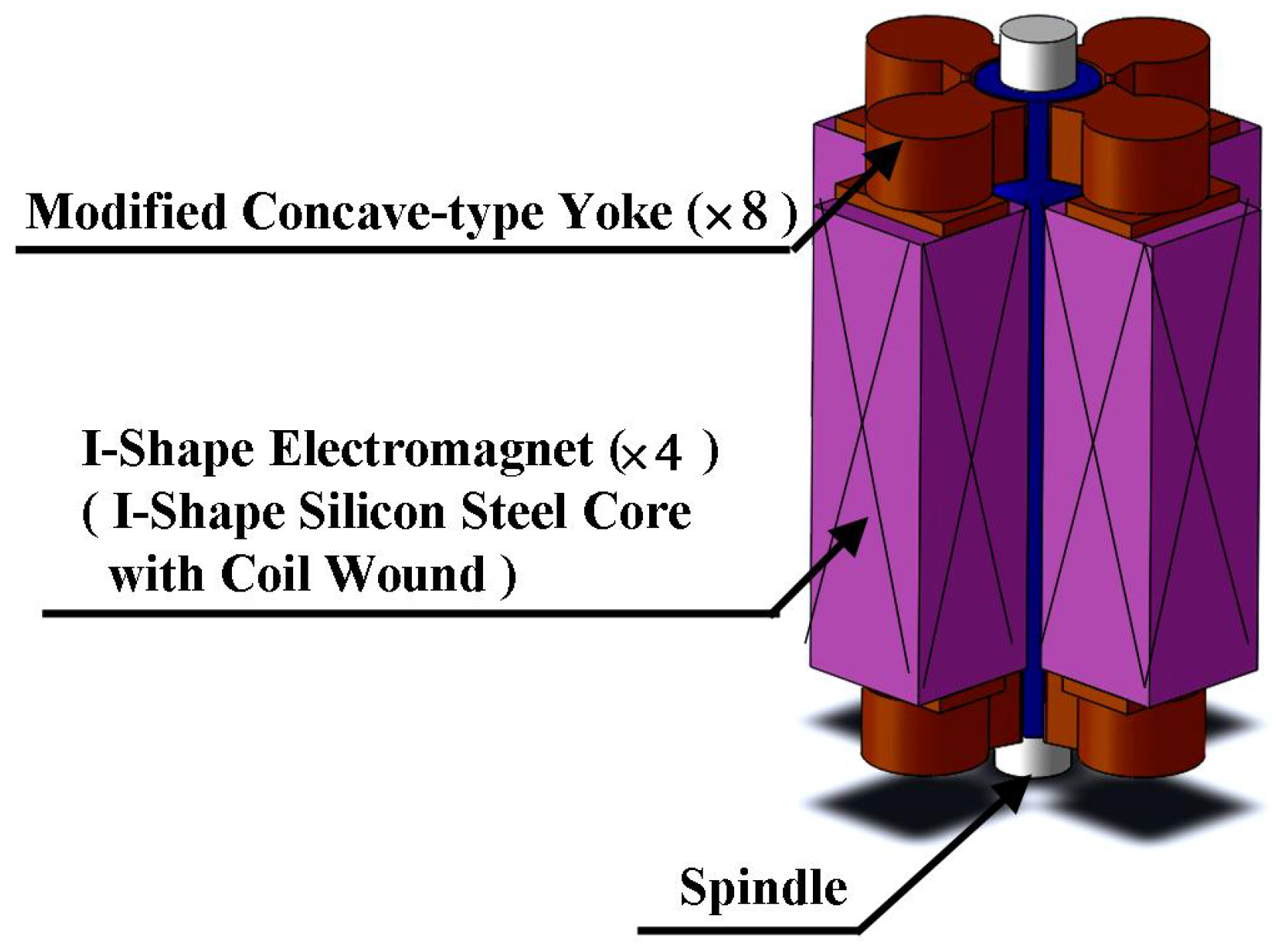
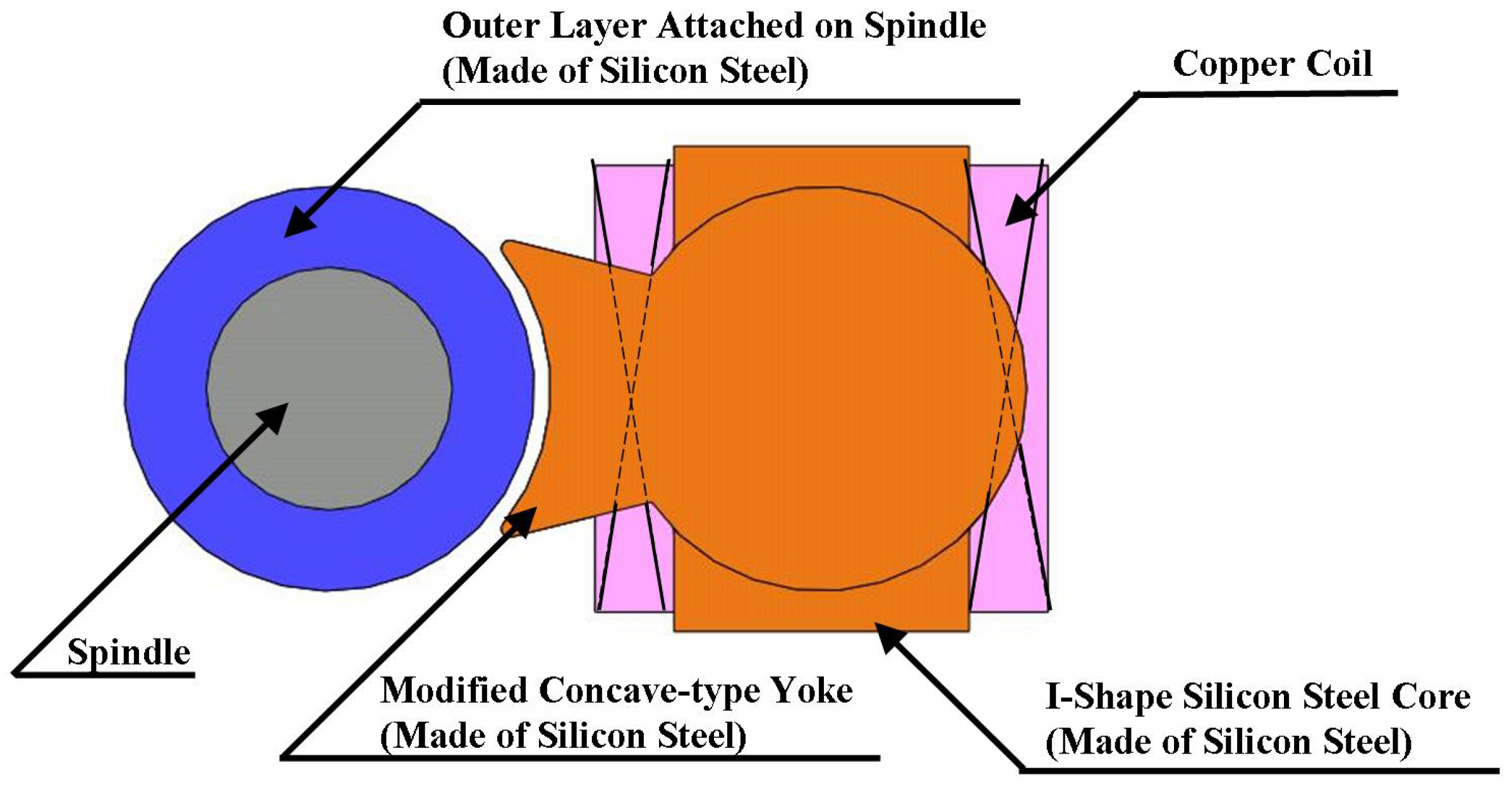
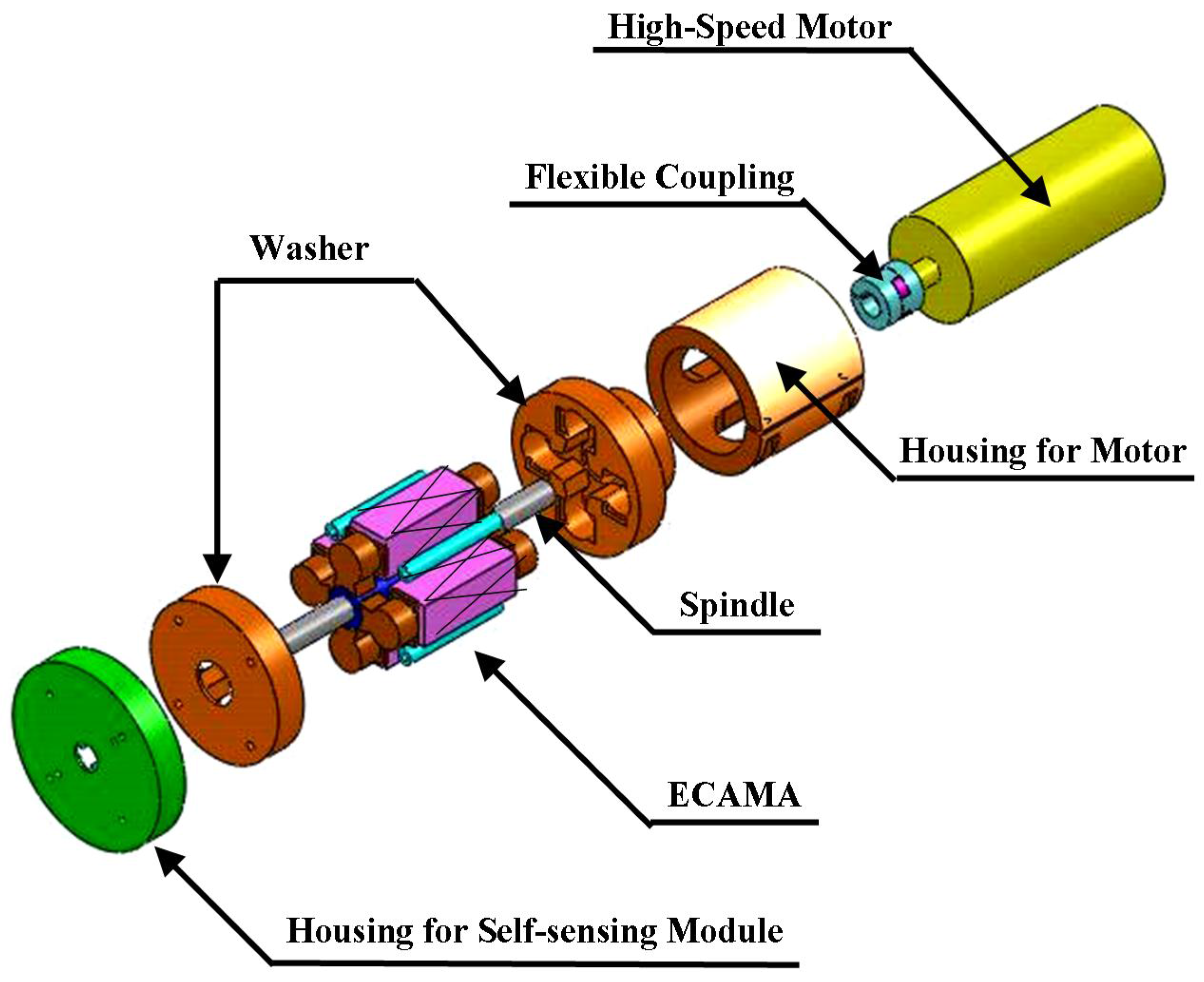
2. Control Strategy for ECAMA against Milling Dynamics
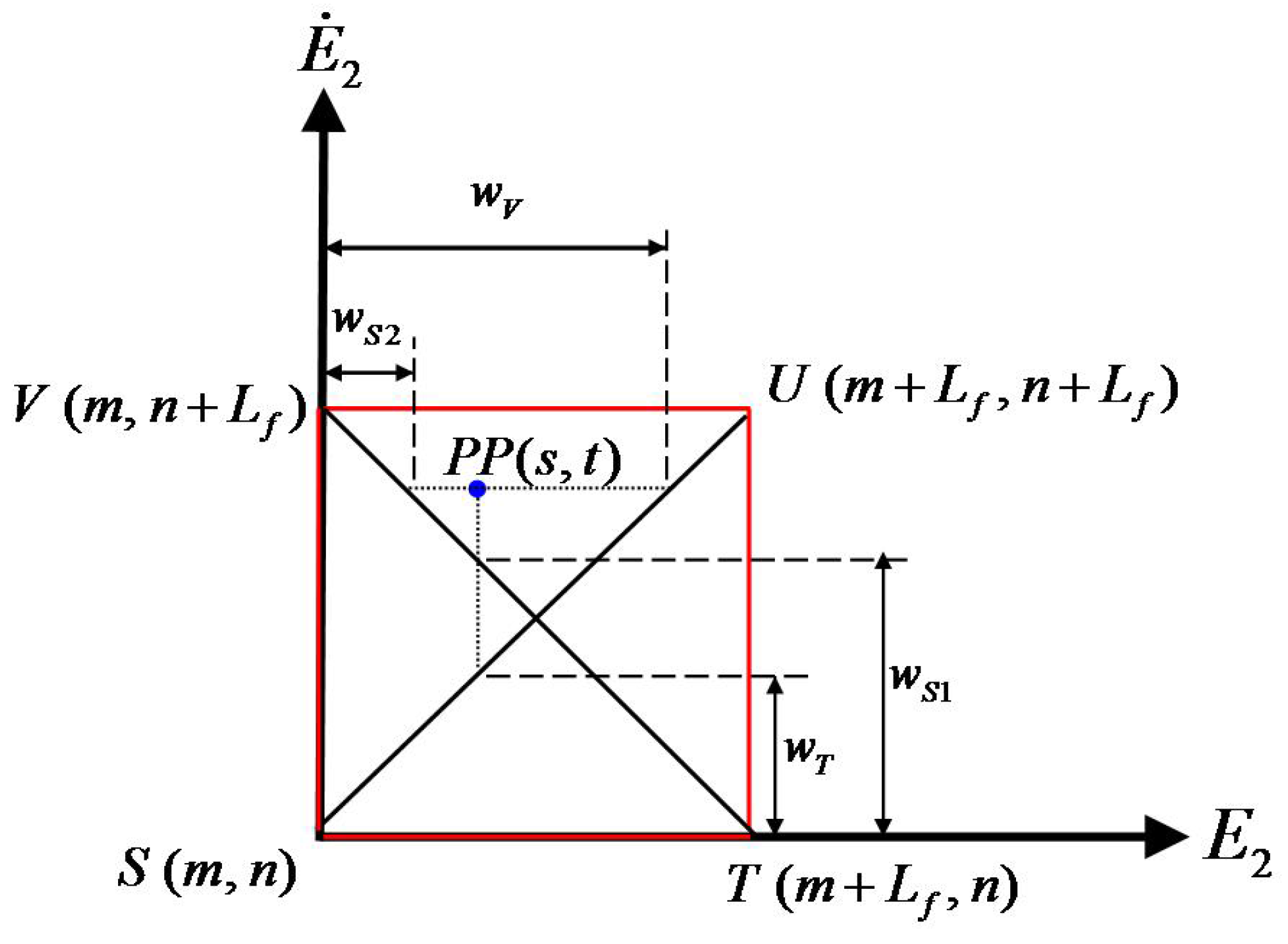
2.1. Control Goal
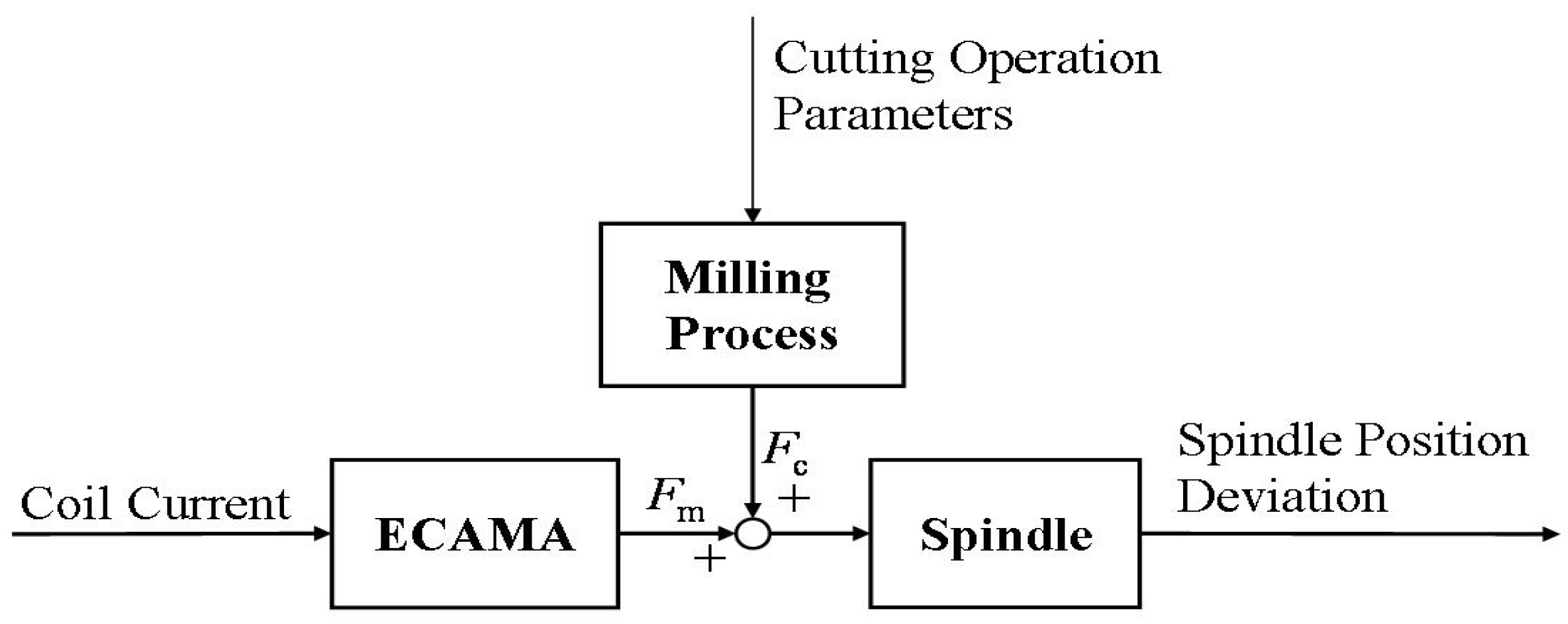
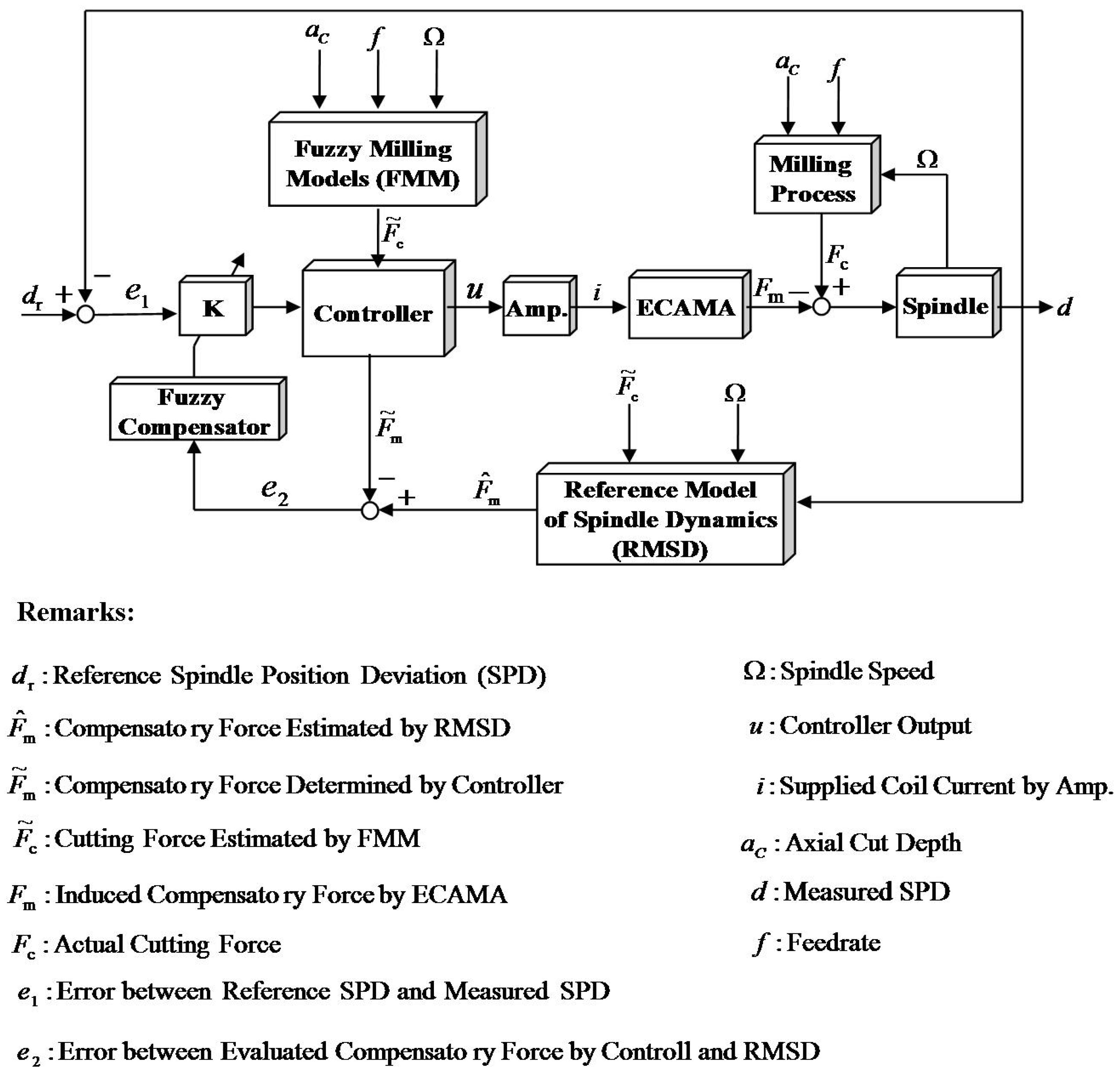
2.2. Fuzzy Model-Reference Adaptive Control (FMRAC)
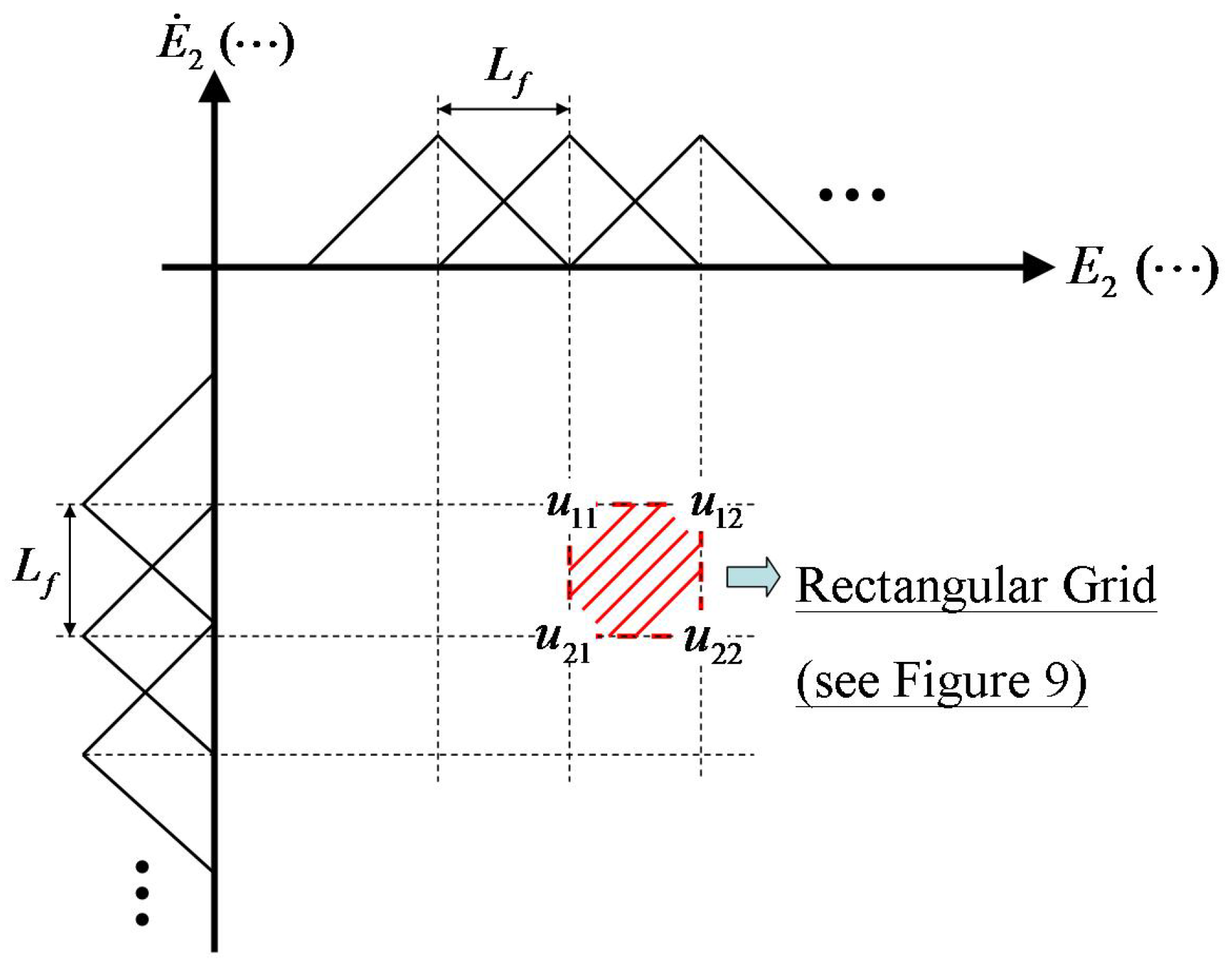
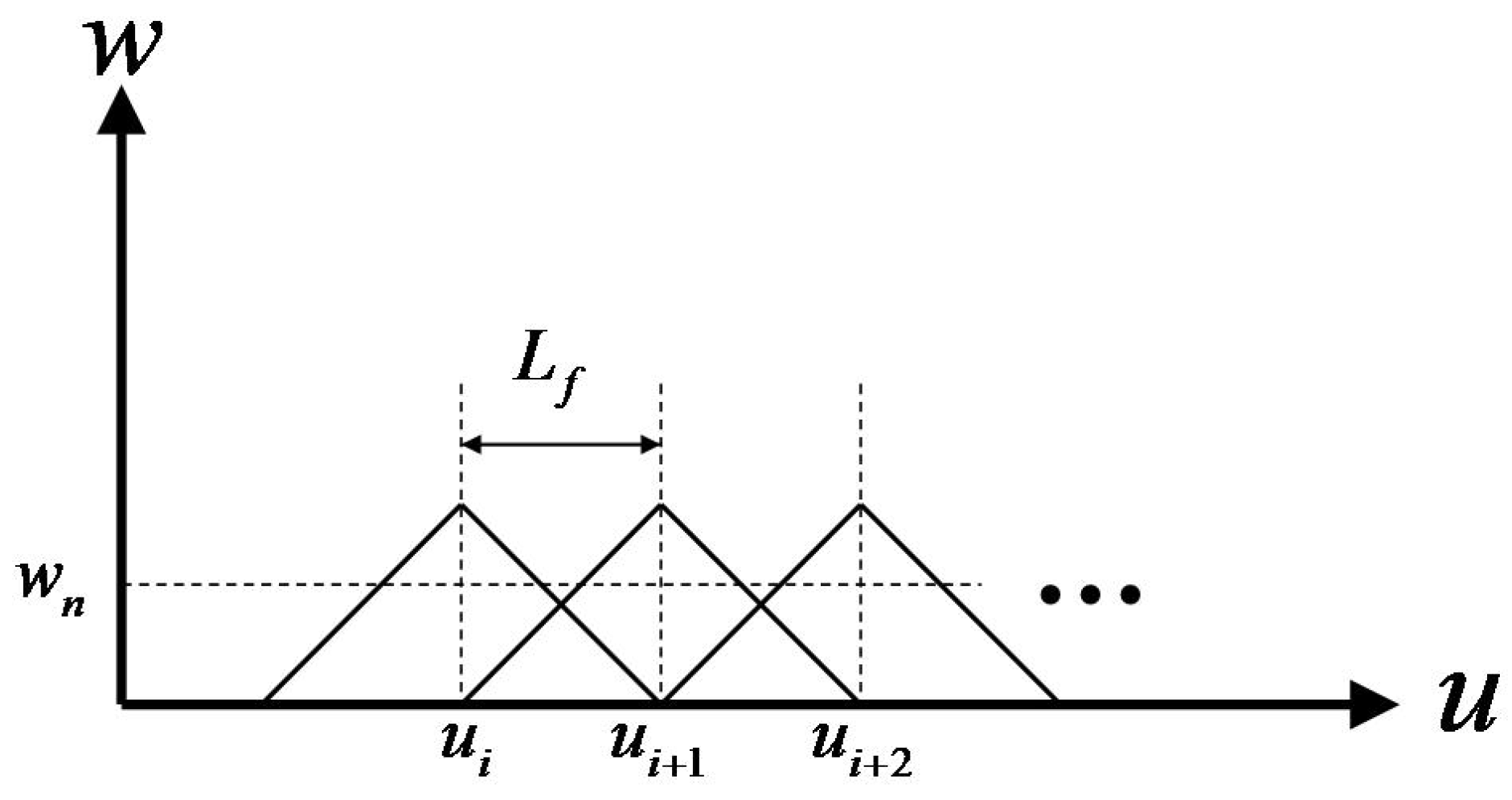
| / | NB | NM | NS | Z | PS | PM | PB |
| NB | NB | NB | NB | NB | NM | NS | Z |
| NM | NB | NB | NB | NM | NS | Z | PS |
| NS | NB | NB | NM | NS | Z | PS | PM |
| Z | NB | NM | NS | Z | PS | PM | PB |
| PS | NM | NS | Z | PS | PM | PB | PB |
| PM | NS | Z | PS | PM | PB | PB | PB |
| PB | Z | PS | PM | PB | PB | PB | PB |
2.3. Performance of the FMRAC
| Parameters | Value |
|---|---|
| Nominal air gap between spindle and yoke | |
| Distance between flexible coupling and top yoke | |
| Distance between flexible coupling and bottom yoke | |
| Distance between flexible coupling and gap self-sensing module | |
| Distance between flexible coupling and cutter tip | |
| Transverse mass moment of inertia of spindle | |
| Polar mass moment of inertia of spindle | |
| Stiffness of current | |
| Stiffness of displacement | |
| Spinning speed of spindle | 10k rpm |
| Feedrate |
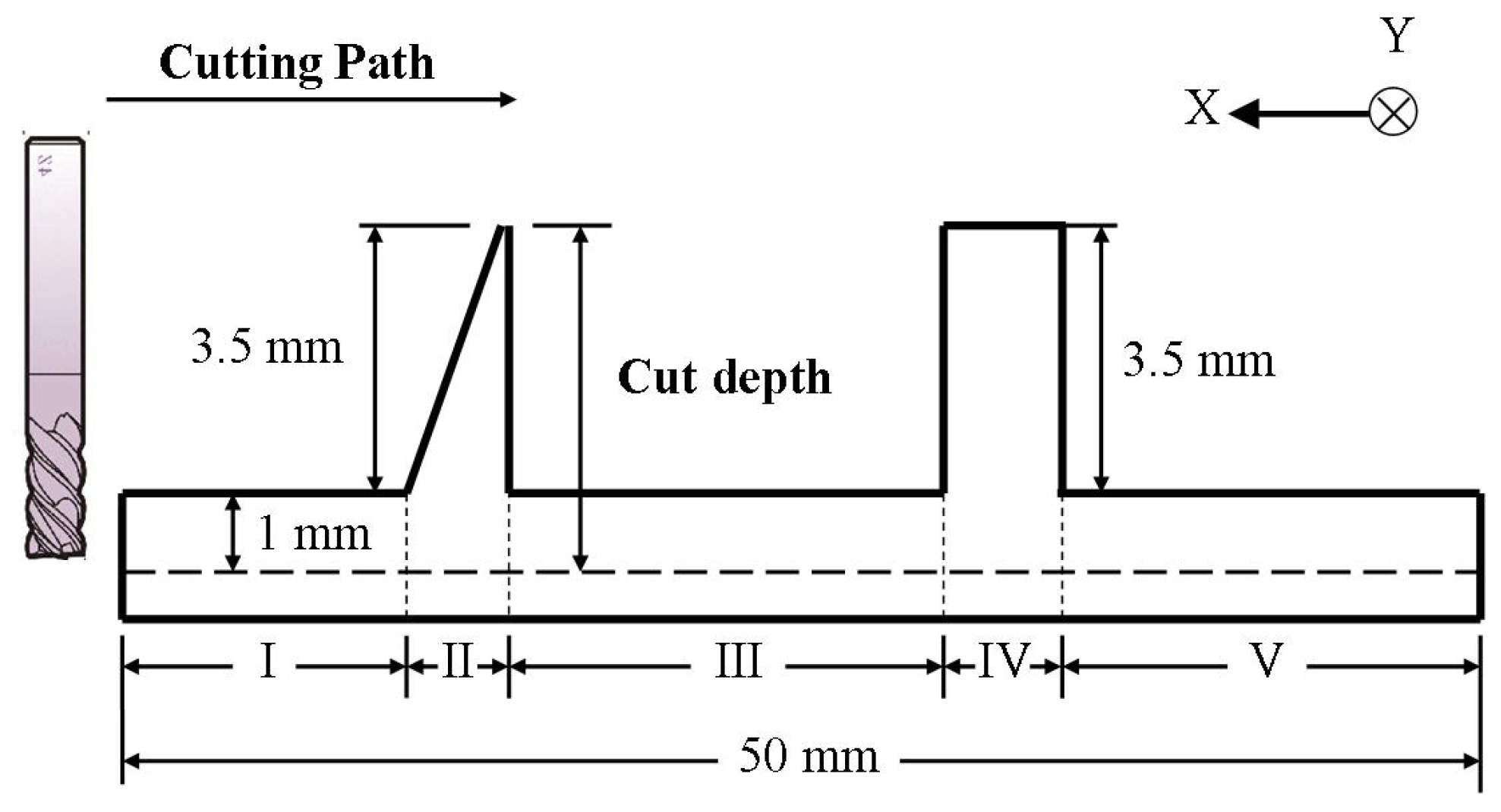
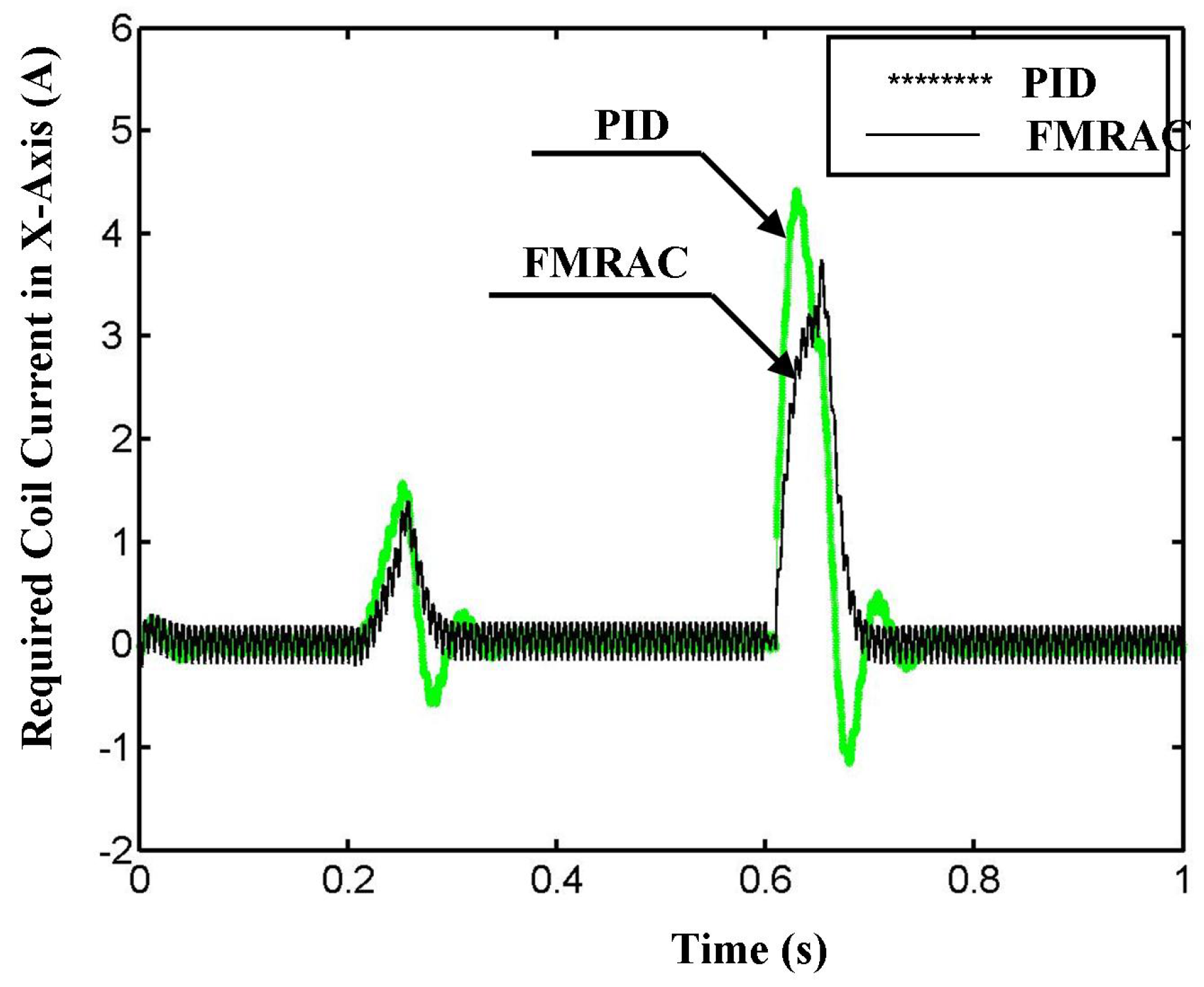
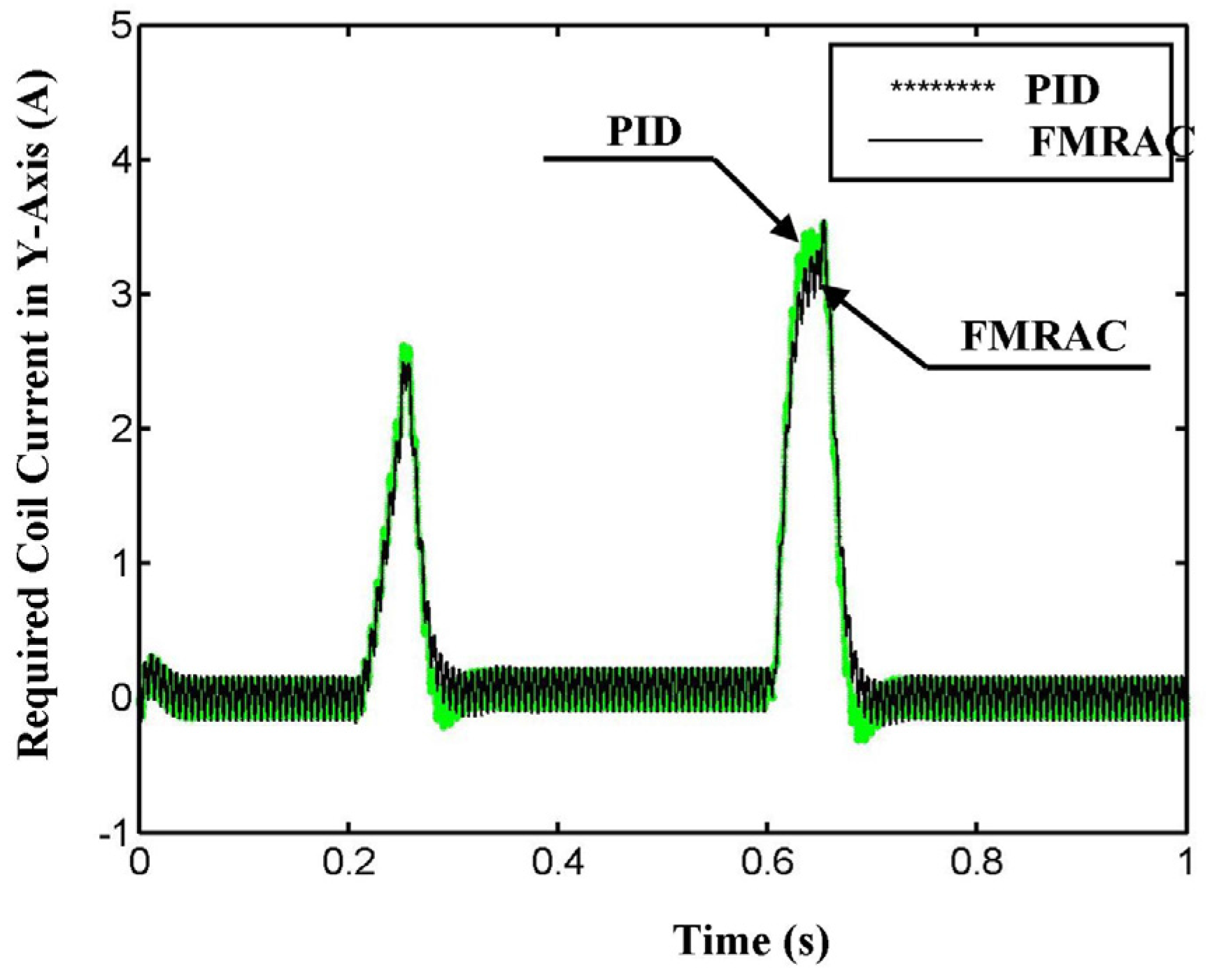
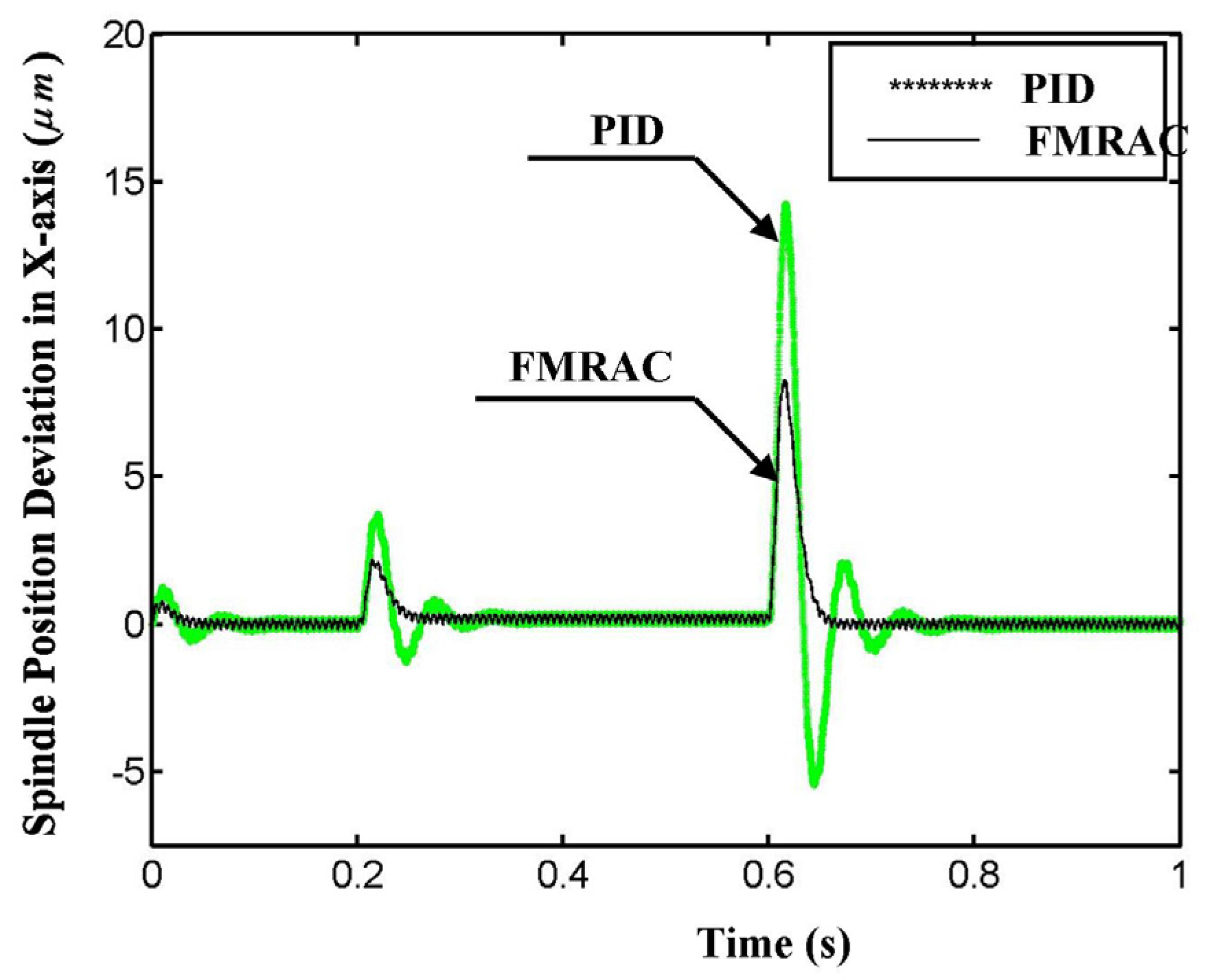
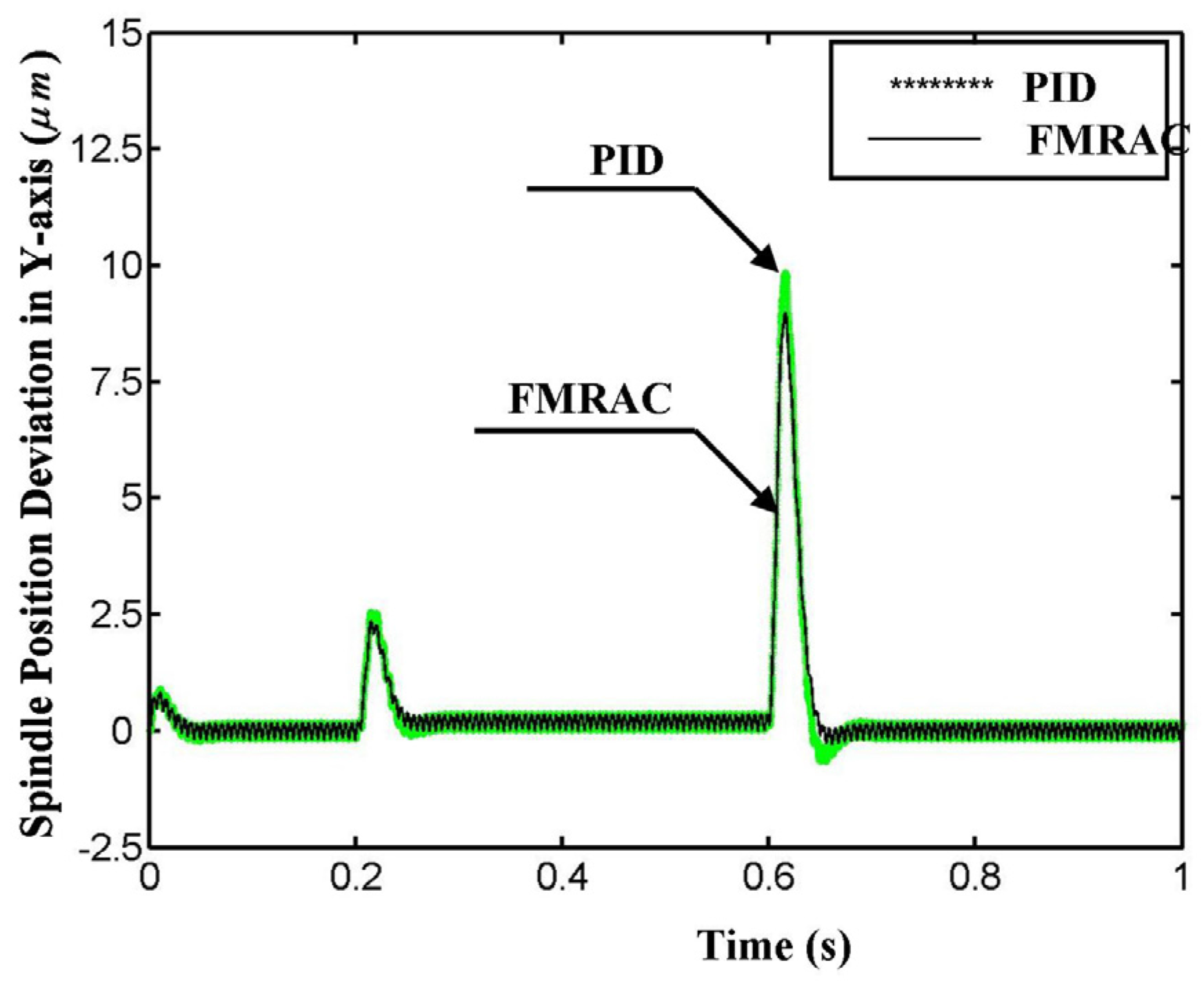
3. Experimental Setup and Results
- ➢
- Axial length of milling module: 40 cm.
- ➢
- Maximum radial length of milling module: 11 cm.
- ➢
- Total weight of milling module: 7.5 kg.
- ➢
- Power of drive motor: 1 kW.
- ➢
- Maximum speed of drive motor: 24k rpm
- ➢
- Total weight of ECAMA: 2.8 kg
- ➢
- Axial length of ECAMA: 12.2 cm
- ➢
- Maximum radial length of ECAMA: 10 cm
- ➢
- Maximum power consumption of ECAMA: 60 W (by an individual I-shape electromagnet)
| Specifications | ECAMA | Modified Radial Design AMB |
|---|---|---|
| Diameter (mm) | 88 | 85 |
| Axial Length (mm) | 122 | 81 |
| Coil Turns | 1200 (on each individual I-shape silicon steel core) | 220 (on each individual pair of electromagnetic poles) |
| Max Induced Magnetic Force (N) | 224 (1.5 A coil current supplied) | 65 (3 A coil current supplied) |
- ➢
- Materials of workpiece: acrylic, aluminum and copper (three types of materials).
- ➢
- Spindle speed (ω): 3000 rpm
- ➢
- Feedrate (f): 300 mm/min.
- ➢
- Axial cut depth (Da): 2.5 mm.
- ➢
- Radial cut depth (Dr): 1 mm.

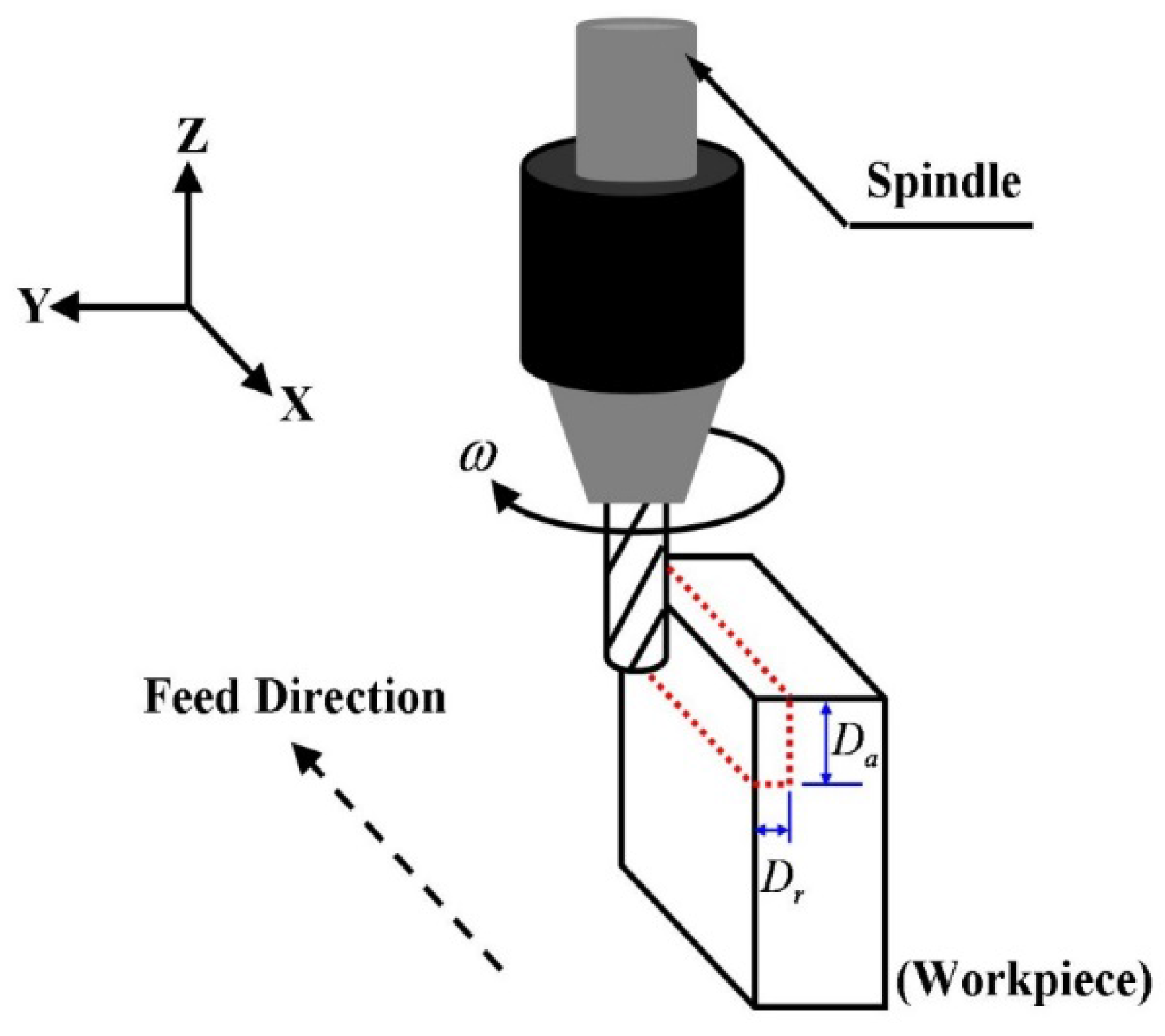
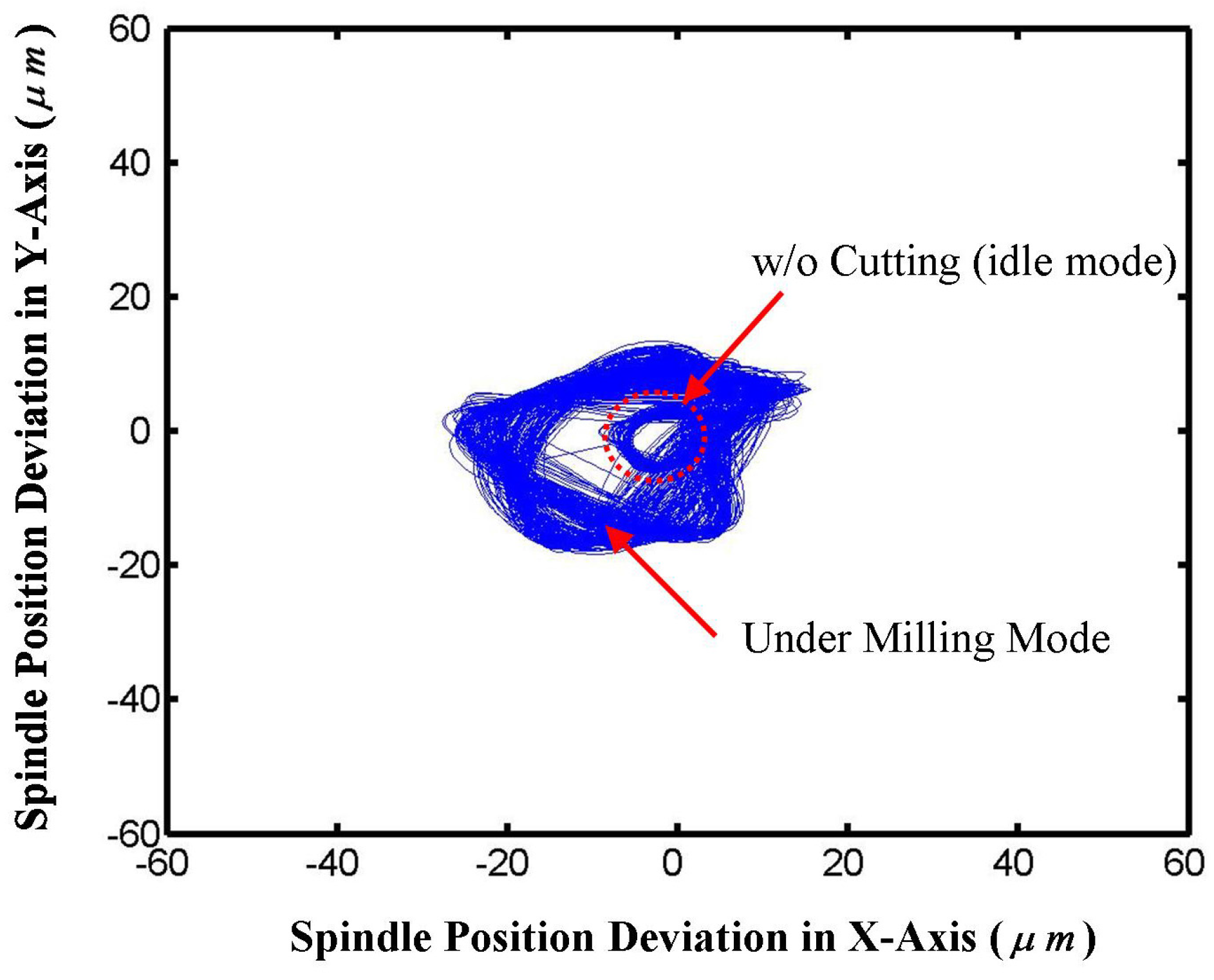
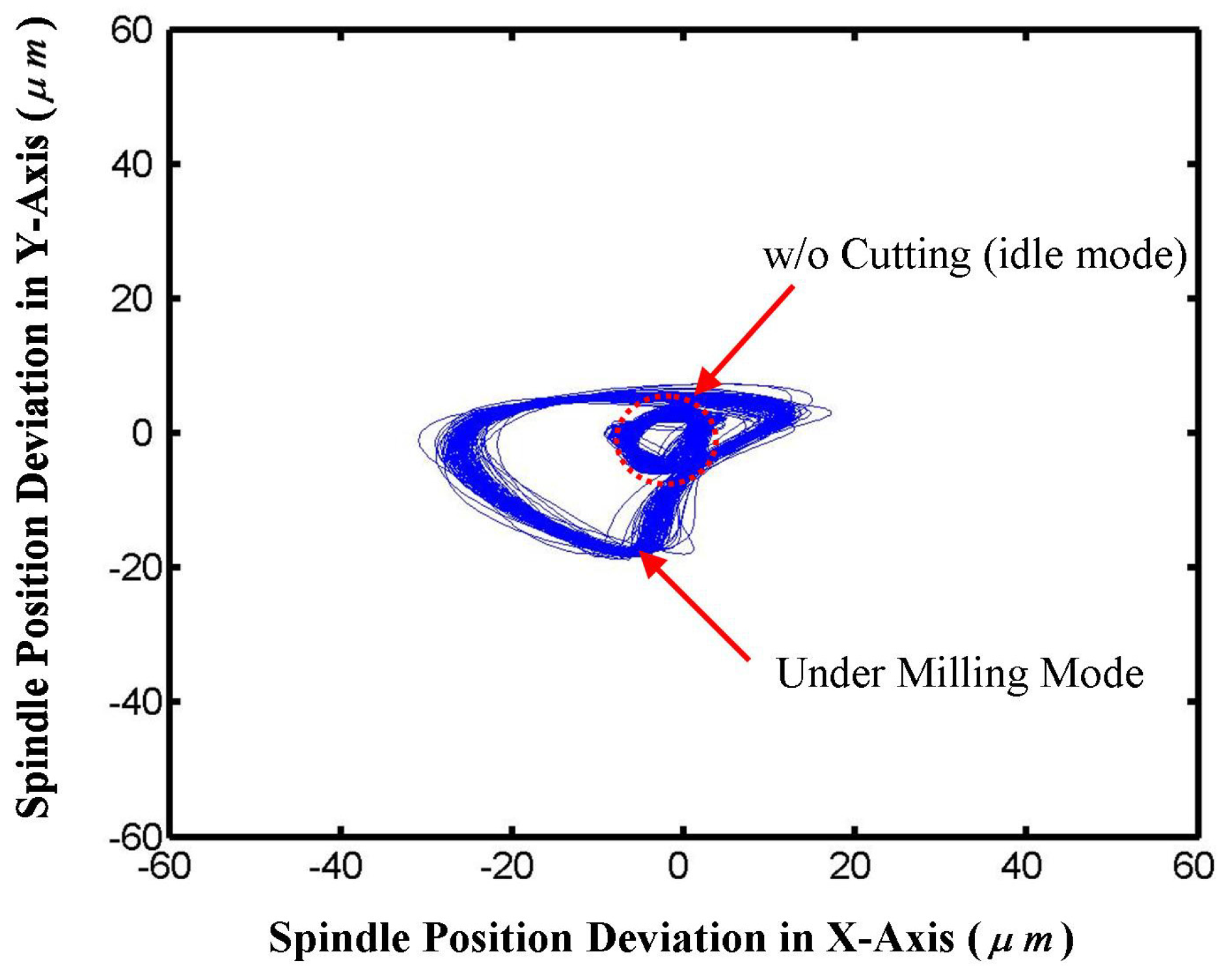
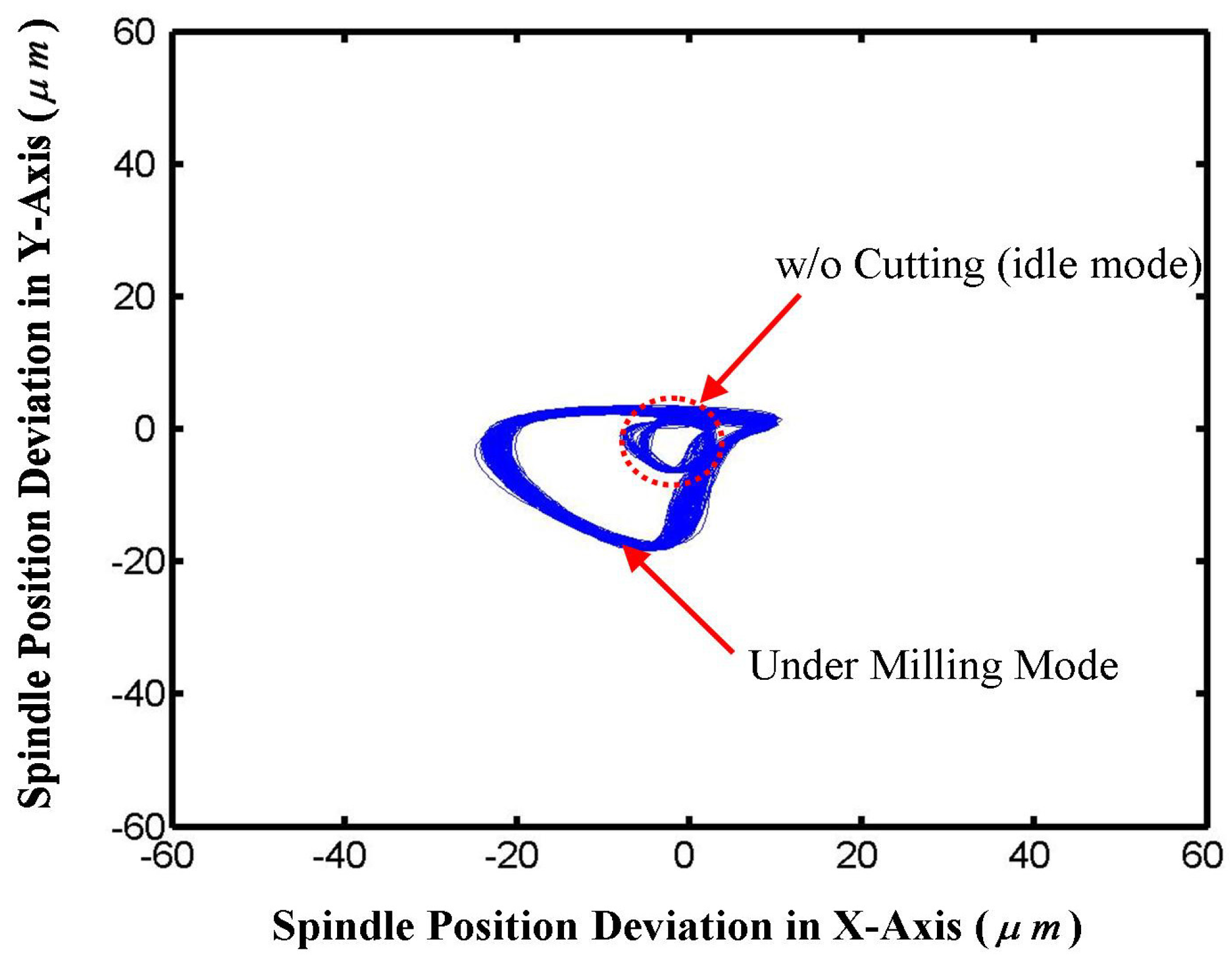
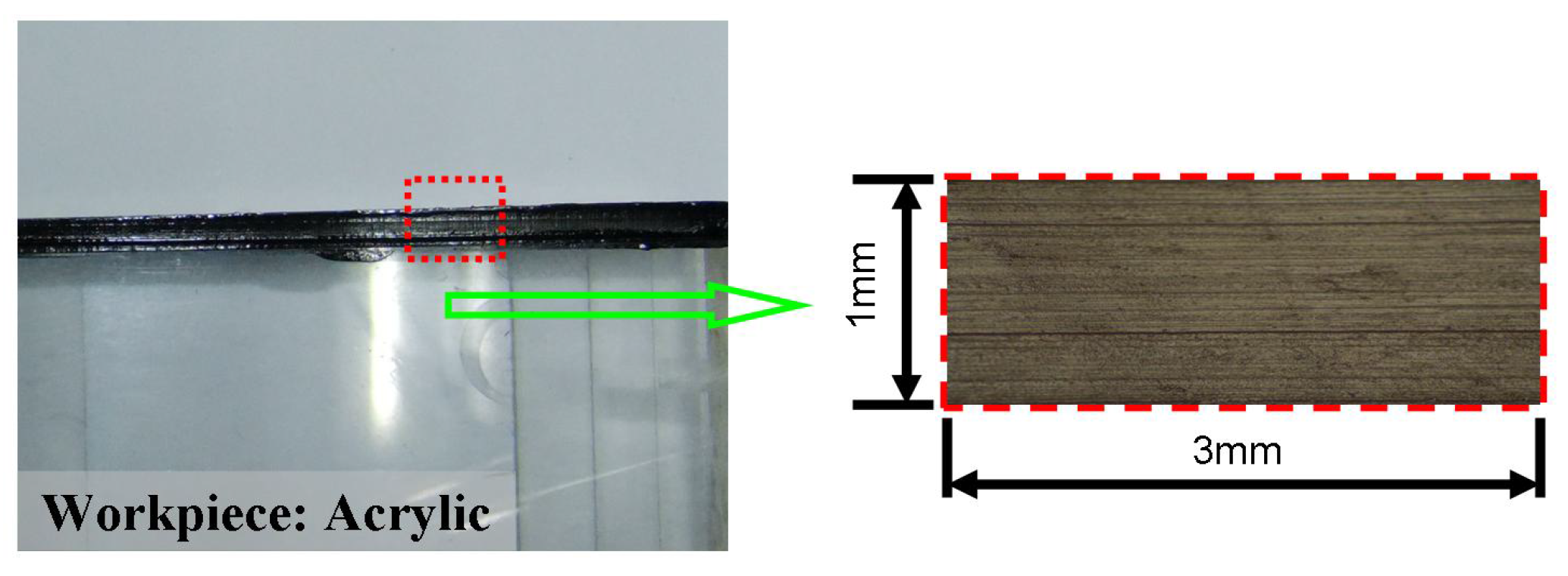
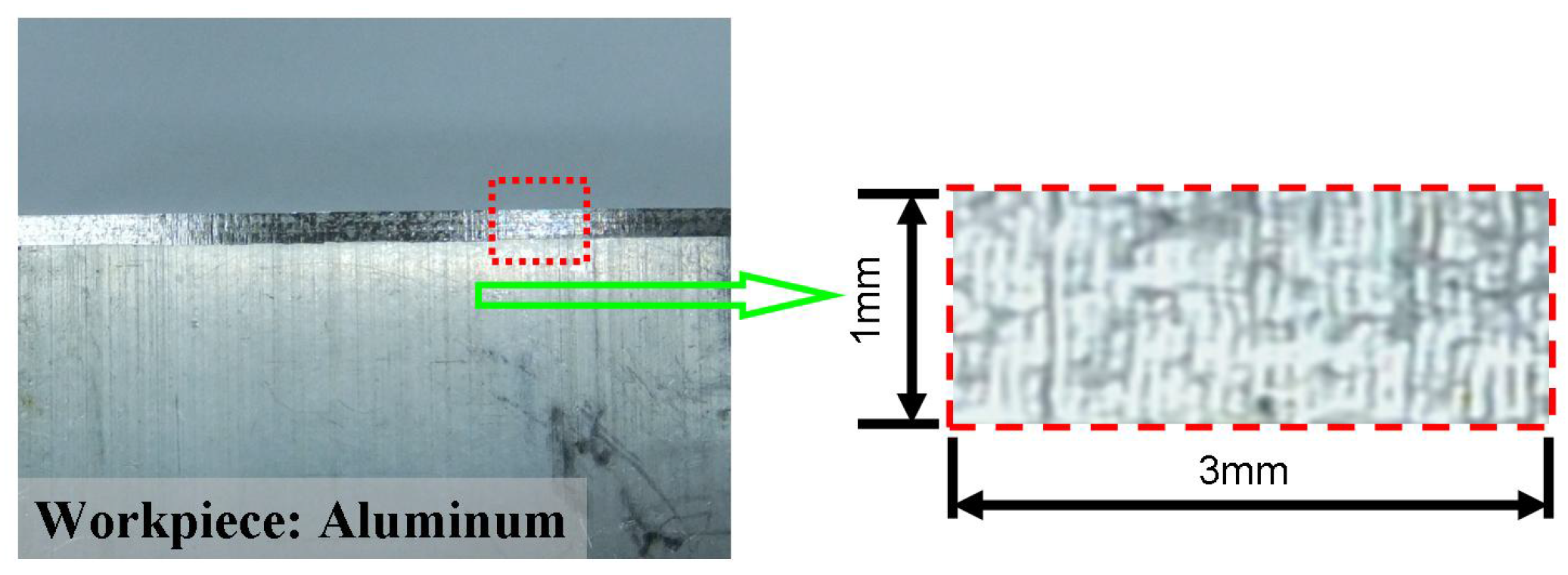
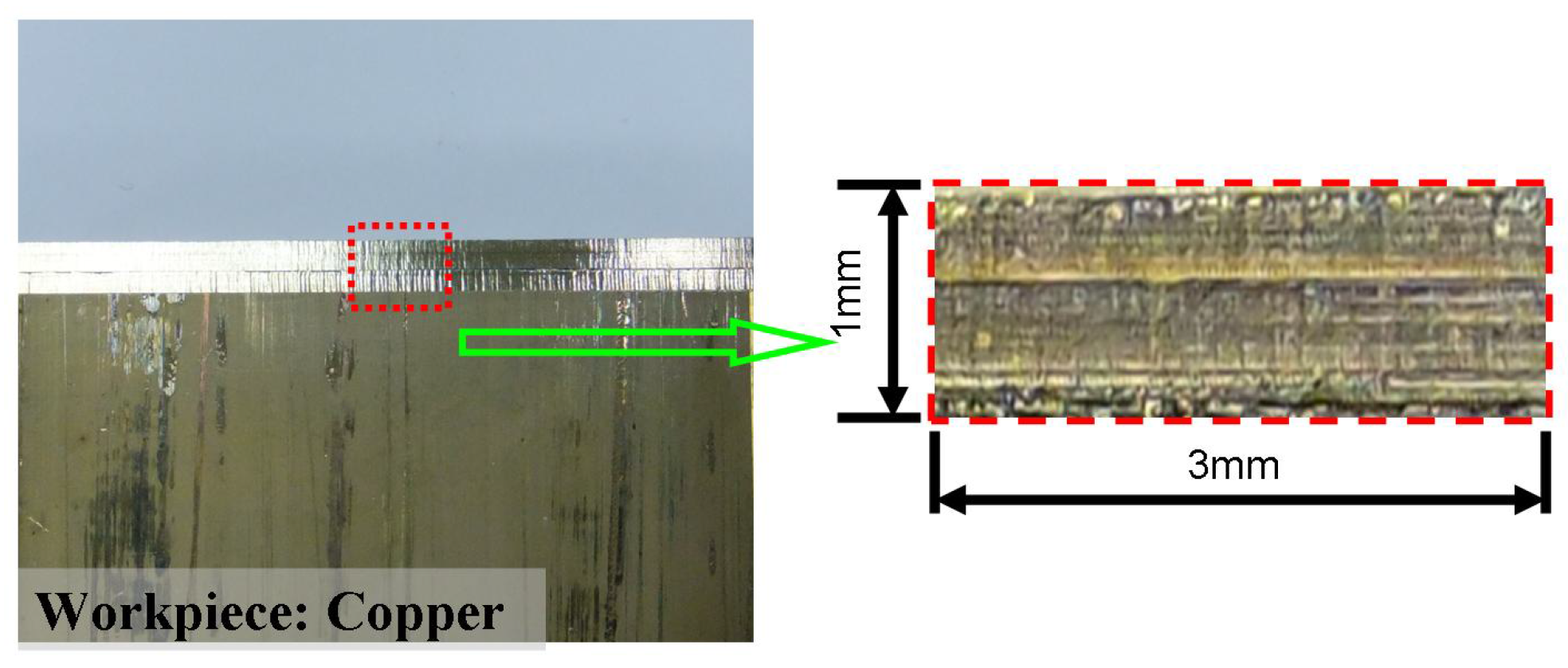
4. Conclusions
- (1)
- The ECAMA is a potential solution for milling applications of AMB. It is designed to deal with the issues of magnetic force intensity and overall AMB size at the same time. That is, the regulation force by AMB can be much enhanced under a reasonable size. However, for regular industrial machinery, the size of the ECAMA should be much larger than that in this work to achieve the requirements of industrial applications.
- (2)
- Since the dynamics of milling processes and magnetic force are both highly nonlinear, estimation errors of the cutting force or magnetic force are definitely met. These force dynamics are investigated by experiments in this work instead of parameters analysis by theoretical methods. The accuracy of experimental models is highly determined by the experiment design. Therefore, the test rig design and the selection of analysis method should be addressed carefully.
- (3)
- A fuzzy compensator is designed to achieve the adaptive gain control. As previously mentioned, the estimation errors are hard to be avoided. A fine-tuning scheme for control gain is, therefore, embedded to diminish the degree of estimation error. For further applications, such as chatter suppression, the membership functions and the decision rules have to be modified to make the regulation behavior faster and more efficient.
Author Contributions
Conflicts of Interest
References
- Kyung, J.H.; Lee, C.W. Controller design for a magnetically suspended milling spindle based on chatter stability analysis. Jpn. Soc. Mech. Eng. Ser. C 2003, 46, 416–422. [Google Scholar] [CrossRef]
- Auchet, S.; Chevrier, P.; Lacour, M.; Lipinski, P. A new method of cutting force measurement based on command voltages of active electro-magnetic bearings. Int. J. Mach. Tools Manuf. 2004, 44, 1441–1449. [Google Scholar] [CrossRef]
- Tsai, N.-C.; Shih, L.-W.; Lee, R.-M. Counterbalance of cutting force for advanced milling operations. Mech. Syst. Signal Process. 2010, 24, 1191–1208. [Google Scholar] [CrossRef]
- Storace, A.F.; Sood, D.; Lyons, J.P.; Preston, M.A. Integration of magnetic bearings in the design of advanced gas turbine engines. J. Eng. Gas Turbines Power 1995, 117, 655–665. [Google Scholar] [CrossRef]
- Swanson, E.E.; Heshmat, H.; Walton, II. Performance of a foil-magnetic hybrid bearing. J. Eng. Gas Turbines Power 2002, 124, 375–382. [Google Scholar] [CrossRef]
- Spirig, M.; Schmied, J.; Jenckel, P.; Kanne, U. Three practical examples of magnetic bearing control design using a modern tool. J. Eng. Gas Turbines Power 2002, 124, 1025–1031. [Google Scholar] [CrossRef]
- Imoberdorf, P.; Zwyssig, C.; Round, S.D.; Kolar, J.W. Combined radial-axial magnetic bearing for a 1 kW, 500,000 rpm permanent magnet machine. In Proceedings of the 22nd Annual IEEE Applied Power Electronics Conference, Anacheim, CA, USA, 25 February–1 March 2007.
- Tsai, N.-C.; Hsu, S.-L. On sandwiched magnetic bearing design. Electromagnetics 2007, 27, 371–385. [Google Scholar] [CrossRef]
- Park, J.-K.; Kyung, J.-H.; Shin, W.-C.; Ro, S.-K. A magnetically suspended miniature spindle and its application for tool orbit control. Int. J. Precis. Eng. Manuf. 2012, 13, 1601–1607. [Google Scholar] [CrossRef]
- Gourc, E.; Seguy, S.; Arnaud, L. Chatter milling modeling of active magnetic bearing spindle in high-speed domain. Int. J. Mach. Tools Manuf. 2011, 51, 928–936. [Google Scholar] [CrossRef]
- Huang, T.; Chen, Z.; Zhang, H.-T.; Ding, H. Active control of an active magnetic bearings supported spindle for chatter suppression in milling process. J. Dyn. Syst. Meas. Control 2015, 137, 111003–111011. [Google Scholar] [CrossRef]
- Smirnov, A.; Pesch, A.H.; Pyrhonen, O.; Sawicki, J.T. High-precision cutting tool tracking with a magnetic bearing spindle. J. Dyn. Syst. Meas. Control 2015, 137. [Google Scholar] [CrossRef]
- Kim, J.H.; Zhao, S.; Kim, G.H.; Lee, S.-K. Rolling bearing-suspended spindle run-out control using repetitive control and adaptive feedforward cancellation. Int. J. Precis. Eng. Manuf. 2013, 14, 2171–2178. [Google Scholar] [CrossRef]
- Kim, J.-H.; Lee, S.-K. Micro-patterning technique using a rotating cutting tool controlled by an electromagnetic actuator. Int. J. Mach. Tools Manuf. 2016, 101, 52–64. [Google Scholar] [CrossRef]
- Qiao, X.; Zhu, C. The active vibration attenuation of a built-in motorized milling spindle. J. Vibrat. Control 2013, 19, 2434–2447. [Google Scholar] [CrossRef]
- Wroblewski, A.C.; Sawicki, J.T.; Pesch, A.H. Rotor model updating and validation for an active magnetic bearing based high-speed machining spindle. J. Eng. Gas Turbines Power 2012, 134. [Google Scholar] [CrossRef]
- Sohnl, J.W.; Paengl, Y.-S.; Choil, S.-B. An active mount using an electromagnetic actuator for vibration control: experimental investigation. J. Mech. Eng. Sci. 2010, 224, 1617–1625. [Google Scholar] [CrossRef]
- Lauderbaugh, L.K.; Ulsoy, A.G. Dynamic modeling for control of milling process. J. Eng. Ind. 1998, 110, 367–375. [Google Scholar] [CrossRef]
- Li, H.Z.; Li, X.P.; Chen, X.Q. A novel chatter stability criterion for the modeling and simulation of the dynamic milling process in the time domain. Int. J. Adv. Manuf. Technol. 2003, 22, 619–625. [Google Scholar] [CrossRef]
- Yang, M.Y.; Lee, T.M. Hybrid adaptive control based on the characteristics of CNC end milling. Int. J. Mach. Tools Manuf. 2002, 42, 489–499. [Google Scholar] [CrossRef]
- Peng, Y.H. On the performance enhancement of self-turning adaptive control for time varying machining processes. Int. J. Adv. Manuf. Technol. 2004, 24, 395–403. [Google Scholar] [CrossRef]
- Chiang, S.-T.; Liu, D.-I.; Lee, A.; Chieng, W. Adaptive control optimization in end milling using neural network. Int. J. Mach. Tools Manuf. 1995, 34, 637–660. [Google Scholar] [CrossRef]
- Kim, M.K.; Cho, M.W.; Kim, K. Application of the fuzzy control strategy to adaptive force control of non-minimum phase end milling operations. Int. J. Mach. Tools Manuf. 1994, 33, 677–696. [Google Scholar] [CrossRef]
- Tarng, Y.S.; Hwang, S.T. Adaptive learning control of milling operations. Mechatronics 1995, 5, 937–948. [Google Scholar] [CrossRef]
- Morita, N.; Yoshida, Y.; Kishioka, S.; Ueno, S. Study on high-speed milling of hard materials. Jpn. Soc. Mech. Eng. Part C 1997, 63, 4347–4353. [Google Scholar] [CrossRef]
- Hegazi, A.S. Comparison between conventional and high speed milling processes. J. Eng. Appl. Sci. 2006, 53, 45–61. [Google Scholar]
- Tang, D.W.; Wang, C.Y.; Hu, Y.N. Finite-element simulation of conventional and high-speed peripheral milling of hardened mold steel. Metall. Mater. Trans. A 2009, 40, 3245–3257. [Google Scholar] [CrossRef]
- Tsai, N.-C.; Lee, R.-M. Regulation of spindle position by magnetic actuator array. Int. J. Adv. Manuf. Technol. 2011, 53, 93–104. [Google Scholar] [CrossRef]
- Allaire, P.E.; Humphris, R.R.; Kelm, R.D. Dynamics of a digitally controlled magnetic bearing. Nippon Kikai Gakkai Ronbunshu 1985, 51, 1095–1100. [Google Scholar]
- Rosyadi, M.; Muyeen, S.M.; Takahashi, R.; Tamura, J. A design fuzzy logic controller for a permanent magnet wind generator to enhance the dynamic stability of wind farms. Appl. Sci. 2012, 2, 780–800. [Google Scholar] [CrossRef]
- Yeh, H.-Y.; Lee, C.-D. The logic-based supervisor control for sun-tracking system of 1 MW HCPV demo plant: Study case. Appl. Sci. 2012, 2, 100–113. [Google Scholar] [CrossRef]
- Sheng, S.; Sun, C. A near-hover adaptive attitude control strategy of a ducted fan micro aerial vehicle with actuator dynamics. Appl. Sci. 2015, 5, 666–681. [Google Scholar] [CrossRef]
- Sheng, S.; Sun, C. Design of a stability augmentation system for an unmanned helicopter based on adaptive control techniques. Appl. Sci. 2015, 5, 575–586. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, R.-M.; Chen, T.-C. Adaptive Control of Active Magnetic Bearing against Milling Dynamics. Appl. Sci. 2016, 6, 52. https://doi.org/10.3390/app6020052
Lee R-M, Chen T-C. Adaptive Control of Active Magnetic Bearing against Milling Dynamics. Applied Sciences. 2016; 6(2):52. https://doi.org/10.3390/app6020052
Chicago/Turabian StyleLee, Rong-Mao, and Tsung-Chia Chen. 2016. "Adaptive Control of Active Magnetic Bearing against Milling Dynamics" Applied Sciences 6, no. 2: 52. https://doi.org/10.3390/app6020052
APA StyleLee, R.-M., & Chen, T.-C. (2016). Adaptive Control of Active Magnetic Bearing against Milling Dynamics. Applied Sciences, 6(2), 52. https://doi.org/10.3390/app6020052






