Optimized Planning of Power Source Capacity in Microgrid, Considering Combinations of Energy Storage Devices
Abstract
:1. Introduction
2. Modeling of Distributed Energy Resources (DERs)
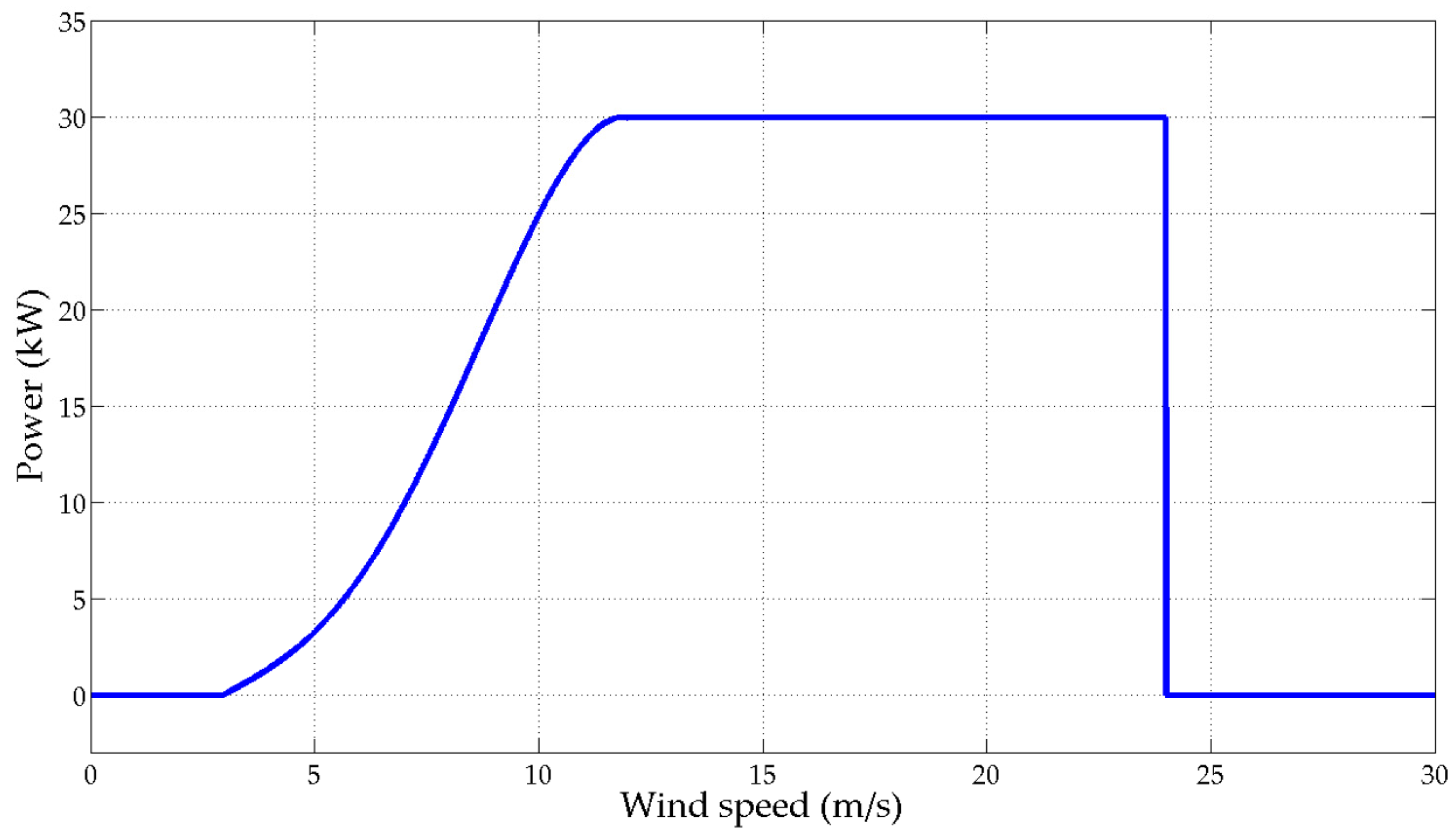
2.1. Modeling of Distributed Generators
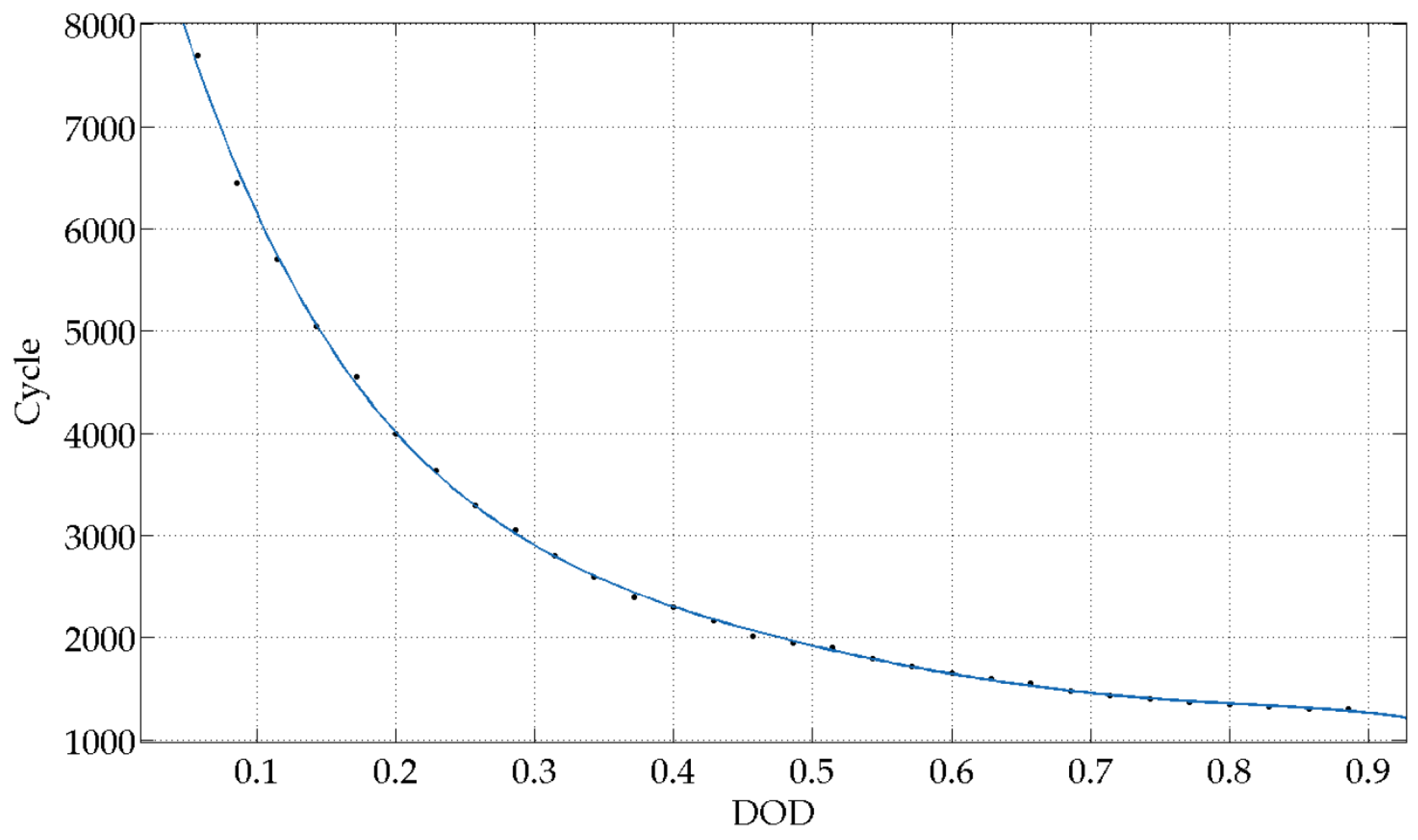
2.2. Modeling and Characteristic Analysis of Energy Storage Devices and Back-Up Source
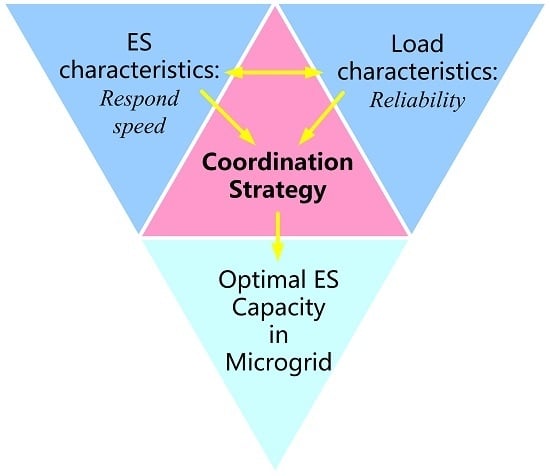
3. Analysis of Power Source and Load Coordination Mechanism
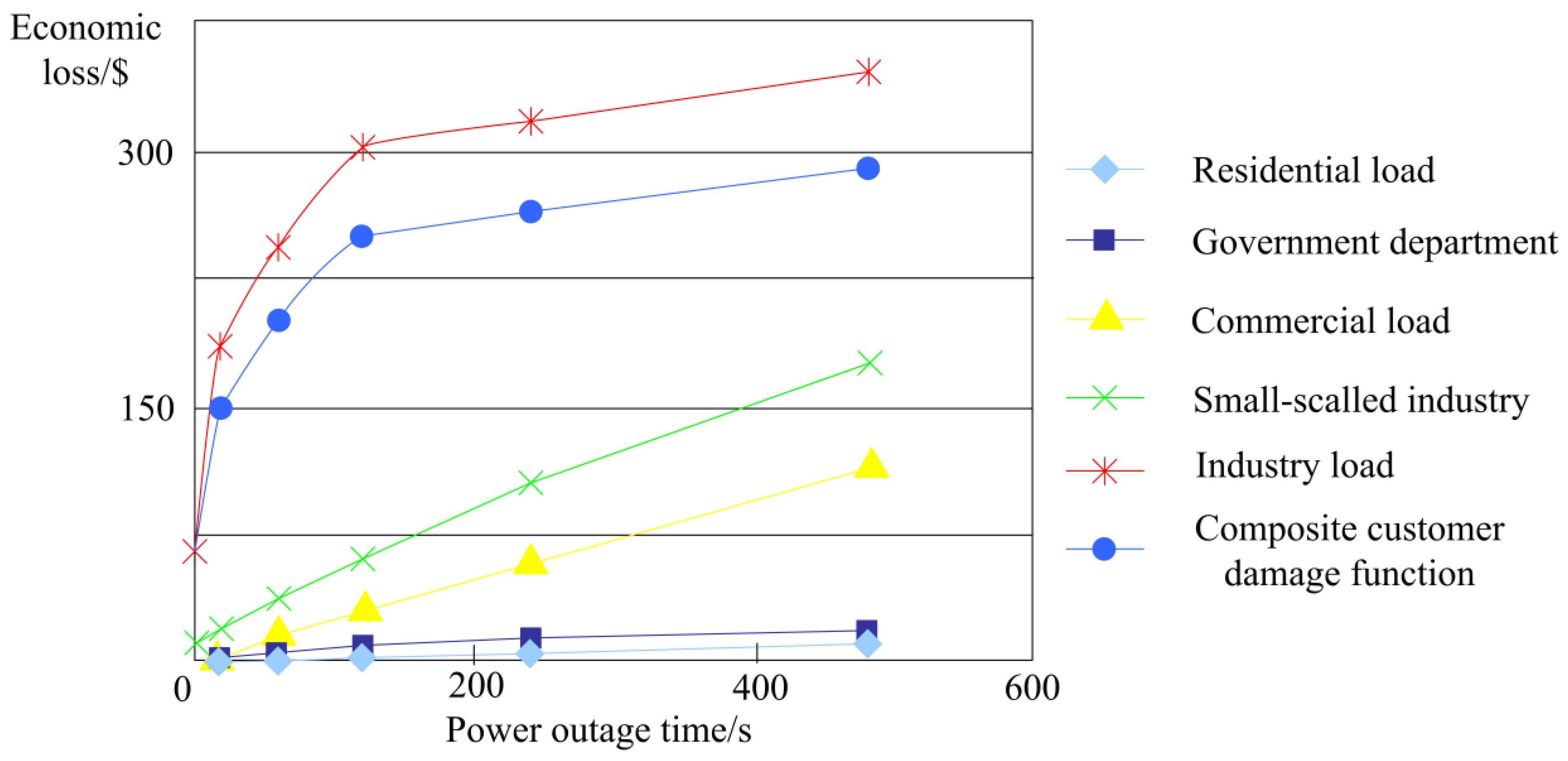
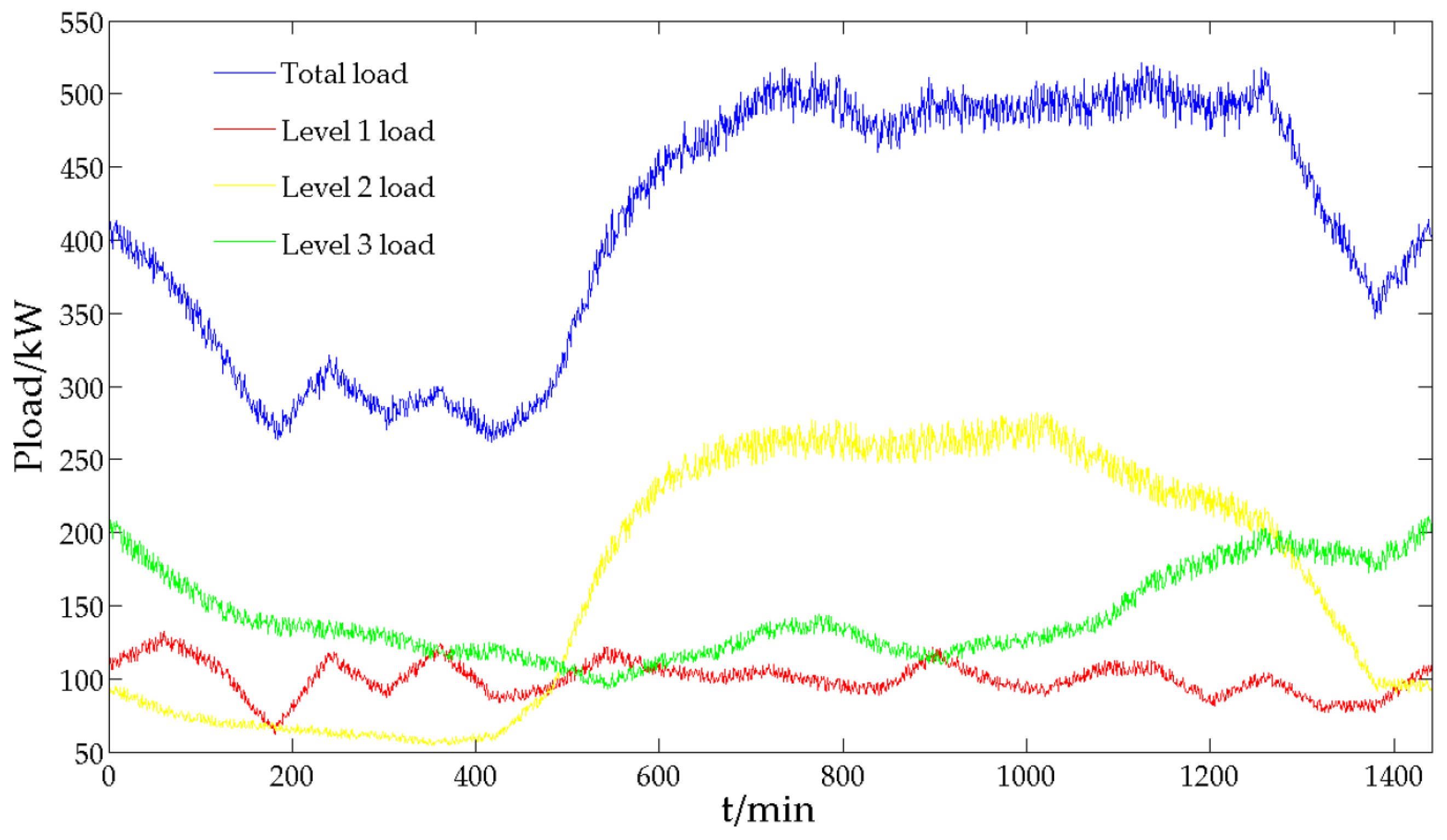
3.1. Load Character Analysis
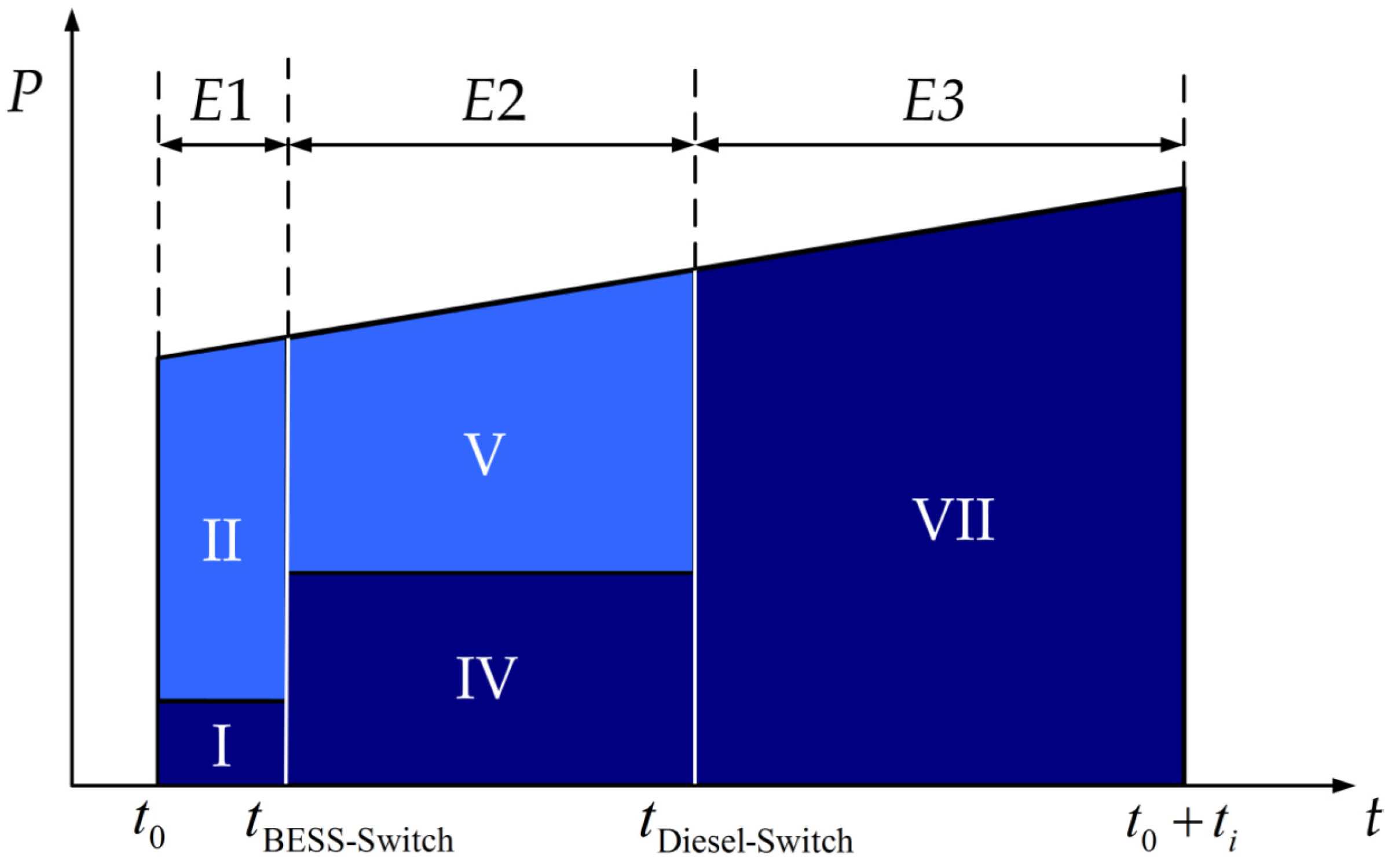
3.2. Power Source Capacity Planning Strategy Considering Source-Load Coordination
4. Optimized Planning of MG Power Source Capacity
4.1. Objective Function
4.2. Constrains
- Constrains of output power of PV, WT and diesel generator:For PV and WT, the limits (especially for minimum values) are associated with the primary source.
- Constrains of charge and discharge power of ES devices:where Pc-max, Pc-min are the maximum and minimum charging power of ES devices.
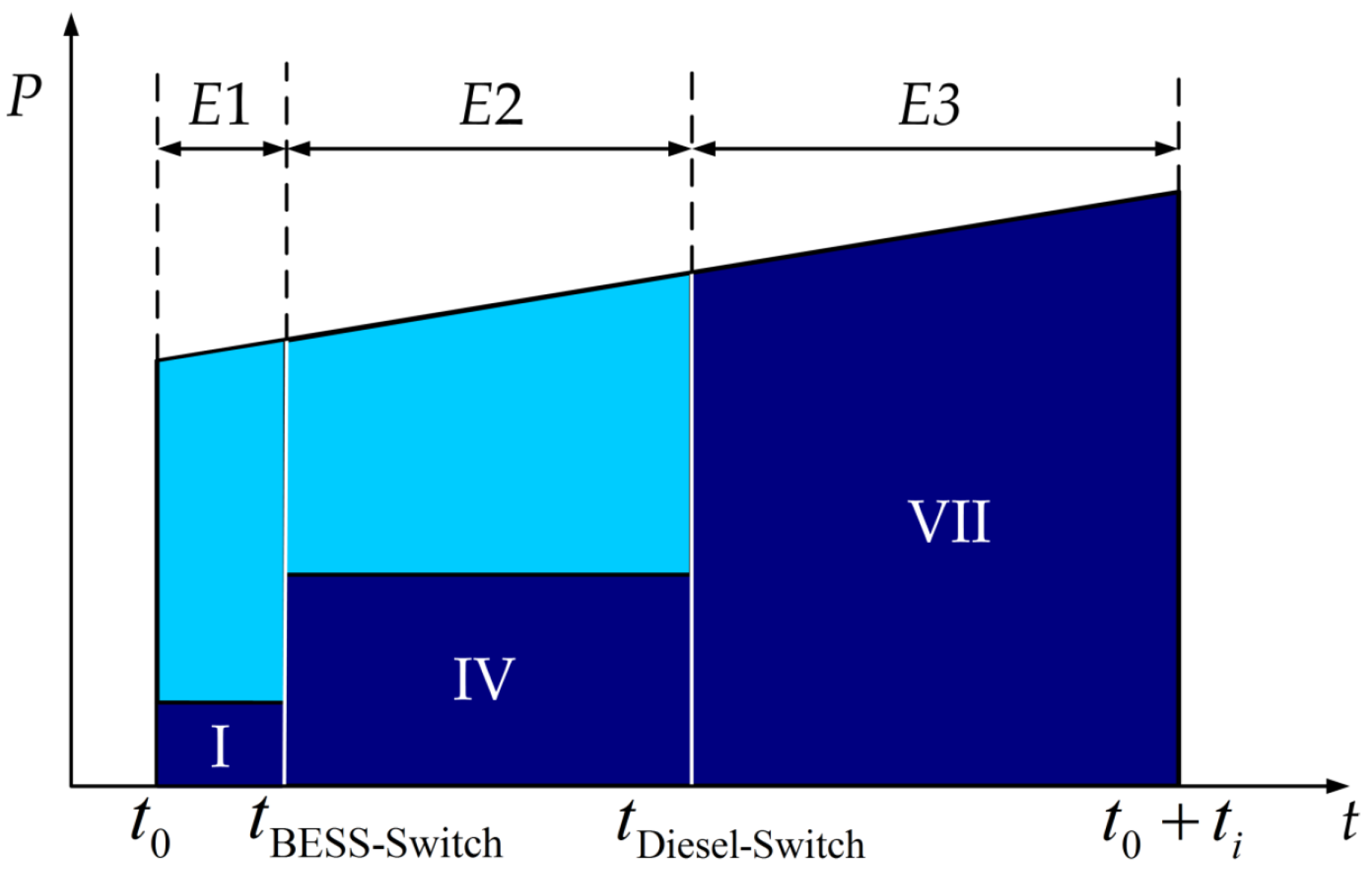
- Constrains of power supply reliability, where the unserved time of level i-th load (Tl-i) shall not exceed its corresponding limit:
- Constrains of ES discharging time span, for each discharging process, the discharging time span of SC and battery shall be limited according to the proposed strategy:
5. Case study
5.1. Parameters
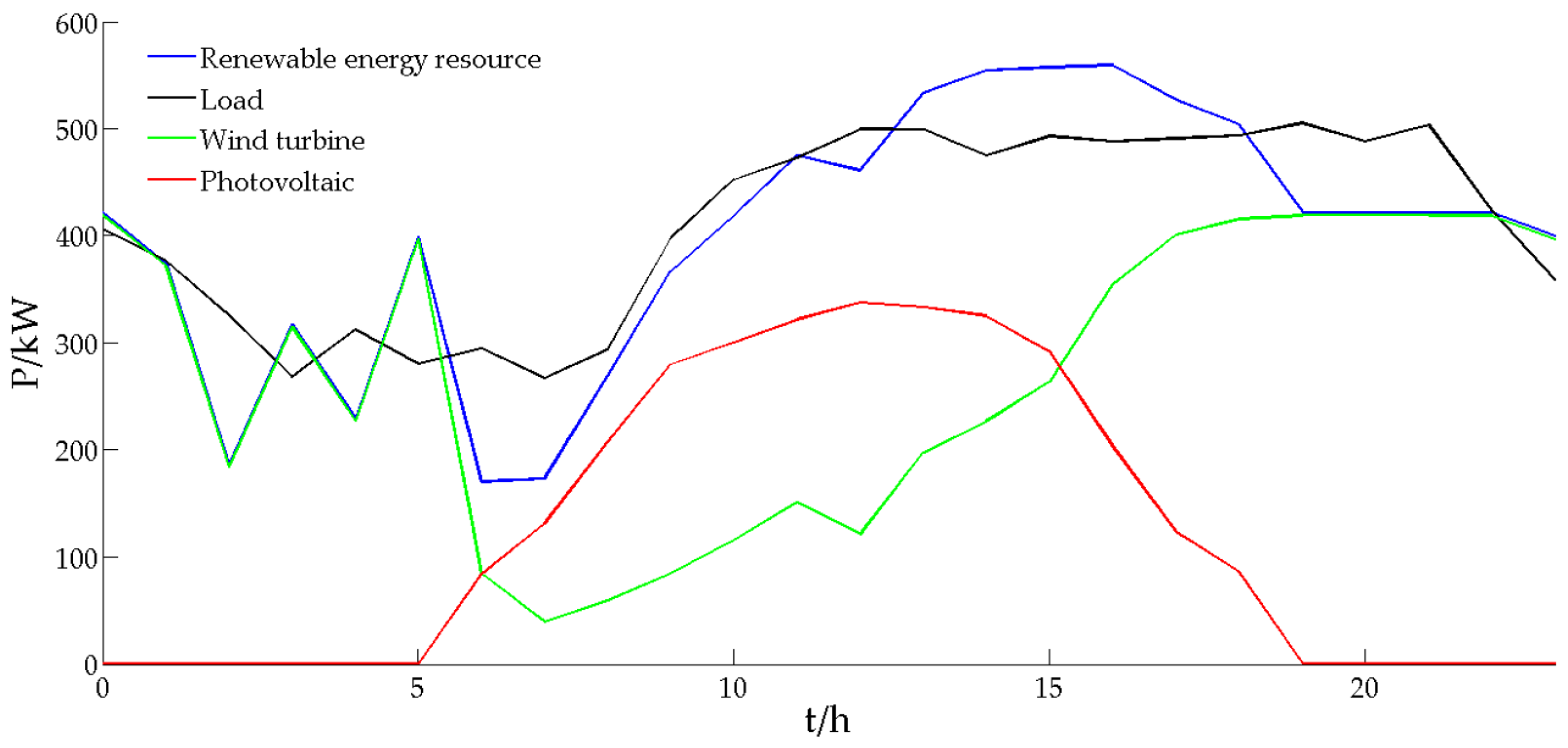
5.2. Load Character and DER Data
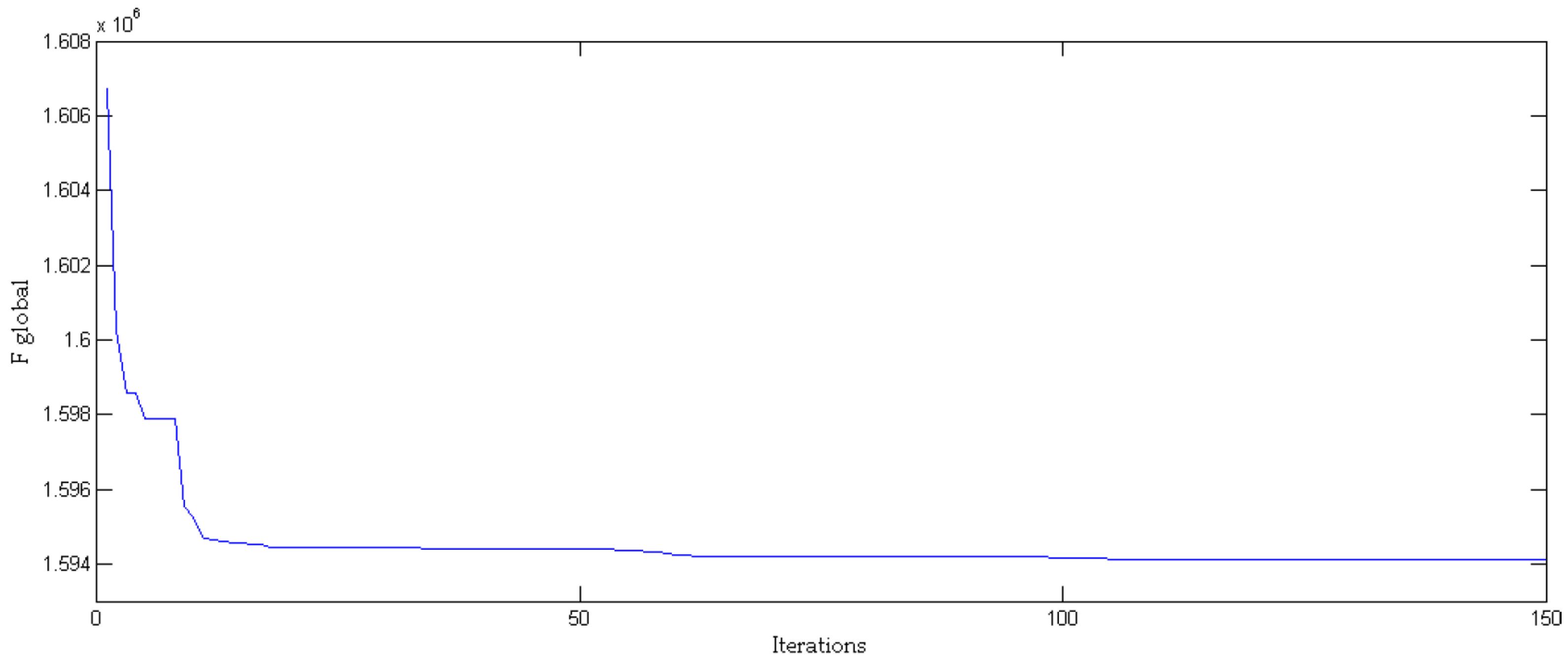
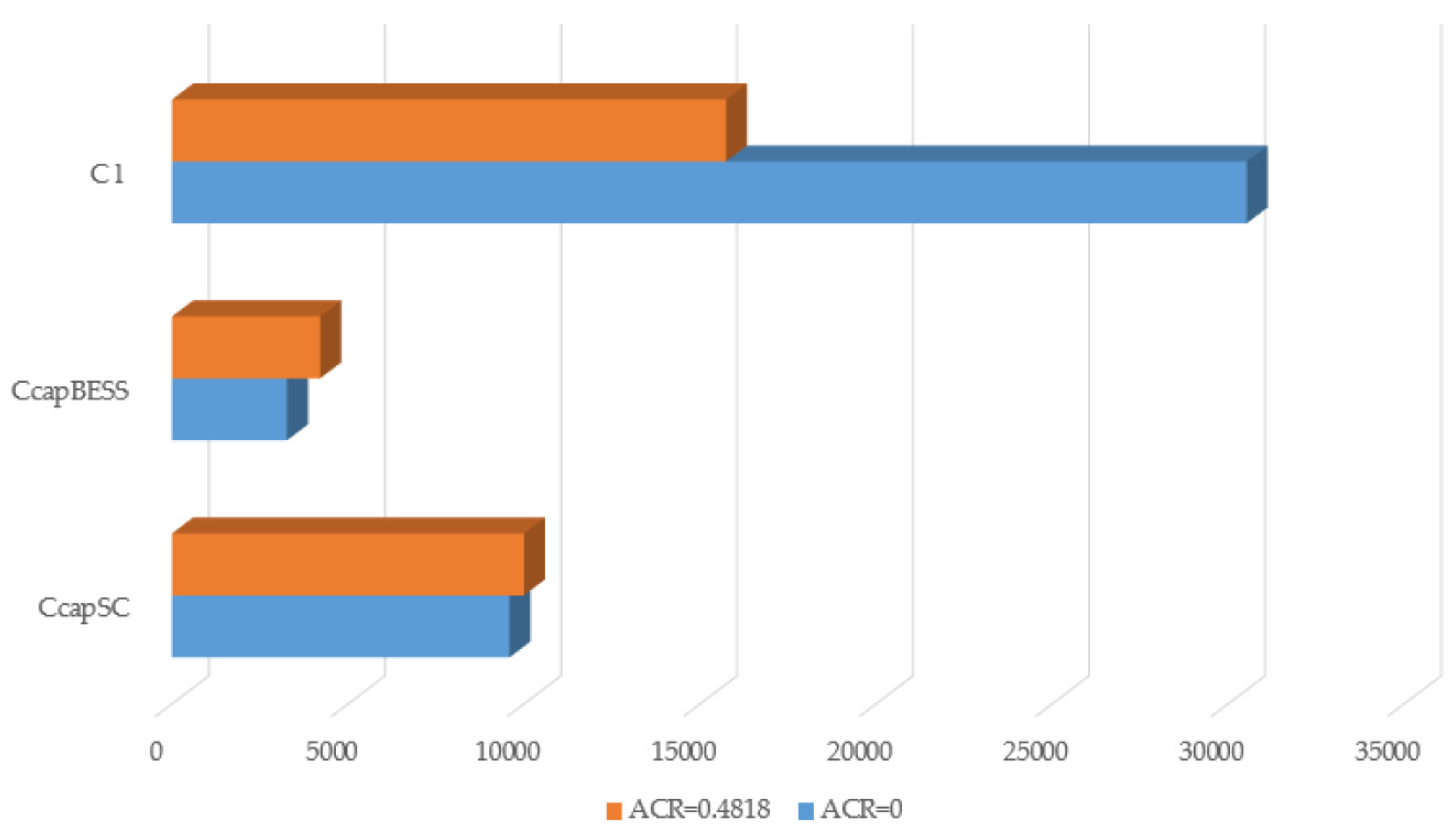
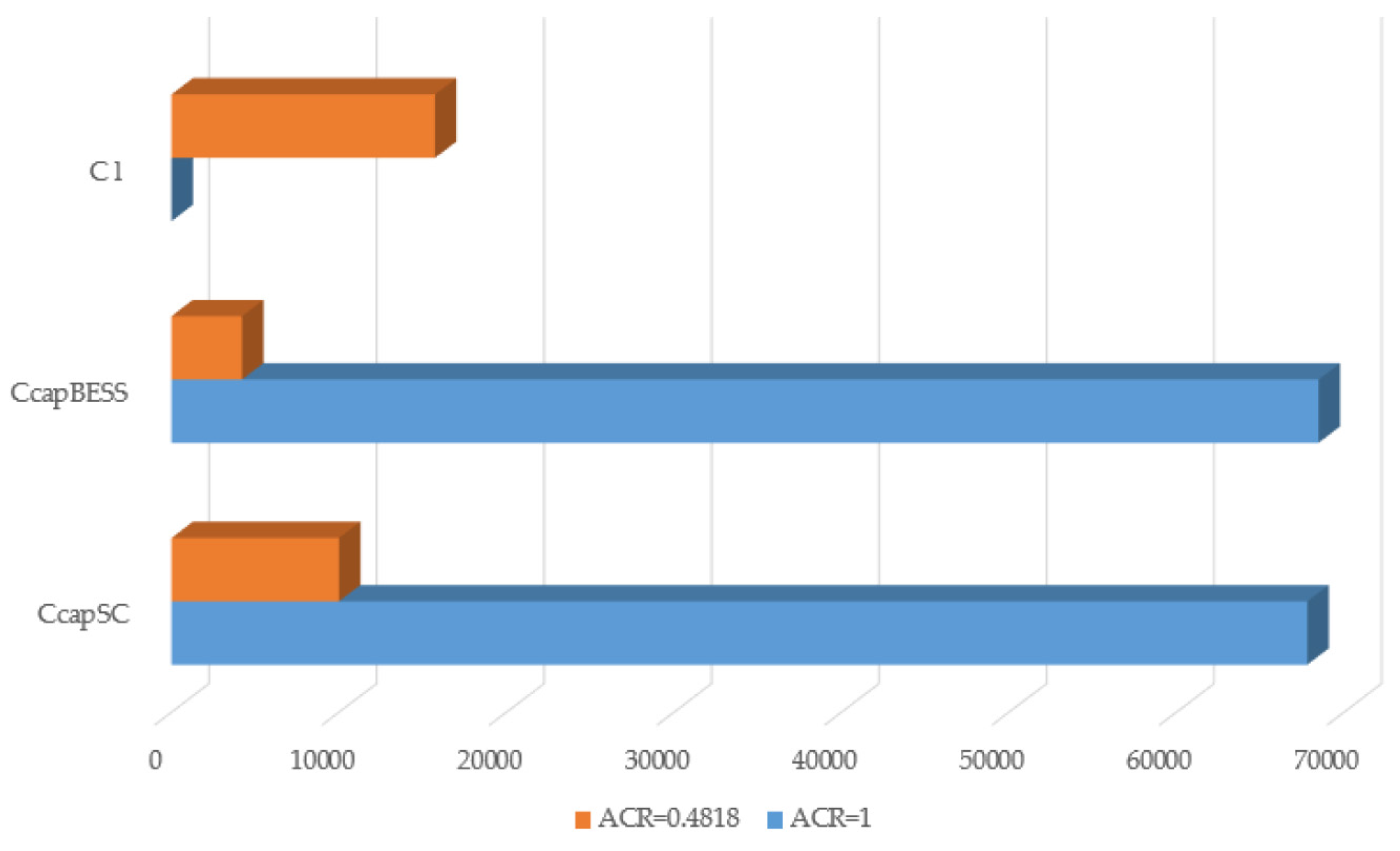
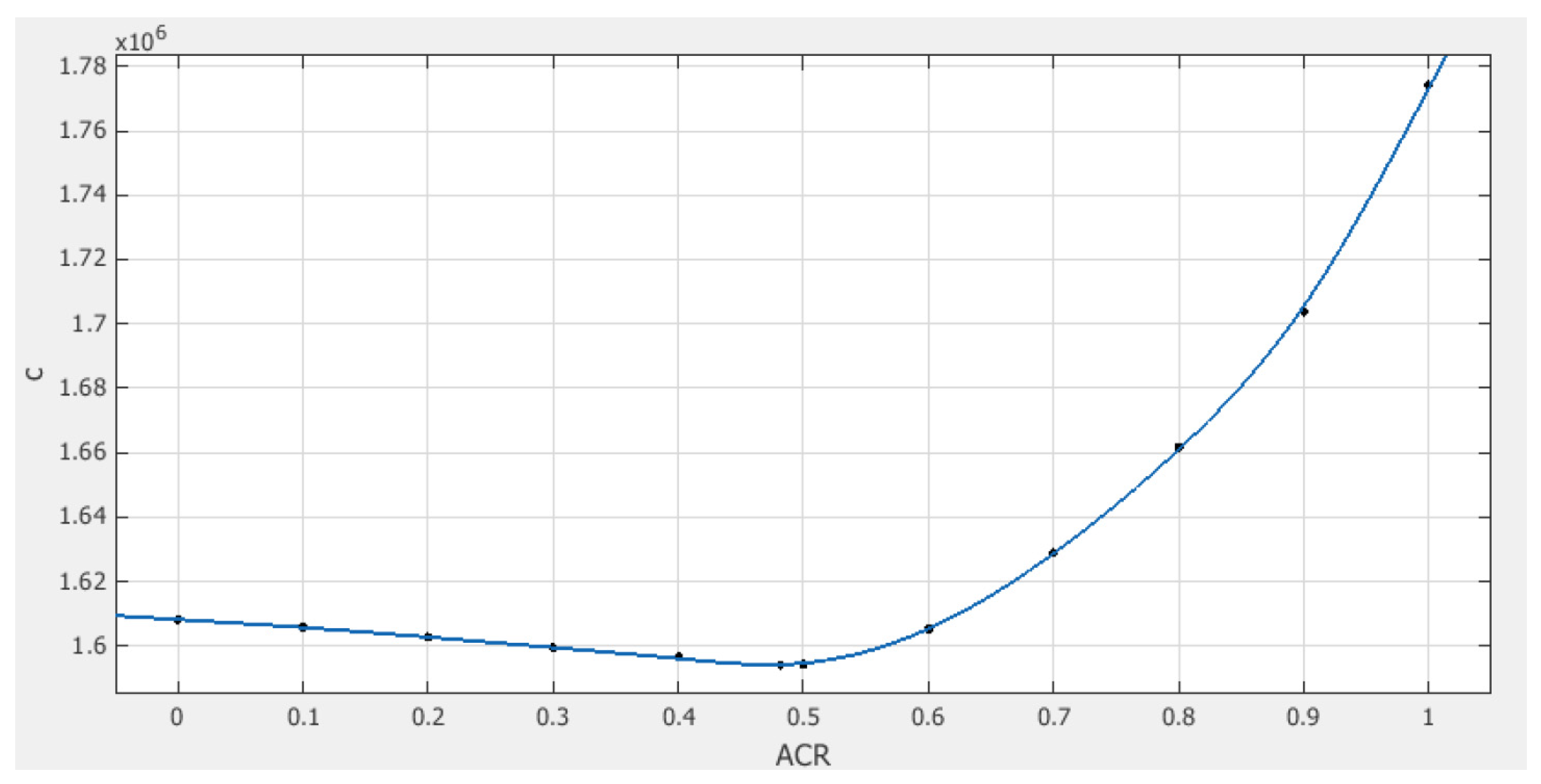
5.3. ES Device Capacity Optimization
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Meisen, P. Linking renewable energy resources: A compelling, global strategy for sustainable development. IEEE Power Eng. Rev. 1998, 18, 16–18. [Google Scholar] [CrossRef]
- Xu, Y.; Singh, C. Adequacy and economy analysis of distribution systems integrated with electric energy storage and renewable energy resources. IEEE Trans. Power Syst. 2012, 27, 2332–2341. [Google Scholar] [CrossRef]
- Marzband, M.; Moghaddam, M.M.; Akorede, M.F.; Khomeyrani, G. Adaptive load shedding scheme for frequency stability enhancement in microgrids. Electr. Power Syst. Res. 2016, 140, 78–86. [Google Scholar] [CrossRef]
- Marzband, M.; Azarinejadian, F.; Savaghebi, M.; Guerrero, J.M. An optimal energy management system for islanded microgrids based on multiperiod artificial bee colony combined with markov chain. IEEE Syst. J. 2015, 100, 1–11. [Google Scholar] [CrossRef]
- Solanki, A.; Nasiri, A.; Bhavaraju, V.; Familiant, Y.L.; Fu, Q. A new framework for microgrid management: Virtual droop control. IEEE Trans. Smart Grid. 2016, 7, 554–566. [Google Scholar] [CrossRef]
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Canizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in microgrid control. IEEE Trans. Smart Grid. 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
- Yang, X.; Du, Y.; Su, J.; Chen, X. An optimal secondary voltage control strategy for islanded microgrid. In Proceedings of the IEEE International Power Electronics and Motion Control Conference, Hefei, China, 22–26 May 2016.
- Li, J.; Li, F.; Li, X.; Liu, H.; Chen, F.; Liu, B. S-shaped droop control method with secondary frequency characteristics for inverters in microgrid. IET Gener. Transm. Dis. 2016, 10, 3385–3392. [Google Scholar] [CrossRef]
- Sun, X.; Hao, Y.; Wu, Q.; Guo, X. A multifunctional and wireless droop control for distributed energy storage units in Islanded AC microgrid applications. IEEE Trans. Power Electr. 2016, 32, 736–751. [Google Scholar] [CrossRef]
- Abdelaziz, M.M.A.; Farag, H.E. An enhanced supervisory control for islanded microgrid systems. IEEE Trans. Smart Grid. 2016, 7, 1941–1943. [Google Scholar] [CrossRef]
- Marzband, M.; Parhizi, N.; Savaghebi, M.; Guerrero, J.M. Distributed smart decision-making for a multimicrogrid system based on a hierarchical interactive architecture. IEEE Trans. Energy Conver. 2016, 31, 644–655. [Google Scholar] [CrossRef]
- Marzband, M.; Sumper, A.; Ruiz-Alvarez, A.; Dominguez-Garcia, J.L.; Tomoiaga, B. Experimental evaluation of a real time energy management system for stand-alone microgrids in day-ahead markets. Appl. Energy 2013, 106, 365–376. [Google Scholar] [CrossRef]
- Marzband, M.; Sumper, A.; Dominguez-Garcia, J.L.; Gumara-Ferret, R. Experimental validation of a real time energy management system for microgrids in islanded mode using a local day-ahead electricity market and MINLP. Energ. Convers. Manag. 2013, 76, 314–322. [Google Scholar] [CrossRef]
- Marzband, M.; Ghadimi, M.; Sumper, A.; Dominguez-Garcia, J.L. Experimental validation of a real-time energy management system using multi-period gravitational search algorithm for microgrids in islanded mode. Appl. Energy 2014, 128, 164–174. [Google Scholar] [CrossRef]
- Marzband, M.; Javadi, M.; Dominguez-Garcia, J.L.; Moghaddam, M.M. Non-cooperative game theory based energy management systems for energy district in the retail market considering DER uncertainties. IET Gener. Transm. Dis. 2016, 10, 2999–3009. [Google Scholar] [CrossRef]
- Marzband, M.; Parhizi, N.; Adabi, J. Optimal energy management for stand-alone microgrids based on multi-period imperialist competition algorithm considering uncertainties: experimental validation. INT Trans. Electr. Energy. 2016, 26, 1358–1372. [Google Scholar] [CrossRef]
- Marzband, M.; Yousefnejad, E.; Sumper, A.; Dominguez-Garcia, J.L. Real time experimental implementation of optimum energy management system in standalone Microgrid by using multi-layer ant colony optimization. Int. J. Electr. Power Energy Syst. 2016, 75, 265–274. [Google Scholar] [CrossRef]
- Zhang, D.; Li, S.; Zeng, P.; Zang, C. Optimal microgrid control and power-flow study with different bidding policies by using powerworld simulator. IEEE Trans. Sustain. Energ. 2014, 5, 282–292. [Google Scholar] [CrossRef]
- Park, S.; Lee, J.; Bae, S.; Hwang, G.; Choi, J.K. Contribution-based energy-trading mechanism in microgrids for future smart grid: A game theoretic approach. IEEE Trans. IND Electron. 2016, 63, 4255–4265. [Google Scholar] [CrossRef]
- Paschalidis, I.C.; Li, B.; Caramanis, M.C. Demand-side management for regulation service provisioning through internal pricing. IEEE Trans. Power Syst. 2012, 27, 1531–1539. [Google Scholar] [CrossRef]
- Misra, S.; Bera, S.; Ojha, T. D2P: Distributed dynamic pricing policy in smart grid for PHEVs management. IEEE Trans. Parall. Distr. 2015, 26, 702–712. [Google Scholar] [CrossRef]
- Arefifar, S.A.; Mohamed, Y.A.R.I.; El-Fouly, T.H.M. Optimum microgrid design for enhancing reliability and supply-security. IEEE Trans. Smart Grid. 2013, 4, 1567–1575. [Google Scholar] [CrossRef]
- Shadmand, M.B.; Balog, R.S. Multi-objective optimization and design of photovoltaic-wind hybrid system for community smart DC microgrid. IEEE Trans. Smart Grid. 2014, 5, 2635–2643. [Google Scholar] [CrossRef]
- Arefifar, S.A.; Mohamed, Y.A.I. DG mix, Reactive sources and energy storage units for optimizing microgrid reliability and supply security. IEEE Trans. Smart Grid. 2014, 5, 1835–1844. [Google Scholar] [CrossRef]
- Dong, J.; Gao, F.; Guan, X.; Zhai, Q.; Wu, J. Storage-reserve sizing with qualified reliability for connected high renewable penetration micro-grid. IEEE Trans. Sustain. Energ. 2016, 7, 732–743. [Google Scholar] [CrossRef]
- Yang, P.; Nehorai, A. Joint optimization of hybrid energy storage and generation capacity with renewable energy. IEEE Trans. Smart Grid. 2013, 5, 1566–1574. [Google Scholar] [CrossRef]
- Xiao, J.; Bai, L.; Li, F.; Liang, H.; Wang, C. Sizing of energy storage and diesel generators in an isolated microgrid using Discrete Fourier Transform (DFT). IEEE Trans. Sustain. Energ. 2014, 5, 907–916. [Google Scholar] [CrossRef]
- Kerdphol, T.; Fuji, K.; Mitani, Y.; Watanabe, M.; Qudaih, Y. Optimization of a battery energy storage system using particle swarm optimization for stand-alone microgrids. Int. J. Electr. Power Energy Syst. 2016, 81, 32–39. [Google Scholar] [CrossRef]
- Mitra, J.; Vallem, M.R.; Singh, C. Optimal deployment of distributed generation using a reliability criterion. IEEE Trans. IND Appl. 2016, 52, 1. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Crow, M.L.; Elmore, A.C. Optimal sizing of a vanadium redox battery system for microgrid systems. IEEE Trans. Sustain. Energ. 2015, 6, 729–737. [Google Scholar] [CrossRef]
- Abeywardana, D.W.; Hredzak, B.; Agelidis, V.; Demetriades, G. Supercapacitor sizing method for energy controlled filter based hybrid energy storage systems. IEEE Trans. Power Electr. 2017, 32, 1626–1637. [Google Scholar] [CrossRef]
- Wang, S.; Tang, Y.; Shi, J.; Gong, K.; Liu, Y.; Ren, L.; Li, J. Design and advanced control strategies of a hybrid energy storage system for the grid integration of wind power generations. IET Renew. Power Gener. 2015, 9, 89–98. [Google Scholar] [CrossRef]
- Hearn, C.S.; Lewis, M.C.; Pratap, S.B.; Hebner, R.E.; Uriarte, F.M.; Chen, D.; Longoria, R.J. Utilization of optimal control law to size grid-level flywheel energy storage. IEEE Trans. Sustain. Energ. 2013, 4, 611–618. [Google Scholar] [CrossRef]
- Specific Configuration of Power Supply and Self-emergency Power Supply for Important Power Users; GB/Z 29328-2012; Standards Press of China: Beijing, China, 2013; pp. 15–21.
- IEEE Recommended Practice for Emergency and Standby Power Systems for Industrial and Commercial Applications. Available online: http://ieeexplore.ieee.org/servlet/opac?punumber=5252 (accessed on 7 December 2016).
- Bowden, G.J.; Barker, P.R.; Shestopal, V.O.; Twidell, J.W. The weibull distribution function and wind power statistics. Wind Eng. 1983, 7, 85–98. [Google Scholar]
- Jian, C.; Wang, C.; Bo, Z.; Zhang, X. Economic operation optimization of a stand-alone microgrid system considering characteristics of energy storage system. Autom. Electric Power Syst. 2012, 36, 25–31. [Google Scholar]
- Bahramirad, S.; Reder, W.; Khodaei, A. Reliability-constrained optimal sizing of energy storage system in a microgrid. IEEE Trans. Smart Grid. 2012, 3, 2056–2062. [Google Scholar] [CrossRef]
- Atia, R.; Yamada, N. Sizing and analysis of renewable energy and battery systems in residential microgrids. IEEE Trans. Smart Grid. 2016, 7, 1–10. [Google Scholar] [CrossRef]
- Jenkins, D.P.; Fletcher, J.; Kane, D. Lifetime prediction and sizing of lead-acid batteries for microgeneration storage applications. IET Renew. Power Gen. 2008, 2, 191–200. [Google Scholar] [CrossRef]
- Kaiser, R. Optimized battery-management system to improve storage lifetime in renewable energy systems. J. Power Sources. 2007, 168, 58–65. [Google Scholar] [CrossRef]
- Dufo-López, R.; Bernal-Agustín, J.L. Multi-objective design of PV–wind–diesel–hydrogen–battery systems. Renew. Energ. 2008, 33, 2559–2572. [Google Scholar] [CrossRef]
- Wacker, G.; Billinton, R. Customer cost of electric service interruptions. Proc. IEEE. 1989, 77, 919–930. [Google Scholar] [CrossRef]
- Skarstein, O.; Uhlen, K. Design considerations with respect to long-term diesel saving in wind/diesel plants. Wind Eng. 1989, 13, 72–87. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November 1995; pp. 1942–1948.
- Selvakumar, A.I.; Thanushkodi, K. A new particle swarm optimization solution to nonconvex economic dispatch problems. IEEE Trans. Power Syst. 2007, 22, 42–51. [Google Scholar] [CrossRef]
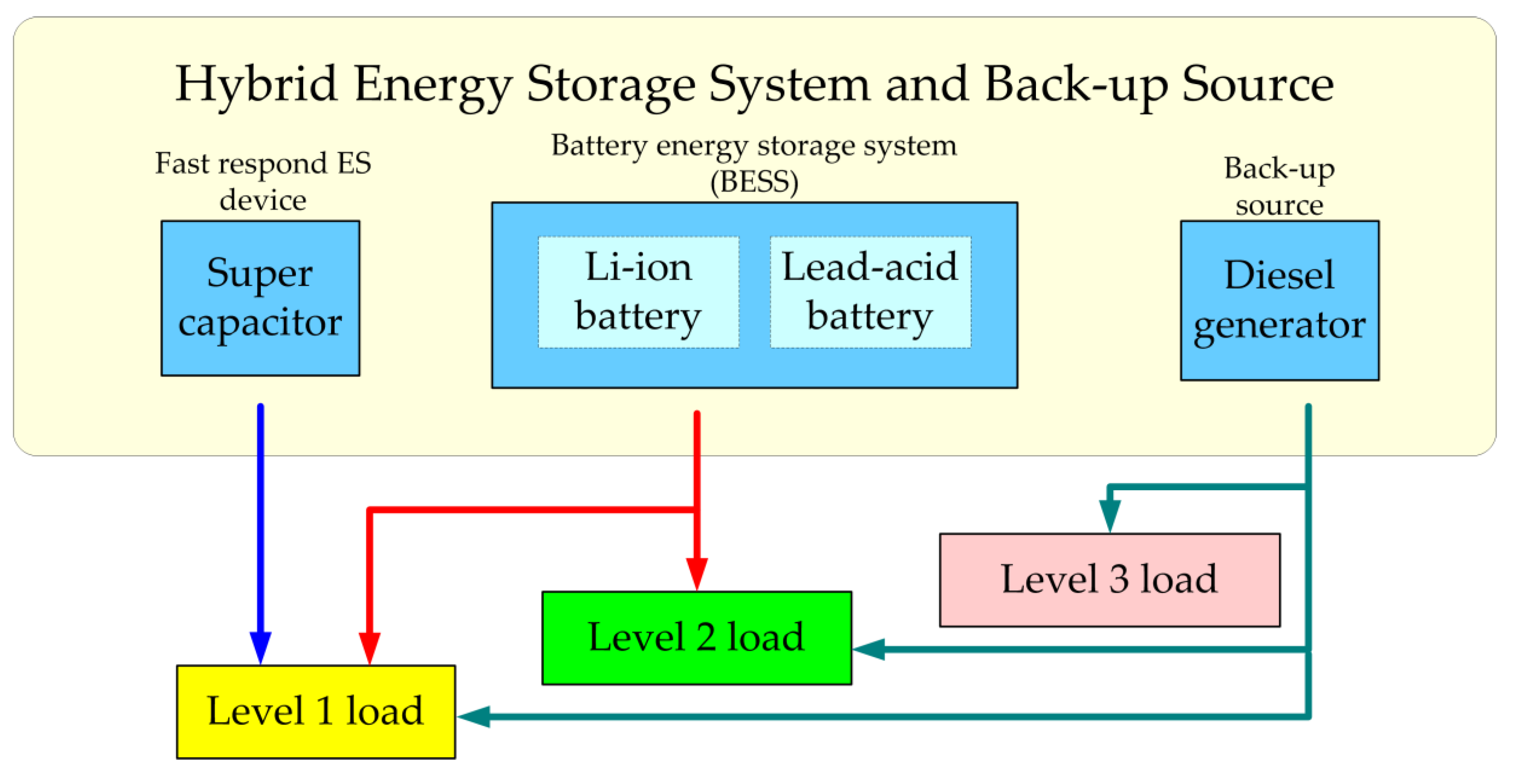
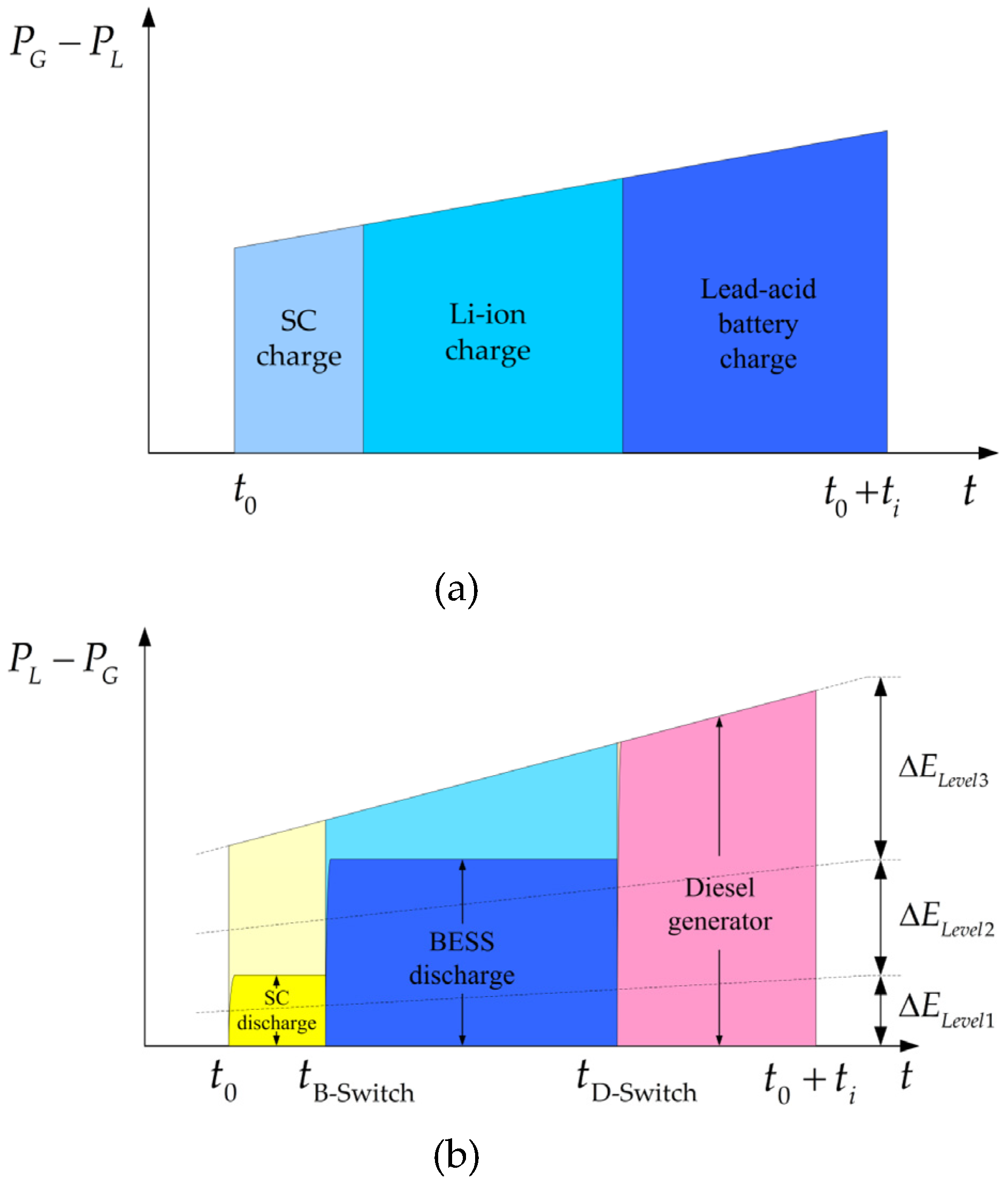
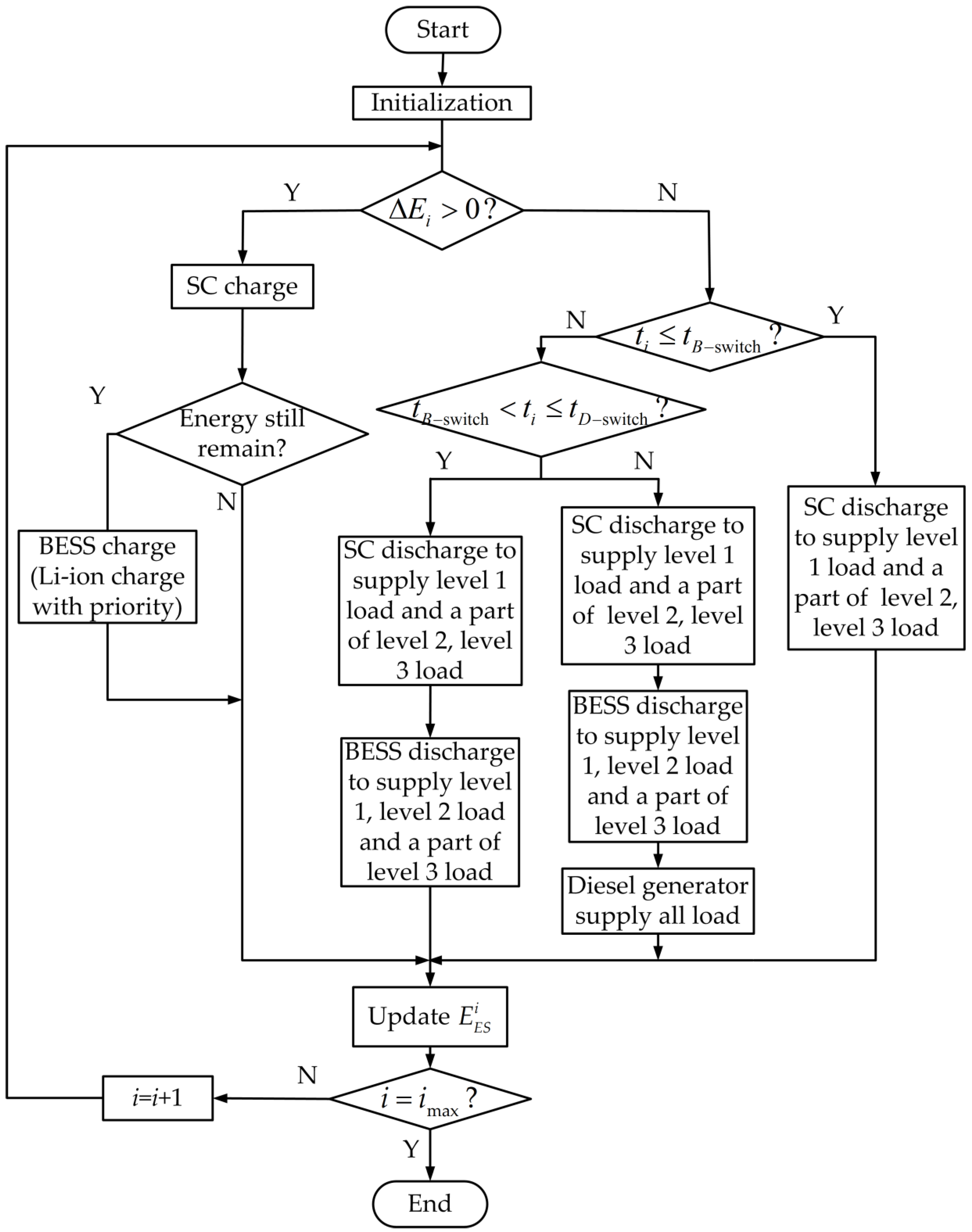
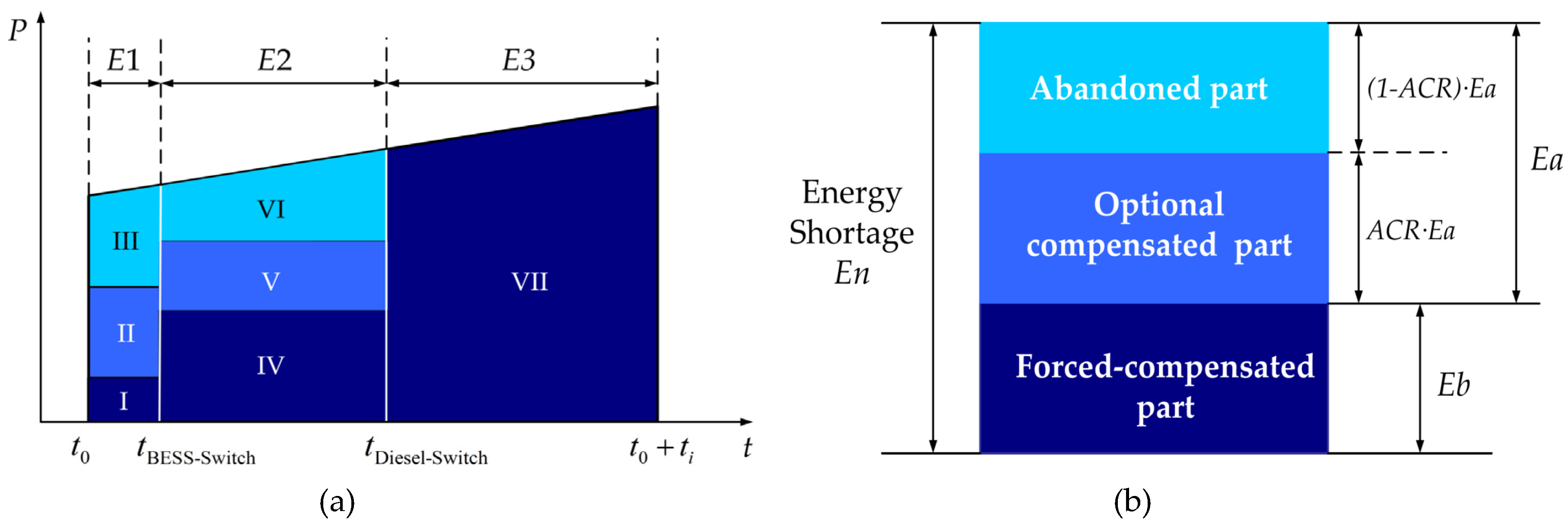
| ES Type | Energy Density (Wh/kg) | Power Density (W/kg) | Investment Cost ($/kWh) | Cycle Times | Response Speed | |
|---|---|---|---|---|---|---|
| Energy type | Lead-acid battery | 30~50 | 75~300 | 70~420 | 103 | medium |
| Li-ion battery | 75~250 | 150~315 | 280~1400 | 103 | medium | |
| Power type | Super capacitor | 0.1~15 | 500~5000 | 420~5600 | 105 | fast |
| Flywheel | 5~130 | 400~1600 | 1400~4900 | 106 | fast | |
| SMES | 0.5~5 | 500~2000 | 980~9800 | 106 | fast | |
| Load Grade | Level 1 | Level 2 | Level 3 |
|---|---|---|---|
| Description | Power supply interrupt may cause: casualty; extremely severe pollution; poisoning, explosion or fire; extremely severe political effect; extremely severe economic loss; massive social chaos. | Power supply interrupt may cause: serious pollution; serious political effect; serious economic loss; areal social chaos. | Load not belonging to first class and level 2 load |
| Supply requirement | Must be supplied without interruption | Should be supplied with minimal interruption | Can be interrupted if necessary |
| Specific Type of Level 1 Load | Electrical Equipment | tinterrupt |
|---|---|---|
| Electronics manufacturing (Chip manufacturing) | Emergency illumination | ≤1 min |
| Fire protection facilities | ≤1 min | |
| Information Technology Computer Integrated Manufacturing (IT CIM) equipment | ≤200 ms | |
| Automatic board feeder | ≤200 ms | |
| Tin scraping machine | ≤200 ms | |
| Solder paste printer | ≤200 ms | |
| High-speed chip mounter | ≤200 ms | |
| High-speed welding furnace | ≤200 ms |
| Types of Level 1 Load | tinterrupt | |
|---|---|---|
| Industrial load | Mining | ≤200 ms |
| Chemical industry | ≤200 ms | |
| Metallurgic industry | ≤1 s | |
| Electronics manufacturing | ≤200 ms | |
| Social load | Communication | ≤800 ms |
| Radio and television | ≤800 ms | |
| Information safety | ≤800 ms | |
| Public services | ≤1 min | |
| Transportation | ≤800 ms | |
| Medical services | ≤0.5 s | |
| Assembly occupancies | ≤1 min | |
| Stage | Component | Stage | Component | Stage | Component | |||
|---|---|---|---|---|---|---|---|---|
| E1 | I | Level 1 load | E2 | IV | Level 1 and level 2 load | E3 | VII | Level 1, level 2 and level 3 load |
| II | Part of Level 2 and Level 3 load | V | Part of Level 3 load | |||||
| III | The rest of Level 2 and Level 3 load | VI | The rest of Level 3 load | |||||
| Distributed Energy Resources (DERs) | Parameter | Value |
|---|---|---|
| Wind turbine (WT) | Unit price | $100,000 |
| Rated power | 30 kW | |
| Rated wind speed | 12 m/s | |
| Cut-in wind speed | 3 m/s | |
| Cut-out wind speed | 24 m/s | |
| Photovoltaic (PV) unit | Unit price | $90 |
| Rated power | 0.2 kWp | |
| Rated sunlight intensity | 1 kW/m2 | |
| Ratedtemperature | 25 °C | |
| Power temperature coefficient | −0.45% | |
| Diesel generator | Unit price | $5000 |
| Rated power | 100 kW | |
| Coefficient A | 0.246 L/kWh | |
| Coefficient B | 0.08145 L/kWh 1 | |
| Super capacitor (SC) | Unit price | $7200 |
| Unit capacity | 1 kWh | |
| Li-ion battery | Unit price | $2.1 |
| Unit capacity | 3.2 V 3000 mAH | |
| Lead-acid battery | Unit price | $184 |
| Unit capacity | 2 V 1000 Ah | |
| Coefficients in lifetime model | a1 = 0, a2 = 7753, a3 = −7.263, a4 = 2603, a5 = −0.8455 2 |
| Time | Wind Speed | Sunlight Intensity | Temperature | Time | Wind Speed | Sunlight Intensity | Temperature |
|---|---|---|---|---|---|---|---|
| (m/s) | (KW/m2) | (°C) | (m/s) | (KW/m2) | (°C) | ||
| 0 | 12 | 0 | 16 | 12 | 6.7 | 0.83 | 18.4 |
| 1 | 10.4 | 0 | 15.2 | 13 | 7.9 | 0.82 | 18.6 |
| 2 | 7.7 | 0 | 14.5 | 14 | 8.3 | 0.8 | 18.6 |
| 3 | 9.5 | 0 | 14.4 | 15 | 8.8 | 0.72 | 19.5 |
| 4 | 8.3 | 0 | 13.8 | 16 | 10.1 | 0.5 | 19.2 |
| 5 | 10.9 | 0 | 13.3 | 17 | 11 | 0.303 | 18.6 |
| 6 | 6 | 0.2 | 13.1 | 18 | 11.5 | 0.21 | 18 |
| 7 | 4.8 | 0.315 | 13.5 | 19 | 12 | 0 | 17.3 |
| 8 | 5.4 | 0.5 | 14.2 | 20 | 12 | 0 | 17.1 |
| 9 | 6 | 0.68 | 15.7 | 21 | 12 | 0 | 16.9 |
| 10 | 6.6 | 0.735 | 17.1 | 22 | 11.8 | 0 | 16.3 |
| 11 | 7.2 | 0.79 | 18.2 | 23 | 10.9 | 0 | 15.8 |
| Device | Capacity | Lifetime/a | Times of Replacement | Total Cost/$ |
|---|---|---|---|---|
| Wind turbine | 450 kW | 20 | 0 | 1,400,000 |
| Photovoltaic | 48 kW | 20 | 0 | 21,600 |
| Super capacitor | 1.38 kWh | 20 | 0 | 10,000 |
| Li-ion battery | 5.73 kWh | 5.87 | 3 | 1722 |
| Lead-acid battery | 27 kWh | 7.13 | 2 | 2490 |
| Diesel generator | 100 kW | 20 | 0 | 5000 |
| Device | Capital Cost/$ | Operation & Maintenance/$ (Considering Pollutant Emission) | Recycling Profit/$ |
|---|---|---|---|
| WT | 1,400,000 | 109,920 | −39,920 |
| PV | 21,600 | 1696 | −616 |
| SC | 10,000 | 393 | −285 |
| BESS | 4212 | 1662 | −346 |
| Diesel | 5000 | 65,219 | −143 |
| LCC Component | Cost/$ |
|---|---|
| Ccap | 1,440,812 |
| Com + Cp | 178,879 |
| Cr | −41,310 |
| Cl | 15,746 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Chen, Y.; Luo, Y.; Zhao, G.; Jin, X. Optimized Planning of Power Source Capacity in Microgrid, Considering Combinations of Energy Storage Devices. Appl. Sci. 2016, 6, 416. https://doi.org/10.3390/app6120416
Liu Z, Chen Y, Luo Y, Zhao G, Jin X. Optimized Planning of Power Source Capacity in Microgrid, Considering Combinations of Energy Storage Devices. Applied Sciences. 2016; 6(12):416. https://doi.org/10.3390/app6120416
Chicago/Turabian StyleLiu, Zifa, Yixiao Chen, Ya Luo, Guankun Zhao, and Xianlin Jin. 2016. "Optimized Planning of Power Source Capacity in Microgrid, Considering Combinations of Energy Storage Devices" Applied Sciences 6, no. 12: 416. https://doi.org/10.3390/app6120416
APA StyleLiu, Z., Chen, Y., Luo, Y., Zhao, G., & Jin, X. (2016). Optimized Planning of Power Source Capacity in Microgrid, Considering Combinations of Energy Storage Devices. Applied Sciences, 6(12), 416. https://doi.org/10.3390/app6120416