Further Investigation on Laminar Forced Convection of Nanofluid Flows in a Uniformly Heated Pipe Using Direct Numerical Simulations
Abstract
:1. Introduction
2. Numerical Approach
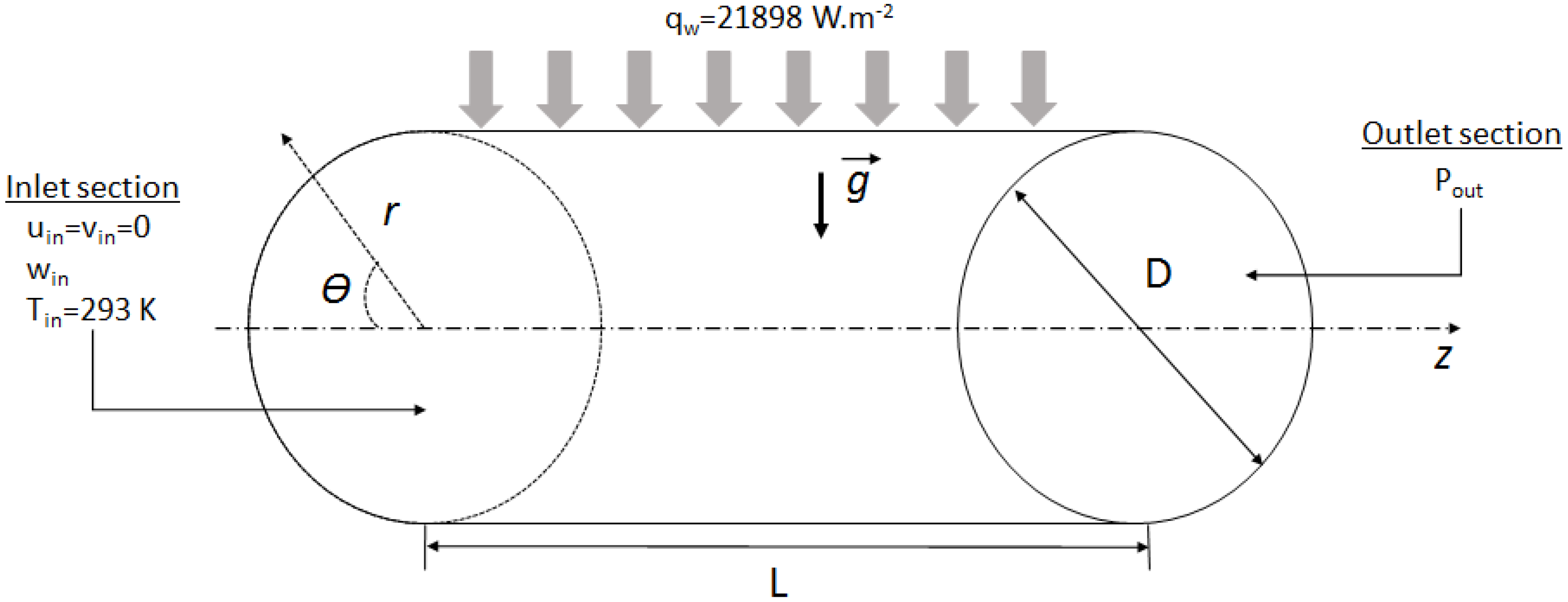
2.1. Geometrical Modeling
2.2. Numerical Method
2.3. Fluid Properties and Two-Phase Modeling
2.3.1. Water Properties
2.3.2. Single-Phase Model
2.3.3. Mixture Model
- Conservation of mass:
- Conservation of momentum:where the mixture velocity, density and viscosity are respectively:
- The drift velocity of the kth phase writes:
- Conservation of energy:
- Conservation of the volume fraction in nanoparticles:
- The slip velocity is defined as the velocity of a second phase (np: nanoparticles) relative to the primary phase (bf: base fluid):
- The drift velocity is related to the relative velocity by:
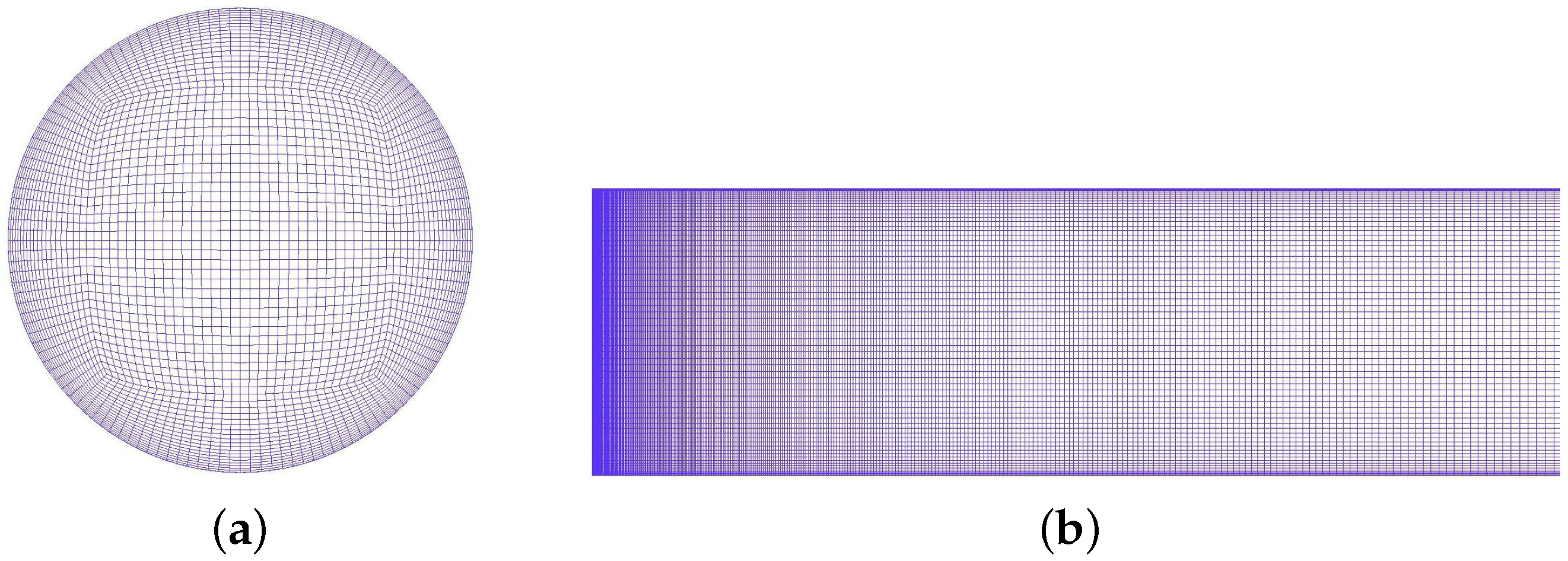
2.3.4. Boundary Conditions and Grid Resolution
- At the inlet ():
- On the pipe wall ():
- At the pipe outlet, the gauge pressure is set equal to zero and all the normal diffusion fluxes and the mass balance correction are applied.
3. Validation of the Numerical Model
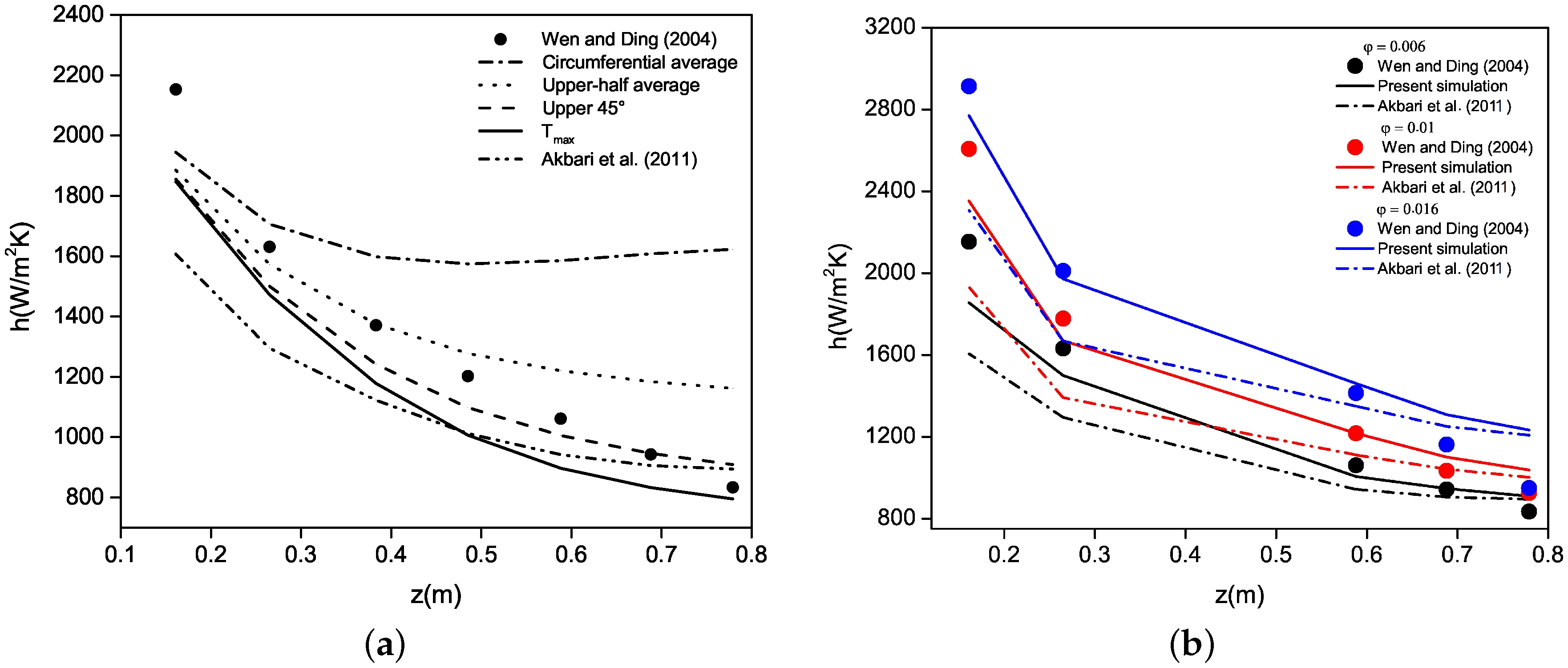
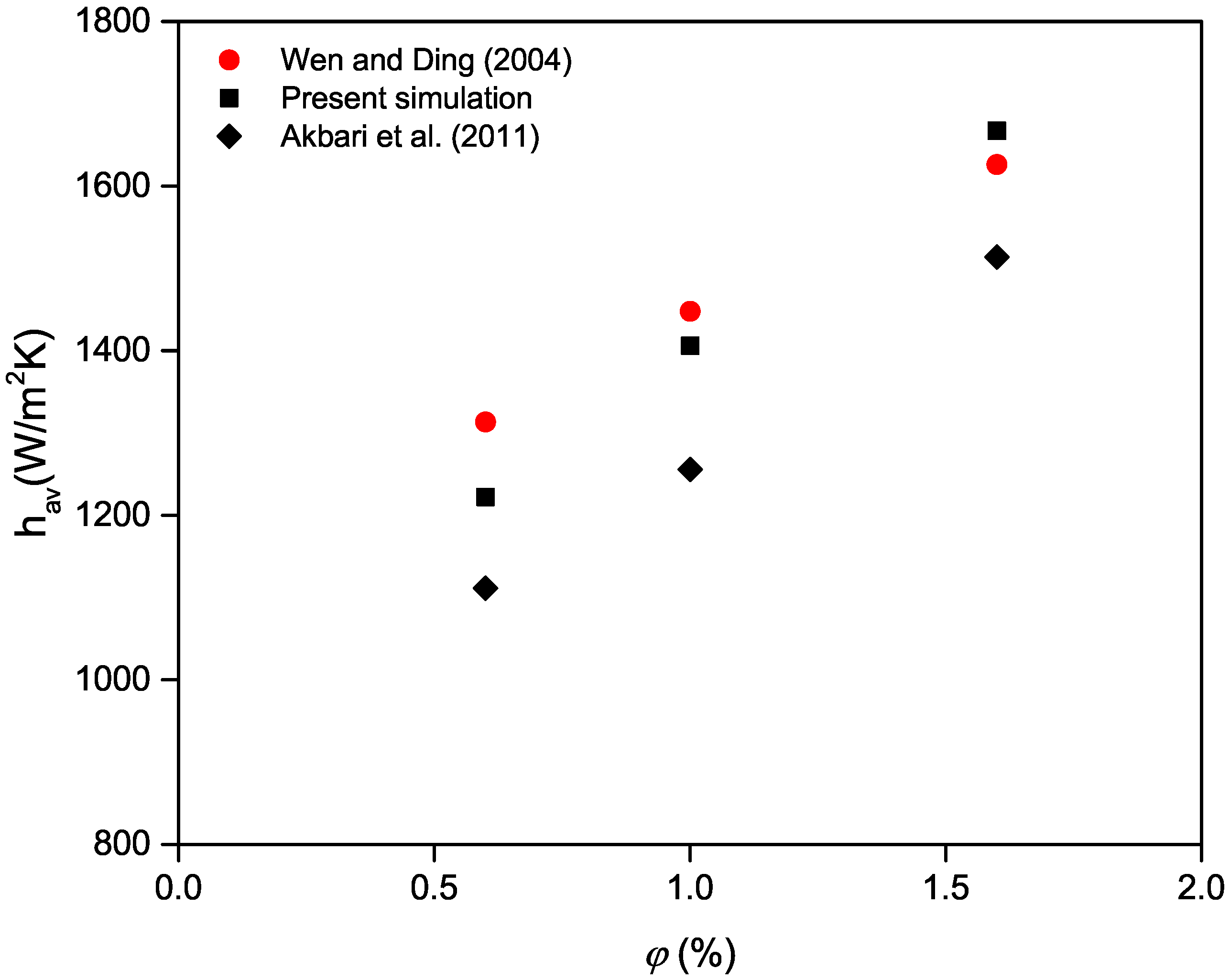
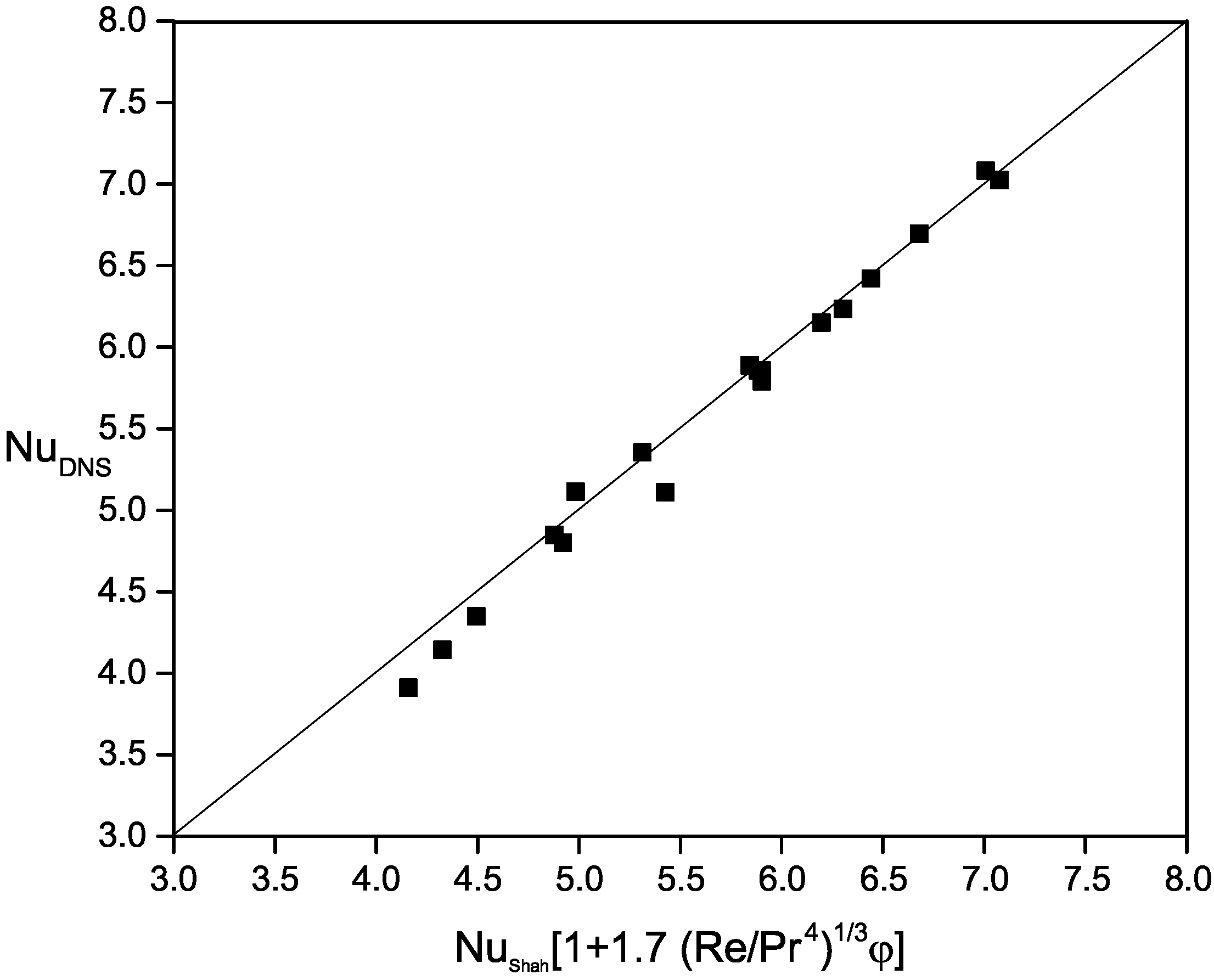
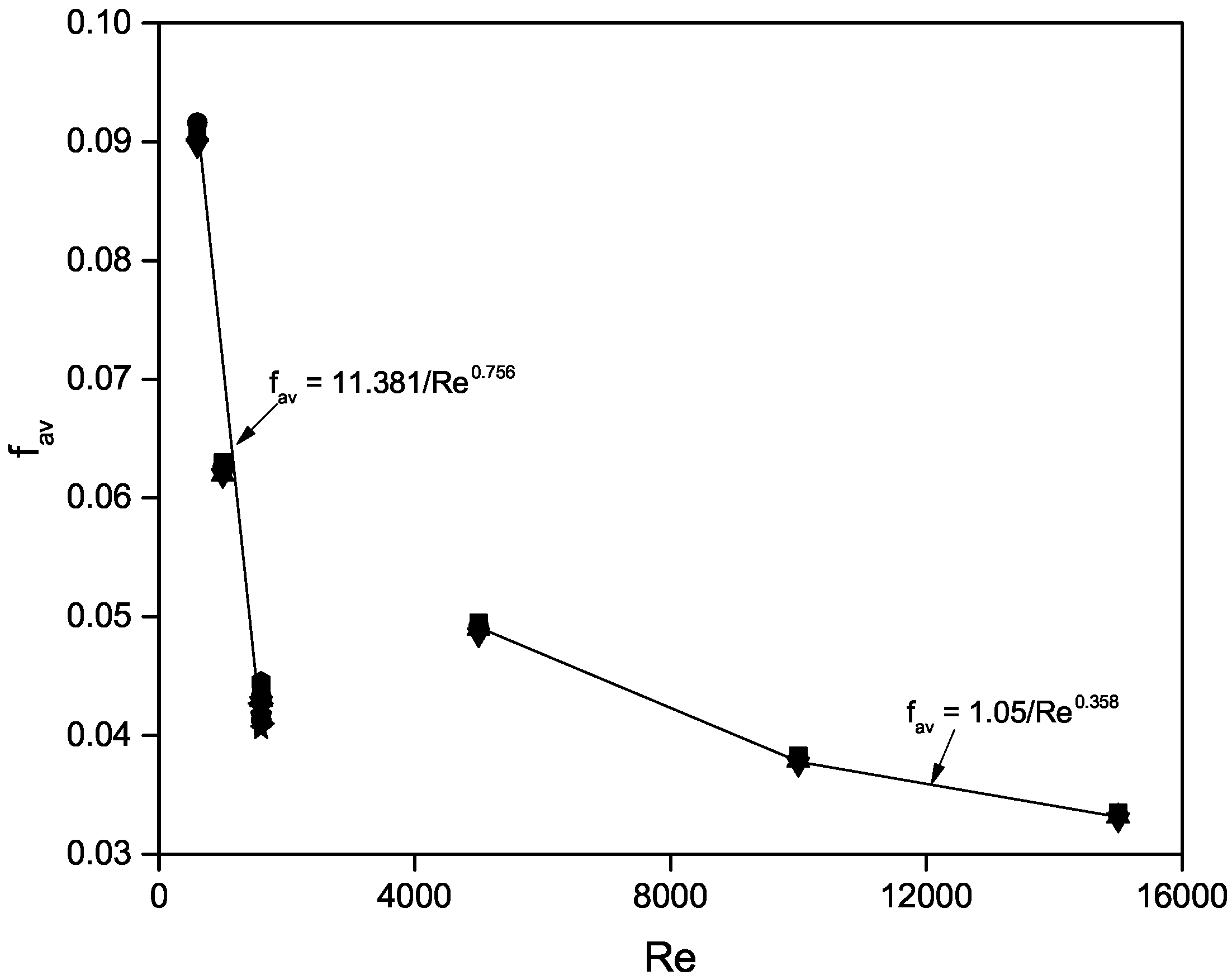
3.1. Performances of the Mixture Model
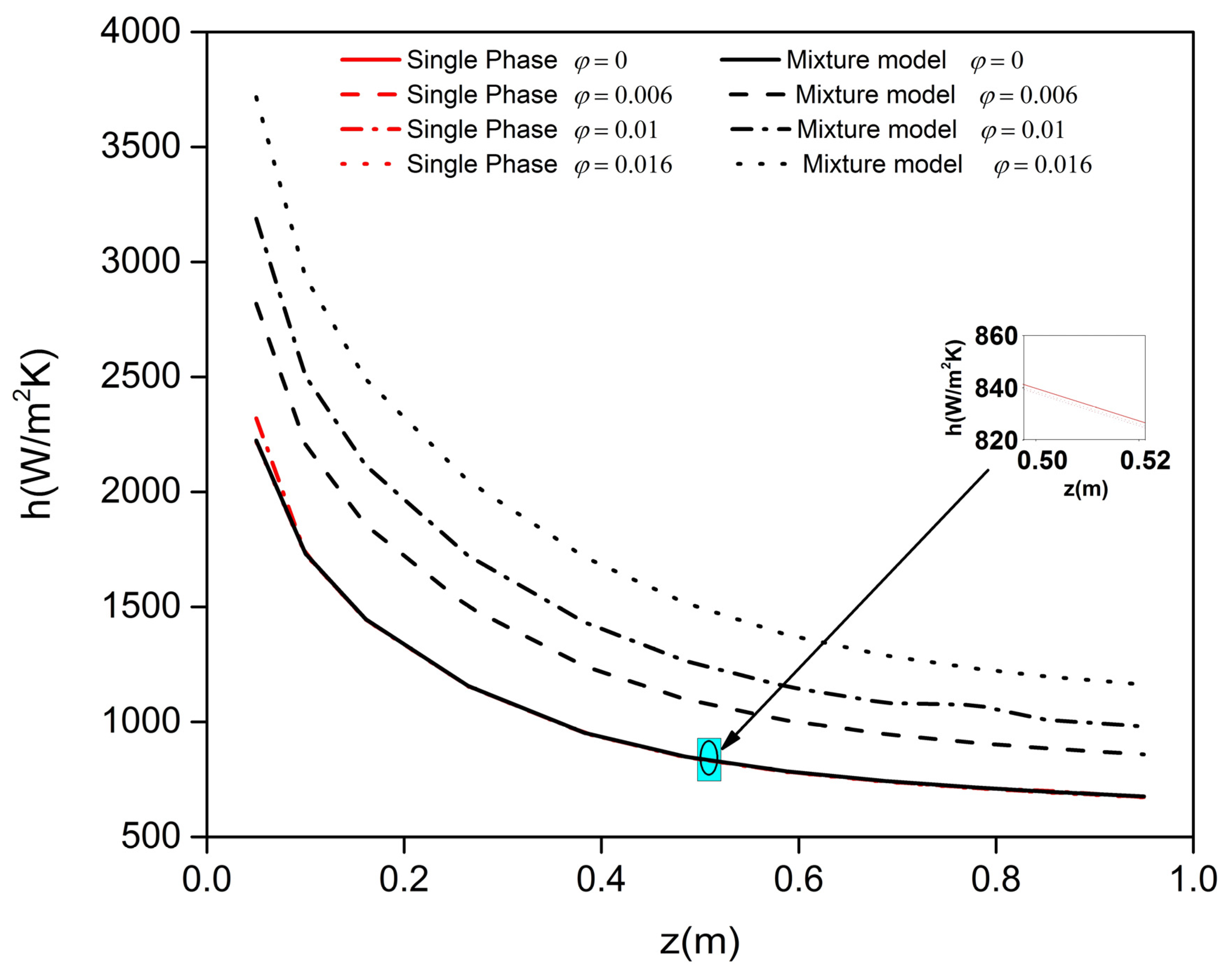
3.2. Comparative Analysis of Single-Phase and Mixture Models
4. Results and Discussion
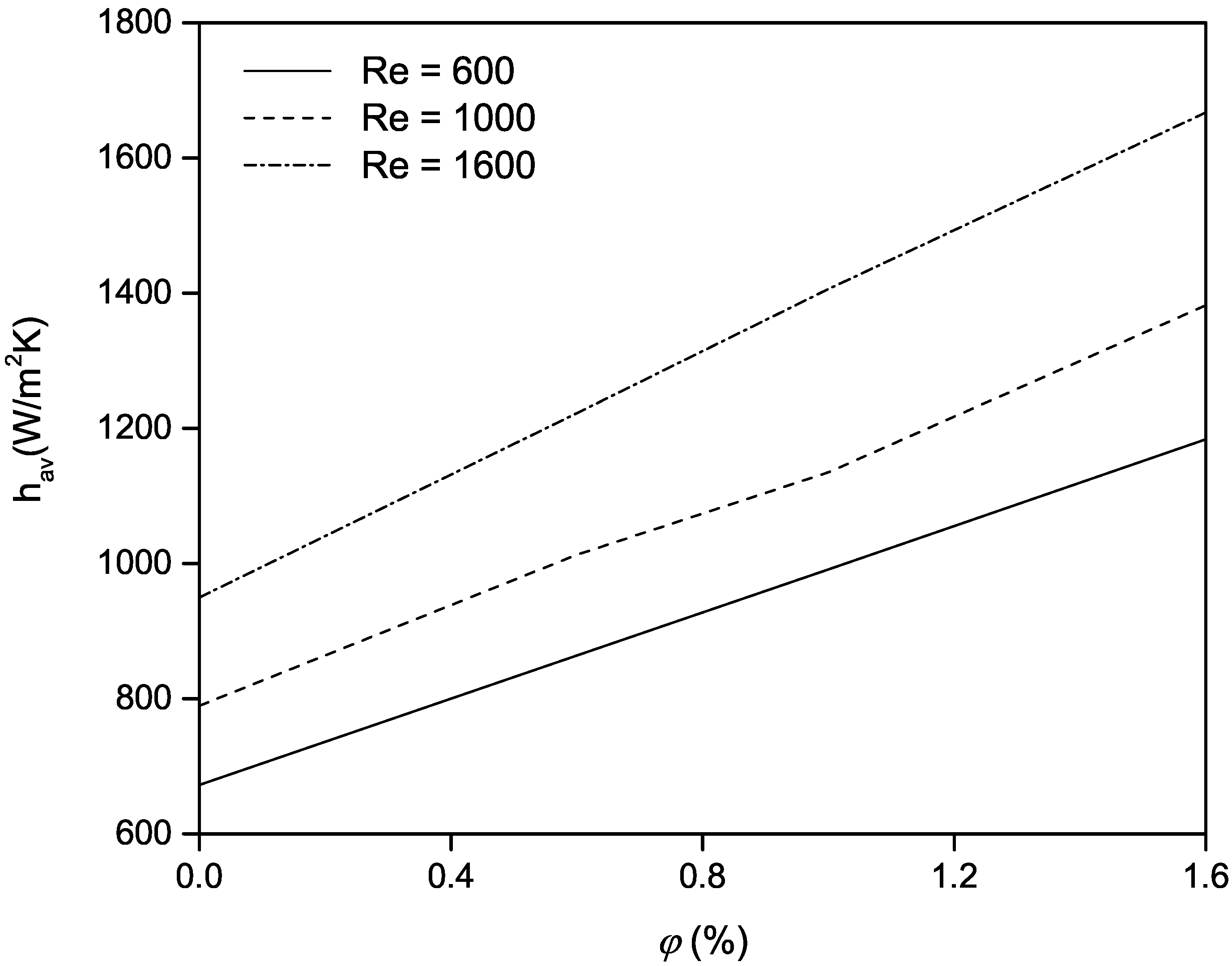
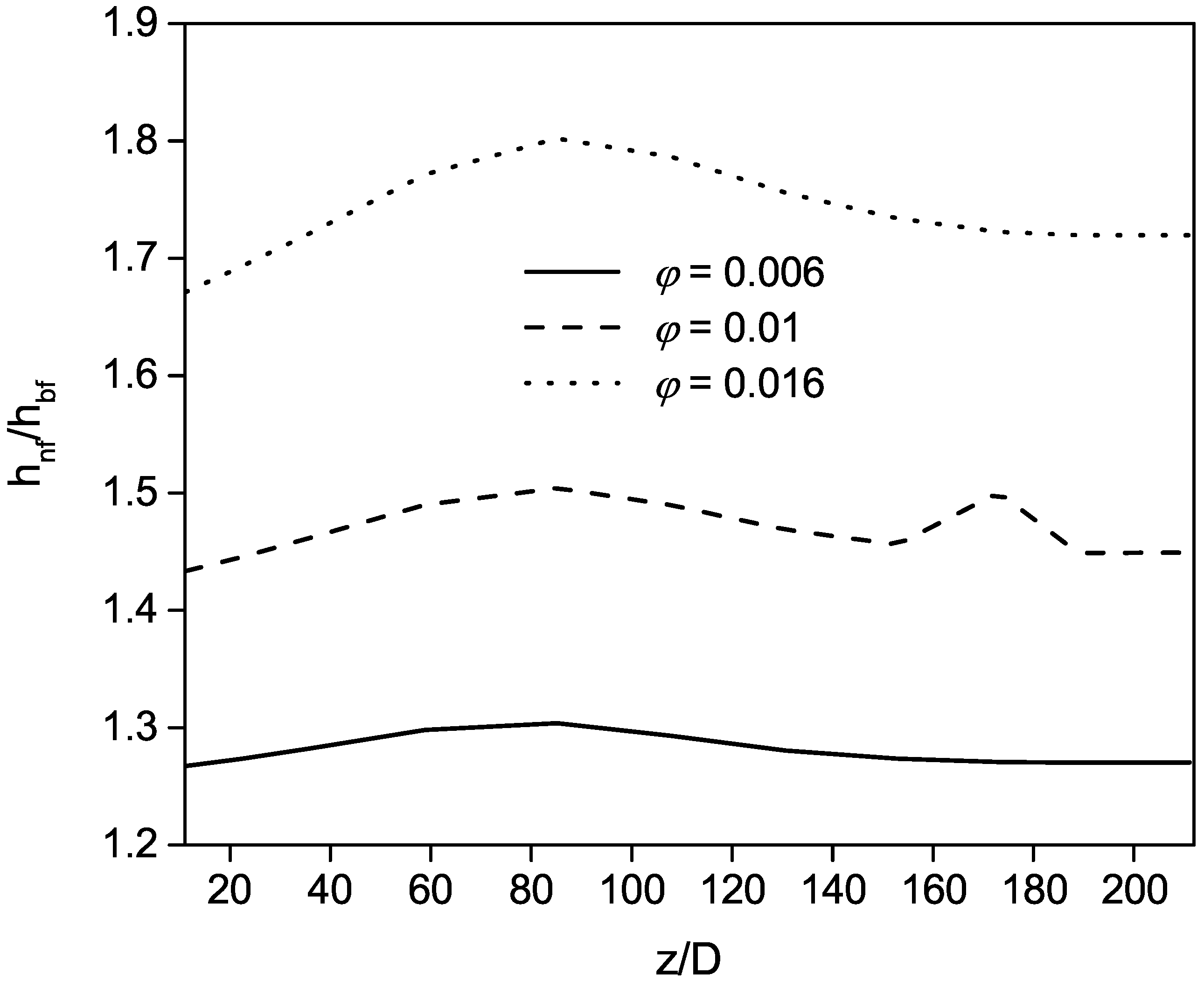
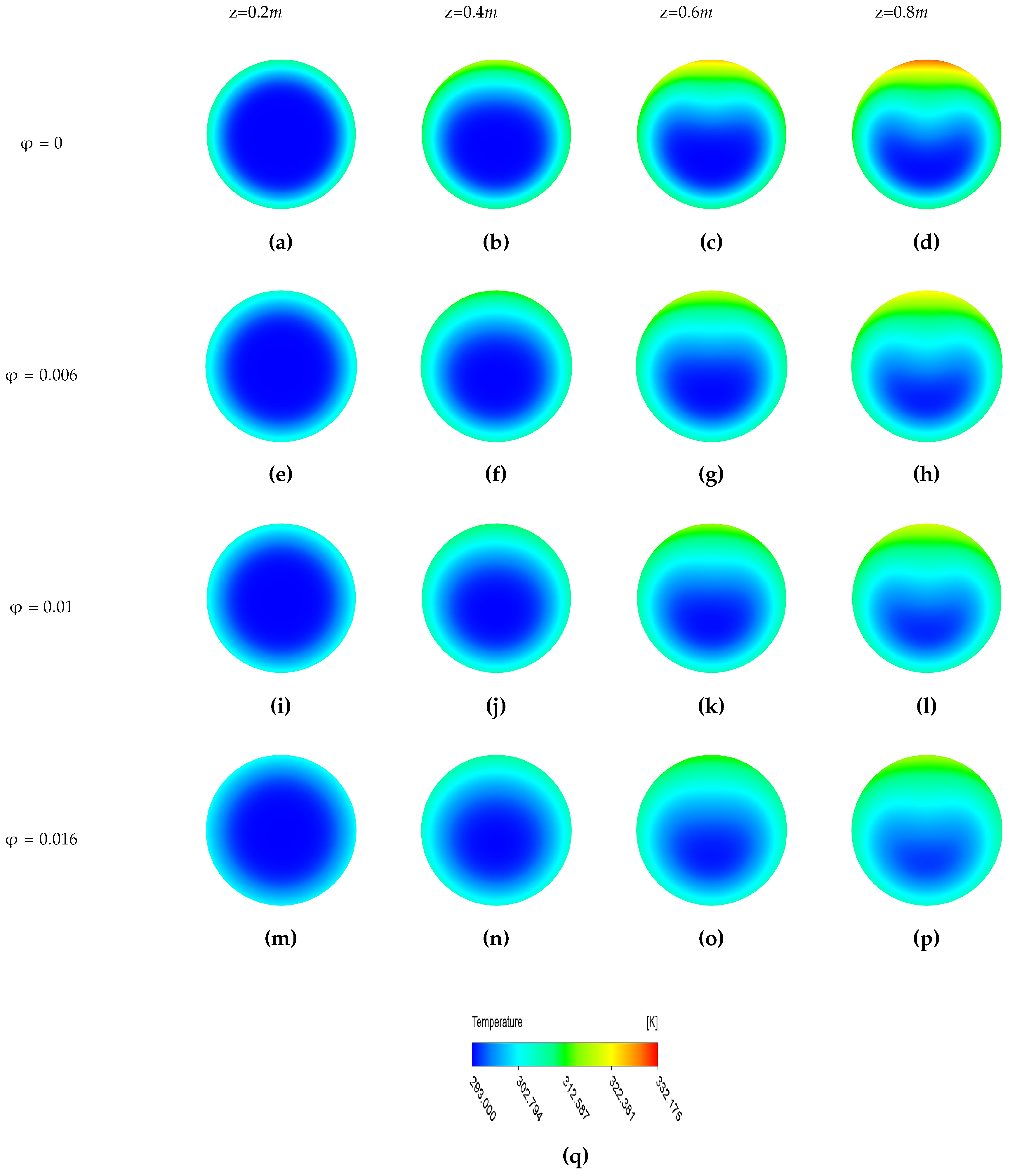
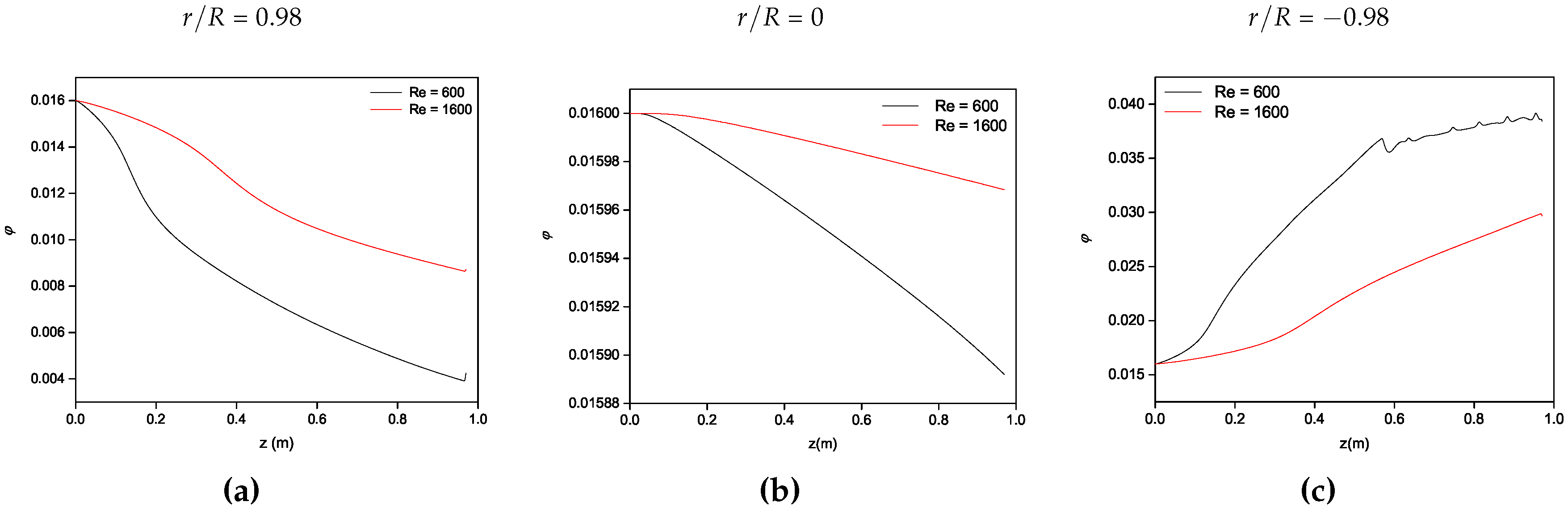
4.1. Influence of the Volume Fraction of Nanoparticles and Reynolds Number for /Water-Based Nanofluids
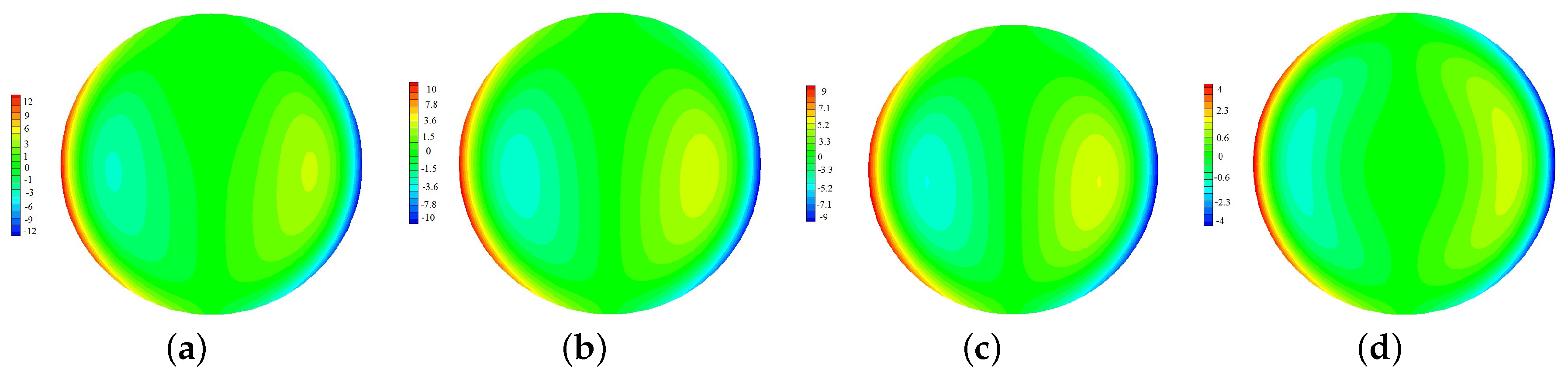
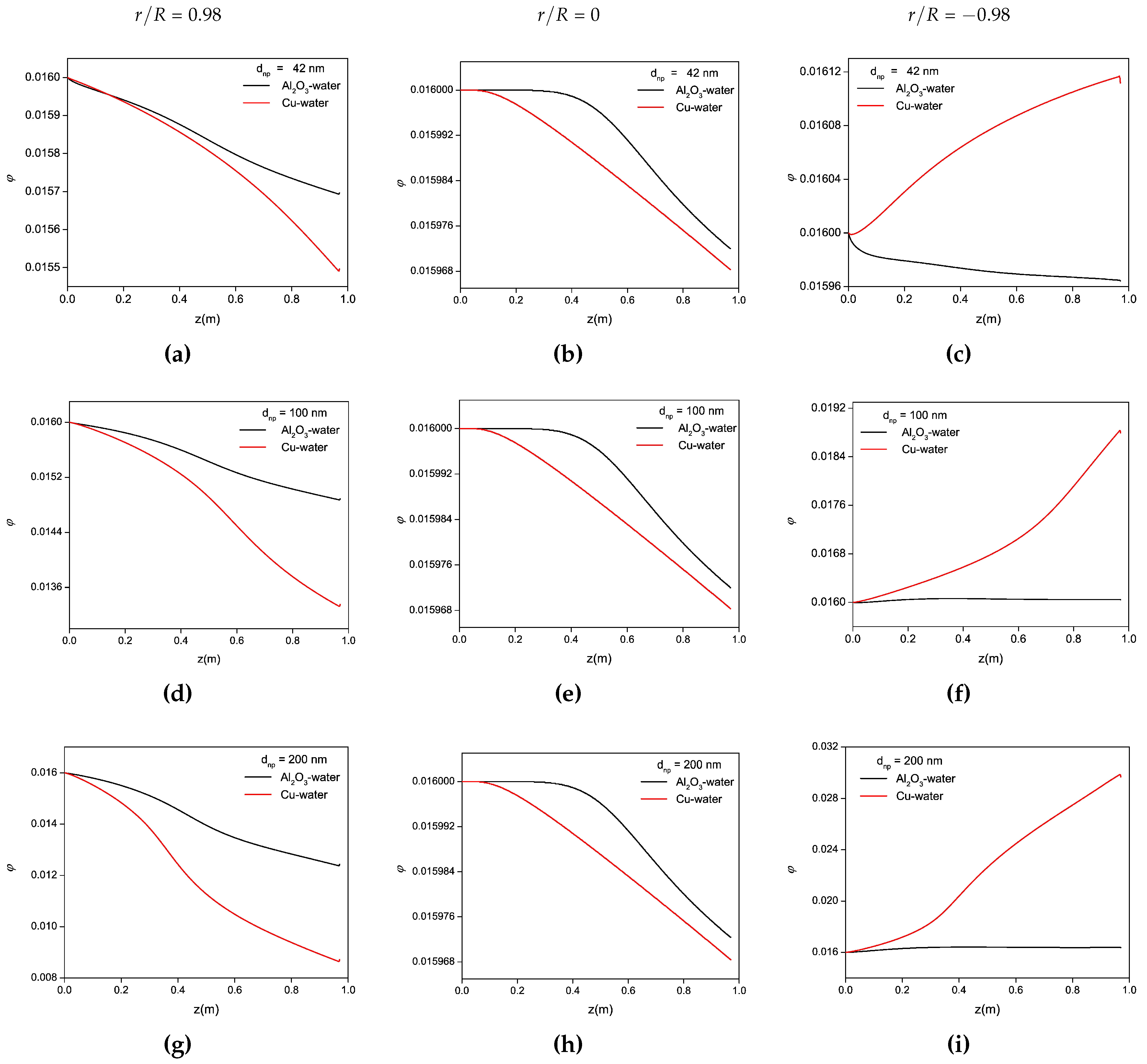
4.2. Influence of the Nanoparticle Diameter for and Cu/Water-Based Nanofluids
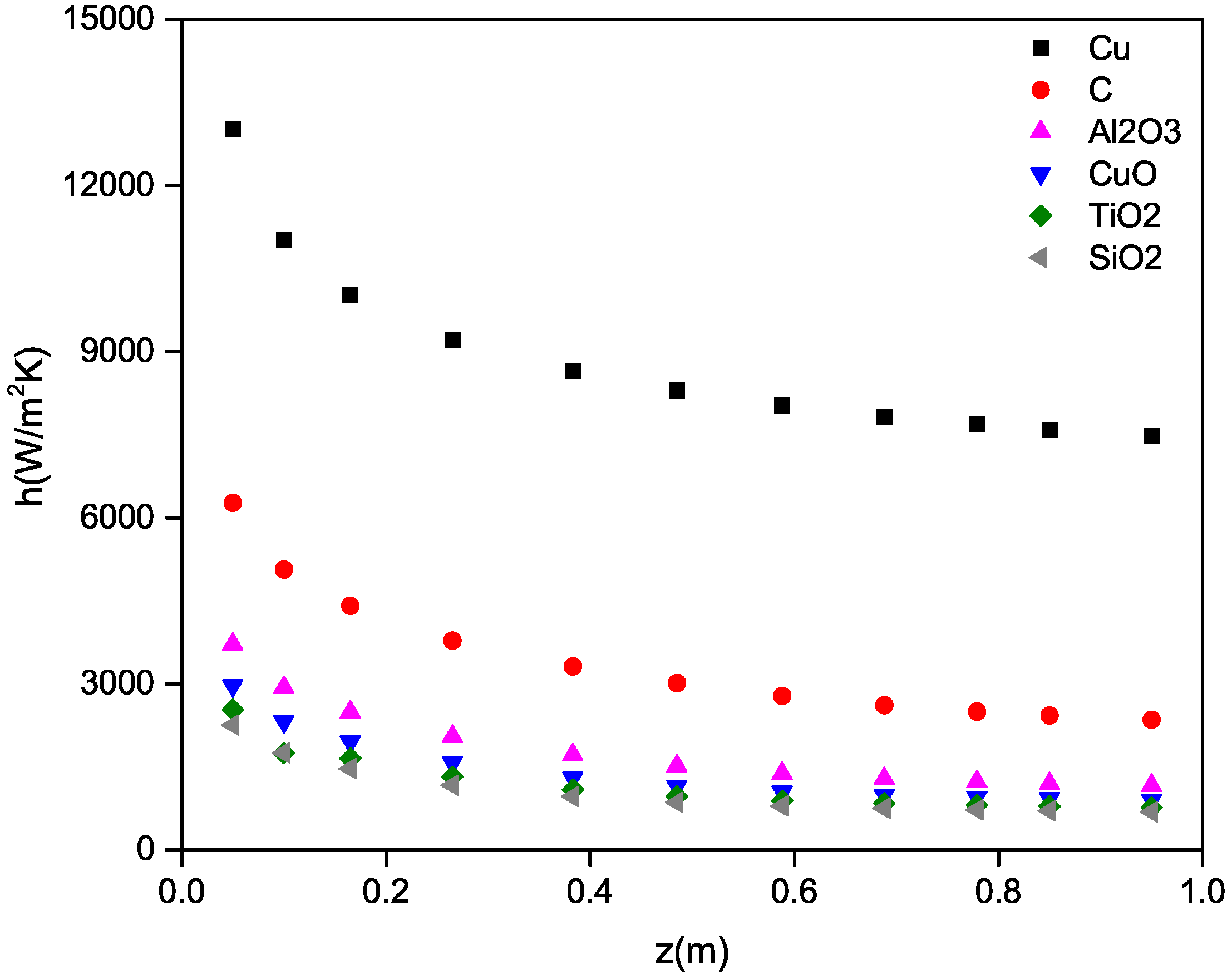
4.3. Influence of the Type of Nanoparticles for Water-Based Nanofluids
4.4. Summary
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| Specific heat, J·K·kg | |
| D | Tube diameter, m |
| Nanoparticle diameter, m | |
| f | Friction factor, - |
| h | Heat transfer coefficient, W·m·K |
| k | Thermal conductivity, W·m·K |
| L | Tube length, m |
| q | Heat flux, W·m |
| R | Tube radius, m |
| r | Radial location, m |
| Global Reynolds number, - | |
| T | Temperature, K |
| w | Axial velocity component, m·s |
| z | Axial position, m |
| Volume fraction, - | |
| Dynamic viscosity, Pa·s | |
| Density, kg·m | |
| τ | Wall shear stress, Pa |
| Average | |
| Base fluid | |
| Effective | |
| Inlet | |
| Mixture | |
| Nanofluid | |
| Nanoparticles | |
| w | Wall |
References
- Wong, K.V.; De Leon, O. Applications of nanofluids: Current and future. Adv. Mech. Eng. 2010, 2010. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Application of nanofluids in heat exchangers: A review. Renew. Sustain. Energy Rev. 2012, 16, 5625–5638. [Google Scholar] [CrossRef]
- Maxwell, J.C. A Treatise on Electricity and Magnetism, 2nd ed.; Clarendon: Oxford, UK, 1881. [Google Scholar]
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles. In Proceedings of the ASME International Mechanical Engineering Congress & Exposition, San Francisco, CA, USA, 12–17 November 1995; Volume 231, pp. 99–106.
- Jang, S.P.; Choi, S.U.S. Effects of various parameters on nanofluid thermal conductivity. J. Heat Transf. 2007, 129, 617–623. [Google Scholar] [CrossRef]
- Khanafer, K.; Vafai, K. A critical synthesis of thermophysical characteristics of nanofluids. Int. J. Heat Mass Transf. 2011, 54, 4410–4428. [Google Scholar] [CrossRef]
- Riazi, H.; Murphy, T.; Webber, G.B.; Atkin, R.; Mostafavi Tehrani, S.S.; Taylor, R.A. Specific heat control of nanofluids: A critical review. Int. J. Therm. Sci. 2016, 107, 25–38. [Google Scholar] [CrossRef]
- Bianco, V.; Manca, O.; Nardini, S.; Vafai, K. Heat Transfer Enhancement with Nanofluids; CRC Press: London, UK, 2015. [Google Scholar]
- Das, S.K.; Choi, S.U.S.; Yu, W.; Pradeep, T. Nanofluids Science and Technology; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Kakac, S.; Pramuanjaroenkij, A. Single-phase and two-phase treatments of convective heat transfer enhancement with nanofluids—A state-of-the-art review. Int. J. Therm. Sci. 2016, 100, 75–97. [Google Scholar] [CrossRef]
- Wen, D.; Ding, Y. Experimental investigation into convective heat transfer of nanofluids at the entrance region under laminar flow conditions. Int. J. Heat Mass Transf. 2004, 47, 5181–5188. [Google Scholar] [CrossRef]
- Heyhat, M.M.; Kowsary, F.; Rashidi, A.M.; Momenpour, M.H.; Amrollahi, A. Experimental investigation of laminar convective heat transfer and pressure drop of water-based Al2O3 nanofluids in fully developed flow regime. Exp. Therm. Fluid Sci. 2013, 44, 483–489. [Google Scholar] [CrossRef]
- Halelfadl, S.; Estellé, P.; Maré, T. Heat transfer properties of aqueous carbon nanotubes nanofluids in coaxial heat exchanger under laminar regime. Exp. Therm. Fluid Sci. 2014, 55, 174–180. [Google Scholar] [CrossRef]
- Maré, T.; Halelfadl, S.; Sow, O.; Estellé, P.; Duret, S.; Bazantay, F. Comparison of the thermal performances of two nanofluids at low temperature in a plate heat exchanger. Exp. Therm. Fluid Sci. 2011, 35, 1535–1543. [Google Scholar] [CrossRef]
- Mehrez, Z.; El Cafsi, A.; Belghith, A.; Le Quéré, P. The entropy generation analysis in the mixed convective assisting flow of Cu-water nanofluid in an inclined open cavity. Adv. Powder Technol. 2015, 26, 1442–1451. [Google Scholar] [CrossRef]
- Labonté, J.; Nguyen, C.T.; Roy, G. Heat Transfer Enhancement in Laminar Flow Using Al2O3-Water Nanofluid Considering Temperature-Dependent Properties. In Proceedings of the 4th WSEAS International Conference on Heat Transfer, Thermal Engineering and Environment, Elounda, Greece, 21–23 August 2006; pp. 21–23.
- Bianco, V.; Chiacchio, F.; Manca, O.; Nardini, S. Numerical investigation of nanofluids forced convection in circular tubes. Appl. Therm. Eng. 2009, 29, 3632–3642. [Google Scholar] [CrossRef]
- Lotfi, R.; Saboohi, Y.; Rashidi, A.M. Numerical study of forced convective heat transfer of nanofluids: Comparison of different approaches. Int. Commun. Heat Mass Transf. 2010, 37, 74–78. [Google Scholar] [CrossRef]
- Akbari, M.; Galanis, N.; Behzadmehr, A. Comparative analysis of single and two-phase models for CFD studies of nanofluid heat transfer. Int. J. Therm. Sci. 2011, 50, 1343–1354. [Google Scholar] [CrossRef]
- Azari, A.; Kalbasi, M.; Rahimi, M. CFD and experimental investigation on the heat transfer characteristics of alumina nanofluids under the laminar flow regime. Braz. J. Chem. Eng. 2014, 31, 469–481. [Google Scholar] [CrossRef]
- Behroyan, I.; Vanaki, S.M.; Ganesan, P.; Saidur, R. A comprehensive comparison of various CFD models for convective heat transfer of Al2O3 nanofluid inside a heated tube. Int. Commun. Heat Mass Transf. 2016, 70, 27–37. [Google Scholar] [CrossRef]
- Bianco, V.; Manca, O.; Nardini, S. Second law analysis of Al2O3-water nanofluid turbulent forced convection in a circular cross section tube with constant wall temperature. Adv. Mech. Eng. 2013, 2013, 1–12. [Google Scholar] [CrossRef]
- Anoop, K.; Sundararajan, T.; Das, S. Effect of particle size on the convective heat transfer in nanofluid in the developing region. Int. J. Heat Mass Transf. 2009, 52, 2189–2195. [Google Scholar] [CrossRef]
- Hwang, K.S.; Jang, S.P.; Choi, S.U.S. Flow and convective heat transfer characteristics of water-based Al2O3 nanofluids in fully developed laminar flow regime. Int. J. Heat Mass Transf. 2009, 52, 193–199. [Google Scholar] [CrossRef]
- Wang, X.; Li, X. Influence of pH on nanofluids’ viscosity and thermal conductivity. Chin. Phys. Lett. 2009, 26. [Google Scholar] [CrossRef]
- Liu, M.; Ding, C.; Wang, J. Modeling of thermal conductivity of nanofluids considering aggregation and interfacial thermal resistance. RSC Adv. 2016, 6, 3571–3577. [Google Scholar] [CrossRef]
- Kakac, S.; Pramuanjaroenkij, A. Review of convective heat transfer enhancement with nanofluids. Int. J. Heat Mass Transf. 2009, 52, 3187–3196. [Google Scholar] [CrossRef]
- Vargaftik, N.B. Tables on the Thermophysical Properties of Liquids and Gases: In Normal and Dissociated States; Hemisphere Publishing Corporation: Washington, DC, USA, 1975. [Google Scholar]
- Chon, C.H.; Kihm, K.D.; Lee, S.P.; Choi, S.U.S. Empirical correlation finding the role of temperature and particle size for nanofluid (Al2O3) thermal conductivity enhancement. Appl. Phys. Lett. 2005, 87. [Google Scholar] [CrossRef]
- Behzadmehr, A.; Saffar-Avval, M.; Galanis, N. Prediction of turbulent forced convection of a nanofluid in a tube with uniform heat flux using a two phase approach. Int. J. Heat Fluid Flow 2007, 28, 211–219. [Google Scholar] [CrossRef]
- De Castro, C.A.N.; Li, S.F.Y.; Nagashima, A.; Trengove, R.D.; Wakeham, W.A. Standard reference data for the thermal conductivity of liquids. J. Phys. Chem. Ref. Data 1986, 15, 1073–1086. [Google Scholar] [CrossRef]
- Xuan, Y.; Roetzel, W. Conceptions for heat transfer correlation of nanofluids. Int. J. Heat Mass Transf. 2000, 43, 3701–3707. [Google Scholar] [CrossRef]
- Khanafer, K.; Vafai, K.; Lightstone, M. Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. Int. J. Heat Mass Transf. 2003, 46, 3639–3653. [Google Scholar] [CrossRef]
- Maiga, S.E.B.; Nguyen, C.T.; Galanis, N.; Roy, G. Heat transfer behaviours of nanofluids in a uniformly heated tube. Superlattices Microstruct. 2004, 35, 543–557. [Google Scholar] [CrossRef]
- Rea, U.; McKrell, T.; Hu, L.; Buongiorno, J. Laminar convective heat transfer and viscous pressure loss of alumina-water and zirconia-water nanofluids. Int. J. Heat Mass Transf. 2009, 52, 2042–2048. [Google Scholar] [CrossRef]
- Hachey, M.; Nguyen, C.; Galanis, N.; Popa, C. Experimental investigation of Al2O3 nanofluids thermal properties and rheology e effects of transient and steady-state heat exposure. Int. J. Therm. Sci. 2014, 76, 155–167. [Google Scholar] [CrossRef]
- Nan, C.W.; Birringer, R.; Clarke, D.R.; Gleiter, H. Effective thermal conductivity of particulate composites with interfacial thermal resistance. J. Appl. Phys. 1997, 81, 6692–6699. [Google Scholar] [CrossRef]
- Manninen, M.; Taivassalo, V.; Kallio, S. On the mixture model for multiphase flow. VTT Publ. 1996, 88, 67. [Google Scholar]
- Schiller, L.; Naumann, Z. A drag coefficient correlation. Z. Ver. Deutsch. Ing. 1935, 77, 318–320. [Google Scholar]
- Heris, S.Z.; Esfahany, M.N.; Etemad, S.G. Experimental investigation of convective heat transfer of Al2O3/water nanofluid in circular tube. Int. J. Heat Fluid Flow 2007, 28, 203–210. [Google Scholar] [CrossRef]
- Bianco, V.; Manca, O.; Nardini, S. Numerical investigation on nanofluids turbulent convection heat transfer inside a circular tube. Int. J. Therm. Sci. 2011, 50, 341–349. [Google Scholar] [CrossRef]
- Keblinski, P.; Phillpot, S.R.; Choi, S.U.S.; Eastman, J.A. Mechanisms of heat flow in suspensions of nano-sized particles (nanofluids). Int. J. Heat Mass Transf. 2002, 45, 855–863. [Google Scholar] [CrossRef]
- Jang, S.P.; Choi, S.U.S. Role of Brownian motion in the enhanced thermal conductivity of nanofluids. Appl. Phys. Lett. 2004, 84, 4316–4318. [Google Scholar] [CrossRef]
- Koo, J.; Kleinstreuer, C. A new thermal conductivity model for nanofluids. J. Nanopart. Res. 2004, 6, 577–588. [Google Scholar] [CrossRef]
- Galanis, N.; Ouzzane, M. Developing mixed convection in an Inclined tube with circumferentially nonuniform heating at its outer surface. Numer. Heat Transf. A Appl. 1999, 35, 609–628. [Google Scholar] [CrossRef]
- Orfi, J.; Galanis, N. Developing laminar mixed convection with heat and mass transfer in horizontal and vertical tubes. Int. J. Therm. Sci. 2002, 41, 319–331. [Google Scholar] [CrossRef]
- Khdher, A.M.; Mamat, R.; Sidik, N.A.C. The Effects of Turbulent Nanofluids and Secondary Flow on the Heat Transfer through a Straight Channel. In Recent Advances in Mathematical and Computational Methods; Springer: Dordrecht, The Netherlands, 2011; pp. 118–124. [Google Scholar]
- Ebrahimnia-Bajestan, E.; Niazmand, H. Convective heat transfer of nanofluids flows through an isothermally heated curved pipe. Iran. J. Chem. Eng. 2011, 8, 81–97. [Google Scholar]
- Colla, L.; Fedele, L.; Buschmann, M.H. Nanofluids Suppress Secondary Flow in Laminar Pipe Flow. In Proceedings of the World Congress on Mechanical, Chemical, and Material Engineering, Barcelona, Spain, 20–21 July 2015; pp. 279-1–279-4.
- Shah, R.K. Thermal Entry Length Solutions for the Circular Tube and Parallel Plates. In Proceedings of the Third National Heat and Mass Transfer Conference, Bombay, India, 11–13 December 1975; Volume 1, pp. 11–75.
- Choi, M.; Cho, K. Effect of the aspect ratio of rectangular channels on the heat transfer and hydrodynamics of paraffin slurry flow. Int. J. Heat Mass Transf. 2001, 44, 55–61. [Google Scholar] [CrossRef]
- Suresh, S.; Chandrasekar, M.; Chandra Sekhar, S. Experimental studies on heat transfer and friction factor characteristics of CuO/water nanofluid under turbulent flow in a helically dimpled tube. Exp. Therm. Fluid Sci. 2011, 35, 542–549. [Google Scholar] [CrossRef]

| (kg·m) | (J·kg·K) | k (W·m·K) | |
|---|---|---|---|
| C | 220 | 710 | 129 |
| 8933 | 385 | 401 | |
| 6510 | 540 | 18 | |
| 3880 | 729 | ||
| 4175 | 692 | ||
| 2220 | 745 |
| Experiments [11] | Simulation 1 | Simulation 2 | |
|---|---|---|---|
| () | () | ||
| () | () |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sekrani, G.; Poncet, S. Further Investigation on Laminar Forced Convection of Nanofluid Flows in a Uniformly Heated Pipe Using Direct Numerical Simulations. Appl. Sci. 2016, 6, 332. https://doi.org/10.3390/app6110332
Sekrani G, Poncet S. Further Investigation on Laminar Forced Convection of Nanofluid Flows in a Uniformly Heated Pipe Using Direct Numerical Simulations. Applied Sciences. 2016; 6(11):332. https://doi.org/10.3390/app6110332
Chicago/Turabian StyleSekrani, Ghofrane, and Sébastien Poncet. 2016. "Further Investigation on Laminar Forced Convection of Nanofluid Flows in a Uniformly Heated Pipe Using Direct Numerical Simulations" Applied Sciences 6, no. 11: 332. https://doi.org/10.3390/app6110332
APA StyleSekrani, G., & Poncet, S. (2016). Further Investigation on Laminar Forced Convection of Nanofluid Flows in a Uniformly Heated Pipe Using Direct Numerical Simulations. Applied Sciences, 6(11), 332. https://doi.org/10.3390/app6110332







