High-Speed Visual Analysis of Fluid Flow and Heat Transfer in Oscillating Heat Pipes with Different Diameters
Abstract
:1. Introduction
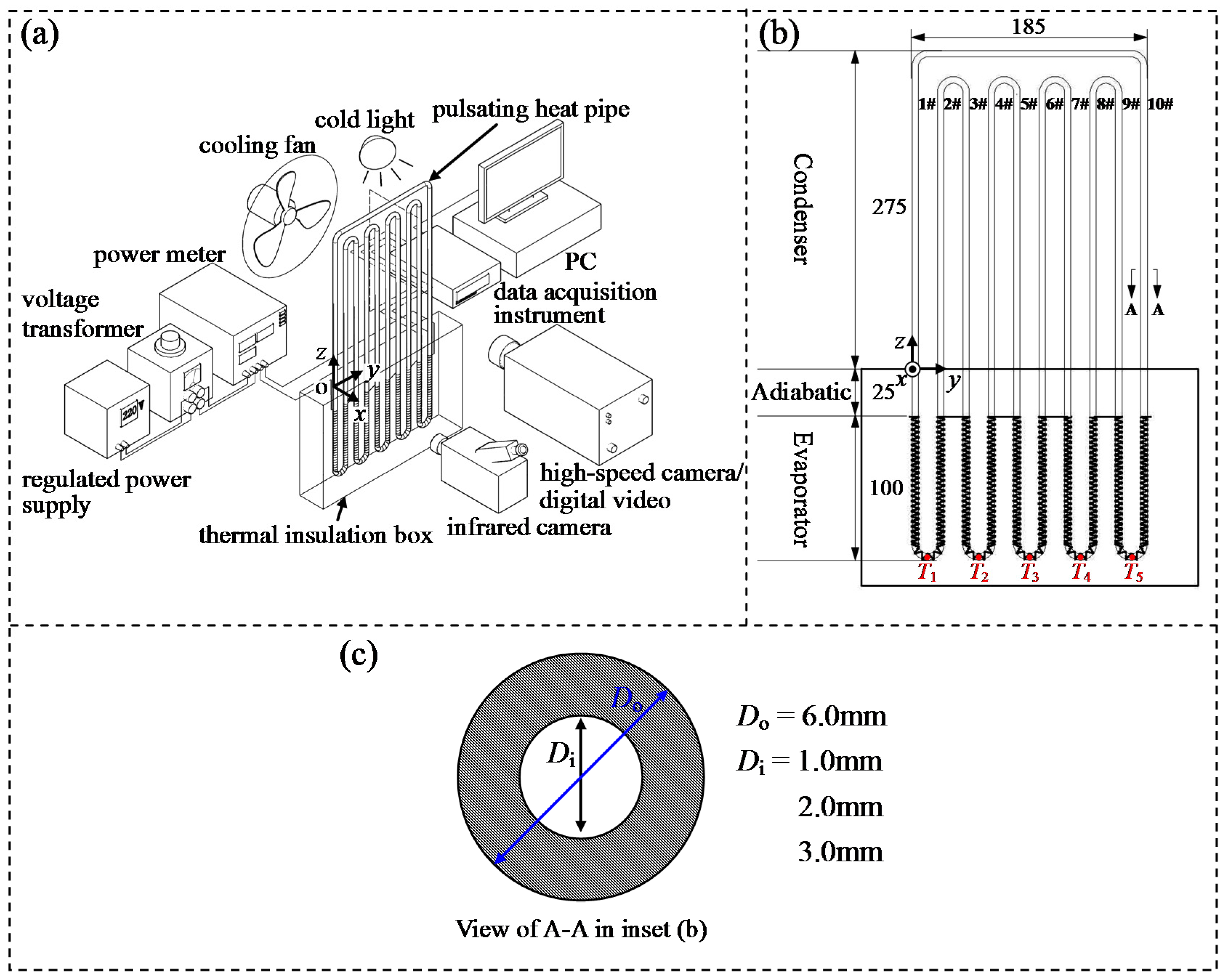
2. Experimental Setup
3. Results and Discussions
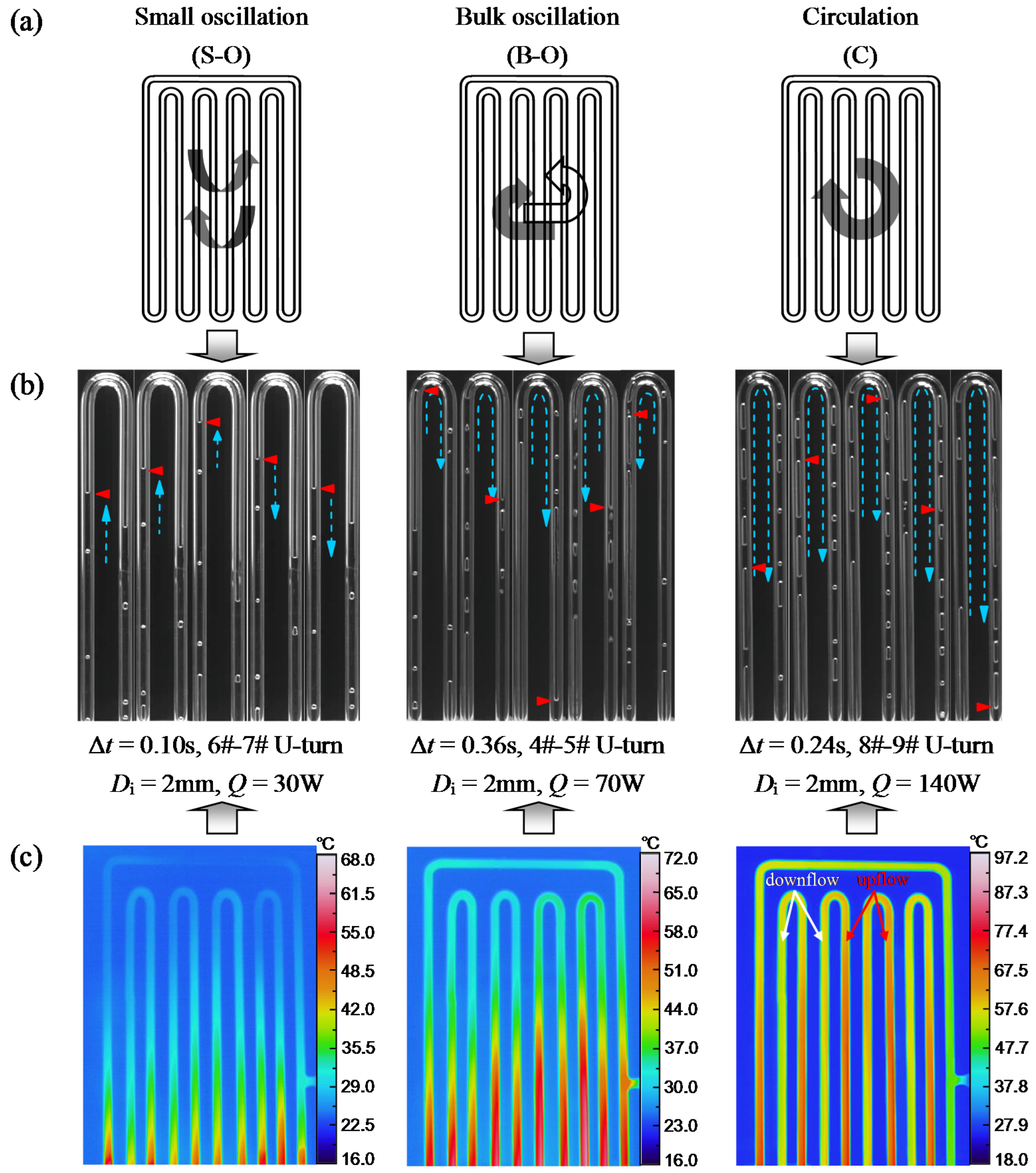
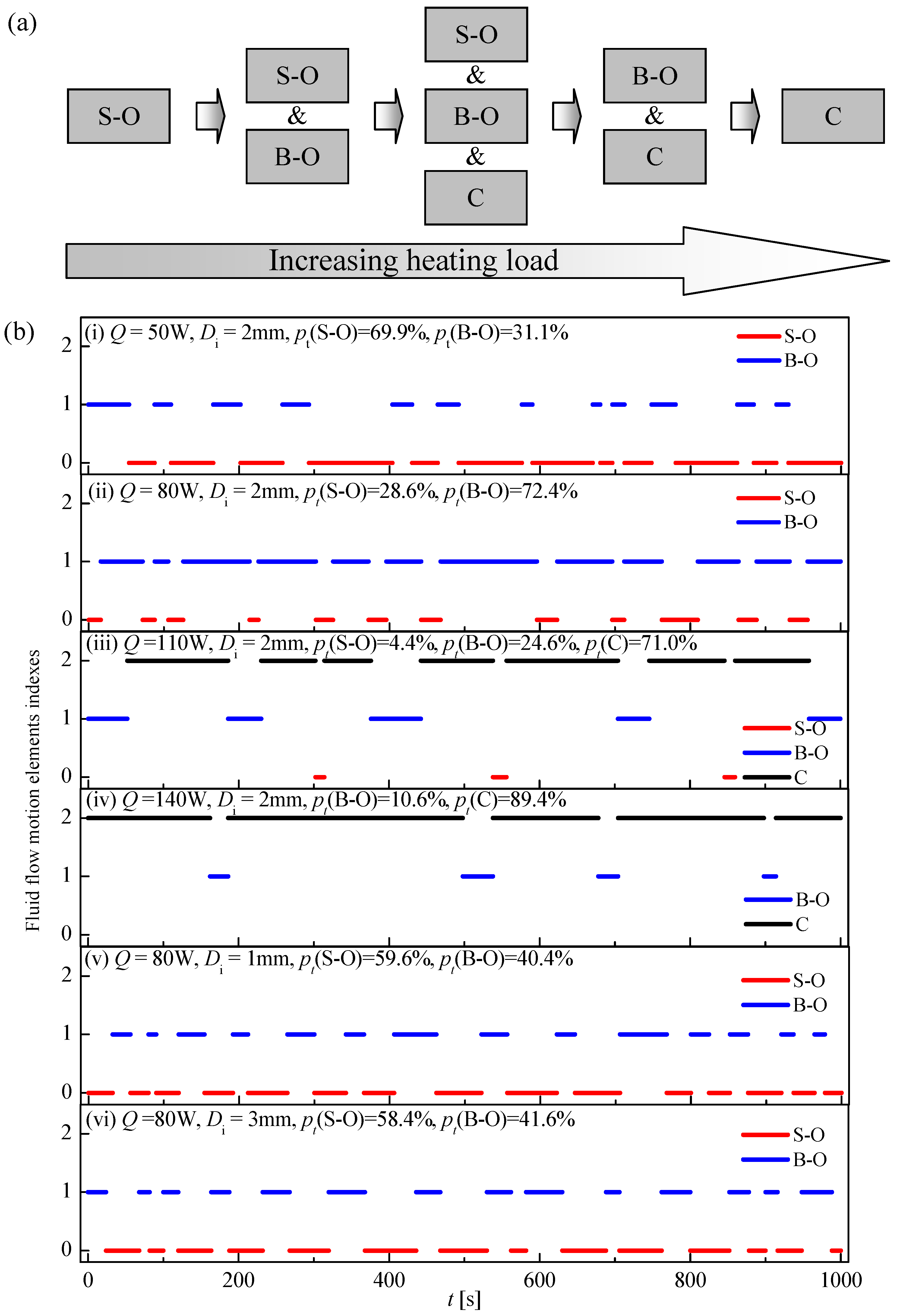
3.1. Fluid Flow Motions inside OHP
3.2. General Flow Patterns in OHP
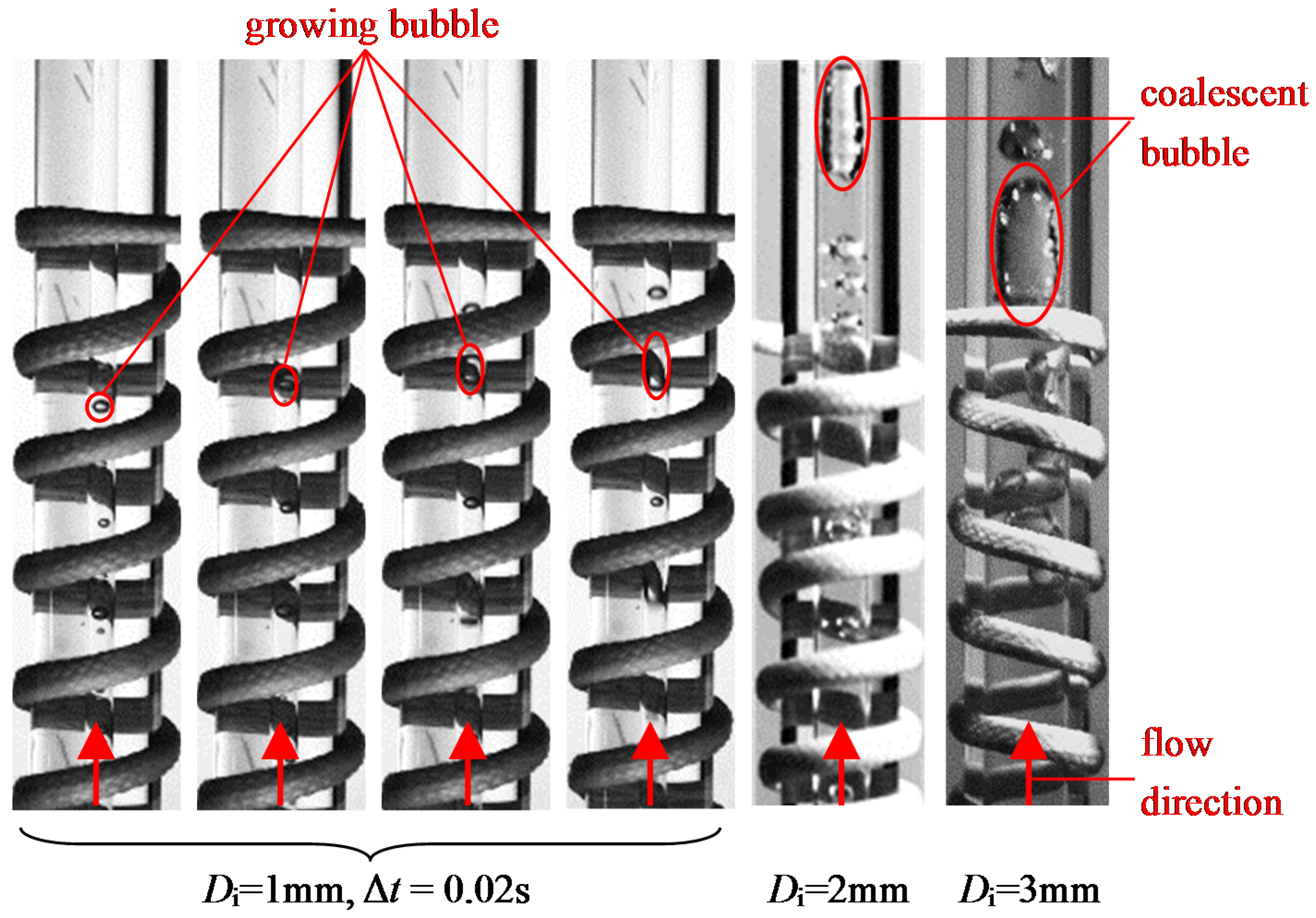
3.2.1. Bubbly Flow
3.2.2. Slug Flow
3.2.3. Annular Flow
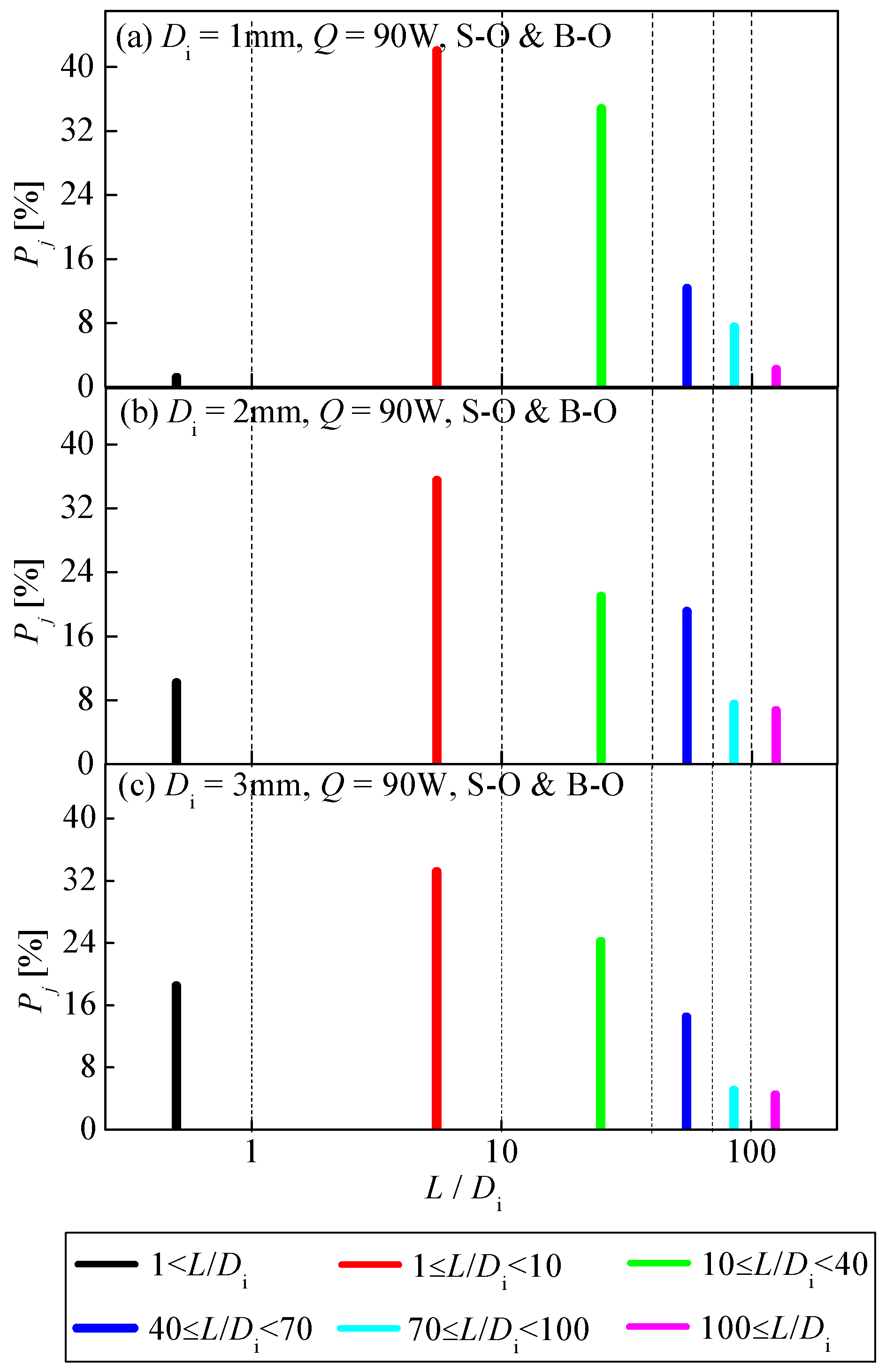
3.3. Flow Pattern Evolutions in Evaporator and Condenser
3.3.1. Flow Pattern Evolutions in Evaporator
3.3.2. Flow Pattern Evolutions in the Condenser
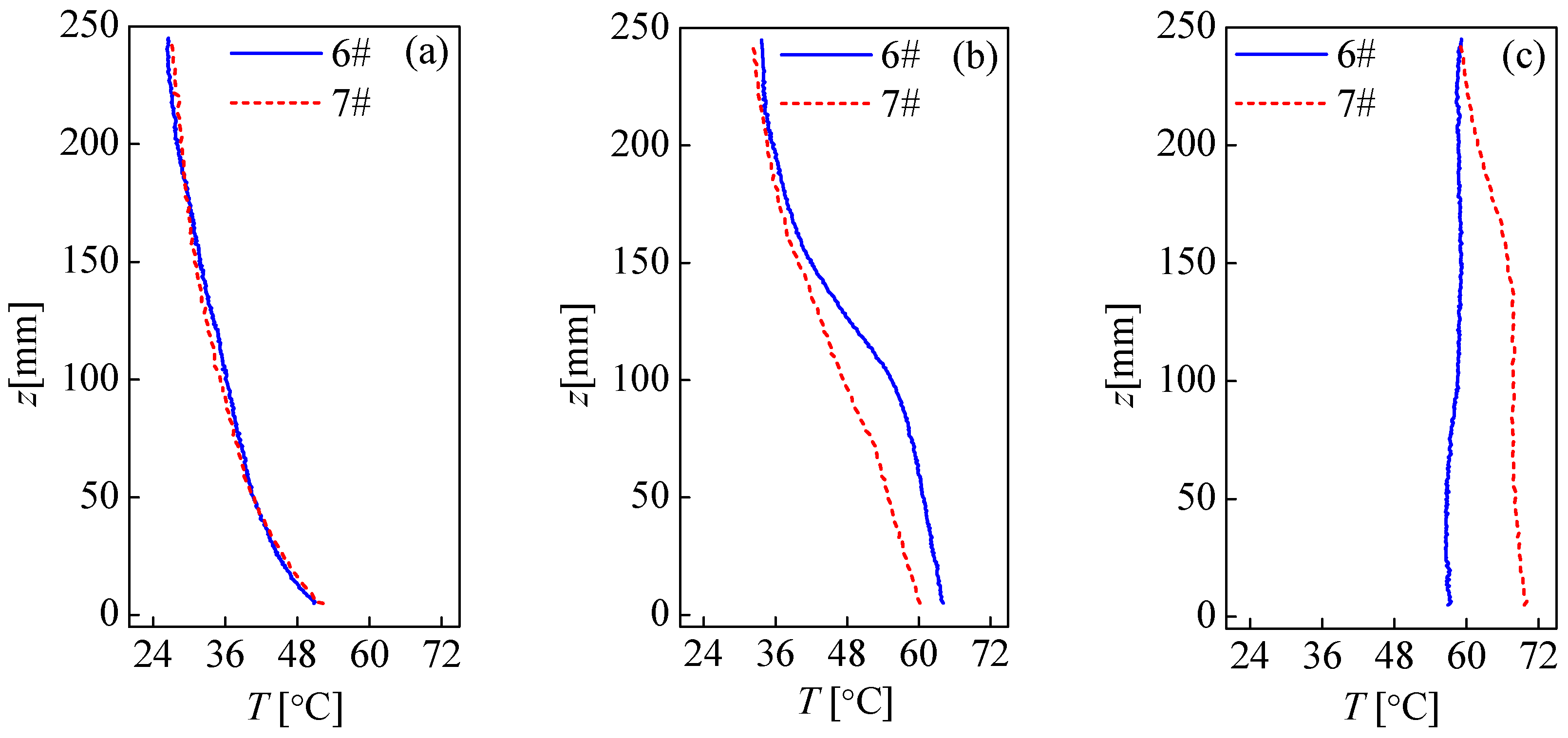
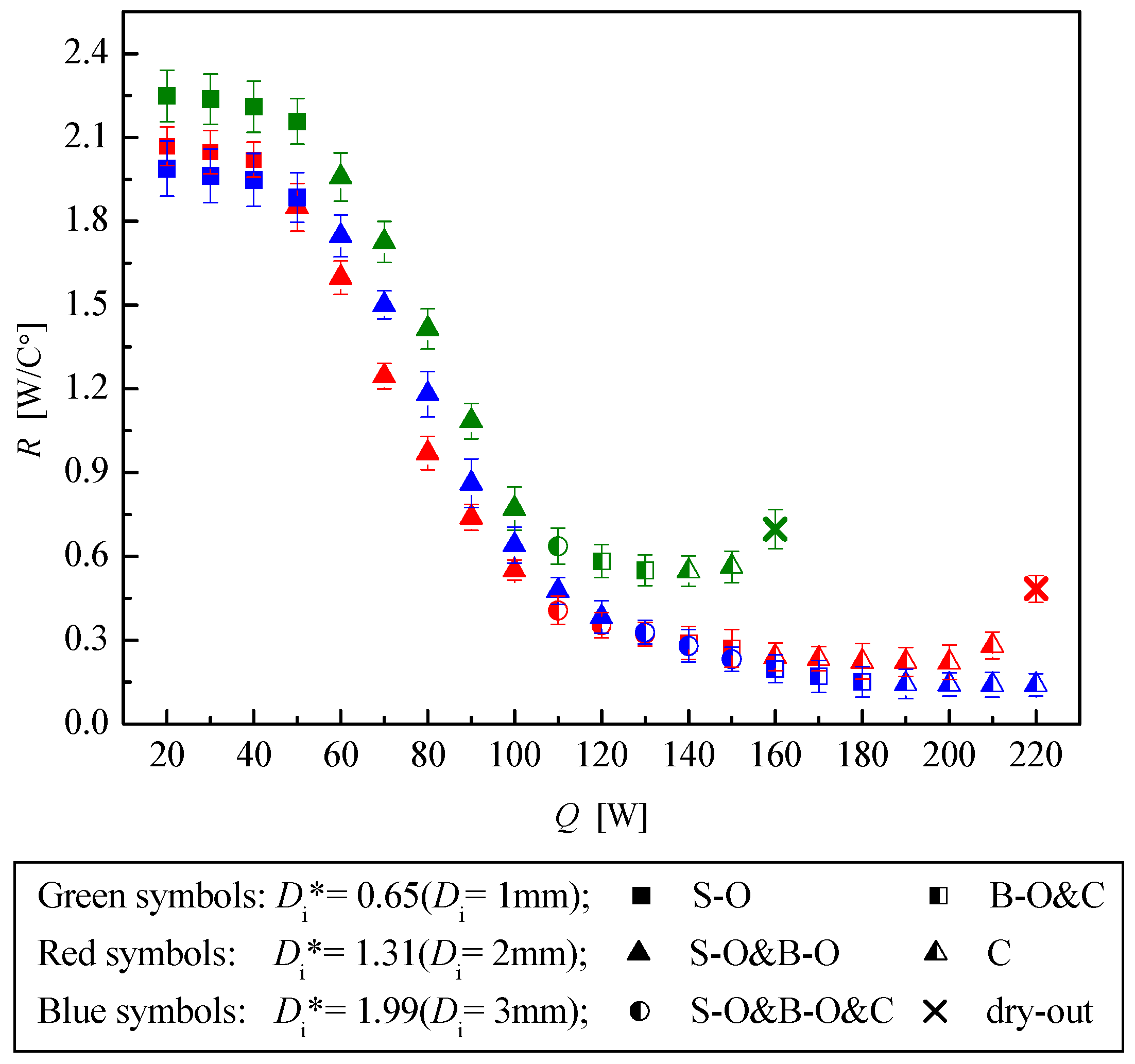
3.4. Thermal Performance
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gasia, J.; Miró, L.; de Gracia, A.; Barreneche, C.; Cabeza, L.F. Experimental evaluation of a paraffin as phase change material for thermal energy storage in laboratory equipment and in a shell-and-tube heat exchanger. Appl. Sci. 2016, 6, 112. [Google Scholar] [CrossRef]
- Bo, Z.; Zhao, Q.; Shuai, X.R.; Yan, J.H.; Cen, K.F. Numerical study on the pressure drop of fluid flow in rough microchannels via the lattice Boltzmann method. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 2022–2031. [Google Scholar] [CrossRef]
- Sun, D.K.; Zhu, M.F.; Wang, J.; Sun, B.D. Lattice Boltzmann modeling of bubble formation and dendritic growth in solidification of binary alloys. Int. J. Heat Mass Transf. 2016, 94, 474–487. [Google Scholar] [CrossRef]
- Tian, F.B.; Bharti, R.P.; Xu, Y.Q. Deforming-Spatial-Domain/Stabilized Space–Time (DSD/SST) method in computation of non-Newtonian fluid flow and heat transfer with moving boundaries. Comput. Mech. 2014, 53, 257–271. [Google Scholar] [CrossRef]
- Jeng, T.-M.; Tzeng, S.-C. Numerical simulation of laminar forced convection of pin-fin heat-sink array in a Channel by Using Porous Approach. Appl. Sci. 2015, 5, 1846–1868. [Google Scholar] [CrossRef]
- Zhao, J.; Huang, S.B.; Gong, L.; Huang, Z.Q. Numerical study and optimizing on micro square pin-fin heat sink for electronic cooling. Appl. Therm. Eng. 2016, 93, 1347–1359. [Google Scholar] [CrossRef]
- Zhao, J.T.; Rao, Z.H.; Liu, C.Z.; Li, Y.M. Experimental study of oscillating heat pipe and phase change materials coupled for thermal energy storage and thermal management. Int. J. Heat Mass Transf. 2016, 99, 252–260. [Google Scholar] [CrossRef]
- Huang, H.J.; Shen, S.C.; Shaw, H.J. Design and fabrication of a novel hybrid-structure heat pipe for a concentrator photovoltaic. Energies 2012, 5, 4340–4399. [Google Scholar] [CrossRef]
- Faghri, A. Review and advances in heat pipe science and technology. J. Heat Transf. 2012, 134, 123001. [Google Scholar] [CrossRef]
- Akachi, H. Structure of a Heat Pipe. U.S. Patent 4,921,041, 1 May 1990. [Google Scholar]
- Akachi, H.; Polasek, F.; Stulc, P. Pulsating heat pipes. In Proceedings of the 5th International Heat Pipe Symposium, Melbourne, Australia, 17–20 November 1996; pp. 208–217.
- Zhang, Y.W.; Faghri, A. Advances and unsolved issues in pulsating heat pipes. Heat Transf. Eng. 2008, 29, 20–44. [Google Scholar] [CrossRef]
- Liao, Q.; Jen, T.C.; Chen, Q.H.; Li, L.J.; Cui, W.Z. Heat transfer performance in 3d internally finned heat pipe. Int. J. Heat Mass Trans. 2007, 50, 1231–1237. [Google Scholar] [CrossRef]
- Li, C.; Peterson, G.P.; Wang, Y. Evaporation/boiling in thin capillary wicks (I)—Wick thickness effects. J. Heat Trans. 2006, 128, 1312–1319. [Google Scholar] [CrossRef]
- Rittidech, S.; Dangeton, W.; Soponronnarit, S. Closed-ended oscillating heat-pipe (CEOHP) air-preheater for energy thrift in a dryer. Appl. Energy 2005, 81, 198–208. [Google Scholar] [CrossRef]
- Meena, P.; Rittidech, S.; Poomsa-ad, N. Application of closed-loop oscillating heat-pipe with check valves (CLOHP/CV) air-preheater for reduced relative-humidity in drying systems. Appl. Energy 2007, 5, 553–564. [Google Scholar] [CrossRef]
- Rittidech, S.; Wannapakne, S. Experimental study of the performance of a solar collector by closed-end oscillating heat pipe (CEOHP). Appl. Therm. Eng. 2007, 27, 1978–1985. [Google Scholar] [CrossRef]
- Rittidech, S.; Donmaung, A.; Kumsombut, K. Experimental study of the performance of a circular tube solar collector with closed-loop oscillating heat-pipe with check valve (CLOHP/CV). Renew. Energy 2009, 34, 2234–2238. [Google Scholar] [CrossRef]
- Burban, G.; Ayel, V.; Alexandre, A.; Lagonotte, P.; Bertin, Y.; Romestant, C. Experimental investigation of a pulsating heat pipe for hybrid vehicle applications. Appl. Therm. Eng. 2013, 50, 94–103. [Google Scholar] [CrossRef]
- Jason, C.; Wang, X. Experimental investigation of pulsating heat pipe performance with regard to fuel cell cooling application. Appl. Therm. Eng. 2013, 50, 268–274. [Google Scholar]
- Shafii, M.B.; Faghri, A.; Zhang, Y.W. Analysis of heat transfer in unlooped and looped pulsating heat pipes. Int. J. Numer. Methods Heat Fluid Flow 2002, 12, 585–609. [Google Scholar] [CrossRef]
- Brian, H.; Faghri, A. Analysis of pulsating heat pipe with capillary wick and varying channel diameter. Int. J. Heat Mass. Trans. 2005, 48, 2635–2651. [Google Scholar]
- Ji, Y.L.; Ma, H.B.; Su, F.M.; Wang, G.Y. Particle size effect on heat transfer performance in an oscillating heat pipe. Exp. Therm. Fluid Sci. 2011, 35, 724–727. [Google Scholar] [CrossRef]
- Qu, J.; Wu, H.Y.; Cheng, P. Thermal performance of an oscillating heat pipe with Al2O3-water nanofluids. Int. Commun. Heat Mass Transf. 2010, 37, 111–115. [Google Scholar] [CrossRef]
- Kim, J.S.; Bui, N.H.; Jung, H.S.; Lee, W.H. The study on pressure oscillation and heat transfer characteristics of oscillating capillary tube heat pipe using mixed working fluid. J. Mech. Sci. Technol. 2003, 17, 1533–1542. [Google Scholar]
- Thompson, S.M.; Cheng, P.; Ma, H.B. An experimental investigation of a three-dimensional flat-plate oscillating heat pipe with staggered microchannels. Int. J. Heat Mass Trans. 2011, 54, 3951–3959. [Google Scholar] [CrossRef]
- Cheng, P.; Thompson, S.; Boswell, J.; Ma, H.B. An investigation of flat-plate oscillating heat pipes. J. Electron. Packag. 2010, 132, 041009. [Google Scholar] [CrossRef]
- Rhodes, M.J.; Taylor, M.R.; Monroe, J.G.; Thompson, S.M. Experimental investigation of a flat-plate oscillating heat pipe with modified evaporator and condenser. In Proceedings of the ASME 2014 International Mechanical Engineering Congress and Exposition, Montreal, QC, Canada, 14–20 November 2014. [CrossRef]
- Han, X.H.; Wang, X.H.; Zheng, H.C.; Chen, G.M. Review of the development of pulsating heat pipe for heat dissipation. Renew. Sustain. Energy Rev. 2016, 59, 692–709. [Google Scholar] [CrossRef]
- Groll, M.; Khandekar, S. Pulsating heat pipe: Progress and prospects. In Proceedings of the International Conference on Energy and the Environment, Shanghai, China, 22–24 May 2003; pp. 723–730.
- Dobson, R.T.; Harms, T.M. Lumped parameter analysis of closed and open oscillatory heat pipes. In Proceedings of the 11th International Heat Pipe Conference, Tokyo, Japan, 12–16 September 1999; pp. 137–142.
- Charoensawan, P.; Terdtoon, P. Thermal performance of horizontal closed-loop oscillating heat pipes. Appl. Therm. Eng. 2008, 28, 460–466. [Google Scholar] [CrossRef]
- Yang, H.H.; Khandekar, S.; Groll, M. Operational limit of closed loop pulsating heat pipes. Appl. Therm. Eng. 2008, 28, 49–59. [Google Scholar] [CrossRef]
- Yang, H.H.; Khandekar, S.; Groll, M. Performance characteristics of pulsating heat pipes as integral thermal spreaders. Int. J. Therm. Sci. 2009, 18, 815–824. [Google Scholar] [CrossRef]
- Rittidech, S.; Pipatpaiboon, N.; Terdtoon, P. Heat-transfer characteristics of a closed-loop oscillating heat-pipe with check valve. Appl. Energy 2007, 84, 565–577. [Google Scholar] [CrossRef]
- Rittidech, S.; Terdtoon, P.; Murakami, M.; Kamonpet, P.; Jompakdee, W. Correlation to predict heat transfer characteristics of a closed-end oscillating heat pipe at normal operating condition. Appl. Therm. Eng. 2003, 23, 497–510. [Google Scholar] [CrossRef]
- Saha, M.; Feroz, C.M.; Ahmed, F.; Mujib, T. Thermal performance of an open loop closed end pulsating heat pipe. Heat Mass Transf. 2012, 48, 259–265. [Google Scholar] [CrossRef]
- Tong, B.Y.; Wong, T.N.; Ooi, K.T. Closed-loop pulsating heat pipe. Appl. Therm. Eng. 2001, 21, 1845–1862. [Google Scholar] [CrossRef]
- Xu, J.L.; Zhang, X.M. Start-up and steady thermal oscillation of a pulsating heat pipe. Heat Transf. 2005, 41, 685–694. [Google Scholar] [CrossRef]
- Khandekar, S.; Charoensawan, P.; Groll, M.; Terdtoon, P. Closed loop pulsating heat pipes Part B: Visualization and semi-empirical modeling. Appl. Therm. Eng. 2003, 23, 2021–2033. [Google Scholar] [CrossRef]
- Khandekar, S.; Groll, M. An insight into thermo-hydrodynamic coupling in closed loop pulsating heat pipes. Int. J. Therm. Sci. 2004, 43, 13–20. [Google Scholar] [CrossRef]
- Khandekar, S.; Gautam, A.P.; Shama, P.K. Multiple quasi-steady states in a closed loop pulsating heat pipe. Int. J. Therm. Sci. 2009, 48, 535–546. [Google Scholar] [CrossRef]
- Borgmeyer, B.; Ma, H.B. Experimental investigation of oscillating motions in a flat plate pulsating heat pipe. J. Thermophys. Heat Transf. 2007, 21, 405–409. [Google Scholar] [CrossRef]
- Wilson, C.; Borgmeyer, B.; Winholtz, R.A.; Ma, H.B.; Jacobson, D.L.; Hussey, D.S.; Arif, M. Visual observation of oscillating heat pipes using neutron radiography. J. Thermophys. Heat Transf. 2008, 22, 366–372. [Google Scholar] [CrossRef]
- Liu, X.D.; Chen, Y.P.; Shi, M.H. Dynamic performance analysis on start-up of closed loop pulsating heat pipes (CLPHPs). Int. J. Therm. Sci. 2012, 65, 224–233. [Google Scholar] [CrossRef]
- Ghiu, C.D.; Joshi, Y.K. Visualization study of pool boiling from thin confined enhanced structures. Int. J. Heat Mass Trans. 2005, 48, 4287–4299. [Google Scholar] [CrossRef]


© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Sun, Q.; Zhang, C.; Wu, L. High-Speed Visual Analysis of Fluid Flow and Heat Transfer in Oscillating Heat Pipes with Different Diameters. Appl. Sci. 2016, 6, 321. https://doi.org/10.3390/app6110321
Liu X, Sun Q, Zhang C, Wu L. High-Speed Visual Analysis of Fluid Flow and Heat Transfer in Oscillating Heat Pipes with Different Diameters. Applied Sciences. 2016; 6(11):321. https://doi.org/10.3390/app6110321
Chicago/Turabian StyleLiu, Xiangdong, Qing Sun, Chengbin Zhang, and Liangyu Wu. 2016. "High-Speed Visual Analysis of Fluid Flow and Heat Transfer in Oscillating Heat Pipes with Different Diameters" Applied Sciences 6, no. 11: 321. https://doi.org/10.3390/app6110321
APA StyleLiu, X., Sun, Q., Zhang, C., & Wu, L. (2016). High-Speed Visual Analysis of Fluid Flow and Heat Transfer in Oscillating Heat Pipes with Different Diameters. Applied Sciences, 6(11), 321. https://doi.org/10.3390/app6110321






