Bolt Looseness Detection Based on Piezoelectric Impedance Frequency Shift
Abstract
:1. Introduction
2. The Proposed Method and Principle
3. The Experimental Setup and Process
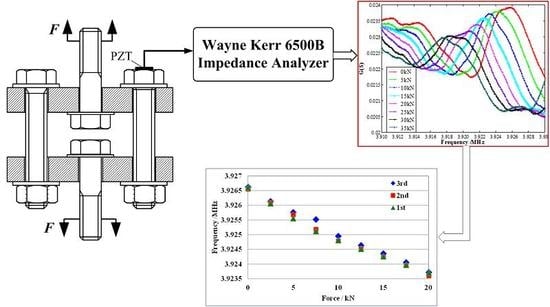
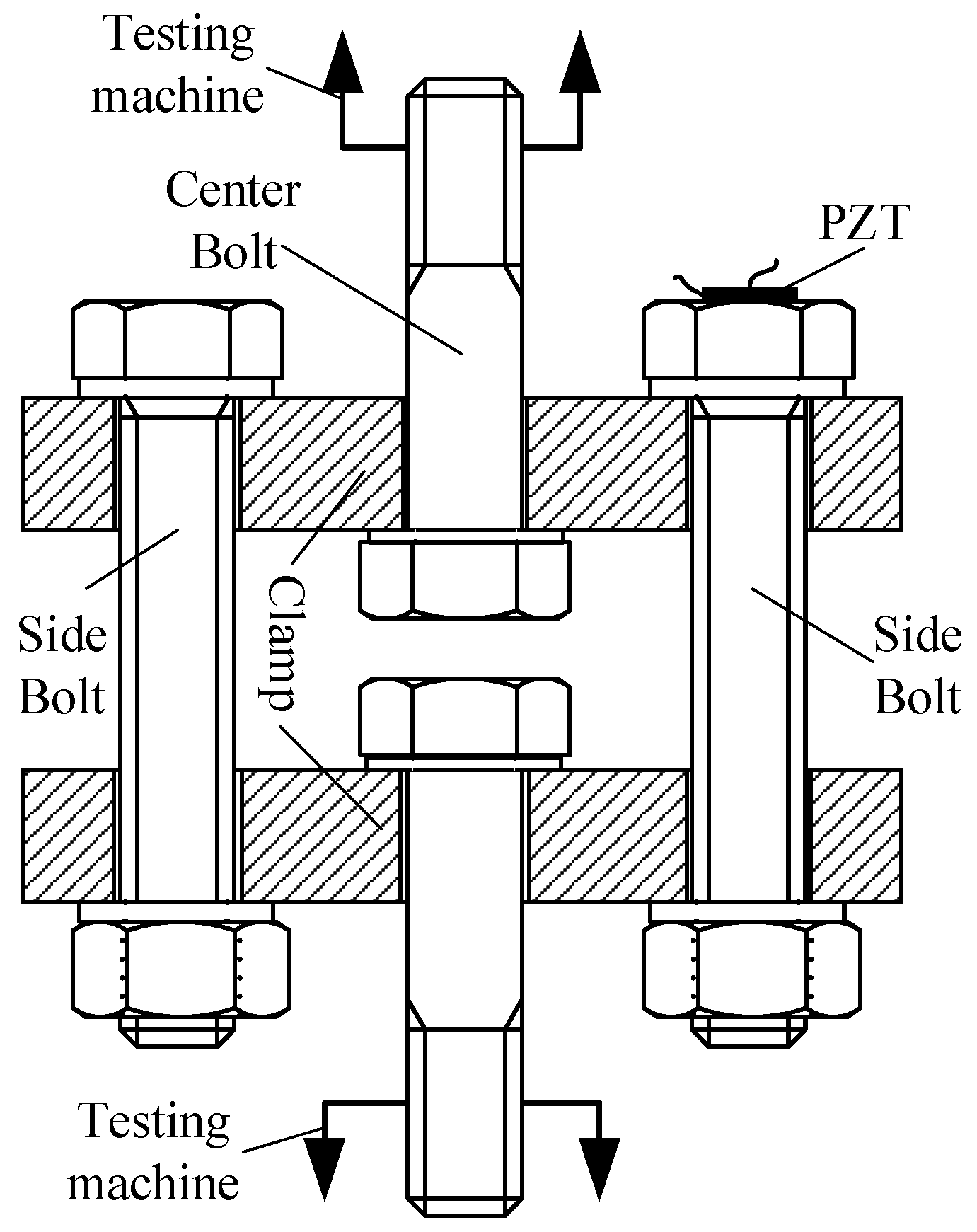
3.1. Experimental Devices
3.2. Experimental Processes
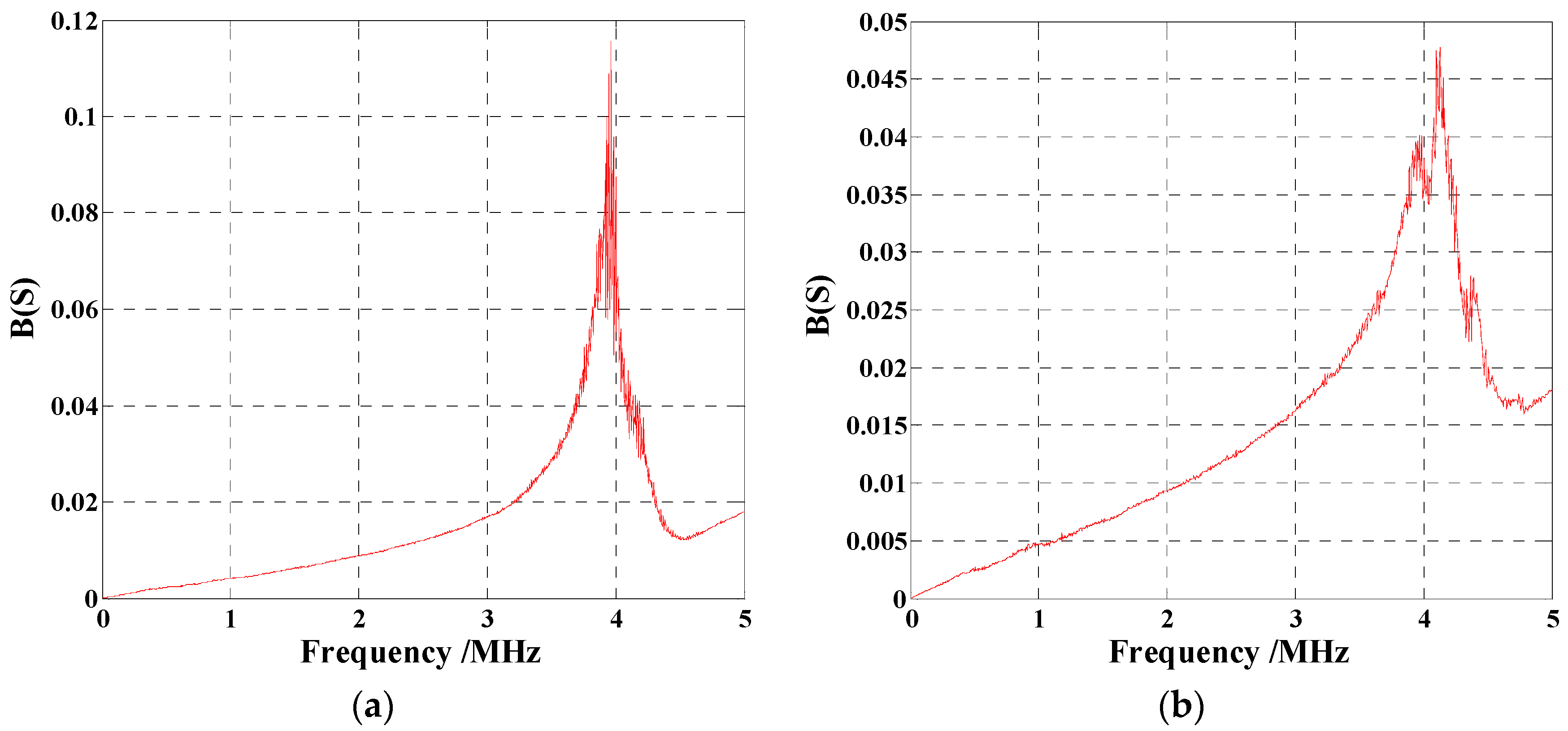
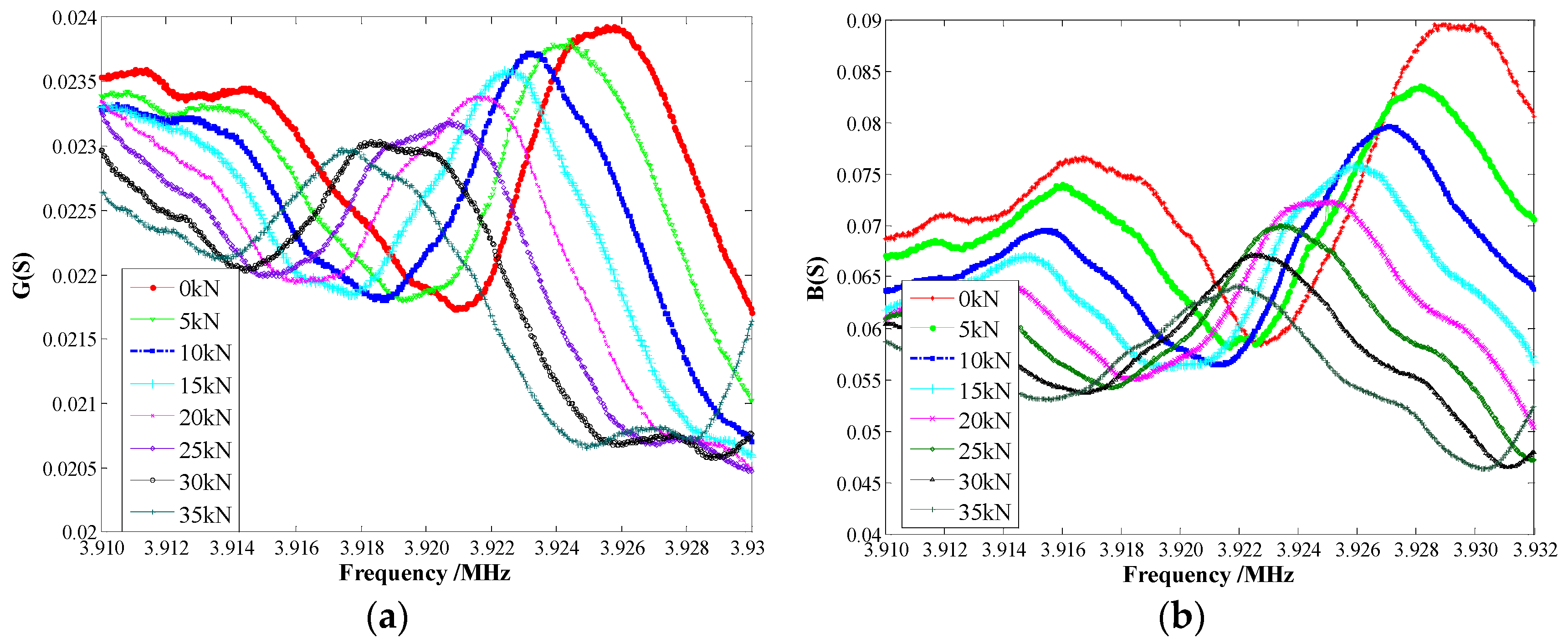
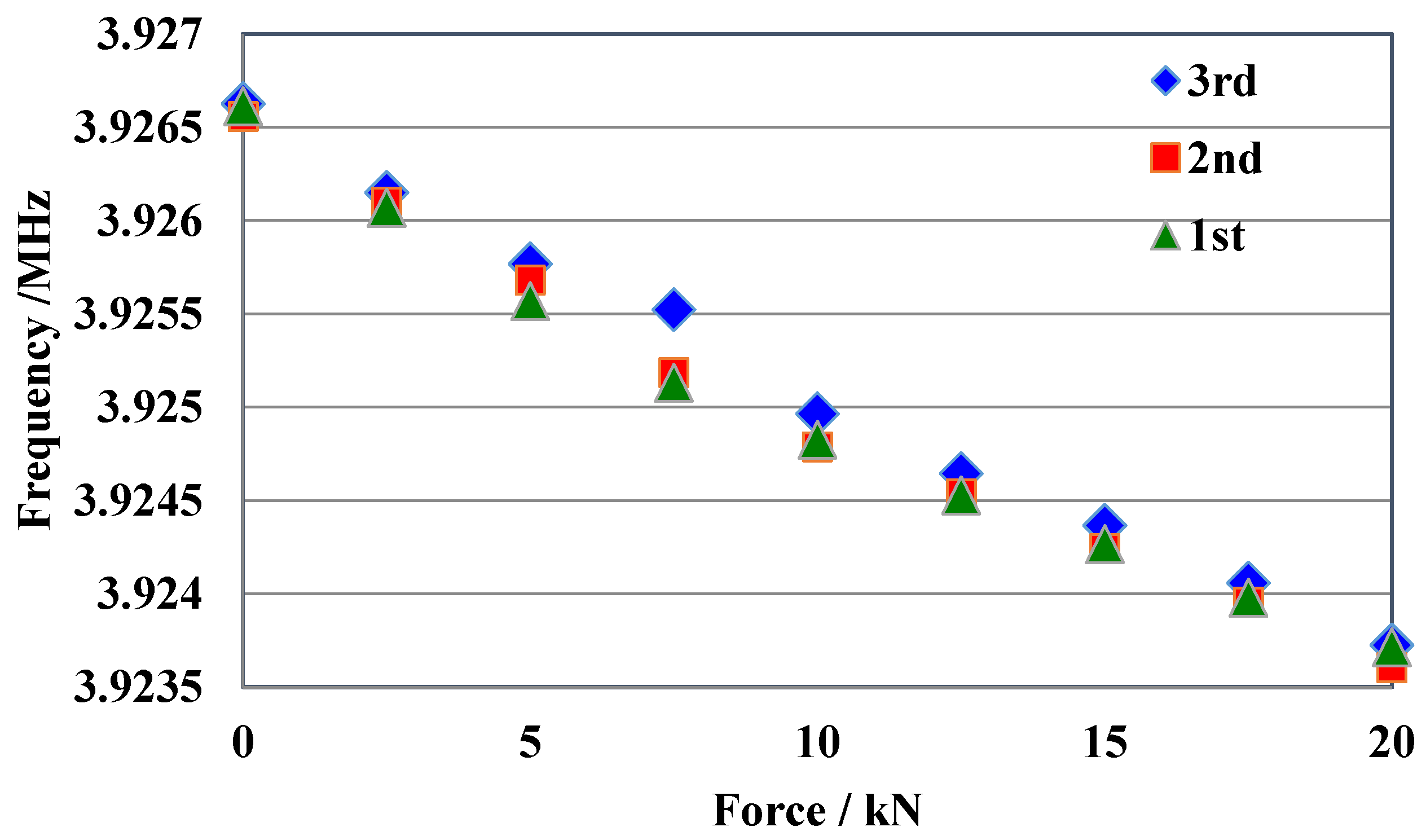
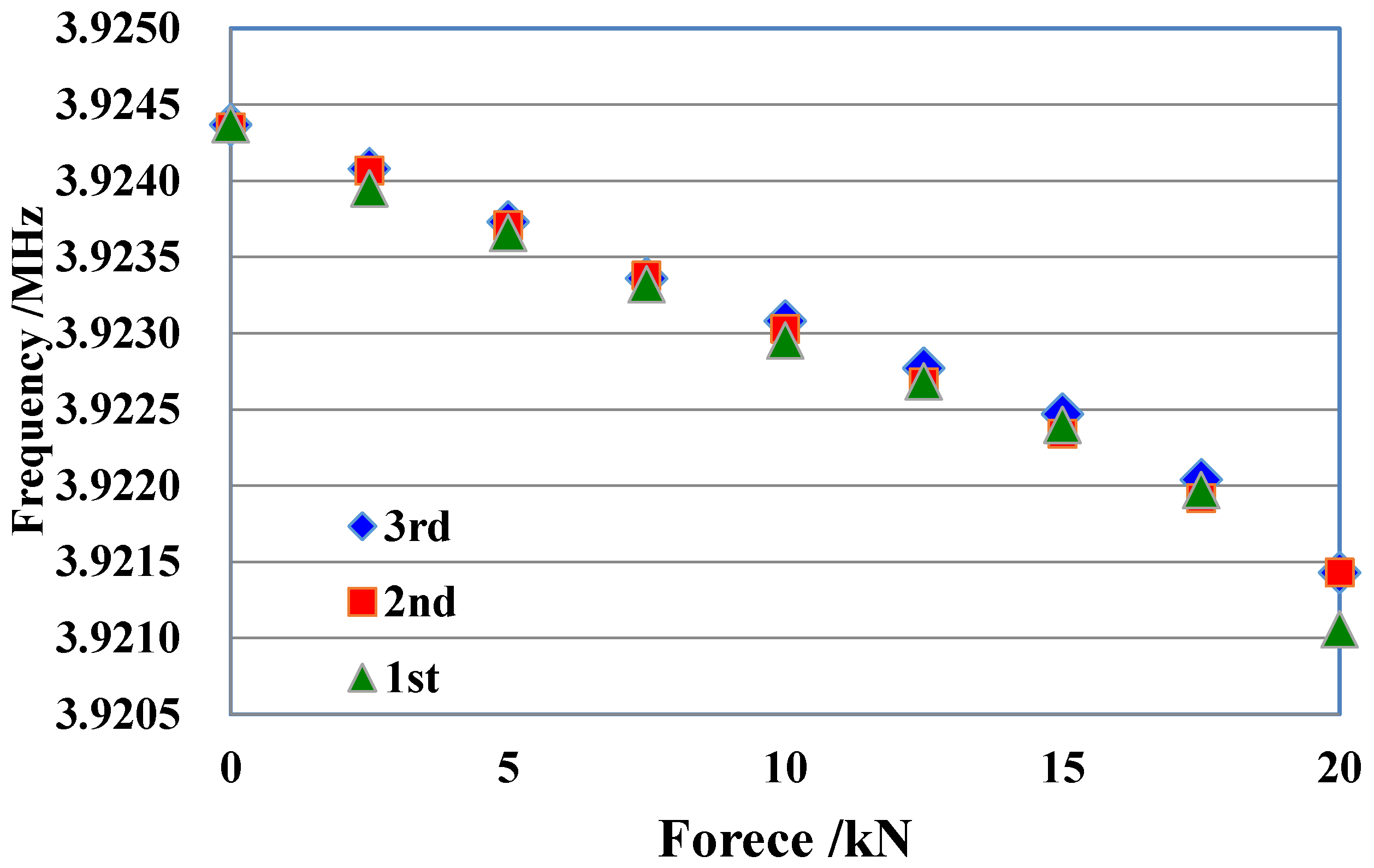
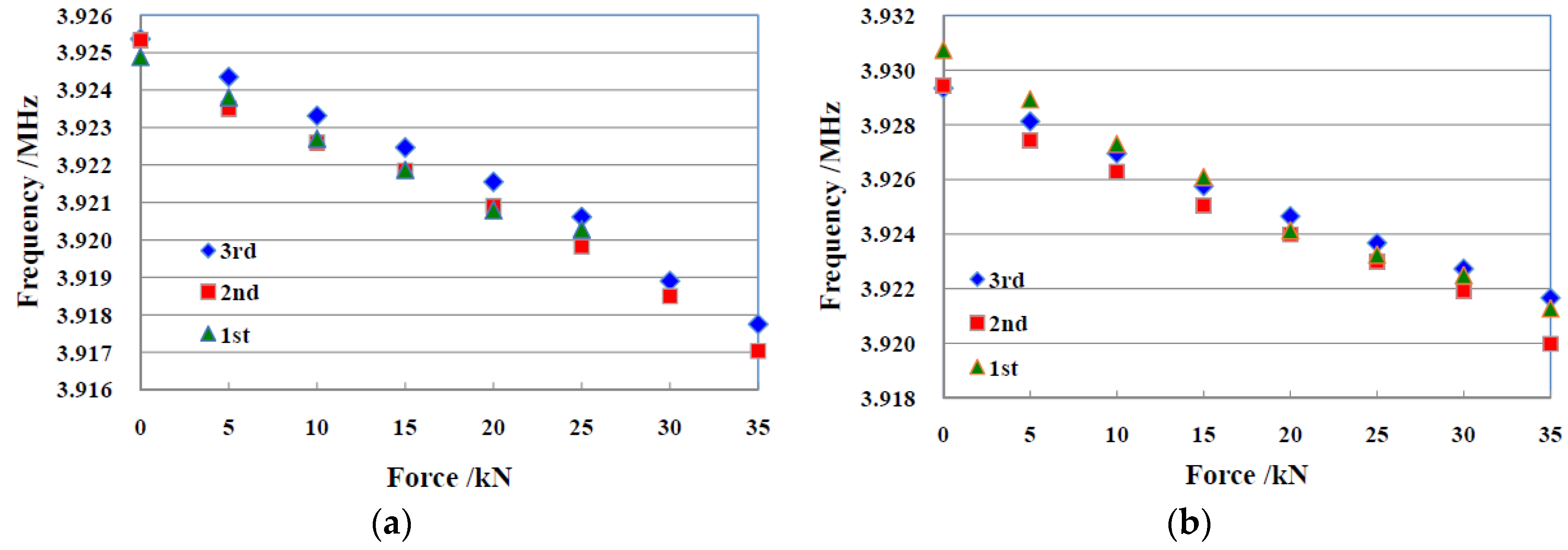
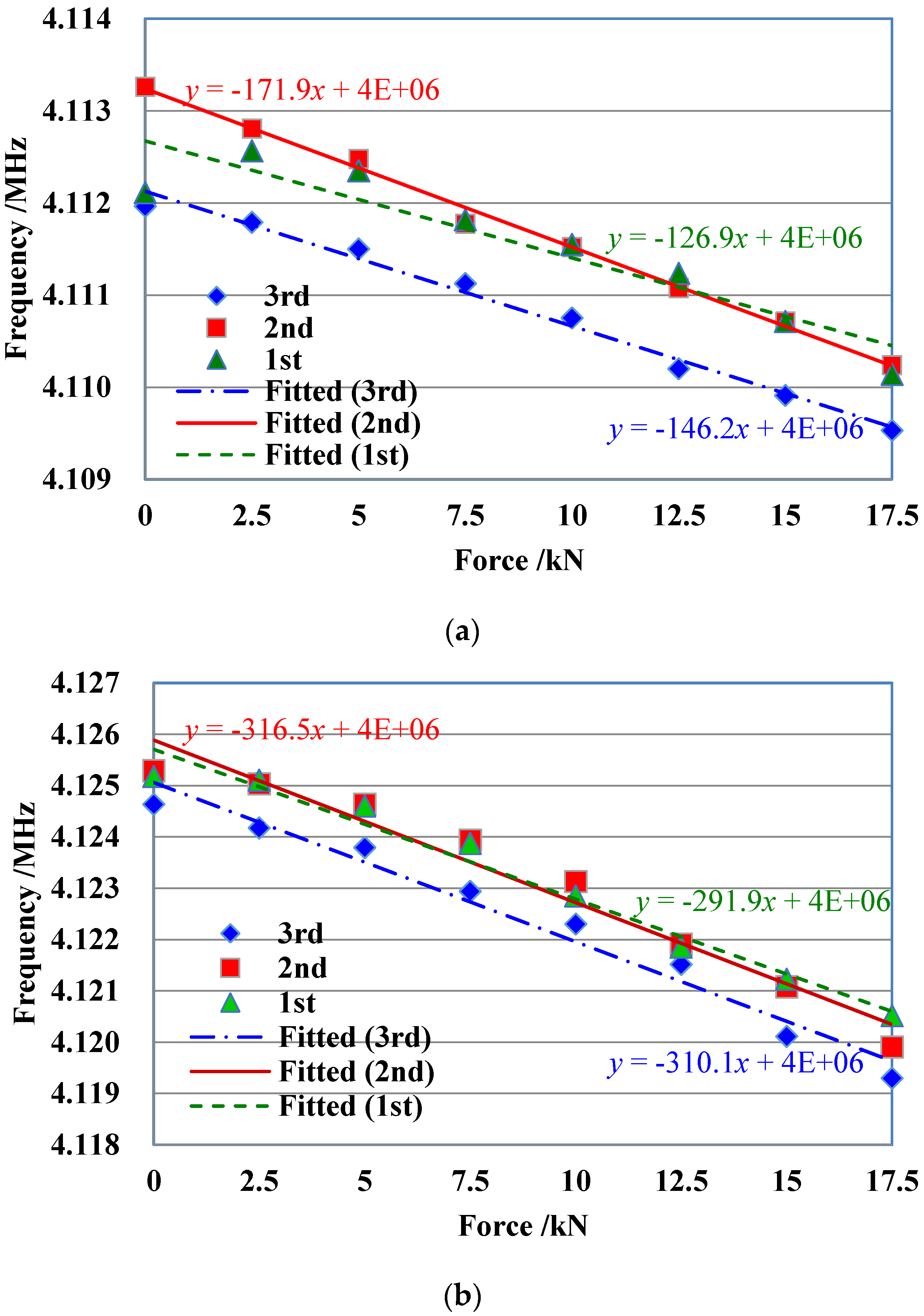
4. The Experimental Results and Analysis
4.1. The M16 Bolt Experimental Results
4.2. The M12 Bolt Experimental Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, T.; Song, G.; Liu, S.; Li, Y.; Xiao, H. Review of Bolted Connection Monitoring. Int. J. Distrib. Sens. Netw. 2013, 2013, 1–8. [Google Scholar] [CrossRef]
- Hirao, M.; Ogi, H.; Yasui, H. Contactless measurement of bolt axial stress using a shear-wave electromagnetic acoustic transducer. NDT & E Int. 2001, 34, 179–183. [Google Scholar]
- Jhang, K.Y.; Quan, H.H.; Ha, J.; Kim, N.Y. Estimation of clamping force in high-tension bolts through ultrasonic velocity measurement. Ultrasonics 2006, 44, e1339–e1342. [Google Scholar] [CrossRef] [PubMed]
- Kim, N.; Hong, M. Measurement of axial stress using mode-converted ultrasound. NDT & E Int. 2009, 42, 164–169. [Google Scholar]
- Chaki, S.; Corneloup, G.; Lillamand, I.; Walaszek, H. Combination of longitudinal and transverse ultrasonic waves for in situ control of the tightening of bolts. J. Press. Vessel Technol. 2007, 129, 383–390. [Google Scholar] [CrossRef]
- Joshi, S.G.; Pathare, R.G. Ultrasonic instrument for measuring bolt stress. Ultrasonics 1984, 22, 261–269. [Google Scholar] [CrossRef]
- Caccese, V.; Mewer, R.; Vel, S.S. Detection of bolt load loss in hybrid composite/metal bolted connections. Eng. Struct. 2004, 26, 895–906. [Google Scholar] [CrossRef]
- Amerini, F.; Barbieri, E.; Meo, M.; Polimeno, U. Detecting loosening/tightening of clamped structures using nonlinear vibration techniques. Smart Mater. Struct. 2010, 19, 085013. [Google Scholar] [CrossRef]
- Amerini, F.; Meo, M. Structural health monitoring of bolted joints using linear and nonlinear acoustic/ultrasound methods. Struct. Health Monit. 2011, 10, 659–672. [Google Scholar] [CrossRef]
- Meyer, J.L.; Harrington, W.B.; Agrawal, B.N.; Song, G. Vibration suppression of a spacecraft flexible appendage using smart material. Smart Mater. Struct. 1998, 7, 95–104. [Google Scholar] [CrossRef]
- Sethi, V.; Song, G. Optimal vibration control of a model frame structure using piezoceramic sensors and actuators. J. Vib. Control 2005, 11, 671–684. [Google Scholar] [CrossRef]
- Song, G.; Gu, H.; Mo, Y.L.; Hsu, T.T.C.; Dhonde, H. Concrete structural health monitoring using embedded piezoceramic transducers. Smart Mater. Struct. 2007, 16, 959–968. [Google Scholar] [CrossRef]
- Laskar, A.; Gu, H.; Mo, Y.L.; Song, G. Progressive collapse of a two-story reinforced concrete frame with embedded smart aggregates. Smart Mater. Struct. 2009, 18, 075001. [Google Scholar] [CrossRef]
- Yang, J.; Chang, F.K. Detection of bolt loosening in C–C composite thermal protection panels: I. Diagnostic principle. Smart Mater. Struct. 2006, 15, 581–590. [Google Scholar] [CrossRef]
- Yang, J.; Chang, F.K. Detection of bolt loosening in C–C composite thermal protection panels: II. Experimental verification. Smart Mater. Struct. 2006, 15, 591–599. [Google Scholar] [CrossRef]
- Wang, T.; Song, G.; Wang, Z.; Li, Y. Proof-of-concept study of monitoring bolt connection status using a piezoelectric based active sensing method. Smart Mater. Struct. 2013, 22, 087001. [Google Scholar] [CrossRef]
- Wang, T.; Liu, S.; Shao, J.; Li, Y. Health monitoring of bolted joints using the time reversal method and piezoelectric transducers. Smart Mater. Struct. 2016, 25, 025010. [Google Scholar] [CrossRef]
- Song, G.; Li, H.; Gajic, B.; Zhou, W.; Chen, P.; Gu, H. Wind turbine blade health monitoring with piezoceramic-based wireless sensor network. Int. J. Smart Nano Mater. 2013, 4, 150–166. [Google Scholar] [CrossRef]
- Ruan, J.; Ho, S.C.M.; Patil, D.; Li, M.; Song, G. Wind turbine blade damage detection using an active sensing approach. Smart Mater. Struct. 2014, 23, 105005. [Google Scholar] [CrossRef]
- Liang, C.; Sun, F.P.; Rogers, C.A. Coupled electro-mechanical analysis of adaptive material systems—Determination of the actuator power consumption and system energy transfer. J. Intell. Mater. Syst. Struct. 1994, 5, 12–20. [Google Scholar] [CrossRef]
- Park, G.; Sohn, H.; Farrar, C.R.; Inman, D.J. Overview of piezoelectric impedance-based health monitoring and path forward. Shock Vib. Dig. 2003, 35, 451–463. [Google Scholar] [CrossRef]
- Gu, H.; Moslehy, Y.; Sanders, D.; Song, G.; Mo, Y.L. Multi-functional smart aggregate-based structural health monitoring of circular reinforced concrete columns subjected to seismic excitations. Smart Mater. Struct. 2010, 19, 065026. [Google Scholar] [CrossRef]
- Ruan, J.; Ho, S.C.M.; Patil, D.; Song, G. Structural health monitoring of wind turbine blade using piezoceremic based active sensing and impedance sensing. In Proceedings of the 2014 IEEE 11th International Conference on Networking, Sensing and Control (ICNSC), Miami, FL, USA, 7–9 April 2014; pp. 661–666.
- Wong, Y.R.; Du, H.; Pang, X. Real-time electrical impedance resonance shift of piezoelectric sensor for detection of damage in honeycomb core sandwich structures. NDT & E Int. 2015, 76, 61–65. [Google Scholar]
- Selva, P.; Cherrier, O.; Budinger, V.; Lachaud, F.; Morlier, J. Smart monitoring of aeronautical composites plates based on electromechanical impedance measurements and artificial neural networks. Eng. Struct. 2013, 56, 794–804. [Google Scholar] [CrossRef]
- Bhalla, S.; Soh, C.K. Structural health monitoring by piezo-impedance transducers. I: Modeling. J. Aerosp. Eng. 2004, 17, 154–165. [Google Scholar] [CrossRef]
- Lim, Y.Y.; Bhalla, S.; Soh, C.K. Structural identification and damage diagnosis using self-sensing piezo-impedance transducers. Smart Mater. Struct. 2006, 15, 987–995. [Google Scholar] [CrossRef]
- Peairs, D.M.; Park, G.; Inman, D.J. Improving accessibility of the impedance-based structural health monitoring method. J. Intell. Mater. Syst. Struct. 2004, 15, 129–139. [Google Scholar] [CrossRef]
- Lu, X.; Zhu, C.; Zhang, J.; Wang, N.; Li, Y. Application of Electro-Mechanical Impedance Method in Crack Detecting of Welding Line. J. Nanjing Univers. Aeron. Astron. 2011, 2, 205–209. [Google Scholar]
- Lim, Y.Y.; Soh, C.K. Fatigue life estimation of a 1D aluminum beam under mode-I loading using the electromechanical impedance technique. Smart Mater. Struct. 2011, 20, 125001. [Google Scholar] [CrossRef]
- Liang, Y.; Li, D.; Parvasi, S.M.; Kong, Q.; Song, G. Bond-slip detection of concrete-encased composite structure using electro-mechanical impedance technique. Smart Mater. Struct. 2016, 25, 095003. [Google Scholar] [CrossRef]
- Martowicz, A.; Sendecki, A.; Salamon, M.; Rosiek, M.; Uhl, T. Application of electromechanical impedance-based SHM for damage detection in bolted pipeline connection. Nondestruct. Test. Eval. 2015, 31, 17–44. [Google Scholar] [CrossRef]
- Ritdumrongkul, S.; Abe, M.; Fujino, Y.; Miyashita, T. Quantitative health monitoring of bolted joints using a piezoceramic actuator-sensor. Smart Mater. Struct. 2003, 13, 20–29. [Google Scholar] [CrossRef]
- Park, G.; Cudney, H.H.; Inman, D.J. Feasibility of using impedance-based damage assessment for pipeline structures. Earthquake Eng. Struct. Dyn. 2001, 30, 1463–1474. [Google Scholar] [CrossRef]
- Wait, J.R.; Park, G.; Farrar, C.R. Integrated structural health assessment using piezoelectric active sensors. Shock Vib. 2005, 12, 389–405. [Google Scholar] [CrossRef]
- An, Y.K.; Sohn, H. Integrated impedance and guided wave based damage detection. Mech. Syst. Signal Process. 2012, 28, 50–62. [Google Scholar] [CrossRef]
- Annamdas, V.G.M.; Yang, Y.; Soh, C.K. Influence of loading on the electromechanical admittance of piezoceramic transducers. Smart Mater. Struct. 2007, 16, 1888–1897. [Google Scholar] [CrossRef]
- Ong, C.W.; Yang, Y.; Naidu, A.S.; Lu, Y.; Soh, C.K. Application of the electro-mechanical impedance method for the identification of in-situ stress in structures. Proc. SPIE 2002, 503–514. [Google Scholar] [CrossRef]
- Lim, Y.Y.; Soh, C.K. Effect of varying axial load under fixed boundary condition on admittance signatures of electromechanical impedance technique. J. Intell. Mater. Syst. Struct. 2012, 23, 815–826. [Google Scholar] [CrossRef]
- Lim, Y.Y.; Liew, W.Y.H.; Soh, C.K. A Parametric Study on Admittance Signatures of a PZT Transducer under Free Vibration. Mech. Adv. Mater. Struct. 2015, 22, 877–884. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, H.; Lv, Y.; Wang, T.; Xu, Z. Detrended Fluctuation Analysis and Hough Transform Based Self-Adaptation Double-Scale Feature Extraction of Gear Vibration Signals. Shock Vib. 2016, 2016, 1–9. [Google Scholar] [CrossRef]
- Lv, Y.; Zhu, Q.; Yuan, R. Fault Diagnosis of Rolling Bearing Based on Fast Nonlocal Means and Envelop Spectrum. Sensors 2015, 15, 1182–1198. [Google Scholar] [CrossRef] [PubMed]

| Parameter | Symbol | Value |
|---|---|---|
| Density | 7800 kg/m3 | |
| Piezoelectric constant | d31 | 150 × 10−12 C/N |
| Dielectric constant | 1.3 × 10−8 F/m |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, J.; Wang, T.; Yin, H.; Yang, D.; Li, Y. Bolt Looseness Detection Based on Piezoelectric Impedance Frequency Shift. Appl. Sci. 2016, 6, 298. https://doi.org/10.3390/app6100298
Shao J, Wang T, Yin H, Yang D, Li Y. Bolt Looseness Detection Based on Piezoelectric Impedance Frequency Shift. Applied Sciences. 2016; 6(10):298. https://doi.org/10.3390/app6100298
Chicago/Turabian StyleShao, Junhua, Tao Wang, Heyue Yin, Dan Yang, and Yourong Li. 2016. "Bolt Looseness Detection Based on Piezoelectric Impedance Frequency Shift" Applied Sciences 6, no. 10: 298. https://doi.org/10.3390/app6100298
APA StyleShao, J., Wang, T., Yin, H., Yang, D., & Li, Y. (2016). Bolt Looseness Detection Based on Piezoelectric Impedance Frequency Shift. Applied Sciences, 6(10), 298. https://doi.org/10.3390/app6100298