Extremely Nonlinear Optics Using Shaped Pulses Spectrally Broadened in an Argon- or Sulfur Hexafluoride-Filled Hollow-Core Fiber
Abstract
:1. Introduction

2. Experimental Section
2.1. Experimental Setup

2.2. Spectral Broadening in a Gas-Filled HCF
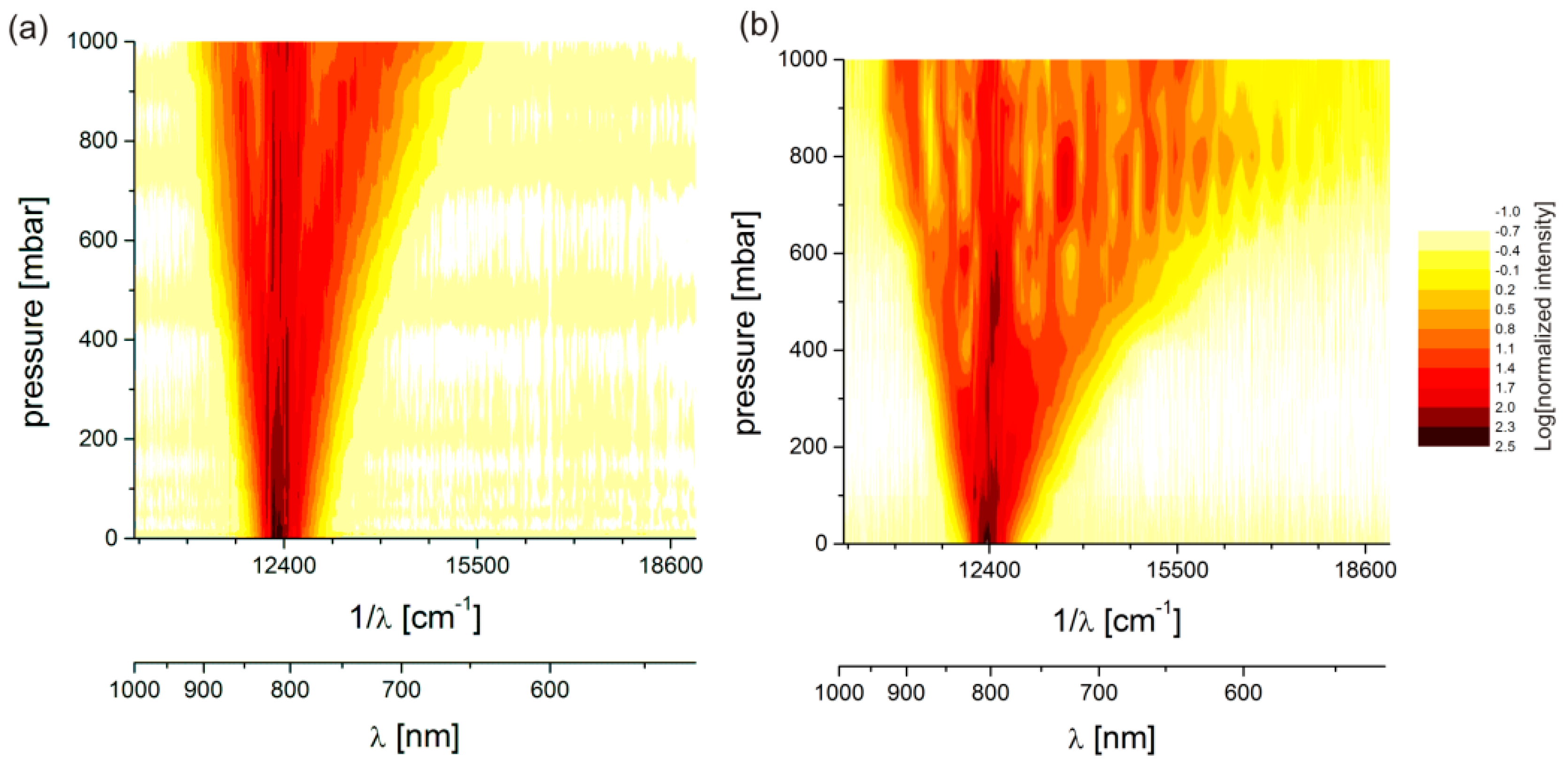
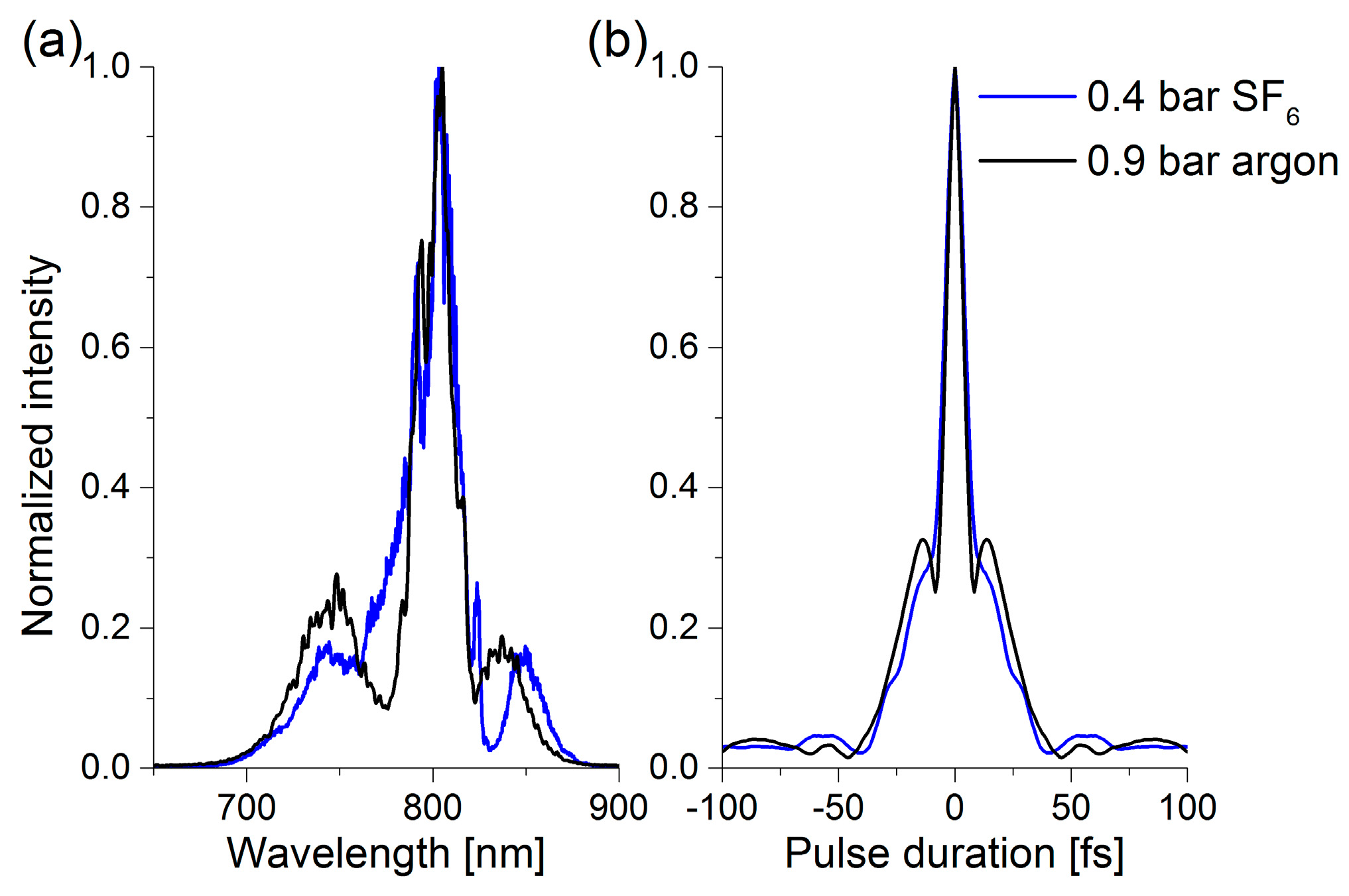
2.3. Tailored High-Harmonic Generation in a Gas-Filled HCF

3. Results and Discussion
3.1. Optimization of the XUV Yield
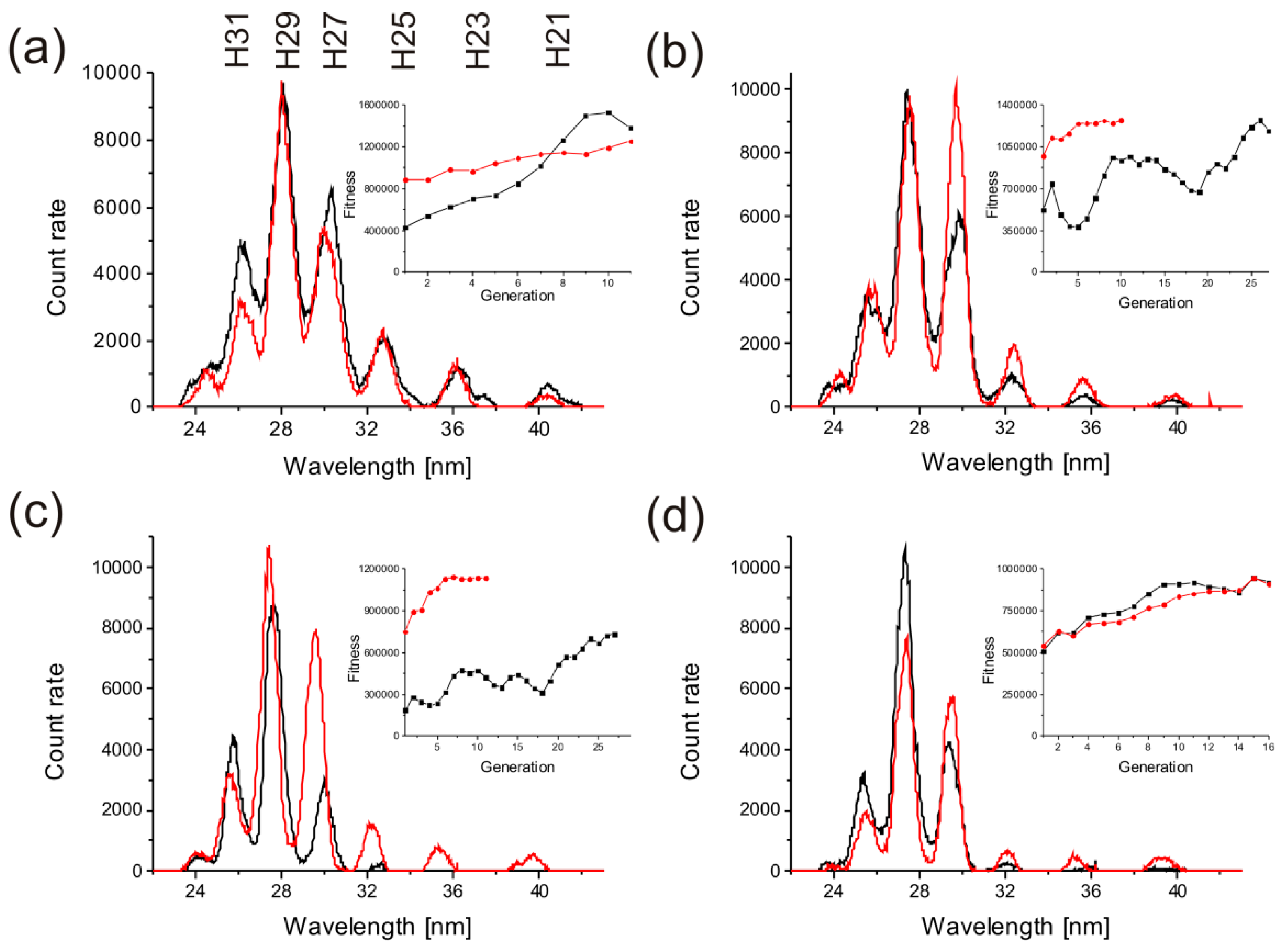
3.2. Selection of Single Harmonics
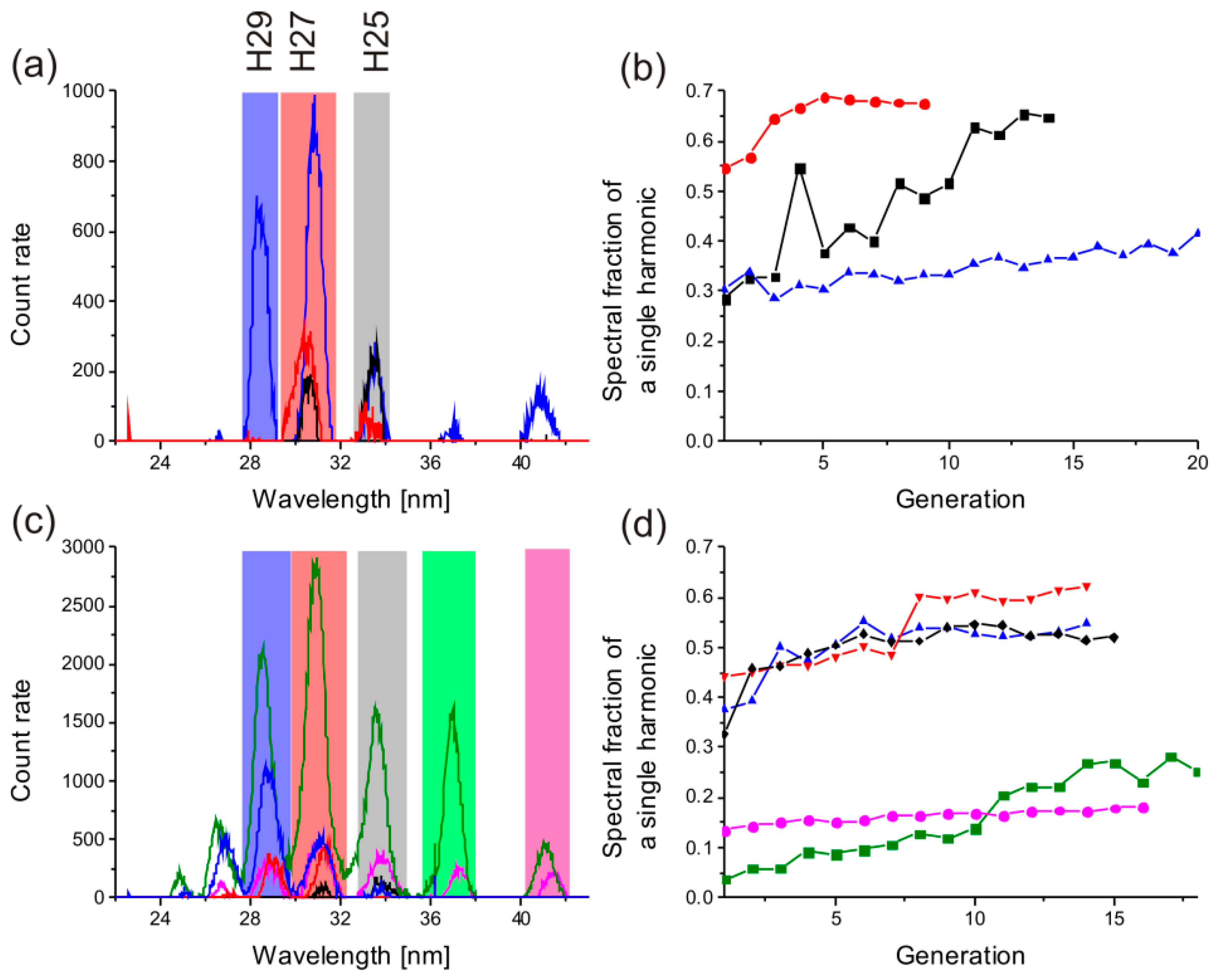
4. Conclusions and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163–234. [Google Scholar] [CrossRef]
- Itatani, J.; Levesque, J.; Zeidler, D.; Niikura, H.; Pepin, H.; Kieffer, J.C.; Corkum, P.B.; Villeneuve, D.M. Tomographic imaging of molecular orbitals. Nature 2004, 432, 867–871. [Google Scholar] [CrossRef] [PubMed]
- Winterfeldt, C.; Spielmann, C.; Gerber, G. Colloquium: Optimal control of high-harmonic generation. Rev. Mod. Phys. 2008, 80, 117–140. [Google Scholar] [CrossRef]
- Pfeifer, T.; Spitzenpfeil, R.; Walter, D.; Winterfeldt, C.; Dimler, F.; Gerber, G.; Spielmann, C. Towards optimal control with shaped soft-X-ray light. Opt. Express 2007, 15, 3409–3416. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Jin, C.; Lin, C.D. Coherent control of high-harmonic generation using waveform-synthesized chirped laser fields. Phys. Rev. A 2014. [Google Scholar] [CrossRef]
- Zürch, M.; Rothhardt, J.; Hädrich, S.; Demmler, S.; Krebs, M.; Limpert, J.; Tünnermann, A.; Guggenmos, A.; Kleineberg, U.; Spielmann, C. Real-time and sub-wavelength ultrafast coherent diffraction imaging in the extreme ultraviolet. Sci. Rep. 2014. [Google Scholar] [CrossRef]
- Zürch, M.; Foertsch, S.; Matzas, M.; Pachmann, K.; Kuth, R.; Spielmann, C. Cancer cell classification with coherent diffraction imaging using an extreme ultraviolet radiation source. JMIOBU 2014. [Google Scholar] [CrossRef]
- Spielmann, C.; Burnett, N.H.; Sartania, S.; Koppitsch, R.; Schnurer, M.; Kan, C.; Lenzner, M.; Wobrauschek, P.; Krausz, F. Generation of coherent X-rays in the water window using 5-femtosecond laser pulses. Science 1997, 278, 661–664. [Google Scholar] [CrossRef]
- Serrat, C.; Roca, D.; Seres, J. Coherent amplification of attosecond light pulses in the water-window spectral region. Opt. Express 2015, 23, 4867–4872. [Google Scholar] [CrossRef] [PubMed]
- Nisoli, M.; de Silvestri, S.; Svelto, O.; Szipocs, R.; Ferencz, K.; Spielmann, C.; Sartania, S.; Krausz, F. Compression of high-energy laser pulses below 5 fs. Opt. Lett. 1997, 22, 522–524. [Google Scholar] [CrossRef] [PubMed]
- Russell, P.S.; Holzer, P.; Chang, W.; Abdolvand, A.; Travers, J.C. Hollow-core photonic crystal fibres for gas-based nonlinear optics. Nat. Photonics 2014, 8, 278–286. [Google Scholar] [CrossRef]
- Okell, W.A.; Witting, T.; Fabris, D.; Austin, D.; Bocoum, M.; Frank, F.; Ricci, A.; Jullien, A.; Walke, D.; Marangos, J.P.; et al. Carrier-envelope phase stability of hollow fibers used for high-energy few-cycle pulse generation. Opt. Lett. 2013, 38, 3918–3921. [Google Scholar] [CrossRef] [PubMed]
- Zhavoronkov, N.; Korn, G. Generation of single intense short optical pulses by ultrafast molecular phase modulation. Phys. Rev. Lett. 2002. [Google Scholar] [CrossRef] [PubMed]
- Turner, F.C.; Strickland, D. Anti-stokes enhancement of multifrequency raman generation in a hollow fiber. Opt. Lett. 2008, 33, 405–407. [Google Scholar] [CrossRef] [PubMed]
- Turner, F.C.; Trottier, A.; Strickland, D.; Losev, L.L. Transient multi-frequency raman generation in SF6. Opt. Commun. 2007, 270, 419–423. [Google Scholar] [CrossRef]
- Zhavoronkov, N. Efficient spectral conversion and temporal compression of femtosecond pulses in SF6. Opt. Lett. 2011, 36, 529–531. [Google Scholar] [CrossRef] [PubMed]
- Landgraf, B.; Hoffmann, A.; Kartashov, D.; Gärtner, F.; Samsonova, Z.; Polynkin, P.; Jacoby, J.; Kühl, T.; Spielmann, C. Generation of multi-millijoule red-shifted pulses for seeding stimulated raman backscattering amplifiers. Opt. Express 2015, 23, 7400–7406. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, A.; Zürch, M.; Gräfe, M.; Spielmann, C. Spectral broadening and compression of sub-millijoule laser pulses in hollow-core fibers filled with sulfur hexafluoride. Opt. Express 2014, 22, 12038–12045. [Google Scholar] [CrossRef] [PubMed]
- Pfeifer, T.; Walter, D.; Winterfeldt, C.; Spielmann, C.; Gerber, G. Controlling the spectral shape of coherent soft X-rays. Appl. Phys. B 2005, 80, 277–280. [Google Scholar] [CrossRef]
- Nibbering, E.T.J.; Grillon, G.; Franco, M.A.; Prade, B.S.; Mysyrowicz, A. Determination of the inertial contribution to the nonlinear refractive index of air, N2, and O2 by use of unfocused high-intensity femtosecond laser pulses. J. Opt. Soc. Am. B 1997, 14, 650–660. [Google Scholar] [CrossRef]
- Carman, R.L.; Mack, M.E. Experimental investigation of transient stimulated raman scattering in a linearly dispersionless medium. Phys. Rev. A 1972. [Google Scholar] [CrossRef]
- Everall, N.J.; Partanen, J.P.; Barr, J.R.M.; Shaw, M.J. Threshold measurements of stimulated raman scattering in gases using picosecond krf laser pulses. Opt. Commun. 1987, 64, 393–397. [Google Scholar] [CrossRef]
- Rundquist, A.; Durfee, C.G.; Chang, Z.H.; Herne, C.; Backus, S.; Murnane, M.M.; Kapteyn, H.C. Phase-matched generation of coherent soft X-rays. Science 1998, 280, 1412–1415. [Google Scholar] [CrossRef] [PubMed]
- Holgado, W.; Alonso, B.; Roman, J.S.; Sola, I.J. Temporal and spectral structure of the infrared pulse during the high order harmonic generation. Opt. Express 2014, 22, 10191–10201. [Google Scholar] [CrossRef] [PubMed]
- Anderson, P.N.; Horak, P.; Frey, J.G.; Brocklesby, W.S. High-energy laser-pulse self-compression in short gas-filled fibers. Phys. Rev. A 2014. [Google Scholar] [CrossRef]
- Serrat, C. Broadband spectral amplitude control in high-order harmonic generation. Appl. Sci. 2012, 2, 816–830. [Google Scholar] [CrossRef]
- Haight, R.; Seidler, P.F. High-resolution atomic core-level spectroscopy with laser harmonics. Appl. Phys. Lett. 1994, 65, 517–519. [Google Scholar] [CrossRef]
- Fruke, R.; Kutzner, J.; Witting, T.; Zacharias, H.; Wilhein, T. Euv scanning transmission microscope operating with high-harmonic and laser plasma radiation. Europhys. Lett. 2005, 72, 915–921. [Google Scholar] [CrossRef]
- Haarlammert, T.; Zacharias, H. Application of high harmonic radiation in surface science. Curr. Opin. Solid State Mater. Sci. 2009, 13, 13–27. [Google Scholar] [CrossRef]
- Berlasso, R.; Dallera, C.; Borgatti, F.; Vozzi, C.; Sansone, G.; Stagira, S.; Nisoli, M.; Ghiringhelli, G.; Villoresi, P.; Poletto, L.; et al. High-order laser harmonics and synchrotron study of transition metals M2,3 edges. Phys. Rev. B 2006. [Google Scholar] [CrossRef]
- Loh, Z.H.; Khalil, M.; Correa, R.E.; Leone, S.R. A tabletop femtosecond time-resolved soft X-ray transient absorption spectrometer. Rev. Sci. Instrum. 2008. [Google Scholar] [CrossRef] [PubMed]
- Guggenmos, A.; Jobst, M.; Ossiander, M.; Radunz, S.; Riemensberger, J.; Schaffer, M.; Akil, A.; Jakubeit, C.; Bohm, P.; Noever, S.; et al. Chromium/scandium multilayer mirrors for isolated attosecond pulses at 145 eV. Opt. Lett. 2015, 40, 2846–2849. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoffmann, A.; Zürch, M.; Spielmann, C. Extremely Nonlinear Optics Using Shaped Pulses Spectrally Broadened in an Argon- or Sulfur Hexafluoride-Filled Hollow-Core Fiber. Appl. Sci. 2015, 5, 1310-1322. https://doi.org/10.3390/app5041310
Hoffmann A, Zürch M, Spielmann C. Extremely Nonlinear Optics Using Shaped Pulses Spectrally Broadened in an Argon- or Sulfur Hexafluoride-Filled Hollow-Core Fiber. Applied Sciences. 2015; 5(4):1310-1322. https://doi.org/10.3390/app5041310
Chicago/Turabian StyleHoffmann, Andreas, Michael Zürch, and Christian Spielmann. 2015. "Extremely Nonlinear Optics Using Shaped Pulses Spectrally Broadened in an Argon- or Sulfur Hexafluoride-Filled Hollow-Core Fiber" Applied Sciences 5, no. 4: 1310-1322. https://doi.org/10.3390/app5041310
APA StyleHoffmann, A., Zürch, M., & Spielmann, C. (2015). Extremely Nonlinear Optics Using Shaped Pulses Spectrally Broadened in an Argon- or Sulfur Hexafluoride-Filled Hollow-Core Fiber. Applied Sciences, 5(4), 1310-1322. https://doi.org/10.3390/app5041310







