Electrically Small Resonators for Planar Metamaterial, Microwave Circuit and Antenna Design: A Comparative Analysis

Abstract

Planar metamaterials and many microwave circuits and antennas are designed by means of resonators with dimensions much smaller than the wavelength at their resonance frequency. There are many types of such electrically small resonators, and the main purpose of this paper is to compare them as building blocks for the implementation of microwave components. Aspects such as resonator size, bandwidth, their circuit models when they are coupled to transmission lines (as is usually required), as well as key applications, will be considered.

1. Introduction

Resonators are key elements in radiofrequency (RF) and microwave engineering. Many passive and active circuits (such as filters, diplexers, oscillators, amplifiers, etc.) and antennas contain resonant elements in their designs [1,2]. There are many types of resonators of interest for RF and microwave applications, such as cavity resonators, dielectric resonators, acoustic wave resonators, lumped element resonators, quartz crystal resonators, transmission line resonators, and semilumped resonators, among others. In this paper, the focus is on semilumped resonators, namely, planar resonators with dimensions much smaller than the signal wavelength, λ, at their fundamental resonance frequency [3]. Transmission line resonators are also planar resonators, but their dimensions scale with the resonance frequency. It is well known, for instance, that a short-circuited λ/2 transmission line behaves as a series resonator, whereas it can be modeled by a parallel resonator if it is open ended [1]. Conversely, for λ/4 lines, a short-circuit load provides a parallel resonance, whereas for an open ended line the input impedance is that of a series resonator. Such transmission line resonators have been used in many microwave applications, such as filters (parallel coupled line bandpass filters, gap coupled λ/2-resonator filters, bandpass and bandstop filters based on shunt stubs, etc.) and antennas (printed dipole and monopole antennas, for instance) [1]. However, the fact that their dimensions scale with frequency is a limiting aspect in terms of device miniaturization.

To reduce device size, a possible strategy is to replace transmission line resonators with semilumped resonators. The advantage of this approach is the full compatibility with planar technology. As mentioned above, semilumped resonators are electrically small resonant elements. In such resonators, the resonance, rather than being related to a distributed Fabry-Perot type phenomenon, can be interpreted in terms of an LC equivalent circuit, with a clearly identifiable inductance, L, and capacitance, C, in the resonator topology. As long as semilumped resonators are small (as compared to transmission line resonators) and fully planar, they are of special interest in applications where size reduction and cost are important. However, as the resonator’s size is reduced, the quality factor, Q, is also degraded, and for certain applications (such as reference oscillators, very narrow band pass filters, etc.), other high-Q resonators (such as cavity resonators, or crystal resonators, among others) are a necessity. Nevertheless, semilumped resonators may find application in a wide variety of scenarios, such as microwave front ends (in image rejection filters, in intermediate frequency −IF− filters, etc.), or as constitutive building blocks of a new class of artificial structures known as metamaterials [4,5,6,7,8,9,10]. Let us now briefly consider in the next section the potentiality of electrically small resonators for the design of microwave circuits and metamaterials based on two illustrative examples. In Section 3, the different semilumped resonators considered in this paper will be presented and analyzed. Some illustrative applications will be presented in Section 4. Finally, the main conclusions will be highlighted in Section 5.

2. Electrically Small Resonators for Metamaterial and Microwave Circuit Design

As we have mentioned before, in semilumped resonators the inductance and capacitance can be associated to a certain element of the resonator topology (in certain cases, a single element can provide the inductive and capacitive behavior). To clarify this aspect, let us consider the implementation of a transmission line with a shunt connecting the series resonator to the ground (Figure 1(a)). From the transmission line theory, it is well known that such resonators can be implemented by means of a λ/4 open stub, as depicted in Figure 1(b) [2]. However, the shunt-connected resonator can be alternatively realized by means of a stepped impedance shunt stub (SISS), as shown in Figure 1(c) [11]. The narrow section of the stub is essentially a series inductance, whereas the wide section behaves as a grounded patch capacitance. Both designs of Figure 1(b,c) provide the same resonance frequency, as derived from the transmission zero present in the transmission coefficient (Figure 1(d)). Such a transmission of zero is caused by the short at the position of the resonator. However, it can be appreciated that the length of the SISS is significantly smaller than the length of the transmission line stub, as corresponds to a semilumped component.

Figure 1. (a) Transmission line loaded with a grounded resonator. (b) Implementation of the resonator by means of a λ/4 open stub. (c) Implementation of the resonator by means of a stepped impedance shunt stub (SISS). (d) Typical frequency response of the line loaded with the λ/4 open stub and SISS.

Figure 1. (a) Transmission line loaded with a grounded resonator. (b) Implementation of the resonator by means of a λ/4 open stub. (c) Implementation of the resonator by means of a stepped impedance shunt stub (SISS). (d) Typical frequency response of the line loaded with the λ/4 open stub and SISS.

The considered SISS is an open resonator, since it is driven by the current generated by the line. Let us now consider electrically small closed resonators, which can be electrically or magnetically driven. It is obvious that if a λ/2 transmission line is closed in a ring configuration, as shown in Figure 2(a), this resonator can be excited by means of an axial time varying magnetic field, or even by means of an electric field in the plane of the particle. Since the electrical length of the ring is λ/2 at resonance, it follows that its diameter is λ/2π at this frequency, i.e., relatively small compared to the wavelength. However, this ring resonator is a distributed element since it operates under the same principle than the unfolded counterpart. In order to reduce the size of a split ring, one possible solution is to add an inner ring with the gap on the opposite side, as depicted in Figure 2(b) [12]. By virtue of the mutual coupling between both rings, the fundamental resonance of the resulting particle is lower than the fundamental resonance of any of the individual rings, and thus the particle is electrically smaller than a single ring resonator [13]. The particle of Figure 2(b) is called split ring resonator (SRR), and, as long as its diameter can be made much smaller than the wavelength, this particle is useful for the implementation of effective media with controllable electromagnetic properties, also called metamaterials. Specifically, since, above SRR resonance, the magnetic field generated by the induced currents in the SRR is opposite to the incident magnetic field, this particle is useful for the synthesis of negative effective permeability media. Figure 2(c) shows the first three-dimensional metamaterial structure that was conceived to exhibit backward (or left-handed) wave propagation [14]. The necessary negative effective permeability and permittivity to achieve left-handedness was due to the presence of SRRs and metallic posts, respectively.

Through these two examples, it is clear that electrically small resonators have a high potentiality in both microwave engineering and metamaterial synthesis. Nevertheless, microwave circuits and antennas based on metamaterial concepts and implemented by means of electrically small resonators like the SRR have been reported. Therefore, the analysis and comparison of such electrically small resonators is of highest interest and is the purpose of the next section.

Figure 2. (a) λ/2 ring resonator. (b) Split ring resonator (SRR). (c) First bulk SRR-based reported structure exhibiting backward wave propagation in a certain frequency band. Photograph courtesy of D.R. Smith.

Figure 2. (a) λ/2 ring resonator. (b) Split ring resonator (SRR). (c) First bulk SRR-based reported structure exhibiting backward wave propagation in a certain frequency band. Photograph courtesy of D.R. Smith.

3. Electrically Small Planar Resonators: A Comparative Analysis and Circuit Models

There are many types of electrically small planar resonators. In this paper, the main focus will be on those resonators of interest for the design of metamaterials or metamaterial-based or inspired microwave circuits and antennas. The list may be too long, hence, it will be limited to the more relevant and useful implementations, according to the authors own experience.

3.1. Topologies and Circuit Models of the Isolated Resonators

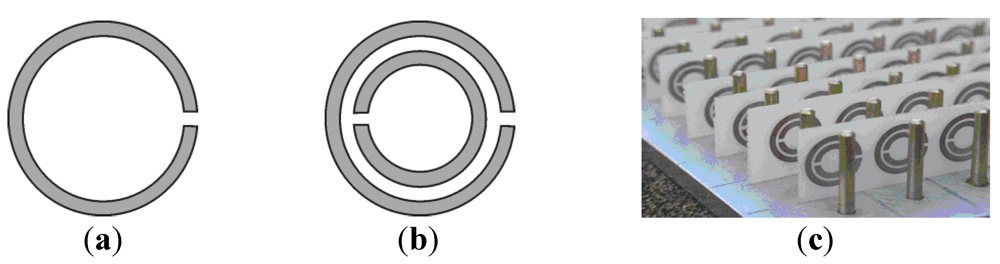
Let us begin with the SRR already considered in the previous section [12]. As long as the distance between both rings is small (i.e., there is significant coupling between them), the particle can be considered to be electrically small and a quasi-static analysis to infer the SRR inductance and capacitance can be applied. Such an analysis was carried out in [7,15]. When the SRR is excited by an external time-varying magnetic field directed along the SRR axis (z-axis in Figure 3), the cuts on each ring force the electric current to flow from one ring to another across the slot between them, taking the form of a strong displacement current. The slot between the rings therefore behaves as a distributed capacitance, and the whole SRR has the equivalent circuit shown in Figure 3(b), where L_s is the SRR self-inductance and C_o/2 is the capacitance associated with each SRR half. This capacitance is C_o = 2πr_oC_pul, where r_o is the mean radius of the SRR, and C_pul is the per unit length capacitance along the slot between the rings. The total capacitance of this circuit is the series connection of the capacitance of both SRR halves, that is, C_o/4. Therefore, the resonance frequency ω_o is given by:

(1)

The inductance L_s can be modeled as the inductance of an average ring of radius r_o, i.e., the mean radius of the ring, and width c. Approximate expressions for L_s, based on a variational calculation, are provided in [16]. Closed expressions for the per unit length capacitance are given in many microwave textbooks [17], and explicit expressions for L_s and C_pul are provided in [7].

The model of Figure 3 is valid as long as the perimeter of the ring can be considered small with regard to half wavelength, and the capacitance associated with the cuts on each ring can be neglected. Under such assumptions, the currents on each ring must vanish at the cuts, and the angular dependence of the currents on each ring can be assumed to be linear (so that the total current on both rings is constant). Such assumptions also imply that the voltage across the slots is constant in both SRR halves. A more detailed circuit model, which takes into account the gap capacitance and includes a transmission line model for the slot between the rings has been reported in [18], but such a model converges to the model of Figure 3 when the capacitance of the cuts is neglected and the electrical length of the SRR is small [18]. As both approximations are usually fulfilled for any practical SRR design, the more simple model reported above is assumed valid in this paper.

Figure 3. SRR topology and its equivalent circuit model.

Figure 3. SRR topology and its equivalent circuit model.

The closer the rings of the SRR of Figure 3 are the lower the resonance frequency and the smaller the electrical size of the particle result. However, in practice, the separation between rings cannot be smaller than a certain value that depends on the fabrication technology (typically 100 µm for PCB technology). This means that the electrical size of edge coupled SRRs cannot be reduced below roughly λ/10. To circumvent this limiting aspect, one possible solution is to print the rings face-to-face on opposite sides of a thin dielectric slab. Whilst this modification does not significantly affect the behavior of the resonator, the per unit length capacitance (i.e., the capacitance of the broadside coupled strips) is markedly increased, and hence the particles can be made as small as λ/30 [15], or even smaller. Obviously, the penalty of these broadside coupled split ring resonators (BC-SRRs) is the need of two metallic levels for their implementation.

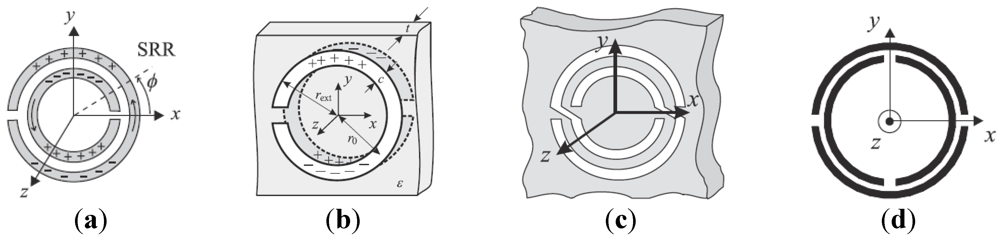
There is, however, another interesting aspect that differentiates the conventional SRR and the BC-SRR. The charge distribution in the SRR (depicted in Figure 4(a)) indicates that there is an electric dipole at the first resonance frequency in the orthogonal direction to the symmetry plane of the particle (such a symmetry plane is an electric wall). This means that the SRR can also be excited by means of a time varying electric field applied in the plane of the particle co-directional to the direction of the electric dipole. Hence, the first SRR resonance can be driven electrically and/or magnetically, i.e., the particle exhibits bianisotropy. For the BC-SRR, charges in the upper half are also images of charges in the lower half, but this charge distribution does not result in a net dielectric dipole (Figure 4(b)). Thus, the BC-SRR is non-bianisotropic. Another possible way to avoid bianisotropy while keeping a uniplanar design is by means of the topology depicted in Figure 4(c) [19]. Essentially, the circuit model of this particle, called non-bianisotropic split ring resonator (NB-SRR), is that of the conventional SRR. However, the NB-SRR, like the BC-SRR, has an inversion symmetry with regard to its center, which means that cross polarization effects are not present, i.e., the first resonance frequency cannot be excited through an electric field.

An alternative way to obtain inversion symmetry, thus overcoming bianisotropy is by introducing additional cuts in the edge coupled SRR, as Figure 4(d) illustrates [19]. This particle, called double slit split ring resonator DS-SRR, exhibits the same inductance as the SRR, but its capacitance is four times smaller since it is the result of the series connected edge capacitances of each SRR quarter. This means that the resonance frequency is twice the resonance frequency of the SRR, and hence the electrical size of the particle cannot be made very small.

Figure 4. Topology and charge distribution of (a) conventional SRR, (b) broadside coupled split ring resonators (BC-SRR), (c) non-bianisotropic split ring resonator (NB-SRR), and (d) double slit split ring resonator (DS-SRR).

Figure 4. Topology and charge distribution of (a) conventional SRR, (b) broadside coupled split ring resonators (BC-SRR), (c) non-bianisotropic split ring resonator (NB-SRR), and (d) double slit split ring resonator (DS-SRR).

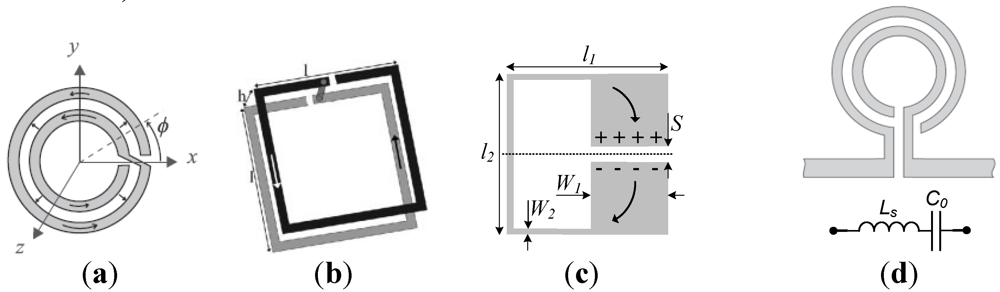
Another interesting particle that combines the advantages of small electrical size and uniplanar configuration is the spiral. The two-turn spiral 2-SR can be considered to be constituted of two rings with cuts in the same position and with an electric short between both rings through cross terminals, as shown in Figure 5(a). A quasistatic analysis of this particle [20,21] reveals that the inductance is that of the SRR with identical dimensions. However, the capacitance is the edge capacitance of the whole circumference. Therefore, the resonance frequency is half the resonance frequency of the SRR. Spirals are therefore very useful in applications where small electrical size combined with a monolayer design is required. Obviously, it is possible to etch the two spiral loops at different levels, one on top of the other, connected through a metallic via [22]. Although the price to pay in this case is the use of two metal levels, this broad side coupled spiral resonator (BC-SR, see Figure 5(b)) exhibits a very small electrical size if the metal levels are separated by a very thin dielectric layer (with this design, particle diameters as small as λ/100 can be achieved).

Figure 5. Topology of the (a) two-turn spiral resonator (2-SR), (b) BC-SR, (c) folded stepped impedance resonator (SIR) and (d) open split ring resonator (OSRR) (including the circuit model).

Figure 5. Topology of the (a) two-turn spiral resonator (2-SR), (b) BC-SR, (c) folded stepped impedance resonator (SIR) and (d) open split ring resonator (OSRR) (including the circuit model).

Another interesting electrically small planar particle is the stepped impedance resonator (SIR). It is well known that the length of a λ/2 resonator can be reduced by narrowing and widening the central and outer sections, respectively, of the particle [23]. If, additionally, we fold it, as depicted in Figure 5(c), the edge capacitance between the patches enhances the capacitance of the particle and hence the electrical length is made smaller. The folded SIR exhibits bianisotropy and combined with transmission lines is very interesting in order to achieve extremely small devices, as will be shown later.

The previous particles are closed particles that can be magnetically and, in some cases, electrically driven. Open particles can also be of interest in applications where the resonator must be excited by means of a voltage or current source. Inspired by the topology of the SRR of Figure 3, the open split ring resonator (OSRR) was presented in 2004 [24]. This particle can be constructed by means of two concentric rings with cuts in the same position. By elongating the rings, shaping them as a hook (Figure 5(d)), we create the two required terminals for particle excitation. The incident current is transferred from one ring to the other through the distributed edge capacitance between the two rings. According to that, it is clear that the resonance frequency of this series resonator is identical to the resonance frequency of the two-turn spiral resonator, 2-SR. Therefore OSRRs are very interesting for applications where small series (open) resonators implemented in one metal layer are required. Indeed, the OSRR, rather than an open SRR, is an open 2-SR. However, we will preserve the original term assigned to this particle in [24].

Concerning open SIRs, the SISS reported in Section 2 is indeed an open version of the SIR. It is an open series resonator shunt connected to the host microstrip line. Open SIRs can also be implemented in CPW structures by etching this particle in the back substrate side, with the wide strip sections below the central strip and ground planes. This enhances the electric coupling between the line and the SIR and hence very small resonance frequencies can be achieved with small particles. Therefore, electrically driven open SIRs can be made electrically very small.

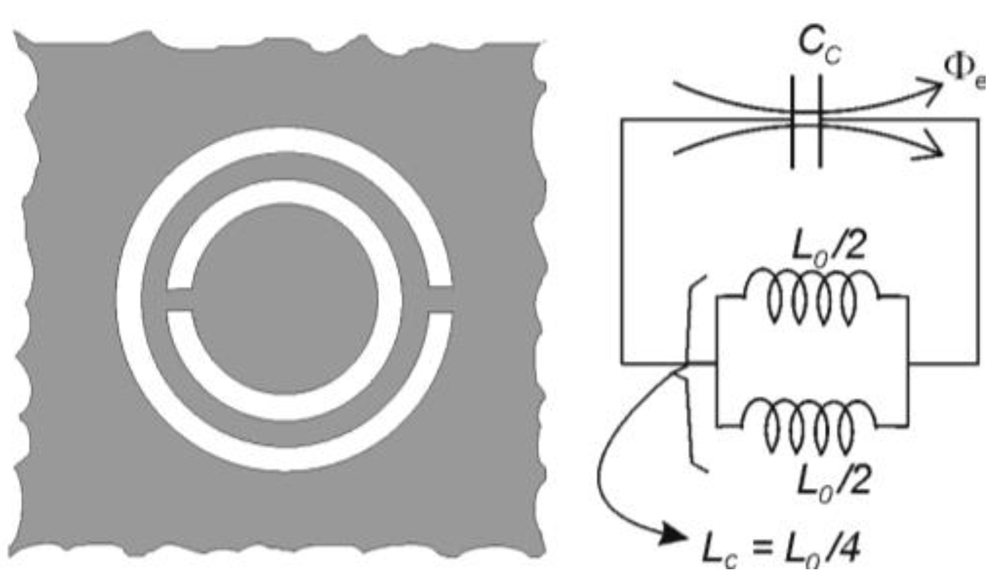
Let us now consider the application of duality to some of the previous particles. If the topology of the SRR is removed from a metallic film, the resulting particle (Figure 6) can be considered the negative image, or the complementary counterpart, of the SRR. For this reason, this particle has been called complementary split ring resonator (CSRR) [25]. It can be easily demonstrated by applying the Babinet principle, that the CSRR can be excited by means of an axial time varying electric field or by means of a magnetic field applied to the plane of the particle [26]. Under ideal conditions, i.e., a perfectly conducting and zero-thickness metallic screen, it can be demonstrated that the resonance frequency of the CSRR is identical to the resonance frequency of the SRR (provided identical dimensions and substrate are considered). Indeed, the capacitance of the CSRR, C_c, is the capacitance of a disk of radius r_o−c/2 surrounded by a ground plane at a distance c of its edge. The inductance is given by the parallel connection of the two inductances of the metallic strips connecting the inner and outer metallic regions of the CSRR. These inductive values are given by L_o/2, where L_o = 2πrL_pul, with L_pul being the per unit length inductance of the CPWs connecting the inner disk to ground.

Figure 6. Complementary split ring resonator (CSRR) topology and its equivalent circuit model. Geometrical parameters of the CSRR are identical to those of Figure 3 referred to the SRR.

Figure 6. Complementary split ring resonator (CSRR) topology and its equivalent circuit model. Geometrical parameters of the CSRR are identical to those of Figure 3 referred to the SRR.

Complementarity can also be applied to the NB-SRR, DS-SRR, 2-SR, SIR and OSRR. Let us consider in certain detail the complementary counterparts of the SIR and OSRR, since they are of special interest for microwave and metamaterial-based circuit design. The complementary version of the open split ring resonator was called open complementary split ring resonator (OCSRR) [27]. The OCSRR is the complementary (negative) image of the OSRR, but it can also be considered to be the open version of the CSRR. However, the OCSRR must be considered with some caution, since the metallic terminals of the OSRR disappear by applying duality. As shown in Figure 7(a), the OCSRR is an open particle with terminals for external connection (excitation) as indicated in the figure. From one terminal to the other there are two possible current paths: On one hand, the inductive path through the strip between the ring slots; on the other hand, the capacitive path through the slots. Therefore the OCSRR is an open parallel resonant tank. The capacitance of the particle is the capacitance of the CSRR, C_c; the inductance is four times larger than the inductance of the CSRR. This means that the OCSRR is smaller than the CSRR by a factor of two. Indeed, the resonance frequency and electrical size of the OSRR and the OCSRR are identical (provided the same dimensions and substrate are considered).

The complementary counterpart of the SIR has been called dumb-bell defected ground structure (DB-DGS). The reason is that this structure is dumb-bell shaped, and it is typically etched in the ground plane of microstrip lines, creating thus a defect, or pattern, in such a ground plane (Figure 7(b)). This structure behaves like a series connected parallel resonant tank, as reported in [28]. Thus, OCSRRs and DB-DGSs are of interest in applications where electrically small open parallel resonators are required.

Figure 7. (a) Open complementary split ring resonator (OCSRR) topology and its equivalent circuit model. (b) Topology of a dumb-bell defected ground structure (DB-DGS) etched in a ground plane of a microstrip transmission line.

Figure 7. (a) Open complementary split ring resonator (OCSRR) topology and its equivalent circuit model. (b) Topology of a dumb-bell defected ground structure (DB-DGS) etched in a ground plane of a microstrip transmission line.

Many other electrically small planar resonant particles, such as multiconductor SRRs or spirals [29], Hilbert shaped resonators [30,31], electrically tunable resonators [32,33] etc., have been considered in the literature, but are out of the scope of this paper. Nevertheless, the authors recommend the books by Marques, Martín and Sorolla [7] and by Solymar and Shamonina [9] for an overview of the resonators considered in this paper and for other electrically small resonant particles.

3.2. Transmission Lines Loaded with Electrically Small Resonators

In microwave applications, rather than isolated, the resonators considered in the previous sub-section are coupled (or connected) to host transmission lines (microstrip lines, CPWs, etc.). Despite the fact that such electrically small particles can also be present in metallic waveguides, the main interest of this paper is planar technology. For this reason, the present section is devoted only to the study of planar transmission lines loaded with semilumped resonators.

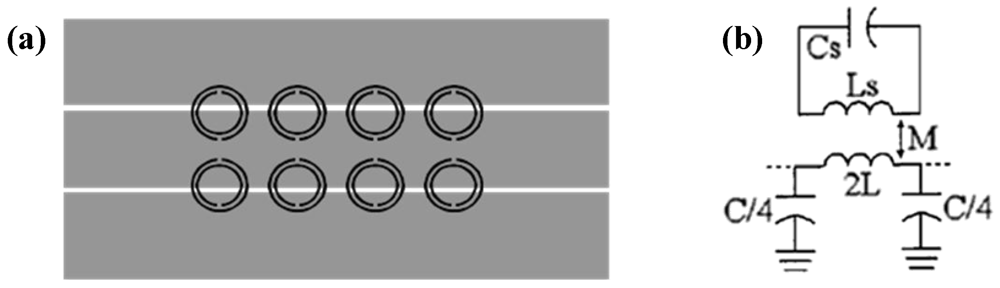
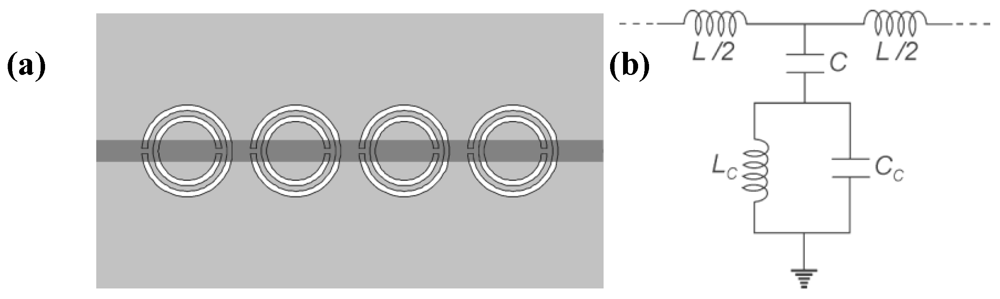
Let us start with the equivalent circuit models of transmission lines loaded with closed resonators. Typically, the SRR (or the 2-SR, NB-SRR, BC-SRR and DS-SRR) are useful particles to load a CPW transmission line. They can also be used by coupling them to a microstrip transmission line, but the corresponding circuit models are not so accurate. The typical topology of a CPW loaded with pairs of SRRs, as well as the lumped element equivalent circuit model of the unit cell, are depicted in Figure 8 [34,35]. The SRRs are etched in the back substrate side, below the slots, so the particles can be excited by the time varying magnetic field generated by the current flowing through the line. The circuit model of the unit cell must take into account the resonator and the line, as well as the coupling between the resonator and the line and, eventually, inter-resonator coupling. In many applications, coupling of the inter-resonator is not required (i.e., the resonators are separated enough) and can be neglected. This is the case considered here. Nevertheless, the analysis of transmission lines loaded with tightly coupled resonators has been carried out in [36]. In the circuit model of Figure 8, L and C are the line inductance and capacitance, L_s and C_s are the inductance and capacitance of the SRR (or the considered coupled particle), and M is the mutual coupling between the line and the SRRs. 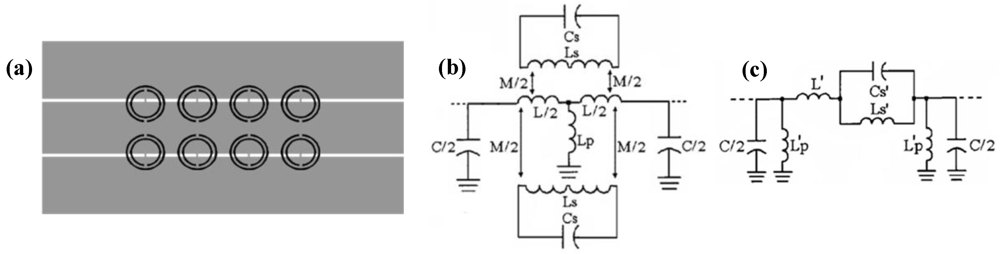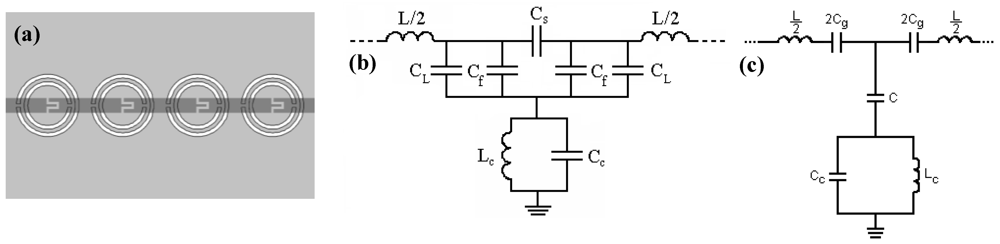The structure of Figure 8 exhibits a stop band behavior that has been interpreted as consequence of the negative effective permeability of the structure (caused by the presence of the SRRs) above resonance, and by the highly positive effective permeability below SRR resonance. To implement a backward wave (or left handed) CPW transmission line, inductive strips between the central strip and the ground planes, above the positions of the SRRs, have been introduced (Figure 9(a)) [34,35]. With the presence of the shunt connected strips, the structure switches its frequency response to a bandpass type response, where wave propagation in the first allowed (narrow) band is backward (typically this structure exhibits a forward wave transmission band at higher frequencies). In this case, the circuit model is that depicted in Figure 9(b), where L_p accounts for the pair of shunt connected strips. The circuit model depicted in Figure 9(b) can be transformed to the circuit depicted in Figure 9(c) [35]. The following transformations apply:

(2)

(3)

(4)

(5)

Figure 8. (a) Typical topology of a SRR loaded CPW. (b) Equivalent circuit model of the unit cell. The magnetic wall concept has been applied, so that the model is that of the one half of the structure.

Figure 8. (a) Typical topology of a SRR loaded CPW. (b) Equivalent circuit model of the unit cell. The magnetic wall concept has been applied, so that the model is that of the one half of the structure.

Figure 9. (a) Typical topology of a SRR- and strip-loaded CPW. (b) Equivalent circuit model of the unit cell. (c) Transformed circuit model.

Figure 9. (a) Typical topology of a SRR- and strip-loaded CPW. (b) Equivalent circuit model of the unit cell. (c) Transformed circuit model.

The circuit model of Figure 9(c) is useful for design purposes since a parameter extractor has been developed [37], namely, from the electromagnetic simulation (or measurement) of the frequency response of a SRR-loaded CPW, we can easily infer the element values of the circuit model. The technique is very useful but it is out of the scope of this paper. Moreover, from the equivalent circuit model of the unit cell, we can easily predict the bandwidth of the allowed bands, as well as the characteristic impedance of the propagating structures in those bands. The bandwidth can be inferred from the dispersion relation, given by:

(6)

with Z_s and Z_p being the series and shunt impedance, respectively, of the π-model of the considered line (for a T-model, the same expression is also valid). The characteristic impedance of a periodic structure whose unit cell can be described by a π-model is:

(7)

and for a T-model, it takes the form:

(8)

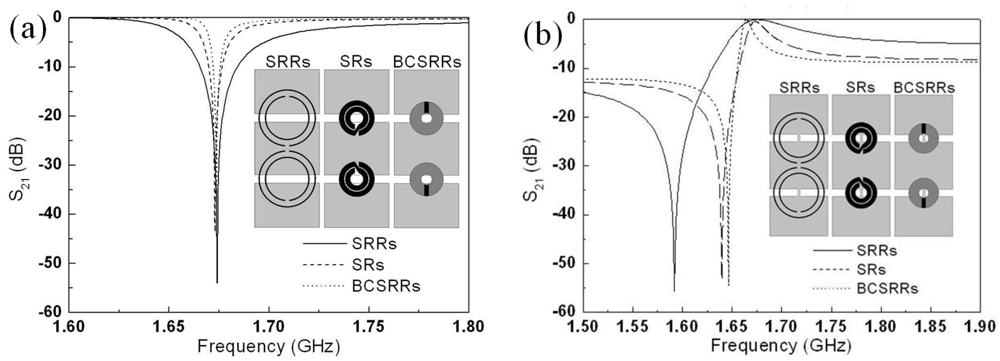
It has been mentioned before that the electrical size of the SRR can be decreased through different strategies. However, as discussed in [38], reducing the particle size has the effect of narrowing the bandwidth. Therefore, a trade-off between size and bandwidth when choosing the loading particles must be taken into account. This important aspect is illustrated in Figure 10, where the transmission coefficient of a CPW transmission line loaded with different resonant elements is depicted. If, for instance, a notch filter with much localized frequency is required, the use of a 2-SR spiral or a BC-2SR, rather than a SRR, is recommended. However, for applications of strip- and resonator-loaded CPW as bandpass filters, SRRs are necessary if the required bandwidth is moderate.

Figure 10. Layouts and transmission coefficients of several CPWs loaded with pairs of SRRs, BC-SRRs and 2-SRs (a) and with shunt strips (b). Relevant dimensions are: Ring width c = 0.2 mm, distance between the rings d = 1 mm, external radius r_ext = 5.4mm for the SRRs; c = 0.961 mm, d = 0.19 mm, r_ext = 3.36 mm for the SRs; and c = 2.12 mm, d = 0.2 mm, r_ext = 3.17 mm for the BCSRRs. For the CPW the central strip width is W_C = 10 mm, the width of the slots is G = 1.59 mm and the length D = 12.2 mm. Shunt strip width w_S = 0.2 mm. The considered substrate characteristics are: dielectric constant ε_r = 10.2 and thickness h = 2.54 mm. From [38]; copyright © 2010, John Wiley & Sons; reprinted with permission.

Figure 10. Layouts and transmission coefficients of several CPWs loaded with pairs of SRRs, BC-SRRs and 2-SRs (a) and with shunt strips (b). Relevant dimensions are: Ring width c = 0.2 mm, distance between the rings d = 1 mm, external radius r_ext = 5.4mm for the SRRs; c = 0.961 mm, d = 0.19 mm, r_ext = 3.36 mm for the SRs; and c = 2.12 mm, d = 0.2 mm, r_ext = 3.17 mm for the BCSRRs. For the CPW the central strip width is W_C = 10 mm, the width of the slots is G = 1.59 mm and the length D = 12.2 mm. Shunt strip width w_S = 0.2 mm. The considered substrate characteristics are: dielectric constant ε_r = 10.2 and thickness h = 2.54 mm. From [38]; copyright © 2010, John Wiley & Sons; reprinted with permission.

Let us now consider microstrip lines loaded with CSRRs. The typical topology and circuit model (unit cell) are depicted in Figure 11 [25]. The line is described by the inductance L and by the capacitance C, which models also the electric coupling between the line and the CSRR, described by the inductance L_c and the capacitance C_c. The structure exhibits a stop band behavior that has been interpreted as being due to the negative effective permittivity of the structure in the vicinity of CSRR resonance. A left handed transmission band can be generated by merely cutting gaps in the microstrip line, above the positions of the CSRRs [26]. In this case the structure is a passband and can be modeled according to the circuit depicted in Figure 12(b), where the gap is modeled by a π-model consisting of the series capacitance C_s plus the fringing capacitances C_f. Such a model can be transformed to the model depicted in Figure 12(c), with the following transformations [39]

(9)

(10)

where C_par = C_f + C_L. Like for the SRR-loaded CPW, CSRR loaded lines can be analyzed through their lumped element equivalent circuit, and expressions (6) and (8). The parameter extraction technique for these CSRR-loaded lines has been published in [40].

Figure 11. (a) Typical topology of a CSRR loaded microstrip line. (b) Equivalent circuit model of the unit cell.

Figure 11. (a) Typical topology of a CSRR loaded microstrip line. (b) Equivalent circuit model of the unit cell.

Figure 12. (a) Typical topology of a CSRR- and gap-loaded microstrip line. (b) Equivalent circuit model of the unit cell. (c) Transformed circuit model.

Figure 12. (a) Typical topology of a CSRR- and gap-loaded microstrip line. (b) Equivalent circuit model of the unit cell. (c) Transformed circuit model.

The circuit models depicted in Figure 11 and Figure 12 also apply for microstrip lines loaded with complementary spirals or with other complementary closed particles. Concerning the trade-off between particle size and bandwidth, the same comments in reference to SRR-loaded lines also apply (see [38] for more details and for numerical calculations).

The main relevant limitation of SRR- and CSRR-loaded lines is the narrow bandwidth, which is related to the limited coupling between the line and the resonator. In band pass structures, moderate and wide bands have been achieved by merging the backward and the forward wave transmission bands [41]. However, the validity of the models of the SRR- and CSRR-loaded lines in the forward wave transmission band is restricted to only a small portion of the band [42]. The DS-SRR (or DS-CSRR) has been considered in order to implement moderate or even wideband stop band structures, but this particle is electrically larger than the SRR (or CSRR), and therefore the accuracy of the circuit model to properly describe lines loaded with such particles is questionable. An alternative approach to implement wide band structures is the combined use of OSRRs and OCSRR in transmission lines.

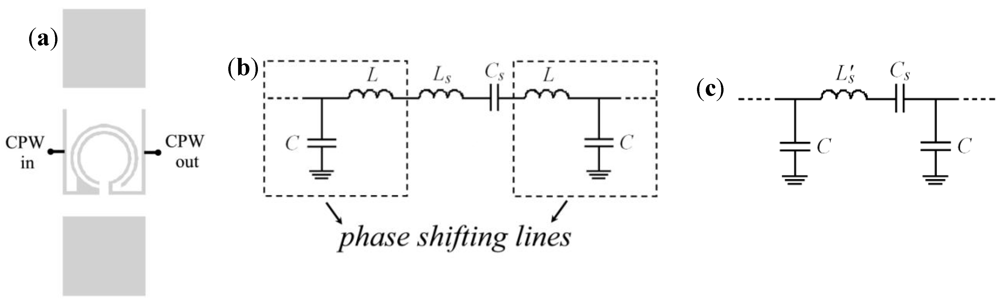
Let us consider a CPW loaded with an OSRR (Figure 13(a)). The circuit model of this structure is not merely a series resonator between the input and output ports of the CPW. As discussed in [43], the line introduces some phase shift that must be taken into account for an accurate modeling. Such phase shift can be accounted for by cascading phase shifting lines to the series resonator, L_s-C_s, modeling the OSRR. In practice, such shifting lines can be modeled by means of a lumped capacitance C and inductance L, and the circuit model is that shown in Figure 13(b), which in turn can be simplified to the model depicted in Figure 13(c). For OCSRR loaded lines (Figure 14), a similar phenomenology applies. That is, the structure cannot be simply modeled by means of a shunt connected parallel resonator. A certain phase shift appears, and the equivalent circuit model is that depicted in Figure 14(b,c). In the models of Figure 13 and Figure 14, L and C must be considered parasitic elements. The frequency response of CPW transmission lines loaded with either OSRRs or OCSRRs reveals that the structures exhibit a band pass behavior with very wide transmission bands. As will be shown in the next section, by cascading OSRR and OCSRR-loaded CPWs, it is possible to implement transmission lines with composite backward and forward characteristics, as well as wide band filters. As compared to other structures based on closed rings, the main advantage of these OSRR and OCSRR based lines, is that the equivalent circuit of the structures models their behavior to a very good approximation within the whole transmission band.

Figure 13. Layout (a), circuit model (b) and simplified circuit model (c) of a CPW transmission line loaded with a series connected open split ring resonator (L’_s = L_s + 2L).

Figure 13. Layout (a), circuit model (b) and simplified circuit model (c) of a CPW transmission line loaded with a series connected open split ring resonator (L’_s = L_s + 2L).

Figure 14. Layout (a), circuit model (b) and simplified circuit model (c) of a CPW transmission line loaded with a pair of open complementary split ring resonators, where C’_p = 2C_p + 2C and L’_p = L_p/2. The backside strips (in dark grey) connecting the different ground plane regions are necessary to prevent the slot mode of the CPW and the second resonance of the open complementary split ring resonators.

Figure 14. Layout (a), circuit model (b) and simplified circuit model (c) of a CPW transmission line loaded with a pair of open complementary split ring resonators, where C’_p = 2C_p + 2C and L’_p = L_p/2. The backside strips (in dark grey) connecting the different ground plane regions are necessary to prevent the slot mode of the CPW and the second resonance of the open complementary split ring resonators.

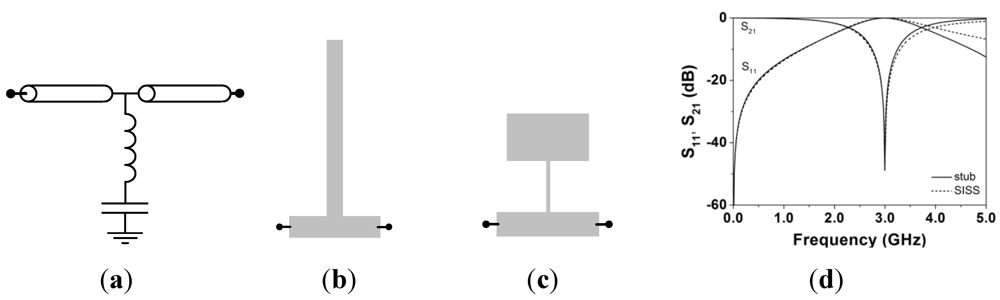
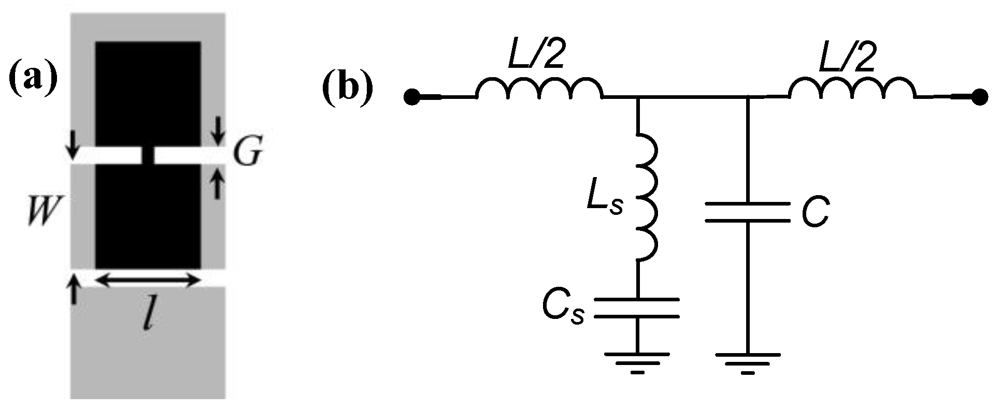
To end this section, we will consider the SIRs coupled to transmission lines. These resonators are useful to implement shunt connected series resonators. In microstrip technology, the SISS topology of Figure 1(c), where the SISS is merely modeled as a series grounded resonator, is very useful (the limitations of this model are discussed in [11]). In CPW technology, SIRs are typically implemented by backside etching the wide SIR strip sections below the central strip and ground planes of the CPW structure, as shown in Figure 15. The equivalent circuit model of the SIR-loaded CPW is also depicted in Figure 15. L and C are the line inductance and capacitance, whereas the SIR is modeled by L_s and C_s.

Figure 15. Typical layout of a SIR-loaded CPW (a) and equivalent circuit model (b).

Figure 15. Typical layout of a SIR-loaded CPW (a) and equivalent circuit model (b).

4. Applications

In this section, three illustrative applications of some of the semilumped resonators considered before are highlighted. Rather than discussing them in detail, the main aim is to point out the key characteristics of the resonators for the considered applications.

4.1. Wideband Bandpass Filters and Dual-band Components based on OSRRs and OCSRRs

OSRRs and OCSRRs can be combined in order to implement artificial transmission lines exhibiting left handed wave propagation at low frequencies and right handed wave propagation at high frequencies. The typical layout of these structures is depicted in Figure 16.

Figure 16. Topology of the unit cell of a CPW composite right/left handed transmission line based on a combination of series connected open split ring resonators in the external stages and a pair of shunt connected open complementary split ring resonators in the central stage. The considered substrate is the Rogers RO3010 with thickness h = 1.27 mm and dielectric constant ε_r = 10.2. Dimensions are: l = 12.3 mm, W = 5 mm, G = 1.28 mm. For the open complementary split ring resonator: r_ext = 2.9 mm, c = 0.5 mm, d = 1.2 mm. For the open split ring resonators: r_ext = 2 mm, c = d = 0.2 mm.

Figure 16. Topology of the unit cell of a CPW composite right/left handed transmission line based on a combination of series connected open split ring resonators in the external stages and a pair of shunt connected open complementary split ring resonators in the central stage. The considered substrate is the Rogers RO3010 with thickness h = 1.27 mm and dielectric constant ε_r = 10.2. Dimensions are: l = 12.3 mm, W = 5 mm, G = 1.28 mm. For the open complementary split ring resonator: r_ext = 2.9 mm, c = 0.5 mm, d = 1.2 mm. For the open split ring resonators: r_ext = 2 mm, c = d = 0.2 mm.

Figure 17. (a) Frequency response of the circuit of Figure 16. (b) Characteristic impedance. (c) Dispersion diagram. The element values of the circuit model are (in reference of Figure 13(c) and Figure 14(c)): L’_s = 6.94 nH, C_s = 0.85 pF, C = 0.28 pF, L = 0.76 nH, L’_p = 1.95 nH and C’_p = 2.43 pF. From [43]; copyright © 2009, IEEE; reprinted with permission.

Figure 17. (a) Frequency response of the circuit of Figure 16. (b) Characteristic impedance. (c) Dispersion diagram. The element values of the circuit model are (in reference of Figure 13(c) and Figure 14(c)): L’_s = 6.94 nH, C_s = 0.85 pF, C = 0.28 pF, L = 0.76 nH, L’_p = 1.95 nH and C’_p = 2.43 pF. From [43]; copyright © 2009, IEEE; reprinted with permission.

Figure 18. Fabricated wideband bandpass filter and frequency response. The substrate is the Rogers RO3010 with thickness h = 0.254 mm and measured dielectric constant ε_r = 11.2. Dimensions are: l = 12.32 mm, W = 5.6 mm, G = 0.574 mm. For the OCSRR: r_ext=2.1 mm, c = 0.5 mm, d = 0.16 mm. For the OSRR: r_ext = 1.9 mm, c = 0.3 mm, d = 0.16 mm. The element values of the circuit model are (in reference of Figure 13c and Figure 14c): C’_p = 1.779 pF, L’_p = 3.216 nH, C_s = 1.08 pF, L_s = 4.89 nH, L = 0.384 nH, C = 0.182 pF and L_hs = 0.2 nH, where an additional shunt inductance L_hs in series with the OCSRR tank has been considered to take into account the shunt inductive effect of the narrow strip connection between the main line and the OCSRR (this being needed to predict the broadband response of the OCSRR). From [44]; copyright ℘ 2011, Elsevier; reprinted with permission.

Figure 18. Fabricated wideband bandpass filter and frequency response. The substrate is the Rogers RO3010 with thickness h = 0.254 mm and measured dielectric constant ε_r = 11.2. Dimensions are: l = 12.32 mm, W = 5.6 mm, G = 0.574 mm. For the OCSRR: r_ext=2.1 mm, c = 0.5 mm, d = 0.16 mm. For the OSRR: r_ext = 1.9 mm, c = 0.3 mm, d = 0.16 mm. The element values of the circuit model are (in reference of Figure 13c and Figure 14c): C’_p = 1.779 pF, L’_p = 3.216 nH, C_s = 1.08 pF, L_s = 4.89 nH, L = 0.384 nH, C = 0.182 pF and L_hs = 0.2 nH, where an additional shunt inductance L_hs in series with the OCSRR tank has been considered to take into account the shunt inductive effect of the narrow strip connection between the main line and the OCSRR (this being needed to predict the broadband response of the OCSRR). From [44]; copyright ℘ 2011, Elsevier; reprinted with permission.

Figure 17 shows the frequency response, as well as the characteristic impedance and dispersion. Clearly, the structure exhibits a composite right/left handed behavior. It is interesting to mention that the equivalent circuit model of the structure (consisting of the cascade of the circuits shown in Figure 13 and Figure 14 for each OSRR and OCSRR section) provides a good estimation of the characteristics of the artificial transmission line up to frequencies that extend beyond the allowed transmission band. If parasitics in the models of Figure 13 and Figure 14 are removed, the equivalent circuit that is obtained by cascading those models of such figures is the model of a canonical composite right left/handed line, which is also the equivalent circuit model of a band pass filter [43,44]. Therefore, combined OSRR and OCSRR structures are useful for the implementation of band pass filters and metamaterial-based microwave components. The key aspect is the fact that the wide bands can be obtained. Hence, these structures are specially suited for the design of wideband filters. An illustrative example is shown in Figure 18, where the agreement between the simulated and measured frequency responses is very reasonable [44].

Another possible application of OSRR and OCSRR-based lines is the design of dual-band components. As compared to dual-band components based on CSRRs [45], a wider band for the first frequency is obtained by using artificial lines based on open particles. Figure 19 depicts a fabricated dual-band power splitter and its frequency response.

Figure 19. Fabricated dual-band power divider and frequency response. (a) Top view. (b) Bottom view. (c) Power division (S₂₁, S₃₁) and matching (S₁₁). The substrate is the Rogers RO3010 with thickness h = 0.635 mm and dielectric constant ε_r = 10.2. Dimensions are: l = 9 mm, W = 4 mm, G = 0.74 mm. For the open complementary split ring resonator: r_ext = 0.9 mm, c = 0.2 mm, d = 0.2 mm. For the open split ring resonators: r_ext = 1.5 mm, c = 0.3 mm, d = 0.2 mm. The wide metallic strip in the back substrate side has been added in order to enhance the shunt capacitance of the open complementary split ring resonator stage, as required to achieve the electrical characteristics of the device. The circuit parameters, referred to the circuits of Figure 13(c) and Figure 14(c) are: C = 0.2 pF, L = 0.25 nH, C_s = 0.66 pF, L’_s = 3.74 nH, C’_p = 2.99 pF and L’_p = 0.83 nH. From [43]; copyright © 2009, IEEE; reprinted with permission.

Figure 19. Fabricated dual-band power divider and frequency response. (a) Top view. (b) Bottom view. (c) Power division (S₂₁, S₃₁) and matching (S₁₁). The substrate is the Rogers RO3010 with thickness h = 0.635 mm and dielectric constant ε_r = 10.2. Dimensions are: l = 9 mm, W = 4 mm, G = 0.74 mm. For the open complementary split ring resonator: r_ext = 0.9 mm, c = 0.2 mm, d = 0.2 mm. For the open split ring resonators: r_ext = 1.5 mm, c = 0.3 mm, d = 0.2 mm. The wide metallic strip in the back substrate side has been added in order to enhance the shunt capacitance of the open complementary split ring resonator stage, as required to achieve the electrical characteristics of the device. The circuit parameters, referred to the circuits of Figure 13(c) and Figure 14(c) are: C = 0.2 pF, L = 0.25 nH, C_s = 0.66 pF, L’_s = 3.74 nH, C’_p = 2.99 pF and L’_p = 0.83 nH. From [43]; copyright © 2009, IEEE; reprinted with permission.

4.2. Ultra Compact Elliptic-function Lowpass Filters Based on SIRs

Elliptic-function lowpass filters are characterized by the presence of transmission zeros that improve the frequency selectivity of the filter. These transmission zeros can be achieved by using grounded series resonators. Therefore, SIRs loading a CPW transmission line are specially suited for this purpose. Figure 20 shows a designed elliptic lowpass filter and its frequency response [46]. The filter characteristics are good, and the device dimensions are very small. The small size of the SIR is in this case the most relevant aspect of the proposed structure.

Figure 20. Layout (a), photograph (b), and frequency response (c) of the fabricated elliptic lowpass filter. Dimensions are: W = 5 mm, G = 0.55 mm, l = 6.6 mm, b = 2.42 mm, c = 2.7 mm. The strips of the meander lines are of 0.2 mm. The filter has been fabricated on the Rogers RO3010 substrate with measured dielectric constant ε_r = 11.2 and thickness h = 254 μm. The circuit simulation corresponds to an ideal elliptic filter with the following characteristics: order-3 elliptic-function LPF with a passband ripple of L_Ar = 0.1 dB, a cutoff frequency of f_c = 1 GHz and a stopband attenuation of L_As = 30.52 dB with the equal-ripple stopband starting normalized frequency Ω_s = 2.5. From [46], copyright © 2010, IEEE; reprinted with permission.

Figure 20. Layout (a), photograph (b), and frequency response (c) of the fabricated elliptic lowpass filter. Dimensions are: W = 5 mm, G = 0.55 mm, l = 6.6 mm, b = 2.42 mm, c = 2.7 mm. The strips of the meander lines are of 0.2 mm. The filter has been fabricated on the Rogers RO3010 substrate with measured dielectric constant ε_r = 11.2 and thickness h = 254 μm. The circuit simulation corresponds to an ideal elliptic filter with the following characteristics: order-3 elliptic-function LPF with a passband ripple of L_Ar = 0.1 dB, a cutoff frequency of f_c = 1 GHz and a stopband attenuation of L_As = 30.52 dB with the equal-ripple stopband starting normalized frequency Ω_s = 2.5. From [46], copyright © 2010, IEEE; reprinted with permission.

4.3. Dual-band Antennas Based on SRs

It has been recently demonstrated that dual-band antennas with very closely spaced operating frequencies (such as those required, for instance, in UHF-RFID applications to cover different regulated bands worldwide), can be implemented by coupling electrically small resonators to mono-band antennas [47]. This perturbs the impedance of the antenna and conjugate impedance matching between the antenna and the integrated circuit at two required frequencies can be achieved. For this application, the key aspect is the resonator’s size. For this reason, the use of a 2-SR is of interest.

Figure 21. Photographs of the mono-band (a) and dual-band (b) fabricated UHF-RFID tags. (c) Measured and simulated read ranges. The dimensions of the tag are 48 mm × 48 mm, and the strip width is 1.4 mm. The other relevant dimensions are l_m = 16.3 mm, w_m = 4.8 mm, d_l = 7.3 mm, d_r = 33.9 mm and d_f = 14.2 mm. The final dimensions concerning the 2-SR and its relative position inside the antenna (shown in Figure 21b) are l_r = 16.1 mm, w_r = 6.8 mm, s_h = 8.3 mm and s_v = 5.4mm. The strip width of the 2-SR is 0.5 mm and the separation between spirals is 0.3 mm. The considered substrate is the Rogers RO3010 with the dielectric constant ε_r = 10.2 and thickness h = 0.127 mm. From [47], copyright © 2011, IEEE; reprinted with permission.

Figure 21. Photographs of the mono-band (a) and dual-band (b) fabricated UHF-RFID tags. (c) Measured and simulated read ranges. The dimensions of the tag are 48 mm × 48 mm, and the strip width is 1.4 mm. The other relevant dimensions are l_m = 16.3 mm, w_m = 4.8 mm, d_l = 7.3 mm, d_r = 33.9 mm and d_f = 14.2 mm. The final dimensions concerning the 2-SR and its relative position inside the antenna (shown in Figure 21b) are l_r = 16.1 mm, w_r = 6.8 mm, s_h = 8.3 mm and s_v = 5.4mm. The strip width of the 2-SR is 0.5 mm and the separation between spirals is 0.3 mm. The considered substrate is the Rogers RO3010 with the dielectric constant ε_r = 10.2 and thickness h = 0.127 mm. From [47], copyright © 2011, IEEE; reprinted with permission.

Figure 21 depicts a conventional mono-band meander line antenna, as well as its dual-band counterpart. The dual-band antenna has been designed to cover the UHF-RFID USA and European regulated bands. As can be seen from the measured read ranges, dual-band functionality, with very reasonable read ranges, is obtained [47].

5. Conclusions

In conclusion, we have reviewed the most used electrically small resonators for the synthesis of metamaterials and metamaterial-based or inspired microwave circuits and antennas. The intrinsic circuit models of these resonators as well as the circuit models of transmission lines coupled to them have been pointed out. Such transmission lines loaded with these electrically small resonators are the building blocks for the design of many microwave components. A comparative analysis in terms of resonator’s size, bandwidth, and suitability for certain applications, has also been carried out. This comparison has been the main relevant aspect of the present paper.