Numerical Simulation on Deformation and Damage Mechanism of Existing Underground Structures Induced by Adjacent Construction of Super-Large-Diameter Tunnels
Abstract
1. Introduction
2. Numerical Simulation and Constitutive Model
2.1. Numerical Model
2.2. CDP Constitutive Model
3. Deformation and Internal Force Variation Patterns of Existing Tunnels Induced by Super-Large-Diameter Shield Undercrossing
3.1. Settlement and Stress Contours
3.2. Settlement Development Patterns of the Existing Tunnel
3.3. Internal Force Variation Pattern of Existing Tunnels
3.3.1. Axial Bending Moment
3.3.2. Axial Shear Force
4. Damage Development Mechanism of the Existing Tunnel
4.1. Damage of the Existing Tunnel
4.2. Damage Mechanism of the Existing Tunnel Based on the Entire Construction Process
5. Conclusions
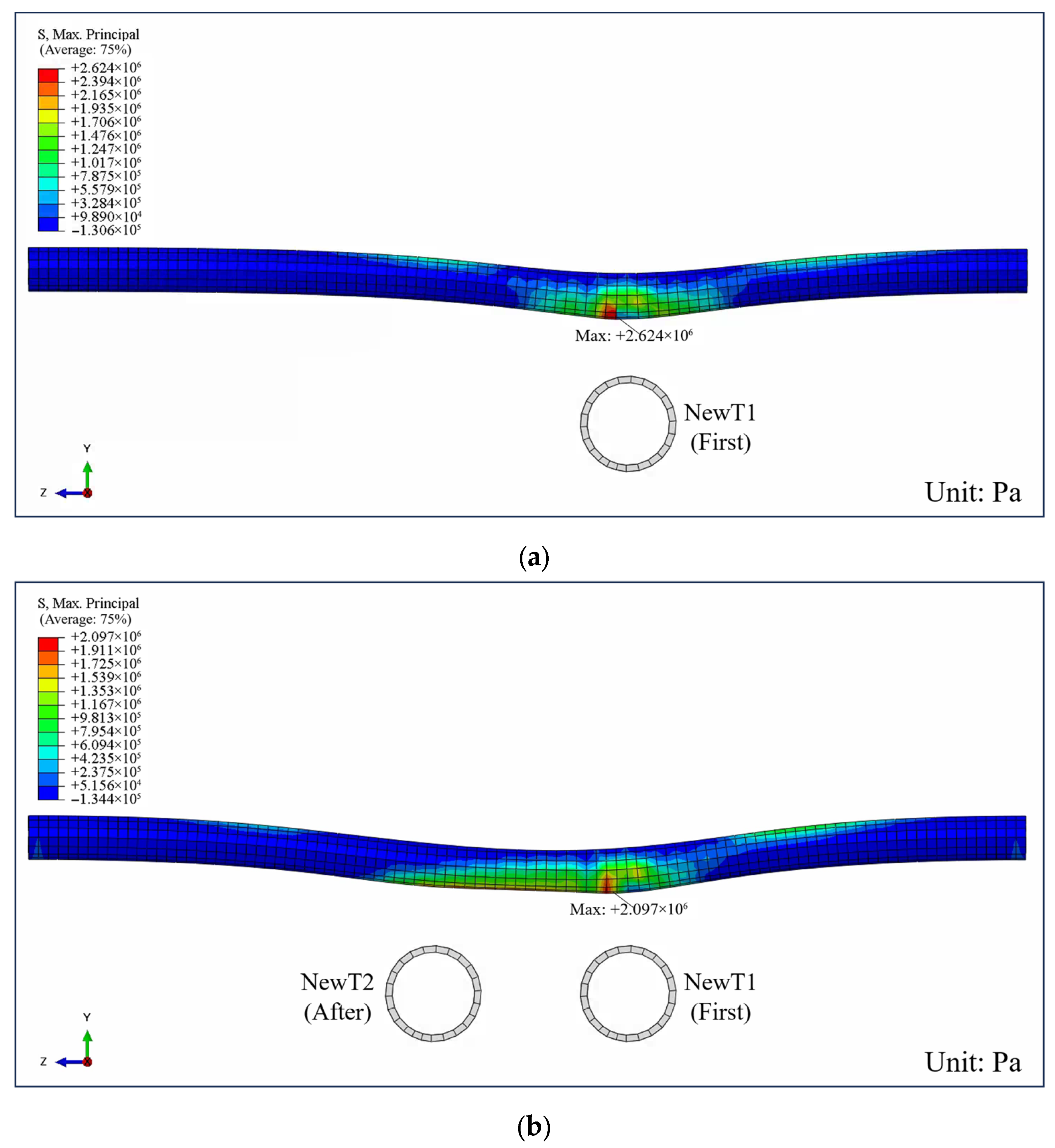
- When the single-line excavation was completed, the maximum settlement of the existing tunnel was −19.70 mm and the settlement trough exhibited a V shape. After the double-line completion, the maximum settlement increased to −24.51 mm, and the settlement trough evolved into a W shape, with the influence range expanding from about 40 m during the single-line stage to about 60 m. The position of the peak settlement shifted from the axis of the first tunnel toward the central axis of the double-line tunnels.
- The vertical bending moment reached its maximum after the completion of single-line excavation, with the peak located above the axis of NewT1. Following the double-line completion, its distribution evolved from a single-peak pattern into a broad, gentle, double-peak pattern, and the influence range expanded significantly. The maximum horizontal bending moment was only 1/8 of the vertical bending moment, confirming that vertical bending is the dominant loading mode. The shear force analysis indicated that the construction of the after tunnel generally increased the vertical shear force values, widened the affected zone, and formed a high-shear risk area between approximately 78 m and 103 m on both sides of the axis of the first tunnel.
- The damage mechanism of the existing tunnel induced by the double-line super-large-diameter shield undercrossing is as follows: damage is triggered by the historical peak stress and accumulates irreversibly, rather than being determined by the final stress state. When the after tunnel advanced six rings (time T6), the stress peak at the tunnel bottom of the existing tunnel reached 2.655 MPa, briefly exceeding the tensile strength of the concrete, and irreversible tensile damage occurred at the tunnel bottom. Although the final stress peak decreased to 2.097 MPa, the final DAMAGET value reached 92.4%, representing a high-damage state. Moreover, the distribution area of the damage highly coincided with the location of the maximum bending moment, indicating that cracking was primarily caused by bending-induced tension.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shen, S.L.; Wu, H.N.; Cui, Y.J.; Yin, Z.Y. Long-term settlement behaviour of metro tunnels in the soft deposits of Shanghai. Tunn. Undergr. Space Technol. 2014, 40, 309–323. [Google Scholar] [CrossRef]
- Liang, R.Z.; Xia, T.D.; Hong, Y.; Yu, F. Effects of above crossing tunnelling on the existing shield tunnels. Tunn. Undergr. Space Technol. 2016, 58, 159–176. [Google Scholar] [CrossRef]
- Ding, Z.; Zhang, M.B.; Zhang, X.; Wei, X.J. Theoretical analysis on the deformation of existing tunnel caused by under crossing of large diameter slurry shield considering construction factors. Tunn. Undergr. Space Technol. 2023, 133, 104913. [Google Scholar] [CrossRef]
- Liu, X.; Fang, Q.; Zhang, D.L. Mechanical responses of existing tunnel due to new tunnelling below without clearance. Tunn. Undergr. Space Technol. 2018, 80, 44–52. [Google Scholar] [CrossRef]
- Yan, C.Z. Research on the Mechanism and Construction Techniques of Interaction for Adjacent Tunneling Preformed by Shield. Master’s Thesis, Tongji University, Shanghai, China, 2007. [Google Scholar]
- Han, K.H.; Zhang, C.P.; Zhang, D.L. Upper-bound solutions for the face stability of a shield tunnel in multilayered cohesive-frictional soils. Comput. Geotech. 2016, 79, 1–9. [Google Scholar] [CrossRef]
- Lu, D.C.; Song, T.; Lin, Q.T.; Meng, X.; Du, X.L. Numerical simulation study on deformation mechanism of existing tunnels induced by shield undercrossing. J. Disaster Prev. Mitig. Eng. 2025, 45, 485–500. [Google Scholar]
- Peng, M.M. Analysis on deformation control of shield tunneling under existing double-line tunnel. J. Guangdong Commun. Polytech. 2025, 24, 17–22. [Google Scholar]
- Liu, M.G.; Liu, Z.J.; Chen, R.D.; Pang, K.; Zhou, C.L.; Zhang, Y. Results of micro-deformation control measures for ultra-diameter shield tunnels crossing the existing tunnels in water-rich sand clay composite stratum. J. Munic. Technol. 2025, 43, 116–125. [Google Scholar]
- Yang, Z. Study on Influence and Control Measures of Shield Tunnel Passing Through Existing Tunnel in Soft Soil. Master’s Thesis, Tianjin University, Tianjin, China, 2023. [Google Scholar]
- Lin, Q.T.; Lu, D.C.; Lei, C.M. Mechanical response of existing tunnels for shield undercrossing in cobble strata based on the model test. Tunn. Undergr. Space Technol. 2022, 125, 104505. [Google Scholar] [CrossRef]
- Fu, J.Y.; Zhao, N.N.; Qu, Y.; Yang, J.S.; Wang, S.Y. Effects of twin tunnel undercrossing excavation on the operational high speed railway tunnel with ballastless track. Tunn. Undergr. Space Technol. 2022, 124, 104470. [Google Scholar] [CrossRef]
- Jin, D.L.; Yuan, D.J.; Li, X.G.; Zheng, H.T. Analysis of the settlement of an existing tunnel induced by shield tunneling underneath. Tunn. Undergr. Space Technol. 2018, 81, 209–220. [Google Scholar] [CrossRef]
- Shao, S.; Wu, Y.M.; Fu, H.L.; Zhang, J.W. Mechanism and optimized design methodology of steel plate reinforcement for tunnel lining void zones. Materials 2025, 18, 4204. [Google Scholar] [CrossRef]
- Nie, B.L. The Study of Cracking Mechanism of an Existing Shield Tunnel Segment Induced by an Adjacent Pit Excavation. Master’s Thesis, Changsha University of Science & Technology, Changsha, China, 2019. [Google Scholar]
- Zhang, W.J.; Lu, Q.W.; Zhang, G.L.; Li, H.L. Study on dynamic response of shield tunnel ring structure by cap location. Chin. J. Undergr. Space Eng. 2020, 16, 116–125. [Google Scholar]
- Wei, C.M. Research on Damage of Existing Tunnel Lining Structure Under Disturbance of Subway Shield Construction. Master’s Thesis, Shenyang Jianzhu University, Shenyang, China, 2024. [Google Scholar]
- Zhang, W.J.; Qi, J.B.; Zhang, G.L.; Niu, R.J.; Zhang, C.; He, L.C.; Lyu, J.R. Full-scale experimental study on failure characteristics of the key segment in shield tunnel with super large cross section. Tunn. Undergr. Space Technol. 2022, 129, 104671. [Google Scholar] [CrossRef]
- Liu, D.J.; Li, M.; Zuo, J.P.; Gao, Y.; Zhong, F.; Zhang, Y.; Chang, Y.Q. Experimental and numerical investigation on cracking mechanism of tunnel lining under bias pressure. Thin-Walled Struct. 2021, 163, 107693. [Google Scholar] [CrossRef]
- Chen, R.P.; Chen, S.; Wu, H.N.; Wu, H.N.; Liu, Y.; Meng, F.Y. Investigation on deformation behavior and failure mechanism of a segmental ring in shield tunnels based on elaborate numerical simulation. Eng. Fail. Anal. 2020, 117, 104960. [Google Scholar] [CrossRef]
- Sharghi, M.; Afshin, H.; Dias, D.; Jeong, H. 3D numerical study of the joint dislocation and spacing impacts on the damage of tunnel segmental linings. Eng. Fail. Anal. 2023, 56, 104878. [Google Scholar] [CrossRef]
- Shi, G.J.; Yang, Y.B.; Liu, C.; Lu, M.J. Research on longitudinal crack development laws and mechanical properties of shield tunnel. Railw. Stand. Des. 2024, 70. [Google Scholar] [CrossRef]
- Cao, S.Y.; Wang, S.M.; Liu, C.K.; He, C.; Lu, D.Y.; Ma, G.Y. Influence of crack location on failure mode of shield tunnel lining structure. J. Southeast Univ. (Nat. Sci. Ed.) 2020, 50, 120–127. [Google Scholar]
- Dong, F. Failure Mechanism and Safety Assessment of Metro Tunnel Lining. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2018. [Google Scholar]
- Xu, G.W.; He, C.; Lu, D.Y.; Wang, S.M. The influence of longitudinal crack on mechanical behavior of shield tunnel lining in soft-hard composite strata. Thin-Walled Struct. 2019, 144, 106282. [Google Scholar] [CrossRef]
- Han, K.H.; Zhai, Z.Y.; Chen, X.S.; Zhang, C.P.; Ju, J.W.W.; Bao, X.H.; Wang, S.Y.; Hou, B.B. A methodology for evaluating the safety resilience of the existing tunnels induced by foundation pit excavation. Tunn. Undergr. Space Technol. 2025, 158, 106362. [Google Scholar] [CrossRef]
- Han, K.H.; Ju, J.W.W.; Zhang, C.P.; Su, D.; Cui, H.Z.; Lin, X.T.; Chen, X.S. A resilience assessment framework for microencapsulated self-healing cementitious composites based on a micromechanical damage-healing model. Int. J. Damage Mech. 2024, 33, 39–56. [Google Scholar] [CrossRef]
- Xu, Z.H.; Yu, T.F.; Li, S.C.; Lin, P.; Ma, W.; Han, T.; Li, S. Intelligent identification of lithology and adverse geology: A state-of-the-art review. Smart Undergr. Eng. 2025, 1, 3–25. [Google Scholar] [CrossRef]
- Chen, W.Z.; Tan, X.Y.; Yang, J.P. Review of state-of-the-art in structural health monitoring of tunnel engineering. Smart Undergr. Eng. 2025, 1, 40–50. [Google Scholar] [CrossRef]
- Zhao, G.F.; Li, Z.; Chen, Y.F.; Gong, Q.M.; Li, S.J.; Wei, X.D. A digital twin-based multiscale framework for predicting full-scale TBM rock cutting performance from miniature point load tests. Smart Undergr. Eng. 2025, 1, 51–63. [Google Scholar] [CrossRef]
- Wang, F.Y.; Zhang, D.M.; Huang, H.W.; Huang, Q. A phase-field-based multi-physics coupling numerical method and its application in soil-water inrush accident of shield tunnel. Tunn. Undergr. Space Technol. 2023, 140, 105233. [Google Scholar] [CrossRef]
- Wang, F.Y.; Zhou, M.L.; Zhang, D.M.; Huang, H.W.; Chapman, D. Random evolution of multiple cracks and associated mechanical behaviors of segmental tunnel linings using a multiscale modeling method. Tunn. Undergr. Space Technol. 2019, 90, 220–230. [Google Scholar] [CrossRef]
- Wang, F.Y.; Huang, H.W.; Zhang, D.M.; Zhou, M.L. Cracking feature and mechanical behavior of shield tunnel lining simulated by a phase-field modeling method based on spectral decomposition. Tunn. Undergr. Space Technol. 2022, 119, 104246. [Google Scholar] [CrossRef]
- Miao, J.B.; Lu, D.C.; Lin, Q.T.; Kong, F.C.; Du, X.L. Time-dependent surrounding soil pressure and mechanical response of tunnel lining induced by surrounding soil viscosity. Sci. China Technol. Sci. 2021, 64, 2453–2468. [Google Scholar] [CrossRef]
- Lin, X.T.; Chen, R.P.; Wu, H.N.; Cheng, H.Z. Deformation behaviors of existing tunnels caused by shield tunneling undercrossing with oblique angle. Tunn. Undergr. Space Technol. 2019, 89, 78–90. [Google Scholar] [CrossRef]
- Lin, X.T.; Chen, R.P.; Wu, H.N.; Cheng, H.Z. Three-dimensional stress-transfer mechanism and soil arching evolution induced by shield tunneling in sandy ground. Tunn. Undergr. Space Technol. 2019, 93, 103104. [Google Scholar] [CrossRef]
- Huang, X.; Schweiger, H.F.; Huang, H.W. Influence of deep excavations on nearby existing tunnels. Int. J. Geomech. 2013, 13, 170–180. [Google Scholar] [CrossRef]
- Liu, C.; Cui, J.; Zhang, Z.X.; Liu, H.; Huang, X.; Zhang, C.Q. The role of TBM asymmetric tail-grouting on surface settlement in coarse-grained soils of urban area: Field tests and FEA modelling. Tunn. Undergr. Space Technol. 2021, 111, 103857. [Google Scholar] [CrossRef]
- Gong, Y.K.; Zhang, C.; Geng, Z.H.; Chen, R.P.; Ren, Y.H. Development and evaluation of a process-oriented 3D finite element model for earth pressure balance shield tunneling. Comput. Geotech. 2024, 171, 106347. [Google Scholar] [CrossRef]
- GB 50010-2010; Code for Design of Concrete Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2010; pp. 19–21.
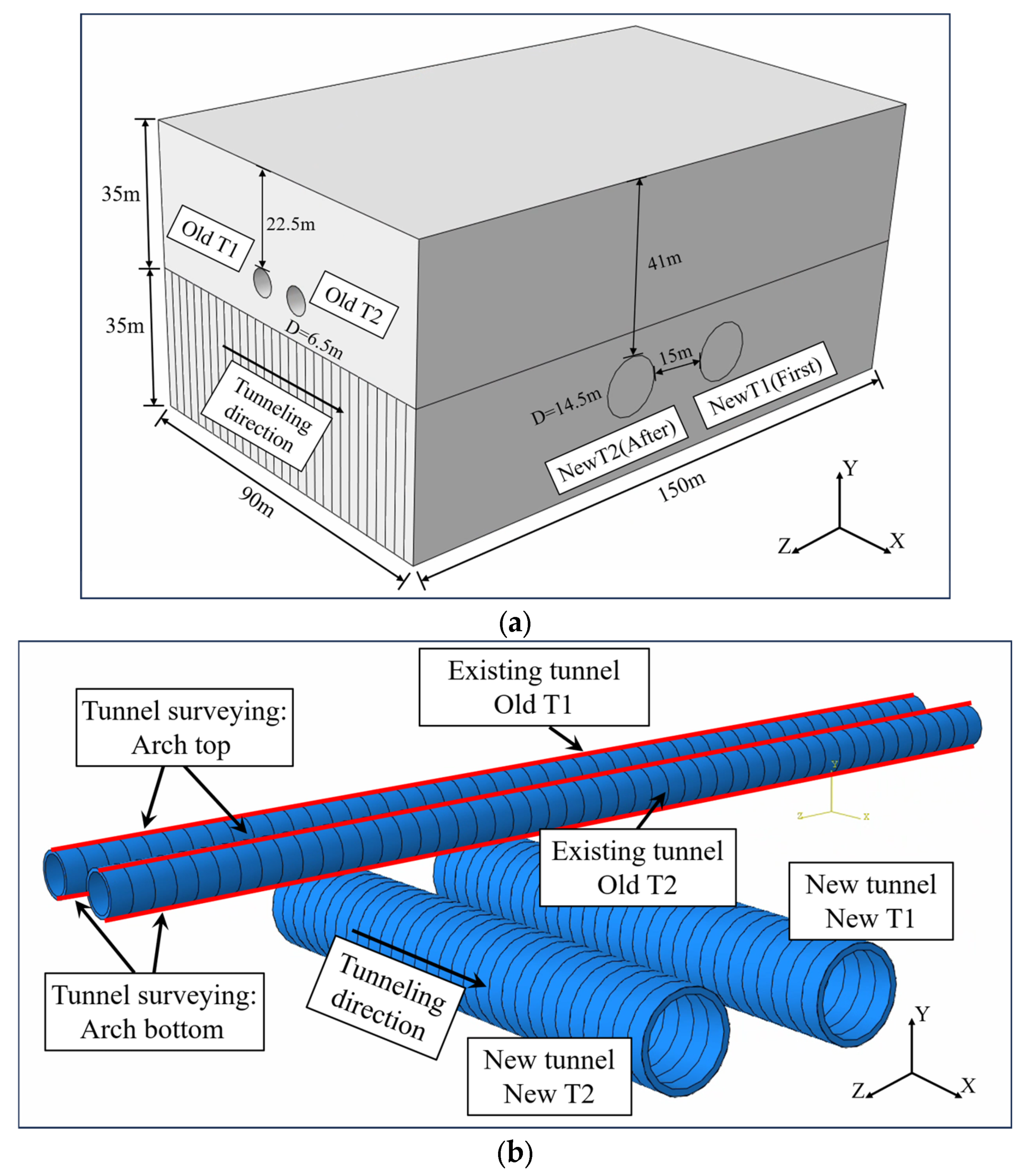







| Material Name | Thickness (m) | Mass Density (kg·m−3) | E (MPa) | Poisson’ s Ratio | Cohesion (kPa) | Internal Friction Angle (°) |
|---|---|---|---|---|---|---|
| Silty clay | 70 | 1900 | 140 | 0.23 | 25.4 | 22.4 |
| New tunnel lining (C50) | 0.55 | 2500 | 33,500 | 0.2 | - | - |
| Shield shell | 0.3 | 7850 | 210,000 | 0.25 | - | - |
| Existing tunnel lining | 0.5 | 2400 | 34,500 | 0.2 | - | - |
| Parameter | Unit | Value | Parameter | Unit | Value |
|---|---|---|---|---|---|
| Mass density | kg/m3 | 2400 | Peak compressive strength | MPa | 36.88 |
| Elastic modulus | GPa | 34.5 | Peak tensile strength | MPa | 2.64 |
| Poisson’s ratio | - | 0.2 | Peak compressive strain | - | 1.85 × 10−3 |
| Dilation angle | - | 38 | Peak tensile strain | - | 1.20 × 10−4 |
| Invariant stress ratio K | - | 0.667 | fb0/fc0 | - | 1.16 |
| Viscosity parameter | - | 0.0005 | Eccentricity | - | 0.1 |
| Times | Tensile Stress Contours | Description |
|---|---|---|
| T1 |  | Tensile stress initially appears, concentrated above the first line NewT1, but with a low magnitude. |
| T2 |  | The stress continues to rise, showing a local high stress zone. |
| T3 |  | The stress continues to increase, and the high stress zone expands slightly to both sides. |
| T4 |  | The stress decreases slightly, but the distribution pattern remains centered above the NewT1 axis. |
| T5 |  | Single-line completion: the high-stress zone remains stable, with a peak value of 2.624 MPa. |
| T6 |  | After tunnel NewT2 advances six rings, stress reaches the process peak of 2.655 MPa, exceeding the tensile strength of C50 concrete. |
| T7 |  | Stress begins to decrease but still maintains a wide distribution of high stress. |
| T8 |  | With continued advancement of the after line, the influence of double-line tunneling superimposes, expanding the distribution range. |
| T9 |  | Stress further decreases, and its distribution becomes more uniform. |
| T10 |  | Double-line completion: the stress peak decreases to 2.097 MPa, but its influence range is the widest. |
| Legend |  | |
| Times | DAMAGET Contours | Description |
|---|---|---|
| T1 |  | No damage; the structure remains intact. |
| T2 |  | Damage begins to appear locally at the tunnel bottom of the existing tunnel directly above NewT1. |
| T3 |  | Damage rapidly expands, forming a relatively distinct high-damage band. |
| T4 |  | Damage continues to accumulate, and its extent extends toward both sides. |
| T5 |  | Single-line completion: damage approaches its maximum value and remains stable in distribution. |
| T6 |  | After tunnel advances 6 rings: damage increases slightly. |
| T7 |  | Damage reaches its peak of 92.4% and stabilizes, though its range expands. |
| T8 |  | Damage remains stable, and its distribution pattern is essentially unchanged. |
| T9 |  | No further propagation of damage; the structure enters a stable damage stage. |
| T10 |  | Construction ends; damage stabilizes at 92.4%, exhibiting a high-damage and low-stress state. |
| Legend |  | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Zhai, Z.; Han, K. Numerical Simulation on Deformation and Damage Mechanism of Existing Underground Structures Induced by Adjacent Construction of Super-Large-Diameter Tunnels. Appl. Sci. 2026, 16, 1398. https://doi.org/10.3390/app16031398
Zhai Z, Han K. Numerical Simulation on Deformation and Damage Mechanism of Existing Underground Structures Induced by Adjacent Construction of Super-Large-Diameter Tunnels. Applied Sciences. 2026; 16(3):1398. https://doi.org/10.3390/app16031398
Chicago/Turabian StyleZhai, Zhiyuan, and Kaihang Han. 2026. "Numerical Simulation on Deformation and Damage Mechanism of Existing Underground Structures Induced by Adjacent Construction of Super-Large-Diameter Tunnels" Applied Sciences 16, no. 3: 1398. https://doi.org/10.3390/app16031398
APA StyleZhai, Z., & Han, K. (2026). Numerical Simulation on Deformation and Damage Mechanism of Existing Underground Structures Induced by Adjacent Construction of Super-Large-Diameter Tunnels. Applied Sciences, 16(3), 1398. https://doi.org/10.3390/app16031398







