Theoretical Analysis of the Vertical Stability of a Floating and Sinking Drilled Wellbore Using Vertical Elastic Supports

Abstract

This study addresses the calculation of vertical stability for shaft walls during floating and sinking processes in deep vertical shaft drilling in Western China. A mechanical model for the elastic support of the drilling shaft wall was developed by analyzing the forces during the transition from floating to sinking, and incorporating the cement filling behind the wall. This model was validated against empirical data. The analysis examined how shaft wall stability is impacted by parameters such as the elastic modulus of vertical support, borehole diameter, and water column height. Key findings include (1) the proposed elastic support model, which incorporates the viscoelastic properties of the cement slurry post setting, accurately reflecting the interaction between the wellbore and the surrounding rock mass; (2) the critical depth of the borehole wall initially increases and then decreases, correlating with cement slurry setting time, peaking about 18 h post initial setting, and stabilizing after 24 h as the support becomes a fixed support; and (3) a significant positive correlation exists between borehole diameter and critical depth, which increases and then decreases as the height of the ballast water rises. These results provide insights essential for assessing the stability of the floating sinking technique in drilling operations.

1. Introduction

Shaft sinking by drilling is a special mechanized shaft sinking technology [1,2,3]. Compared with other drilling methods, it has the characteristics of avoiding well drilling and being intrinsically safe [4,5,6]. It has been adeptly implemented for the construction of extensive and deep vertical shafts within the weakly cemented Cretaceous–Jurassic formations in Western China [7,8,9]. The sinking of a floating shaft and the filling of the wall with cement are key processes in the construction of a drilled borehole [10,11,12]. In recent years, with vertical shaft drilling construction increasingly involving projects that are both deep and large [13,14,15], calculating vertical stability for wellbore wall structures with a depth greater than 500 m and a net diameter greater than 6 m using existing Mining Engineering Design Manual [16] theoretical methods is no longer consistent with engineering practice [17]; such approaches cannot meet engineering needs and new methods must be studied and implemented urgently.

In recent years, domestic scholars have made some progress regarding theoretical research on the calculation of wellbore stability during floating and sinking. Niu Xuechao [18,19] simplified the shaft lining in the surrounding ground to a mechanical model with a tubular ballast element at the bottom of the shaft, and studied the stability of the shaft lining during the process of floating and sinking, in combination with a test model. Based on the principles of the energy method, Cheng Hua et al. [20,21,22] obtained a formula for calculating the critical depth at which a variable cross-section partially submerged drilled shaft lining remains vertically stable, using subsectional integral summation. This was then used with ABAQUS 6.3 to study the vertical structural stability of drilled shaft linings under different working conditions. Yao Zhishu [23] established a new calculation model and a new formula for calculating the critical depth at which a shaft lining floats and sinks affects vertical stability, before and after the first section is filled, by analyzing the forces of floating and sinking exert on the shaft bottom. Cheng Helan [24] studied the stress and deformation of the shaft lining during the floating and sinking process. By using the superposition method, the analytical expression of stress–strain at any point of the shaft lining during the floating sinking process could be obtained. Velychkovych, A. References [25,26] conducted a study on the adaptive behavior of elastic components of drilling dampers as the amplitude of external loads increases. Additionally, a novel numerical analysis model for the performance of friction dampers, based on a spirally cut shell, was established. These studies mainly consider how the variable cross-section of the borehole wall, the height to which the ballast water fills the wellbore, and the uneven distribution of ground density impact the vertical stability of the borehole wall.

Without further exploring the real boundary conditions of the contact between the wellbore and the surrounding rock–cement slurry, the sinking of the floating bottom of the wellbore is still used as the hinged boundary condition and the model for calculating the critical depth at which the vertical stability of the structure is established. However, a gap remains between the results of the critical depth calculation formula and engineering practice.

Therefore, this study takes the air shaft of Longgu Mine as its research object, establishes a calculation model based on an in-depth analysis of the contact between the bottom of the caisson wall and the surrounding ground and the filling and the stress conditions of the cement slurry wall under the sinking of the floating drilling wellbore, where the boundary conditions of the bottom of the caisson wall are regarded as the horizontal hinged and vertical elastic supports. The calculation formula for the vertical stability of the corresponding floating and sinking of the is derived and verified as part of this project. The main factors affecting the critical depth for vertical structure stability are analyzed. The research results can provide a reference for evaluating the stability of the shaft lining for drilled wellbores during floating and sinking, and for improving the filling technology for behind the wall.

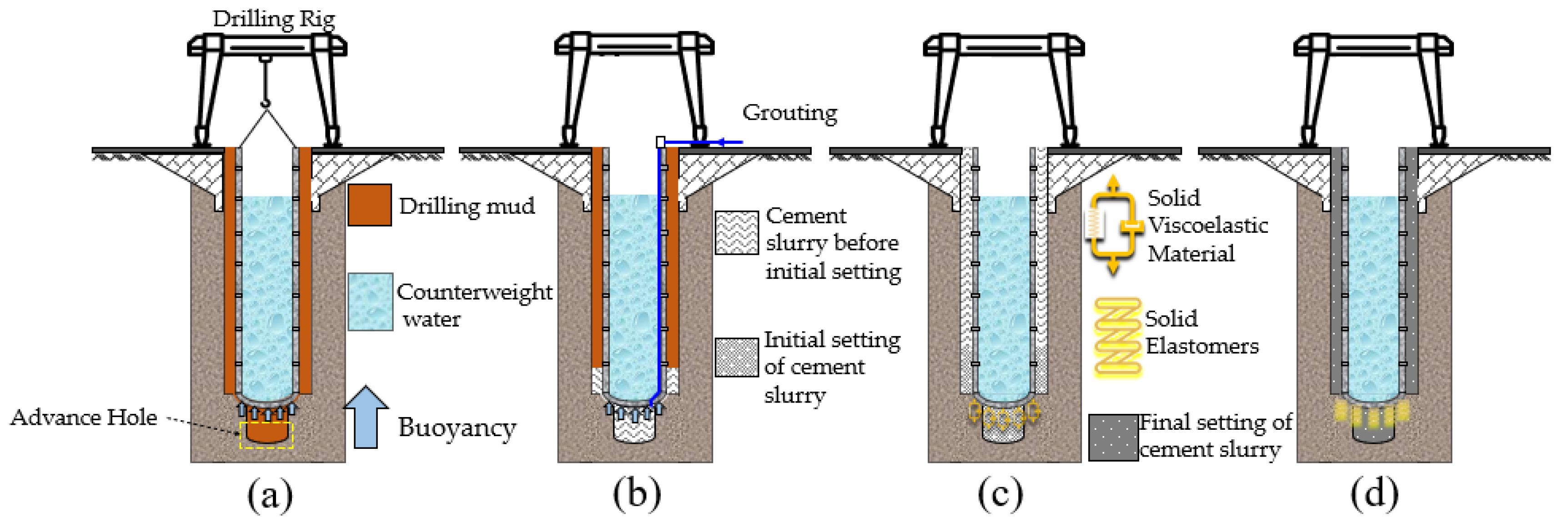
2. Analysis of Stress Evolution of Bottom Filling of Shaft Lining

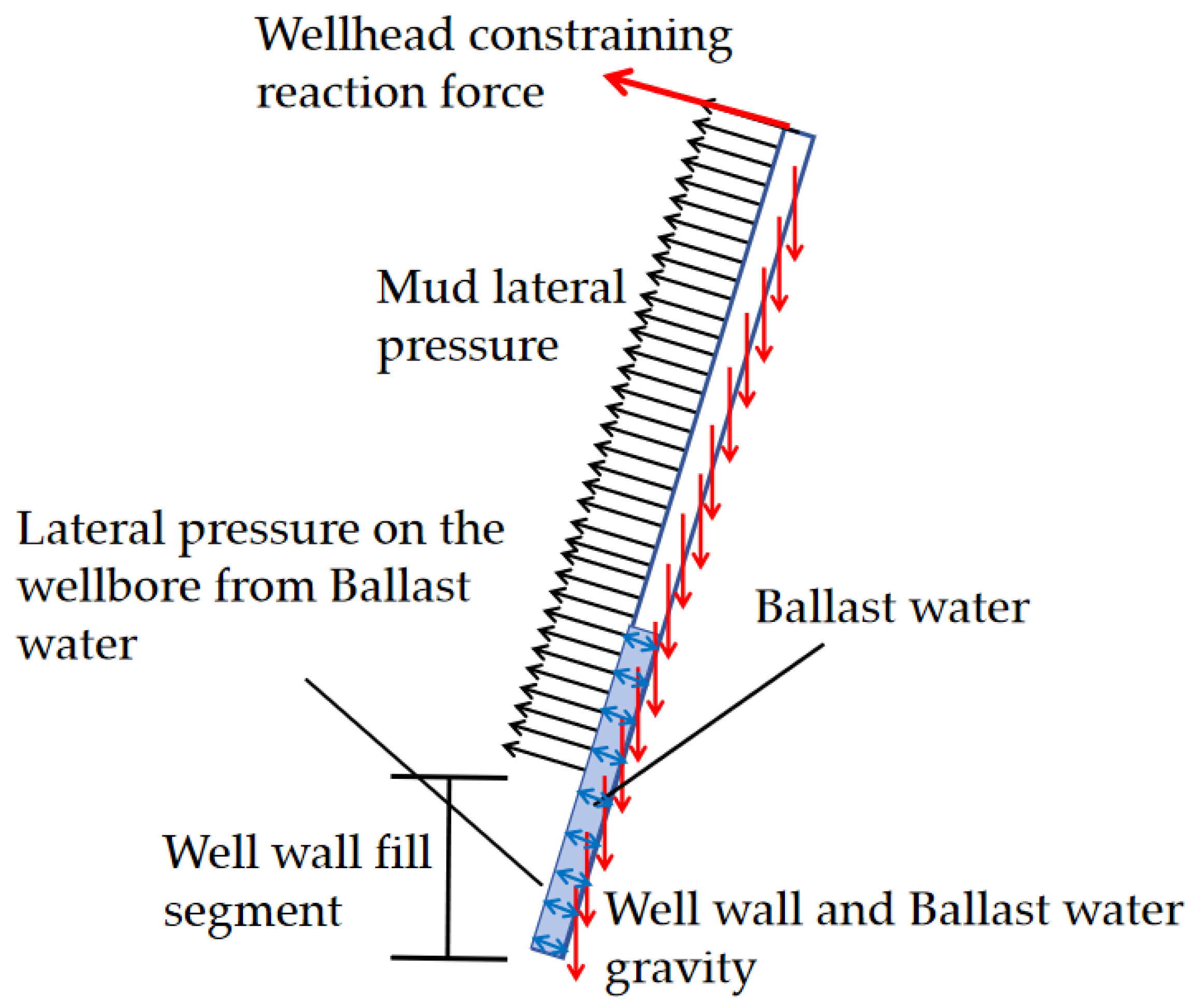
2.1. Analysis of the Stress Evolution of Bottom Filling in Wellbore Walls

Upon reaching the designated depth by drilling, the process involves circulating mud, adjusting mud parameters, and conducting ultrasonic logging. Within the mud-filled wellbore, the prefabricated wellbore bottom and wellbore sections are sequentially hoisted into place. Each segment of the wellbore is interconnected via flanges, and counterweight water is introduced to facilitate the buoyancy and sinking of the drilling wellbore until it reaches the bottom of the well. For wellbores with a net diameter exceeding 6 m, the construction methodology primarily employs a single expanding well technique. The depth of the advance borehole typically exceeds the design depth of the wellbore by approximately 5 m. Once the wall descends to the bottom and is rectified, the backfilling of the wall takes place. At this juncture, the residual mud in the advance borehole and the liquid within the wellbore impart a buoyancy effect prior to the filling of the first section of wall (approximately 80 m) with a cement slurry (Figure 1a). Subsequently, the inner tube method is utilized to introduce the initial section of the high-density cement slurry, which imparts buoyancy to the wellbore bottom prior to the onset of initial setting (Figure 1b). Following this, the first filled advance borehole and the cement slurry at the wellbore bottom transition into the initial setting state, resulting in the instantaneous cessation of the buoyancy exerted by the cement slurry [27,28,29]. The stability of the wellbore structure significantly decreases; however, during the process from the initial setting to the final setting of the cement slurry, the slurry begins to form solid particles and develops a certain level of strength. The weight of the wellbore and the injected counterweight water is conveyed to the bottom of the wellbore through the cement slurry after the initial setting period. At this point, the cement slurry in the advance borehole exerts a vertical support reaction force on the bottom of the wellbore. Due to the rigidity of the cement slurry after initial setting, it undergoes elastic deformation under pressure. Therefore, it can be regarded as an elastic support. This elastic support has a certain capacity for elastic deformation within a specific range. When the wellbore experiences support reaction forces, this vertical elastic support is capable of actively absorbing the bending strain energy of the wellbore wall and buffering the vertical displacements. Additionally, the deformation of the elastic support facilitates the release of high localized stress, which is then transmitted to adjacent areas, thereby preventing stress from concentrating at the bottom of the wellbore. This, in turn, and to a certain extent, enhances the stability of the wellbore. At this stage, the cement slurry is regarded as a solid viscoelastic body, marking a period when vertical structural instability is most likely to emerge following the floating and sinking of the wellbore (Figure 1c). Finally, as the initial high-fill cement slurry progresses towards the final solidification stage from bottom to top, the hydration reaction of the cement slurry is essentially complete, resulting in the formation of a stable crystalline framework within the paste, with a significant reduction in free water and the stabilization of the pore structure. At this stage, the material transitions from a viscoelastic flow state to a continuous medium predominantly characterized by elasticity, with the viscous flow effects significantly diminished. Once the cement slurry has fully set, it forms a strong bond with the bottom of the wellbore and the surrounding rock in the advance drilled section. At this stage, the cement slurry on the bottom of the wellbore can be described as exerting the same effect as a fixed support; the stress state of the wellbore is significantly enhanced, greatly improving its vertical resistance to instability (Figure 1d).

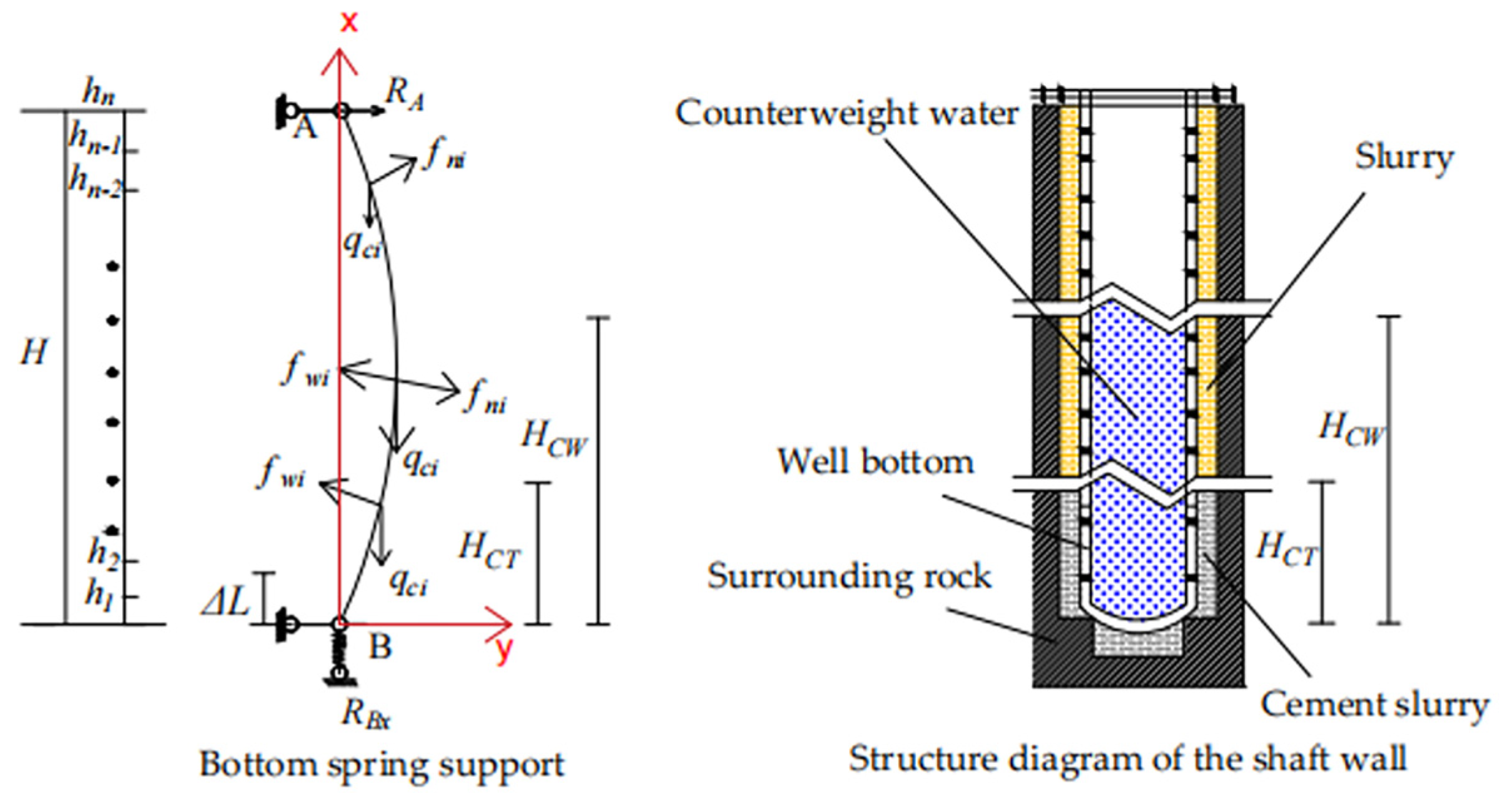
2.2. Computational Model for Assessing the Vertical Structural Integrity of Shaft Lining

Fundamental Assumptions:

(1)

The shaft lining is conceptualized as a slender compression member, articulated at both extremities, with the vertical support at the base simplified as an elastic foundation.

(2)

The vertical deflection profile of the shaft lining exhibits sinusoidal characteristics.

(3)

The shaft comprises n sections of wall, taking into account the effects of the thickness, material properties, and the height of the counterbalancing water of each wall section in terms of structural stability.

The analytical model of vertical stability of the shaft lining structure is established in accordance with the aforementioned assumptions, as depicted in Figure 2.

2.3. Calculation Formula for Vertical Structural Stability of Shaft Lining

During the initial stage of backfill grouting, the hydration reaction is intense. After the initial setting of the grout slurry, it begins to develop strength and can be treated as a solid viscoelastic body. At this point, the cylindrical structure of the shaft lining is no longer subjected to buoyancy. In the model of member compression, the bottom vertical support can be considered a spring support, while the lateral supports are treated as hinged supports.

The entire shaft comprises n segments of lining. Commencing from the bottom of the shaft, let M_i denote the bending moment of the i-th segment; let E_i represent the elastic modulus of the i-th segment; let d_i indicate the inner diameter of the i-th segment; let D_i signify the outer diameter of the shaft lining; let h_i denote the height of the i-th structural segment; and let I_i be the moment of inertia of the i-th segment. Additionally, a segments of the shaft lining are situated below the level of the counterweight water, with the height of the counterweight water indicated as H_CW, and b segments are positioned below the level of the backfill slurry, with the backfill height denoted as H_CT.

Under these conditions, the shaft lining’s cylindrical structure is not subject to buoyancy, and the lateral pressures from the surrounding mud slurry and backfill slurry on the shaft lining cylinder counteract each other. Therefore, the shaft lining cylinder is only subjected to its own weight, support reactions, and the pressure from the counterweight water.

Taking the vertical displacement at the bottom shaft support as y, and according to the principles of the mechanics of materials, the deflection curve can be approximated as

$$y=\delta \sin {\displaystyle \frac{\pi (x+\Delta L)}{H+\Delta L}}$$

(1)

The pressure exerted on the inner wall of the shaft lining by the counterweight water per unit length is $f_{wi}={\displaystyle \frac{\pi }{4}}{\gamma }_w{d_i}^2\sin \alpha =q_{wi}\sin \alpha$.

The pressure exerted on the outer wall of the shaft lining by the slurry per unit length is $f_{ni}={\displaystyle \frac{\pi }{4}}{\gamma }_n{d_i}^2\sin \alpha =q_{ni}\sin \alpha$.

Both the shaft bottom and shaft collar satisfy the geometric boundary conditions and natural boundary conditions, namely: $y(-\Delta L)=0$, $M(-\Delta L)=0$, $y(H)=0$, $M(H)=0$.

After the initial setting of the cement slurry, the gravitational load of the shaft, previously borne by the backfill fluid, is now supported by the bottom elastic support. Let the spring constant of the elastic support composed of the cement slurry be denoted as $K_n$. The compression displacement is denoted as $\Delta L_n$, the spring constant of the elastic support formed by the pre-drilled surrounding rock is $K_s$, and its compression displacement is $\Delta L_s$. The support reaction force is

$$R_{B_x}=K_s\Delta L_s+K_n\Delta L_n=G$$

(2)

The total strain energy of the entire shaft lining cylinder is

$$U={\displaystyle \sum _{i=1}^n\frac{1}{2}{E}_i{I}_i{\displaystyle {\int }_{h_{i-1}}^{h_i}{(y^{″})}^2}}\mathrm{d}x$$

(3)

Let the vertical displacement at the centroid of the shaft lining be $\Delta L_z$. The cumulative work exerted by the weight of the shaft lining, the weight of the counterbalancing water, and the lateral pressure exerted by the slurry on the cylindrical structure of the shaft lining can be calculated as follows:

$$W_1={\displaystyle \sum _{i=1}^n{q}_{ci}{\displaystyle {\int }_{h_{i-1}}^{h_i}\lambda (x)\mathrm{d}x}}+{\displaystyle \sum _{i=1}^a{\displaystyle {\int }_{h_{i-1}}^{h_i}{q}_{wi}\lambda (x)\mathrm{d}x+{\displaystyle \sum _{i=1}^n{\displaystyle {\int }_{h_{i-1}}^{h_i}{q}_{ni}\sin \mathsf{\alpha }\mathsf{\lambda }(\mathrm{x})\mathrm{d}x}}}}$$

(4)

The sum of the work done by the spring support and its energy loss is

$$W_2=-K_s\Delta {L_s}^2-K_n\Delta {L_n}^2$$

(5)

Therefore, when the cylindrical structure of the shaft lining transitions from a vertical state to a slightly bent state, the total work done by the external forces is

$$\Delta W=W_1+W_2$$

(6)

For a solid with a constant cross-section, given its elastic modulus E, applied force as F, cross-sectional area as A, height as L, and compressive deformation as ΔL, the spring constant K can be expressed as

$$K={\displaystyle \frac{\sigma A}{\Delta L}}={\displaystyle \frac{EA\epsilon }{\Delta L}}={\displaystyle \frac{EA\frac{\Delta L}{L}}{\Delta L}}={\displaystyle \frac{EA}{L}}={\displaystyle \frac{F}{\Delta L}}$$

(7)

According to the study by Hu Changming [30], for a linear viscoelastic model, the relationship between the elastic modulus of the cement slurry and time can be expressed as [31,32,33]

$$E(t)=E_m(1-e^{(-{\displaystyle \frac{E_m}{\eta }})t})=E_m(1-e^{(-{\displaystyle \frac{E_m}{H(t)}})})$$

(8)

where $E_m$ is the elastic modulus of the fully hardened cement paste (Pa), and $H(t)=\eta (t)/t$ is the viscous parameter (Pa).

Combining Equations (7) and (8) yields

$$K_n={\displaystyle \frac{E_m(1-e^{(-\frac{E_m}{H(t)})})A}{L}}$$

(9)

when the shaft lining cylinder is in a critical equilibrium state, $\Delta W=\Delta U$, which simplifies to

$${H_{cr}}^3={\displaystyle \frac{{\pi }^2{\displaystyle \sum _{i=1}^n{E}_i{I}_i\left(\frac{{\alpha }_i-{\alpha }_{i-1}}{2}-\frac{(\sin 2\pi {\alpha }_i-\sin 2\pi {\alpha }_{i-1})}{4\pi }\right)}}{{\displaystyle \sum _{i=1}^n{q}_i[\frac{{{\alpha }_i}^2-{{\alpha }_{i-1}}^2}{4}-\frac{1}{8{\pi }^2}(\cos 2\pi {\alpha }_i-\cos 2\pi {\alpha }_{i-1})]}+\frac{2}{{\delta }^2{\pi }^2}\left(G\Delta L_z-K_s\Delta {L_s}^2-K_n\Delta {L_n}^2\right)}}$$

(10)

Let $E_s$ represent the elastic modulus of the pre-drilled surrounding rock. By simultaneously solving Equations (9) and (10), the final formula for the critical depth of the shaft lining is obtained by

$$H_{cr}=\sqrt[3]{{\displaystyle \frac{{\pi }^2{\displaystyle \sum _{i=1}^n{E}_i{I}_i\left(\frac{{\alpha }_i-{\alpha }_{i-1}}{2}-\frac{(\sin 2\pi {\alpha }_i-\sin 2\pi {\alpha }_{i-1})}{4\pi }\right)}}{{\displaystyle \sum _{i=1}^n{q}_i[\frac{{{\alpha }_i}^2-{{\alpha }_{i-1}}^2}{4}-\frac{1}{8{\pi }^2}(\cos 2\pi {\alpha }_i-\cos 2\pi {\alpha }_{i-1})]}+B}}}$$

(11)

where $B={\displaystyle \frac{2}{{\delta }^2{\pi }^2}}(G\Delta L_z-{\displaystyle \frac{E_{s}A}{L}}\Delta {L_s}^2-{\displaystyle \frac{E_m(1-e^{(-\frac{E_m}{H(t)})})A}{L}}\Delta {L_n}^2)$. When B = 0, Equation (11) simplifies to the formula for calculating the critical depth for vertical structural stability of a multi-section shaft lining with variable cross-sections, as specified in the Mining Engineering Design Handbook [17].

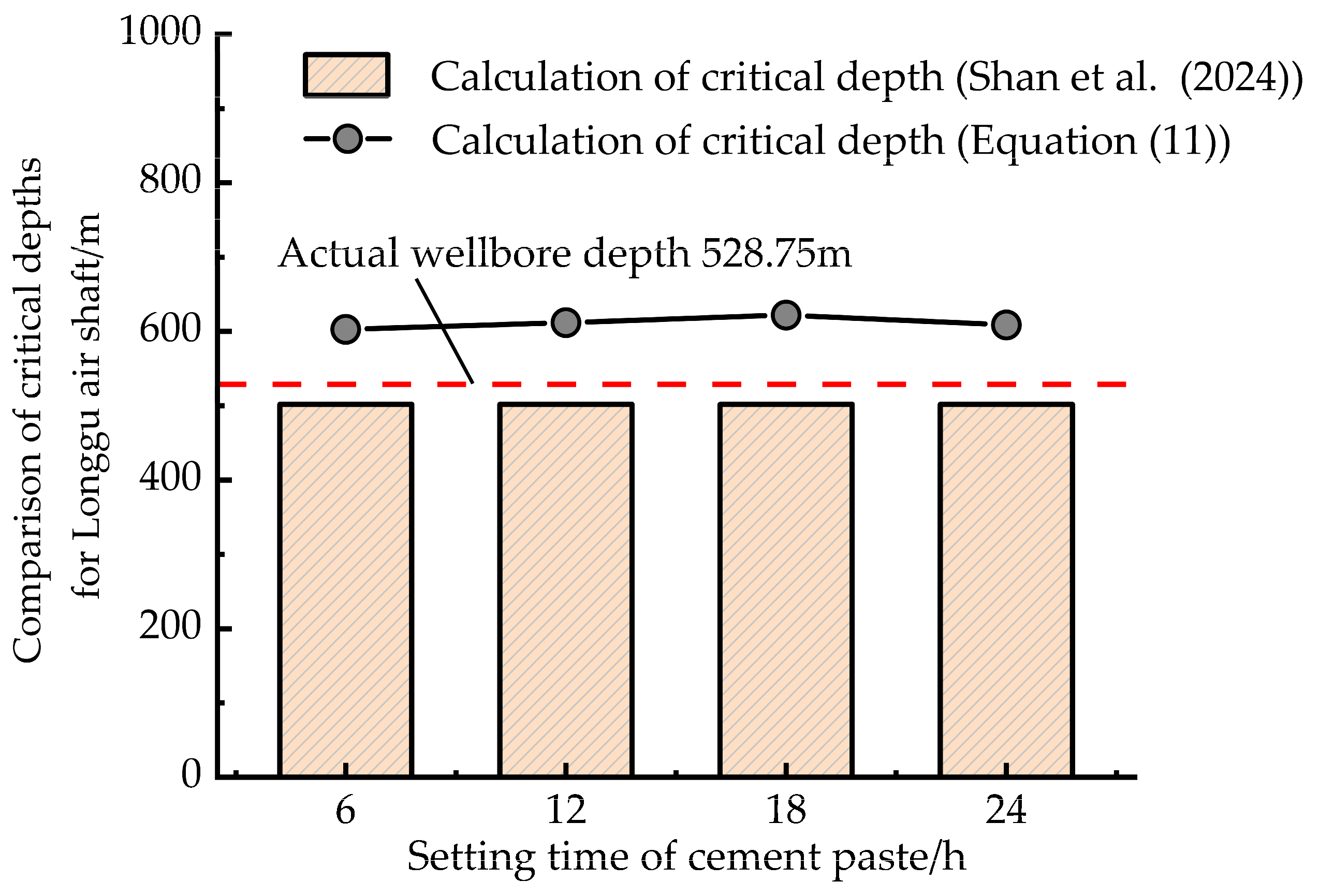
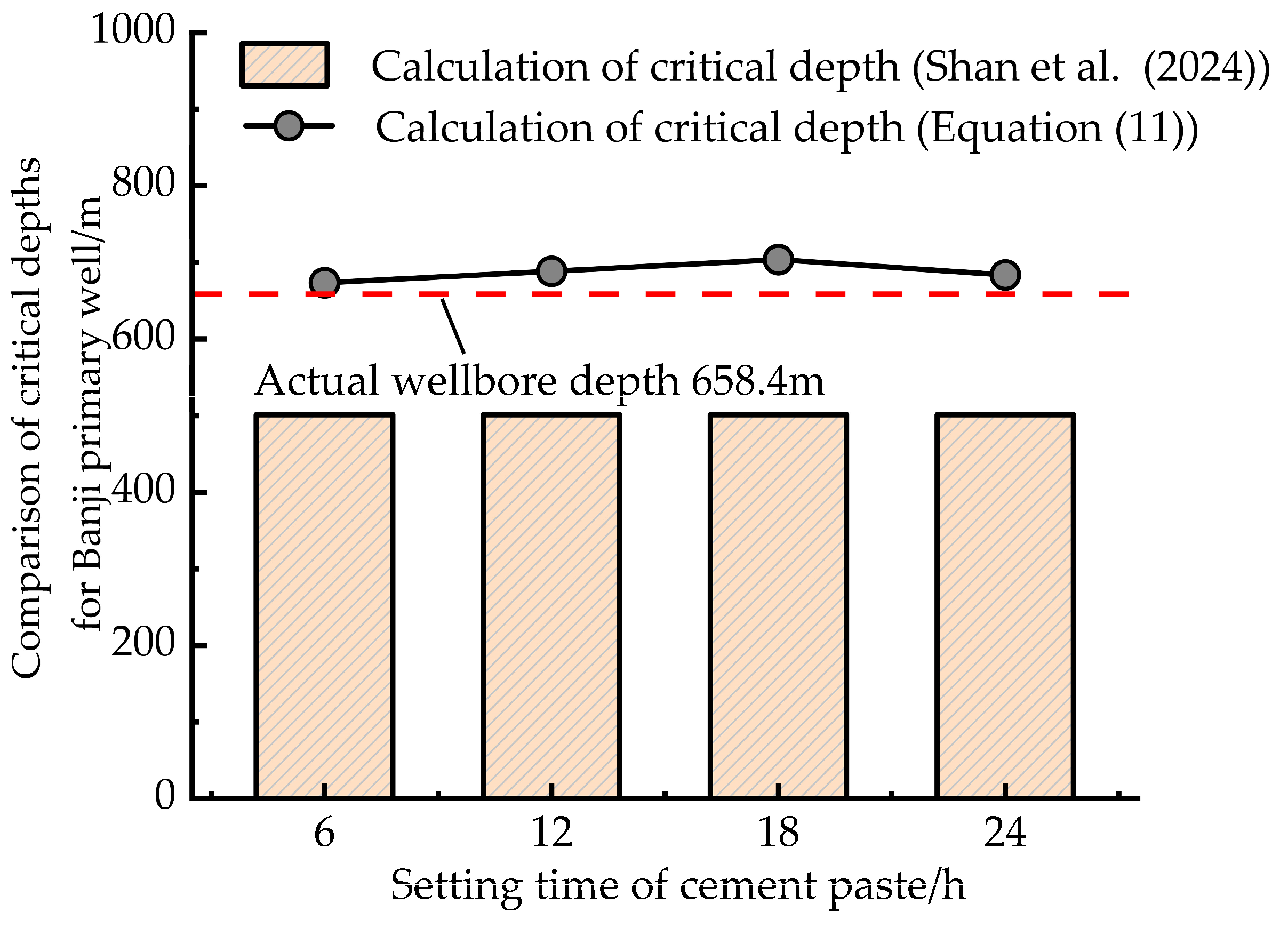
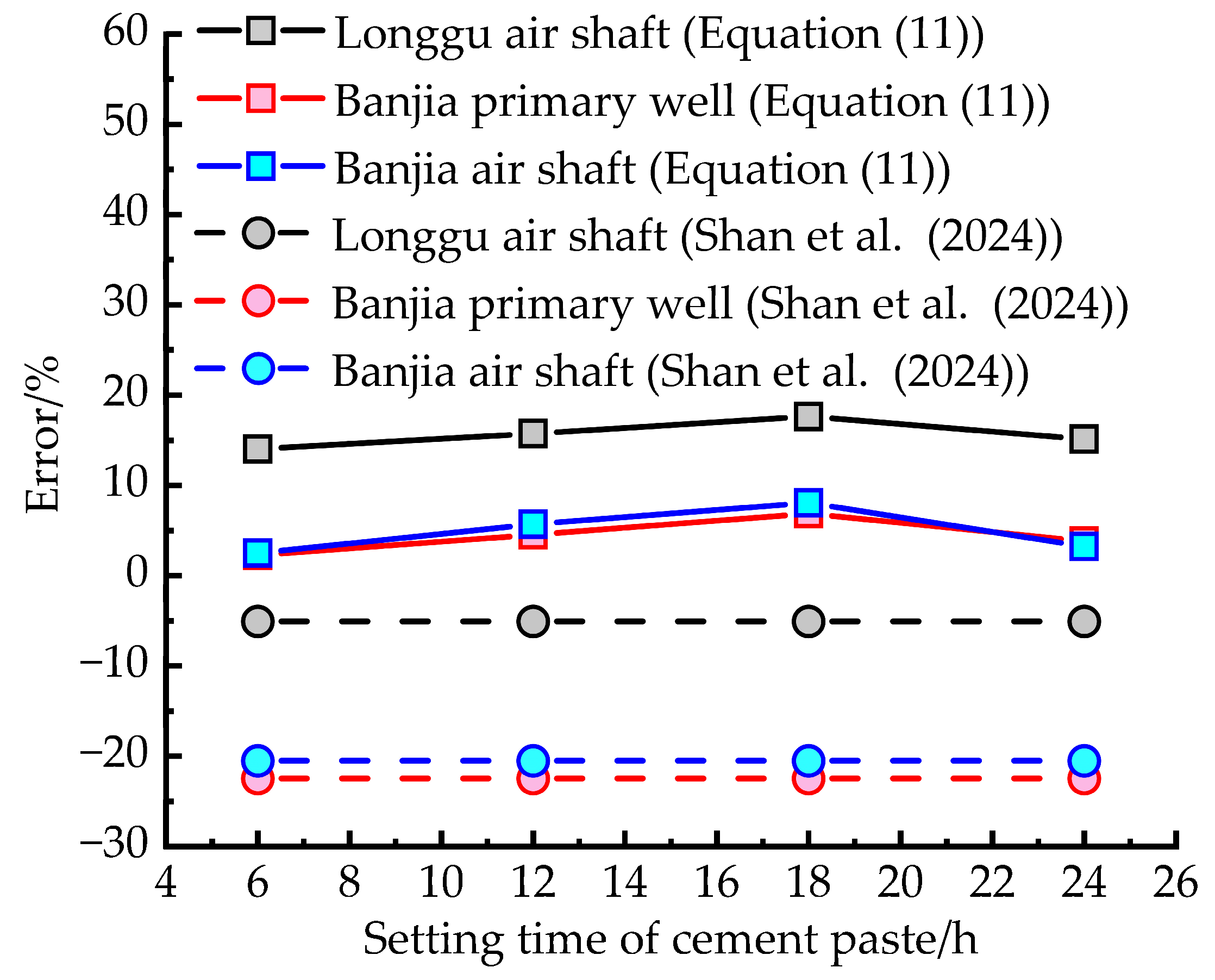
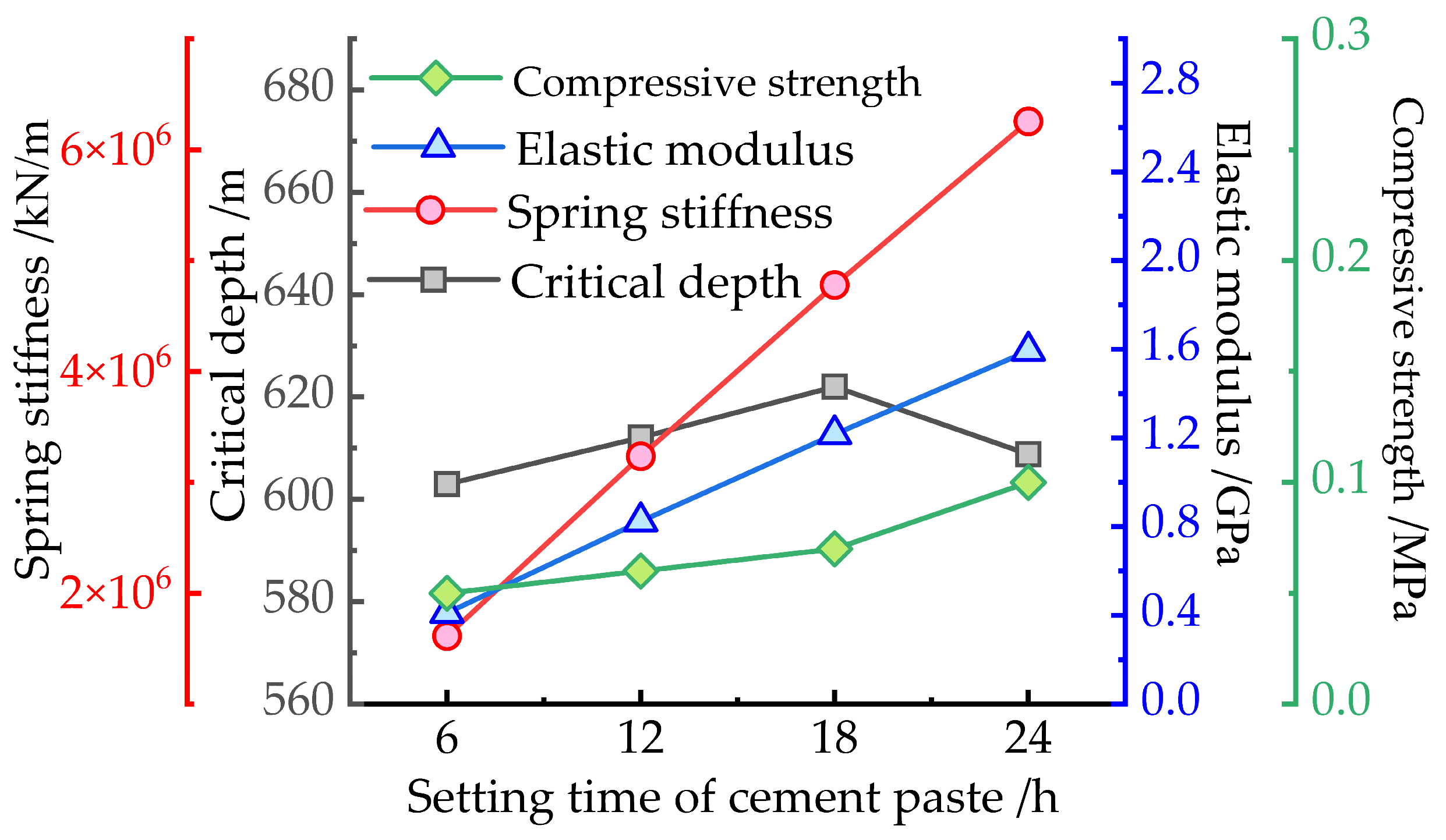
3. Results

According to the numerical calculation results from Reference [17], the maximum deflection of the borehole wall in a state of vertical stability is only a few millimeters. This study employs the elastic modulus data of cement slurry at different time points provided in Reference [30] (6 h: 0.411 GPa; 12 h: 0.824 GPa; 18 h: 1.218 GPa; and 24 h: 1.594 GPa) and utilizes Equation (11) to perform vertical structural stability calculations for the Longgu air shaft, the main board collection well, and the ventilation well. The calculation results are presented in Figure 3, Figure 4 and Figure 5.

Simultaneously, the critical depth for vertical stability of the borehole’s mid-section wall was calculated using the method outlined in the Mining Engineering Design Manual [17], revealing that the computed value is less than the actual subsidence depth of the borehole wall, and indicating the presence of stability risks. However, engineering practice indicates that the three mentioned borehole shafts did not experience instability during the lifting and sinking processes, suggesting that the critical depth calculation results provided by the manual [17] are overly conservative. In contrast, the vertical stability critical depths calculated using Equation (11) exceed the actual subsidence depths of the borehole walls, indicating no risk of instability, which aligns more closely with actual engineering conditions. As shown in Figure 3, Figure 4 and Figure 5.

Figure 6 illustrates the comparative analysis of the errors that arise in calculating the critical depth of the borehole wall using Equation (11) and the formula from Reference [17]. The analysis shows that the critical depth calculated with the formula from Reference [17] is less than the actual engineering value, exhibiting a negative error, and suggesting that this method yields overly conservative results, which are not favorable for guiding field operations. In contrast, the results derived from Equation (11) are consistently greater than the actual engineering values, with all errors being positive. Under a cement setting time of 6 h, the maximum error is only 14.04% (Longgu air shaft), and under a setting time of 18 h, the maximum error is only 17.64% (Longgu air shaft). This demonstrates that the results obtained using Equation (11) are closer to the actual engineering conditions, thus validating the scientific basis of the elastic support model for the vertical stability of the borehole wall proposed in this study.

4. The Influence of Different Factors on the Critical Depth of the Well Wall

Based on the floating and sinking of the shaft wall of Longgu air shaft [17], the influence on the critical depth of the shaft wall of the elastic coefficient of the vertical bearing, the diameter of the advance borehole, and the height of the ballast water in the well is discussed in this section.

4.1. Vertical Bearing Elastic Coefficient (K_n)

Integrating the findings from Reference [30] and laboratory tests, Figure 7 illustrates the interrelationships among the elastic coefficient of the cement slurry, its maximum compressive strength, the critical depth of the shaft wall, the elastic coefficient of the vertical bearing (K_n), and the setting times of the cement slurry. The critical depth of the borehole wall initially increases before subsequently decreasing throughout the cement slurry condensation process. In contrast, the elastic coefficient of the cement slurry, the maximum compressive strength, and the elastic coefficient of the vertical bearing (K_n) tend to rise in an approximately linear manner as the cement slurry gradually consolidates. The critical depth attains its maximum value of 622.04 m at 18 h; notably, the critical depth at 24 h (608.82 m) consistently surpasses that observed at 6 h (602.99 m).

As the setting time of the cement slurry increases, the elastic coefficient of the vertical bearing perpetuates its increase, favorably reducing the compression of the vertical bearing. Simultaneously, the compressive strength of the cement slurry increases gradually, enhancing the compression exerted on the vertical bearing. Between the setting time intervals of 6 to 18 h, compressive strength emerges as the primary controlling factor, leading to a continuous augmentation of the critical depth. Conversely, from 18 to 24 h, it is the elastic coefficient that predominates as the critical factor, resulting in a decrement in the critical depth. Once the setting period exceeds 24 h, the cement slurry ultimately fully solidifies, and the support becomes fixed.

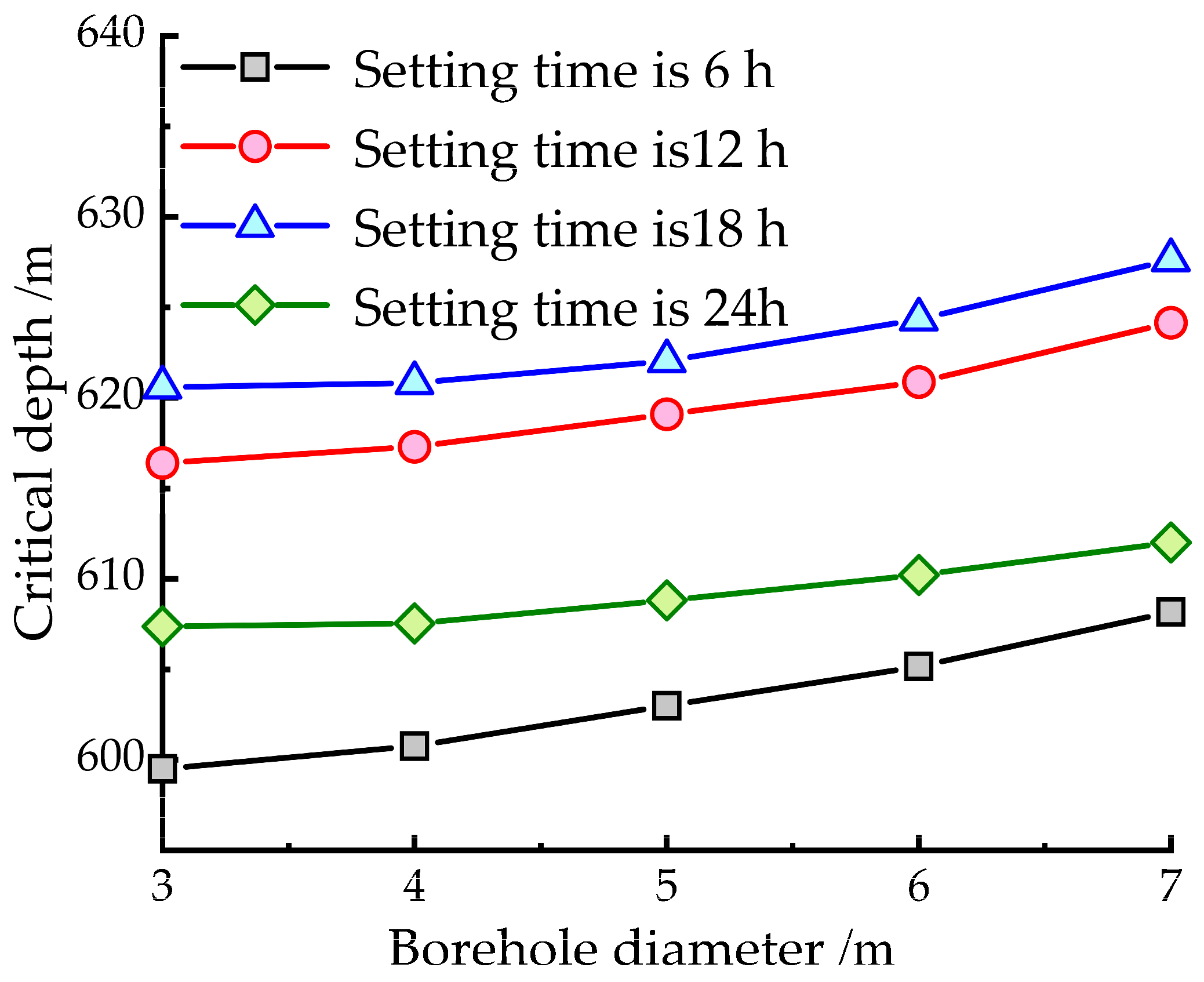
4.2. Borehole Diameter

The correlation between the critical depth of the borehole wall and the radius of the advance borehole is illustrated in Figure 8. Under varying setting times for the cement slurry, the critical depth of the borehole wall exhibits a positive correlation with the diameter of the advance borehole, peaking when this diameter reaches 7 m. More specifically, at setting times of 6, 12, 18, and 24 h, the critical depths are 8.68 m, 7.74 m, 7.03 m, and 4.63 m, respectively. The rate of increase in the critical depth of the borehole wall, in response to the expanding radius of the drill, varies depending on the initial setting time of the cement slurry. For instance, at a radius of 6 m, the growth rate reaches a maximum at 6 h, measuring 3.02, while it diminishes to a minimum of 1.79 at 24 h.

As the diameter of the advance borehole (r) expands, the contact area between the base of the casing and the cement slurry increases, consequently elevating the pressure exerted on the cement slurry. This, in turn, generates an increase in the strain energy of the borehole wall and increases the critical depth. Furthermore, during the initial setting phase, the compressive strength of the cement slurry is relatively low, resulting in it accommodating only a fraction of the total pressure, while the remainder is borne by the rock surrounding the advance drilled section. The elastic support provided by the surrounding rock can also absorb a portion of the strain energy exerted on the borehole wall when compressed. Notably, at a setting time of 6 h, the hydration reaction is at its most vigorous, leading to a substantial consumption of the free water in the cement slurry, a rapid growth in the elastic modulus, and the significantly enhanced capacity of the elastic support to absorb strain energy. Conversely, at 24 h, the hydration reaction slows, the rate of increase in the elastic modulus of the cement slurry declines, and the capability of the elastic support to withstand strain energy experiences only slight improvement.

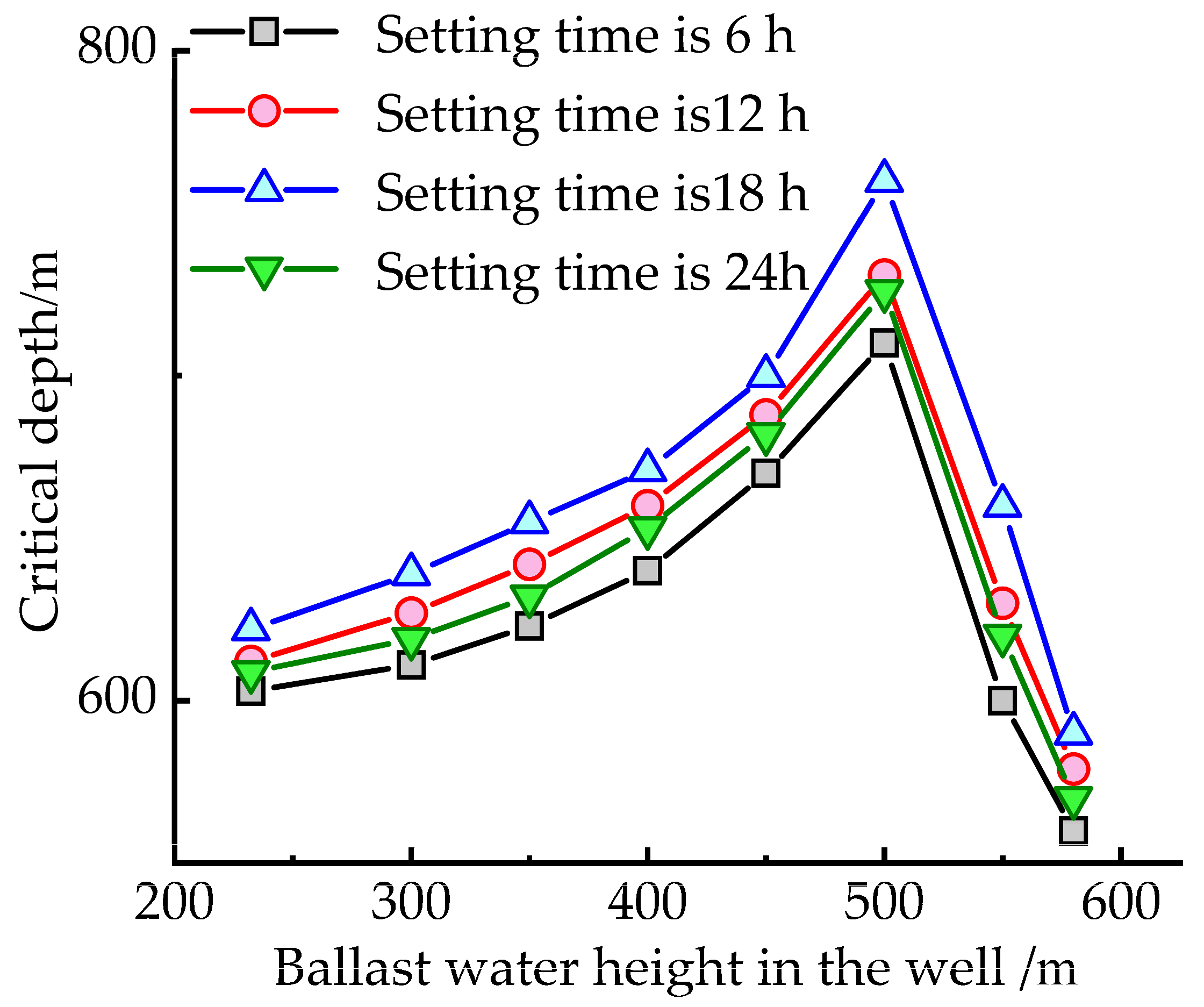
4.3. Ballast Water Height in the Well

The relationship between the critical depth of the wellbore and the height of the ballast water within the well is illustrated in Figure 9. At different cement paste setting times, both the critical depth of the wellbore and the height of the ballast water exhibit a trend of first increasing and then decreasing, reaching their peak when the ballast water height reaches 500 m. This behavior can be attributed to the initial phase where as the weight of the liquid in the wellbore increases, the overall center of gravity of the wellbore gradually shifts downward. The ballast water inside the well exerts pressure on the wellbore wall, partially resisting bending deformation, and thus increasing the critical depth of the wellbore. However, in the subsequent phase, as the height of the ballast water continues to rise, the elevation of the liquid level causes the center of gravity of the wellbore system to shift upward. The increase in the mass of the liquid significantly enhances the total weight of the wellbore wall, and the resultant additional bending moments and axial pressures greatly reduce its stability, leading to a decrease in the critical depth. The effect of the ballast fluid on the wellbore is illustrated in Figure 10.

For the cement slurry setting times of 6, 12, 18, and 24 h, the peak critical depths (H_cr) recorded are 720.92 m, 731.87 m, 760.06 m, and 726.41 m, respectively. When the height of the ballast water varies, the differences in the growth rate of Hcr are notable. As the water height increases from 232 m to 500 m, the increase in the critical depth of the wellbore with a prolonged cement paste setting time initially rises and then falls, with the change being most pronounced at the initial setting time of 18 h. Therefore, when calculating the critical depth of the wellbore wall, it is essential to adequately consider the impact of the ballast water height on the vertical stability of the wellbore structure.

5. Discussion

(1)

Although the model established in this study demonstrates good applicability in both theoretical derivation and engineering validation, it still has several limitations. The model treats the wellbore as a completely elastic medium, without considering the plastic deformation and damage accumulation effects experienced by the concrete materials during the actual stress process. Additionally, factors such as temperature variations, hydration reaction processes, and material mixing ratios—which could significantly influence the time-dependent mechanical properties of the cement slurry—are not included in the current model. Future research will further investigate the influence of different material properties on the stability of the wellbore.

(2)

Existing studies indicate that, under such engineering conditions, the contact state between the bottom of the wellbore and the surrounding rock is generally stable, with a low probability of occurrences such as unilateral contact, local unloading, contact failure, nonlinear stiffness-displacement responses, bond performance degradation, or interface slippage [18,19,20]. Therefore, this study does not incorporate these complex contact mechanisms into the model. Subsequent studies will combine physical model experiments with long-term field monitoring to further elucidate the variation patterns of the critical depth of the wellbore under different working conditions.

(3)

In establishing the analysis model for the vertical stability of the wellbore, this study simplified the upper boundary condition to a hinged support. However, in actual engineering scenarios, there may be other construction scenarios and control measures, such as using a wellhead locking device, that induce the wellbore top to approach the characteristics of a fixed support under actual working conditions. Changes in such boundary conditions will directly affect the buckling mode and critical load of the wellbore, subsequently impacting the stability assessment. Future research will further explore the influence of different upper boundary conditions on the stability of the wellbore.

6. Conclusions

In the transition from the sinking of the wellbore to the initial elevation of the backfill, the cement slurry situated at the bottom of the wellbore undergoes an immediate shift into its initial setting state, resulting in the instantaneous loss of buoyancy exerted by the slurry on the bottom of the wellbore. This phase presents the greatest propensity for the vertical structural instability of the bottom of the wellbore. A computational model addressing the vertical structural stability of shaft linings, predicated on elastic support, has been proposed. This model incorporates the viscoelastic properties of the filling cement slurry post initial setting, accurately reflecting the stress conditions experienced by the shaft lining during the critical phases of floating and subsiding, as well as during the backfilling process against the wall. The elastic coefficient of vertical bearing (K_n) exhibits a positive correlation with changes to the elastic modulus and strength of the cement slurry throughout the consolidation phase, significantly impacting the critical depth of the shaft lining. Initially, the critical depth of the shaft lining increases before subsequently decreasing as the elastic coefficient of vertical support rises, which, in turn, correlates positively with the diameter of the advance borehole and demonstrates a similar trend—an initial increase followed by a decrease—as the height of the ballast water within the well increases.