MSHI-Mamba: A Multi-Stage Hierarchical Interaction Model for 3D Point Clouds Based on Mamba

Abstract

Mamba, based on the state space model (SSM), offers an efficient alternative to the quadratic complexity of attention, showing promise for long-sequence data processing and global modeling in 3D object detection. However, applying it to this domain presents specific challenges: traditional serialization methods can compromise the spatial structure of 3D data, and the standard single-layer SSM design may limit cross-layer feature extraction. To address these issues, this paper proposes MSHI-Mamba, a Mamba-based multi-stage hierarchical interaction architecture for 3D backbone networks. We introduce a cross-layer complementary cross-attention module (C3AM) to mitigate feature redundancy in cross-layer encoding, as well as a bi-shift scanning strategy (BSS) that uses hybrid space-filling curves with shift scanning to better preserve spatial continuity and expand the receptive field during serialization. We also develop a voxel densifying downsampling module (VD-DS) to enhance local spatial information and foreground feature density. Experimental results obtained on the KITTI and nuScenes datasets demonstrate that our approach achieves competitive performance, with a 4.2% improvement in the mAP on KITTI, validating the effectiveness of the proposed components.

1. Introduction

As the core data form for representing the real 3D world, 3D point cloud technology has shown irreplaceable application value in fields such as autonomous driving, robotics, and virtual reality. Unlike the dense arrays of 2D images, the disorder, irregularity, and multi-scale geometric–semantic complexity of point cloud data pose significant challenges to efficient representation learning and cross-task transfer. Early sparse convolutional neural networks (sparse CNNs) can obtain effective features [1,2,3,4,5,6], but their fixed convolution kernels struggle to dynamically adapt to complex geometric structures. Another type of Transformer-based model [7,8,9,10,11], which relies on serialization, features a global attention mechanism; however, its quadratic computational complexity limits its application in long-sequence point clouds. Furthermore, single-stage detection methods [12,13] often face issues such as insufficient multi-scale information fusion and poor coherence in geometric reconstruction during self-supervised pre-training tasks.

We have noted recent progress in state space models (SSMs) [14,15]. Among these, Mamba models propose an efficient hardware-aware algorithm that enables efficient training and inference through linear-complexity dynamic modeling. Recent related work [16,17,18,19,20,21] has successfully transferred 1D sequence Mamba from NLP to 2D vision tasks. For 3D point cloud data with more complex spatial structures, frameworks such as those in [12,22,23] also leverage the dynamic selectivity mechanism of SSMs to overcome the efficiency–accuracy trade-off bottleneck in traditional methods, enabling the efficient processing of long point cloud sequences. Such frameworks capture cross-level geometric dependencies via implicit state variables across multiple Mamba layers and adaptively fuse multi-scale feature information, thereby enhancing global semantic consistency while preserving sensitivity to local details.

On this basis, our work introduces a Mamba-based multi-stage hierarchical interaction architecture. Through multiple stages, it realizes the progressive modeling of spatial geometry, effectively capturing geometric and semantic information at multiple resolutions. To optimize the fusion of multi-scale information between stages and within layers of each stage, we introduce a cross-layer complementary cross-attention mechanism. This mechanism divides Mamba layers into two types: ordinary Mamba layers and interactive Mamba layers that incorporate a complementary cross-attention module. Ordinary Mamba layers perform conventional sequence modeling, while interactive Mamba layers dynamically fuse current-layer features with historical interactive features. This interactive module captures two types of historical information: single-scale features from the immediate previous layer and multi-scale features from multiple preceding interactive layers. By complementarily fusing these two types of features, the mechanism overcomes the locality limitations of traditional hierarchical structures, enhances cross-layer and cross-stage interactive fusion between shallow detail features and deep semantic features, and improves the model’s hierarchical expressive capacity for complex patterns, while reducing information redundancy.

To enhance the spatial proximity of voxel serialization, we also propose two modules. One is the bi-shift scanning strategy module, which combines multi-mapping paths of space-filling curves and spatial displacement. This strategy rearranges voxel blocks according to the logical scanning order in 3D space. By utilizing the complementary path planning of the Hilbert curve and its variant, the Trans-Hilbert curve, it constructs a two-way geometric association mapping, effectively resolving the limitations of traditional single-path scanning and minimizing proximity loss during sequence encoding. By introducing spatial displacement, it dynamically adjusts the starting position of the scanning block to capture a wider range of spatial relationships. Our other module introduces a voxel downsampling operation between stages. This paradigm leverages submanifold sparse feature downsampling to further mitigate the degradation in local spatial proximity caused by voxel serialization operations. Specifically, submanifold convolution is used to accurately extract the surface geometric features of non-empty voxels, supplemented by sparse convolution to dynamically expand the effective receptive field. In addition, in the downsampling module, we selectively identify high-response regions of 3D features for voxel generation, achieving feature focus on key regions and reducing redundant background calculations.

Our contributions are summarized as follows:

(1)

We propose MSHI-Mamba, a Mamba-based multi-stage hierarchical interaction architecture for 3D voxels, which enables the interactive fusion of feature information across layers and stages.

(2)

We define a cross-layer complementary cross-attention mechanism, enhancing feature complementarity between layers, reducing information redundancy, and further improving the network’s cross-layer representation capabilities.

(3)

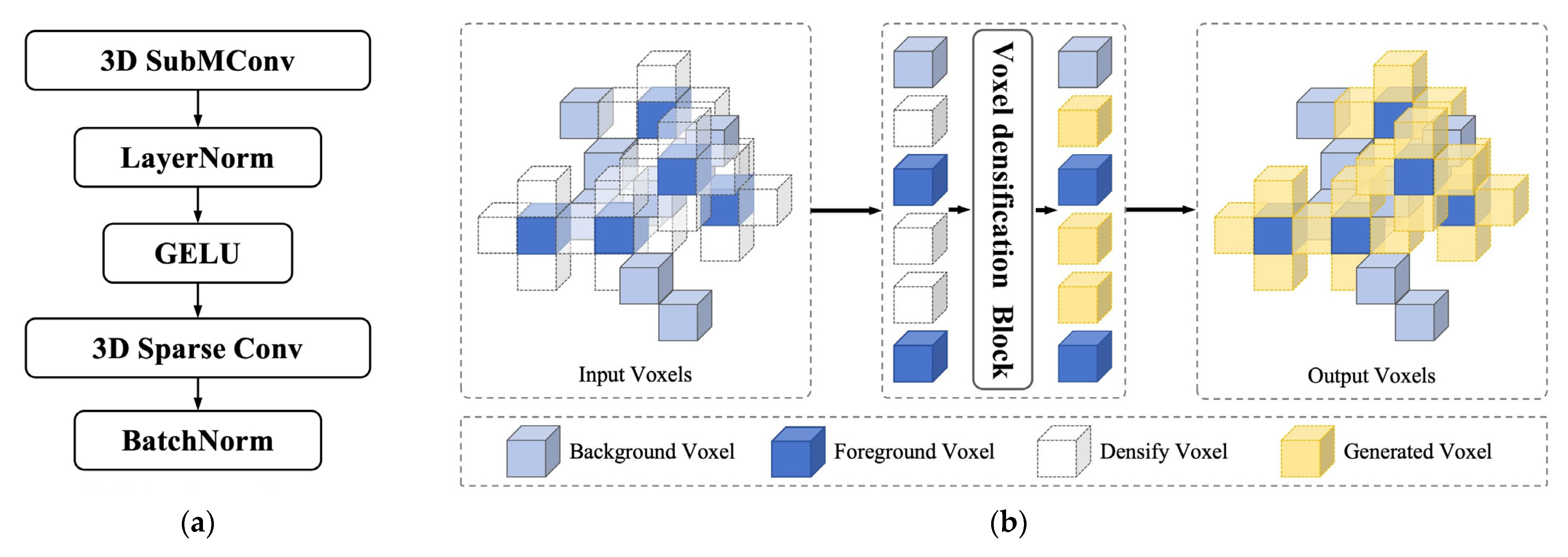
To mitigate spatial proximity loss caused by voxel serialization and expand the model’s perception range, we propose a bi-shift scanning strategy and voxel densification downsampling. These enhance local spatial information, selectively generate key foreground voxels, and enable cross-regional spatial information perception.

(4)

Our experimental results demonstrate the effectiveness of the proposed approach. On the KITTI dataset, MSHI-Mamba achieves a 4.2% improvement in the mAP compared to the baseline method. Competitive performance is also observed on the nuScenes dataset.

2. Related Work

2.1. Three-Dimensional Object Detection Based on Point Clouds

In autonomous driving and robotics, accurate 3D spatial perception is a pivotal prerequisite for reliable system operation. Point cloud-based 3D object detection methods fulfill this task by directly processing the geometric features of raw point clouds, and such approaches are primarily categorized into three representative paradigms: voxel-based, point-based, and voxel-point hybrid methods. Voxel-based methods, such as Voxel R-CNN and VoxelNeXt [2,3,5], convert unordered point clouds into regular grids via voxelization and leverage 3D sparse convolution for feature extraction. These methods fully exploit the sparsity of voxelized data, thus achieving an effective trade-off between inference efficiency and detection accuracy. Point-based methods, such as PointRCNN and 3DSSD [24,25,26], preserve the fine-grained geometric details of point clouds through downsampling operations combined with architectures like PointNet++ [27], yet they typically suffer from excessive computational overhead. Voxel-point hybrid methods, such as PV-RCNN and BADet [4,28,29], integrate the merits of both voxel and point representations. By means of multi-scale feature aggregation, they boost the detection performance, with a particularly notable improvement for small object detection. From the perspective of the model architecture, 3D point cloud detection methods can be further divided into sparse CNN-based methods and sequence-based modeling methods. Sparse CNN-based methods reduce redundant computations through sparsity constraints and demonstrate strong capabilities in local feature capture. Nevertheless, their receptive fields are inherently limited by the adoption of small convolutional kernels, which impairs their ability to model global contextual information.

2.2. Three-Dimensional Point Cloud Transformers

Due to the powerful global modeling abilities of Transformers, 3D object detection based on Transformers has become one of the mainstream architectures for point cloud analysis tasks. They can break through the local receptive field limitations of traditional convolutional neural networks (sparse CNNs) and achieve the efficient perception of complex 3D scenes. Some works [9,13,30,31,32,33] introduce and modify point cloud/voxel Transformer architectures to guide 3D representation learning, further enhancing the performance and efficiency of Transformers across different tasks. For example, Point-BERT [13] and Point-MAE [30] directly introduce standard Transformer architectures applicable to self-supervised learning. OctFormer [31] uses octrees to sort point clouds, while DSVT [9] uses dynamic sparse window attention, which supports the efficient parallel computing of local windows with varying sparsity. The point cloud processing component of 3DMMF [34] applies a context-aware channel expansion based on the self-attention mechanism to the PointPillars [35] detection network, effectively improving model performance. Recent works, such as BEVFormer v2 [32] and RTDETRv3 [33], significantly improve the real-time detection performance by optimizing the query mechanism and sparse feature indexing of Transformer decoders. They also introduce implicit motion compensation in time-series modeling to enhance the robustness in tracking dynamic targets. Although Transformers show strong global modeling potential in 3D detection, their computational complexity and multi-modal feature alignment efficiency remain focuses of current research.

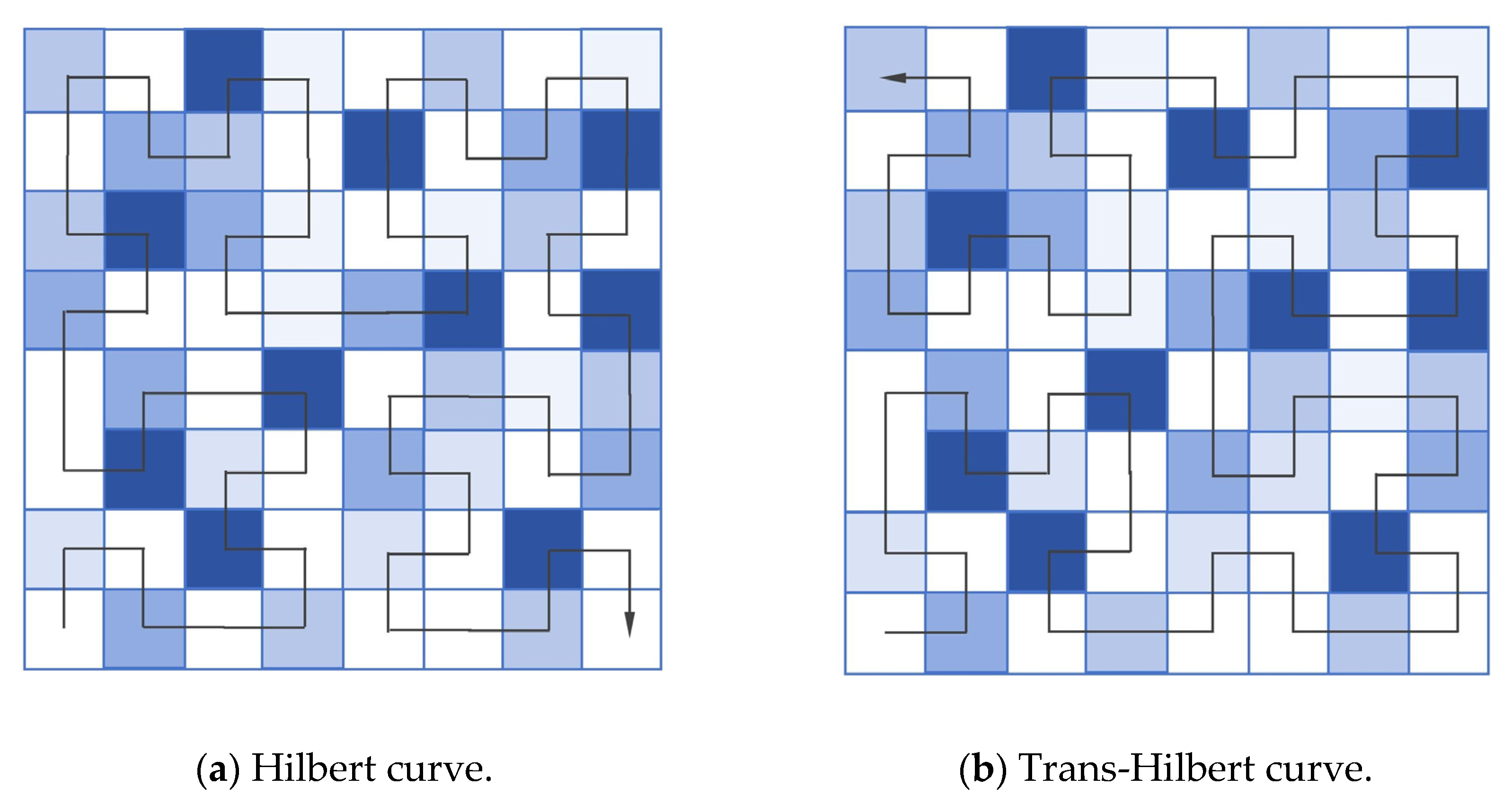
2.3. State Space Models and Space-Filling Curves

In large-scale sparse point cloud scenes, the state space model (SSM) relies on linear-complexity sequence modeling, which breaks through the bottleneck of traditional methods in terms of computational efficiency and long-range dependence modeling. Its selective state transfer mechanism effectively addresses the quadratic complexity problem caused by global attention calculations in Transformers, balancing local geometric details and global context awareness. For disordered point cloud or voxel features, a major technical challenge is achieving efficient serialization to adapt to the recursive computing paradigm of the SSM. The space-filling curve traverses each point in multi-dimensional space through a fractal path, maintaining spatial topology and local proximity during dimensionality reduction and serialization. Current techniques [12,36,37,38] apply it to sparse data processing. In 3D perception tasks, PointMamba [12] combines the spatial traversal advantages of the Hilbert curve to convert disordered point clouds into a one-dimensional sequence with local causality, embedding a selective SSM module to achieve efficient global modeling. Voxel Mamba [22] integrates the Hilbert curve with a voxel feature pyramid network, using an SSM to perform the cross-level dynamic fusion of multi-scale voxel features and model long-range dependencies through linear recursion. Additionally, the voxel grouping method FlatFormer [10] uses window scanning curves to parallelize large-scale voxels, significantly improving the hardware execution efficiency. The collaborative design of space-filling curves and SSMs can mitigate the damage to spatial structures caused by serialization. Therefore, we adopt this idea to design a double-shift scanning strategy to maintain the local proximity of voxel features and achieve efficient global context perception.

3. Method

In this section, we introduce MSHI-Mamba, a Mamba-based multi-stage hierarchical interaction 3D backbone. Figure 1 shows the details of the network architecture. In the backbone network, we aggregate voxel features across multiple stages (described in Section 3.1), enabling the network to gradually extract and integrate voxel feature information from different levels and dimensions; in each stage, efficient inter-layer information interaction is achieved through a cross-layer complementary cross-attention module (described in Section 3.2), which effectively enhances the model’s representational capabilities. Each layer applies a bi-shift scanning strategy to serialize all scene voxels into a one-dimensional sequence (described in Section 3.3) and feeds them into the Mamba block for feature extraction. This not only preserves spatial proximity but also enables cross-region shift operations, enhancing the mode’s ability to model long-range dependencies. To facilitate the flow of feature information between stages, we also design a voxel densification downsampling module (described in Section 3.4) for foreground feature densification and effective downsampling. Through the synergy of these two functions, the integration and transmission of feature information across different stages are achieved, further improving the model’s overall performance. The architecture proposed in this paper can seamlessly replace the 3D backbone in existing methods and enhance the 3D perception performance of autonomous driving systems.

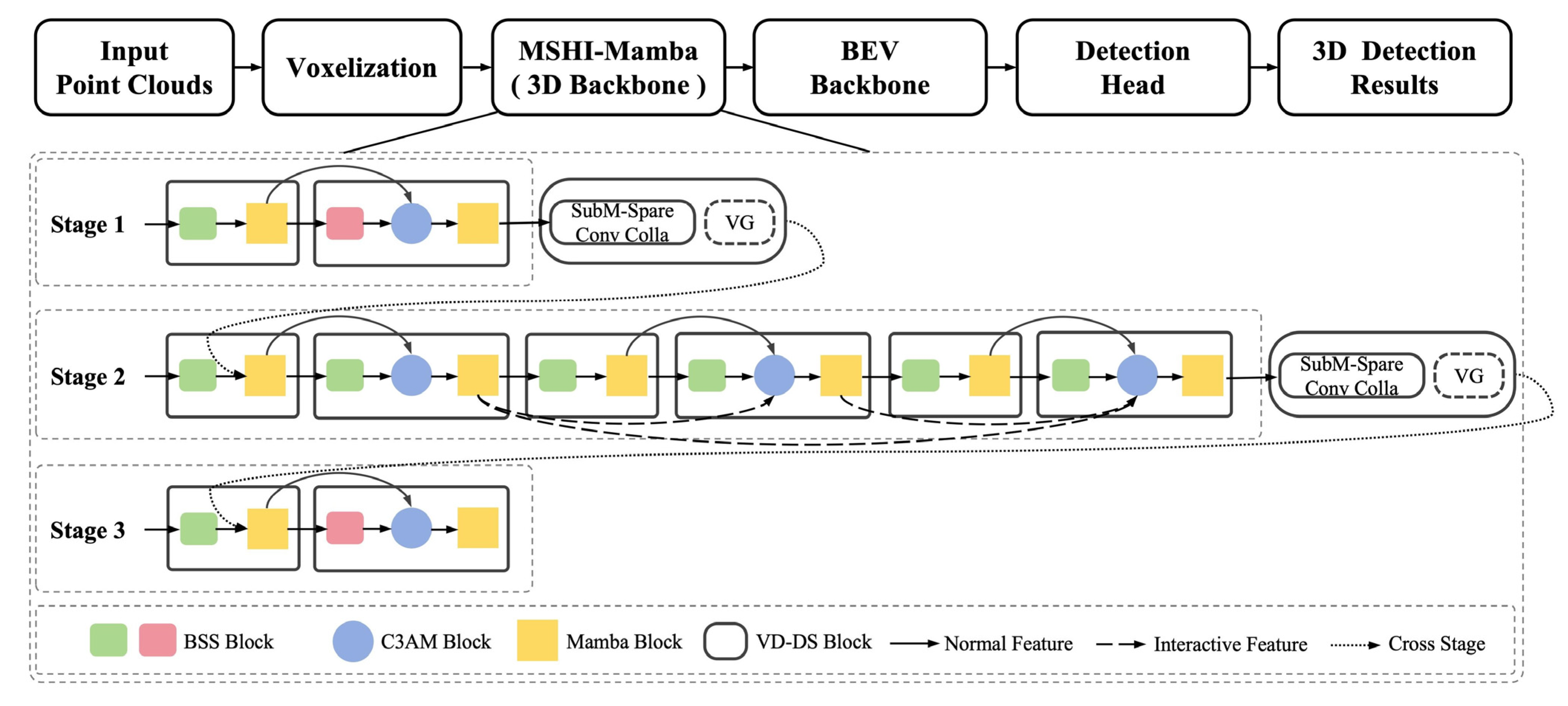
3.1. Multi-Stage Hierarchical Interaction Architecture (MSHI)

Our designed Mamba-based multi-stage hierarchical interaction 3D backbone, MSHI-Mamba, adopts a three-stage progressive architecture, with its specific structure shown in Figure 1. The first stage performs lightweight geometric perception and uses a two-Mamba-layer structure. At this shallow stage, the network processes high-resolution voxel features, and the presence of fewer layers prevents the premature introduction of global dependencies that could disrupt local topologies. This reduces the computational complexity while maintaining the initial spatial continuity, enabling the network to ensure information integrity, reduce the unnecessary consumption of computing resources, and improve the efficiency when processing large amounts of high-resolution feature data. The second stage functions as the middle layer, containing six Mamba layers and serving as the network’s core feature extraction layer for semantic abstraction. Stacking Mamba layers achieves hierarchical receptive field expansion, captures long-range dependencies, improves the understanding of complex autonomous driving scenes, and enhances the accuracy and reliability of network detection. The third stage remains a lightweight stage. Although the voxel feature resolution is the lowest at this stage, excessive Mamba layers may cause information redundancy, which impairs model performance. Therefore, we only set up a simplified two-Mamba-layer architecture. These two Mamba layers effectively integrate shallow detail features and deep semantic features, enhancing the integrity of semantic information while restoring spatial details.

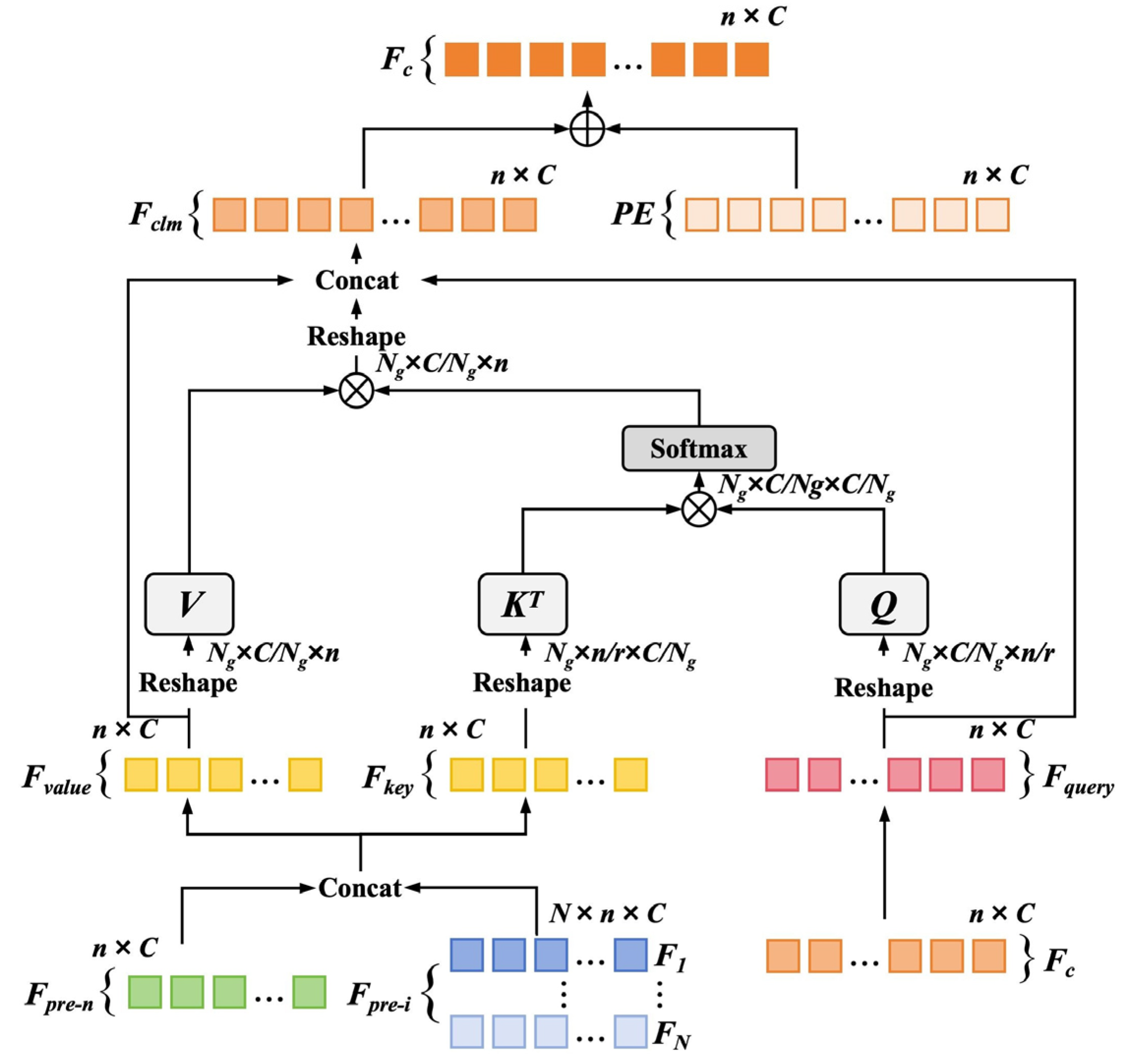
3.2. Cross-Layer Complementary Cross-Attention

In a Mamba-based network, features extracted from different Mamba layers exhibit a degree of complementarity and redundancy. To capture this inter-layer complementarity while minimizing redundant information reuse, we introduce two structurally distinct types of Mamba layers: ordinary Mamba layers and interactive Mamba layers. Each interactive layer is integrated with a cross-layer complementary cross-attention module, inspired by SparX [39]. Our module implements two distinct cross-layer data connection mechanisms to facilitate information flow: (1) sequential feature transmission—features from the immediately preceding ordinary layer are passed sequentially to the current layer; this provides the foundational voxel feature information necessary for subsequent layer processing; (2) selective interactive feature connection—the current interactive layer connects to the N nearest preceding interactive layers; this constraint limits connections to a defined number of interactive layers, thereby preventing the feature confusion and excessive computational overhead that would arise from connecting to all previous layers, while still ensuring efficient cross-layer information transmission. Furthermore, we introduce a spacing parameter M to control the density of interactive Mamba layers within each network stage. Within a stage, ordinary and interactive layers are arranged alternately. This design ensures that the final output of each stage retains rich semantic information while managing the computational complexity. Typically, each stage concludes with an interactive Mamba layer, allowing for final feature optimization and integration at the stage boundary. To promote information flow across stages, the first interactive Mamba layer of each stage is additionally connected with the downsampled features from the previous stage, enabling smooth information circulation and sharing throughout the network hierarchy.

Within each interactive Mamba layer, the C3AM selectively retrieves complementary information by modeling interactions between the current layer and a selected set of adjacent layers. The module measures the feature similarity between the current layer and its connected layers, mines effective complementary information, and employs token compression to reduce the spatial dimensionality, thereby lowering the computational cost. Specifically, as shown in Figure 2, $F_{pre\_n}\in R_n\times C$ and $F_{pre\_i}=\{F_1,F_2,\dots F_N\}\in R_n\times C$ represent the feature sets from the preceding ordinary layer and the preceding N interactive layers, respectively. These features are concatenated, projected to a channel dimension of 2C via a linear layer, and then evenly split into $F_{key}$ and $F_{value}$. The current interactive layer feature $F_c\in R_n\times C$ is denoted as $F_{query}$. We then divide the feature channels into $N_g$ groups and compute group-wise cross-attention separately within each group. This design, inspired by grouped convolution, reduces the computational complexity while enhancing the model’s capacity to learn relationships within different feature subgroups, allowing it to capture distinct interaction patterns and mine complementary information per group. Concurrently, following [40,41], the number of spatial tokens in $F_{key}$ and $F_{value}$ is compressed from n to n/r, which reduces the computational time and improves the efficiency while preserving the spatial resolution. The final complementary features $F_{clm}$ are concatenated with $F_c$ and $F_{value}$, projected via another linear layer, and finally fed into the core Mamba module for further feature extraction. The process is formulated as follows:

$$F_{key},F_{value}=Seg(W^L(Cat(F_{pre\_n},F_{pre\_i})))$$

(1)

$$Q=W^Q(S{r}^Q(F_c)),K=W^K(S{r}^K(F_{key})),V=W^V(F_{value})$$

(2)

$$F_{clm}=(Softmax({\displaystyle \frac{Q{K}^T}{\sqrt{C}}}))V$$

(3)

where $W^L,W^Q,W^K,W^V\in R^{n\times C}$ refer to linear projections. Seg splits the concatenated features into 2C channels along a specified dimension. $S{r}^Q,S{r}^K$ represent the operations of reducing the number of spatial tokens. $\{Q,K\}\in R^{{\displaystyle \frac{n}{r}}\times {\displaystyle \frac{C}{N_g}}\times N_g}$, $V\in R^{n\times {\displaystyle \frac{C}{N_{\mathrm{g}}}}\times N_g}$, $F_{clm}\in R^{n\times 2C}$.

3.3. Bi-Shift Scanning Strategy

Due to Mamba’s unidirectional modeling characteristic, modeling unstructured point clouds is challenging. Space-filling curves traverse all elements in a space without repetition, enabling dimensionality reduction while preserving the spatial topological structure of point clouds. We choose the Hilbert curve to reorder the voxel sequence. Compared with random sequences, the Hilbert curve better maintains the proximity of spatial voxels—adjacent key voxels in the scanning sequence often have geometrically close positions. In the lightweight shallow feature extraction stage, we apply two different space-filling curves to the two Mamba layers: the Hilbert curve and the Trans-Hilbert curve. As shown in Figure 3, scanning path planning prioritizes the x/y axis to capture neighborhood features in the x/y direction, overcoming the limitation of relying on a single sequence’s neighborhood relationships. This allows the model to aggregate local features from different directions, improving the completeness of local geometric feature capture. In the intermediate semantic abstraction stage, we introduce a shift scan operator, which enables multi-scale perceptual field expansion by dynamically adjusting the scan starting coordinates (x0, y0, z0). This effectively extends the model’s receptive field beyond adjacent voxels, allowing it to capture a wider range of spatial relationships. The entire bijective shift scanning strategy can be expressed as follows:

$$E(v_i)=\Phi ((v_i\oplus \Delta i)\mathrm{mod}L)$$

(4)

where $\Phi :Z^3\to N$ is the spatial mapping of the Hilbert space-filling curve and its Trans-Hilbert variant, which establishes a mapping from 3D voxel coordinates $v_i\in Z^3$ to a 1D sequence via recursive partitioning, preserving spatial locality. The shift scan operator $\Delta i\in R^3$ implements non-destructive coordinate offsets for voxels. The modular arithmetic parameter $L=2^{3k}$ (where k is the voxel density parameter) ensures the topological closure of the traversal path, while mod L ensures that shifted parameters remain within the curve’s valid range, supporting cyclic traversal.

3.4. Voxel Densification Downsampling

When voxel features are flattened into a one-dimensional continuous feature sequence, spatial proximity information may be lost. As shown by the two parts in Figure 4, during serialization encoding into a 1D spatial representation, the distance between spatially adjacent parts in the 3D space increases in the 1D space, weakening the topological structure and spatial relationships of 3D features. To this end, we design a joint optimization downsampling module to ensure the integrity of local spatial information in voxel features and effectively expand the receptive field. Figure 5a shows the structure of our double convolution co-downsampling module. Firstly, the submanifold convolution structure captures geometric details in the neighborhood, and only positions with the same topological structure in the input feature map undergo convolution. The input voxel feature is V, with the submanifold convolution kernel $K_{sub}$; after the submanifold convolution operation $C_{sub}(V,K_{sub})$, the output feature $V_{sub}$ maximizes the preservation of geometric details in the neighborhood of V, maintains local topological invariance, and ensures that spatial proximity information remains undestroyed during downsampling. Secondly, the sparse convolution structure constructs multi-scale perceptual units to effectively expand the perceptual radius. With the sparse convolution kernel $K_{sparse}$, after performing the sparse convolution operation $C_{sparse}(V,K_{sparse})$ on the input feature V, the resulting output feature $V_{sparse}$ captures broader information across different scales. Through the synergy of submanifold convolution and sparse convolution structures, this collaborative downsampling module enhances local spatial information, enables flexible receptive field expansion, and balances computational efficiency with feature representational capabilities. Furthermore, addressing the sparsity of foreground voxels, we design an optional voxel densification module. As shown in Figure 5b, we diffuse voxels in foreground regions by first calculating feature importance scores along the channel dimension. Let the feature vector of a voxel along the channel dimension be $F=\left[f_1,f_2,\dots ,f_n\right]$ (where n is the number of channels). We then select the top-K values as the feature subset $F_{top-K}$ for regional voxel diffusion. For the diffused voxels, the initial feature is zero-initialized, and voxel feature values are dynamically generated in subsequent modules, which makes foreground region features denser and easier for the model to focus on.

4. Experiments

4.1. Datasets and Evaluation Indicators

KITTI [42] is a classic benchmark dataset in autonomous driving, comprising data collected from real road scenarios. It consists of 7481 training samples and 7518 testing samples, including three categories of data: LiDAR point clouds, high-resolution camera images, and sensor calibration parameters. Following the standard split protocol, the training samples are divided into a training set of 3712 samples and a validation set of 3769 samples, used for model training and performance tuning, respectively. For the 3D object detection task, the dataset focuses on three categories of road objects: cars, pedestrians, and cyclists. It classifies the detection difficulty into three levels (easy, medium, hard) based on the object size, occlusion, and truncation degree. For evaluation, the average precision across 11 recall thresholds (R11) is adopted as the primary metric, with distinct intersection over union (IoU) thresholds set for each category: 0.7 for cars and 0.5 for both pedestrians and cyclists.

nuScenes [43] is a large-scale multi-modal benchmark dataset for autonomous driving, containing 1000 driving scene sequences (approximately 1.4 million images and 390,000 LiDAR point cloud frames). It encompasses diverse scenarios and features 10 categories of road objects. The dataset is partitioned into a training set of 700 sequences, a validation set of 150 sequences, and a test set of 150 sequences. These sets are designated for model training, hyperparameter tuning and validation, and official benchmark evaluation, respectively. nuScenes employs the mean average precision (mAP) and the nuScenes detection score (NDS) as the primary metrics for the evaluation of model performance.

4.2. Implementation Details

We implement our method based on the open-source framework OpenPCDet and evaluate it on both the KITTI and nuScenes datasets.

On the KITTI dataset, we set the voxel size to [0.16, 0.16, 0.125]. Our backbone network consists of three stages with a channel dimension of C = 128, containing 2, 6, and 2 Mamba layers sequentially. This design facilitates progressive feature extraction from local to global contexts, thereby effectively enhancing model performance. In the proposed cross-layer complementary cross attention module (C3AM), the number of adjacent interactive layers is set to N = 2, and the token compression ratios for each stage are configured as [4, 2, 1]. This reduces the computational load while maintaining performance. In the bi-shift scanning strategy (BiShift-Scan), the shift steps for each stage are set as [[0, 0], [0, 1, 2, 3, 4, 5], [0, 0]]. For the nuScenes dataset, we adjust the voxel size to [0.225, 0.225, 0.25] to accommodate its different point cloud density and scene scale. The backbone network architecture, channel dimension, and Mamba layer configuration remain consistent with the KITTI setup to ensure the generalizability of our approach. The configurations of the C3AM and BiShift-Scan modules are kept identical to those used for KITTI.

All experiments are performed on an RTX 4090 GPU. We employ the Adam optimizer with a dynamically adjusted learning rate to improve the training efficiency. Specifically, the models are trained on KITTI for 24 epochs with a learning rate of 0.0025. For nuScenes, training lasts for 30 epochs with a learning rate of 0.003, tailored to the dataset’s size and complexity. All other hyperparameters align with those of CenterPoint [44] to ensure a fair experimental comparison.

For ablation studies, we design a baseline algorithm that stacks 10 vanilla Mamba layers across three stages. In this baseline, inter-stage interaction is limited to sparse convolution, omitting the voxel densification downsampling module. Feature serialization per layer relies solely on the Hilbert curve, without incorporating the proposed BiShift-Scan strategy or the C3AM module. Comparisons with this baseline clearly demonstrate the innovativeness of our architectural and strategic contributions, as well as their significant positive impacts on model performance.

4.3. Main Results

4.3.1. Three-Dimensional Detection Results

The experimental results are evaluated on the KITTI and nuScenes validation sets. For KITTI, we adopt the 3D average precision under 11 recall thresholds (3D AP_R11) as the main metric. For nuScenes, we follow the official evaluation protocol and use the mean average precision (mAP) as the core metric to comprehensively assess the detection performance across diverse scenarios. On the KITTI validation set, we compare the proposed model with several representative methods, shown in

Table 1. Effectiveness on the KITTI validation set for car, pedestrian, and cyclist. Results marked with * are reproduced by us, all settings except the 3D backbone are kept consistent to ensure a fair comparison. Bold indicates the best result in the table.

Model	Car			Pedestrian			Cyclist			mAP
	Easy	Med.	Hard	Easy	Med.	Hard	Easy	Med.	Hard
VoxelNet [45]	77.5	65.1	57.7	39.5	33.7	31.5	61.2	48.4	44.4	51.0
SECOND [46]	83.1	73.7	66.2	51.1	42.6	37.3	70.5	53.9	46.9	58.4
PointPillars [35]	79.1	75.0	68.3	52.1	43.5	41.5	75.8	59.1	52.9	60.8
PointRCNN [24]	85.9	75.8	68.3	49.4	41.8	38.6	73.9	59.6	53.6	60.8
TANet [47]	83.8	75.4	67.7	54.9	46.7	42.4	73.8	59.9	53.3	62.0
Flatformer * [10]	86.5	75.6	74.1	54.4	48.2	43.3	80.6	62.9	61.1	65.2
DSVT-Voxel * [9]	86.4	77.8	75.8	60.8	55.4	52.1	85.1	66.8	63.9	69.3
MSHI-Mamba (Baseline)	83.8	74.8	73.5	54.2	47.3	43.3	82.6	62.9	59.7	64.7
MSHI-Mamba (Ours)	88.9	78.2	75.9	61.1	50.8	46.8	86.4	67.2	63.6	68.9

, including VoxelNet, SECOND, PointPillars, PointRCNN, TANet, Flatformer, and DSVT-Voxel (results marked with * are reproduced by us; all settings except the 3D backbone are kept consistent to ensure fair comparison). The results show that our model achieves the best 3D AP_R11 for the car and cyclist categories. Compared to the baseline, it improves the performance by 3.4%, 3.5%, and 4.6% for cars, pedestrians, and cyclists, respectively, under medium difficulty.

On the nuScenes test set, as seen in

Table 2. Effectiveness on the nuScenes test set. Bold indicates the best result in the table.

Model	mAP	NDS
PointPillars [35]	30.5	45.3
3DSSD [25]	42.6	56.4
CenterPoint [44]	58.0	65.5
Voxel Mamba [22]	69.0	73.0
DSVT [9]	68.4	72.7
MSHI-Mamba (Ours)	59.3	67.7

, while the proposed model outperforms traditional methods such as PointPillars, 3DSSD, and CenterPoint, a performance gap remains compared to the state-of-the-art Voxel Mamba. This indicates that further enhancements are needed to boost its competitiveness on large-scale, complex datasets, which will be a focus of our future work.

4.3.2. Inference Efficiency

Table 3. Comparison with other architectures in terms of GPU memory.

Model	Backbone	Memory (GB)
Part-A2 [48]	SpCNN	2.9
PV-RCNN++ [49]		17.2
SST [50]	Transformers	6.8
DSVT-Voxel [9]		4.2
Voxel Mamba [22]	SSMs	3.7
MSHI-Mamba (Ours)		4.3

and

Table 4. Comparison of FPS on KITTI.

Model	FPS
PointRCNN [24]	10.0
PV-RCNN [4]	8.9
SECOND [46]	30.4
TANet [47]	28.7
PointPillars [35]	42.4
MSHI-Mamba (Ours)	10.7

compare the MSHI-Mamba model against other 3D detection methods in terms of inference speed (frames per second, FPS) and GPU memory consumption. Regarding inference speed, MSHI-Mamba operates faster than PV-RCNN and PointRCNN. While methods like SECOND and PointPillars achieve higher FPS, they suffer from significantly lower accuracy. In terms of GPU memory usage, our method is compared with Transformer-based and sparse convolution (SpCNN)-based architectures. MSHI-Mamba requires only an additional 0.6 GB of memory compared to Voxel Mamba, and it maintains a lower overall memory footprint than Transformer-based methods. This demonstrates the efficiency advantage of the Mamba architecture. Although the introduced cross-attention mechanism partially offsets the complexity reduction gains from Mamba, it preserves the core optimization benefits.

4.4. Ablation Study

We conduct a series of ablation studies on the KITTI validation set to thoroughly evaluate MSHI-Mamba. All models are trained for 20 epochs following the OpenPCDet pipeline.

4.4.1. Ablation Study of Cross-Layer Complementary Cross-Attention (C3AM)

We study the effectiveness of the cross-layer complementary cross-attention module (C3AM). The experiment is carried out on the KITTI validation set (car), with the 3D AP_R11@0.7 as the core index. The baseline model is constructed using a multi-stage architecture with stacked ordinary Mamba layers (mAP = 77.3%), which provides an important reference standard for subsequent comparative analysis. We then gradually introduce new modules and mechanisms to observe their impacts on model performance. The ablation experiment results for the cross-layer complementary cross-attention module are shown in

Table 5. Ablation study of cross-layer complementary cross-attention module (%). Bold indicates the best result in the table. √ indicates that the module is included in the model, while ✗ indicates the opposite.

Model	C3AM		Car				Pedestrian	Cyclist
	CSI	IML	Easy	Med.	Hard	mAP	Med.	Med.
Baseline	✗	✗	83.8	74.8	73.5	77.3	47.3	62.6
MSHI-Mamba	√	N = 1	86.6	76.9	74.4	79.3	48.5	64.9
	√	N = 2	87.5	77.2	74.7	79.8	48.8	65.8
	√	N = 3	86.7	77.0	74.6	79.4	48.1	65.2
	✗	N = 2	85.8	76.1	74.2	78.7	47.6	64.7

. After introducing the interactive Mamba layer (IML, N = 1), the mAP increases to 79.3%, which proves that the cross-layer feature complementary interaction mechanism can effectively enhance the model’s representational ability. Next, we discuss the influence of the number of interactive layers N on performance. When N = 2, the mAP reaches a peak of 79.8%, with optimal performance. When N = 3, due to interference from redundant information, the model’s detection accuracy decreases, with the mAP dropping to 79.4%. Based on the experimental results, we finally select N = 2 as the optimal configuration of the cross-layer complementary cross-attention module (C3AM) to ensure that the model achieves an optimal balance between performance and computing resources. In addition, we evaluate the role of the cross-stage interaction mechanism (CSI) in the model. Disabling the transfer of downsampled features across stages (i.e., retaining only intra-stage interactions) causes a 1.1% mAP drop to 78.7%, which clearly demonstrates that cross-scale global information alignment is indispensable. The cross-stage interaction mechanism facilitates the fusion of multi-scale features, which enhances the model’s ability to capture vehicle characteristics across varying sizes and improves the overall detection accuracy.

4.4.2. Ablation Study of Bi-Shift Scanning Strategy (BSS)

To verify the effectiveness of the bi-shift scanning strategy (BSS), we design ablation experiments on the KITTI validation set (car) to analyze its effects on the 3D detection performance. The baseline model adopts a non-shift strategy based only on the Hilbert curve (mAP = 77.3%). The comparison results of the ablation experiment for the double-shift scanning strategy are shown in

Table 6. Ablation study of double-shift scanning strategy (%). Bold indicates the best result in the table. √ indicates that the module is included in the model, while ✗ indicates the opposite.

Model	BSS	Car				Pedestrian	Cyclist
		Easy	Med.	Hard	mAP	Med.	Mod.
Baseline	✗	83.8	74.8	73.5	77.3	47.3	62.6
MSHI-Mamba	√	86.8	77.2	74.2	79.4	48.4	65.7

. When we use dual-path space-filling curves—the Hilbert curve and the Trans-Hilbert curve—the performance of the model is significantly improved. The mAP increases from 77.3% (baseline) to 79.4%, representing a 2.1% improvement. The results show that maintaining spatial proximity and cross-region shifting play a key role in enhancing the model’s ability to model long-range dependencies. The spatial proximity preservation strategy enables the model to better capture local features and spatial correlations of targets, while the cross-region shift strategy helps the model to break through local constraints and effectively establish long-distance feature dependencies, thereby improving model performance.

4.4.3. Ablation Study of Voxel Densification Downsampling

We further verify the effectiveness of the voxel densification downsampling module (VD-DS). We continue to design ablation experiments on the KITTI validation set (car), focusing on the module’s influence on the detection accuracy. The comparison results of the voxel densification downsampling module’s ablation experiments are shown in

Table 7. Ablation study of voxel dense downsampling (%). Bold indicates the best result in the table. √ indicates that the module is included in the model, while ✗ indicates the opposite.

Model	C3AM	BSS	VD-DS	Car				Pedestrian	Cyclist
				Easy	Med.	Hard	mAP	Med.	Med.
Baseline	✗	✗	✗	83.8	74.8	73.5	77.3	47.3	62.6
MSHI-Mamba	√	✗	✗	86.8	77.2	74.2	79.4	48.4	65.7
	√	√	✗	87.4	77.9	75.1	80.2	49.9	66.1
	√	√	√	88.9	78.2	75.9	81.0	50.8	67.2

. Compared with the MSHI-Mamba model without the voxel densification downsampling module (VD-DS), the model with VD-DS achieves a 0.8% mAP improvement. An analysis of the experimental results indicates that the VD-DS module can better capture local feature information around car targets, thereby enhancing the recognition and positioning capabilities for target objects.

4.5. Limitations and Assumptions

The performance of the proposed MSHI-Mamba backbone network depends on predefined hyperparameters, including the number of Mamba layers, shift-scan configurations, and the voxel densification strategy. All optimizations are tailored to conventional road scene datasets; thus, the model is not fully adapted to the characteristics of extreme weather, complex urban environments, or rare objects. Furthermore, the model balances computational complexity through grouped cross-attention and token compression. While this design improves the inference efficiency, it may result in the loss of fine-grained features in scenarios involving high-resolution point clouds or long-range dependencies. Additionally, the top-K feature selection strategy within the voxel densification module is sensitive to the choice of K and lacks adaptive adjustment, which may limit the model’s generalizability across diverse autonomous driving scenarios. We plan to address these limitations in future work to enhance the model’s overall robustness.

5. Conclusions

In this paper, we propose MSHI-Mamba, a Mamba-based multi-stage hierarchical interaction architecture for 3D point cloud detection. The framework systematically addresses key challenges through three novel components: a cross-layer complementary cross-attention module (C3AM) that reduces feature redundancy by dynamically selecting complementary inter-layer information, a bi-shift scanning strategy (BSS) based on hybrid space-filling curves to preserve spatial continuity and expand the receptive field during serialization, and a voxel densifying downsampling module (VD-DS) to enhance local spatial information and foreground feature density. Experimental results demonstrate that MSHI-Mamba achieves a 4.2% improvement in the mean average precision (mAP) over the established baseline on the KITTI dataset while maintaining competitive performance on the more challenging nuScenes dataset. These findings validate that the proposed modules collectively improve cross-layer feature interaction, spatial structure preservation, and local feature enhancement, offering a more effective architectural design for Mamba-based 3D detection backbones.