Cooling Performance of Impingement–Effusion Double-Wall Configurations Under Atmospheric and Elevated Pressures

Abstract

The combustor liner of the modern aero-engine operates under extreme thermal loads with limited coolant supply, necessarily making efficient cooling approaches important. Impingement–effusion double-wall cooling integrates impingement, convection, and film cooling, but most studies testing this approach have been conducted at atmospheric pressure, limiting the application of the technology in real engines. This work experimentally and numerically evaluates the cooling performance of baseline and optimized configurations, focusing on the effects of pressure drop, initial cooling filmand operating pressure under atmospheric and elevated pressures up to 0.3 MPa. The results show that increasing the pressure drop enhances cooling effectiveness, which can be attributed to enhanced jet momentum and cooling film coverage, though benefits diminish when the pressure drop further increases to over 4%. Introducing initial film cooling extends upstream protection, improves downstream uniformity, and stabilizes overall effectiveness across varying pressure drops. Elevated operating pressure further enhances the cooling effectiveness of impingement–effusion cooling, as higher coolant density promotes stronger impingement and more coherent cooling film formation. The simulations confirm that pressure-induced density effects dominate the cooling process, whereas blowing-ratio-based similarity fails to capture these dependencies. The results highlight the limitations of atmospheric evaluations and provide physical insights for designing efficient combustor liners under realistic pressure conditions.

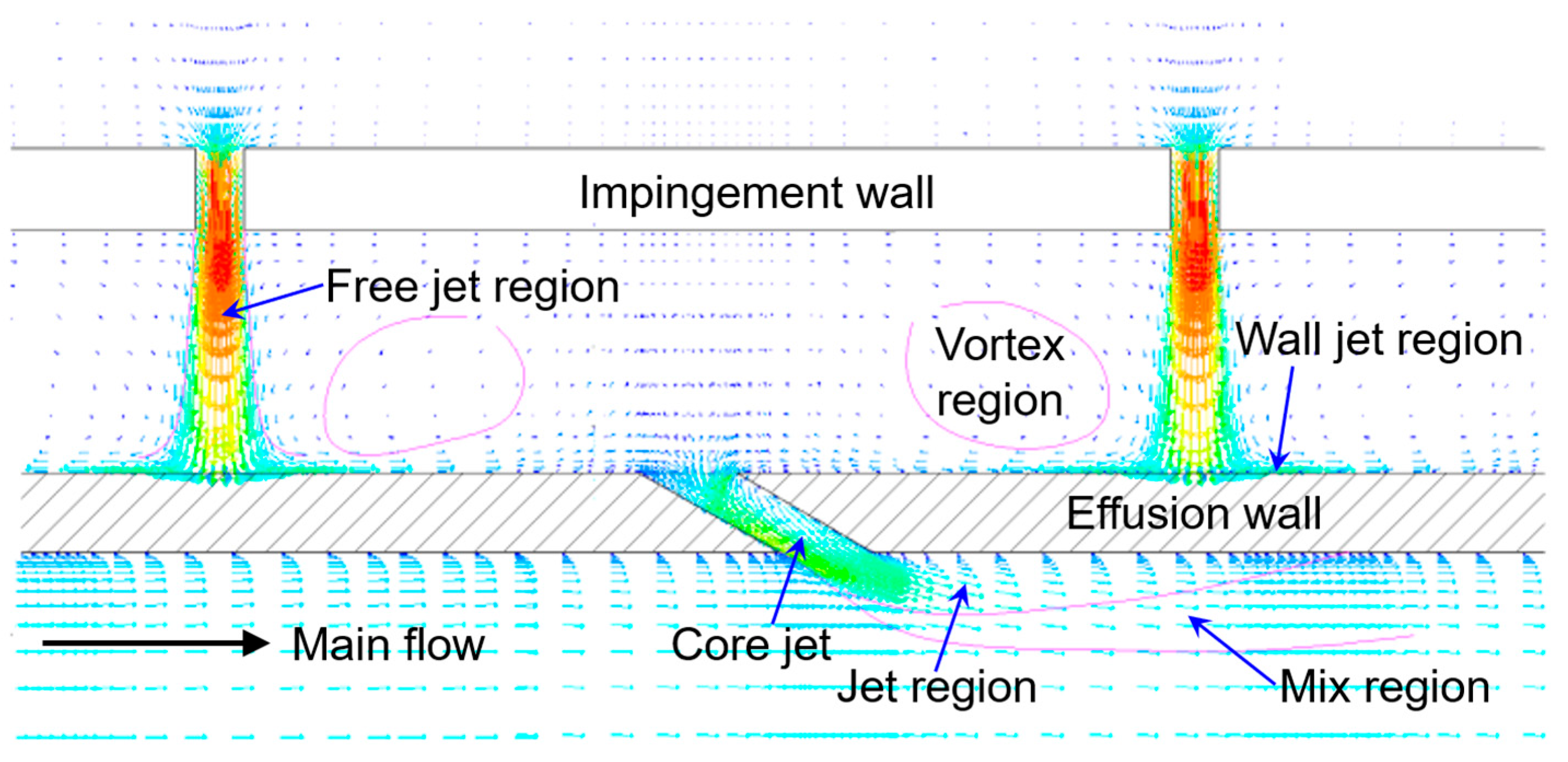
1. Introduction

With the continuous efforts toward higher efficiency and lower emissions in modern aero-engines, the operating temperature and pressure of combustors have substantially increased. In high-temperature-rise combustors, the combustor liner operates under extreme thermal loads, while the limited availability of cooling air poses challenges for its durability. Efficient liner cooling is therefore essential to ensure safe and reliable operation. Among the available cooling techniques, impingement–effusion cooling is one of the most effective approaches, integrating the benefits of impingement, effusion, and convective and film cooling within a single configuration [1].

As illustrated in Figure 1, coolant initially passes through impingement orifices in the outer-layer (impingement) wall, forming high-speed jets that impact on the inner-layer (effusion) wall and generate free jets and wall jets and recirculating vortex structures in the near-wall region. The coolant subsequently flows through multiple inclined effusion orifices into the combustor chamber, confining the hot gas (main flow), and forming a continuous protective cooling film along the inner liner surface.

An extensive number of studies have investigated the effects of geometric and operating parameters on impingement–effusion cooling performance. Orifice arrangement has been a particular focus. Rhee et al. [2] compared staggered, square and hexagonal arrangements, and found that the staggered arrangement features the highest heat transfer coefficient due to the increased effusion-to-injection area ratio. Similarly, Xie et al. [3] demonstrated that staggered orifices provide higher cooling effectiveness (η_c) relative to overlapped ones at the same blowing ratios (M) and injection distances (H). Both studies confirmed that reducing H increases jet momentum, suppresses crossflow, and improves η_c. Other parameters, such as the overall orifice area ratio (δ = A_coolant/A_wall) and Reynolds number (Re), also play important roles. Niu et al. [4] reported that increasing δ from 0.5% to 0.8% enhances area-averaged η_c by 17.3%, whereas raising Re from 800 to 2000 reduces η_c by up to 6%. Li et al. [5] investigated the impacts of the inclination angle of effusion orifices (α = 30–90°) and blowing ratios (M = 0.5–2.0), showing that smaller α and higher M improve film-cooling effectiveness but increase structural stresses around the orifices, indicating a trade-off between cooling performance and structural durability. Wu et al. [6] compared forward and backward effusion injection and found that backward effusion injection enhances lateral spreading of the cooling film and reduces sensitivity to M, albeit with deeper cooling jet penetration into mainstream hot gas.

Beyond conventional parameter optimization, various novel structural concepts have been developed to improve the uniformity and cooling efficiency of impingement–effusion cooling configurations [7,8,9,10]. Rao et al. [7] introduced pin-fins in the impingement channel to suppress crossflow and improve both uniformity and overall η_c. Xu et al. [8] proposed a hollow-pillar configuration that reduces internal fluid resistance and improves external cooling film coverage through vortex interaction and bypass flow. Chen et al. [9] examined conformal-pin and fan-shaped film-cooling orifices, showing 5%–40% higher η_c than conventional round-shaped orifices at Re = 470–3780. These developments highlight the strong potential of geometric optimization to balance cooling effectiveness, pressure loss, and mechanical integrity. Furthermore, comparisons with other cooling techniques confirm the advantages of impingement–effusion cooling [2,11,12,13,14,15,16,17,18]. For aero-engine combustors with moderate temperature rise (<850 K) and inlet temperature (<900 K), impingement–effusion cooling can reduce coolant demand to 5.0–6.5 kg/(s·m²·MPa), which is nearly 50% lower than film cooling alone [11,12]. Experimental studies [2,12,13,14,15,16] consistently show that staggered orifice arrangements provide higher heat transfer coefficients than in-line layouts; this is attributed to the stronger suction at orifice inlets, while direct comparisons indicate that impingement–effusion cooling achieves roughly a 30% higher cooling effectiveness relative to pure effusion cooling [17]. Moreover, optimization studies reveal the importance of pressure-drop distribution across the double-wall liner. Allocating approximately 90% of the pressure drop to the impingement wall enhances convection and improves cooling effectiveness [18]. These results show that both geometric and hydraulic parameters must be co-optimized under a limited coolant supply.

Overall, the cooling performance of impingement–effusion configurations arises from three synergistic mechanisms [19,20,21]: (a) high heat transfer coefficients due to impingement jets impacting on the effusion wall, (b) enlarged convective cooling surface area and increased boundary-layer suction induced by inclined effusion orifices, and (c) a full-coverage cooling film that protects the wall from the mainstream hot gas [22,23,24,25]. These mechanisms provide the theoretical basis for optimizing impingement–effusion double-wall liners in advanced aero-engine combustors.

Despite the extensive number of studies, the crucial limitation remains that most existing studies have been conducted under atmospheric pressure. This condition differs significantly from the elevated pressures (typically several to tens of bars) encountered in practical aero-engine combustors. Elevated pressure changes density ratios, jet discharge characteristics, and coolant–mainstream interaction, potentially modifying both impingement cooling heat transfer and film cooling behavior. To the best of our knowledge, very limited efforts have explored pressure effects, and systematic assessments of coolant utilization, pressure-drop allocation, and similarity in film cooling between atmospheric and elevated pressures are largely absent. This knowledge gap restricts the applicability of existing design correlations and undermines the accurate prediction of liner cooling performance under practical operating pressures.

To address these limitations, the present study combines controlled-pressure experiments and validated simulations to evaluate the effects of liner pressure drop, initial film-cooling addition and operating pressure on double-wall impingement–effusion cooling performance. The applicability of cooling effectiveness measurements at atmospheric pressure to elevated pressure is assessed for the first time, providing a practical reference for cooling design. In addition, the simulations further reveal the respective heat-transfer contributions and mechanisms of impingement–effusion cooling under elevated pressures. These results would establish a more complete understanding of pressure-dependent behavior, enabling more reliable design and optimization of impingement–effusion cooling systems for advanced aero-engine combustors.

2. Methodologies

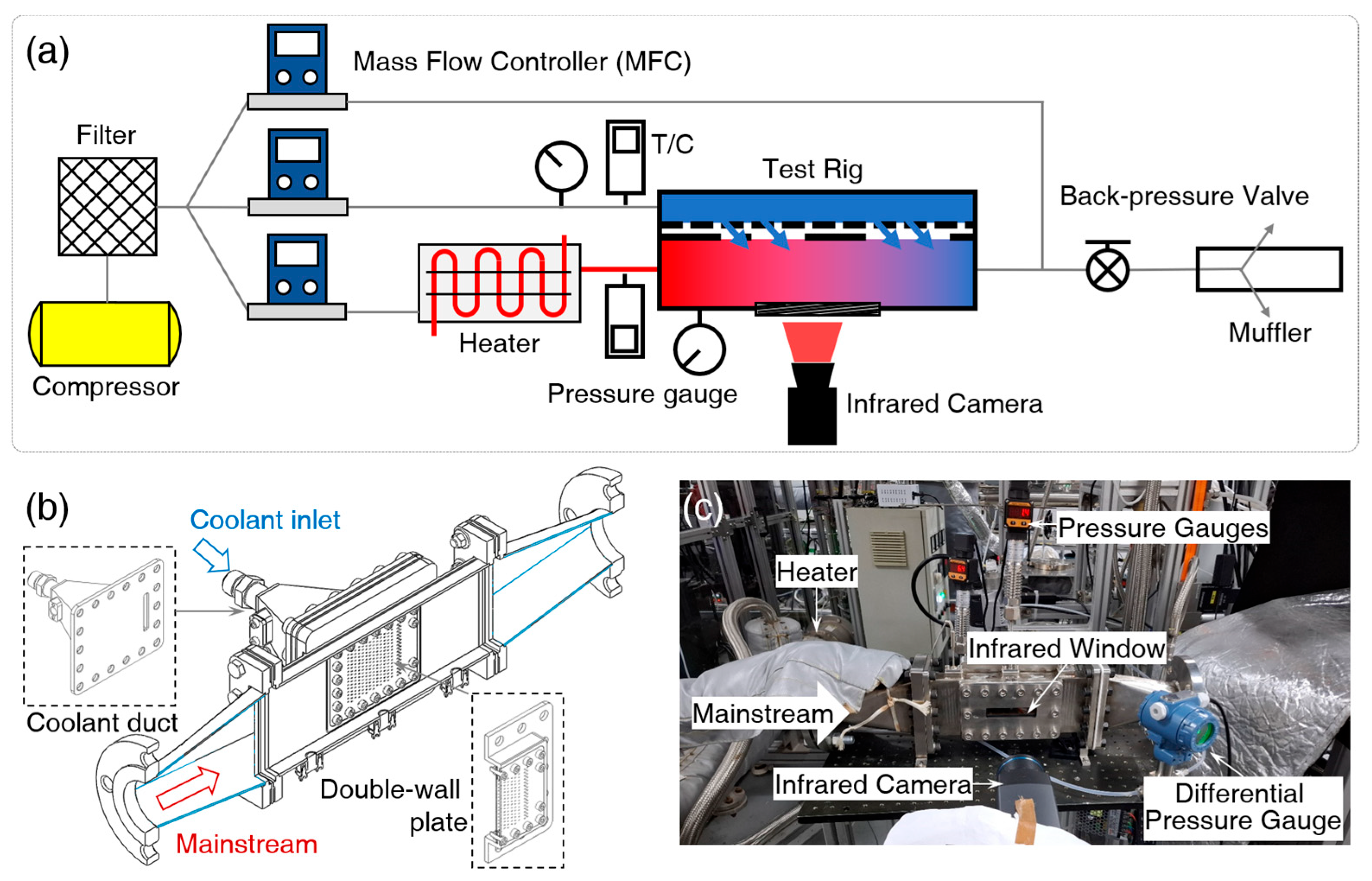
2.1. Experimental Setup and Test Section

The experimental setup, as shown in Figure 2a, mainly consists of an air compressor, an electric heater, three mass flow controllers (MFCs), thermal couples (T/Cs), pressure gauges, the test rig, and an infrared (IR) camera. Compressed air from the compressor is first filtered and then divided into three flow branches, each regulated by an individual MFC with an uncertainty of ±1%. The first branch is heated by the electric heater and supplied to the test rig as the mainstream flow, with the temperature maintained at 473 ± 3 K. The second branch serves as the coolant flow entering the cooling-air duct through the coolant inlet. The third branch, equipped with a back-pressure valve, is used to regulate the operating pressures of the mainstream flow. The wall temperature of the effusion plate is monitored using the IR camera with an uncertainty of ±1.5 K. Multiple K-type T/Cs and pressure gauges distributed along the mainstream and coolant flow paths provide continuous real-time data to the data acquisition system, with uncertainties of ±2 K and ±0.5%, respectively. The operating pressure and the total pressure drop of the double-wall configurations are manipulated by adjusting the MFCs. To suppress acoustic noise and flow pulsation under elevated pressures, a muffler is installed at the outlet.

A cross-sectional view of the test rig (impingement–effusion cooling double-wall plates) is shown in Figure 2b. During the operation, hot mainstream gas and coolant air are introduced into the test section perpendicularly, and different combinations of impingement and effusion plates are evaluated using the representative double-wall configurations. An infrared-transparent ZnSe window is mounted on the wall opposite the coolant duct to enable direct observation and IR imaging. The overall arrangement of the experimental apparatus is shown in Figure 2c.

2.2. Data Reduction and Operating Conditions

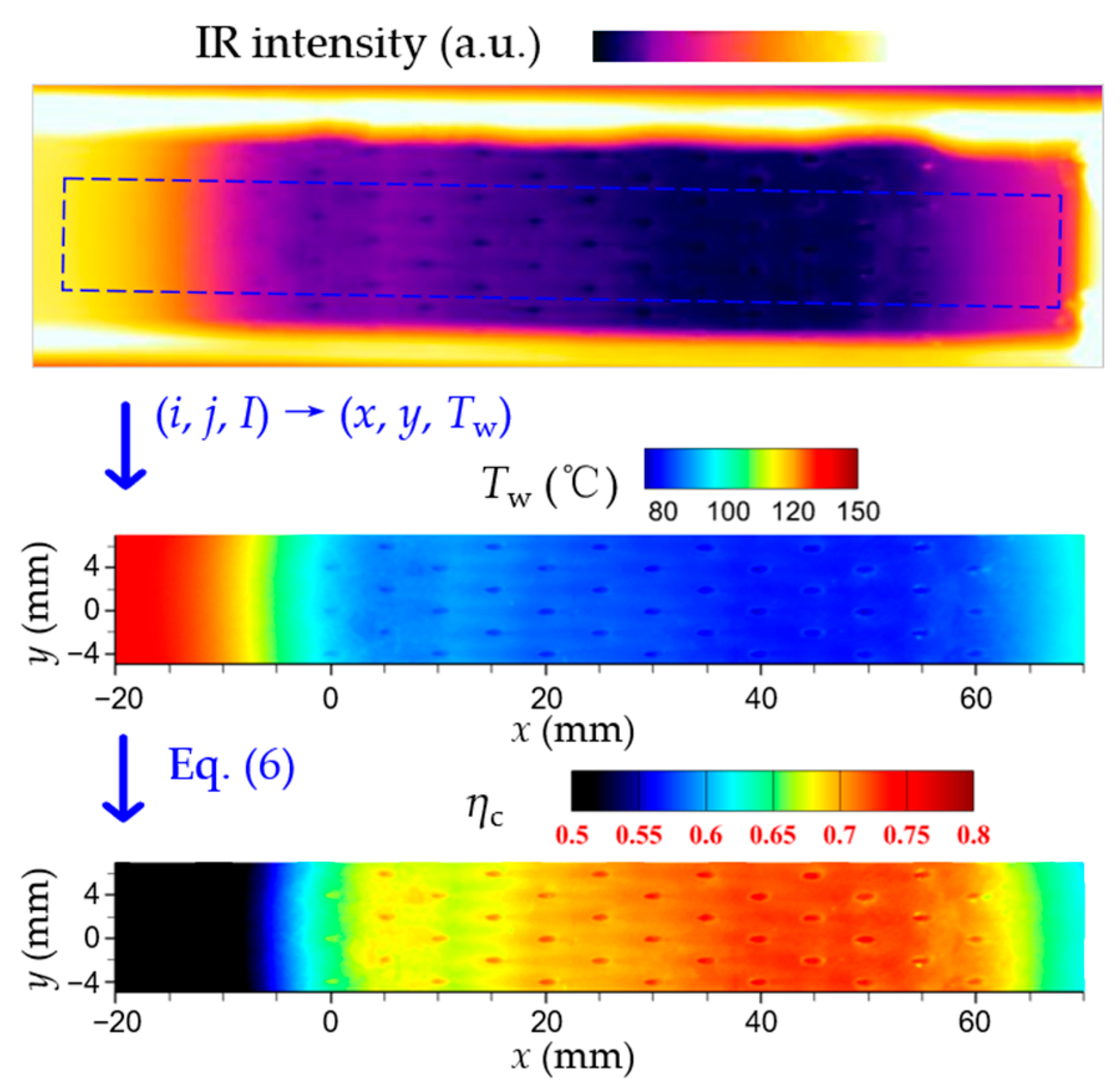
2.2.1. Data Reduction Methods and Measurement Error Evaluation

The impingement–effusion double-wall cooling structure can be regarded as a sequential flow system in which the coolant successively passes through the impingement and effusion plates. For analytical convenience, the entire process can be equivalently modeled as a single flow channel with equivalent hydraulic characteristics. The corresponding equivalent flow area and the overall discharge coefficient of the double-wall configuration are determined using the following equations [22]:

$${\displaystyle \frac{1}{A_{\mathrm{o}}^2}}={\displaystyle \frac{1}{A_{\mathrm{i}}^2}}+{\displaystyle \frac{1}{A_{\mathrm{e}}^2}}$$

(1)

$${Cd}_{\mathrm{o}}={\displaystyle \frac{{\dot{m}}_c}{A_{\mathrm{o}}\sqrt{2\rho \left(\mathrm{\Delta }p\right)}}}$$

(2)

where A_i and A_e denote the total orifice areas of the impingement and effusion plates, respectively; A_o denotes the equivalent orifice area of the double-wall structure. ${\dot{m}}_c$ is the coolant mass flow rate monitored by the MFC. Δp represents the total pressure drop across the double-wall configuration. The pressure-loss coefficient ($\zeta$), defined as the ratio of the pressure drop between the coolant inlet and mainstream to the total pressure of the coolant inlet, is calculated as

$$\zeta ={\displaystyle \frac{\mathrm{\Delta }p}{p_{\mathrm{c}}}}={\displaystyle \frac{p_{\mathrm{c}}-p_{\mathrm{g}}}{p_{\mathrm{c}}}}$$

(3)

where Δp is measured directly by a differential pressure gauge (shown in Figure 2c) with an uncertainty of ±20 Pa, p_c is the total pressure of the coolant, and p_g is the static pressure of the mainstream.

The blowing ratio (M), defined as the ratio of the coolant to mainstream momentum flux, is expressed as

$$M={\displaystyle \frac{{\rho }_{\mathrm{c}}{u}_{\mathrm{c}}}{{\rho }_{\mathrm{g}}{u}_{\mathrm{g}}}}$$

(4)

where ρ_c and u_c are the averaged density and velocity of coolant flow inside the effusion orifices, and ρ_g and u_g are those of the mainstream, respectively.

The specific coolant mass flow rate (G_c), representing the coolant mass flow rate per unit cooling-film covered area and per unit operating pressure, is defined as

$$G_{\mathrm{c}}={\displaystyle \frac{{\dot{m}}_{\mathrm{c}}}{A_{\mathrm{c}}·p_{\mathrm{g}}}}$$

(5)

where A_c is the surface area on the effusion plate.

The overall cooling effectiveness (η_c) of the impingement–effusion cooling configuration is defined as [17]:

$${\eta }_{\mathrm{c}}={\displaystyle \frac{T_{\mathrm{g}}-T_{\mathrm{w}}}{T_{\mathrm{g}}-T_{\mathrm{c}}}}$$

(6)

where T_g and T_c are the temperatures of the mainstream hot gas and coolant air, respectively; T_w is the local temperature on the surface of the effusion plate at the hot side, captured by the IR camera. Figure 3 illustrates the post-processing procedure for extracting the overall cooling effectiveness from the recorded IR image. Pixel positions are converted to Cartesian coordinates through spatial calibration, and the infrared signals are transformed into temperature values using the temperature-calibration correlations of the IR camera.

To obtain the streamwise profiles of cooling effectiveness, the local η_c values at each streamwise position x are spanwise-averaged, as shown in Equation (7).

$${\eta }_{\mathrm{a}\mathrm{v}}{|}_{x=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.}={\left({\displaystyle \frac{\sum _{i=1}^N{\eta }_{\mathrm{c},i}}{N}}\right)}_{x=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.}$$

(7)

The measurement error of overall cooling effectiveness is derived based on the error-propagation theorem, expressed as Equation (8).

$$∆\eta =\sqrt{{{\left(\mathrm{\Delta }{T}_{\mathrm{c}}\right)}^2\left({\displaystyle \frac{\partial \eta }{\partial T_{\mathrm{c}}}}\right)}^2+{{\left(\mathrm{\Delta }{T}_{\mathrm{g}}\right)}^2\left({\displaystyle \frac{\partial \eta }{\partial T_{\mathrm{g}}}}\right)}^2+{{\left(\mathrm{\Delta }{T}_{\mathrm{w}}\right)}^2\left({\displaystyle \frac{\partial \eta }{\partial T_{\mathrm{w}}}}\right)}^2}$$

(8)

where the absolute uncertainties of T_g, T_c, and T_w are denoted as ΔT_g, ΔT_c, and ΔT_w, respectively.

Further expansion from Equations (6) and (8) yields the expression for estimating the measurement error of the overall cooling effectiveness from the absolute uncertainties of the individual temperature measurements. The resulting three partial-derivative terms are presented in Equation (9).

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial \eta }{\partial T_{\mathrm{c}}}}={\displaystyle \frac{T_{\mathrm{g}}-T_{\mathrm{w}}}{{\left(T_{\mathrm{g}}-T_{\mathrm{c}}\right)}^2}}\\ {\displaystyle \frac{\partial \eta }{\partial T_{\mathrm{g}}}}={\displaystyle \frac{T_{\mathrm{w}}-T_{\mathrm{c}}}{{\left(T_{\mathrm{g}}-T_{\mathrm{c}}\right)}^2}}\\ {\displaystyle \frac{\partial \eta }{\partial T_{\mathrm{w}}}}=-{\displaystyle \frac{1}{T_{\mathrm{g}}-T_{\mathrm{c}}}}\end{array}\right.$$

(9)

Substituting Equation (9) into Equation (8) gives the absolute uncertainty, expressed as Equation (10).

$$∆\eta =\sqrt{{\displaystyle \frac{\left[{\left(\mathrm{\Delta }{T}_{\mathrm{c}}\right)}^2{\left(T_{\mathrm{g}}-T_{\mathrm{w}}\right)}^2+{\left(\mathrm{\Delta }{T}_{\mathrm{g}}\right)}^2{\left(T_{\mathrm{w}}-T_{\mathrm{c}}\right)}^2\right]}{{\left(T_{\mathrm{g}}-T_{\mathrm{c}}\right)}^4}}+{\displaystyle \frac{{\left(\mathrm{\Delta }{T}_{\mathrm{w}}\right)}^2}{{\left(T_{\mathrm{g}}-T_{\mathrm{c}}\right)}^2}}}$$

(10)

Given that the mainstream temperature T_g and the coolant temperature T_c were measured using K-type T/Cs with an uncertainty of ±2 K, the corresponding absolute uncertainties are ΔT_g = 2 K and ΔT_c = 2 K. The wall temperature T_w, measured by the IR camera, has an uncertainty of approximately ΔT_w = 1.5 K. For the present test conditions, T_g = 473 ± 3 K, T_c = 303 ± 3 K, while the measured wall temperature T_w ranges from 323 K to 473 K. The associated temperature differences are therefore (T_g − T_w) _max = 150 K and (T_g − T_w) _max = 170 K. Substituting these values into Equation (10) determines the maximum error of the overall cooling effectiveness as (Δη)_max = 0.014.

2.2.2. Operating Conditions

In this work, the impingement and effusion orifices were arranged in a rhombus pattern, as shown in Figure 4. The impingement-orifice diameter is 1.2 mm, and the effusion-orifice diameter is 0.62 mm. The gap between the impingement and effusion plates (H) is 4.5 mm, and the inclination angle of the effusion orifice (α) is 20°. The streamwise spacing (S) and spanwise spacing (P) are 5 mm and 4 mm, respectively, as illustrated in Figure 4c. Figure 4a,b show photographs of the baseline and the optimized effusion plates, where the additional initial film-cooling orifices are highlighted by red squares. The optimized configuration introduced additional two-row impingement orifices and three-row effusion orifices at the initial streamwise position of the double-wall configuration. Except for the streamwise spacing S_initial = 4 mm, all parameters of these additional impingement orifices are identical to those of the baseline configuration. Similarly, the steamwise spacing of the additional effusion orifices S_initial is 2 mm, with other parameters identical to the baseline.

The experiments were conducted for three test cases, as listed in

Table 1. Operating conditions of the experiments.

Case	No. 1	No. 2	No. 3
pg, MPa	0.1	0.3	0.3
Tg, K	473	473	473
$\zeta$	4%	4%	1%, 2%, 4%, 4.8%
ug, m/s	12	12	12
Orifice arrangement	baseline	optimized	baseline

. Case No. 3 was tested at p_g = 0.3 MPa with four pressure drops (ζ = 1%, 2%, 4%, and 4.8%). Case No. 1 was tested at p_g = 0.1 MPa and ζ = 4%, and No. 2 was tested at p_g = 0.3 MPa and ζ = 4%, using the baseline and optimized configurations, respectively. The mainstream temperature and velocity were maintained at 473 K and 12 m/s for all cases. Moreover, numerical simulations were conducted for cases No. 1 and No. 3 for comparison.

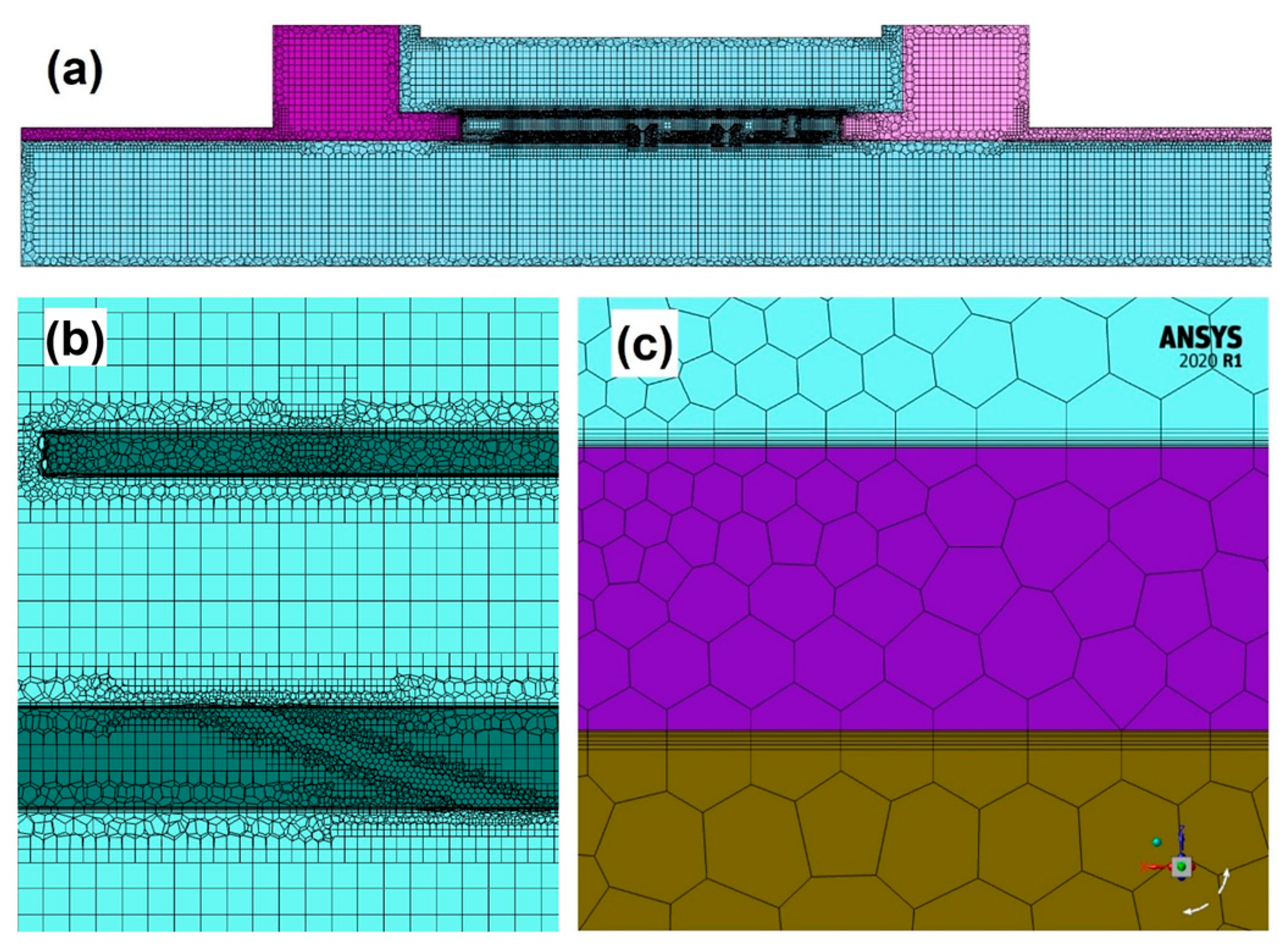
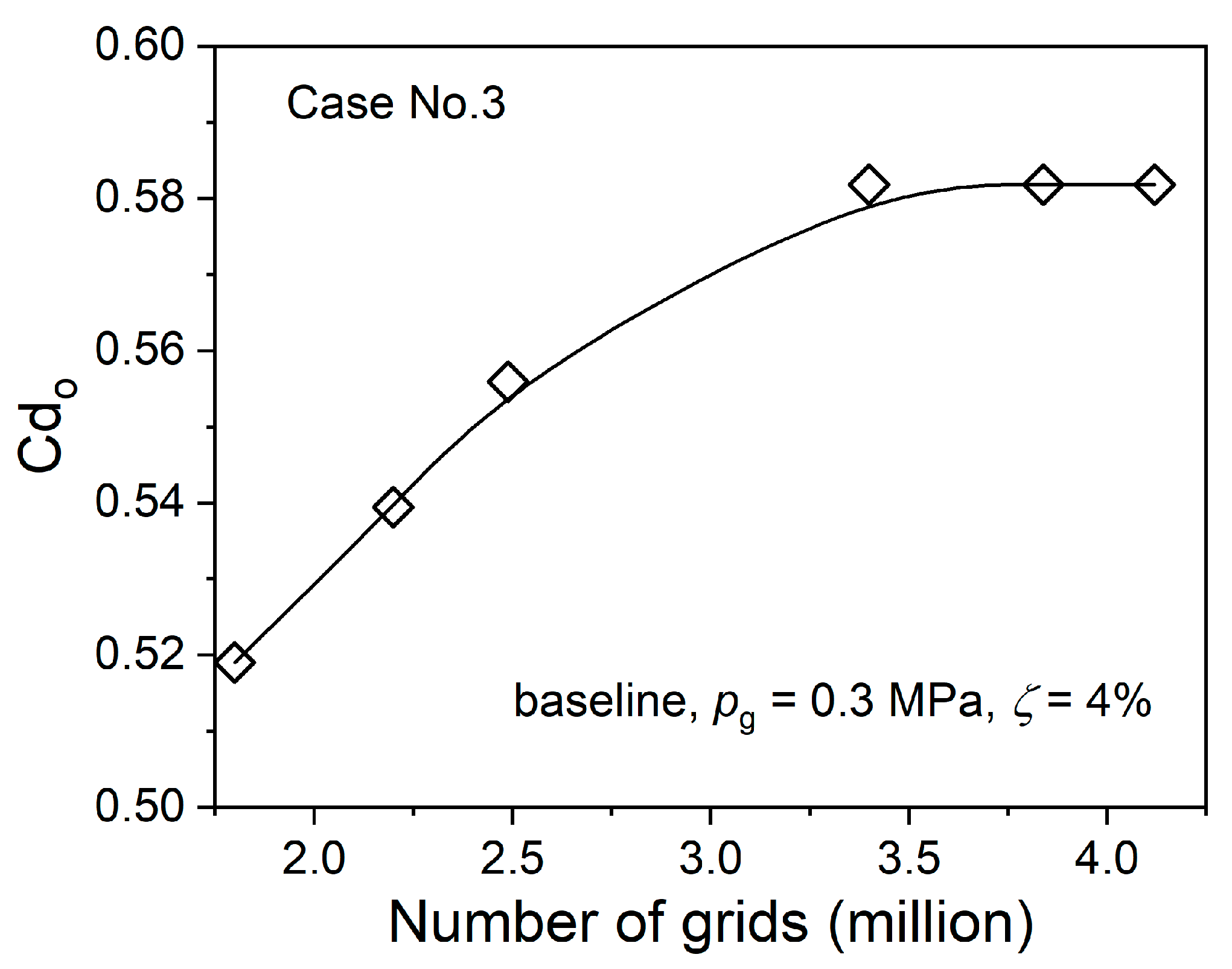
2.3. Numerical Simulation Approach

ANSYS Fluent (2020R1) is used to simulate the steady-state, three-dimensional flow and heat-transfer characteristics of the impingement–effusion double-wall configurations. The governing equations to be solved for steady turbulent flow and heat transfer can be expressed in tensor form as

$$\nabla ·\left(\rho \overrightarrow{u}\varphi \right)={\displaystyle \frac{\partial }{\partial x_i}}\left(\mathsf{\Gamma }{\displaystyle \frac{\partial \varphi }{\partial x_i}}\right)+S$$

(11)

where ϕ denotes general variables such as u, v, w, and T. Γ is the diffusion coefficient and S is the source term. The diffusion coefficients and source terms corresponding to each solved variable ϕ, expressed in tensor form, are listed in

Table 2. The diffusion coefficients and source terms in Equation (11).

General Variables, ϕ	Diffusion Coefficients, Γ	Source Term, S
u, v, w (uj, j = 1–3)	${\mu }_{\mathrm{e}\mathrm{f}\mathrm{f}}=\mu +{\mu }_{\mathrm{t}}$	$-{\displaystyle \frac{\partial p}{\partial x_i}}+{\displaystyle \frac{\partial }{\partial x_j}}\left({\mu }_{\mathrm{e}\mathrm{f}\mathrm{f}}{\displaystyle \frac{\partial u_j}{\partial x_i}}\right)$
T	${\displaystyle \frac{\mu }{P_r}}+{\displaystyle \frac{{\mu }_{\mathrm{t}}}{{\sigma }_T}}$

.

According to the turbulence-model accuracy comparisons for predicting impingement and film cooling flows provided by Kwon et al. [26], the k-ω SST and k-ε turbulence models exhibit average deviations of 7.2% and 26.5% from the experiments, respectively. Given its better predictive capability, the k-ω SST model with enhanced wall treatment is adopted in the present work, and the governing equations of k and ω are provided in the ANSYS Fluent User Manual [27]. Pressure–velocity coupling is solved using the SIMPLE algorithm, and second-order upwind schemes are applied to the convective terms.

The computational domain is simplified based on the test rig and the geometry of the impingement–effusion double-wall cooling configuration. It consists of a mainstream channel, a coolant supply channel, and the double-wall cooling section. The hot gas flows through the mainstream channel, which has a chamber height of 30 mm. The double-wall cooling section has a streamwise length of 90 mm, and the mainstream domain extends 150 mm both upstream and downstream to ensure fully developed inlet and outlet flow conditions.

For the double-wall configuration, the impingement and effusion plates have thicknesses of 0.6 mm and 1.5 mm, respectively. In the spanwise direction, a periodic region of 12 mm is selected as the computational domain. Given the spanwise spacing P = 4 mm, this periodic region covers six staggered columns of cooling orifices. Unless otherwise stated, a Cartesian coordinate is adopted, in which the x-, y-, and z-axes correspond to the streamwise, spanwise and wall-normal directions. The origin is located at the center of the first row of orifices (excluding the additional rows). As shown in Figure 5, the computational domain is discretized using the poly-hexcore meshing method in ANSYS Fluent Meshing. The detailed meshing parameters are as follows:

• Maximum global mesh size: 2 mm; minimum global mesh size: 0.1 mm.
• Mesh size on effusion plate: 0.5 mm.
• Boundary-layer grids were generated at all fluid–solid interfaces, with a first-layer height of 0.01 mm, a growth ratio of 1.2, and six layers in total.
• Mesh size of computional zone inside the orifices: 0.1 mm.

A grid independence study (GIS) was performed by refining the mesh using velocity-gradient adaption, resulting in grid sizes varying from 1.8 to 4.2 million cells. Figure 6 shows the simulated overall discharge coefficient of the double-wall configuration (Cd_o) for the different refined meshes. Since the coolant mass flow rate is directly governed by Cd_o at a constant pressure drop, Cd_o serves as an appropriate parameter for evaluating grid independence. The simulated Cd_o becomes nearly constant once the mesh size reaches approximately 3.4 million, which is therefore adopted for all numerical simulations in the present work.

To validate the present computational approach, a benchmark case was simulated based on the impingement–effusion cooling configuration and the experimental data reported by Yang et al. [3]. The same mesh generation strategy and numerical methods described above were used. The tested configuration features an impingement-orifice diameter of 1.6 mm, an effusion-orifice diameter of 1.9 mm, and a streamwise spacing of 3 mm. Figure 7 compares the predicted η_c with the measurements at various G_c (kg/(s·m²·MPa). The simulated cooling effectiveness under varying coolant mass flows shows good agreement with the measured results, with consistent streamwise trends. Therefore, the present computational approach is validated as feasible and accurate.

The boundary conditions in the present work were specified as follows. The mainstream inlet was defined as a velocity inlet with u_g = 12 m/s and T_g = 473 K. The coolant air inlet was defined as a pressure inlet at the designed ζ, with T_c = 300 K. The outlet was set as a pressure outlet at different operating pressures (0.1, 0.3 MPa).

3. Results and Discussion

3.1. Measured Overall Cooling Effectiveness of Impingement–Effusion Configurations

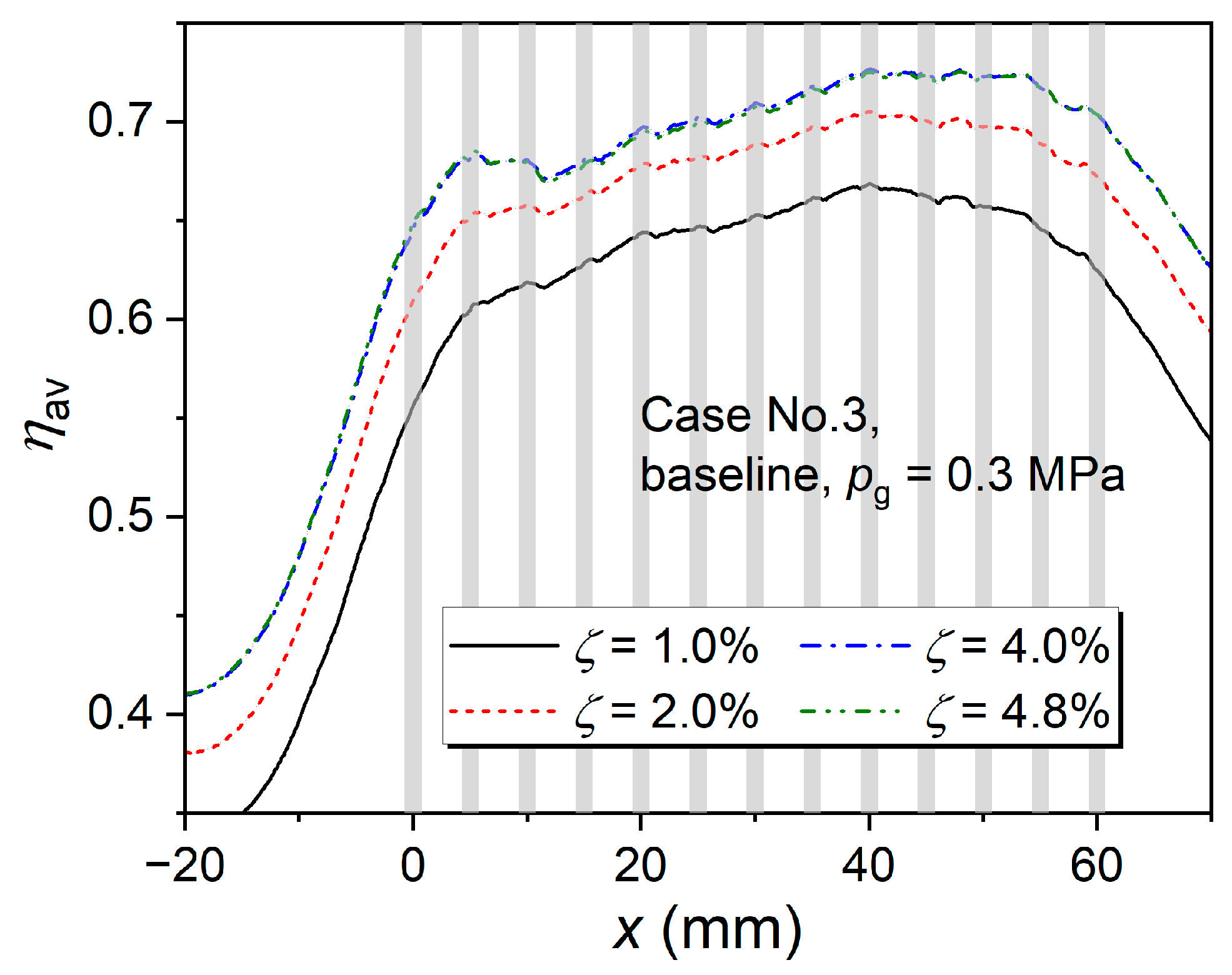
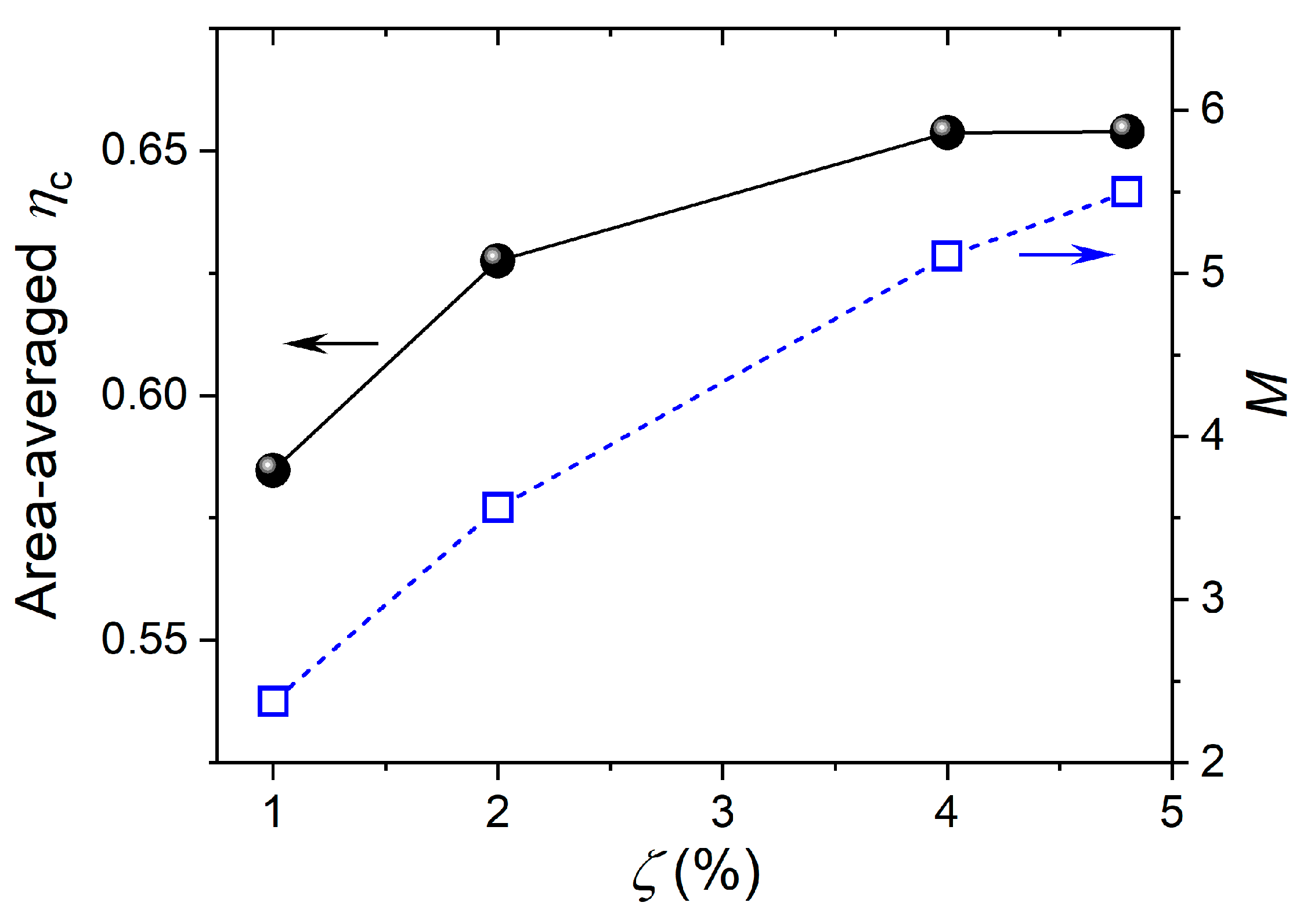
3.1.1. Effect of Pressure-Loss Coefficient

Figure 8 presents the contour maps of the overall cooling effectiveness distribution on the effusion plate under various pressure-loss coefficients. As ζ increases from 1% to 4%, the overall cooling effectiveness rises sharply, particularly within the streamwise region of 20–60 mm, where local improvements of up to 10% are observed. The region at x = 0–20 mm also exhibits a clear increase in cooling effectiveness. However, within this range, further increasing the pressure drop exerts limited influence on the expansion of the effective cooling coverage. When ζ further increases from 4% to 4.8%, almost no discernible change occurs in the cooling effectiveness distribution.

The streamwise profiles of spanwise-averaged cooling effectiveness (η_av), shown in Figure 9, quantitatively illustrate the influence of the pressure-loss coefficient. The trends of η_av agree with those derived from the contour maps: the curves corresponding to ζ = 4% and ζ = 4.8% almost overlap, demonstrating that further increasing pressure loss has little effect on cooling performance enhancement. Notably, the evolution of curve shapes with respect to the effusion orifice positions (indicated by gray bands) reveals key insights. As ζ increases from 1% to 4%, the η_av profile transitions from a single-peak to a double-peak shape. At ζ = 4%, an additional local maximum appears near the second row of orifices. Because variations in pressure drop mainly result in an overall upward shift of the curves, the locations of the peaks remain nearly unchanged.

Figure 10 shows the relationships between ζ, M, and area-averaged η_c. Increasing ζ directly raises the coolant flow rate and M in an almost linear manner, while the area-averaged η_c increases nonlinearly. Although higher flow rates and impingement jet velocities enhance impingement cooling, the diminishing improvement in total cooling performance results from competing effects. A higher M weakens the wall attachment of the effusion-cooling film, causing partial detachment from the surface and reducing film-cooling effectiveness. Because film cooling plays an important role in total heat removal, the overall cooling efficiency cannot be further improved. In particular, when ζ increases from 4% to 4.8%, the enhancement of impingement cooling is completely offset by the degradation of film cooling, leading to a negligible change in total effectiveness.

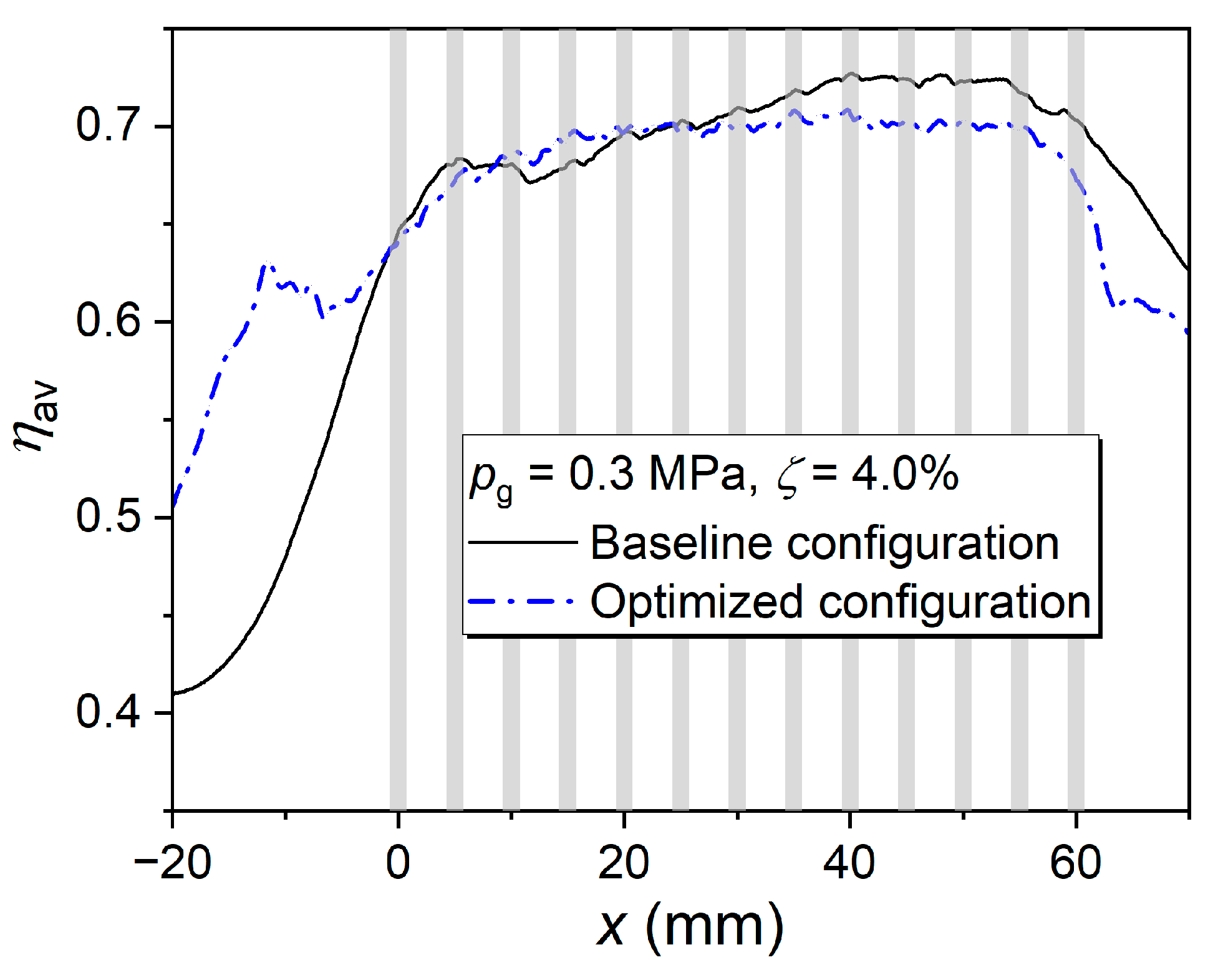
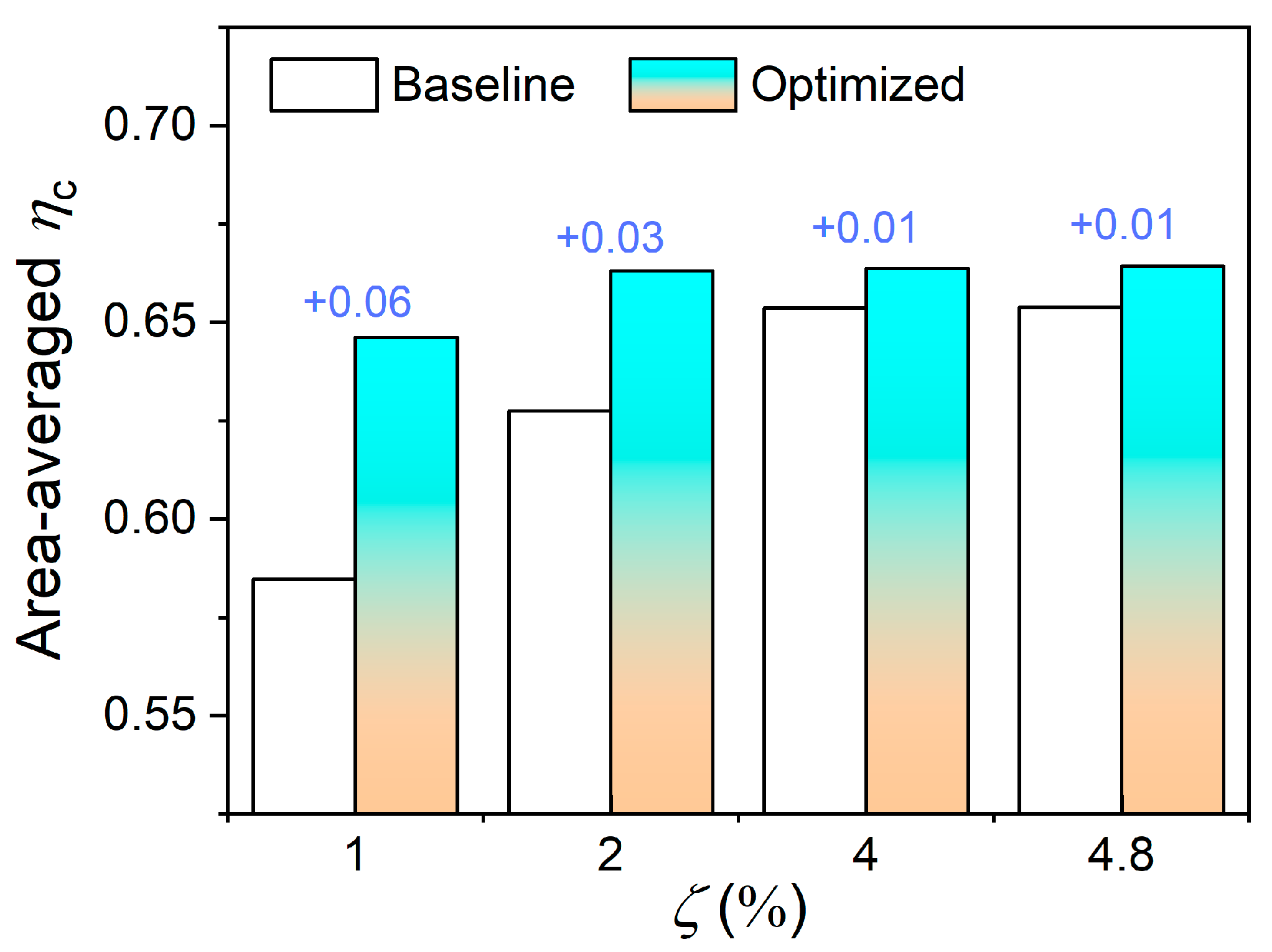
3.1.2. Effect of Initial Cooling Film

Figure 11 illustrates the influence of the introduction of initial film cooling on the overall cooling effectiveness of the impingement–effusion configuration. Although the peak η_c slightly decreases, the distribution uniformity of η_c improves significantly, and the effective cooling region extends upstream from 0 mm to approximately −20 mm. This improvement is attributed to the redistribution of coolant through the initial film-cooling orifices.

As observed in Figure 6, the cooling film in the baseline case primarily accumulates between 20 mm and 60 mm, while the cooling film closer to the leading edge is easily destroyed by the mainstream, resulting in weaker cooling performance. The addition of an initial film cooling modifies the coolant distribution and enhances jet uniformity within the plane, thereby improving the overall uniformity of cooling effectiveness. Moreover, the initial cooling film thickens the downstream cooling-film layer, reducing its erosion by the mainstream and stabilizing the surface protection.

The spanwise-averaged cooling effectiveness along the streamwise direction, shown in Figure 12, further confirms these effects. The initial film cooling significantly enhances cooling in the previously uncooled region, increasing local effectiveness by nearly 20% near the first-row film-cooling orifices. In the perforated region, redistribution of cooling air slightly reduces the peak effectiveness but improves downstream uniformity, maintaining values of approximately 0.7 from the fourth to the twelfth row. Hence, the inclusion of initial film-cooling orifices effectively expands the protected surface area and achieves more uniform thermal protection, which would be an advantage for engineering applications.

Figure 13 compares the pressure-drop dependence of cooling effectiveness for the baseline and optimized configurations. With the introduction of initial film-cooling orifices, higher effectiveness is achieved at lower pressure drops. For instance, the cooling effectiveness at ζ = 1% matches that of the baseline at ζ = 4%. Furthermore, the area-averaged cooling effectiveness of the optimized configuration remains stable over a wider range of pressure drops, demonstrating its robustness under the variable operating conditions typical of practical gas turbine combustors.

3.2. Insights into the Pressure Effects on Overall Cooling Performance

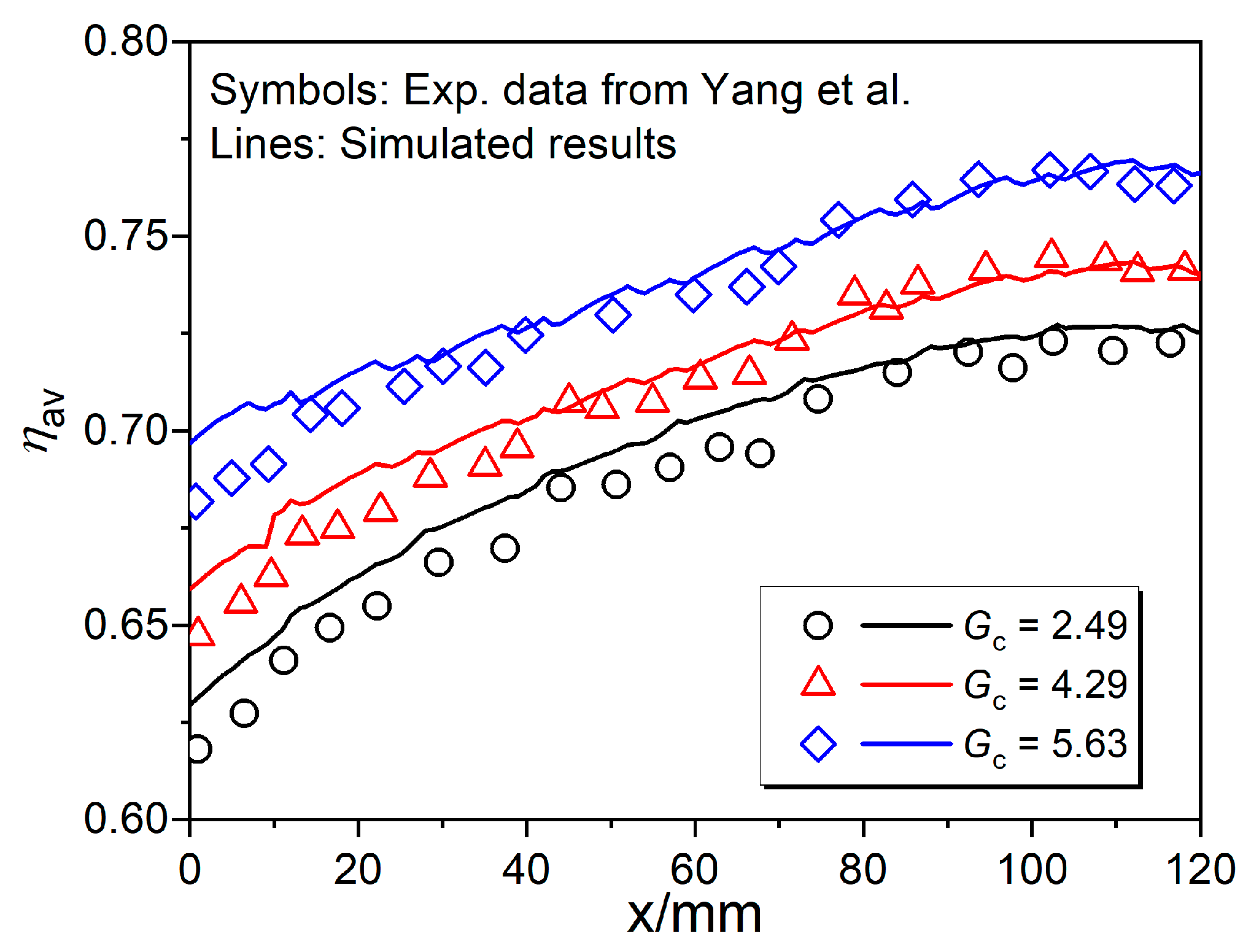
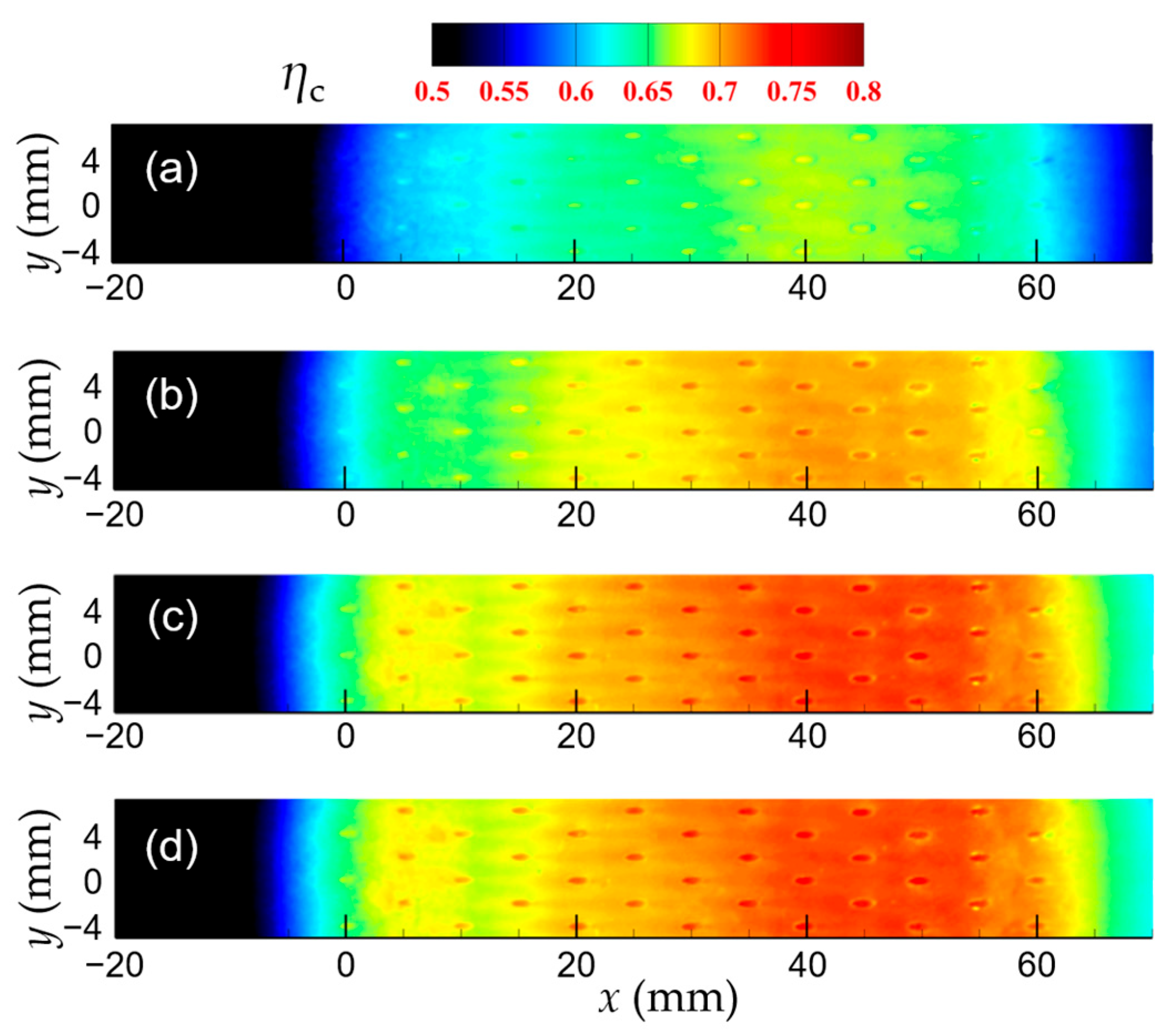
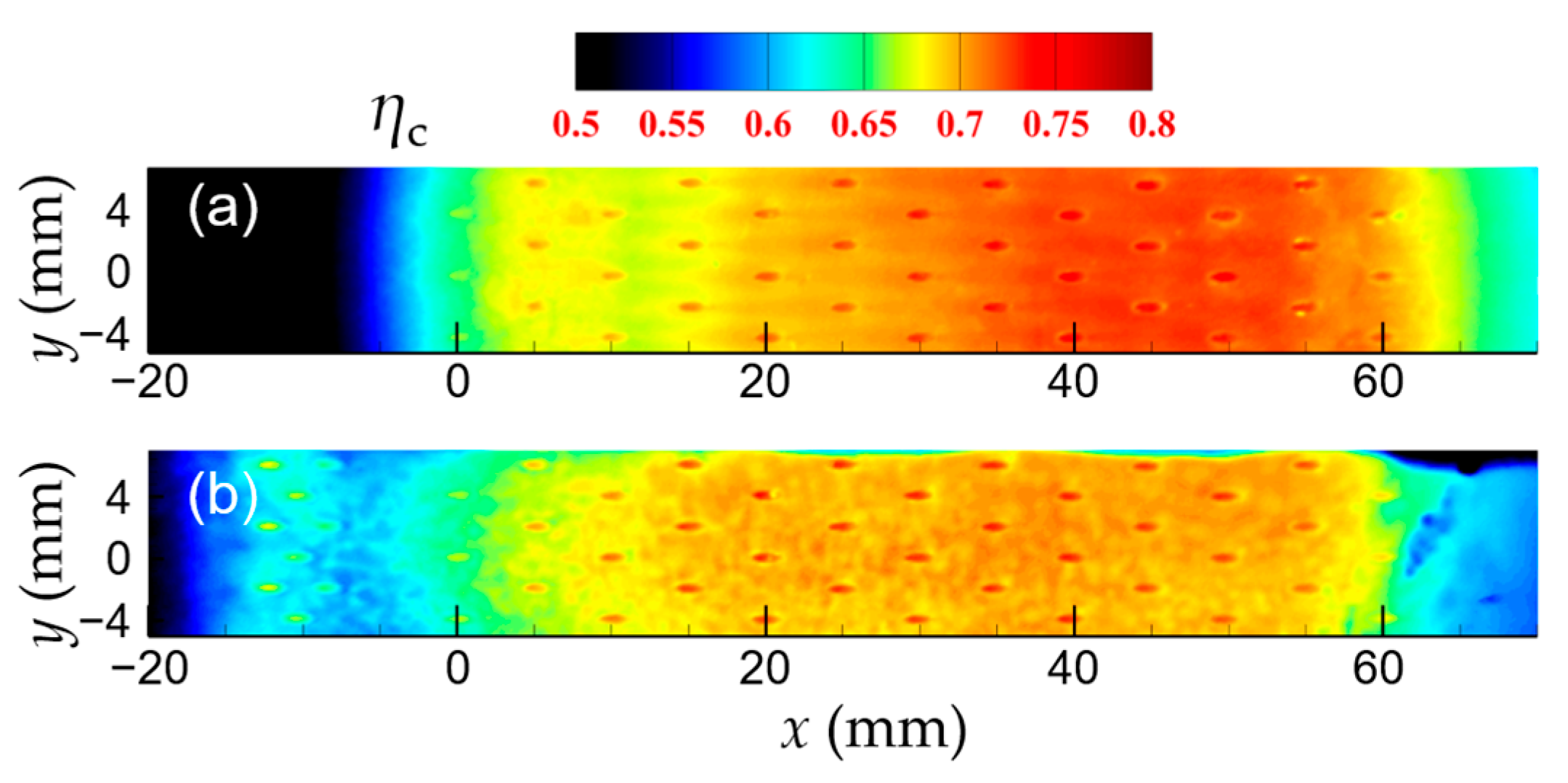
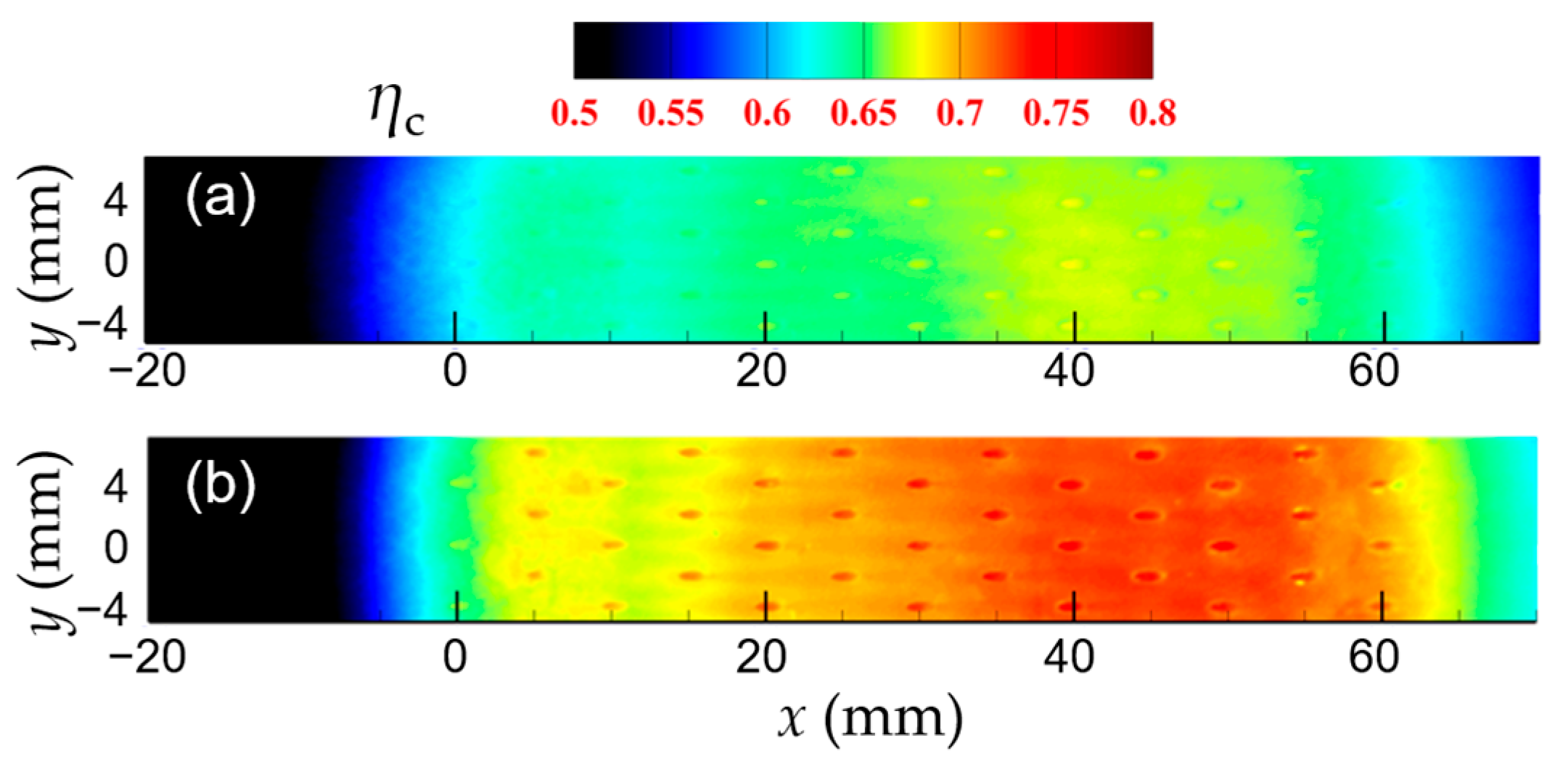
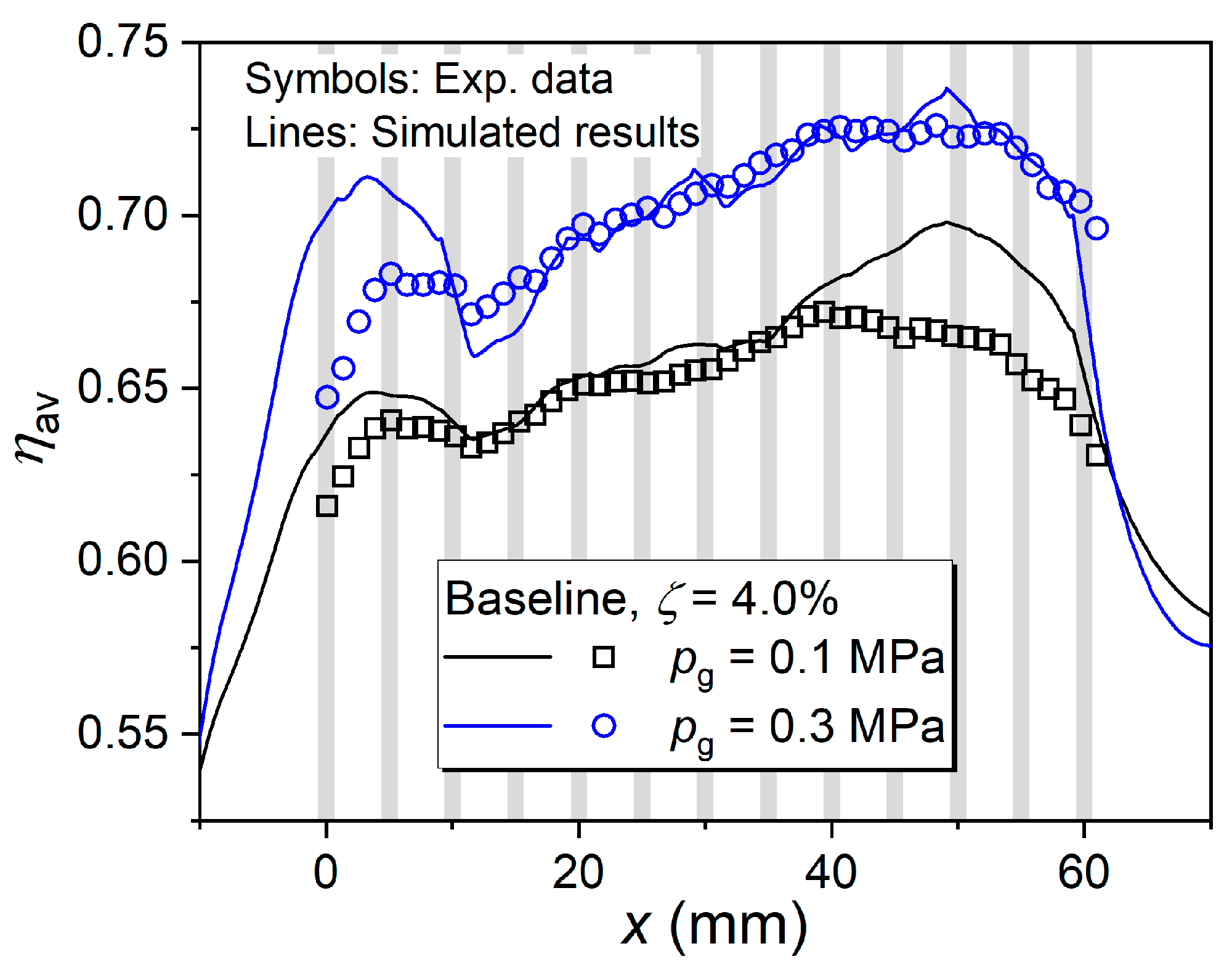
3.2.1. Comparisons of Cooling Effectiveness Under Atmospheric and Elevated Pressures

To examine the influence of operating pressure on the impingement–effusion cooling performance, experiments were conducted at p_g = 0.1 MPa and 0.3 MPa and constant ζ = 4%, as shown in Figure 14. The results reveal that the cooling effectiveness at 0.1 MPa is markedly lower than that at 0.3 MPa. These findings demonstrate that laboratory measurements conducted at atmospheric pressure may substantially underestimate the cooling performance under actual engine conditions. Therefore, accurate evaluation and scaling of impingement–effusion cooling require explicit consideration of operating pressure effects.

Figure 15 shows the measured and simulated spanwise-averaged cooling-effectiveness (η_av) profiles along the streamwise direction at p_g = 0.1 MPa and p_g = 0.3 MPa under a constant ζ of 4.0%. The simulated results agree well with the measurements, confirming the reliability of the numerical approach in capturing the pressure-dependent flow and heat-transfer behavior. Both the contour distribution in Figure 14 and the streamwise profiles in Figure 15 show that elevated operating pressure significantly enhances cooling performance across the entire surface. At p_g = 0.3 MPa, the peak cooling effectiveness well exceeds 0.7, and this is accompanied by notable improvement over the upstream region influenced by the several rows of effusion orifices. These combined observations and simulated results indicate that atmospheric-pressure measurements cannot reproduce the heat-transfer characteristics observed under elevated pressures, even when Reynolds-number similarity is maintained.

Figure 16 further shows that the observed improvement in cooling effectiveness at elevated pressure cannot be explained solely by blowing ratio, since M remains nearly constant. Instead, the enhancement arises from pressure-induced changes in density, jet coherence, and cooling-film stability. Higher pressure increases the coolant density and jet momentum flux, which strengthens impingement heat transfer and promotes more coherent cooling-film formation downstream. These combined effects improve the persistence of surface protection under engine-relevant pressures.

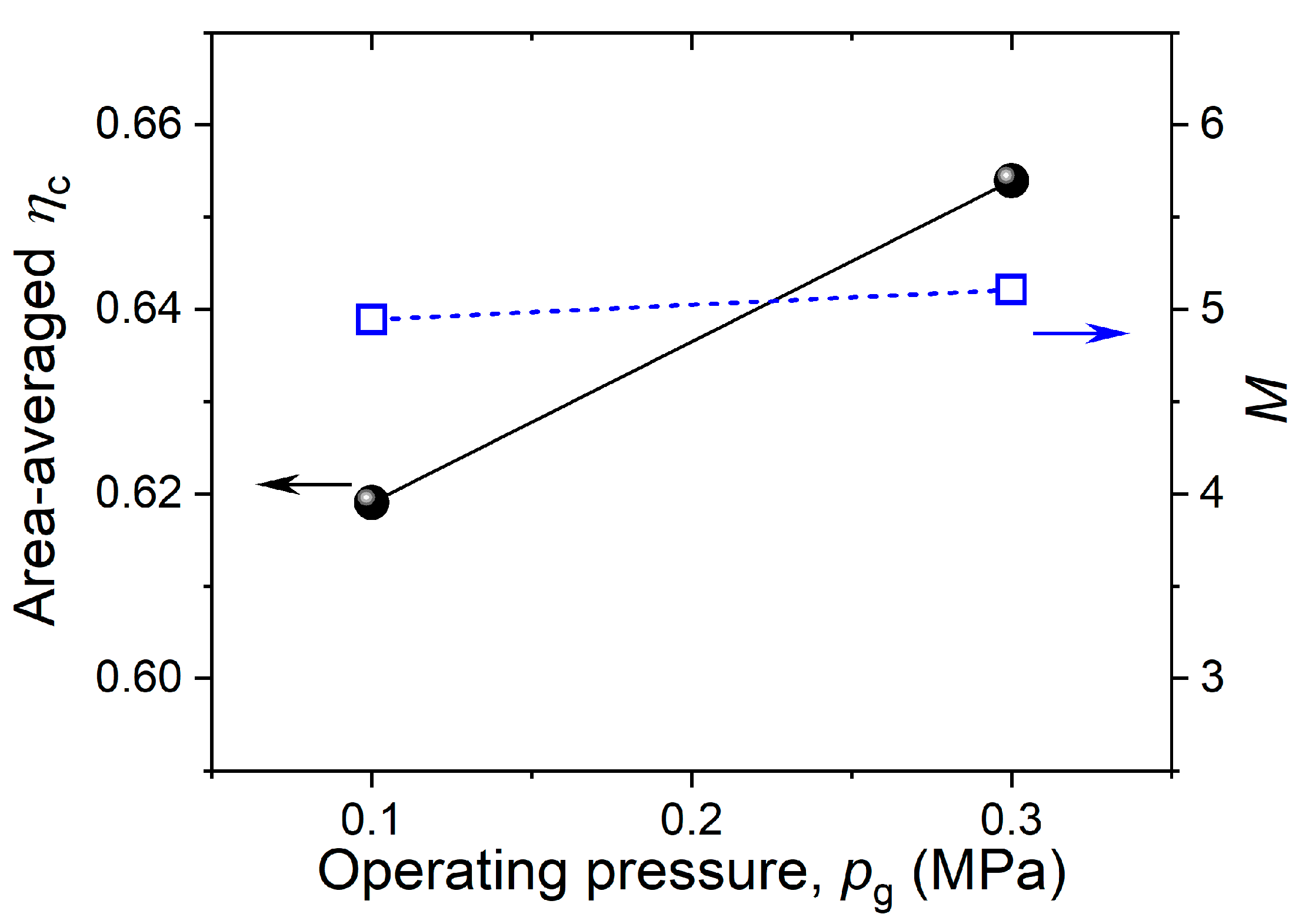
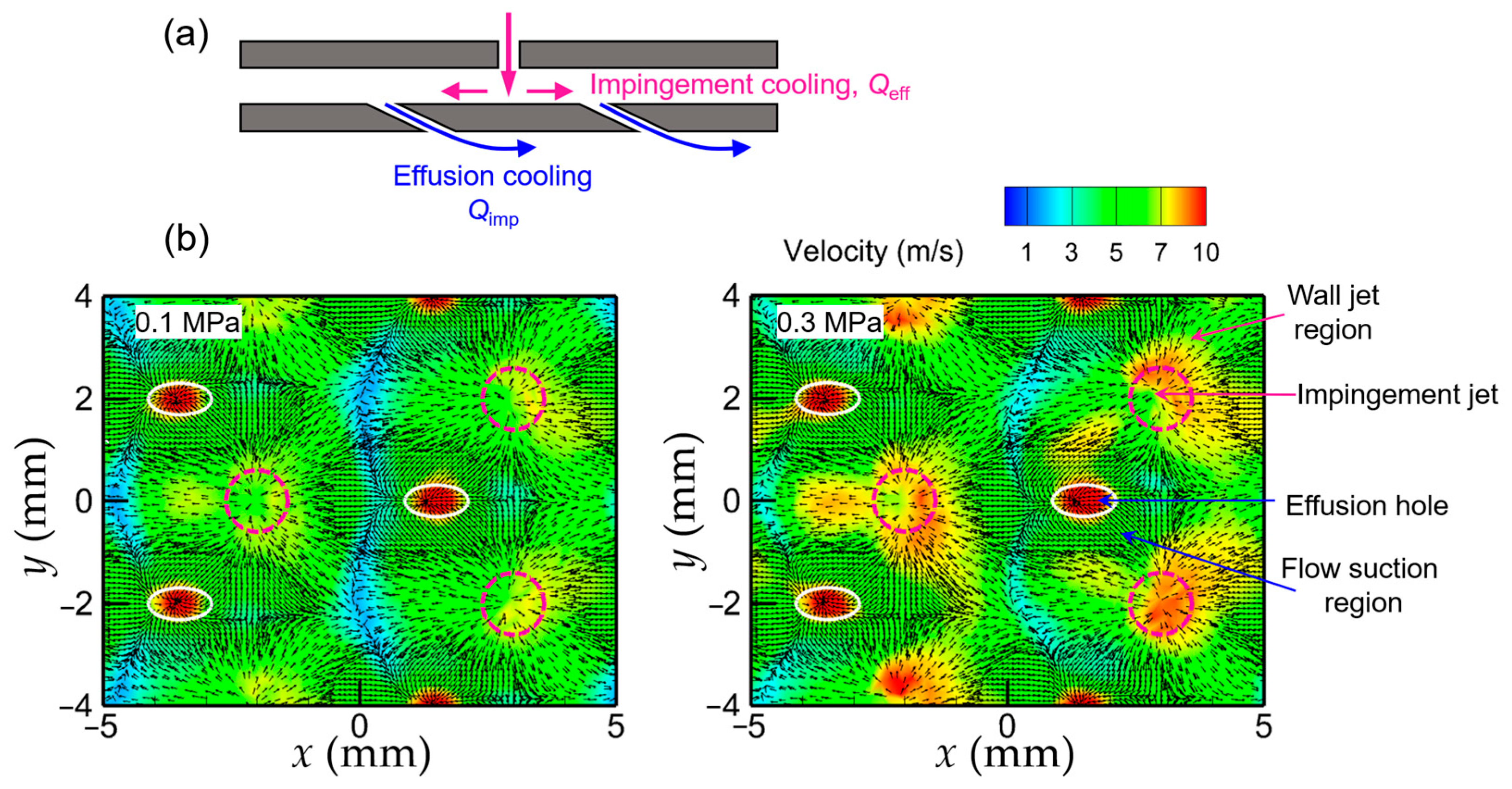
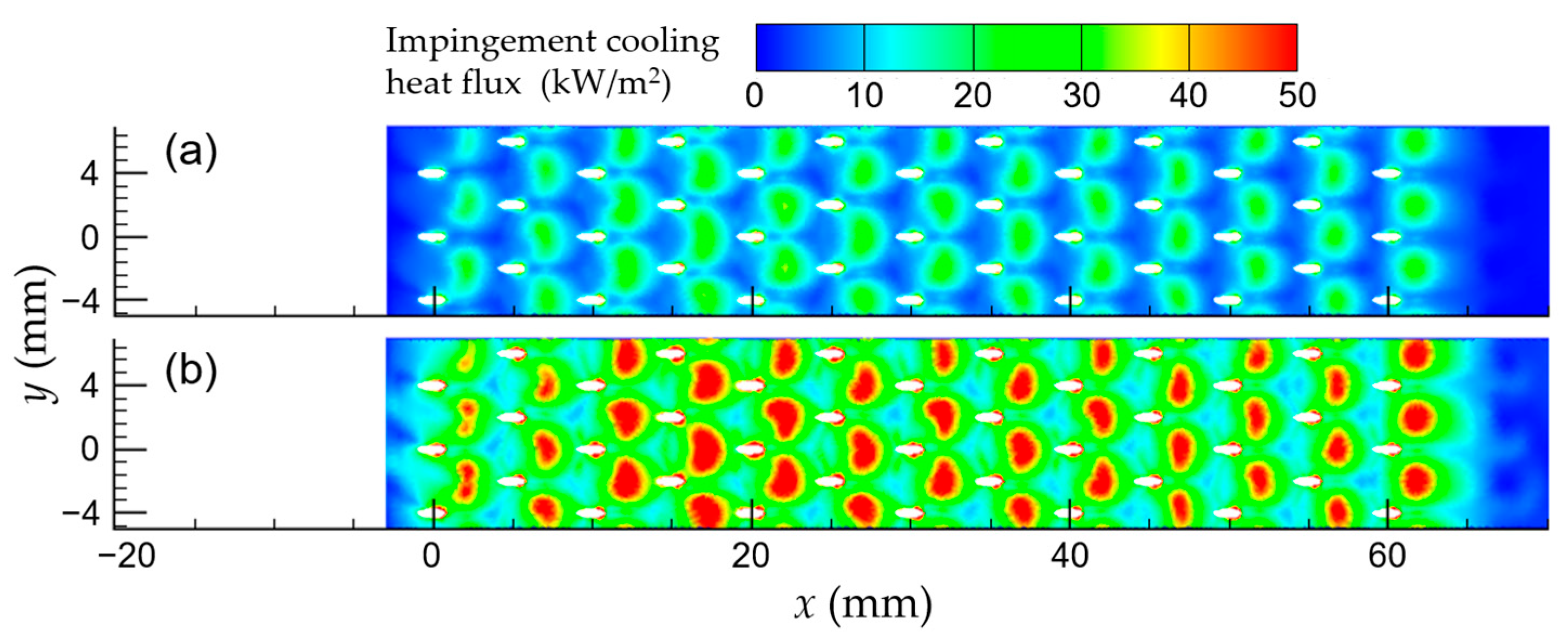
3.2.2. Contributions of Impingement and Convective Cooling Under Different Pressures

Previous studies [19,20,21] have clarified the mechanisms of heat transfer enhancement in impingement–effusion double-wall cooling configurations. As illustrated in Figure 17a, these mechanisms include jet impingement heat transfer on the cold side of the effusion plate, near-wall lateral flow inside the impingement channel [28], and forced convection induced beneath the effusion plate. Accordingly, a cross-section located 0.3 mm from the cold-side wall of the effusion plate within the impingement cavity was selected to analyze the flow characteristics. As shown in Figure 17b, the dominant flow features are generally consistent with those presented in Figure 1, including the impingement jet stagnation zone, near-wall lateral flow region, and suction-induced flow through the effusion orifice. These forced convection flows contribute significantly to enhancing the heat transfer performance along the wall surface [29,30]. A comparison between the atmospheric and pressurized mainstream conditions reveals that the local flow velocity is higher under elevated pressure, particularly in the regions of the impingement jet and the suction flow induced by the effusion orifices.

Further analysis of the wall heat flux was conducted, focusing on the heat flux along the cold side of the effusion plate (Q_imp) and within the effusion orifices (Q_eff). As shown in Figure 18, both distributions exhibit similar patterns under the two pressure conditions. The impingement jet stagnation zones correspond to the highest heat fluxes, and localized enhancement around the effusion orifices is attributed to suction-induced convection. However, the magnitude of heat flux under pressurized conditions is significantly greater than that under atmospheric conditions.

Table 3. Comparisons of simulated heat transfer parameters for the impingement–effusion cooling plate at p_g = 0.1 and 0.3 MPa.

pg (MPa)	Gc (kg/(m2·s·MPa))	Cdo	M	Qimp (W/m2)	Qeff (W/m2)	Qimp/pg (W/(m2·MPa))	Qeff/pg (W/(m2·MPa))
0.1	5.32	0.502	5.1	9629	3095	96,292	30,955
0.3	5.88	0.556	5.6	23,665	7025	78,549	23,417

summarizes the simulated flow and heat transfer parameters. Under high-pressure conditions, both Q_imp and Q_eff exceed twice the corresponding values at atmospheric pressure. The coolant mass flux per unit area (G_c) slightly increases from 5.32 to 5.88 kg/(m²·s·MPa), and the discharge coefficient (Cd_o) rises from 0.502 to 0.556, confirming that the greater coolant mass flow rate at constant pressure loss is the primary reason for enhanced heat transfer. These results highlight that similarity modeling of cooling performance comparing atmospheric and pressurized conditions may introduce substantial errors if variations in flow and heat transfer coefficients are neglected. Therefore, accurate evaluation of liner cooling performance must explicitly incorporate the effects of pressure, as atmospheric-pressure data cannot reliably represent conditions in practical gas turbines.

4. Conclusions

This study systematically evaluated the impingement–effusion cooling performance under atmospheric and elevated pressures through experiments and simulations, focusing on the effects of pressure drop, initial film-cooling addition, and operating pressure. The main findings are summarized as follows.

• Pressure drop strongly affects cooling effectiveness. Increasing the pressure drop across the impingement wall enhances jet momentum and cooling-film attachment, thereby improving overall cooling. However, when the drop exceeds about 4%, further gains diminish, as excessive blowing weakens cooling-film adhesion.
• Initial film-cooling addition redistributes coolant flow, slightly reducing local peak effectiveness but broadening surface protection and improving cooling uniformity. Comparable effectiveness to the baseline case at a high pressure drop can thus be achieved with lower coolant consumption.
• Elevated operating pressure substantially enhances cooling persistence and stability. Higher gas density increases jet momentum flux, promotes coherent impingement, and stabilizes cooling-film coverage, yielding greater overall effectiveness compared to the same at atmospheric pressure.
• Blowing-ratio-based similarity fails to account for pressure-dependent density and jet-mainstream interactions. Reliable scaling from laboratory to engine conditions, therefore, requires explicit inclusion of pressure effects.

In summary, although the conclusions of this study are limited to the operating conditions investigated (up to 473 K, 0.3 MPa), the results clearly reveal the trend that elevated pressure significantly affects impingement–effusion cooling performance. Properly accounting for pressure-driven effects is essential for accurate liner-cooling design. These findings provide both physical insight and practical guidance for developing next-generation, high-efficiency aero-engine combustors.