A Generative Model Approach for LiDAR-Based Classification and Ego Vehicle Localization Using Dynamic Bayesian Networks
Abstract
1. Introduction
- Innovative Classification Framework: We developed a robust method to classify static and dynamic tracks using LiDAR data, leveraging a combination of probabilistic models, including DBNs and interaction dictionaries.
- Self-Aware Localization Strategy: We introduced a novel ego vehicle localization approach that does not rely on external odometry data during testing, enhancing autonomy in dynamic environments.
- Simultaneous Multi-Track Interaction Modeling: We proposed a combined interaction dictionary that enables simultaneous modeling of multiple track interactions and ensures continuity during missing observations.
- Integration of Interaction Dictionaries: We designed a methodology that combines multiple static track interactions into a unified dictionary framework, ensuring robust localization even in the absence of continuous observations.
- Hybrid Inference with MJPF: We implemented an MJPF filter that supports hybrid discrete and continuous inference for trajectory prediction.
- Generative Localization Model: We developed a generative localization model capable of statistical filtering and divergence-based anomaly detection during trajectory estimation.
- MJPF Enhancement for Ego Vehicle Localization: We incorporated MJPF into the localization process to refine ego vehicle positioning by continuously predicting and updating its estimated trajectory based on static track interactions.
2. Related Works
2.1. Classification of LiDAR Data
2.2. Ego Vehicle Localization
3. Proposed Framework
3.1. Offline Training Phase
3.1.1. Detection and Tracking
3.1.2. Odometry Sensor
3.1.3. Null Force Filter
3.1.4. Track Classifications
3.2. Implementation Details: Interaction Dictionary and Algorithmic Configurations
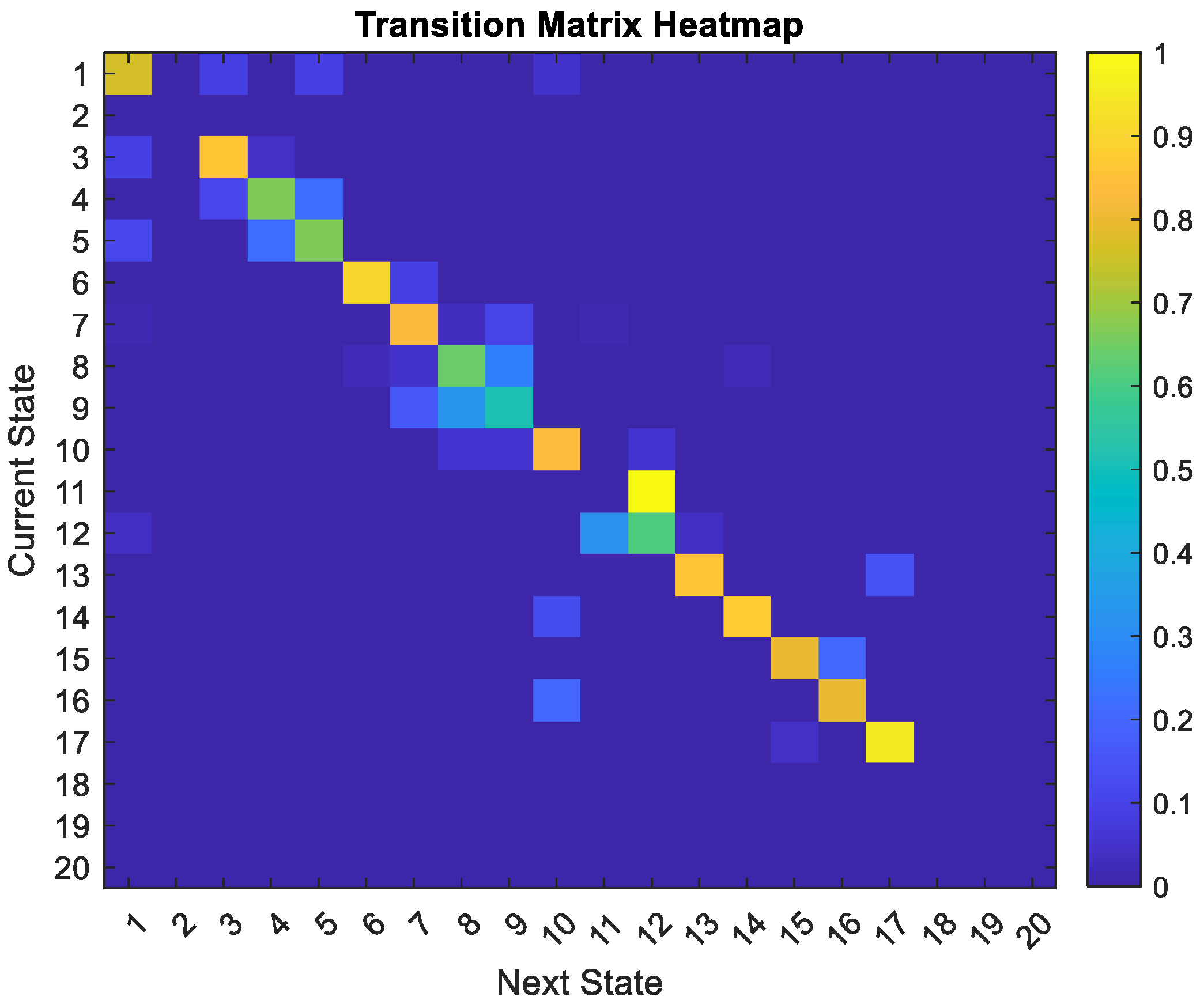
3.2.1. Construction of the Interaction Dictionary
3.2.2. Parameter Configuration for JPDA and GNG
3.3. Online Testing Phase
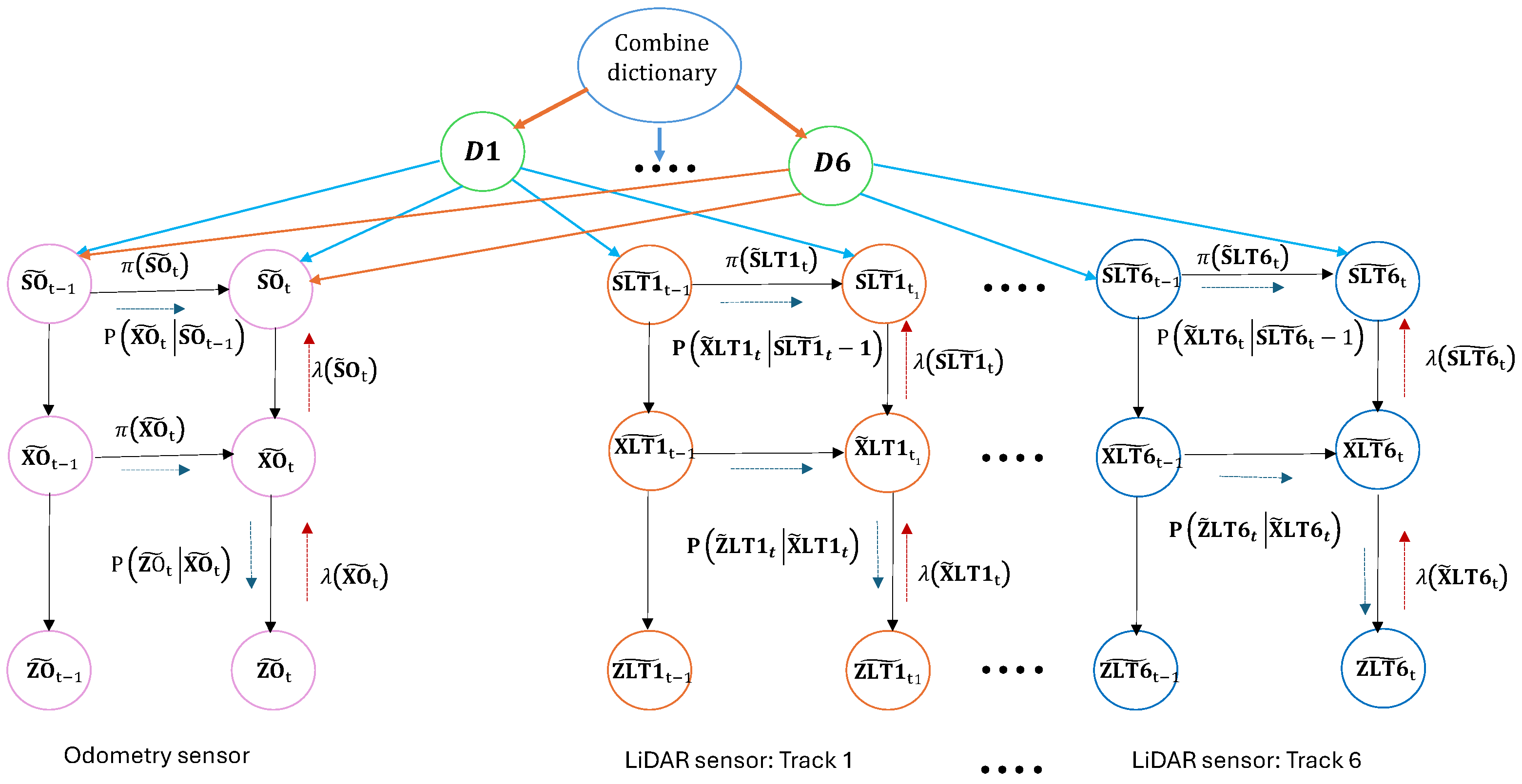
3.4. Localization with Combined Dictionary
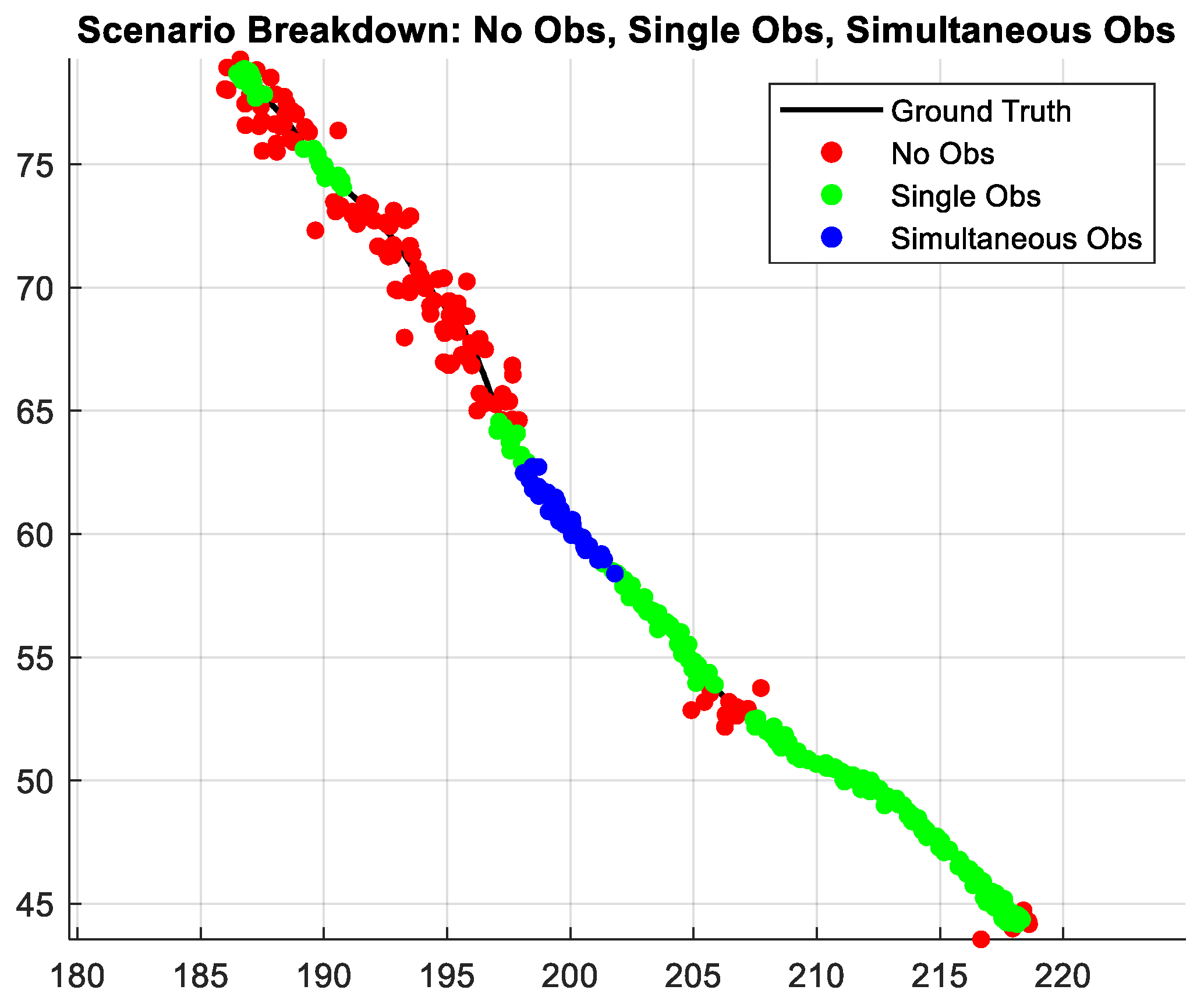
- Simultaneous Track Interactions: When multiple static tracks are observed at the same instant, combining dictionaries can refine ego-vehicle position estimates by leveraging cross-track constraints.
- Extended No Observation Periods: In some time intervals, no new LiDAR observations of static tracks may be available (e.g., occlusion or sensor dropout). Incorporating combined dictionaries can help maintain stable localization by relying on prior learned interactions across multiple tracks.
- Isolated Track Interactions: Even when only one track is observed, the combined dictionary framework can cross-validate with other track dictionaries (now unused) to check for consistency, thereby reducing ambiguity.
3.4.1. Steps to Create a Combined Dictionary
3.4.2. Bhattacharyya Distance to Match Observed Tracks
3.4.3. Particle Initialization for Multiple Tracks
3.4.4. Prediction Phase (Per Track and Ego Vehicle)
3.4.5. Update Phase (Measurements + Combined Interaction)
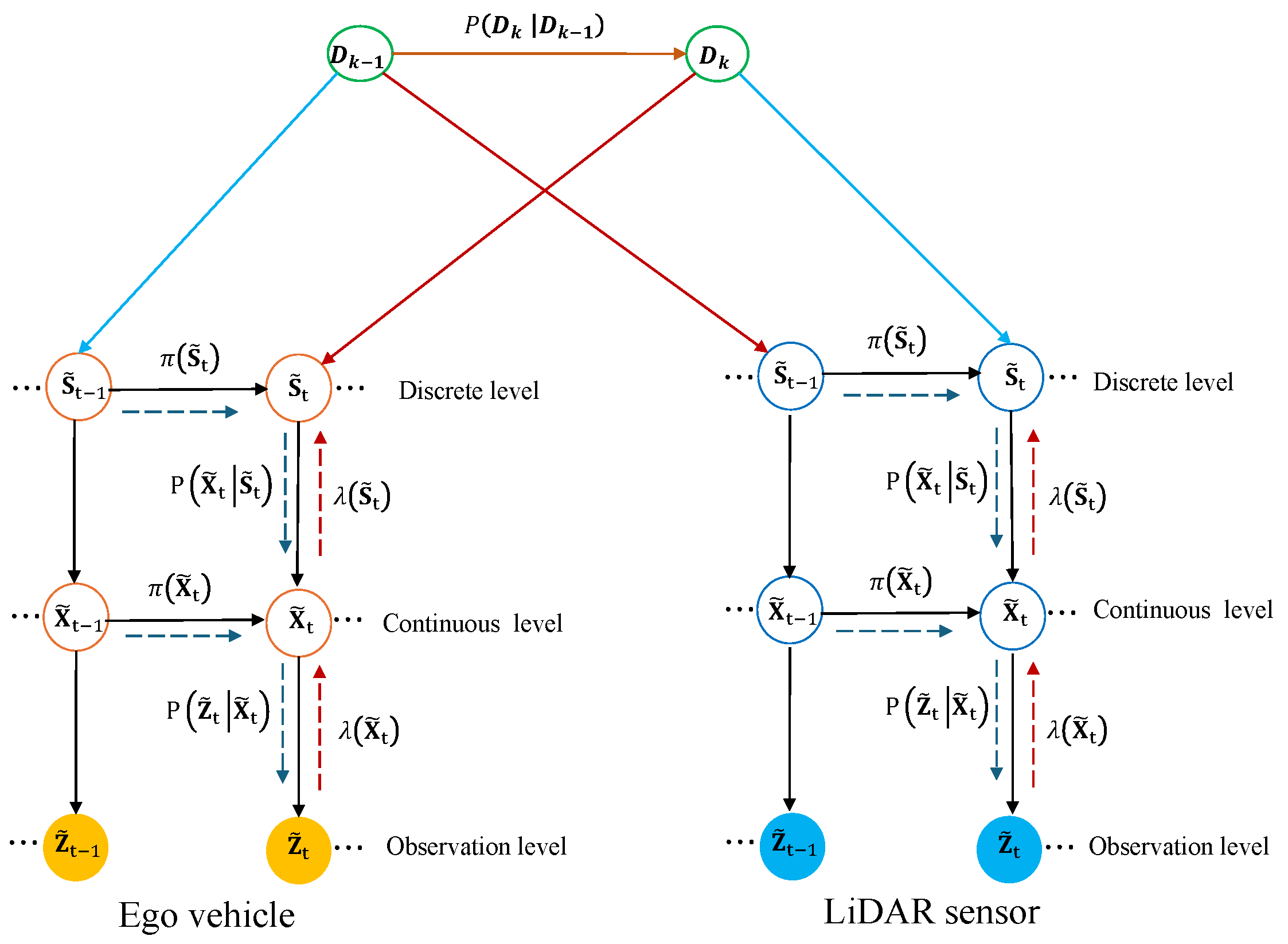
3.4.6. DBN Structure During Training
- Sensor Integration: The lower-level nodes in the DBN represent the ego vehicle’s state, including its hidden state , predicted position , and observed position . These nodes are connected via transition probabilities , modeling the odometry-based motion dynamics.
- LiDAR-Based Track Classification: At the track level, the DBN models individual static tracks, such as , where represents the hidden state of the track and represents its observed position. Transition probabilities capture the temporal evolution of these static objects in the LiDAR dataset.
- Dictionary Fusion: A higher-level node integrates the outputs of all track-level nodes into a unified combined dictionary. This dictionary serves as a probabilistic repository of interactions between the ego vehicle and the classified tracks. It encodes cross-track consistency and enables robust ego position estimations across different scenarios.
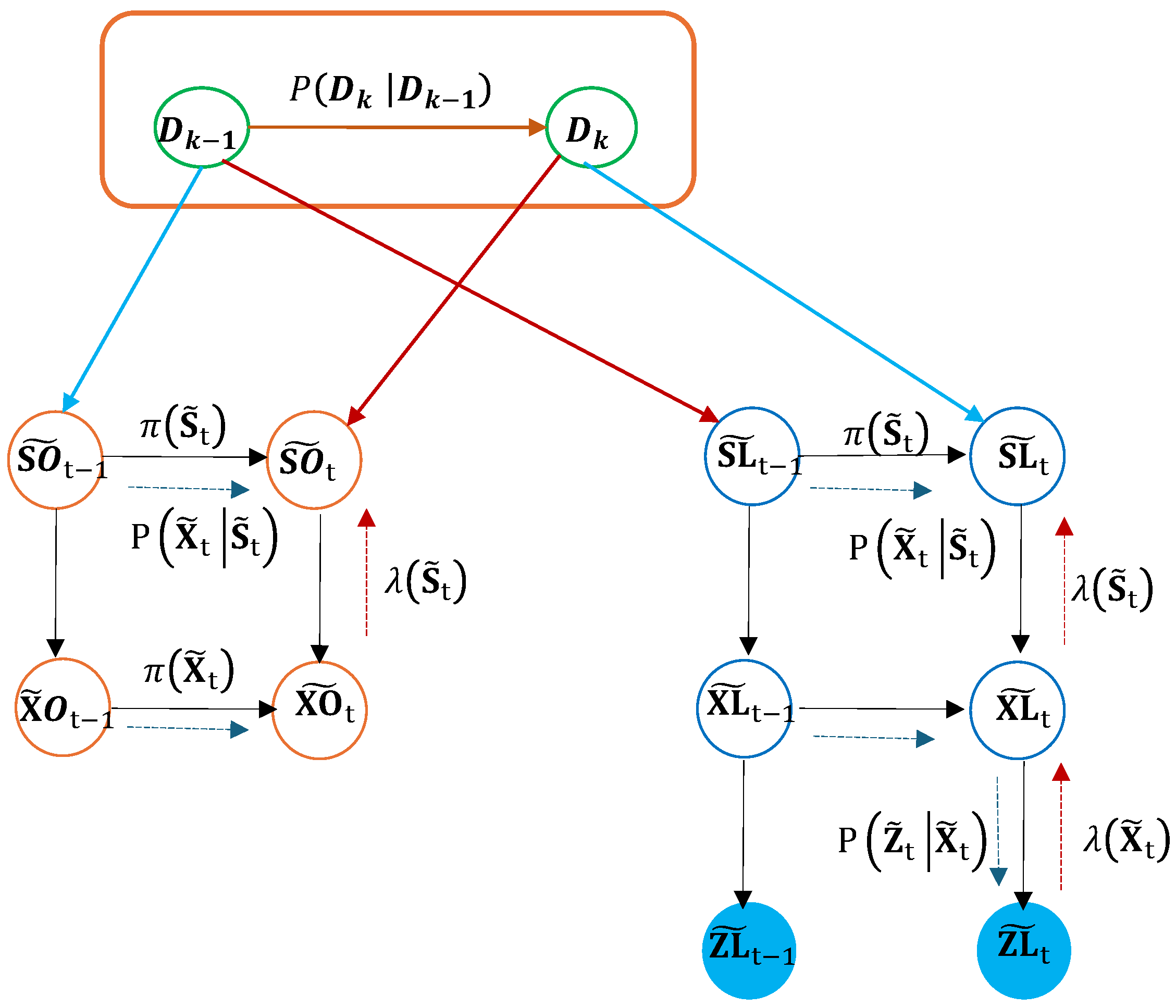
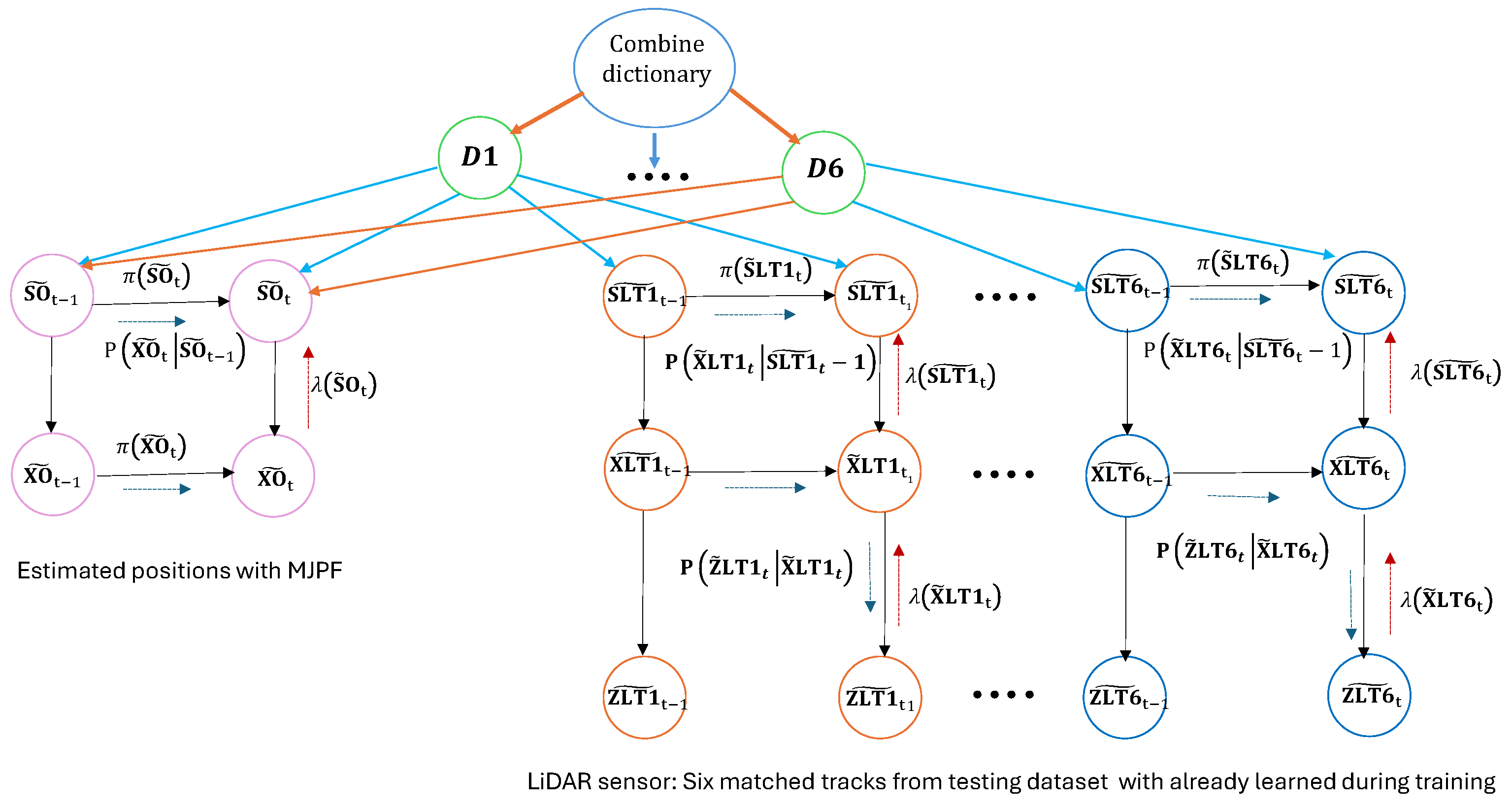
3.4.7. DBN Structure During Testing
- Track Matching: Observed tracks in the LiDAR testing dataset are matched with the learned static tracks using the Bhattacharyya distance. This step ensures that the six static tracks identified during training are accurately re-associated with their counterparts in the testing environment, which shares a similar structure.
- Prediction with MJPF: Once the tracks are matched, the MJPF predicts the ego vehicle’s positions. The MJPF leverages the matched tracks as static references, using the learned motion dynamics and interaction models to estimate the ego state.
- Dictionary Fusion for Robust Estimation: The matched track dictionaries are combined into a unified dictionary, as in the training phase. This fused dictionary incorporates all static tracks and provides probabilistic corrections to the MJPF predictions, ensuring that the ego vehicle’s trajectory remains consistent with the observed environment.
- Final Ego Position Estimation: The leftmost nodes of the DBN represent the final estimated positions of the ego vehicle. These nodes aggregate probabilistic influences from all matched tracks and the fused dictionary, enabling accurate localization even in the absence of direct odometry input.
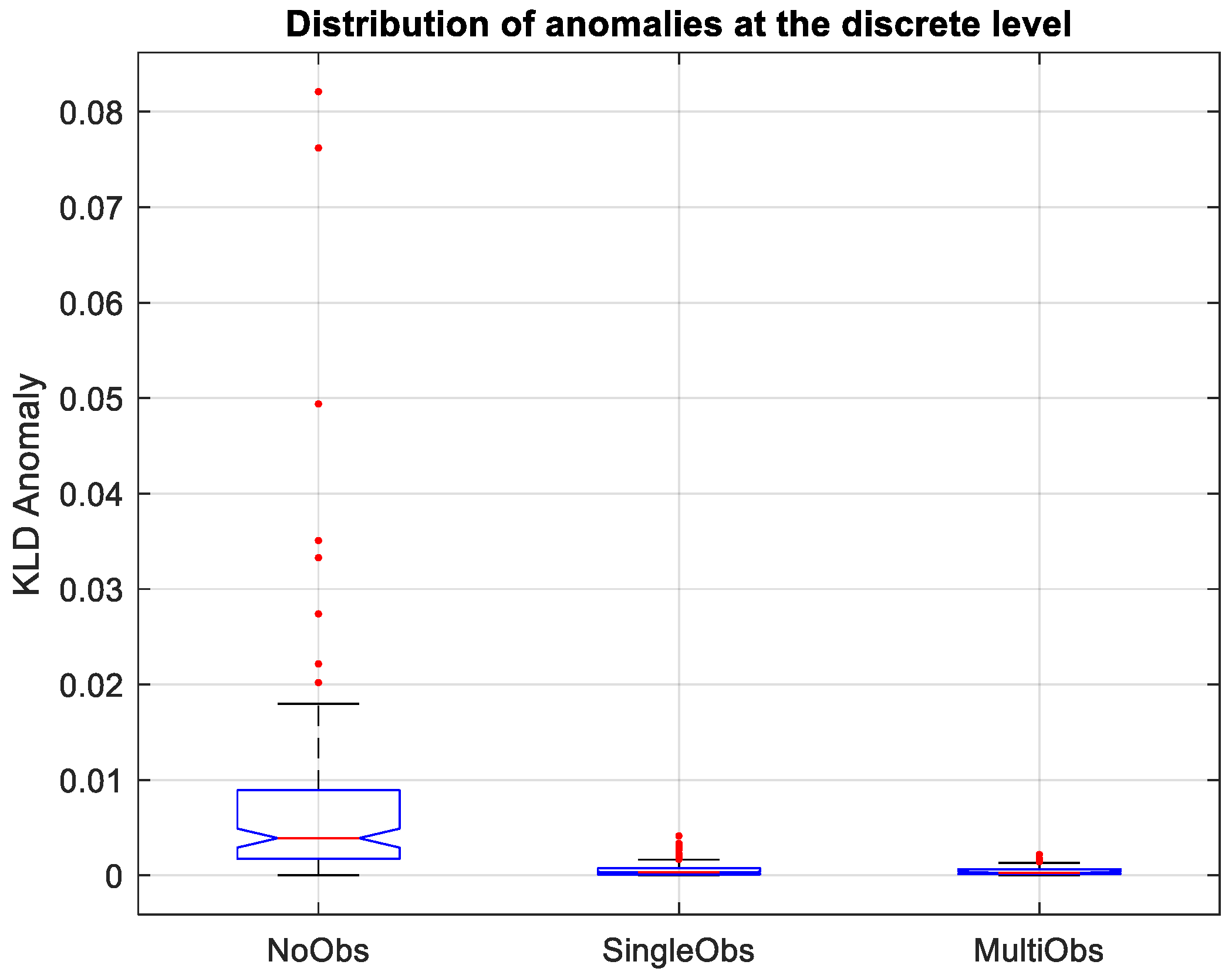
4. Results and Discussion
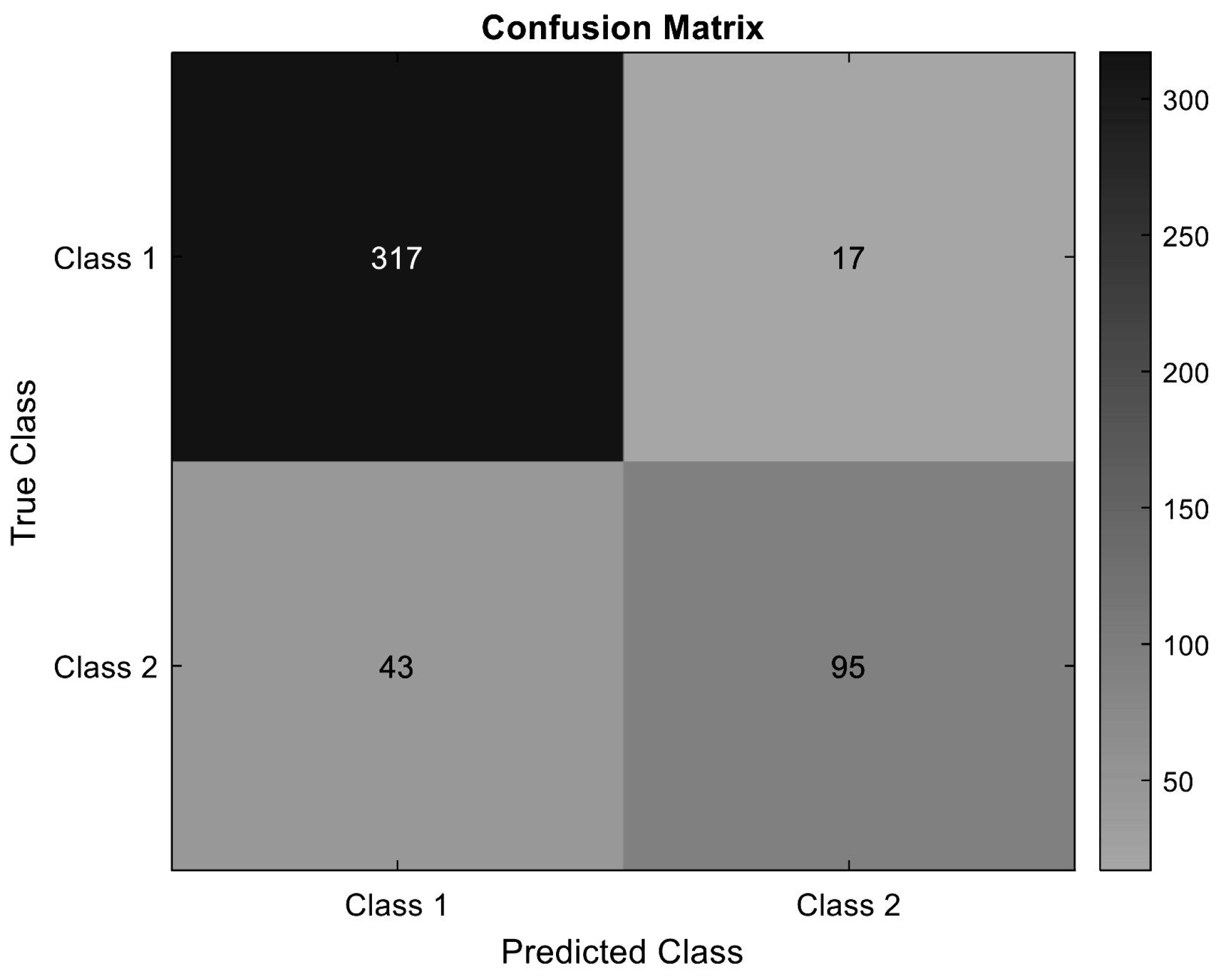
4.1. Classification Results
- True positive (TP): The 317 dynamic interactions are correctly classified.
- True negative (TN): The 95 static interactions are correctly classified.
- False positive (FP): 43 static interactions are misclassified as dynamic.
- False negative (FN): 17 dynamic interactions are misclassified as static.
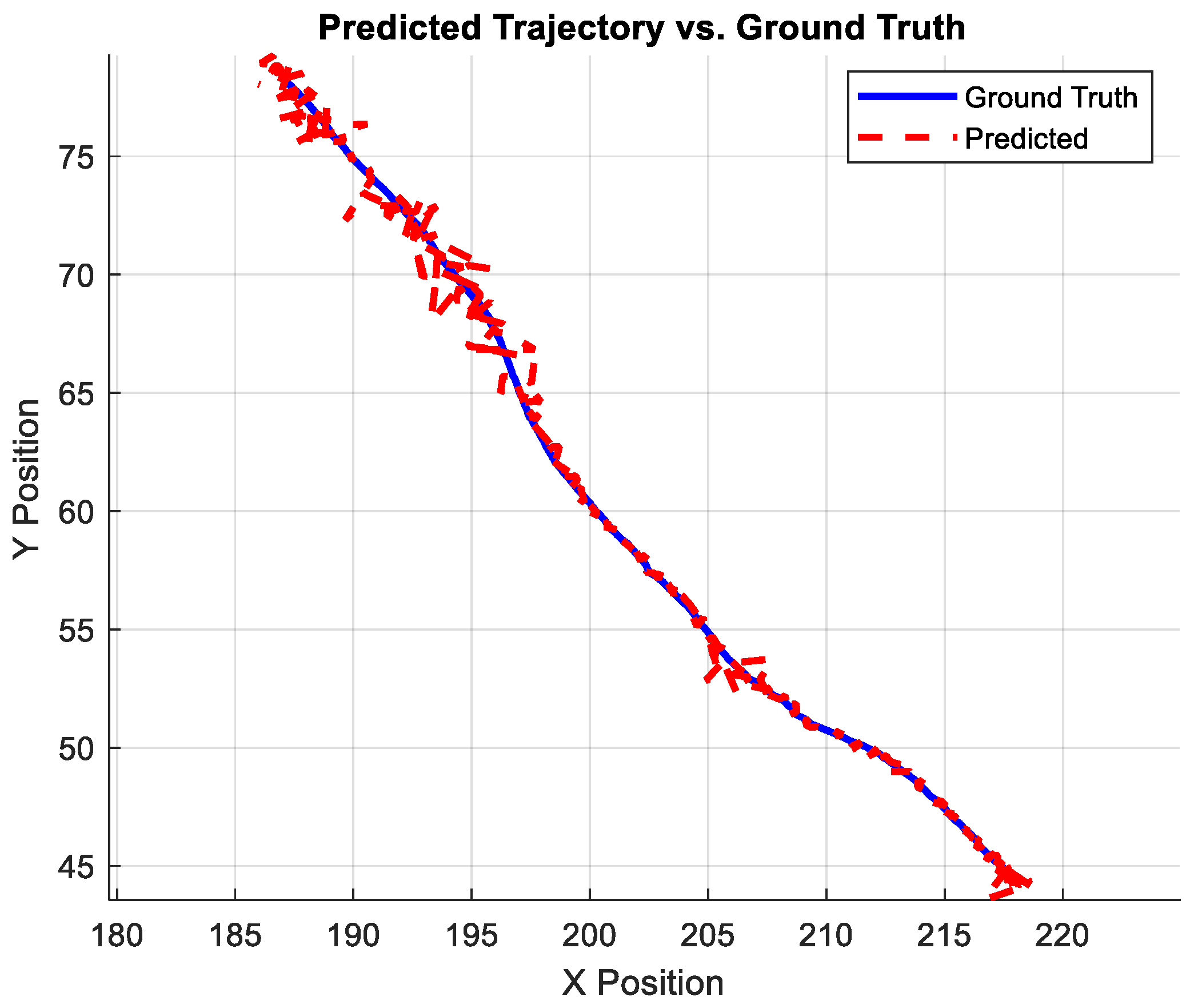
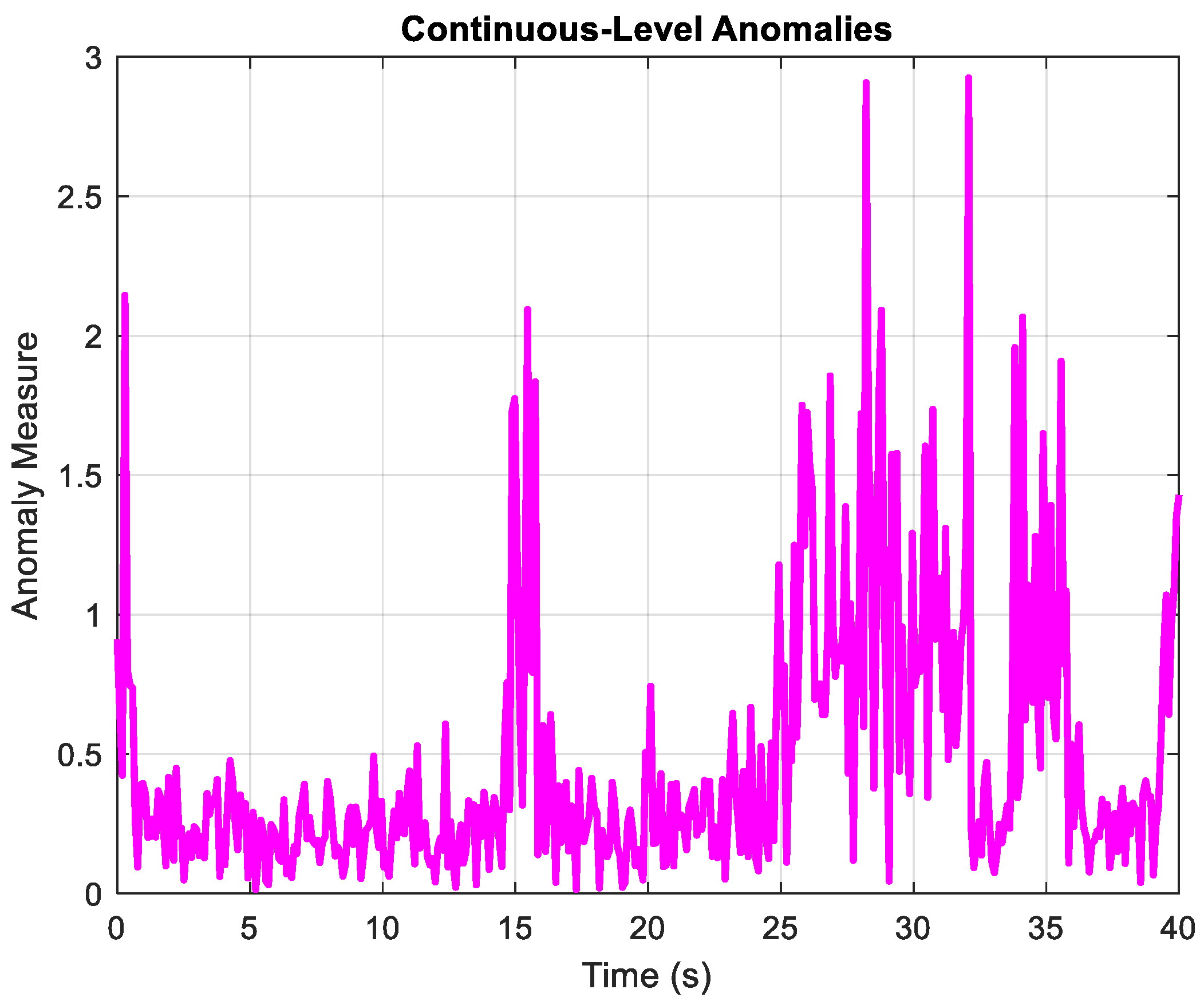
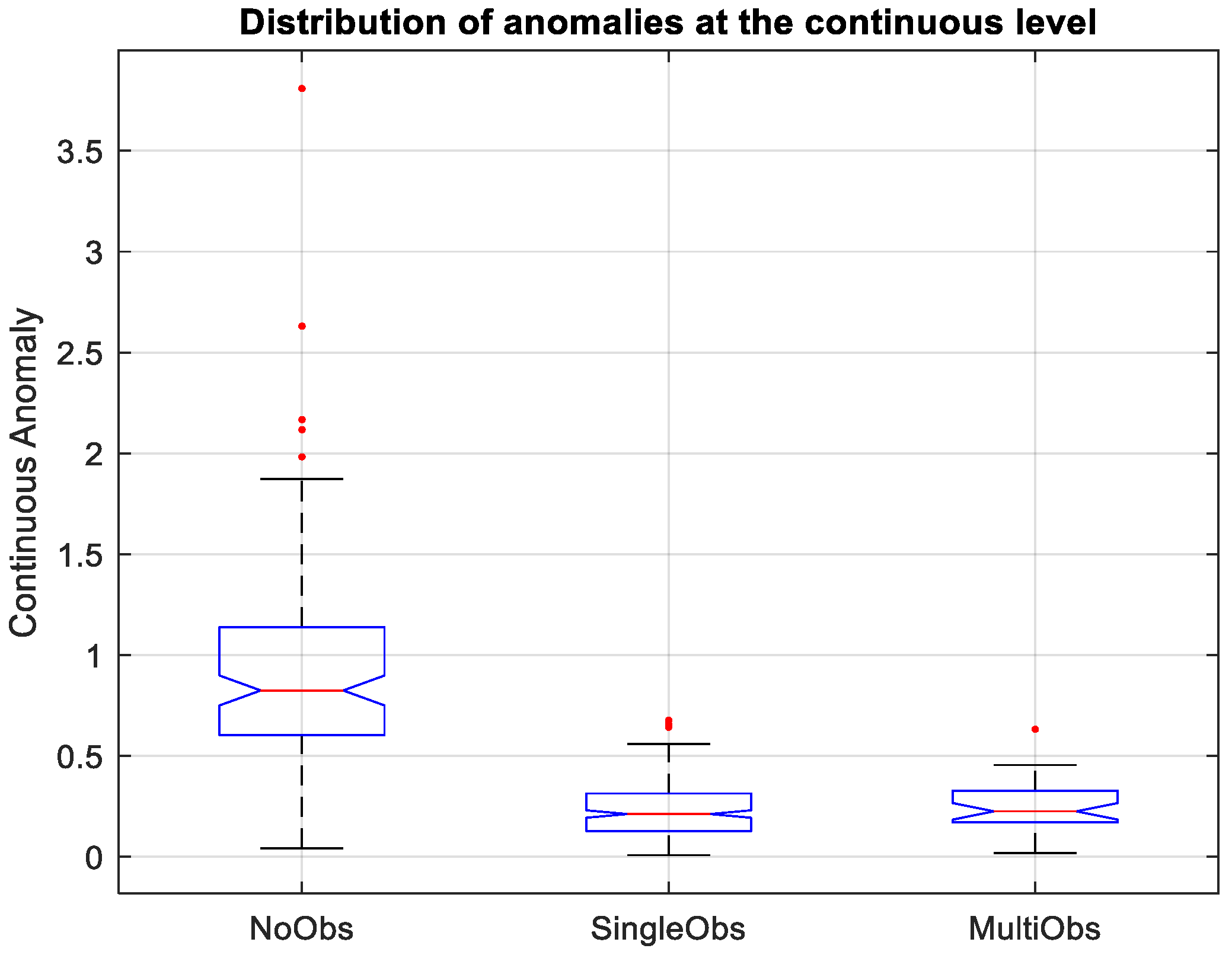
4.2. Localization Results Using a Combined Dictionary
4.3. Computational Efficiency Analysis
- Cluster Matching Optimization: Only the most relevant clusters are matched using Bhattacharyya distance, significantly reducing the number of comparisons during track association.
- Selective Kalman Updates: Kalman filter prediction and update steps are performed exclusively for those clusters actively involved in interactions, avoiding unnecessary computations.
- Efficient MJPF Design: The Markov Jump Particle Filter marginalizes linear components within the state space, which reduces the number of particles and accelerates inference.
4.4. Ablation Study of Core Components
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
List of Abbreviations
| AV | Autonomous Vehicle |
| LiDAR | Light Detection and Ranging |
| MJPF | Markov Jump Particle Filter |
| DBN | Dynamic Bayesian Network |
| GNG | Growing Neural Gas |
| JPDA | Joint Probabilistic Data Association |
| NFF | Null Force Filter |
| KF | Kalman Filter |
| PF | Particle Filter |
| CLA | Continuous-Level Anomaly |
| KLDA | Kullback–Leibler Divergence Anomaly |
| KITTI | Karlsruhe Institute of Technology and Toyota Technological Institute dataset |
| MSE | Mean Squared Error |
| RMSE | Root Mean Squared Error |
| DBSCAN | Density-Based Spatial Clustering of Applications with Noise |
| CIFs | Covariance Intersection Filters |
| VAE | Variational Autoencoder |
| CMJPF | Coupled Markov Jump Particle Filter |
References
- Yurtsever, E.; Lambert, J.; Carballo, A.; Takeda, K. A survey of autonomous driving: Common practices and emerging technologies. IEEE Access 2020, 8, 58443–58469. [Google Scholar] [CrossRef]
- Chong, Y.S.; Tay, Y.H. Abnormal event detection in videos using spatiotemporal autoencoder. In Proceedings of the Advances in Neural Networks-ISNN 2017: 14th International Symposium, ISNN 2017, Sapporo, Hakodate, and Muroran, Hokkaido, Japan, 21–26 June 2017; Proceedings, Part II 14. Springer: Berlin/Heidelberg, Germany, 2017; pp. 189–196. [Google Scholar]
- Nozari, S.; Krayani, A.; Marin, P.; Marcenaro, L.; Gomez, D.M.; Regazzoni, C. Modeling autonomous vehicle responses to novel observations using hierarchical cognitive representations inspired active inference. Computers 2024, 13, 161. [Google Scholar] [CrossRef]
- Kotseruba, I.; Tsotsos, J.K. 40 years of cognitive architectures: Core cognitive abilities and practical applications. Artif. Intell. Rev. 2020, 53, 17–94. [Google Scholar] [CrossRef]
- Morin, A. Levels of consciousness and self-awareness: A comparison and integration of various neurocognitive views. Conscious. Cogn. 2006, 15, 358–371. [Google Scholar] [CrossRef] [PubMed]
- Alemaw, A.S.; Slavic, G.; Zontone, P.; Marcenaro, L.; Gomez, D.M.; Regazzoni, C. Modeling Interactions between Autonomous Agents in a Multi-Agent Self-Awareness Architecture. IEEE Trans. Multimed. 2025, 1–16. [Google Scholar] [CrossRef]
- Slavic, G.; Zontone, P.; Marcenaro, L.; Gómez, D.M.; Regazzoni, C. Vehicle localization in an explainable dynamic Bayesian network framework for self-aware agents. Inf. Fusion 2025, 122, 103136. [Google Scholar] [CrossRef]
- Janai, J.; Güney, F.; Behl, A.; Geiger, A. Computer vision for autonomous vehicles: Problems, datasets and state of the art. Found. Trends® Comput. Graph. Vis. 2020, 12, 1–308. [Google Scholar] [CrossRef]
- Van Brummelen, J.; O’brien, M.; Gruyer, D.; Najjaran, H. Autonomous vehicle perception: The technology of today and tomorrow. Transp. Res. Part C Emerg. Technol. 2018, 89, 384–406. [Google Scholar] [CrossRef]
- Aminosharieh Najafi, T.; Affanni, A.; Rinaldo, R.; Zontone, P. Drivers’ Mental Engagement Analysis Using Multi-Sensor Fusion Approaches Based on Deep Convolutional Neural Networks. Sensors 2023, 23, 7346. [Google Scholar] [CrossRef]
- Zontone, P.; Affanni, A.; Piras, A.; Rinaldo, R. Convolutional Neural Networks Using Scalograms for Stress Recognition in Drivers. In Proceedings of the 2023 31st European Signal Processing Conference (EUSIPCO), Helsinki, Finland, 4–8 September 2023; pp. 1185–1189. [Google Scholar]
- Lo Grasso, A.; Zontone, P.; Rinaldo, R.; Affanni, A. Advanced Necklace for Real-Time PPG Monitoring in Drivers. Sensors 2024, 24, 5908. [Google Scholar] [CrossRef]
- Abbasi, R.; Bashir, A.K.; Alyamani, H.J.; Amin, F.; Doh, J.; Chen, J. Lidar point cloud compression, processing and learning for autonomous driving. IEEE Trans. Intell. Transp. Syst. 2022, 24, 962–979. [Google Scholar] [CrossRef]
- Xie, X.; Bai, L.; Huang, X. Real-time LiDAR point cloud semantic segmentation for autonomous driving. Electronics 2021, 11, 11. [Google Scholar] [CrossRef]
- Adnan, M.; Slavic, G.; Martin Gomez, D.; Marcenaro, L.; Regazzoni, C. Systematic and Comprehensive Review of Clustering and Multi-Target Tracking Techniques for LiDAR Point Clouds in Autonomous Driving Applications. Sensors 2023, 23, 6119. [Google Scholar] [CrossRef] [PubMed]
- Luo, C.; Yang, X.; Yuille, A. Exploring simple 3d multi-object tracking for autonomous driving. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 10488–10497. [Google Scholar]
- Zermas, D.; Izzat, I.; Papanikolopoulos, N. Fast segmentation of 3d point clouds: A paradigm on lidar data for autonomous vehicle applications. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; IEEE: New York, NY, USA, 2017; pp. 5067–5073. [Google Scholar]
- Liu, Z.; Cai, Y.; Wang, H.; Chen, L. Surrounding objects detection and tracking for autonomous driving using LiDAR and radar fusion. Chin. J. Mech. Eng. 2021, 34, 1–12. [Google Scholar] [CrossRef]
- Hamieh, I.; Myers, R.; Rahman, T. LiDAR Based Classification Optimization of Localization Policies of Autonomous Vehicles; Technical report, SAE Technical Paper; SAE International: Warrendale, PA, USA, 2020. [Google Scholar]
- Kumar, G.A.; Lee, J.H.; Hwang, J.; Park, J.; Youn, S.H.; Kwon, S. LiDAR and camera fusion approach for object distance estimation in self-driving vehicles. Symmetry 2020, 12, 324. [Google Scholar] [CrossRef]
- Sualeh, M.; Kim, G.W. Dynamic multi-lidar based multiple object detection and tracking. Sensors 2019, 19, 1474. [Google Scholar] [CrossRef]
- Nunes, L.; Wiesmann, L.; Marcuzzi, R.; Chen, X.; Behley, J.; Stachniss, C. Temporal consistent 3d lidar representation learning for semantic perception in autonomous driving. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 5217–5228. [Google Scholar]
- Regazzoni, C.S.; Marcenaro, L.; Campo, D.; Rinner, B. Multisensorial generative and descriptive self-awareness models for autonomous systems. Proc. IEEE 2020, 108, 987–1010. [Google Scholar] [CrossRef]
- Schütz, A.; Sánchez-Morales, D.E.; Pany, T. Precise positioning through a loosely-coupled sensor fusion of GNSS-RTK, INS and LiDAR for autonomous driving. In Proceedings of the 2020 IEEE/ION Position, Location and Mavigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; IEEE: New York, NY, USA, 2020; pp. 219–225. [Google Scholar]
- Tang, L.; Shi, Y.; He, Q.; Sadek, A.W.; Qiao, C. Performance test of autonomous vehicle lidar sensors under different weather conditions. Transp. Res. Rec. 2020, 2674, 319–329. [Google Scholar] [CrossRef]
- Chen, X. LiDAR-Based Semantic Perception for Autonomous Vehicles. Ph.D. Thesis, Universitäts-und Landesbibliothek Bonn, Bonn, Germany, 2022. [Google Scholar]
- Li, F.; Fu, C.; Sun, D.; Li, J.; Wang, J. SD-SLAM: A semantic SLAM approach for dynamic scenes based on LiDAR point clouds. Big Data Res. 2024, 36, 100463. [Google Scholar] [CrossRef]
- Tian, X.; Zhu, Z.; Zhao, J.; Tian, G.; Ye, C. DL-SLOT: Dynamic lidar slam and object tracking based on collaborative graph optimization. arXiv 2022, arXiv:2212.02077. [Google Scholar]
- Adnan, M.; Zontone, P.; Marcenaro, L.; Gómez, D.M.; Regazzoni, C. Classifying Static and Dynamic Tracks for LiDAR-Based Navigation of Autonomous Vehicle Systems. In Proceedings of the 2024 9th International Conference on Frontiers of Signal Processing (ICFSP), Paris, France, 12–14 September 2024; IEEE: New York, NY, USA, 2024; pp. 111–117. [Google Scholar]
- Liu, T.; Xu, C.; Qiao, Y.; Jiang, C.; Yu, J. Particle filter slam for vehicle localization. arXiv 2024, arXiv:2402.07429. [Google Scholar]
- Farag, W. Real-time autonomous vehicle localization based on particle and unscented kalman filters. J. Control Autom. Electr. Syst. 2021, 32, 309–325. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y.; Sun, Z. LiDiff: Generative Diffusion Model for LiDAR-based Human Motion Forecasting. arXiv 2023, arXiv:2301.04556. [Google Scholar]
- Xu, Q.; Pang, Y.; Liu, Y. Air traffic density prediction using Bayesian ensemble graph attention network (BEGAN). Transp. Res. Part C Emerg. Technol. 2023, 153, 104225. [Google Scholar] [CrossRef]
- Giuliari, F.; Hasan, I.; Cristani, M.; Galasso, F. Transformer Networks for Trajectory Forecasting. In Proceedings of the 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021. [Google Scholar]
- Adnan, M.; Zontone, P.; Marcenaro, L.; Gómez, D.M.; Regazzoni, C. Autonomous Vehicle Localization via LiDAR-Based Classification of Dynamic and Static Tracks in Complex Environments. In Proceedings of the IEEE International Joint Conference on Neural Networks (IJCNN 2025), Rome, Italy, 30 June–5 July 2025. [Google Scholar]
- Aksoy, E.E.; Baci, S.; Cavdar, S. Salsanet: Fast road and vehicle segmentation in lidar point clouds for autonomous driving. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 19 October–13 November 2020; IEEE: New York, NY, USA, 2020; pp. 926–932. [Google Scholar]
- Wang, Y.; Mao, Q.; Zhu, H.; Deng, J.; Zhang, Y.; Ji, J.; Li, H.; Zhang, Y. Multi-modal 3d object detection in autonomous driving: A survey. Int. J. Comput. Vis. 2023, 131, 2122–2152. [Google Scholar] [CrossRef]
- Alaba, S.Y.; Ball, J.E. A survey on deep-learning-based lidar 3d object detection for autonomous driving. Sensors 2022, 22, 9577. [Google Scholar] [CrossRef] [PubMed]
- Haidar, S.A.; Chariot, A.; Darouich, M.; Joly, C.; Deschaud, J.E. Are We Ready for Real-Time LiDAR Semantic Segmentation in Autonomous Driving? arXiv 2024, arXiv:2410.08365. [Google Scholar]
- Guo, Y.; Wang, H.; Hu, Q.; Liu, H.; Liu, L.; Bennamoun, M. Deep learning for 3d point clouds: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 4338–4364. [Google Scholar] [CrossRef]
- Fang, S.; Li, H.; Yang, M. LiDAR SLAM based multivehicle cooperative localization using iterated split CIF. IEEE Trans. Intell. Transp. Syst. 2022, 23, 21137–21147. [Google Scholar] [CrossRef]
- Akai, N.; Hirayama, T.; Murase, H. Persistent homology in LiDAR-based ego-vehicle localization. In Proceedings of the 2021 IEEE Intelligent Vehicles Symposium (IV), Nagoya, Japan, 11–17 July 2021; IEEE: New York, NY, USA, 2021; pp. 889–896. [Google Scholar]
- Liu, K.; Zhou, X.; Chen, B.M. An enhanced lidar inertial localization and mapping system for unmanned ground vehicles. In Proceedings of the 2022 IEEE 17th International Conference on Control & Automation (ICCA), Naples, Italy, 27–30 June 2022; IEEE: New York, NY, USA, 2022; pp. 587–592. [Google Scholar]
- Hong, Z.; Petillot, Y.; Wallace, A.; Wang, S. RadarSLAM: A robust simultaneous localization and mapping system for all weather conditions. Int. J. Robot. Res. 2022, 41, 519–542. [Google Scholar] [CrossRef]
- He, Y.; Liang, S.; Rui, X.; Cai, C.; Wan, G. Egovm: Achieving precise ego-localization using lightweight vectorized maps. arXiv 2023, arXiv:2307.08991. [Google Scholar]
- Marín-Plaza, P.; Beltrán, J.; Hussein, A.; Musleh, B.; Martín, D.; de la Escalera, A.; Armingol, J.M. Stereo vision-based local occupancy grid map for autonomous navigation in ros. In Proceedings of the International Conference on Computer Vision Theory and Applications, Rome, Italy, 27–29 February 2016; SciTePress: Setúbal, Portugal, 2016; Volume 4, pp. 701–706. [Google Scholar]
- Behley, J.; Garbade, M.; Milioto, A.; Quenzel, J.; Behnke, S.; Stachniss, C.; Gall, J. SemanticKITTI: A Dataset for Semantic Scene Understanding of LiDAR Sequences. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 9297–9307. [Google Scholar]
- Himmelsbach, M.; Hundelshausen, F.V.; Wuensche, H.J. Fast segmentation of 3D point clouds for ground vehicles. In Proceedings of the 2010 IEEE Intelligent Vehicles Symposium, La Jolla, CA, USA, 21–24 June 2010; IEEE: New York, NY, USA, 2010; pp. 560–565. [Google Scholar]
- Arya Senna Abdul Rachman, A. 3D-LIDAR Multi Object Tracking for Autonomous Driving: Multi-Target Detection and Tracking Under Urban Road Uncertainties. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2017. [Google Scholar]
- Slavic, G.; Marin, P.; Martin, D.; Marcenaro, L.; Regazzoni, C. Interpretable anomaly detection using a generalized Markov Jump particle filter. In Proceedings of the 2021 IEEE International Conference on Autonomous Systems (ICAS), Montréal, QC, Canada, 11–13 August 2021; IEEE: New York, NY, USA, 2021; pp. 1–5. [Google Scholar]
- Slavic, G.; Plaza, P.M.; Marcenaro, L.; Gómez, D.M.; Regazzoni, C. Simultaneous Localization and Anomaly Detection from First-Person Video Data through a Coupled Dynamic Bayesian Network Model. In Proceedings of the 2022 18th IEEE International Conference on Advanced Video and Signal Based Surveillance (AVSS), Madrid, Spain, 29 November–2 December 2022; IEEE: New York, NY, USA, 2022; pp. 1–8. [Google Scholar]
- Christodoulou, L.; Kasparis, T.; Marques, O. Advanced statistical and adaptive threshold techniques for moving object detection and segmentation. In Proceedings of the 2011 17th International Conference on Digital Signal Processing (DSP), Corfu, Greece, 6–8 July 2011; IEEE: New York, NY, USA, 2011; pp. 1–6. [Google Scholar]
- Amin, F.; Mahmoud, M. Confusion matrix in binary classification problems: A step-by-step tutorial. J. Eng. Res. 2022, 6, 1. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The KITTI vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; IEEE: New York, NY, USA, 2012; pp. 3354–3361. [Google Scholar]

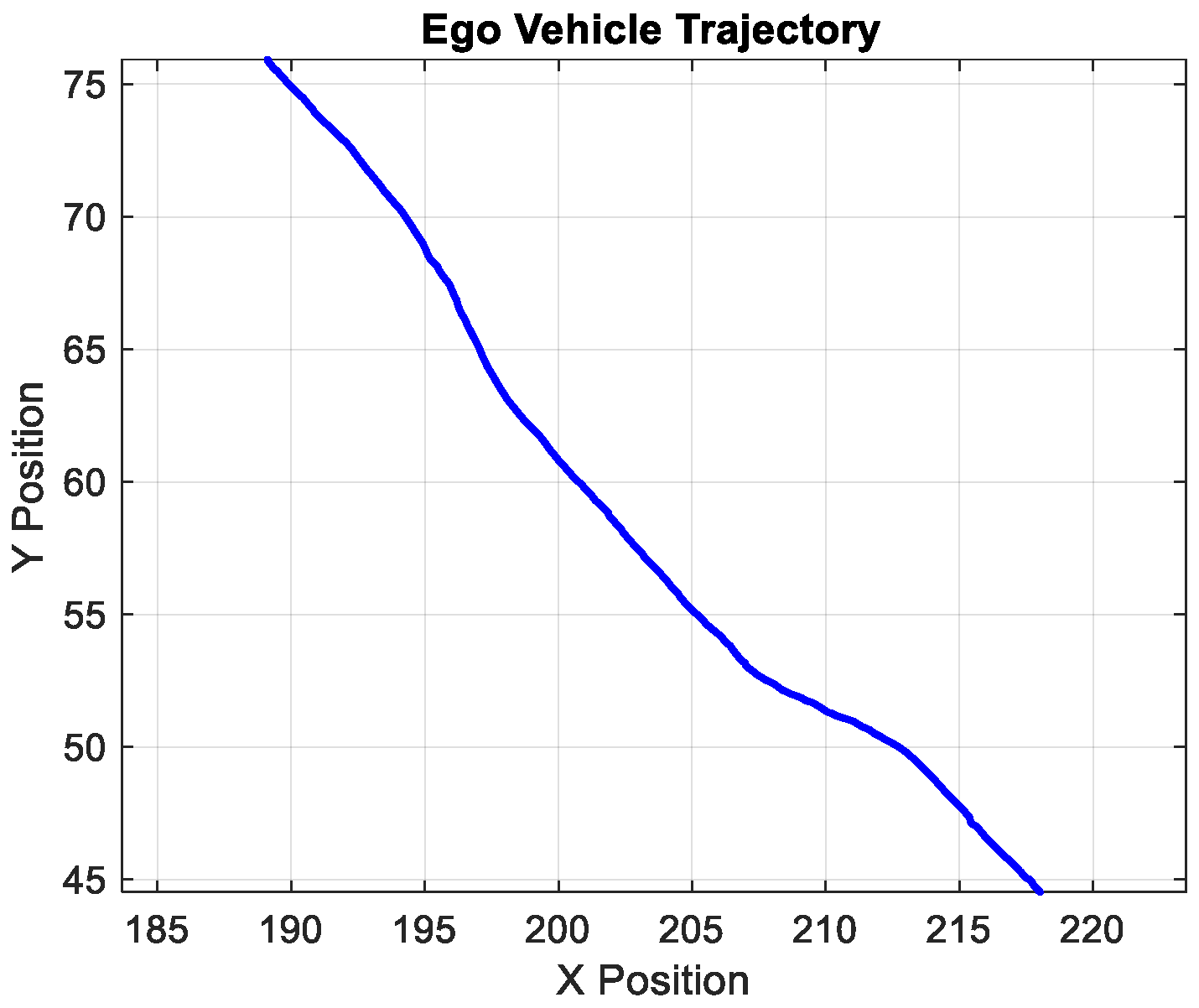
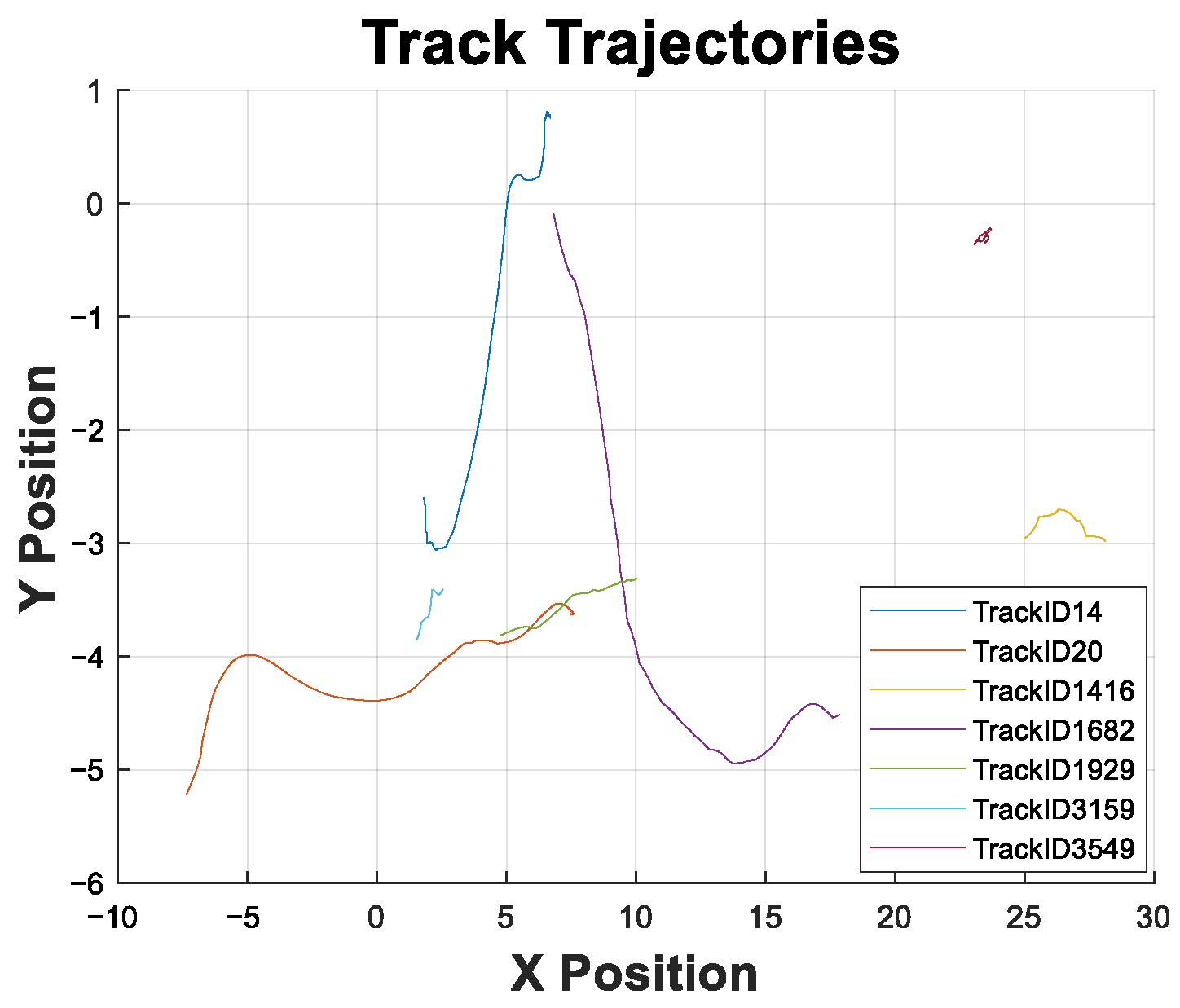
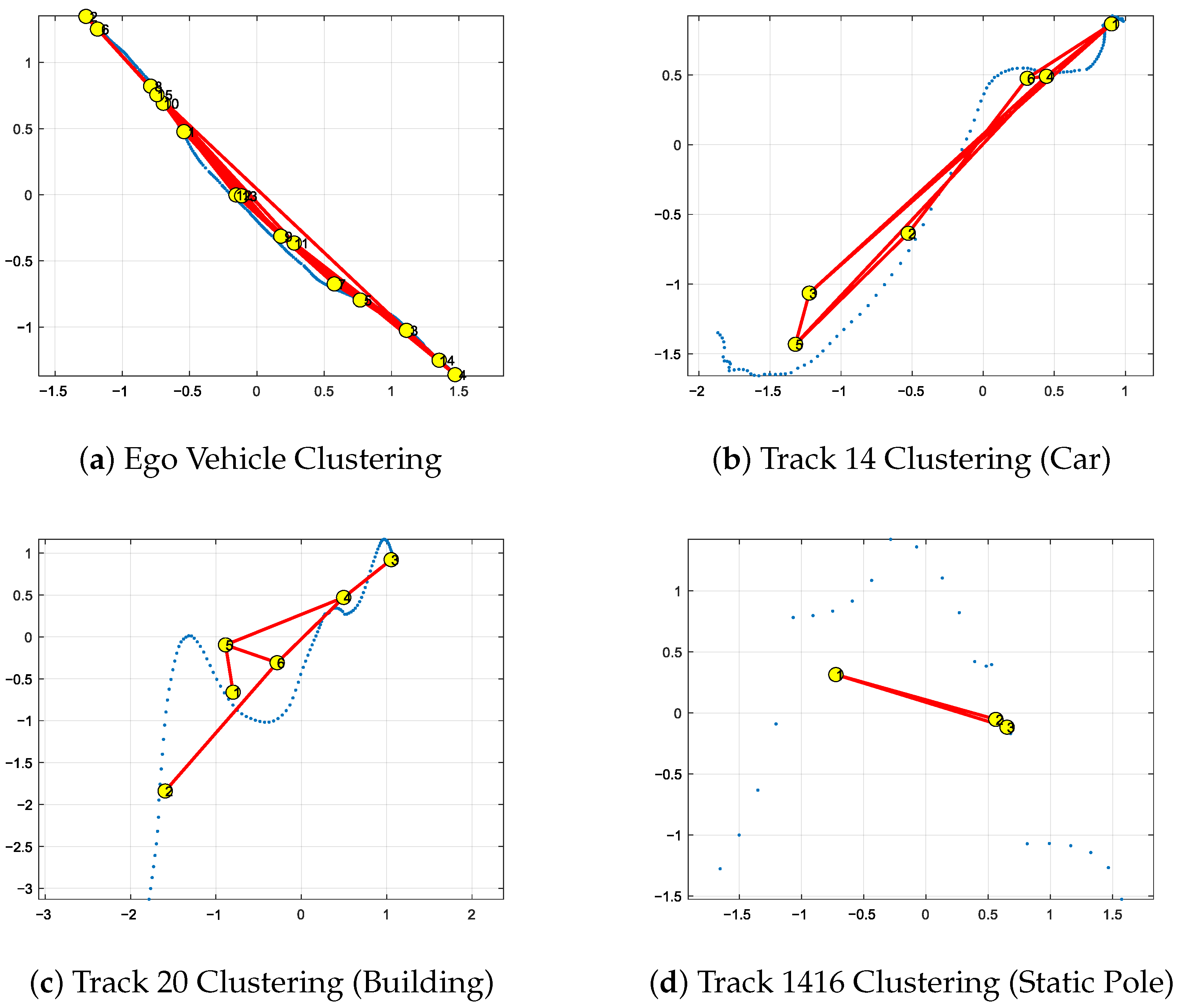
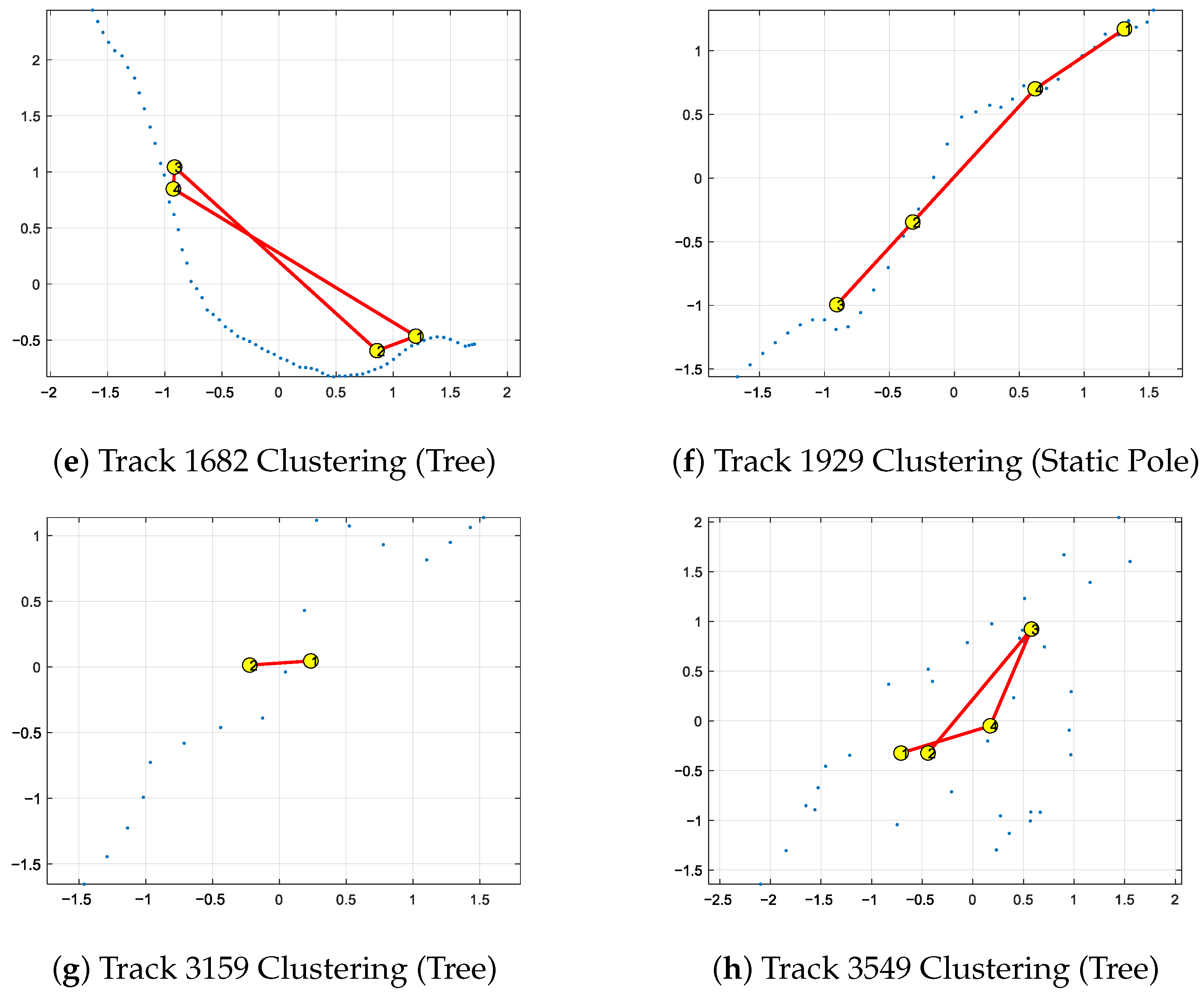
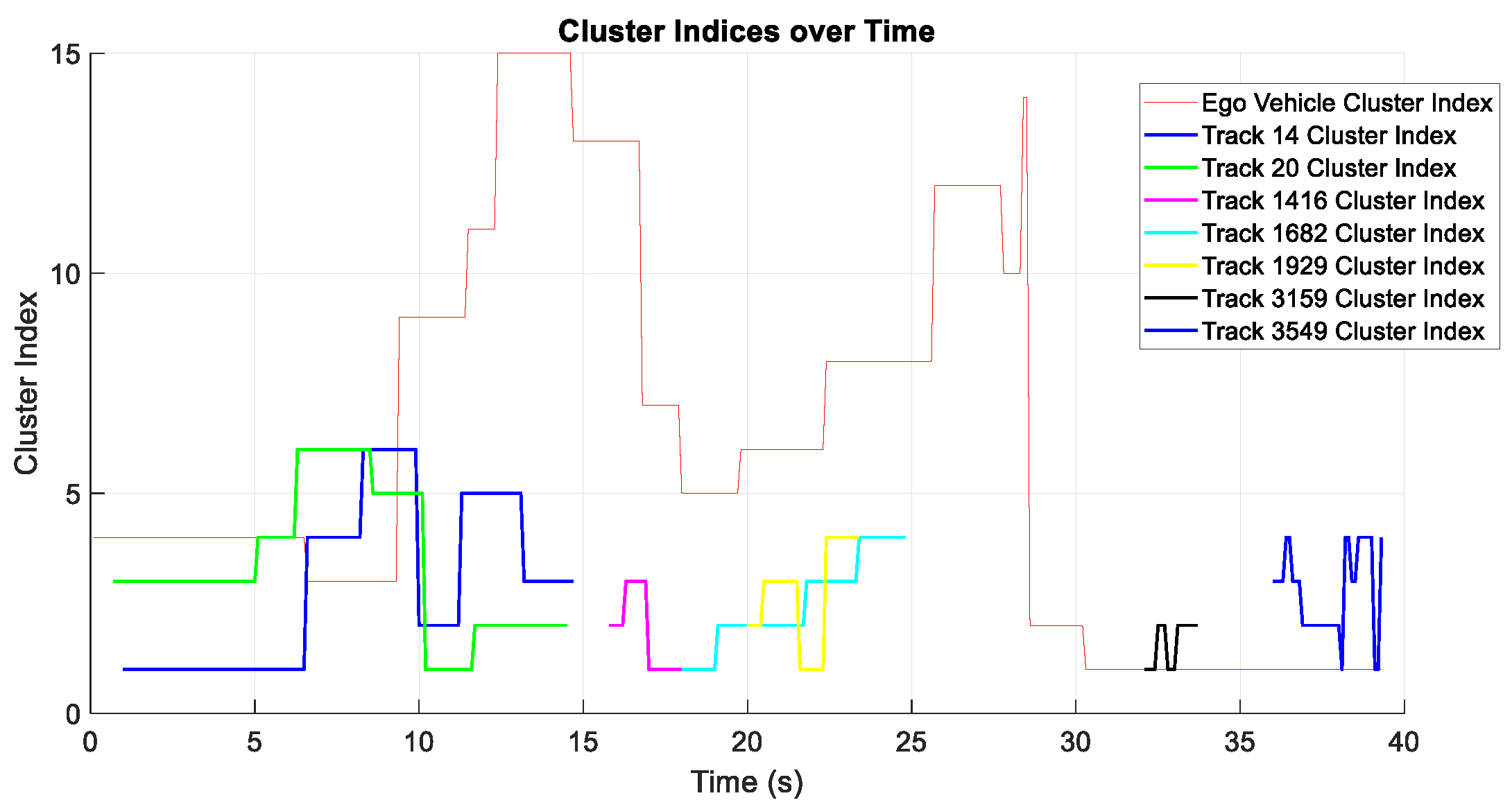
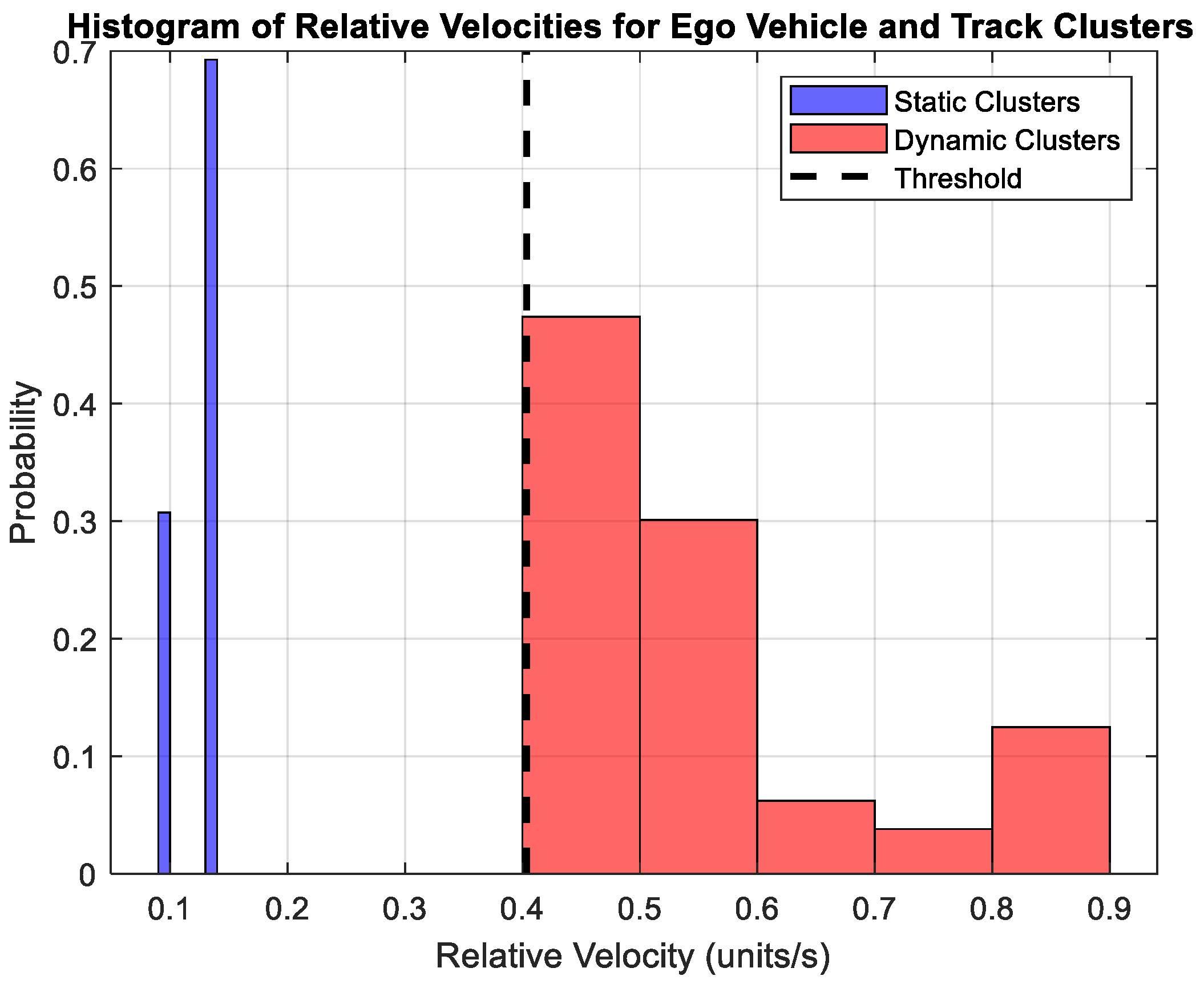


| Time (s) | Track Cluster | Label | Ego Cluster | Ego x Position (m) | Ego y Position (m) |
|---|---|---|---|---|---|
| 0.1000 | 4 | 0 | 0 | 218.0021 | 44.5398 |
| 0.2000 | 4 | 0 | 0 | 218.0051 | 44.5382 |
| 0.3000 | 4 | 0 | 0 | 218.0092 | 44.5362 |
| 0.4000 | 4 | 0 | 0 | 218.0013 | 44.5405 |
| 0.5000 | 4 | 0 | 0 | 217.9974 | 44.5423 |
| 0.6000 | 4 | 0 | 0 | 217.9942 | 44.5441 |
| 0.7000 | 4 | 0 | 0 | 217.9893 | 44.5475 |
| 0.8000 | 4 | 0 | 0 | 217.9881 | 44.5494 |
| 0.9000 | 4 | 0 | 0 | 217.9875 | 44.5504 |
| 1.0000 | 4 | 1 | 5 | 217.9887 | 44.5512 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| Step | Description |
|---|---|
| 1 | Temporal Alignment: Synchronize LiDAR and odometry timestamps to associate ego and track observations frame-wise. |
| 2 | Track Association: Identify active TrackIDs using the JPDA filter at each frame. |
| 3 | Cluster Assignment: Assign ego and track positions to their respective GNG clusters to extract cluster indices. |
| 4 | Interaction Labeling: If ego and track positions fall within a defined spatial proximity, label the interaction as ; otherwise . |
| 5 | Dictionary Population: Store the interaction entry as , where is the ego vehicle position. |
| Module | Parameter | Description and Value |
|---|---|---|
| JPDA Tracker | Gating threshold | 0.8 (based on Mahalanobis distance) |
| Confirmation count | 3 consecutive detections required | |
| Missed detection tolerance | Up to 5 missed updates allowed | |
| GNG Clustering | Maximum number of nodes | 100 (adaptive per trajectory length) |
| Learning rate (winner) | 0.05 | |
| Learning rate (neighbor) | 0.0006 | |
| Maximum edge age | 50 iterations | |
| Node insertion interval | Every 100 steps | |
| Error decay factor | 0.0005 |
| Metric | iCAB | KITTI |
|---|---|---|
| Accuracy | 87% | 82% |
| Precision | 88% | 80% |
| Recall | 94% | 89% |
| F1 Score | 91% | 85% |
| Method | Mean Error (m) |
|---|---|
| Full Framework (MJPF + Combined Dictionary) | 0.17 |
| Without Combined Dictionary (Single Track Only) | 0.23 |
| Without MJPF (Kalman Only) | 0.29 |
| Without Dictionary (Odometry Only, No LiDAR) | 0.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adnan, M.; Zontone, P.; Martín Gómez, D.; Marcenaro, L.; Regazzoni, C. A Generative Model Approach for LiDAR-Based Classification and Ego Vehicle Localization Using Dynamic Bayesian Networks. Appl. Sci. 2025, 15, 5181. https://doi.org/10.3390/app15095181
Adnan M, Zontone P, Martín Gómez D, Marcenaro L, Regazzoni C. A Generative Model Approach for LiDAR-Based Classification and Ego Vehicle Localization Using Dynamic Bayesian Networks. Applied Sciences. 2025; 15(9):5181. https://doi.org/10.3390/app15095181
Chicago/Turabian StyleAdnan, Muhammad, Pamela Zontone, David Martín Gómez, Lucio Marcenaro, and Carlo Regazzoni. 2025. "A Generative Model Approach for LiDAR-Based Classification and Ego Vehicle Localization Using Dynamic Bayesian Networks" Applied Sciences 15, no. 9: 5181. https://doi.org/10.3390/app15095181
APA StyleAdnan, M., Zontone, P., Martín Gómez, D., Marcenaro, L., & Regazzoni, C. (2025). A Generative Model Approach for LiDAR-Based Classification and Ego Vehicle Localization Using Dynamic Bayesian Networks. Applied Sciences, 15(9), 5181. https://doi.org/10.3390/app15095181












