Abstract
Graph neural networks (GNNs) are widely used for graph-structured data. However, GNNs are vulnerable to membership inference attacks (MIAs) in graph classification tasks, which determine whether a graph was in the training set, risking the leakage of sensitive data. Existing MIAs rely on prediction probability vectors, but they become ineffective when only prediction labels are available. We propose a Graph-level Label-Only Membership Inference Attack (GLO-MIA), which is based on the intuition that the target model’s predictions on training data are more stable than those on testing data. GLO-MIA generates a set of perturbed graphs for the target graph by adding perturbations to its effective features and queries the target model with the perturbed graphs to obtain their prediction labels, which are then used to calculate the robustness score of the target graph. Finally, by comparing the robustness score with a predefined threshold, the membership of the target graph can be inferred correctly with high probability. Experimental evaluations on three datasets and four GNN models demonstrate that GLO-MIA achieves an attack accuracy of up to 0.825, outperforming baseline work by 8.5% and closely matching the performance of probability-based MIAs, even with only prediction labels.
1. Introduction
Graph-structured data are widespread in numerous fields in the real world, including biology [1], social networks [2], and other fields. However, the non-Euclidean nature of these data makes their analysis more challenging. In recent years, graph neural networks (GNNs) have been widely applied to various tasks related to graph structures, such as node classification [3], link prediction [4,5], graph classification [6], etc., due to their ability to capture hidden patterns in graph-structured data, and they have achieved state-of-the-art performance. However, the risk of privacy leakage from GNNs has raised significant concerns.
Previous studies have shown that GNNs are vulnerable to a privacy attack called a membership inference attack (MIA) [7,8,9,10,11], where the adversary can infer whether the given data have been used for the training of the model, leading to serious privacy leakage, especially in sensitive applications. For example, in drug research, where the training data include protein interaction networks and molecular properties, the adversary can leverage the model’s prediction probability vectors to infer whether specific proteins or molecules are used in the training set, leaking sensitive molecular data or compromising drug development confidentiality. Therefore, it is important and urgent to study membership inference attacks against GNNs.
Membership inference attacks exploit the model’s memorization of the training data, finding the differences in the model’s output between the training data (members) and the testing data (non-members) to infer membership. In graph classification tasks, MIAs aim to infer the membership of the given graph. Existing MIAs usually utilize prediction probability vectors to infer membership. However, if GNNs only provide prediction labels rather than probability vectors, these MIAs become ineffective. The label-only scenarios for GNNs are widely prevalent and more practical for MIAs, for example, molecular activity or toxicity prediction systems only output binary labels (e.g., active/inactive, toxic/non-toxic), not probability vectors. Therefore, it is necessary to investigate whether there exists an MIA threat against GNNs in graph classification tasks when only prediction labels are available to the adversary, which, to the best of our knowledge, remains insufficiently explored.
We propose a Graph-level Label-Only Membership Inference Attack (GLO-MIA) against GNNs, revealing the vulnerability of GNNs to such threats. Specifically, given a target graph, GLO-MIA generates a set of perturbed graphs based on the target graph. Then, these perturbed graphs are used to query the target model to obtain their prediction labels. Next, the robustness score of the target graph is calculated based on these prediction labels. Finally, the robustness score of the target graph is compared with a predefined threshold. If it is greater than the threshold, the target graph is considered a member; otherwise, it is considered a non-member. In the label-only scenario, the adversary cannot use sufficient model information for membership inference, but the adversary can utilize a shadow dataset with a distribution similar to the target dataset to train a shadow model that mimics the behavior of the target model. GLO-MIA leverages the shadow model to determine the perturbation magnitude and threshold to distinguish members and non-members. Due to the diverse feature distributions and types of graph data, we propose a general perturbation method that applies small, uniformly sampled numerical values to the graph’s effective features.
The performance of GLO-MIA is evaluated on four GNN models and three datasets. The experimental results show that GLO-MIA achieves an accuracy of up to 0.825, surpassing the baseline work by up to 8.5%. Even using only prediction labels, GLO-MIA achieves performance close to that of probability-based MIAs. Furthermore, we analyze the impact of perturbation magnitude and the number of perturbed graphs on the attack performance. Finally, we discuss the impact of regularization techniques as a possible defense against GLO-MIA.
In summary, our main contributions are as follows:
- We propose GLO-MIA, which, to the best of our knowledge, is the first label-only membership inference attack against graph neural networks in graph classification tasks, revealing the vulnerability of GNNs to such threats.
- We propose a general perturbation method to implement GLO-MIA, which infers membership by leveraging the robustness of graph samples to the perturbations.
- We evaluate GLO-MIA using four representative GNN methods on three real-world datasets and analyze the factors that influence attack performance. Experimental results show that GLO-MIA can achieve an attack accuracy of up to 0.825, outperforming baselines by up to 8.5%. Even in the most restrictive black-box scenario, GLO-MIA achieves performance comparable to that of probability-based MIAs that utilize prediction probability vectors of the model.
2. Background
In this section, we introduce the basic notations of graph neural networks (GNNs) and describe four representative GNN models.
2.1. Notations
We define an undirected, unweighted attributed graph as , where is the set of all nodes in the graph; represents the number of the nodes; and E is the set of edges, where represents the number of edges. For any two nodes , indicates that there exists an edge between and . A is the adjacency matrix of the graph. If , ; otherwise, . represents the feature matrix of the nodes in the graph, where d is the feature dimension.
2.2. Graph Neural Networks
Graph neural networks (GNNs) are a class of neural networks specifically designed to handle graph-structured data. They take the node feature matrix and the graph topology structure as inputs to learn the representation of a single node or the entire graph. Most of the existing GNNs utilize the message passing mechanism. By iteratively performing the “aggregate–update” operation, node embeddings are generated. After l aggregation iterations, the node representation captures the information of l-hop neighbors. The lth layer of a GNN can be expressed as follows:
where represents the embedding of node at the lth layer, denotes the set of neighbors of node , aggregates information from node and its neighbors, and applies a nonlinear transformation to the aggregated information. The differences among GNN models primarily lie in the implementation strategies of these two functions. We select four GNNs, including Graph Convolutional Network (GCN) [3], Graph Attention Network (GAT) [12], SAmple and aggreGatE (GraphSAGE) [13], and Graph Isomorphism Network (GIN) [6].
GCN employs symmetric normalization, and the node embedding is represented as follows:
where and . The embedding of each node aggregates as a weighted average of the node itself and its neighboring nodes; is the activation function, which generates new embeddings from the aggregated results.
GAT employs an attention mechanism, and the node embedding is represented as follows:
where represents the attention coefficient between node pairs, indicating the strength of the connection between nodes.
GraphSAGE characterizes the central node by aggregating information from a fixed number of randomly sampled neighbor nodes. It supports various aggregation methods, including mean aggregation, LSTM-based aggregation, and max-pooling aggregation. In our work, we employ mean aggregation, and the node embedding is represented as follows:
where denotes the mean aggregation function.
GIN is based on graph isomorphism testing, and its aggregation method preserves the strict distinguishability of neighbor features. The current node embedding is summed with the aggregation results and then passed through a multilayer perceptron (MLP):
where is a learnable parameter used to adjust the weight of the central node.
After obtaining the final node embeddings, GNNs can perform tasks such as node classification, link prediction, and graph classification. This paper focuses on graph classification, where GNNs aggregate all node embeddings into a single graph-level embedding using a readout layer, represented as follows:
where represents a readout function.
3. Related Work
In this section, we discuss the related work on membership inference attacks (MIAs).
In recent years, various privacy attacks have been instantiated on graph neural networks (GNNs), which can be generally categorized into four types based on the adversary’s targets: Model stealing attacks aim to obtain a substitute model that has similar predictions to the target model [14,15]. Property inference attacks aim to reveal sensitive data properties [16,17]. Graph reconstruction attacks aim to reconstruct the structure of the target graph [16,18,19]. Membership inference attacks aim to determine whether any given data record was used in the training of the target model [7,8,9,10,11].
Membership inference attacks are generally categorized into two types: training-based MIAs and threshold-based MIAs. Training-based MIAs use shadow models and shadow datasets to construct attack features and train an attack model to infer membership. Threshold-based MIAs compare scores (e.g., maximum confidence and prediction cross-entropy) with a predefined threshold to infer the membership of data. In the field of traditional machine learning, extensive research on membership inference attacks has been conducted [20,21,22,23,24,25].
Membership inference attacks on GNNs have attracted increasing attention. MIAs on GNNs include node-level [7,11], link-level [26], and graph-level MIAs [9,10]. Node-level MIAs determine the membership of a node. Link-level MIAs focus on determining whether a link between two nodes exists in the training graph. Graph-level MIAs identify the membership of an entire graph.
In graph-level MIAs, the adversary usually utilizes the difference in the output distribution of the target model between members and non-members. Wu et al. [9] proposed the first graph-level black-box MIA in graph classification tasks, leveraging the model’s prediction probability vectors to construct attack features and training a binary classifier. They also introduced multiple types of probability-based metrics to assess membership privacy leakage. Yang et al. [10] proposed combining one-hot class labels with prediction probability vectors as attack features to train the attack model. Furthermore, they utilized a class-dependent threshold to implement the attack based on modified prediction entropy. However, existing MIAs rely on the model providing prediction probability vectors and cannot be implemented when the model only outputs prediction labels.
Research on label-only membership inference attacks on graphs is still insufficient, but in non-graph domains, several studies have explored label-only MIAs [23,24,27,28,29]. In the graph domain, Conti et al. [11] utilized the fixed properties of a node, the prediction correctness of the target model, the node’s features and neighborhood information to construct attack features, training an attack model to identify the membership of the node. However, graph-level label-only MIAs remain insufficiently explored. Therefore, we propose GLO-MIA, the first label-only membership inference attack against graph classification tasks.
4. Graph-Level Label-Only Membership Inference Attack
In this section, we introduce the threat model and implementation details of our GLO-MIA.
4.1. Threat Model
4.1.1. Formalization of the Problem
In the graph classification tasks of GNNs, membership inference attacks aim to determine whether a given graph belongs to the training set of the target GNN model. Formally, given a trained target GNN model that only provides the prediction labels, a target graph , and the external knowledge obtained by the adversary, our attack can be expressed as follows:
where 1 indicates is in the training set of , while 0 indicates the opposite.
4.1.2. Adversary’s Knowledge and Capability
Label-Only Black-Box Setting. It is assumed that the adversary cannot access the parameters or internal representations of the target model and can only query the target model. The target model only provides prediction labels rather than prediction probability vectors. This represents a realistic scenario that is the most restrictive scenario, making it significantly more challenging for the adversary to attack.
Shadow Dataset and Shadow Model. It is assumed that the adversary owns a shadow dataset from the same domain as the target model’s training dataset, with no overlap between the shadow and target datasets. Additionally, the adversary knows the architecture and training algorithm of the target model, as well as the membership and non-membership status of the samples in the shadow dataset used for the shadow model. The adversary can use the shadow dataset to train a shadow model with the same architecture as the target model to mimic its behavior.
4.2. Attack Methodology
4.2.1. Attack Intuition
In the label-only setting, the adversary can obtain nothing more than the label-only output from the target model, making it impossible to rely on prediction probability vectors for the attack. Choquette-Choo et al. [24] evaluated the robustness of the model’s prediction labels under perturbations of the input to infer membership, and their proposed MIAs could be applied in the image, audio, and natural language domains. Inspired by their work, we infer membership of the target graph by calculating the robustness score, which is defined as follows:
where denotes the robustness score of a given target graph , the target graph corresponds to the ground-truth label y, is the label of predicted by the target model , is a set of perturbed graphs of , and is one of the perturbed graphs. represents the number of elements in . The function is the indicator function: if , it is recorded as 1; otherwise, it is 0. Graphs with relatively high robustness scores are considered members.
4.2.2. Attack Overview
Our attack process is shown in Figure 1; it consists of following three steps:
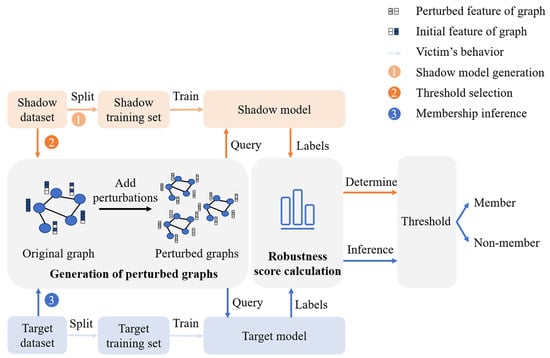
Figure 1.
Illustration of GLO-MIA (step 1: shadow model generation; step 2: threshold selection; step 3: membership inference).
(1) Shadow model generation. The adversary splits the shadow dataset into training and testing sets and trains a shadow model on the training set to mimic the target model’s behavior.
(2) Threshold selection.
- (a)
- The adversary generates a set of perturbed graphs for each shadow graph using Algorithm 1, as introduced in Section 4.2.3.
- (b)
- The adversary calculates robustness scores using the prediction labels via Equation (8), as introduced in Section 4.2.1.
- (c)
- The adversary labels the robustness scores of the shadow training data as “member” and those of the shadow testing data as “non-member” to construct the attack dataset, by which a threshold for the robustness score can be selected.
(3) Membership inference.
- (a)
- The adversary perturbs the target graph to generate a set of perturbed graphs.
- (b)
- The adversary calculates the robustness score of the target graph.
- (c)
- The adversary compares the robustness score of the target graph with the selected threshold. If the score is above the threshold, the graph is a member; otherwise, it is a non-member.
4.2.3. Generation of Perturbed Graphs
A method for generating perturbed graphs is proposed to distinguish between members and non-members by perturbing the effective (i.e., non-zero) features on the graph, as described in Algorithm 1. Specifically, our method consists of the following steps:
(1) Identify non-zero features. Given a target graph , its non-zero features are identified. The positions of non-zero features are indicated by , which is a boolean matrix with shape where the element value true indicates the presence of a non-zero value, while the element value false denotes a zero value (lines 1–2 in Algorithm 1).
(2) Adjust perturbation range. The perturbation range is initialized from to . A scaler s is used to adjust the perturbation range for different datasets. The perturbation range after adjustment is from to (line 3).
(3) Generate perturbed graphs. Initialize an empty set for storing perturbed graphs (line 4). Then, repeat the following steps (a) to (e) until N perturbed graphs have been generated (lines 5–12):
- (a)
- Create a copy of the input graph as to ensure that the perturbations are applied to without affecting (line 6).
- (b)
- Initialize the perturbation matrix (denoted by ) as a zero matrix of shape , where n and d represent the number of nodes and the feature dimension of the input graph, respectively. It stores perturbation values, which are calculated as follows (line 7):where is a random perturbation value uniformly sampled from the perturbation range that is adjusted by the scaler s.
- (c)
- Initialize the operator matrix (denoted by ) as a zero matrix of shape , and store the arithmetic operators at the non-zero feature positions indicated by . The arithmetic operators are generated according to the following equation (line 8):where is an integer randomly sampled between 0 and 1. The values of elements of the matrix can only be or , representing the addition or subtraction of a perturbation value.
- (d)
- Perform element-wise multiplication of perturbation values by their corresponding operators and add them to the features of , ensuring that perturbations are added only to non-zero features, while the others remain unchanged (lines 9–10).
- (e)
- Finally, add to the set , which is the set of perturbed graphs (line 11).
The perturbations that we perform are irrelevant to the feature types, and our purpose is to distinguish between members and non-members rather than to cause severe model misclassifications or to make the perturbations imperceptible.
| Algorithm 1 Generation_of_Perturbed_Graphs () |
|
4.2.4. Perturbation Magnitude Estimation and Threshold Selection
As described in Algorithm 1, a scaler s is used to adjust the perturbation range, which controls the perturbation magnitude of graphs. However, perturbations that are either too large or too small fail to identify the membership of the target graph, which is validated in Section 5.3. Therefore, appropriate perturbations need to be found to distinguish between members and non-members, which can be roughly estimated using the shadow dataset and model.
During estimation, s is gradually increased in small steps. At each step, the following processes are performed:
(1) Calculate the robustness scores of the shadow data using the current s.
(2) Label the robustness scores of the shadow training data as “member”, while labeling those of the shadow testing data as “non-member” to construct the attack dataset.
(3) Maximize the classification accuracy of distinguishing between shadow members and non-members under current s by iteratively selecting a threshold using the ROC curve. Record the current AUC and accuracy, which jointly reflect the classification performance of the estimation.
(4) If both the AUC and accuracy begin to decline, terminate the process, and record the last s and threshold before the decline for use in the attack on the target model. Otherwise, increment s by a small step and repeat steps (1) to (3).
5. Experiments
In this section, we systematically evaluate the performance of GLO-MIA. In Section 5.1, we introduce the experimental setup. In Section 5.2, we evaluate GLO-MIA using three graph classification datasets and four GNN models, and we compare the experimental results with those of the baselines. In Section 5.3, and Section 5.4, we analyze the impact of perturbation magnitude and the number of perturbed graphs on the performance of the proposed MIA, respectively. Finally, we investigate regularization techniques as a possible defense against GLO-MIA in Section 5.5.
5.1. Experimental Setup
5.1.1. Datasets
TUDataset [30] is a collection of benchmark datasets for graph classification and regression tasks. We evaluate GLO-MIA on three publicly available bioinformatics datasets from TUDataset, including DD [31], ENZYMES [32,33], and PROTEINS_full [31,32]. Each dataset consists of multiple independent graphs, which have different numbers of nodes and edges. Each graph is labeled for graph classification tasks.
The DD dataset is used to classify protein structures into enzymes and non-enzymes. The labels in the PROTEINS_full dataset show whether a protein is an enzyme. The ENZYMES dataset assigns enzymes to six classes, which reflect the catalyzed chemical reactions. The statistical details of these datasets are provided in Table 1.

Table 1.
Statistical information of datasets.
We randomly divide the dataset into two non-overlapping subsets, including the target dataset and the shadow dataset. To ensure fairness, we use training sets and testing sets of the same size. Training sets are constructed with randomly assigned samples: 150 for ENZYMES and 250 each for DD and PROTEINS_full.
5.1.2. Model Architectures and Training Settings
The experimental models are four popular GNN models, including GCN [3], GAT [12], GraphSAGE [13], and GIN [6]. All of these models are based on a two-layer architecture, which is a common setting in practice. We use the cross-entropy loss function and the Adam optimizer for training, with 1000 epochs and a batch size of 64. The implementation is developed in Python using PyTorch (v2.0.0) and PyTorch Geometric (v2.2.0) as the main development libraries.
5.1.3. Metrics
We adopt attack accuracy ( ACC) and the area under the ROC curve (AUC) as metrics to evaluate the attack performance of GLO-MIA.
(1) Attack accuracy (ACC): Attack accuracy (ACC) represents the percentage of all samples whose membership is inferred correctly by MIAs. It is calculated as follows:
(2) Area under the ROC curve (AUC): The area under the ROC curve (AUC) is computed as the area under the curve of the attack receiver operating characteristic (ROC), which is a threshold-independent metric.
5.1.4. Baselines
Our evaluation aims to confirm whether GLO-MIA outperforms the gap attack [21] and achieves performance comparable to that of probability-based MIAs based on prediction probability vectors [9,10], even if the adversary only uses the prediction labels rather than prediction probability vectors.
(1) Gap attack [21]. This is a naïve baseline commonly used for label-only MIAs [23,24]. It determines membership based on whether the target model’s prediction label is correct. Samples that are correctly predicted are regarded as members, while those incorrectly predicted are considered non-members. The attack accuracy of the gap attack is directly related to the gap between training and testing accuracy of the target model. If the adversary’s target data are equally likely to be members or non-members of the training set, the attack accuracy of the gap attack can be calculated as follows [24]:
where and are the accuracy of the target model on the training dataset and the testing dataset, respectively. If the model overfits its training data, which means it has higher accuracy on the training set, the gap attack will achieve non-trivial performance.
(2) Probability-based MIAs. We implement two advanced probability-based MIAs that utilize the prediction probability vectors of the target model in graph classification tasks.
- (a)
- Cross-entropy-based MIA [9]. This method assumes that the loss of members should be smaller than that of non-members.
- (b)
- Modified prediction entropy-based MIA [10]. This method assumes that members are expected to have lower modified prediction entropy than non-members.
5.2. Experimental Results
We train a shadow model with the same architecture as the target model using a non-overlapping shadow dataset that has the same distribution as the target dataset. Then, we apply GLO-MIA on different GNN models. The number of perturbed graphs is set to 1000 for each dataset, which ensures a sufficient number of perturbed samples for obtaining an appropriate threshold, thereby enabling GLO-MIA to achieve higher attack accuracy, as analyzed in Section 5.4. To avoid the impact of randomness, we conduct GLO-MIA five times in all experiments and report the average results.
We compare GLO-MIA with the gap attack, and the results are shown in Table 2. In Table 2, we record the “train–test gap”, which represents the gap between the training and testing classification accuracy to measure the overfitting of the target model. The best attack performance for each dataset is highlighted in bold. The experimental results show that GLO-MIA is effective on different GNN models and datasets. For example, on GraphSAGE trained on the DD dataset, it is possible to achieve an attack accuracy of 0.738, which is 5.6% higher than that of the gap attack. On the ENZYMES dataset, the highest attack accuracy can reach 0.825, which is 8.5% higher than that of the gap attack. Furthermore, our experimental results show that the attack performance on the GIN models is lower than that on other GNN models in most cases. For example, the attack accuracy achieved on GIN trained on the DD dataset is 0.713, surpassing that of the gap attack by only 2.5%, which is lower than those of other models on the DD dataset, even though it performs more overfitted (train–test gap = 0.376). This phenomenon is also observed on the ENZYMES dataset. These observations may suggest that GIN may have higher inherent robustness against GLO-MIA. In contrast, GraphSAGE is relatively more vulnerable to GLO-MIA, which is likely due to its aggregation mechanism being more sensitive to feature perturbations in graphs.

Table 2.
Comparison of attack accuracy between GLO-MIA and the gap attack.
Moreover, we compare GLO-MIA to two advanced threshold-based MIAs on graph classification tasks using prediction probability vectors under the same conditions as in Table 2. Since the threshold selection strategies are different and AUC is a threshold-independent evaluation metric, we adopt AUC to assess the performance of GLO-MIA and the probability-based MIAs. The performance of these MIAs is shown in Table 3, with the best attack performance for each model-dataset combination highlighted in bold. We further visualize the results in Figure 2. From the figure, we can see that GLO-MIA achieves performance close to that of the probability-based MIAs and, in most cases, outperforms the cross-entropy-based MIA. This further confirms the effectiveness of GLO-MIA.

Table 3.
Comparison of AUC between GLO-MIA and two probability-based MIAs (CELoss: cross-entropy-based MIA, Mentr: modified prediction entropy-based MIA).
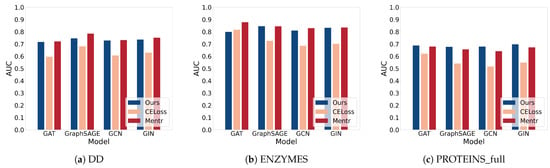
Figure 2.
Visualization of Table 3.
5.3. The Impact of Perturbation Magnitude
In this section, we analyze the impact of the perturbation magnitude on GLO-MIA. In GLO-MIA, the perturbation magnitude is controlled by adjusting the scaler size. We evaluate the performance of GLO-MIA under the different scaler sizes. The results are shown in Figure 3, where the x-axis represents scaler size and the y-axis represents attack accuracy. The red and blue lines represent the attack accuracy of the gap attack and GLO-MIA, respectively. From the figure, we observe that as the size of the scaler increases, the attack accuracy initially improves and then declines.
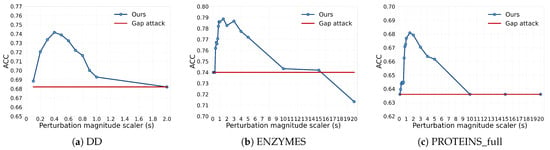
Figure 3.
Impact of perturbation magnitude on the performance of the attacks (blue line: GLO-MIA; red line: gap attack; x-axis: scaler size; y-axis: attack accuracy).
To analyze this phenomenon, we further plot the robustness score distributions of members and non-members of the ENZYMES dataset with scaler sizes of 0.1, 1.5, and 15.0, as shown in Figure 4. The red and blue bars represent the robustness scores of members and non-members, respectively. We observe that when the perturbation is too small (s = 0.1), the model predictions are not effectively disturbed, resulting in highly overlapping robustness score distributions of members and non-members, and the attack accuracy remains similar to that of the gap attack. When the perturbation is effective (s = 1.5), the robustness scores of non-members decrease significantly, while members maintain relatively high robustness, leading to a clear distinction between the two distributions. At this point, the attack accuracy of GLO-MIA outperforms the baseline by approximately 5%. However, when the perturbation is too large (s = 15.0), both members and non-members are misclassified, causing their distributions to overlap again and significantly reducing the attack performance even below that of the gap attack (s = 20.0).
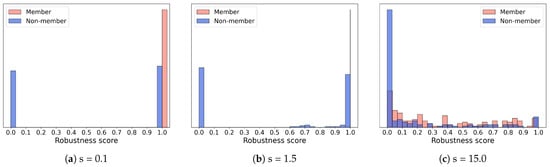
Figure 4.
Robustness score distributions of members and non-members under different perturbation magnitude scaler sizes (s: scaler size; red: members; blue: non-members).
The experimental results demonstrate that the choice of perturbation magnitude is a critical factor for the performance of GLO-MIA, and suitable perturbations can effectively enhance the distinguishability of members and non-members.
5.4. The Impact of the Number of Perturbed Graphs
We further investigate the impact of the number of perturbed graphs on the attack performance of GLO-MIA, evaluating it on three datasets and four GNN models. The results are shown in Figure 5, where the x-axis represents the number of perturbed graphs and the y-axis represents attack accuracy; the red and blue lines represent the attack accuracy of the gap attack and GLO-MIA, respectively. From the figure, we observe that as the number of perturbed graphs increases, the attack performance generally improves and approaches convergence, indicating that increasing the number of perturbed graphs enhances the attack’s effectiveness. When the number of perturbed graphs is small (e.g., one to ten), the attack accuracy is relatively low but still effective, which means that GLO-MIA remains a threat even with limited query budgets. In practical applications, if computational resources permit, increasing the number of perturbed graphs can improve the attack accuracy.
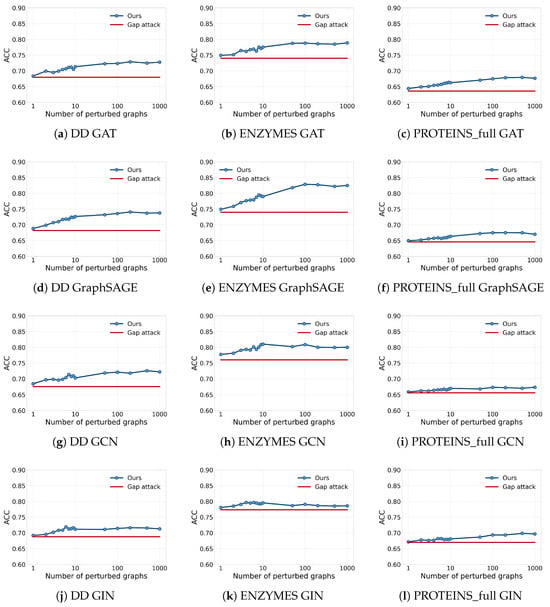
Figure 5.
Impact of the number of perturbed graphs on the performance of the attacks (blue line: GLO-MIA; red line: gap attack; x-axis: number of perturbed graphs; y-axis: attack accuracy).
5.5. Possible Defense
Similar to other MIAs [9,10,20,23,24], GLO-MIA exploits the model’s overfitting. Regularization techniques such as weight decay are used to reduce overfitting. As a representative case, multiple GCN models are trained on the ENZYMES dataset using different weight decay coefficients. The GLO-MIA is evaluated on these GCN models. The results are shown in Figure 6, where the x-axis represents the weight decay coefficient. In Figure 6a, the y-axis denotes classification accuracy, while in Figure 6b, it represents attack accuracy. As the regularization technique is strengthened, the train–test accuracy gap generally shows a downward trend, indicating that the prediction difference between the training set and the testing set decreases, and the attack accuracy of the GLO-MIA shows a significant decrease. However, we observe that excessive regularization degrades the model’s performance. Therefore, balancing model effectiveness and defense against attacks is critical.
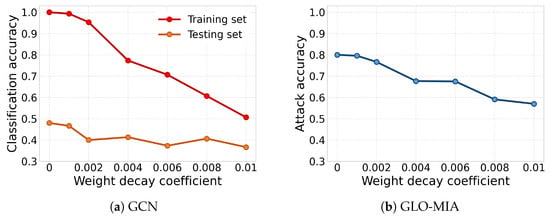
Figure 6.
Impact of regularization on GLO-MIA and model performance (red line: classification accuracy on training set; orange line: classification accuracy on testing set; blue line: GLO-MIA; x-axis: weight decay coefficient; y-axis: accuracy).
6. Conclusions and Future Work
This paper proposes GLO-MIA, the first label-only MIA against GNNs in graph classification tasks, revealing the vulnerability of GNNs to such threats. Based on the intuition that the target model’s predictions on the training data are more stable than those on testing data, GLO-MIA can effectively infer the membership of given graph samples by comparing their robustness scores with a predefined threshold. Our empirical evaluation results on four popular GNN models (GCN, GAT, GraphSAGE and GIN) and three benchmark datasets show that the attack accuracy of GLO-MIA can reach up to 0.825 at best, with a maximum improvement of 8.5% compared with the gap attack, and the performance of GLO-MIA is close to that of probability-based MIAs. Furthermore, we analyze the impact of perturbation magnitude and the number of perturbed graphs on the attack performance. Finally, we discuss the impact of regularization techniques as a possible defense on the attack performance.
However, GLO-MIA applies under the assumption that the shadow dataset and target dataset follow the same distribution, and it is currently applicable to small/medium-scale undirected attributed graphs. In future work, we will enhance GLO-MIA’s adaptability to diverse graph types (e.g., large-scale graphs) and improve its attack generalization capability across different distribution scenarios. We will also study other label-only MIAs in graph classification tasks and defense methods against these MIAs.
Author Contributions
Writing—original draft preparation, Y.L.; writing—review and editing, J.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the Shanghai Natural Science Foundation under grant number 22ZR1422600.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
You can find the datasets we use in this experiment at https://chrsmrrs.github.io/datasets/docs/datasets/ (accessed on 1 November 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hirst, J.D.; Sternberg, M.J. Prediction of Structural and Functional Features of Protein and Nucleic Acid Sequences by Artificial Neural Networks. Biochemistry 1992, 31, 7211–7218. [Google Scholar] [CrossRef] [PubMed]
- Borgatti, S.P.; Mehra, A.; Brass, D.J.; Labianca, G. Network Analysis in the Social Sciences. Science 2009, 323, 892–895. [Google Scholar] [CrossRef] [PubMed]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Kipf, T.N.; Welling, M. Variational Graph Auto-Encoders. arXiv 2016, arXiv:1611.07308. [Google Scholar]
- Pan, S.; Hu, R.; Long, G.; Jiang, J.; Yao, L.; Zhang, C. Adversarially Regularized Graph Autoencoder for Graph Embedding. arXiv 2018, arXiv:1802.04407. [Google Scholar]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How Powerful Are Graph Neural Networks? arXiv 2018, arXiv:1810.00826. [Google Scholar]
- He, X.; Wen, R.; Wu, Y.; Backes, M.; Shen, Y.; Zhang, Y. Node-Level Membership Inference Attacks against Graph Neural Networks. arXiv 2021, arXiv:2102.05429. [Google Scholar]
- Olatunji, I.E.; Nejdl, W.; Khosla, M. Membership Inference Attack on Graph Neural Networks. In Proceedings of the 2021 Third IEEE International Conference on Trust, Privacy and Security in Intelligent Systems and Applications (TPS-ISA), Atlanta, GA, USA, 13–15 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 11–20. [Google Scholar]
- Wu, B.; Yang, X.; Pan, S.; Yuan, X. Adapting Membership Inference Attacks to GNN for Graph Classification: Approaches and Implications. In Proceedings of the 2021 IEEE International Conference on Data Mining (ICDM), Auckland, New Zealand, 7–10 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1421–1426. [Google Scholar]
- Yang, J.; Li, H.; Fan, W.; Zhang, X.; Hao, M. Membership Inference Attacks Against the Graph Classification. In Proceedings of the GLOBECOM 2023–2023 IEEE Global Communications Conference, Kuala Lumpur, Malaysia, 4–8 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 6729–6734. [Google Scholar]
- Conti, M.; Li, J.; Picek, S.; Xu, J. Label-Only Membership Inference Attack against Node-Level Graph Neural Networks. In Proceedings of the 15th ACM Workshop on Artificial Intelligence and Security, Los Angeles, CA, USA, 7–11 November 2022; pp. 1–12. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive Representation Learning on Large Graphs. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Wu, B.; Yang, X.; Pan, S.; Yuan, X. Model Extraction Attacks on Graph Neural Networks: Taxonomy and Realisation. In Proceedings of the 2022 ACM on Asia Conference on Computer and Communications Security; Association for Computing Machinery: New York, NY, USA, 2022; pp. 337–350. [Google Scholar]
- Shen, Y.; He, X.; Han, Y.; Zhang, Y. Model Stealing Attacks Against Inductive Graph Neural Networks. In Proceedings of the 2022 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 22–26 May 2022; pp. 1175–1192. [Google Scholar]
- Zhang, Z.; Chen, M.; Backes, M.; Shen, Y.; Zhang, Y. Inference attacks against graph neural networks. In Proceedings of the 31st USENIX Security Symposium (USENIX Security 22), Boston, MA, USA, 10–12 August 2022; pp. 4543–4560. [Google Scholar]
- Wang, X.; Wang, W.H. Group Property Inference Attacks Against Graph Neural Networks. In Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security, Los Angeles, CA, USA, 7–11 November 2022; pp. 2871–2884. [Google Scholar]
- Duddu, V.; Boutet, A.; Shejwalkar, V. Quantifying Privacy Leakage in Graph Embedding. In Proceedings of the MobiQuitous 2020-17th EAI International Conference on Mobile and Ubiquitous Systems: Computing, Networking and Services, Darmstadt, Germany, 7–9 December 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 76–85. [Google Scholar]
- Zhang, Z.; Liu, Q.; Huang, Z.; Wang, H.; Lee, C.K.; Chen, E. Model Inversion Attacks Against Graph Neural Networks. IEEE Trans. Knowl. Data Eng. 2022, 35, 8729–8741. [Google Scholar] [CrossRef]
- Shokri, R.; Stronati, M.; Song, C.; Shmatikov, V. Membership Inference Attacks against Machine Learning Models. In Proceedings of the 2017 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 3–18. [Google Scholar]
- Yeom, S.; Giacomelli, I.; Fredrikson, M.; Jha, S. Privacy Risk in Machine Learning: Analyzing the Connection to Overfitting. In Proceedings of the 2018 IEEE 31st Computer Security Foundations Symposium (CSF), Oxford, UK, 9–12 July 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 268–282. [Google Scholar]
- Salem, A.; Zhang, Y.; Humbert, M.; Berrang, P.; Fritz, M.; Backes, M. ML-Leaks: Model and Data Independent Membership Inference Attacks and Defenses on Machine Learning Models. arXiv 2018, arXiv:1806.01246. [Google Scholar]
- Li, Z.; Zhang, Y. Membership Leakage in Label-Only Exposures. In Proceedings of the 2021 ACM SIGSAC Conference on Computer and Communications Security, Virtual Event, 15–19 November 2021; pp. 880–895. [Google Scholar]
- Choquette-Choo, C.A.; Tramer, F.; Carlini, N.; Papernot, N. Label-Only Membership Inference Attacks. In Proceedings of the 38th International Conference on Machine Learning (PMLR), Virtual, 18–24 July 2021; PMLR; pp. 1964–1974. [Google Scholar]
- Song, C.; Shmatikov, V. Auditing Data Provenance in Text-Generation Models. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 196–206. [Google Scholar]
- He, X.; Jia, J.; Backes, M.; Gong, N.Z.; Zhang, Y. Stealing Links from Graph Neural Networks. In Proceedings of the 30th USENIX Security Symposium (USENIX Security 21), Online, 11–13 August 2021; pp. 2669–2686. [Google Scholar]
- Zhang, G.; Liu, B.; Zhu, T.; Ding, M.; Zhou, W. Label-Only Membership Inference Attacks and Defenses in Semantic Segmentation Models. IEEE Trans. Dependable Secur. Comput. 2022, 20, 1435–1449. [Google Scholar] [CrossRef]
- Lu, Z.; Liang, H.; Zhao, M.; Lv, Q.; Liang, T.; Wang, Y. Label-Only Membership Inference Attacks on Machine Unlearning without Dependence of Posteriors. Int. J. Intell. Syst. 2022, 37, 9424–9441. [Google Scholar] [CrossRef]
- He, Y.; Li, B.; Liu, L.; Ba, Z.; Dong, W.; Li, Y.; Qin, Z.; Ren, K.; Chen, C. Towards Label-Only Membership Inference Attack Against Pre-Trained Large Language Models. arXiv 2025, arXiv:2502.18943. [Google Scholar]
- Morris, C.; Kriege, N.M.; Bause, F.; Kersting, K.; Mutzel, P.; Neumann, M. TUDataset: A Collection of Benchmark Datasets for Learning with Graphs. arXiv 2020, arXiv:2007.08663. [Google Scholar]
- Dobson, P.D.; Doig, A.J. Distinguishing Enzyme Structures from Non-Enzymes without Alignments. J. Mol. Biol. 2003, 330, 771–783. [Google Scholar] [CrossRef] [PubMed]
- Borgwardt, K.M.; Ong, C.S.; Schoenauer, S.; Vishwanathan, S.V.N.; Smola, A.J.; Kriegel, H.P. Protein Function Prediction via Graph Kernels. Bioinformatics 2005, 21, i47–i56. [Google Scholar] [CrossRef] [PubMed]
- Schomburg, I.; Chang, A.; Ebeling, C.; Gremse, M.; Heldt, C.; Huhn, G.; Schomburg, D. BRENDA, the enzyme database: Updates and major new developments. Nucleic Acids Res. 2004, 32, D431–D433. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).