Experimental and Numerical Analysis of Freeze–Thaw-Induced Mechanical Degradation in the Coarse-Grained Soil of the Southeastern Qinghai–Xizang Plateau
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. Test Methods
- FT Cycle Test
- 2.
- Triaxial Shear Test
3. Experimental Results and Analysis
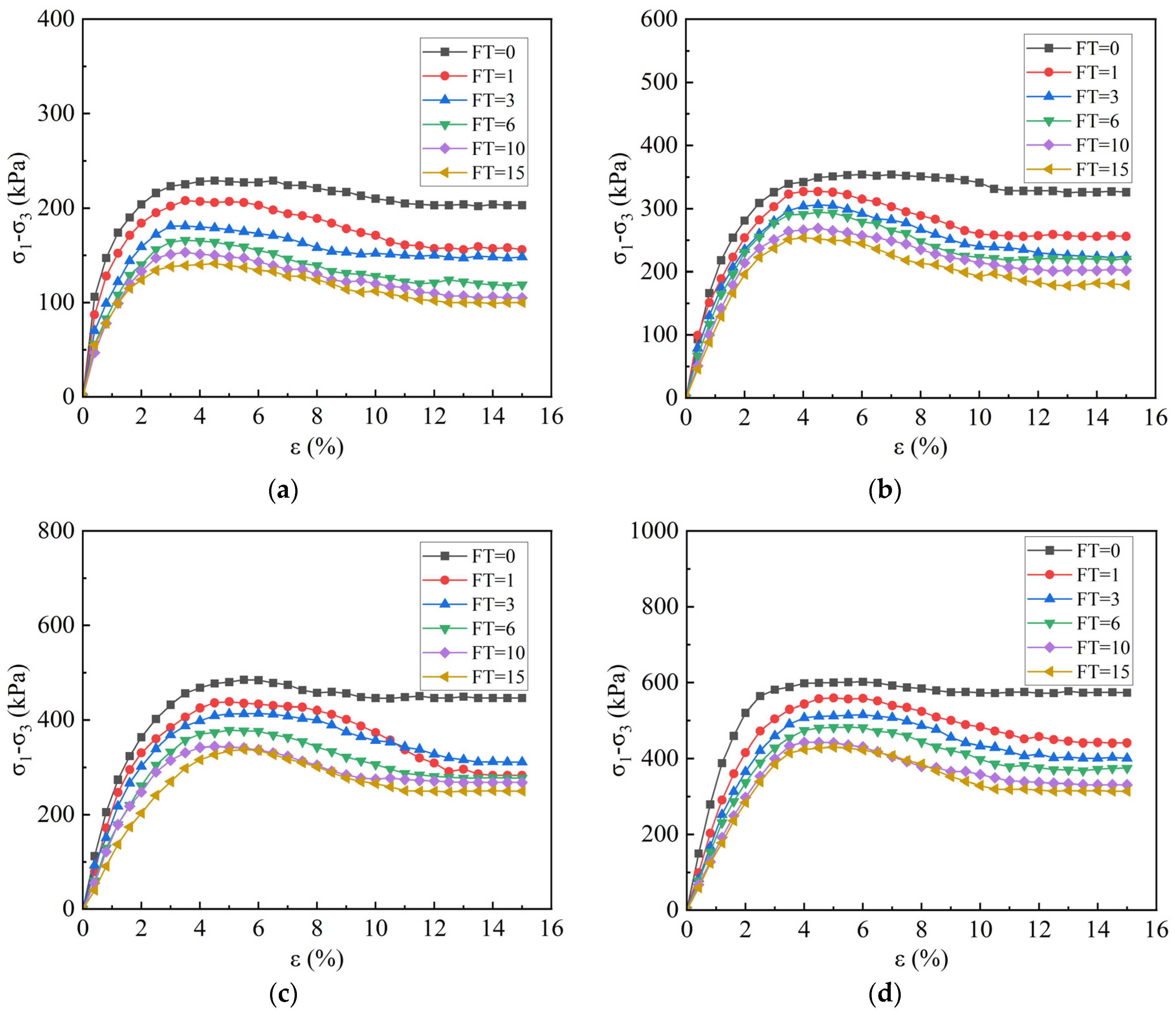
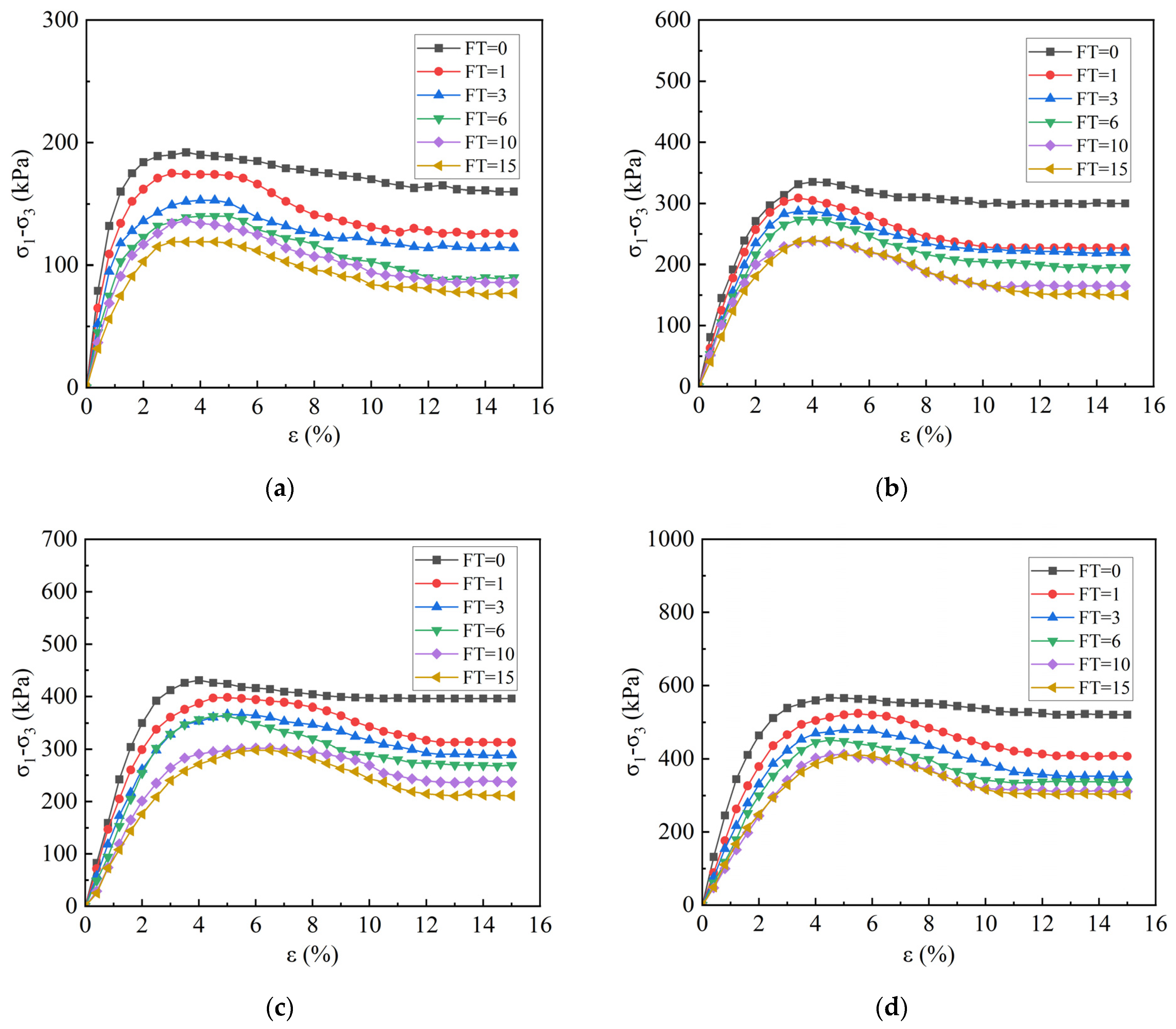
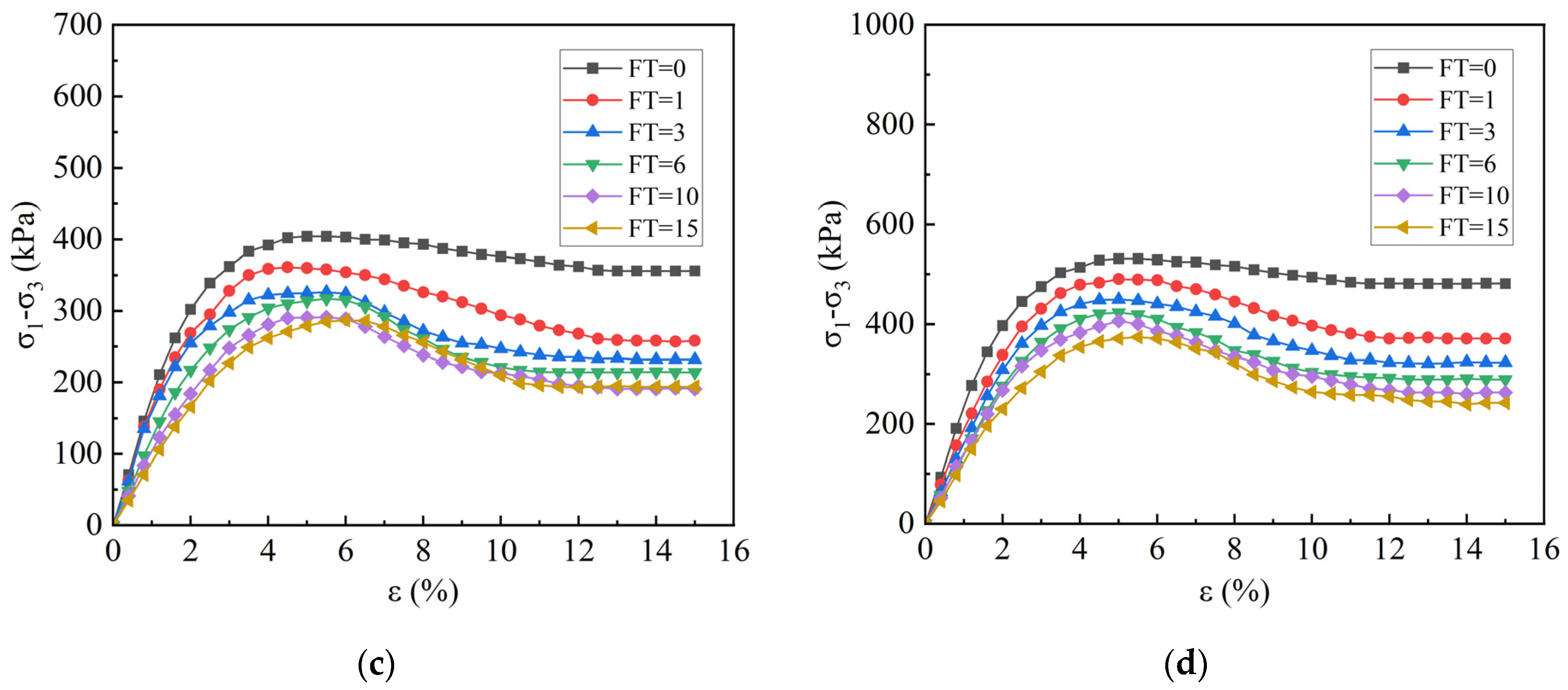
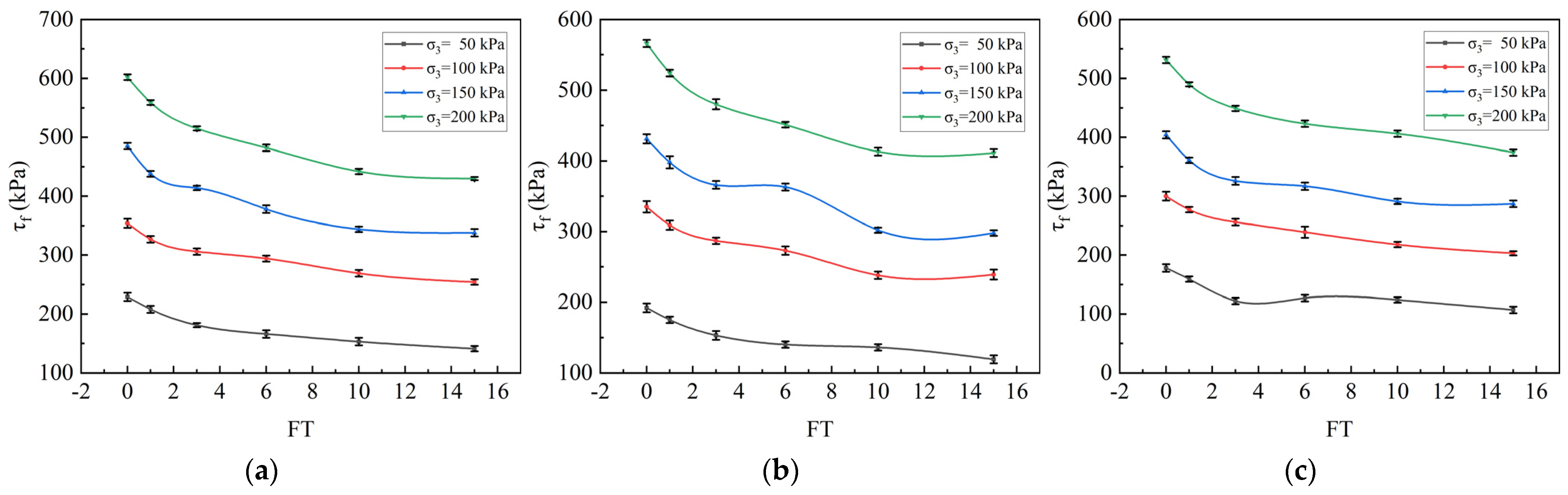
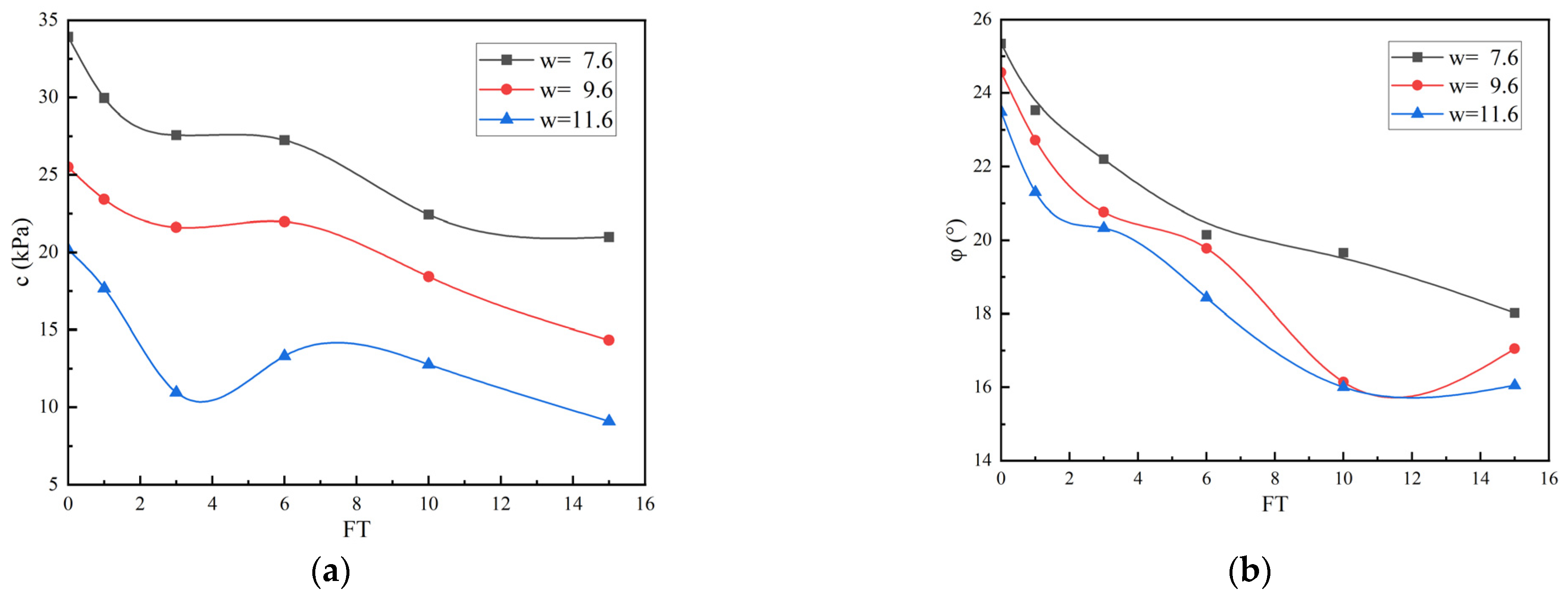
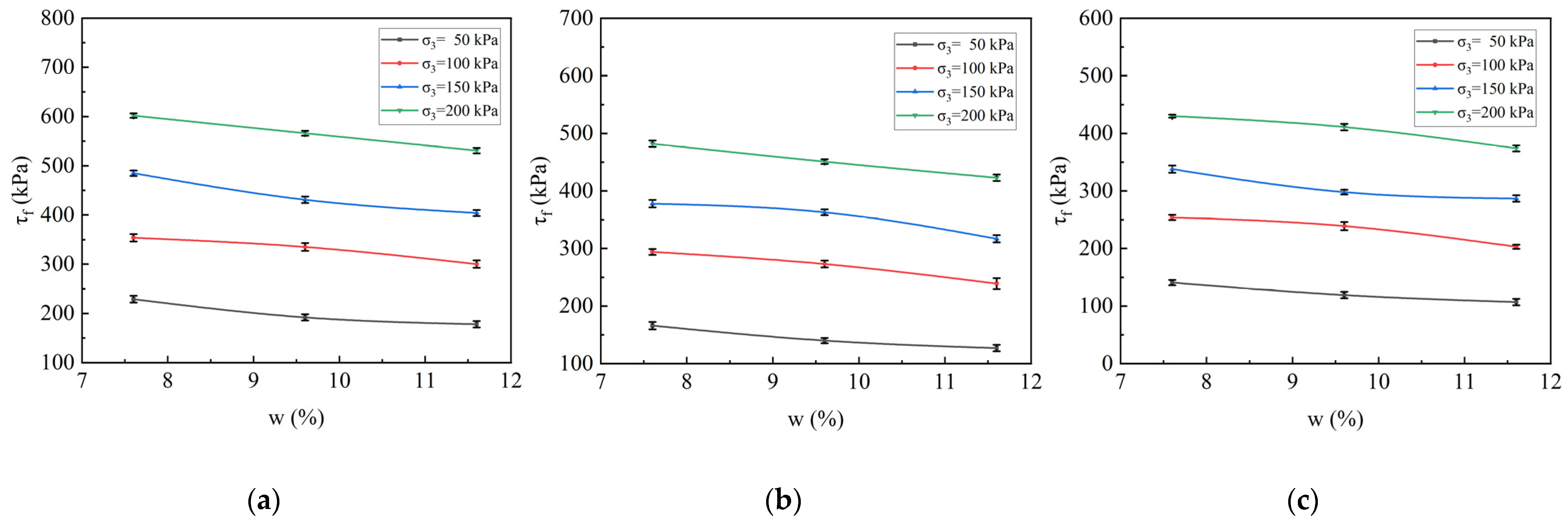
3.1. Effect of FT Cycles and Confining Pressure on the Mechanical Properties of Specimens
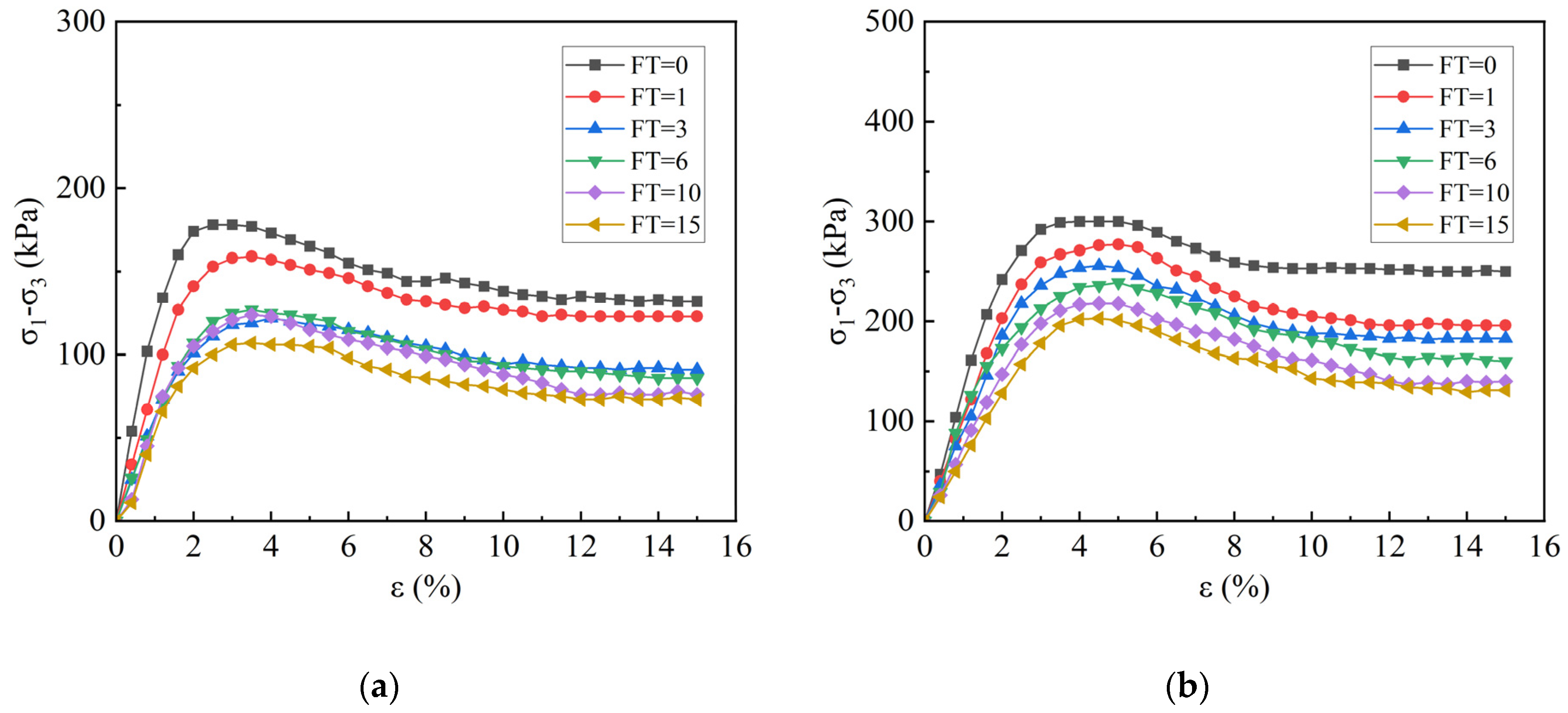
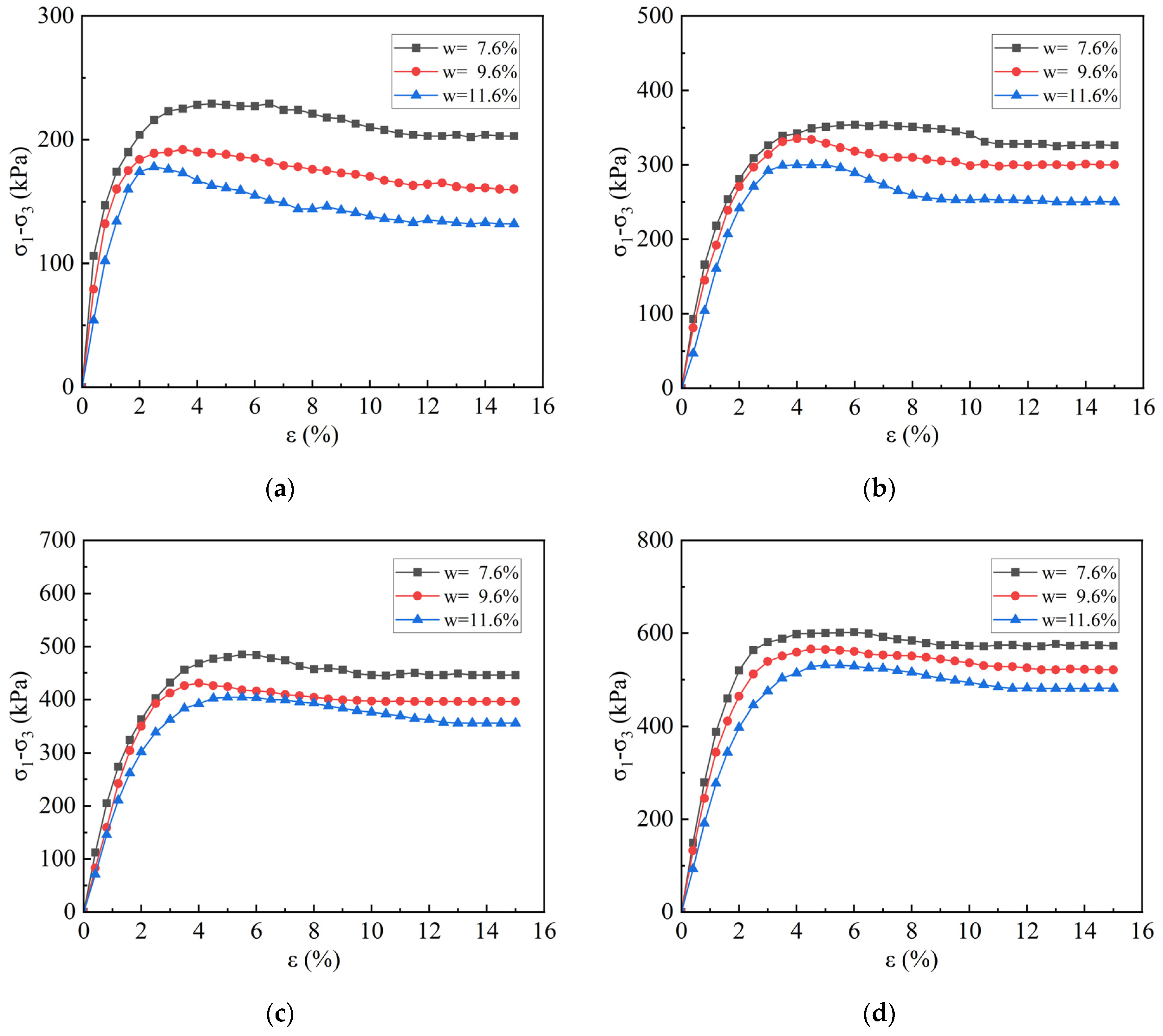
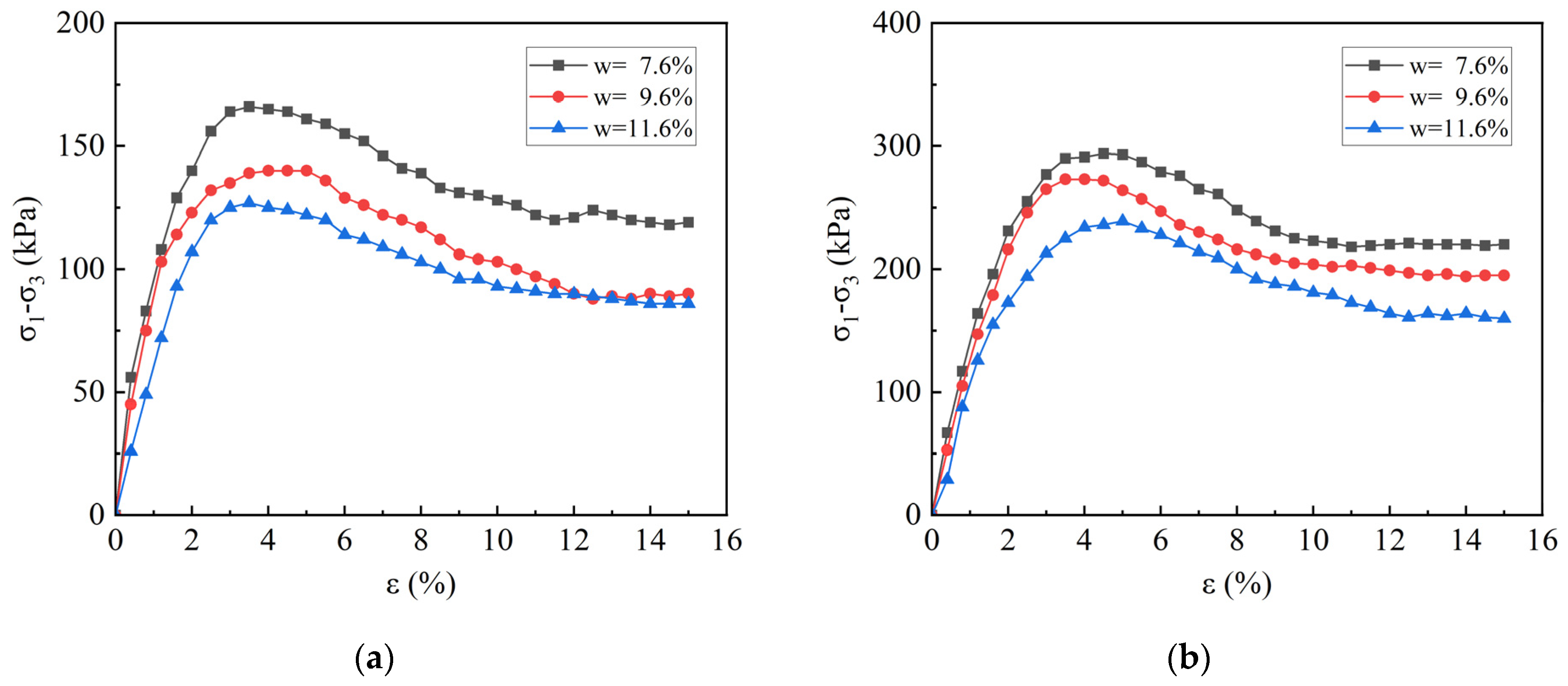
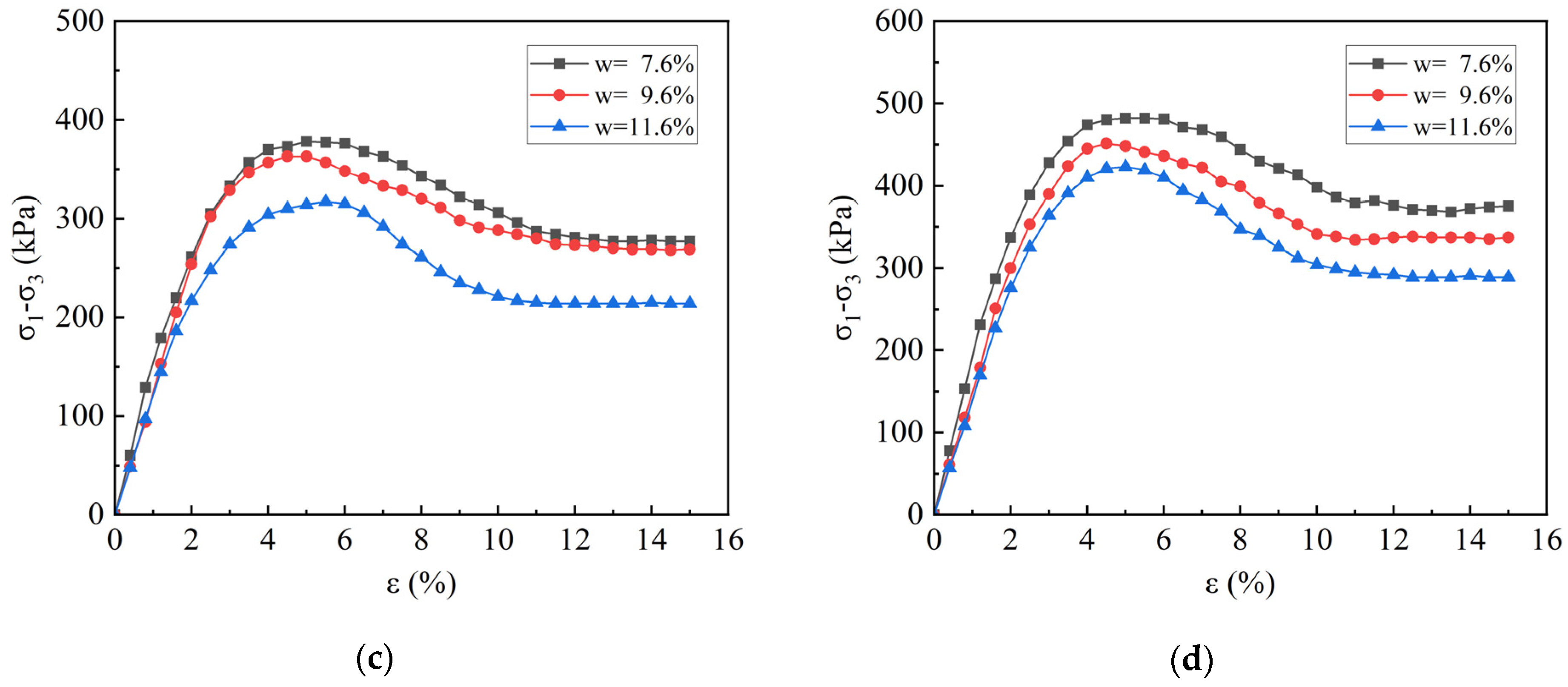
3.2. The Effect of Water Content and Confining Pressure on the Mechanical Properties of Samples
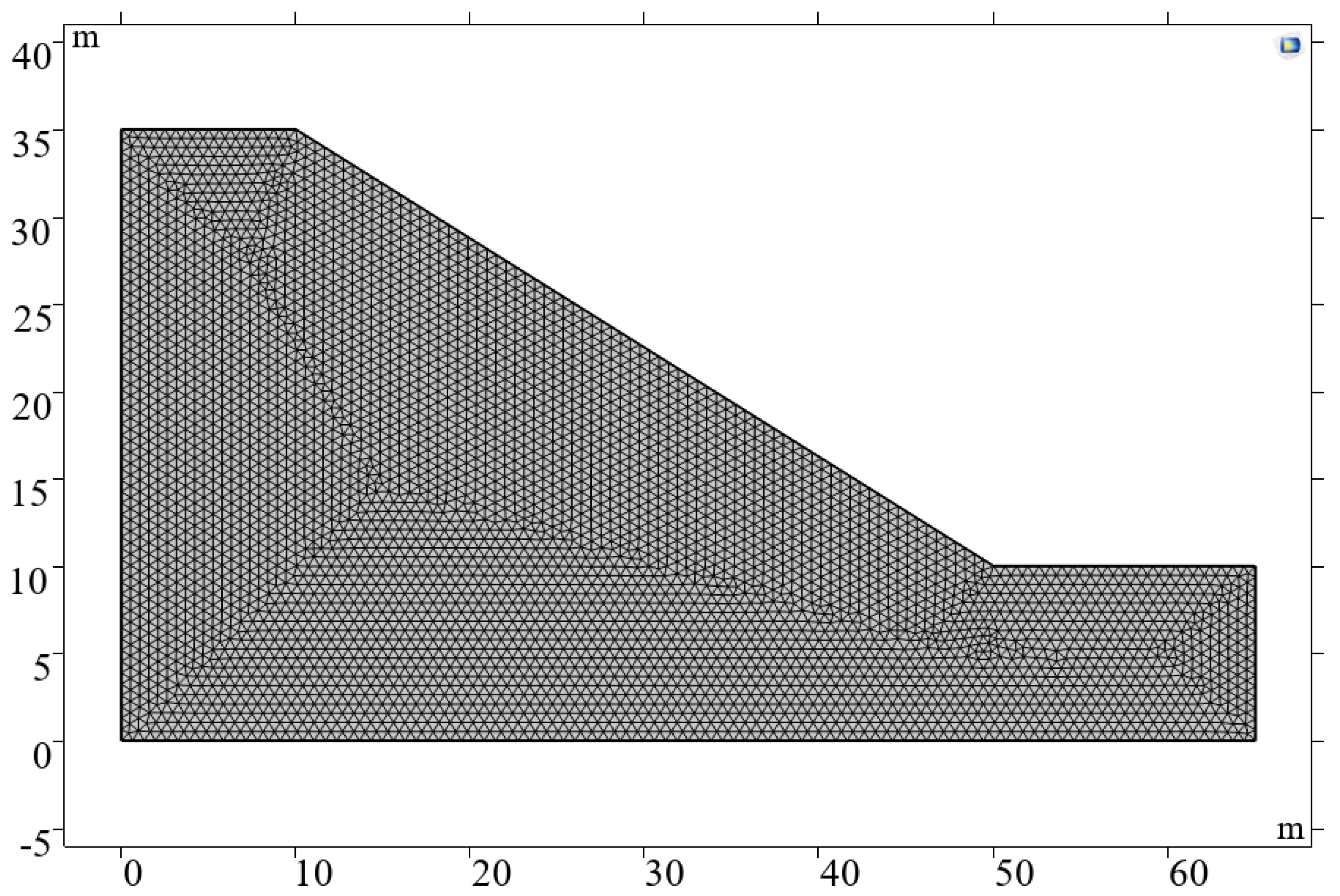
4. Numerical Analysis of the Slope Stability of Coarse-Grained Soil Based on COMSOL Multiphysics
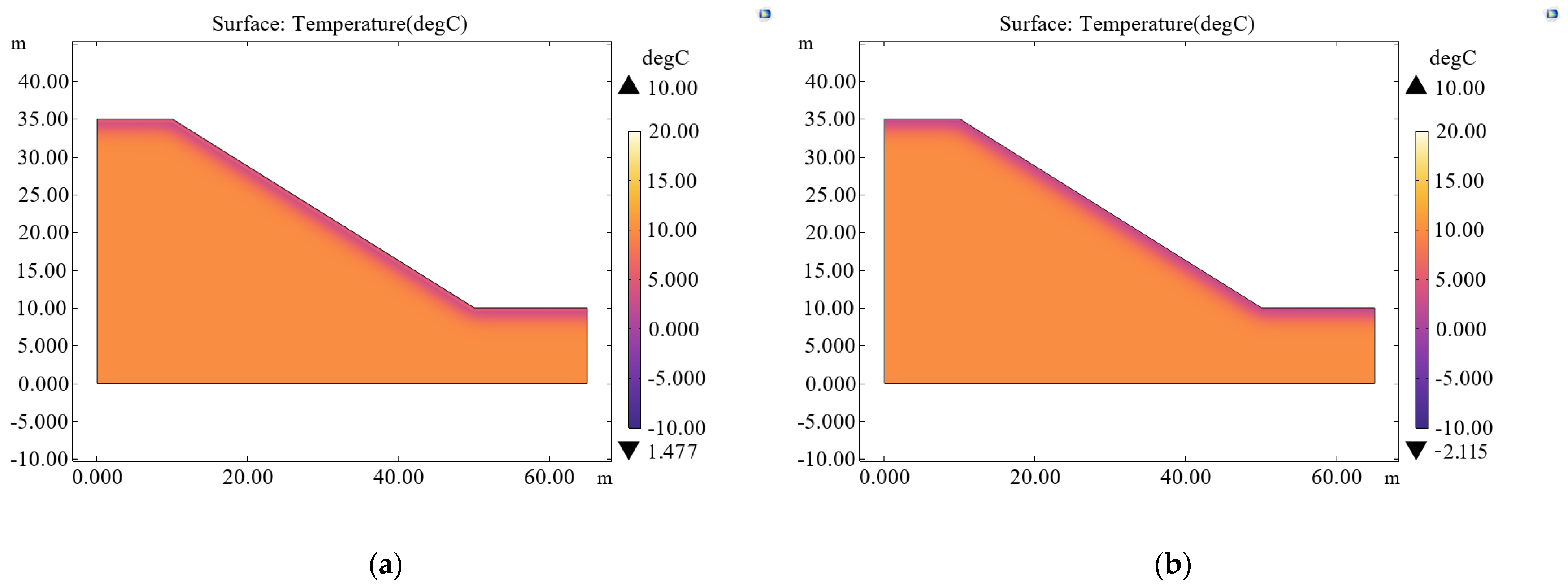
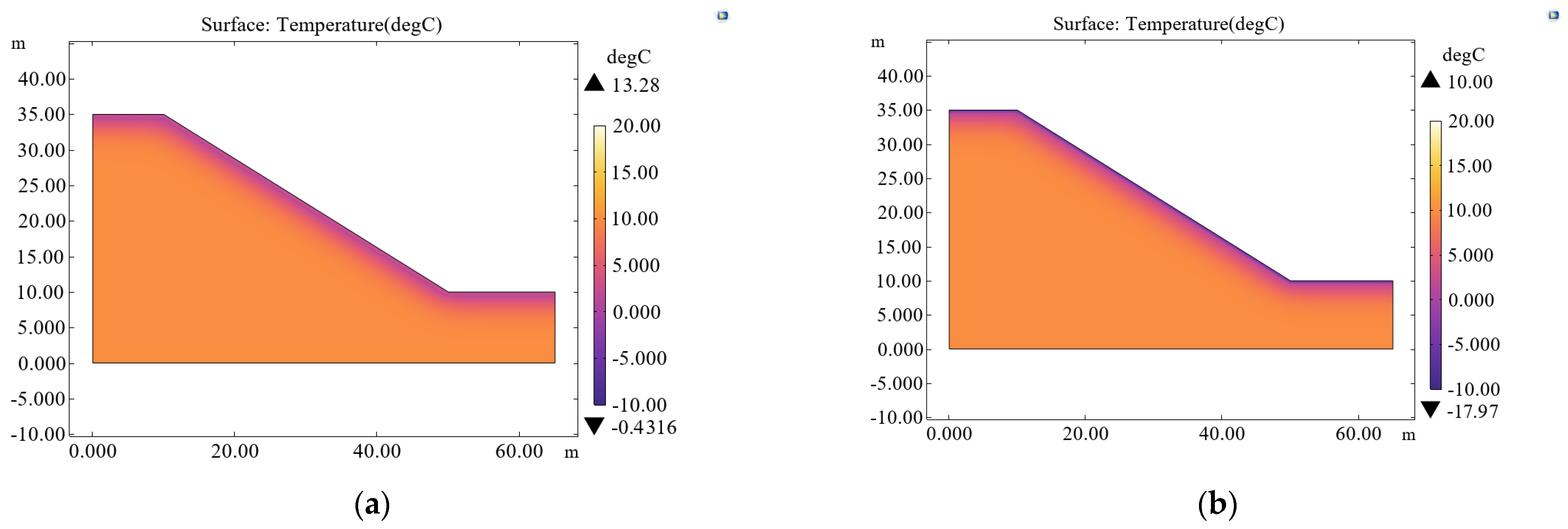
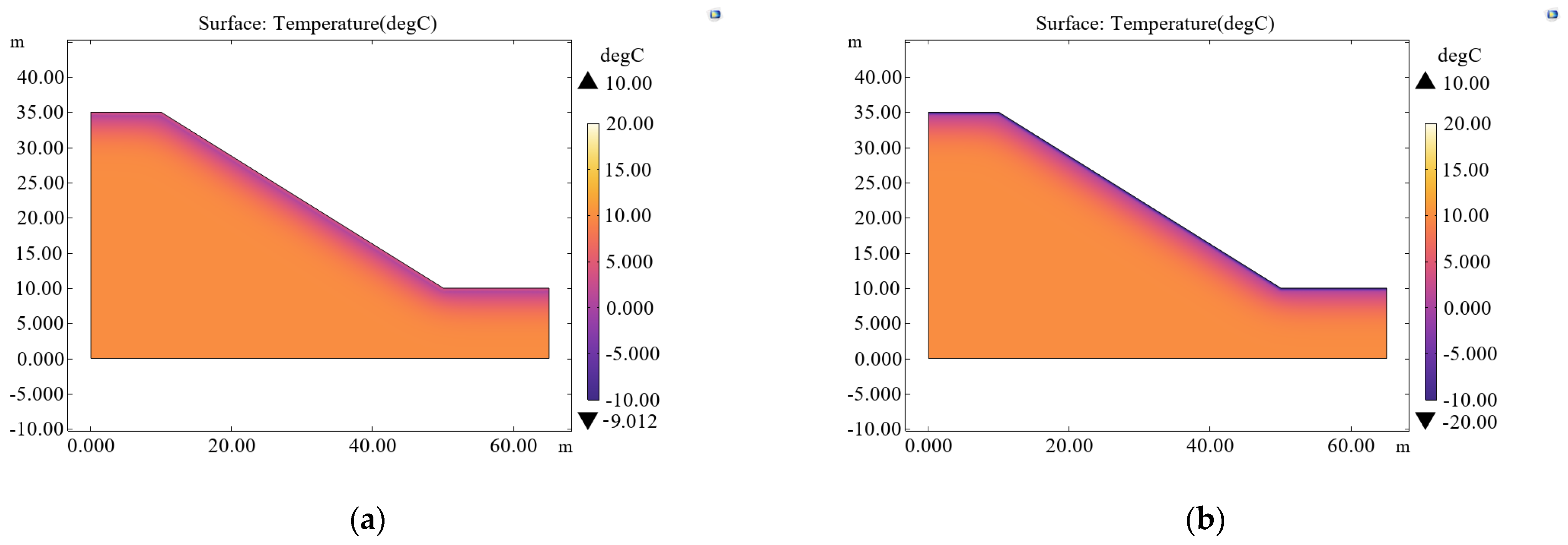
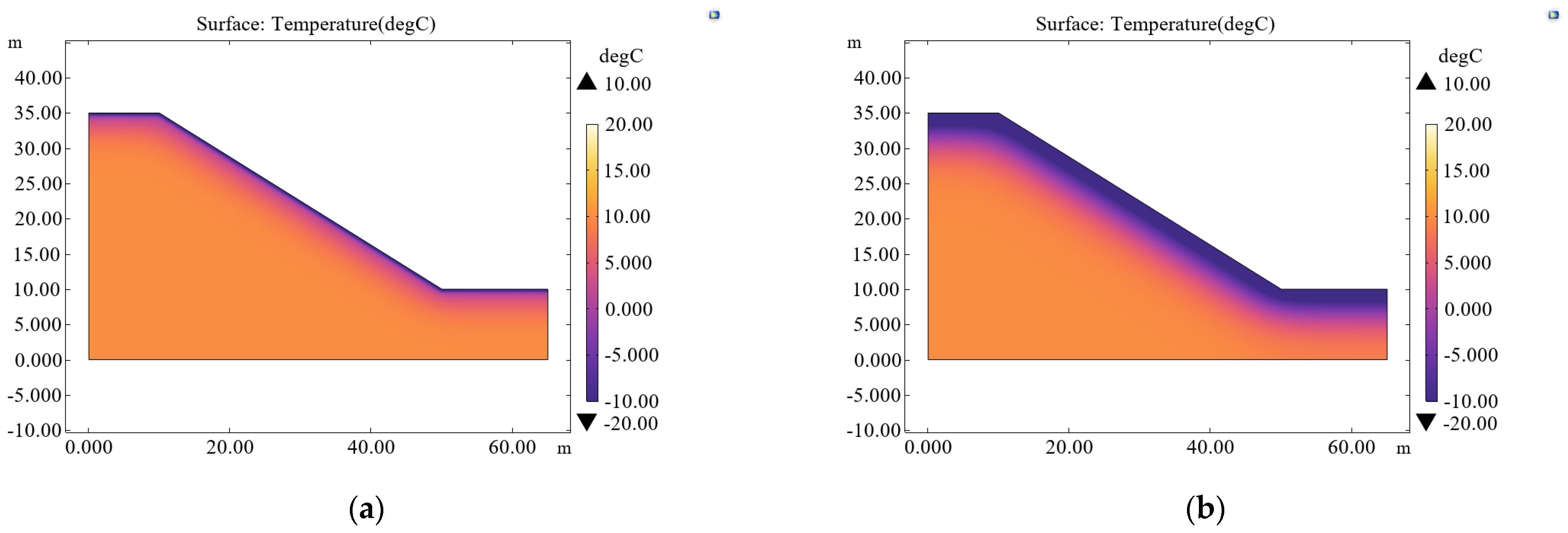
4.1. The Temperature Variation of the Slope’s Soil Under the Action of FT Cycles
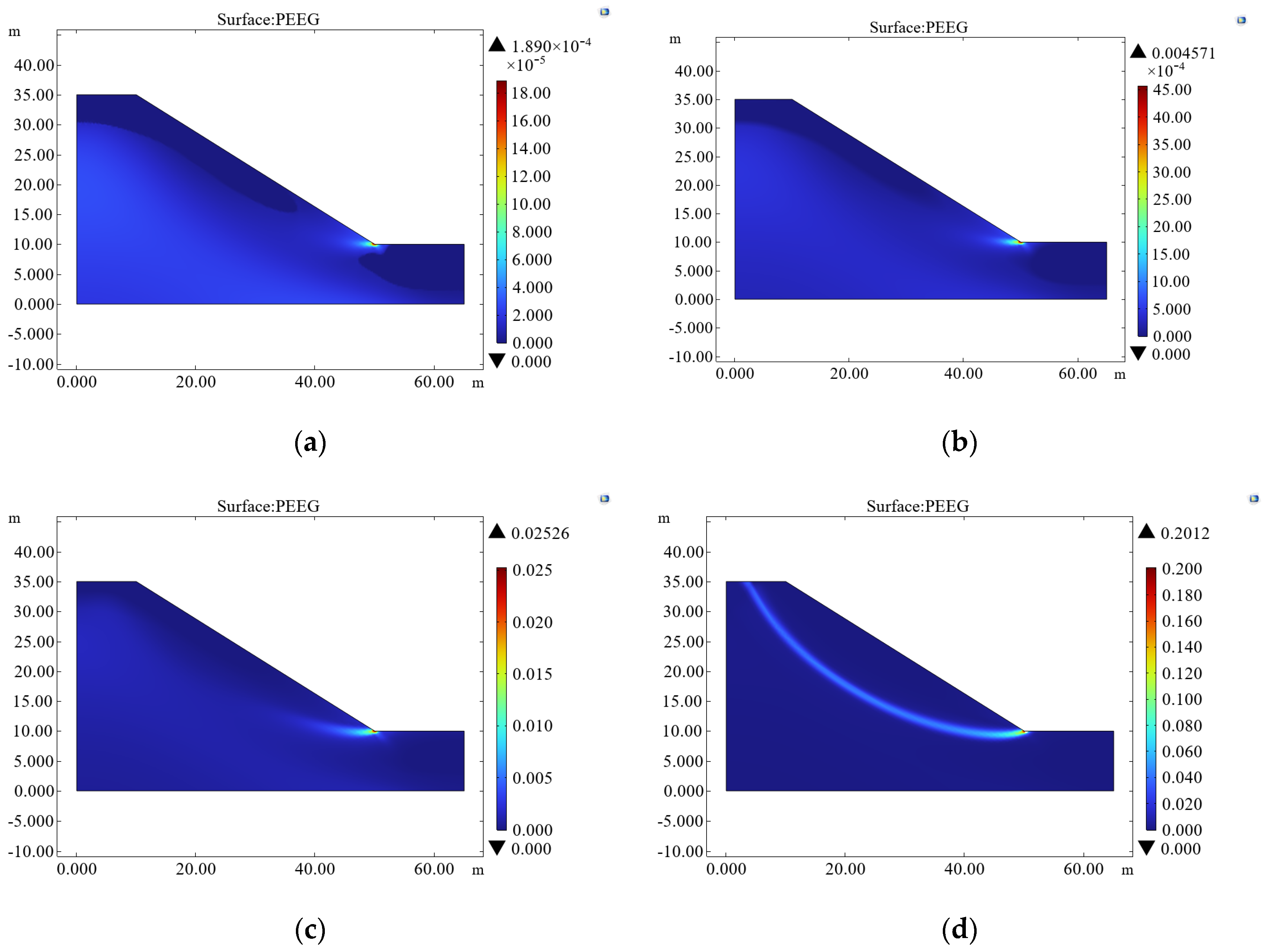
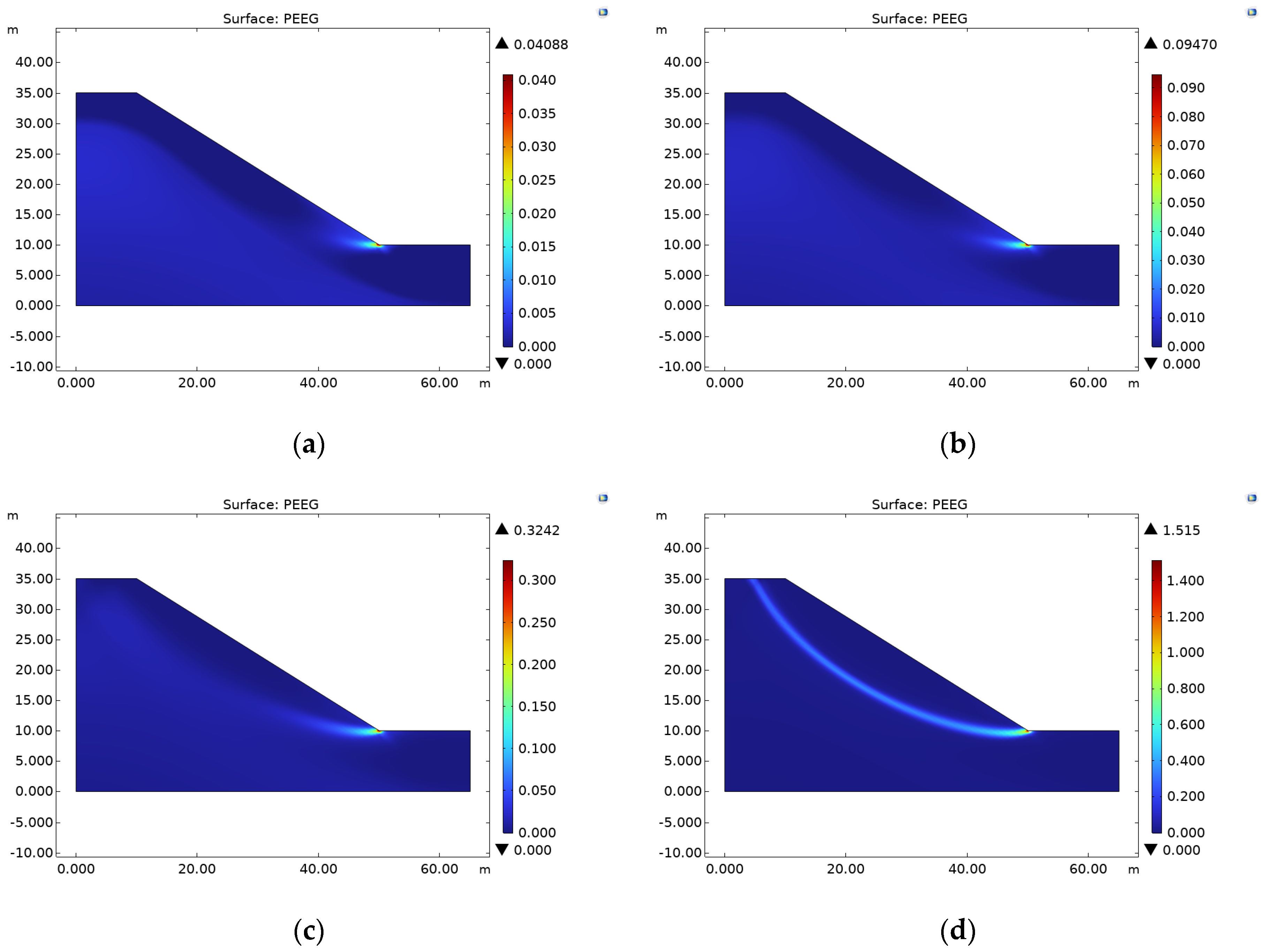
4.2. Changes in Slope Soil Stability Under FT Cycles
5. Conclusions
- (1)
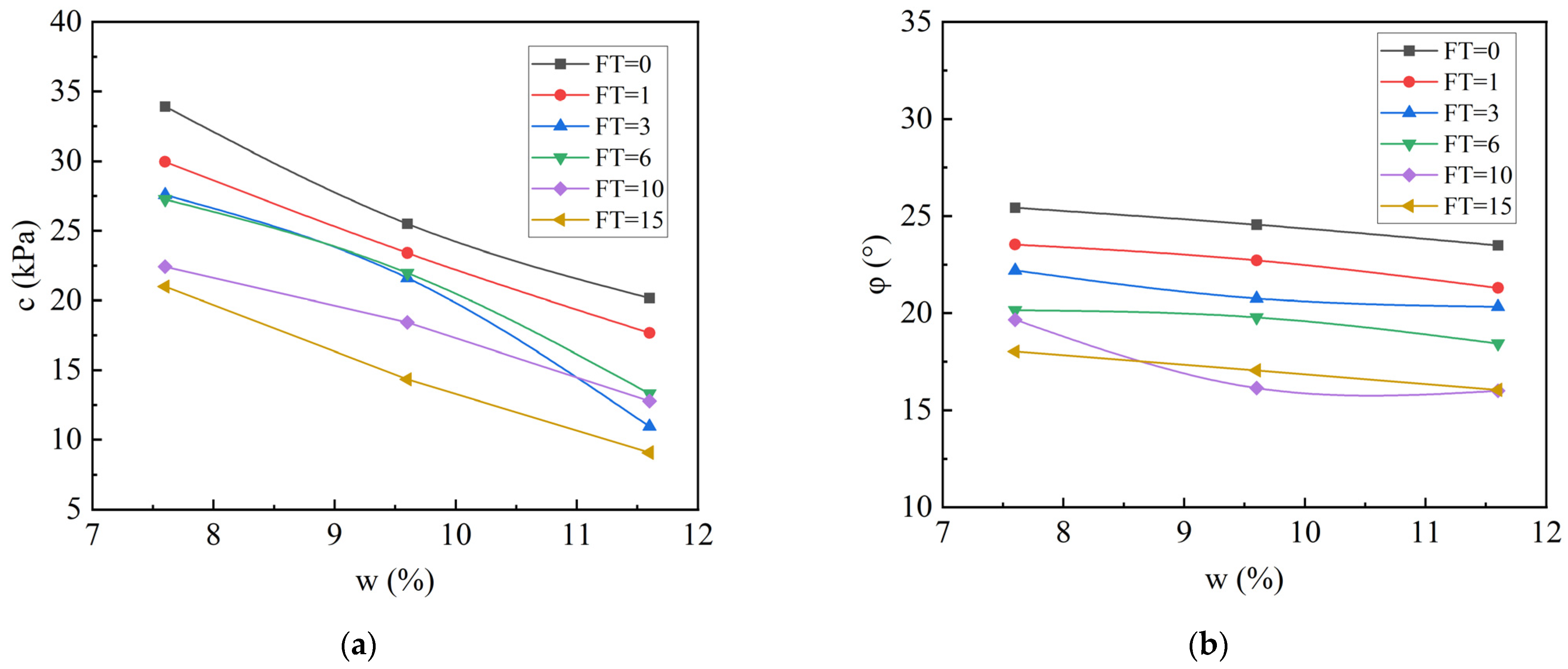
- FT cycles significantly degrade the mechanical properties of coarse-grained soil in southeastern Xizang. The stress–strain curve of the samples initially shows a higher slope and stable peak value. After one FT cycle, the peak stress decreases by 8.4%, and after fifteen cycles, the overall reduction reaches approximately 31.2%. The cohesion and internal friction angle decrease by an average of 26.5 kPa (38~55%) and about 7.4° (29~32%), respectively, with changes stabilizing after 10 cycles.
- (2)
- An increase in moisture content leads to an increase in pore water pressure, weakening the particle interlocking effect. As the moisture content increases from 7.6% to 11.6%, the strain softening degree increases from 8.0% to 16.0% in the non-FT samples, and after FT cycles, it increases further to 27.9~33.7%. This indicates that the shear strength degradation is more pronounced at higher moisture levels.
- (3)
- Increased confining pressure significantly enhances shear strength. Under conditions where the confining pressure increases from 50 kPa to 200 kPa, the peak stress increases by as much as 89.7%, effectively inhibiting the structural degradation caused by FT cycles and high moisture levels.
- (4)
- The two-dimensional slope model constructed using COMSOL Multiphysics shows that, at a lower moisture content (7.6%), the maximum plastic strain at the critical instability of the slope is approximately 0.20. At moisture contents of 9.6% and 11.6%, instability occurs earlier at 106 and 15 FT cycles, respectively, with the maximum plastic strain increasing to 1.515 and 2.465, indicating that the moisture content has a decisive impact on slope stability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Ding, J.; Piao, S. Does the continuous wetting of the Tibetan Plateau contribute to the accelerated degradation of permafrost? Sci. China Earth Sci. 2024, 67, 1714–1718. [Google Scholar] [CrossRef]
- Liu, W.; Wen, J.; Chen, J.; Wang, Z.; Lu, X.; Wu, Y.; Jiang, Y. Characteristic analysis of the spatio-temporal distribution of key variables of the soil freeze-thaw processes over the Qinghai-Tibetan Plateau. Cold Reg. Sci. Technol. 2022, 197, 103526. [Google Scholar] [CrossRef]
- Zhao, L.; Hu, G.; Liu, G.; Zou, D.; Wang, Y.; Xiao, Y.; Du, E.; Wang, C.; Xing, Z.; Sun, Z.; et al. Investigation, Monitoring, and Simulation of Permafrost on the Qinghai-Tibet Plateau: A Review. Permafr. Periglac. Process. 2024, 35, 412–422. [Google Scholar] [CrossRef]
- Leuther, F.; Schlüter, S. Impact of freeze–thaw cycles on soil structure and soil hydraulic properties. Soil 2021, 7, 179–191. [Google Scholar] [CrossRef]
- Dai, L.; Guo, X.; Zhang, F.; Du, Y.; Ke, X.; Li, Y.; Cao, G.; Li, Q.; Lin, L.; Shu, K.; et al. Seasonal dynamics and controls of deep soil water infiltration in the seasonally-frozen region of the Qinghai-Tibet plateau. J. Hydrol. 2019, 571, 740–748. [Google Scholar] [CrossRef]
- Luo, S.; Wang, J.; Pomeroy, J.W.; Lyu, S. Freeze–thaw changes of seasonally frozen ground on the Tibetan Plateau from 1960 to 2014. J. Clim. 2020, 33, 9427–9446. [Google Scholar] [CrossRef]
- Lancuo, Z.; Hou, G.; Xu, C.; Liu, Y.; Zhu, Y.; Wang, W.; Zhang, Y. Simulating the route of the Tang-Tibet Ancient Road for one branch of the Silk Road across the Qinghai-Tibet Plateau. PLoS ONE 2019, 14, e0226970. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Peng, W.; Li, J.; Luo, Q.; Jiang, B.; Yu, Y.; Liu, E. Effects of Freeze–Thaw Cycle on Permeability and Compression Properties of Aeolian Soil–Bentonite Mixture. Iranian Journal of Science and Technology, Transactions of Civil Engineering 2024, 48, 3621–3641. [Google Scholar] [CrossRef]
- Yu, S.; Huang, S.; Liu, F.; Cai, H.; Ye, Y. Quantification of pore structure evolution and its correlation with the macroscopic properties of sandstones under freeze–thaw action. Bull. Eng. Geol. Environ. 2024, 83, 3. [Google Scholar] [CrossRef]
- Chen, J.; Wang, E.; Xue, J.; Cui, L.; Zheng, X.; Du, Q. Effects of soil particle size and gradation on the transformation between shallow phreatic water and soil water under laboratory freezing-thawing action. J. Hydrol. 2023, 619, 129323. [Google Scholar] [CrossRef]
- Chen, H.; Xu, N.; Jiang, P.; Jiang, L. Study on the Effect of Freeze–Thaw Action on the Electrical Conductivity and Sensing Properties of Graphene-Based Cement Composites. Materials 2023, 16, 855. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Lu, X.; Liu, Z.; Wang, N.; Xu, P.; Li, P. Experimental study on the engineering properties and failure mechanism of moraine in Southeast Tibet under freeze–thaw cycles conditions. Eng. Fail. Anal. 2024, 163, 108551. [Google Scholar] [CrossRef]
- Liu, Z.; Xiang, Y.; Liu, W.; Huang, J.; Liang, Z.; Zhang, Q.; Li, W. Effect of Freeze–Thaw Cycles on Microstructure and Hydraulic Characteristics of Claystone: A Case Study of Slope Stability from Open-Pit Mines in Wet Regions. Water 2024, 16, 640. [Google Scholar] [CrossRef]
- Xiang, B.; Liu, E.; Yang, L. Influences of freezing–thawing actions on mechanical properties of soils and stress and deformation of soil slope in cold regions. Sci. Rep. 2022, 12, 5387. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; He, Y.; Yu, S.; Cai, C. Experimental investigation and prediction model for UCS loss of unsaturated sandstones under freeze-thaw action. Int. J. Min. Sci. Technol. 2022, 32, 41–49. [Google Scholar] [CrossRef]
- Li, S.; Wang, C.; Yang, J.; Lai, Y.; Jiang, Q.; Wan, X. Thermo-hydro-mechanical process and damage mechanism of a cold-region canal under coupled wetting–drying and freezing–thawing cycles. Acta Geotech. 2022, 17, 4655–4665. [Google Scholar] [CrossRef]
- Ling, X.; Tian, S.; Tang, L.; Li, S. A damage-softening and dilatancy prediction model of coarse-grained materials considering freeze–thaw effects. Transp. Geotech. 2020, 22, 100307. [Google Scholar] [CrossRef]
- Tian, S.; Tang, L.; Ling, X.; Kong, X.; Li, S.; Cai, D. Cyclic behaviour of coarse-grained materials exposed to freeze-thaw cycles: Experimental evidence and evolution model. Cold Reg. Sci. Technol. 2019, 167, 102815. [Google Scholar] [CrossRef]
- Li, A.; Niu, F.; Zheng, H.; Akagawa, S.; Lin, Z.; Luo, J. Experimental measurement and numerical simulation of frost heave in saturated coarse-grained soil. Cold Reg. Sci. Technol. 2017, 137, 68–74. [Google Scholar] [CrossRef]
- Liu, Y.; Deng, H.; Xu, J.; Tian, G.; Deng, J. Association study on the pore structure and mechanical characteristics of coarse-grained soil under freeze–thaw cycles. Minerals 2022, 12, 314. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, E.; Liu, X.; Zhang, G.; Song, B. A new strength criterion for frozen soils considering the influence of temperature and coarse-grained contents. Cold Reg. Sci. Technol. 2017, 143, 1–12. [Google Scholar] [CrossRef]
- Qu, Y.L.; Ni, W.K.; Niu, F.J.; Mu, Y.H.; Chen, G.L.; Luo, J. Mechanical and electrical properties of coarse-grained soil affected by cyclic freeze-thaw in high cold regions. J. Cent. South Univ. 2020, 27, 853–866. [Google Scholar] [CrossRef]
- Wang, D.; Liu, E.; Yang, C.; Wang, P.; Song, B. Micromechanics-based binary-medium constitutive model for frozen soil considering the influence of coarse-grained contents and freeze–thaw cycles. Acta Geotech. 2023, 18, 3977–3996. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2021: The Physical Science Basis; Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- GB/T 50123-2019; Standard for Soil Test Methods. Ministry of Housing and Urban-Rural Development: Beijing, China, 2019.
- Kloffel, T.; Larsbo, M.; Jarvis, N.; Barron, J. Freeze-thaw effects on pore space and hydraulic properties of compacted soil and potential consequences with climate change. Soil Tillage Res. 2024, 239, 106041. [Google Scholar] [CrossRef]
- Mutaz, E.; Serati, M.; Rimmelin, R.; Williams, D.J. Variation of apparent cohesion and friction angle under polyaxial stress conditions in concrete. Presented at the ISRM International Symposium—EUROCK 2021, Virtual, 21–24 September 2021. ISRM-EUROCK-2021-013. [Google Scholar]
- Zhao, Y.D.; Hu, X. How do freeze–thaw cycles affect the soil pore structure in alpine meadows considering soil aggregate and soil column scales? J. Soil Sci. Plant Nutr. 2022, 22, 4207–4216. [Google Scholar] [CrossRef]
- Wang, D.; Yang, X.; Wan, Q.; Zhang, S. Experimental study on the dynamic characteristics of coarse-grained saline soil embankments in the high-cold saline lake area under freeze-thaw cycle action. Case Stud. Constr. Mater. 2024, 21, e04040. [Google Scholar] [CrossRef]
- Li, D.; Sun, B.; Yang, L.; Wang, W. Mechanical and thermal properties of recycled coarse aggregate concrete incorporating microencapsulated phase change materials and recycled tire rubber granules and its freeze-thaw resistance. J. Build. Eng. 2025, 101, 111821. [Google Scholar] [CrossRef]
- Song, B.; Nakamura, D.; Kawaguchi, T.; Kawajiri, S.; Rui, D. Quantifying the shear behavior of fine-grained soil with herbaceous plant roots under freeze-thaw conditions using X-ray CT scan. Soil Tillage Res. 2025, 246, 106326. [Google Scholar] [CrossRef]
- Shu, H.; Yu, Q.; Niu, C.; Wang, Q. The crack characteristics and microscopic mechanism of composite solidified soil under alternating wet-dry and freeze-thaw cycles. Cold Reg. Sci. Technol. 2025, 235, 104479. [Google Scholar] [CrossRef]
- Liu, R.; Zhang, W.; Han, S.; Du, H.; Cui, P.; Ma, Z.; Feng, X.; Zhang, W. A numerical heat transfer model and performance evaluation of coaxial geothermal heat exchanger under soil freezing conditions. Appl. Therm. Eng. 2025, 266, 125538. [Google Scholar] [CrossRef]
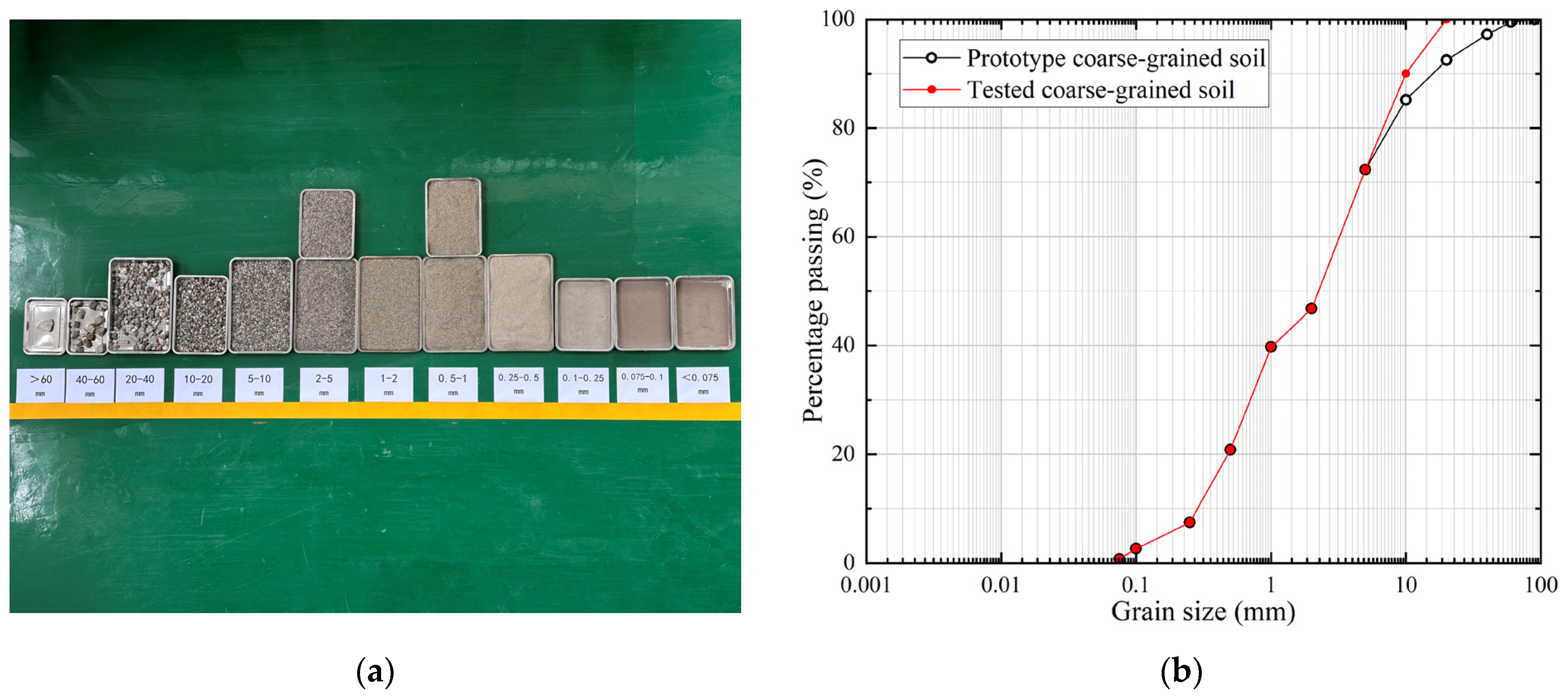




| Parameter | Natural Density (g/cm3) | Maximum Dry Density (g/cm3) | Minimum Dry Density (g/cm3) | Optimum Moisture Content (%) | Natural Moisture Content (%) | Specific Gravity (g/cm3) |
|---|---|---|---|---|---|---|
| Measured Value | 1.97 | 2.15 | 1.76 | 7.6 | 1.2 | 2.65 |
| Parameter | Density (kg/m3) | Thermal Conductivity (W/(m·K)) | Specific Heat Capacity (J/(kg·K)) | Porosity (%) | Young’s Modulus (MPa) | Poisson’s Ratio | Cohesion (kPa) | Internal Friction Angle (rad) |
|---|---|---|---|---|---|---|---|---|
| Initial Slope | 2150 | 3 | 1500 | 30 | 120 | 0.2 | 33.92 | 0.442 |
| Moisture Content | Cohesion c (Pa) | Internal Friction Angle φ (rad) |
|---|---|---|
| 7.6% | c = 31,728*exp(−0.002*FT) | φ = 0.4206*exp(−0.002*FT) |
| 9.6% | c = 25,128*exp(−0.003*FT) | φ = 0.4032*exp(−0.002*FT) |
| 11.6% | c = 17,181*exp(−0.003*FT) | φ = 0.3864*exp(−0.002*FT) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, H.; Wang, P.; Chen, L.; Sang, D.; Li, C.; Shi, C.; Zhang, W. Experimental and Numerical Analysis of Freeze–Thaw-Induced Mechanical Degradation in the Coarse-Grained Soil of the Southeastern Qinghai–Xizang Plateau. Appl. Sci. 2025, 15, 4900. https://doi.org/10.3390/app15094900
Niu H, Wang P, Chen L, Sang D, Li C, Shi C, Zhang W. Experimental and Numerical Analysis of Freeze–Thaw-Induced Mechanical Degradation in the Coarse-Grained Soil of the Southeastern Qinghai–Xizang Plateau. Applied Sciences. 2025; 15(9):4900. https://doi.org/10.3390/app15094900
Chicago/Turabian StyleNiu, Huan, Peiqing Wang, Liang Chen, Ding Sang, Chao Li, Congyou Shi, and Wengang Zhang. 2025. "Experimental and Numerical Analysis of Freeze–Thaw-Induced Mechanical Degradation in the Coarse-Grained Soil of the Southeastern Qinghai–Xizang Plateau" Applied Sciences 15, no. 9: 4900. https://doi.org/10.3390/app15094900
APA StyleNiu, H., Wang, P., Chen, L., Sang, D., Li, C., Shi, C., & Zhang, W. (2025). Experimental and Numerical Analysis of Freeze–Thaw-Induced Mechanical Degradation in the Coarse-Grained Soil of the Southeastern Qinghai–Xizang Plateau. Applied Sciences, 15(9), 4900. https://doi.org/10.3390/app15094900








