An Axial Compression Transformer for Efficient Human Pose Estimation

Abstract

Transformer has a wide range of applications in human posture estimation. It can model the global dependence relationship of images through the self-attention mechanism to obtain key human body information. However, Transformer consumes a lot of computation. An axial compression pose transformer (ACPose) method is proposed to reduce part of the computational cost of Transformer by the axial compression of the input matrix, while maintaining the global receptive field by feature fusion. A Local Enhancement Module is constructed to avoid the loss of too much feature information in the compression process. In the COCO dataset experiment, there was a significant reduction in computational cost compared to those of state-of-the-art transformer-based algorithms.

1. Introduction

Two-dimensional (2D) human pose estimation is a crucial task in computer vision, aiming to detect and localize the keypoints of the human body from a given image. With the advancement of deep learning methods, 2D human pose estimation has achieved significant improvements in both accuracy and real-time performance, enabling its wide application in various real-world scenarios, such as motion analysis [1,2,3,4,5] and human–computer interaction [6,7,8,9,10,11].

In the field of motion analysis, human pose estimation technology provides technical support for athletes. By capturing an athlete’s posture, their technique can be analyzed to adjust its standardization and accuracy, facilitating coaches in refining technical details and customizing training plans. In virtual reality and augmented reality fields, human pose estimation technology is a crucial component for human–computer interaction. By recognizing human postures and mapping them to the virtual world, real-time human–computer interaction is enabled, enhancing immersion and interactivity.

Over the last decade, Convolutional Neural Networks (CNNs) have been widely adopted for human pose estimation due to their ability to capture local features through local receptive fields, allowing them to focus on keypoint information [12,13,14]. However, CNNs’ strong reliance on local features limits their capacity to capture global contextual information, which is crucial for accurate pose estimation as it requires a comprehensive understanding of the image content.

The introduction of Transformer architectures has brought about significant breakthroughs in this field. Compared to the traditional methods, Transformers leverage their self-attention mechanism to effectively capture the relationships between different parts of an input sequence, leading to a superior performance in keypoint detection tasks (as shown in [15,16,17,18,19,20]). Furthermore, the multi-layer self-attention mechanism enhances the model’s ability to recognize complex poses. To combine the advantages of CNNs and Transformers, other researchers have proposed various hybrid architectures [21]. For instance, TransPose [22] utilizes CNNs for feature extraction and Transformers to capture global dependencies, while TokenPose [23] introduces keypoint tokens to further improve performance. However, these methods often face a high computational cost, which hinders their deployment in real-time applications.

Addressing this challenge, we propose an axial compression module designed to simplify the network structure within a Transformer, while preserving crucial information, enabling efficient global modeling. Our method integrates the axial compression module into the Transformer architecture. The input data undergo lightweight processing, followed by attention calculations. Specifically, we employ average pooling operations to compress the input along both the horizontal and vertical axes, generating two matrices. These are then processed through a multi-head attention mechanism to capture the relative positional information of the keypoints. Additionally, our unique design for splitting attention heads allows for each head to focus more intently on specific directional position information (horizontal or vertical), thereby enhancing the model’s understanding of the global features associated with keypoints. To recover the potentially lost local visual features during the axial compression process, we introduce a Local Enhancement Module. Specifically, after obtaining the output from the axial compression module, we calculate the residual difference between the original input and the compressed output. This residual is then subjected to average pooling dimensionality reduction, followed by multi-head self-attention operations, effectively extracting local information missed by the axial compression module. By fusing this extracted local information with the output of the axial compression module, we achieve a synergistic combination of global features and local details. The basic principle is as follows:

(1)

Text is human-generated, highly condensed information, while images are natural information containing a lot of redundancy and noise. Compression operations can reduce the useless information in images.

(2)

For human pose estimation tasks, compression operations do not significantly lose global semantic information. CNNs initially extract the local features from images, while Transformer structures tend to establish global dependencies.

(3)

From a biological perspective, human vision can partially fill in missing parts of an image. Similarly, the performance loss caused by missing some visual information in Transformers is relatively low.

Compared to other lightweight methods, such as pruning [24,25], upsampling [26], and depthwise convolution [27], our axial compression module significantly reduces the computational cost, while retaining keypoint global feature information. The experimental results demonstrate that this method effectively decreases the model parameter count and the computational cost, while maintaining high detection accuracy, providing a novel solution for lightweight human pose estimation tasks.

Building upon this idea, we propose a new and efficient attitude estimation method based on axial compression Transformer, named ACPose. Figure 1 illustrates the ACPose architecture, we utilizes TokenPose [23] as the baseline network. It first extracts feature maps using CNNs, flattens them into visual tokens, and adds randomly initialized keypoint tokens to represent human keypoints. These tokens are then fed into Transformer. Subsequently, the input Transformer’s feature matrix undergoes horizontal and vertical average pooling. Multi-head attention is applied to the compressed matrices, and the results are fused. The difference matrix obtained by subtracting the fused matrix from the original Transformer input is average-pooled and subjected to self-attention. This result is then merged with the output of the axial compression stage. Finally, we use the traditional heatmap methods to predict the keypoints.

In summary, this article has the following three contributions:

• Novel Compress–Merge Strategy: This paper introduces a novel compress–merge strategy, implemented in the proposed axial compression pose Transformer (ACPose) network for efficient human pose estimation. By employing compression operations to reduce the computational cost, while utilizing feature fusion to maintain Transformer’s global receptive field, this strategy mitigates performance degradation caused by irrelevant information in human pose estimation tasks.
• Local Enhancement Method: This work proposes a local enhancement method that leverages the difference between the compressed and original inputs to amplify the lost local details. This technique effectively enhances the extraction of local features, leading to a significant improvement in prediction accuracy.
• Competitive Performance with Reduced Complexity: Extensive experiments conducted on prominent public datasets demonstrate that our approach achieves a substantial 81.2% reduction in computational cost of the Transformer part, while maintaining competitive accuracy. These results highlight the effectiveness of our proposed method in achieving lightweight, yet high-performing human pose estimation.

2. Related Work

2.1. Efficient Vision Transformer

In recent years, we have witnessed significant advancements in vision Transformers, with notable contributions in areas such as image classification, object detection, and image segmentation. While some methods have achieved impressive accuracy at a high computational cost, their resource demands often hinder practical applications. Consequently, some researchers have explored techniques to streamline Transformer architectures and design efficient vision Transformer models. For instance, BEiT [28] employs a masked learning strategy by randomly masking portions of an image and training the model to predict the occluded content. This approach enables the model to learn global contextual information, while reducing the computational costs. SeaFormer [29] utilizes a combination of axial compression and convolutional fusion to simultaneously capture both global and local image information. DilateFormer [30] focuses on the self-attention mechanism, selecting a limited number of patches surrounding each query patch for attention computation. By employing different dilation rates across different heads, it effectively reduces the computational cost of the Transformer layers.

2.2. Transformer-Based Pose Estimation Methods

The multi-head self-attention mechanism within Transformers effectively captures the long-range dependencies between human keypoints, which is crucial for accurately predicting their relationships. Recognizing this, some researchers have applied vision Transformers to the field of human pose estimation, resulting in the emergence of numerous Transformer-based human pose estimation networks.

Several notable works have applied Transformers to human pose estimation. TFPose [31] recasts the task as a sequence prediction problem utilizing Transformer encoder-decoder architecture for keypoint regression. VITpose [32], based on the ViT [12] backbone, employs a simple Transformer baseline and enhances accuracy by increasing the model size. HRFormer [33] leverages parallel multi-resolution streams to jointly learn features and integrates them through a multi-scale fusion module, achieving the fusion of different distance attention mechanisms. TokenPose [18] extracts features using CNNs and introduces the concept of keypoint tokens, enabling Transformer to learn the global constraints. These methods demonstrate the effectiveness of Transformers in human pose estimation, with TokenPose [18] achieving competitive accuracy, while maintaining a relatively small model size. Consequently, this paper adopts TokenPose [18] as the baseline network for experimentation.

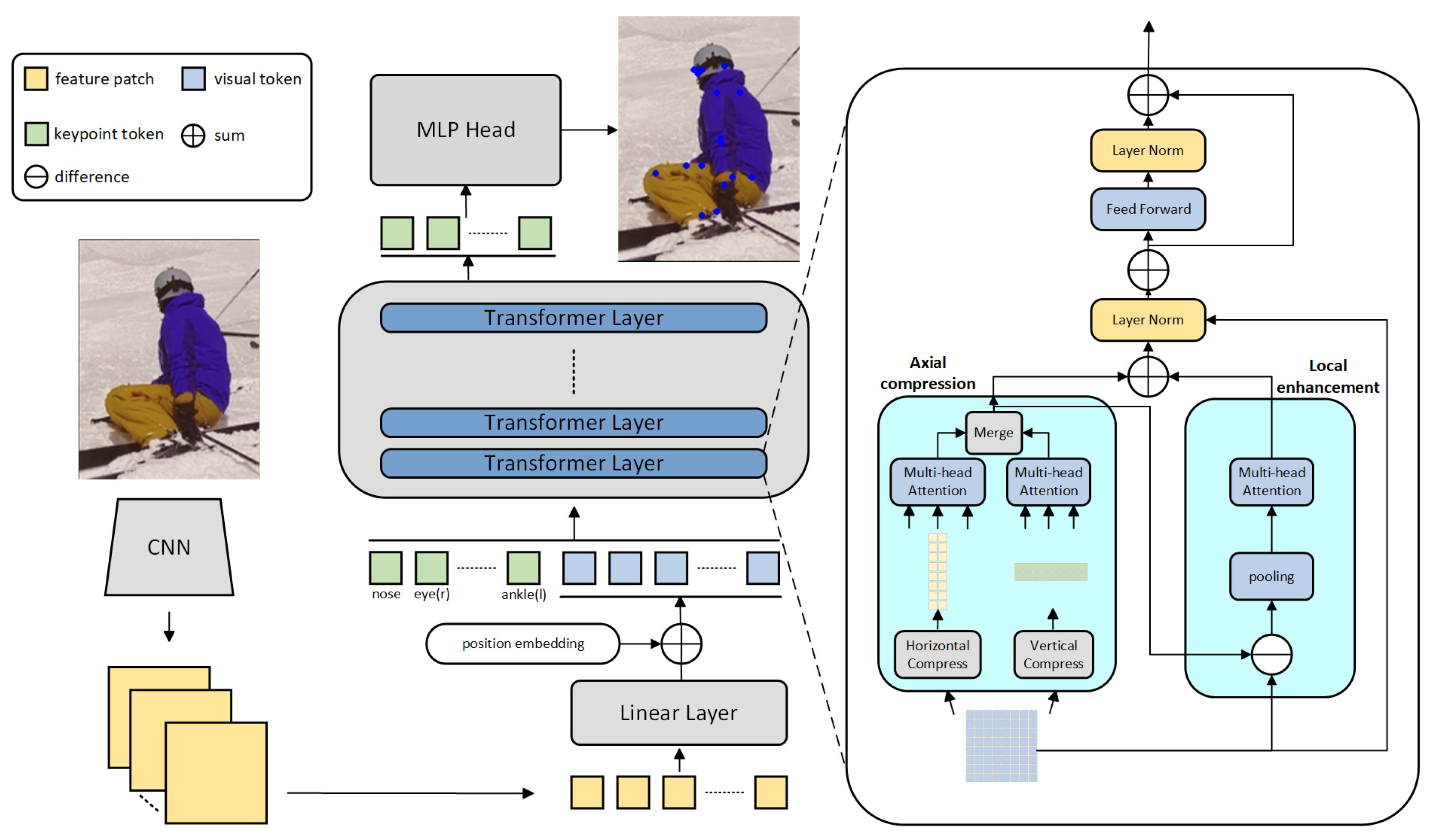
3. Methods

Our objective is to develop a model capable of efficiently performing human pose estimation. The proposed approach first extracts features from input human images using CNNs. These feature maps are then partitioned into patches and flattened into one-dimensional vectors, which are combined with randomly initialized keypoint tokens and fed into Transformer. Within Transformer, we replace the standard multi-head attention operation with axial compression and Local Enhancement Modules. Finally, the output is mapped to a heatmap through an MLP, and then decoded to obtain the keypoint coordinates, yielding the final prediction results. The following five sections present the details of our approach.

3.1. Tokenization

Feature extraction and tokenization are performed using a CNN. An input image is fed into the CNN to extract features. To enhance model efficiency, we employ the first three stages of HRNet [34], which have a parameter count one-fourth that of the complete HRNet. Following convolutional network feature extraction, the output feature map has dimensions 1/4 the size of the original input image (denoted as $x\in {ℝ}^{H\times W\times C}$). This output feature map is then divided into a grid along both the height (H) and width (W) dimensions, resulting in ${\displaystyle \frac{H}{P_h}}\times {\displaystyle \frac{W}{P_w}}$ grid cells. Each grid cell has a size of $x_p\in {ℝ}^{P_h\times P_w\times C}$. Each grid cell is flattened into a one-dimensional sequence of size $P_h\times P_w\times C$, which is then mapped to a visual token through a linear layer. Since accurate keypoint localization is crucial for human pose estimation, two-dimensional positional embedding $p{e}_i$ is incorporated into each specific visual token $v_i$, resulting in a visual token of $\left\{v_1+p{e}_1, v_2+p{e}_2,\cdots , v_L+p{e}_L\right\}$, where L represents the total number of visual tokens. Concurrently, N keypoint tokens are randomly initialized to represent the human keypoints, with N determined by the number of keypoints in the dataset. Finally, these two types of token are connected and input into Transformer for training.

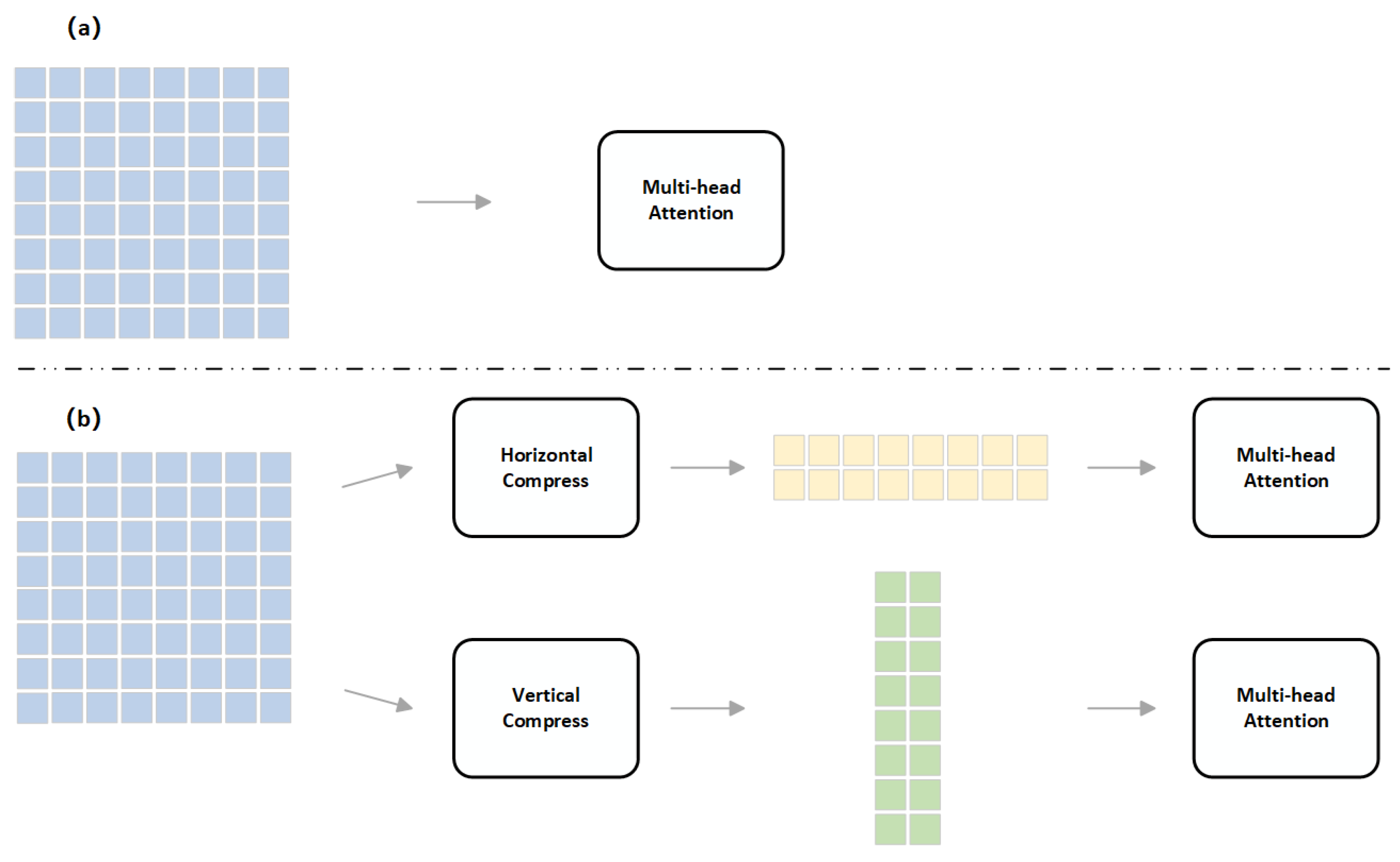
3.2. Axial Compression Module

This paper proposes an axial compression module for lightweight network architectures. Figure 2a depicts the traditional approach, while Figure 2b shows a schematic diagram of the method proposed in this paper. Within Transformer, the input data are first processed by this axial compression module for lightweight computation and attention calculation. Specifically, assuming the input is $X\in {ℝ}^{n\times d}$, where n denotes the number of sequences and d denotes the sequence length, we employ average pooling to simplify the network structure, while emphasizing the relative positions of the keypoints. X is averaged along both the horizontal and vertical axes, resulting in two compressed matrices, $X_h\in {ℝ}^{n\times h}$ and $X_v\in {ℝ}^{h\times d}$, respectively. Here, h represents the number of heads in the multi-head attention mechanism. This effectively compresses the global information into these two matrices. Subsequently, $X_h$ and $X_v$ are linearly mapped to generate two sets of matrices: the query ($Q_n$, $Q_d$), the key ($K_n$, $K_d$), and the value ($V_n$, $V_d$). These qkv matrix pairs are then fed into a multi-head attention module to compute the attention scores.

$$y_h={\displaystyle \sum _{p=1}^{n}softma{x}_p\left(\frac{q_{\left(\mathrm{h}\right)p}\times {k_{\left(h\right)}}^T}{\sqrt{d_k}}\right)\cdot {v_{\left(h\right)}}_p}$$

(1)

$$y_v={\displaystyle \sum _{p=1}^{d}softma{x}_p\left(\frac{q_{\left(v\right)p}\times {k_{\left(v\right)}}^T}{\sqrt{d_k}}\right)\cdot {v_{\left(v\right)}}_p}$$

(2)

In this context, $d_k$ represents the key dimension. The attention score determines the attention level that the current query token should give to each key. Furthermore, when splitting the attention heads, $q_{\left(h\right)}$, $k_{\left(h\right)}$, and $v_{\left(h\right)}$ are divided into h heads of size n × 1, and $q_{\left(v\right)}$, $k_{\left(v\right)}$, and $v_{\left(v\right)}$ are divided into h heads of size 1 × d. This operation allows for multiple attention heads to capture richer horizontal and vertical positional information. The two output matrices, $y_h$ and $y_v$, are then fused to form a global positional feature representation. To ensure that the fused representation fully establishes global dependencies, the matrices $y_h$ and $y_v$, which participate in fusion, must acquire comprehensive information along each individual axis, both horizontally and vertically. Therefore, after obtaining the feature matrices $y_h\in {ℝ}^{n\times h}$ and $y_v\in {ℝ}^{h\times d}$ through the self-attention mechanism, they are subjected to average pooling operations along both the horizontal and vertical axes, and further compressed into $y_{h1}\in {ℝ}^{n\times 1}$ and $y_{v1}\in {ℝ}^{1\times d}$, respectively. This aggregates the multi-dimensional information obtained from the multi-head attention mechanism onto a single axis. Subsequently, to fuse these two axial feature matrices, we use the repeat operation to expand the matrices $y_{h2}\in {ℝ}^{n\times d}$ and $y_{v2}\in {ℝ}^{n\times d}$ into $y_{h2}\in {ℝ}^{n\times d}$ and $y_{v2}\in {ℝ}^{n\times d}$, resulting in two feature matrices with the same shape. Finally, by summing $y_{h2}$ and $y_{v2}$, we obtain the feature matrix $y_o$. Each point in this matrix encompasses both the horizontal positional features and the vertical positional features, indicating that the keypoint tokens have acquired comprehensive global positional information and established long-range dependencies with visual features.

3.3. Detail Augmentation Module

To recover local visual features that may be lost during the compression process, we propose a Local Enhancement Module. Specifically, after obtaining the output $y_o$ from the axial compression module, we subtract the output $y_o$ from the original Transformer input X. The resulting difference is then subjected to average pooling with a kernel size of $k \times k$ (where k takes on values of 2, 3, and 4) to reduce dimensionality and maintain computational efficiency. Subsequently, multi-head self-attention is applied to the pooled matrix to effectively extract local information that may have been overlooked by the axial compression module. Finally, the output is fused with $y_o$. Since the dimension of the pooled matrix is reduced, we employ bilinear interpolation to expand it back to its original dimension before matching $y_o$’s dimensions. The final result, obtained by adding this expanded output to $y_o$, represents the output of the Local Enhancement Module.

3.4. Transformer Architecture

Depending on the version setup, we use different Transformer layers as the encoder, as illustrated in Figure 1. These Transformer layer primarily consists of an axial compression module, a feature fusion module, and a feed-forward network. Furthermore, both the axial compression module and the feed-forward network are preceded by regularization and residual connection mechanisms. The computational formula for this is as follows:

$$LayerNorm\left(X+MultiHeadAttention\left(X\right)\right)$$

(3)

$$LayerNorm\left(X+FeedForward\left(X\right)\right)$$

(4)

where $MultiHeadAttention\left(X\right)$ represents the output of the multi-head attention layer, and $FeedForward\left(X\right)$ represents the output of the feed-forward network layer; their output shapes are consistent with the original input X, allowing for direct summation.

Human keypoint detection is a complex task primarily focused on obtaining keypoint coordinates. While the standard Transformer methods utilize self-attention mechanisms to acquire global receptive fields for extracting positional information, this often comes with a significant computational burden. Therefore, addressing these concerns, we compress the matrices during self-attention operations, streamlining the network structure while simultaneously achieving a global receptive field comparable to that of standard Transformers through the fusion of information along two axes. Unlike other prevalent Pose Transformer architectures, our proposed Transformer presents a more efficient and lightweight network structure.

3.5. Heatmap

During the output stage of Transformer, we select only N keypoint tokens as the output and process them through a multi-layer perceptron (MLP). This mapping results in a two-dimensional heatmap $P\in {ℝ}^{N\times H\times W}$, where H and W represent 1/4 the size of the original image dimensions. Subsequently, a reshape operation transforms this heatmap into $P\in {ℝ}^{N\times H^{*}\times W^{*}}$, matching the dimensions of the original image. We can then locate the human keypoints by identifying the position of the maximum response value on this heatmap, as illustrated in Figure 3. The location corresponding to the maximum response represents our predicted human keypoint. During model training, we employ the Mean Squared Error (MSE) loss function to compare the predicted heatmap with the ground truth heatmap. The mathematical formula for the MSE loss function is as follows:

$$L_{MSE}={\displaystyle \frac{1}{2}}{\displaystyle \sum _{i=1}^N‖P_i{-{P_i}^{^}‖}^2}$$

(5)

where N represents the number of human keypoints, which varies depending on the dataset; $P_i$ denotes the ground truth heatmap, and ${P_i}^{^}$ represents the predicted heatmap.

4. Results

4.1. Setup

In this paper, we designed three versions of ACPose, as shown in

Table 1. Structure configuration table of different ACPose models.

Model	#Params	CNN Backbone	Heads	Layers	GFLOPs
ACPose-Base	13.9M	HRNetW32-stage3	8	12	5.1
ACPose-Large/D6	20.8M	HRNetW48-stage3	8	6	9.1
ACPose-Large/D24	27.5M	HRNetW48-stage3	12	24	9.8

. The base utilizes the first three stages of HRNet-W32 as the backbone for the CNN stage, large employs the first three stages of HRNet-W48 as the backbone, and D24 denotes Transformer with 24 layers.

During training, the images from the COCO dataset are cropped to 256 × 192 dimensions, while those from the MPII dataset are cropped to 256 × 256. We employ the Adam optimizer with a total of 300 epochs and an initial learning rate of 1 × 10⁻³. The learning rate is adjusted to 1 × 10⁻⁴ and 1 × 10⁻⁵ at epochs 200 and 260, respectively. To address the uncertainty caused by insufficient model training and limited training data, we adjusted the batch size during model training, conducting multiple trainings with settings of 32, 64, and 128. The experiments are conducted on a hardware environment consisting of two NVIDIA RTX 4090 24G GPUs with a software environment comprising PyTorch 2.3.0 and CUDA 12.1. The manufacturer is ASUS and the location is Shanghai, China.

4.2. Quantitative Results

The COCO dataset comprises over 200,000 images and 250,000 person instances; each instance is annotated with 17 keypoints. The COCO dataset is divided into train, validation, and test-dev sets, containing 57k, 5k, and 20k images, respectively. We trained our model on the COCO train2017 set and evaluated it on the COCO validation and COCO test-dev sets. A commonly used evaluation metric for the COCO dataset is Average Precision (AP), which is calculated based on Object Keypoint Similarity (OKS). The formula for calculating OKS is as follows:

$$OKS={\displaystyle \frac{{\displaystyle {\sum }_i{e}^{-d_i^2/2s^2{k}_i^2\delta \left(v_i>0\right)}}}{{\displaystyle {\sum }_i\delta \left(v_i>0\right)}}}$$

(6)

In this case, $d_i$ represents the Euclidean distance between the predicted keypoint coordinates and their corresponding ground truth values. $v_i$ indicates whether each keypoint is visible. $s$ represents the area of the human part of it, and $k_i$ represents the weight assigned to each keypoint.

The formula for calculating AP is as follows:

$$A{P}_t={\displaystyle \frac{{\displaystyle {\sum }_p\delta \left(OKS>t\right)}}{{\displaystyle {\sum }_{p}1}}}$$

(7)

When t = 0.5 and 0.75, AP is represented as $A{P}^{50}$ and $A{P}^{75}$, while $A{P}^L$ and $A{P}^M$ represent evaluation metrics for large-scale and medium-scale objects, respectively. Additionally, we also employ Average Recall (AR) as an evaluation metric.

We use GFLOPs as the evaluation standard for model computational cost, where FLOP stands for floating-point operations, s represents seconds, and FLOPs represent the number of floating-point operations per second. Therefore, GFLOPs represent billions of operations per second. We utilize the thop library to output the GFLOPs in the model network.

As shown in

Table 2. Performance comparison between ACPose and mainstream models on COCO dataset.

Method	#Params	GFLOPs	$\mathit{G}\mathit{F}\mathit{L}\mathit{O}\mathit{P}{\mathbf{s}}^{\mathit{T}}$	AP	$\mathbf{A}{\mathbf{P}}^{50}$	$\mathbf{A}{\mathbf{P}}^{75}$	$\mathbf{A}{\mathbf{P}}^{\mathbf{L}}$	$\mathbf{A}{\mathbf{P}}^{\mathbf{M}}$	AR
TransPose-R-A4	6.0M	8.9	3.38	72.6	89.1	79.9	68.8	79.8	78.0
TransPose-H-S	8.0M	10.2	4.88	74.2	89.6	80.8	70.6	81.0	79.5
TransPose-H-A6	17.5M	21.8	11.4	75.8	90.1	82.1	71.9	82.8	80.8
TokenPose-B *	13.5M	5.7	1.29	75.6	89.8	81.4	71.3	81.4	80.0
TokenPose-L/D6 *	20.8M	10.3	1.97	77.7	90.0	81.8	71.8	82.4	80.4
ViTPose-Base	86.0M	18.6	-	75.8	90.7	83.2	78.4	68.7	81.1
SHaRPose-Base	93.9M	17.1	-	75.5	90.6	82.3	82.2	72.2	80.8
ACPose-B *	13.9M	5.1 (−11%)	0.68 (−47.3%)	75.7 (+0.1%)	92.5	82.7	72.8	80.0	78.2
ACPose-L/D6 *	21.0M	8.8 (−15%)	0.37 (−81.2%)	77.4 (−0.4%)	93.6	84.8	74.3	81.8	79.9
ACPose-L/D24 *	27.5M	9.9	1.52	77.4	93.6	83.8	74.4	81.9	79.9

* The asterisk indicates the usage of GTBox; $GFLOP{\mathrm{s}}^T$ represents the computational cost of the Transformer part.

, we evaluated the performance of ACPose on the mainstream COCO dataset. The results demonstrate that our ACPose model achieves a more significant reduction in computational cost compared to those of the other prevailing models, while maintaining competitive AP scores. Specifically, compared to TokenPose-L/D6, our ACPose-L/D6 reduces the Transformer-related computational cost by 81.2% with only a 0.4% decrease in accuracy; the results show that the original method, TokenPose, generates a large number of matrix operations due to the excessive data volume in the Transformer layers, resulting in high GFLOPs. Our method significantly reduces the data volume through compression operations, thereby substantially lowering the GFLOPs, primarily within the Transformer structure. Furthermore, our ACPose-B achieves a 47.3% reduction in the Transformer-related computational cost, while improving accuracy by 0.1%.

Compared to TransPose-H-A6, our method exhibits substantial reductions in computational cost and demonstrates superior accuracy. Additionally, as evident from the table, our approach out-performs the ViTPose and SHaRPose methods by reducing the computational cost without compromising the performance.

The MPII dataset comprises over 25,000 images and 40,000 person instances, each instance annotated with 16 human keypoints. In the MPII dataset, we primarily utilize the Percentage of Correct Keypoints (PCKs) as the evaluation metric, specifically PCK@0.5 as our final experimental result.

As shown in

Table 3. Performance comparison between ACPose and mainstream models on MPII dataset.

Method	#Params	$\mathit{G}\mathit{F}\mathit{L}\mathit{O}\mathit{P}{\mathbf{s}}^{\mathit{T}}$	Hea	Sho	Elb	Wri	Hip	Kne	Ank	Mean
SimpleBaseline-R50	34.0M	-	96.4	95.3	89.0	83.2	88.4	84.0	79.6	88.5
SimpleBaseline-R101	53.0M	-	96.9	95.9	95.9	84.4	88.4	84.5	80.7	89.1
SimpleBaseline-R152	53.0M	-	97.0	95.9	90.0	85.0	89.2	85.3	81.3	89.6
HRNetW32	28.5M	-	96.9	96.0	90.6	85.8	88.7	86.6	82.6	90.1
TokenPose-L/D6	21.4M	0.64	97.1	95.9	91.0	85.8	89.5	86.1	82.7	90.2
ACPose-L/D6 (Ours)	21.66M	0.39 (−39.0%)	97.1	96.1	90.9	86.1	88.9	86.1	81.6	90.0 (−0.2%)

$GFLOP{\mathrm{s}}^T$ represents the GFLOPs of the Transformer part. Bold indicates the optimal indicator.

, we evaluated our model on the MPII dataset. Compared to the other mainstream methods, our model demonstrates a significant reduction in the computational cost. Compared to the TokenPose [18] method, $GFLOP{\mathrm{s}}^T$ is reduced by 39.0%, with only a 0.2% loss in accuracy. Specifically, ACPose-L/D6 achieves 96.1% and 86.1% prediction accuracy for the shoulder joint (Sho) and wrist joint (Wri), respectively, surpassing the TokenPose-L/D6 method. This indicates that our approach does not compromise overall prediction accuracy, while achieving a well-balanced efficient human pose estimation network in terms of both precision and computational cost.

4.3. Qualitative Results

Figure 4 presents the comparative analysis of our method, ACPose, and the TokenPose [18] method on the COCO dataset. As illustrated in the figure, ACPose demonstrates a more accurate inference of the human keypoint locations. The first image reveals that ACPose excels at identifying the keypoints in overlapping images and exhibits heightened sensitivity in recognizing smaller human targets within an image. This suggests that ACPose’s Local Enhancement Module effectively enhances the recognition capability for fine-grained details within images. The second and third images showcase ACPose’s superior accuracy in predicting the human keypoints even under occlusion conditions. In conclusion, ACPose consistently out-performs the other methods in terms of pose estimation accuracy.

4.4. Ablation Study

To investigate the impact of the pooling kernel size k in the Local Enhancement Module on both prediction accuracy and computational cost, we conducted ablation experiments on the MPII dataset. The aim was to identify the optimal balance between resource consumption and model performance. As shown in

Table 4. Performance comparison of different size pooled cores on MPII datasets.

Model	k	#Params	GFLOPs	$\mathbf{G}\mathbf{F}\mathbf{L}\mathbf{O}\mathbf{P}{\mathbf{s}}^{\mathbf{T}}$	Mean
TokenPose-L/D6	-	21.49 M	11.85	0.64	90.2
ACPose-L/D6	4	21.49 M	11.56	0.35 (−45.3%)	89.4 (−0.9%)
ACPose-L/D6	3	21.53 M	11.57	0.36 (−43.8%)	89.8 (−0.4%)
ACPose-L/D6	2	21.66 M	11.60	0.39 (−39.0%)	90.0 (−0.2%)

, we varied the matrix compression size during the pooling stage within the Local Enhancement Module. The results demonstrate that as the pooling kernel size k decreases, both the computational cost and the parameter count gradually increase, accompanied by a corresponding improvement in the performance metrics. Specifically, when k = 4, $GFLOP{s}^T$ is reduced by 45.3% with a 0.9% decrease in accuracy. When k = 3, $GFLOP{s}^T$ is reduced by 43.8% with a 0.4% decrease in accuracy. When k = 2, $GFLOP{s}^T$ is reduced by 39.0% with a 0.2% decrease in accuracy. Based on this analysis, we conclude that k = 2 achieves the optimal balance between computational cost and accuracy, representing the most favorable combination.

To verify the influence of different compression degrees in axial compression on the results and obtain the optimal compression size, ablation experiments were conducted on the MPII dataset. The experiments mainly focused on adjusting the parameter h in the axial compression module to investigate the impact of the compression degree on the performance metrics. As shown in

Table 5. Performance comparison of different compression degrees h on MPII datasets.

Model	h	#Params	GFLOPs	$\mathbf{G}\mathbf{F}\mathbf{L}\mathbf{O}\mathbf{P}{\mathbf{s}}^{\mathbf{T}}$	Mean
TokenPose-L/D6	-	21.49 M	11.85	0.64	90.2
ACPose-L/D6	36	21.96 M	11.78	0.57 (−10.9%)	90.1 (−0.1%)
ACPose-L/D6	24	21.73 M	11.66	0.45 (−29.7%)	90.0 (−0.2%)
ACPose-L/D6	12	21.66 M	11.60	0.39 (−39.0%)	90.0 (−0.2%)

, as h decreases, the compression degree gradually increases, the computational cost and the parameter amount gradually decrease, and the accuracy metrics remain basically consistent. Specifically, when h is 36, $GFLOP{s}^T$ is reduced by 10.9%; when h is 24, $GFLOP{s}^T$ is reduced by 29.7%; and when h is 12, $GFLOP{s}^T$ is reduced by 39.0%. Based on the above analysis, we believe that when h is 12, a balance between computational cost and performance is achieved, making it the optimal compression choice.

5. Discussion

This paper demonstrates the higher efficiency of Transformer structures in focusing on global feature extraction. We propose ACPose, an efficient human pose estimation method that achieves significant reductions in model consumption without sacrificing accuracy, thereby addressing the balance between accuracy and speed in human pose estimation. Through the careful design of axial compression and Local Enhancement Modules, ACPose achieves competitive results on both the COCO and MPII datasets. The qualitative experiments show that our method can more accurately predict keypoint locations compared to other lightweight models when applied to human pose estimation. Furthermore, ablation studies were conducted to determine the optimal parameter settings for our model.

Despite achieving outstanding performance on the public datasets, we encountered certain challenges during our research. Specifically, while reducing dimensionality within Transformer, effectively lowering complexity, the current method does not differentiate the contribution of various tokens to human keypoint prediction during compression. This results in a degree of accuracy loss. Therefore, addressing this issue and exploring more nuanced token-specific compression strategies will be the focus of our future work.