Optimal Design and Seismic Performance of Base-Isolated Structures with Varying Heights Equipped with Tuned Inerter Dampers Subjected to Far-Fault and Near-Fault Ground Motions
Abstract
1. Introduction
2. Optimal Design of the TID
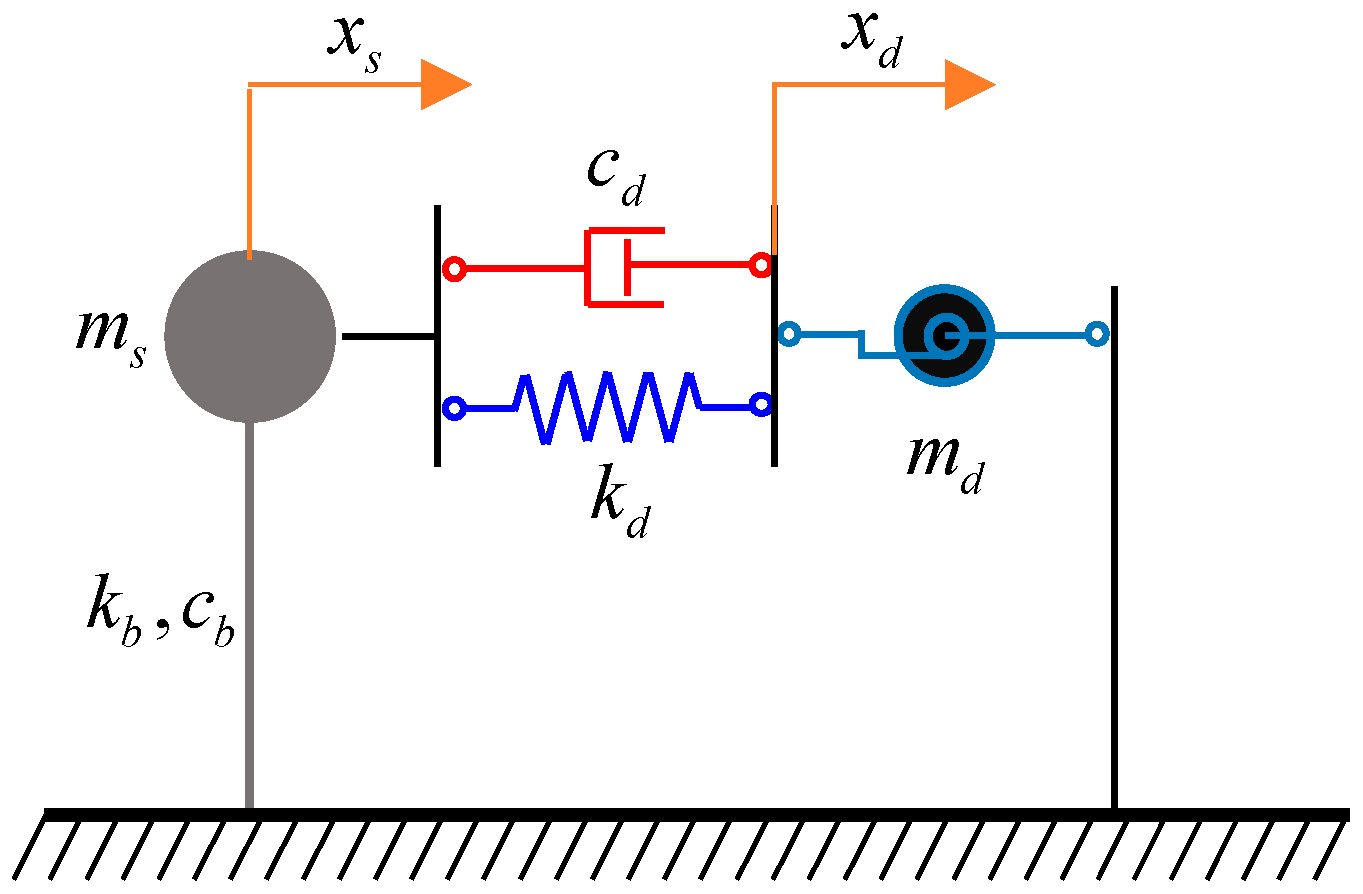
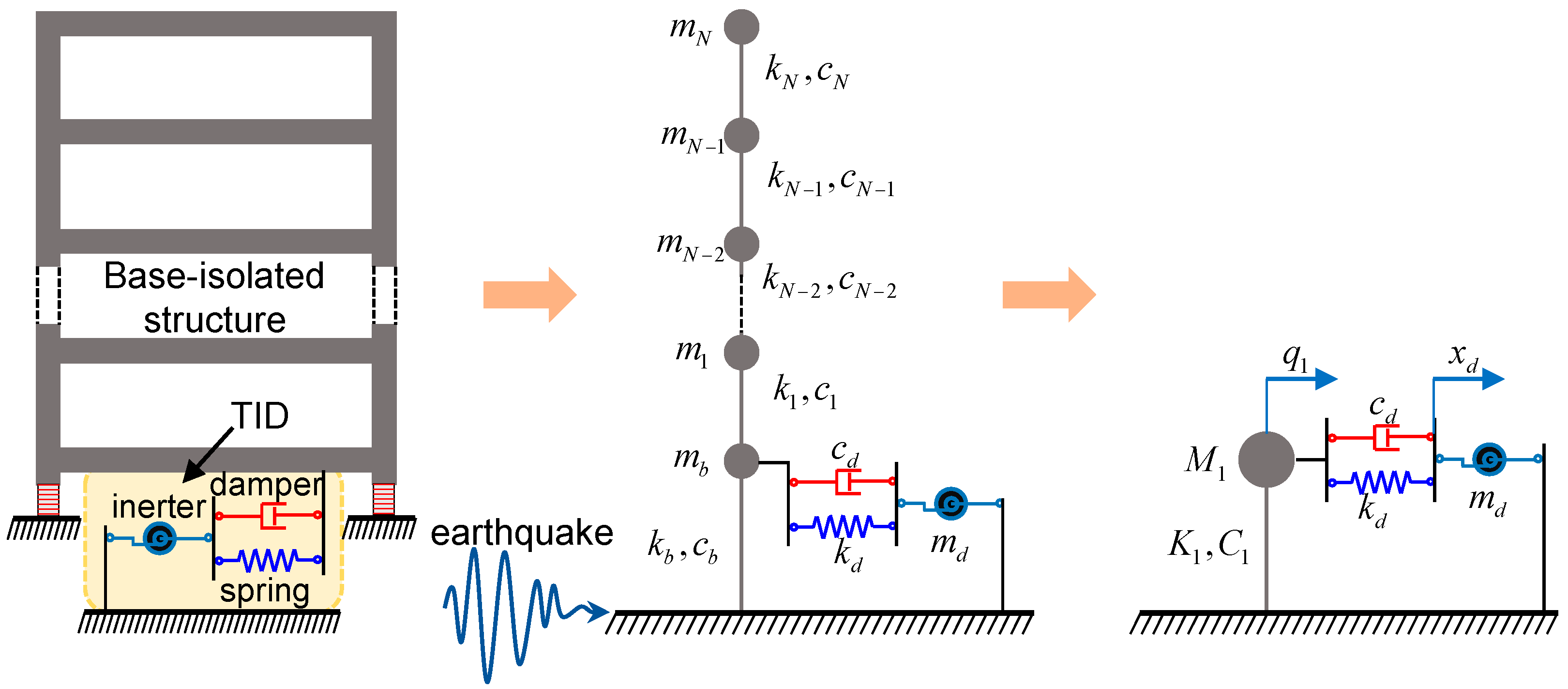
2.1. Mathematical Modelling
2.2. Optimization Problem
2.3. Optimization Method
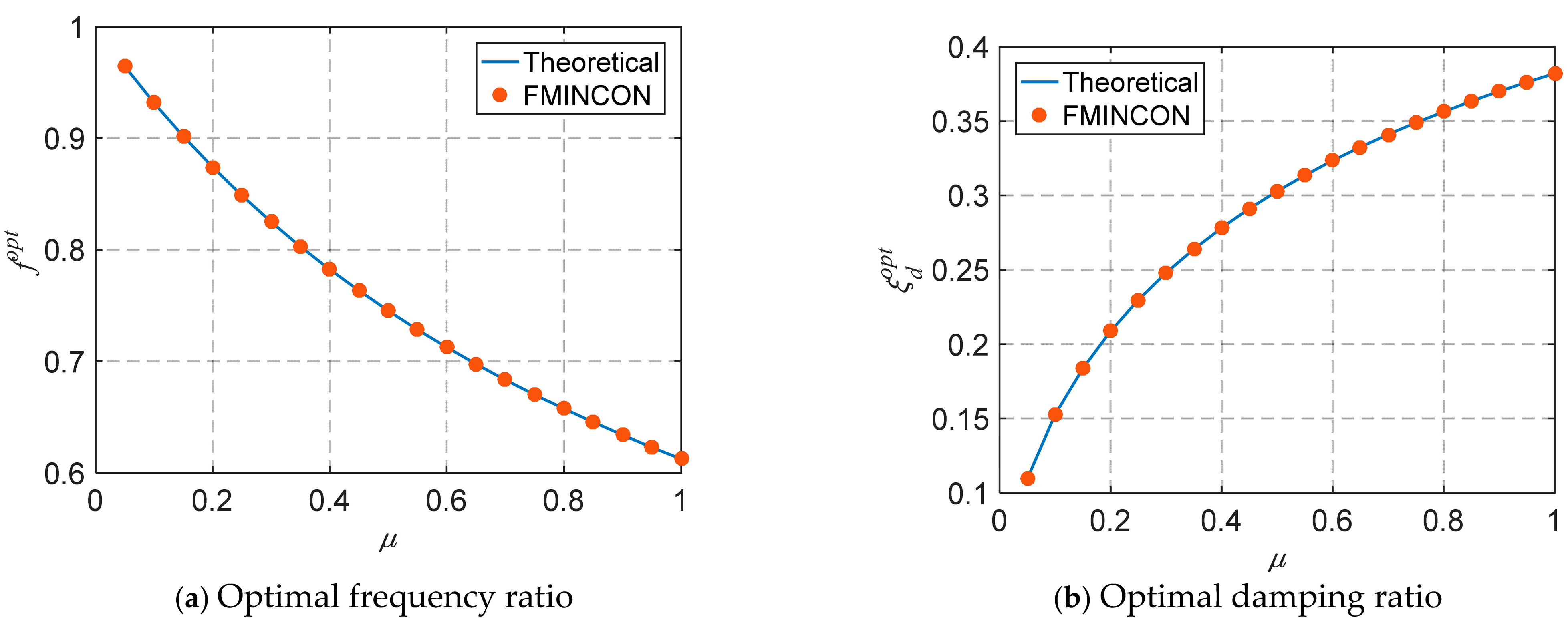
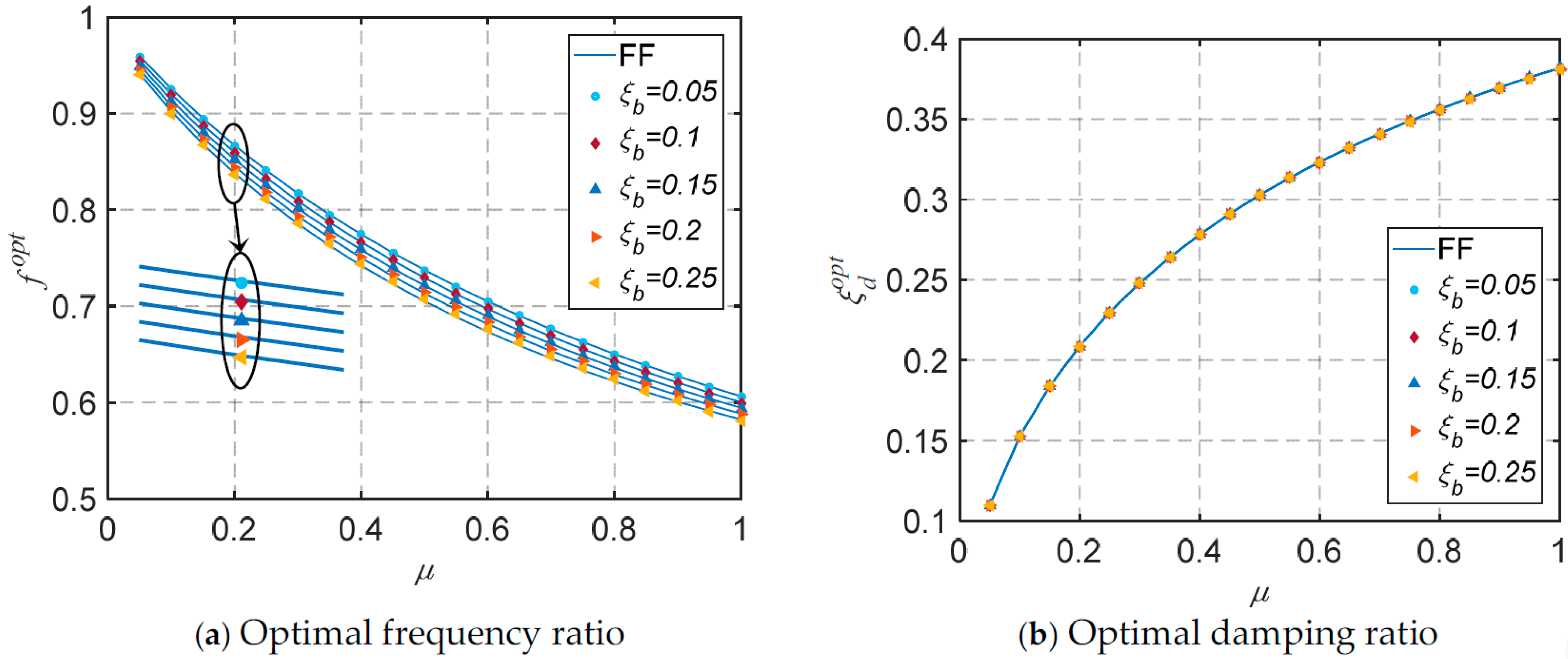
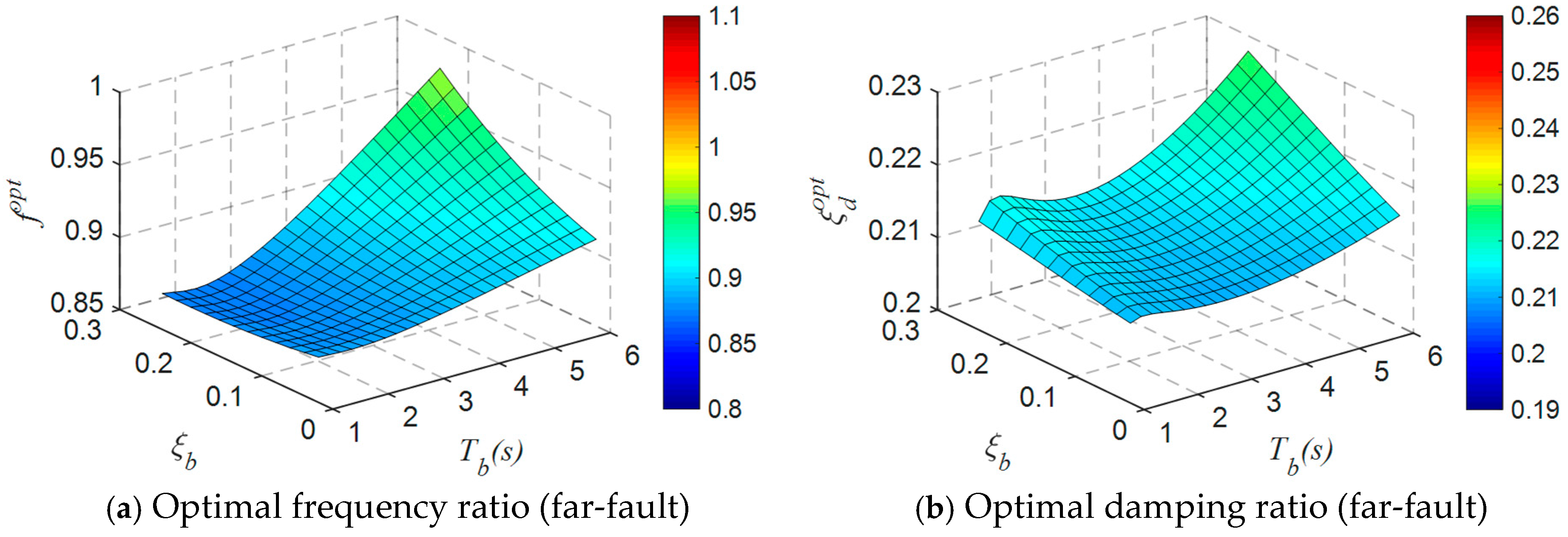
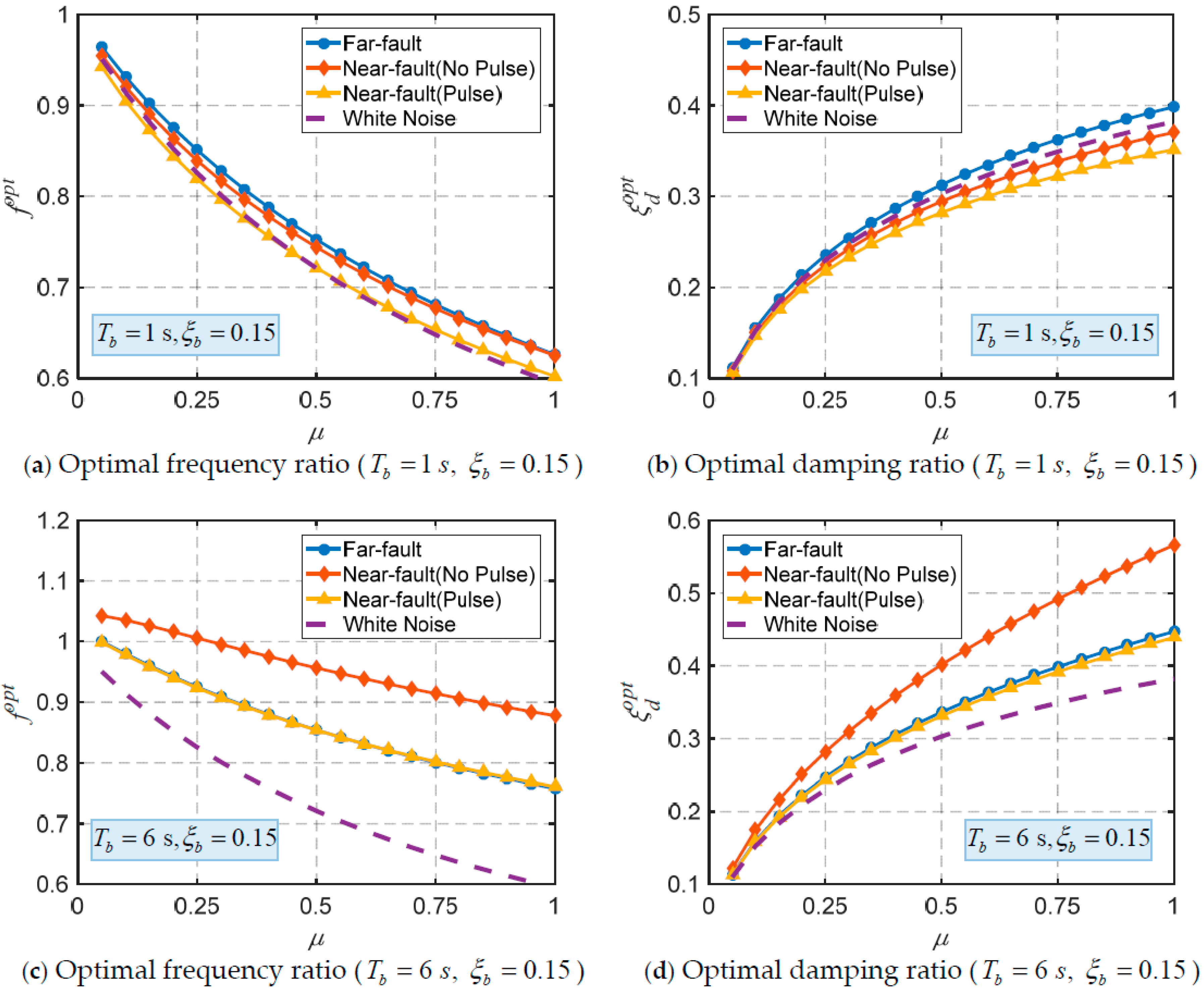
2.4. Optimization Results
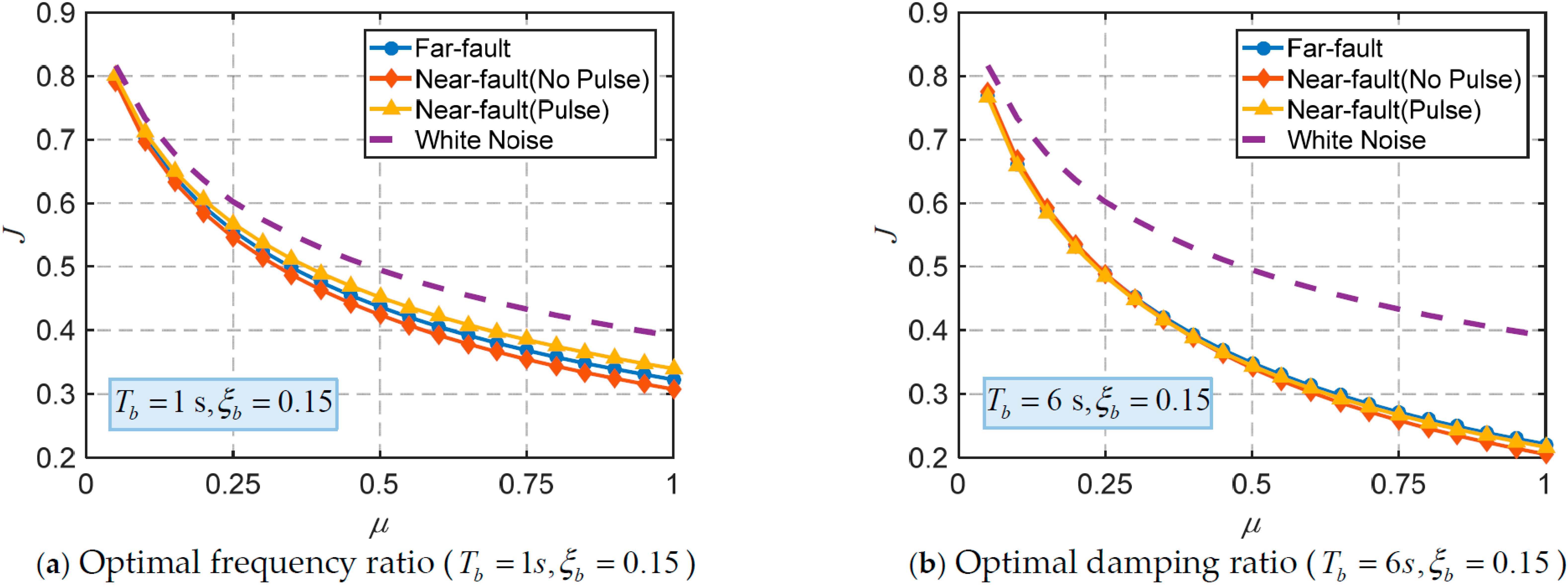
2.5. Control Effectiveness
3. Seismic Control Effectiveness of the TID for Base-Isolated Structures
3.1. Optimal Design of Base-Isolated Structures Equipped with a TID
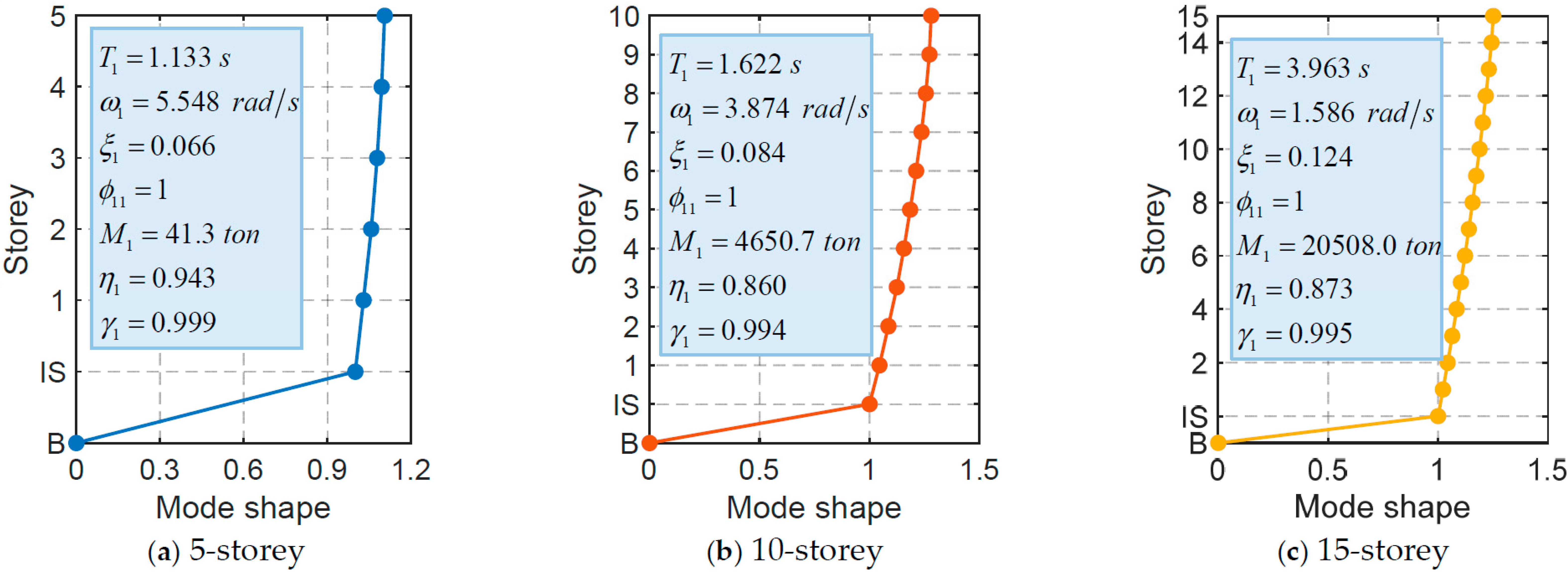
3.2. Structure Information
3.3. TID Parameters and Time History Analysis
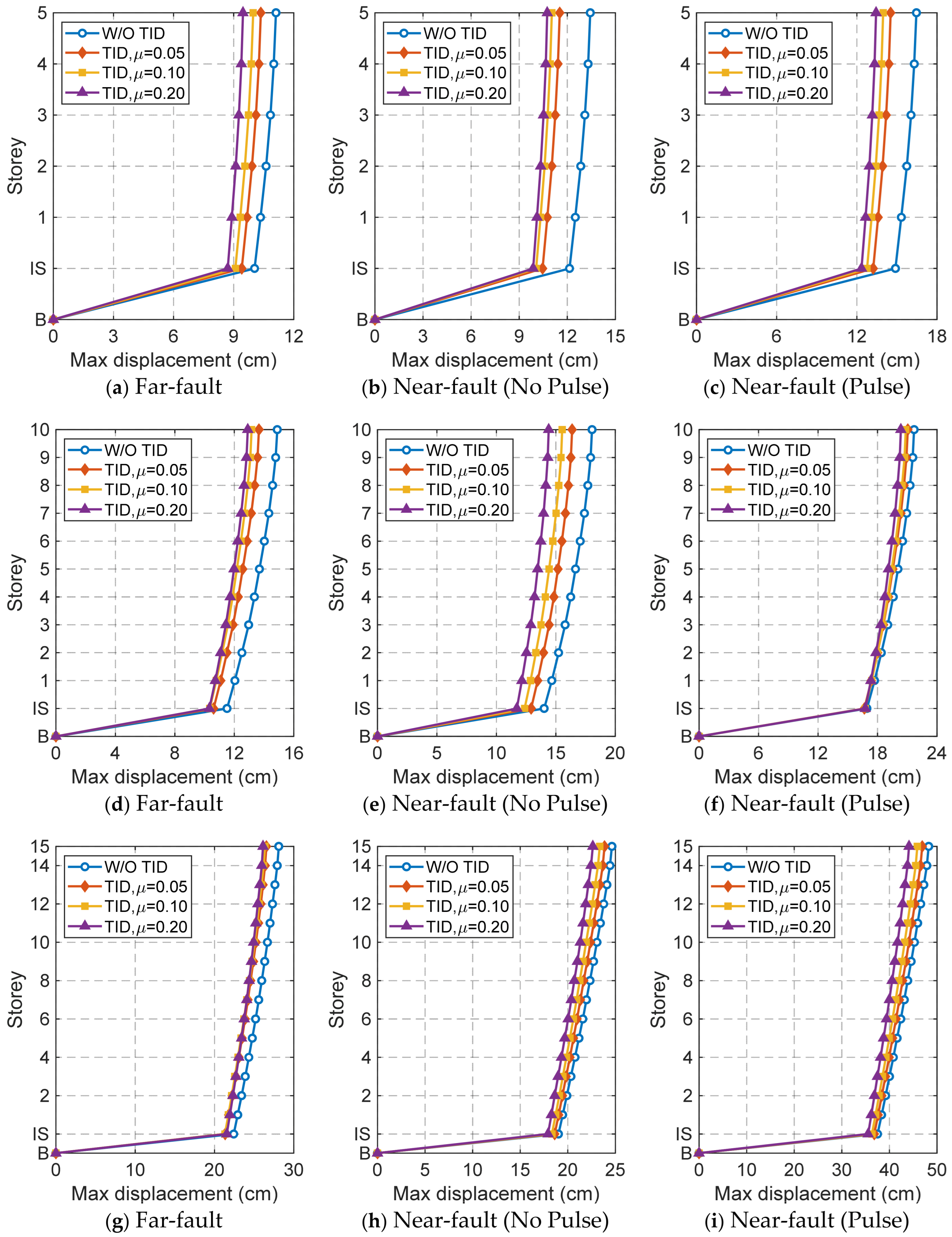
3.4. Displacement Response
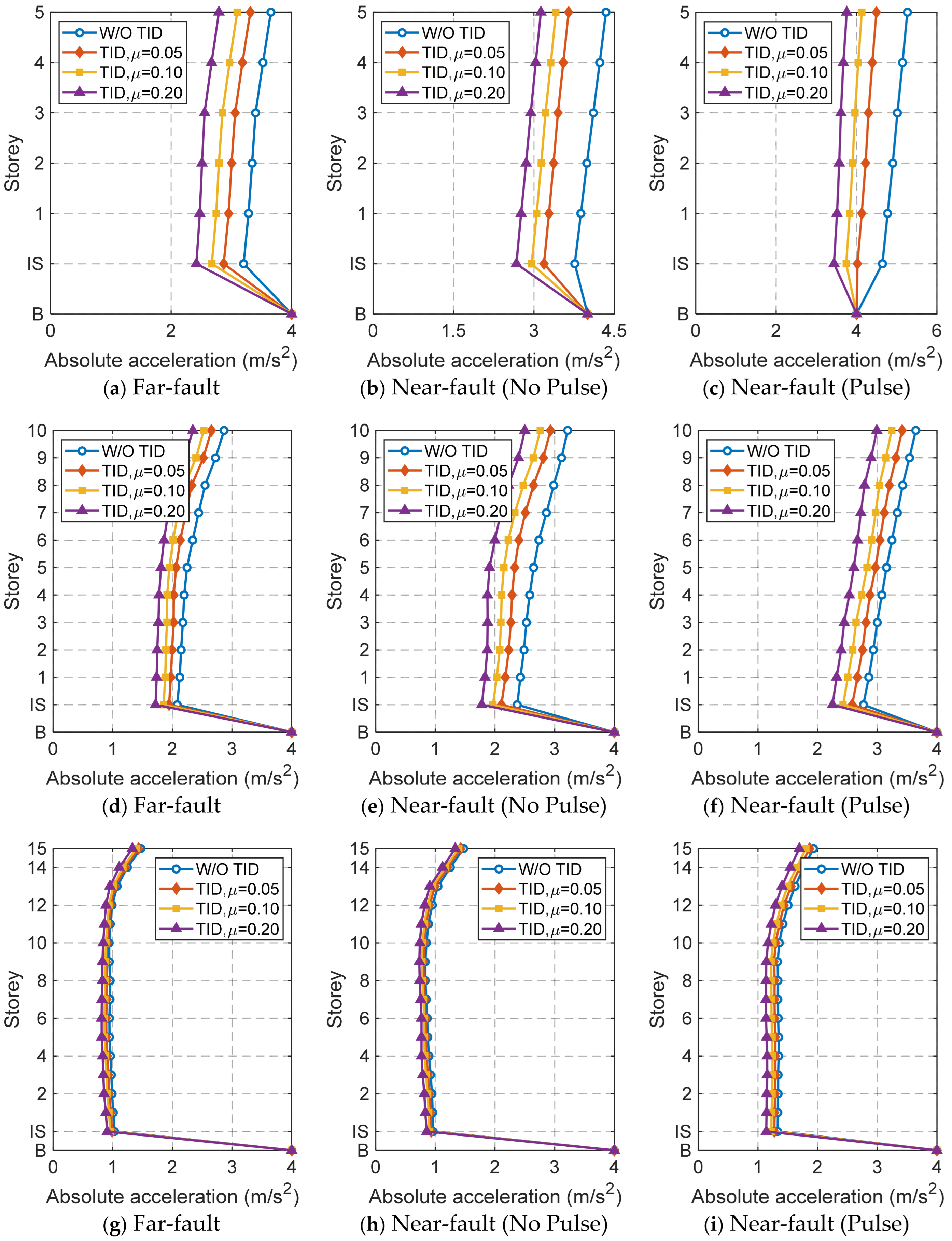
3.5. Absolute Acceleration Response
4. Conclusions
- (1)
- Considering the impact of ground motion characteristics, the optimal parameters for the base-isolated structure equipped with the TID have been determined. As the natural period and damping ratio of the base-isolated structure increase, both the optimal frequency ratio and damping ratio tend to rise. Due to the impracticality of deriving or fitting simple and accurate closed-form solutions, a parameter optimization analysis based on design conditions has been proposed.
- (2)
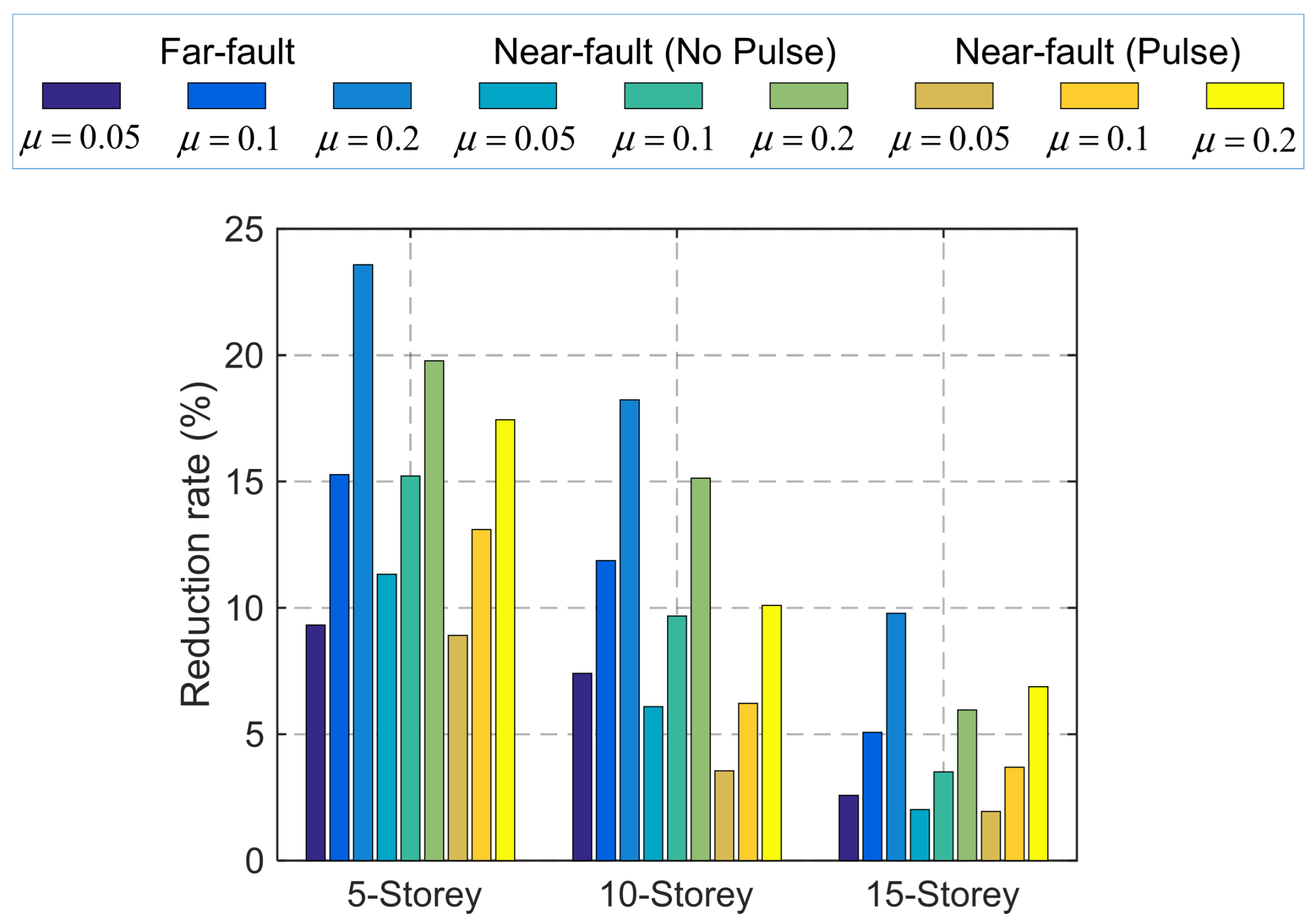
- The TID is more effective and stable for seismic control of base-isolated structures under far-fault ground motions than under near-fault ground motions. Additionally, the TID is more suitable for low-rise base-isolated structures. The control effectiveness of the TID improves with the mass ratio, however, when the mass ratio exceeds 0.2, the additional benefits of increasing the mass ratio diminish.
- (3)
- The TID provides excellent control over the mean square displacement response of the base-isolated structure, but its control effect on the peak displacement response is less significant due to the control hysteresis of the TID. Additionally, the TID demonstrates effective control over the absolute acceleration response of low-rise base-isolated structures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Saaed, T.E.; Nikolakopoulos, G.; Jonasson, J.-E.; Hedlund, H. A state-of-the-art review of structural control systems. J. Vib. Control 2015, 21, 919–937. [Google Scholar] [CrossRef]
- Ramírez, A.; Tomás-Rodríguez, M.; Sierra-García, J.E.; Santos, M. Metaheuristic optimized semi-active structural control approaches for a floating offshore wind turbine. Appl. Sci. 2024, 14, 11368. [Google Scholar] [CrossRef]
- Parulekar, Y.M.; Reddy, G.R. Passive response control systems for seismic response reduction: A state-of-the-art review. Int. J. Struct. Stab. Dyn. 2011, 9, 151–177. [Google Scholar] [CrossRef]
- Lee, S.J.; Kim, J.H. Effect of nonlinear hysteresis details of isolation system on in-structure response spectra. Appl. Sci. 2025, 15, 62. [Google Scholar] [CrossRef]
- Xu, Y.; Guo, T.; Xiong, J.; Chen, B.; Zhi, Q.; Yang, J. Optimization design of triple friction pendulums for base-isolated high-rise buildings based on bearing displacement and collapse fragility. Structures 2022, 43, 1091–1099. [Google Scholar] [CrossRef]
- Shang, J.; Tan, P.; Han, J.; Zhang, Y.; Li, Y. Performance of seismically isolated buildings with variable friction pendulum bearings under near-fault ground motions. J. Build. Eng. 2022, 45, 103584. [Google Scholar] [CrossRef]
- Habieb, A.B.; Valente, M.; Milani, G. Implementation of a simple novel Abaqus user element to predict the behavior of unbonded fiber reinforced elastomeric isolators in macro-scale computations. Bull. Earthq. Eng. 2019, 17, 2741–2766. [Google Scholar] [CrossRef]
- Chen, H.; Xu, H.; Liu, Y.; Ren, X. Seismic demand estimation of isolated buildings with nonlinear bearings subjected to linear response spectra. J. Build. Eng. 2023, 67, 105995. [Google Scholar] [CrossRef]
- Kelly, J.M. The role of damping in seismic isolation. Earthq. Eng. Struct. Dyn. 1999, 28, 3–20. [Google Scholar] [CrossRef]
- Bhagat, S.; Wijeyewickrema, A.C.; Subedi, N. Influence of near-fault ground motions with fling-step and forward-directivity characteristics on seismic response of base-isolated buildings. J. Earthq. Eng. 2021, 25, 455–474. [Google Scholar] [CrossRef]
- Elias, S.; Matsagar, V. Research developments in vibration control of structures using passive tuned mass dampers. Annu. Rev. Control 2017, 44, 129–156. [Google Scholar] [CrossRef]
- Li, D.; Ikago, K. Optimal design of nontraditional tuned mass damper for base-isolated building. J. Earthq. Eng. 2023, 27, 2841–2862. [Google Scholar] [CrossRef]
- De Angelis, M.; Perno, S.; Reggio, A. Dynamic response and optimal design of structures with large mass ratio TMD. Earthq. Eng. Struct. Dyn. 2012, 41, 41–60. [Google Scholar] [CrossRef]
- Kang, Y.J.; Peng, L.Y. Optimisation design and damping effect analysis of large mass ratio tuned mass dampers. Shock Vib. 2019, 8376781. [Google Scholar] [CrossRef]
- Kang, Y.-J.; Peng, L.-Y.; Peng, P.; Wang, H.-S.; Xiao, G.-Q. Seismic performances of a structure equipped with a large mass ratio multiple tuned mass damper. Struct. Des. Tall Spec. 2020, 29, e1803. [Google Scholar] [CrossRef]
- Yahyai, M.; Zebarjad, L.; Head, M.; Shokouhian, M. Optimum parameters for large mass ratio tmds using frequency response function. J. Earthq. Eng. 2021, 25, 2127–2146. [Google Scholar] [CrossRef]
- Kang, Y.-J.; Peng, L.-Y.; Pan, P.; Xiao, G.-Q.; Wang, H.-S. Shaking table test and numerical analysis of a coal-fired power plant equipped with large mass ratio multiple tuned mass damper (LMTMD). J. Build. Eng. 2021, 43, 102852. [Google Scholar] [CrossRef]
- Shu, Z.; Li, S.; Sun, X.; He, M. Performance-based seismic design of a pendulum tuned mass damper system. J. Earthq. Eng. 2019, 23, 334–355. [Google Scholar] [CrossRef]
- de Souza Pippi, A.; Avila, S.M.; Doz, G. A review on the use of the inerter device in the structural coupling technique for adjacent building vibration control. Structures 2022, 42, 480–501. [Google Scholar] [CrossRef]
- Ma, R.; Bi, K.; Hao, H. A novel rotational inertia damper for amplifying fluid resistance: Experiment and mechanical model. Mech. Syst. Signal Process. 2021, 149, 107313. [Google Scholar] [CrossRef]
- Xu, K.; Bi, K.; Han, Q.; Li, X.; Du, X. Using tuned mass damper inerter to mitigate vortex-induced vibration of long-span bridges: Analytical study. Eng. Struct. 2019, 182, 101–111. [Google Scholar] [CrossRef]
- Makris, N.; Kampas, G. Seismic protection of structures with supplemental rotational inertia. J. Eng. Mech. 2016, 142, 04016089. [Google Scholar] [CrossRef]
- Ikago, K.; Saito, K.; Inoue, N. Seismic control of single-degree-of-freedom structure using tuned viscous mass damper. Earthq. Eng. Struct. Dyn. 2012, 41, 453–474. [Google Scholar] [CrossRef]
- Hwang, J.S.; Kim, J.; Kim, Y.M. Rotational inertia dampers with toggle bracing for vibration control of a structure. Eng. Struct. 2007, 29, 1201–1208. [Google Scholar] [CrossRef]
- Gonzalez-Buelga, A.; Lazar, I.F.; Jiang, J.Z.; Neild, S.A.; Inman, D.J. Assessing the effect of nonlinearities on the performance of a tuned inerter damper. Struct. Control Health Monit. 2017, 24, e1879. [Google Scholar] [CrossRef]
- Nakamura, Y.; Fukukita, A.; Tamura, K.; Yamazaki, I.; Matsuoka, T.; Hiramoto, K.; Sunakoda, K. Seismic response control using electromagnetic inertial mass dampers. Earthq. Eng. Struct. Dyn. 2014, 43, 507–527. [Google Scholar] [CrossRef]
- Lazar, I.F.; Neild, S.A.; Wagg, D.J. Using an inerter-based device for structural vibration suppression. Earthq. Eng. Struct. Dyn. 2014, 43, 1129–1147. [Google Scholar] [CrossRef]
- He, H.; Tan, P.; Hao, L.; Xu, K.; Xiang, Y. Optimal design of tuned viscous mass damper for acceleration response control of civil structures under seismic excitations. Eng. Struct. 2022, 252, 113685. [Google Scholar] [CrossRef]
- Di Egidio, A.; Contento, A. Seismic benefits from coupling frame structures with a hysteretic mass damper inerter. Appl. Sci. 2023, 13, 5017. [Google Scholar] [CrossRef]
- Djerouni, S.; Ounis, A.; Elias, S.; Abdeddaim, M.; Rupakhety, R. Optimization and performance assessment of tuned mass damper inerter systems for control of buildings subjected to pulse-like ground motions. Structures 2022, 38, 139–156. [Google Scholar] [CrossRef]
- Chen, H.; Jia, S.; He, X. Dynamic characteristics of multiple inerter-based dampers for suppressing harmonically forced oscillations. Struct. Eng. Mech. 2019, 72, 747–762. [Google Scholar]
- Wen, Y.; Chen, Z.; Hua, X. Design and evaluation of tuned inerter-based dampers for the seismic control of MDOF structures. J. Struct. Eng. 2016, 143, 04016207. [Google Scholar] [CrossRef]
- Jangid, R.S. The role of a simple inerter in seismic base isolation. Appl. Sci. 2024, 14, 1056. [Google Scholar] [CrossRef]
- Pan, C.; Zhang, R. Design of structure with inerter system based on stochastic response mitigation ratio. Struct. Control Health Monit. 2018, 25, e2169. [Google Scholar] [CrossRef]
- Chen, H.; Bi, K.; Yanhui, L.; Ping, T. Performance evaluation of multiple tuned inerter-based dampers for seismic induced structural vibration control. Struct. Control Health Monit. 2022, 29, e2860. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, M.Z.Q. Performance evaluation for inerter-based dynamic vibration absorbers. Int. J. Mech. Sci. 2015, 99, 297–307. [Google Scholar] [CrossRef]
- Xu, K.-F.; Zhang, Y.-W.; Niu, M.-Q.; Chen, L.-Q. Dynamics analysis of a variable stiffness tuned mass damper enhanced by an inerter. Appl. Sci. 2023, 13, 1404. [Google Scholar] [CrossRef]
- Zuo, H.; Bi, K.; Hao, H.; Ma, R. Influences of ground motion parameters and structural damping on the optimum design of inerter-based tuned mass dampers. Eng. Struct. 2021, 227, 111422. [Google Scholar] [CrossRef]
- Javidialesaadi, A.; Wierschem, N.E. Design and performance evaluation of inerter-based tuned mass dampers for a ground acceleration excited structure. Soil Dyn. Earthq. Eng. 2021, 140, 106463. [Google Scholar] [CrossRef]
- Barredo, E.; Blanco, A.; Colín, J.; Penagos, V.M.; Abúndez, A.; Vela, L.G.; Meza, V.; Cruz, R.H.; Mayén, J. Closed-form solutions for the optimal design of inerter-based dynamic vibration absorbers. Int. J. Mech. Sci. 2018, 144, 41–53. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, M.Z.; Shu, Z.; Huang, L. Analysis and optimisation for inerter-based isolators via fixed-point theory and algebraic solution. J. Sound Vib. 2015, 346, 17–36. [Google Scholar] [CrossRef]
- Sun, H.; Zuo, L.; Wang, X. Exact H2 optimal solutions to inerter-based isolation systems for building structures. Struct. Control Health Monit. 2019, 26, e2357. [Google Scholar] [CrossRef]
- De Domenico, D.; Ricciardi, G. Improving the dynamic performance of base-isolated structures via tuned mass damper and inerter devices: A comparative study. Struct. Control Health Monit. 2018, 25, e2234. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, M.; Li, Z.; Zhu, L.; Meng, Y. Optimal design and seismic performance of base-isolated storage tanks using friction pendulum inerter systems. Structures 2022, 43, 234–248. [Google Scholar] [CrossRef]
- Djerouni, S.; Elias, S.; Abdeddaim, M.; Rupakhety, R. Optimal design and performance assessment of multiple tuned mass damper inerters to mitigate seismic pounding of adjacent buildings. J. Build. Eng. 2022, 48, 103994. [Google Scholar] [CrossRef]
- De Domenico, D.; Impollonia, N.; Ricciardi, G. Soil-dependent optimum design of a new passive vibration control system combining seismic base isolation with tuned inerter damper. Soil Dyn. Earthq. Eng. 2018, 105, 37–53. [Google Scholar] [CrossRef]
- Qian, F.; Luo, Y.; Sun, H.; Tai, W.C.; Zuo, L. Optimal tuned inerter dampers for performance enhancement of vibration isolation. Eng. Struct. 2019, 198, 109464. [Google Scholar] [CrossRef]
- De Angelis, M.; Giaralis, A.; Petrini, F.; Pietrosanti, D. Optimal tuning and assessment of inertial dampers with grounded inerter for vibration control of seismically excited base-isolated systems. Eng. Struct. 2019, 196, 109250. [Google Scholar] [CrossRef]
- Djerouni, S.; Abdeddaim, M.; Eliasa, S.; Rupakhety, R. Optimum double mass tuned damper inerter for control of structure subjected to ground motions. J. Build. Eng. 2021, 44, 103259. [Google Scholar] [CrossRef]
- Masnata, C.; Matteo, A.D.; Adam, C.; Pirrotta, A. Assessment of the tuned mass damper inerter for seismic response control of base-isolated structures. Struct. Control Health Monit. 2020, 28, e2665. [Google Scholar] [CrossRef]
- Masnata, C.; Di Matteo, A.; Adam, C.; Pirrotta, A. Smart structures through nontraditional design of Tuned Mass Damper Inerter for higher control of base isolated systems. Mech. Res. Commun. 2020, 105, 103513. [Google Scholar] [CrossRef]
- Ren, C.; Wang, J.; Looi, D.T.W.; Hong, M. Optimal design and performance evaluation of a tuned inertial damper considering soil-structure interaction effects. Soil Dyn. Earthq. Eng. 2025, 194, 109338. [Google Scholar] [CrossRef]
- Tong, S.; Zeng, J.; Miao, Z.; Chen, G. Parameter optimization of tuned inerter damper for vibration suppression in structures with damping. J. Sound Vib. 2025, 597, 118827. [Google Scholar] [CrossRef]
- Greco, R.; Morga, M. Optimum design of tuned mass dampers for different earthquake ground motion parameters and models. J Struct. Des. Tall Spec. Build. 2019, 28, e1672. [Google Scholar] [CrossRef]
- Applied Technical Council. Federal Emergency Management Agent. Quantification of Seismic Performance Factors; FEMA: Washington, DC, USA, 2009.
- Wang, H.; Shen, W.; Li, Y. Dynamic behavior and seismic performance of base-isolated structures with electromagnetic inertial mass dampers: Analytical solutions and simulations. Eng. Struct. 2021, 246, 113072. [Google Scholar] [CrossRef]
- Liu, T.; Zordan, T.; Briseghella, B. An improved equivalent linear model of seismic isolation system with bilinear behavior. Eng. Struct. 2014, 61, 113–126. [Google Scholar] [CrossRef]
- Far, H.; Fatahi, B.; Ghabraie, K. Evaluation of numerical procedures to determine seismic response of structures under influence of soil-structure interaction. Struct. Eng. Mech. 2015, 56, 27–47. [Google Scholar]
- Wang, Q.; Qiao, H.; De Domenico, D.; Zhu, Z.; Tang, Y. Seismic response control of adjacent high-rise buildings linked by the Tuned Liquid Column Damper-Inerter (TLCDI). Eng. Struct. 2020, 223, 111169. [Google Scholar] [CrossRef]
- Qiao, H.; Huang, P.; De Domenico, D.; Wang, Q. Structural control of high-rise buildings subjected to multi-hazard excitations using inerter-based vibration absorbers. Eng. Struct. 2022, 266, 114666. [Google Scholar] [CrossRef]




| No. | Earthquake | Year | M | Station | Distance (km) | Site Class | Vs_30 (m/s) | Component |
|---|---|---|---|---|---|---|---|---|
| 1 | Northridge | 1994 | 6.7 | Canyon Country-WLC | 11.9 | D | 309 | NORTHR/LOS000 |
| 2 | Duzce | 1999 | 7.1 | Bolu | 12.2 | D | 326 | DUZCE/BOL000 |
| 3 | Hector Mine | 1999 | 7.1 | Hector | 11.2 | C | 685 | HECTOR/HEC000 |
| 4 | Imperial Valley | 1979 | 6.5 | Delta | 22.25 | D | 275 | IMPVALL/H-DLT262 |
| 5 | Kobe | 1995 | 6.9 | Nishi-Akashi | 16.15 | C | 609 | KOBE/NIS000 |
| 6 | Kobe | 1995 | 6.9 | Shin-Osaka | 23.8 | D | 256 | KOBE/SHI000 |
| 7 | Kocaeli | 1999 | 7.5 | Duzce | 14.5 | D | 276 | KOCAELI/DZC180 |
| 8 | Kocaeli | 1999 | 7.5 | Arcelik | 12.05 | C | 523 | KOCAELI/ARC000 |
| 9 | Landers | 1992 | 7.3 | Yermo Fire Station | 23.7 | D | 354 | LANDERS/YER270 |
| 10 | Landers | 1992 | 7.3 | Coolwater | 19.85 | D | 271 | LANDERS/CLW-LN |
| 11 | Loma Prieta | 1989 | 6.9 | Capitola | 22.1 | D | 289 | LOMAP/CAP000 |
| 12 | Loma Prieta | 1989 | 6.9 | Gilroy Array #3 | 12.5 | D | 350 | LOMAP/G03000 |
| 13 | Manjil | 1990 | 7.4 | Abbar | 12.8 | C | 724 | MANJIL/ABBAR--L |
| 14 | Superstition Hills | 1987 | 6.5 | El Centro Imp. Co. | 18.35 | D | 192 | SUPERST/B-ICC000 |
| 15 | Superstition Hills | 1987 | 6.5 | Poe Road (temp) | 11.45 | D | 208 | SUPERST/B-POE270 |
| 16 | Cape Mendocino | 1992 | 7.0 | Rio Dell Overpass | 11.1 | D | 312 | CAPEMEND/RIO270 |
| 17 | Chi-Chi | 1999 | 7.6 | CHY101 | 12.75 | D | 259 | CHICHI/CHY101-E |
| 18 | Chi-Chi | 1999 | 7.6 | TCU045 | 26.4 | C | 705 | CHICHI/TCU045-E |
| 19 | San Fernando | 1971 | 6.6 | LA—Hollywood Stor | 24.35 | D | 316 | SFERN/PEL090 |
| 20 | Friuli | 1976 | 6.5 | Tolmezzo | 15.4 | C | 425 | FRIULI/A-TMZ000 |
| No. | Earthquake | Year | M | Station | Distance (km) | Site Class | Vs_30 (m/s) | Component |
|---|---|---|---|---|---|---|---|---|
| 1 | Gazli, USSR | 1976 | 6.8 | Karakyr | 4.7 | C | 660 | GAZLI/GAZ000 |
| 2 | Imperial Valley-06 | 1979 | 6.5 | Bonds Corner | 2.25 | D | 223 | IMPVALL/H-BCR140 |
| 3 | Imperial Valley-06 | 1979 | 6.5 | Chihuahua | 7.85 | D | 275 | IMPVALL/H-CHI012 |
| 4 | Nahanni, Canada | 1985 | 6.8 | Site 1 | 6.05 | C | 660 | NAHANNI/S1010 |
| 5 | Nahanni, Canada | 1985 | 6.8 | Site 2 | 2.45 | C | 660 | NAHANNI/S2240 |
| 6 | Loma Prieta | 1989 | 6.9 | Corralitos | 2.05 | C | 462 | LOMAP/CLS000 |
| 7 | Cape Mendocino | 1992 | 7.0 | Cape Mendocino | 3.5 | C | 514 | CAPEMEND/CPM000 |
| 8 | Northridge-01 | 1994 | 6.7 | LA—Sepulveda VA | 4.2 | C | 380 | NORTHR/SPV270 |
| 9 | Northridge-01 | 1994 | 6.7 | Northridge—Saticoy | 6.05 | D | 281 | NORTHR/STC090 |
| 10 | Chi-Chi, Taiwan | 1999 | 7.6 | TCU067 | 3.55 | C | 434 | CHICHI/TCU067-E |
| 11 | Chi-Chi, Taiwan | 1999 | 7.6 | TCU084 | 5.6 | C | 553 | CHICHI/TCU084-E |
| 12 | Denali, Alaska | 2002 | 7.9 | TAPS Pump Sta. #10 | 4.45 | C | 553 | DENALI/PS10-047 |
| No. | Earthquake | Year | M | Station | Distance (km) | Site Class | Vs_30(m/s) | Component |
|---|---|---|---|---|---|---|---|---|
| 1 | Imperial Valley | 1979 | 6.5 | El Centro Array #6 | 1.75 | D | 203 | IMPVALL/H-E06140 |
| 2 | Imperial Valley | 1979 | 6.5 | El Centro Array #7 | 2.1 | D | 211 | IMPVALL/H-E07140 |
| 3 | Loma Prieta | 1989 | 6.9 | Saratoga-Aloha | 8.05 | C | 371 | LOMAP/STG000 |
| 4 | Erzican | 1992 | 6.7 | Erzincan | 2.2 | D | 275 | ERZIKAN/ERZ-EW |
| 5 | Cape Mendocino | 1992 | 7.0 | Petrolia | 4.1 | C | 713 | CAPEMEND/PET000 |
| 6 | Landers | 1992 | 7.3 | Lucerne | 2.95 | C | 685 | LANDERS/LCN260 |
| 7 | Northridge | 1994 | 6.7 | Rinaldi Receiving Sta | 3.25 | D | 282 | NORTHR/RRS228 |
| 8 | Northridge | 1994 | 6.7 | Sylmar-Olive View | 3.5 | C | 441 | NORTHR/SYL090 |
| 9 | Chi-Chi | 1999 | 7.6 | TCU065 | 3.65 | D | 306 | CHICHI/TCU065-E |
| 10 | Chi-Chi | 1999 | 7.6 | TCU102 | 4.6 | C | 714 | CHICHI/TCU102-E |
| 5-Storey | IS | 1 | 2 | 3 | 4 | 5 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mass (103 kg) | 6.8 | 6.0 | 6.0 | 6.0 | 6.0 | 6.0 | ||||||||||
| Stiffness (103 kN/m) | 1.2 | 33.7 | 29.1 | 28.6 | 25.0 | 19.0 | ||||||||||
| Damping (kN/m/s) | 30 | 67 | 58 | 57 | 50 | 38 | ||||||||||
| 10-Storey | IS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||||
| Mass (103 kg) | 380 | 380 | 380 | 380 | 280 | 280 | 280 | 275 | 275 | 275 | 275 | |||||
| Stiffness (103 kN/m) | 60 | 1200 | 1200 | 1100 | 1100 | 1100 | 950 | 850 | 800 | 650 | 650 | |||||
| Damping (103 kN/m/s) | 3 | 5 | 5 | 4.8 | 4.7 | 4.7 | 4 | 3.7 | 3.4 | 2.8 | 2.8 | |||||
| 15-Storey | IS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Mass (103 kg) | 981 | 981 | 981 | 981 | 981 | 981 | 981 | 981 | 981 | 981 | 981 | 981 | 981 | 981 | 981 | 981 |
| Stiffness (103 kN/m) | 45 | 1913 | 1864 | 1815 | 1717 | 1668 | 1570 | 1520 | 1422 | 1275 | 1177 | 1030 | 883 | 687 | 490 | 400 |
| Damping (103 kN/m/s) | 8 | 18.5 | 18.0 | 17.5 | 16.6 | 16.1 | 15.2 | 14.7 | 13.7 | 12.3 | 11.4 | 10.0 | 8.5 | 6.6 | 4.7 | 3.9 |
| Ground Motions Type | Far-Fault | Near-Fault (No Pulse) | Near-Fault (Pulse) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Structure | Parameter | md (ton) | fopt | md (ton) | fopt | md (ton) | fopt | |||
| 5-Storey | μ = 0.05 | 2.067 | 0.964 | 0.111 | 2.067 | 0.962 | 0.110 | 2.067 | 0.957 | 0.109 |
| μ = 0.1 | 4.135 | 0.933 | 0.154 | 4.135 | 0.930 | 0.152 | 4.135 | 0.922 | 0.150 | |
| μ = 0.2 | 8.269 | 0.878 | 0.212 | 8.269 | 0.875 | 0.207 | 8.269 | 0.864 | 0.204 | |
| 10-Storey | μ = 0.05 | 232.535 | 0.963 | 0.111 | 232.535 | 0.966 | 0.110 | 232.535 | 0.961 | 0.110 |
| μ = 0.1 | 465.071 | 0.931 | 0.155 | 465.071 | 0.935 | 0.154 | 465.071 | 0.928 | 0.152 | |
| μ = 0.2 | 930.141 | 0.876 | 0.213 | 930.141 | 0.883 | 0.211 | 930.141 | 0.873 | 0.208 | |
| 15-Storey | μ = 0.05 | 1025.385 | 0.975 | 0.111 | 1025.385 | 0.999 | 0.114 | 1025.385 | 0.973 | 0.111 |
| μ = 0.1 | 2050.770 | 0.948 | 0.155 | 2050.770 | 0.980 | 0.160 | 2050.770 | 0.945 | 0.155 | |
| μ = 0.2 | 4101.539 | 0.900 | 0.214 | 4101.539 | 0.945 | 0.223 | 4101.539 | 0.897 | 0.213 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, Y.; Zhang, Z.; Zhang, Z.; Zhang, X.; Liu, Q. Optimal Design and Seismic Performance of Base-Isolated Structures with Varying Heights Equipped with Tuned Inerter Dampers Subjected to Far-Fault and Near-Fault Ground Motions. Appl. Sci. 2025, 15, 4739. https://doi.org/10.3390/app15094739
Kang Y, Zhang Z, Zhang Z, Zhang X, Liu Q. Optimal Design and Seismic Performance of Base-Isolated Structures with Varying Heights Equipped with Tuned Inerter Dampers Subjected to Far-Fault and Near-Fault Ground Motions. Applied Sciences. 2025; 15(9):4739. https://doi.org/10.3390/app15094739
Chicago/Turabian StyleKang, Yingjie, Zewen Zhang, Zeyu Zhang, Xinyu Zhang, and Qingkuan Liu. 2025. "Optimal Design and Seismic Performance of Base-Isolated Structures with Varying Heights Equipped with Tuned Inerter Dampers Subjected to Far-Fault and Near-Fault Ground Motions" Applied Sciences 15, no. 9: 4739. https://doi.org/10.3390/app15094739
APA StyleKang, Y., Zhang, Z., Zhang, Z., Zhang, X., & Liu, Q. (2025). Optimal Design and Seismic Performance of Base-Isolated Structures with Varying Heights Equipped with Tuned Inerter Dampers Subjected to Far-Fault and Near-Fault Ground Motions. Applied Sciences, 15(9), 4739. https://doi.org/10.3390/app15094739





