A Novel Temperature Reconstruction Method for Acoustic Pyrometry Under Strong Temperature Gradients and Limited Measurement Points
Abstract
1. Introduction
2. Basic Principles and Methodologies
2.1. Basic Principle of Acoustic Pyrometry
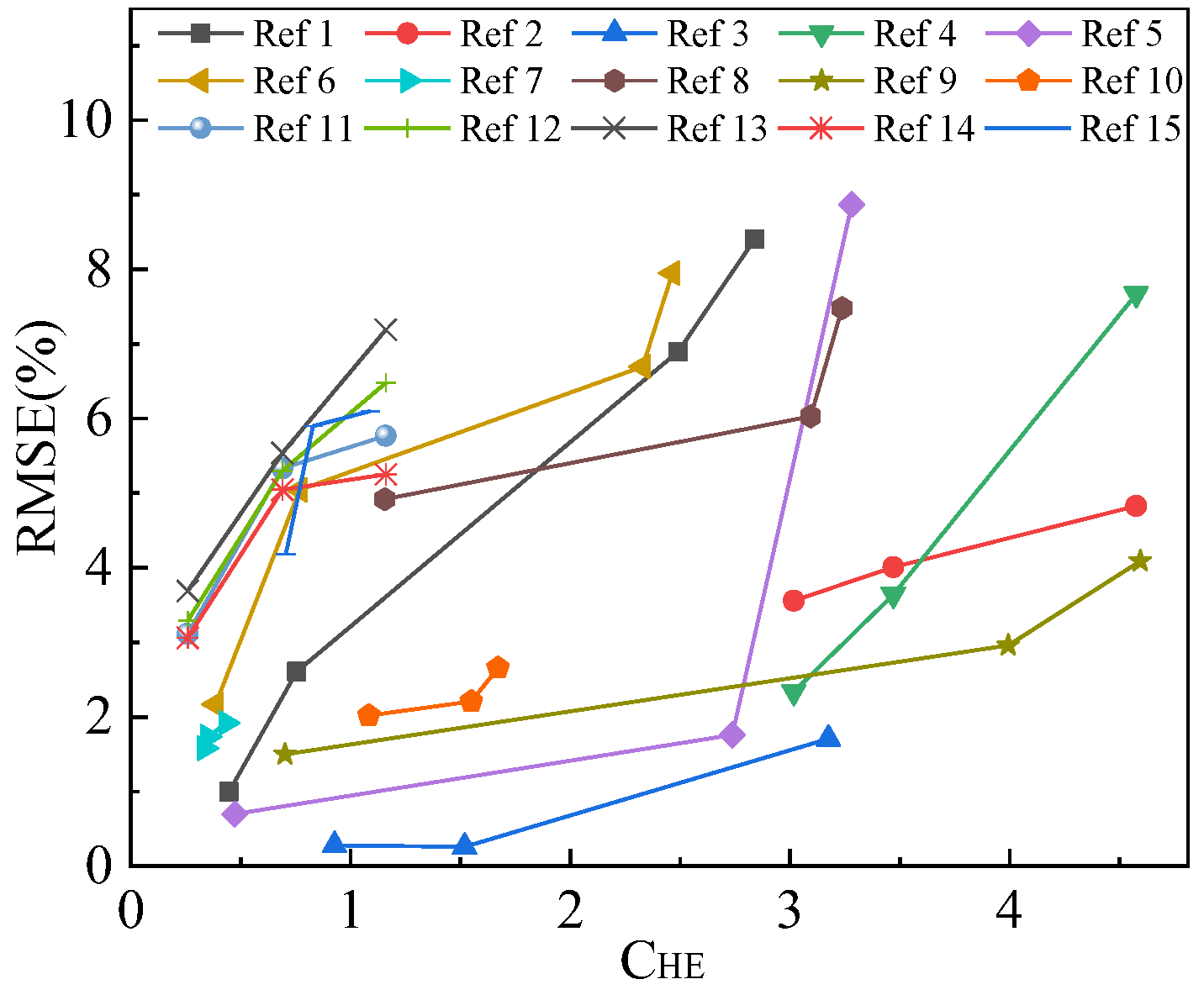
2.2. The Coefficient of Heating Effect
2.3. Improvements to the Reconstruction of High-Gradient Temperature Fields with Limited Measurement Points
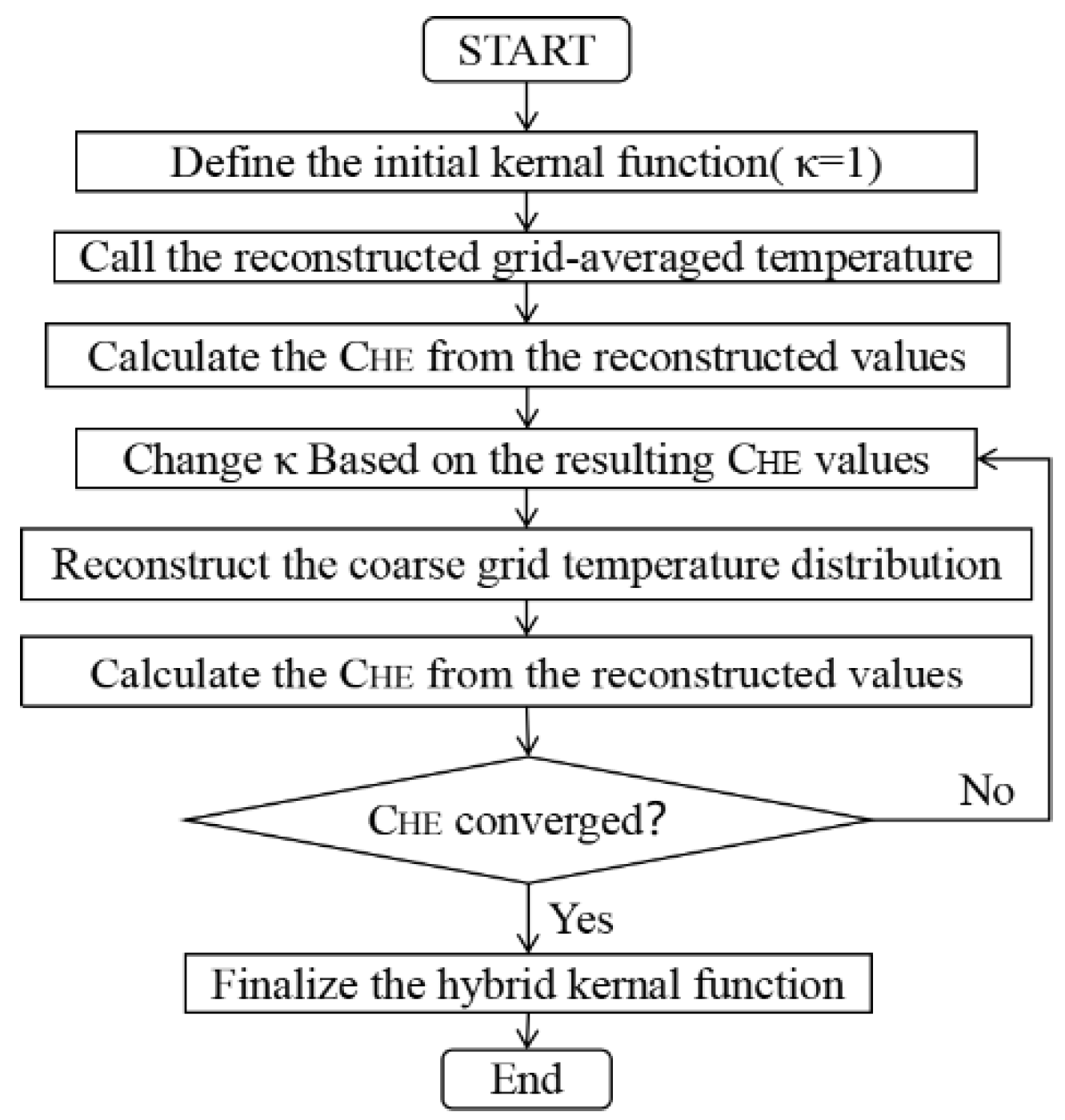
2.3.1. RBF Approximation and the Adaptive Hybrid Kernel Method
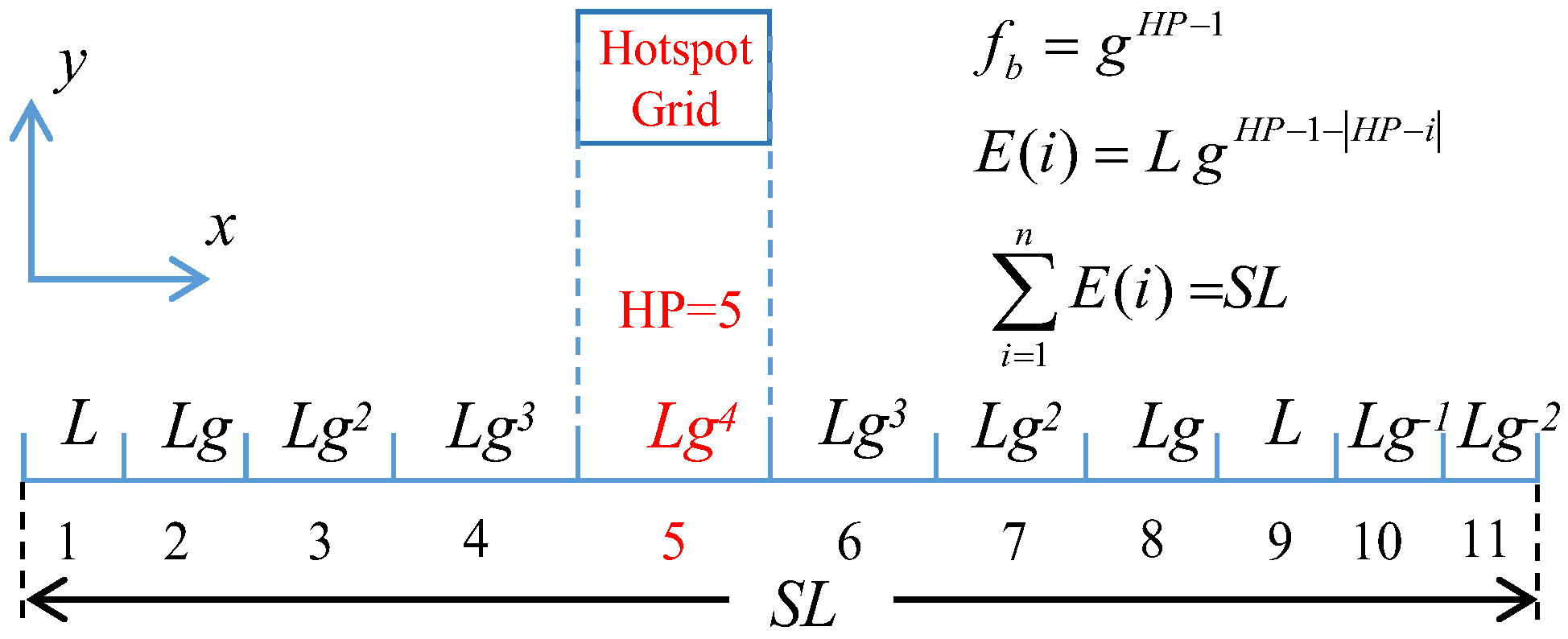
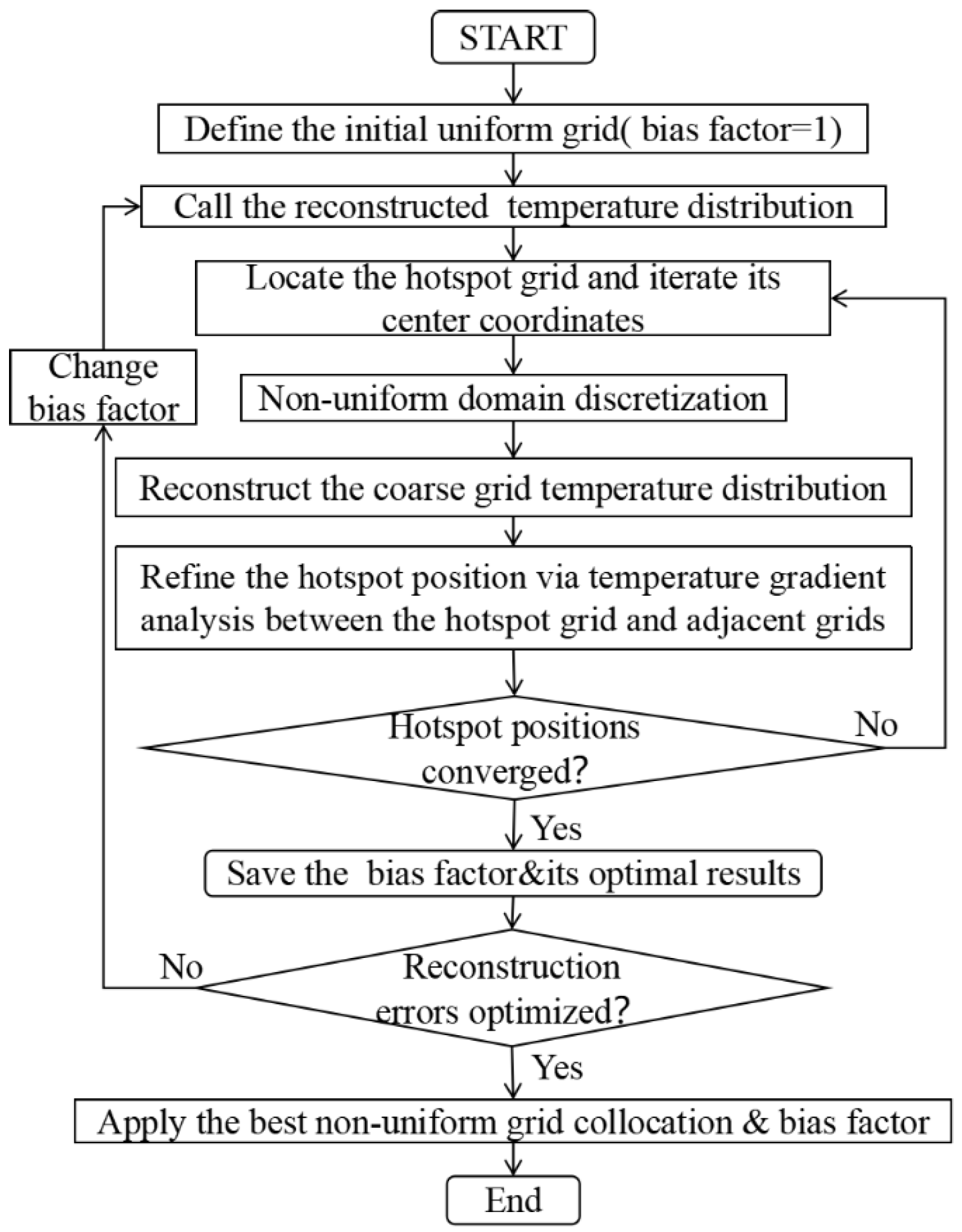
2.3.2. Domain Discretization and the Adaptive Grid Evolution Strategy
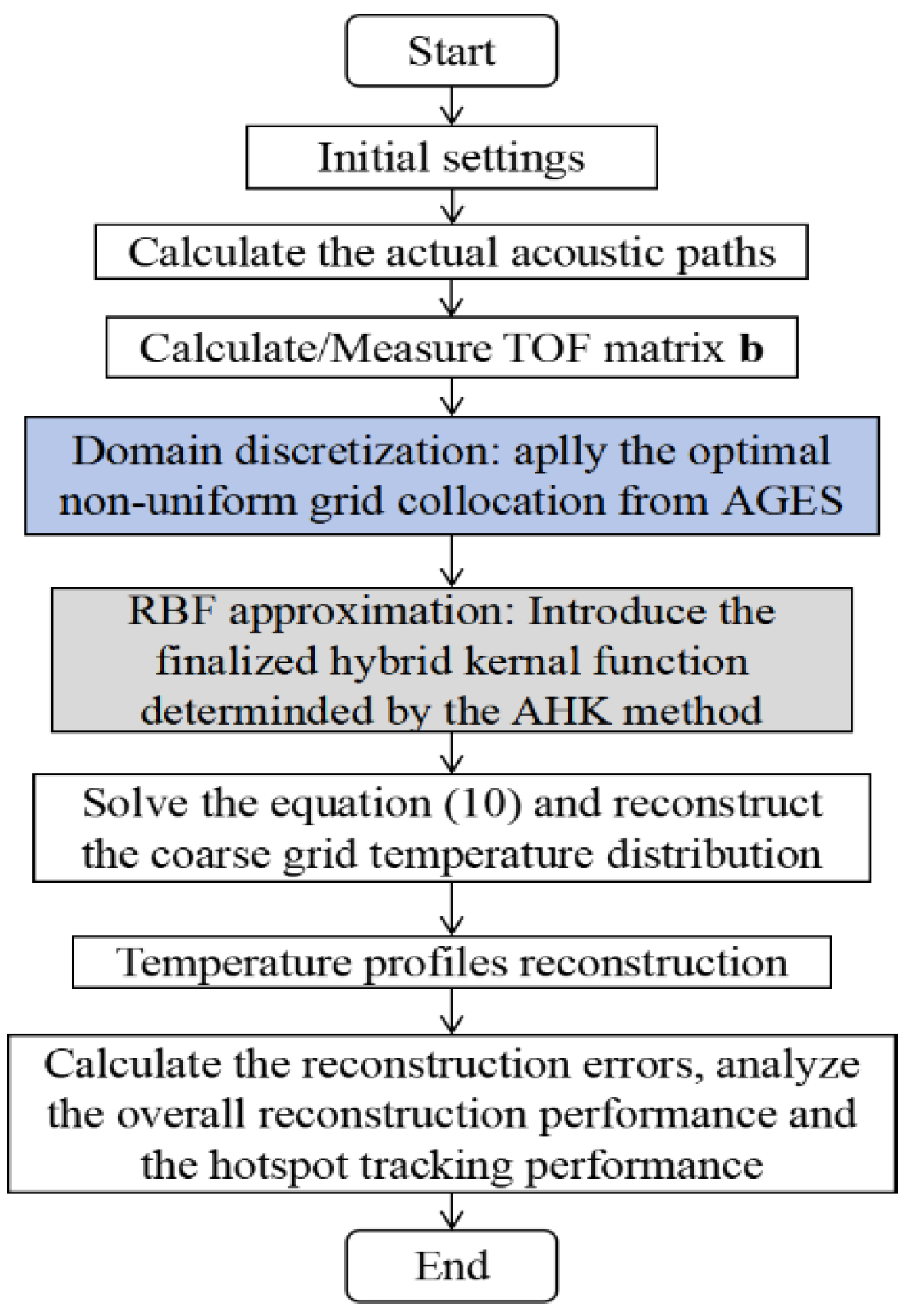
2.3.3. AGES-AHK Method
3. Results and Discussion
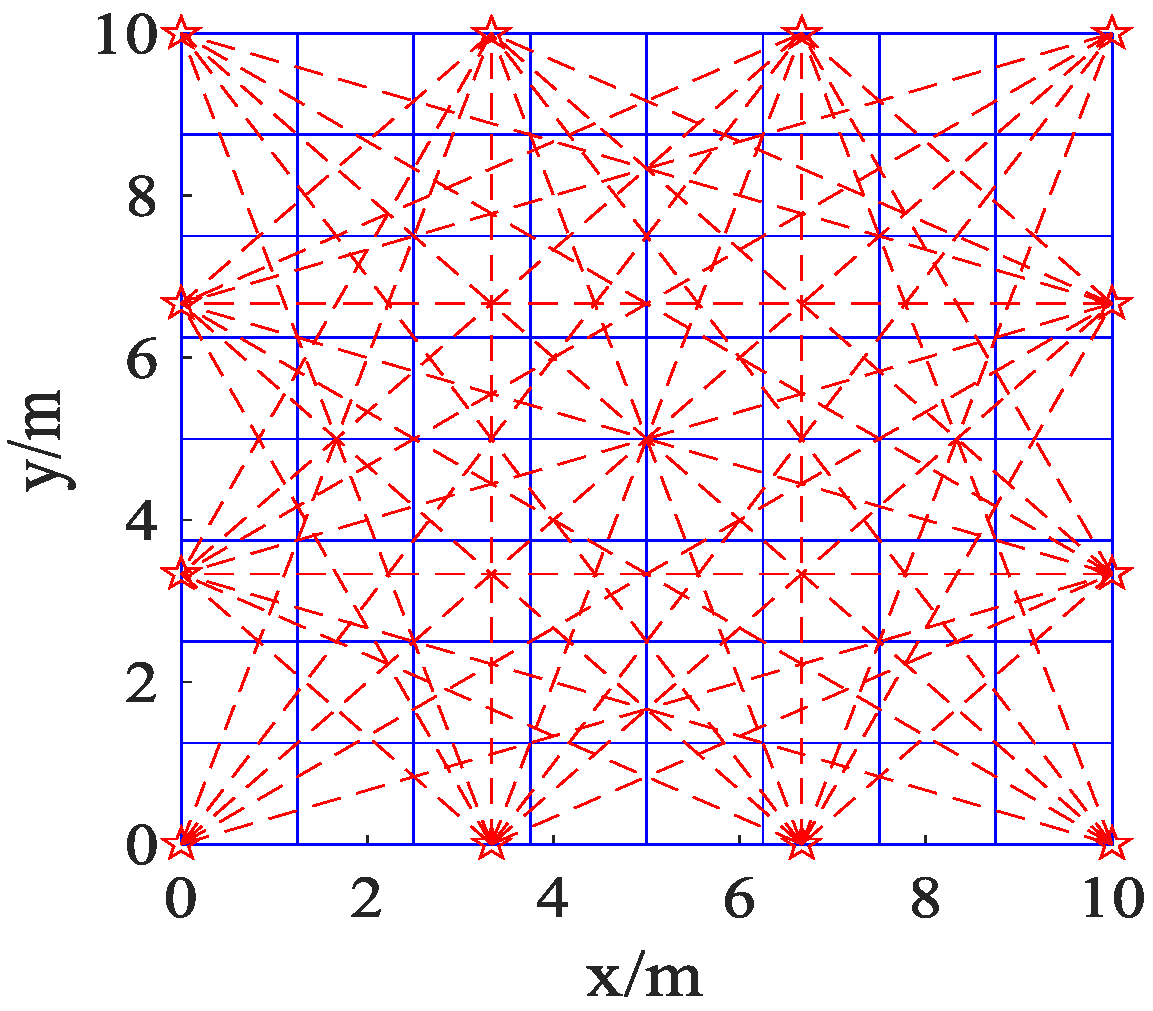
3.1. Initial Settings
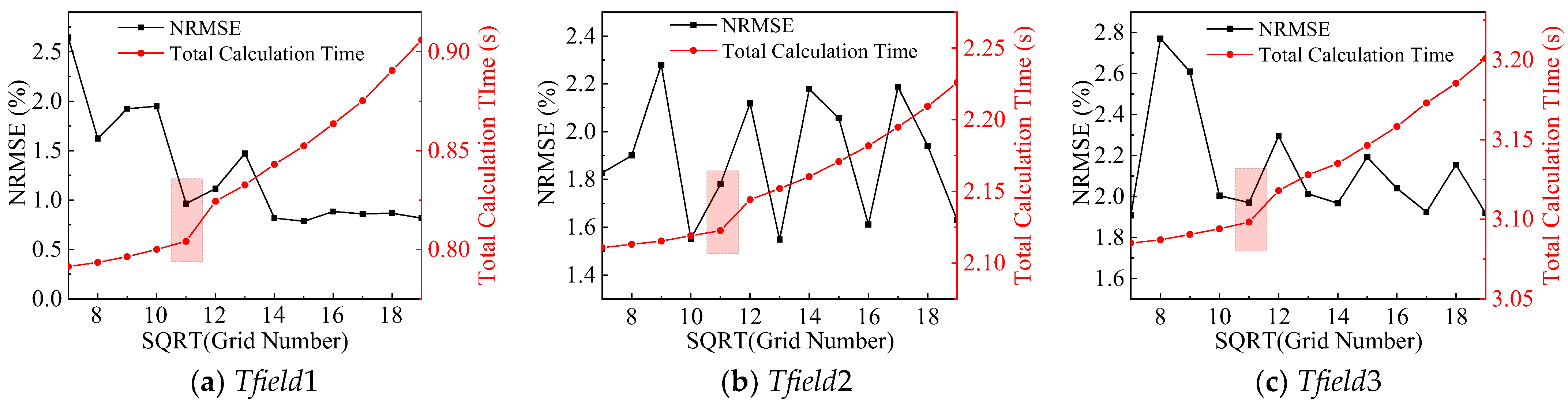
3.2. Parametric Investigation of the Initial Reconstruction Result
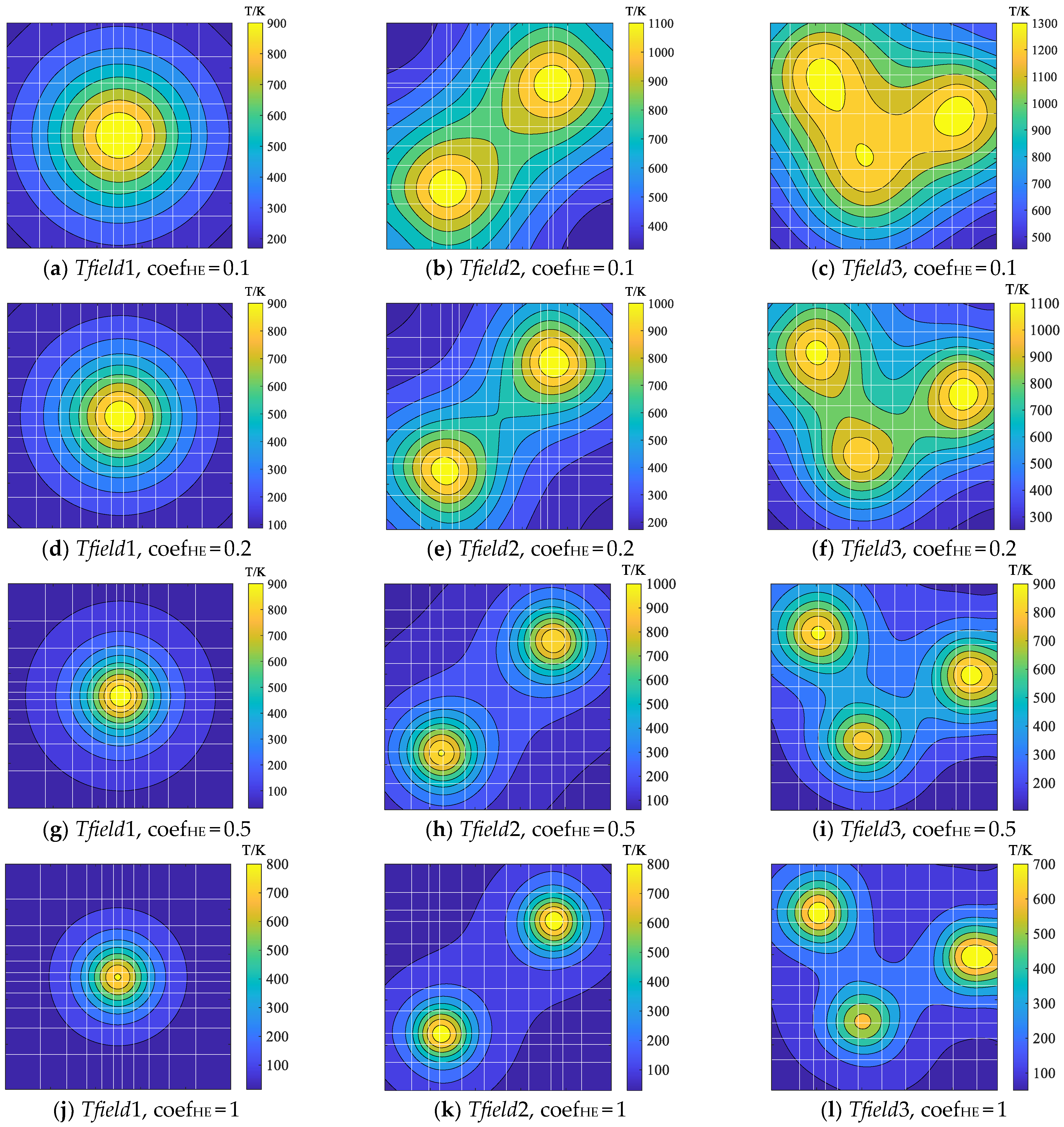
3.3. The Reconstruction Results of the AGES-AHK Method
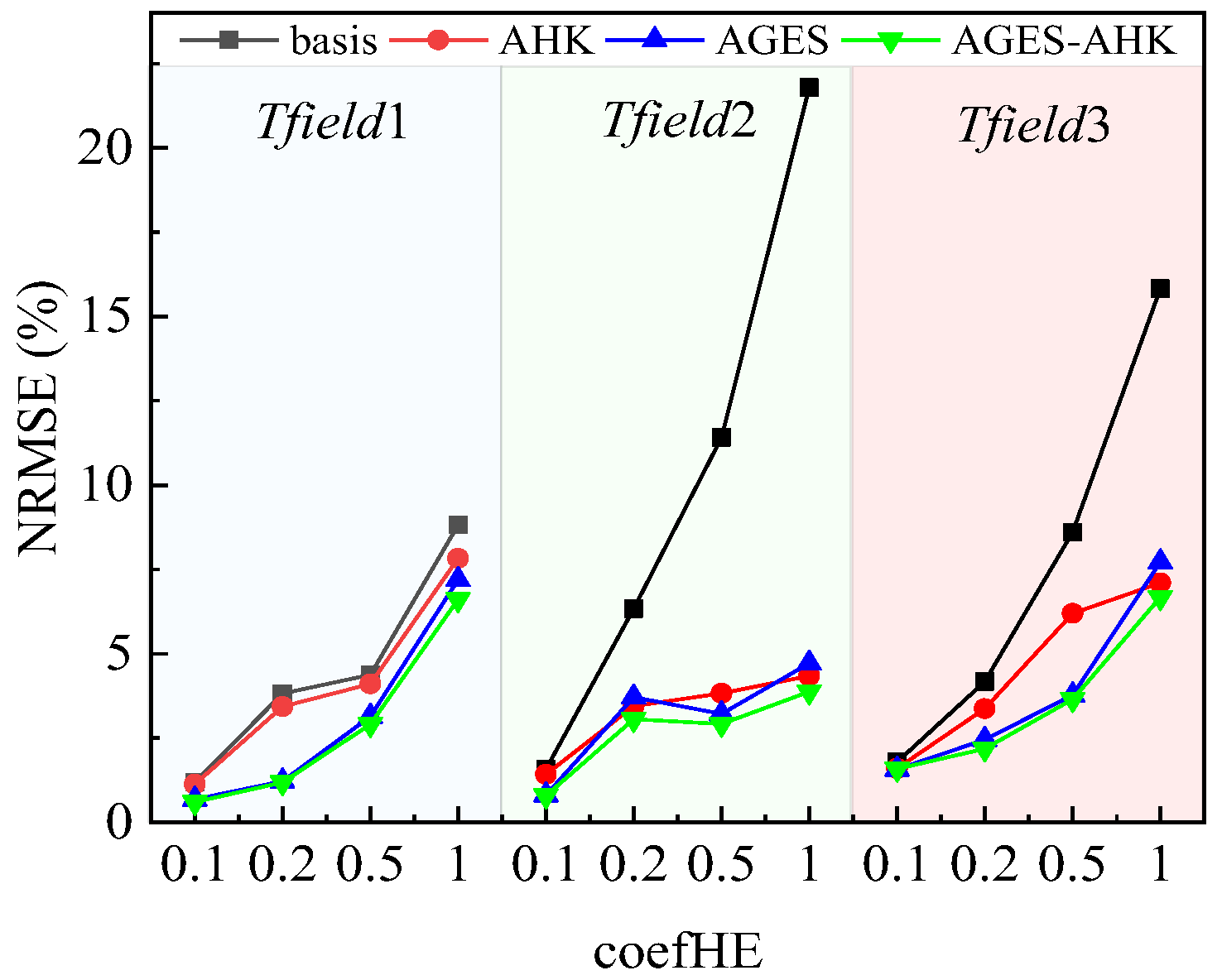
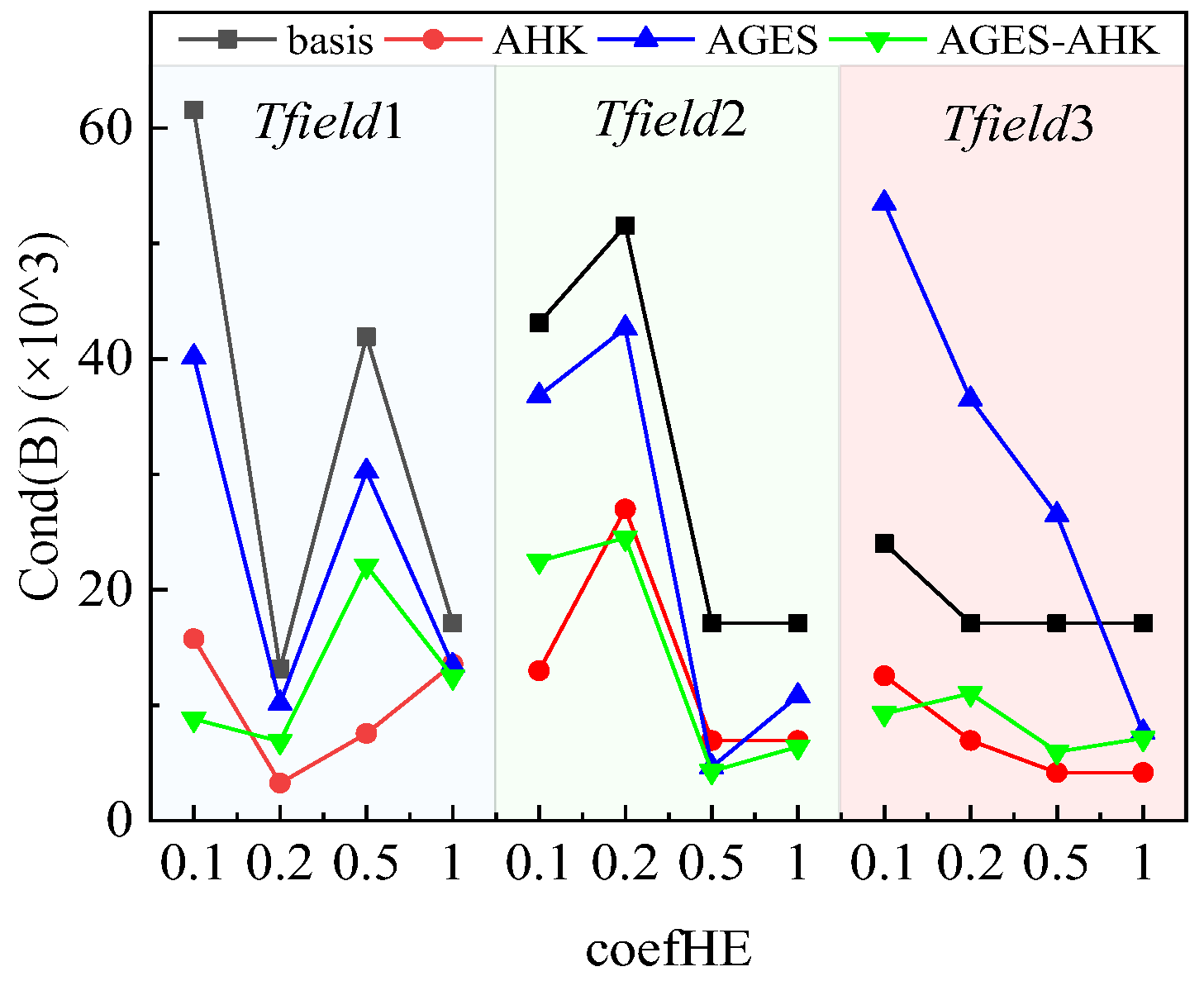
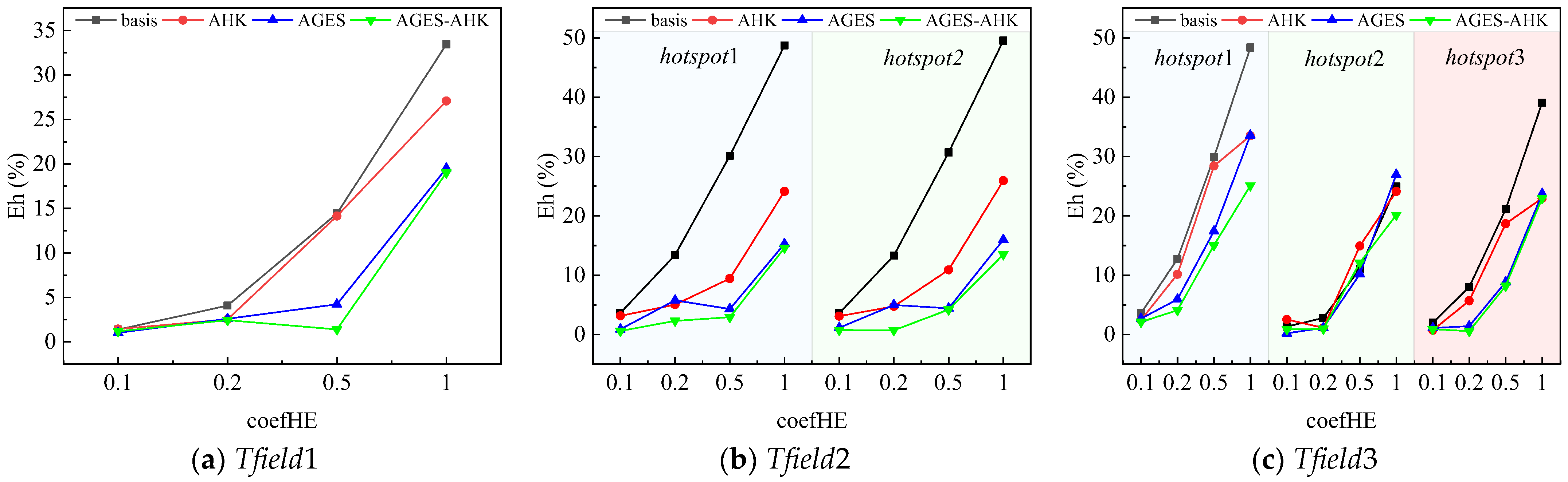
3.4. The Discussion of the Overall Reconstruction Error and the Hotspot Tracking Performance
3.5. The Discussion of the Practical Challenges and Future Advancements
4. Conclusions
- (1)
- The effect of the intrinsic characteristics of the reconstructed temperature field (CHE) on the difficulty of reconstruction is verified through literature reviews and reconstruction results.
- (2)
- The finalized adaptive hybrid kernel from the AHK method combines the sharp spatial localization characteristics of G with the global characterization of MQ, thereby alleviating the ill-conditioned nature of the problem and enhancing the suitability for reconstructing large-gradient temperature fields.
- (3)
- By implementing adaptive nonuniform meshing without increasing the total grid number, AGES pre-optimizes grid density distribution to match the temperature field topography, thereby facilitating improvement in the reconstruction performance.
- (4)
- The finalized AGES-AHK method integrates the optimization of AHK and AGES, achieving significant improvements over basis data in both reconstruction fidelity and hotspot characterization. At CHE levels below 15, the AGES-AHK method achieved the lowest NRMSE of less than 3.7%, Eh of less than 15% and Dh of less than 2.24%, representing its superior overall reconstruction performance and hotspot tracking ability. Even at the highest CHE level of 30, the AGES-AHK method was still able to reproduce the overall temperature field topography and qualitatively track the hotspots.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, S.; Shen, G.; An, L.; Niu, Y. Online monitoring of the two-dimensional temperature field in a boiler furnace based on acoustic computed tomography. Appl. Therm. Eng. 2015, 75, 958–966. [Google Scholar] [CrossRef]
- FAN, B.; SHEN, C.; WANG, K. Simulation on spray combustion flow field of the air heater. J. Rocket Propuls. 2023, 49, 13–22. [Google Scholar]
- Bramanti, M.; Salerno, E.A.; Tonazzini, A.; Pasini, S.; Gray, A. An acoustic pyrometer system for tomographic thermal imaging in power plant boilers. IEEE Trans. Instrum. Meas. 1996, 45, 159–167. [Google Scholar] [CrossRef]
- Shen, X.; Xiong, Q.; Shi, X.; Wang, K.; Liang, S.; Gao, M. Ultrasonic temperature distribution reconstruction for circular area based on Markov radial basis approximation and singular value decomposition. Ultrasonics 2015, 62, 174–185. [Google Scholar] [CrossRef] [PubMed]
- Pan, G.; Niu, X.; Pan, L.; Zheng, M.; Sun, J.; Ding, Z. Analysis on outlet temperature uniformity of hydrogen/oxygen preburner with high-pressure and low-mixture-ratio. J. Rocket Propuls. 2023, 49, 29–35. [Google Scholar]
- Kong, Q.; Jiang, G.; Liu, Y.; Sun, J. 3D Temperature Distribution Reconstruction in Furnace Based on Acoustic Tomography. Math. Probl. Eng. 2019, 2019, 1830965. [Google Scholar] [CrossRef]
- Zhang, S.; Shen, G.; An, L.; Niu, Y.; Jiang, G. Monitoring ash fouling in power station boiler furnaces using acoustic pyrometry. Chem. Eng. Sci. 2015, 126, 216–223. [Google Scholar] [CrossRef]
- Tsai, W.-Y.; Chen, H.-C.; Liao, T.-L. High accuracy ultrasonic air temperature measurement using multi-frequency continuous wave. Sens. Actuators A Phys. 2006, 132, 526–532. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, S.; Lei, J.; Liu, J.; Schlaberg, H.I.; Yan, Y. A method for simultaneous reconstruction of temperature and concentration distribution in gas mixtures based on acoustic tomography. Acoust. Phys. 2015, 61, 597–605. [Google Scholar] [CrossRef]
- Tsai, W.-Y.; Huang, C.-F.; Liao, T.-L. New implementation of high-precision and instant-response air thermometer by ultrasonic sensors. Sens. Actuators A Phys. 2005, 117, 88–94. [Google Scholar] [CrossRef]
- Liu, S.; Liu, S.; Ren, T. Acoustic Tomography Reconstruction Method for the Temperature Distribution Measurement. IEEE Trans. Instrum. Meas. 2017, 66, 1936–1945. [Google Scholar] [CrossRef]
- Xie, L.B.; Liu, T.; Zhang, Z.G.; Shao, W. 2-D temperature reconstruction based on the algorithm of interpolation and iterative. Proc. Chin. Soc. Electr. Eng. 2004, 24, 249–252. [Google Scholar]
- Andersen, A.; Kak, A.C. Simultaneous Algebraic Reconstruction Technique (SART): A Superior Implementation of the ART Algorithm. Ultrason. Imaging 1984, 6, 81–94. [Google Scholar] [CrossRef]
- Kong, Q.; Jiang, G.; Liu, Y.; Sun, J. 3D high-quality temperature-field reconstruction method in furnace based on acoustic tomography. Appl. Therm. Eng. 2020, 179, 115693. [Google Scholar] [CrossRef]
- Wang, R.; An, L.; Shen, G.; Zhang, S. Acoustic reconstruction of three-dimensional temperature field based on regularized SVD algorithm. Chin. J. Comput. Phys. 2015, 32, 195–201. [Google Scholar] [CrossRef]
- Zhang, J.; Qi, H.; Jiang, D.; He, M.; Ren, Y.; Su, M.; Cai, X. Acoustic tomography of two dimensional velocity field by using meshless radial basis function and modified Tikhonov regularization method. Measurement 2021, 175, 109107. [Google Scholar] [CrossRef]
- Zhang, J.; Qi, H.; Ren, Y.; Su, M.; Cai, X. Acoustic tomography of temperature and velocity fields by using the radial basis function and alternating direction method of multipliers. Int. J. Heat Mass Transf. 2022, 188, 122660. [Google Scholar] [CrossRef]
- Fan, W.; Chen, Y.; Pan, H.; Ye, Y.; Cai, Y.; Zhang, Z. Experimental study on underwater acoustic imaging of 2-D temperature distribution around hot springs on floor of Lake Qiezishan, China. Exp. Therm. Fluid Sci. 2010, 34, 1334–1345. [Google Scholar] [CrossRef]
- Yan, H.; Li, X.; Wang, S. Reconstruction of three dimensional temperature field based on least square method and Kriging interpolation. J. Shenyang Univ. Technol. 2014, 36, 303–307. [Google Scholar] [CrossRef]
- Shen, X.; Xiong, Q.; Shi, W.; Liang, S.; Shi, X.; Wang, K. A New Algorithm for Reconstructing Two-Dimensional Temperature Distribution by Ultrasonic Thermometry. Math. Probl. Eng. 2015, 2015, 1–10. [Google Scholar] [CrossRef][Green Version]
- Lu, J.; Wakai, K.; Takahashi, S.; Shimizu, S. Acoustic computer tomographic pyrometry for two-dimensional measurement of gases taking into account the effect of refraction of sound wave paths. Meas. Sci. Technol. 2000, 11, 692. [Google Scholar] [CrossRef]
- Yan, H.; Chen, G.; Zhou, Y.; Liu, L. Primary study of temperature distribution measurement in stored grain based on acoustic tomography. Exp. Therm. Fluid Sci. 2012, 42, 55–63. [Google Scholar] [CrossRef]
- Zhang, S.; Shen, G.; An, L.; Li, G. Ash fouling monitoring based on acoustic pyrometry in boiler furnaces. Appl. Therm. Eng. 2015, 84, 74–81. [Google Scholar] [CrossRef]
- Kong, Q.; Jiang, G.; Liu, Y.; Sun, J. Location of the Leakage From a Simulated Water-Cooling Wall Tube Based on Acoustic Method and an Artificial Neural Network. IEEE Trans. Instrum. Meas. 2021, 70, 1–18. [Google Scholar] [CrossRef]
- Soma, P.; Fu-Sung, L.; Ching-Chuan, H.; Ya-Han, L.; Chen-Yuan, L.; Shan-Wen, D.; Chih-Hsien, H. An Acoustic Hotspot Tracking Algorithm for Highly Centralized Gas Temperature Distribution. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 68, 1370. [Google Scholar] [CrossRef]
- Yu, Y.; Xiong, Q.; Li, Q.; Wu, C.; Wang, K.; Gao, M.; Liang, S. A method for ultrasound thermal image distribution reconstruction. Meas. Sci. Technol. 2019, 30, 095007. [Google Scholar] [CrossRef]
- Jia, R.; Xiong, Q.; Xu, G.; Wang, K.; Liang, S. A method for two-dimensional temperature field distribution reconstruction. Appl. Therm. Eng. 2017, 111, 961–967. [Google Scholar] [CrossRef]
- Yu, Y.; Xiong, Q.; Yang, M.; Wu, C.; Zhu, Q.; Wang, K.; Gao, M. Krylov Subspace Methods for Regularized Models in Acoustic Temperature Reconstruction from Simulated and Real Measurements. IEEE Trans. Instrum. Meas. 2021, 70, 9514111. [Google Scholar] [CrossRef]
- Yu, Y.; Xiong, Q.; Li, Q.; Wu, C.; Gao, M.; Wang, K. A hybrid kernel function approach for acoustic reconstruction of temperature distribution. Measurement 2020, 166, 108238. [Google Scholar] [CrossRef]
- Sreeram, B.; Chaitanya, S.K.; Jaswanth, K.K.A.; Srinivasan, K. Precise temperature reconstruction in acoustic pyrometry: Impact of domain discretization and transceiver count. Appl. Therm. Eng. 2024, 238, 122009. [Google Scholar] [CrossRef]
- Lifeng, Z.; Jing, L. Acoustic Tomography Temperature Reconstruction Based on Virtual Observation and Residual Network. IEEE Sens. J. 2022, 22, 17054–17064. [Google Scholar] [CrossRef]
- Ruixi, J.; Qingyu, X.; Shan, L. Acoustic imaging for temperature distribution reconstruction. AIP Adv. 2016, 6, 125018. [Google Scholar] [CrossRef]
- Sha, L.; Shi, L.; Guowei, T.; Guowei, T. Reconstruction method for inversion problems in an acoustic tomography based temperature distribution measurement. Meas. Sci. Technol. 2017, 28, 115005. [Google Scholar] [CrossRef]
- Qian, K.; Genshan, J.; Yuechao, L. Research on Temperature Field Reconstruction Based on RBF Approximation with Polynomial Reproduction Considering the Refraction Effect of Sound Wave Paths. Sound Vib. 2018, 52, 9–20. [Google Scholar] [CrossRef]
- Zhou, X.; Dong, C.; Zhao, C.; Bai, X. Temperature-field reconstruction algorithm based on reflected sigmoidal radial basis function and QR decomposition. Appl. Therm. Eng. 2020, 171, 114987. [Google Scholar] [CrossRef]
- Li, Z.; Xinzhi, Z.; Chenlong, D.; Yuhui, W.; Hailin, W. Ultrasonic Thermometry Algorithm Based on Inverse Quadratic Function. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 68, 1876–1884. [Google Scholar] [CrossRef]
- Yuhui, W.; Xinzhi, Z.; Li, Z.; Chenlong, D.; Hailin, W. A Method for Reconstruction of Boiler Combustion Temperature Field Based on Acoustic Tomography. Math. Probl. Eng. 2021, 2021, 9922698. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, X.; Yang, Q.; Chen, J.; Dong, C.; Zhao, L. A Reconstruction Method of Boiler Furnace Temperature Distribution Based on Acoustic Measurement. IEEE Trans. Instrum. Meas. 2021, 70, 9600413. [Google Scholar] [CrossRef]
- Zhang, J.; Qi, H.; Ji, Y.; Ren, Y.; He, M.; Su, M.; Cai, X. Nonlinear Acoustic Tomography for Measuring the Temperature and Velocity Fields by Using the Covariance Matrix Adaptation Evolution Strategy Algorithm. IEEE Trans. Instrum. Meas. 2022, 71, 4500214. [Google Scholar] [CrossRef]
- Aster, R.C.; Borchers, B.; Thurber, C.H. Chapter Three—Rank Deficiency and Ill-Conditioning. In Parameter Estimation and Inverse Problems, 3rd ed.; Aster, R.C., Borchers, B., Thurber, C.H., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 55–91. [Google Scholar]
- Bao, Y.; Jia, J. Nonlinear temperature field reconstruction using acoustic tomography. In Proceedings of the 2017 IEEE International Conference on Imaging Systems and Techniques (IST), Beijing, China, 18–20 October 2017; pp. 1–6. [Google Scholar]
- Yan, H.; Wang, S.; Liu, L.; Zhou, Y. A reconstruction algorithm of temperature field taking into account the bending of sound wave paths. Acta Acust. 2014, 39, 705–713. [Google Scholar]
- Roberts, S.M.; Shipman, J.S. Two-Point Boundary value Problems: Shooting Methods; Elsevier: New York, NY, USA, 1972. [Google Scholar]
- Buhmann, M.D. Radial Basis Functions: Theory and Implementations; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Majdisova, Z.; Skala, V. Radial basis function approximations: Comparison and applications. Appl. Math. Model. 2017, 51, 728–743. [Google Scholar] [CrossRef]
- Kong, Q.; Jiang, G.; Liu, Y.; Yu, M. Numerical and experimental study on temperature field reconstruction based on acoustic tomography. Appl. Therm. Eng. 2020, 170, 114720. [Google Scholar] [CrossRef]
- Chaitanya, S.K.; Alapati, J.K.K.; Srinivasan, K. Evaluation of regularization methods for acoustic pyrometry. Measurement 2022, 198, 111356. [Google Scholar] [CrossRef]
- Jia, R.; Xiong, Q.; Wang, K.; Wang, L.; Xu, G.; Liang, S. The study of three-dimensional temperature field distribution reconstruction using ultrasonic thermometry. AIP Adv. 2016, 6, 075007. [Google Scholar] [CrossRef]
- Rippa, S. An algorithm for selecting a good value for the parameter c in radial basis function interpolation. Adv. Comput. Math. 1999, 11, 193–210. [Google Scholar] [CrossRef]
- Fasshauer, G.E.; Zhang, J.G. On choosing “optimal” shape parameters for RBF approximation. Numer. Algorithms 2007, 45, 345–368. [Google Scholar] [CrossRef]
- Bayona, V.; Moscoso, M.; Kindelan, M. Optimal constant shape parameter for multiquadric based RBF-FD method. J. Comput. Phys. 2011, 230, 7384–7399. [Google Scholar] [CrossRef]
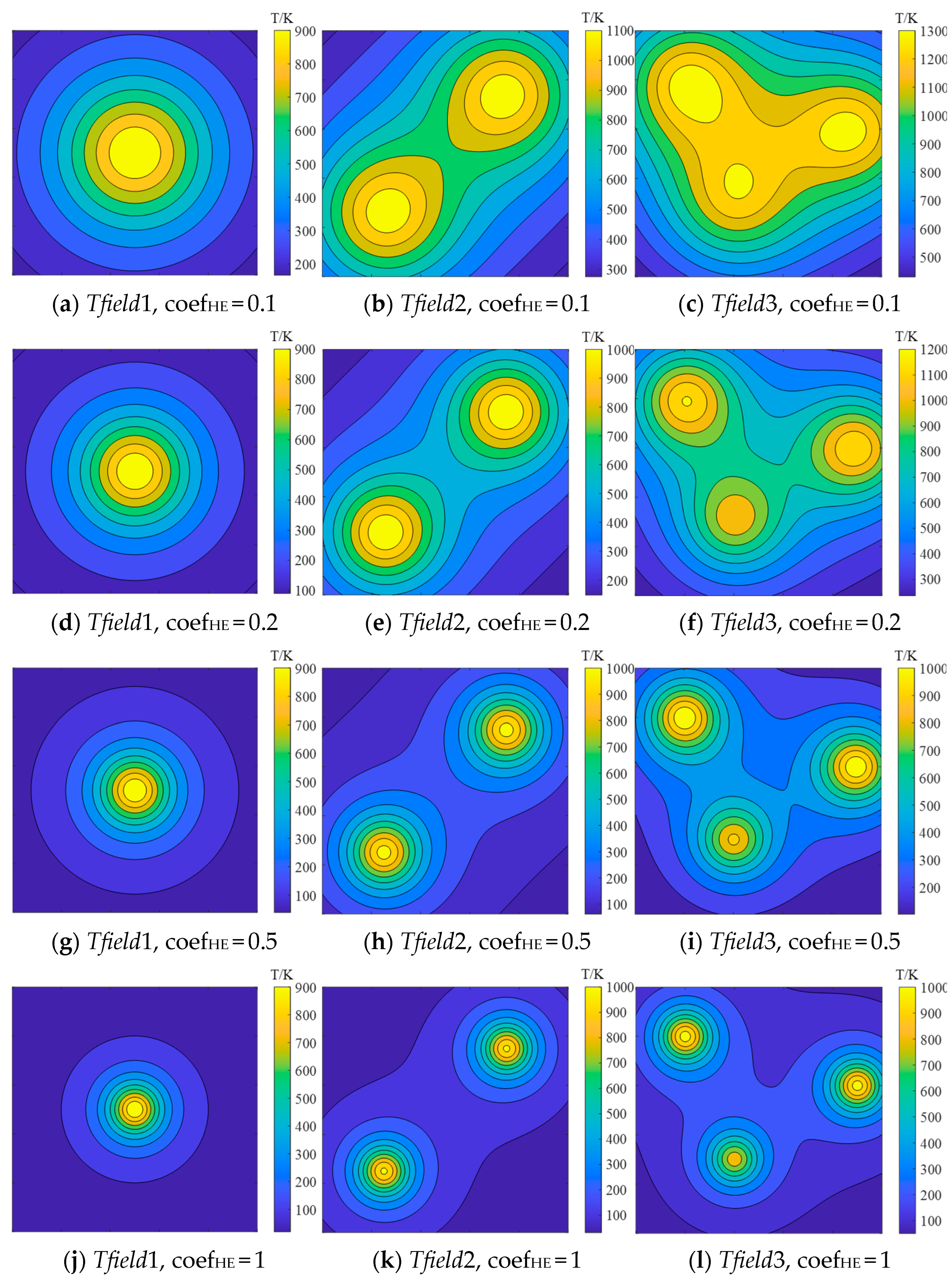
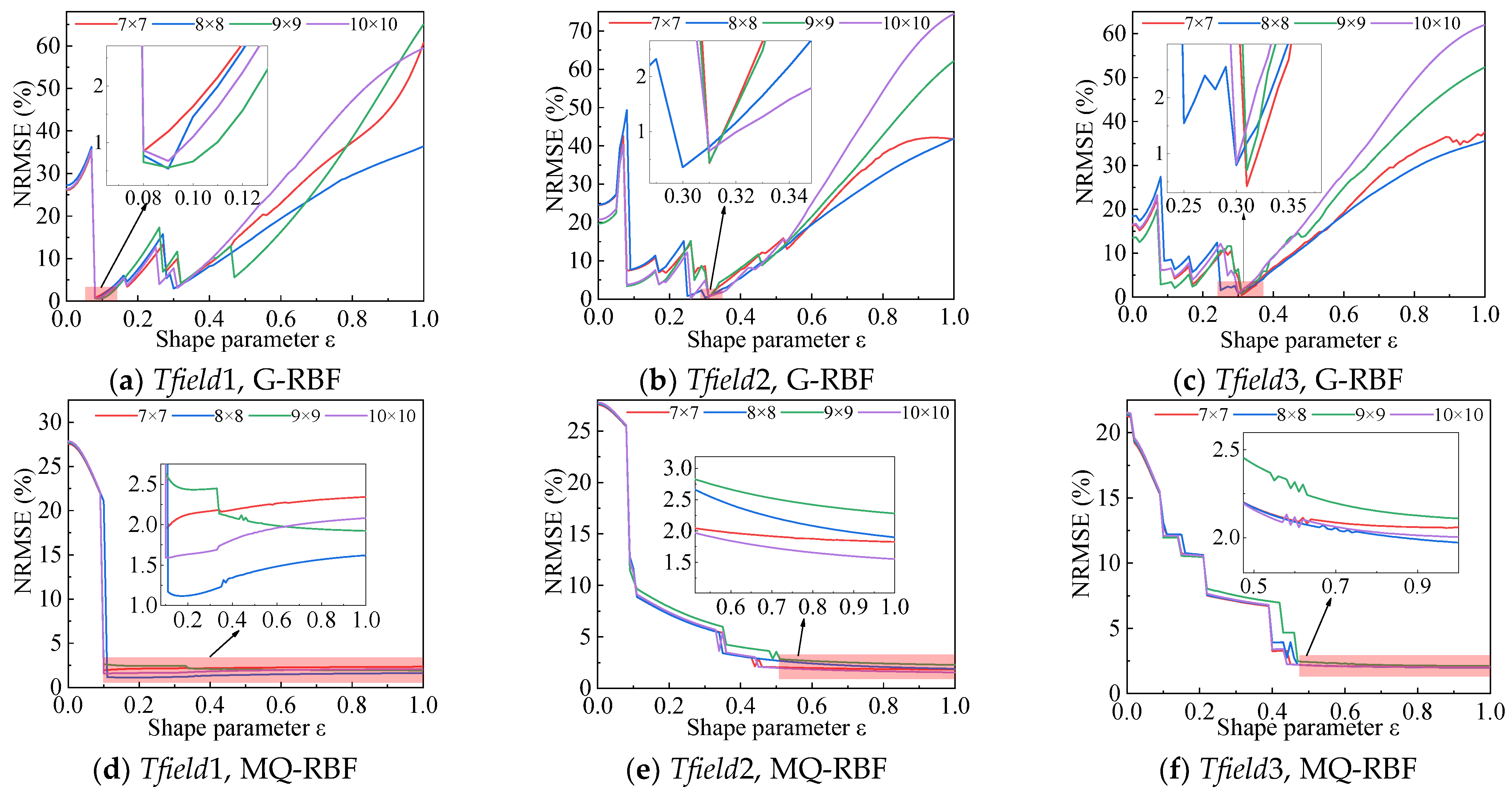
| coefHE | CHE | ||
|---|---|---|---|
| Tfield1 | Tfield2 | Tfield3 | |
| 0.1 | 3.26 | 2.23 | 2.34 |
| 0.2 | 6.51 | 5.22 | 4.08 |
| 0.5 | 16.53 | 14.96 | 15.28 |
| 1 | 32.04 | 31.33 | 34.02 |
| Case | coefHE | Input Values | NRMSE/% | Eh/% | Dh/% |
|---|---|---|---|---|---|
| Tfield1 | 0.1 | fb = 0.3, κ = 1.5 × 10−4 | 0.60 | 1.19 | 0 |
| 0.2 | fb = 0.4, κ = 1.5 × 10−4 | 1.18 | 2.43 | 0 | |
| 0.5 | fb = 0.2, κ = 1.5 × 10−4 | 2.90 | 1.39 | 0 | |
| 1 | fb = 0.25, κ = 1 × 10−4 | 6.61 | 19.01 | 0 | |
| Tfield2 | 0.1 | fb = 0.1, κ = 1.5 × 10−4 | 0.79 | 0.58, 0.74 | 1.41, 1.41 |
| 0.2 | fb = 0.2, κ = 1.5 × 10−4 | 3.06 | 2.28, 0.70 | 1.41, 1.41 | |
| 0.5 | fb = 0.5, κ = 9 × 10−5 | 2.92 | 2.91, 4.18 | 0, 0 | |
| 1 | fb = 0.4, κ = 7 × 10−5 | 3.87 | 14.59, 13.49 | 0, 0 | |
| Tfield3 | 0.1 | fb = 0.8, κ = 1.5 × 10−4 | 1.58 | 2.10, 0.86, 0.89 | 1.41, 3, 2 |
| 0.2 | fb = 0.4, κ = 7.5 × 10−5 | 2.18 | 4.08, 0.95, 0.55 | 1.41, 2.41, 1 | |
| 0.5 | fb = 0.5, κ = 3 × 10−5 | 3.65 | 14.94, 12.09, 8.20 | 2.24, 0, 1.41 | |
| 1 | fb = 0.5, κ = 1 × 10−4 | 6.67 | 24.98, 20.12, 22.96 | 1.41, 1, 0 |
| coefHE | Dh/% | |||
|---|---|---|---|---|
| Basis | AHK | AGES | AGES-AHK | |
| 0.1 | 0 | 0 | 0 | 0 |
| 0.2 | 0 | 0 | 0 | 0 |
| 0.5 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| coefHE | Dh/% | |||
|---|---|---|---|---|
| Basis | AHK | AGES | AGES-AHK | |
| 0.1 | 1.41, 1.41 | 1.41, 1.41 | 0, 1.41 | 1.41, 1.41 |
| 0.2 | 0.14, 1.41 | 1.41, 1.41 | 1.41, 1.41 | 1.41, 1.41 |
| 0.5 | 0, 0 | 0, 0 | 0, 0 | 0, 0 |
| 1 | 0, 0 | 0, 0 | 0, 0 | 0, 0 |
| coefHE | Dh/% | |||
|---|---|---|---|---|
| Basis | AHK | AGES | AGES-AHK | |
| 0.1 | 1, 3.16, 6.32 | 1.41, 2, 3.16 | 1.41, 3, 3 | 1.41, 3, 2 |
| 0.2 | 3, 2.24, 3.16 | 1, 2.24, 2 | 1.41, 0, 3 | 1.41, 2.41, 1 |
| 0.5 | 2.24, 0, 2 | 2.24, 0, 2.24 | 1.41, 0, 1 | 2.24, 0, 1.41 |
| 1 | 2, 2, 1.41 | 1.41, 1.41, 1 | 2, 1, 1 | 1.41, 1, 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, J.; Chen, L.; Li, N.; Zhou, Q.; Gao, Z.; Zhou, J. A Novel Temperature Reconstruction Method for Acoustic Pyrometry Under Strong Temperature Gradients and Limited Measurement Points. Appl. Sci. 2025, 15, 4728. https://doi.org/10.3390/app15094728
Tan J, Chen L, Li N, Zhou Q, Gao Z, Zhou J. A Novel Temperature Reconstruction Method for Acoustic Pyrometry Under Strong Temperature Gradients and Limited Measurement Points. Applied Sciences. 2025; 15(9):4728. https://doi.org/10.3390/app15094728
Chicago/Turabian StyleTan, Jingkao, Lehang Chen, Na Li, Qulan Zhou, Zhongquan Gao, and Jie Zhou. 2025. "A Novel Temperature Reconstruction Method for Acoustic Pyrometry Under Strong Temperature Gradients and Limited Measurement Points" Applied Sciences 15, no. 9: 4728. https://doi.org/10.3390/app15094728
APA StyleTan, J., Chen, L., Li, N., Zhou, Q., Gao, Z., & Zhou, J. (2025). A Novel Temperature Reconstruction Method for Acoustic Pyrometry Under Strong Temperature Gradients and Limited Measurement Points. Applied Sciences, 15(9), 4728. https://doi.org/10.3390/app15094728






