Security-Enhanced Lightweight Authentication Key-Agreement Protocol for Unmanned Aerial Vehicle Communication
Abstract
1. Introduction
- (a)
- An authenticated key-agreement protocol with low computational complexity and only four scalar multiplication operations is proposed, and the performance analysis shows that our protocol has a lower computational cost than representative protocols.
- (b)
- A key-agreement scheme is designed to compute the session key by combining the identity identifier and a temporary session random number. This scheme ensures the security of the session key when information on the temporary session random number is leaked.
- (c)
- A formal analysis and ProVerif simulation [29] are performed to verify the performance of the proposed protocol. Both the theoretical analysis and experimental verification show that the proposed protocol has higher security properties and a lower computational cost than representative protocols.
2. Analysis of Limitations of Existing Representative Methods
2.1. Analysis of Security Vulnerabilities in the Chaudhry Protocol
- (a)
- Attacker C obtains the message by listening to the public channel: ;
- (b)
- Leveraging the publicly available and the obtained , the adversary can calculate through the scalar–point-multiplication operation ;
- (c)
- Attacker C obtains the by calculating because ;
- (d)
- Attacker C obtains the by calculating .
2.2. An Analysis of the Security Vulnerabilities in the Ren Protocol
- (a)
- Attacker C receives the message by listening to the public channel: ;
- (b)
- Attacker C obtains through the temporary session;
- (c)
- Attacker C calculates through the elliptic-curve scalar multiplication operation.
- (d)
- Attacker C obtains the by calculating .
2.3. Analysis of Security Vulnerabilities in the Tsobdjou Protocol
- (a)
- Attacker C obtains the message by listening to the public channel M.
- (b)
- Attacker C obtains the session key directly by calculating .
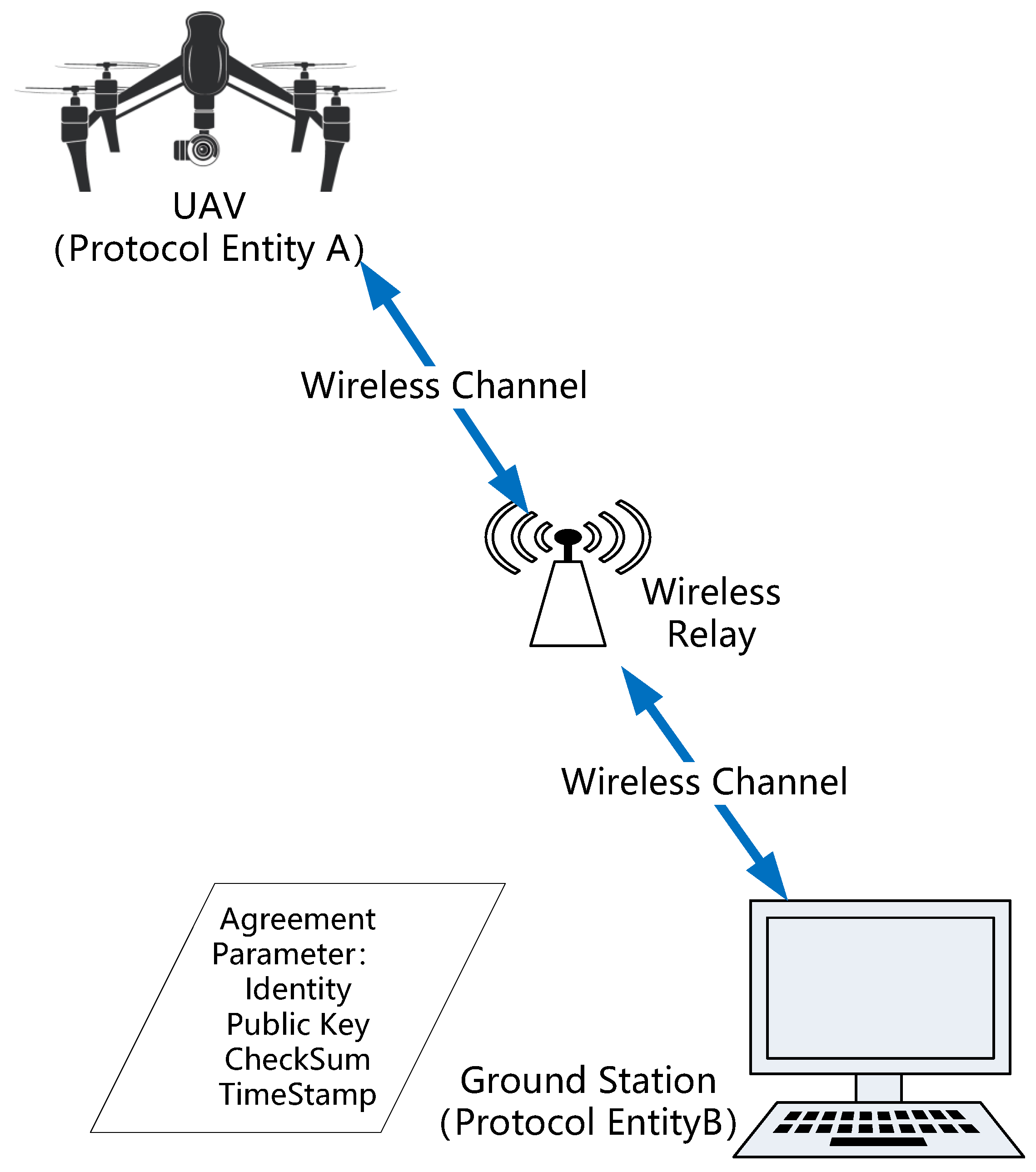
3. A Security-Enhanced Authenticated Key-Agreement Protocol: SE-UAVAKA
3.1. Related Theories and Definitions
3.1.1. Security Attribute Definition
- Impersonation attack resistance: If the attacker cannot obtain the long-term key of protocol entity A, they will not be able to impersonate A and communicate with other protocol entities.
- Replay attack resistance: An attacker cannot deceive the target host by sending data packets that the target host has already received.
- Known session-specific temporary information attack resistance: The disclosure of temporary intermediate results does not affect the security of the session key.
- Perfect forward security: The disclosure of long-term keys of all protocol units has no influence on the security of the previously created session keys.
- Known-key security: Even if an attacker gets hold of some previous session keys, they cannot obtain the current session key.
- User anonymity: During the execution of the protocol, attackers cannot find out the identity of the protocol instance.
- Mutual authentication: Protocol units can authenticate each other, and the authentication process cannot be falsified by attackers.
3.1.2. Some Notations Used in the Protocols
3.2. SE-UAVAKA Initialization Phase
- (a)
- Select a large prime number p and the parameters as an elliptic curve : A finite field exists on and satisfies . The prime p is chosen to be sufficiently large (e.g., 256+ bits for modern security), while a and b are randomly selected from such that , ensuring the curve is nonsingular (free from cusps or self-intersections) to maintain cryptographic integrity by avoiding singular points where discrete logarithm problems become computationally tractable.
- (b)
- Select point P as the base point of the elliptic curve. This point is selected because it generates a large cyclic subgroup of prime order, ensuring resistance to attacks like Pohlig–Hellman, and its cofactor is minimized to maintain cryptographic robustness.
- (c)
- Select a one-way hash function (e.g., SHA-256, representing robust collision resistance and standardized security) and a symmetric encryption/decryption function (e.g., AES-128, ensuring strong confidentiality and widespread cryptographic acceptance).
- (d)
- Enter the ID (a constant identity ID that uniquely identifies the protocol instance, ensuring immutability and persistence throughout the device lifecycle) of the trusted protocol instance in the database (which is normally saved when the device leaves the factory;
- (e)
- Use a cryptographically secure pseudorandom number generator (CSPRNG, e.g., AES-CTR_DRBG from Linux/dev/urandom, FIPS 140-2 certified) to generate the global private key (where n is the order of the elliptic-curve group), then compute the RC’s global public key via scalar multiplication: (with “·” denoting elliptic-curve scalar multiplication).
- (f)
- Transfer all public parameters to all protocol entities.
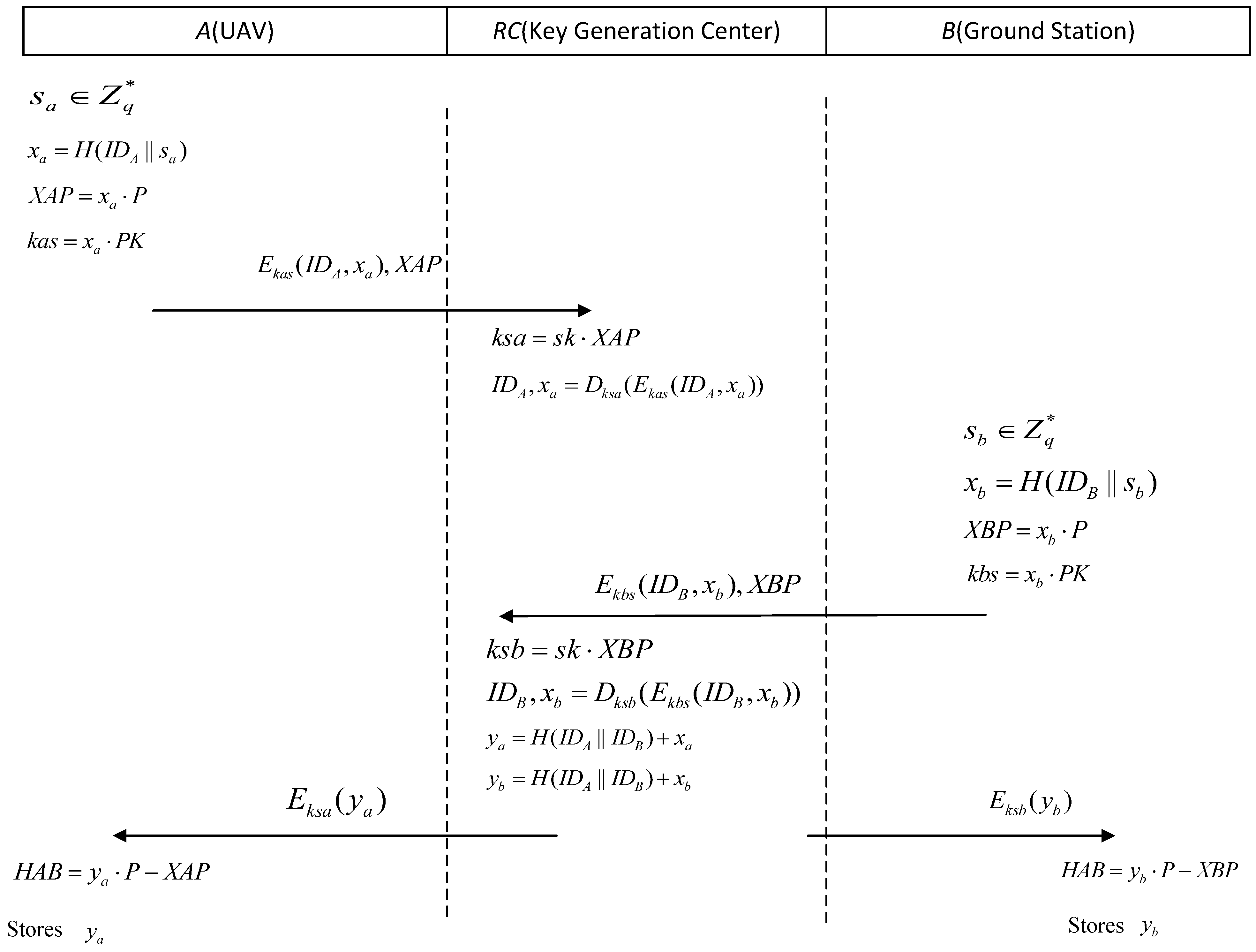
3.3. SE-UAVAKA Registration Phase
- (a)
- Use the random number generator described in the initialization phase to generate a random number (where represents a set of positive integers), and use a one-way hash function to calculate (where is a connector, indicating that two elements are concatenated together);
- (b)
- Using the scalar multiplication of elliptic curves, compute ;
- (c)
- Calculate the symmetric key for the temporary encryption (the global public key generated during the initialization phase);
- (d)
- Use symmetric encryption technology to encrypt the identities and to obtain (for example, when using the AES-128 algorithm, the string formed by concatenating and is used as the parameter to be encrypted, and is used as the symmetric encryption key for calculation);
- (e)
- Send and to the key-generation center RC.
- (a)
- Combine the global private key and issued by protocol instance B and use the scalar multiplication operation of the elliptic curve to compute (because , ; therefore, );
- (b)
- Use for decryption to obtain the ID and of protocol unit A: , and then wait for the message from B.
- (a)
- Use the random number generator described in the initialization phase to generate a random number and use a one-way hash function to calculate ;
- (b)
- Using the scalar multiplication of elliptic curves, compute ;
- (c)
- Calculate the symmetric key for the temporary encryption ;
- (d)
- Encrypt identity and using symmetric encryption to obtain ;
- (e)
- Send and to the key-generation center RC.
- (a)
- Combine the global private key and issued by protocol instance B and use the scalar multiplication operation of the elliptic curve to compute (because , ; therefore, );
- (b)
- Use for decryption to obtain the ID and of protocol unit A: , and then wait for the message from B;
- (c)
- Calculate and calculate ;
- (d)
- Encrypt using and , respectively, and send them to A and B.
- (a)
- Decrypt with ;
- (b)
- Store .
- (a)
- Decrypt using ;
- (b)
- Store .
3.4. SE-UAVAKA Authentication Key-Agreement Phase
3.4.1. Detailed Steps of Authentication Key-Agreement Phase
- (a)
- Retrieve the data obtained during the registration phase from the local secure storage.
- (b)
- Select a random number and use scalar multiplication to calculate .
- (c)
- Generate the current timestamp .
- (d)
- Calculate using a one-way hash function.
- (e)
- XOR of the x-axis of point of the elliptic curve to obtain .
- (f)
- XOR encryption of the x-axis of point of the elliptic curve to obtain .
- (g)
- Use the symmetric encryption algorithm to encrypt the ID to obtain .
- (h)
- Send parameters to protocol entity B through an open channel.
- (a)
- Decode the x-axis information of to obtain .
- (b)
- Decode the y-axis information of to obtain .
- (c)
- Combine the above x- and y-axis information to obtain .
- (d)
- Decrypt the information using the symmetric decryption algorithm to obtain the ID of protocol entity A: .
- (e)
- Calculate using a one-way hash function.
- (f)
- Compare with the obtained : If the comparison is successful, B authenticates A successfully.
- (g)
- Fetch the data obtained during the registration phase from the local secure storage.
- (h)
- Select a random number and use scalar multiplication to calculate .
- (i)
- Generate the current timestamp .
- (j)
- Calculate using a one-way hash function.
- (k)
- XOR of the x-axis of point of the elliptic curve to obtain .
- (l)
- XOR encryption of the x-axis of point of the elliptic curve to obtain .
- (m)
- Use the symmetric encryption algorithm to encrypt the ID to obtain .
- (n)
- Calculate the session key .
- (o)
- Send the parameters to protocol entity A through an open channel.
- (a)
- Decode the x-axis information of to obtain .
- (b)
- Decode the y-axis information of to obtain .
- (c)
- By combining the above x- and y-axis information, we obtain .
- (d)
- Decrypt the information using the symmetric decryption algorithm to obtain the ID of protocol entity A: .
- (e)
- Calculate using a one-way hash function.
- (f)
- Compare with the obtained : If the comparison is successful, A authenticates B successfully.
- (g)
- Calculate the session key: .
3.4.2. Explanation of Key Processes in the Authentication Key-Agreement Phase
3.4.3. Security Mechanisms and Design Rationale
- Elliptic-Curve Scalar Multiplication: The proposed scheme employs scalar multiplication () to generate cryptographic parameters, establishing direct binding between and ephemeral value as impersonation resistance. Without knowledge of both and the drone’s long-term secret , adversaries cannot feasibly forge valid parameters.
- XOR-based Parameter Obfuscation: The XOR operation () serves dual security purposes: (1) Obscures sensitive coordinate data from elliptic-curve operations during transmission, preventing eavesdroppers from directly reconstructing ; (2) leverages as session-specific secrets generated during registration to enforce dual-key decryption requirements. This design withstands known temporary parameter attacks since derivation requires both and , remaining secure even if gets compromised.
- Timestamp and Hash Validation: The protocol incorporates timestamp validation (, ) to ensure message freshness, complemented by hash commitments and for parameter integrity verification. Any tampering during transmission alters the resulting hash values, triggering verification failure at the recipient side.
- Identity-Protected Symmetric Encryption: Anonymous authentication is achieved through session-specific symmetric encryption of identifiers (). Without access to the long-term secret —securely stored in device memory and never exposed in communication channels—attackers cannot correlate sessions with specific drones or ground stations.
3.4.4. Main Improvements of This Protocol
- Improved efficiency: The protocol reduces scalar multiplication operations to four (two per entity), significantly lowering computational latency compared to prior works (e.g., Chaudhry’s eight operations).
- Resistance to Known Session-Specific Attacks: A key innovation lies in binding the session key to both long-term identities (, ) and ephemeral parameters (, ). Even if temporary values (, ) leak, an adversary cannot compute without knowing and , which are protected via XOR obfuscation and encrypted channels. This contrasts with vulnerabilities in Chaudhry’s and Ren’s protocols, where session keys become directly computable from leaked temporaries.
- Mutual Authentication Guarantees: The protocol enforces mutual authentication through bidirectional hash verification. Entity B validates to confirm that was generated by a legitimate UAV with knowledge of and . Similarly, Entity A verifies to authenticate the ground station. This dual-check mechanism ensures that neither party can proceed to key derivation without successful authentication.
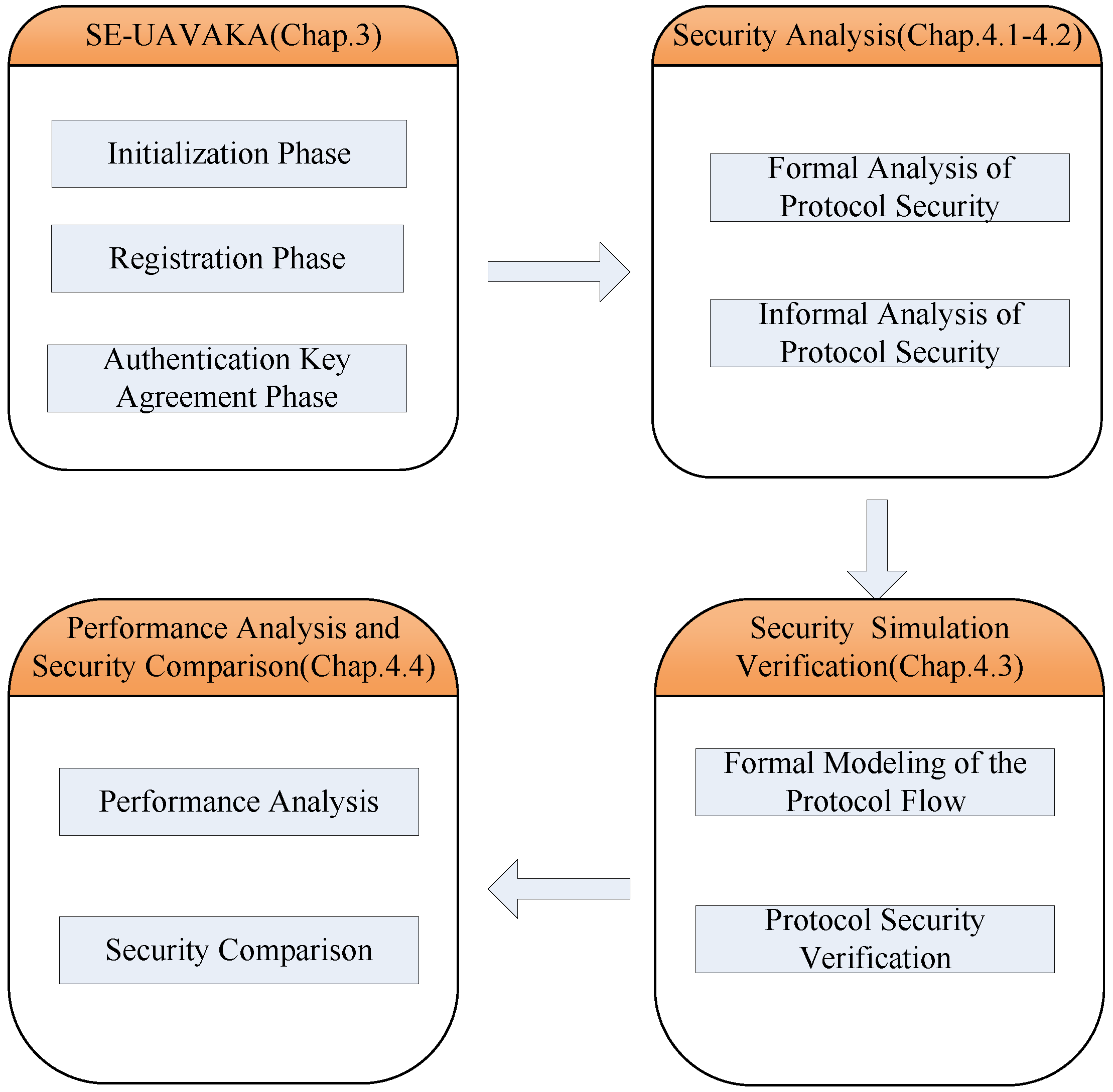
4. Security Analysis and Simulation Verification
4.1. Formal Analysis of Protocol Security
4.1.1. Detailed Steps for Formal Security Analysis
Mutual Authentication
- (a)
- Message meaning rule: If the entity U believes that K is a shared key between the entities U and V, and U receives a message encrypted with K, then the entity U believes that V has sent a message M, the formulas are as follows:
- (b)
- Checking freshness rule: If the entity U believes that the message M was sent by V and is fresh, then the entity U believes that the entity V trusts the message M. The formulas are as follows: .
- (c)
- Arbitration rule: If the entity U believes that the entity V has control over the message M, and the entity U believes that V trusts the message M, then the entity U trusts the message M. The formulas are as follows: .
- (d)
- Fresh-connections rule: If the entity U believes that the message M is fresh, then the entity U also believes that the message simply concatenated by M and N is also fresh. The formulas are as follows: .
- (e)
- Trust rule: If the entity U trusts a message that is simply a concatenation of the messages M and N, then the entity U believes this message M. The formulas are as follows: .
- (f)
- Sending rule: If the entity U believes that the entity V has sent a message connected by M and N, then the entity U believes that V has sent the message M. The formulas are as follows: .
- Goal 1: (protocol entity B believes that protocol entity A trusts the message ).
- Goal 2: (protocol entity B believes that protocol entity A trusts the message).
- Goal 3: (protocol entity B trusts the message ).
- Goal 4: (protocol entity A trusts the message ).
- Step 1: :.
- Step 2: :.
Anti-Attack Against Known Session-Specific Temporary Information
- (a)
- occurs and the temporary session information is obtained.
- (b)
- Retrieve messages transmitted through the public channel: .
- (c)
- occurs; obtain and decrypt the message to obtain .
- (d)
- Determine the message transmitted through the public channel: .
- (e)
- Decrypt the message to obtain .
- (f)
- The session key is obtained by calculation: .
User Anonymity
- (a)
- Obtain the message transmitted through the public channel .
- (b)
- occurs, and is received according to or is received according to .
4.1.2. Interpretation and Result Evaluation
Clarification of BAN Logic and Probabilistic Analysis
Applicability of Analytical Methods
- Relevance of BAN Logic: Addressing the fundamental requirement of mutual authentication, BAN logic rigorously formalizes trust transfer mechanisms between protocol entities through axiomatic rules (e.g., message freshness and jurisdiction rules). Its “belief-action” framework effectively models dependency relationships among critical authentication parameters. The logic systematically characterizes how entities establish trust in session keys and ephemeral values through message exchanges, thereby ensuring logical consistency throughout the authentication process. For example, it formalizes the derivation of trust through sequential verification steps during protocol execution.
- Complementarity of Probabilistic Analysis: Through formal definitions of adversary success events (Event1–Event7) and computation of their probabilistic bounds, this approach transforms protocol security into mathematically quantifiable propositions. The methodology establishes explicit connections between session-key compromise probabilities and the computational intractability of the elliptic-curve discrete logarithm problem (ECDLP), aligning with modern cryptography’s provable security paradigm. This dual perspective enables rigorous security evaluation under practical attack conditions, particularly when temporary session parameters become compromised, while maintaining alignment with computational complexity assumptions.
4.2. Informal Analysis of Protocol Security
4.2.1. Detailed Steps for Formal Security Analysis
Anti-Imitation Attack
- (a)
- Select a random number . Because the registration fails, a random number is selected as the long-term key. Calculate .
- (b)
- Generate the timestamp .
- (c)
- Calculate the summary value .
- (d)
- Obtain by XOR scrambling the x-axis of point of the elliptic curve: .
- (e)
- Obtain by XOR scrambling the y-axis of the point of the elliptic curve : .
- (f)
- Send the message to protocol entity B.
- (a)
- Decrypt the x-axis information: .
- (b)
- Decrypt the y-axis information: .
- (c)
- By combining the above x- and y-axis information, we obtain .
- (d)
- Decrypt by using a symmetric decryption algorithm to obtain the ID: .
- (e)
- Calculate using a one-way hash function: .
- (f)
- Because is not legally registered, the calculated ; that is, , and thus, the session is rejected.
Perfect Forward Security
Anti-Repetition Attack
Known Key Security
4.2.2. Interpretation and Result Evaluation
4.3. Formal Simulation Verification of Protocol Security
4.3.1. Formal Modeling of the Protocol Flow
| Algorithm 1 Formal modeling algorithm for the authentication-key-agreement phase of entity A. |
| Input: Null Output: Process let pEa= event startAuthB; new ra:Random; let Na = computeNx(ra,ida,P) in let hab = Minus(ya,xa) in let EaxEay = exor(Na,hab) in new TSSeeda:bitstring; let TSa = generate_Timeline(TSSeeda) in let Ha = threeElementsHash(ida,TSa,Na) in let eIDa = symenc(ida,hab) in out (c,(eIDa,EaxEay,Ha,TSa)); in (c,(xeIDb:bitstring,xEbxEby:bitstring,xHb:bitstring,xTSb:TimeLine)); let xNb = dxor(xEbxEby,hab) in let xidb = symdec(xeIDb,hab) in let xxHb = threeElementsHash(xidb,xTSb,xNb) in if (xxHb = xHb) then let SKAB = computeKeySK(ra,ida,xNb) in let SSKAB = oneElementHash(SKAB) in event endAuthA. |
| Algorithm 2 Formal modeling algorithm for the authentication key-agreement phase of entity B. |
| Input: Null Output: Process let pEb= event startAuthA; in (c,(xva:bitstring,xhida:bitstring,xTSa:TimeLine,xla:bitstring,xSAP:Point)); in (c,(xeIDa:bitstring,xEaxEay:bitstring,xHa:bitstring,xTSa:TimeLine)); new rb:Random; let Nb = computeNx(rb,idb,P) in let hba = Minus(yb,xb) in let EbxEby = exor(Nb,hba) in new TSSeedb:bitstring; let TSb = generate_Timeline(TSSeedb) in let Hb = threeElementsHash(idb,TSb,Nb) in let eIDb = symenc(idb,hba) in let xNa = dxor(xEaxEay,hba) in let xida = symdec(xeIDa,hba) in let xxHa = threeElementsHash(xida,xTSa,xNa) in if (xxHa = xHa) then let SKBA = computeKeySK(rb,idb,xNa) in let SSKBA = oneElementHash(SKBA) in out (c,(eIDb,EbxEby,Hb,TSb)); event endAuthB. |
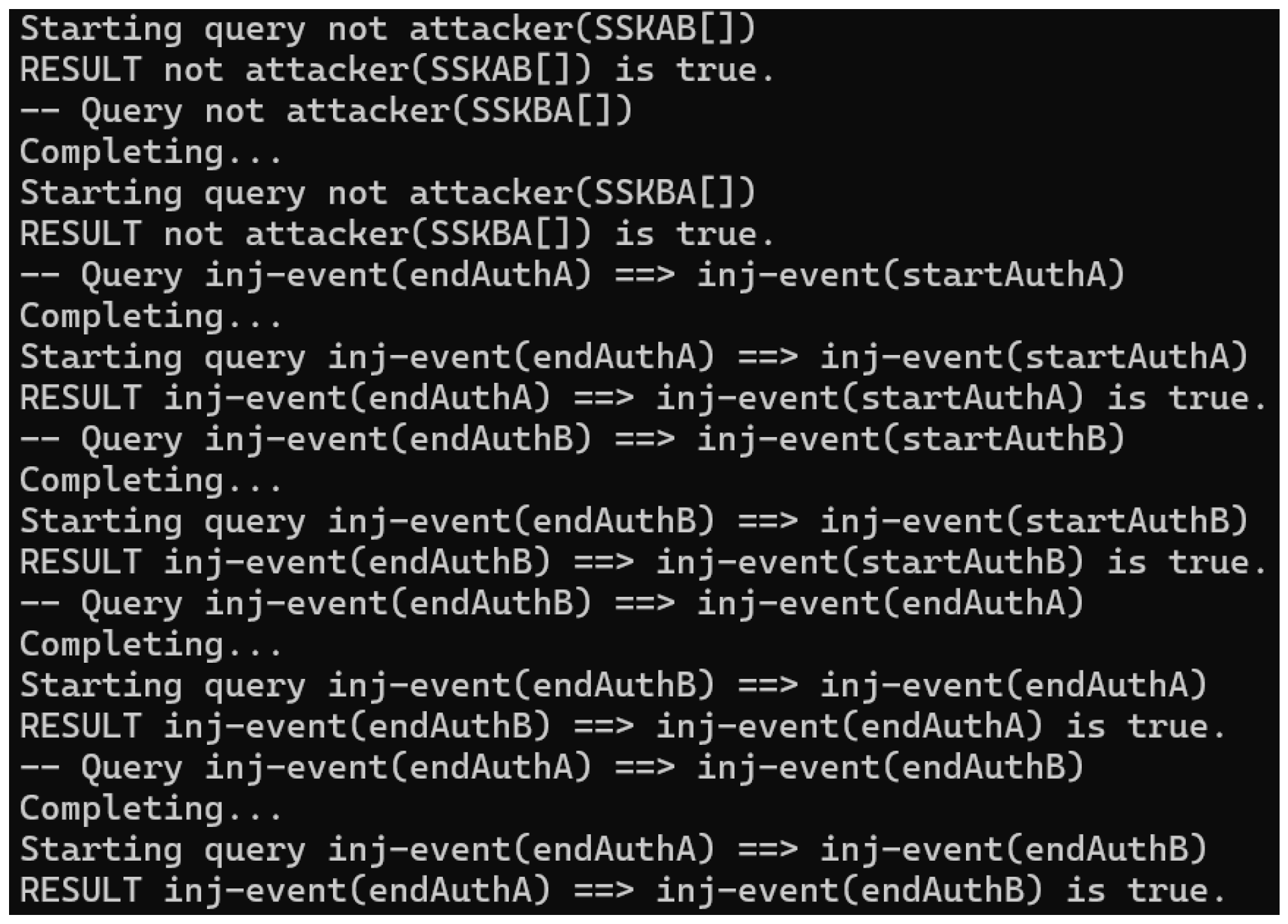
4.3.2. Protocol Security Verification Results
4.3.3. Interpretation and Result Evaluation
4.4. Performance Analysis and Security Comparison
4.4.1. Performance Analysis
4.4.2. Security Comparison
4.4.3. Interpretation and Result Evaluation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAV | Unmanned Aerial Vehicle |
| ECC | Elliptic-Curve Cryptography |
| DH | Diffie–Hellman |
| RC | Key-Generation Center |
| PK | Public key of the key-generation center |
| sk | Private key of the key-generation center |
| TS | Timestamp information |
| SSK | Session keys of protocol entities |
References
- Ghamari, M.; Rangel, P.; Mehrubeoglu, M.; Tewolde, G.S.; Sherratt, R.S. Unmanned aerial vehicle communications for civil applications: A review. IEEE Access 2022, 10, 102492–102531. [Google Scholar] [CrossRef]
- Albeaino, G.; Gheisari, M.; Franz, B.W. A systematic review of unmanned aerial vehicle application areas and technologies in the AEC domain. J. Inf. Technol. Constr. 2019, 24, 381–405. [Google Scholar]
- Wang, L.; Chen, Y.; Wang, P.; Yan, Z. Security threats and countermeasures of unmanned aerial vehicle communications. IEEE Commun. Stand. Mag. 2021, 5, 41–47. [Google Scholar] [CrossRef]
- Jacobsen, R.H.; Marandi, A. Security threats analysis of the unmanned aerial vehicle system. In Proceedings of the MILCOM 2021—2021 IEEE Military Communications Conference (MILCOM), San Diego, CA, USA, 29 November–2 December 2021; IEEE: New York, NY, USA, 2021; pp. 316–322. [Google Scholar]
- Zeng, Y.; Zhang, R.; Lim, T.J. Wireless communications with unmanned aerial vehicles: Opportunities and challenges. IEEE Commun. Mag. 2016, 54, 36–42. [Google Scholar] [CrossRef]
- Abdussami, M.; Amin, R.; Vollala, S. Provably secured lightweight authenticated key agreement protocol for modern health industry. Ad Hoc Netw. 2023, 141, 103094. [Google Scholar] [CrossRef]
- Guo, Y.; Guo, Y. CS-LAKA: A lightweight authenticated key agreement protocol with critical security properties for IoT environments. IEEE Trans. Serv. Comput. 2023, 16, 4102–4114. [Google Scholar] [CrossRef]
- Hasan, M.K.; Weichen, Z.; Safie, N.; Ahmed, F.R.A.; Ghazal, T.M. A Survey on Key Agreement and Authentication Protocol for Internet of Things Application. IEEE Access 2024, 12, 61642–61666. [Google Scholar] [CrossRef]
- Mahmood, K.; Chaudhry, S.A.; Naqvi, H.; Kumari, S.; Li, X.; Sangaiah, A.K. An elliptic curve cryptography based lightweight authentication scheme for smart grid communication. Future Gener. Comput. Syst. 2018, 81, 557–565. [Google Scholar] [CrossRef]
- Abbasinezhad-Mood, D.; Nikooghadam, M. Design and hardware implementation of a security-enhanced elliptic curve cryptography based lightweight authentication scheme for smart grid communications. Future Gener. Comput. Syst. 2018, 84, 47–57. [Google Scholar] [CrossRef]
- Liestyowati, D. Public key cryptography. Proc. J. Phys. Conf. Ser. 2020, 1477, 052062. [Google Scholar] [CrossRef]
- Braeken, A. Public key versus symmetric key cryptography in client–server authentication protocols. Int. J. Inf. Secur. 2022, 21, 103–114. [Google Scholar] [CrossRef]
- Adhikari, S.; Ray, S.; Obaidat, M.S.; Biswas, G. Efficient and secure content dissemination architecture for content centric network using ECC-based public key infrastructure. Comput. Commun. 2020, 157, 187–203. [Google Scholar] [CrossRef]
- Alladi, T.; Bansal, G.; Chamola, V.; Guizani, M. SecAuthUAV: A novel authentication scheme for UAV-ground station and UAV-UAV communication. IEEE Trans. Veh. Technol. 2020, 69, 15068–15077. [Google Scholar] [CrossRef]
- Nyangaresi, V.O.; Ibrahim, A.; Abduljabbar, Z.A.; Hussain, M.A.; Al Sibahee, M.A.; Hussien, Z.A.; Ghrabat, M.J.J. Provably secure session key agreement protocol for unmanned aerial vehicles packet exchanges. In Proceedings of the 2021 International Conference on Electrical, Computer and Energy Technologies (ICECET), Cape Town, South Africa, 9–10 December 2021; IEEE: New York, NY, USA, 2021; pp. 1–6. [Google Scholar]
- Rodrigues, M.; Amaro, J.; Osório, F.S.; Branco Kalinka, R.L.J.C. Authentication methods for UAV communication. In Proceedings of the 2019 IEEE Symposium on Computers and Communications (ISCC), Barcelona, Spain, 29 June–3 July 2019; IEEE: New York, NY, USA, 2019; pp. 1210–1215. [Google Scholar]
- Yu, S.; Lee, J.; Sutrala, A.K.; Das, A.K.; Park, Y. LAKA-UAV: Lightweight authentication and key agreement scheme for cloud-assisted Unmanned Aerial Vehicle using blockchain in flying ad-hoc networks. Comput. Netw. 2023, 224, 109612. [Google Scholar] [CrossRef]
- Gupta, K.; Silakari, S. Ecc over rsa for asymmetric encryption: A review. Int. J. Comput. Sci. Issues (IJCSI) 2011, 8, 370. [Google Scholar]
- Li, N. Research on Diffie-Hellman key exchange protocol. In Proceedings of the 2010 2nd International Conference on Computer Engineering and Technology, Chengdu, China, 16–18 April 2010; IEEE: New York, NY, USA, 2010; Volume 4, p. 634. [Google Scholar]
- Verri Lucca, A.; Mariano Sborz, G.A.; Leithardt, V.R.Q.; Beko, M.; Albenes Zeferino, C.; Parreira, W.D. A review of techniques for implementing elliptic curve point multiplication on hardware. J. Sens. Actuator Netw. 2020, 10, 3. [Google Scholar] [CrossRef]
- Kapoor, V.; Abraham, V.S.; Singh, R. Elliptic curve cryptography. Ubiquity 2008, 2008, 1–8. [Google Scholar] [CrossRef]
- Chen, Y.; Yin, F.; Hu, S.; Sun, L.; Li, Y.; Xing, B.; Chen, L.; Guo, B. ECC-based authenticated key agreement protocol for industrial control system. IEEE Internet Things J. 2022, 10, 4688–4697. [Google Scholar] [CrossRef]
- Islam, S.H.; Biswas, G. Design of two-party authenticated key agreement protocol based on ECC and self-certified public keys. Wirel. Pers. Commun. 2015, 82, 2727–2750. [Google Scholar] [CrossRef]
- Challa, S.; Das, A.K.; Odelu, V.; Kumar, N.; Kumari, S.; Khan, M.K.; Vasilakos, A.V. An efficient ECC-based provably secure three-factor user authentication and key agreement protocol for wireless healthcare sensor networks. Comput. Electr. Eng. 2018, 69, 534–554. [Google Scholar] [CrossRef]
- Farhdi Moghadam, M.; Mohajerzdeh, A.; Karimipour, H.; Chitsaz, H.; Karimi, R.; Molavi, B. A privacy protection key agreement protocol based on ECC for smart grid. In Handbook of Big Data Privacy; Springer: Cham, Switzerland, 2020; pp. 63–76. [Google Scholar]
- Chaudhry, S.A.; Nebhan, J.; Yahya, K.; Al-Turjman, F. A privacy enhanced authentication scheme for securing smart grid infrastructure. IEEE Trans. Ind. Inform. 2022, 18, 5000–5006. [Google Scholar] [CrossRef]
- Ren, S.; Liu, Y.; Yu, B.; Liu, J.; Li, D. Provable Secure Anonymous Device Authentication Protocol in IoT Environment. IEEE Internet Things J. 2024, 11, 12266–12277. [Google Scholar] [CrossRef]
- Tsobdjou, L.D.; Pierre, S.; Quintero, A. A new mutual authentication and key agreement protocol for mobile client—server environment. IEEE Trans. Netw. Serv. Manag. 2021, 18, 1275–1286. [Google Scholar] [CrossRef]
- Blanchet, B.; Smyth, B.; Cheval, V.; Sylvestre, M. ProVerif 2.00: Automatic cryptographic protocol verifier, user manual and tutorial. Version 2018, 16, 5–16. [Google Scholar]
- Yogesh, P.R. Formal verification of secure evidence collection protocol using BAN logic and AVISPA. Procedia Comput. Sci. 2020, 167, 1334–1344. [Google Scholar] [CrossRef]
- Küsters, R.; Truderung, T. Using ProVerif to analyze protocols with Diffie-Hellman exponentiation. In Proceedings of the 2009 22nd IEEE Computer Security Foundations Symposium, Port Jefferson, NY, USA, 8–10 July 2009; IEEE: New York, NY, USA, 2009; pp. 157–171. [Google Scholar]
- Hu, S.; Chen, Y.; Zheng, Y.; Xing, B.; Li, Y.; Zhang, L.; Chen, L. Provably secure ECC-based authentication and key agreement scheme for advanced metering infrastructure in the smart grid. IEEE Trans. Ind. Inform. 2022, 19, 5985–5994. [Google Scholar] [CrossRef]
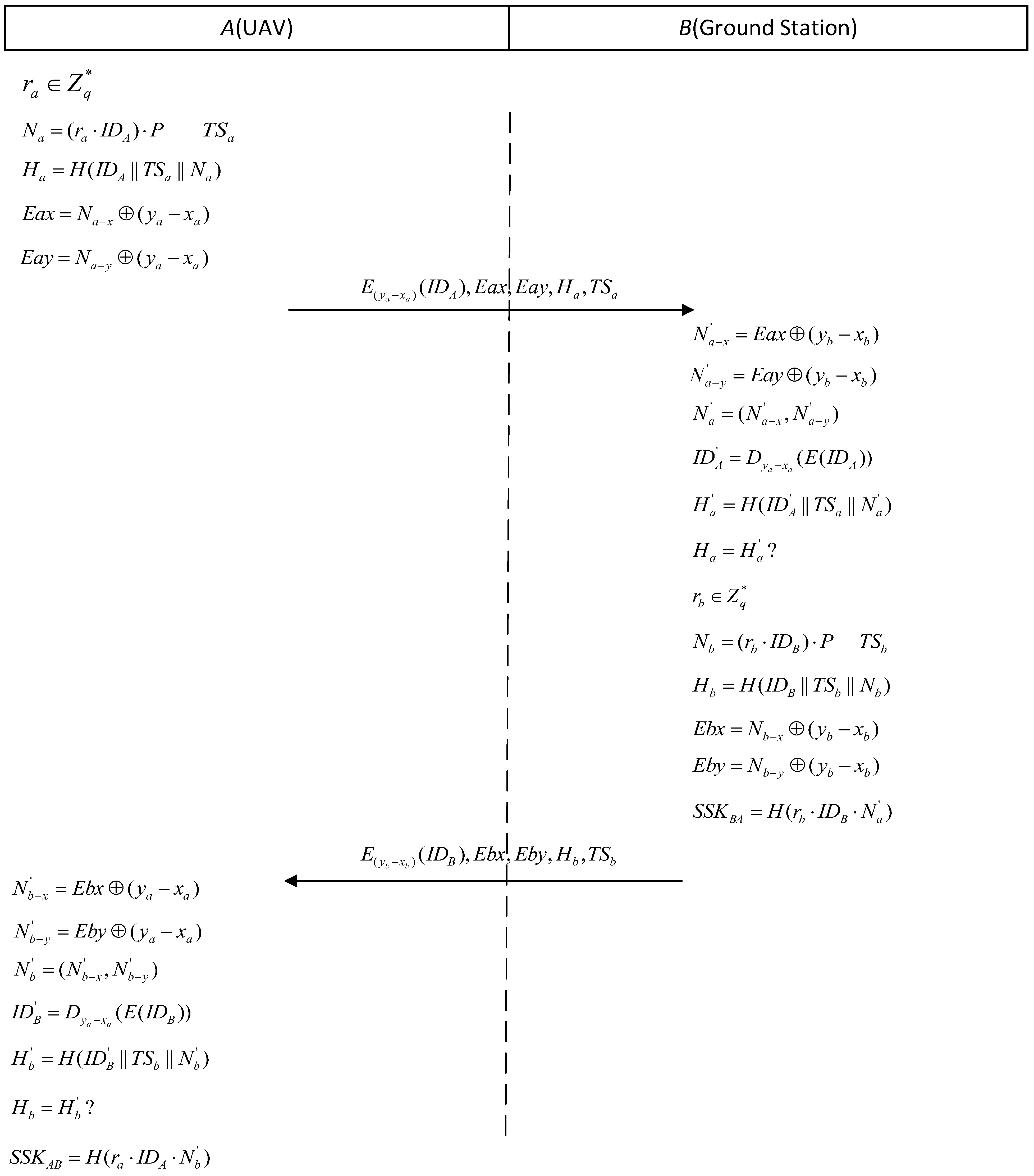
| Notation | Description |
|---|---|
| A | Agreement Entity A |
| B | Agreement Entity B |
| Key-generation center | |
| Public key of the key-generation center | |
| Private key of the key-generation center | |
| Identification of the protocol entity | |
| Integers in finite fields | |
| Symmetric encryption function | |
| Symmetric decryption function | |
| ⊕ | Bitwise XOR Operator |
| Timestamp information | |
| One-way hash function | |
| Session keys of protocol entities |
| Notation | Description |
|---|---|
| Entity U believes the statement M | |
| Entity U receives message M | |
| Entity U once sent message M | |
| Entity U has control over message M | |
| Message M is fresh | |
| The message is composed of M and N | |
| is part of the message | |
| is encrypted by the key K | |
| U and V communicate using the key K |
| Operation | Average Time per Session (PC) | Average Time per Session (ARM Cortex-M3) |
|---|---|---|
| Mul | 2.1780 ms | 87 ms |
| Add | 0.0239 ms | 0.36 ms |
| Hash | 0.0186 ms | 0.065 ms |
| Xor | 0.0091 ms | 0.1 ms |
| Protocol | Number of Tests | Agreement Time (PC) | Agreement Time (ARM Cortex-M3) |
|---|---|---|---|
| Chaudhry | 17.621 ms | 697.24 ms | |
| Tsobdjou | 13.235 ms | 522.72 ms | |
| Ren | 13.2168 ms | 522.52 ms | |
| Proposed | 8.9328 ms | 349.59 ms |
| Properties | Ren | Chaudhry | Tsobdjou | Proposed |
|---|---|---|---|---|
| IAR | ✓ | ✓ | ✓ | ✓ |
| RAR | ✓ | ✓ | ✓ | ✓ |
| UA | ✓ | ✓ | ✓ | ✓ |
| MA | ✓ | ✓ | ✓ | ✓ |
| PFS | ✓ | ✓ | ✓ | ✓ |
| KKS | ✓ | ✓ | ✓ | ✓ |
| KSTR | ☓ | ☓ | ☓ | ✓ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z.; Zheng, Y.; Chen, S.; Du, Z.; Liu, S.; Zhang, K. Security-Enhanced Lightweight Authentication Key-Agreement Protocol for Unmanned Aerial Vehicle Communication. Appl. Sci. 2025, 15, 4680. https://doi.org/10.3390/app15094680
He Z, Zheng Y, Chen S, Du Z, Liu S, Zhang K. Security-Enhanced Lightweight Authentication Key-Agreement Protocol for Unmanned Aerial Vehicle Communication. Applied Sciences. 2025; 15(9):4680. https://doi.org/10.3390/app15094680
Chicago/Turabian StyleHe, Zhoucan, Yilong Zheng, Sisi Chen, Zhongze Du, Shuyuan Liu, and Kailong Zhang. 2025. "Security-Enhanced Lightweight Authentication Key-Agreement Protocol for Unmanned Aerial Vehicle Communication" Applied Sciences 15, no. 9: 4680. https://doi.org/10.3390/app15094680
APA StyleHe, Z., Zheng, Y., Chen, S., Du, Z., Liu, S., & Zhang, K. (2025). Security-Enhanced Lightweight Authentication Key-Agreement Protocol for Unmanned Aerial Vehicle Communication. Applied Sciences, 15(9), 4680. https://doi.org/10.3390/app15094680






