MWMOTE-FRIS-INFFC: An Improved Majority Weighted Minority Oversampling Technique for Solving Noisy and Imbalanced Classification Datasets

Abstract

In view of the data of fault diagnosis and good product testing in the industrial field, high-noise unbalanced data samples exist widely, and such samples are very difficult to analyze in the field of data analysis. The oversampling technique has proved to be a simple solution to unbalanced data in the past, but it has no significant resistance to noise. In order to solve the binary classification problem of high-noise unbalanced data, an enhanced majority-weighted minority oversampling technique, MWMOTE-FRIS-INFFC, is introduced in this study, which is specially used for processing noise-unbalanced classified data sets. The method uses Euclidean distance to assign sample weights, synthesizes and combines new samples into samples with larger weights but belonging to a few classes, and thus solves the problem of data scarcity in smaller class clusters. Then, the fuzzy rough instance selection (FRIS) method is used to eliminate the subsets of synthetic minority samples with low clustering membership, which effectively reduces the overfitting tendency of minority samples caused by synthetic oversampling. In addition, the integration of classification fusion iterative filters (INFFC) helps mitigate synthetic noise issues, both raw data and synthetic data noise. On this basis, a series of experiments are designed to improve the performance of 6 oversampling algorithms on 8 data sets by using the MWMOTE-FRIS-INFFC algorithm proposed in this paper.

1. Introduction

Data-driven constitutes a form of actuarial analysis in which data serves as the guiding principle of reality. However, in practical applications, it can be observed that the levels of different data types vary widely, which actually indicates a serious imbalance in the data set. In the field of industry and fault prediction, this imbalance ratio ranges from 1:1000 to 1:100,000, and in some cases of precision systems engineering [1], the imbalance ratio is even more obvious. From a disciplinary perspective, limited numbers of samples tend to exhibit greater representativeness, especially in the context of disease data, failure data, and defect data, highlighting the important utility of these samples. Serious damage to the balance of data sets will lead to overfitting of some data, resulting in the concentration of sample classification, the decline of robustness of classification methods, and the decline of data analysis accuracy [2]. Oversampling techniques such as majority-weighted Minority Oversampling (MWMOTE) can effectively deal with a small number of characteristics of fault samples in unbalanced data and can also produce a better processing effect on noise. For example, the KNN method can effectively deal with local noise when the value of neighborhood parameter k is reasonable, but without prior experience, the KNN method may lead to insufficient or excessive recognition [3]. The double challenge of an unbalanced data set with noise poses new challenges to both the KNN algorithm and the original MWMOTE algorithm, so we propose an improved algorithm. Fuzzy-Rough Instance Selection (FRIS) and Iterative Noise Filter Based on the Fusion of Classifiers (INFFC), it realizes adaptive noise processing and unbalanced data processing, uses Euclidean distance and density screening to eliminate true noise and suspected noise, and enriches the original unbalanced samples by over-sampling technology. In this paper, the algorithm is renamed as a majority-class weighted minority-class oversampling algorithm (MWMOTE-FRIS-INFFC) based on the fusion of fuzzy rough instance selection and iterative noise classification fusion filtering. Moreover, it avoids the generation of new noise. Moreover, it can also overcome the expansion of inter-class imbalance and intra-class imbalance.

Through the experimental results, it can be seen that the algorithm proposed in this study is due to other common algorithms.

Oversampling technology constitutes a countermeasure algorithm addressing the imbalance of data in the realm of data analysis [4]. Initially, oversampling techniques employed methods such as data interpolation, data fusion, and dataset expansion to augment the count of minor samples, thereby attaining a balanced dataset. Subsequently, diverse oversampling techniques have been introduced for various domains, encompassing random oversampling, synthetic minority oversampling, adaptive synthetic sampling [5], safety level synthetic minority oversampling, and majority weighted minority oversampling. Nevertheless, despite these advancements, oversampling techniques applied to data in the domain of assembly still exhibit certain shortcomings. Even the aforementioned algorithms possess deficiencies in their handling of public datasets [6], which are outlined as follows:

(1) Partial oversampling technology introduces data volume to solve the imbalance between classes, but there is still a lot of noise in the added data, resulting in increased overlap and ambiguity between data classes.

(2) The experimental results of some algorithms are relatively good, but the practical application requires a lot of time and hardware support, resulting in insufficient universality.

(3) For the binary classification and diagnosis of data in the fault field, conventional algorithms tend to cause the convergence speed of the data aggregation classification process to be too fast, resulting in the sudden boundary fitting ignoring the knowledge content of the boundary, which is not conducive to the observation of some boundary knowledge [7]. According to the data in the field of equipment safety diagnosis, it is very important to reduce the convergence rate of sampling for the construction and use of knowledge graphs.

(4) None of the above algorithms deal with noise reasonably. In fact, the processing of noise directly affects the distribution of new instances, that is, directly affects the sampling effect of the algorithm.

In the field of conventional production line fault detection, the main form of data is the binary classification problem, that is, fault state and normal state. The subsequent fault cause analysis is a data processing problem that requires multi-data and multi-dimensional comprehensive analysis, but the binary classification problem of the first step is the primary task to achieve early warning and production line safety assurance [8]. Through the analysis of operation and maintenance data, there are serious class imbalance and noise problems in the production line fault detection data. In order to solve the above problems, this paper proposes a majority-class weighted minority-class oversampling technique based on fuzzy rough instances combined with classification fusion iterative filtering. The algorithm can effectively solve the problem of sample imbalance in binary classification problems and can significantly reduce the overfitting failure of synthetic samples to the original clustering problem. Subsequently, the classifier can integrate iterative filtering to filter out the influence of noise as a whole and finally complete the classification task. The algorithm shows good ability in solving practical problems. This study first introduces the basic principle of the algorithm and then adopts 8 public data sets and 5 similar algorithms of other scholars as the experimental basis and verifies the effectiveness of the algorithm by using the measurement standards commonly used in the industry (accuracy, G-mean, and F-measure). (Note: In order to ensure the accuracy of the experiment, the randomness of the experiment was ignored in this study, and the 5-fold stratified crossover experiment was adopted and repeated three times.) Based on the above experimental design and results, the proposed majority-class weighted minor-class oversampling technique is discussed and evaluated in depth.

First of all, from the experimental results, this algorithm shows a higher classification accuracy and a lower false positive rate when dealing with the binary classification problem of fault detection in the production line. This is mainly due to the algorithm’s effective handling of the problem of sample imbalance and the filtering ability of noisy data. By comparing similar algorithms of other scholars, the algorithm proposed in this paper has improved in various performance indicators, especially in the two comprehensive evaluation indicators of G-mean and F-measure, showing better performance.

Second, the algorithm design of this paper fully considers the actual demand of production line fault detection. In the production line environment, the fault data are often relatively rare, and the normal data occupies the vast majority. This unevenness of data distribution can have a serious impact on the performance of the classifier. The algorithm proposed in this paper alleviates this problem effectively by means of weighting and oversampling so that the classifier can better adapt to the actual data distribution.

In addition, the iterative filtering mechanism in the algorithm also greatly improves the robustness and stability of the classifier. In the production line environment, noisy data are difficult to avoid. These noisy data may negatively affect the performance of the classifier. However, by means of iterative filtering, the algorithm can effectively identify and filter out these noisy data, thus improving the accuracy and reliability of the classifier.

Finally, the experimental design of this paper fully considers the reliability and repeatability of the experiment. The stability and reliability of the experimental results were ensured by using a 4-fold layered crossover experiment and repeating it three times. This kind of experimental design also makes it more convenient for other researchers to reproduce the experimental results of this paper and conduct more in-depth research and discussion.

In summary, the majority-class weighted minority-class oversampling technique proposed in this paper is an effective fault detection algorithm for production lines. The algorithm shows excellent performance in dealing with sample imbalance and noise problems, with high classification accuracy and a low false positive rate. At the same time, the algorithm also fully considers the actual demand of production line fault detection and has high practicability and application value.

2. Materials and Methods

Based on the existing data rules, there is a limited impact on data classification [9]. Currently, several well-established methods incorporate random oversampling technology, which entails randomly duplicating data within data clusters containing limited amounts of data post-classification and integrating them into the database to balance the volume of data post-classification. Nonetheless, this approach tends towards rudimentary analysis and heavily emphasizes the entity problem, thereby inducing overfitting phenomena and affecting the data classification boundary [10]. Later researchers enhanced the oversampling technique through synthesis and introduced a synthetic minority oversampling technique. Its fundamental principle involves adding new data to the data cluster through linear distance interpolation. Although this data lacks substantial significance, the synthesized data are generally guaranteed to remain within the cluster boundary, and a safe zone can be ensured based on distance settings [11]. However, the synthetic oversampling technique is prone to being influenced by data noise. In scenarios with excessive data noise, it readily generates new noise points, which traditional data cleaning methods struggle to eliminate, ultimately impairing classification accuracy. Furthermore, this synthetic oversampling technique necessitates a relatively high level of expertise in parameter setting for synthetic data, encompassing not only algorithmic application experience but also industry data application experience. The setting of K value and c value in certain K-NN algorithms necessitates industry data analysis experience to ensure the precision of classification for synthetic data within the original clustering cluster, thereby preventing breaches of classification boundaries [12].

Currently, this study of the noise impact of synthetic oversampling techniques remains a pivotal concern in the industry. B-SMOTE, for instance, employs a limited amount of boundary instance data as a foundation, refines sampling rules, and integrates data pertaining to a select few boundary data points. This approach exhibits improved resilience to noise, albeit with the presence of overlap. Subsequently, this concept has undergone continual evolution, resulting in adaptive synthetic sampling algorithms such as ADASYN, which leverage the k-value to ascertain the optimal allocation of weights. Nonetheless, all these algorithms hinge upon the utilization of the boundary to establish a so-called “safe zone” within which data synthesis and oversampling occur. However, the data synthesized in this manner inherently possesses a natural distance from the perimeter of the safe zone, thereby mitigating the influence of noise on the data. Nevertheless, this approach can expedite convergence during the classification process, potentially altering the centroid position of clusters, thereby affecting subsequent cluster analysis. Notably, this issue is not particularly apparent in traditional data samples; however, it becomes increasingly challenging in the processing of time-series data, logical data, and knowledge graph-based data, constituting an inherent limitation of the algorithm.

3. MWMOTE-FRIS-INFFC

The MWMOTE-FRIS-INFFC approach, a majority-class weighted minority-class oversampling technique, is formulated through a fusion of fuzzy rough instances and iterative classification fusion filtering. This represents a concerted effort in integrating multiple technologies. Rooted in the principles of majority weighted minority oversampling, the original MWMOTE algorithm nonetheless adopted a similar exhaustive approach to data handling, reassigning appropriate weights based on importance and assigning rational weights in accordance with the samples’ positioning within the decision boundaries of cluster classifications. This approach also addresses class imbalance by augmenting data in underrepresented classes, thus reducing the disproportionate classification rates.

However, when the original dataset contains significant noise, the synthesized samples may introduce new noise if preliminary filtering fails to mitigate the noise effectively. Conversely, if the MWMOTE algorithm performs extensive filtering and denoising operations in its initial stages, it may exacerbate the imbalance in the distribution of furniture samples, adversely impacting subsequent classification and data learning processes. Therefore, the algorithm proposed in this study leverages multiple iterations of noise filtering to develop a synthetic classifier, subsequently cleansing the data to ensure that classifier output is generated only after the completion of filtering. This approach facilitates the attainment of accurate results.

3.1. Preliminaries

3.1.1. Majority Weighted Minority Oversampling Technique (MWMOTE)

To solve the problem of unbalanced samples, Sukarna Barua et al. [13] designed a new minority oversampling algorithm (MWMOTE), which improved the way of selecting minority samples and generating samples, mainly in the following three stages: the first stage is to first identify the data in the original data set, build a new subset after finding a few class samples, continue to find samples that are difficult to learn in the new subset, and complete the construction of the set Si (min). The second stage is to assign weight Sw based on data importance in the new subset. The third stage is to use synthetic oversampling technology to synthesize new samples in Si (min) and add them to get a new output sample set Sout (min). The specific algorithm steps are shown as Algorithm 1.

Algorithm 1. Majority Weighted Minority Oversampling Technique (MWMOTE)

Input: Minority sample and majority sample (Smin and Smaj) Procedure: (1) The total number of samples of a few classes is recorded as Smin; Calculate k1 neighbors of each sample belonging to minority class Smin based on Euclidean distance, where the minority class is denoted as NN (xi). (2) If NN (xi) = 0 means that k1 neighbors near the i minority sample have no minority sample, the sample is a noise sample; Sminf is used to represent the number of Smin samples left after removing the noise sample. (3) For each sample belonging to the minority class Sminf, calculate its k2 neighbors belonging to the majority class according to the Euclidean distance, denoted as Nmaj (xi). (4) Combine the results of (3) to get most class boundary data sets, denoted as Sbmaj; (5) For each sample belonging to Sbmaj, calculate its k3 neighbors belonging to the minority class according to Euclidean distance, which are denoted as Nmin (yi). (6) Combine the results of (5) to get a few class information sets, which are denoted as Simin. (7) For each sample belonging to Simin, the information weight Iw (yi, xi) is calculated according to the location distance and density factors of the sample. The closer the sample is to most types of samples, the lower the density will be, making it easier to draw. (8) The step is equivalent to the normalization step, dividing the current information weight by the total information weight to get the selection weight of each xi, that is, the probability of being selected to synthesize new samples.   Cluster Smin into M clusters, draw samples from Simin according to probability, and then randomly select samples from M clusters for interpolation of the SMOTE formula; repeat (9) until the desired number is satisfied. end Output: The oversampled minority sets.

The primary advantage of this algorithm lies in its capacity to precisely select a limited set of class samples suitable for learning. Additionally, its proficiency in allocating weights to samples and clusters is noteworthy. The newly created minority class samples, by virtue of this algorithm, largely ensure that the synthesized samples mitigate both inter-class and intra-class imbalances. Notably, the algorithm does not broaden the range of certain class samples during the weight computation process, thus preserving the convergence speed and preventing overfitting. However, a significant limitation of this algorithm is its struggle with data noise, particularly weak and false noise. During the generation of class samples, there is a propensity to interpolate more of these undesirable noise types, necessitating the adjustment of various algorithm parameters for different data types, which introduces a considerable workload. Consequently, optimization efforts may be directed towards both noise processing and the noise introduced in newly generated samples.

3.1.2. Fuzzy-Rough Instance Selection (FRIS)

In the preceding deliberations, the MWMOTE algorithm employs the K-NN approach to interpolate samples for the internal boundary weights of minority classes, subsequently generating novel samples distinct from the original dataset. However, in the context of unbalanced samples containing noise, excessive noise elimination during initial data preprocessing can inadvertently eliminate pseudo-noise and weak noise information, thereby compounding the complexity of machine learning classification. Consequently, the current data preprocessing efforts may be insufficient for noise reduction, leading to an augmentation of noise in the subsequently interpolated data. To address this, the present study adopts the fuzzy rough set theory to assess the availability of information within the positive domain of the data and its carrying of critical information, ultimately determining its retention or removal.

The fuzzy rough data set theory, originating from the mathematical domain, can effectively eliminate certain data inappropriately weighted by the MWMOTE algorithm during the data sorting process. Nevertheless, the elimination of data, apart from affecting a few class samples, may also influence the majority of class samples, thereby compromising the precision of sample classification boundaries. Additionally, the deleted data can alter the boundary overlap, leading to variations in the data quantity and domain scope within the cluster domain. Therefore, in the application of the FRIS algorithm, utmost care is taken to avoid data discrimination in the boundary domain. Instead, the Euclidean distance between boundary data and the cluster center is utilized to compute the weight, with the positive distance serving as a substitute for the negative correlation degree for sorting purposes. This approach ensures the deletion of redundant data while maintaining the compliance of all object attributes within the domain.

3.1.3. Iterative Noise Filter Based on the Fusion of Classifiers (INFFC)

After an objective analysis of the data sources of assembly line failures, we found that with the increase in the complexity of industrial production, more and more non-homologous and non-same-type equipment constitute extremely complex production lines. In the process of data normalization, there will be very complex noise sources due to the impact of data collection format, equipment, environment, and other aspects. In particular, the subsequent minority class synthesis oversampling technology will synthesize some pseudo-noise in a few class samples, which puts forward higher requirements for noise processing. In this paper, the classifier is synthesized with multiple filters for the first time, and a variety of filtering strategies and classifier synthesis methods are used to transform the information from different noise sources so as to complete the filtering, make the filtering more targeted, and improve the filtering sensitivity. In this study, the four classifiers are combined, and the focus is on C4.5, 3-NN, SVM, and LR. This step can be used to remove noise through multiple iterations. In the process of multiple iterations, if the classifier determines the noise point, the data will be eliminated, and then some unrecognized data will be constructed into another filter. In this filter, all instances of previous iterations can be detected to see if they are noise points. Because each iteration forms a relatively clean data set, the subsequent filtering results are relatively accurate.

3.2. The Proposed Method

The algorithm proposed in this study is an algorithm based on majority class synthesis and minority class oversampling, and then it combines with fuzzy rough sets to eliminate some unreasonable synthesis algorithms, and finally it combines the method of synthetic multi-classifier filtering to propose noisy data to obtain more accurate classification results. The basic flow of the algorithm is shown as Algorithm 2.

Algorithm 2. MWMOTE-FRIS-INFFC

Input: Set of D∈{min, maj}, where min means minority class and maj means majority class. Rmin:Rmaj means unbalanced sample target ratio. FC = SVM, 3-NN, C4.5, LR. Output: Balanced data set DBalanced Procedure: 1. Creates a data S∈D in the original data set. 2. Create new samples from a few class samples according to the MWMOTE algorithm. 3. Fuzzy rough data set theory (FIRS) is used to delete some unqualified synthetic examples. 4. Find the min value in the set composed of S data to replace the D set. 5. By synthesizing multi-classifier noise filtering FC to eliminate noise, data sets with noise scores lower than the threshold are obtained to achieve the purpose of noise elimination, and data are input into data set DBalanced for output. end

4. Algorithm Testing and Discussion

In order to verify the effectiveness of the algorithm proposed in this study, it is necessary to verify it on the data set and search for algorithms with similar efficacy as control algorithms to comprehensively evaluate the effectiveness of the algorithm. To ensure the confidence and generality of the results, we have selected eight reality-imbalanced datasets with different dimensions or spatial complexity from the UCI machine learning repository [14] and other publicly available datasets [15]. The binary classification of the data follows the setting in the relevant literature. After extensive research, we selected the following algorithms: (1) Random Oversampling (ROS), (2) SMOTE (Nitesh V. 2002), (3) ADASYN (He. 2008), (4) Cluster-SMOTE (Cieslak. 2006), and (5) A-SUWO (Nekooeimehr. 2016) [16,17,18,19,20]. All the data simulation was completed on MATLAB 2016b with a 64-bit operating system, 16 GB of running memory, and a 4.0 GHz cpu. The classifier adopts the neural network classifier, and all parameters adopt the preset values. Furthermore, a 5-fold stratified cross experiment was used, and the method of calculating the average value of three experiments was adopted as the final result [16]. A summary table of unbalanced data sets is shown in

Table 1. Unbalanced data and information summary.

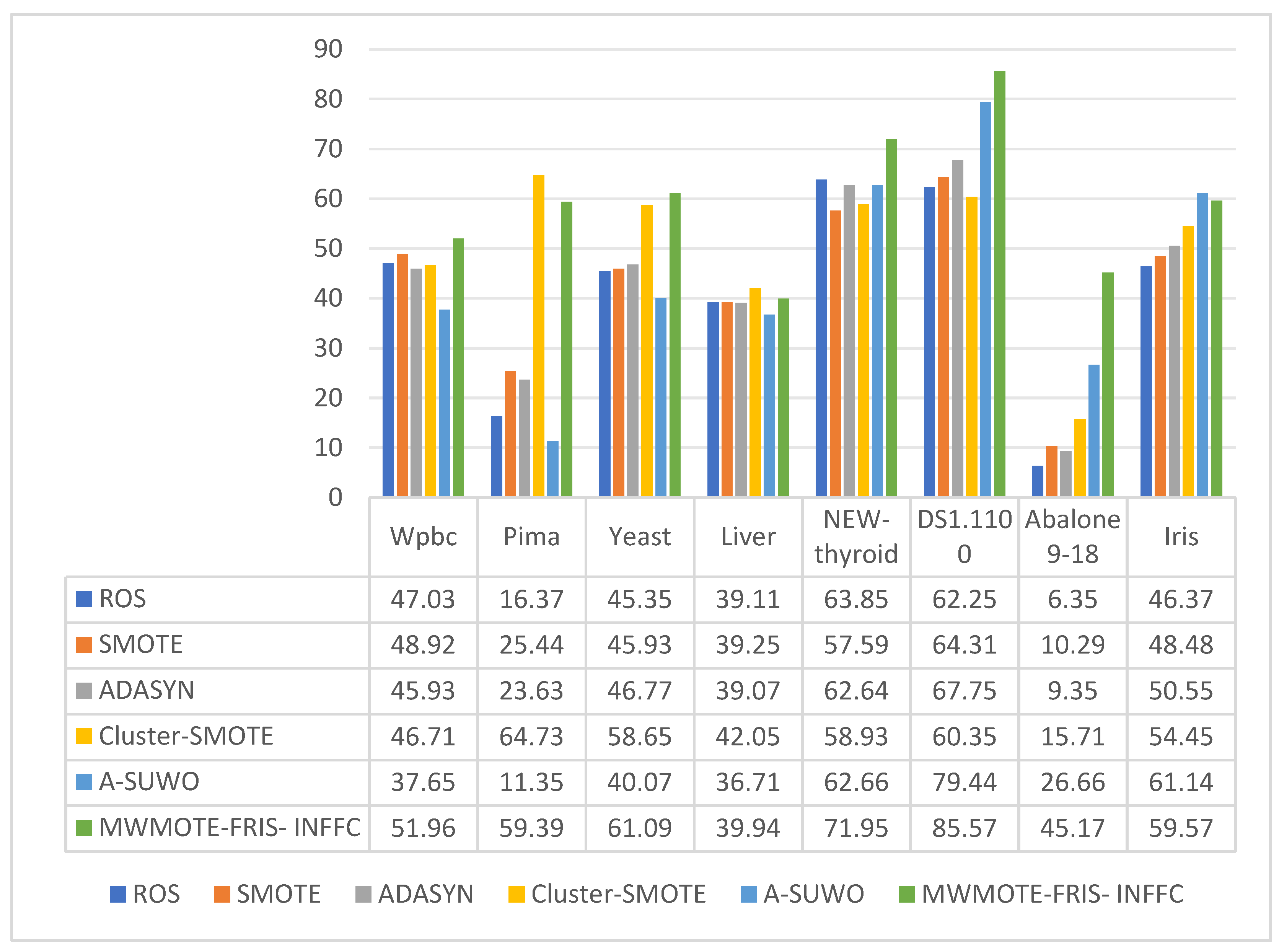
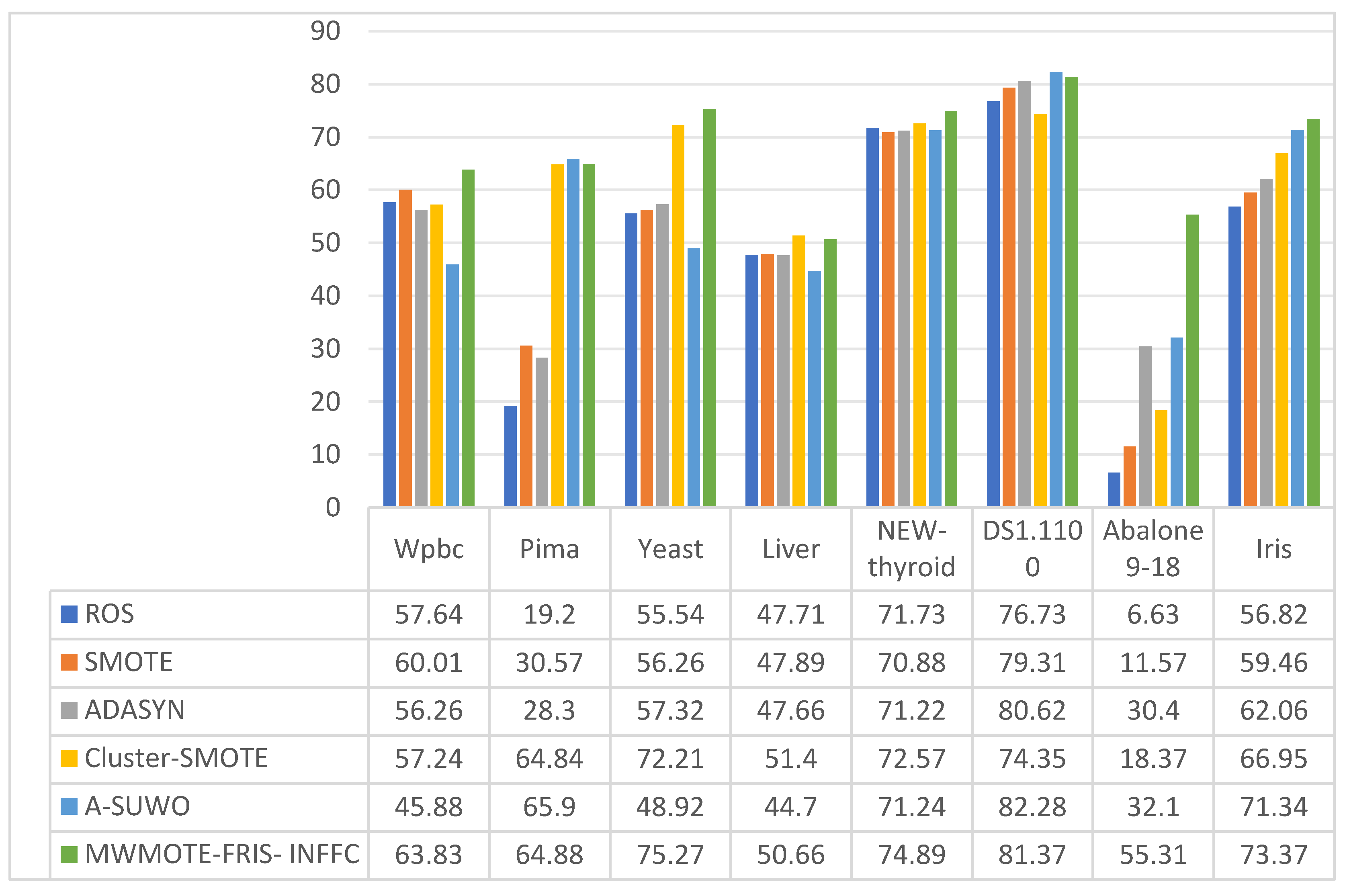
NO.	NAME	Minority Class	Majority Class	Minority Quantity	Majority Quantity	Total Quantity	Imbalanced Ratios
1	Wpbc	N	R	47	151	198	1/3.23
2	Pima	1	0	268	500	768	1/1.87
3	Yeast	ME3/MEW/EXC/VAC/POX/ERL	Other	304	1180	1484	1/3.88
4	Liver	1	Other	71	107	178	1/1.37
5	NEW-thyroid	2	Other	35	180	215	1/5.15
6	DS1.1100	1	0	804	25,929	26,733	1/32.25
7	Abalone9-18	18	9	42	689	731	1/16.41
8	Iris	2	Other	50	100	150	1/2

.

4.1. Evaluation Criteria

The traditional methods and parameters for evaluating the accuracy of algorithms and the algorithm for classifying unbalanced samples are not applicable, because if the classification accuracy is only calculated, a relatively high classification accuracy can be obtained as long as a small number of samples in the unbalanced sample are correctly classified [21]. Binary classification problems can include the following four categories: true positive, true negative, false positive, and false negative, abbreviated as TP, TN, FP, and FN, respectively. After calculation based on statistical confidence conditions, the parameters that need to be paid attention to include three key parameters: precision (4-1), G-mean (4-2), and F-measure (4-3) [22].

$$\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}=\mathrm{T}\mathrm{P}/(\mathrm{F}\mathrm{P}+\mathrm{T}\mathrm{P})$$

(1)

$$\mathrm{G}-\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}=\sqrt{{\displaystyle \frac{\mathrm{T}\mathrm{P}\mathrm{\ast }\mathrm{T}\mathrm{N}}{(\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N})\mathrm{\ast }(\mathrm{T}\mathrm{N}+\mathrm{F}\mathrm{P})}}})$$

(2)

$$\mathrm{F}-\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}={\displaystyle \frac{2\mathrm{T}\mathrm{P}\mathrm{\ast }\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}}/({\displaystyle \frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}}+\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n})$$

(3)

When TP means models are classified as correct and labeled as correct instances, TN means models are classified as correct and labeled as incorrect instances, FP means models are classified as an error and labeled as a correct instance, and FN means models are classified as an error and an instance is labeled as an error. A higher precision value means that the model has a stronger ability to identify correct samples. The larger the G-mean, the stronger the actual classification ability of the model. The larger the F-measure, the stronger the ability of correct sample allocation, and the model is less interfered with by external factors [23,24,25,26].

4.2. Comparison of Algorithm Evaluation Results

The precision summary results of different algorithms in different data sets are shown in Figure 1. The G-mean summary results of different data sets and different algorithms are shown in Figure 2. The summary results of the F-measure under different data sets and different algorithms are shown in Figure 3. The optimal value of the data result is displayed in bold font. (Because the algorithm classifier proposed in this paper chooses the combination of multiple classifiers and iterative filtering algorithms, it has obvious advantages over other algorithms [27,28], so the subsequent classifiers of other algorithms all use the same neural network classifier, because, according to the research of other scholars, the neural network classifier has the best effect and is not affected by the filtering algorithm proposed in this study.).

According to the analysis in Figure 1, Figure 2 and Figure 3, the algorithm proposed in this paper (MWMOTE-FRIS-INFFC) has the best comprehensive performance. For example, on most data sets, the classification accuracy of the algorithm proposed in this paper exceeds 75% without training a large number of data samples. The accuracy rate is relatively high. Some other algorithms also have some ability to deal with unbalanced samples and anti-noise. According to the analysis in Figure 2, the algorithm proposed in this paper still has the best overall effect. The optimal value of the algorithm proposed in this paper is generally higher. According to the analysis in Figure 3, in addition, under the classification performance of different data sets, the overall classification result of the proposed algorithm is relatively good, and the classification accuracy of the liver data set is the lowest, which is 39.94%. In addition, the classification performance of other data sets is also relatively good, among which the DS1.1100 data set shows the best classification results, and the classification accuracy is 85.57%. At the same time, the overall trend is similar in terms of the performance of G-mean and F-measure analysis [29,30,31]. The performance of the algorithm proposed in this study is relatively good, and the overall value fluctuation is relatively stable, which proves that the algorithm proposed in this study has similar working effects on different data sets and can complete the work of anti-noise and unbalanced sample classification.

4.3. Comparison of Classification of Unbalanced Samples with High Noise

Comparing the MWMOTE-FRIS-INFFC algorithm with other methods on multiple data sets, the results show that MWMOTE-FRIS-INFFC has certain advantages. For further confirmation, we selected datasets with noise ratios above 20% for further comparison and analyzed the classification performance of MWMOTE-FRIS-INFFC on high noise and sample imbalance datasets. The basic parameter settings are the same as above. Classification lasts for 5 times. After each classification, the best classification algorithm records the result and adds 1. Finally, 5 classification results are accumulated. The number of records of algorithms with the best performance is shown in

Table 2. Results of classification and comparison of highly noisy and severely unbalanced data sets.

Data Set (Noise Ratios)	Meas	ROS	SMOTE	ADASYN	Cluster-SMOTE	A-SUWO	MWMOTE-FRIS-INFFC
Ecoli3 (20.0%)	Precision	0	0	0	1	0	4
	G-mean	0	0	0	0	0	5
	F-measure	0	0	0	1	0	4
Ds1.100 (31.72%)	Precision	0	0	1	0	0	4
	G-mean	0	0	0	0	2	3
	F-measure	0	0	1	0	0	4
Haberman (24.69%)	Precision	0	0	0	2	0	3
	G-mean	0	0	0	1	0	4
	F-measure	0	0	0	1	0	4

.

In practical applications, the presence of samples with high noise and significant imbalance is commonplace. Initially, severely imbalanced samples exacerbate the challenges posed by inter-class and intra-class imbalances, thereby necessitating a thorough evaluation of algorithmic capabilities. Based on the analysis of data results, it is evident that the MWMOTE-FRIS-INFFC classification approach exhibits superior performance [32]. Specifically, this algorithm demonstrates a superior capacity in balancing data samples, efficiently achieving the intended goal of expanding, interpolating, and increasing minority class samples to balance the sample ratio, thereby approximating data balance across classes. The MWMOTE algorithm effectively balances data during minority class synthesis and majority class weighting, particularly in cases of highly imbalanced datasets, exhibiting resilience against overfitting caused by a limited number of samples [33].

However, during the process of data expansion and interpolation, the occurrence of boundary overlap and noise overlap in certain data can augment the difficulty in learning from minority class samples. Consequently, this study aimed to mitigate this issue by employing fuzzy rough set theory to eliminate inappropriate samples, thereby enhancing the membership degree of new samples and achieving the goal of balancing genuine samples. Ultimately, a combination of image classification and data classification was utilized, incorporating multiple iterative filtering techniques to address noise issues. This approach effectively mitigates noise in industrial datasets, particularly preventing excessive loss of genuine samples and minority samples during the processing of imbalanced samples by certain simpler classifiers. The retention of available instance data is maximized to the greatest extent possible.

5. Conclusions

As the various algorithms in the realm of big data continue to evolve and advance, scientists have observed that research conducted at the foundational level of data frequently offers a more telling representation of scientific veracity. Within the industrial sector, the binary classification issue arises frequently, yet its outcomes are often markedly imbalanced. Although a minor proportion of samples possess analytical significance, their scant representation can readily lead to inaccuracies in data classification algorithms. Furthermore, from a pragmatic perspective, data noise emerges as a pivotal concern in image algorithmic applications. Thus, the key findings of this study can be condensed as follows:

(1) At present, the processing methods of unbalanced samples are mostly oversampling and undersampling. Among them, the over-sampling technology has a better effect on the data of industrial manufacturing processing. In this study, the oversampling technology is also used to process data samples, and part of the sampling process is modified in the process of use, forming a majority class synthesis minority class oversampling technology.

(2) In the process of using industrial data information, the noise problem is a common problem, but when the noise problem is fused with unbalanced samples, the way of data pre-noising is easy to lose effective data instances, so it is necessary to propose targeted noise processing algorithms.

(3) This study proposes a majority-class weighted minority-class oversampling technique (MWMOTE-FRIS-INFFC) based on the combination of fuzzy rough instances and classification fusion iterative filtering. In the process of inter-class identification, the majority-class-weighted minority-class oversampling technique is used to expand the data set to a certain extent, thus effectively solving the problem of unbalanced data. The Euclidean distance is used to assign sample weights so as to synthesize and insert new samples in the samples with large weights and a few classes so as to solve the problem of insufficient data clusters in the sample class of a few classes. Subsequently, fuzzy rough instance selection (FRIS) is used to remove some of the synthetic minority samples with low membership degree to the cluster, which can effectively solve the overfitting phenomenon of synthetic oversampling to the minority samples. Then, it is necessary to introduce the classification fusion iterative filter (INFFC) to solve the integrated noise problem, such as original noise and synthetic data noise, and then complete the data processing.

(4) In this study, 8 data sets and 5 unbalanced and noisy sample classification models proposed by other scholars of the same type were used to carry out cross experiments, and the test was carried out under the condition of unified experimental conditions as far as possible. The test results show that the algorithm proposed in this study has the best effect. In the subsequent separate test process of high-noise data sets, it is found that the algorithm proposed in this study is still the best and has a good processing effect against high noise.

With the development of subsequent study, this study will further improve the algorithm to improve the computational efficiency of the algorithm and even continue to expand the algorithm, including three-classification, four-classification, multi-classification, and other problems; the algorithm can have good adaptability.