Station Maintenance for Low-Orbit Large-Scale Constellations Based on Absolute and Relative Control Strategies

Abstract

With the development of commercial space technology and the proposal of concepts such as “Black Jack”, the Space Transport Layer (STL), and the commercial space-based Internet, large-scale low-orbit satellite constellations have become a research hotspot in the aerospace field. Large-scale low-orbit satellite constellations consist of a huge number of satellites, which makes the networking control and operation management of the constellations more complicated. It also increases the difficulty of achieving the economical and efficient networking of the constellations as well as ensuring their safe and stable operation. In this study, aiming at the problem of large-scale constellation phase control in low orbit, strategies for constellation station holding were examined. First, aiming at the problem of station keeping of large-scale constellations in low orbit, the characteristics of satellite phase drift and phase keeping were analyzed, and absolute and relative station-keeping strategies were proposed. Second, a phase-holding loop control method combining semi-major axis overshoot control and passive control was proposed, and a relative phase-maintenance scheme based on a dynamic reference satellite was designed. Then, the absolute and relative station controls of different low-orbit constellations were simulated. The simulation results showed that in order for all satellites in the constellation to maintain a phase angle deviation within ±0.1° in a low-solar-activity year, about 13 days were required on average to adjust the semi-major axis of the satellites by about 71 m. The relative position control of small-scale constellations was simulated, and only four orbital maneuvers were needed to achieve the phase angle maintenance within the threshold of ±5° for all satellites in the constellation within 300 days. Finally, it was concluded that absolute control was suitable for large-scale constellation phase preservation, and relative control was more suitable for small-scale constellation phase preservation. This paper can provide a reference and suggestions for future large-scale constellation deployment and maintenance control strategies of low-orbit constellations.

1. Introduction

With the deployment of huge satellite groups, constellation networking has ushered in new challenges. In particular, orbit-control technology and orbit-maintenance technology have become the constraints of large-scale constellation networking control. Determining how to efficiently, economically, and stably control large-scale constellation initialization and constellation configuration maintenance in low orbit has become a challenging problem that needs to be focused on and solved in the field of large-scale constellation orbit control. Constellation orbit control involves aspects such as control technology, control methods, and optimal control. Among them, the selection of the orbit operation control strategy will directly affect the constellation networking efficiency and the constellation operation cost, and further affect the geometric integrity, structural stability, and service availability of the constellation system. Large-scale constellation networking in low orbit is mainly based on constellation service characteristics and satellite orbit characteristics, which are crucial for completing the establishment and maintenance of the overall constellation geometry. The main tasks of a constellation network are the deployment and maintenance of the constellation orbital plane and the satellite phase in the orbital plane.

In terms of drag, Finley et al. proposed a phase space method for accomplishing differential drag maneuvers, based on the relative phase drift rate and collision avoidance of the satellite constellation. In this method, orbit modification was the only means of collision avoidance of the satellite constellation [1]. Foster et al. proposed a differential drag control method for a large fleet of propulsionless satellites deployed in the same orbit and used the simulated annealing algorithm to minimize the required phasing time given the available control authority [2]. He et al. proposed a station-keeping strategy to compensate for perturbations due to the atmospheric drag, in which the errors in the orbital measurements and control as well as in the estimation of the semimajor axis decay rate were taken into account [3]. Ulybyshev proposed a new linear quadratic controller for satellite constellations, which helped to increase the formation-keeping accuracy for the low-altitude satellite constellations affected by atmospheric drag [4].

In terms of low thrust, Li et al. applied Hamiltonian theory to transform the low-thrust station-keeping optimization problem into a two-point boundary value problem, which was used for the station-keeping strategy of satellites with low thrust [5]. Fan et al. established a long-term perturbation model for relative motion based on a Hamiltonian model. By analyzing the long-term evolution process of the BDS medium Earth orbit (MEO) constellation over 10 years, the validity of the proposed analytical perturbation compensation calculation method was verified [6].

In terms of perturbations, Li et al. employed perturbation analysis to formulate the relative perturbation motion equations for constellation orbits, elucidating the orbital perturbation principles and the overall drift characteristics of relative perturbation motion. In addition, they established the governing equations for both absolute and relative motion in the context of constellation orbital perturbation compensation control [7,8]. Hu et al. conducted an in-depth analysis of the orbital evolution process influenced by Earth’s oblateness perturbation and satellite orbit deviations. Their findings indicated that Earth’s oblateness perturbation resulted in the general drift of the constellation structure, while satellite orbit deviations played a critical role in determining the stability of the constellation geometry [9,10]. Oliveira et al. accounted for three-body and $J_2$ perturbations based on the integral over time of the undesired perturbation forces. This approach helped to map orbits that had a high potential to require less fuel consumption for station-keeping maneuvers [11]. In terms of constellation configuration maintenance, Wang et al. proposed a method of calculating the major semi-axis deviations indirectly from the change in the relative phase and deduced the evolution of the relative phase with a limit cycle control method, which met the requirements of long-term orbit preservation [12]. Jiang et al. analyzed the orbital perturbations and configurational phase drift of constellation satellites, and they presented a numerical differential correction method for constellation configurations [13].

Chu et al. employed a relative configuration preservation method to minimize the average drift deviation and implemented a free-segment-maintenance strategy. This approach effectively decreased the control frequency and achieved orderly and decentralized constellation management in both temporal and spatial dimensions [14]. Sun et al. derived a formula to calculate the maintenance control amount for the semi-major axis by considering the phase drift caused by the attenuation of the satellite’s orbital semi-major axis. They also analyzed the maintenance control rules for satellites with varying surface mass ratios during periods of both low and high solar activity. The orbital altitude changes of the on-orbit satellites in the Starlink constellation have verified that this method can effectively maintain the satellite phase within the desired interval and ensure a stable and consistent control frequency [15,16]. Yang et al. developed a second-order consistent control methodology for maintaining a constellation’s relative configuration, which effectively compensated for the configuration drift caused by variations in the surface mass ratios. This method effectively compensates for the configuration drift caused by the changes in the ratio of the cross-sectional area to the mass [17,18].

Li et al. introduced a dual-bias strategy to significantly mitigate the relative drift. The initial bias was derived by fitting the relative drift of the constellation in its unbiased state. Subsequently, the second bias was obtained by fitting the residual relative drift after applying the first bias. By superimposing these two bias components, the overall relative drift was substantially reduced [19]. Chen et al. employed the principle of satellite initial parameter bias compensation to model and adjust for the cumulative effects of various perturbations, thereby mitigating long-term orbital deviations caused by these factors and preserving the stability of the constellation configuration [20]. Chen et al. conducted an in-depth analysis of the laws of motion of satellites and the evolution characteristics of constellation configurations under perturbations. They proposed a relative phase-maintenance strategy anchored on a reference satellite, which effectively reduced the complexity and frequency of the constellation configuration maintenance, conserved fuel, and shortened the orbit-control time [21]. Hu et al. developed a relative phase-maintenance strategy for a constellation based on dynamic adjustments to this reference orbit. By computing the relative phase deviation and the rate of change for each satellite with respect to the reference orbit, they ensured that the phase deviations of all the satellites remained within allowable limits [22].

Liu et al. developed a method for calculating the phase-holding period and changes in the semi-major axis using limit cycle theory. They subsequently proposed a high-precision phase-holding method grounded in limit cycle principles [23]. Qi et al. utilized high-precision latitude angle data obtained from satellite-based global navigation satellite system (GNSS) receivers to approximate the changes in the relative semi-major axis during constellation configuration maintenance. This approach aimed to fulfill the requirements for future large-scale constellation-independent high-precision configuration maintenance [24]. Arnas et al. designed a novel method for two-dimensional lattice-preserving flower constellations that maintained the initial distribution of satellites and the initial symmetries over time, i.e., relative station keeping. Moreover, the amount of fuel required to achieve the absolute station keeping with this procedure was very low. Relative and absolute station-keeping methods for the maintenance of a constellation were established for $J_2$ perturbations [25].

For low Earth orbit (LEO) near-circular satellites, the nominal semi-major axis and orbital inclination of satellites within the same orbital plane in a constellation should be consistent. The perturbation and drift patterns of the orbital elements for these constellations are also uniform. However, in practical engineering applications, initial deviations in the capture of satellite orbital elements (such as pre-bias in the orbital inclination) can occur, which may be negligible but will cause the constellation configuration to drift over time. When the phase angle deviation exceeds the permissible theoretical threshold, adjustments to the satellite phase angle are required. Therefore, maintaining the constellation’s station position primarily involves maintaining the satellite phase.

At present, the research objects of satellite positioning are mostly independent satellites or small satellite constellations, and there is relatively little research on the station keeping of large-scale low-orbit constellations. At the same time, the configuration maintenance of large-scale constellations is more stringent, and the cost constraints are more prominent. Therefore, based on the station keeping of a single satellite or a small-scale satellite constellation, this paper conducts research on the configuration maintenance strategy of large-scale low-orbit constellations. This article proposes a large-scale constellation phase-keeping loop control method based on a fixed reference star and a relative phase control method for large-scale constellations based on a dynamic reference star, thus providing the necessary conditions for the station keeping of large-scale low-orbit constellations. At the same time, a phase-keeping loop control scheme combining semi-major axis overshoot control and passive control and a relative phase maintenance scheme based on dynamic reference satellites are designed. During the initialization and configuration maintenance processes of large-scale low-orbit constellations, most satellites use continuous and efficient low thrust to complete the orbital maneuvering tasks for constellation networking. For example, during the constellation initialization stage, tasks such as raising the satellite orbital altitude and adjusting the eccentricity are carried out, and during the constellation configuration maintenance stage, tasks like maintaining the satellite phase angle are performed.

This paper is structured as follows. Section 2 presents the analysis of the constellation station-keeping methods. In Section 3 and Section 4, the absolute and relative control models for constellations are established, the phase-drift and phase-keeping rules of satellites are analyzed, and the corresponding station-keeping strategies are evaluated and validated. In Section 5, the simulation results are presented to assess the impacts of various control strategies on the constellation availability and operational costs, with a focus on minimizing costs. Finally, Section 6 presents the conclusions and further discussion.

2. Constellation Station Maintenance Analysis

At present, the low-orbit large-scale constellation orbit-control strategy still faces many challenges, mainly in the following aspects [6].

• The maintenance degree of the constellation configuration is more complicated.

Compared with MEO constellations, LEO constellations have larger numbers of satellites and larger scales, and the orbital elements of satellites in different orbital planes are quite different, so the initial deployment degrees of LEO constellations are more complicated. For example, currently, the number of satellites in orbit of the Starlink system exceeds several thousand, according to the publicly available website www.space-track.org (accessed on 22 October 2024). These satellites are deployed on multiple orbital planes in a process that roughly follows a complex orbital maneuver (or docking orbit) from the initial orbit to the operational orbit. Due to the differences in orbital elements, such as the initial orbital altitude, right ascension, and phase difference of satellites with the same and different orbital planes, the constellation initialization control strategy should be designed from the top overall level. The maintenance of the constellation configuration should be comprehensively considered from the existing satellite–Earth measurement and control. As a result, the initialization of the constellation deployment and the maintenance of the constellation configuration are more complicated.

2.

The main perturbative effects and drift rules of the constellation are not assimilated.

Compared with MEO constellations, due to the differences in the main perturbation forces, the orbital drift characteristics of the low-orbit constellations are different. For example, an initial deviation of the semi-major axis of an LEO satellite on the order of 100 m causes a phase difference of nearly 36° over the course of a year, while an MEO satellite’s phase difference is only 1.5°. Due to the relatively low orbital altitude of the satellite, the atmospheric drag is greatly affected, and the orbital altitude of the satellite decreases continuously with the atmospheric drag. The orbital deviations of the initial orbital elements of the satellite and the capture error of the ground measurement and control system cause the cumulative drift of the phase angle, resulting in the continuous divergence of the overall geometry of the constellation. Therefore, satellite orbit deviations and perturbation forces are important factors affecting the constellation coverage characteristics and mission realization. To compensate for the satellite orbital altitude attenuation caused by atmospheric drag, the control laws, control methods, and control strategy analysis of the satellite relative phase angle in the same orbital plane and the right ascension of different orbital planes are also different.

3.

Constellation orbit-control mode and orbit-control technology are more integrated.

The control and maintenance technologies and the control methods of medium- and high-orbit constellations mainly include perturbation compensation methods based on the average orbit root number and the constellation-configuration numerical differential correction method based on the instantaneous root number. Compared with MEO constellations, large-scale low-orbit constellations have large numbers of satellites, low orbital altitudes, and large cumulative influences of initial deviations and capture error perturbations. Therefore, the stable and safe operation requirements of large-scale low-orbit constellations are more stringent, and constellation geometry maintenance tasks occur more frequently. There are still many theoretical problems to be studied and many engineering application problems to be solved if the existing orbit-control and orbit-maintenance technology, control methods, and control modes of medium- and high-orbit constellations or small low-orbit satellite constellations are extended to large-scale low-orbit satellite constellations.

In this context, this paper summarizes and compares the literature on constellation orbit-control strategies from around the world. The existing research results, existing problems, and areas to be further studied are analyzed, and the geometric configuration maintenance law, orbit-control methods, and constellation orbit-control strategies of large-scale low-orbit constellations are studied. The aim is to realize the optimal design of large-scale constellation orbit control in low orbit and to provide a reference for the future engineering planning and control operation of the Internet of Constellations.

2.1. Contents of Station Keeping

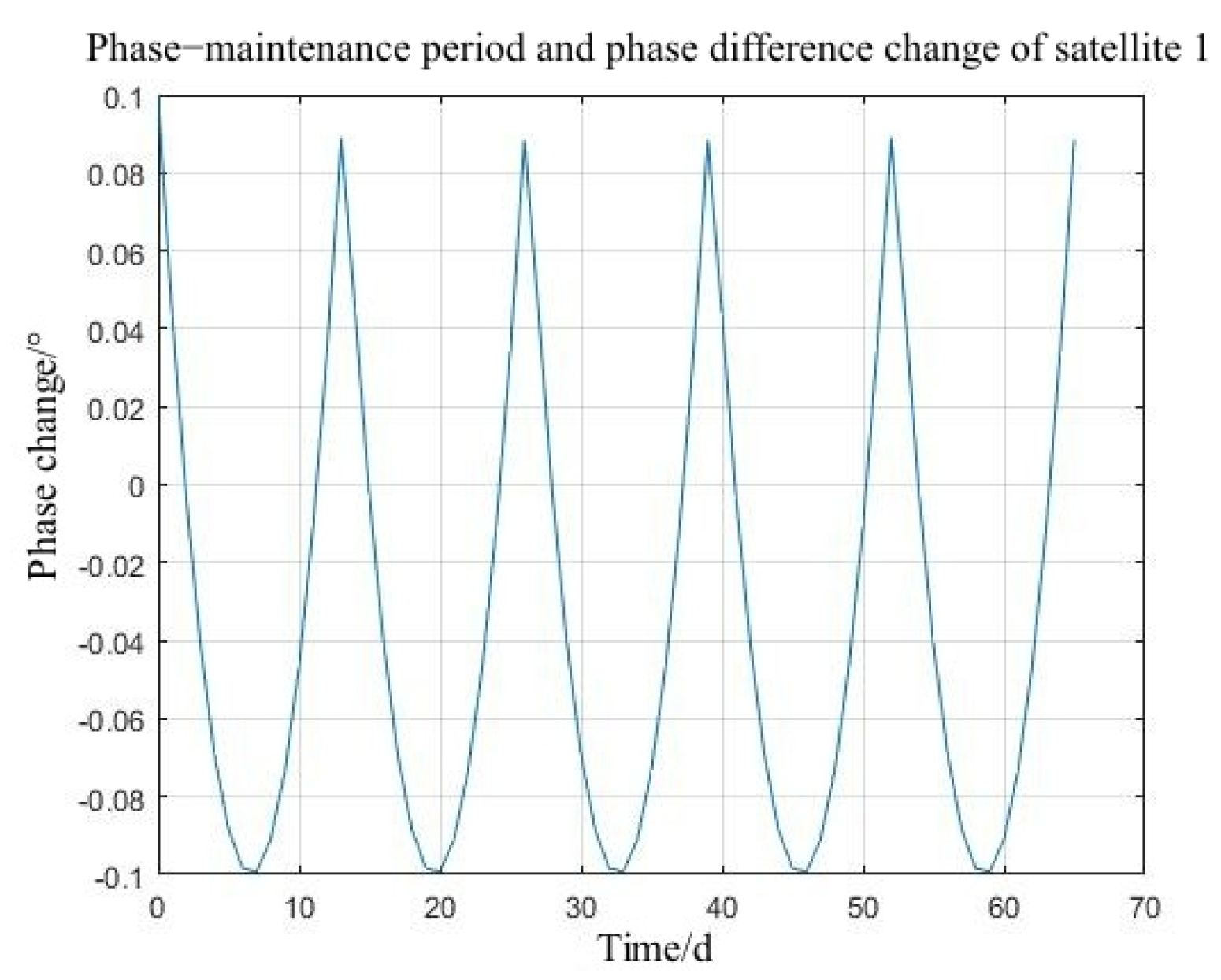
Ideally, for low-orbit near-circular orbit satellites, the nominal orbital semi-major axes and orbital inclinations of satellites in the same orbital plane within a constellation should be consistent. If only the perturbation of the Earth‘s non-spherical $J_2$ term and atmospheric drag are considered, the perturbation and drift laws of the orbital elements of low-orbit constellation satellites are also consistent. However, in general practical engineering, there are initial deviations in the capture of satellite orbital elements (among them, for the orbital inclination, according to practical engineering applications, the method of pre-biasing is generally adopted, and the initial deviation amount can be ignored). Under the influence of the Earth‘s non-spherical $J_2$ term and atmospheric drag, the decay of the satellite‘s semi-major axis and the phase change will be inconsistent, which in turn causes the constellation configuration to drift.

After the constellation configuration is established, under the influence of atmospheric drag and the perturbation of the Earth‘s non-spherical $J_2$ term, the deviation of the satellite‘s semi-major axis will lead to the inconsistent decay of the satellite‘s semi-major axis. Within an orbital period, the differences in the running speeds of satellites will cause the drift of the phase angle. When the deviation of the phase angle exceeds the allowable theoretical boundary value, the satellite‘s phase angle needs to be adjusted. Therefore, the content of constellation station keeping is the maintenance of the satellite‘s phase.

2.2. The Content of Satellite Constellation Station Keeping

The phase angle deviations between satellites in a constellation need to be calculated for constellation station holding. Therefore, a satellite needs to be selected as the reference basis for constellation phase holding. There are generally two methods for selecting the reference basis of constellation station position keeping. One method is to select a fixed satellite (the first satellite of the first orbital plane or the nominal orbit of the constellation in general) among all the satellites of the constellation as the reference basis and then calculate the phase angle difference between the other satellites and the reference satellite [15]. The other method is to dynamically select any satellite from all the satellites of the constellation as the reference basis and calculate the phase angle difference between the remaining satellites and the reference satellite [21].

• Fixed-reference-star method.

In the constellation, a designated satellite (typically the first satellite in the initial orbital plane or nominal orbit of the constellation) is chosen as the reference star. This satellite, denoted as $(1,1)$, serves as the phase control basis for the constellation, while the reference satellite $(1,1)$ remains uncontrolled, with its standard phase denoted as ${\lambda }_{1,1}$. If the actual phase of any other satellite $(i,j)$ in the constellation is ${\lambda }_{ij}$, then $\Delta \lambda ={\lambda }_{ij}-{\lambda }_{11}-\Delta \stackrel{\wedge }{\lambda }$ represents the phase difference between satellite $(i,j)$ and the reference star, where $\Delta \stackrel{\wedge }{\lambda }$ denotes the designed theoretical value of the phase difference between satellites $(i,j)$ and $(1,1)$. When the deviation $\Delta \lambda$ in the phase angle exceeds the permissible limits, it becomes necessary to implement phase-maintenance control for satellite $(i,j)$.

2.

Dynamic-reference-star method.

The procedure for referencing the dynamic reference star is as follows. A satellite $(j,i)$ is dynamically chosen as the reference star from all the satellites in the constellation. The phase angle difference between other satellites $(i,j)$ and the reference star $(j,i)$ is denoted as $\Delta \lambda ={\lambda }_{ij}-{\lambda }_{11}-\Delta \stackrel{\wedge }{\lambda }$, where $\Delta \stackrel{\wedge }{\lambda }$ represents the designated value of the nominal phase difference between satellite $(i,j)$ and satellite $(j,i)$. When the phase angle deviation $\Delta \lambda$ exceeds the permissible boundary value, it becomes necessary to implement phase-maintenance control for satellite $(i,j)$.

2.3. Analysis of Satellite Constellation Phase Evolution

The Earth’s non-spherical perturbation terms can be divided into zonal harmonics and tesseral harmonics. Among them, the influence of the first term of the zonal harmonics is much greater than that of other terms. Therefore, this paper only considers the perturbation influence of this term. As a conservative force, the Earth’s non-spherical perturbation does not have a long-term perturbation effect on the orbital elements $a, e, i$ of a circular orbit, but will only cause periodic fluctuations [21].

$$\left\{\begin{array}{l}\dot{\Omega }=-{\displaystyle \frac{3J_2{R}_e^2}{2p^2}}n\cos i\\ \dot{\lambda }=-{\displaystyle \frac{3J_2{R}_e^2}{2p^2}}n\left[\left(2-{\displaystyle \frac{5}{2}}{\sin }^{2}i\right)-\left(1-{\displaystyle \frac{3}{2}}{\sin }^{2}i\right)\sqrt{1-e^2}\right]\end{array}\right.,$$

(1)

In the formula, $\dot{\Omega }$ is the drift rate of the right ascension of the ascending node, $J_2$ is the Earth’s non-spherical perturbation term, $\dot{\lambda }$ is the drift rate of the phase angle, $R_e$ is the radius of the Earth, $p$ is the semi−latus rectum, $n$ is the average angular velocity of the satellite’s motion, $i$ is the orbital inclination, and $e$ is the eccentricity.

As the orbital altitude gradually increases, the drift rate of the phase angle shows a significant linear decrease. Therefore, the change in the satellite’s orbital altitude plays a major role in the process of the phase angle drift.

Ideally, for low-orbit satellites in near-circular orbits, the nominal orbital semi-major axes and orbital inclinations of satellites within the same orbital plane of the constellation should be consistent. If only the perturbations of the Earth’s non-spherical J2 term and atmospheric drag are considered, the perturbation and drift laws of the orbital elements of low-orbit constellation satellites are also consistent. However, for satellites in different orbital planes of the constellation, under the influence of the Earth’s non-spherical J2 term and atmospheric drag, the attenuation of the satellite’s semi-major axis and the laws of the phase change are inconsistent, so they need to be discussed separately. In view of this, the subsequent analysis of the evolution of the satellite phase is applicable only to the satellites within the same orbital plane of the low-orbit satellite constellation in near-circular orbits.

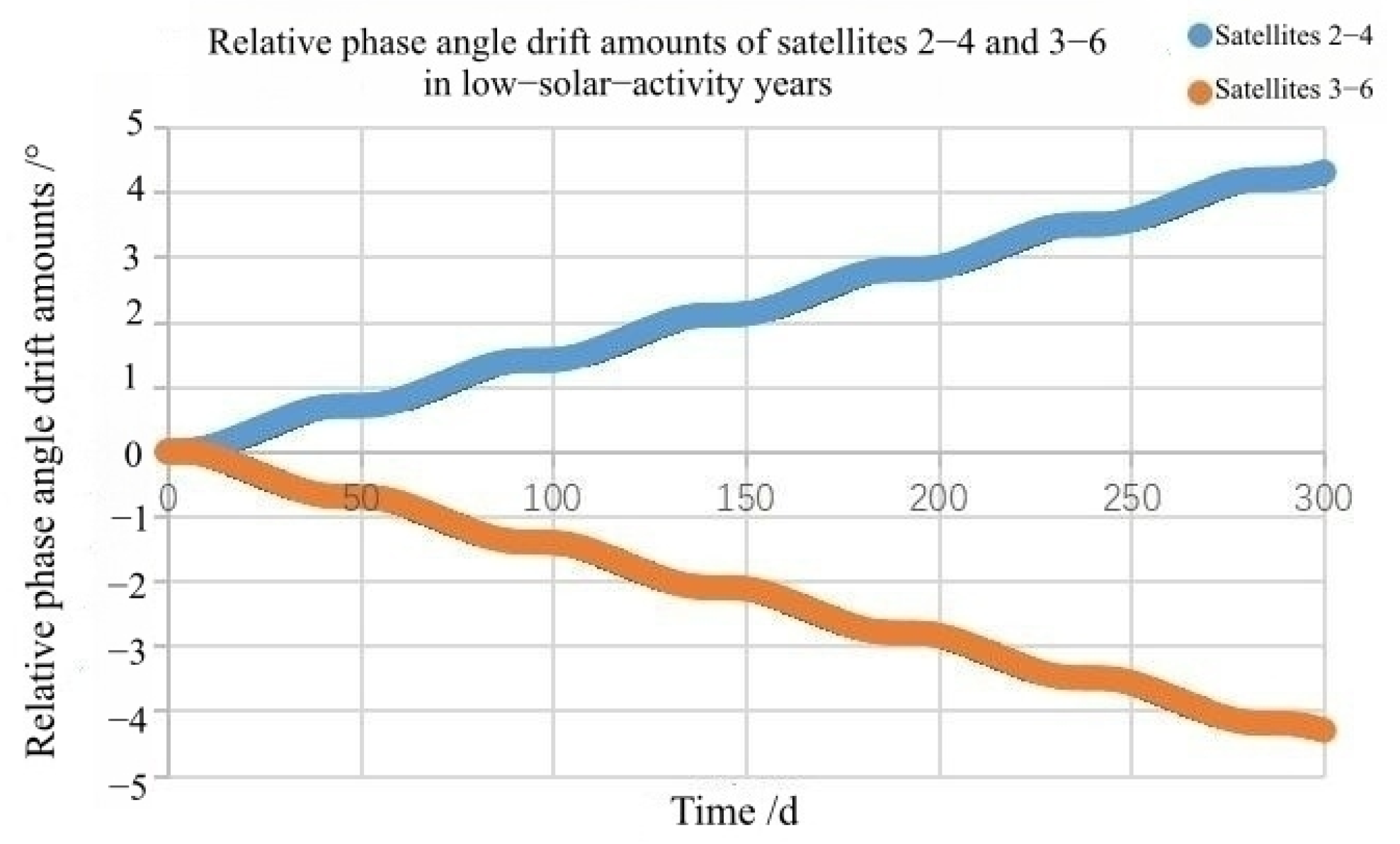
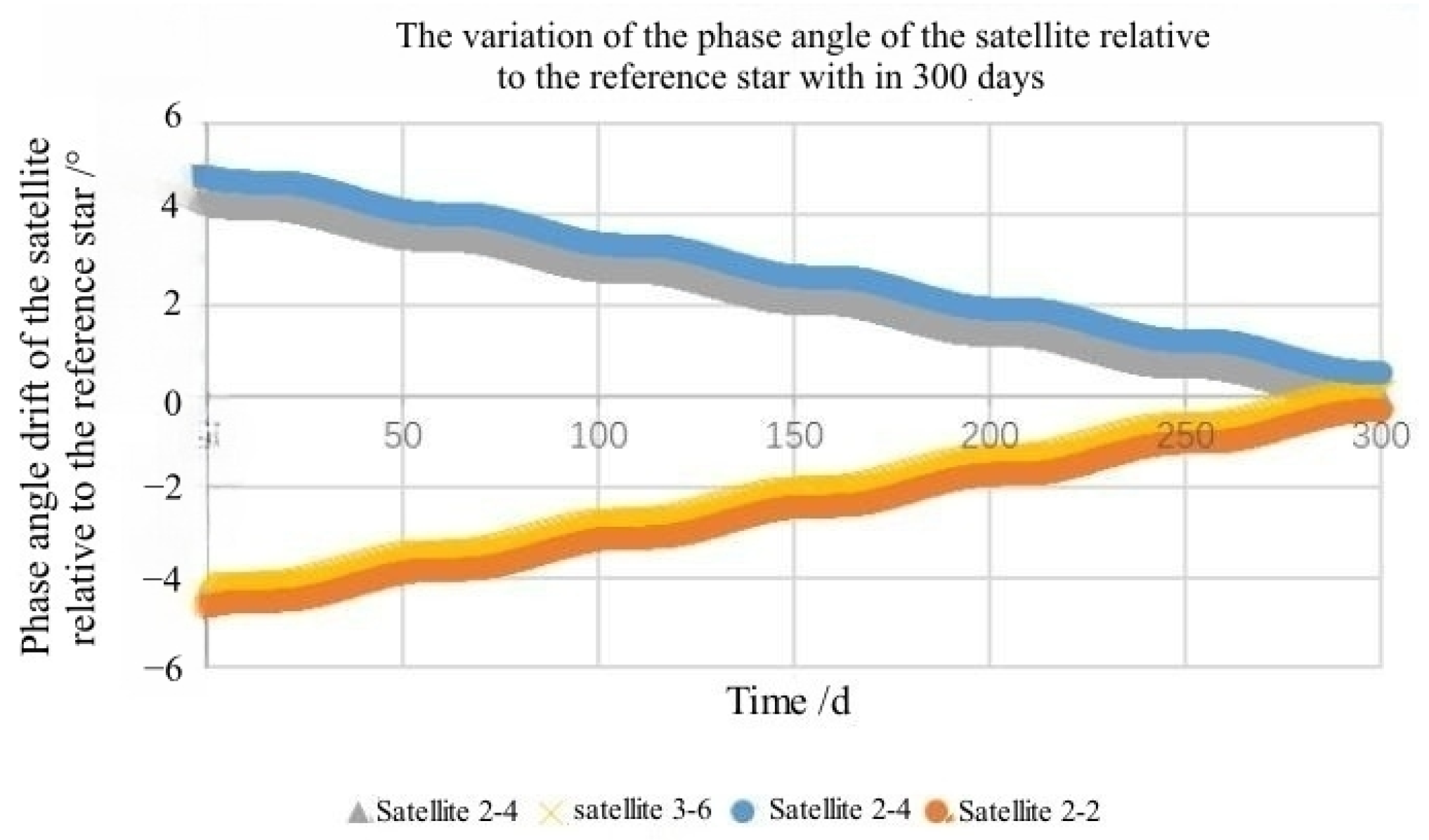
For low-orbit satellites in near-circular orbit, the attenuation of the orbital semi-major axis caused by atmospheric drag will cause a relative phase drift of the satellite. The relationship between the phase angle drift rate and the semi-major axis attenuation can be written as follows [15]:

$$\Delta \stackrel{·}{\lambda }\left(t\right)=-{\displaystyle \frac{3}{2}}\sqrt{\mu }{a}^{-{\displaystyle \frac{5}{2}}}\Delta a,$$

(2)

By integrating the above formula, the relative rate of change in the phase angle can be regarded as a function of the semi-major axis and the rate of change of the semi-major axis. The relationship between the phase angle drift and the semi-major axis attenuation is [15].

$$\Delta \lambda \left(t\right)=-{\displaystyle \frac{3}{2}}\sqrt{\mu }{a}^{-{\displaystyle \frac{5}{2}}}\Delta at.$$

(3)

where $\Delta a$ is the amount of attenuation caused by atmospheric drag.

According to the phase calculation formula of the reference star,

$$\Delta \lambda =\Delta \lambda \left(t\right)+\Delta \stackrel{\wedge }{\lambda }.$$

(4)

When the phase deviation $\Delta \lambda$ of the satellite relative to the reference star exceeds the threshold value, the following condition is satisfied:

$$\left|\Delta \lambda \right|>{\lambda }_{\max }.$$

(5)

The orbit control of the satellite needs to be implemented.

3. Constellation Station Maintenance Method

After the satellite is inserted into the initial orbit, it runs in the nominal orbit. Due to the influence of atmospheric drag perturbations, the orbital altitude of the satellite keeps decreasing and the operation period keeps becoming shorter within one orbital period. As a result, the actual phase of the satellite will deviate from the nominal value (theoretical value). To maintain the constellation configuration and phase requirements, the semi-major axis of the orbit needs to be corrected regularly. The frequency of correction mainly depends on the atmospheric density (related to the solar activity cycle), the satellite’s windward area, and the satellite phase drift range constraints. At present, the common method of constellation station position maintenance is the phase-holding ring method.

3.1. Phase-Maintenance Circulation Orbit Method

The idea of the phase-holding ring method is as follows. Using the attenuation characteristics of the satellite phase and the orbit semi-major axis (under the influence of atmospheric drag perturbations, the drift acceleration of the actual phase of the satellite is always forward), when the satellite phase is located at the forward boundary of the drift ring, a positive bias occurs on the orbital semi-major axis. Thus, the actual phase of the satellite gradually shifts to the backward boundary, and with the gradual decrease in the semi-major axis (the actual value gradually becomes less than the nominal value), the actual phase of the satellite gradually drifts forward. When the phase of the satellite reaches the forward boundary of the drift ring, the operation of lifting the orbital semi-major axis is needed to start a new drift cycle. Therefore, to reduce the frequency of orbit-control tasks and lower the fuel consumption, a suitable control quantity of semi-major axis maintenance tasks is selected, and the phase maintenance ring is fully utilized. The limit cycle control method combining overshoot control and passive control is adopted.

The specific implementation process of the phase-holding ring method is described as follows. The relative phase control box of the constellation satellite is set. The left and right boundaries correspond to the control range of the relative phase of $\left(-\Delta {\lambda }_0,\Delta {\lambda }_0\right)$. The lower boundary corresponds to the nominal flat root of the semi-major axis of the reference orbit $a_0$. The upper boundary corresponds to the maximum bias of the semi-major axis $\Delta a_0$ (greater than 0). The initial relative phase of the satellite is near the right boundary $\Delta {\lambda }_0$ of the control box. Since the change rate of the semi-major axis $\dot{a}$ is less than 0, the satellite’s flat root of the semi-major axis decreases with time. The relative phase angle of the satellite gradually drifts to the left boundary $-\Delta {\lambda }_0$ of the control box and returns to the right boundary after a complete drift period. When the drift reaches the right boundary of the control box, the semi−major axis is lifted repeatedly. Figure 1 shows the approximate relationship between the satellite phase drift and the semi-major axis. Each time the phase drifts out of the most forward boundary, semi-major axis overshoot control is applied to the already decayed orbit to ensure that the phase angle deviation remains within the required permissible range.

3.2. Calculation of Phase-Holding Limit Loop Control Parameters

Due to the influence of atmospheric drag, the actual phase of the satellite will deviate from the theoretical nominal value in one orbital period. According to Formula (1), which provides the relationship between the amount of satellite phase angle drift and the amount of semi-major axis attenuation, it can be seen that the change in the semi-major axis after satellite control is approximately a straight line, and the trend of the phase difference change is approximately a parabola. It is assumed that the variation trend of the satellite phase difference over time after satellite control is as follows:

$$\Delta \lambda \left(t\right)=\lambda \left(0\right)-{\displaystyle \frac{3}{2}}\sqrt{\mu }{a}^{-{\displaystyle \frac{5}{2}}}\left(a_{0}t+{\displaystyle \frac{1}{2}}{\dot{a}}_d{t}^2\right).$$

(6)

According to the implementation idea of the phase-holding ring method, when the relative drift of the semi-major axis is 0,

$$a_0=-{\dot{a}}_{d}t.$$

(7)

Thus, the time of half a drift cycle of the phase difference is

$$t=-{\displaystyle \frac{a_0}{{\dot{a}}_d}}.$$

(8)

This formula is combined with Formula (5) to obtain

$$\lambda \left(0\right)={\displaystyle \frac{3}{4}}\sqrt{\mu }{a}^{-{\displaystyle \frac{5}{2}}}{\displaystyle \frac{a_0^2}{{\dot{a}}_d}}.$$

(9)

The following is defined:

$$\lambda \left(0\right)={2\lambda }_0.$$

(10)

Then, the attenuation of the semi-major axis in a phase-holding period is

$$a_0={\left({\displaystyle \frac{8{\dot{a}}_d{a}^{\frac{5}{2}}\Delta {\lambda }_0}{3\sqrt{\mu }}}\right)}^{{\displaystyle \frac{1}{2}}}.$$

(11)

The target value of the semi-major axis deviation of the phase-keeping orbit maneuver is

$$\Delta a=4{\left({\displaystyle \frac{2{\dot{a}}_d{a}^{\frac{5}{2}}\Delta {\lambda }_0}{3\sqrt{\mu }}}\right)}^{{\displaystyle \frac{1}{2}}}.$$

(12)

The time interval required for two semi-major axis controls is

$$\Delta t=4{\left({\displaystyle \frac{2a^{\frac{5}{2}}\Delta {\lambda }_0}{3{\stackrel{·}{a}}_d\sqrt{\mu }}}\right)}^{{\displaystyle \frac{1}{2}}}.$$

(13)

For a quasi-circular orbit, according to the simplified satellite continuous small-thrust perturbation equation, the tangential velocity increment required by the change in the semi-major axis of the phase-maintaining orbit maneuver can be written as

$$\Delta V={\displaystyle \frac{n}{2}}\Delta a.$$

(14)

Based on the influence of the space atmospheric density and solar activity, the change rate of the satellite’s average value of the semi-major axis is also different due to the different orbital altitudes and satellite windward areas (or surface-to-mass ratios) of different satellites in the constellation. Therefore, the phase-holding control period and semi-major axis adjustment amounts of different satellites in the constellation should be calculated correspondingly.

4. Analysis of Position-Holding Strategy of Constellation Stations

The strategy of constellation station holding can be divided into two types: absolute station holding and relative station holding.

• Absolute control strategy.

Absolute control means that each satellite in the constellation is controlled independently to keep it within a control range centered on the control reference satellite. The absolute control method is relatively mature and reliable. It is the same as the control method of a single satellite. It has a certain engineering application basis and is highly reliable for the constellation control system.

The launch of multiple satellites with one launcher is considered an example. After the satellite is in orbit, the control of the initial orbit acquisition is preliminarily completed based on the nominal orbit. The absolute control strategy is based on the orbit of the nominal constellation as a reference. By controlling the semi-major axis, inclination, and right ascension of a single satellite one by one, the constellation configuration can be established within a specified time limit. Due to the influence of various perturbations, the satellite will gradually deviate from the originally designed orbit during orbit operation, the safe positions between the satellites in the constellation will change, and the overall structure of the constellation will be destroyed. It is necessary to maintain the long-term and periodic orbit of the constellation to ensure the integrity of the constellation’s performance.

Considering the measurement errors and onboard control errors in the ground measurement and control system, the absolute control strategy is to control each satellite one by one. By improving the measurement accuracy of the semi-major axis, the average orbit-control period can be increased, and the number of orbit-control tasks during the lifetime can be reduced, thereby reducing the configuration maintenance frequency.

2.

Relative control strategy.

Relative control is to control the constellation globally, rather than independently controlling each satellite. The control target also changes from the absolute position of each satellite to the relative position between satellites to keep the configuration of the whole constellation unchanged within certain precision requirements.

Different from the absolute control strategy, the relative position-holding strategy requires a ground measurement and control system to conduct precise orbit determination and orbit prediction for the whole satellite network. Then, the reference orbit and control strategy of each satellite are calculated and combined with the relative control strategy. The relative control strategy occupies more ground satellite tracking telemetry and command (TT&C) resources, and the scheduling algorithm is more complex. At the same time, a relative control strategy requires high on-board autonomy. Considering Internet Constellation does not have the function of directly measuring the orbital parameters of adjacent satellites, it can only rely on the GNSS of the satellites to obtain precise orbital data and transmit it back to the ground control center through inter-satellite links and satellite-Earth mode.

A relative control strategy synthesizes the orbital perturbation deviation of the whole network satellite and only corrects the parts that affect the relative geometric configuration of the constellation. The propellant consumption, orbital control frequency, and control period are more advantageous than those of the absolute control strategy, but the control process is relatively complicated and the reliability is low.

3.

Comparison of absolute and relative control strategies.

The absolute holding strategy has the advantages of simple control, high reliability, and mature control methods. Due to the pressure on the ground measurement and control system, the absolute holding strategy requires fewer measurements and control resources. Before the relative control strategy is controlled, the reference track should be optimized, and the reference track parameters should be updated to reduce the control frequency, which is of high complexity and low reliability. The absolute phase control method is simple and mature, with high reliability. Relative phase control is more suitable for constellations with fewer satellites. Absolute phase control is recommended for large constellations.

Table 1. Comparison of control strategies.

Control Strategy	Advantages	Disadvantages
Absolute control	Simple control, high reliability, mature control methods	Many orbital control tasks, large relative fuel consumption
Relative control	Reduced frequency of control and lower fuel consumption	Measurement and control system is under great pressure, scheduling algorithm is complex, onboard autonomy is required to be high

shows a detailed comparison of the control strategies.

4.1. Constellation Absolute-Station-Holding Strategy

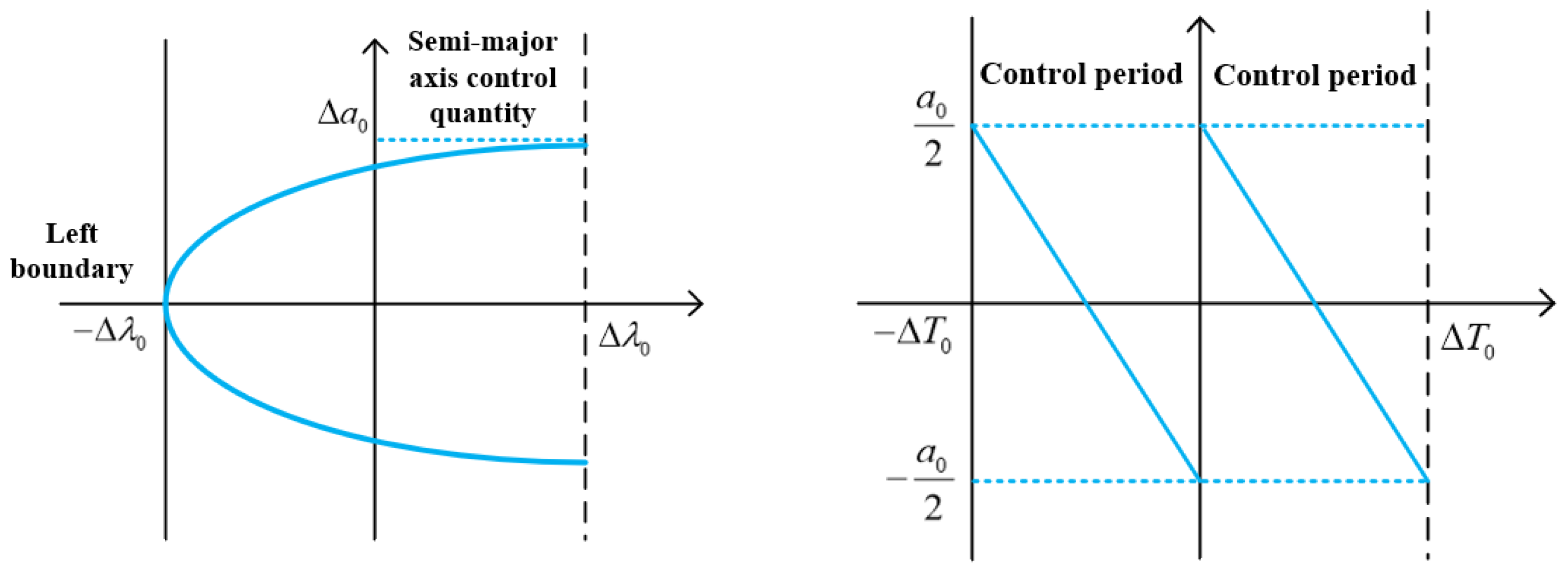
Based on the relationship between the semi-major axis deviation and the phase deviation, as well as the calculation method of the limit cycle control period and the semi-major axis change, the absolute-phase-holding strategy of the satellite constellation is presented in this section. Absolute phase holding is a method for the autonomous phase holding control of a single satellite, and it is suitable for the absolute station holding of large low-orbit constellations. The control flow chart of the satellite absolute control strategy is shown in Figure 2.

The control process of the satellite absolute control strategy is as follows:

• The initial semi-major axis deviation relative to the reference star before satellite control $a_0$ and the corresponding initial phase angle deviation ${\lambda }_0$ are obtained.
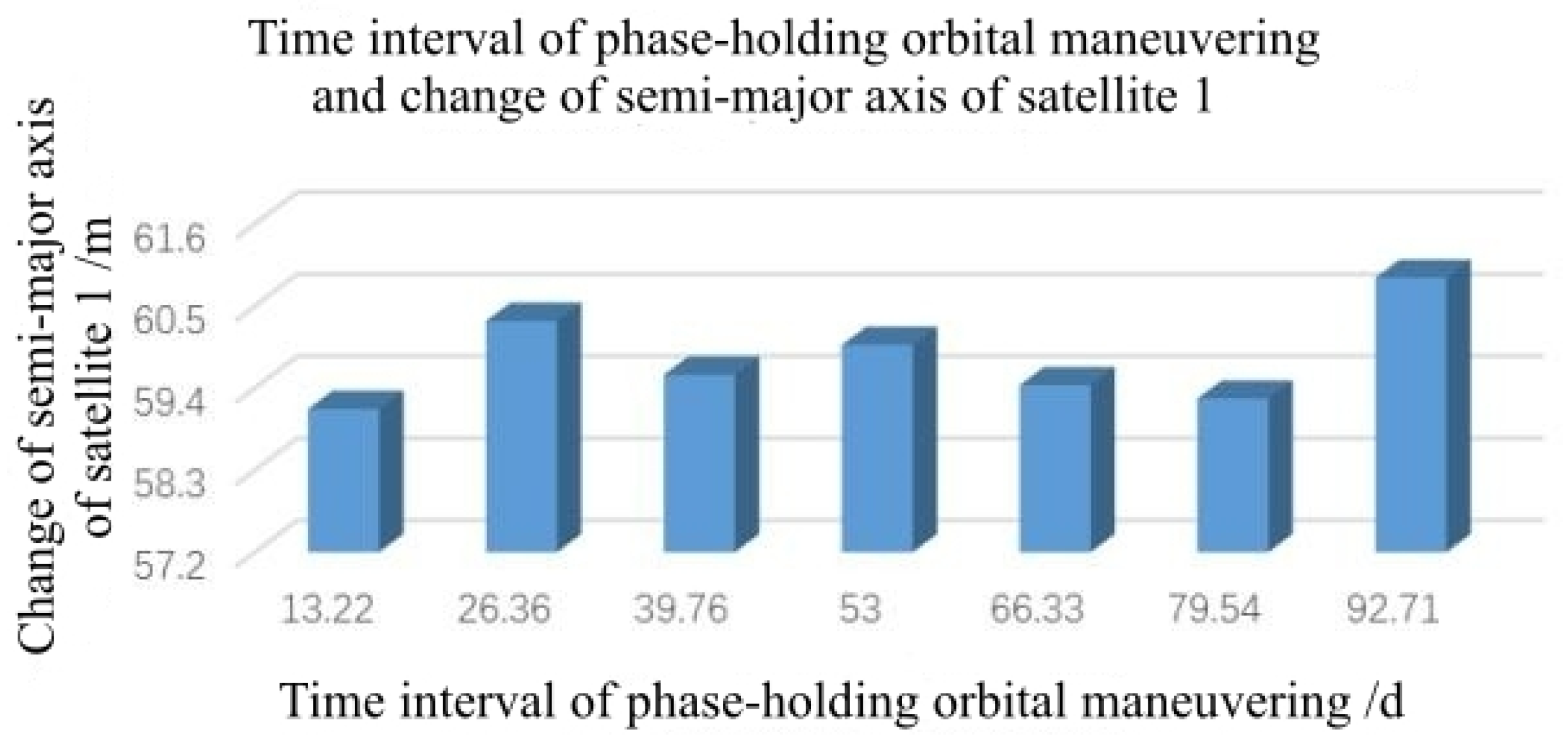
• The high−precision orbit propagator (HPOP) model was used to extrapolate the satellite orbit’s average value of the semi-major axis and phase angle. The attenuation rate of the satellite’s average value of the semi-major axis was calculated by curve fitting the variations of the average value of the semi-major axis attenuation rate ${\dot{a}}_d$ and the range of the phase angle drift ring $2\Delta {\lambda }_0$.
• Based on the average value of the semi-major axis attenuation rate ${\dot{a}}_d$ and phase angle drift ring range $2\Delta {\lambda }_0$, the semi-major axis deviation target value of the phase-holding orbit maneuver within a phase-holding period $\Delta a$ is calculated.
• The change in the semi-major axis that maintains control is calculated: $\Delta a_w=\Delta a+\Delta a_0$.
• The disparity between $2\Delta {\lambda }_0$ and ${\lambda }_0$ is calculated. If the disparity is less than the tolerance value ($d\lambda <\epsilon$), the process proceeds to step 6; otherwise, the process returns to step 1 for iterative correction.
• Orbit control (lifting or lowering the semi-major axis of the satellite) is carried out on the satellite at this moment to achieve the goal of satellite phase maintenance.

4.2. Relative Station Position-Keeping Strategy of Constellation

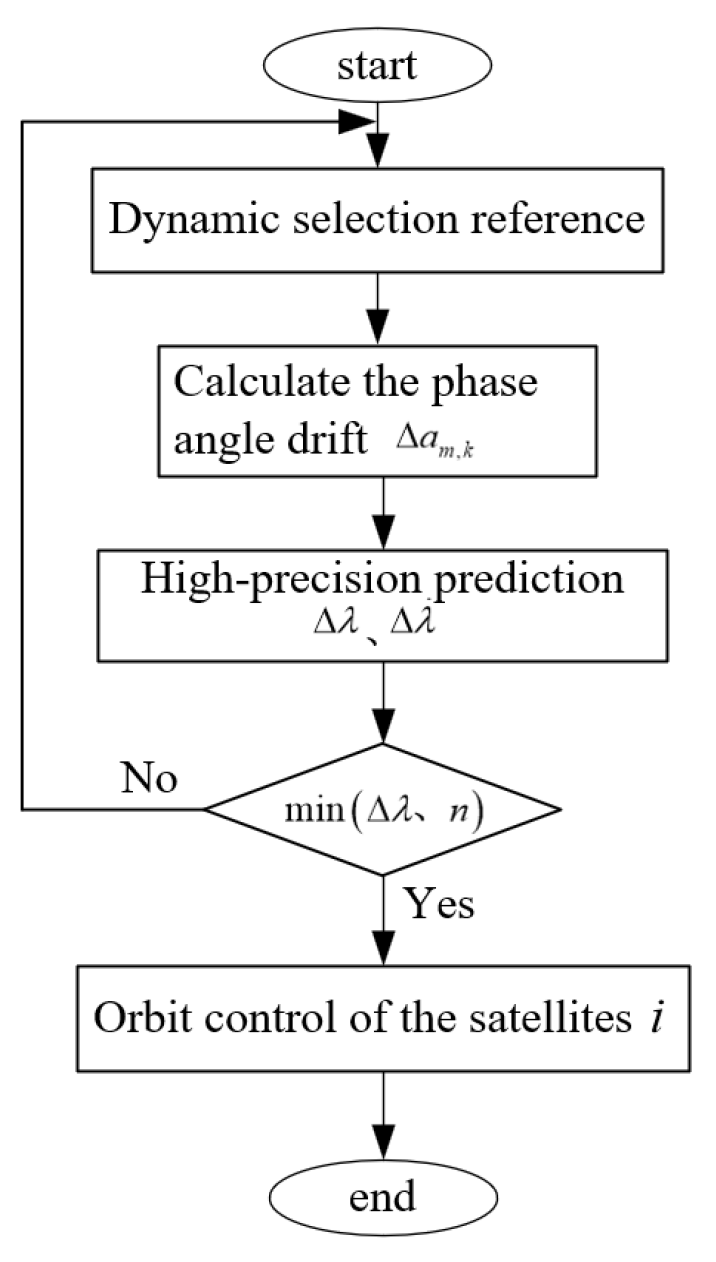
In this section, a relative phase control strategy based on a dynamic reference satellite is designed based on the method of referring to a dynamic reference star. The specific process is as follows. Any satellite in the constellation is dynamically selected as the reference star, and then the sum of the phase drifts of other satellites in the constellation and the reference satellite is calculated. The satellite with the minimum cumulative value of the phase angle drift and the minimum number of satellites to be controlled is selected as the control reference, and the relative station position maintenance of the constellation is carried out. The control flow chart of the satellite relative control strategy is shown in Figure 3.

The control process of the relative phase-maintenance strategy based on a dynamic reference satellite is as follows:

• All the satellites in the constellation are utilized as dynamic reference stars, and the phase angle drift $\Delta {\lambda }_{m,k}=\Delta {\lambda }_k-\Delta {\lambda }_m-\Delta \widehat{\lambda }$ of the other satellites relative to the reference satellite is computed. Here, $m=1,2,\dots n$, $k=1,2,\dots n$, and $\Delta \widehat{\lambda }$ represent the designated nominal value of the phase difference between satellite k and satellite m.
• The orbit extrapolation of a satellite in the constellation is carried out by a high-precision orbit forecaster to calculate the satellite phase deviation $\Delta \lambda$. With the change rate of the phase deviation $\Delta \dot{\lambda }$, the phase angle summation $\Delta {\lambda }_m$ ($\Delta {\lambda }_m={\displaystyle {\sum }_{k=1}^n\Delta {\lambda }_{m,k}}$) is selected. In addition, the number of phase maintenance satellites $i$ and the smallest satellite $k$ ($k=1,2,\dots n$) should be used as the reference satellite.
• Based on the reference satellite $k$, orbit control is implemented for satellite $i$ to adjust its semi-major axis (raising or lowering) to alter the phase drift direction between the satellites and maintain the phase angle of the constellation.

According to the perturbation variational equation of the relative phase angle, the cumulative semi-major axis control quantity can be deduced as

$$\Delta a_i={\displaystyle \frac{4a_k\Delta {\lambda }_0}{\left(3n+7\Delta \dot{\lambda }\right)\Delta t}}+\Delta a_0,$$

(15)

where $\Delta {\lambda }_0$ is the maximum allowable drift of the phase difference, $\Delta t$ is the phase drift time, and $\Delta a_0$ is the absolute value of the semi-major axis deviation between the reference satellite and the control satellite.

5. Simulation and Analysis of Positioning Strategy of Constellation Station

5.1. Simulation Scheme and Result Analysis of Absolute Station-Holding Strategy

• Setting of simulation conditions.

The large-scale Walker constellation selected in the simulation had a configuration of Walker 60/3/1. (The concept of the Walker-δ constellation was first proposed by J.G. Walker of the Royal Aircraft Establishment in the UK in 1971. The Walker-δ constellation can be represented by the configuration code N/P/F. Among them, N represents the total number of satellites in the constellation, P represents the total number of orbital planes in the constellation, and F represents the phase factor of satellites in adjacent orbital planes of the constellation [26]). It also had an orbital altitude of 550 km and an orbital inclination of 53°. The satellite phase angle drift ring was simulated within a range of ±0.1°. The perturbation model was the Earth non-spherical $J_2$ perturbation model. The Jacchia 71 atmospheric density model (set) was used, and the orbit prediction model was the HPOP model. The satellite surface-to-mass ratio was 0.01, the phase retention mission period was 100 days, and $C_d=2.2$.

Table 2. Initial orbital elements of the satellite.

Satellite Number	Initial Semi-Major Axis /km	Dip Angle /°	Initial Phase /°	Surface-to-Mass Ratio/m2/kg
1	6925.6	53.0	0	0.01

presents the details for satellite number 1 in the constellation.

2.

Simulation results.

The optical pressure coefficient was set to 1.0. In low-solar-activity years, the solar radiation index was F_10.7 = 100, and the solar activity index K_p = 2.0. In high-solar-activity years, the solar radiation index was F_10.7 = 200, and the solar activity index K_p = 2.0. The decay rates of satellite 1 in different solar years were obtained by simulations, and the results are shown in Figure 4 and Figure 5. The average daily decay rate of satellite 1 in low-solar-activity years was 4.5 m, and that of satellite 1 in high-solar-activity years was 25.6 m.

Based on the relationship between the semi-major axis deviation and the phase deviation, as well as the limit cycle control period and the calculation method of the semi-major axis change, the maximum semi-major axis adjustment corresponding to satellite 1 and the maximum time interval between two orbit control tasks were calculated. The results are shown in

Table 3. Satellite control parameter settings.

Satellite Number	Initial Semi-Major Axis/km	Maximum Adjustment Amount of Average Value of the Semi-Major Axis in Years of Low Solar Activity/m	Maximum Adjustment of Semi-Major Axis of High-Solar-Activity Year/m	Maximum Interval of Adjustment Time for Average Value of the Semi-Major Axis of Low-Solar-Activity Year/d	Maximum Interval for Adjustment of Average, Average, and Semi-Major Axis in High-Solar-Activity Years/d
1	6925.6	29.4	70.7	13.1	5.5

.

The phase-holding task of satellite 1 was simulated. The statistical results of the phase-holding period and semi-major axis change of satellite 1 are shown in Figure 6, and those of the phase-maintenance period and phase difference change of satellite 1 are shown in Figure 7. As can be seen from the simulation results, in the nearly 100-day phase-holding period of satellite 1, the phase-holding control period was about 13.1 days, the maximum adjustment of the semi-major axis was about 70.7 m, and the phase angle deviation was basically kept within ±0.1°. These results verified the effectiveness of the absolute station phase-holding ring method and achieved the expected phase-holding task.

The statistical results of the time interval of the orbit maneuvering and the change of the semi-major axis during phase holding are shown in

Table 4. Orbital maneuver time interval and semi-major axis change.

No.	Control Time/d	Interval from Last Control Moment/d	Maximum Adjustment of Semi-Major Axis/m
1	13.22	13.14	59.12
2	26.36	13.40	60.3
3	39.76	13.24	59.58
4	53.00	13.33	59.98
5	66.33	13.21	59.44
6	79.54	13.17	59.26
7	92.71	13.53	60.88
Average	/	13.29	59.79
Total	92.71	/	418.56

. The average holding period of satellite 1 in a single phase-holding mission was 13.29 days, and the change in the semi-major axis in a single orbital maneuver was 59.79 m. In the whole phase-holding task, the orbital maneuver time totaled 92.71 days, and the total orbital maneuver semi-major axis change was 418.56 m.

Figure 8 more directly reflects the time interval of the orbital maneuvering and the change of the semi-major axis of satellite 1 in the phase-holding task. The deviation of the orbital maneuvering was within 5%. Therefore, the absolute station position autonomous phase-holding method could complete the satellite phase-holding task. This method can be extended to the absolute station position holding of the constellation phase, which has significant advantages in large−scale constellation station holding.

5.2. Simulation Scheme and Result Analysis of Relative Station-Position-Holding Strategy

• Setting of simulation conditions.

Since relative phase control is more suitable for constellations with small numbers of satellites, the configuration of the low-orbit Walker constellation selected in the simulation test was 18/3/1, with an orbital altitude of 550 km and an orbital inclination of 53°. The perturbation model of the simulation test was the Earth non-spherical $J_2$ perturbation model, and the Jacchia 71 atmospheric density model (set) was used. The satellite surface-to-mass ratio was 0.01, the orbit forecast model was the HPOP model, and the range of the constellation phase-angle-deviation drift ring was maintained by the simulation analysis. The simulation phase-holding task period was 300 days, and $C_d=2.2$.

2.

Simulation results.

According to the evolution of the constellation configuration caused by the phase deviation drift, the nominal orbit of the constellation was taken as a reference, and the relative phase angle drift amounts of satellites 2−4 and 3−6 in low-solar-activity years were obtained. The main reason for the satellite phase angle drift shown in Figure 9 was that the semi-major axis of the orbit had an initial deviation from the nominal orbit. Therefore, the satellite phase angle showed nonlinear changes over time under the action of atmospheric drag.

According to the relative phase-maintenance strategy steps based on dynamic datum satellites, satellites 1−1, 1−2, 1−3, 2−1, …, and 3−3 were taken as the reference satellites, and the relative phase drift amounts of other satellites in the constellation were calculated. When satellite 1-2 was taken as the reference satellite, the total phase deviation beyond the critical threshold was the minimum, and the number of satellites to be controlled was the minimum.

Table 5. Relative phase drift amounts of satellites in the constellation with reference.

	Relative Star	1−3	2−2	2−4	3−6
Reference Star
1−2		4.35	4.13	4.38	4.37

shows the phase drift amounts of satellites in the constellation that exceeded the critical threshold of the phase deviation relative to reference star 1−2. Based on the statistical results and relative control process, satellite 1−2 was selected as the control reference, and orbit control was carried out on satellites 1−3, 2−2, 2−4, and 3−6. The results over 30 days after orbit control for the phase maintenance of the constellation satellites are shown in Figure 10. The phase angle deviation of satellite 2−4 relative to reference satellite 1−2 gradually decreased with time, and the change rate of the phase difference was about −0.0147°. The phase angle deviation of satellite 3−6 relative to the reference star 1−2 gradually increased, and the phase difference change rate was about 0.0153°.

Based on the HPOP forecaster, orbit extrapolation and curve fitting were carried out on the satellite implementing orbit control. The changes in the satellite’s relative phase angle to the reference star within 300 days were obtained, as shown in Figure 11. The simulation data showed that the phase angle drift amounts of all the satellites in the constellation were maintained within the range of ±5° over 300 days, which was in line with the expectations.

5.3. Comparative Analysis of Constellation-Maintenance Strategy Simulation Results

The evaluation of the absolute and relative control strategies of the constellation was based on their ability to satisfy the availability and serviceability requirements of the constellation, as well as the availability of mature and reliable control technology. The overall orbital transformation time, fuel consumption, and minimum use of the measurement and control resources of the constellation satellites were taken as measurement indicators.

The simulation results of the absolute control strategy showed that in low-solar-activity years, satellite 1 achieved the maintenance task of a ±0.1° phase angle deviation. The maintenance control period was 13.29 days, and the change in the semi-major axis of each orbit-control maneuver was 59.79 m. The simulation results of the relative control strategy showed that in low-solar-activity years, the Walker constellation with the constellation configuration of Walker 18/3/1 only needed to carry out four orbit-control tasks for satellites 1−3, 2−2, 2−4, and 3−6. The phase-angle-maintenance task within the threshold of ±5° for all the satellites in the constellation was realized over 300 days. A comparison of the simulation results with the control strategies are shown in

Table 6. Comparison of simulation results with control strategies.

Control Strategy	Frequency of Orbit Control	Occupied Resources
Absolute control	A single star maintained a control period of 13.29 days and consumed more fuel.	Each satellite in the constellation was controlled independently, requiring fewer measurement and control resources. This method is suitable for large-scale constellation phase maintenance.
Relative control	Only four orbit-control tasks were needed for satellites 1−3, 2−2, 2−4, and 3−6, consuming less fuel.	The calculations were complex, and the resource consumption was large. This method is suitable for small-scale constellation phase maintenance.

.

6. Conclusions

Aiming at the problem of large-scale constellation phase control in low orbit, the strategy of constellation station holding was investigated in this study. First, the relationship between the satellite phase angle drift rate and the semi-major axis attenuation was analyzed mathematically. A phase-holding loop control method combining semi-major axis overkill control and passive control was proposed. In addition, the calculation process of the phase-holding control parameters (maintenance control period and semi-major axis control amount) was derived, which provides theoretical support for constellation station holding. Second, the absolute station position control of large-scale constellations was simulated. The simulation results showed that to ensure the phase angle deviations were within the range of ±0.1° for all the satellites in the constellation in low-solar-activity years, about 13 days were required on average to adjust the satellite’s semi-major axis by about 71 m. The relative position control of small constellations was simulated. The simulation results showed that only four orbital maneuvers were needed to achieve the ±5° phase angle threshold maintenance task over 300 days for all satellites in the constellation. Finally, the comparison of the control strategy simulation results provides data support for the selection of maintenance control strategies for different-scale LEO constellations.