MCANet: An Unsupervised Multi-Constraint Cascaded Attention Network for Accurate and Smooth Brain Medical Image Registration

Abstract

Brain medical image registration is a fundamental premise for the computer-assisted treatment of brain diseases. The brain is one of the most important and complex organs of the human body, and it is very challenging to perform accurate and fast registration on it. Aiming at the problem of voxel folding in the deformation field and low registration accuracy when facing complex and fine objects, this paper proposed a fully convolutional multi-constraint cascaded attention network (MCANet). The network is composed of two registration sub-network cascades and performs coarse-to-fine registration of input image pairs in an iterative manner. The registration subnetwork is called the dilated self-attention network (DSNet), which incorporates dilated convolution combinations with different dilation rates and attention gate modules. During the training of MCANet, a double regularization constraint was applied to punish, in a targeted manner, the excessive deformation problem, so that the network can generate relatively smooth deformation while having high registration accuracy. Experimental results on the Mindboggle101 dataset showed that the registration accuracy of MCANet was significantly better than several existing advanced registration methods, and the network can complete relatively smooth registration.

1. Introduction

Using medical images to diagnose and treat diseases has always been the main development direction in the field of medical image processing. Deformable registration techniques for brain images have found many medical applications, such as brain tumor localization, neurosurgery assistance, and treatment response assessment. The aim of deformable registration is to establish a set of optimal spatial correspondence between a fixed image and a moving image in the same space, so that the difference regions between the two images tend to be aligned. According to different medical scenarios, it is possible to perform atlas-to-patient registration, patient-to-patient registration, multimodal image registration, multi-view image registration, etc. At the same time, the results of image registration can also be applied to many other medical image processing techniques, such as image segmentation, image fusion, etc. Recently, methods based on deep learning have been widely used in the field of image analysis and processing, and they have demonstrated advantages such as improved accuracy, faster processing speed, and the ability to handle complex deformations, surpassing traditional algorithms. Since AlexNet [1] achieved outstanding performance, the convolutional neural network (CNN) has become one of the most successful models in deep learning. CNN has also made a major breakthrough in the field of medical image registration by virtue of its ability to efficiently process highly structured data. The CNN-based medical image registration methods can be divided into two categories: one is the iterative registration method using CNN for similarity prediction, and the other is the method of using CNN for transformation parameter prediction. The former can be called the method based on deep similarity, which mainly uses CNN to measure the similarity between multimodal images. Traditional intensity-based similarity measures such as cross-correlation (CC), square sum distance (SSD), and mean square distance (MSD) are very effective for the registration of single-modality images with the same intensity distribution. CC measures the linear correlation between two images, SSD calculates the sum of squared differences between corresponding pixels, and MSD is the average of squared differences, providing a robust measure of similarity. But for multimodal image registration, the performance of traditional similarity measures is not satisfactory. Consequently, some researchers have proposed using CNNs to measure the similarity between images, which has yielded promising results. However, these methods [2,3,4] still rely on traditional image registration algorithms for iterative optimization, which results in lower registration efficiency. The second category includes both supervised [5,6,7] and unsupervised [8,9] learning-based registration approaches. Unlike the methods based on deep similarity, the above two methods infer the transformation parameters at one time in the forward prediction (a direct inference process that predicts transformation parameters without iterative optimization), which greatly improves the registration efficiency. The difference between these two methods is that the supervised models need some label information during the training to help the model to learn. However, it is usually difficult to obtain these required real information or ground truth. These data often need to be manually marked by experts [10] or generated by traditional registration algorithms [11,12] or by random transformation [13]. The ground truth obtained by these methods may also be inconsistent with actual physiological changes, as it cannot always reflect real-world biological variability. In addition, these data will also limit the upper limit of registration. In contrast, unsupervised learning retains the benefits of supervised learning while not being constrained by the need for ground truth, making it increasingly favored by researchers. More and more studies have begun to explore how to use unsupervised methods to improve registration performance, such as the work by Zheng et al. [14].

A key challenge in unsupervised learning for registration networks has been determining the appropriate loss function in the absence of supervised information. With the introduction of the space transformation network (STN) [15], this problem was perfectly solved. As a differentiable module, STN can be arbitrarily inserted into any position of the neural network, and it can carry out gradient backpropagation along with the network as a whole. The insertion of the STN made it possible to warp the moving image to generate warped images during the training process, perform similarity calculations [16] by applying STN to the field of medical images for the first time, and perform end-to-end registration of 2D cardiac cine MR scans, and it achieved comparable accuracy to traditional deformable registration methods and greatly shortened registration time. Later, Balakrishnan et al. [17] proposed VoxelMorph, which is a deformable registration model based on an unsupervised full convolutional neural network. The model is trained by punishing the appearance difference between images and the spatial gradient of the deformation field. This model also achieves the same results as the most advanced traditional registration algorithm. Kuang et al. [18] proposed a lightweight unsupervised registration model, FAIM, and strengthened the penalty for irreversible deformation. Later, Zhao et al. [19] proposed a deep-learning framework VTN for unsupervised affine and deformable registration and used it for 3D cardiac cine MRI and 4D chest CT registration. The results showed that although the smoothness of deformation is a problem, the registration performance of this method exceeds that of traditional algorithms, such as Elastix [20], and has achieved remarkable results in other aspects. In addition, Chen et al. [21] introduced TransMorph, a hybrid Transformer ConvNet model for volume medical image registration.

Accurate patient-to-patient registration is extremely challenging due to the variability in brain structures across different individuals. In addition, voxel folding in the deformation field can significantly affect image topology and deformation authenticity. Voxel folding refers to the overlapping of voxels during deformation, leading to inaccuracies. In order to solve the above problems, the traditional registration algorithm can effectively deal with the problems of voxel folding and deformation smoothness based on mathematical models and optimization methods, especially in maintaining the local structure and overall consistency, but it has a slow registration speed in large-scale data or real-time applications, and low registration accuracy when dealing with complex deformation or nonlinear transformation. Deep-learning-based registration algorithms can achieve faster and more accurate registration by learning transformation patterns from large datasets. These algorithms perform better than traditional methods, especially when dealing with complex nonlinear deformations. However, they may still struggle with voxel folding and maintaining deformation smoothness. To enhance registration speed and accuracy, while also addressing voxel folding and deformation smoothness, we propose the multi-constraint cascaded attention network (MCANet). The network architecture consists of two identical subnets, one of which is the extended self-attention network (DSNet). This paper introduces an attention mechanism based on attention gates to the convolutional neural network. This improves the network’s sensitivity to regions with large differences between patient images by inhibiting feature activation in the alignment region. As a result, the network better adapts to inter-patient image variations, enhancing registration accuracy. By applying additional regularization constraints to reduce noise and discontinuities in the registration process, and to make the deformation results smoother and more realistic, our main contributions in this paper are as follows:

• We have successfully applied the dilated convolution combination and attention mechanism to the registration of 3D brain MRI images, so that the network can expand the receptive field without adding too much computational cost and network parameters and obtain multi-scale features, and the network can better understand the global structure and local details of the image and improve the ability to accurately detect the deformed region.
• Through the cascading network architecture, the deformation registration of the input image from coarse to fine is realized, which greatly improves the accuracy of registration. This method of step-by-step refinement of registration results can effectively improve the accuracy of registration results and can handle registration tasks of different scales and complexities. At the same time, the double regularization constraint is used to ensure the smoothness and authenticity of the image registration, avoid the excessive deformation and discontinuity of the registration results, and make the registration results more in line with the actual situation.
• The proposed network model adopts an unsupervised end-to-end training method. It is not limited by ground-based facts and enables near-real-time brain MRI registration between patients.

Compared with traditional algorithms and existing deep-learning-based algorithms, the algorithm in this paper is able to perform alignment efficiently and accurately, and also promotes alignment smoothness and suppresses severe bending deformations under the constraints of dual regularization, which greatly improves the performance in all aspects.

2. Materials and Methods

2.1. Experimental Data

The data used for the brain MRI alignment experiments in this paper were obtained from the Mindboggle101 dataset [22] and from the Neurite OASIS sample data, which is freely and publicly accessible, and which was derived from T1-weighted brain MR images from 101 participants. The Neurite OASIS [23] sample data contains 413 brain MRI scans from multiple centers. These data were processed using FreeSurfer version 7.4.1 and the neuronal software package SAMSEG. Four data subsets from the Mindboggle101 dataset, including MMRR-21, NKI-RS-22, NKI-TRT-20, and OASIS-TRT-20, totaling 83 3D brain MR images, were initially used in this study. For image preprocessing, all images were subjected to a cranial stripping operation and strictly aligned to the MNI152 template space. Thirty-one cortical regions were manually labeled according to the Desikan–Killiany–Tourville (DKT) protocol. In the Mindboggle101 dataset, three subsets of MMRR-21, NKI-RS-22, and NKI-TRT-20 totaling 63 brain images (3906 pairs) were used as part of the training data. The test subset includes 20 images (380 pairs) from OASIS-TRT-20. In order to improve the generalization ability of the model, the study simultaneously used 413 3D brain MR images from Neurite OASIS and divided them into training, validation, and test sets in the ratio of 7:2:1. Specifically, 0.7 of the data (382 images) were used for training, 0.2 of the data (89 images) for validation, and 0.1 of the data (45 images) for testing. This strategy not only enlarges the size of the experimental data but also improves the adaptability of the model to different imaging protocols and population variations, thus enhancing the generalizability of the model in various clinical settings. In addition, in this study, the images were intensity normalized and the image size was cropped from the original 181 × 217 × 181 to 160 × 208 × 160 to make the images suitable for the proposed network. Also, linear affine alignment was performed on all images using the ANTs software version 2.4.3 package [24]. The newly introduced validation set plays a crucial role in hyperparameter tuning and model selection to ensure optimal model performance while minimizing the risk of overfitting.

2.2. MCANet Network Structure

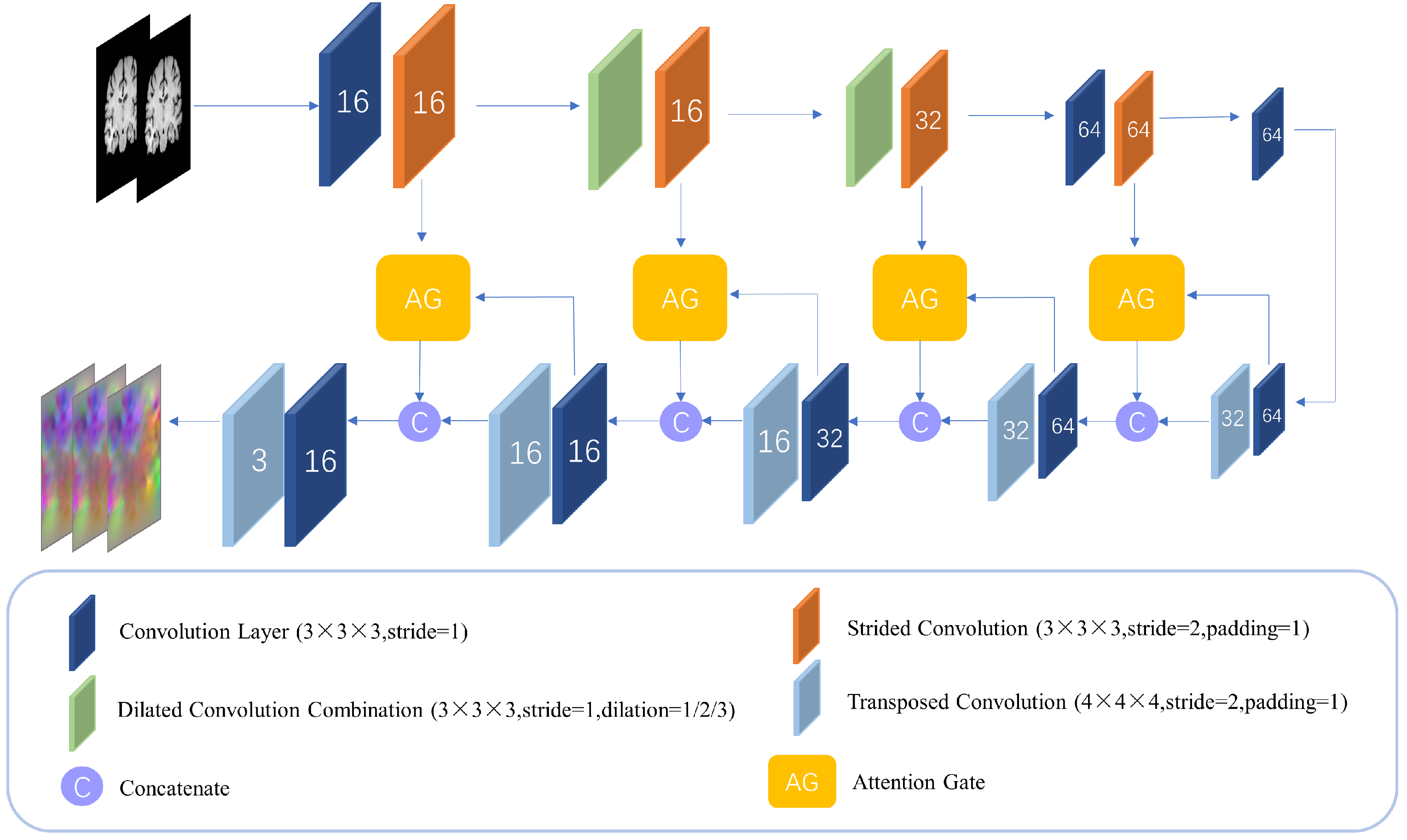
MCANet consists of two levels of identical registration subnet cascade, each of which incorporates an expanded self-attention design. Since the use of downsampling to enhance the receptive field of features will cause the deep feature map to lose the local detail information in the image, MCANet uses an expanded convolution group with different expansion rates to explicitly increase the receptive field without adding additional parameters, so that the network can capture more contextual information during the convolution process. The self-attention mechanism with the attention gate as the main form is added, and the shallow feature map is downsampled by step–step convolution, so that the size of the feature map is consistent with that of the gated feature map. Through the gating mechanism, the attention gate combines the attention-adjusted features with the original features, which can effectively increase the receptive field of the network without adding a large number of parameters, and at the same time inhibit the feature activity of the alignment region to improve the sensitivity of the network to the difference region and implicitly improve the deformation field smoothing problem. The transposed convolution is then used for upsampling to restore the obtained feature map to its original size in the input image. For the two-subnet cascade structure, double regularization constraints are explicitly applied to resolve the voxel folding problem, thereby comprehensively improving registration quality.

2.3. Cascade Network Registration Method

The input of the deformable image registration model is usually an image pair that has been affine aligned, where the image to be registered is called the fixed image and the image to be registered is called the moving image. For a pair of fixed image, F, and moving image, M, CNN can generate a displacement vector field (DVF) $\phi$ for floating image warping by performing feature extraction and deformation prediction on them. In the registration task, the training process of CNN is the process of continuously updating the network parameters to obtain the optimal DVF. After obtaining the DVF, the STN can be used to perform trilinear interpolation on the floating image according to the deformation information in the DVF, thereby obtaining the deformed image. For the MCANet proposed in this paper, the floating image needs to go through two stages of deformation in total, as shown in Figure 1.

In the first stage, M and F are passed into the registration subnet together as the initial input. After the deformation field ${\phi }_1$ is generated by the registration subnet $U_1$, the first warping deformation is performed on M to obtain a rough deformed image $I_1$. This stage can be expressed as Equation (1):

$$I_1=U_1(M,{\phi }_1)=M\circ {\phi }_1,$$

(1)

After obtaining the deformed image $I_1$, it enters the second stage of registration. At this time, $I_1$ is sent to the registration subnet $U_2$ together with F again as the moving image. After the prediction of $U_2$, the deformation field ${\phi }_2$ between F and $I_1$ can be generated. According to the voxel displacement in ${\phi }_2$, rough deformed image $I_1$ is warped again, and then we can obtain the fine deformed image $I_2$. This process can be expressed by Equation (2):

$$I_2=U_2(M\circ {\phi }_1,{\phi }_2)=U_2(I_1,{\phi }_2)=I_1\circ {\phi }_2,$$

(2)

Since $I_1$ is the moving image in the second stage, after the spatial transformation in the first stage, $I_1$ may lose part of the spatial information in the original moving image M. Therefore, in this study, the deformation field ${\phi }_1$ is input to the end of $U_2$ as auxiliary information to assist in the generation of ${\phi }_2$. Through the above process, the network architecture completes the coarse-to-fine registration of the original input images.

2.4. Dilated Self-Attention Network

The deformable registration network in this paper is composed of two encoder–decoder networks with the same structure, which we call the dilated self-attention network (DSNet), as shown in Figure 2. In this network, we use dilated convolutions to increase the receptive field of the convolutional layer and thereby improve the performance of the network. In the deep neural network, downsampling is often used to increase the receptive field. However, due to the limited number of downsampling in the shallow network, the receptive field of the low-level features cannot be effectively expanded. It is difficult for the extracted features to fully reflect the differences between the input images. Therefore, some studies [25] have increased the receptive field of low-level features by adding Inception modules to the network. But for 3D convolution, especially in the shallow layer of the network (the size of the feature map is large at this time), the use of any large-scale convolution will bring huge memory and calculation consumption. But dilated convolution can bypass this problem. Dilated convolution can explicitly increase the receptive field of the feature map without adding additional parameters, enabling the network to capture more contextual information during the convolution process. At the same time, because there is no downsampling, the loss of detailed information in the image is avoided, and the ability of low-level features to perceive the difference in detail in the image is preserved. In computer vision, acquiring multi-scale features is crucial for object region detection. By adjusting the dilation rate of dilated convolutions, the size of the receptive field can be directly changed, and the network can capture features of different scales.

Previous research [26] has elucidated that dilation convolution employs sparse sampling techniques, which, if a single dilation rate is used, can lead to a checkerboard pattern effect within the perceptual field of a pixel. In this case, voxels within the depth feature map can only perceive the underlying information in a checkerboard pattern, resulting in a large loss of local information. At the same time, the information correlation between voxels that are far away from each other is not strong, and the checkerboard effect reduces the coherence and consistency of the local information. For this reason, this study uses a cascade of three dilation convolutions with different dilation rates $r\in \{1,2,3\}$ and integrates them into one module. This cascade of dilation convolutions with different dilation rates is able to expand the sensory field of the output of each layer without increasing the number of parameters, which makes the parameter utilization more efficient in capturing the long-term dependence and global information in the input data, and thus simplifies the complexity of the model to a certain extent. In addition, the dilation convolution with different dilation rates is able to capture features at different scales, and by integrating these multi-scale features, information can be extracted more optimally, which in turn enhances the model’s representation of the input data. As the sequence of dilation rates is redesigned, this will further optimize the feature extraction process and enhance the model’s ability to recognize subtle features. This approach not only improves the model’s sensitivity to local features but also enhances its understanding of global features, thus achieving better performance in various visual tasks. In this way, the model is able to achieve the in-depth mining of multi-dimensional features of the input data while keeping the number of parameters constant, which is important for improving the generalization ability and adaptability of the model. Adopting the dilation convolution cascade strategy with different dilation rates can not only effectively solve the checkerboard grid problem caused by a single dilation rate but also further improve the feature extraction ability and expression ability of the model through the integration of multi-scale features, which provides new ideas and methods for the design of deep-learning models.

Attention gate has been shown to be successfully applied to dense prediction tasks for images [27]. A network model trained with an attention gate can implicitly learn the ability to focus on task-relevant regions in an image and suppress responses to task-irrelevant features [28]. This study incorporates attention gates into the design of the registration subnet DSNet. Figure 3 shows the structure of the attention gate module. The attention gate uses feature maps of two adjacent scales as input; through the attention gate, the interrelated regions in the input image can be selectively learned, and the saliency of unrelated regions can be suppressed, which avoids the introduction of additional human supervision in the network construction process. The attention gates can enhance the model’s response to critical regions and improve the final registration accuracy. Among them, the deep feature map on the decoding path is input into the network as a gating signal, which contains rich context information; the attention gate can dynamically adjust the degree of attention of the model to the input features, which can be used to screen image features closely related to the registration task and determine key deformation areas in the image. For the gating feature map and the weighted feature map, this paper used the additive attention mechanism [29] to calculate the attention weight. Compared with the multiplicative attention mechanism [30], although the additive attention requires more computational cost, it will achieve better performance than the multiplicative attention. Therefore, this study used the additive attention mechanism to complete the calculation of attention weights. The attention mechanism helps the network identify salient features related to the task by continuously optimizing the attention weights. The calculation of the attention weight is:

$$x_j={\sigma }_1(W_l^T{l}_i^j+W_g^T{g}_i+b_1),$$

(3)

$$y_j={\sigma }_2(W_x^T{x}_i^j+b_2),$$

(4)

where $l_i^j$ and $g_i$ represent the low-level feature map and the gated feature map of layer j in the network, respectively. $W_h^T,W_g^T,W_x^T$ represent the linear transformation parameters of convolution. The low-level feature map $l_i^j$ is downsampled using strided convolution so that $l_i^j$ has the same size as the gating feature map $g_i$. $b_1$ and $b_2$ are bias terms of the operation. ${\sigma }_1$ is the ReLU activation function, and ${\sigma }_2$ is the sigmoid activation function, which are used to enhance nonlinear expression. Afterwards, the attention weight coefficient ${\alpha }_i^{\prime }$ can be obtained by resampling $y_i^j$ using trilinear interpolation. Finally, the attention weighted feature map $h_i^j$ can be obtained by multiplying $l_i^{\prime }$ and ${\alpha }_i^{\prime }$ element-wise.

$$h_i^j=l_i^j·{\alpha }_i^j,$$

(5)

By adding the attention gates to the skip connections of each scale, the multi-scale imaging information can be aggregated in the gating signal, which helps the network to achieve more accurate feature selection and weight assignment, thereby achieving better deformation prediction. In addition, the attention gate is also a differentiable module whose parameters can be updated in backpropagation.

2.5. Loss Function and Double Regularization Constraint

In this paper, we trained the two registration subnetworks as a whole and minimized the loss function in an end-to-end training manner to achieve the highest registration accuracy. The loss function usually consists of two parts: one is the similarity loss between the fixed image and the moving image, and the other is the regularization of the DVF. In this paper, normalized cross-correlation (NCC) [31] was used to measure the similarity between the deformed image and the fixed image, and its negative value is taken as the similarity loss. The relevant calculation can be performed according to Equation (6):

$$\begin{array}{cc}\hfill L_{sin}& =-NCC(F,M\circ \phi )\hfill \\ & =\sum _{p\in \mathrm{\Omega }}{\displaystyle \frac{{\left({\sum }_{p_i}(F\left(p_i\right)-\overline{F}\left(p\right))([M\circ \phi ]\left(p_i\right)-[\overline{M}\circ \phi ]\left(p\right))\right)}^2}{\left({\sum }_{p_i}{(F\left(p_i\right)-\overline{F}\left(p\right))}^2\right)\left({\sum }_{p_i}{([M\circ \phi ]\left(p_i\right)-[\overline{M}\circ \phi ]\left(p\right))}^2\right)}},\hfill \end{array}$$

(6)

where p represents the voxel point in the image and $\mathrm{\Omega }$ represents the image domain. $F\left(p\right)$ and $[\overline{M}\circ \phi ]\left(p\right)$ denote the average voxel intensity within a local window centered at p in the fixed and deformed images, respectively. In this paper, the window size is $9^3$.

If the network is optimized only with similarity loss, the network parameters are updated towards making the deformed image infinitely close to the fixed image. But at this time, the DVF predicted by CNN will be excessively warped, and even the voxels in the DVF will be folded. Therefore, it is necessary to carry out some spatial regularization on the DVF. Considering that the dual-subnetwork registration model used in this study may produce large deformation predictions, imposing a single regularization constraint is not enough to meet the smooth requirements of the deformation field, so double regularization constraints are implemented. The first regularization term is diffusion regularization, which penalizes the spatial gradient of the DVF:

$$R_{diffision}\left(\phi \right)=\sum _{p\in \mathrm{\Omega }}{\parallel \nabla \phi \left(p\right)\parallel }^2=\sum _{p\in \mathrm{\Omega }}[{({\displaystyle \frac{\partial \phi \left(p\right)}{\partial x}})}^2+{({\displaystyle \frac{\partial \phi \left(p\right)}{\partial y}})}^2+{({\displaystyle \frac{\partial \phi \left(p\right)}{\partial z}})}^2],$$

(7)

The second regularization is the bending energy [32], which penalizes severe bending deformation by applying a loss to the second derivative of the voxel displacement in the DVF. It is defined as:

$$R_{\mathrm{dending}}\left(\phi \right)=\sum _{p\in \mathrm{\Omega }}{∥{\nabla }^2\phi \left(p\right)∥}^2,$$

(8)

The double regularization constraint in this paper can be expressed as:

$$R=\gamma R_{diffusion}\left(\phi \right)+\beta R_{bendng}\left(\phi \right),$$

(9)

where $\gamma$ and $\beta$ represent the trade-off coefficients between the two regularization terms.

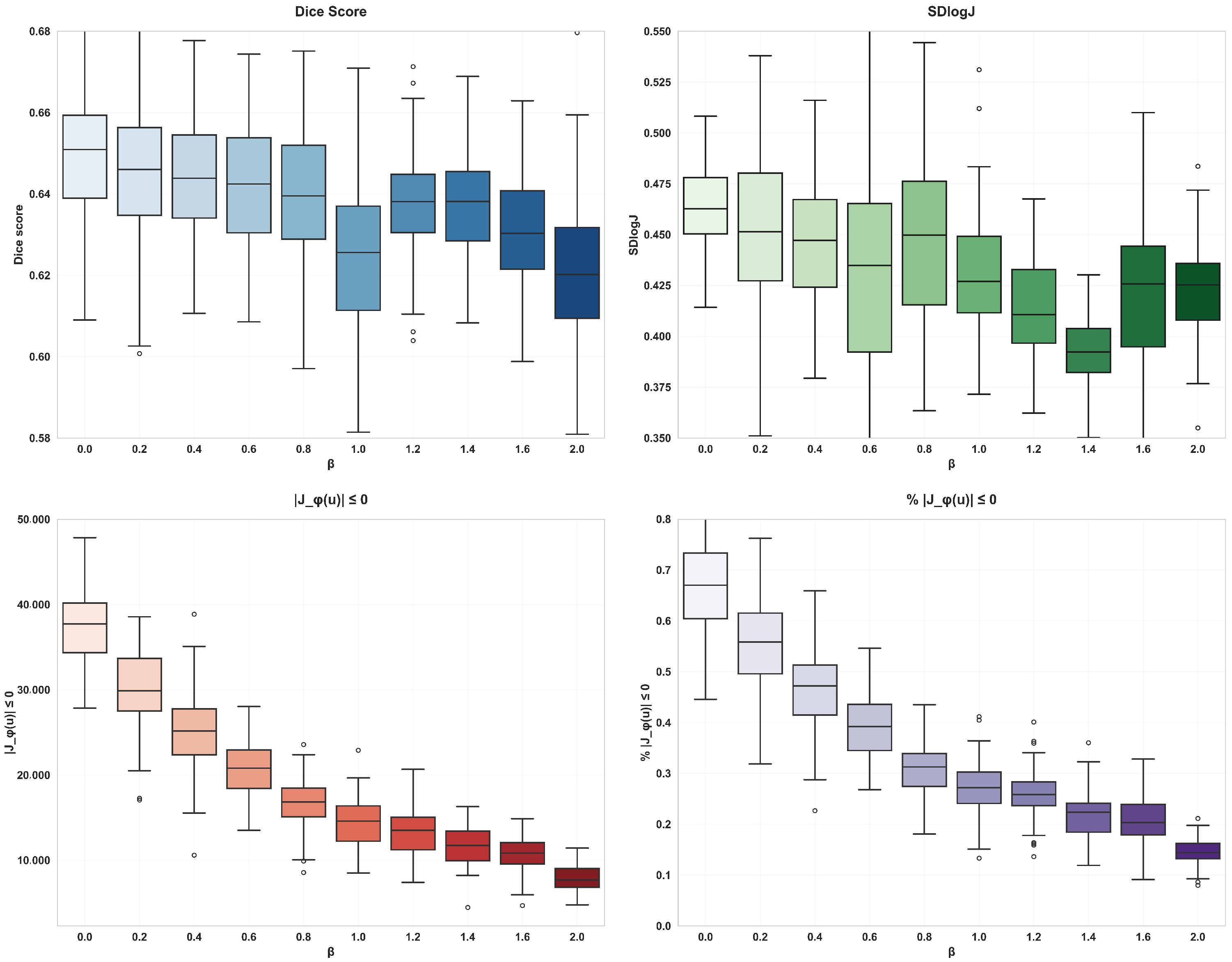
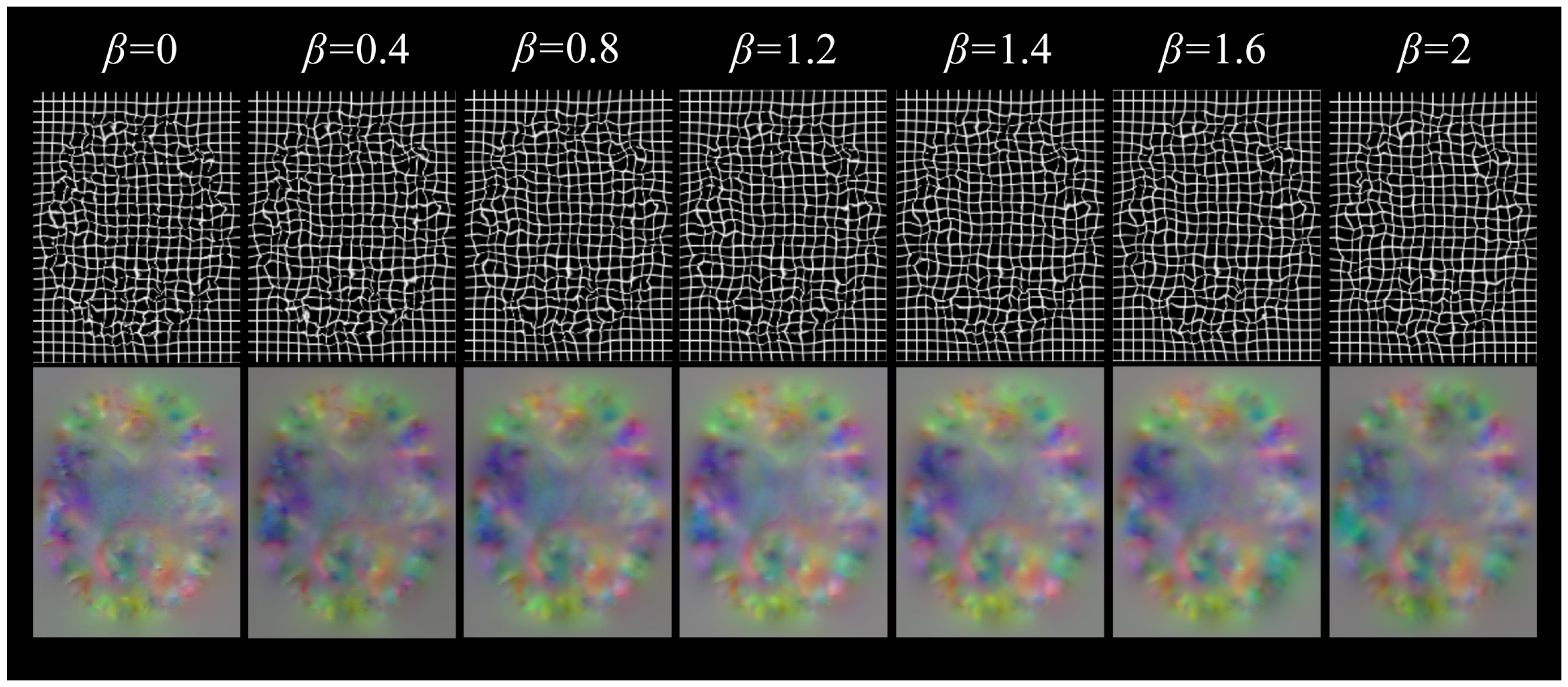
The diffusion regularization term is used to punish the spatial gradient of the displacement field, so as to promote the smoother displacement field, which helps to avoid overly complex local deformation and maintain the continuity of the overall deformation. The bending energy regularization term can not only promote the smoothness of the displacement field and inhibit the serious bending deformation at the same time but also effectively control the complexity of the model and reduce the risk of overfitting. With the increase of the $\beta$ of the weight coefficient of bending energy, the degree of voxel folding decreases significantly, but the Dice score also decreases, so when using double regularization constraints, the voxel folding problem can be effectively alleviated by adjusting the weight coefficient and ensuring smooth deformation.

2.6. Evaluation Method

In this paper, the Dice equation was used to calculate the volume overlap of the same anatomical tissues between the fixed image and the deformed image, and the Dice scores of all labeled tissues were averaged to quantitatively evaluate the registration accuracy. The calculation equation is as follows:

$$Dice(S_F,S_W)=2{\displaystyle \frac{\mid S_F\cap S_W\mid }{\mid S_F\mid +\mid S_W\mid }},$$

(10)

where $S_F$ and $S_W$ represent the corresponding brain anatomical tissues in the fixed image and the warped image, respectively. At the same time, in order to quantify the regularization of the DVF during registration, we also counted the number of folded voxels in the DVF, which was obtained by calculating the number of voxels with non-positive Jacobian determinant in the DVF (i.e., $\left|J_{\phi }\right|\le 0$).

In order to better measure the smoothness of the deformation field, SDlogJ is also used in the study. SDlogJ is an index used to evaluate the regularity of the deformation field, mainly to calculate the logarithmic standard deviation of the Jacobian determinant. The calculation formula is as follows:

$$SDlogJ=\sqrt{{\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\left(log|J_{\phi }\left(i\right)|-\mu \right)}^2},$$

(11)

In this formula, N represents the total number of voxels. $|J_{\phi }\left(i\right)|$ denotes the absolute value of the Jacobian determinant for the i-th voxel, and $\mu$ is the mean of the logarithm of the Jacobian determinants across all voxels. Additionally, the study introduces Sensitivity to evaluate the model’s ability to detect positive samples. Sensitivity is calculated using the following formula:

$$Sensitivity={\displaystyle \frac{TP}{TP+FN}},$$

(12)

where $TP$ is the number of true positive samples (correctly identified as positive) and $FN$ is the number of false negative samples (positive samples incorrectly classified as negative). This metric quantifies the proportion of actual positives that are correctly identified by the model.

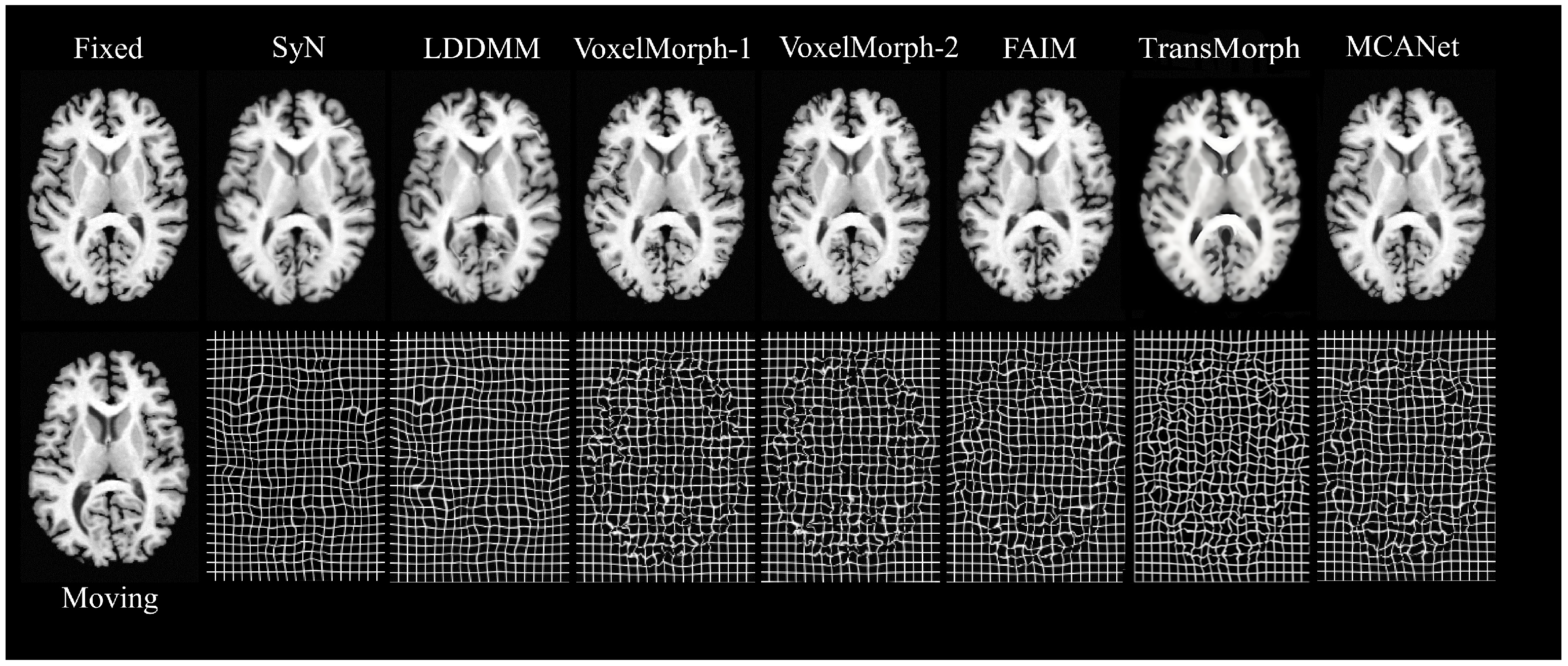
In order to intuitively demonstrate the performance of MCANet, this study introduced several other advanced registration methods as baselines, including SyN [33], LDDMM [34], VoxelMorph-1, VoxelMorph-2, FAIM, and Transmorph [21] DIF-VM. SyN, as an excellent representative of traditional registration algorithms, has been proven to perform effective inter-patient brain registration. We used the ANTs software package to conduct SyN experiments with cross-correlation as the similarity measure and a gradient step size of 0.2. The second traditional algorithm baseline was LDDMM, which aimed to solve large deformation image registration and can handle inter-patient registration with varying brain structures very well. In our experiment, the mean square error (MSE) was used as the objective function, the smoothing kernel size was 5, the smoothing kernel power was 2, the matching item coefficient was 4, the regular item coefficient was 8, and the number of iterations was 500. Moreover, this paper also selected VoxelMorph based on unsupervised learning as the baseline. There were two variants of this model: VoxelMorph-1 and VoxelMorph-2. In this study, it was retrained according to the optimal parameters given in Ref. [15], and the registration evaluation was completed on the test dataset of this paper. FAIM is a lightweight unsupervised registration model that can achieve high-precision registration with a small number of network parameters. In addition, FAIM also incorporates a regularization term that directly penalizes folded voxels during training. According to Ref. [16], in this study, the weight coefficient of this regularization term was set to $1\times {10}^{-5}$ to ensure the balance between the registration accuracy and the smoothness of the deformation field. In addition to the above methods, two baseline methods for deep learning have been chosen for this paper. DIF-VM is a probabilistic differential homography-based alignment method that uses CNNs to estimate the displacement vector field and diffusion regularization to ensure the smoothness of the deformation field. TransMorph, as a novel Transformer-based unsupervised alignment framework, effectively captures long-range spatial relations through a self-attention mechanism. In this study, the optimal parameters from Ref. [21] are used for retraining, and the Adam optimizer is used during training with an initial learning rate of $1\times {10}^{-5}$, a batch size of 1, and a total number of iterations of 10,000. The loss function consists of similarity loss (negative mutual information) and regularization loss (bending energy) to ensure the smoothness and biomechanical soundness of the deformation field.

2.7. Implementation

The MCANet proposed in this paper was implemented using the deep-learning framework PyTorch version 1.12.0. All experiments were performed on a single NVIDIA Tesla P100 GPU from NVIDIA Corporation, Santa Clara, CA, USA and Intel Xeon Silver 4210 CPU from Intel Corporation, Santa Clara, CA, USA. All models were trained for 500 epochs (63,000 iterations) using the Adam gradient optimizer to minimize the training loss and update the network parameters, with a batch size of 1. In training, the initial learning rate was set to $1\times {10}^{-4}$, and this decreased automatically with the increase of training times. The weight coefficient $\gamma$ was set to 1 based on experimental experience.

3. Results

3.1. Comparative Experiment

To evaluate the registration performance of MCANet and other advanced registration methods on both the Mindboggle101 and Neurite OASIS datasets, we conducted comprehensive comparative experiments. The results, listed in

Table 1. Registration results of Affine, SyN, LDDMM, DIF-VM, VoxelMorph-1, VoxelMorph-2, FAIM, Transmorph, and MCANet.

Method	Dice Score	SDlogJ	${\mathit{J}}_{\mathit{o}}\left(\mathit{u}\right)\le 0$	Sensitivity	Time (s)
Mindboggle101:
Affine	$0.385\pm 0.021$	–	–	–	–
SyN	$0.508\pm 0.055$	$0.581\pm 0.075$	$1297\pm 982$	$44.517$	$781.543$
LDDMM	$0.492\pm 0.048$	$0.612\pm 0.081$	$1156\pm 652$	$43.371$	$86.837$
DIF-VM	$0.538\pm 0.105$	$0.531\pm 0.121$	$13,523\pm 2351$	$43.267$	$0.517$
VoxelMorph-1	$0.581\pm 0.063$	$0.502\pm 0.037$	$51,415\pm 8463$	$46.812$	$0.092$
VoxelMorph-2	$0.603\pm 0.020$	$0.498\pm 0.058$	$48,906\pm 7183$	$45.785$	$0.264$
FAIM	$0.619\pm 0.016$	$0.564\pm 0.052$	$11,975\pm 3085$	$43.123$	$0.261$
Transmorph	$0.635\pm 0.046$	$0.477\pm 0.041$	$11,703\pm 1652$	$46.227$	$0.423$
MCANet	$0.637\pm 0.013$	$0.445\pm 0.036$	$11,693\pm 2418$	$47.551$	$0.733$
Neurite OASIS:
Affine	$0.532\pm 0.151$	–	–	–	–
SyN	$0.663\pm 0.071$	$0.575\pm 0.155$	$1786\pm 874$	$49.486$	1058
LDDMM	$0.584\pm 0.068$	$0.533\pm 0.07$	$1569\pm 528$	$45.283$	$123.765$
DIF-VM	$0.636\pm 0.121$	$0.541\pm 0.126$	$14,875\pm 1985$	$44.916$	$0.863$
VoxelMorph-1	$0.718\pm 0.060$	$0.421\pm 0.054$	$52,035\pm 8762$	$51.854$	$0.568$
VoxelMorph-2	$0.732\pm 0.031$	$0.417\pm 0.048$	$47,452\pm 6827$	$50.349$	$0.576$
FAIM	$0.736\pm 0.018$	$0.524\pm 0.032$	$11,825\pm 2843$	$46.786$	$0.412$
Transmorph	$0.764\pm 0.034$	$0.462\pm 0.036$	$11,681\pm 2631$	$49.281$	$0.732$
MCANet	$0.762\pm 0.023$	$0.405\pm 0.076$	$11,951\pm 1493$	$54.641$	$0.917$

, include average Dice scores, the degree of folding of the deformation field (measured by the number and percentage of folded voxels), and other registration performance indicators. The data clearly demonstrate that MCANet achieves the highest registration accuracy across both datasets. On the Mindboggle101 dataset, MCANet significantly outperforms traditional methods, improving the Dice score by 0.252 compared to Affine (p < 0.001), 0.129 compared to SyN (p < 0.01), and 0.145 compared to LDDMM (p < 0.001). In terms of registration speed, MCANet is markedly faster than SyN and LDDMM (p < 0.001 for both comparisons). On the Neurite OASIS dataset, MCANet also shows substantial improvements, with a Dice score increase of 0.250 over Affine, 0.119 over SyN, and 0.198 over LDDMM, all with p-values less than 0.001. Compared to deep-learning-based methods, MCANet achieves a Dice score improvement of 0.018 over FAIM (p < 0.05), 0.056 over VoxelMorph-1 (p < 0.001), and 0.034 over VoxelMorph-2 (p < 0.01) on Mindboggle101. On Neurite OASIS, MCANet attains a Dice score of 0.782 ± 0.023, slightly lower than Transmorph (0.784 ± 0.054) but significantly better than other deep-learning methods.

Figure 4 clearly shows the remarkable effect of MCAnet. In the box graph of Dice score in the upper left corner, MCAnet outperforms or is equivalent to traditional algorithms on both datasets, which indicates that MCAnet has advantages in maintaining high registration accuracy. The centerline map of SDlogJ box shows that the deformation field of MCANet is smoother, which is a significant advantage compared with the traditional algorithm, because, although the traditional algorithm performs well in the smoothness of the deformation field, it needs to carefully adjust the parameters, and with the increase of parameters the folding rate of the deformation field increases linearly, which may lead to complex and difficult to explain deformation results. In the box graph at the lower left corner and the lower right corner, MCAnet shows excellent performance, and its deformation field folding rate is low, which further proves the ability of MCAnet in generating natural deformation results. MCANet can provide accurate registration results while maintaining high sensitivity. Although deep-learning methods such as MCANet perform well in accuracy and smoothness, they usually require a significant amount of training data and computing resources and are sensitive to changes in data distribution. However, MCANet has found an optimal balance point in these challenges, which can efficiently provide high-precision and natural registration results. The boxplot in Figure 4 intuitively shows the advantages of MCANet in different indicators, especially in Dice score and SDlogJ, proving its effectiveness and reliability in image registration tasks.

While traditional algorithms exhibit advantages in deformation field smoothness, this performance is contingent upon meticulous parameter tuning. Our experiments reveal that, as the gradient step in SyN increases, registration accuracy improves, but so does the deformation field folding rate, increasing linearly. This indicates that traditional algorithms may generate overly complex and uninterpretable deformation results with higher parameter settings. In contrast, MCANet not only surpasses traditional algorithms in registration speed but also in accuracy. Among the deep-learning methods, although MCANet often achieves higher or comparable Dice scores, it is not without drawbacks. Deep-learning algorithms typically require substantial training data and computational resources, and their performance can be sensitive to variations in data distribution. In comparison with Transmorph and DIF-VM, MCANet usually obtains higher or comparable Dice scores as well as lower SDlogJ, which indicates that MCANet usually has higher accuracy and smoother deformation fields. Deep-learning algorithms typically require large amounts of training data and computational resources, and their performance is very sensitive to changes in data distribution. Thus, the complexity of these models sometimes leads to longer training times and higher hardware requirements. Despite these challenges, MCANet achieves an optimal balance, efficiently delivering highly accurate and natural registration results. As shown in Figure 5, MCANet generates the most accurate and visually appealing alignment results on cross-sectional slices of the brain, effectively reconciling the trade-off between accuracy and computational efficiency.

In summary, MCANet demonstrates exceptional registration performance across both the Mindboggle101 and Neurite OASIS datasets. Compared with traditional algorithms and other deep-learning-based methods, MCANet has obvious advantages in terms of registration accuracy and time efficiency and can generate more accurate and natural deformation results.

3.2. Ablation Result

In order to evaluate the impact of each network component on registration performance, we conducted an effectiveness experiment on the structures of the registration subnetwork DSNet and the cascaded structure of the dual subnetwork on the Mindboggle101 dataset. This experiment tested the registration capability of DSNet and performed an ablation study on it.

Table 2. Registration results of MCANet ablation studies.

Model	Dice Score	SDlogJ	$|{\mathit{J}}_{\mathit{\phi }}\left(\mathit{u}\right)|\le 0$	%$|{\mathit{J}}_{\mathit{\phi }}\left(\mathit{u}\right)|\le 0$	Time (s)
MCANet	$0.649\pm 0.016$	$0.458\pm 0.036$	$36,706\pm 4812$	$0.689\pm 0.090$	$0.733$
DSNet	$0.612\pm 0.022$	$0.481\pm 0.024$	$30,244\pm 4362$	$0.568\pm 0.082$	$0.367$
DSNet(w/o DC)	$0.607\pm 0.020$	$0.487\pm 0.036$	$47,484\pm 6239$	$0.892\pm 0.117$	$0.343$
DSNet(w/o AG)	$0.611\pm 0.019$	$0.476\pm 0.019$	$48,069\pm 5959$	$0.903\pm 0.112$	$0.354$
DSNet(w/o DC+AG)	$0.606\pm 0.018$	$0.492\pm 0.061$	$48,505\pm 6154$	$0.911\pm 0.116$	$0.330$

lists three variants of DSNet, where “DC” represents dilated convolution combinations with different dilation rates and “AG” represents attention gate components. In “DSNet (w/o DC)”, the dilated convolution combinations were removed and replaced with ordinary 3D convolutions, which can reflect the impact of a large receptive field on registration performance. In “DSNet (w/o AG)”, the four attention gate components of different scales were replaced by skip connections. The “DSNet (w/o DC + AG)” variant removed both the dilated convolution combinations and the attention mechanism, retaining only the basic network structure, to verify the compatibility of dilated convolution combinations and attention gate components. The experimental data in Table 2 shows that the designs added to the encoder–decoder in this paper are fully effective.

3.3. Regularization Analysis

This paper proposed a double regularization constraint on the model during training, hoping to avoid the excessive deformation and voxel folding problems that may be caused by two-stage registration. In this section, we analyzed the impact of the additional bending energy loss on the registration performance.

Table 3. The effect of regularization coefficient $\beta$ on registration performance.

$\mathit{\beta }$	Dice Score	SDlogJ	$|{\mathit{J}}_{\mathit{\phi }}\left(\mathit{u}\right)|\le 0$	%$|{\mathit{J}}_{\mathit{\phi }}\left(\mathit{u}\right)|\le 0$
0	$0.649\pm 0.016$	$0.462\pm 0.025$	$36,706\pm 4812$	$0.689\pm 0.090$
0.2	$0.645\pm 0.017$	$0.451\pm 0.084$	$30,019\pm 4473$	$0.564\pm 0.084$
0.4	$0.647\pm 0.015$	$0.446\pm 0.033$	$24,922\pm 4420$	$0.468\pm 0.083$
0.6	$0.643\pm 0.015$	$0.430\pm 0.052$	$20,965\pm 3117$	$0.394\pm 0.059$
0.8	$0.641\pm 0.016$	$0.436\pm 0.041$	$16,878\pm 2758$	$0.317\pm 0.052$
1	$0.627\pm 0.018$	$0.429\pm 0.026$	$14,274\pm 2776$	$0.268\pm 0.052$
1.2	$0.639\pm 0.013$	$0.416\pm 0.065$	$13,560\pm 2412$	$0.255\pm 0.045$
1.4	$0.637\pm 0.013$	$0.394\pm 0.021$	$11,693\pm 2418$	$0.219\pm 0.045$
1.6	$0.630\pm 0.016$	$0.418\pm 0.042$	$10,585\pm 2227$	$0.199\pm 0.042$
2	$0.618\pm 0.016$	$0.421\pm 0.023$	$7672\pm 1557$	$0.144\pm 0.029$

presents the registration accuracy and the percentage of folded voxels of MCANet when the bending energy weight coefficient $\beta$ took different values, and the data are presented in the form of a line chart in Figure 6.

To intuitively show the constraint of the bending energy regularization term on the deformation field, Figure 7 visualizes the deformation field under different values of $\beta$. By observing the visualization results of the deformation field, it can be seen that, with the increase of $\beta$, the folded gridlines (white areas) in the gridded deformation field were significantly reduced, and the distortion of the gridlines became more natural and smoother. The median of Dice score, SDlogJ, and folded voxel percentage of MCANet under different $\beta$ values can be seen in Figure 6. It can be seen that the Dice score shows a slight decrease with increasing $\beta$, but this stabilizes at $\beta$ = 1.4, indicating a maintained registration accuracy at higher $\beta$ values. SDlogJ decreases significantly with the increase of $\beta$, reflecting the increase of smoothness and the decrease of deformation in the deformation field. However, when $\beta$ increases to 1.4 or higher, SDlog tends to decrease. The number and percentage of folded voxels also decrease markedly with higher $\beta$, highlighting reduced folding and enhanced deformation quality. Overall, $\beta$ = 1.4 emerges as an optimal choice, balancing high registration accuracy with smooth and authentic deformation.

3.4. Remarks of the Experimental Results

Remark 1. 

In the comparative experiment part, the Mindboggle101 and Neurite OASIS datasets are used to verify the generalization ability of the model. Compared with the traditional registration methods Affine, SyN, and the existing registration algorithms FAIM and VoxelMorph based on deep learning, MCANet’s Dice score has been greatly improved, and compared with the latest algorithm Transmorph, it also has some improvement in smoothness and Dice score. Compared with traditional algorithms, MCAN shows absolute advantages, because it has faster registration speed, and MCANet has obvious advantages in time efficiency. Compared with the registration method of deep learning, MCANet has better smoothness and better Dice score, so the algorithm in this paper is feasible.

Remark 2. 

In the ablation experiment part, we proved the impact of each module on the network; adding an expanded convolutional group can improve the registration accuracy by increasing the receptive field, adding an attention gate component can enhance the response of the model to the key region and improve the registration accuracy of the network, and the simultaneous use of the two can make the network expand the receptive field without adding too much computational cost and network parameters, obtain multi-scale features, improve the voxel folding problem, and improve the over-deformation problem. The network is able to better understand the global structure and local details of the image, improving the ability to accurately detect deformed areas.

Remark 3. 

Regularization analysis part: We perform double regularization constraints on the model during the training process and analyze the influence of the bending energy weight coefficient β on the registration accuracy and smoothness. When the bending energy weight coefficient β increases, the degree of voxel folding decreases, and the Dice score also decreases to a certain extent. Through a large number of experiments, we choose the weight coefficient β taking 1.4, which can not only ensure the smoothness and authenticity of the deformation but also maintain a high registration accuracy.

4. Discussion

3D brain MRI alignment is important in observing structural brain lesions and performing brain health treatments. Traditional deformation alignment algorithms take a significant amount of time to align image pairs and require several manual adjustments of parameters to achieve optimal results. In addition, the optimal alignment parameters are different from one image to another, so the traditional methods are highly dependent on manual operation, which is both troublesome and time-consuming. With the improvement of hardware performance and the increase of network model size, the traditional methods gradually become unsatisfactory in terms of alignment time and accuracy. In contrast, the model proposed in this paper can learn the best parameters for predicting deformations through continuous optimization and can be directly applied to unseen images, completing the alignment at near real-time speed without human involvement. The network can automatically complete the deformation prediction based on the features of the input image, which is efficient and accurate. Although some traditional algorithms still have an advantage in deformation smoothing, FAIM and MCANet have made great strides in this area as well. When the weights of the regularization terms are large enough, they can achieve very smooth deformation without unnecessary sacrifices. While VoxelMorph has been a benchmark for unsupervised alignment due to its alignment accuracy, speed, and robustness, MCANet introduces several key architectural improvements. Specifically, MCANet incorporates attention gates to focus on critical anatomical regions and employs dilated convolutions to expand the receptive field without increasing computational complexity. These enhancements significantly improve deformation smoothness, reduce voxel folding, and enable more precise alignment of complex anatomical structures. Additionally, MCANet’s multi-scale context aggregation mechanism further refines the deformation field, making it particularly effective in scenarios requiring high-precision registration.When the model has a large receptive field and can focus on key areas of deformation, its deformation of deformed images will become more natural and accurate. As can be seen from the data of the ablation experiments in Table 2, the addition of attention gates and regularization terms significantly reduces voxel folding, a common issue in learning-based methods. When combined with dilated convolutions, the proportion of folded voxels decreases by 0.3%, and the smoothness of the deformation field improves by 38%. Bending energy regularization further enhances these improvements by reducing voxel folding, though with a slight decrease in alignment accuracy (as shown in Table 3). This trade-off is justified as it leads to more biologically plausible deformations, which are critical in medical imaging.

FAIM, a lightweight unsupervised network model that directly incorporates the value of a non-orthonormal comparable determinant as part of the loss function, has also made some progress. Although MCANet is larger than FAIM in terms of network architecture and number of parameters, it is significantly better than the latter in terms of alignment accuracy, which remains one of the most important metrics for evaluating models and algorithms. Compared to Transmorph, another advanced deep-learning-based registration method, MCANet demonstrates superior performance in deformation smoothness and voxel folding reduction. While Transmorph achieves competitive registration accuracy, MCANet excels in generating more natural and interpretable deformation fields, which is crucial for medical applications. MCANet’s ability to balance alignment precision with computational efficiency makes it a standout choice for image registration tasks, particularly in scenarios where high-precision and biologically plausible deformations are required. In summary, the model proposed in this paper has made progress in terms of alignment accuracy, speed, and robustness, and the advantages of the model are verified by ablation experiments and comparative analysis.

5. Conclusions

In this paper, we propose a multi-constraint cascade attention network (MCANet) based on unsupervised learning for deformable brain MRI registration. In the subnet design, we combine the expansion convolution combination and the attention mechanism strategy. These methods have played an active role in improving many factors that affect the registration effect. We tested MCANet using the Mindboggle101 and Neurite OASIS datasets, and calculated Dice scores and SDlogJ. The number of voxels folded and registration time were used to quantitatively evaluate the registration effect of 3D brain MRI. The experimental results show that, compared with several existing advanced registration methods (including traditional algorithms and learning based methods), MCANet achieves the highest level of registration accuracy and can smoothly deform moving images. This indicates that MCANet performs well in aligning two brain MR images, and this research has made substantial progress in this field. However, MCANet still has some limitations and needs further improvement in future research.

• Although the network structure and regularization constraint mechanism of MCANet can theoretically solve the voxel folding problem and ensure smooth deformation, they still need to be further optimized in practical applications. In the future, we plan to further improve the smoothness and biological rationality of deformation by introducing more complex regularization strategies (such as deformation models based on physical constraints).
• MCANet is currently mainly aimed at the registration task of brain MRI, but its applicability has not been verified in the 3D image registration of other organs. In the future, we plan to expand MCANet to other medical imaging fields, such as abdomen, chest, and other organ registration tasks, to verify its versatility and cross domain applicability.
• The training process of MCANet relies on unsupervised learning. Although it avoids the need to annotate data, its performance may be affected by the quality and distribution of training data. In the future, we plan to explore semi-supervised learning or self-supervised learning methods to further improve the performance and robustness of the model.

In conclusion, MCANet has shown good performance in brain MRI registration tasks, but it still needs to be improved in data set size, network structure optimization, cross domain applicability, and experimental comparative analysis. We believe that through these improvements, MCANet will be able to play a greater role in the field of medical image registration and provide a valuable reference for related research.