Calculation of Time-Varying Mesh Stiffness of Internal Mesh Transmission and Analysis of Influencing Factors
Abstract
1. Introduction
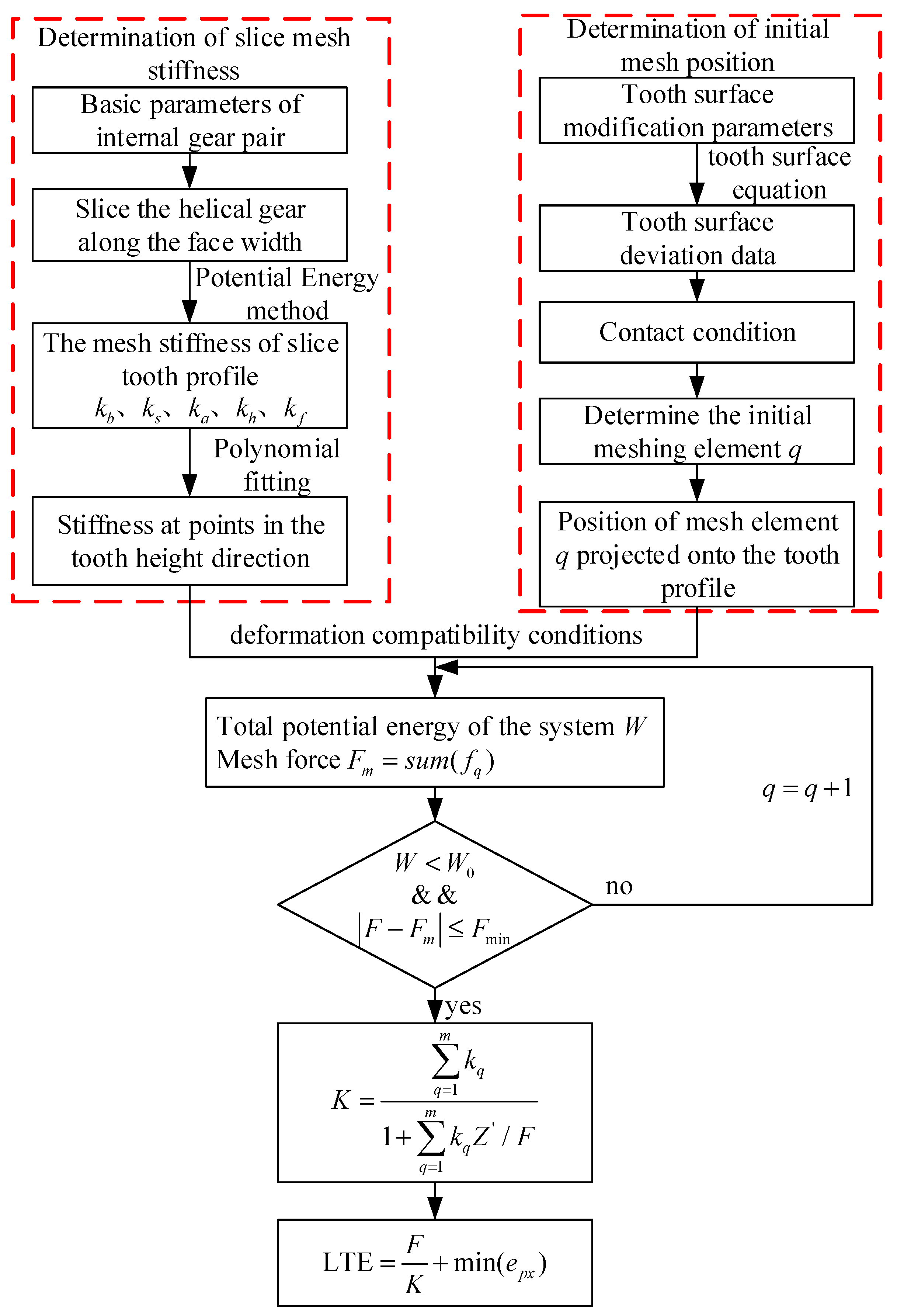
2. Analytical Model of Mesh Stiffness of the Internal Gear Pair
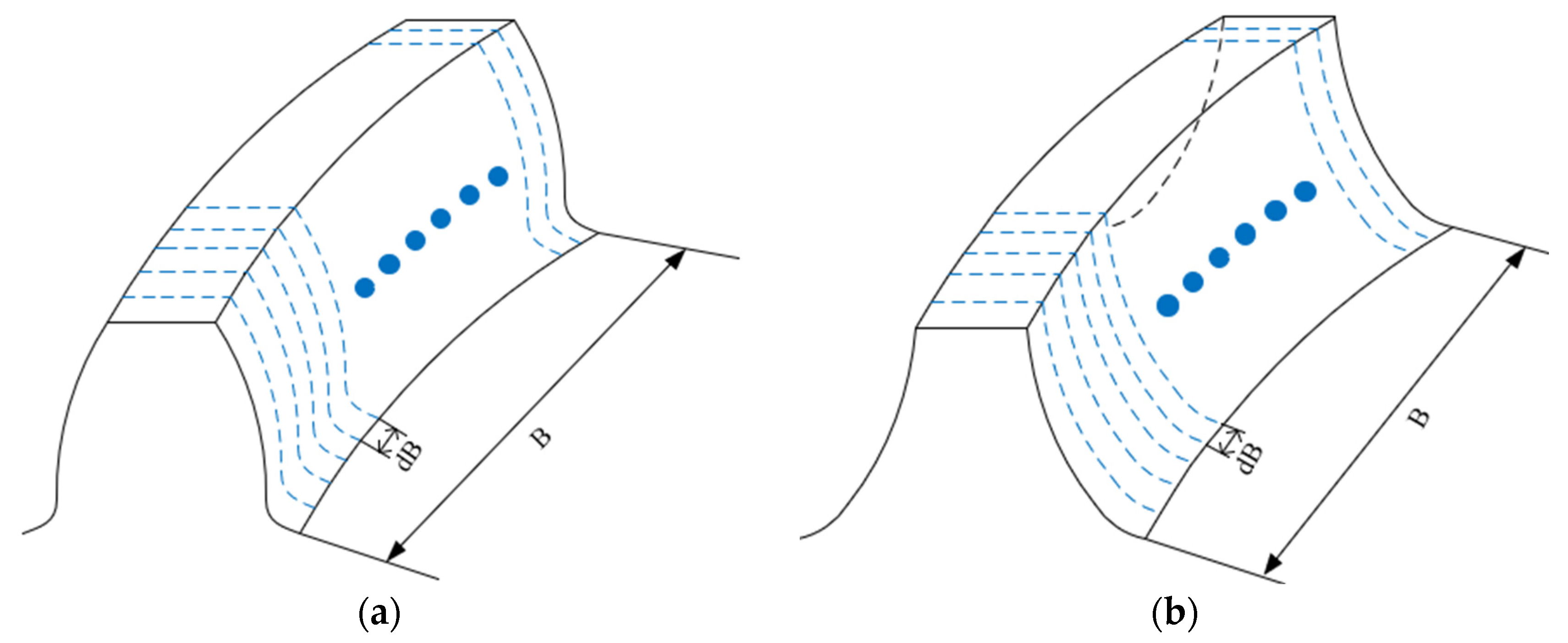
2.1. Establishment of Slice Model for the Internal Gear Pair
2.2. Calculation of Slice Mesh Stiffness
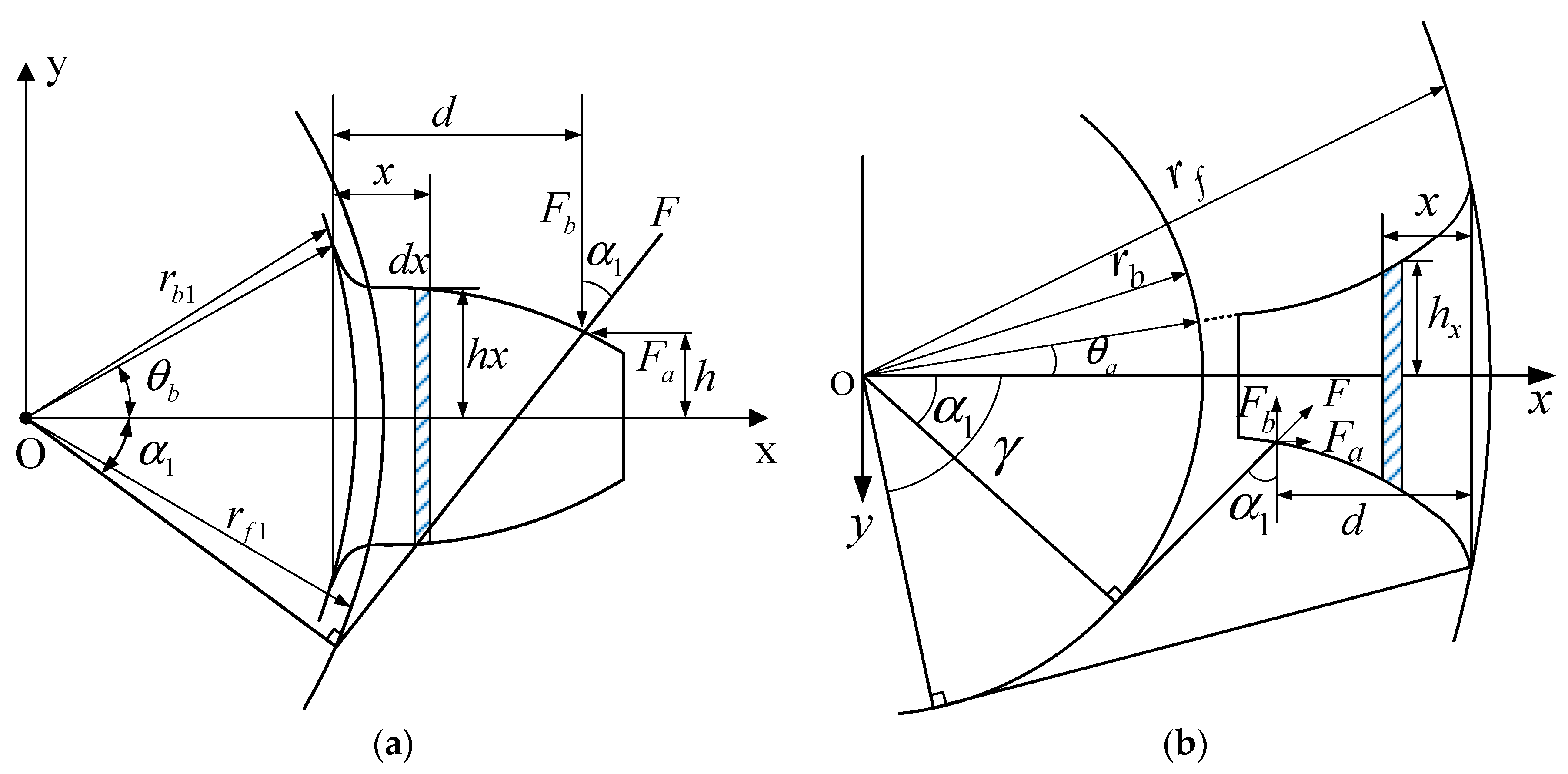
2.2.1. Tooth Stiffness
2.2.2. Contact Stiffness
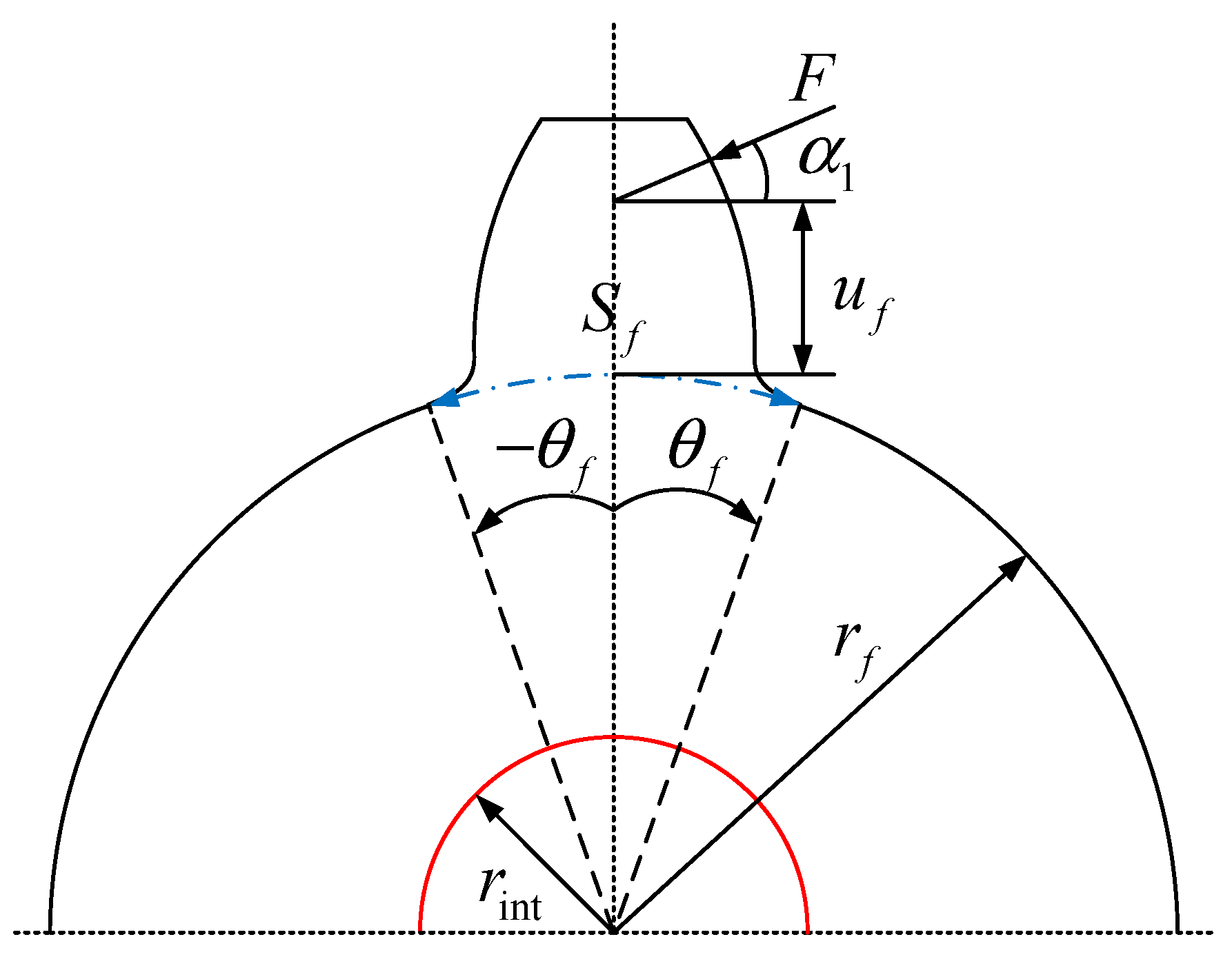
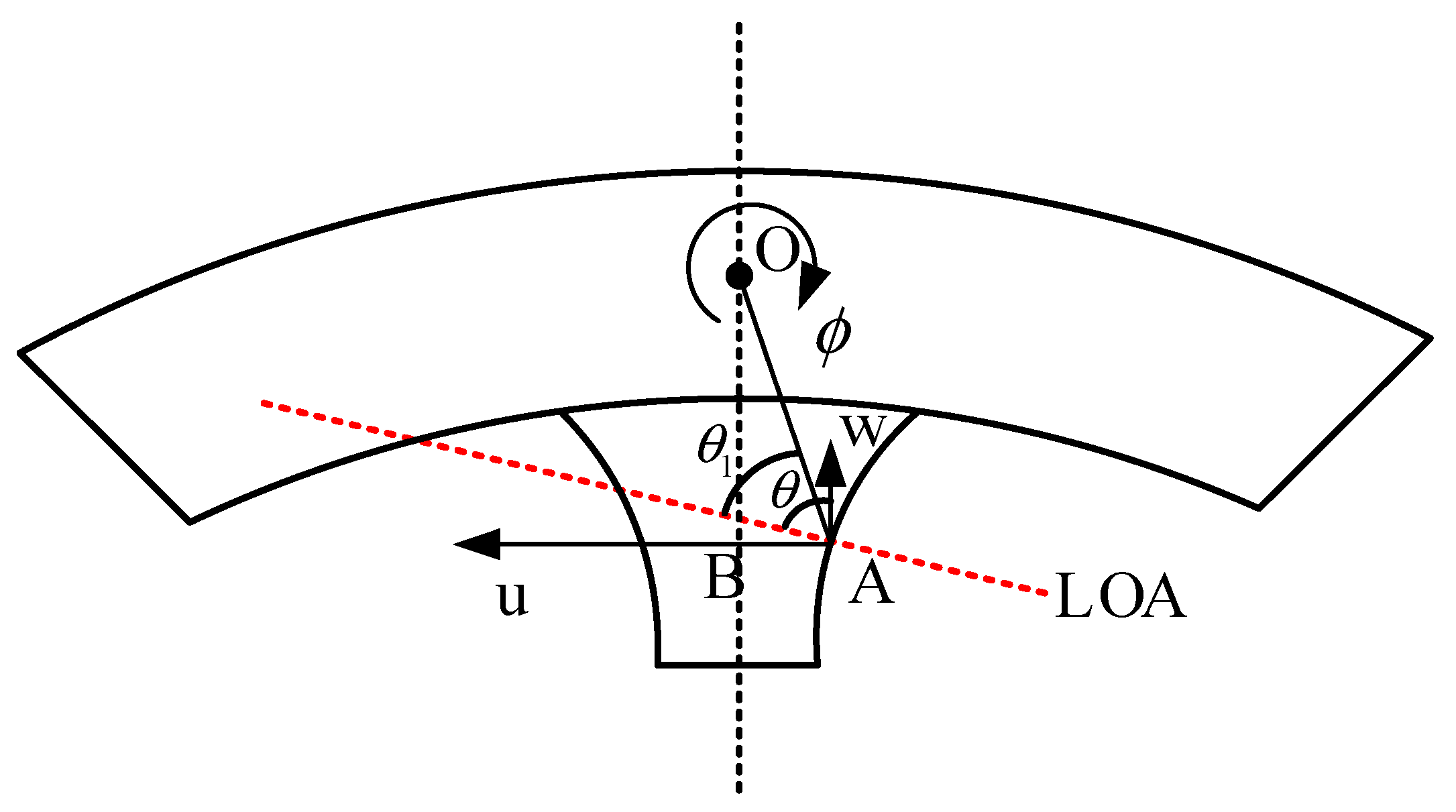
2.2.3. Gear Foundation Stiffness
- (1)
- Foundation stiffness of the external gear
- (2)
- Foundation stiffness of the internal gear ring
3. TVMS Based on Load Tooth Contact Analysis
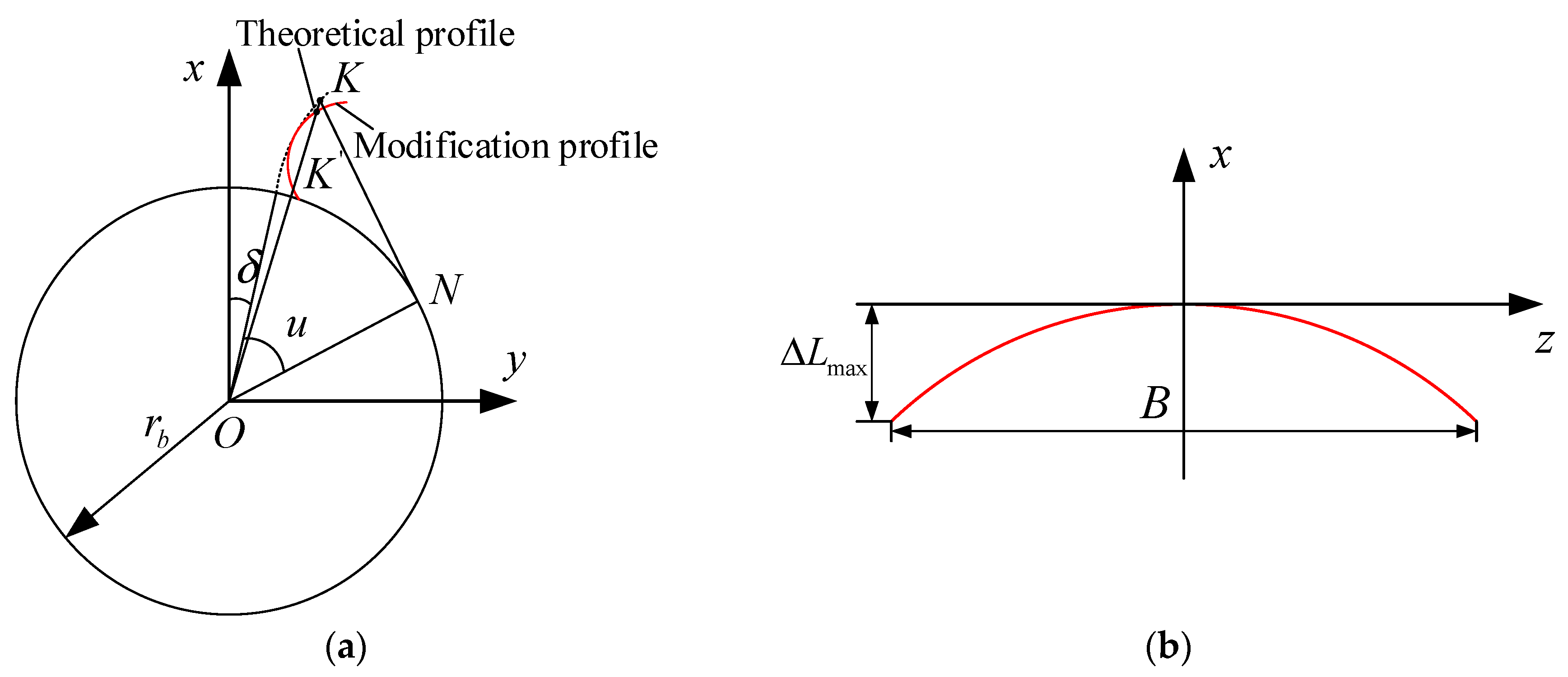
3.1. Calculation of Topological Modification Tooth Surface Deviation
3.2. Calculation of Time-Varying Mesh Stiffness
4. Numerical Simulation Results and Validation
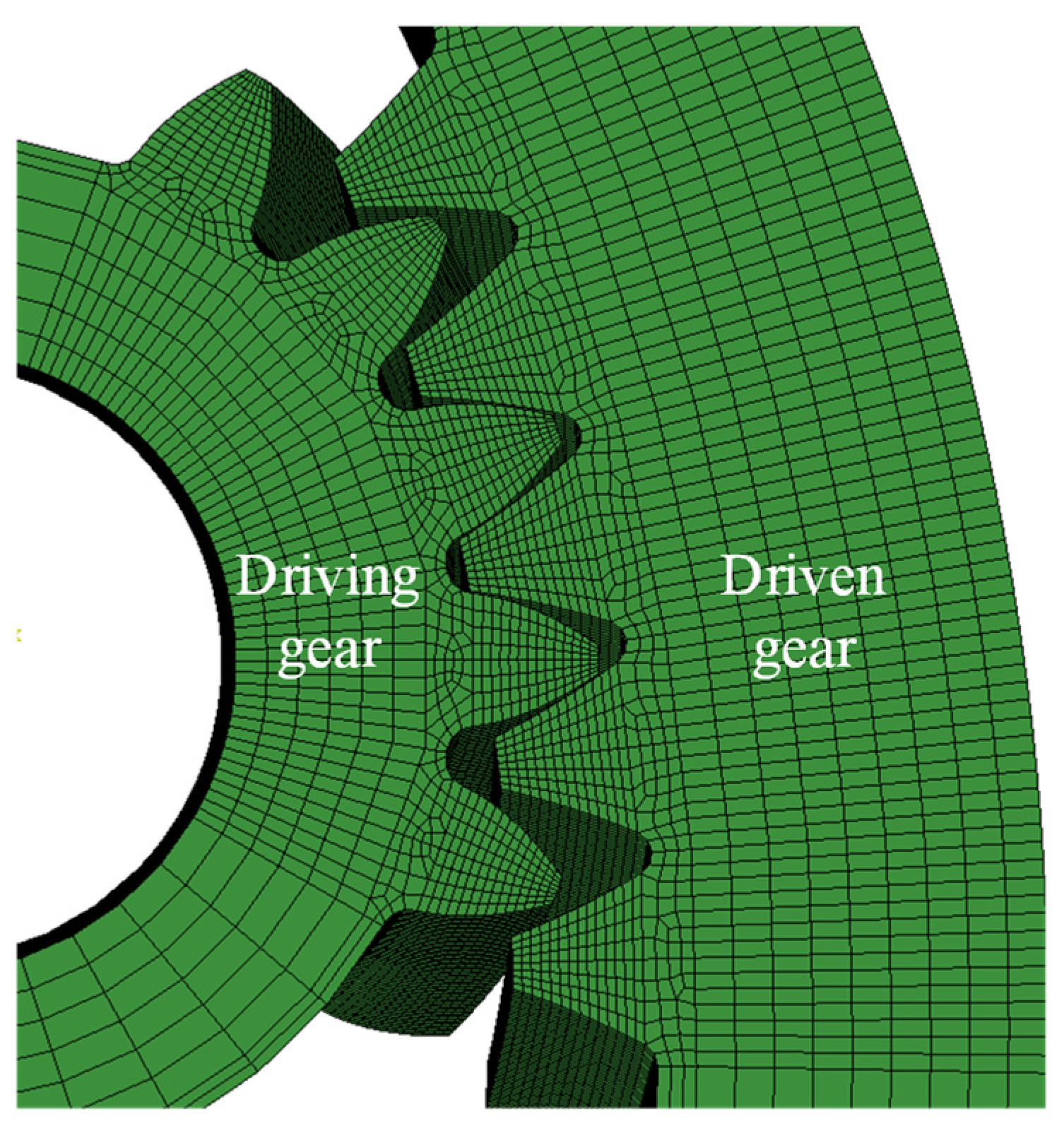
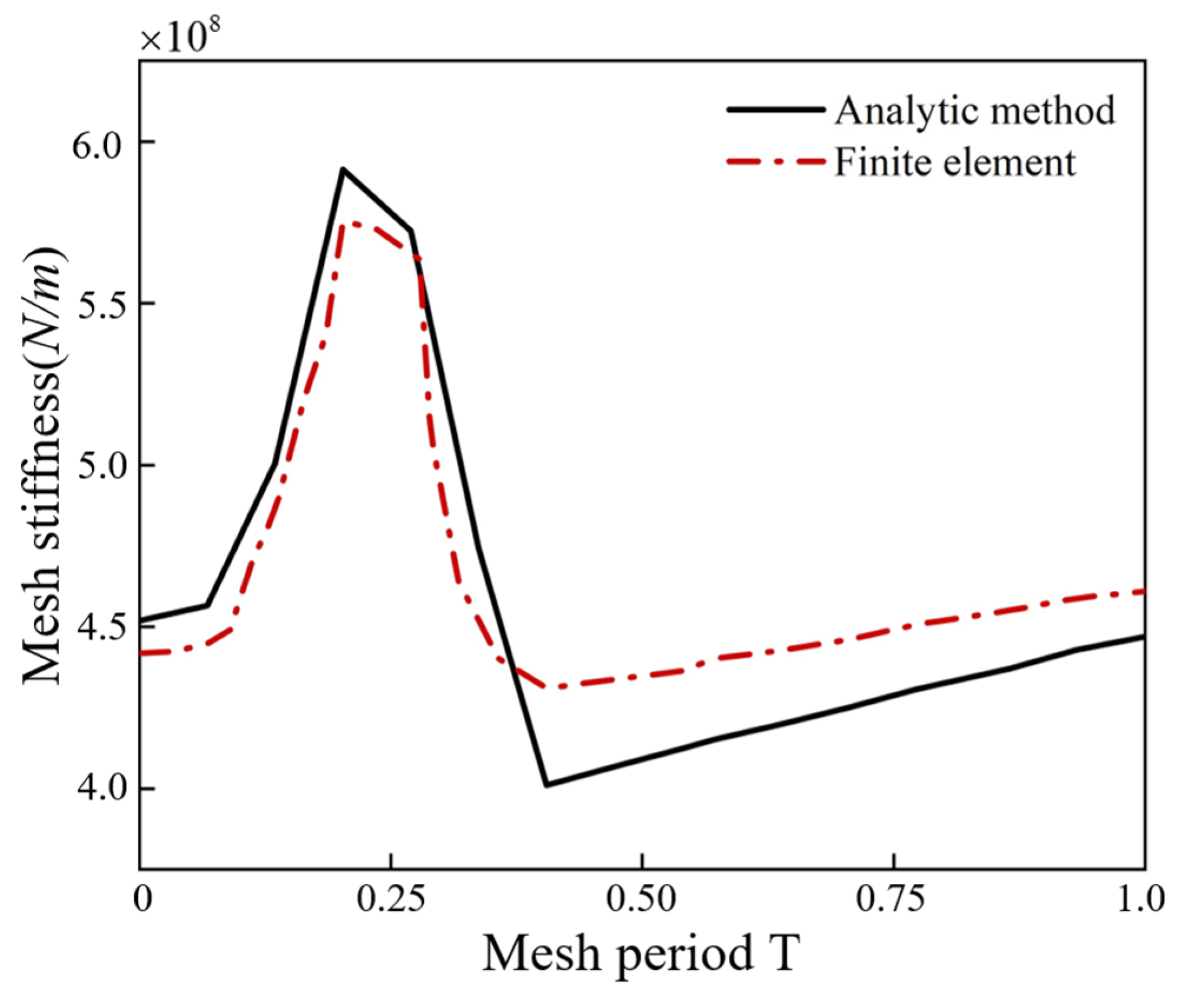
4.1. Validation of Finite Element Results
4.2. The Influence of Different Factors on TVMS and LTE
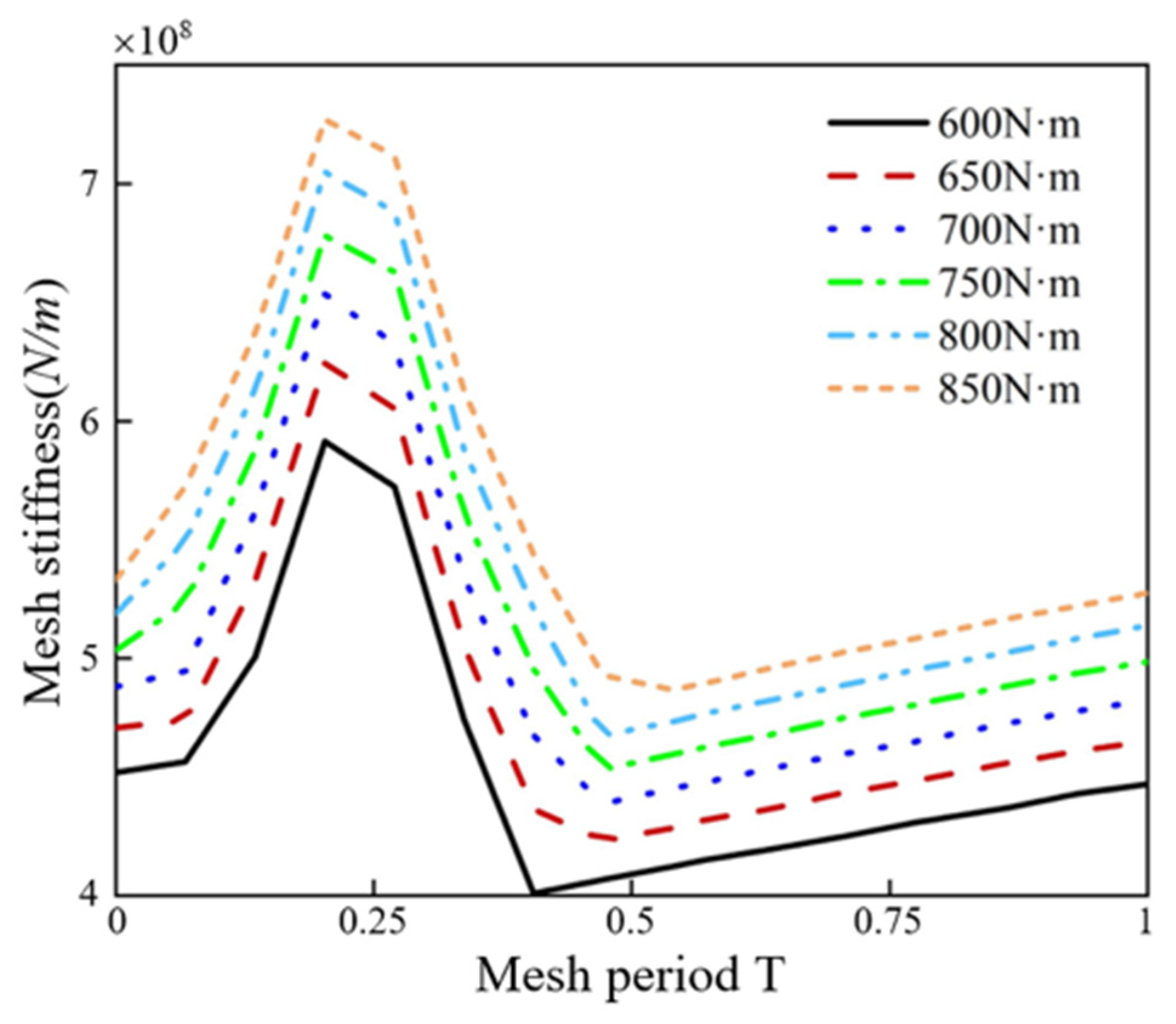
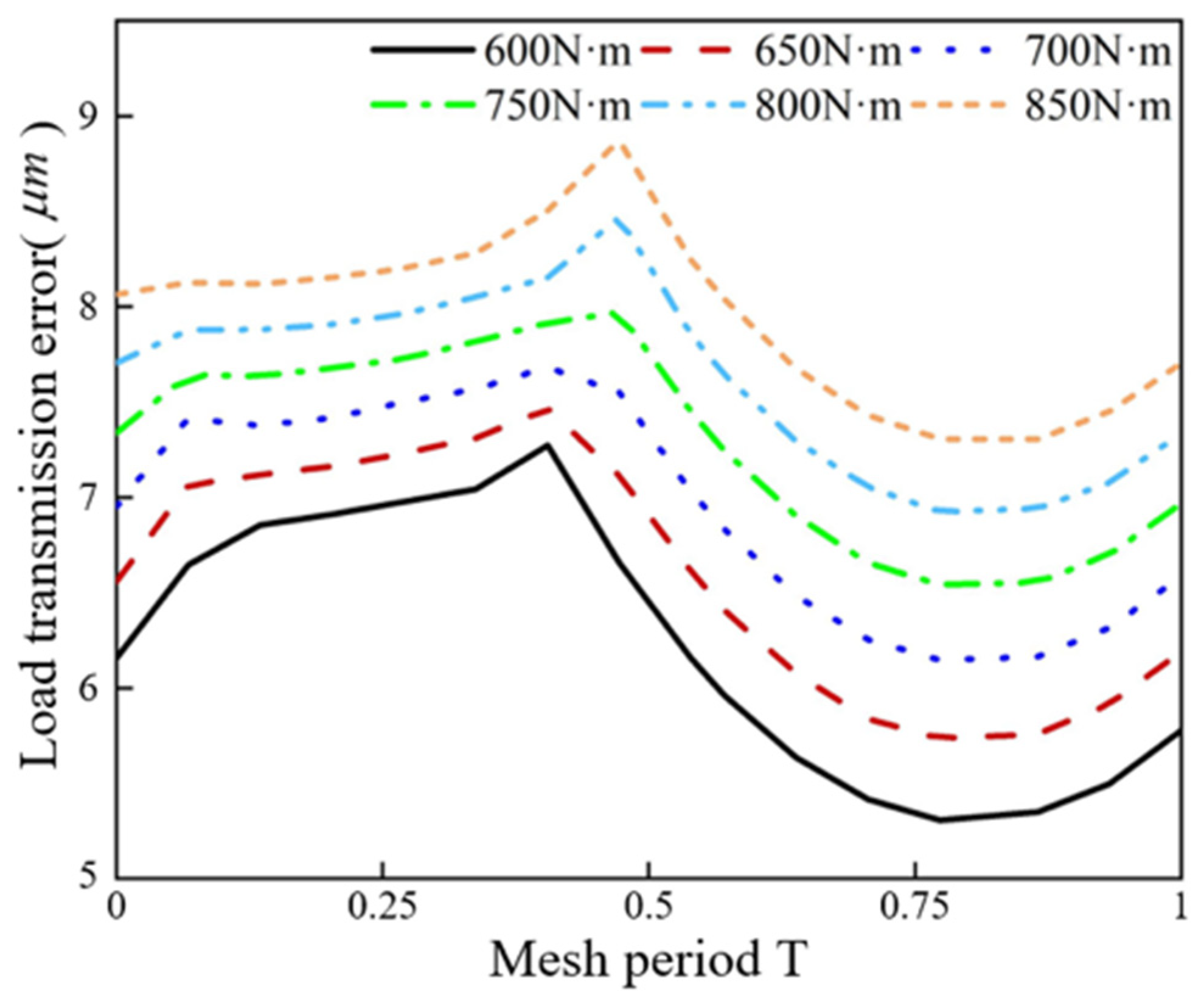
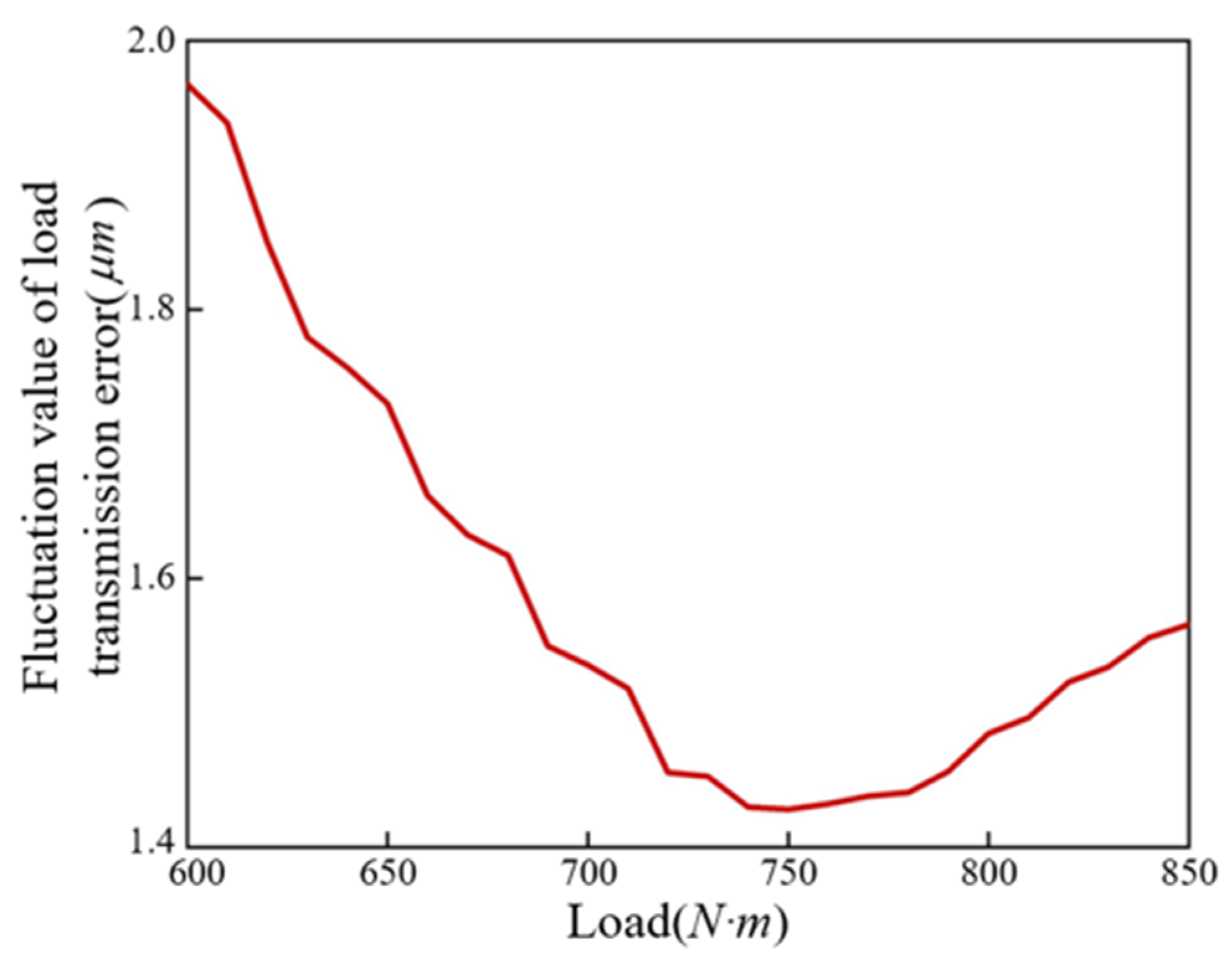
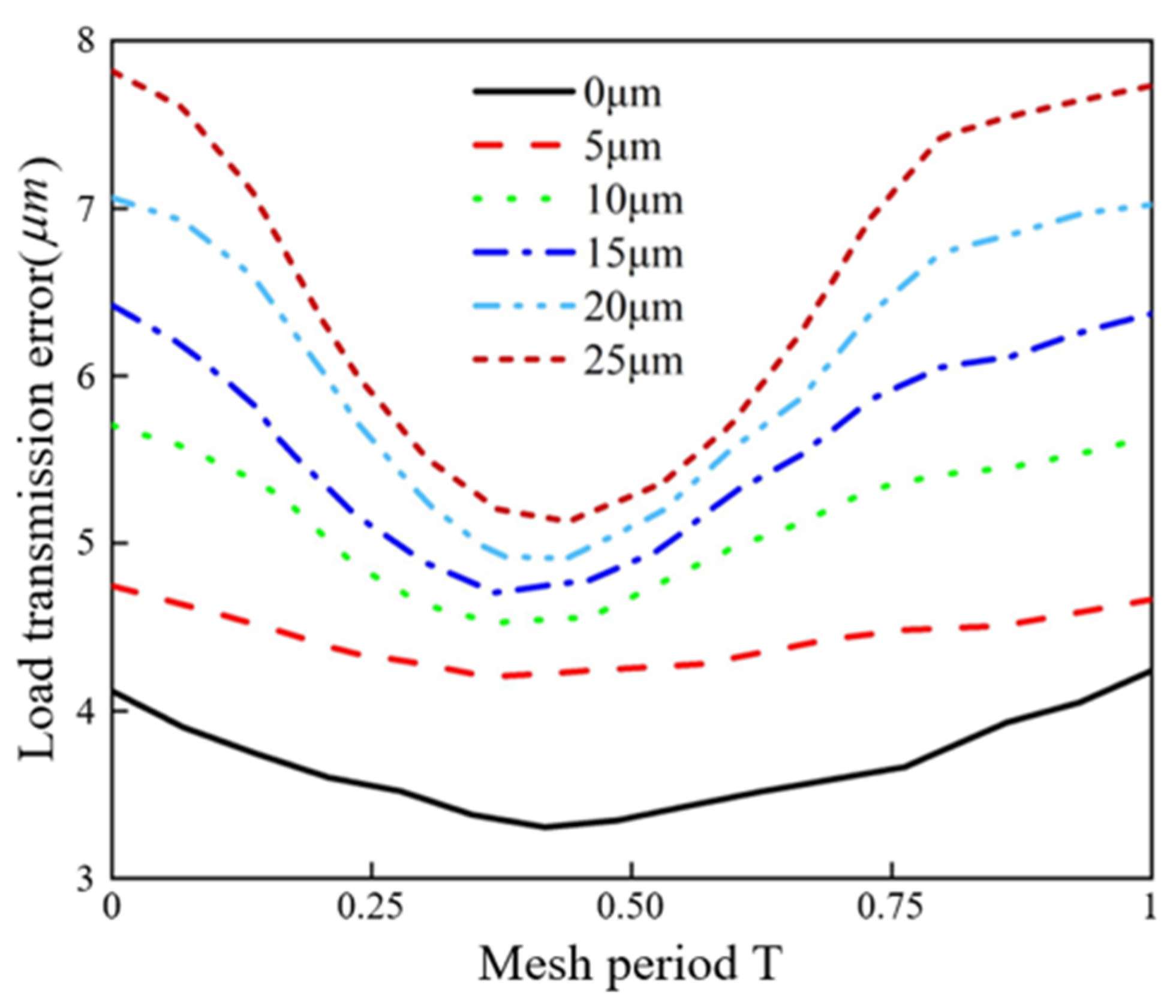
4.2.1. The Influence of Load on TVMS and LTE
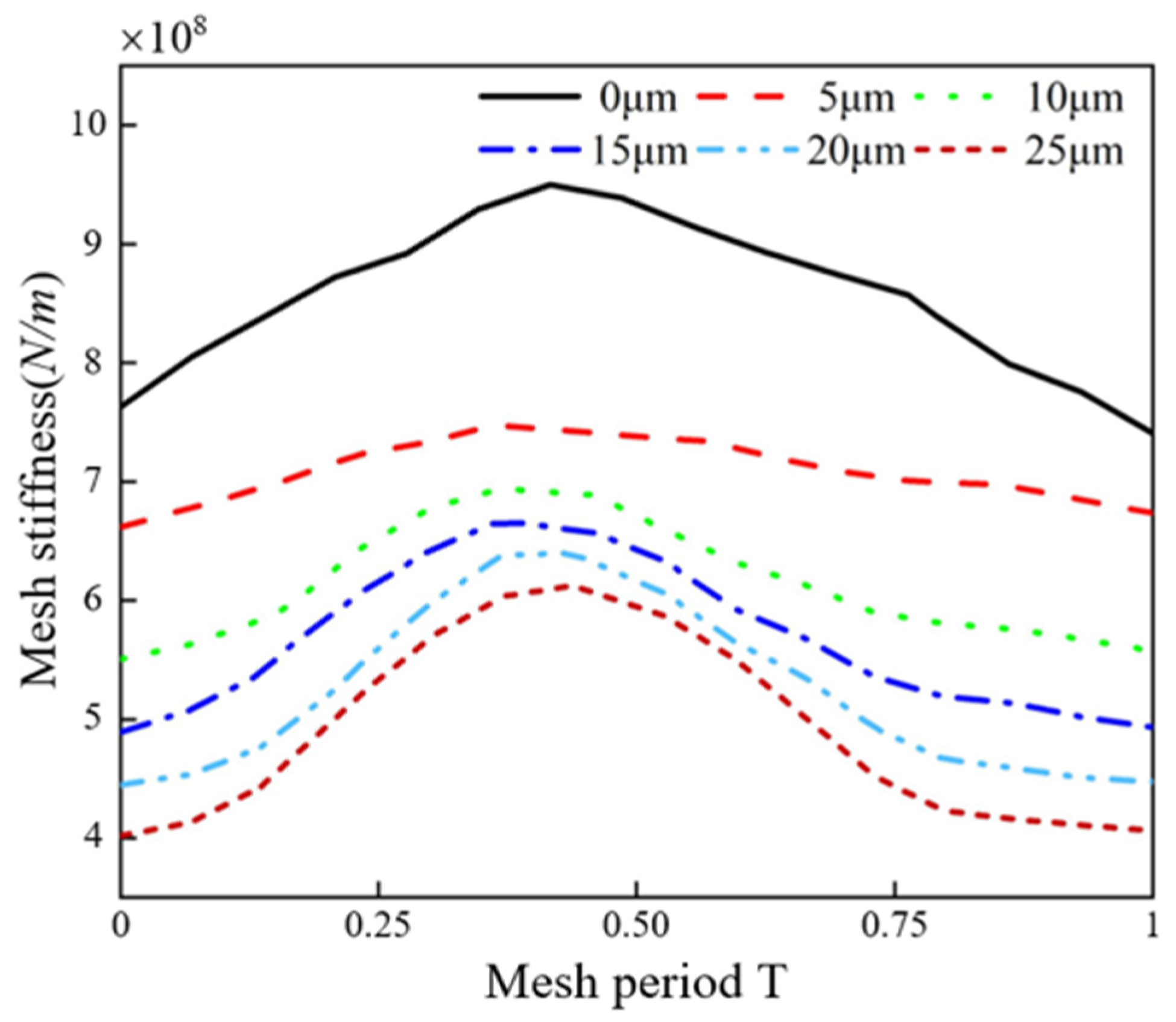
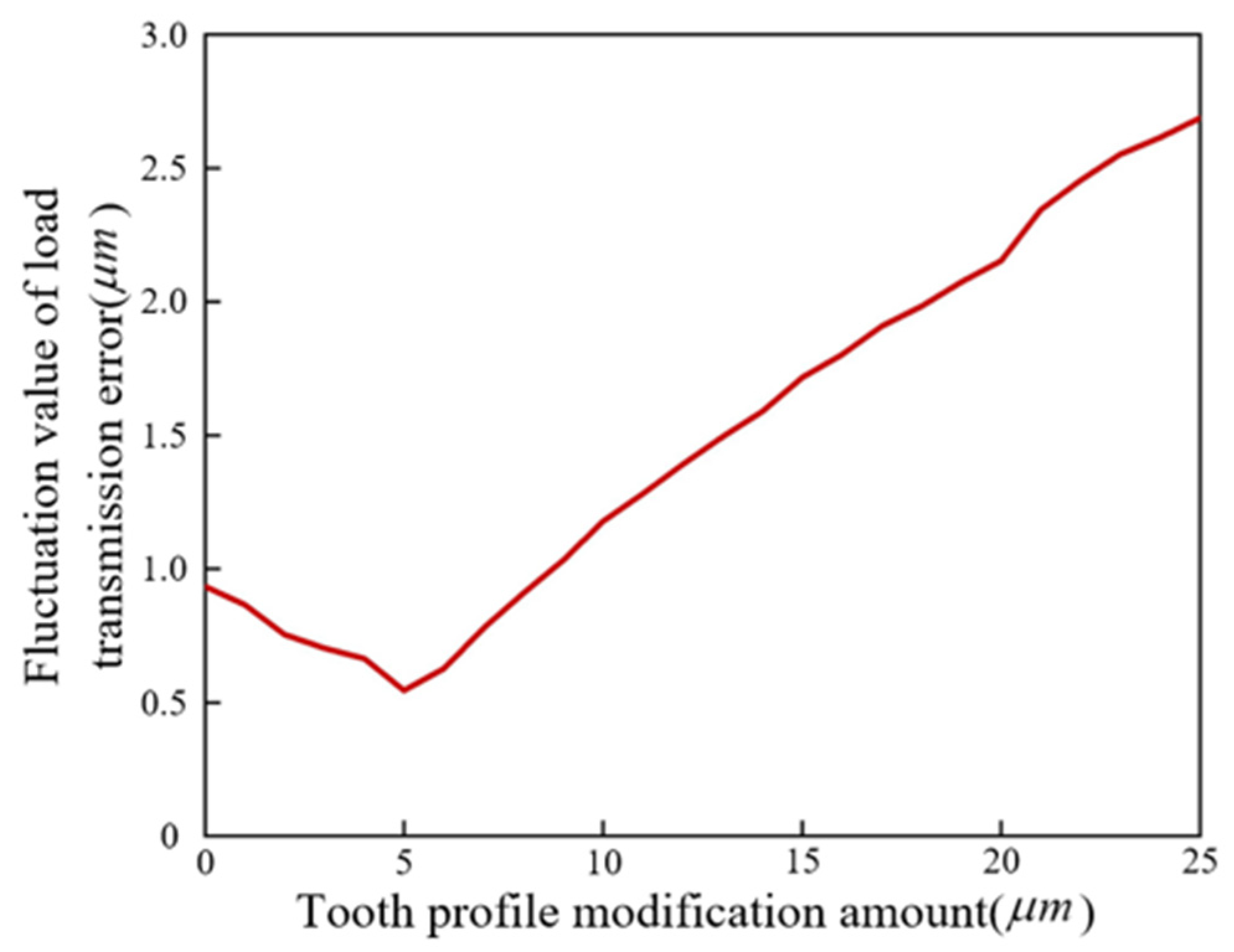
4.2.2. The Influence of Modification Amount on TVMS and LTE
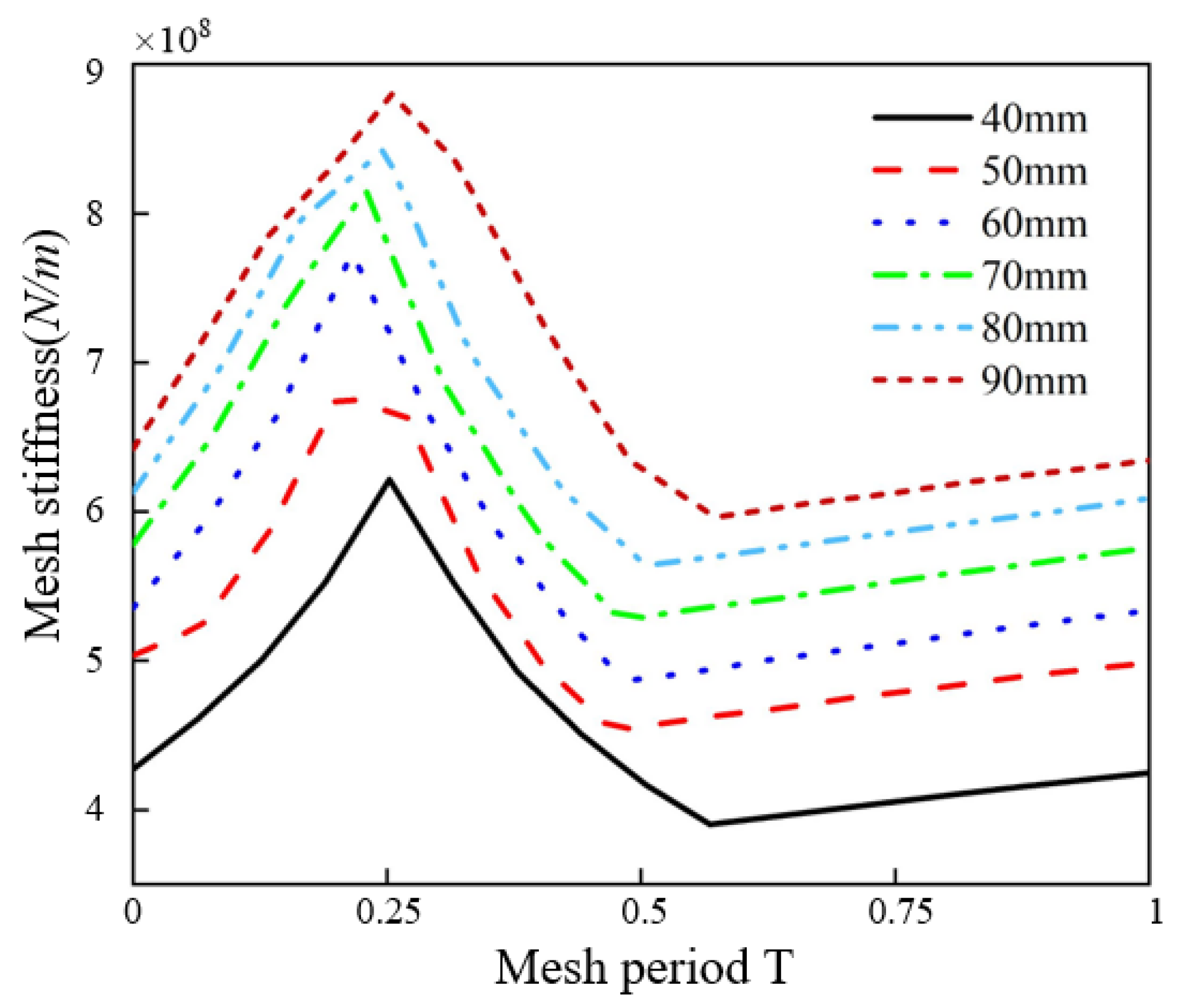
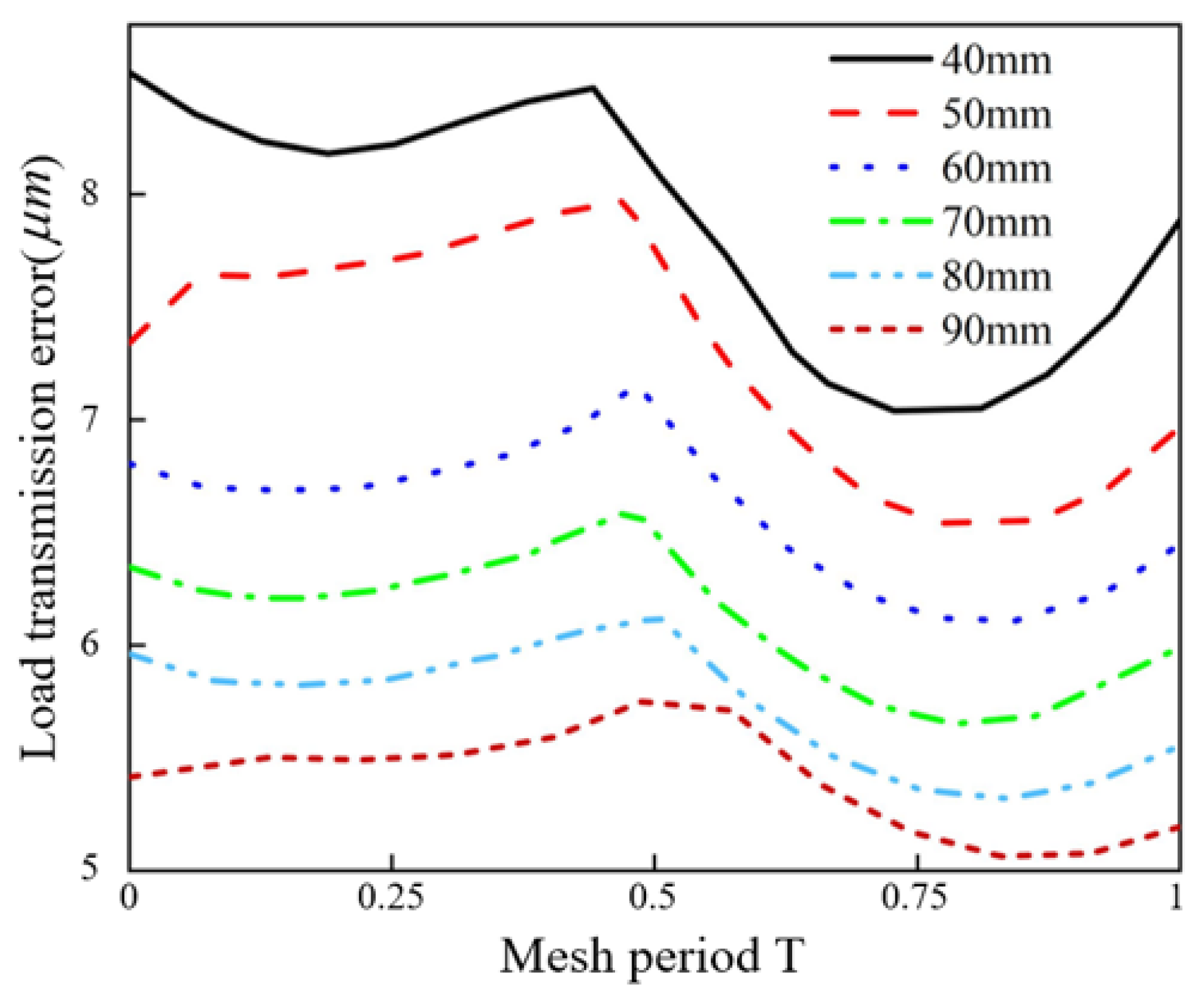
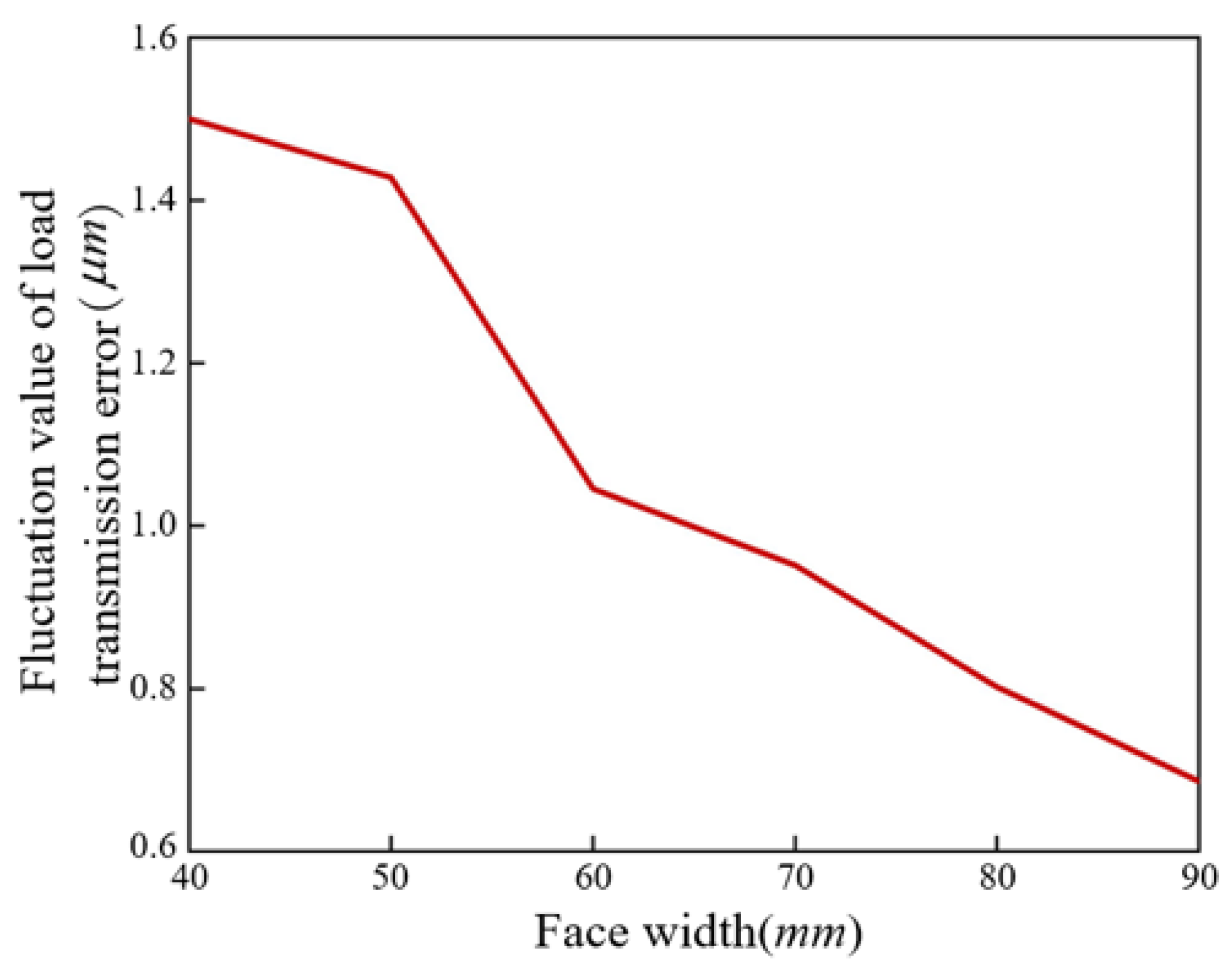
4.2.3. The Influence of Face Width on TVMS and LTE
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| TVMS | Time-varying mesh stiffness |
| LTE | Load transmission error |
| Nomenclature | |
| B | Face width |
| dB | Slice element thickness |
| t | Number of slices |
| Bending, shear, compressive, contact, and gear foundation potential energies | |
| Bending, shear, compressive, contact, and gear foundation stiffness | |
| F | Mesh force |
| E | Elastic modulus |
| G | Shear modulus |
| v | Poisson’s ratio |
| M | Torque |
| Moment of inertia | |
| Cross-sectional area of the microelement | |
| Mesh force component | |
| Mesh angle | |
| d | Effective energy storage length |
| h | Distance between mesh point and tooth midline |
| Half tooth thickness corresponding to microelements | |
| w | Radial displacement |
| u | Circumferential displacement |
| Cross-section rotation | |
| Tooth foundation stiffness correction factor, subscript i denotes the internal gear and external gear | |
| Tooth profile modification function | |
| Flank line crowning function | |
| Coefficients of tooth profile modification function | |
| Coefficients of flank line crowning function | |
| The generating line length at of the modified tooth profile | |
| Helix parameter | |
| Normal module | |
| Helix angle | |
| Rotation angle of the point around the z-axis on the modified tooth profile. | |
| Tooth number of modified gear | |
| Rolling angle | |
| Tooth thickness half-angle of base circle | |
| Base circle radius of modified gear | |
| Deformation of slice tooth pairs on the contact line, the subscript x represents the contact line on the front tooth, the current tooth, and the rear tooth | |
| Tooth surface deviations, subscript x represents the contact line on the front tooth, the current tooth, and the rear tooth | |
| Relative values of tooth surface deviation at the contact line ridge points, subscript x indicates the front and rear teeth relative to the current tooth j | |
| Tooth surface clearance of the slice element on the contact line, subscript x represents the front tooth, the current tooth, and the rear tooth | |
| Mesh clearance, subscript x represents the front tooth, the current tooth, and the rear tooth | |
| Mesh clearance arrangement matrix | |
| Mesh force of slice element pair | |
| Deformation of slice element pair | |
| W | Potential energy |
| K | Time-varying mesh stiffness |
| T | Torque |
| Angle difference | |
| Theoretical rotation angle of the driven gear | |
| Actual rotation angle of the driven gear | |
References
- Chang, L.H.; Liu, G.; Wu, L.Y. A robust model for determining the mesh stiffness of cylindrical gears. Mech. Mach. Theory 2014, 87, 93–114. [Google Scholar] [CrossRef]
- Rezaei, M.; Poursina, M.; Jazi, S.H.; Aboutalebi, F.H. Calculation of time dependent mesh stiffness of helical planetary gear system using analytical approach. J. Mech. Sci. Technol. 2018, 32, 3537–3545. [Google Scholar] [CrossRef]
- Wang, Q.B.; Chen, K.K.; Zhao, B.; Ma, H.; Kong, X.G. An analytical-finite-element method for calculating mesh stiffness of spur gear pairs with complicated foundation and crack. Eng. Fail. Anal. 2018, 94, 339–353. [Google Scholar] [CrossRef]
- Raghuwanshi, N.K.; Parey, A. Mesh stiffness measurement of cracked spur gear by photoelasticity technique. Measurement 2015, 73, 439–452. [Google Scholar] [CrossRef]
- Raghuwanshi, N.K.; Parey, A. Experimental measurement of gear mesh stiffness of cracked spur gear by strain gauge technique. Measurement 2016, 86, 266–275. [Google Scholar] [CrossRef]
- Benatar, M.; Handschuh, M.; Kahraman, A.; Talbot, D. Static and dynamic transmission error measurements of helical gear pairs with various tooth modifications. J. Mech. Des. 2019, 141, 103301. [Google Scholar] [CrossRef]
- Wan, Z.G.; Cao, H.R.; Zi, Y.Y.; He, W.P.; Chen, Y.M. Mesh stiffness calculation using an accumulated integral potential energy method and dynamic analysis of helical gears. Mech. Mach. Theory 2015, 92, 447–463. [Google Scholar] [CrossRef]
- Yu, W.; Mechefske, C.K. A new model for the single mesh stiffness calculation of helical gears using the slicing principle. Iran J. Sci. Technol.-Trans. Mech. Eng. 2019, 43, 503–515. [Google Scholar] [CrossRef]
- Huang, W.K.; Ma, H.; Zhao, Z.F.; Wang, P.F.; Peng, Z.K.; Zhang, X.X.; Zhao, S.T. An iterative model for mesh stiffness of spur gears considering slice coupling under elastohydrodynamic lubrication. J. Cent. South Univ. 2023, 30, 3414–3434. [Google Scholar] [CrossRef]
- Chen, K.K.; Huangfu, Y.F.; Ma, H.; Xu, Z.T.; Li, X.; Wen, B.C. Calculation of mesh stiffness of spur gears considering complex foundation types and crack propagation paths. Mech. Syst. Signal Proc. 2019, 130, 273–292. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, H.W.; Lu, F.X.; Wang, C.; Zhang, J.C.; Qin, M.J. A New Fast Calculating Method for Meshing Stiffness of Faulty Gears Based on Loaded Tooth Contact Analysis. Processes 2023, 11, 2003. [Google Scholar] [CrossRef]
- Chen, Z.G.; Shao, Y.M. Mesh stiffness calculation of a spur gear pair with tooth profile modification and tooth root crack. Mech. Mach. Theory 2013, 62, 63–74. [Google Scholar] [CrossRef]
- Autiero, M.; Paoli, G.; Cirelli, M.; Valentini, P.P. The effect of different profile modifications on the static and dynamic transmission error of spur gears. Mech. Mach. Theory 2024, 201, 105752. [Google Scholar] [CrossRef]
- Sánchez, M.B.; Pleguezuelos, M.; Pedrero, J.I. Influence of profile modifications on meshing stiffness, load sharing, and trasnsmission error of involute spur gears. Mech. Mach. Theory 2019, 139, 506–525. [Google Scholar] [CrossRef]
- Hu, Z.H.; Tang, J.Y.; Zhong, J.; Chen, S.Y.; Yan, H.Y. Effects of tooth profile modification on dynamic responses of a high speed gear-rotor-bearing system. Mech. Syst. Signal Proc. 2016, 76, 294–318. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Ji, P.F. Research on the variation of mesh stiffness and transmission error for spur gear with tooth profile modification and wear fault. Eng. Fail. Anal. 2021, 122, 105184. [Google Scholar] [CrossRef]
- Sun, Z.; Chen, S.Y.; Hu, Z.H.; Tao, X. Improved mesh stiffness calculation model of comprehensive modification gears considering actual manufacturing. Mech. Mach. Theory 2022, 167, 104470. [Google Scholar] [CrossRef]
- Dai, H.; Long, X.H.; Chen, F.; Xun, C. An improved analytical model for gear mesh stiffness calculation. Mech. Mach. Theory 2021, 159, 104262. [Google Scholar] [CrossRef]
- Pedrero, J.I.; Sánchez, M.B.; Pleguezuelos, M. Analytical model of meshing stiffness, load sharing, and transmission error for internal spur gears with profile modification. Mech. Mach. Theory 2024, 197, 105650. [Google Scholar] [CrossRef]
- Shen, Z.X.; Qiao, B.J.; Yang, L.H.; Luo, W.; Chen, X.F. Evaluating the influence of tooth surface wear on TVMS of planetary gear set. Mech. Mach. Theory 2019, 136, 206–223. [Google Scholar] [CrossRef]
- Karpat, F.; Engin, B.; Dogan, O.; Yuce, C.; Yilmaz, T.G. Effect of Rim Thickness on Tooth Root Stress and Mesh Stiffness of Internal Gears; ASME International Mechanical Engineering Congress and Exposition: Montreal, ON, Canada, 2014. [Google Scholar]
- Wang, G.J.; Luo, Q.; Zou, S.D. Time-varying meshing stiffness calculation of an internal gear pair with small tooth number difference by considering the multi-tooth contact problem. J. Mech. Sci. Technol. 2021, 35, 4073–4083. [Google Scholar] [CrossRef]
- Yang, D.C.H.; Sun, Z.S. A rotary model for spur gear dynamics. ASME J. Mech. Trans. Aut. Des. 1985, 107, 529–535. [Google Scholar] [CrossRef]
- Liang, X.H.; Zuo, M.J.; Patel, T.H. Evaluating the time-varying mesh stiffness of a planetary gear set using the potential energy method. Proc. Inst. Mech. Eng. Part C J. Eng. Mech. Eng. Sci. 2014, 228, 535–547. [Google Scholar] [CrossRef]
- Sainsot, P.; Velex, P.; Duverger, O. Contribution of gear body to tooth deflections—A new bidimensional analytical formula. J. Mech. Des. 2004, 126, 748–752. [Google Scholar] [CrossRef]
- Chen, Z.G.; Shao, Y.M. Mesh stiffness of an internal spur gear pair with ring gear rim deformation. Mech. Mach. Theory 2013, 69, 1–12. [Google Scholar] [CrossRef]
- Wang, Q.B.; Zhang, Y.M. A model for analyzing stiffness and stress in a helical gear pair with tooth profile errors. J. Vib. Control 2017, 23, 272–289. [Google Scholar] [CrossRef]
- Ma, H.; Zeng, J.; Feng, R.J.; Pang, X.; Wen, B.C. An improved analytical method for mesh stiffness calculation of spur gears with tip relief. Mech. Mach. Theory 2016, 98, 64–80. [Google Scholar] [CrossRef]
- Meng, Z.; Zhang, Y.; Pang, X.S.; Jin, Y.S.; Li, J.M.; Fan, F.J. Measurement and evaluation of time-varying meshing stiffness of faulty gears under different types. Meas. Sci. Technol. 2023, 34, 095127. [Google Scholar] [CrossRef]
- Wang, Y.N.; Li, K.Y.; Qiao, B.J.; Shen, Z.X.; Chen, X.F. Theoretical Investigation of Mesh Relationship and Mesh Stiffness of Internal Spur Gears with Tooth Wear. Appl. Sci. 2023, 13, 2022. [Google Scholar] [CrossRef]



| Parameters | Pinion | Gear |
|---|---|---|
| Teeth number Z | 18 | 68 |
| Normal module mn (mm) | 5 | |
| Pressure angle α (°) | 20 | |
| Face width B (mm) | 50 | |
| Helix angle β (°) | 13 | |
| Young’s modulus E (GPa) | 210 | |
| Poisson’s ratio v | 0.3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Zhao, H.; Ren, Y.; Yang, J. Calculation of Time-Varying Mesh Stiffness of Internal Mesh Transmission and Analysis of Influencing Factors. Appl. Sci. 2025, 15, 4599. https://doi.org/10.3390/app15094599
Li J, Zhao H, Ren Y, Yang J. Calculation of Time-Varying Mesh Stiffness of Internal Mesh Transmission and Analysis of Influencing Factors. Applied Sciences. 2025; 15(9):4599. https://doi.org/10.3390/app15094599
Chicago/Turabian StyleLi, Jubo, Hengbo Zhao, Yanbo Ren, and Jianjun Yang. 2025. "Calculation of Time-Varying Mesh Stiffness of Internal Mesh Transmission and Analysis of Influencing Factors" Applied Sciences 15, no. 9: 4599. https://doi.org/10.3390/app15094599
APA StyleLi, J., Zhao, H., Ren, Y., & Yang, J. (2025). Calculation of Time-Varying Mesh Stiffness of Internal Mesh Transmission and Analysis of Influencing Factors. Applied Sciences, 15(9), 4599. https://doi.org/10.3390/app15094599





