Abstract
To address the intense mining pressure and dynamic accidents, such as shield collapse during mining in shallow coal seams crossing the Maoliang terrain, this study focuses on Panel 30206 of the Yanghuopan Coal Mine. Through theoretical analysis, numerical simulation, and field measurements, the stress transfer patterns and dynamic changes in shield loads during mining were analyzed, and the mechanism of dynamic mining pressure and calculation method for maximum support resistance were determined. The results show that when the working face enters the load-affected zone of the Maoliang terrain, the base load ratio of the overburden increases. The fracturing of the roof strata causes a synchronized motion between the key stratum and the overlying surface layer. The fracture and instability of the key stratum under mining-induced terrain loads significantly increase the shield resistance and intensify the mining pressure, with a hysteresis effect. Field measurements indicate a maximum shield working resistance of 8974 kN at Panel 30206, showing a 3.25% deviation from the theoretical value of 9266 kN, with a 25 m lag behind the peak load in the Maoliang terrain. This research provides criteria for support selection and ground control in Maoliang terrain mining, ensuring safe production.
1. Introduction
The Yushenfu mining area exhibits favorable geological conditions characterized by shallow-buried thick coal seams overlaid by Quaternary loess and Tertiary clay deposits. Since the Quaternary period, alternating loess deposition and erosional processes have formed a highly fragmented terrain dominated by dense gully networks and interconnected Maoliang valley systems [1,2]. Field observations indicate that intersecting loess ridges critically constrain the extraction of shallow coal seams. Modifications to the surface topography during mining operations induce abrupt increases in the overburden base load ratio, thereby generating intense dynamic loading phenomena during face advancement through Maoliang zones [3,4,5]. Therefore, elucidating the influence of the Maoliang terrain on the strata pressure distribution in shallow coal seams, alongside clarifying the overburden movement mechanisms and stress transfer pathways, is imperative for ensuring safe and efficient mining practices in such geomorphologically complex regions.
Researchers in China have made substantial advances in the theoretical frameworks, mechanical analyses, and control strategies for shallow coal seam mining [6,7,8]. Notably, Huang et al. [9,10,11] developed structural models of the “short voussoir beam” and “step rock beam” specific to shallow coal seams, while further identifying the “activation” effect induced in overlying roof strata during close-distance mining. Concerning dynamic loading mechanisms in face support systems, Zhang et al. [12] established a composite bearing structure model to quantify the support resistance. Ren [13] advanced a cantilever-articulated rock beam theory, identifying the primary mechanism underlying shield collapse incidents. Furthermore, Shang et al. [14] derived interburden failure criteria by considering adjacent seam pillar stresses. Regarding valley terrain impacts, Lai et al. [15,16] established theoretical criteria for the initial fracture span of high-level key strata under rotational and sliding instability modes. Liu et al. [17] systematically investigated the synergistic coupling effects of valley morphology. Concurrently, Zhang et al. [18] demonstrated that fracture propagation in non-uniformly loaded rock beams serves as the predominant trigger of dynamic pressure events at valley bottoms. Building on these findings, Xie et al. and Fu et al. [19,20] quantitatively characterized the spatiotemporal patterns and mechanical drivers of strata damage during shallow multi-seam extraction in gully terrain. Furthermore, Wang et al. [21] and Wang et al. [22] validated that the mining advance direction, gully slope angle, and extracted seam thickness collectively govern the critical thresholds for gully slope stability degradation. In the context of shallow coal seam mining across Maoliang terrain, Huang et al. [23] quantitatively characterized dynamic load fluctuations in hydraulic shields and developed a computational method for estimating shield loads during roof weighting under goaf-induced stress conditions. Through parametric simulations, Di et al. [24] established that the slope gradient and vertical relief exert a dominant control over the strata pressure magnitude. A comparative analysis by Wang et al. [25] further elucidated the lithology-dependent regulatory mechanisms of strata pressure, demonstrating distinct overburden failure patterns between the sandy and rocky Maoliang formations. Concurrently, Wang et al. [26] investigated underground pressure distribution patterns during Maoliang terrain mining and identified peak pressure intensities at the Maoliang base that progressively attenuated with face advancement. Zhao et al. [27] and Yang et al. [28] revealed that pressure-arch instability in shallow overburden strata governs periodic roof weighting and surface subsidence. Research on strata pressure dynamics in shallow coal seams has provided critical insights. For example, Du et al. [29] demonstrated that intense dynamic pressures originate from the reverse rotational movement of key block-articulated structures during the coal pillar penetration stage. Concurrently, Zhao et al. [30] established that the stress concentration at the leading arch foot, driven by the formation of continuous pressure-arch structures and subsequent elastic energy accumulation, triggers severe roof weighting events. Furthermore, Hu et al. [31] and Liu et al. [32] systematically quantified the spatiotemporal evolution of the support stress and overburden compaction strength during close-distance multi-seam mining. These findings collectively refine the mechanistic models of strata pressure behavior and underpin the development of safety protocols for mining operations under analogous geological constraints.
While existing studies have established fundamental theories for shallow coal seam mining, critical gaps persist in understanding the stress transfer mechanisms within the Maoliang terrain and dynamic shield load evolution during cross-terrain excavation, particularly regarding transient strata pressure dynamics. To resolve these limitations, this study systematically analyzed the stress transfer laws and dynamic variations in shield loads within shallow coal seams crossing the Maoliang terrain by applying theoretical analyses, numerical simulations, and field measurements. Through integrated analyses, we quantify stress redistribution patterns and shield load fluctuations during Maoliang mining, reveal the mechanisms of dynamic pressure generation, and propose a predictive model for maximum support resistance. These results advance the theoretical frameworks for strata pressure control and support optimization in Maoliang terrains, while offering actionable strategies to ensure mining safety under complex topographical constraints.
2. Working Face Overview
Panel 30206 of the Yanghuopan Coal Mine is located in the northwest section of the mining field, featuring complex topography with alternating Maoliang ridges and intersecting gullies. Bordered by Shifo Gully to the east, Yanghuopan Village to the south, Moshiwan Branch to the west, and Sunyingyicha Coal Mine to the north, the panel extends 1562.4 m in the east-west orientation with a 313-m face width. The coal seam has an average mining height of 2.2 m, and dips 1−2°, with a maximum burial depth of 121 m. The overburden consists of a 46-m thick bedrock and 25–75 m of unconsolidated layers in the borehole columnar section shown in Figure 1. The Maoliang ridge crest elevation reaches +1250 m with a 50-m relative height, as shown in the overburden profile in Figure 2.
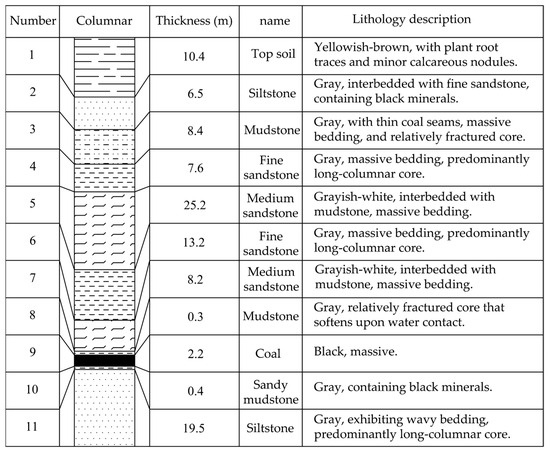
Figure 1.
Borehole columnar section of Panel 30206.
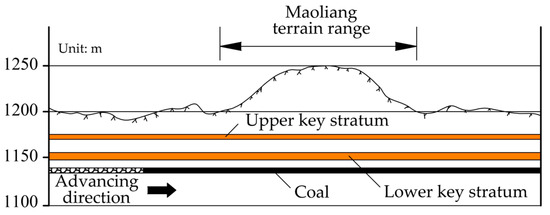
Figure 2.
Topographic profile of Panel 30206.
3. Strata Stress Distribution Characteristics
3.1. Mechanical Model Analysis
Under shallow coal seam mining conditions, the thickness of the surface overburden significantly affects the strata pressure manifestation at the working faces. Based on soil mechanics principles, when a concentrated load P is applied to the ground surface, the horizontal stress σx, vertical stress σy, and shear stress τxy induced at any point M within the plane can be expressed as [33]
Empirical evidence indicates that the height and morphology of the Maoliang terrain are the primary factors influencing the strata pressure manifestation at the working faces. Based on the overlying Maoliang terrain characteristics, terrain loading can be modeled mechanistically as a semi-infinite plane body subjected to distributed-boundary forces. This complex loading system was simplified into a parabolic load perpendicular to the face advancement direction, expressed as
In this formula, A and B are parameters related to the morphology of the Maoliang terrain.
A terrain profile along the panel strike direction was established, and a mechanical model of static loading stress transfer in the Maoliang terrain was constructed, as shown in Figure 3.
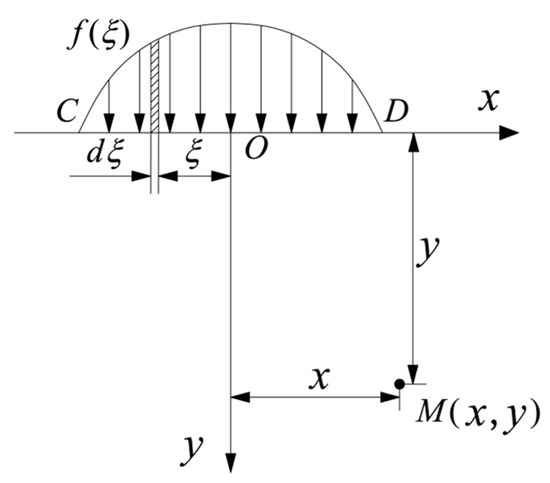
Figure 3.
Mechanical model of static loading stress transfer in the Maoliang terrain.
Within the loaded segment CD, considering a differential element dξ located at a distance ξ from the coordinate origin O, the concentrated load acting on this element can be expressed as
In this formula, is the average unit weight of the soil layer in the Maoliang terrain, N/m3.
Therefore, the vertical and horizontal distances from point M to the concentrated load are y and , respectively. Under these conditions, the stress at point M induced by the concentrated load can be derived from the following equation:
From the parabolic load distribution equation , the coordinates of boundary points C and D in the Maoliang terrain are determined as and , respectively. To facilitate quantitative analysis, a characteristic parameter is defined, enabling the expression of stress at any point M in the underlying strata under Maoliang terrain loading as:
Through integration, the stress induced at any point M in the underlying strata can be obtained as
In this formula, are expressed as
In addition, with an increase in burial depth, the stress generated by the self-weight of the stratum gradually increases. Therefore, the influence of the self-weight load of the stratum on the vertical stress should be considered in the stress calculation. The corrected vertical stress can be expressed as
3.2. Strata Stress Distribution Patterns
According to the terrain characteristics of the Yanghuopan 30206 working face, the terrain parameters and are considered. The vertical stress, horizontal stress and tangential stress at different positions of the underlying strata under the load of the Maoliang terrain can be calculated from Formula (6), and the distribution law is shown in Figure 4.
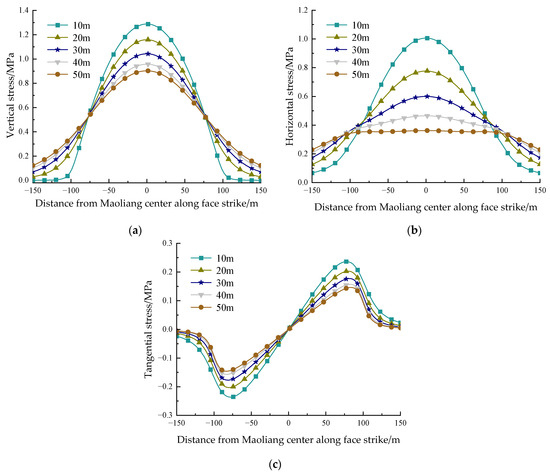
Figure 4.
Stress distribution in the underlying strata under Maoliang terrain loading. (a) Vertical stress (b) Horizontal stress (c) Tangential stress.
As shown in Figure 4, within a horizontal distance of 50 m from the center of the Maoliang terrain, the vertical stress, horizontal stress, and tangential stress all decrease with increasing burial depth, and the rate of stress reduction gradually diminishes, indicating that as burial depth increases, the influence of the Maoliang terrain load on the formation stress gradually weakens.
Among these, the distribution patterns of the vertical and horizontal stresses were similar, both exhibiting a symmetric peak distribution, reaching maximum values at the center of the Maoliang terrain, and decreasing significantly toward both sides. At a burial depth of 10 m, the peak values of the vertical and horizontal stresses are 1.3 MPa and 1.0 MPa, respectively. The closer the location is to the center of the Maoliang terrain, the more pronounced the influence of burial depth on the stresses, with a greater effect on the horizontal stress than on the vertical stress. In contrast, the tangential stress displays a center-symmetric distribution: it is zero at the center of the Maoliang terrain, increases first, and then decreases toward both sides. At a burial depth of 10 m, the peak tangential stress is 0.25 MPa, occurring at a horizontal distance of approximately 75 m from the center of the Maoliang terrain, indicating that the Maoliang terrain load induces significant shear deformation in the edge region.
4. Strata Pressure Manifestation Mechanism
4.1. Evolution Characteristics of Overburden Structures
Coal seam mining causes a redistribution of the original rock stress, resulting in the fracturing of the key layer of the overburden and interlocking of the key blocks [34,35]. Subsequently, the lower key layer subsides and collapses above the goaf, forming a step rock beam structure. As the working face advances continuously, both the interburden and the upper key layer gradually fracture and collapse. Once the upper key layer fractures, it rotates and subsides, thereby forming a hinged masonry beam structure.
When the working face enters the influence zone of the Maoliang terrain load, the thickness of the overlying soil layer increases, thereby intensifying the load on the overburden rock structure. This leads to an increased bearing ratio of the overburden and a strong abutment pressure on the working face, as shown in Figure 5. The fracturing of the roof rock layer causes the upper key layer and its overlying soil layer to move in a coordinated manner, transferring the load to the hinged masonry beam structure formed by the upper key layer. Under the influence of mining, both the hinged masonry and step rock beam structures gradually slip and become unstable, which further results in a significant increase in support resistance.
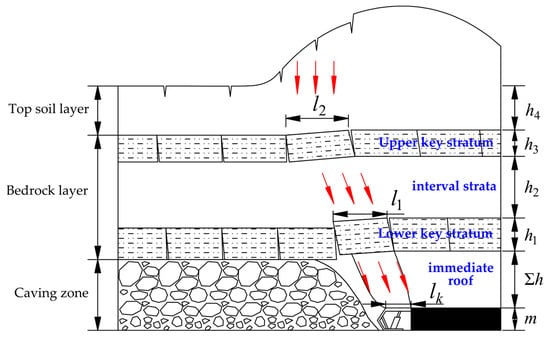
Figure 5.
Mechanical model of dynamic evolution of overburden structures during mining across Maoliang terrain.
4.2. Dynamic Roof Failure and Stress Transfer Mechanisms
According to the above analysis, the load exerted on the working face supports is not simply the sum of the weight of all the overlying strata but is closely related to the characteristics of the roof structure and the stress transfer path [36]. Stress is transmitted along specific paths within the key layer of the overburden, such that the actual load on the supports is controlled by the structure formed after the fracture of the key layer [37,38]. After the dual key layers of the roof fracture, a lower-step rock beam structure and an upper-hinged masonry beam structure are formed, and their mechanical model is shown in Figure 6.
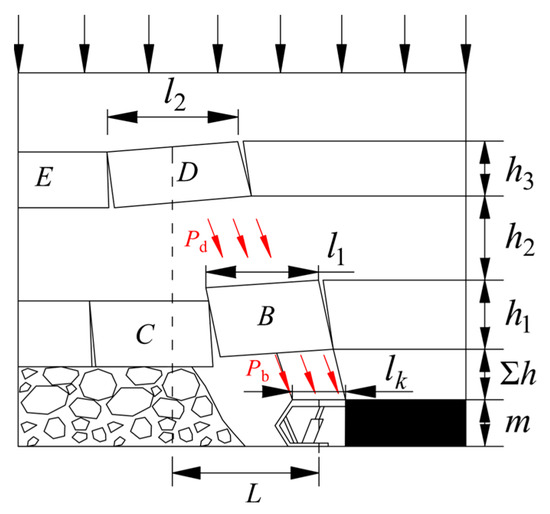
Figure 6.
Mechanical model of stress transfer in the roof strata.
Based on the step rock beam theory in Reference [23], the load acting on the supports can be obtained as
In this formula, is the support roof control distance, m; is the support width, m; is the immediate roof thickness, m; is the blockiness of the step rock beam; is the average unit weight of the bedrock, N/m3; is the rotation angle of the step rock beam, °; is the maximum rotation angle of the step rock beam, °; is the load borne by key block B, N.
is composed of the self-weight of key block B and the load transferred from the overlying strata, and is expressed as
In this formula, is the thickness of the lower key layer, m; is the thickness of the interburden, m; is the length of step rock beam B, m; is the stress transfer coefficient, where K = 1 when h2 < 2.5l1; is the load transferred downward by the hinged masonry beam, N.
Under the influence of mining, the sliding instability of the hinged masonry beam structure has a load transfer effect on the interburden and the lower-step rock beam. Therefore, the stability calculation of the stepped rock beam structure must consider the instability load of the overlying hinged masonry beam structure. Thus, based on the masonry beam theory formula, the load transferred downward by the hinged masonry beam is expressed as
In this formula, is the block size of the hinged masonry beam; is the rotation angle of the hinged masonry beam, °; is the load borne by key block D, N.
is composed of the self-weight of key block D and the overlying Maoliang terrain load. From Equation (6), it can be seen that the Maoliang terrain load follows a nonlinear distribution, and its magnitude depends on the burial depth and horizontal position of that point. Therefore, to simplify the calculation, the stress at the center of the upper surface of key block D is taken as the average value for key block D. Thus, can be expressed as
In this formula, is the thickness of the upper key layer, m; is the vertical stress at the center of the upper surface of key block D under the action of the Maoliang terrain load, Pa.
From Equation (12), the vertical stress can be expressed as
In this formula, is the thickness of the surface soil layer before entering the Maoliang terrain area, m.
By solving Equations (13)–(17) simultaneously, the support load P can be expressed as
The mining pressure on the working face is most intense when the upper-hinged masonry beam and the lower-step rock beam fail simultaneously. At this moment, the fracture angle formed by the overlying strata failure is , and the horizontal distance L between the working face support and key block D can be expressed as:
5. Strata Pressure Evolution Laws
Taking the 3-1 coal seam of Yanghuopan Coal Mine as the background, an FLAC3D numerical model of the 30206 working face was established to simulate the mining pressure distribution during excavation through the Maoliang terrain area. The model dimensions are 400 m in the strike direction, 100 m in the dip direction, and 160 m in depth, as shown in Figure 7.
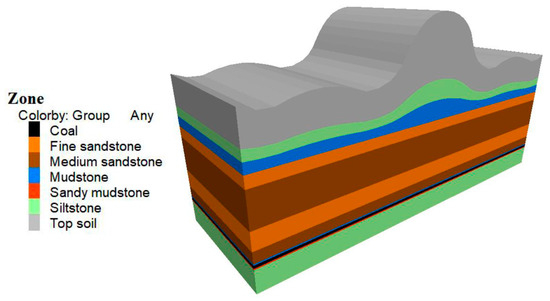
Figure 7.
Numerical calculation model.
In terms of the model boundary conditions, a free boundary is applied at the top to allow free deformation and movement of the overlying strata under the mining disturbance. Fixed boundaries are set on the sides and bottom to restrict displacement at the model boundaries, simulating the constraint effects of actual geological bodies on the mining area and ensuring the stability and accuracy of the model calculations [39,40].
The constitutive relationship of the model blocks is selected as the Mohr-Coulomb yield criterion model to simulate the elastoplastic deformation and failure characteristics of coal and rock masses under stress. To investigate the mechanical response of coal and rock masses and the law of mining pressure behavior during mining in the Maoliang terrain area, and to accurately reflect the mechanical properties of each rock stratum, relevant parameters for different lithologies were obtained based on the on-site geological survey data of the 30206 working face at the Yanghuopan Coal Mine. Rock mechanics tests were conducted in the laboratory to determine the physical and mechanical parameters of the coal and rock masses, with the specific parameters presented in Table 1.

Table 1.
Numerical simulation core parameters.
A cross-section along the central inclination of the working face reveals that when the working face advances to 0 m, 50 m, and 100 m from the Maoliang terrain boundary, the influence range of the front abutment pressure is approximately 20 m. The closer the working face is to the Maoliang terrain center, the more pronounced the abutment pressure concentration becomes. When the working face advances to the middle of the Maoliang terrain, the peak abutment pressure reaches a maximum of 8.33 MPa, located 10 m in front of the coal wall. The influence range of the abutment pressure extends to 70 m, with a stress concentration factor of approximately 2.6, as shown in Figure 8.
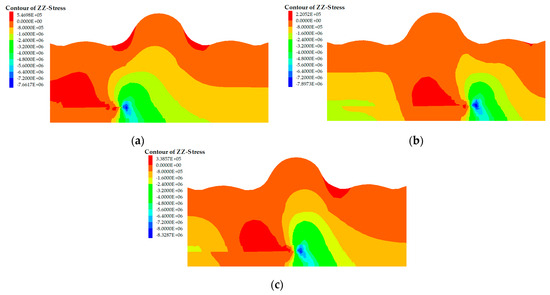
Figure 8.
Distribution of front abutment pressure at different face advancement distances. (a) 0 m from Maoliang terrain endpoint; (b) 50 m from Maoliang terrain endpoint; (c) 100 m from Maoliang terrain endpoint.
Meanwhile, during the advancement of the working face, the front abutment pressure was dynamically monitored, and the monitoring results are shown in Figure 9. The data indicate that after the working face enters the Maoliang terrain area, the peak abutment pressure increases significantly, reaching a maximum at 100 m of advancement, which is approximately 0.83 MPa higher than that before entering the Maoliang terrain. As the working face continues to advance and exits the Maoliang terrain area, the peak abutment pressure gradually decreases and stabilizes. However, the stabilized pressure peak remains higher than that before entering the Maoliang terrain, indicating that while the direct influence of the Maoliang terrain load on the abutment pressure weakens after exiting the area, a residual pressure effect still persists.
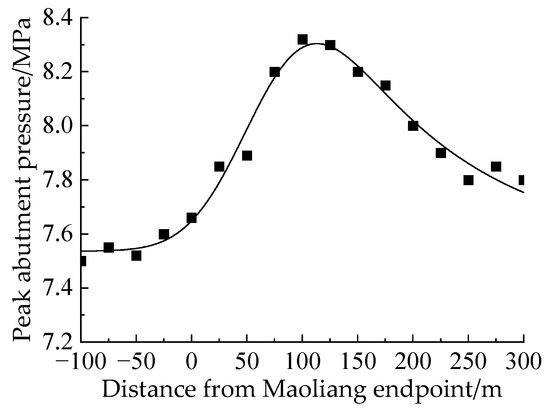
Figure 9.
Variation curve of the peak front abutment pressure.
6. Engineering Case Validation
6.1. Calculation of Maximum Support Working Resistance
To verify the reliability of the calculation formula for the working face support resistance, the 30206 working face of the 3-1 coal seam in Yanghuopan Coal Mine was selected as the research object, and a computational analysis was conducted based on the actual mining conditions. According to geological data, the Maoliang terrain extends approximately 200 m along the strike of the working face, with a topographic height of about 50 m. Given the overlying Maoliang terrain characteristics, it can be simplified as a parabolic distributed load perpendicular to the working face advancement direction, expressed by equation . Using Equation (6), the maximum vertical stress transferred from the Maoliang terrain load to key block D is calculated to be 1.05 MPa. The remaining calculation parameters are as follows: ; ; ; ; ; ; ; ; ; ; ; ; ; ; .
Substituting the above parameters into Equation (18), the maximum working resistance of the support during mining through the Maoliang terrain is obtained as:
6.2. Dynamic Variation Patterns of Support Loads
To investigate the dynamic variation of the support load during mining through the Maoliang terrain, the above parameters are substituted into Equation (10), and the dynamic variation of the support load during mining through the Maoliang terrain is shown in Figure 10.
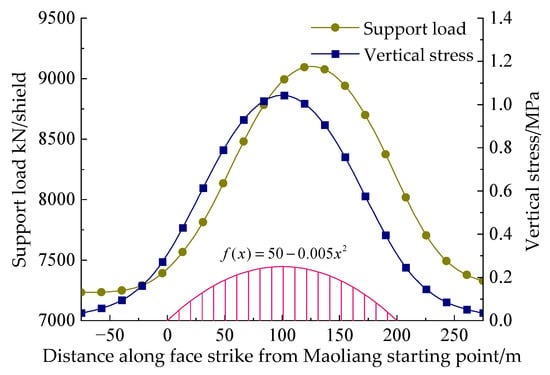
Figure 10.
Dynamic variation of support loads during mining across the Maoliang terrain.
As shown in Figure 10, it can be observed that as the working face advances, there is a significant difference in the variation trend between the support load and the Maoliang terrain load, showing a lag in the support load response. Before entering the Maoliang terrain zone, the support load is 7237 kN per support. When the working face advances 25 m into the Maoliang terrain zone, the support load gradually increases, reaching a peak value of 9266 kN per support at 125 m, which is a 28.04% increase compared to the pre-entry load. At this point, the peak position of the support load lags behind the peak Maoliang terrain load by approximately 25 m. As the working face further advances 25 m beyond the Maoliang terrain zone, the support load gradually decreases and returns to its original level. These results indicate that the Maoliang terrain load has a significant impact on the support load and exhibits a lag effect with a lag distance of approximately 25 m.
The lag phenomenon is closely related to the interaction mechanism between the surface soil layer and key bedrock strata, which is manifested in the following three ways:
- Spatiotemporal differences in key stratum fracturing
In the Maoliang terrain zone, the thick surface soil layer transfers its self-weight load to the working face through an upper key stratum. Due to the large span and high flexural stiffness of the upper key stratum, more strain energy must accumulate before fracturing, causing its fracturing position to lag behind that of the lower key stratum. The lower key stratum fractures earlier, forming a “step rock beam” structure, while the “hinged masonry beam” structure formed by the fractured upper key stratum gradually transfers the soil layer load to the supports. This results in the peak support load responding later than the peak Maoliang terrain load.
- 2.
- Synergistic deformation effect between soil and bedrock
The surface soil layer has low mechanical strength and cannot bear loads independently, relying on the deformation of the key bedrock strata. When the upper key stratum starts to rotate and subside, the soil layer deforms synchronously with the key stratum blocks, forming a “surface soil-key stratum synergistic deformation body”. The time lag between the compressive deformation of the soil layer and the fracture displacement of the key stratum introduces a delay in the load transfer.
- 3.
- Hierarchical adjustment of stress transfer paths
Before entering the Maoliang zone, the support loads primarily originated from fracturing of the immediate roof and lower key strata. After entering the zone, the stress transfer path transforms into a multi-level mode: “surface soil layer → upper key stratum → lower key stratum → supports”. Following the fracture of the upper key stratum, loads are transmitted gradually through contact stresses at the articulated joints between blocks rather than direct vertical loading, causing delays in stress wave propagation. Additionally, the parabolic load distribution of the Maoliang terrain (with higher central loads and lower lateral loads) causes the middle of the key stratum to reach the fracturing strength first, and the time required for fracturing to propagate laterally further exacerbates the lag in load transfer.
6.3. Field Monitoring Analysis of Support Working Resistance
The ZY8000/14/25D shield hydraulic support is employed for roof—support operations in the 30206 working face, with a rated working resistance of 8000 kN. During the advancement of the working face, pressure sensors were installed on the supports to obtain data on the working resistance of the supports. Multiple monitoring points were evenly arranged along the strike of the working face for data collection, ensuring a comprehensive reflection of the working resistance of the supports at different positions. The monitoring frequency was set to collect data once per minute to achieve dynamic real—time monitoring of the support working resistance. Throughout the monitoring period, the maximum opening ratio of the support safety valve during the advancement of the working face was 23%, the active column of the support shrank significantly, and the coal wall experienced severe spalling. An analysis of the support working resistance monitoring data for the 30206 working face resulted in the support working resistance variation curve shown in Figure 11. The monitoring results show that the maximum working resistance of the support is 8974 kN, with an error of 3.25% compared to the theoretical calculation result of 9266 kN. The area of strong mining pressure occurs within 25 to 225 m from the Maoliang terrain zone endpoint, lagging behind the Maoliang terrain zone by about 25 m. Within this range, the average working resistance of the support is 7865 kN, and a total of 17 cycles of pressure increase occur, with an average step distance of 12.3 m per cycle. This indicates that the theoretical calculation model is both reasonable and feasible.
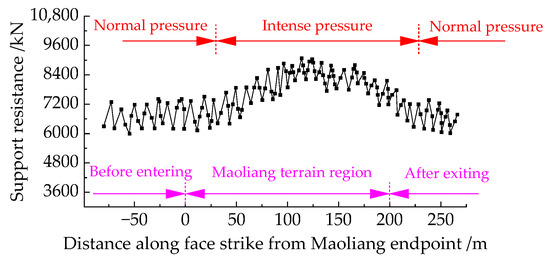
Figure 11.
Variation curve of working resistance for supports in Panel 30206.
7. Discussion
This study investigates the mechanism of dynamic mining pressure and support resistance during shallow coal seam mining across the Maoliang terrain, yielding a series of findings. A comparative analysis with the existing literature is presented as follows:
In terms of the stress distribution law in strata under Maoliang terrain loads, the mechanical model of static load stress transfer for the Maoliang terrain constructed in this study clarifies that vertical and horizontal stresses exhibit a symmetric peak distribution. Although previous studies have addressed stress-related issues in shallow coal seam mining, few have explored such detailed stress distributions under Maoliang terrain loads. The results of this study further refine the theory of stress distribution in shallow coal seams influenced by Maoliang topography, providing a basis for considering stress factors in subsequent mining designs.
Regarding the evolution characteristics of the overburden structure and stress transfer laws during mining in Maoliang terrain areas, this study reveals that Maoliang terrain loads exacerbate the fracturing and instability of key overburden strata, leading to increased support loads, intense mining pressure, and a lag phenomenon. While Huang et al. [11] have studied the dynamic loads on supports and the variation laws of advanced abutment pressure, this study systematically analyzes the dynamic evolution of the overburden structure and the detailed process of stress transfer. This supplements the details of how the changes in the overburden structure affect the stress transfer and support loads at different mining stages, leading to a deeper understanding of the problem.
Concerning the calculation method for support resistance, the method derived from the mechanical model of roof stress transfer in this study was validated in the 30206 working face of Yanghuopan Coal Mine, with a small error compared with the field measurement results. Compared with previous research, this achievement improves the accuracy and practicality of the calculations, providing a more reliable reference for support selection in actual mining operations.
8. Conclusions
- (1)
- By constructing a static load stress transmission mechanical model for the Maoliang terrain, the stress distribution pattern of the strata under the Maoliang load was determined. Under the Maoliang load, both the vertical and horizontal stresses in the underlying strata show symmetrical peak distributions, reaching their maximum at the Maoliang center and significantly decreasing toward both sides. As the burial depth increases, the influence of the load on these stresses gradually diminishes.
- (2)
- A mechanical model of the overburden structure during mining in the Maoliang terrain zone was established, revealing the evolution characteristics of the overburden structure and stress transmission patterns in the working face. The Maoliang load has a significant impact on the peak support pressure and the support load ahead of the coal face, with a noticeable delay. The mining-induced disturbance exacerbates the failure and instability of the key overburden layers, leading to a significant increase in support load and more intense mining pressure.
- (3)
- Based on the roof stress transmission mechanical model, a calculation method for the support resistance in the Maoliang terrain zone was developed. The maximum support working resistance for the 30206 working face is 8974 kN, with an error of 3.25% compared to the theoretical calculation result of 9266 kN. Compared to the situation before entering the Maoliang zone, the support load increased by 28.04%. The range of strong mining pressure extends from 25 m to 225 m from the Maoliang endpoint, lagging behind the Maoliang load by approximately 25 m.
- (4)
- Future research directions will primarily focus on the following aspects: First, to deeply investigate the transmission laws of Maoliang terrain loads under complex geological conditions and their influences on mining pressure, and to construct more accurate mechanical models by incorporating more geological factors. Second, to expand the scope of field measurements, studies should be conducted in different mining areas to validate and refine the research results, thereby enhancing their universality. Third, advanced monitoring technologies and numerical simulation methods should be integrated for the real-time monitoring and simulation of overburden structure changes and stress distribution during mining, to provide more effective technical support for mining pressure control.
Author Contributions
Methodology, G.Q. and T.Y.; software, G.Q. and B.W.; investigation, Y.H. and S.G.; data curation, Y.H. and S.G.; writing—original draft preparation, G.Q.; writing—review and editing, J.Z. and T.Y.; supervision, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant number 52404144) and the Natural Science Basic Research Program of Shaanxi (grant number 2024JC-YBQN-0594).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The relevant data in this manuscript were obtained from field measurements and tests, which are real and effective.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, S.; Wei, J.; Song, S.; Hou, E.; Sun, T. Study on overburden and surface damage characteristics of shallow-buried coal seam mining in loess gully area. Coal Sci. Technol. 2022, 50, 1–9. [Google Scholar]
- Song, S.; Ruan, H.; Wei, J.; Niu, R.; Cheng, X.; Chen, B. The Influence of the Key Characteristics of Overburden Rock Structure on the Development Height of Water-Conducting Fracture in Yushenfu Coal Mine Area, China. Appl. Sci. 2024, 14, 10537. [Google Scholar] [CrossRef]
- Zhang, D.; Fan, G.; Wang, X. Characteristics and stability of slope movement response to underground mining of shallow coal seams away from gullies. Int. J. Min. Sci. Technol. 2012, 22, 47–50. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, Z.; Zhang, C.; Fan, Z.; Lu, Z.; Huang, Z.; Lu, C.; Xue, J.; Wang, C.; Chen, F.; et al. Review on roof disaster and prevention technology for coal mining face in China. J. Min. Strat. Control. Eng. 2024, 6, 16–41. [Google Scholar]
- Song, G.; Zhang, B.; Fu, X.; Du, F.; Bi, Z.; Wang, Y.; Yang, Y. Formation mechanism and application of “main control Layer-weak layer” composite structure in shallow coal seam. J. Min. Saf. Eng. 2021, 38, 286–294. [Google Scholar]
- Wang, J.; Xu, J.; Yang, S.; Wang, Z. Development of strata movement and its control in underground mining: In memory of 40 years of Voussoir Beam Theory proposed by Academician Minggao Qian. Coal Sci. Technol. 2023, 51, 80–94. [Google Scholar]
- Zhao, B.; Guo, Y.; Sun, H.; Yang, X.; Wang, J.; Zhao, Y. Stability research on the water-resistant strata under mining in nearly shallow coal seam based on location of main key stratum. J. Min. Saf. Eng. 2022, 39, 653–662. [Google Scholar]
- Hou, Z. Study on key stratum in shallow seam. J. China Coal Soc. 1999, 24, 359–363. [Google Scholar]
- Huang, Q. Ground pressure behavior and definition of shallow seams. Chin. J. Rock Mech. Eng. 2002, 21, 1174–1177. [Google Scholar]
- Huang, Q.; Qian, M.; Shi, P. Structural analysis of main roof stability during periodic weighting in longwall face. J. China Coal Soc. 1999, 24, 581–585. [Google Scholar]
- Huang, Q.; Wang, X.; He, Y.; Li, K.; Li, J.; Liu, J.; Wang, S. Activated roof structure and support dynamic load inshallow-buried close coal seam mining. J. Min. Saf. Eng. 2022, 39, 857–866. [Google Scholar]
- Zhang, J.; He, Y. Research on the fracture evolution law and combined bearing structure load of shallow buried coal seam group. Coal Sci. Technol. 2023, 51, 65–76. [Google Scholar]
- Ren, Y. Presentation and verification of “cantilever beam-articulated rock beam” composite structure in shallow buried working face. J. China Coal Soc. 2019, 44, 1–8. [Google Scholar]
- Shang, T.; Wang, J.; Liu, Y.; Suo, Y.; Wang, Z.; Fu, S.; Zhang, F. A Study on the Instability Mechanisms of Coal Pillars in Shallow Coal Seams Group Mining. Adv. Civ. Eng. 2023, 2023, 4646450. [Google Scholar] [CrossRef]
- Lai, X.; Zhu, H.; Guo, Z.; Gu, H.; Li, X.; Zhao, Q.; Shan, P. Breaking dynamic load mechanism and application of high key strata in gully area of shallow coal seam. J. Min. Saf. Eng. 2024, 41, 879–888. [Google Scholar]
- Lai, X.; Qiao, H.; Shan, P.; Wu, L.; Zhu, H.; Zhao, H.; Dai, Z. Evolution characteristics of water flowing fracture in shallow buried coal seam in water abundance gully valley area. Coal Sci. Technol. 2024, 52, 1–11. [Google Scholar]
- Liu, C.; Li, J.; Zhao, J.; Chen, Y.; Zhang, H.; Yu, X. Dynamic strata pressure mechanism and distribution characteristics of overburden air leakage fissures in the condition of shallow thick coal seam in gully area. J. Min. Saf. Eng. 2023, 40, 965–971. [Google Scholar]
- Zhang, J.; Long, J.; Yang, T.; Wang, B.; Zhou, F. Study on dynamic loading mechanism of mining in gully area of shallow coal seam. J. Min. Saf. Eng. 2019, 36, 1222–1227. [Google Scholar]
- Xie, X.; Hou, E.; Zhao, B.; Feng, D.; Hou, P. Investigating the Evolution Law and Fracture Mechanism of Overlying Coal-Bearing Strata Caused by Shallow Multi-Seam Mining in a Gully Area. Appl. Sci. 2025, 15, 2649. [Google Scholar] [CrossRef]
- Fu, Y.; Li, C.; He, Y. Research on the Movement of Overlying Strata in Shallow Coal Seams with High Mining Heights and Ultralong Working Faces. Appl. Sci. 2024, 14, 4685. [Google Scholar] [CrossRef]
- Wang, X.F.; Zhang, D.S.; Zhang, C.G.; Fan, G.W. Mechanism of mining-induced slope movement for gullies overlaying shallow coal seams. J. Mt. Sci. 2013, 10, 388–397. [Google Scholar] [CrossRef]
- Wang, B.; Liu, H.; Liu, D.; Zhang, J.; Lin, H. Study on Deformation Mechanism and Surrounding Rock Strata Control in End-Mining Retracement Roadway in Closely Spaced Coal Seams. Appl. Sci. 2025, 15, 436. [Google Scholar] [CrossRef]
- Huang, Q.; Wang, X.; Hu, J.; Zhou, H.; Li, J.; He, Y. Activated roof structure and dynamic load of support under goaf of shallow-buried close coal seams in loess hilly area. J. Min. Saf. Eng. 2023, 40, 983–990. [Google Scholar]
- Di, S.; Wang, J.; Li, D.; Qi, X.; Wang, Y. Influence of hill topography on ground pressure feature of shallow buried 7.0 m working face. China Saf. Sci. J. 2018, 28, 164–169. [Google Scholar]
- Wang, Y.; Zhang, X.; Xu, Q. Study on strata behavior characteristics of fully mechanized mining face at near shallow buried coal seam with superimposed static and dynamic loading in hill terrain. J. Saf. Sci. Technol. 2017, 13, 115–121. [Google Scholar]
- Wang, X.; Zhang, D.; Fan, G.; Zhang, C. Underground pressure characteristics analysis in back-gully mining of shallow coal seam under a bedrock gully slope. Min. Sci. Technol. 2011, 21, 23–27. [Google Scholar]
- Zhao, Y.; Wang, S.; Zou, Y.; Wang, X.; Huang, B.; Zhang, X. Pressure-Arching Characteristics of Fractured Strata Structure during Shallow Horizontal Coal Mining. Teh. Vjesn. 2018, 25, 1457–1466. [Google Scholar]
- Yang, D. Analysis on fracture mechanics theory of roof cutting instability mechanism with large mining height face in shallow coal seam. Front. Earth Sci. 2023, 10, 900144. [Google Scholar] [CrossRef]
- Du, F.; Yuan, R.; Zheng, J.; Song, G. Mechanism of abnormal strata pressure of mining under coal pillar in close distance shallow coal seams. J. China Coal Soc. 2017, 42, 24–29. [Google Scholar]
- Zhao, Y.; Wang, S.; Hagan, P.; Guo, W. Evolution Characteristics of Pressure-Arch and Elastic Energy during Shallow Horizontal Coal Mining. Teh. Vjesn. 2018, 25, 867–875. [Google Scholar]
- Hu, S.; Yu, T. Study on overlying rock movement and mine pressure behavior in shallow-buried close coal multi-seam mining. Alex. Eng. J. 2024, 105, 578–587. [Google Scholar] [CrossRef]
- Liu, Y.; Kong, D.; Li, P.; Wen, Z.; Li, F.; Zuo, Y.; Wu, G. The migration and evolution law of overlying strata and the instability and failure characteristics of end face roof under the condition of ascending mining in close distance coal seam: Case study. Eng. Fail. Anal. 2024, 165, 108809. [Google Scholar]
- Zhang, J.; Sun, J.; He, Y.; Zhang, Y.; Pang, H.; Wu, H.; Zhang, J.; Peng, B. Study on floor stress distribution law and roadway layout of contiguous coal seams. Coal Sci. Technol. 2024, 52, 11–22. [Google Scholar]
- Yuan, Y.; Yuan, C.F.; Zhu, C.; Liu, H.X.; Wang, S.Z. Study on the disaster reduction mechanism of presplitting blasting and reasonable blasting parameters for shallowly buried remnant pillars. Energy Sci. Eng. 2019, 7, 2884–2894. [Google Scholar] [CrossRef]
- Lan, T.; Liu, Y.; Yuan, Y.; Liu, H.; Liu, H.; Zhang, S.; Wang, S. Mine pressure behavior law of isolated island working face under extremely close goaf in shallow coal seam. Sci. Rep. 2023, 13, 20576. [Google Scholar] [CrossRef]
- Ren, Y. Influence of surface mountain load on mining pressure of shallow buried deep working face. Min. Saf. Environ. Prot. 2020, 47, 77–81+87. [Google Scholar]
- Ju, J.; Xu, J. Surface stepped subsidence related to top-coal caving longwall mining of extremely thick coal seam under shallow cover. Int. J. Rock Mech. Min. Sci. 2015, 78, 27–35. [Google Scholar] [CrossRef]
- Li, L.; Wu, G.; Liu, Q. Study on Overburden Movement and Fissure Evolution Law of Protective Layer Mining in Shallow Coal Seam. Energies 2022, 15, 1831. [Google Scholar] [CrossRef]
- Makarov, V.; Perov, M.; Bilan, T.; Novoseltsev, O.; Zaporozhets, A. Technological State of Coal Mining in Ukraine. In Geomining: Studies in Systems, Decision and Control; Springer: Cham, Switzerland, 2024; Volume 224, pp. 31–34. [Google Scholar]
- Makarov, V.; Kaplin, M.; Bilan, T.; Perov, M.; Zaporozhets, A. Forecasting the Technological Development of the Coal Industry. In Geomining: Studies in Systems, Decision and Control; Springer: Cham, Switzerland, 2024; Volume 224, pp. 165–177. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).