Model Updating of Bridges Using Measured Influence Lines
Abstract
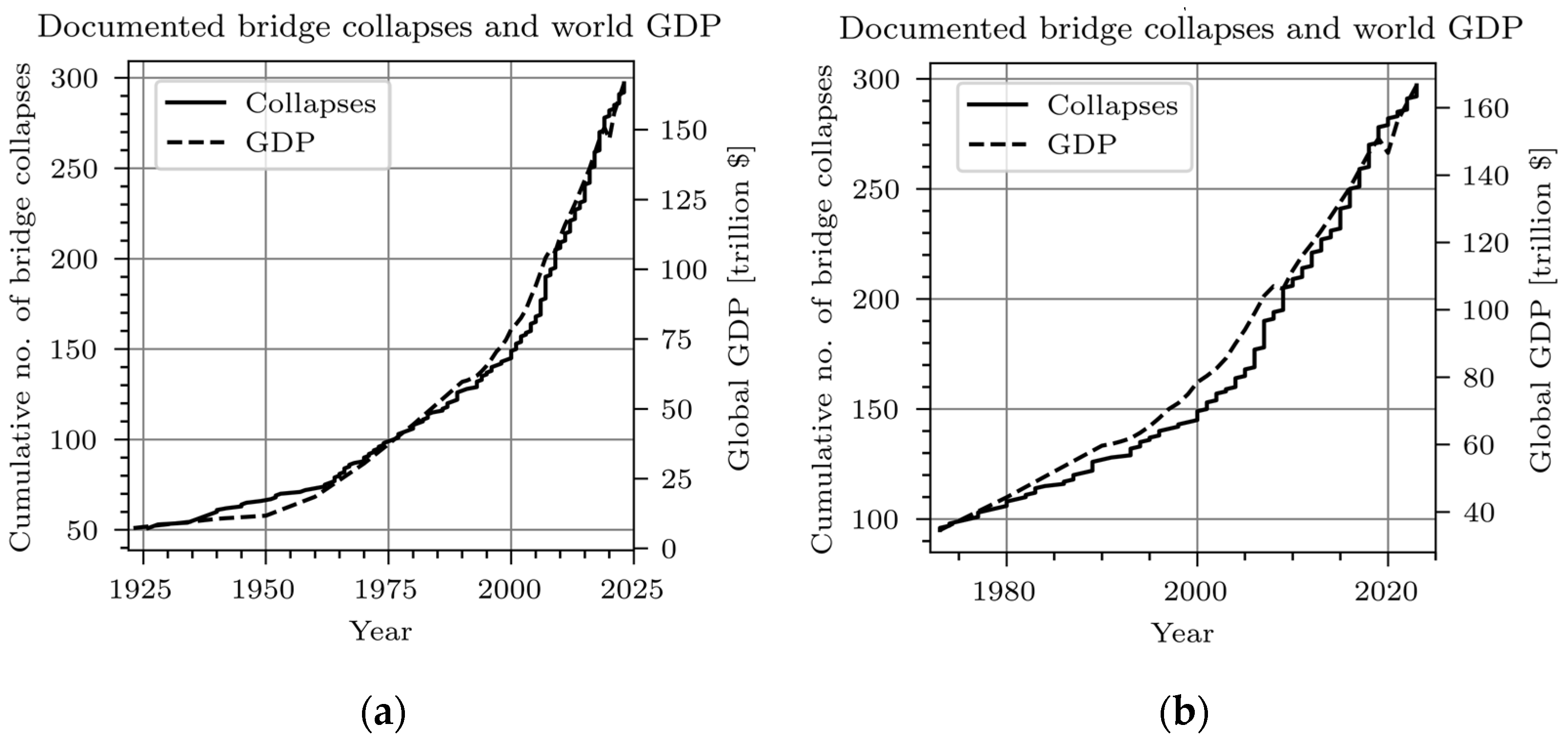
1. Introduction
2. Materials and Methods
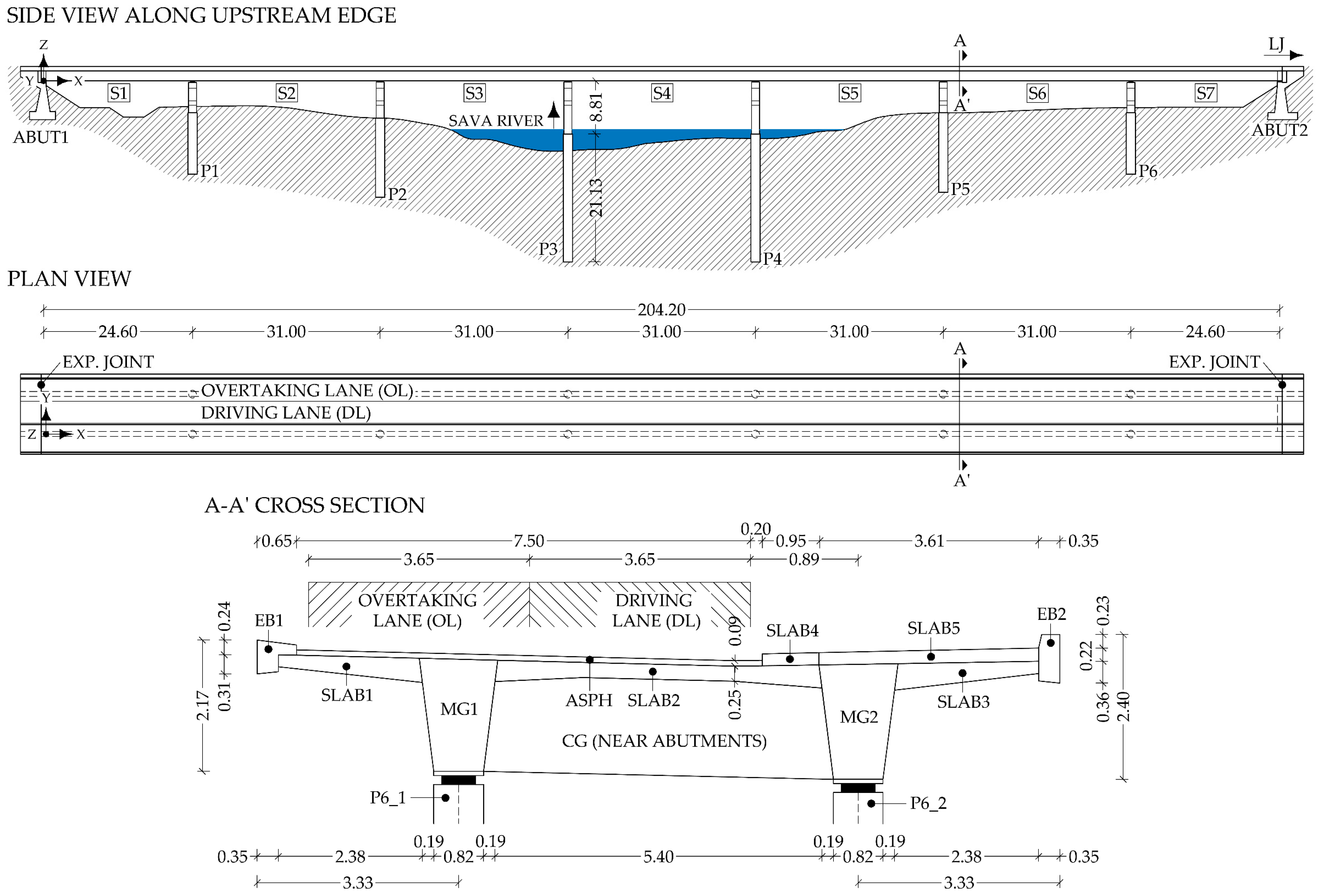
2.1. Description of the Case Study Bridge
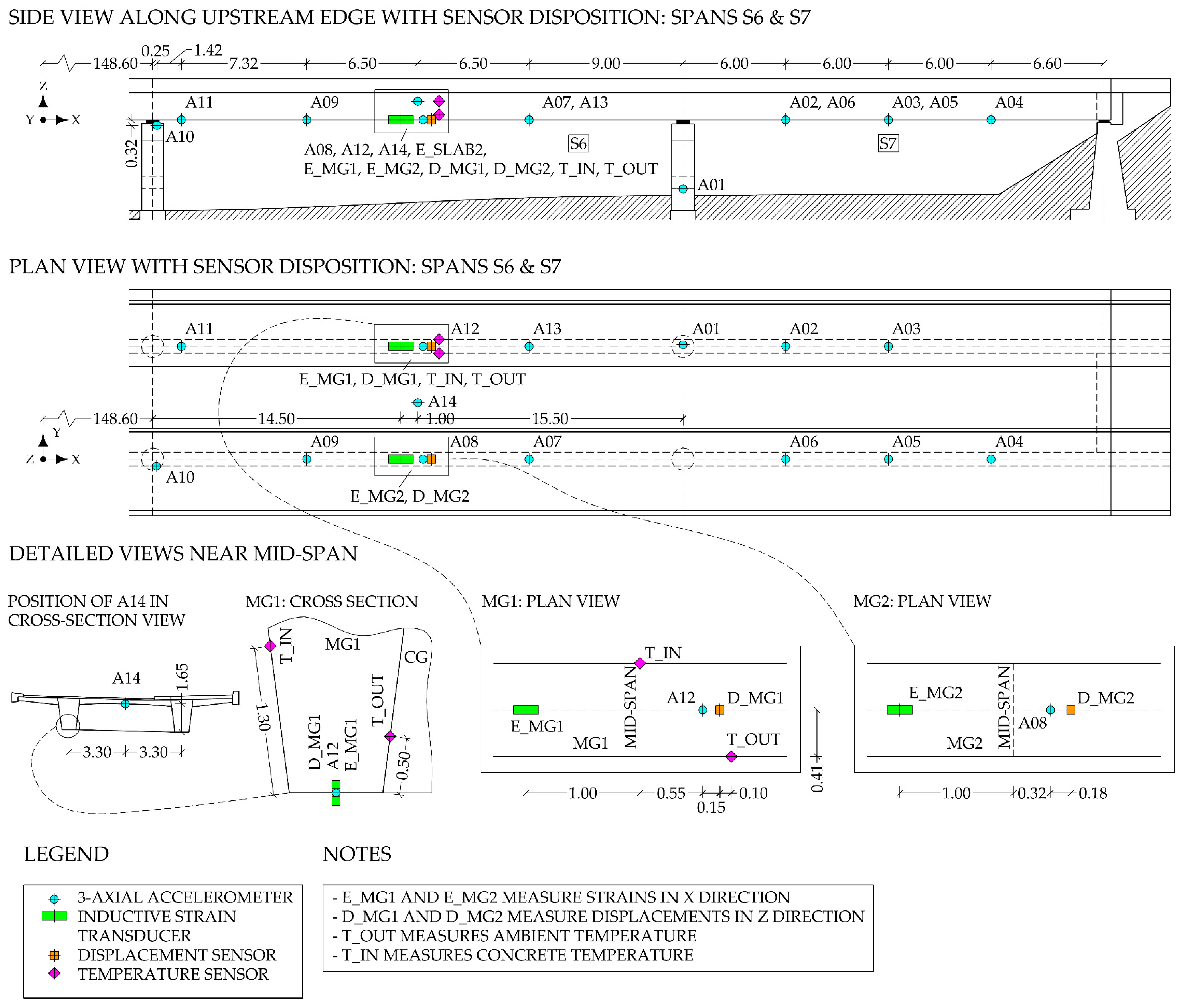
2.2. Measurements
- Fourteen Dewesoft-type IOLITEi 3xMEMS-ACC tri-axial MEMS accelerometers (Dewesoft, Trbovlje, Slovenia) measuring the ambient and traffic-induced vibrations and to determine the modal parameters of the bridge;
- Two inductive strain transducers (denoted in the paper as B-WIM sensors) measuring traffic-induced strains on both girders, and to obtain input for the B-WIM measurements;
- Two linear variable differential transformers (denoted as LVDTs or. displacement sensors) (HBK, Darmstadt, Germany) measuring traffic-induced vertical displacements on both main girders;
- Two temperature sensors, T_OUT (Dewesoft, Trbovlje, Slovenia)measuring environmental temperature and T_IN, measuring the temperature approximately 5 cm inside the main girder MG1.
2.2.1. Strain and Displacement Measurements Under the Calibration Vehicle Crossings
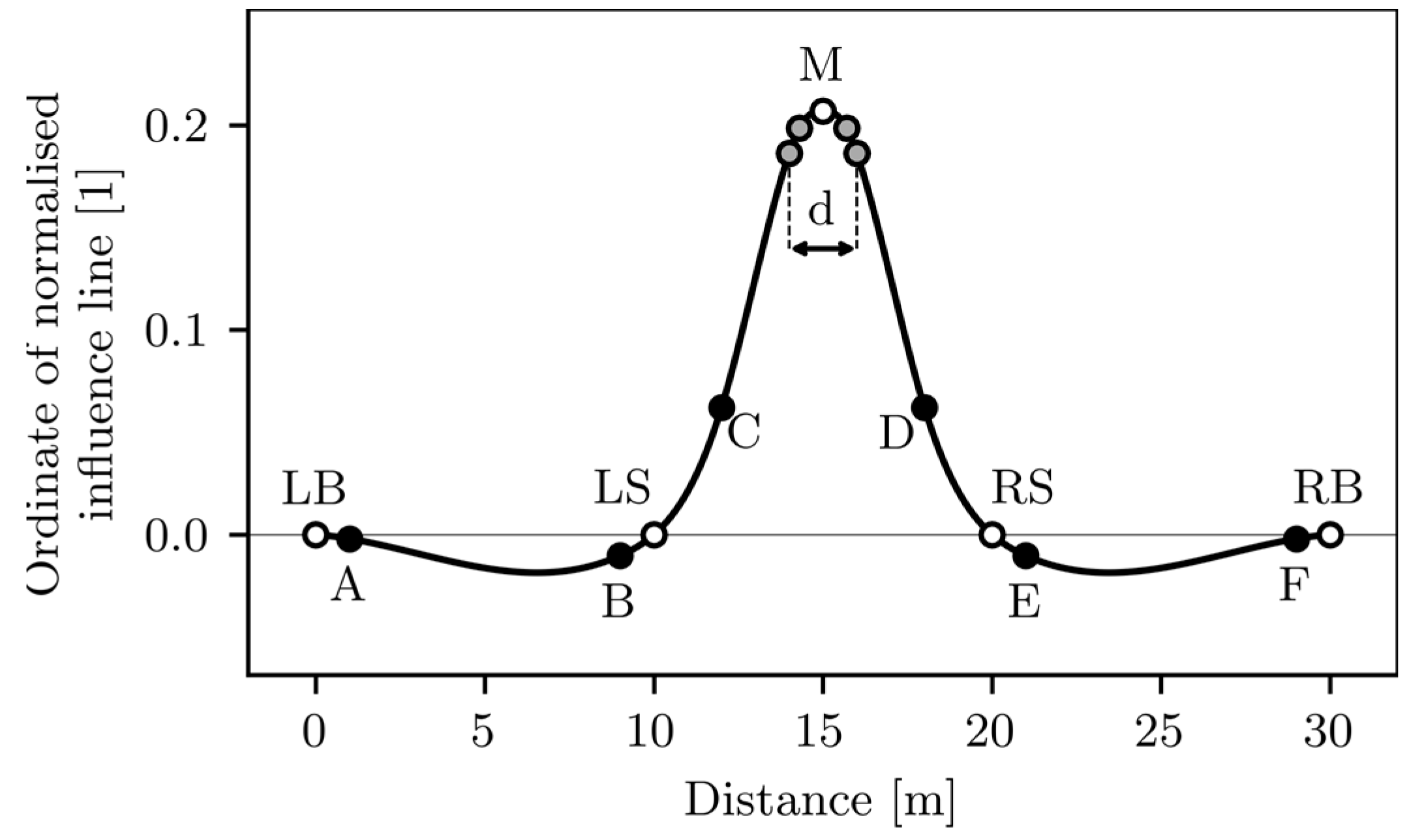
2.2.2. Extraction of the Strain Influence Line (IL) from the Strain Measurements
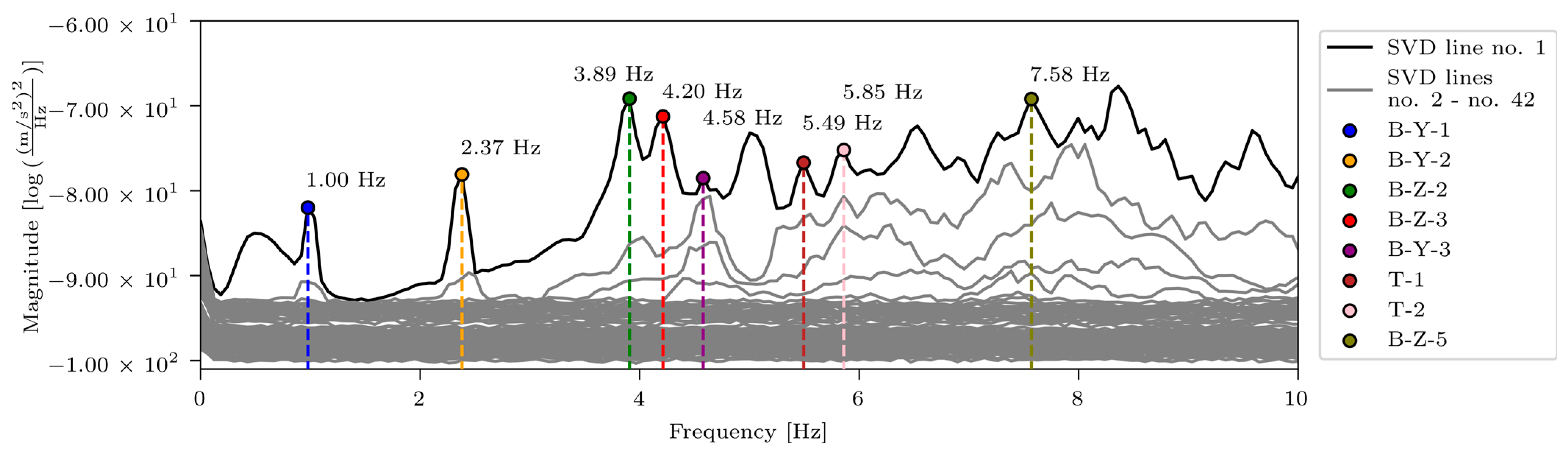
2.2.3. Ambient and Traffic-Induced Vibration Test
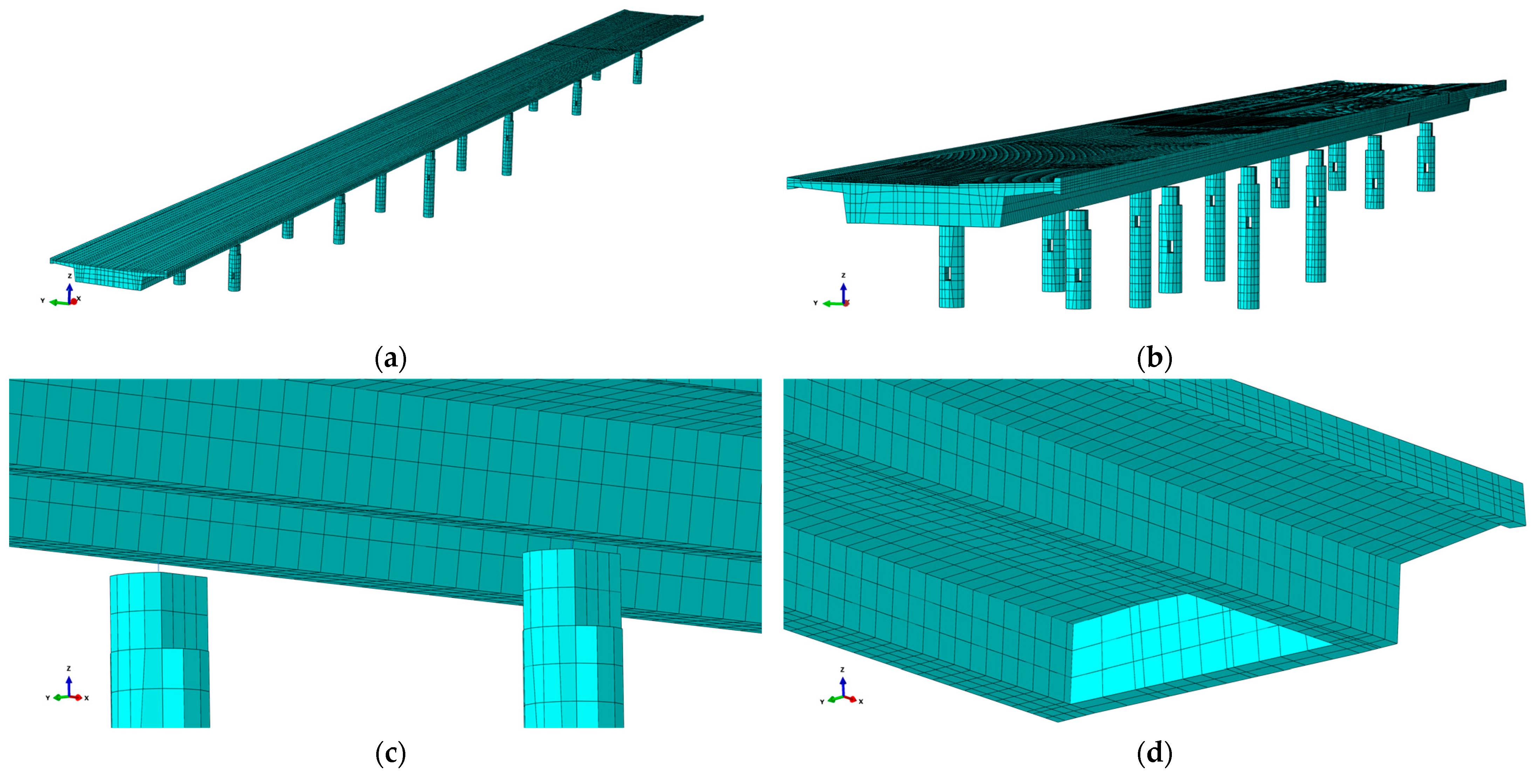
2.3. Finite Element (FE) Model
2.3.1. Geometry and Materials
| Element | Abbreviation | Young’s Modulus (GPa) | Poisson Ratio | Density (t/m3) |
|---|---|---|---|---|
| Asphalt | ASPH | 8.00 | 0.35 | 2.582 |
| Edge beam 1 | EB1 | 31.00 | 0.20 | 2.710 |
| Edge beam 2 | EB2 | 31.00 | 0.20 | 2.580 |
| Main girder 1 | MG1 | 35.00 | 0.20 | 2.500 |
| Main girder 2 | MG2 | 35.00 | 0.20 | 2.500 |
| Slab 1 | SLAB1 | 35.00 | 0.20 | 2.500 |
| Slab 2 | SLAB2 | 35.00 | 0.20 | 2.500 |
| Slab 3 | SLAB3 | 35.00 | 0.20 | 2.500 |
| Slab 4 | SLAB4 | 35.00 | 0.20 | 3.573 |
| Slab 5 | SLAB5 | 14.59 | 0.20 | 1.177 |
| Pier (bottom part) 1 | PIER_BOTTOM | 31.00 | 0.20 | 2.500 |
| Pier (upper part, bearing region) 1 | PIER_TOP | 34.00 | 0.20 | 2.500 |
| Cross girder | CG | 35.00 | 0.20 | 2.500 |
2.3.2. Interactions and Boundary Conditions
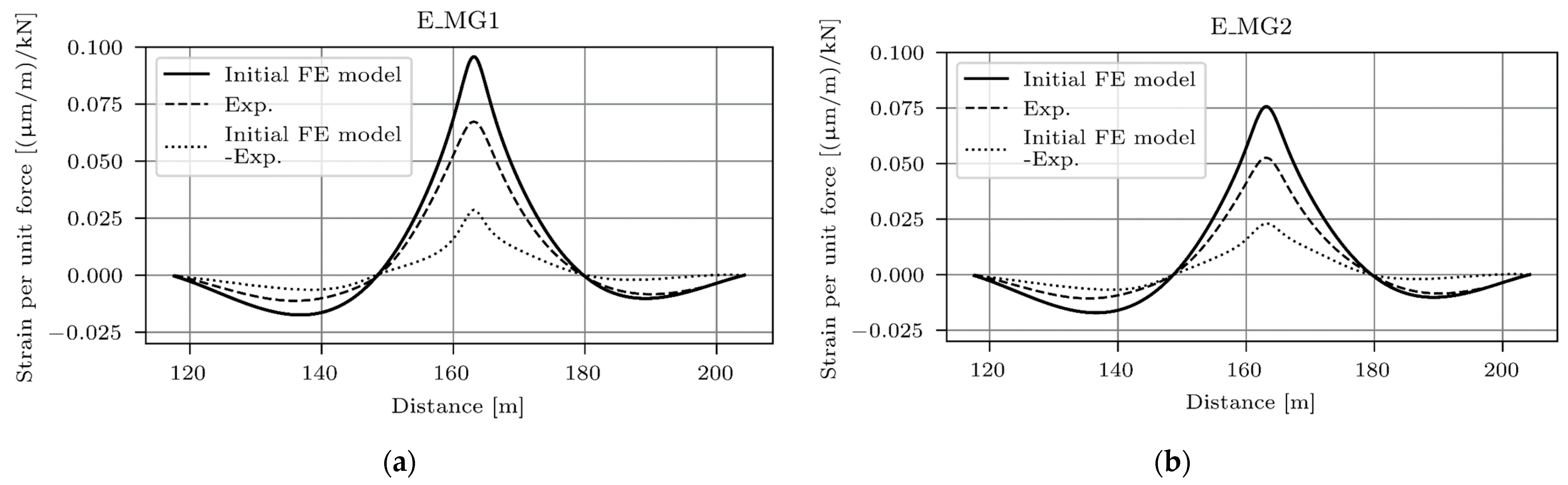
2.4. Comparison of the Initial FE Model and Measurements
2.4.1. Strain IL
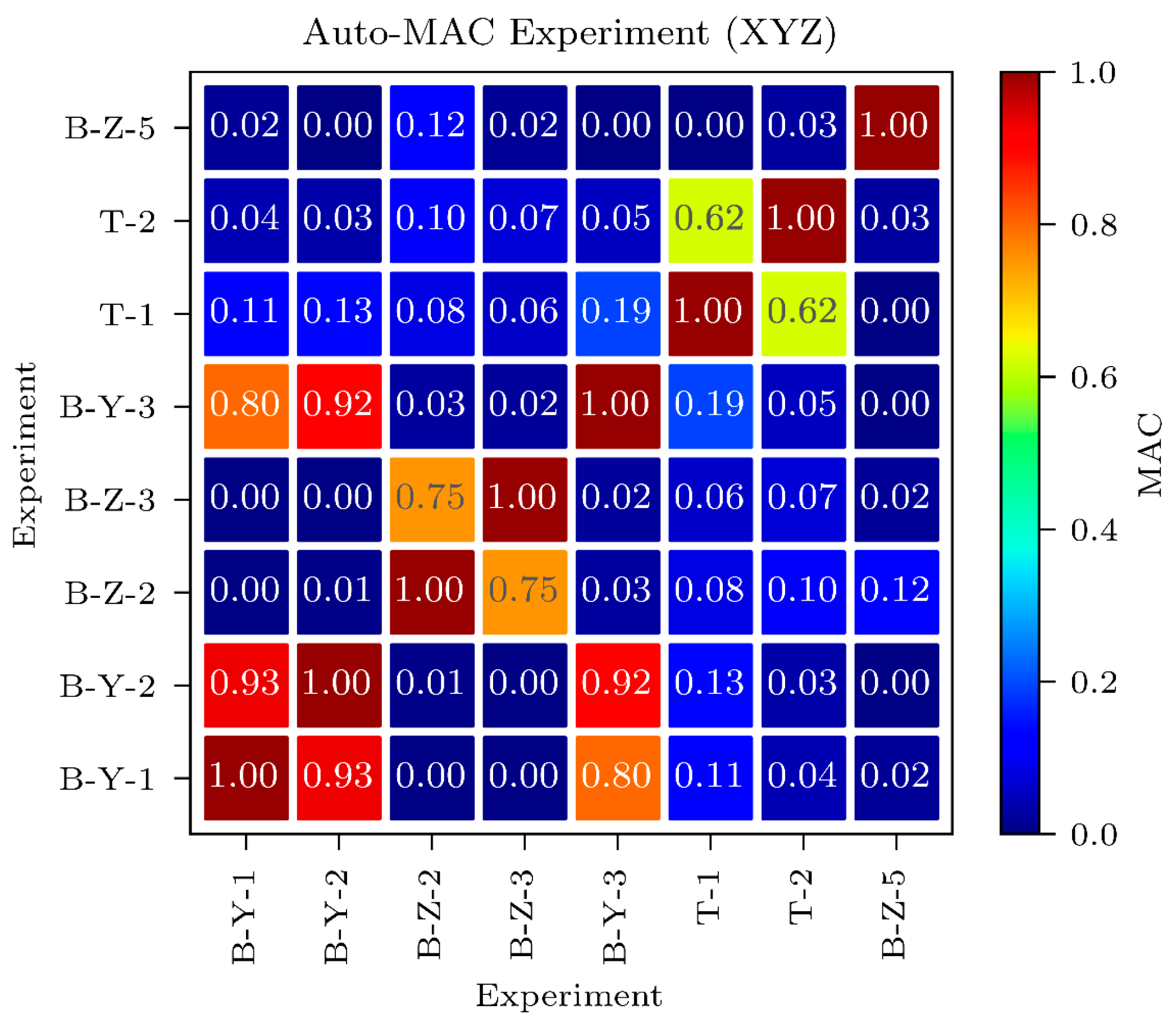
2.4.2. Natural Frequencies and Mode Shapes
2.5. Finite Element Model Updating (FEMU): Error-Domain Model Falsification (EDMF)
3. Results
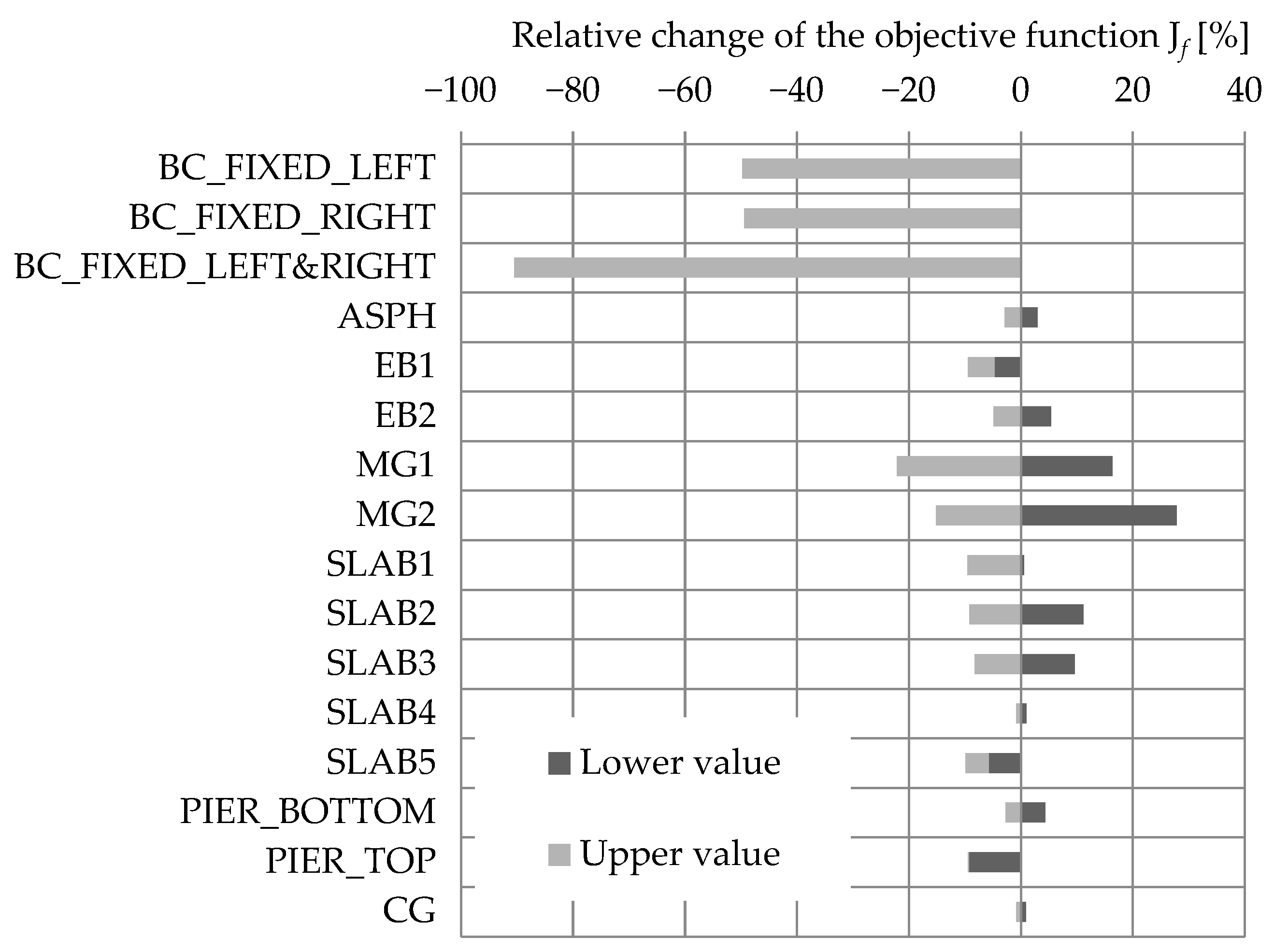
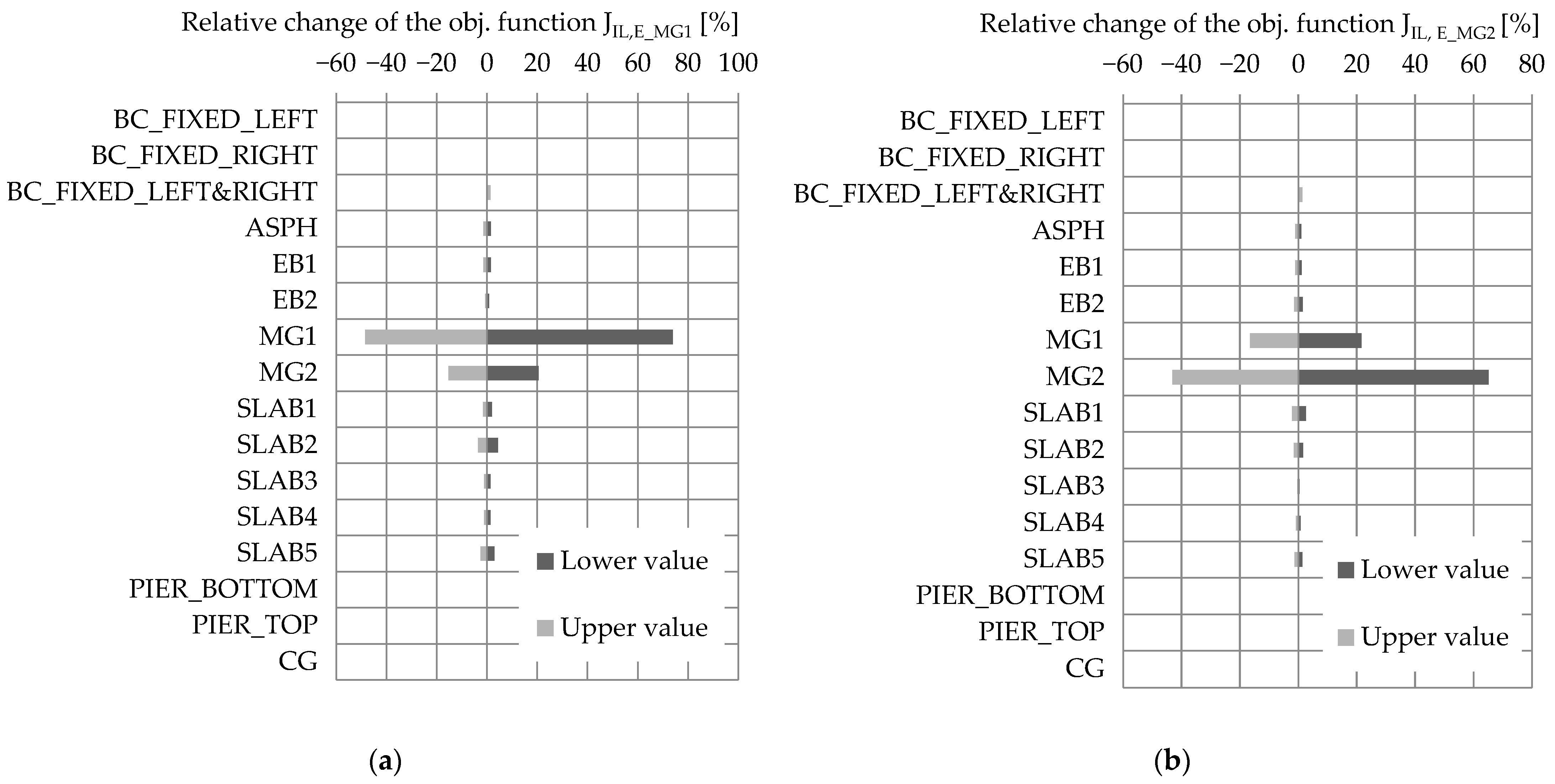
3.1. Sensitivity Study
3.1.1. Natural Frequencies
3.1.2. Strain IL
3.2. Updated FE Model
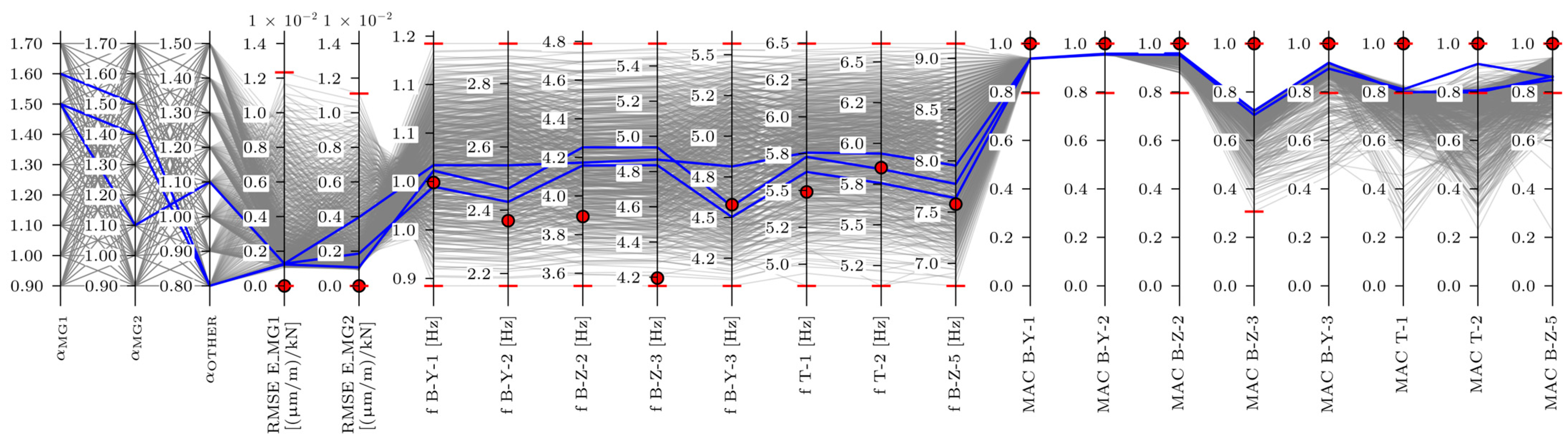
3.2.1. Frequency-Based EDMF
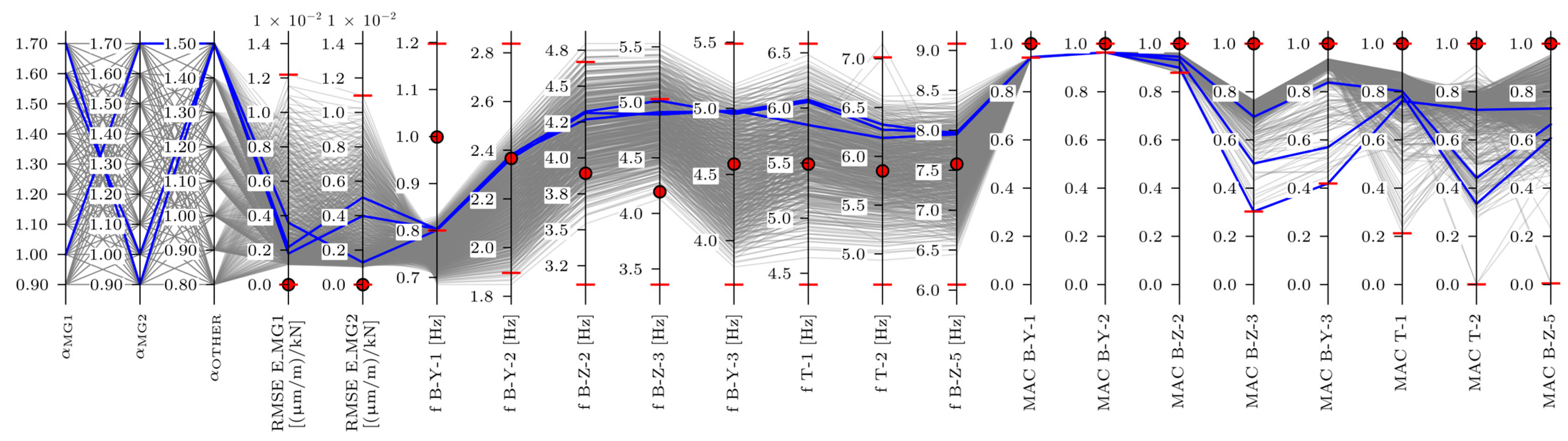
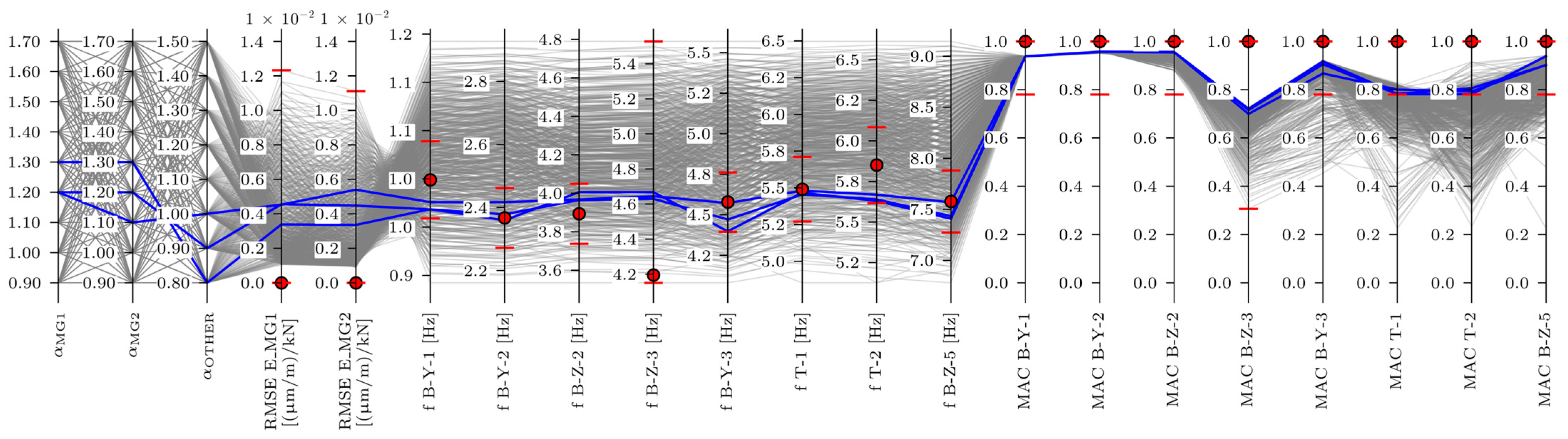
3.2.2. MAC-Based EDMF
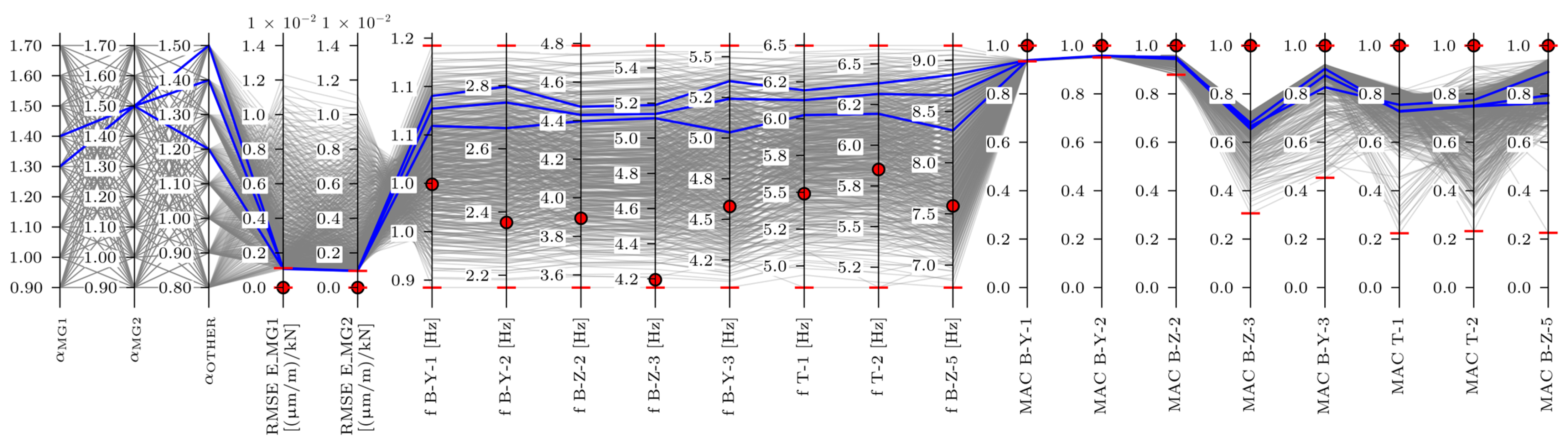
3.2.3. Frequency & MAC-Based EDMF
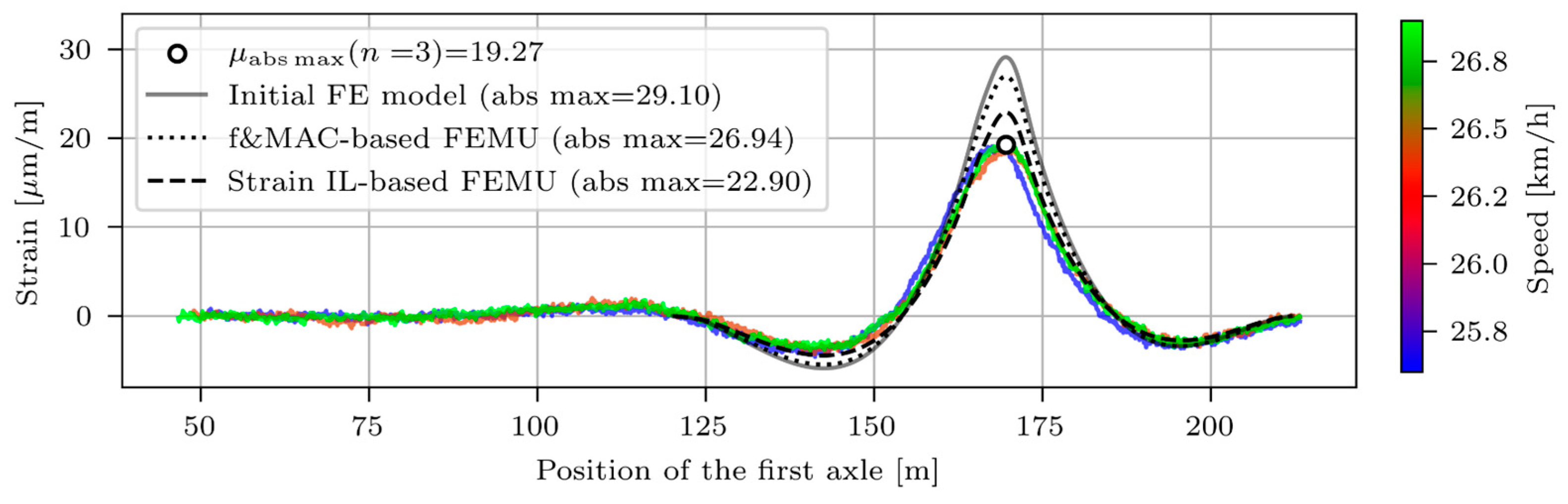
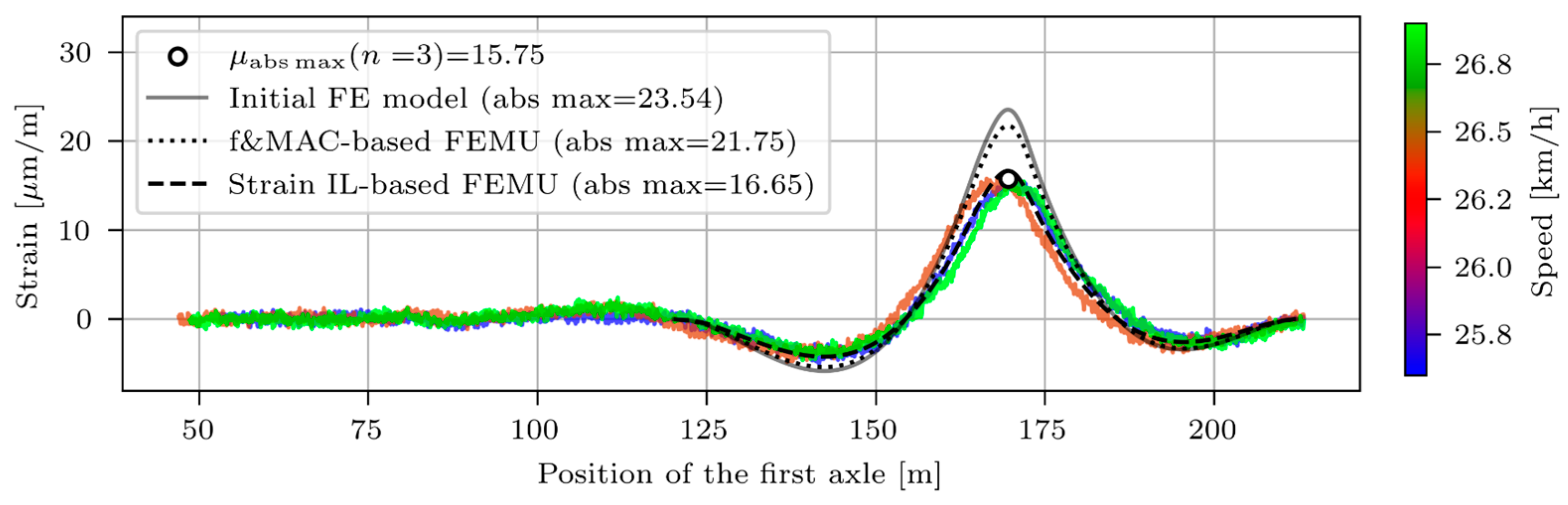
3.2.4. Strain IL-Based EDMF
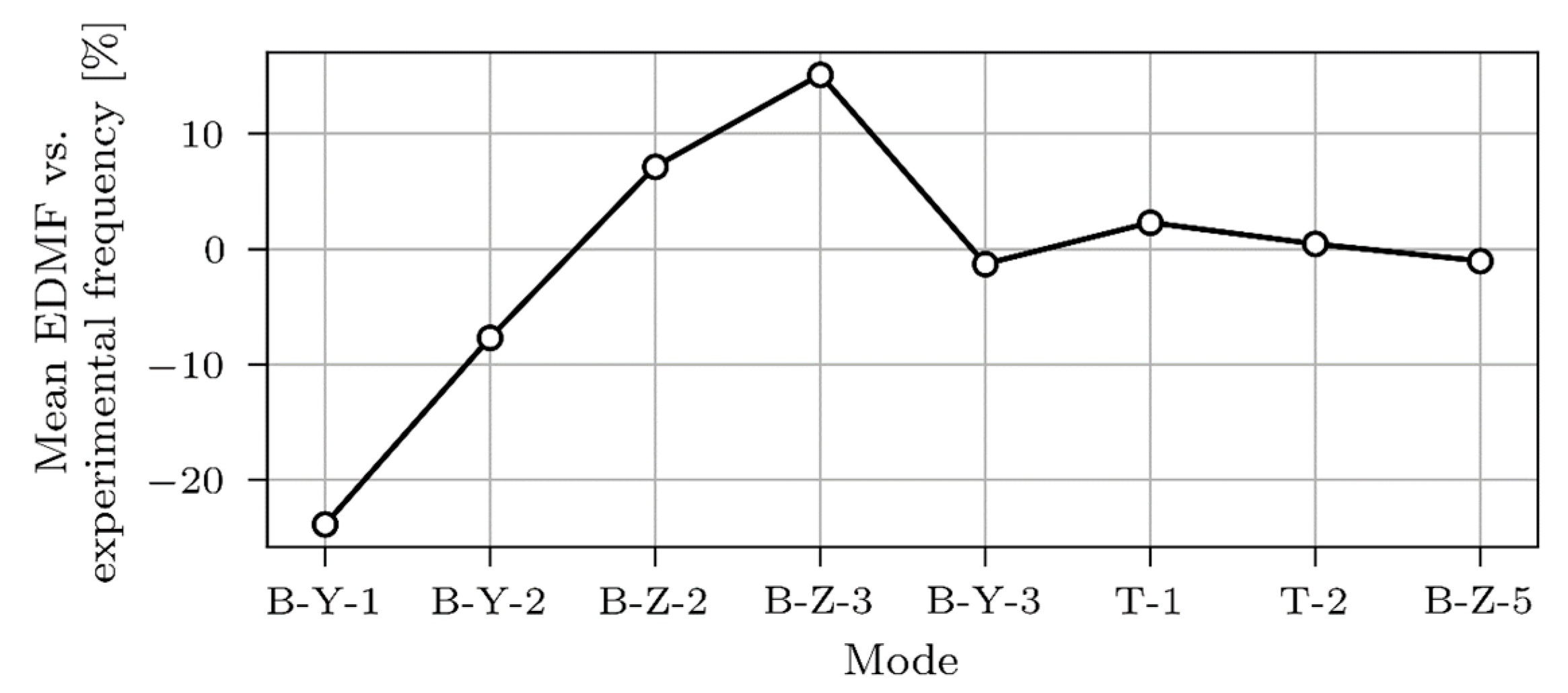
3.2.5. Comparison of EDMF Results
- Setting bearings ABUT1 and ABUT2 to fixed improved the B-Y-1 and B-Y-2 modelled vs. measured frequency values;
- Frequency-based EDMF primarily improved the frequency values; a minor improvement was also seen for E_MG1 and E_MG2 strain ILs. The MAC values decreased;
- MAC-based improved MAC values, improvement in E_MG1 and E_MG2 strain ILs was greater than that in the frequency-based EDMF;
- Frequency and MAC-based EDMF improved frequencies and MACs, closely matching the results of frequency-based EDMF (for frequencies) and MAC-based EDMF (for MAC values), while both strain ILs did not align more closely with the measured ones;
- Strain-based EDMF only improved both strain ILs. Frequency and MAC values were even worse than for the initial FE model.
3.3. Validation of the Updated FE Models with Measured Strains and Displacements Under Calibration Vehicle Passages
3.3.1. Strains
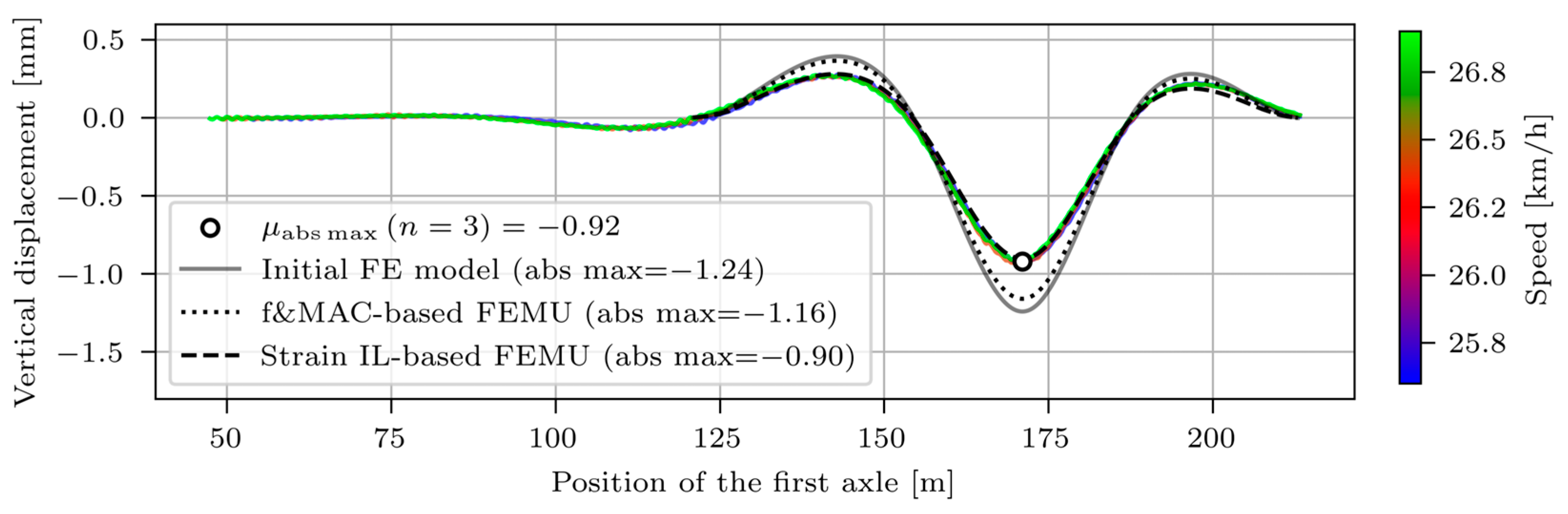
3.3.2. Displacements
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Žnidarič, A.; Pakrashi, V.; OBrien, E.J.; O’Connor, A. A Review of Road Structure Data in Six European Countries. Proc. Inst. Civ. Eng.-Urban Des. Plan. 2011, 164, 225–232. [Google Scholar] [CrossRef]
- Wikipedia Contributors. List of Bridge Failures. Available online: https://en.wikipedia.org/w/index.php?title=List_of_bridge_failures&oldid=1268499764 (accessed on 31 January 2025).
- World Bank; Bolt, J.; van Zanden, J.L. Maddison Project Database 2023; Maddison Database 2010—With Major Processing by Our World in Data. Global GDP over the Long Run—World Bank, Maddison Project Database, Maddison Database—Historical Data. Available online: https://ourworldindata.org/grapher/global-gdp-over-the-long-run (accessed on 31 January 2025).
- Mottershead, J.E.; Friswell, M.I. Model Updating In Structural Dynamics: A Survey. J. Sound Vib. 1993, 167, 347–375. [Google Scholar] [CrossRef]
- Hester, D.; Koo, K.; Xu, Y.; Brownjohn, J.; Bocian, M. Boundary Condition Focused Finite Element Model Updating for Bridges. Eng. Struct. 2019, 198, 109514. [Google Scholar] [CrossRef]
- Ticona Melo, L.R.; Malveiro, J.; Ribeiro, D.; Calçada, R.; Bittencourt, T. Dynamic Analysis of the Train-Bridge System Considering the Non-Linear Behaviour of the Track-Deck Interface. Eng. Struct. 2020, 220, 110980. [Google Scholar] [CrossRef]
- Wang, H.; Li, A.; Li, J. Progressive Finite Element Model Calibration of a Long-Span Suspension Bridge Based on Ambient Vibration and Static Measurements. Eng. Struct. 2010, 32, 2546–2556. [Google Scholar] [CrossRef]
- Bertola, N.J.; Smith, I.F.C. A Methodology for Measurement-System Design Combining Information from Static and Dynamic Excitations for Bridge Load Testing. J. Sound Vib. 2019, 463, 114953. [Google Scholar] [CrossRef]
- Xiao, F.; Mao, Y.; Tian, G.; Chen, G.S. Partial-Model-Based Damage Identification of Long-Span Steel Truss Bridge Based on Stiffness Separation Method. Struct. Control Heal. Monit. 2024, 2024, 5530300. [Google Scholar] [CrossRef]
- Calò, M.; Ruggieri, S.; Buitrago, M.; Nettis, A.; Adam, J.M.; Uva, G. An ML-Based Framework for Predicting Prestressing Force Reduction in Reinforced Concrete Box-Girder Bridges with Unbonded Tendons. Eng. Struct. 2025, 325, 119400. [Google Scholar] [CrossRef]
- OBrien, E.; Quilligan, M.J.; Karoumi, R. Calculating an Influence Line from Direct Measuremetns. Proc. Inst. Civ. Eng. Bridge Eng. 2005, 159, 31–34. [Google Scholar]
- Yan, W.-J.; Yuen, K.-V. A New Probabilistic Frequency-Domain Approach for Influence Line Extraction from Static Transmissibility Measurements under Unknown Moving Loads. Eng. Struct. 2020, 216, 110625. [Google Scholar] [CrossRef]
- Frøseth, G.; Rønnquist, A.; Cantero, D.; Øiseth, O. Influence Line Extraction by Deconvolution in the Frequency Domain. Comput. Struct. 2017, 189, 21–30. [Google Scholar] [CrossRef]
- Li, J.-A.; Feng, D.; Li, Z.; Zhang, H. Bridge Influence Line Identification Using an Adaptive Enhanced Variational Mode Decomposition. Eng. Struct. 2025, 326, 119561. [Google Scholar] [CrossRef]
- Žnidarič, A.; Kalin, J.; Kreslin, M. Improved Accuracy and Robustness of Bridge Weigh-in-Motion Systems. Struct. Infrastruct. Eng. 2017, 14, 13. [Google Scholar] [CrossRef]
- Žnidarič, A.; Kalin, J. Using Bridge Weigh-in-Motion Systems to Monitor Single-Span Bridge Influence Lines. J. Civ. Struct. Health Monit. 2020, 10, 743–756. [Google Scholar] [CrossRef]
- DEWESoft DewesoftX, Version 2023.5; Available online: https://dewesoft.com/products/dewesoftx (accessed on 26 December 2023).
- Jacob, B.; OBrien, E.J.; Jehaes, S. (Eds.) Weigh-in-Motion of Road Vehicles: Final Report of the COST 323 Action; LCPC: Paris, France, 2002. [Google Scholar]
- Žnidarič, A. Influence of Number and Quality of Weigh-in-Moiton Data on Evaluation of Load Effects on Bridges. Ph.D. Thesis, University of Ljubljana, Ljubljana, Slovenia, 2017. [Google Scholar]
- Moses, F. Weigh-in-Motion System Using Instrumented Bridges. J. Transp. Eng. 1979, 105, 233–249. [Google Scholar] [CrossRef]
- Zheng, X.; Yang, D.H.; Yi, T.H.; Li, H.N. Development of Bridge Influence Line Identification Methods Based on Direct Measurement Data: A Comprehensive Review and Comparison. Eng. Struct. 2019, 198, 109539. [Google Scholar] [CrossRef]
- Solution, S.V. ARTeMIS Modal Pro. Available online: https://www.svibs.com/artemis-modal-pro/ (accessed on 26 December 2023).
- Dassault Systemes User Assistance; R2023x; Dassault Systèmes: Vélizy-Villacoublay, France, 2023.
- Technical Report About the General Project of the Tomačevo Bridge; Industrijski projektni zavod Zagreb: Zagreb, Croatia, 1980. (In Croatian)
- Cross Section of the Tomačevo Bridge; Industrijski projektni zavod Zagreb: Zagreb, Croatia, 1980. (In Croatian)
- Detail of the Sidewalk of the Tomačevo Bridge; Industrijski projektni zavod Zagreb: Zagreb, Croatia, 1980. (In Croatian)
- Static Analysis of the Tomačevo Bridge; Industrijski projektni zavod Zagreb: Zagreb, Croatia, 1980. (In Croatian)
- Goulet, J.-A.; Smith, I.F.C. Structural Identification with Systematic Errors and Unknown Uncertainty Dependencies. Comput. Struct. 2013, 128, 251–258. [Google Scholar] [CrossRef]
- Pai, S.G.S.; Smith, I.F.C. Methodology Maps for Model-Based Sensor-Data Interpretation to Support Civil-Infrastructure Management. Front. Built Environ. 2022, 8, 801583. [Google Scholar] [CrossRef]
- Schlune, H.; Plos, M.; Gylltoft, K. Improved Bridge Evaluation through Finite Element Model Updating Using Static and Dynamic Measurements. Eng. Struct. 2009, 31, 1477–1485. [Google Scholar] [CrossRef]
- Jiménez-Alonso, J.F.; Naranjo-Perez, J.; Pavic, A.; Sáez, A. Maximum Likelihood Finite-Element Model Updating of Civil Engineering Structures Using Nature-Inspired Computational Algorithms. Struct. Eng. Int. 2021, 31, 326–338. [Google Scholar] [CrossRef]
- Cao, W.-J.; Koh, C.G.; Smith, I.F.C. Enhancing Static-Load-Test Identification of Bridges Using Dynamic Data. Eng. Struct. 2019, 186, 410–420. [Google Scholar] [CrossRef]
- Hekič, D.; Kosič, M.; Kalin, J.; Žnidarič, A.; Anžlin, A. Challenges of Implementing Bridge Weigh-in-Motion on a Century-Old Steel-Riveted Railway Bridge. In Bridge Maintenance, Safety, Management, Digitalization and Sustainability; CRC Press: Boca Raton, FL, USA, 2024; pp. 1429–1436. [Google Scholar]
- Hekič, D.; Ribeiro, D.; Anžlin, A.; Žnidarič, A.; Češarek, P. Improved Finite Element Model Updating of a Highway Viaduct Using Acceleration and Strain Data. Sensors 2024, 24, 2788. [Google Scholar] [CrossRef] [PubMed]
- Ewins, D.J. Model Validation: Correlation for Updating. Sadhana 2000, 25, 221–234. [Google Scholar] [CrossRef]
- Allemang, R. The Modal Assurance Criterion—Twenty Years of Use and Abuse. Sound Vib. 2003, 37, 14–23. [Google Scholar]
- Rainieri, C.; Fabbrocino, G. Operational Modal Analysis of Civil Engineering Structures, An Introduction and a Guide for Applications; Springer: New York, NY, USA, 2014; ISBN 978-1-4939-0767-0. [Google Scholar]
- Solís, M.; He, L.; Lombaert, G.; De Roeck, G. Finite Element Model Updating of a Footbridge Based on Static and Dynamic Measurements. In Proceedings of the 4th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Kos Island, Greece, 12–14 June 2013; pp. 1432–1449. [Google Scholar] [CrossRef]
- Anžlin, A.; Hekič, D.; Kalin, J.; Kosič, M.; Ralbovsky, M.; Lachinger, S. Assets4rail Deliverable D3.3: Improved Fatigue Consumption Assessment Through Structural and On-Board Monitoring; European Comission: Brussels, Belgium, 2020. [Google Scholar]




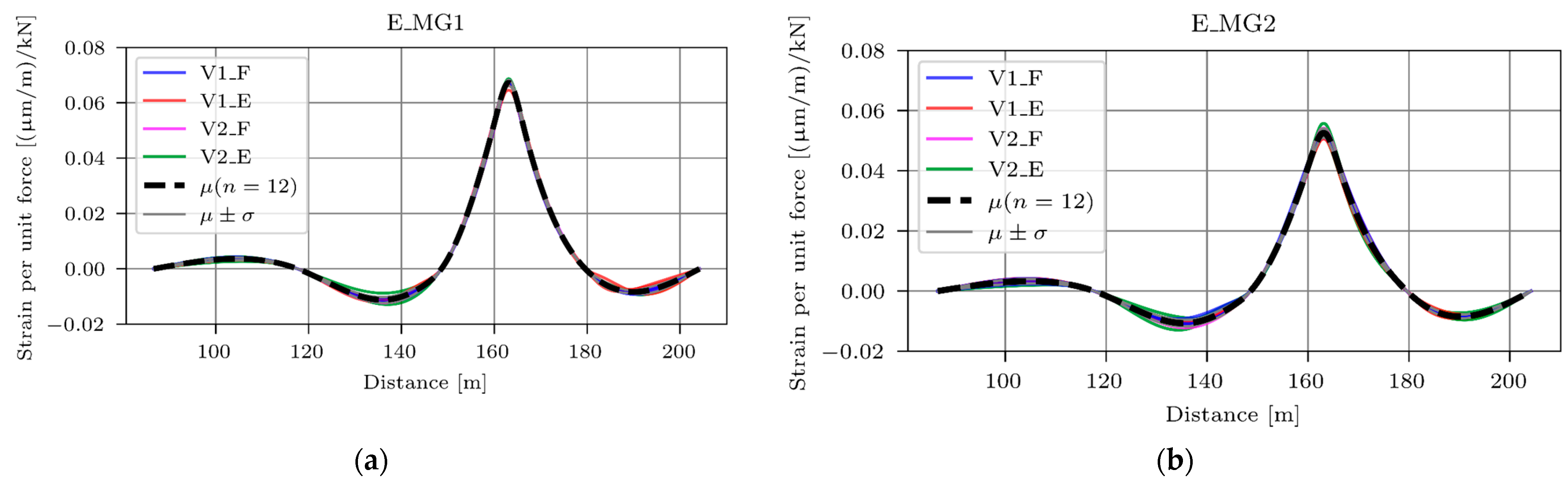




| 1st Axle | 2nd Axle | 3rd Axle | 4th Axle | 5th Axle | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Vehicle 1 | Load (kN) | Spacing (m) | Load (kN) | Spacing (m) | Load (kN) | Spacing (m) | Load (kN) | Spacing (m) | Load (kN) | GVW (kN) |
| V1_F | 68.67 | 3.42 | 73.58 | 1.37 | 71.61 | / | / | / | / | 213.86 |
| V1_E | 57.88 | 3.42 | 37.28 | 1.37 | 36.30 | / | / | / | / | 131.45 |
| V2_F | 69.65 | 3.60 | 90.25 | 2.82 | 64.75 | 1.31 | 61.80 | 1.31 | 59.84 | 346.29 |
| V2_E | 56.90 | 3.60 | 29.43 | 2.82 | 14.72 | 1.31 | 15.70 | 1.31 | 14.72 | 131.45 |
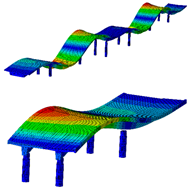
| B-Y-1 | B-Y-2 | B-Z-2 | B-Z-3 |
| 1.00 Hz | 2.37 Hz | 3.89 Hz | 4.20 Hz |
 | 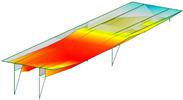 | 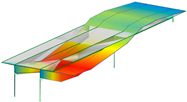 | 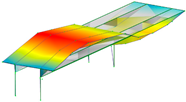 |
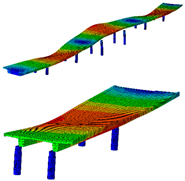
| B-Y-3 | T-1 | T-2 | B-Z-5 |
| 4.58 Hz | 5.49 Hz | 5.85 Hz | 7.58 Hz |
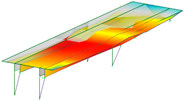 |  | 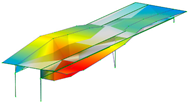 | 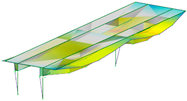 |
| Bearing | Position (Abutment, Pier) | Translational Stiffness (kN/m) | Vertical Stiffness (kN/m) | Rotational Stiffness (kNm) | |
|---|---|---|---|---|---|
| X Direction | Y Direction | ||||
| Elastomeric bearing type 1 | P1, P6 | 3.18 × 103 | 3.18 × 103 | 1.77 × 106 | 3.41 × 104 |
| Elastomeric bearing type 2 | P2, P3 | 3.61 × 103 | 3.61 × 103 | 2.01 × 106 | 3.90 × 104 |
| Elastomeric bearing type 3 | P4, P5 | 4.19 × 103 | 4.19 × 103 | 2.33 × 106 | 4.55 × 104 |
| Unidirectional pot bearing | ABUT1, ABUT2 | Free | Rigid | Rigid | Free (<0.01°) |
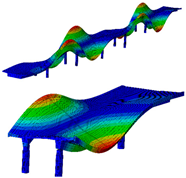
| B-Y-1 | B-Y-2 | B-Z-2 | B-Z-3 |
| 0.72 Hz | 2.01 Hz | 3.79 Hz | 4.41 Hz |
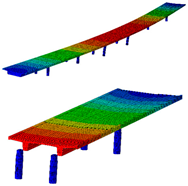 | 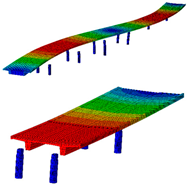 |  |  |
| B-Y-3 | T-1 | T-2 | B-Z-5 |
| 4.16 Hz | 4.98 Hz | 5.28 Hz | 6.89 Hz |
 |  | 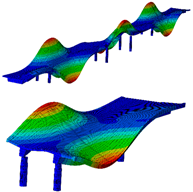 | 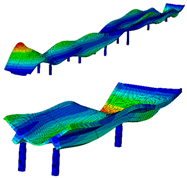 |
| Element/Variable/Property | Lower Value 1 | Upper Value 1 | Description |
|---|---|---|---|
| BC_FIXED_LEFT | DY = DZ = 0 (same as design) | DX = DY = DZ = 0 | Movements in X direction are restrained at the left abutment’s bearings |
| BC_FIXED_ RIGHT. | DY = DZ = 0 (same as design) | DX = DY = DZ = 0 | Movements in X direction are restrained at the right abutment’s bearings |
| BC_FIXED_LEFT&RIGHT | DY = DZ = 0 (same as design) | DX = DY = DZ = 0 | Movements in X direction are restrained at the left and right abutment’s bearings |
| ASPH, EB1, EB2, MG1, MG2, SLAB1, SLAB2, SLAB3, SLAB4, SLAB5, PIER_BOTTOM, PIER_TOP, CG | 0.75 × design | 1.25 × design | Young’s modulus change |
| Output | Experiment | Initial FE Model 1 | Frequency- Based | MAC- Based | Frequency and MAC-Based | Strain IL- Based | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bottom | Upper | Bottom | Upper | Bottom | Upper | Bottom | Upper | |||
| RMSE E_MG1 ((µm/m)/kN) | 0 | 0.00821 | 0.00208 | 0.00642 | 0.00123 | 0.00128 | 0.00339 | 0.00456 | 0.00107 | 0.00112 |
| RMSE E_MG2 ((µm/m)/kN) | 0 | 0.00776 | 0.00300 | 0.00709 | 0.00107 | 0.00396 | 0.00336 | 0.00540 | 0.00095 | 0.00096 |
| f B-Y-1 (Hz) | 1.00 | 0.72 | 0.97 | 0.98 | 0.99 | 1.02 | 0.97 | 0.98 | 1.06 | 1.09 |
| f B-Y-2 (Hz) | 2.37 | 2.01 | 2.41 | 2.42 | 2.43 | 2.54 | 2.36 | 2.42 | 2.67 | 2.80 |
| f B-Z-2 (Hz) | 3.89 | 3.79 | 3.96 | 3.97 | 4.16 | 4.25 | 3.96 | 4.01 | 4.40 | 4.47 |
| f B-Z-3 (Hz) | 4.20 | 4.41 | 4.62 | 4.63 | 4.84 | 4.94 | 4.63 | 4.67 | 5.11 | 5.19 |
| f B-Y-3 (Hz) | 4.58 | 4.16 | 4.56 | 4.59 | 4.50 | 4.81 | 4.40 | 4.57 | 5.03 | 5.35 |
| f T-1 (Hz) | 5.49 | 4.98 | 5.50 | 5.60 | 5.63 | 5.76 | 5.46 | 5.48 | 6.02 | 6.19 |
| f T-2 (Hz) | 5.85 | 5.28 | 5.70 | 5.84 | 5.76 | 5.94 | 5.63 | 5.67 | 6.19 | 6.38 |
| f B-Z-5 (Hz) | 7.58 | 6.89 | 7.56 | 7.61 | 7.64 | 7.95 | 7.41 | 7.57 | 8.32 | 8.86 |
| MAC B-Y-1 | 1.00 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 |
| MAC B-Y-2 | 1.00 | 0.96 | 0.95 | 0.96 | 0.95 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 |
| MAC B-Z-2 | 1.00 | 0.95 | 0.93 | 0.95 | 0.95 | 0.96 | 0.95 | 0.96 | 0.94 | 0.95 |
| MAC B-Z-3 | 1.00 | 0.76 | 0.52 | 0.70 | 0.71 | 0.72 | 0.70 | 0.72 | 0.65 | 0.68 |
| MAC B-Y-3 | 1.00 | 0.93 | 0.65 | 0.91 | 0.90 | 0.92 | 0.87 | 0.92 | 0.83 | 0.90 |
| MAC T-1 | 1.00 | 0.83 | 0.68 | 0.77 | 0.80 | 0.81 | 0.78 | 0.80 | 0.73 | 0.75 |
| MAC T-2 | 1.00 | 0.78 | 0.42 | 0.76 | 0.80 | 0.92 | 0.78 | 0.81 | 0.75 | 0.77 |
| MAC B-Z-5 | 1.00 | 0.86 | 0.83 | 0.90 | 0.85 | 0.86 | 0.90 | 0.94 | 0.76 | 0.89 |
| FEMU Results | |||
|---|---|---|---|
| Initial FE model | 1.0 | 1.0 | 1.0 |
| Frequency-based | 1.0–1.5 | 0.9–1.4 | 1.0 |
| MAC-based | 1.5–1.6 | 1.1–1.5 | 0.8–1.1 |
| Frequency and MAC-based | 1.2–1.3 | 1.1–1.3 | 0.8–1.0 |
| Strain IL-based | 1.3–1.4 | 1.5 | 1.2–1.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hekič, D.; Kalin, J.; Žnidarič, A.; Češarek, P.; Anžlin, A. Model Updating of Bridges Using Measured Influence Lines. Appl. Sci. 2025, 15, 4514. https://doi.org/10.3390/app15084514
Hekič D, Kalin J, Žnidarič A, Češarek P, Anžlin A. Model Updating of Bridges Using Measured Influence Lines. Applied Sciences. 2025; 15(8):4514. https://doi.org/10.3390/app15084514
Chicago/Turabian StyleHekič, Doron, Jan Kalin, Aleš Žnidarič, Peter Češarek, and Andrej Anžlin. 2025. "Model Updating of Bridges Using Measured Influence Lines" Applied Sciences 15, no. 8: 4514. https://doi.org/10.3390/app15084514
APA StyleHekič, D., Kalin, J., Žnidarič, A., Češarek, P., & Anžlin, A. (2025). Model Updating of Bridges Using Measured Influence Lines. Applied Sciences, 15(8), 4514. https://doi.org/10.3390/app15084514









