A Novel Fuzzy Kernel Extreme Learning Machine Algorithm in Classification Problems

Abstract

Today, numerous methods have been developed to address various problems, each with its own advantages and limitations. To overcome these limitations, hybrid structures that integrate multiple techniques have emerged as effective computational methods, offering superior performance and efficiency compared to single-method solutions. In this paper, we introduce a basic method that combines the strengths of fuzzy logic, wavelet theory, and kernel-based extreme learning machines to efficiently classify facial expressions. We call this method the Fuzzy Wavelet Mexican Hat Kernel Extreme Learning Machine. To evaluate the classification performance of this mathematically defined hybrid method, we apply it to both an original dataset and the JAFFE dataset. The method is enhanced with various feature extraction methods. On the JAFFE dataset, the algorithm achieved an average classification accuracy of 94.55% when supported with local binary patterns and 94.27% with a histogram of oriented gradients. Moreover, these results outperform those of previous studies conducted on the same dataset. On the original dataset, the proposed method was compared with an extreme learning machine and wavelet neural network, and it was found that the method has remarkable efficiency compared to the other two methods.

1. Introduction

Data have become the cornerstone of modern research and are available in a rapidly expanding range of forms. Communication and body language, for example, serve as important sources of data. Nonverbal communication, defined as the transfer of information without the use of words, accounts for about 93% of overall communication. Of this, facial expressions, body movements, and the perception of distance account for 55%, and the tone of voice for 38%. Facial expressions provide important information about people’s emotions, thoughts, and states of mind, and play a vital role in human-to-human communication. Hundreds of different variations in facial expressions complicate the process of accurate identification and classification. Research has shown that humans can make around 250,000 different expressions with their faces. Initially, psychologists focused on facial expression identification and classification analysis as a research topic. In 1978, researchers for the first time used image sets as inputs to analyze facial expressions and entered the field of image processing [1]. Since then, thanks to technological advancement, successful progress has been made in the fields of face detection, tracking, and face recognition, and work on analyzing facial expressions has accelerated [2]. Recently, simultaneously with the advancing technological environment, soft methodologies including neural networks, fuzzy structure (logic), and wavelet structure have been applied to categorize facial expressions [3,4,5]. For example, Sahoolizadeh et al. proposed a robust Gabor wavelet-based approach for facial gesture recognition and face identification that can reduce dimensions and improve discriminative capabilities as well as perform linear discriminant analysis. In their experiments, the proposed Gabor wavelet metric achieved a maximum 93% correct recognition rate on the ORL dataset without any preprocessing steps [6]. Zong and Huang showed that Kernel ELM, an extreme learning machine based on least square solutions, can be implemented using kernels for face recognition problems. The performances of kernel ELM were compared with traditional least squares support vector machines on a face recognition dataset [7]. Abidin and Alamsyah classified facial expression images into seven classes using BPNNs as classifiers. They applied three wavelet transforms (Haar, Daubechies, and Coiflet) for feature extraction and tested their method on the JAFFE database with promising results [8]. Mahmud and Maun presented an ELM-based facial expression recognition (FER) model. In their experiments, the face image is first captured and then some salient facial features such as the eyes, mouth, and nose are detected. The feature segments are extracted to form feature vectors through morphological image processing and edge detection techniques. Using ELM, facial expressions are classified into six basic categories on the JAFFE facial expression database [9]. Sailaja and Deepthi used Log Gabor wavelet filters for feature extraction in their study. This is because the wavelet structure is “sensitive to changes in light and variations in pose”. In the classification stage, SVM was run on the JAFFE database [10]. Kar et al. conducted extensive experiments on two reference datasets, JAFFE and Cohn-Kanade Extended (CK+). Their proposed methodology integrates meta-heuristic optimization algorithms (Whale) and a relatively new decomposition algorithm, Variational Mode Decomposition with KELM. The methodology was used as a classifier for the FER system [11]. Padmanabhan and Kanchikere proposed an optimized KELM algorithm with ANFIS for an efficient FR system. In the experiment, the success of the hybrid technique was compared with the performance of existing methods in terms of various parameters (precision, sensitivity, etc.) and it was shown that the proposed FR system produced more efficient results [12].

Undoubtedly, these methods have both strengths and disadvantages. Therefore, recent studies have proposed more efficient hybrid algorithms by combining their strengths and camouflaging their weaknesses. For example, Takagi and Sugeno integrated neural networks with a fuzzy structure to solve complex problems with uncertain parameters more efficiently [13]. Ho, Zhang, and Xu created a new algorithm called Fuzzy Wavelet Neural Network, which aims to test the time frequency and multiresolution of a wavelet structure and its capacity to independently stop a set of responses [14]. In ‘Extreme Learning Machine: RBF Network Case’, Huang and Siew extended the LMM structure to the radial basis function (RBF) network case [15]. Later, Huang, Zhu, and Siew introduced a single hidden layer FF neural network, called the extreme learning machine (ELM), to overcome the problems of classical neural networks such as long computation time and becoming stuck at local optima [16]. Pati and Krishnaprasad proposed the WNN structure integrating wavelet structure and neural networks to overcome the disadvantage that backpropagation approaches local minima when adopting a sigmoidal activation function [17,18]. Subasi et al. integrated wavelet neural networks (WNNs) with an FF error backpropagation artificial neural network (FEBANN) and used the algorithm as a classifier [19]. Yilmaz and Oysal introduced the FWNN model by replacing the THEN structure of the Takagi–Sugeno–Kang fuzzy rule set with a wavelet function [20]. Finally, Golestaneh, Zekri, and Sheikholeslam combined a fuzzy wavelet structure with ELM methods to reduce network complexity and introduced the fuzzy wavelet extreme learning machine (FW-ELM) framework [21].

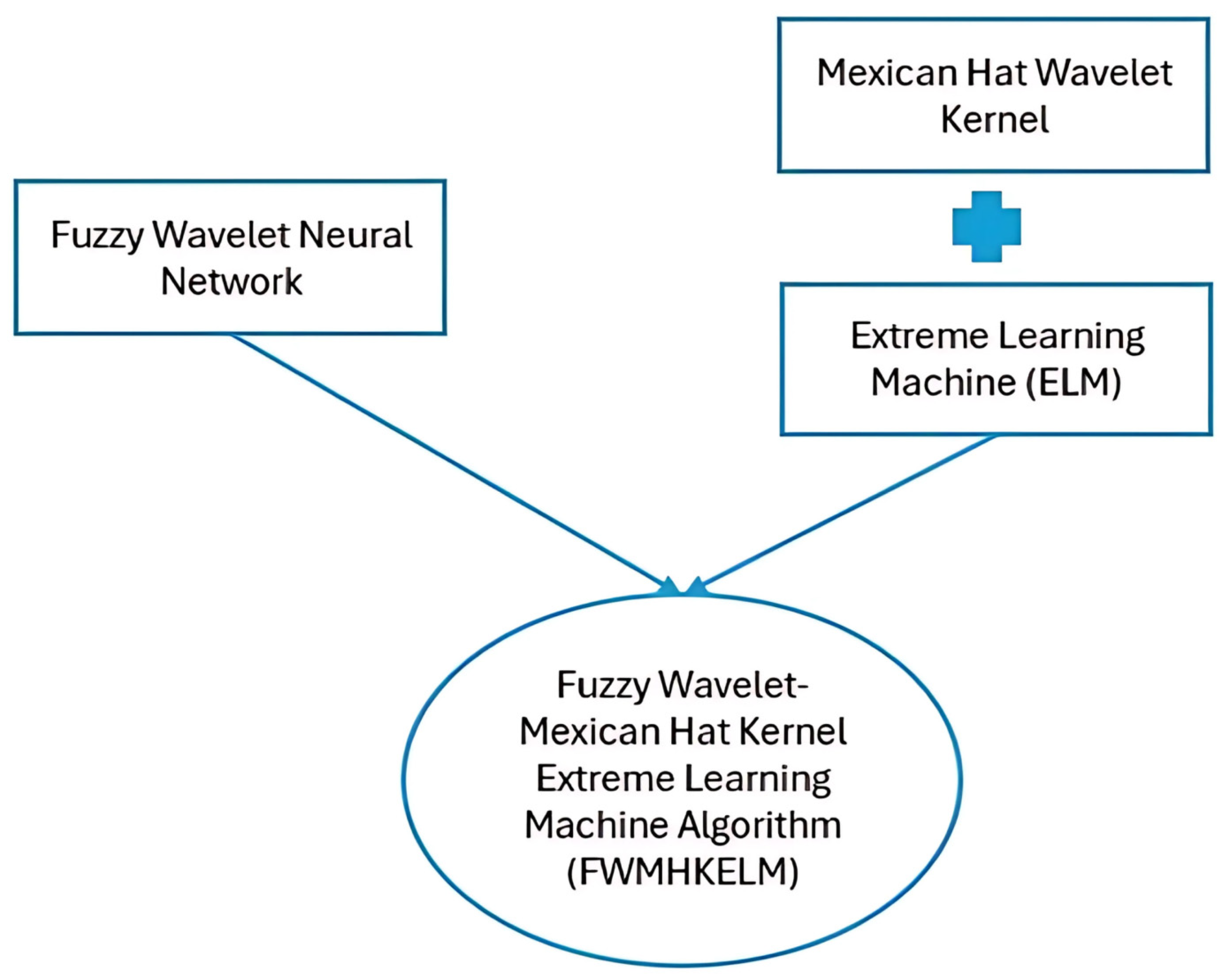
Considering all the above-mentioned issues, in this study we suggest a hybrid baseline algorithm based on fuzzy logic, wavelet structure, and kernel-based extreme learning machines (KELMs) for facial expression classification problems. The hybrid approach is composed of a fuzzy wavelet network and a KELM to form a simple network structure, improve performance accuracy, and mitigate the effect of parameters randomly assigned by the researcher, and the structure is named FWMHKELM and is presented in Figure 1.

The main motivation of the paper is to present the construction of a hybrid baseline algorithm that provides robust results in solving problems related to facial expression classification. Unlike iterative learning algorithms, our hybrid approach analytically determines the framework learning parameters and captures the diversity of network behaviors from the learning function by using wavelets with different parameters in each of the fuzzy rules. Finally, this study aims to contribute a new facial expression dataset to the literature.

The rest of the paper can be summarized as follows: In Section 2, we briefly recall the KELM and FWNN algorithms and then show the mathematical structure of our hybrid approach. In this context, we show the equivalence of a KELM with an FW model by using the proof of the theorem that the Mexican hat wavelet is an admissible ELM kernel. In the hybrid algorithm, all fuzzy rules consist of the IF-THEN structure and the algorithm uses the sigmoid activation function and the Mexican hat wavelet kernel function, respectively. In Section 3, to evaluate the performance of the hybrid algorithm, we present the experiments we designed, the datasets we used, the results of the experiments, and the comparison results with classical baseline methods to evaluate the performance of the hybrid model. In Section 4, all findings are discussed, and recommendations for future studies are made in Section 5.

2. Methods

In this section, we provide a brief overview of the FWNN and Kernel ELM methods, and then, in the final subsection, we focus on integrating a Mexican hat wavelet kernel-based ELM structure into a fuzzy wavelet structure, as the Mexican hat (MH) wavelet is an adaptive ELM kernel according to the translation–invariant theorem.

2.1. Kernel-Based ELM

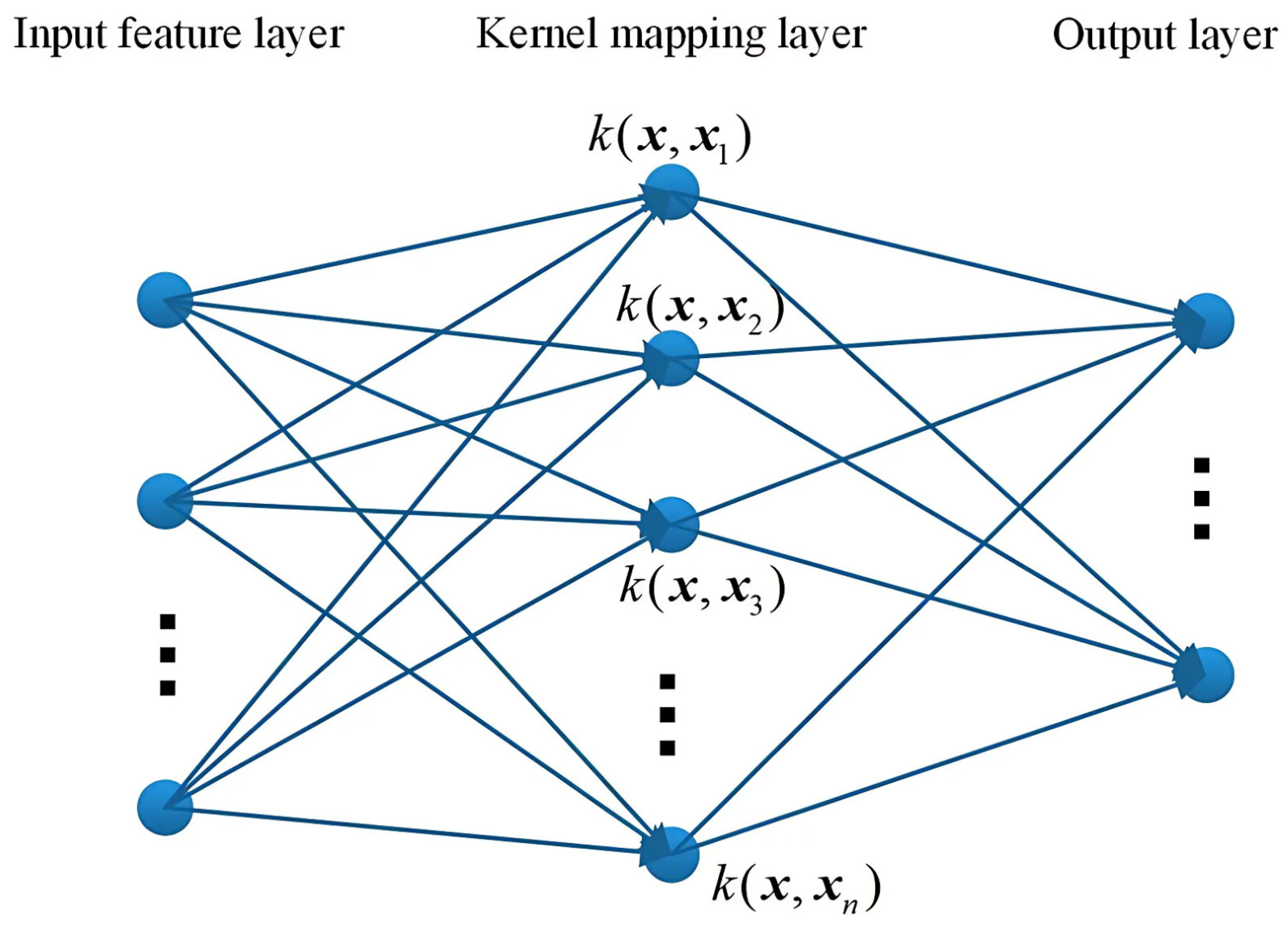
The ELM was introduced to train single hidden layer (HL) feed-forward neural networks (SLFNs), the most widely used artificial neural network structure. A traditional SLFN consists of three layers—the input, hidden, and output layers. The goal of an ELM is to minimize both training errors and the output weight norm simultaneously. To achieve this, an ELM randomly selects input weights and biases, and then computes output neurons using the Moore–Penrose generalized inverse [22]. The weakness of the classical ELM model is that involving randomly assigned weights gives rise to the computation of different accuracies in various trials. However, to eliminate this inconvenience, the proposed kernel-based ELM executes tasks with a modification of random weight assignment between the input and hidden layers [23]. A brief overview of the KELM model will follow. The structure of the KELM is shown in Figure 2.

The mathematical framework of an ELM can be summarized as in Equation (1) [24]:

$$\sum _{\mathrm{i}=1}^{\mathrm{N}}{\mathsf{\beta }}_{\mathrm{i}}\mathrm{f}\left({\mathrm{w}}_{\mathrm{i}}{\mathrm{x}}_{\mathrm{j}}+{\mathrm{b}}_{\mathrm{i}}\right)={\mathrm{t}}_{\mathrm{j}},\hspace{1em}\mathrm{i}=1,2,3,\dots ,\mathrm{K}$$

(1)

where t is the output vector, x is the input feature vector, w is the weight vector between the input layer (IL) and the hidden layer (HL), b is the bias, N is hidden nodes, and K is the training sample. Assuming optimal conditions, the difference between the target value (t) and the model output (o) is expected to be zero error [23].

In this case, Equation (1) can be rewritten as Equation (2):

$$\sum _{\mathrm{i}=1}^{\mathrm{N}}{\mathsf{\beta }}_{\mathrm{i}}\mathrm{f}\left({\mathrm{w}}_{\mathrm{i}}{\mathrm{x}}_{\mathrm{j}}+{\mathrm{b}}_{\mathrm{i}}\right)={\mathrm{o}}_{\mathrm{j}},\hspace{1em}\mathrm{i}=1,\dots ,\mathrm{K}$$

(2)

As a result, the formula expressed by Equation (2) can be shortened to be represented by Equation (3).

$$\mathrm{H}\mathsf{\beta }=\mathrm{T}$$

(3)

Since Equation (3) is a linear problem, it is obtained by the Moore–Penrose inverse known as ${\mathrm{H}}^{†}$.

$$\mathsf{\beta }={\mathrm{H}}^{†}\mathrm{T}$$

(4)

In a KELM, the kernel structure maps the data from the input layer to the hidden layer and computes the ${\mathrm{H}}^{†}$ matrix by applying the orthogonal projection procedure. Applying Mercer’s condition to define the kernel matrix of KELM operates as follows [25]:

$${\Omega }_{\mathrm{N}}={\mathrm{H}}_{\mathrm{N}}{{\mathrm{H}}_{\mathrm{N}}}^{\mathrm{T}}:{\Omega }_{{\mathrm{N}}_{\mathrm{i},\mathrm{j}}}=\mathrm{h}\left({\mathrm{x}}_{\mathrm{i}}\right)-\mathrm{h}\left({\mathrm{x}}_{\mathrm{j}}\right)=\mathrm{K}\left({\mathrm{x}}_{\mathrm{i}},{\mathrm{x}}_{\mathrm{j}}\right)$$

(5)

where ${\mathrm{H}}_{\mathrm{N}}$ is the hidden layer’s output matrix, ${\Omega }_{{\mathrm{N}}_{\mathrm{i},\mathrm{j}}}$ is the kernel matrix, and $\mathrm{K}\left({\mathrm{x}}_{\mathrm{i}},{\mathrm{x}}_{\mathrm{j}}\right)$ is the kernel function. The output of the KELM model is calculated using Equations (6) and (7).

$$\mathrm{f}\left({\mathrm{x}}_{\mathrm{p}}\right)={\left[\begin{array}{c}\mathrm{K}\left({\mathrm{x}}_{\mathrm{p}},{\mathrm{x}}_1\right)\\ ⋮\\ \mathrm{K}\left({\mathrm{x}}_{\mathrm{p}},{\mathrm{x}}_{\mathrm{N}}\right)\end{array}\right]}^{\mathrm{T}}{\mathsf{\alpha }}_{\mathrm{N}}$$

(6)

$${\mathsf{\alpha }}_{\mathrm{N}}={\left({\displaystyle \frac{{\mathrm{I}}_{\mathrm{N}}}{\mathrm{C}}}+{\Omega }_{\mathrm{N}}\right)}^{-1}{\mathrm{T}}_{\mathrm{N}}$$

(7)

where ${\Omega }_{\mathrm{N}}$ is the kernel function matrix of X [25].

2.2. Fuzzy Wavelet Neural Network (FWNN)

Wavelets may be defined as mathematical functions used for representing data or other functions. A wavelet is such a waveform possessing an effectiveness of finite duration with an average value equal to zero. The underlying theme connected to wavelet neural networks is related to the combination of wavelet structure and neural networks. This successful synthesis is called WNN. The novelty of these networks is that they prefer the wavelet as the HL activation function in classical neural networks. The output of the network is given in Equation (8).

$$\mathrm{g}\left(\mathrm{x}\right)=\sum _{\mathrm{k}=1}^{\mathrm{n}}{\mathsf{\omega }}_{\mathrm{k}}\mathsf{\Psi }\left({\displaystyle \frac{\mathrm{x}-{\mathrm{b}}_{\mathrm{k}}}{{\mathsf{\alpha }}_{\mathrm{k}}}}\right)$$

(8)

where n is the size of the input, and ${\mathsf{\omega }}_{\mathrm{k}}$ the weight coefficient. ${\mathrm{b}}_{\mathrm{k}}$ and ${\mathsf{\alpha }}_{\mathrm{k}}$ are free parameters to be initialized.

By synthesizing the FIS and the WNN, the structure of the FWNN was created. FWNN incorporates fuzzy rules, wavelet functions, and neural networks. Therefore, it has some of the strengths of these structures. For example, the high reasoning capability of fuzzy logic or the high-precision approximation performance of the wavelet structure. A set of fuzzy rules that influence the operation of this network is shown in Equation (9) [21].

$${\mathrm{R}}^{\mathrm{i}}=\mathrm{I}\mathrm{F} {\mathrm{x}}_1 \mathrm{i}\mathrm{s} {{\mathrm{A}}_1}^{\mathrm{i}}; \dots ; {\mathrm{x}}_{\mathrm{m}} \mathrm{i}\mathrm{s} {{\mathrm{A}}_{1\mathrm{m}}}^{\mathrm{i}} \mathrm{T}\mathrm{h}\mathrm{e}\mathrm{n} {\mathrm{y}}_{\mathrm{i}}={\mathrm{w}}_{\mathrm{i}}\sum _{\mathrm{i}=1}^{\mathrm{q}}{\mathsf{\psi }}_{\mathrm{i}\mathrm{j}}\left({\mathrm{x}}_{\mathrm{j}}\right)\hspace{1em}\hspace{1em}\mathrm{i}=1:\mathrm{c}$$

(9)

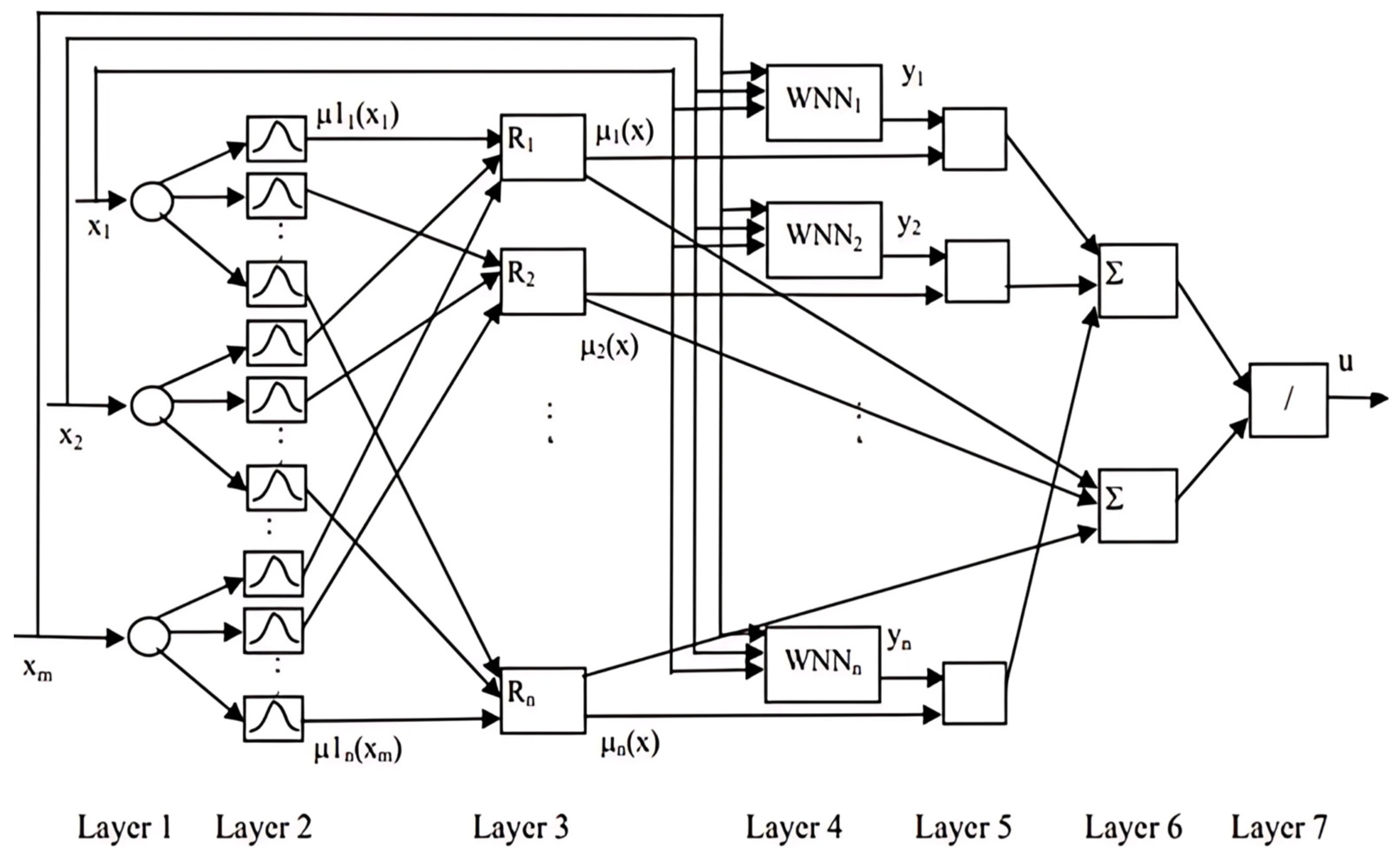
where c and m are the number of fuzzy rules and the size of the input. The output of the FWNN is given in Equation (10) and its general structure is given in Figure 3.

It has seven layers. In the first layer, nodes equal to the number of input signals send the signals. In the second layer, each node corresponds to a linguistic term. For each signal input into the system, the degree of membership to the fuzzy set to which the input value belongs is calculated. In the third layer, each node represents a fuzzy rule. Here, the AND (min) operation is used to calculate the values of the output signals of the layer. The fourth layer is where the wavelets are incorporated into the neural network mechanism. In layer five, the output signals from layer three are multiplied by output signals from the WNNs. Defuzzification is carried out in the sixth and seventh layers to determine the final output of the entire network [14].

$$\widehat{\mathrm{y}}={\displaystyle \frac{{\sum }_{\mathrm{i}=1}^{\mathrm{c}}\left[{\prod }_{\mathrm{j}=1}^{\mathrm{m}}{\mathrm{A}}_{\mathrm{j}}^{\mathrm{i}}\left({\mathrm{x}}_{\mathrm{j}}\right)\right]{\mathrm{y}}_{\mathrm{i}}}{{\sum }_{\mathrm{i}=1}^{\mathrm{c}}\left[{\prod }_{\mathrm{j}=1}^{\mathrm{m}}{\mathrm{A}}_{\mathrm{j}}^{\mathrm{i}}\left({\mathrm{x}}_{\mathrm{j}}\right)\right]}}$$

(10)

2.3. Fuzzy Wavelet Mexican Hat Wavelet Kernel Extreme Learning Machine (FWMHKELM) Algorithm

In this section, we will introduce our proposed basic hybrid algorithm. The work cited in [21] showed the equivalence of the FW structure and the ELM structure. However, edge detection or robustness to noise are important steps in facial expression classification. Therefore, in this study, the FW structure is integrated with a KELM. A Mexican hat wavelet is selected as the kernel. The MH wavelet is defined as the second derivative of the Gaussian function (Equation (11)). This derivative property helps to detect more precisely the distinct change points in the signal or data. In classification and pattern recognition problems, it is important to capture sharp transitions. The MH wavelet kernel was chosen for this study due to its better edge detection; its real-valued, positive semi-definite robustness to noise; and its better performance over a wide spectrum.

The hybrid model has a hierarchical and sequential fusion structure. The operation of the model follows a hierarchical structure—First, the input data are disambiguated by fuzzification (FIS). Then, the frequency components of the data are analyzed by applying the wavelet transform. Finally, classification is performed with the MHKELM. This process is also sequential in nature, as it proceeds in successive steps.

We have mentioned that the MH wavelet function is an acceptable ELM kernel [25]. For this case, Wang et al. proved that the Fourier transform of the MH wavelet is nonnegative according to the translation–invariant theorem [25]. This proof is based on the theorem that the Fourier transform is nonnegative and is given [26]; we will not repeat it in this paper.

When the MH wavelet is used as the mother wavelet, the MH wavelet kernel function is derived as in Equations (11) and (12):

$$\mathsf{\psi }\left(\mathrm{x}\right)=\left(1-{\mathrm{x}}^2\right)\exp \left(-{\displaystyle \frac{{\mathrm{x}}^2}{2}}\right)$$

(11)

$$\mathrm{K}\left({\mathrm{x}}_{\mathrm{i}},{\mathrm{x}}_{\mathrm{j}}\right)=\prod _{\mathrm{d}=1}^{\mathrm{D}}\left[1-{\left({\displaystyle \frac{{\mathrm{x}}_{\mathrm{d}\mathrm{i}}-{\mathrm{x}}_{\mathrm{d}\mathrm{j}}}{\mathrm{a}}}\right)}^2\right] \mathrm{e}\mathrm{x}\mathrm{p}\left[-{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{{\mathrm{x}}_{\mathrm{d}\mathrm{i}}-{\mathrm{x}}_{\mathrm{d}\mathrm{j}}}{\mathrm{a}}}\right)}^2\right]$$

(12)

Also, the Fourier transform of the MH wavelet is shown in Equation (13):

$$(\mathsf{\omega })={\left(2\mathsf{\pi }\right)}^{{\displaystyle \raisebox{1ex}{$\mathrm{D}$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{\mathrm{a}}^{\mathrm{D}}{\prod }_{\mathrm{d}=1}^{\mathrm{D}}\exp \left(-{\displaystyle \frac{1}{2}}{\mathrm{a}}^2{\mathrm{w}}_{\mathrm{d}}^2\right)\left\{{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\displaystyle \frac{1}{2}}{\left({\mathrm{x}}_{\mathrm{d}}+{\mathrm{j}\mathrm{a}\mathsf{\omega }}_{\mathrm{d}}\right)}^2\right]\mathrm{d}{\mathrm{x}}_{\mathrm{d}}-{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\mathrm{x}}_{\mathrm{d}}^2\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\displaystyle \frac{1}{2}}{\left({\mathrm{x}}_{\mathrm{d}}+\mathrm{j}\mathrm{a}{\mathsf{\omega }}_{\mathrm{d}}\right)}^2\right]\mathrm{d}{\mathrm{x}}_{\mathrm{d}}\right\}$$

(13)

Equation (14) is obtained when this is solved by a series of integral partial integrations.

$$\mathrm{F}\left(\mathsf{\omega }\right)=(2\mathsf{\pi }{)}^{\mathrm{D}}{\mathrm{a}}^{3\mathrm{D}}\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\displaystyle \frac{\mathrm{a}}{2}}{\sum }_{\mathrm{d}=1}^{\mathrm{D}}{\mathsf{\omega }}_{\mathrm{d}}^2\right){\prod }_{\mathrm{d}=1}^{\mathrm{D}}{\mathsf{\omega }}_{\mathrm{d}}^2.$$

(14)

The focus of the paper is how to combine the MH wavelet, mentioned above as being an adaptive ELM kernel, and the ELM method into the fuzzy wavelet structure. In this context, it will be argued that the fuzzy wavelet (FW) structure is equivalent to the MH wavelet kernel-based extreme learning machine structure and, finally, the steps of the proposed algorithm will be presented.

The fuzzy wavelet (FW) structure is equivalent to the kernel-based extreme learning machine structure. A TSK model with k inputs and r outputs is defined as in Equation (15) [21]:

$${\mathrm{R}}^{\mathrm{i}}:\mathrm{I}\mathrm{f} {\mathrm{x}}_1 \mathrm{i}\mathrm{s} {{\mathrm{A}}_1}^{\mathrm{i}}; {\mathrm{x}}_2 \mathrm{i}\mathrm{s} {{\mathrm{A}}_2}^{\mathrm{i}}; \dots ; {\mathrm{x}}_{\mathrm{k}} \mathrm{i}\mathrm{s} {{\mathrm{A}}_{\mathrm{k}}}^{\mathrm{i}} \mathrm{T}\mathrm{h}\mathrm{e}\mathrm{n} \left({\mathrm{y}}_1,{\mathsf{\gamma }}_1^{\mathrm{i}}\right),\dots ,\left({\mathrm{y}}_{\mathrm{r}},{\mathsf{\gamma }}_{\mathrm{r}1}^{\mathrm{i}}\right)$$

(15)

where

• $\mathrm{x}={\left[{\mathrm{x}}_1,{\mathrm{x}}_2,\dots ,{\mathrm{x}}_{\mathrm{n}\mathrm{k}}\right]}^{\mathrm{T}}$ is the input vector;
• $\mathrm{y}={\left[{\mathrm{y}}_1,{\mathrm{y}}_2,\dots ,\mathrm{r}\right]}^{\mathrm{T}}$ the output vector;
• ${\mathrm{A}}_{\mathrm{j}}^{\mathrm{i}}\left(\mathrm{j}=1,2,\dots ,\mathrm{n}; \mathrm{i}=1,2,\dots ,\mathrm{c}\right)$ is the fuzzy membership function for rule $\mathrm{i}$;
• ${\mathsf{\gamma }}_{\mathrm{i}}=\left[{{\mathsf{\gamma }}_1}^{\mathrm{i}},{{\mathsf{\gamma }}_2}^{\mathrm{i}},\dots ,{{\mathsf{\gamma }}_{\mathrm{m}}}^{\mathrm{i}}\right]$ is calculated with the help of Equation (16) [18]:

  $${{\mathsf{\gamma }}_{\mathrm{k}}}^{\mathrm{i}}={\mathrm{q}}_{\mathrm{i}\mathrm{k},0}+{\mathrm{q}}_{\mathrm{i}\mathrm{k},1}{\mathrm{x}}_1+\cdots +{\mathrm{q}}_{\mathrm{i}\mathrm{k},\mathrm{n}}{\mathrm{x}}_{\mathrm{n}}$$

  (16)

When an FW model is called an FIS model, Equations (15) and (16) are expressed as Equations (17) and (18):

$${\mathrm{R}}^{\mathrm{i}}:\mathrm{I}\mathrm{f} {\mathrm{x}}_1 \mathrm{i}\mathrm{s} {{\mathrm{A}}_1}^{\mathrm{i}}; {\mathrm{x}}_2 \mathrm{i}\mathrm{s} {{\mathrm{A}}_2}^{\mathrm{i}}; \dots ; {\mathrm{x}}_{\mathrm{k}} \mathrm{i}\mathrm{s} {{\mathrm{A}}_{\mathrm{k}}}^{\mathrm{i}} \mathrm{T}\mathrm{h}\mathrm{e}\mathrm{n} \left({\mathrm{y}}_1,{\mathrm{s}\mathsf{\beta }}_1^{\mathrm{i}}\right),\dots ,\left({\mathrm{y}}_{\mathrm{r}},{\mathrm{s}\mathsf{\beta }}_{\mathrm{r}}^{\mathrm{i}}\right)$$

(17)

where ${\mathrm{s}\mathsf{\beta }}_{\mathrm{n}}^{\mathrm{i}}$ is a combination of the wavelet function and is calculated as in Equation (18).

$${{\mathrm{s}\mathsf{\beta }}_{\mathrm{n}}}^{\mathrm{i}}={\mathrm{q}}_{\mathrm{i}\mathrm{n},0}+{\mathrm{q}}_{\mathrm{i}\mathrm{n},1}{\mathsf{\Psi }}_{\mathrm{i}1}\left({\mathrm{x}}_1\right)+\cdots +{\mathrm{q}}_{\mathrm{i}\mathrm{n},\mathrm{k}}{{\mathsf{\Psi }}_{\mathrm{i}\mathrm{k}}(\mathrm{x}}_{\mathrm{k}})$$

(18)

In Equation (18), s denotes the FW structure and ${{\mathsf{\Psi }}_{\mathrm{j}}}^{\mathrm{i}}(\mathrm{j}=1,2,\dots ,\mathrm{k}; \mathrm{i}=1,2,\dots ,\mathrm{c})$ denotes the wavelet function of the jth input of the ith rule. In Equations (17) and (18), the THEN part considers one coefficient for each of the inputs; the number of coefficients for all c rules is $(\mathrm{n}+1)\times \mathrm{c}$. Furthermore, the output of the FWNN is shown in Equation (10) and can again be restated as in Equation (19).

$$\widehat{\mathrm{y}}={\displaystyle \frac{{\sum }_{\mathrm{i}=1}^{\mathrm{L}}\left[{\prod }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{A}}_{\mathrm{i}}^{\mathrm{j}}\left({\mathrm{x}}_{\mathrm{j}}\right)\right]{\mathrm{y}}_{\mathrm{i}}}{{\sum }_{\mathrm{i}=1}^{\mathrm{L}}\left[{\prod }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{A}}_{\mathrm{i}}^{\mathrm{j}}\left({\mathrm{x}}_{\mathrm{j}}\right)\right]}}=\sum _{\mathrm{i}=1}^{\mathrm{L}}\mathrm{s}{\mathsf{\beta }}_{\mathrm{i}}{\Omega }_{\mathrm{i}\mathrm{j}}{\mathrm{G}}_{\mathrm{F}\mathrm{W}}(\mathrm{x}; {\mathrm{c}}_{\mathrm{i}},{\mathsf{\alpha }}_{\mathrm{i}})$$

(19)

When Equation (19) and (1) are compared, it can be seen that the KELM and FW models are equivalent. Moreover, both models have similar constraints on the number of hidden nodes (N) and the number of rules (c), a power that fires each rule and an activation function that enables communication between each hidden node. FWMHKELM structure—the FW structure is defined as follows:

$${\mathrm{R}}^{\mathrm{i}}:\mathrm{I}\mathrm{f} {\mathrm{x}}_1 \mathrm{i}\mathrm{s} {{\mathrm{A}}_1}^{\mathrm{i}}; {\mathrm{x}}_2 \mathrm{i}\mathrm{s} {{\mathrm{A}}_2}^{\mathrm{i}}; \dots ; {\mathrm{x}}_{\mathrm{k}} \mathrm{i}\mathrm{s} {{\mathrm{A}}_{\mathrm{k}}}^{\mathrm{i}} \mathrm{T}\mathrm{h}\mathrm{e}\mathrm{n} \left({\mathrm{y}}_1,{\mathsf{\gamma }}_1^{\mathrm{i}}\right),\dots ,\left({\mathrm{y}}_{\mathrm{r}},{\mathsf{\gamma }}_{\mathrm{r}1}^{\mathrm{i}}\right)$$

(20)

Depending on whether n is odd or even, ${{\mathsf{\beta }}_{\mathrm{n}}}^{\mathrm{i}}$ is represented by Equations (21) and (22):

$${{\mathsf{\beta }}_{\mathrm{n}}}^{\mathrm{i}}={\mathrm{q}}_{\mathrm{i}\mathrm{n},0}+{\mathrm{q}}_{\mathrm{i}\mathrm{n},1}\sum _{\mathrm{j}=1}^2{{\mathsf{\Psi }}_{\mathrm{i}\mathrm{j}}(\mathrm{x}}_{\mathrm{j}})+{\mathrm{q}}_{\mathrm{i}\mathrm{n},2}\sum _{\mathrm{j}=3}^4{{\mathsf{\Psi }}_{\mathrm{i}\mathrm{j}}(\mathrm{x}}_{\mathrm{j}})+\cdots +{\mathrm{q}}_{\mathrm{i}\mathrm{k},\left[{\displaystyle \frac{\mathrm{n}}{2}}\right]}\sum _{\mathrm{j}=\mathrm{n}-1}^{\mathrm{n}}{\mathsf{\Psi }}_{\mathrm{i}\mathrm{j}}\left({\mathrm{x}}_{\mathrm{j}}\right)\hspace{1em}\hspace{1em}\mathrm{i}\mathrm{f} \mathrm{n}=\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n}$$

(21)

$${{\mathsf{\beta }}_{\mathrm{n}}}^{\mathrm{i}}={\mathrm{q}}_{\mathrm{i}\mathrm{n},0}+{\mathrm{q}}_{\mathrm{i}\mathrm{n},1}\sum _{\mathrm{j}=1}^2{{\mathsf{\Psi }}_{\mathrm{i}\mathrm{j}}(\mathrm{x}}_{\mathrm{j}})+{\mathrm{q}}_{\mathrm{i}\mathrm{n},2}\sum _{\mathrm{j}=3}^4{{\mathsf{\Psi }}_{\mathrm{i}\mathrm{j}}(\mathrm{x}}_{\mathrm{j}})+\dots +{\mathrm{q}}_{\mathrm{i}\mathrm{n},\left[{\displaystyle \frac{\mathrm{n}}{2}}\right]-1}\sum _{\mathrm{j}=\mathrm{n}-2}^{\mathrm{n}-1}{{\mathsf{\Psi }}_{\mathrm{i}\mathrm{j}}(\mathrm{x}}_{\mathrm{j}})+{\mathrm{q}}_{\mathrm{i}\mathrm{n},\left[{\displaystyle \frac{\mathrm{n}}{2}}\right]}{\mathsf{\Psi }}_{\mathrm{i}\mathrm{n}}({\mathrm{x}}_{\mathrm{n}})\hspace{1em}\hspace{1em}\mathrm{i}\mathrm{f} \mathrm{n}=\mathrm{o}\mathrm{d}\mathrm{d}$$

(22)

In Equation (20), the sigmoid function is used in the IF part of the rule, while the Mexican line wavelet kernel is used in the THEN part. The functions are shown in Equations (23) and (24):

$$\mathrm{A}\left(\mathrm{x}\right)=\mathrm{s}\mathrm{i}\mathrm{g}\left(\mathrm{x};\mathrm{a},\mathrm{t}\right)={\displaystyle \frac{1}{1+{\mathrm{e}}^{-\mathrm{a}\left(\mathrm{x}-\mathrm{t}\right)}}}$$

(23)

where $\mathrm{t}$ is the center and $\mathsf{\alpha }$ is the slope point at $\mathrm{x}=\mathrm{t}$.

$$\mathsf{\psi }\left(\mathrm{x}\right)=\left(1-{\mathrm{x}}^2\right)\exp \left(-{\displaystyle \frac{{\mathrm{x}}^2}{2}}\right)$$

(24)

In an arbitrary $\left({\mathrm{x}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{i}}\right)$ training dataset, ${\mathrm{x}}_{\mathrm{i}}={\left[{\mathrm{x}}_{\mathrm{i}1},{\mathrm{x}}_{\mathrm{i}2},\dots ,{\mathrm{x}}_{\mathrm{i}\mathrm{n}}\right]}^{\mathrm{T}}$ is the input vector, ${\mathrm{t}}_{\mathrm{i}}={\left[{\mathrm{t}}_{\mathrm{i}1},{\mathrm{t}}_{\mathrm{i}2},\dots ,{\mathrm{t}}_{\mathrm{i}\mathrm{m}}\right]}^{\mathrm{T}}$ is the output vector, and c is the number of fuzzy rules.

The mathematical model of FW can be defined as Equations (25) and (26):

$${\mathrm{f}}_{\mathrm{c}}\left({\mathrm{x}}_{\mathrm{j}}\right)=\sum _{\mathrm{i}=1}^{\mathrm{c}}{{\Omega }_{\mathrm{M}\mathrm{H}\mathrm{W}}{\mathsf{\beta }}_{\mathrm{i}}\mathrm{G}}_{\mathrm{F}\mathrm{W}}\left({\mathrm{x};\mathrm{t}}_{\mathrm{i}},{\mathsf{\alpha }}_{\mathrm{i}}\right)={\mathrm{t}}_{\mathrm{j}},\hspace{1em}\hspace{1em}\mathrm{j}=1,2,\dots ,\mathrm{N}.$$

(25)

$${\Omega }_{\mathrm{M}\mathrm{H}\mathrm{W}}{\mathrm{H}}_{\mathrm{F}\mathrm{W}}\mathrm{Q}=\mathrm{T}.$$

(26)

where $\Omega$ is the MH wavelet kernel (MHW-KELM) matrix and it can be defined as Equation (27):

$${\Omega }_{\mathrm{i}\mathrm{j}}=\prod _{\mathrm{d}=1}^{\mathrm{D}}\left[1-{\left({\displaystyle \frac{{\mathrm{x}}_{\mathrm{d}\mathrm{i}}-{\mathrm{x}}_{\mathrm{d}\mathrm{j}}}{\mathrm{a}}}\right)}^2\right] \mathrm{e}\mathrm{x}\mathrm{p}\left[-{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{{\mathrm{x}}_{\mathrm{d}\mathrm{i}}-{\mathrm{x}}_{\mathrm{d}\mathrm{j}}}{\mathrm{a}}}\right)}^2\right]$$

(27)

Equation (25) can be compactly written as follows:

$$\mathrm{H}=\left[{\mathsf{\psi }}_{\mathrm{i}\mathrm{e}}^{\mathrm{T}}\left({\mathrm{x}}_{\mathrm{j}}; {\mathrm{b}}_1,{\mathrm{d}}_1\right){\mathrm{G}}_{\mathrm{F}\mathrm{W}}\left({\mathrm{x}}_{\mathrm{j}}; {\mathrm{t}}_1,{\mathrm{a}}_1\right),\dots ,{\mathsf{\psi }}_{\mathrm{i}\mathrm{e}}^{\mathrm{T}}\left({\mathrm{x}}_{\mathrm{j}}; {\mathrm{b}}_{\mathrm{c}},{\mathrm{d}}_{\mathrm{c}}\right){\mathrm{G}}_{\mathrm{F}\mathrm{W}}\left({\mathrm{x}}_{\mathrm{j}}; {\mathrm{t}}_{\mathrm{c}},{\mathrm{a}}_{\mathrm{c}}\right)\right]$$

(28)

where $\Omega$ is the hidden matrix.

The output equation of the new classifier is shown as Equation (29):

$$\mathrm{f}\left(\mathrm{x}\right)={\mathrm{H}}_{\mathrm{F}\mathrm{W}}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}\left\{{\left[\begin{array}{c}\mathrm{K}\left({\mathrm{x}}_{\mathrm{p}},{\mathrm{x}}_1\right)\\ ⋮\\ \mathrm{K}\left({\mathrm{x}}_{\mathrm{p}},{\mathrm{x}}_{\mathrm{N}}\right)\end{array}\right]}^{\mathrm{T}}{\left(\mathrm{I}\mathrm{C}+\Omega \right)}^{-1}\mathrm{T}\right\}$$

(29)

The steps of the FWMHKELM algorithm are summarized below:

Step 1: Randomly select the parameters for the membership function and wavelet coefficients.

Step 2: Construct the hidden matrix using Equations (26) and (28).

Step 3: Calculate the matrix Q.

3. Experimental Results and Analysis

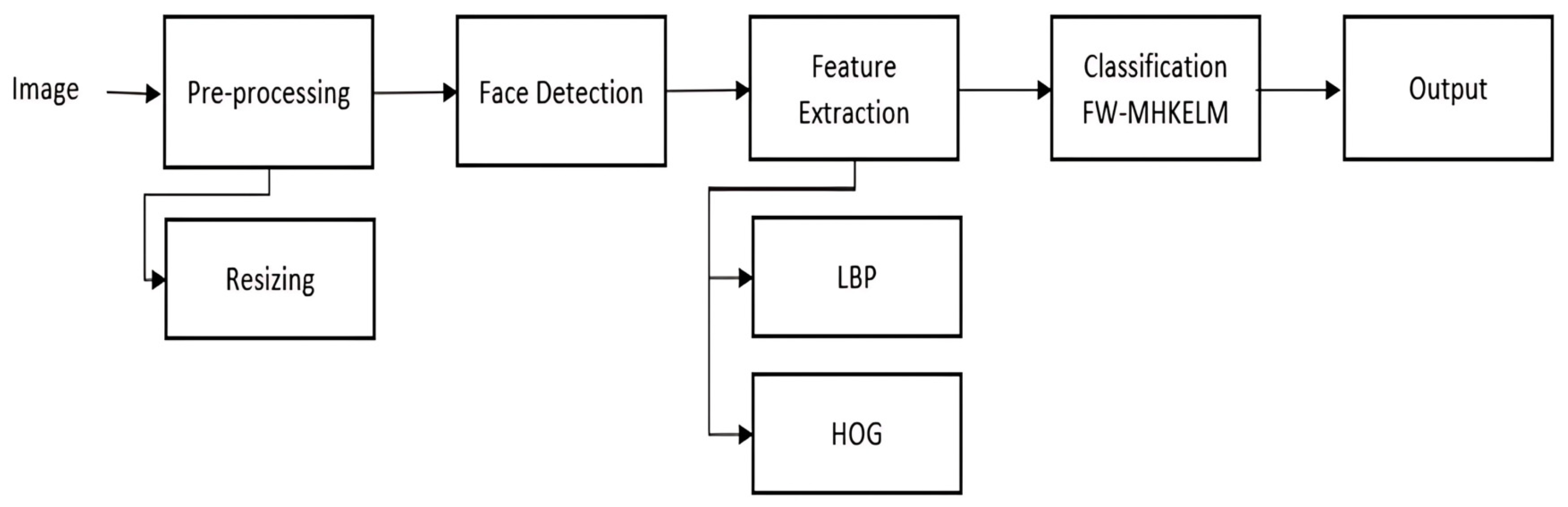
In this study, two experiments were designed, and the first one utilized the JAFFE dataset, which is available in the literature and is frequently used in facial expression classification problems. Access to the Jaffe dataset is publicly available [27]. It consists of 213 black-and-white facial photographs of 10 Japanese women with 7 basic emotional expressions. Each participant displayed each emotional expression more than once. The workflow of the algorithm developed for use in facial expression classification problems is shown in Figure 4.

Examples of these 256 × 256-pixel images are shown in Figure 5.

During preprocessing, image intensities were normalized, and only the region containing the face expressing the emotion was resized. We resized the original image of size 256 × 256 to 168 × 120 by removing background effects. An example is presented in Figure 6.

Additionally, histogram equalization was applied to remove lighting effects. For feature extraction, we employed the local binary pattern (LBP) method. To evaluate the effectiveness of LBP, we also tested the histogram of oriented gradients (HOG) method for comparison.

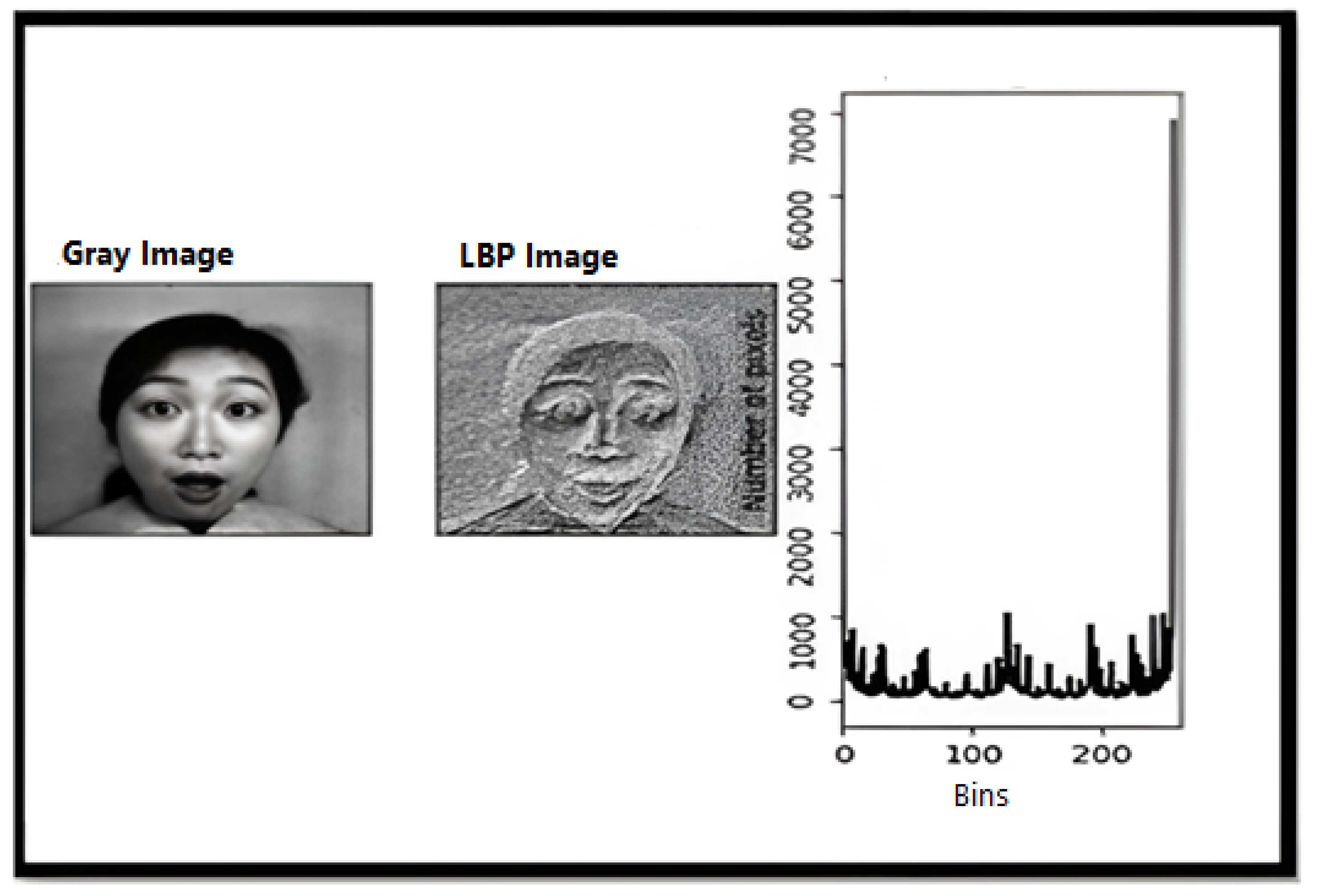
The output image (Figure 7) shows that the LBP-processed image has improved the facial landmark boundaries. Moreover, it is very important to analyze the changes in the pixel positions of key regions such as the eyebrows, eyes, and mouth with respect to a given reference point in facial expression detection. We also test other feature representations such as HOG for comparison. For the classification phase of the facial expression recognition problem, the architecture (network structure) of the proposed algorithm needs to be established. In the developed algorithm, the wavelet coefficients are randomly generated and remain constant. In addition, the initial parameters are all user inputs and are randomly defined. At this stage, the structure of the network is created.

In this study, the structure of the network was defined with user input. Accordingly, the number of neurons/ fuzzy rules in the HL was set as 10, and the minimum error was set as 0.001. To calculate the average classification measure, the experiment was performed with 10-fold cross-validation. Because the number of images in the dataset is limited, after training the dataset, the test image is classified using the proposed hybrid algorithm classifier. All analyses were performed using MATLAB R2021b.

When a dataset contains more than two classes or an unequal distribution of observations across classes, the calculated accuracy rate may be misleading. Therefore, in addition to accuracy, a confusion matrix was generated to summarize the classification algorithm’s performance. The confusion matrix provides preliminary information about the types of errors made by the model.

Table 1. Classification results: the confusion matrix of the LBP + FWMHKELM approach.

	H	S	A	F	D	Sur.	N.
Happy (H)	96.13	1.29	0	0	0.65	0	1.93
Sad (S)	2.58	94.96	0	0.55	0.62	0	1.29
Anger (A)	0	0	94	0.65	2.67	0	2.67
Fear (F)	0	2.5	0.63	91.89	1.88	3.1	0
Disgust (D)	0	0.69	0	2.76	96.55	0	0
Surprise (Sur.)	0	0.37	0	0.67	0	97.63	1.33
Neural (N)	2.76	5.27	0.62	0.67	0	0	90.67

provides a detailed confusion matrix showing classification performance across various facial expressions.

According to Table 1, the performance of the classifier for the expression of happiness is 96.13%. The performance is 91.89% for fear, and 97.63% for surprise. It was determined that over 90% of the classifications for all expressions performed by the proposed algorithm were correct. The average classification accuracy was calculated as 94.55%. In parallel, the experiment was repeated on the same dataset using different methods in the face feature extraction step. Thus, the aim was to observe how the proposed algorithm performs with different facial feature extraction algorithms. In the experiment, HOG was used in the face feature extraction step. In the classification phase, the FWMHKELM algorithm was applied, and the confusion matrix was obtained again. The confusion matrix obtained for this experiment is presented in

Table 2. Classification results: the confusion matrix of the HOG + FWMHKELM approach.

	H	S	A	F	D	Sur.	N
H	97.78	1.11	0	0	0	0	1.11
S	0	95.65	3.24	0	0	1.11	0
A	0	0	97.78	1.11	1.11	0	0
F	0	1.11	0	98.89	0	0	0
D	0	0	0	0	84.22	15.78	0
Sur.	2.22	0	0	4.44	0	90.01	3.33
N	3.33	0	1.11	0	0	0	95.56

.

Table 2 shows that the performance of the classifier is 97.78% for happiness, 98.89% for fear and 84.22% for disgust. When the algorithm was run with histograms of oriented gradients, it was found that the algorithm correctly classified over 90% for all expressions except disgust. The average classification accuracy was calculated as 94.27%. The developed algorithm is also compared with other existing studies in the literature using the same dataset and the results are presented in

Table 3. Performance comparison of various classification methods.

Methods	Average Recognition Rates (%)
LBP + FWMHKELM	94.55
HOG + FWMHKELM	94.27
Fisherface + BPNN [28]	86.85
MIP + ELM [9]	90.16
HOG + ELM [29]	94.37
PCA + FLD + WNN [30]	90.00
LM + FWNN [31]	92.00

.

Table 3 shows that the hybrid algorithm and the local binary pattern algorithm work together in feature detection to achieve more efficient results.

In the second experiment, original images were used to test our approach. The dataset consists of images of 38 people of Turkish origin, 17 males and 21 females, each showing six basic facial expressions (happy, sad, fearful, angry, surprised, and neutral). In the first step of the process, Ethics Committee Approval was obtained for the creation of the dataset and the necessary personal data sharing consents were obtained from the participants through the Voluntary Participation Form. To balance gender and age distribution and reduce sampling bias, the study protocol was designed to include stratified participant recruitment. Neutral images were captured twice under controlled lighting conditions to minimize within-dataset bias. The original image size is 768 × 1024 pixels. Image samples from the database are shown in Figure 8.

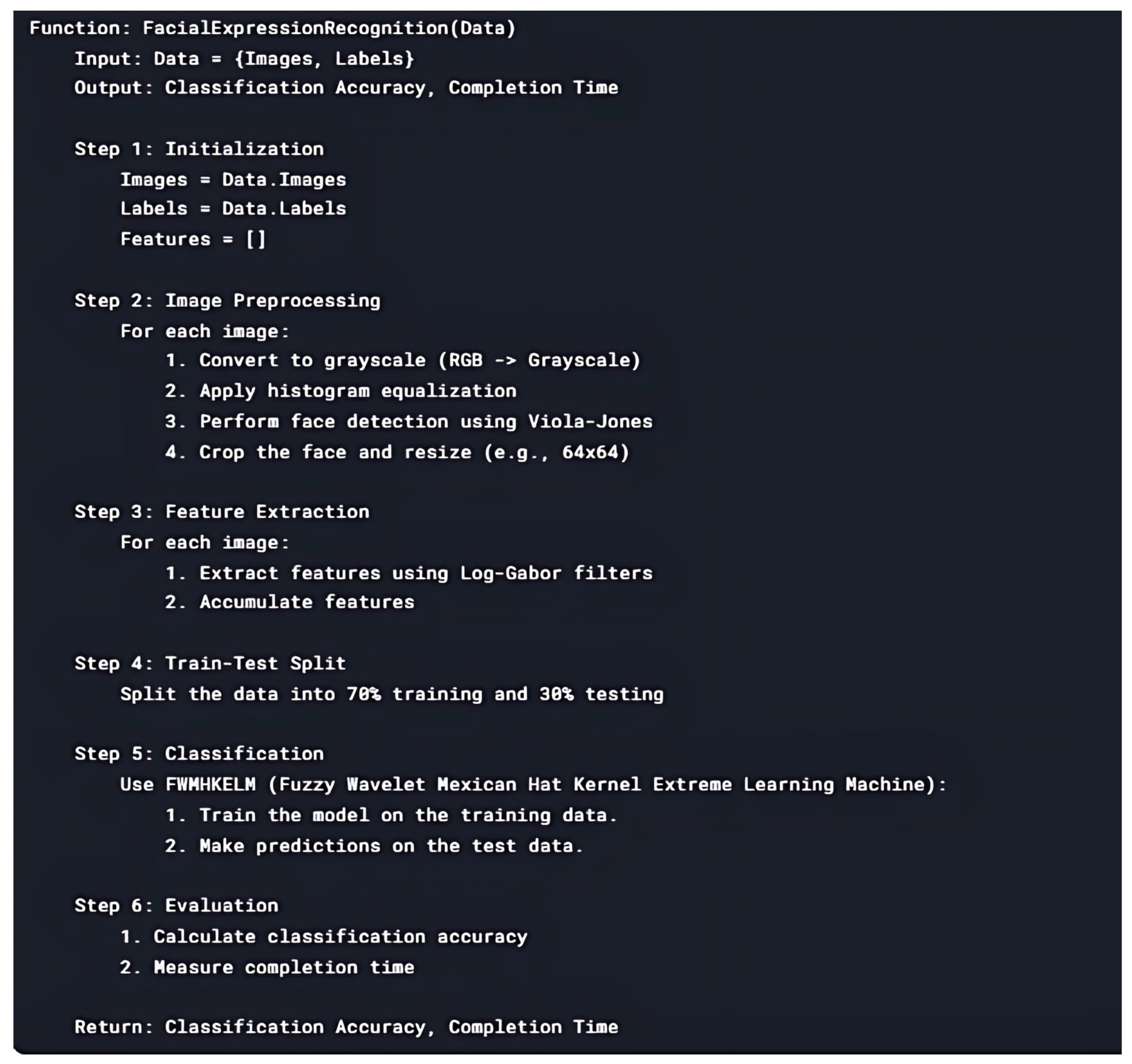
The pseudocode of this experiment is presented in Figure 9. The hybrid method was again run on MATLAB R2021b software. The data were split 70:30 into training data and test data. This ratio was chosen because the neural network was intended to be trained with maximum data, and the remaining images were sufficient to test the accuracy of the algorithm. In the preprocessing step, the image intensities were normalized and only the image consisting of a face expressing an emotion was preprocessed and resized. On the other hand, gray processing was used on the face images to remove the effects of lighting. Histogram equalization was applied for gray processing. Using the Viola–Jones algorithm, certain features in the images were cropped and the face region of the image was extracted. Log Gabor filters were used for feature extraction.

Figure 10 and Figure 11 show an example of the image processing and feature extraction phases.

In the classification phase, the initial parameters were chosen by the user. For example, the number of neurons in the HL was set to 5, in LR it was 0.25, the minimum error was 0.001, and the maximum iteration number was 250. After training the database, the test image was classified using the FWMHKELM classifier. The results are presented in

Table 4. Performance metrics comparison for various methods of face recognition.

Methods	Accura. (%)	Train Time (s)	Test Time(s)
ELM	77.8%	155	2.85
WNN	72.2%	242	5.16
Hybrid Algorithm (FWMHKELM)	80.6%	313	5.26

.

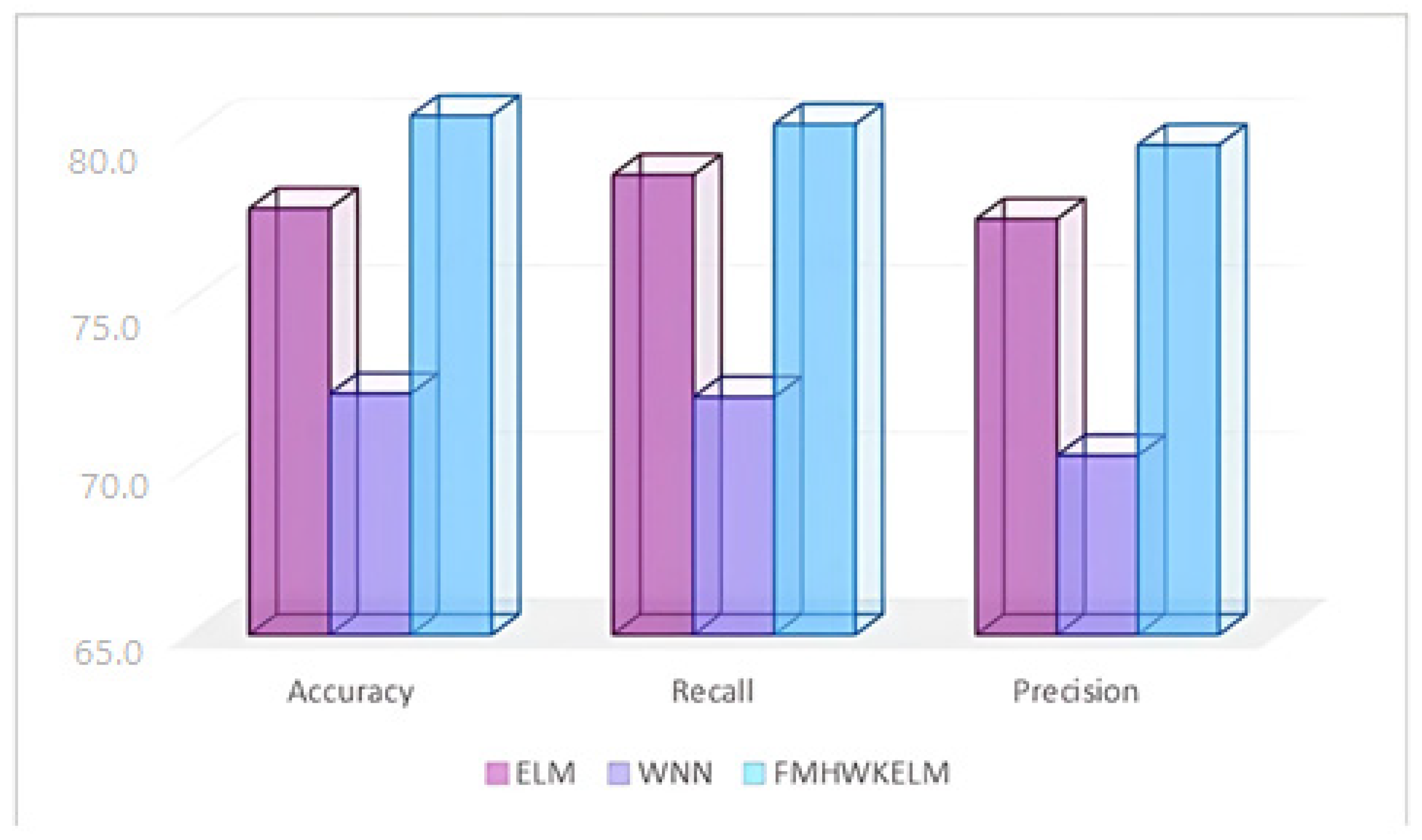
As can be seen in Table 4, the FWMHKELM algorithm demonstrates better classification performance compared to the ELM and WNN algorithms. However, its training time is longer than that of the other algorithms. This increased training time can be attributed to the use of fuzzy rules within the model. To evaluate the classification performance of FWMHKELM, we calculated the accuracy, precision, and recall parameters. The accuracy value of the test is calculated by comparing the test data with the results predicted using real labels. The average accuracy value was calculated as 80.6%. Figure 12 graphically shows the comparison of all algorithms categorized by the accuracy, recall, and precision parameters. The study shows that our proposed FWMHKELM algorithm showed better results than the ELM and WNN.

4. Discussion

The current work presents a hybrid method that will bring a new perspective to the problem of facial expression classification. The structure of the hybrid method includes fuzzy rules, wavelet structure, and a kernel-based ELM. We call this structure FWMHKELM for short. The key advantage of FWMHKELM lies in its simplicity and its high accuracy and generalization performance.

Building on this theoretical foundation, the mathematical framework of the FWMHKELM model was used to classify facial expressions. The facial expression classification helps build a flexible facial expression identification model in terms of mapping behavioral features against physiological biometric features. People have distinct physiognomic expressions associated with emotions such as happiness, sadness, shock, and fear. In the classification system, these expressions are identified through established matching templates based on the geometry of the face.

The mathematical basis of the structure is presented in the paper. Taking advantage of the fact that the Mexican hat wavelet is an acceptable ELM kernel, it is discussed how to integrate a fuzzy wavelet into a fuzzy wavelet neural network and into a kernel-based extreme learning machine algorithm. The theoretical equivalence between the fuzzy wavelet structure and the Mexican hat (MH) kernel-based ELM, as demonstrated in Equations (19) and (26), ensures that the model captures both the local and global features of facial expressions through wavelet decomposition and fuzzy rule-based reasoning. The high classification accuracies (94.55% with LBP, 94.27% with HOG) empirically validate this synergy—the MH kernel’s edge-detection properties (Equations (11) and (12)) enhance feature discrimination, while fuzzy rules handle inherent uncertainties in expression data. For instance, the confusion matrices (Table 1 and Table 2) reflect the model’s ability to leverage wavelet-transformed features (e.g., eyebrow/mouth movements) via the MH kernel, with misclassifications primarily occurring between expressions with overlapping geometric cues (e.g., fear/disgust). This alignment between theory and results underscores how the hybrid structure’s mathematical design—combining fuzzy adaptability, wavelet multiresolution analysis, and the ELM’s efficient optimization—directly translates into superior performance metrics (Figure 12). Future work could further dissect this relationship by visualizing feature maps or kernel responses for specific expressions.

In this study, the coding for the algorithm and all other comparison algorithms was performed in MATLAB (R2021b). The combination of the algorithm with feature extraction algorithms involved in the classification of facial expression datasets (Log Gabor filters, local binary patterns, and histograms of oriented gradients) tends to produce highly successful classes. The integration of feature extraction techniques such as LBP and HOG further improves the classification performance by capturing critical geometric and textural features of facial expressions. Comparison with existing techniques in the literature, such as ELM and WNN, shows the superiority of the proposed method, especially in handling the intrinsic uncertainty associated with human emotions and expressions.

In the experiments, it was observed that the hybrid algorithm failed to classify fear and disgust expressions. One of the main reasons why the FWMHKELM model misclassifies some facial expressions is the feature overlap problem between expressions such as “fear” and “disgust”. These expressions can show highly correlated features because they involve similar movements of facial muscles. For example, both expressions have similar visual cues, such as nose wrinkling, eyebrows pulling in, and lips stretching. This can limit the discrimination ability of the model, especially when using classical feature extraction methods. To reduce misclassifications, the overall performance of the model can be improved by generating synthetic data with more variations in these expressions in the training set, or dynamic data augmentation and 3D morphable techniques can be integrated to reduce anatomical similarities.

Regarding dataset considerations, while the original dataset used in this study (Section 3) was carefully curated with ethical approval and demographic diversity (38 participants with balanced gender representation), we acknowledge that its smaller scale compared to benchmark datasets (e.g., JAFFE) may raise concerns about potential biases. To mitigate this, we employed two strategies: (1) cross-dataset validation, where the model’s performance was first rigorously tested on the JAFFE benchmark (achieving 94.55% accuracy), demonstrating consistency with established literature (Table 3); and (2) feature augmentation via Log Gabor filters and LBP/HOG, which reduce sensitivity to dataset-specific artifacts by emphasizing universal texture/edge features (Figure 7 and Figure 11), as demonstrated in [10]. These steps collectively enhance the model’s robustness to dataset-specific artifacts while preserving expression-related features across diverse populations. Nevertheless, biases could persist in subtle cultural expressions (e.g., Turkish vs. Japanese facial norms in JAFFE). Future work will expand the dataset with multicultural samples (CK+, FER2013) and integrate adversarial training to further minimize demographic bias.

5. Conclusions

In summary, this study presents a novel and fundamental approach to the facial expression classification problem through the proposed Fuzzy Wavelet Mexican Hat Kernel Extreme Learning Machine (FWMHKELM) framework. The FWMHKELM framework combines high accuracy with efficient feature extraction techniques, offering an important contribution to the problem. As the study provides the basic structure, we would like to highlight several areas of improvement in the work that can guide future research. One problem is the random initialization of parameters, which can affect the consistency of the results. This problem can be addressed by using heuristic optimization algorithms such as Genetic Algorithms, Whale, or Grey Wolf Optimization to automatically determine optimal parameter values. With a better pre-processing approach, the area that is likely to be a face can be minimized. Instead of the Mexican hat wavelet used in the proposed structure, it can be integrated with different wavelet kernel structures (such as Morlet or Haar). Comparative analyses with deep learning architectures (e.g., ResNet or Vision Transformer) will be conducted in future studies to evaluate the competitiveness of the model more comprehensively. Thanks to the use of fuzzy logic in our study, we believe that the model has a certain level of interpretability. Fuzzy rules allow the decision mechanism to be analyzed with a certain degree of clarity. However, the combination of a fuzzy wavelet and an ELM may cause the model to be perceived as a “black box”. Considering this point, in future studies, model stability can be supported with explainability techniques such as SHAP or LIME to support the explainability of the proposed model.

With further refinements, the FWMHKELM framework has the potential to set a new benchmark in affective computing and pattern recognition. Its hybrid nature bridges the gap between traditional machine learning and modern deep learning, offering a scalable solution for applications requiring both high accuracy and explainability. Future work could also explore edge deployment for low-power devices, enabling real-time emotion detection in IoT and wearable technologies.

In conclusion, this study lays a solid foundation for advancing facial expression classification systems. By addressing the outlined limitations and integrating cutting-edge techniques, the proposed framework can evolve into a versatile tool for both academic research and industrial applications, paving the way for innovative solutions in emotion-aware AI systems.