Seismic Response Analysis of Buried Nuclear Power Plant Structures in Non-Bedrock Sites
Abstract
1. Introduction
1.1. Embedded Nuclear Power Plant Structure
1.2. Earthquake Records and Site Information
1.3. Artificial Boundary and Seismic Input Method
- KBN: Normal spring coefficient.
- KBT: Tangential spring coefficient.
- CBN: Normal damping coefficient.
- CBT: Tangential damping coefficient.
- ρ: Medium density.
- A, B: Dimensionless empirical parameters (recommended values: 0.8 and 1.1).
- r: Near-field structure characteristic length.
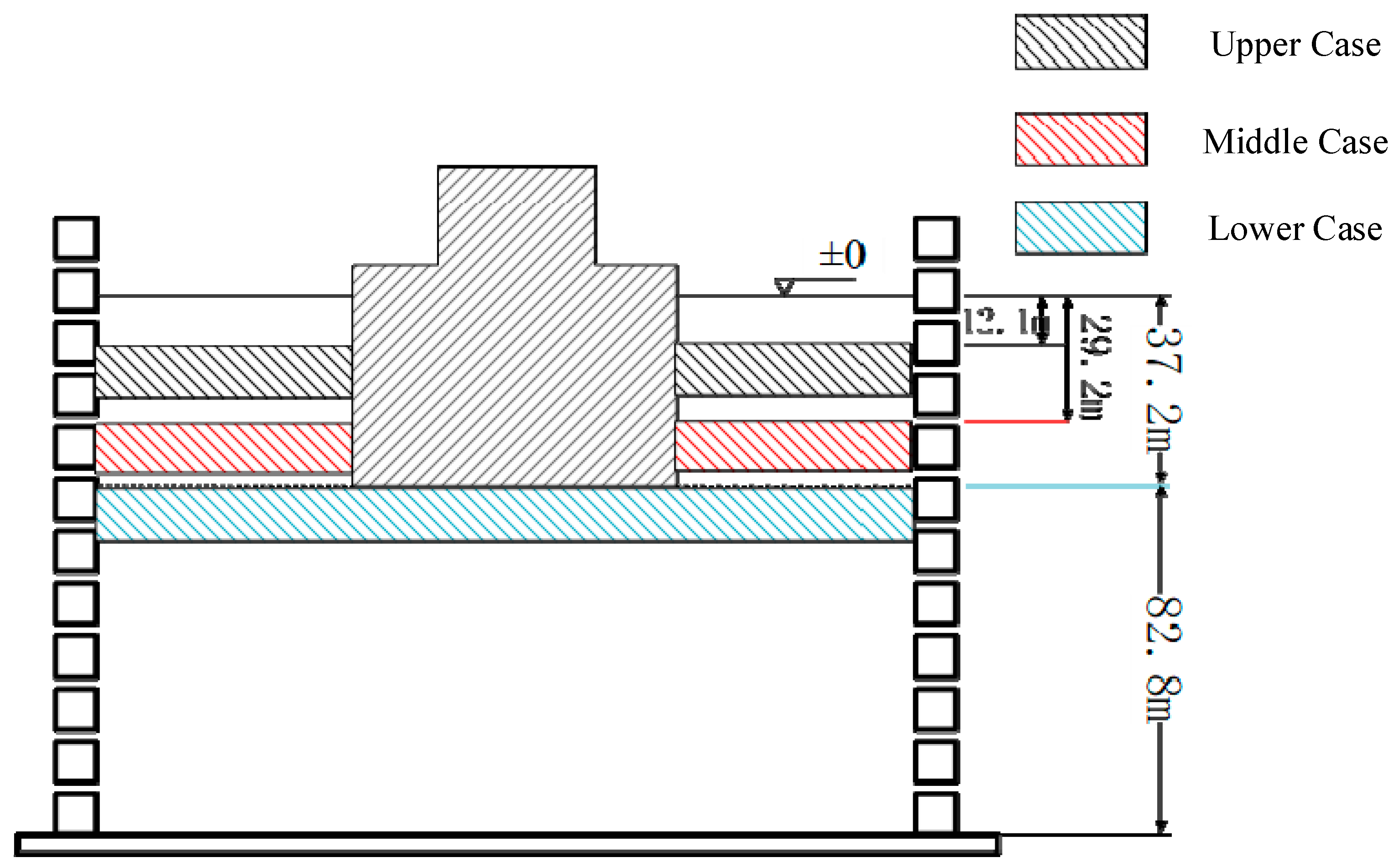
1.4. Operating Conditions
1.5. Davidenkov–Chen–Zhao Liquefaction Constitutive Model
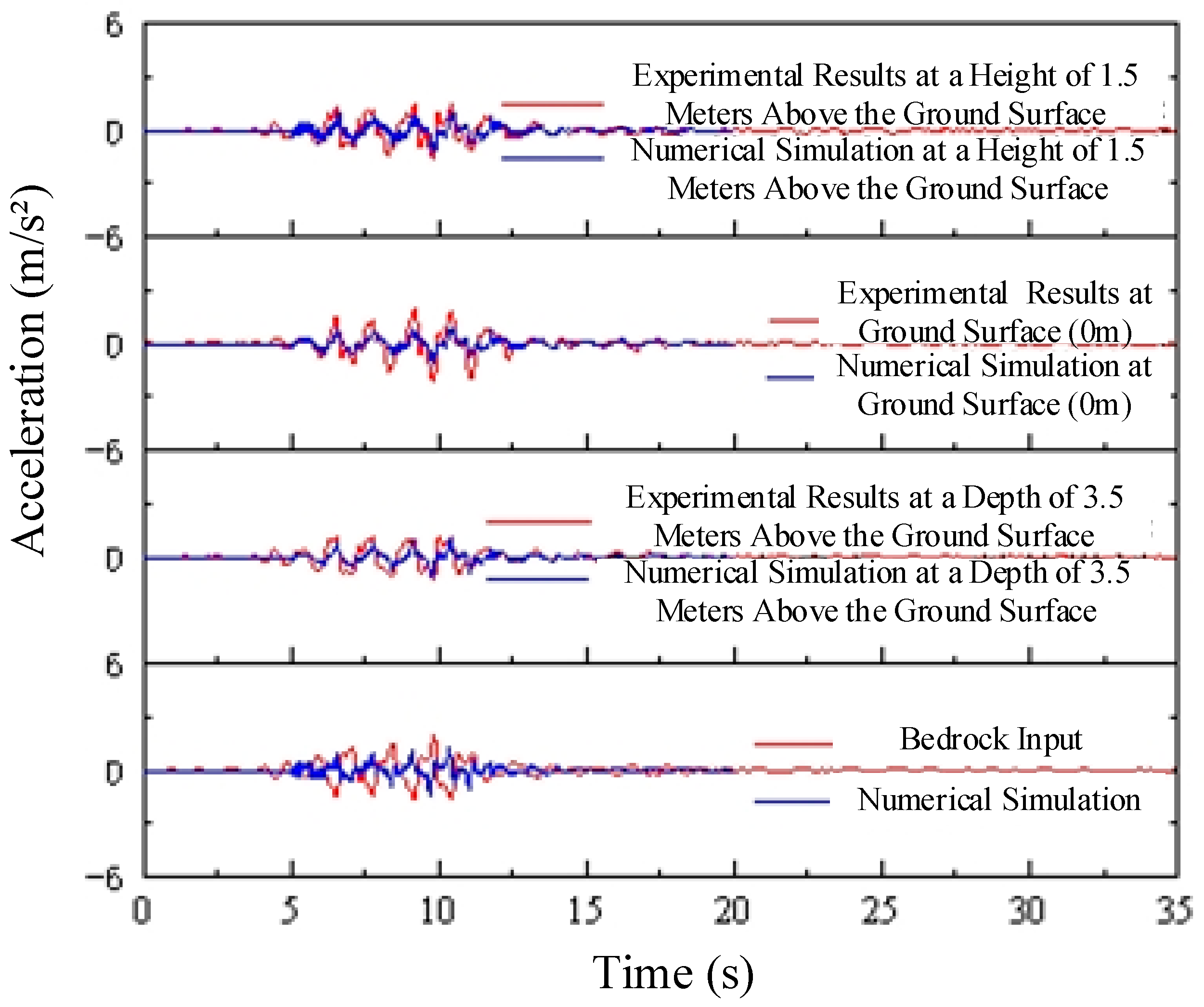
1.6. Comparison Between Numerical Simulation and Experimental Results
1.6.1. Site Horizontal Acceleration
1.6.2. Structural Acceleration
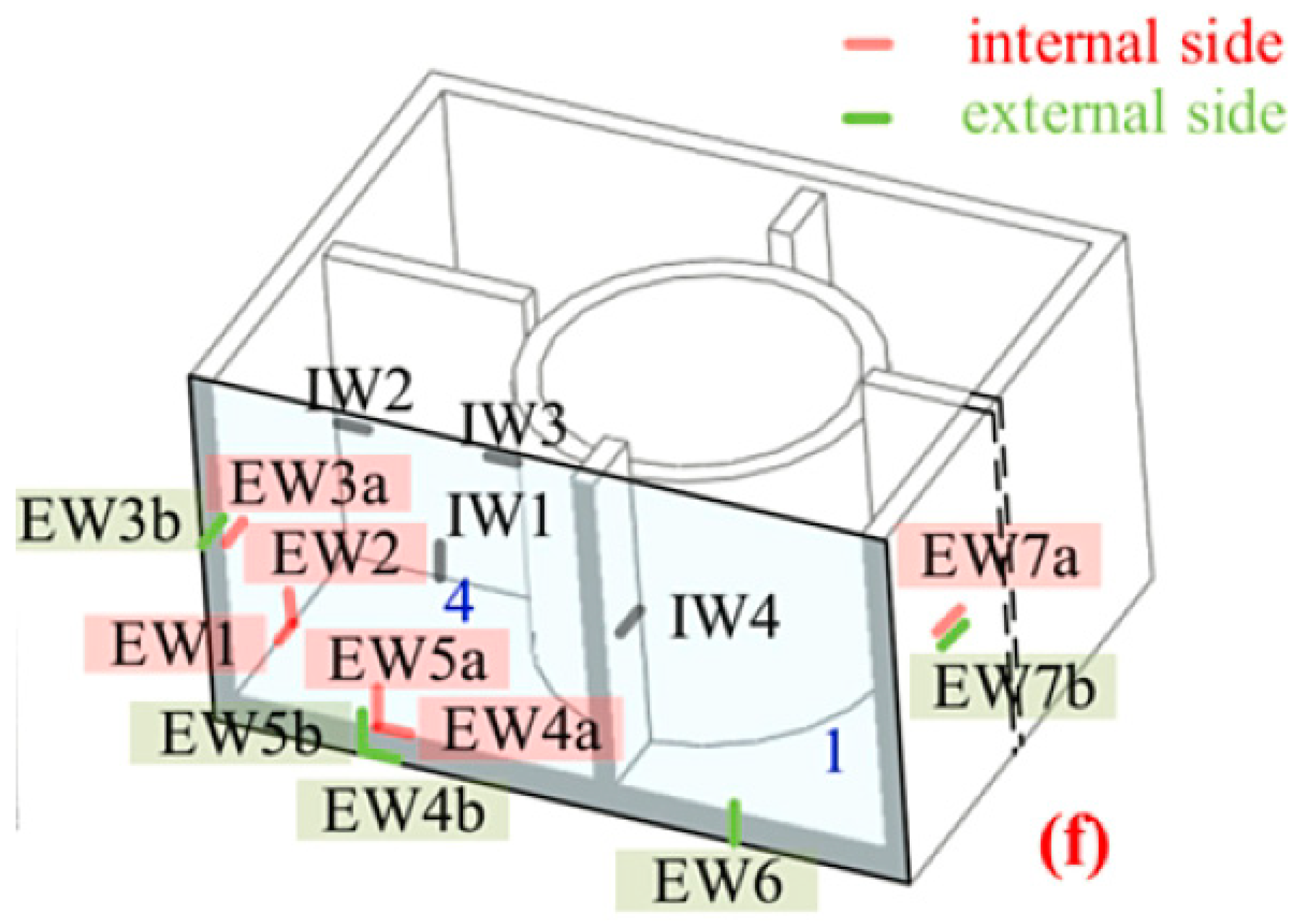
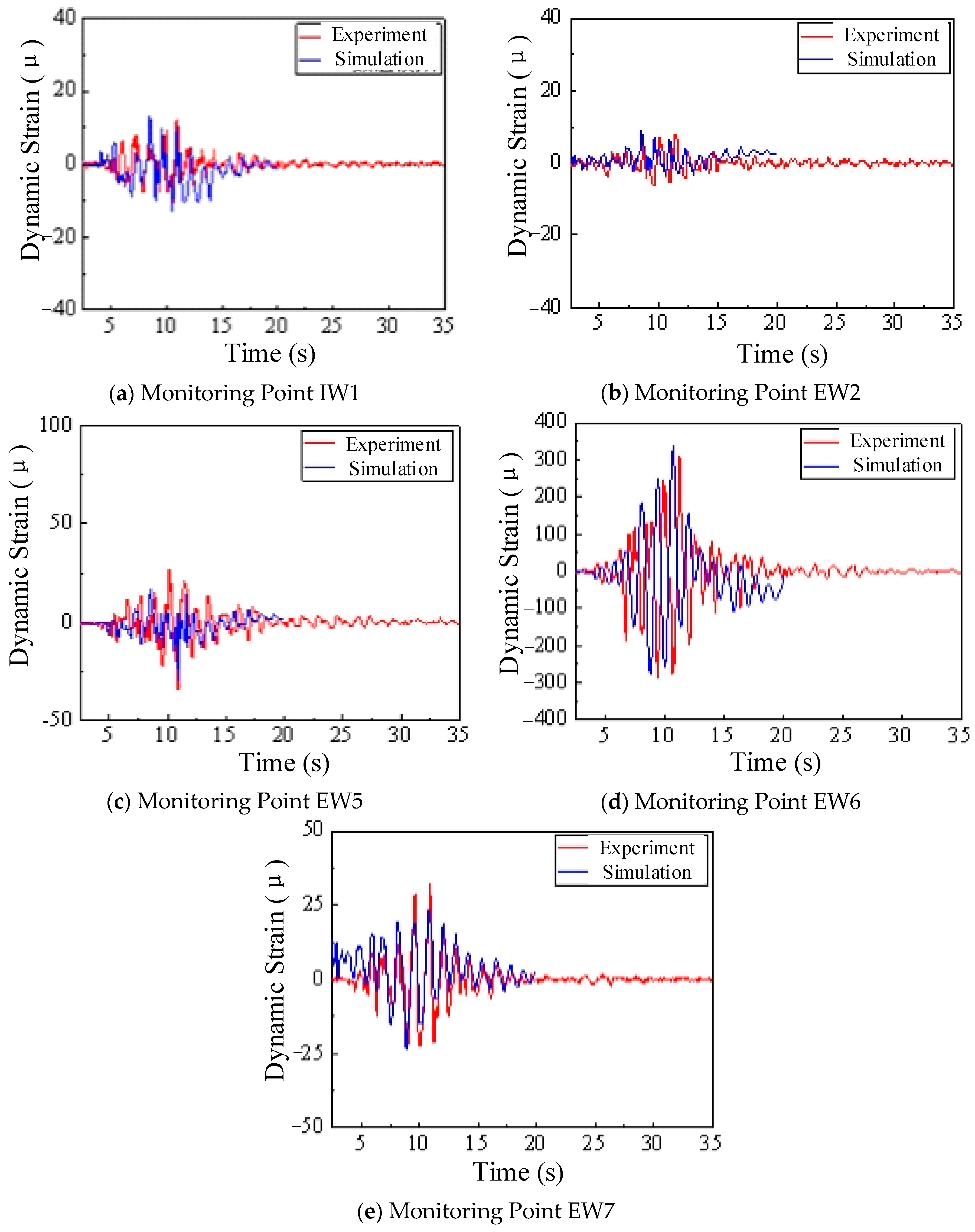
1.6.3. Structural Dynamic Strain
2. Seismic Response Analysis of Site-Embedded NPP Structural Systems
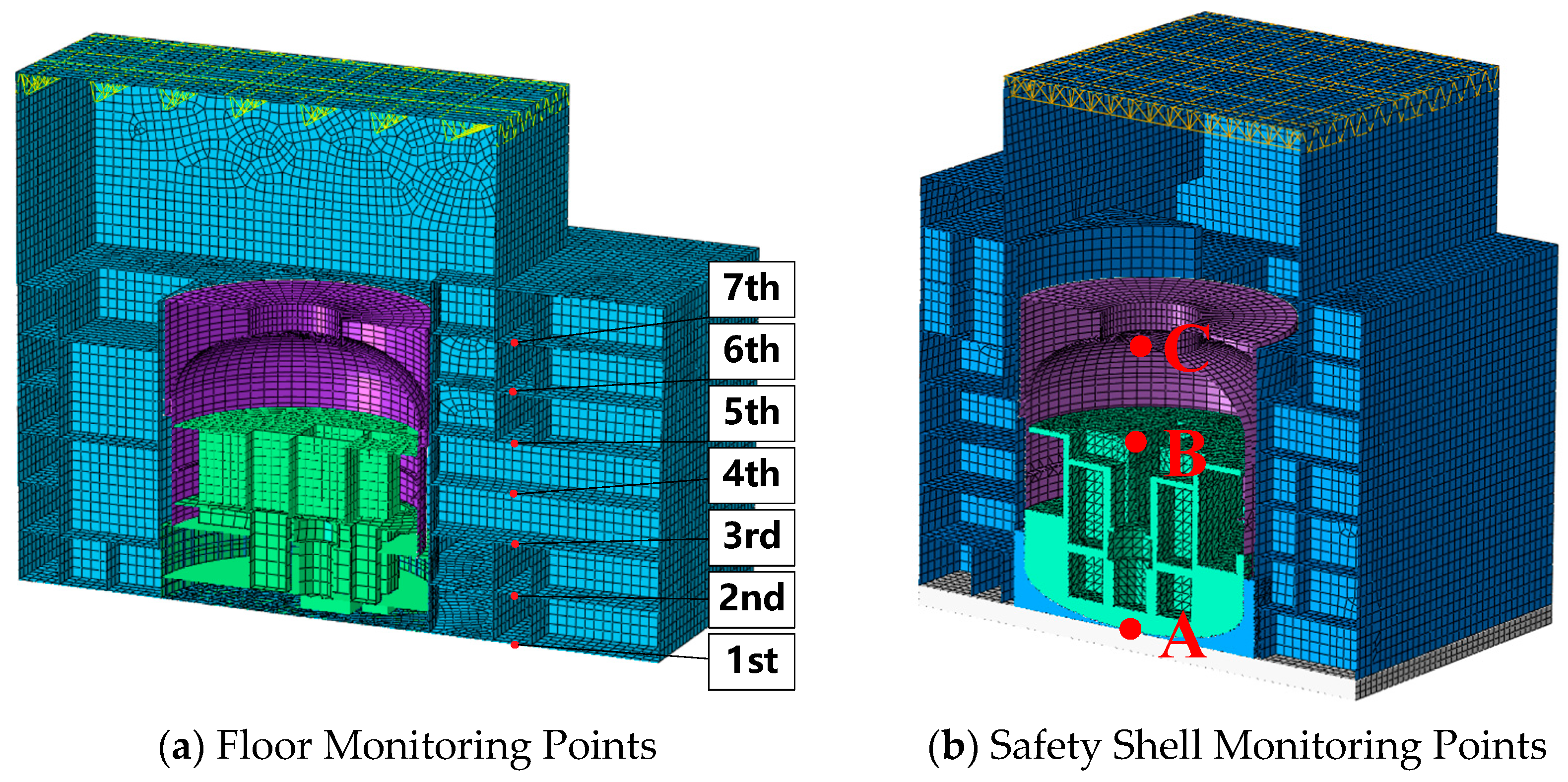
2.1. Auxiliary Building
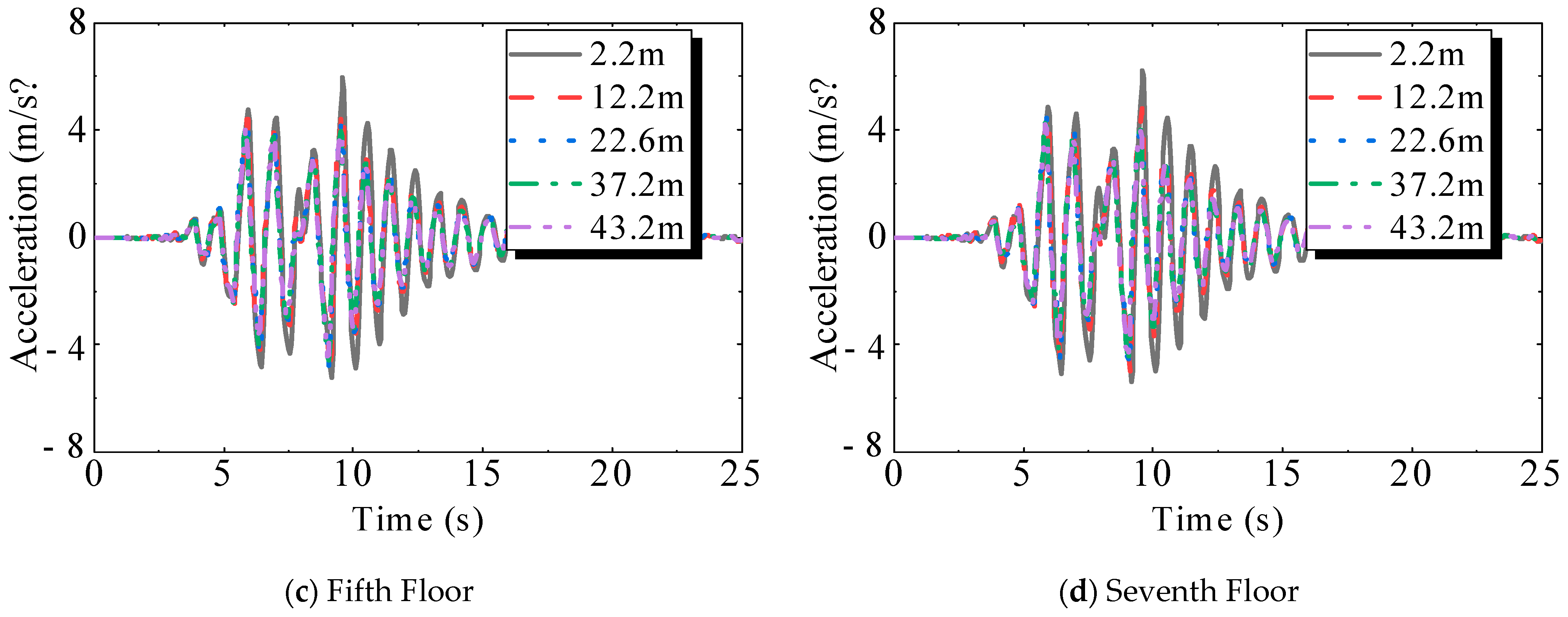
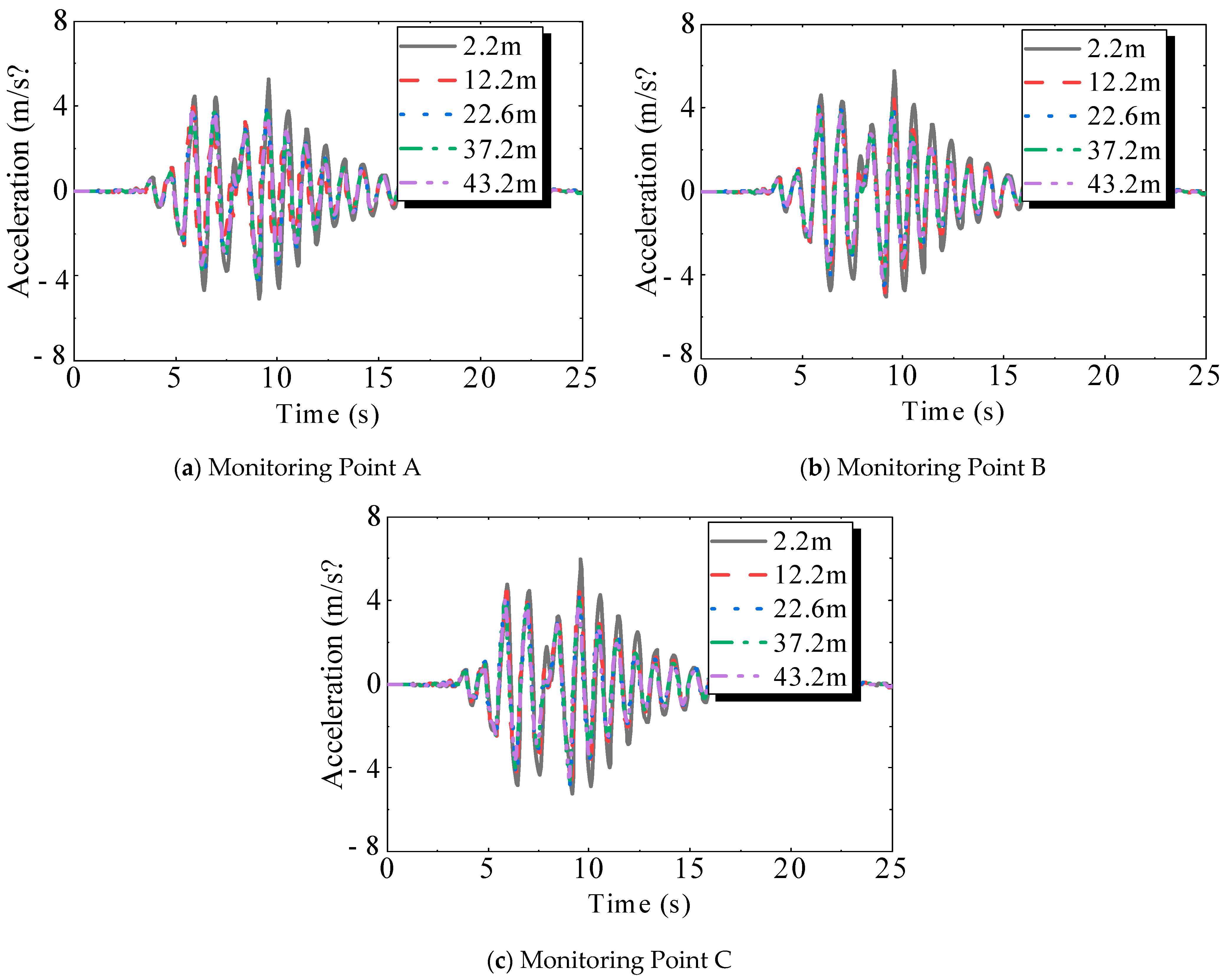
2.1.1. Acceleration of Floors
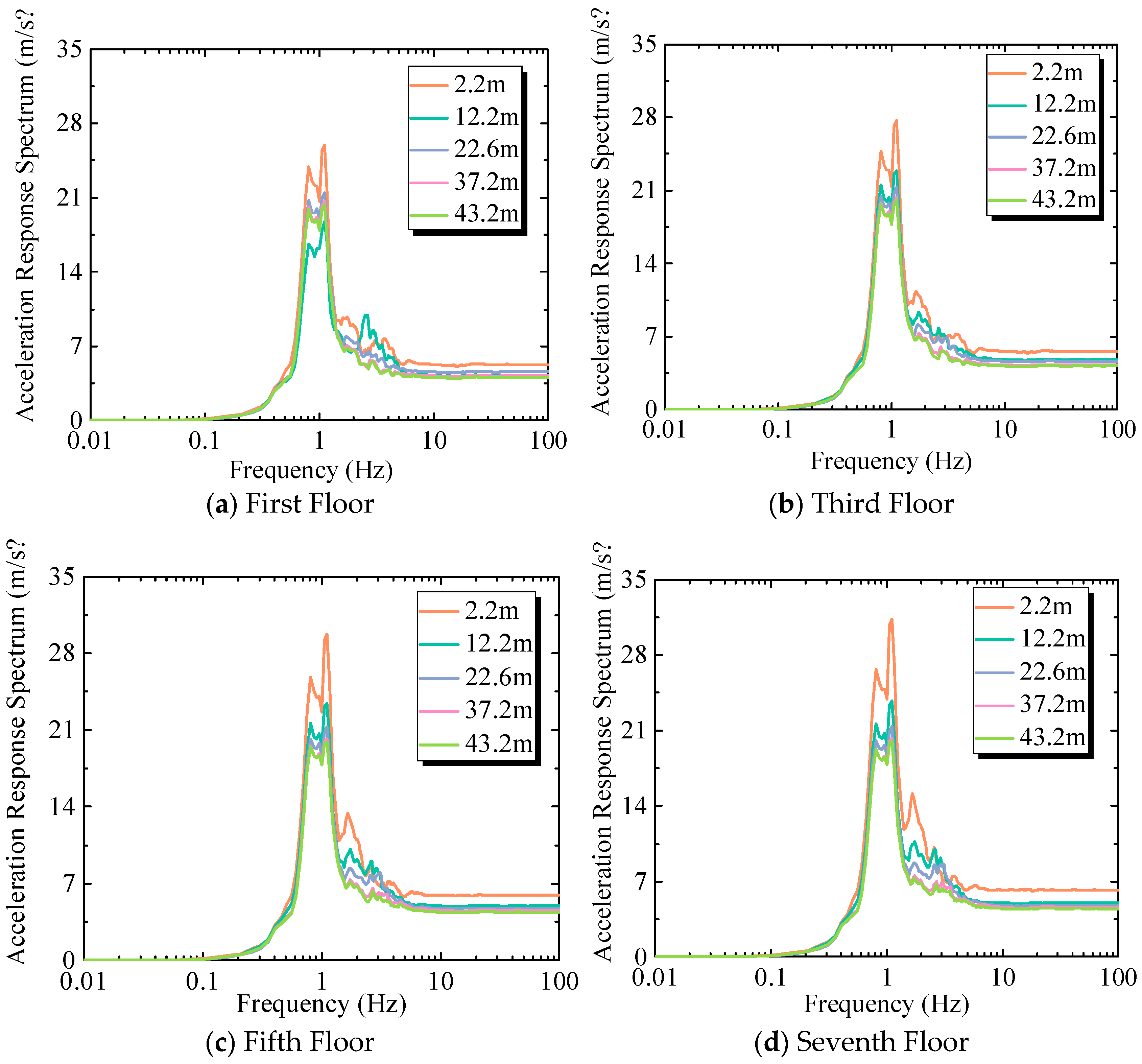
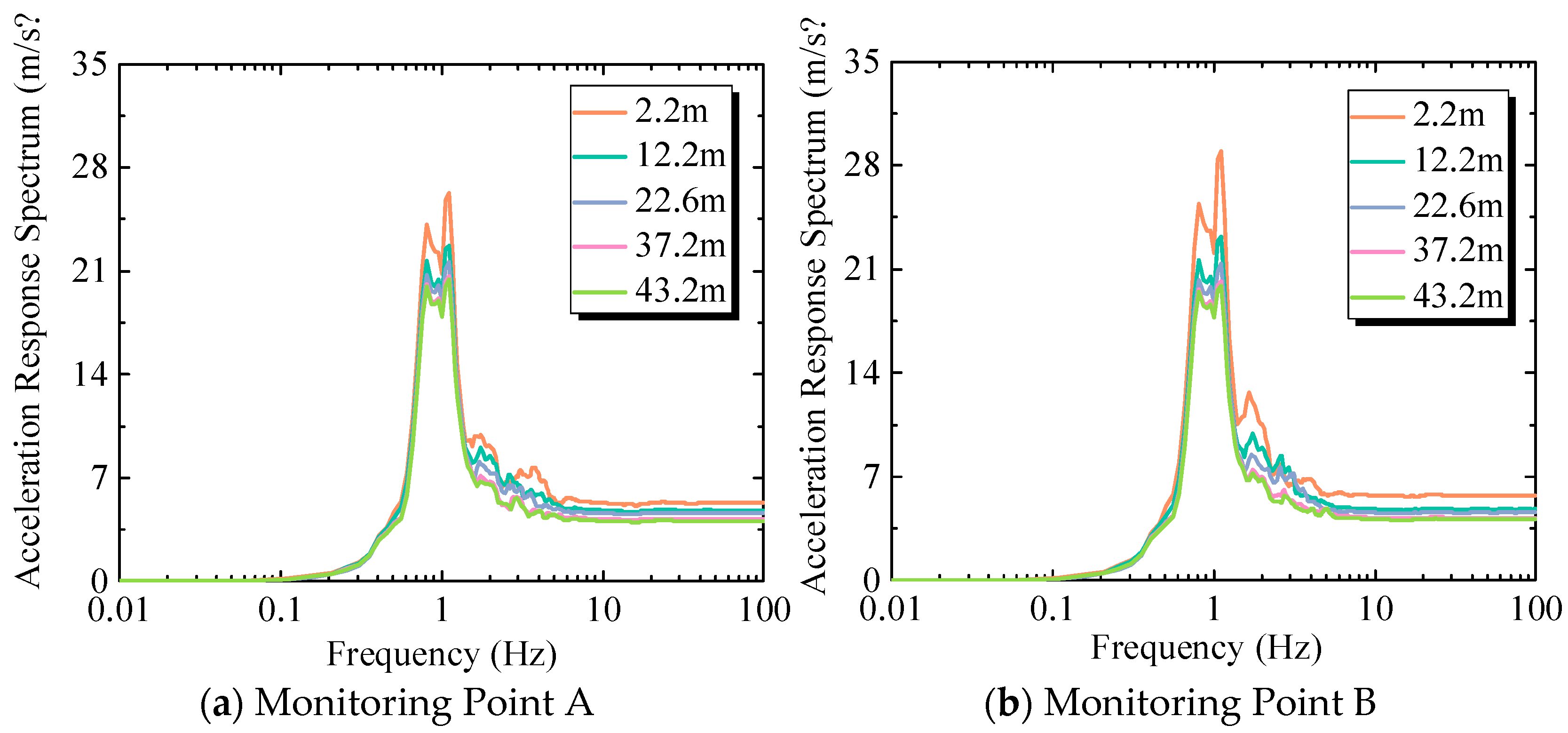
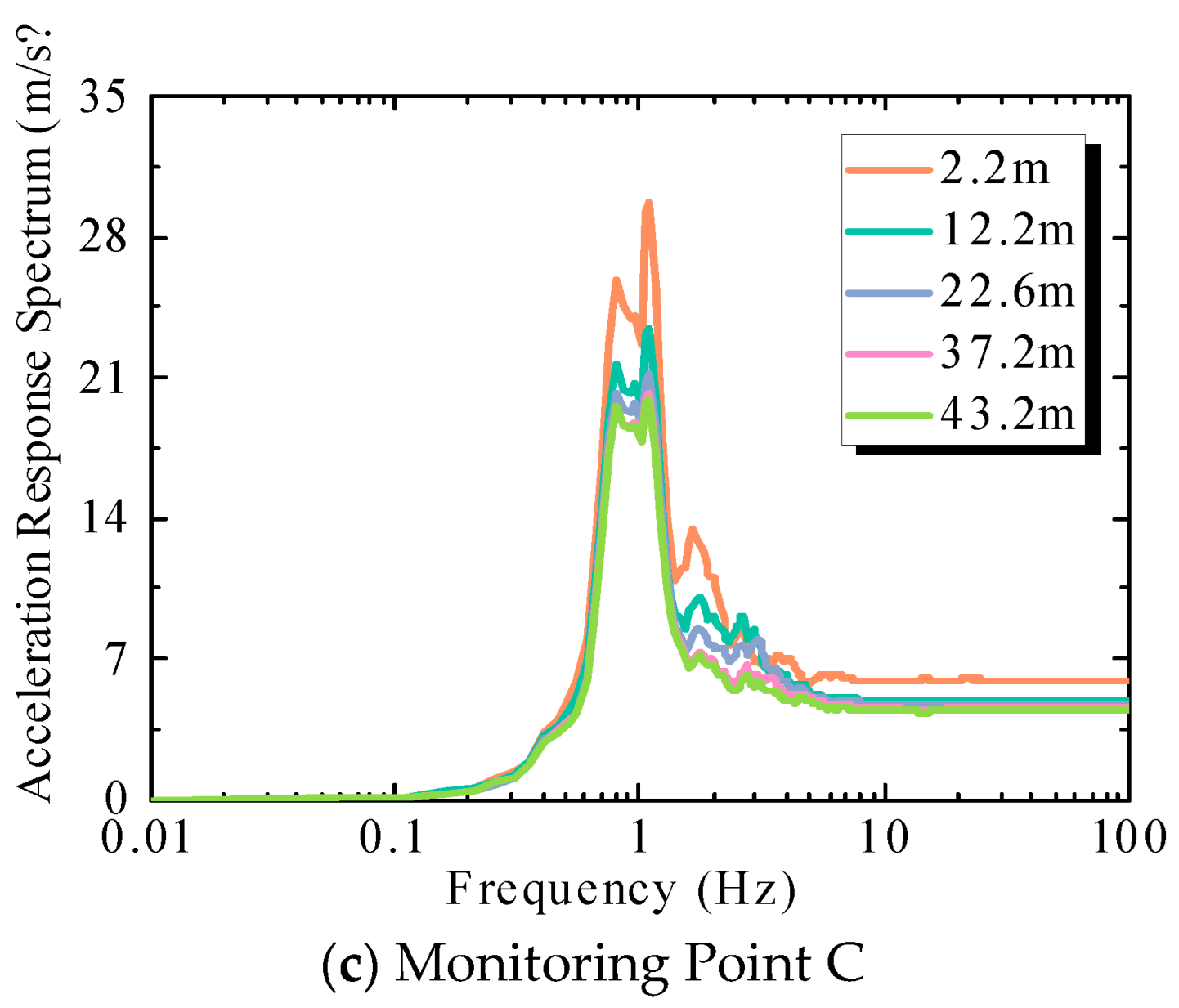
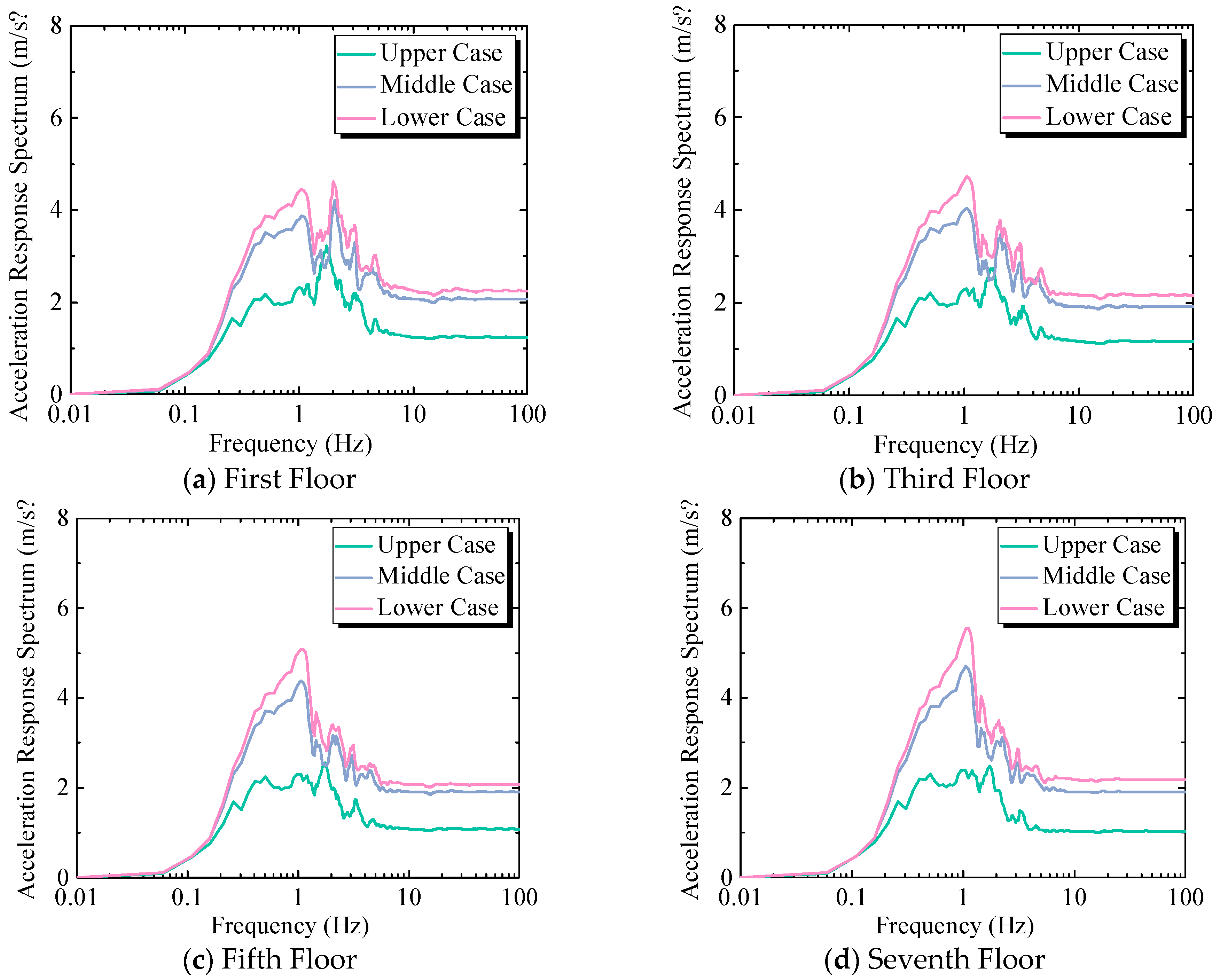
2.1.2. Acceleration Response Spectrum of Floors
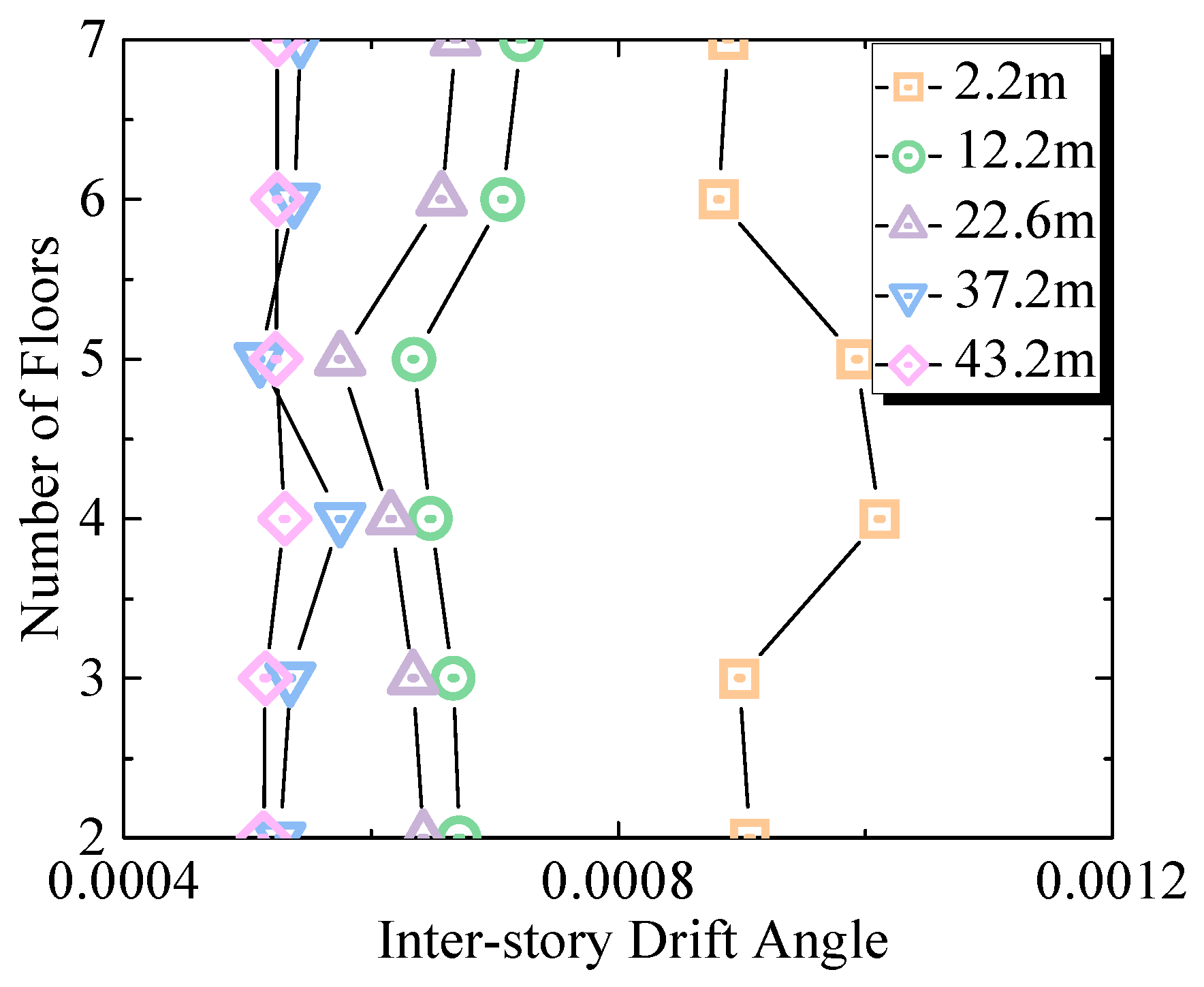
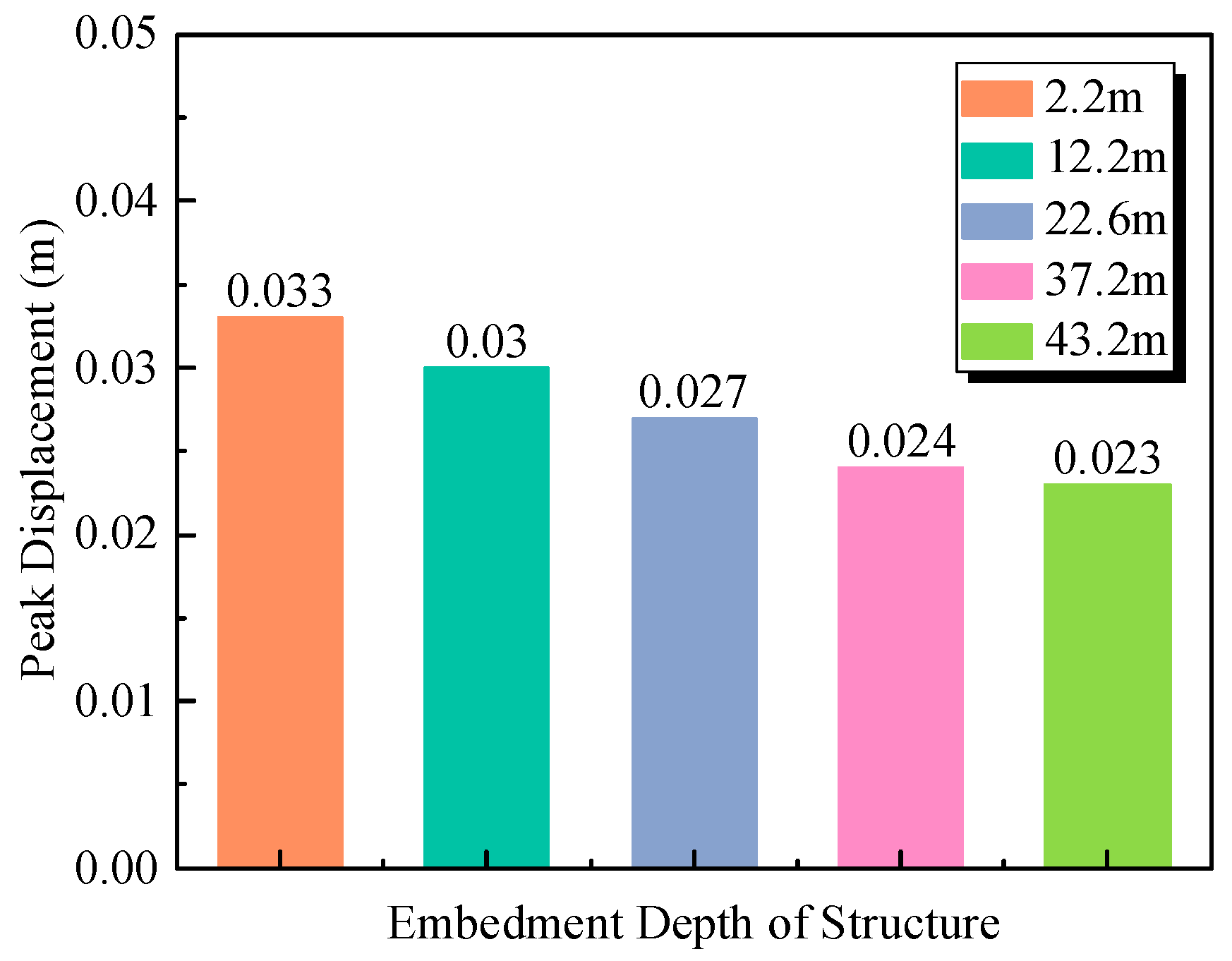
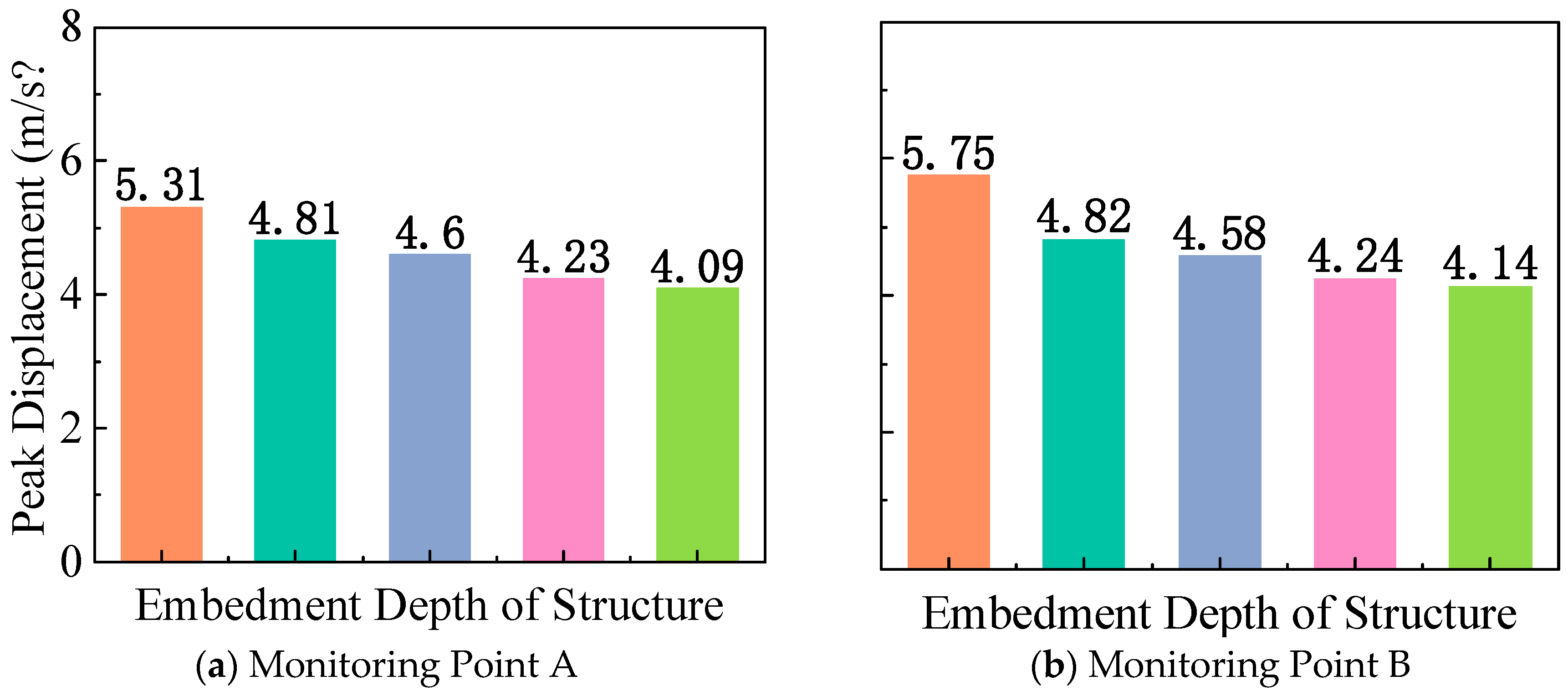
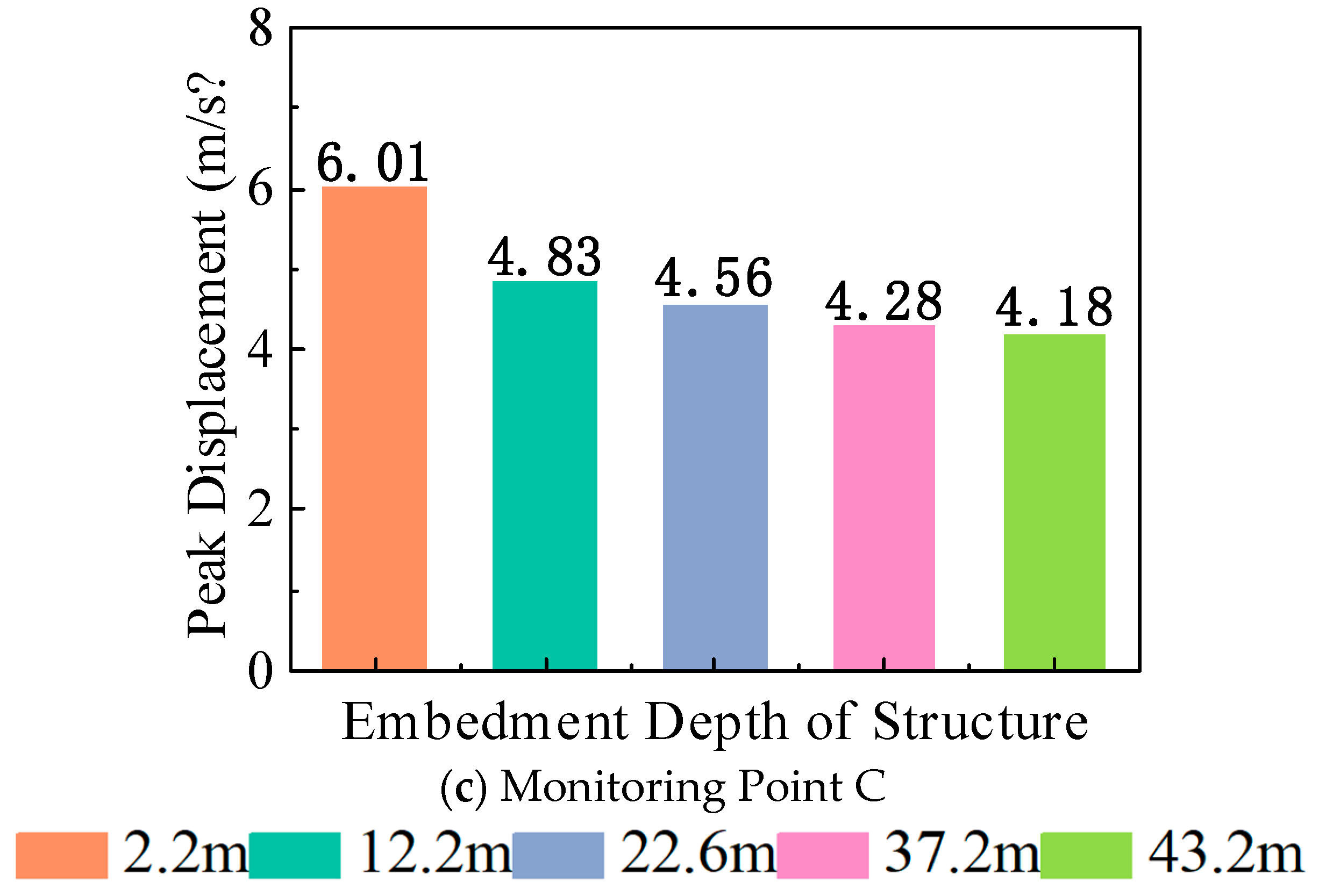
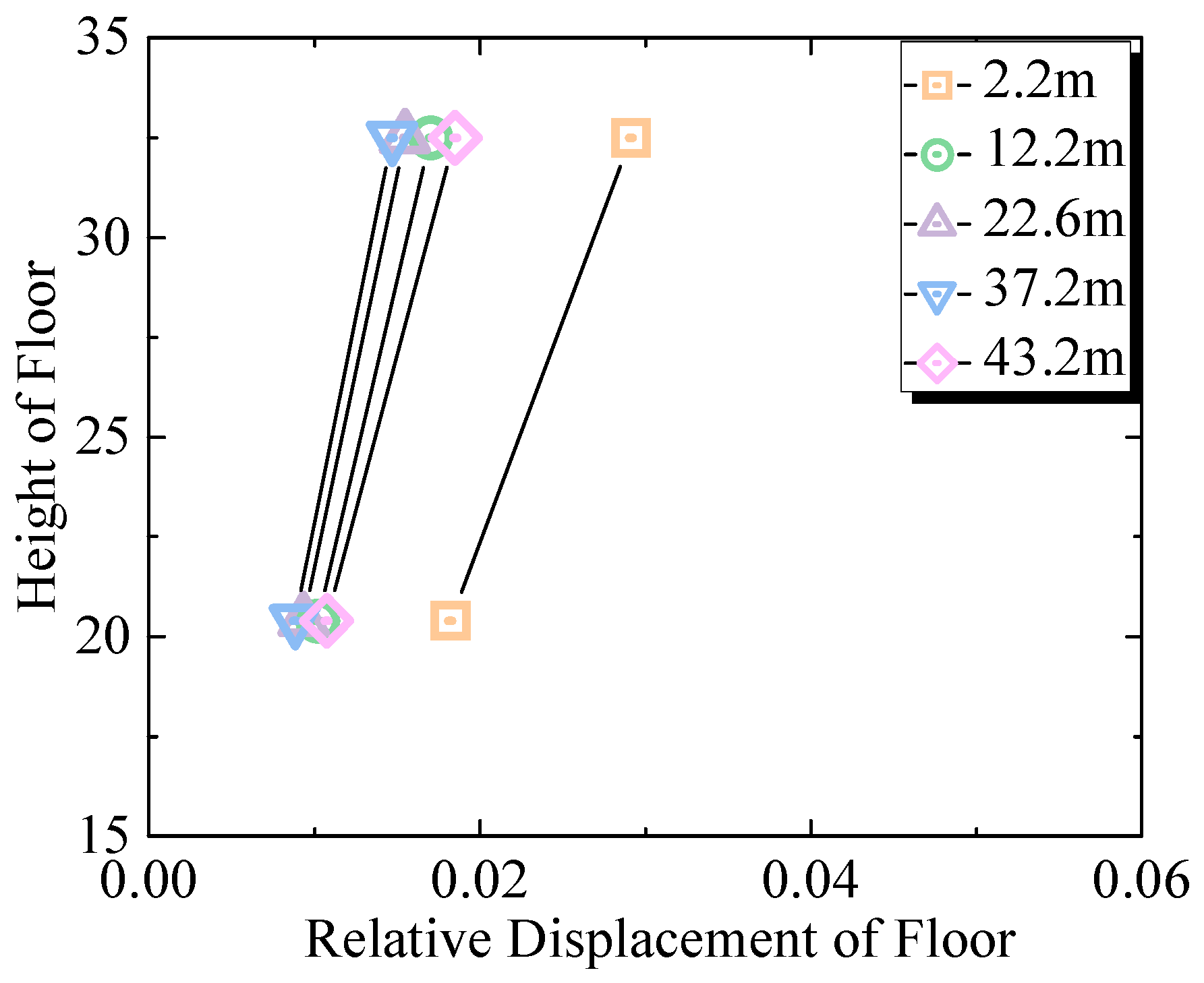
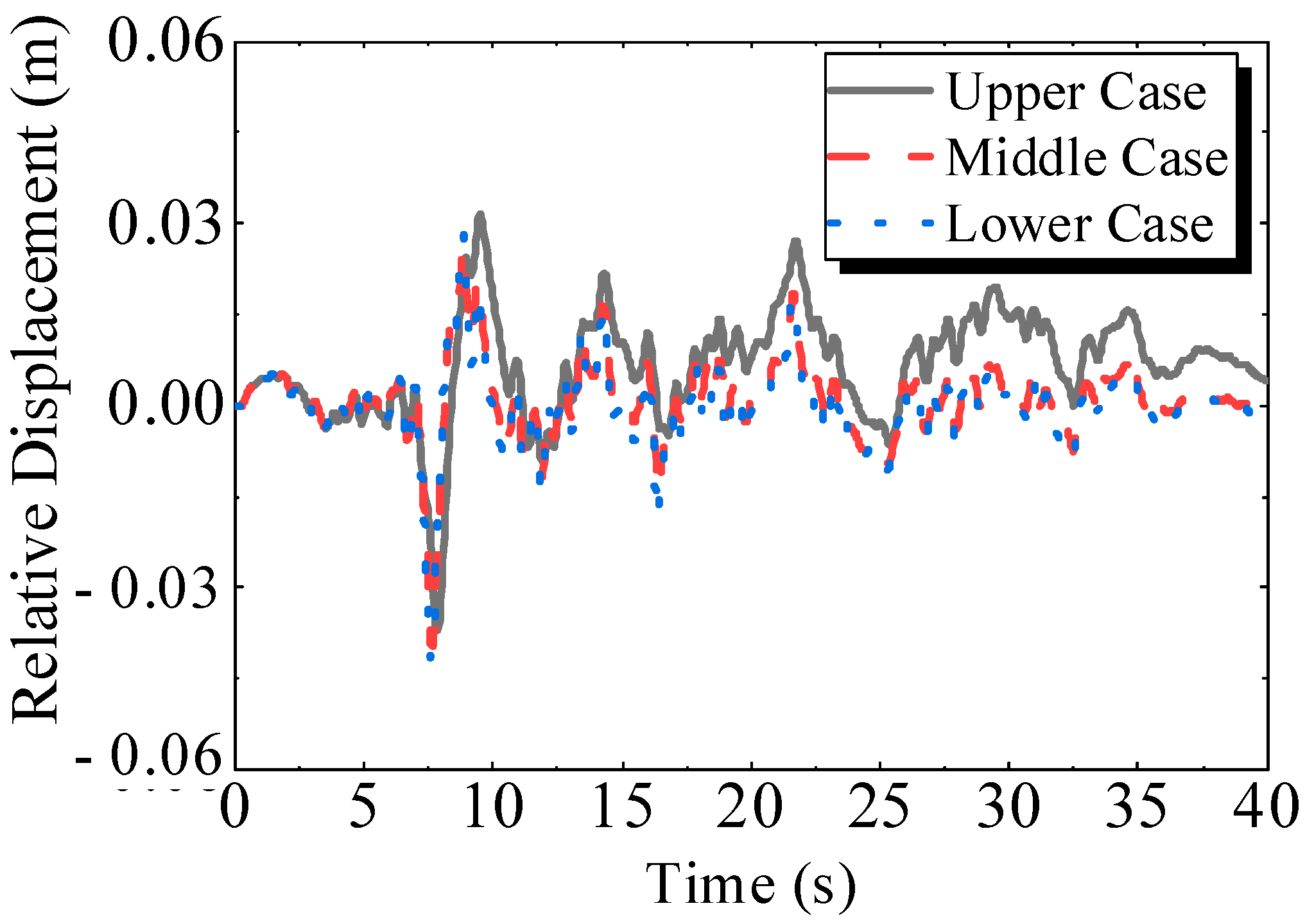
2.1.3. Relative Displacement of Floors
2.2. Containment Structure
2.2.1. Acceleration
2.2.2. Acceleration Response Spectrum
2.2.3. Relative Displacement
3. Seismic Response Analysis of Site-Embedded Nuclear Power Structure Systems with Different Liquefaction Layer Positions
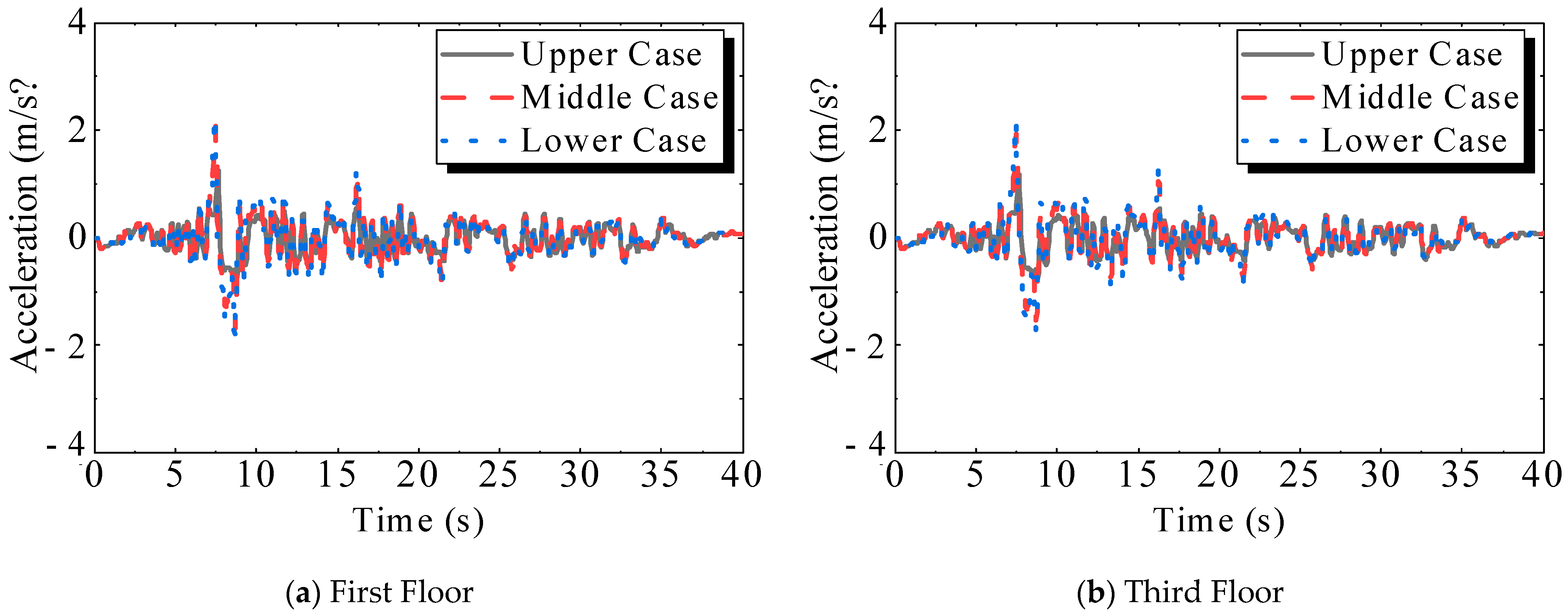
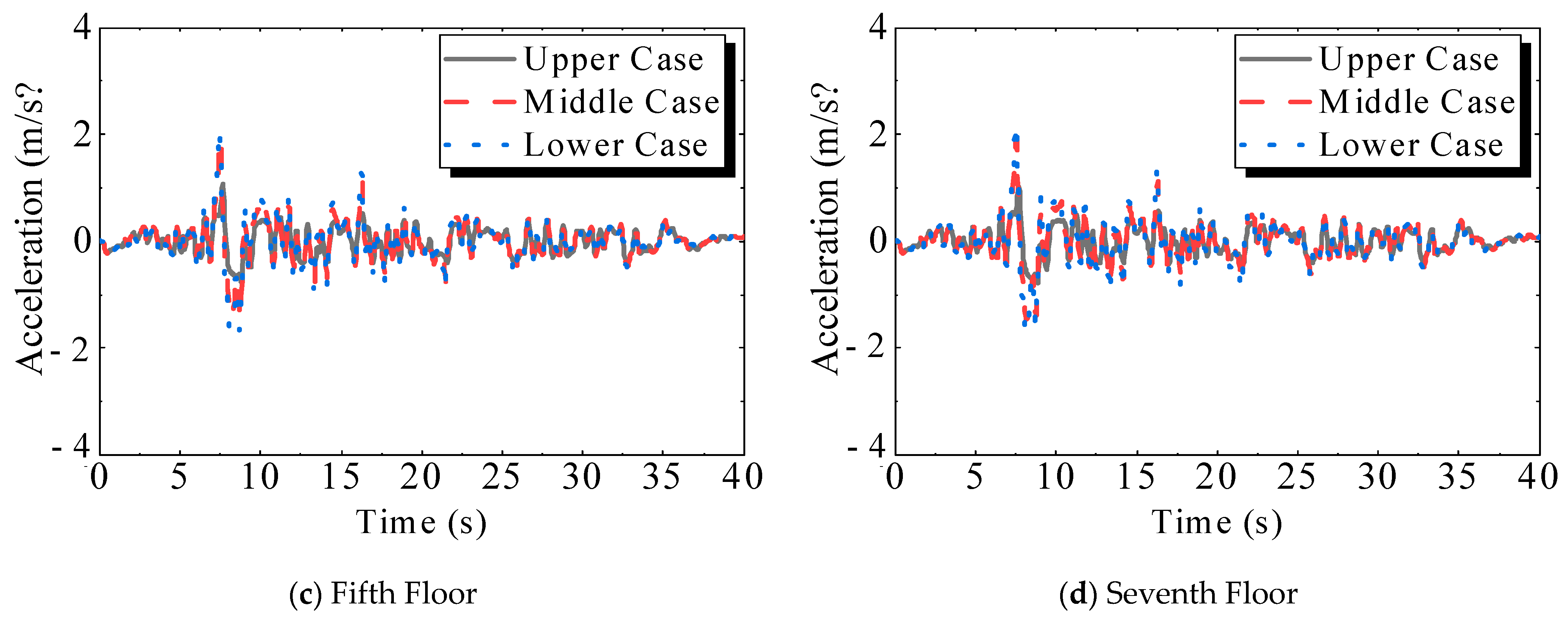
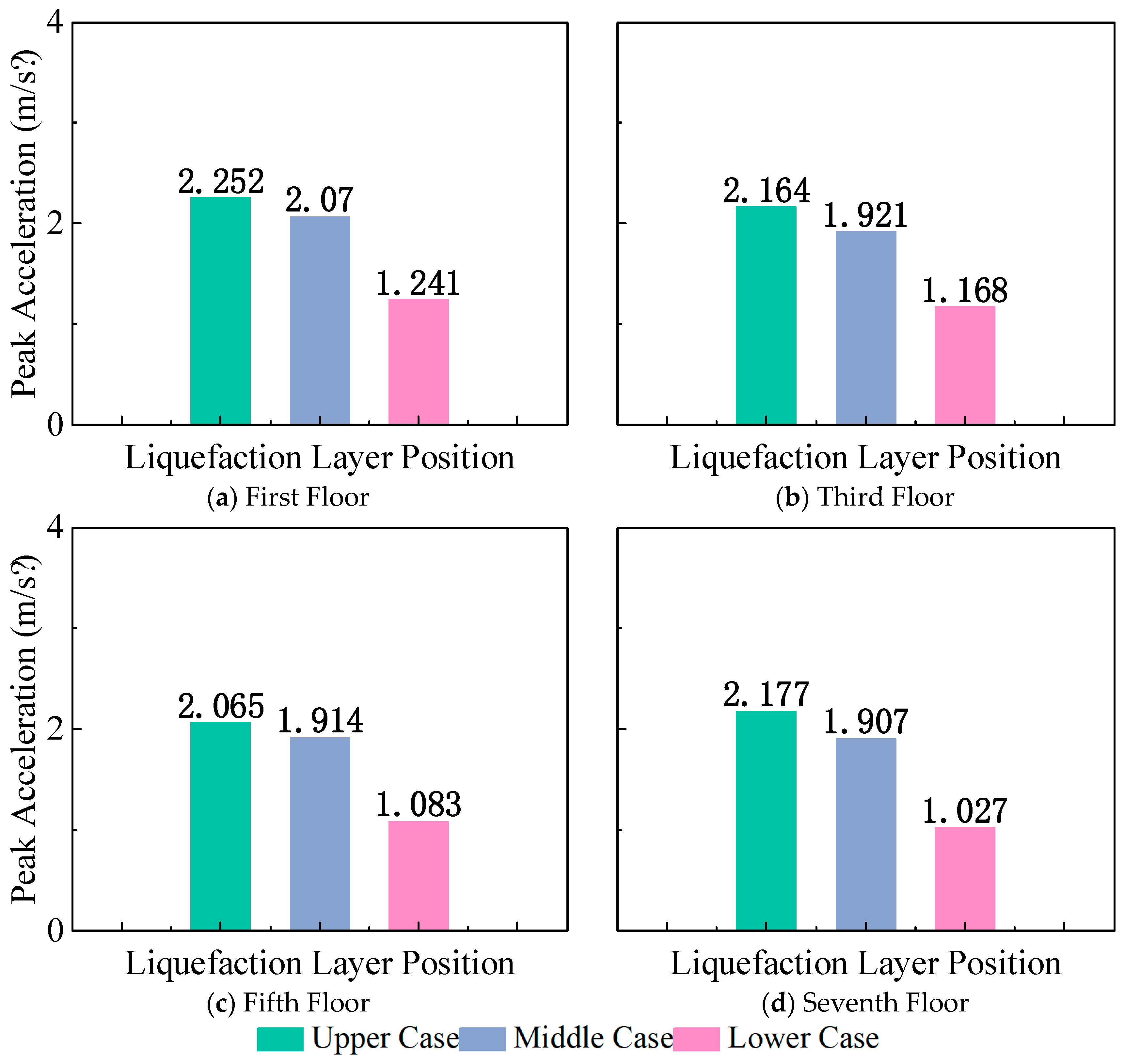
3.1. Auxiliary Building
3.1.1. Acceleration of Floors
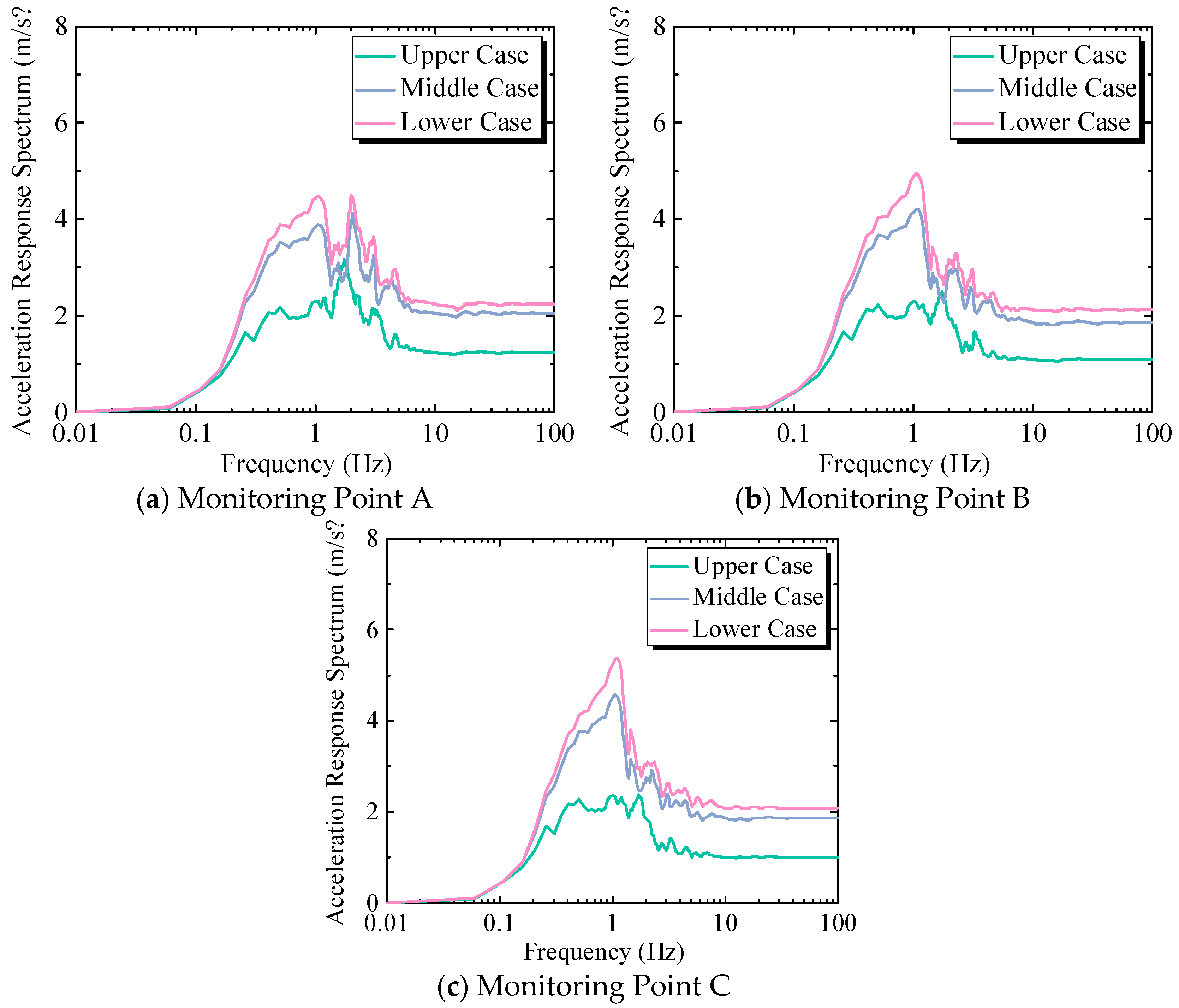
3.1.2. Acceleration Response Spectrum of Floors
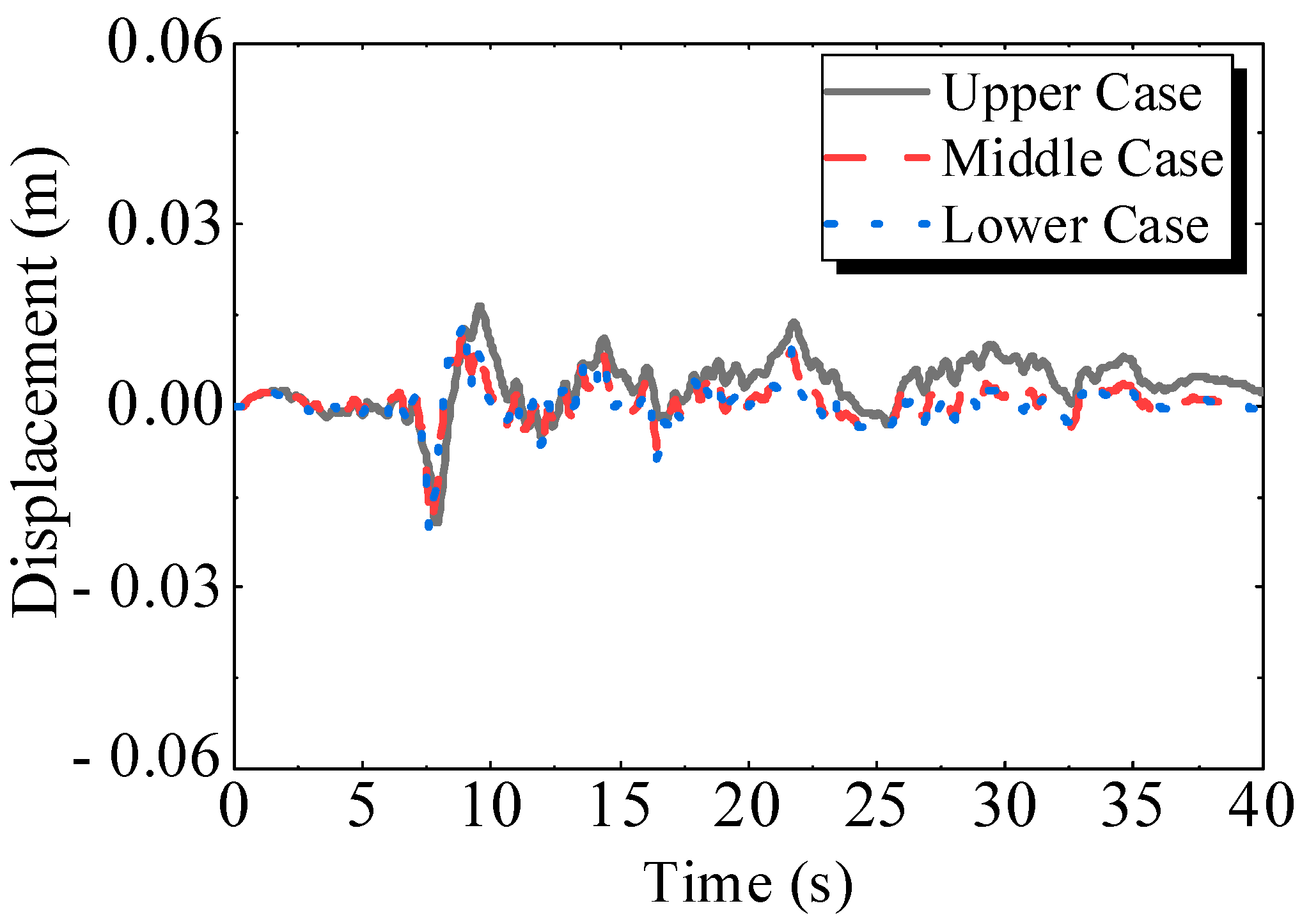
3.1.3. Relative Displacement
3.2. Containment Structure
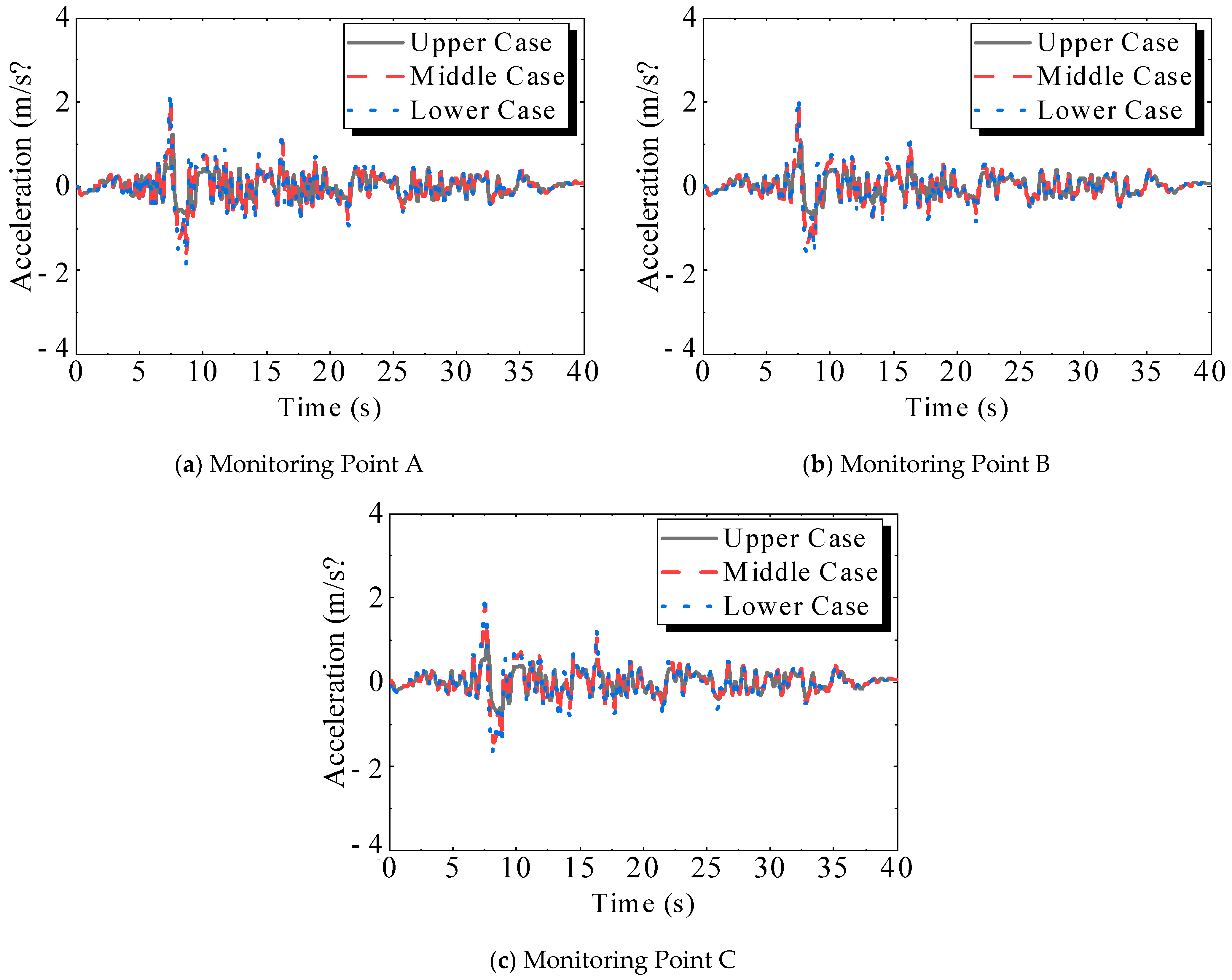
3.2.1. Acceleration
3.2.2. Acceleration Response Spectrum
3.2.3. Relative Displacement
3.3. Liquefiable Site
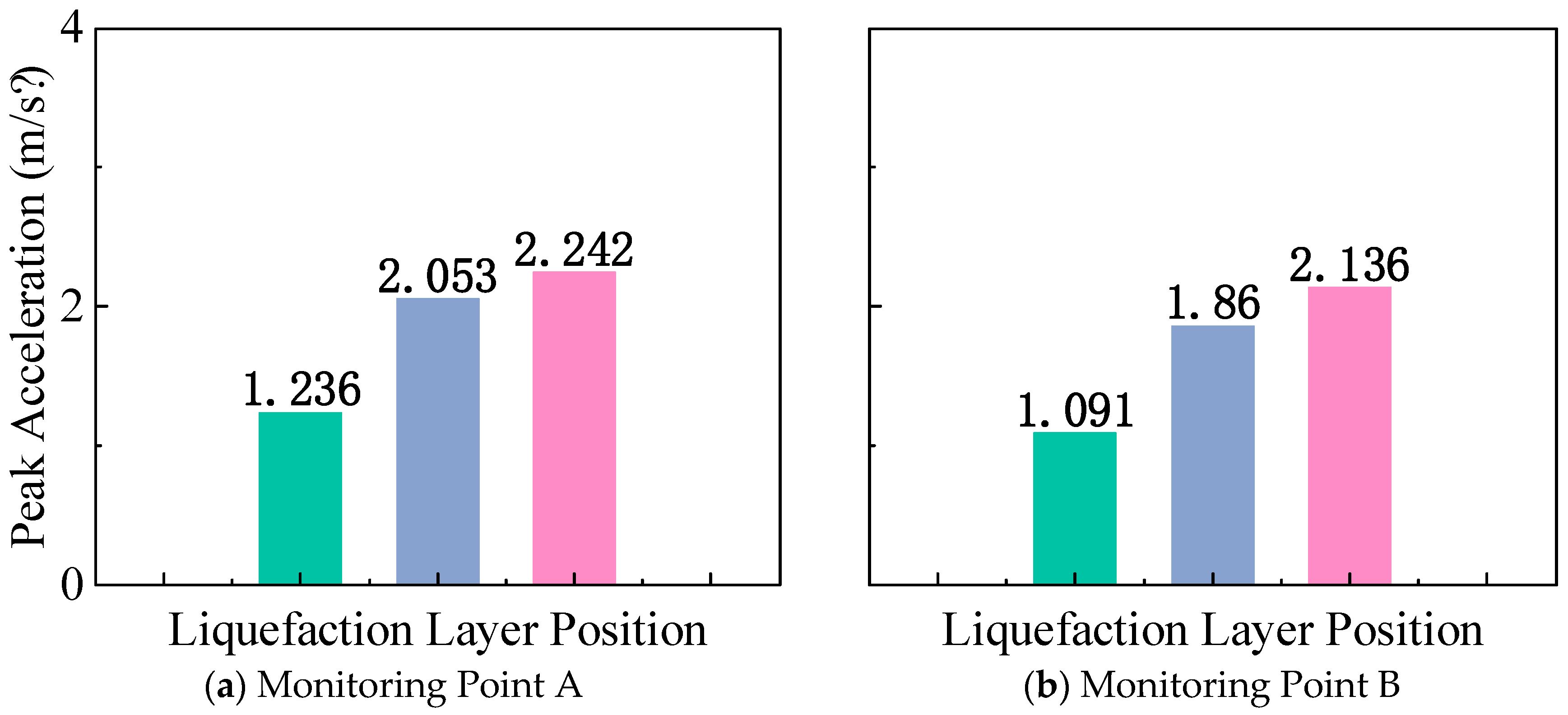
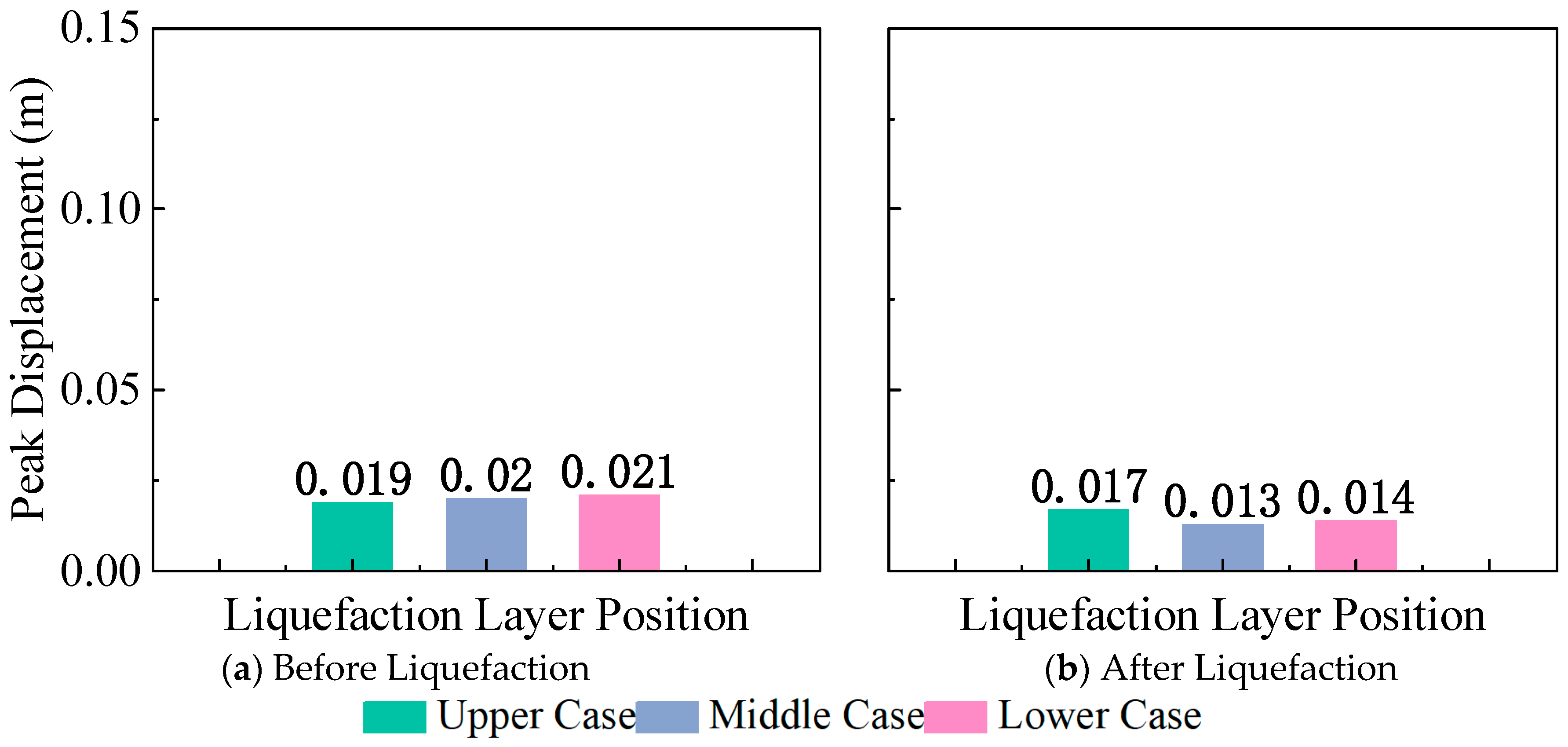
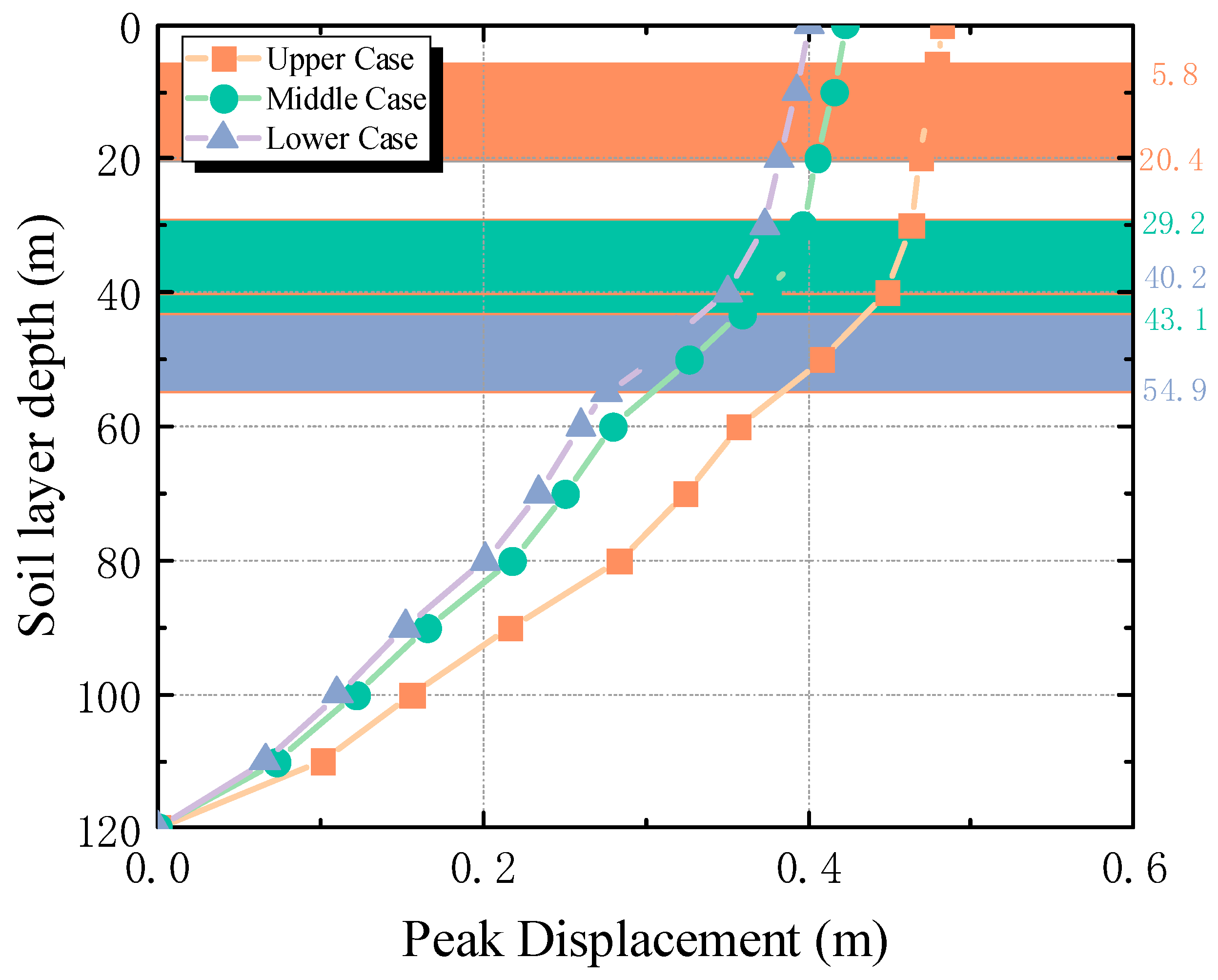
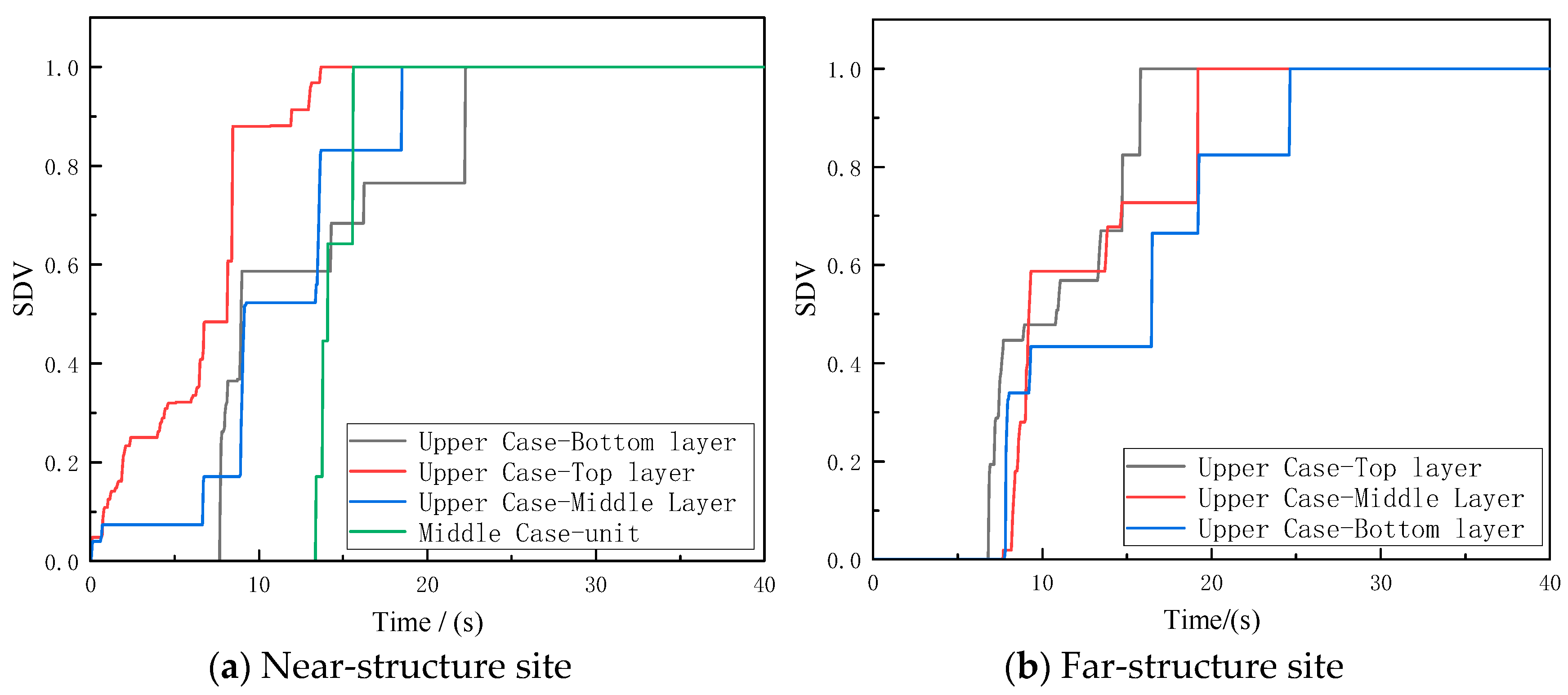
3.3.1. Displacement
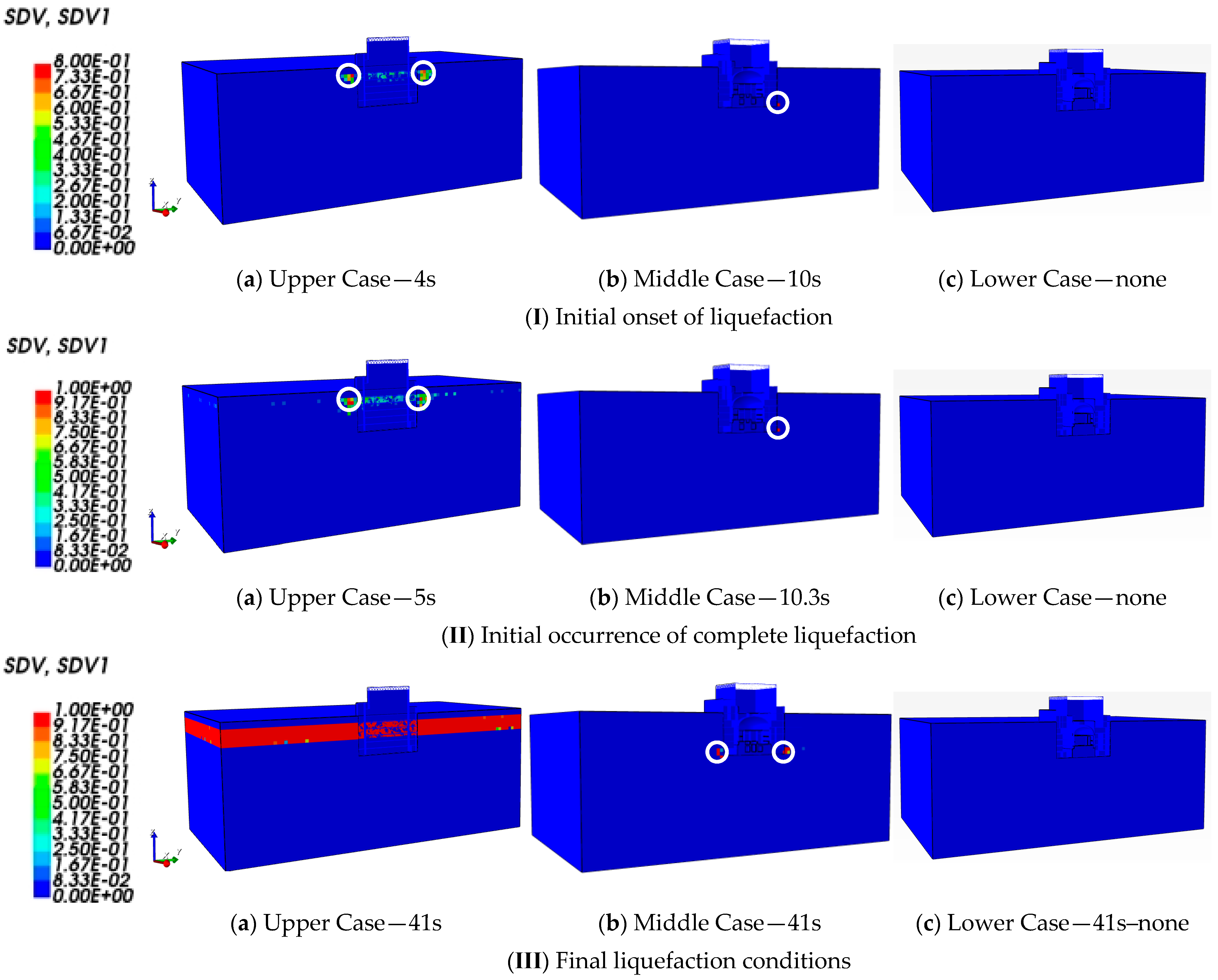
3.3.2. Liquefaction Phenomenon
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Nuclear Performance Report 2024; World Nuclear Association: London, UK, 2024.
- Kobayashi, T.; Yoshikawa, K.; Takaoka, E.; Nakazawa, M.; Shikama, Y. Time history nonlinear earthquake response analysis considering materials and geometrical nonlinearity. Nucl. Eng. Des. 2002, 212, 145–154. [Google Scholar] [CrossRef]
- Zadoyan, P.; Simos, N. Seismic Reevaluation of the Armenian NPP Unit 2: Issues and Engineering Approach. In Proceedings of the 10th International Conference on Nuclear Engineering, Arlington, VA, USA, 14–18 April 2002; pp. 715–726. [Google Scholar]
- Nakamura, N.; Yabushita, N.; Suzuki, T.; Yamada, J.; Tsunashima, N.; Nakano, T. Analyses of Reactor Building by 3D Nonlinear FEM Models Considering Basemat Uplift for Simultaneous Horizontal and Vertical Ground Motions. Nucl. Eng. Des. 2008, 238, 3551–3560. [Google Scholar] [CrossRef]
- Johnson, J.J.; Schneider, O.; Schuetz, W.; Monette, P.; Asfura, A.P. Effects of SSI on EPRTM In-Structure Response for a Rock Site: Coherent High Frequency Ground Motion. In Proceedings of the ASME 2010 Pressure Vessels and Piping Division/K-PVP Conference, Bellevue, WA, USA, 18–22 July 2010; pp. 271–281. [Google Scholar]
- Nakaki, D.K.; Hashimoto, P.S.; Johnson, J.J.; Bayraktarli, Y.; Zuchuat, O. Probabilistic Seismic Soil Structure Interaction Analysis of the Mühleberg Nuclear Power Plant Reactor and SUSAN Buildings. In Proceedings of the ASME 2010 Pressure Vessels and Piping Division/K-PVP Conference, Bellevue, WA, USA, 18–22 July 2010; pp. 79–88. [Google Scholar]
- Chen, Y. Floor Response Spectrum Analysis of Nuclear Power Plant Structures Based on Three-Dimensional Solid Model. Ph.D. Thesis, Tianjin University, Tianjin, China, 2005. [Google Scholar]
- Wu, Z.H. Study on Practical Analysis Method of the Inner Containment in Nuclear Power Plant Reactor Building. Ph.D. Thesis, Institute of Engineering Mechanics, China Earthquake Administration, Harbin, China, 2014. [Google Scholar]
- Li, N. Seismic Dynamic Response of Nuclear Island Structure Considering the Influence of Equipment. Ph.D. Thesis, Institute of Engineering Mechanics, China Earthquake Administration, Harbin, China, 2020. [Google Scholar]
- GB 50267-2019; China Earthquake Administration (CEA). Standard for Seismic Design of Nuclear Island Structure. China Planning Press: Beijing, China, 2019.
- American Society of Civil Engineers (ASCE). Seismic Analysis of Safety-Related Nuclear Structures and Commentary; ASCE/SEI Standard: Reston, VA, USA, 2017; pp. 4–16. [Google Scholar]
- Westinghouse Electric Co. LLC. Westinghouse AP1000 Design Control Document, Revision 19; Nuclear Regulatory Commission: Butler County, PA, USA, 2011. [Google Scholar]
- Li, X.J.; He, Q.M.; Zhang, H.Y.; Lei, Y. Effect of ground motion velocity pulse on seismic performance of foundation isolation structures with different aspect ratio. J. Build. Struct. 2018, 33, 35–42. [Google Scholar]
- Liu, P.X.; Li, X.J.; Zhou, Z.H. Analysis of influence of types of strong seismic observation stations on ground motion. Acta Seismol. Sin. 2022, 44, 1083–1098. [Google Scholar]
- de Borbón, F.; Domizio, M.; Ambrosini, D.; Curadelli, O. Influence of various parameters in the seismic soil-structure interaction response of a nuclear power plant. Eng. Struct. 2020, 217, 110820. [Google Scholar] [CrossRef]
- Li, L.; Chen, Q.; Pan, R. Analysis of the Influence of Structure-Soil-Structure Interaction on the Seismic Response for Nuclear Power Plant ASTS. Energies 2023, 16, 194. [Google Scholar] [CrossRef]
- Patil, G.; Choudhury, D.; Mondal, A. Nonlinear dynamic soil-foundation-superstructure interaction analysis for a reactor building supported on a combined piled-raft system. Int. J. Geomech. 2023, 23, 04023009. [Google Scholar] [CrossRef]
- Firoj, M.; Maheshwari, B. Effect of CPRF on nonlinear seismic response of an NPP structure considering raft-pile-soil-structure-interaction. Soil Dyn. Earthq. Eng. 2022, 158, 107295. [Google Scholar] [CrossRef]
- Firoj, M.; Maheshwari, B.K. A new nonlinear spring-dashpot model of CPRF of NPP structure based on coupled BEM-FEM approach. Earthq. Eng. Struct. Dyn. 2023, 52, 932–955. [Google Scholar] [CrossRef]
- Maheshwari, B.K.; Firoj, M. Settlement of combined piled raft foundation of a nuclear power plant in non-liquefiable and liquefiable soils. Nucl. Eng. Des. 2023, 413, 112518. [Google Scholar] [CrossRef]
- Firoj, M.; Maheshwari, B.K. Dynamic impedances of CPRF using coupled BEM-FEM approach: A parametric study and application. Eng. Anal. Bound. Elem. 2023, 156, 8–19. [Google Scholar] [CrossRef]
- Yang, Y.; Fan, H.; Cheng, Y.P.; Gong, W.; Dai, G.; Liang, F.; Jia, Y. Seismic response of nuclear power station with disconnected pile-raft foundation using dynamic centrifuge tests. J. Clean. Prod. 2022, 379, 134572. [Google Scholar] [CrossRef]
- Amorosi, A.; Boldini, D. Numerical modeling of the transverse dynamic behavior of circular tunnels in clayey soils. Soil Dyn. Earthq. Eng. 2009, 59, 1059–1072. [Google Scholar] [CrossRef]
- Argyroudis, S.A.; Pitilakis, K.D. Seismic fragility curves of shallow tunnels in alluvial deposits. Soil Dyn. Earthq. Eng. 2012, 35, 1–12. [Google Scholar] [CrossRef]
- Chen, H.; Li, X.; Yan, W.; Chen, S.; Zhang, X. Shaking table test of immersed tunnel considering the geological condition. Eng. Geol. 2017, 227, 93–107. [Google Scholar] [CrossRef]
- Tsinidis, G. Response characteristics of rectangular tunnels in soft soil subjected to transversal ground shaking. Tunn. Undergr. Space Technol. 2017, 62, 1–22. [Google Scholar] [CrossRef]
- Patil, M.; Choudhury, D.; Ranjith, P.G.; Zhao, J. Behavior of shallow tunnel in soft soil under seismic conditions. Tunn. Undergr. Space Technol. 2018, 82, 30–38. [Google Scholar] [CrossRef]
- Chen, G.; Zhu, S.; Chen, W.; Li, X.; Juang, C.H. 3D seismic response characteristics of apile-mat-founded AP1000 nuclear-island building considering nonlinear hysteretic behavior of soil. Bull. Earthq. Eng. 2022, 20, 7077–7106. [Google Scholar] [CrossRef]
- Gao, Z.; Zhao, M.; Huang, J.; Du, X.; Wu, L. Three-dimensional nonlinear seismic response analysis of subway station crossing longitudinally inhomogeneous geology under obliquely incident P waves. Eng. Geol. 2021, 293, 106341. [Google Scholar] [CrossRef]
- Jiang, J.; El Naggar, M.H.; Huang, W.; Xu, C.; Zhao, K.; Du, X. Seismic vulnerability analysis for shallow-buried underground frame structure considering 18 existing subway stations. Soil Dyn. Earthq. Eng. 2022, 162, 107479. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, M.; Guan, J.; Yang, J.; Du, X.; Zhao, X. Site effect on seismic response of buried nuclear power plant structure. Soil Dyn. Earthq. Eng. 2024, 183, 108759. [Google Scholar] [CrossRef]
- Kazemi, F.; Asgarkhani, N.; Jankowski, R. Machine learning-based seismic fragility and seismic vulnerability assessment of reinforced concrete structures. Soil Dyn. Earthq. Eng. 2023, 166, 107761. [Google Scholar] [CrossRef]
- Zhuang, H.; Hu, Z.; Wang, X.; Chen, G. Seismic responses of a large underground structure in liquefied soils by FEM numerical modelling. Bull. Earthq. Eng. 2015, 13, 3645–3668. [Google Scholar] [CrossRef]
- Cheng, X.; Sun, Z. Effects of Burial Depth on the Seismic Response of Subway Station Structure Embedded in Saturated Soft Soil. Adv. Civ. Eng. 2018, 1, 8978467. [Google Scholar] [CrossRef]
- Shen, Y.; Zhong, Z.; Li, L.; Du, X.; El Naggar, M.H. Seismic response of shield tunnel structure embedded in soil deposit with liquefiable interlayer. Comput. Geotech. 2022, 152, 105015. [Google Scholar] [CrossRef]
- Bao, X.; Xia, Z.; Ye, G.; Fu, Y.; Su, D. Numerical analysis on the seismic behavior of a large metro subway tunnel in liquefifiable ground. Tunn. Undergr. Space Technol. 2017, 66, 91–106. [Google Scholar] [CrossRef]
- Lu, C.C.; Hwang, J.H. Safety assessment for a shield tunnel in a liquefifiable deposit using a practical dynamic effffective stress analysis. Eng. Fail. Anal. 2019, 102, 369–383. [Google Scholar] [CrossRef]
- Zhao, M.; Ding, Q.; Cao, S.; Li, Z.; Du, X. Large-scale seismic soil-structure interaction analysis via efficient finite element modeling and multi-GPU parallel explicit algorithm. Comput.-Aided Civ. Infrastruct. Eng. 2024, 39, 1886–1908. [Google Scholar] [CrossRef]
- Zhang, G.; Zhao, M.; Zhang, J.; Wang, J.; Du, X. Scaled boundary perfectly matched layer for wave propagation in a three-dimensional poroelastic medium. Appl. Math. Model. 2024, 125, 108–138. [Google Scholar] [CrossRef]
- Chen, G.; Zhuang, H. Developed nonlinear dynamic constitutive relations of soils based on davidenkov skeleton curve. Chin. J. Geotech. Eng. 2005, 27, 860–864. [Google Scholar]
- Wang, Y.; Zhao, D.; Chen, G.; Liang, K. A new nonlinear effective stress method for one-dimensional seismic site response analysis and its validation. Chin. J. Geotech. Eng. 2021, 43, 502–510. [Google Scholar]
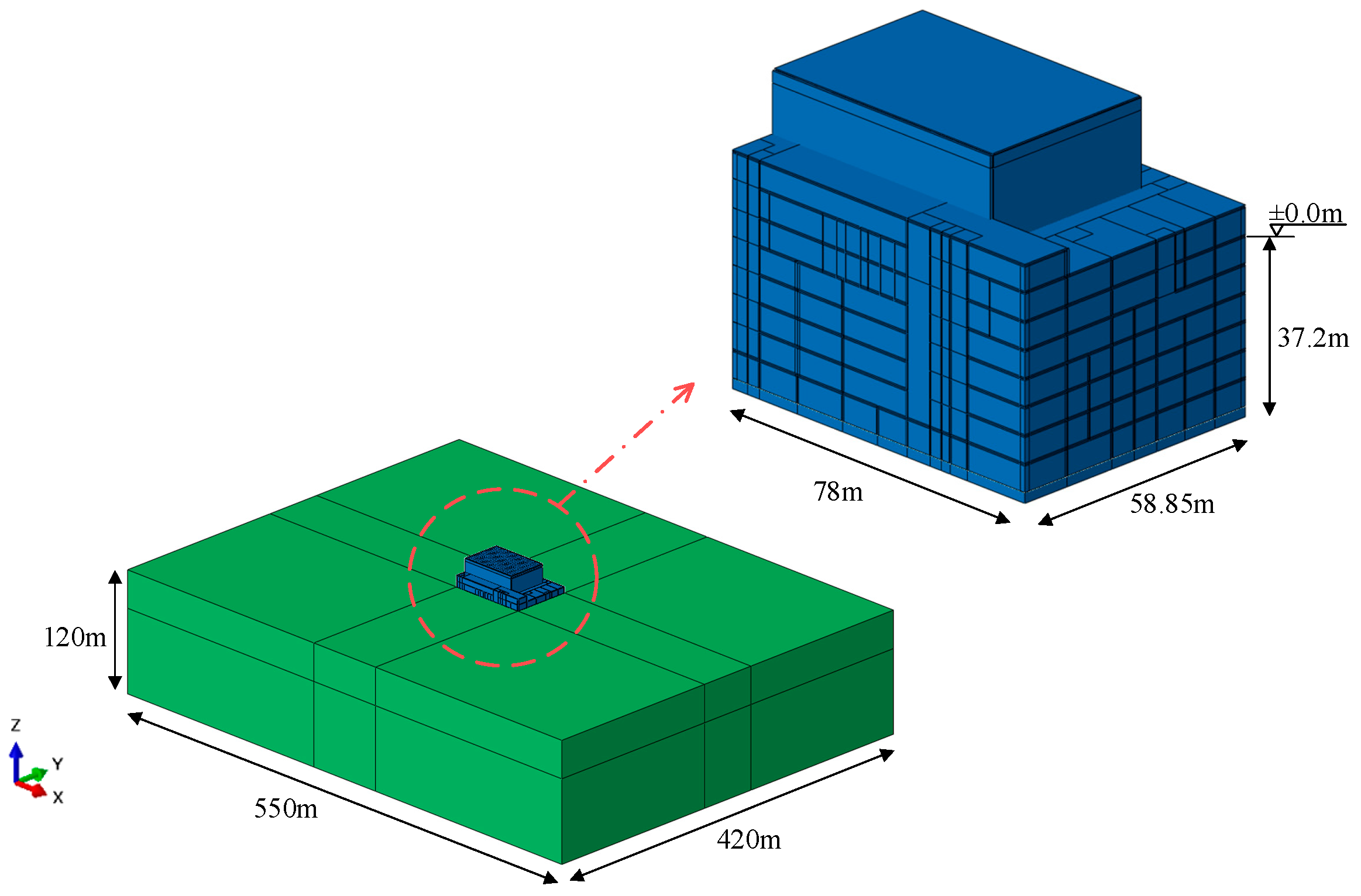

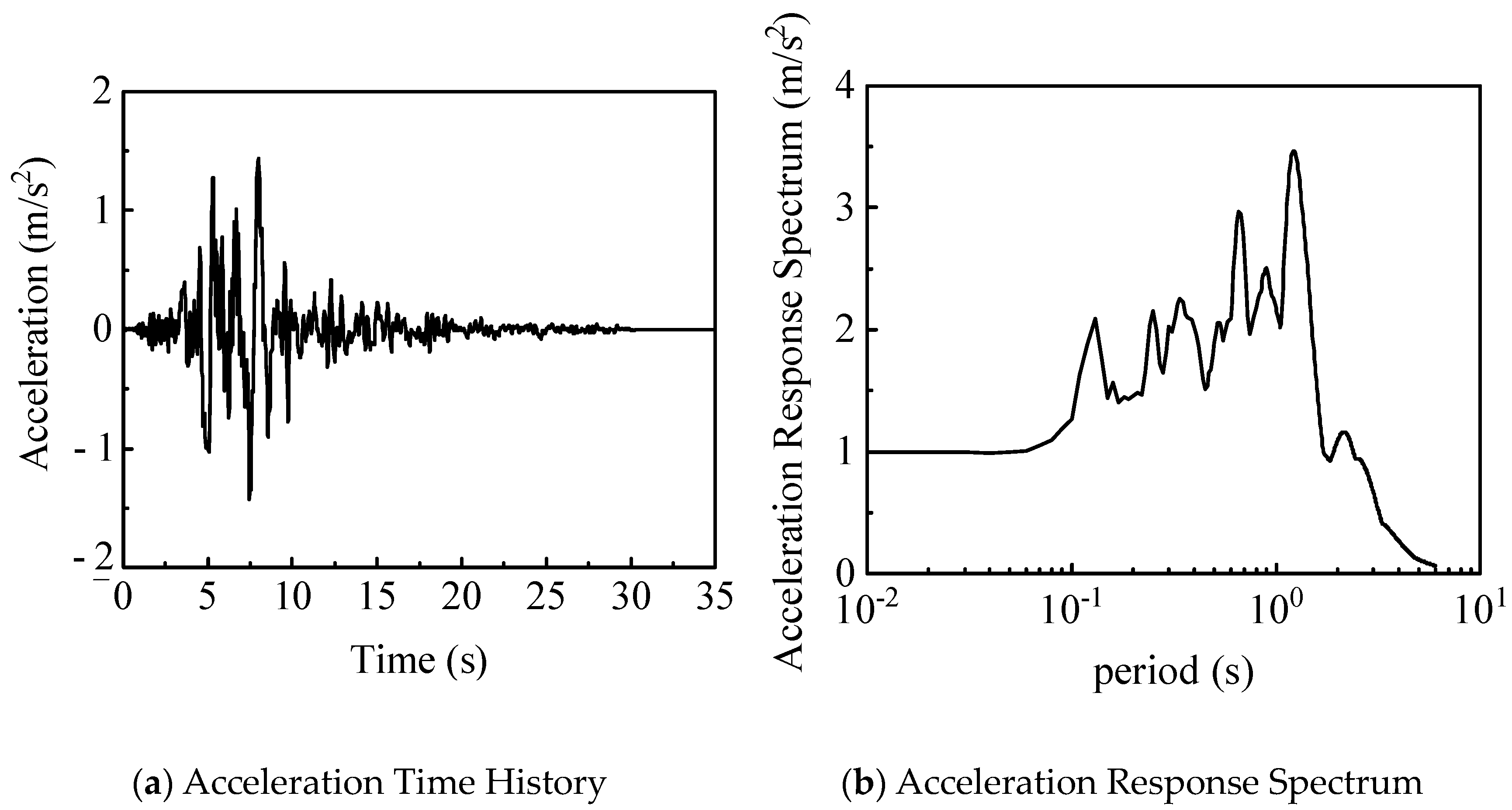
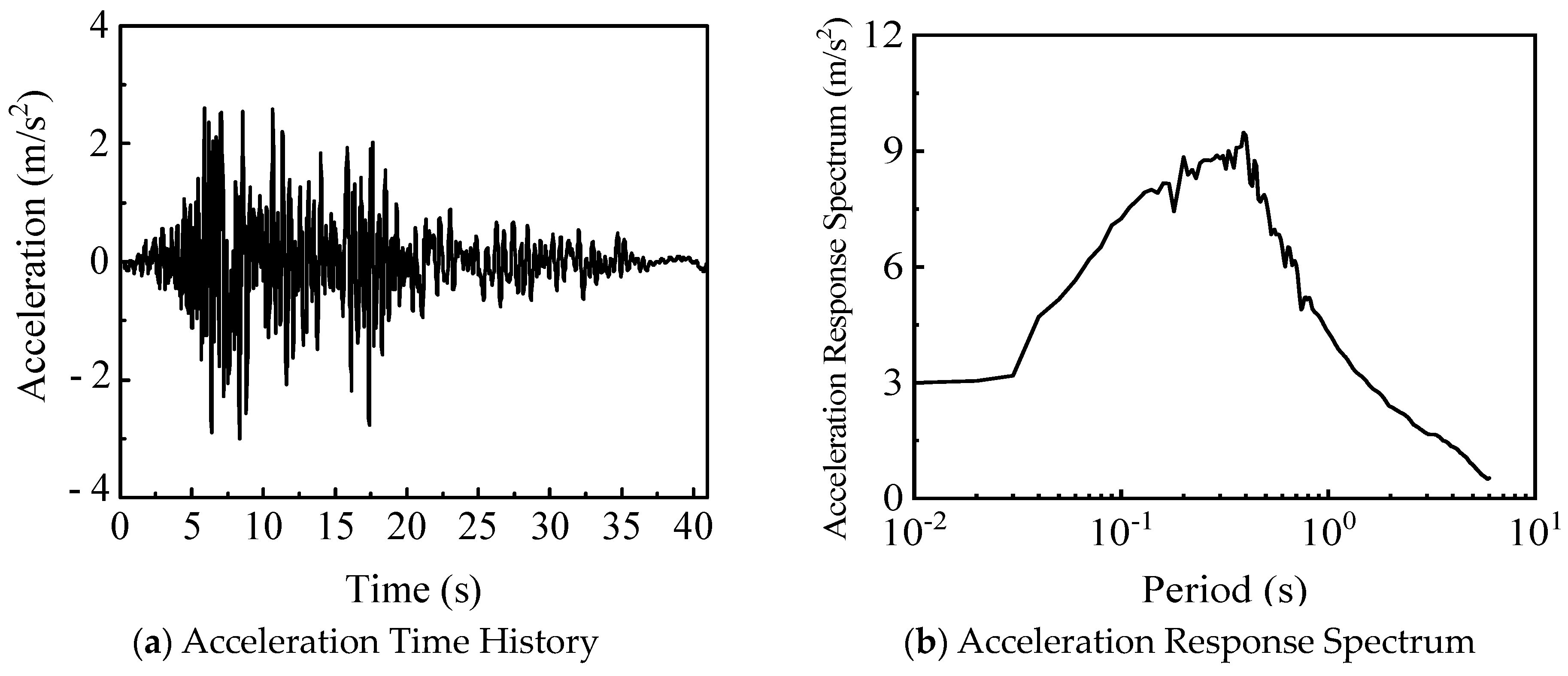





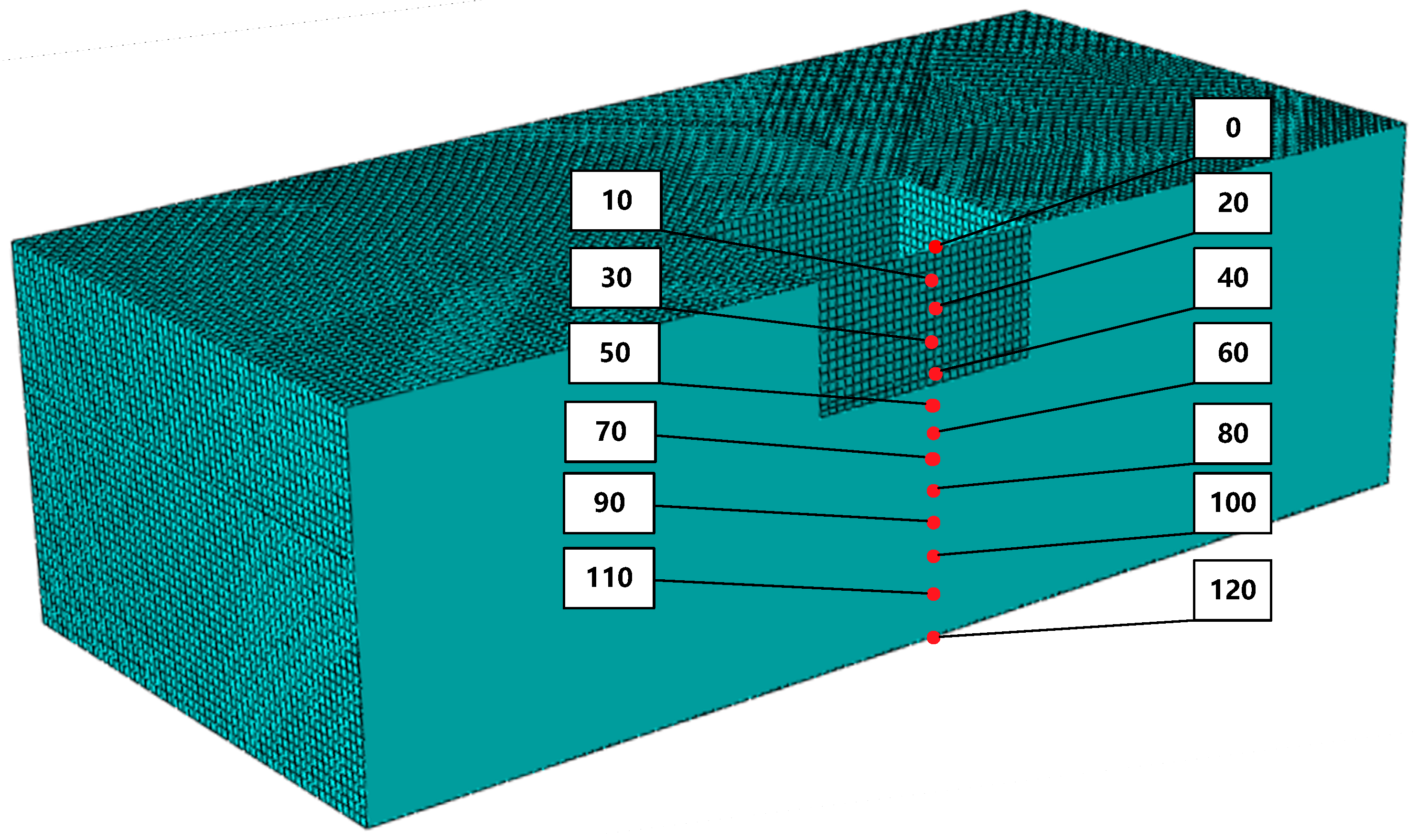


| Soil Layer | Density (kg/m3) | Soil Layer Thickness (m) | Elastic Modulus (MPa) | Shear Wave Velocity (m/s) |
|---|---|---|---|---|
| 1 | 2500 | 120 | 1593 | 565 |
| Soil Layer | Density (kg/m3) | Soil Layer Thickness (m) | Elastic Modulus (MPa) | Shear Wave Velocity (m/s) |
|---|---|---|---|---|
| 1 | 1765 | 30.7 | 219.024 | 208.46 |
| 2 | 1953 | 25.55 | 389.376 | 274.70 |
| 3 | 1989 | To Rock | 744.808 | 385.96 |
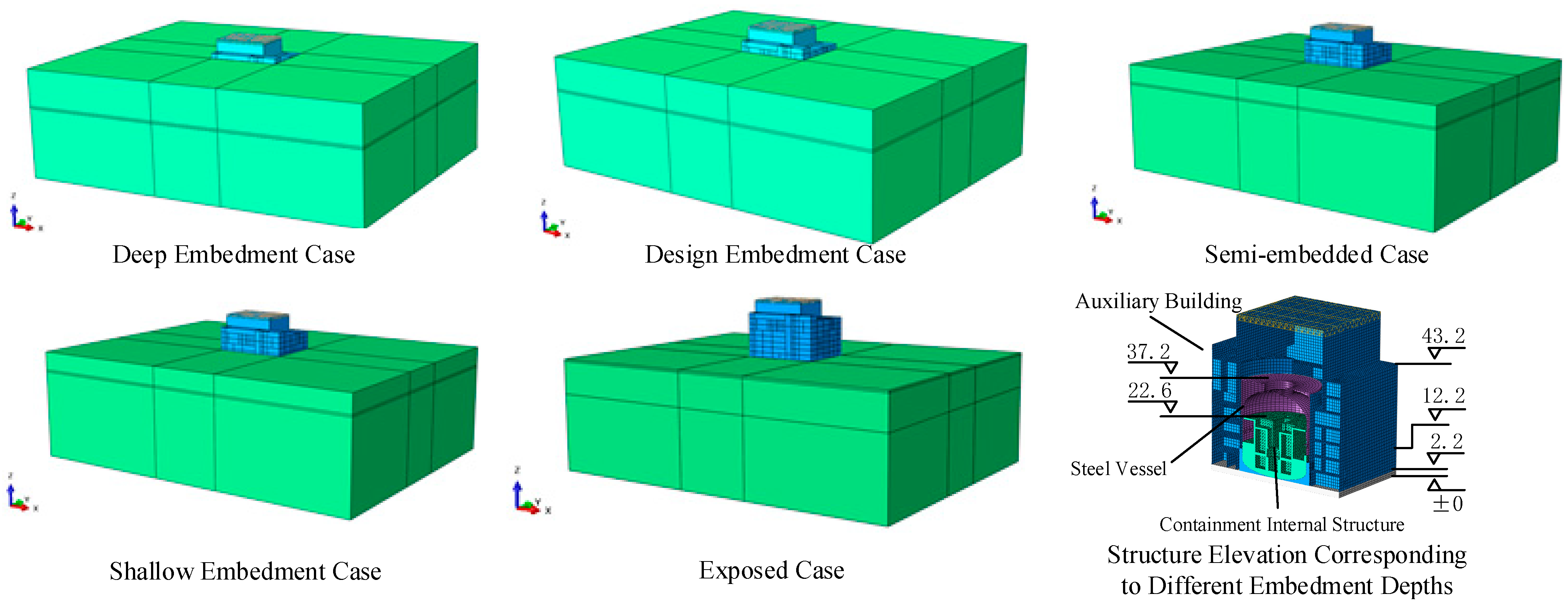
| Cases | Embedment Depth of Structural Embedment Depth | Case Names |
|---|---|---|
| 1 | 43.2 m | Deep Embedment Case |
| 2 | 37.2 m | Design Embedment Case |
| 3 | 22.6 m | Semi-embedded Case |
| 4 | 12.2 m | Shallow Embedment Case |
| 5 | 2.2 m | Exposed Case |
| 6 | 37.2 m | Upper Case |
| 7 | 37.2 m | Middle Case |
| 8 | 37.2 m | Exposed Case |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, J.; Gao, Z.; Zhao, M.; Du, X. Seismic Response Analysis of Buried Nuclear Power Plant Structures in Non-Bedrock Sites. Appl. Sci. 2025, 15, 4378. https://doi.org/10.3390/app15084378
Guan J, Gao Z, Zhao M, Du X. Seismic Response Analysis of Buried Nuclear Power Plant Structures in Non-Bedrock Sites. Applied Sciences. 2025; 15(8):4378. https://doi.org/10.3390/app15084378
Chicago/Turabian StyleGuan, Jiacheng, Zhidong Gao, Mi Zhao, and Xiuli Du. 2025. "Seismic Response Analysis of Buried Nuclear Power Plant Structures in Non-Bedrock Sites" Applied Sciences 15, no. 8: 4378. https://doi.org/10.3390/app15084378
APA StyleGuan, J., Gao, Z., Zhao, M., & Du, X. (2025). Seismic Response Analysis of Buried Nuclear Power Plant Structures in Non-Bedrock Sites. Applied Sciences, 15(8), 4378. https://doi.org/10.3390/app15084378





