Synchronous Rectification Method for CLLC Resonant Converters Based on State-Trajectory Models
Abstract
1. Introduction
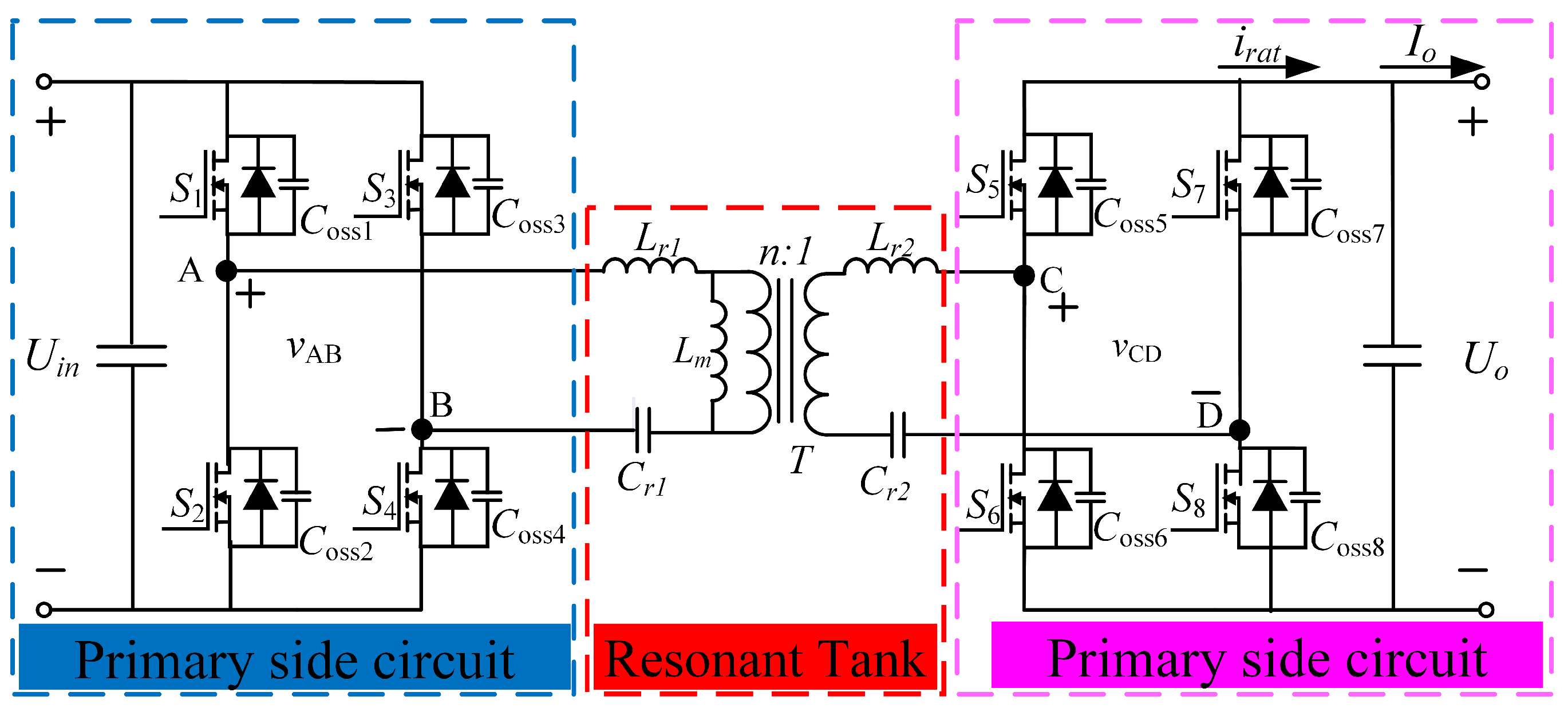
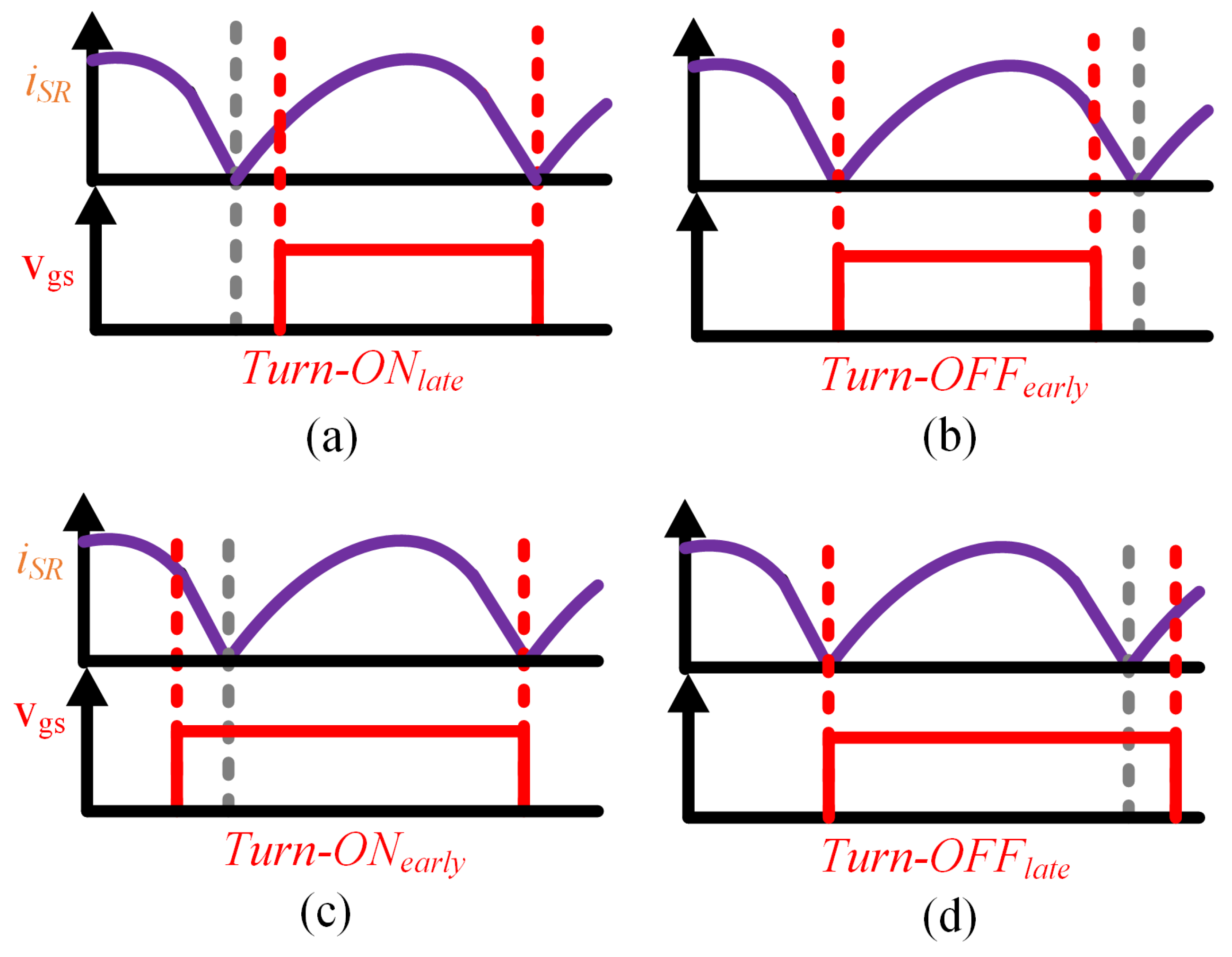
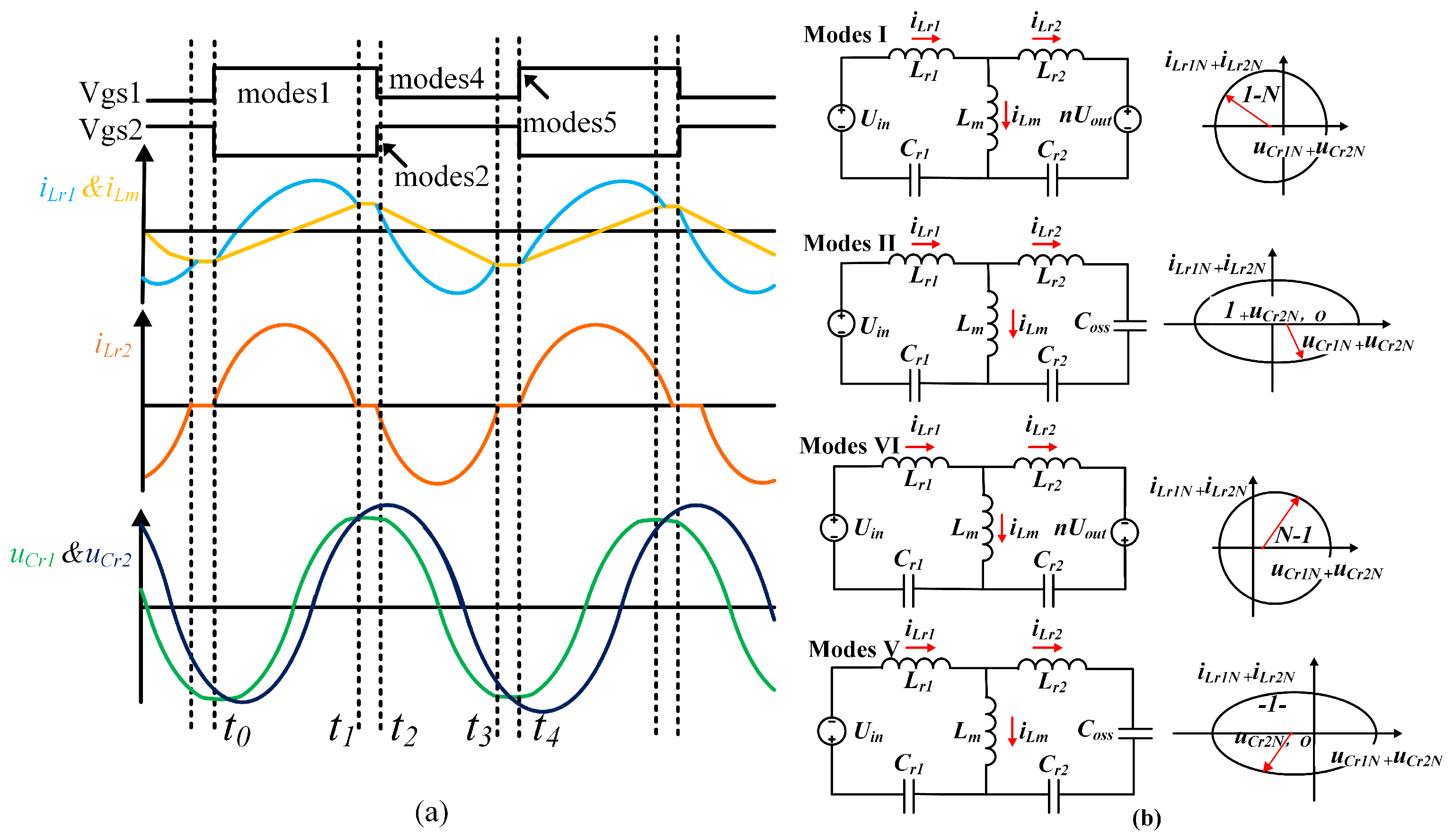
2. The SR Process for CLLC Resonant Converter
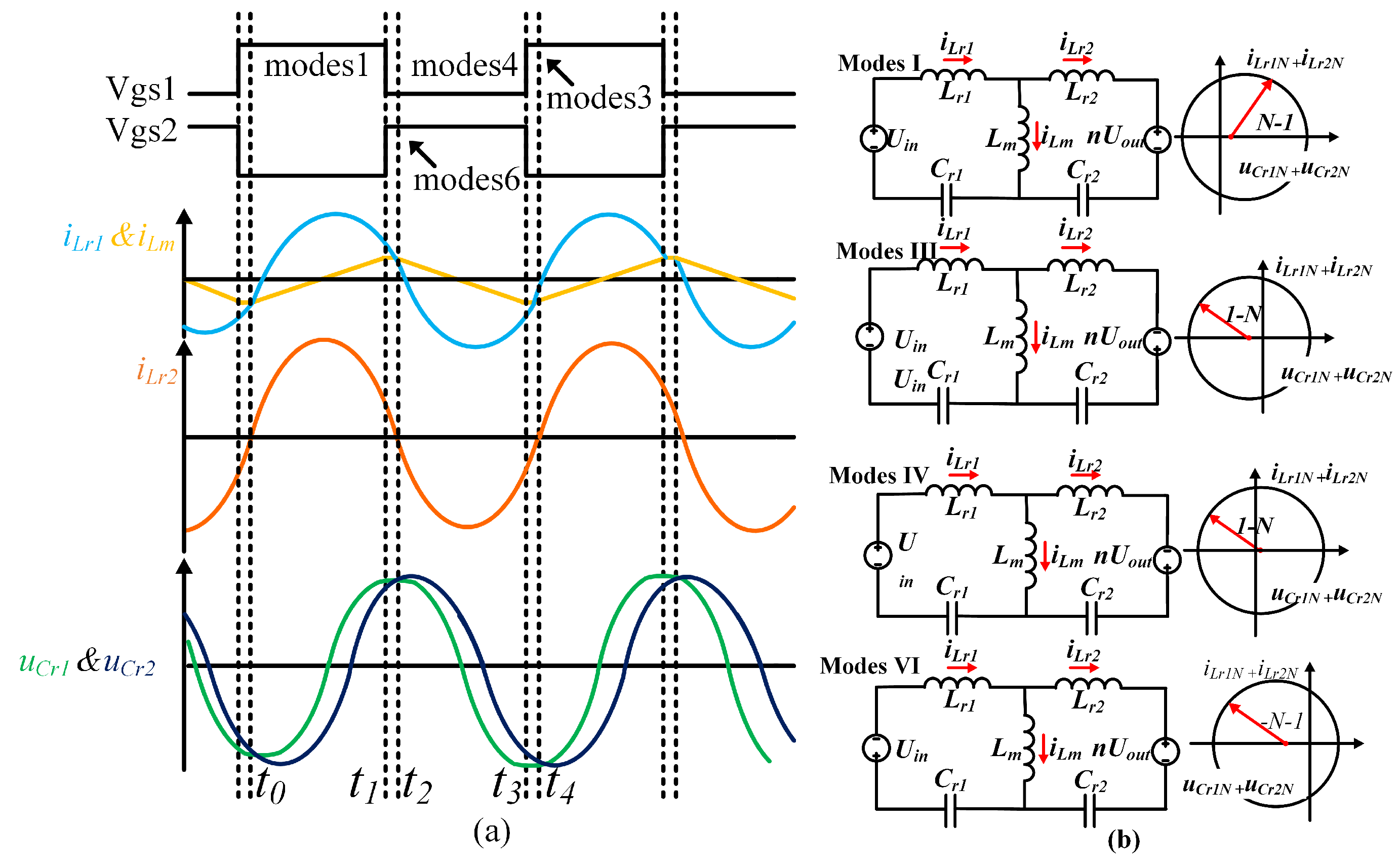
2.1. Below-Resonant State
2.2. Above-Resonant State
3. SR Method for CLLC Resonant Converters Based on State-Trajectory Models
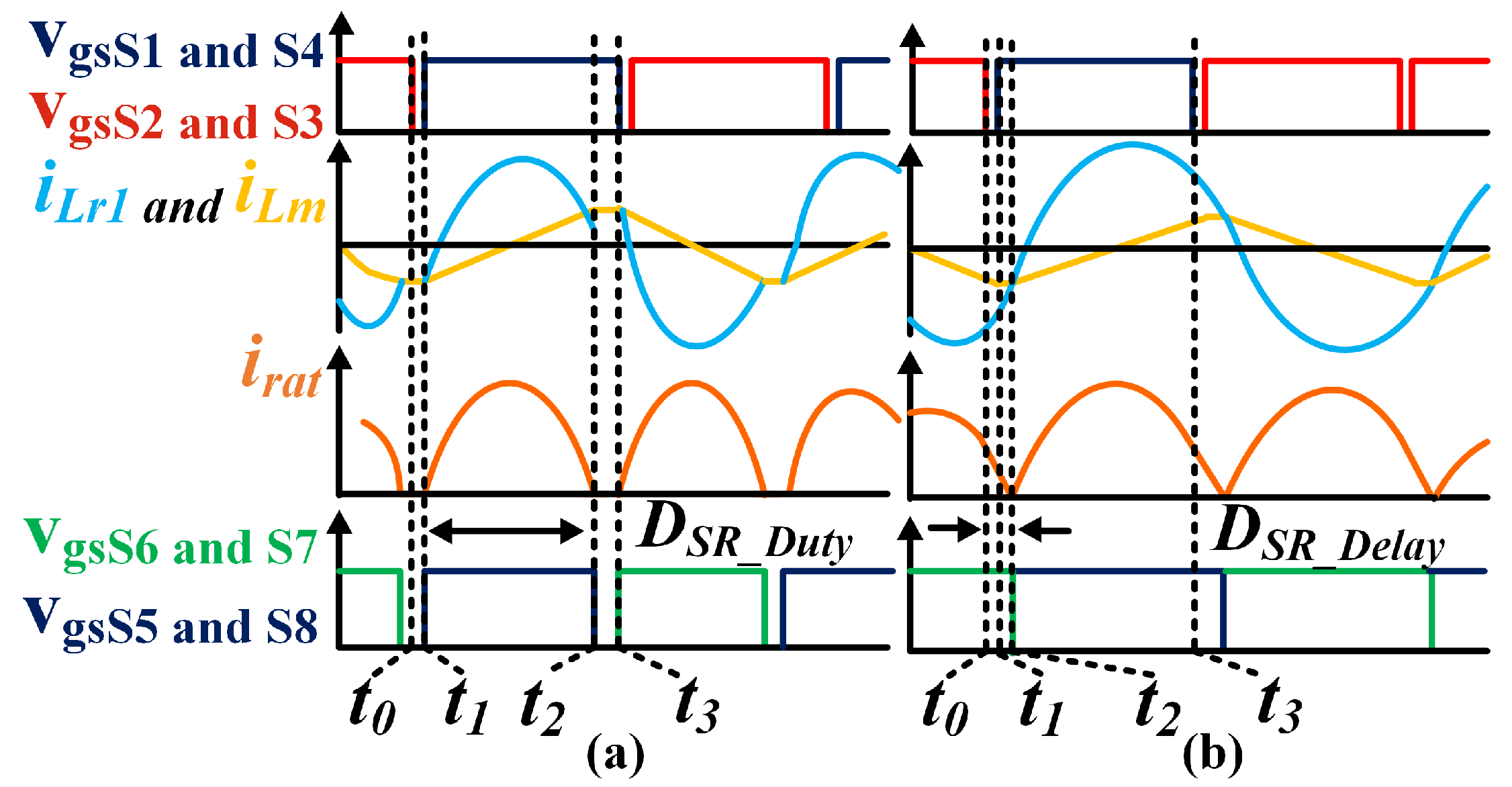
3.1. Above-Resonant Synchronous Rectification Method
3.2. SR Method in the Below-Resonance Region
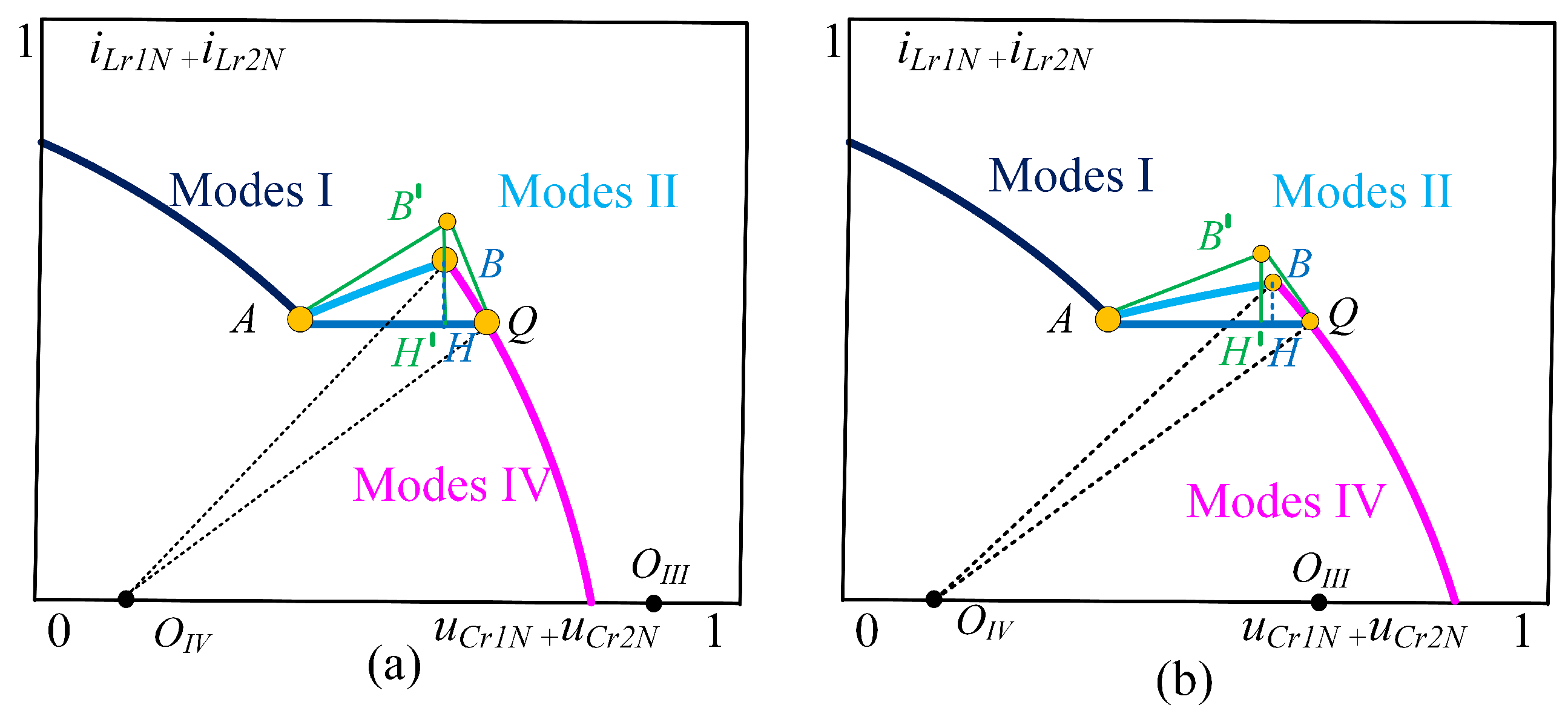
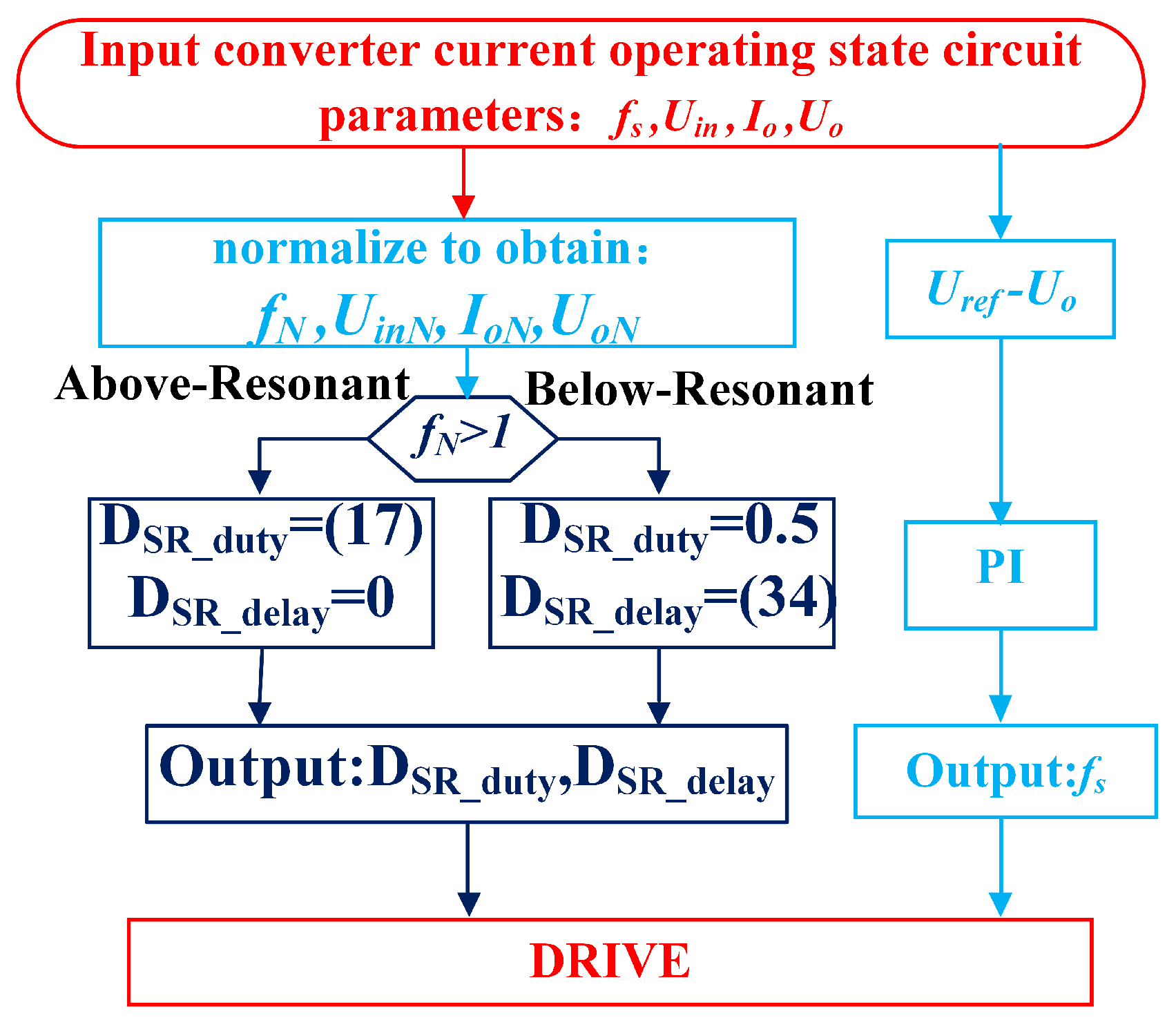
3.3. SR Strategy Based on State Trajectories
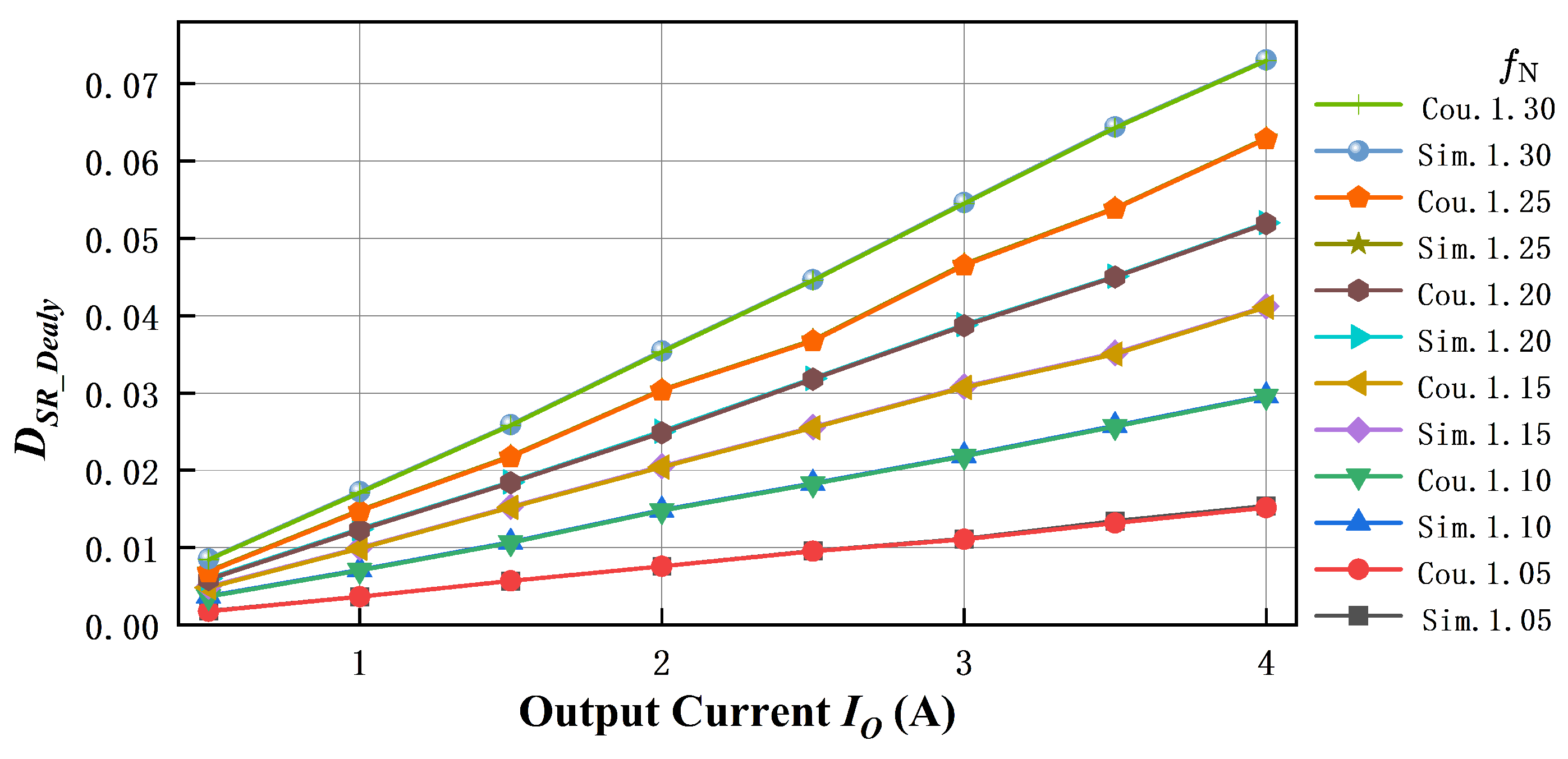
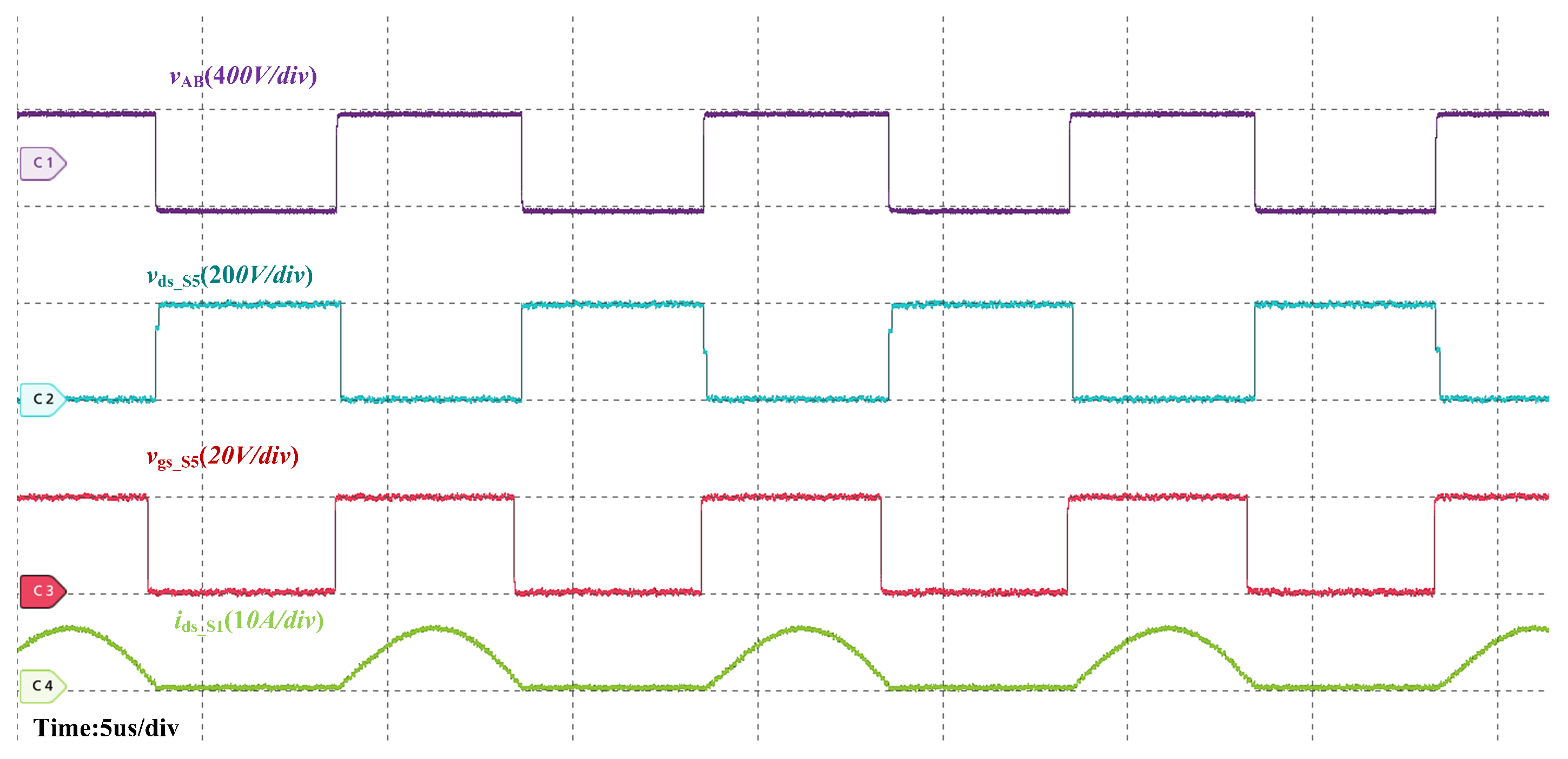
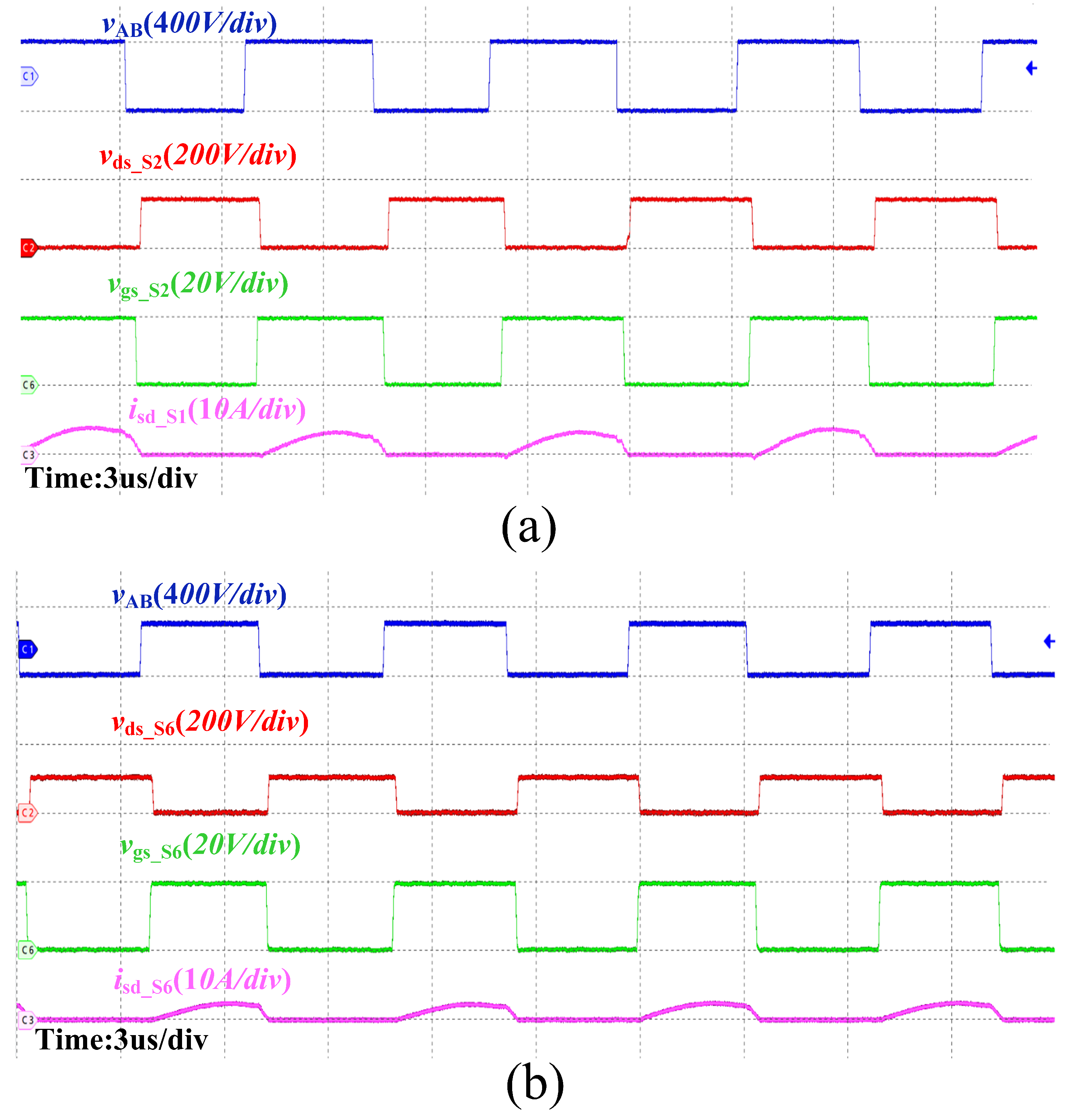
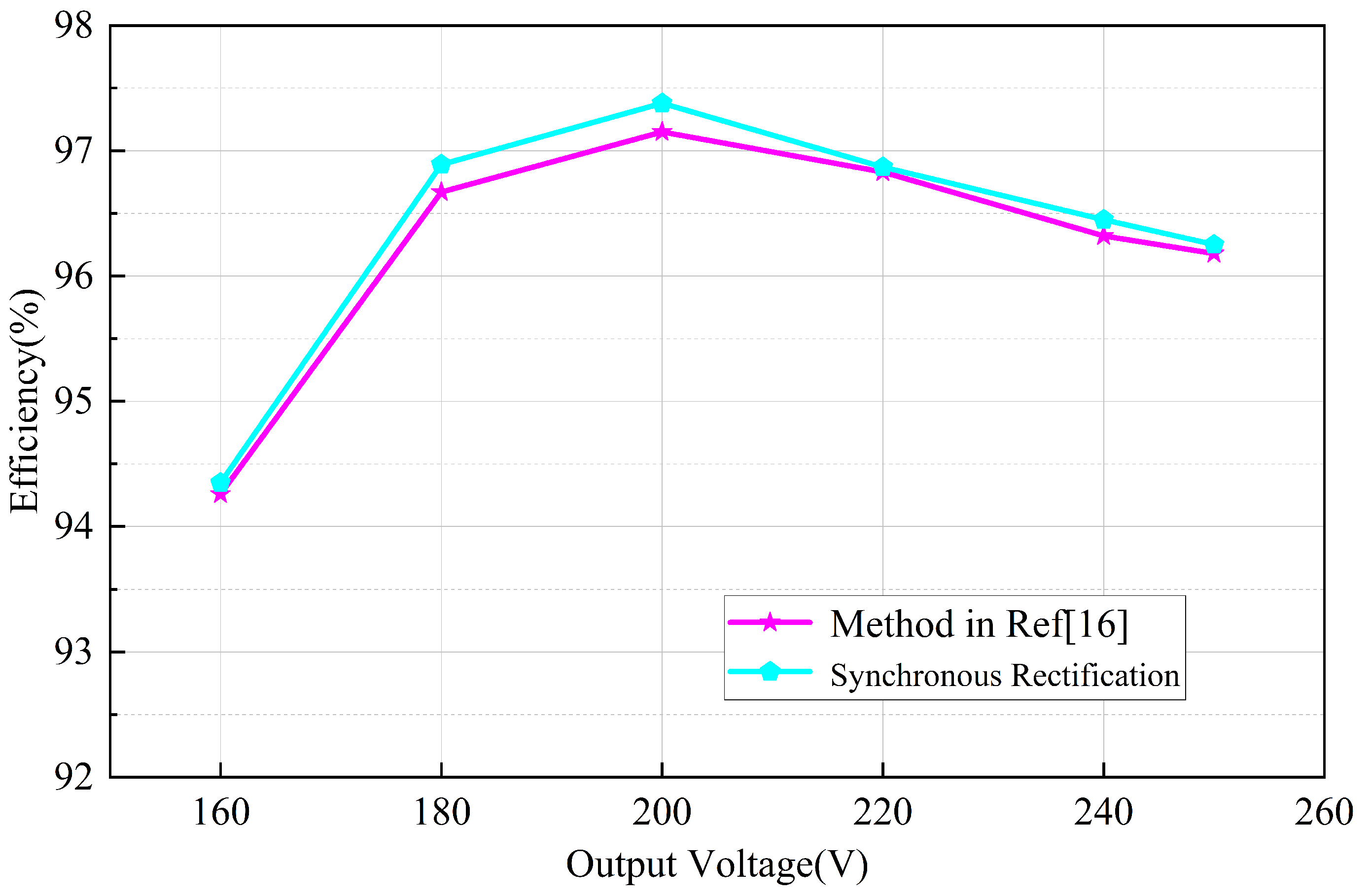
3.4. Simulation Verification
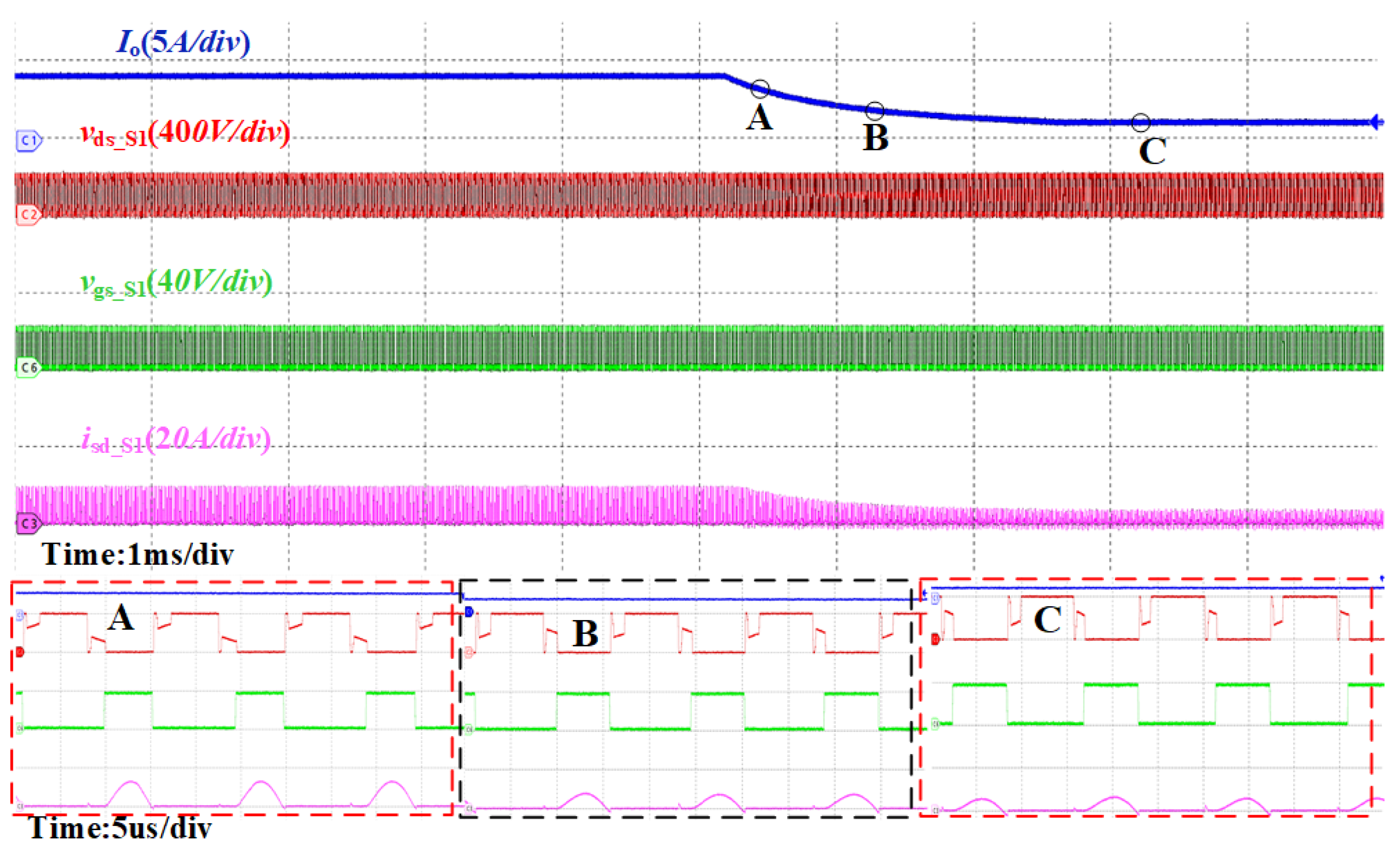
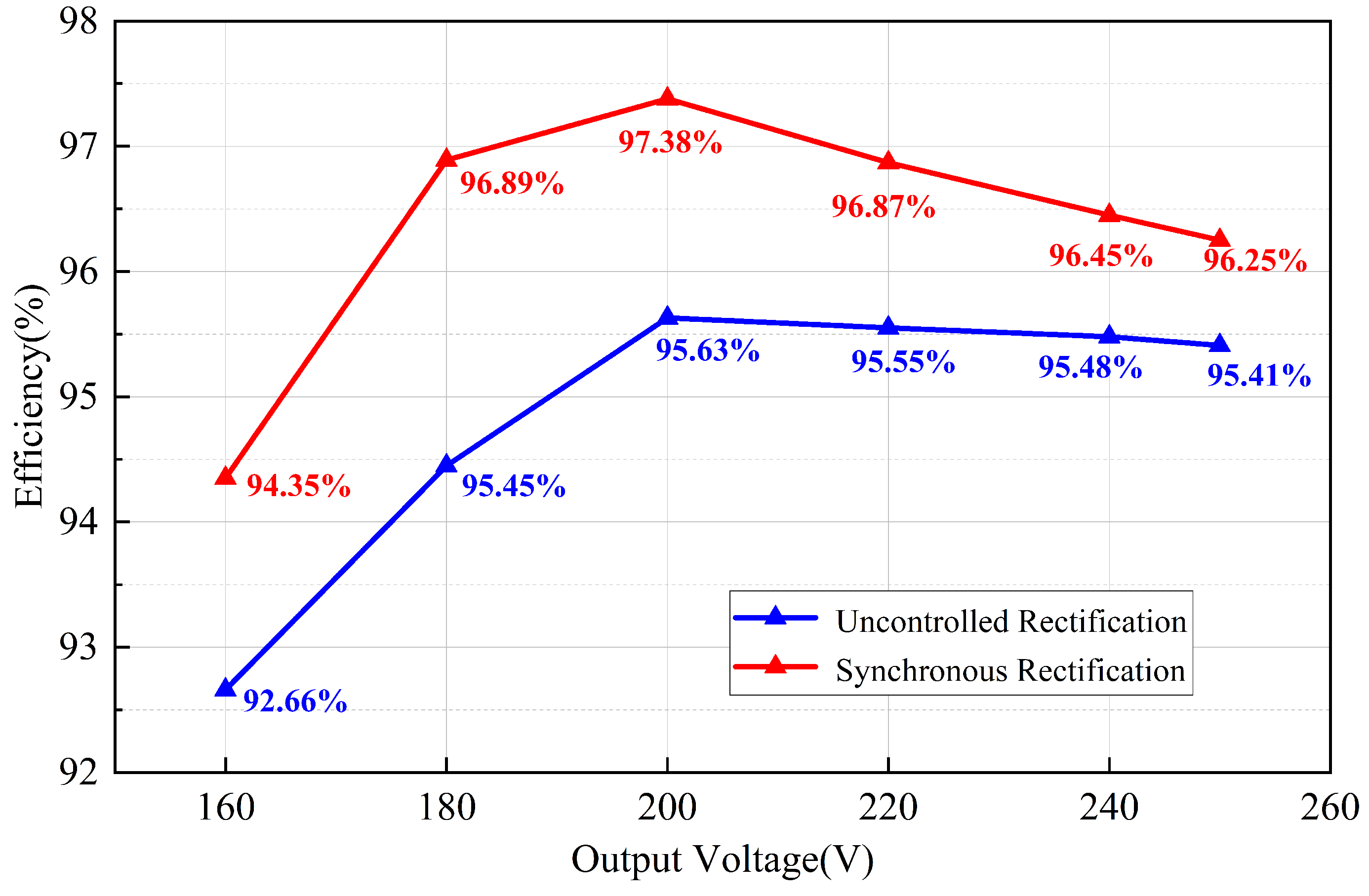
4. Discussion
Verification of Accuracy
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, J.; Yuan, L.; Gu, Q.; Duan, R.; Lu, Z.; Zhao, Z. Design-Oriented Comprehensive Time-Domain Model for CLLC Class Isolated Bidirectional DC-DC Converter for Various Operation Modes. IEEE Trans. Power Electron. 2020, 35, 3491–3505. [Google Scholar] [CrossRef]
- Jung, J.-H.; Kim, H.-S.; Ryu, M.-H.; Baek, J.-W. Design Methodology of Bidirectional CLLC Resonant Converter for High-Frequency Isolation of DC Distribution Systems. IEEE Trans. Power Electron. 2013, 28, 1741–1755. [Google Scholar] [CrossRef]
- Zahid, Z.U.; Dalala, Z.M.; Chen, R.; Chen, B.; Lai, J.-S. Design of Bidirectional DC–DC Resonant Converter for Vehicle-to-Grid (V2G) Applications. IEEE Trans. Transp. Electrif. 2015, 1, 232–244. [Google Scholar] [CrossRef]
- Li, B.; Jing, L.; Wang, X.; Chen, N.; Liu, B.; Chen, M. A Smooth Mode-Switching Strategy for Bidirectional OBC Base on V2G Technology. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019. [Google Scholar]
- Rojas-Dueñas, G.; Riba, J.-R.; Moreno-Eguilaz, M. A Deep Learning-Based Modeling of a 270 V-to-28 V DC-DC Converter Used in More Electric Aircrafts. IEEE Trans. Power Electron. 2022, 37, 509–518. [Google Scholar] [CrossRef]
- Emamalipour, R.; Lam, J. A Multi-Mode Full-Bridge/Modified-Stacked-Switches Structured CLLC Resonant Converter for Energy Storage Applications. IEEE Trans. Power Electron. 2024, 39, 5967–5981. [Google Scholar] [CrossRef]
- Ravariu, C. Vacuum Nano-Triode in Nothing-On-Insulator Configuration Working in Terahertz Domain. IEEE J. Electron Devices Soc. 2018, 6, 1115–1123. [Google Scholar] [CrossRef]
- Pei, L.; Jia, L.; Wang, L.; Zhao, L.; Cao, W.; Zhu, L.; Pei, Y. Accurate Extraction of Body-Diode-Conduction for Synchronous Rectification of CLLC Resonant Converters in High-Voltage Application. IEEE Trans. Power Electron. 2024, 39, 5009–5013. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, C.; Si, Y.; Liu, Y.; Lei, Q. Investigation of Adaptive Synchronous Rectifier (SR) Driving Scheme for LLC/CLLC Resonant Converter in EV On-Board Chargers. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020; pp. 2185–2191. [Google Scholar] [CrossRef]
- Chen, N.; Chen, M.; Li, B.; Wang, X.; Sun, X.; Zhang, D.; Jiang, F.; Han, J. Synchronous Rectification Based on Resonant Inductor Voltage for CLLC Bidirectional Converter. IEEE Trans. Power Electron. 2022, 37, 547–561. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, D.; Chen, N.; Li, B.; Wang, X.; Sun, X.; Jiang, F. A Coupled Inductor Scheme for CLLC Bidirectional Converter and Optimized Current Detection Method. IEEE Trans. Power Electron. 2022, 37, 11546–11551. [Google Scholar] [CrossRef]
- Schobre, T.; Siebke, K.; Mallwitz, R. Design of a GaN based CLLC converter with synchronous rectification for on-board vehicle charger. In Proceedings of the PCIM Europe 2019, International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 7–9 May 2019; pp. 1–5. [Google Scholar]
- Schobre, T.; Siebke, K.; Mallwitz, R. Operation Analysis and Implementation of a GaN Based Bidirectional CLLC Converter with Synchronous Rectification. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE ’19 ECCE Europe), Genova, Italy, 2–5 September 2019; pp. P.1–P.10. [Google Scholar] [CrossRef]
- Zou, S.; Lu, J.; Mallik, A.; Khaligh, A. 3.3 kW CLLC converter with synchronous rectification for plug-in electric vehicles. In Proceedings of the 2017 IEEE Industry Applications Society Annual Meeting, Cincinnati, OH, USA, 1–5 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Zou, S.; Lu, J.; Mallik, A.; Khaligh, A. Bi-Directional CLLC Converter with Synchronous Rectification for Plug-In Electric Vehicles. IEEE Trans. Ind. Appl. 2018, 54, 998–1005. [Google Scholar] [CrossRef]
- Sankar, A.; Mallik, A.; Khaligh, A. Extended Harmonics Based Phase Tracking for Synchronous Rectification in CLLC Converters. IEEE Trans. Ind. Electron. 2019, 66, 6592–6603. [Google Scholar] [CrossRef]
- Li, B.; Chen, M.; Wang, X.; Chen, N.; Sun, X.; Zhang, D. An Optimized Digital Synchronous Rectification Scheme Based on Time-Domain Model of Resonant CLLC Circuit. IEEE Trans. Power Electron. 2021, 36, 10933–10948. [Google Scholar] [CrossRef]
- Li, H.; Sun, Y.; Wang, S.; Zhang, Z.; Ren, X.; Zhang, P.; Yang, G.; Hu, C. Bidirectional Control with Fitting Model-Based Synchronous Rectification and Input Ripple Current Feedforward for SiC Bidirectional CLLC EV Charger. IEEE Trans. Ind. Electron. 2023, 70, 9136–9146. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, F.; Zhuo, F.; Yu, K.; Tian, J.; Song, R. Analysis of High Performance Synchronous Rectified CLLC Resonant Converter with Reactive Power Optimization. IEEE Trans. Power Electron. 2023, 38, 15253–15271. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, F.; Zhuo, F.; Yu, K.; Tian, J.; Zhang, X. Synchronous Rectification and Parameter Design Based on Accurate Time-Domain Model for Asymmetrical CLLC Resonant Converter. IEEE Trans. Transp. Electrif. 2025, 11, 4681–4697. [Google Scholar] [CrossRef]
- Pei, L.; Jia, L.; Wang, L.; Zhao, L.; Song, S.; Pei, Y.; Yang, X.; Gan, Y. A Time-Domain-Model-Based Digital Synchronous Rectification Algorithm for CLLC Resonant Converters Utilizing a Hybrid Modulation. IEEE Trans. Power Electron. 2022, 37, 2815–2829. [Google Scholar] [CrossRef]
- Chen, H.; Sun, K.; Shi, H.; Ha, J.I.; Lee, S. A Battery Charging Method With Natural Synchronous Rectification Features for Full-Bridge CLLC Converters. IEEE Trans. Power Electron. 2022, 37, 2139–2151. [Google Scholar] [CrossRef]
- Ren, X.; Pei, L.; Song, S.; Zhang, J.; Pei, Y.; Wang, L. A Digital Sensor-less Synchronous Rectification Algorithm for Symmetrical Bidirectional CLLC Resonant Converters. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020; pp. 962–968. [Google Scholar] [CrossRef]
- Rezayati, M.; Tahami, F.; Schanen, J.-L.; Sarrazin, B. Generalized State-Plane Analysis of Bidirectional CLLC Resonant Converter. IEEE Trans. Power Electron. 2022, 37, 5773–5785. [Google Scholar] [CrossRef]
- Chen, H.; Wang, L.; Sun, K.; Lu, L. A Switching Delay Strategy for Sensorless Synchronous Rectification in CLLC Converters. IEEE Trans. Power Electron. 2024, 39, 280–293. [Google Scholar] [CrossRef]







| Circuit Specification | Symbol | Normalized Variable |
|---|---|---|
| Resonant frequency | − | |
| Resonant angular frequency | − | |
| Inductor ratio | − | |
| Characteristic impedance | − | |
| Second characteristic impedance | − | |
| Input voltage | ||
| Output voltage | ||
| Output current | ||
| Resonant capacitor voltage | ||
| Resonant inductor current | ||
| Magnetizing inductor current | ||
| Rectified current | ||
| Magnetizing inductor voltage | ||
| Switching frequency |
| Parameters | Values |
|---|---|
| 160∼250 V | |
| and | 32.25 H:32.25 H |
| and | 78.56 nF:78.56 nF |
| 167.7 H | |
| 70∼130 KHz | |
| n | 1 |
| Category | Accuracy | Application Complexity | Operating Range | Additional Sensors |
|---|---|---|---|---|
| FHA method [2,13,14] | low | simple | restricted | no |
| Accurate time-domain methods [16] | high | complex | wide | no |
| Simplified time-domain approach [21] | moderate | moderate | wide | no |
| Frequency-domain fitting methods [20] | moderate | simple | restricted | no |
| Voltage detection methods [7,8,9,10] | high | complex | wide | yes |
| Current detection methods [11,12] | high | complex | wide | yes |
| The methodology proposed | high | simple | wide | no |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Zhang, T.; Ruan, C.; Yu, Q.; Feng, C. Synchronous Rectification Method for CLLC Resonant Converters Based on State-Trajectory Models. Appl. Sci. 2025, 15, 4372. https://doi.org/10.3390/app15084372
Sun Z, Zhang T, Ruan C, Yu Q, Feng C. Synchronous Rectification Method for CLLC Resonant Converters Based on State-Trajectory Models. Applied Sciences. 2025; 15(8):4372. https://doi.org/10.3390/app15084372
Chicago/Turabian StyleSun, Zhenao, Tuanlong Zhang, Chuanpeng Ruan, Qingshuai Yu, and Chuxiang Feng. 2025. "Synchronous Rectification Method for CLLC Resonant Converters Based on State-Trajectory Models" Applied Sciences 15, no. 8: 4372. https://doi.org/10.3390/app15084372
APA StyleSun, Z., Zhang, T., Ruan, C., Yu, Q., & Feng, C. (2025). Synchronous Rectification Method for CLLC Resonant Converters Based on State-Trajectory Models. Applied Sciences, 15(8), 4372. https://doi.org/10.3390/app15084372





