Regional Seismicity of the Northeastern Tibetan Plateau Revealed by Crustal Magnetic Anomalies
Abstract
1. Introduction
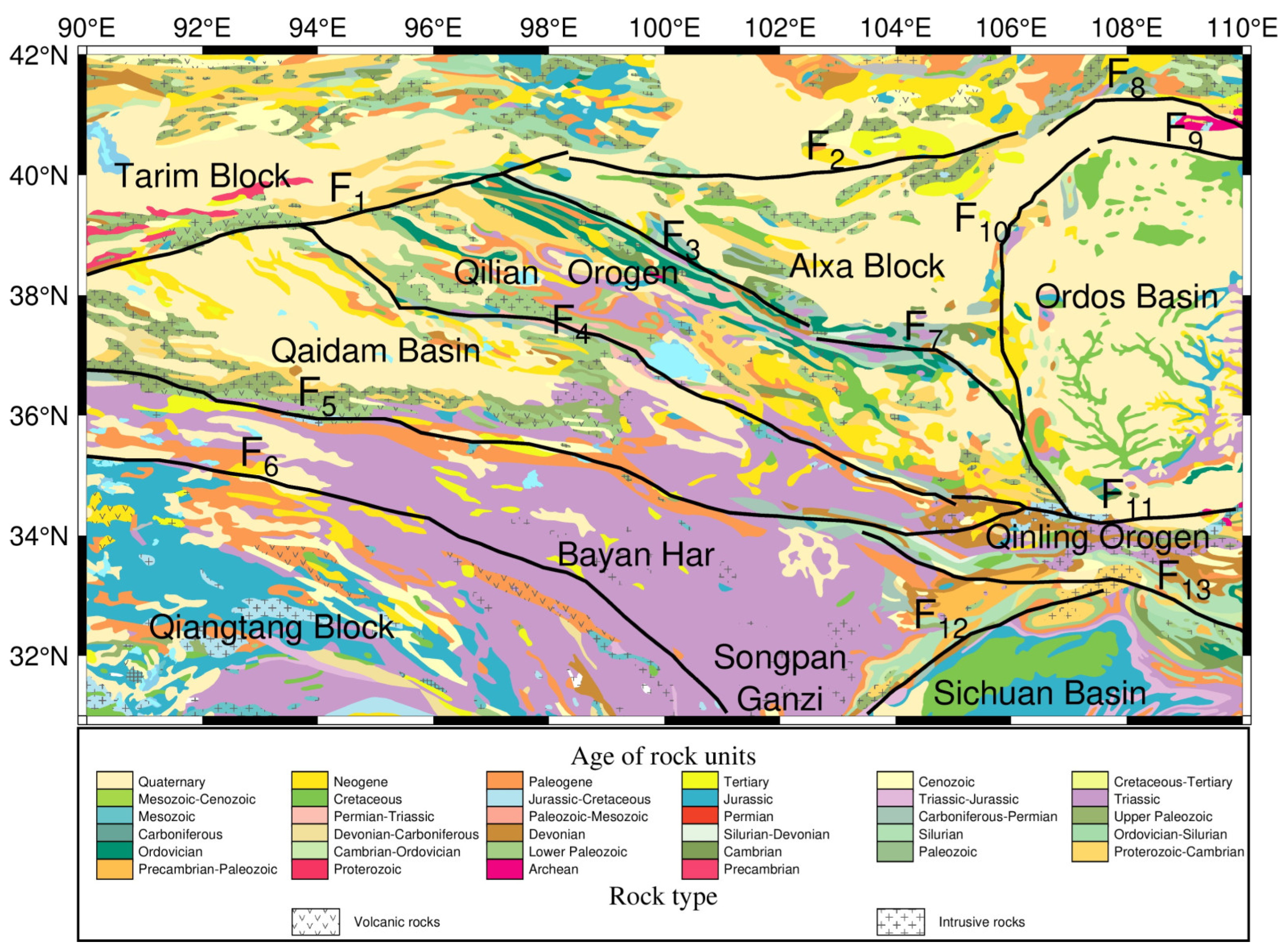
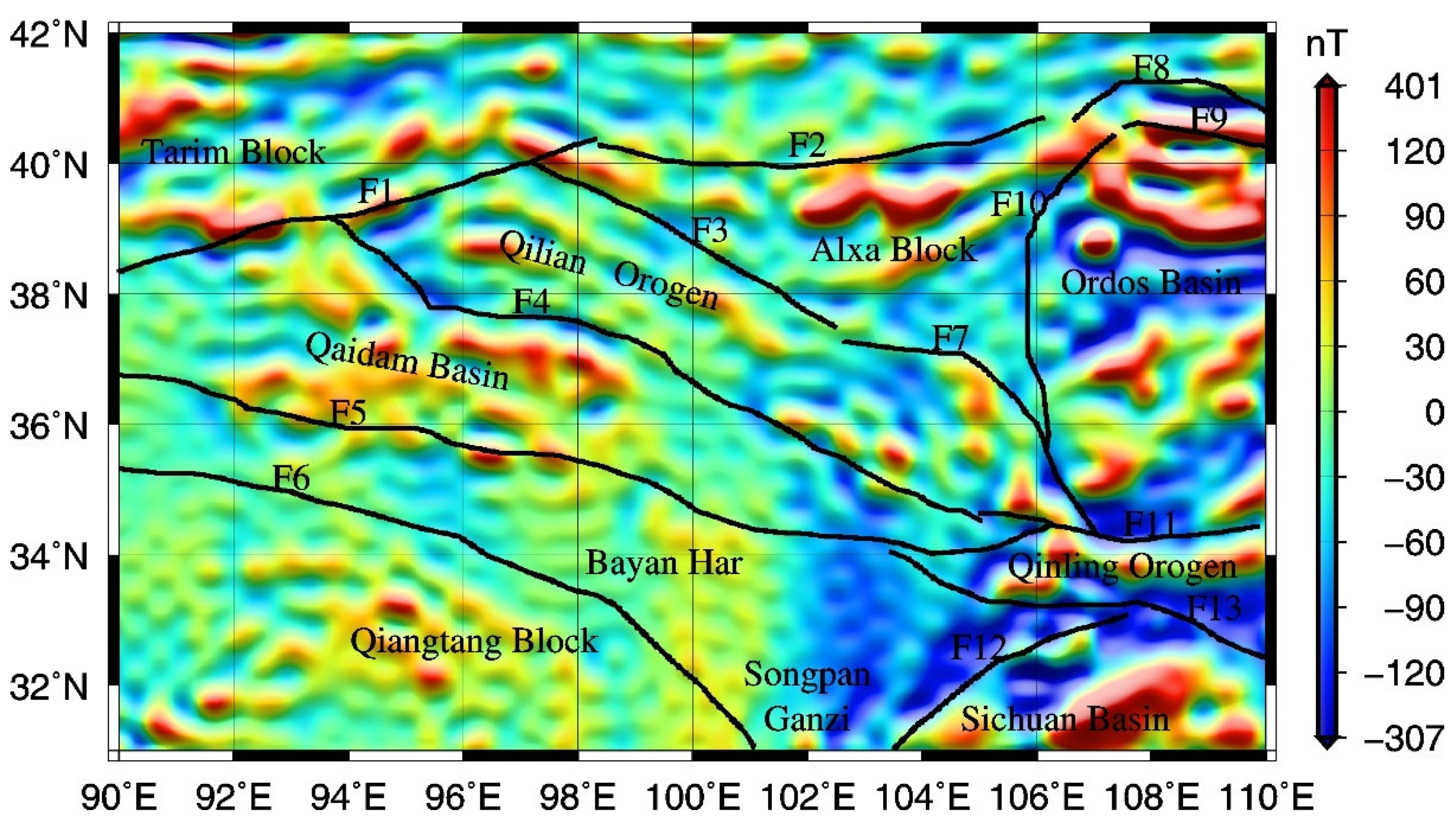
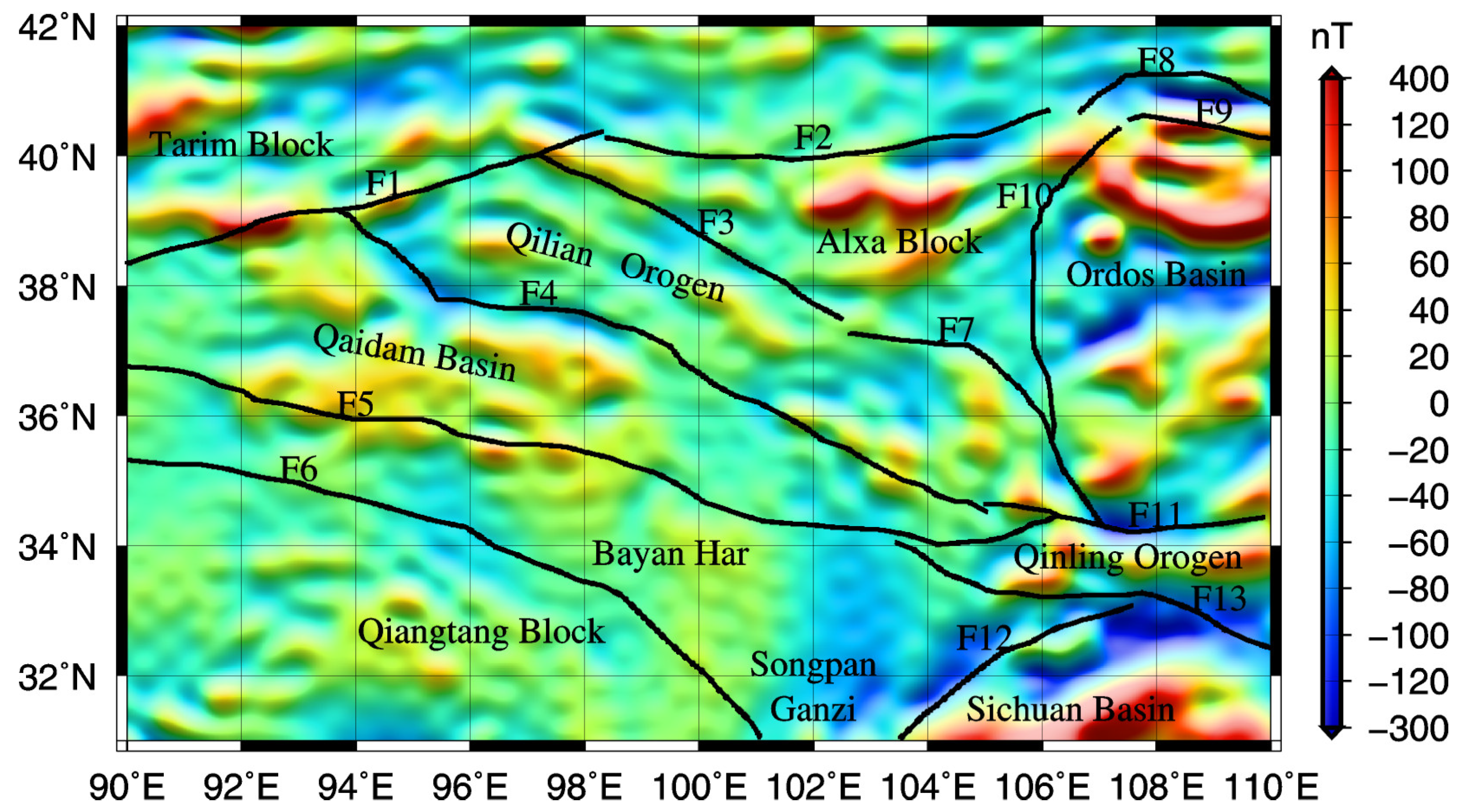
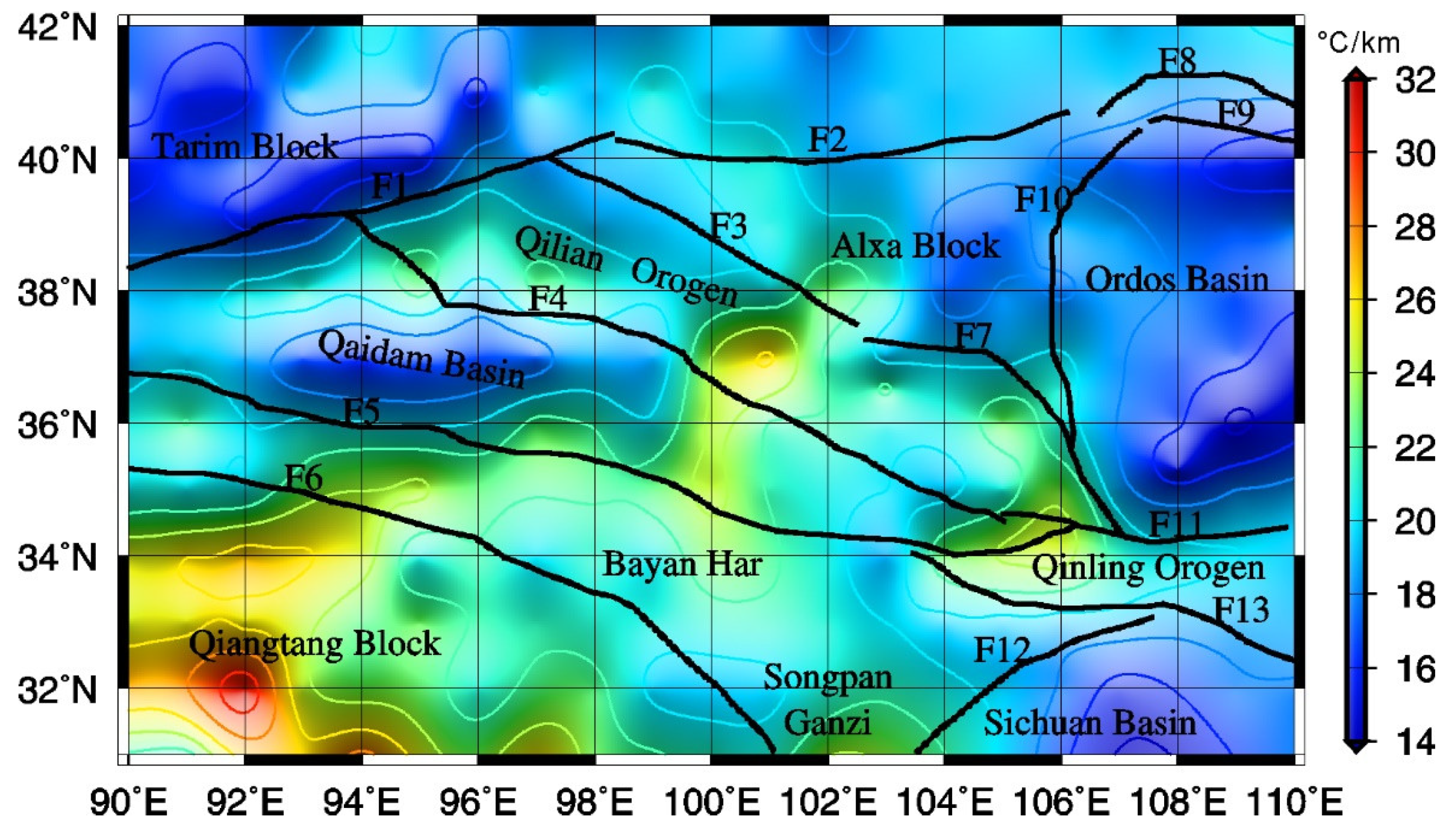
2. Geological Setting
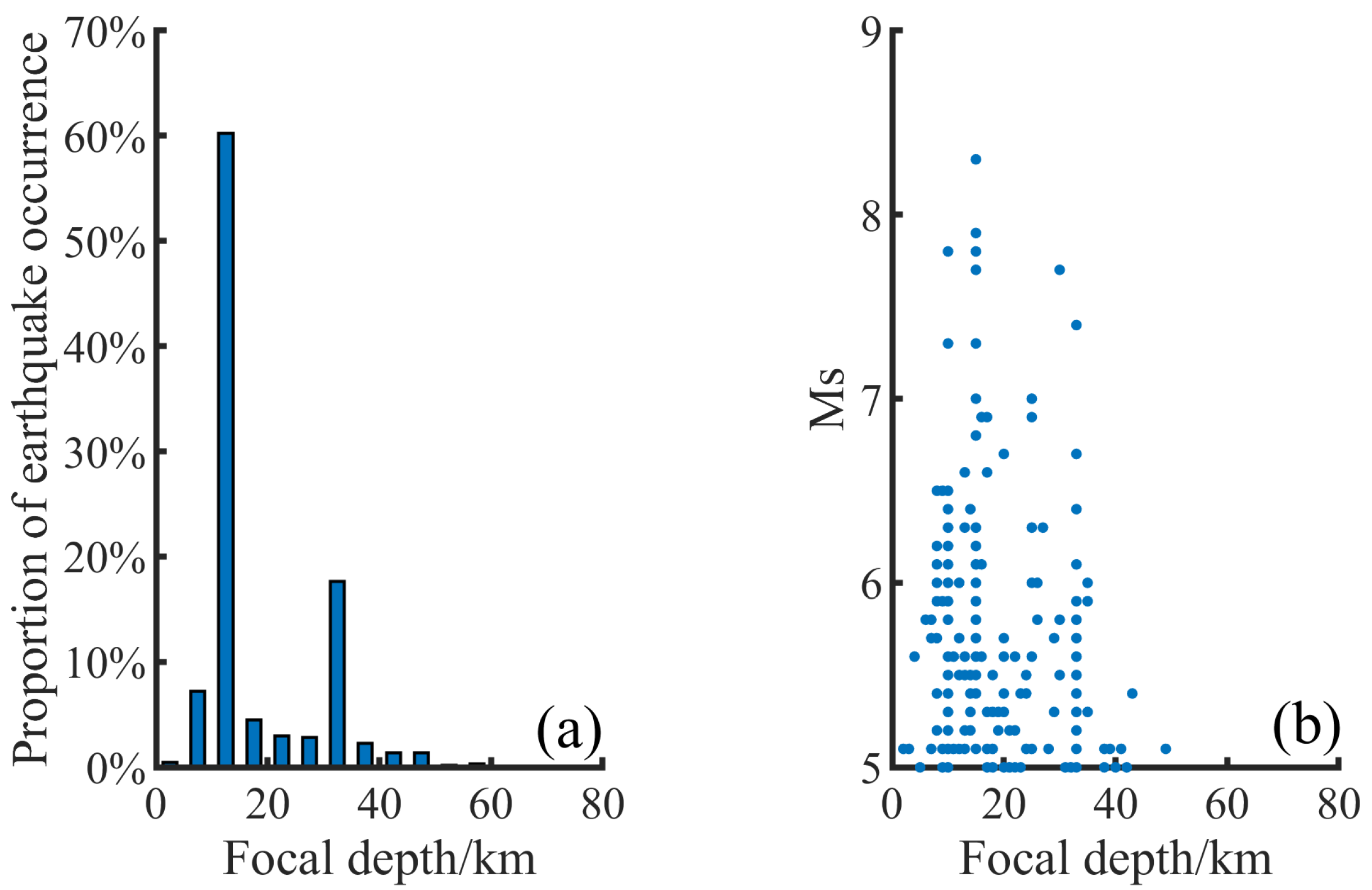
3. Regional Seismicity
4. Methodology
4.1. Data Sources
4.2. Inversion of the CPD
5. Crustal Magnetic Anomalies
5.1. Crustal Magnetic Anomalies and Aeromagnetic Anomalies
5.2. Distribution of Crustal Magnetic Anomalies
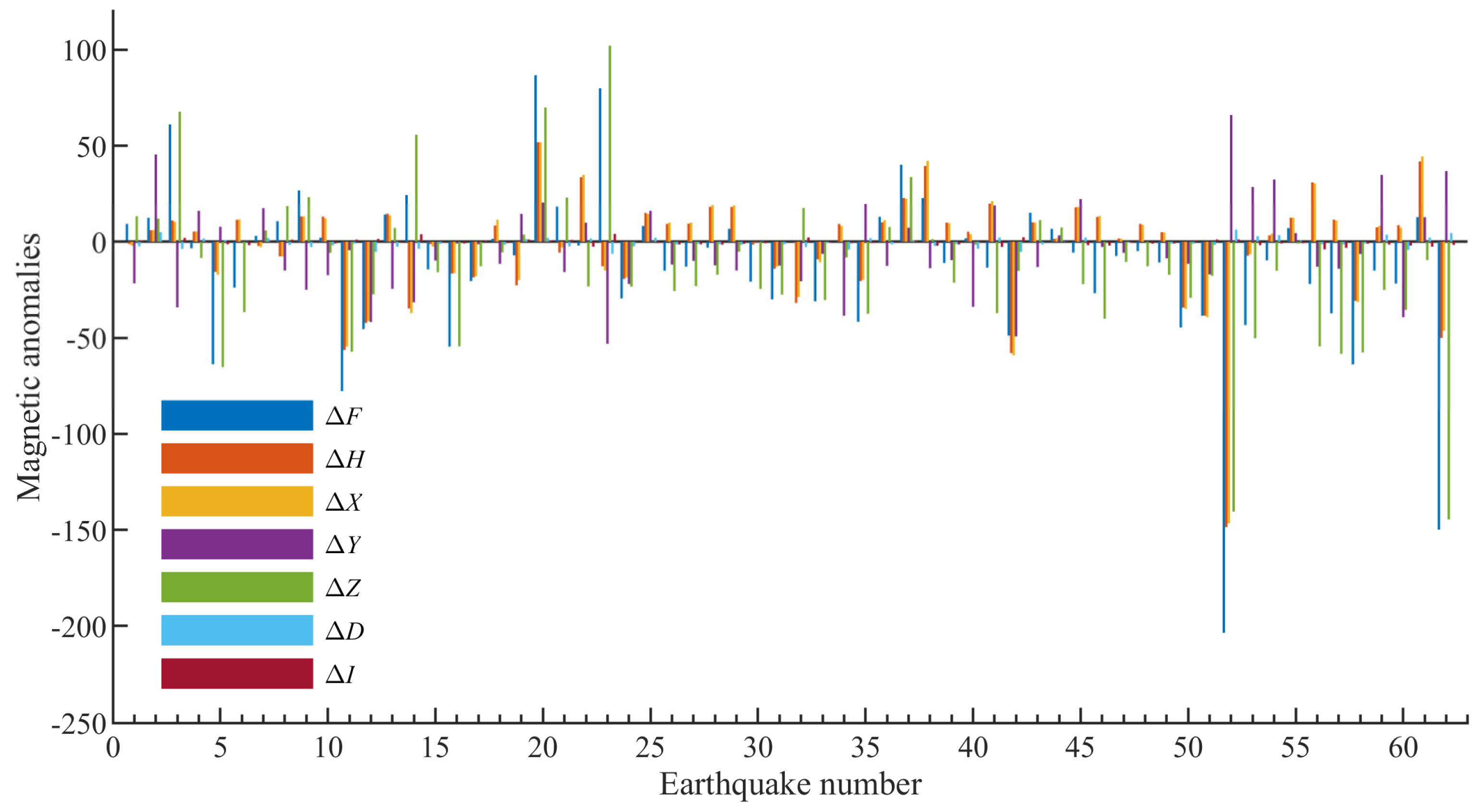
6. Relationships Between the Magnetic Anomalies and Earthquakes
7. Curie Point Depths
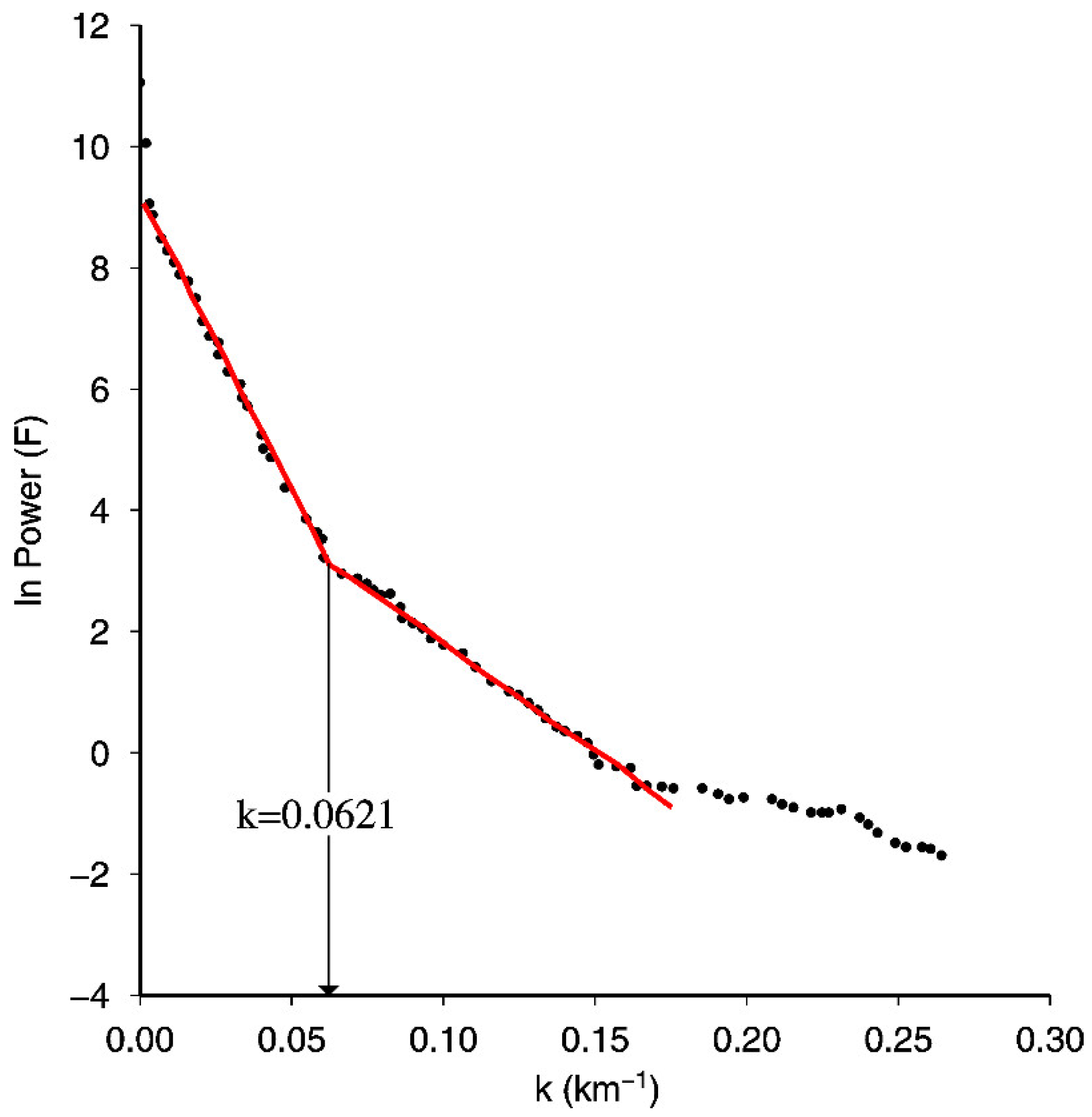
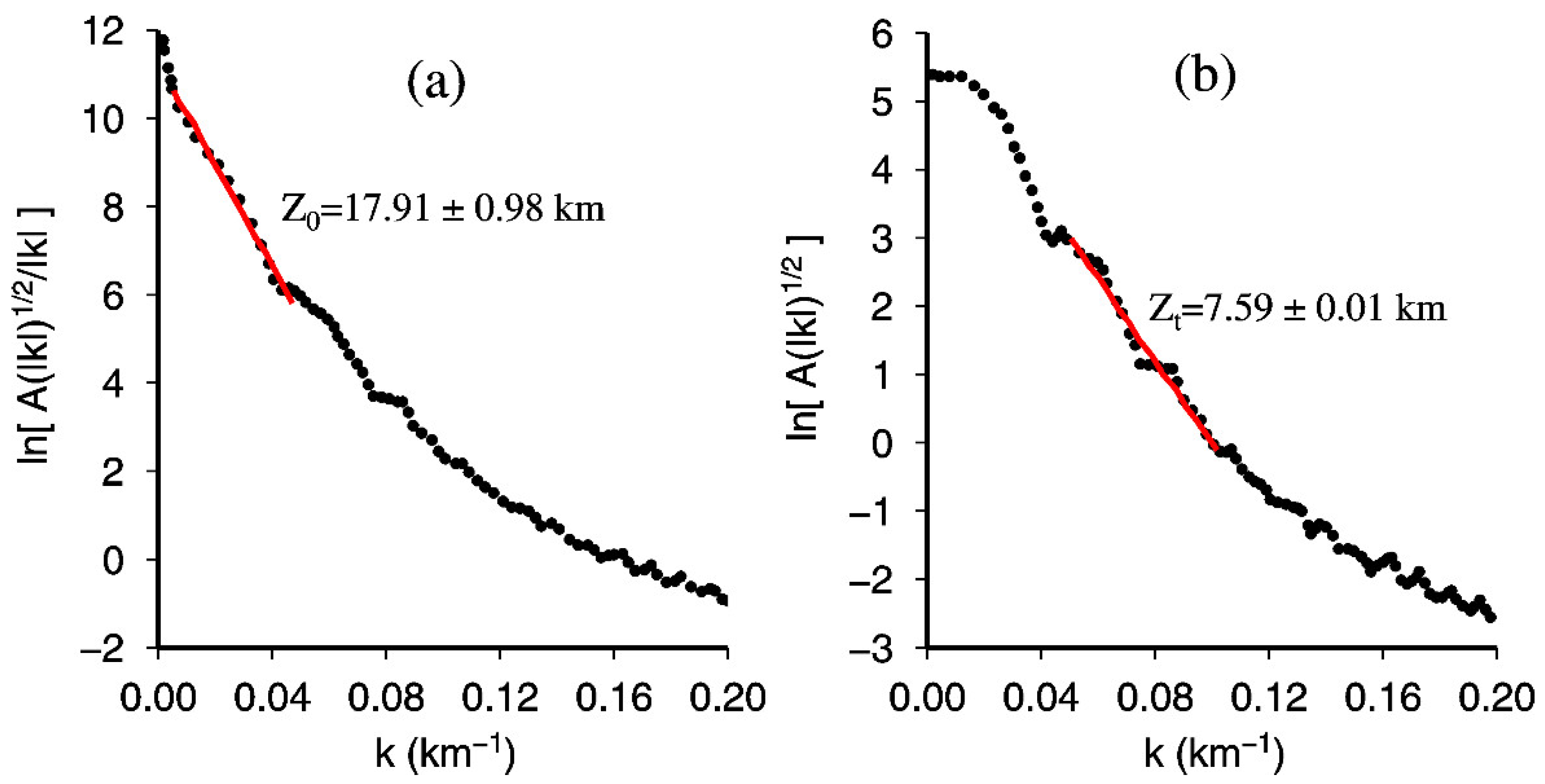
7.1. Calculation of the Curie Point Depth
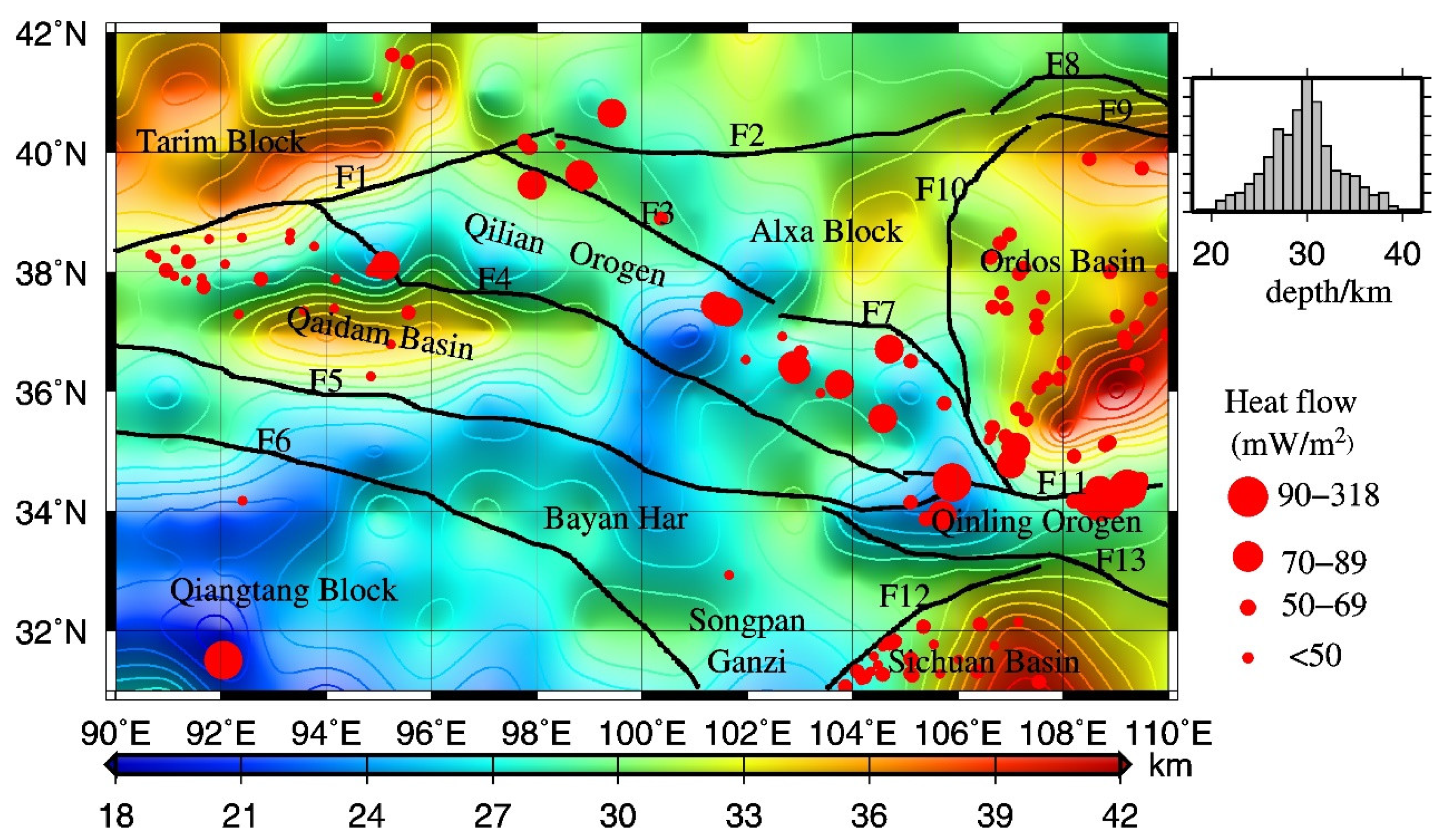
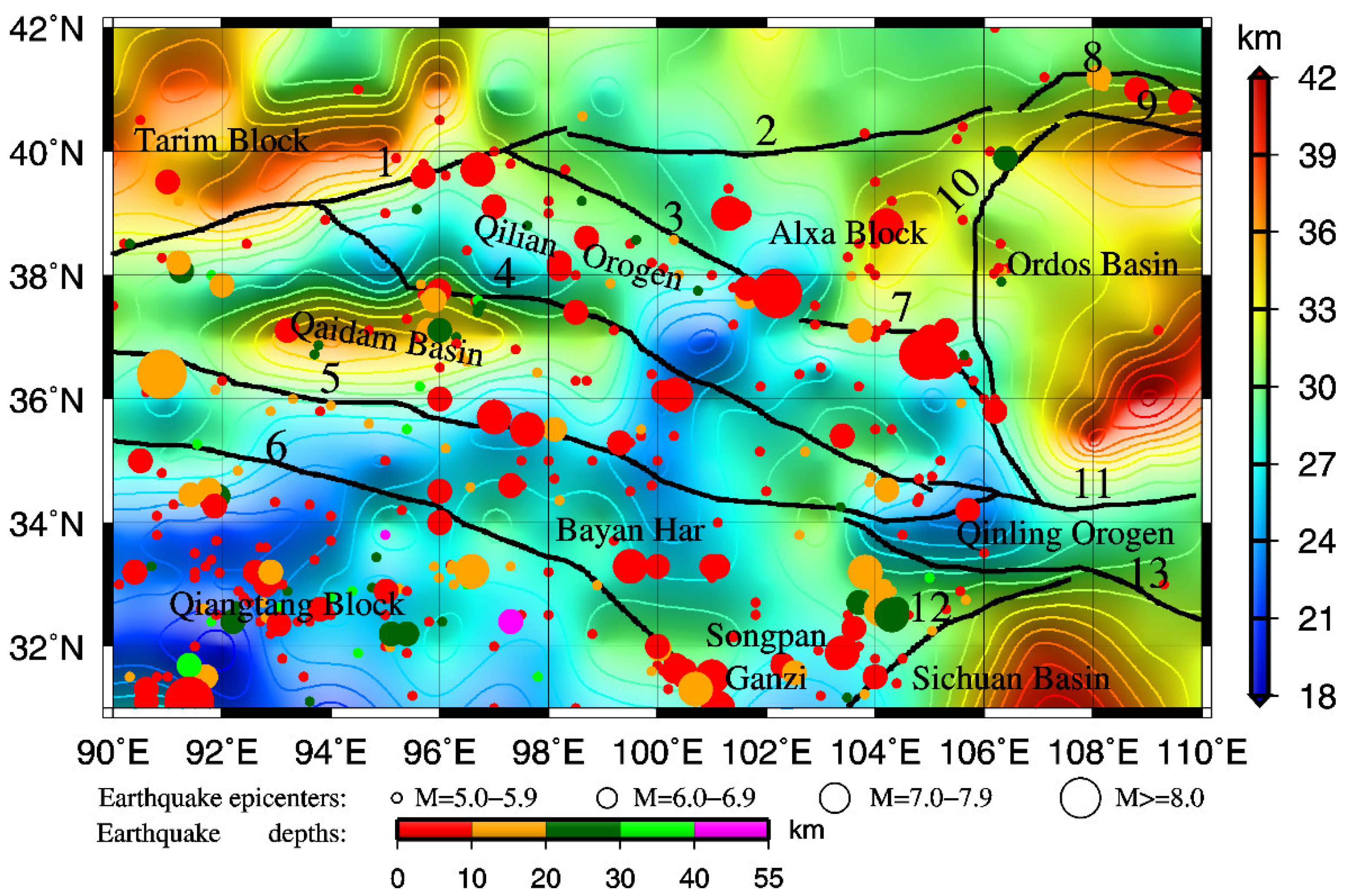
7.2. Distribution of Curie Point Depths
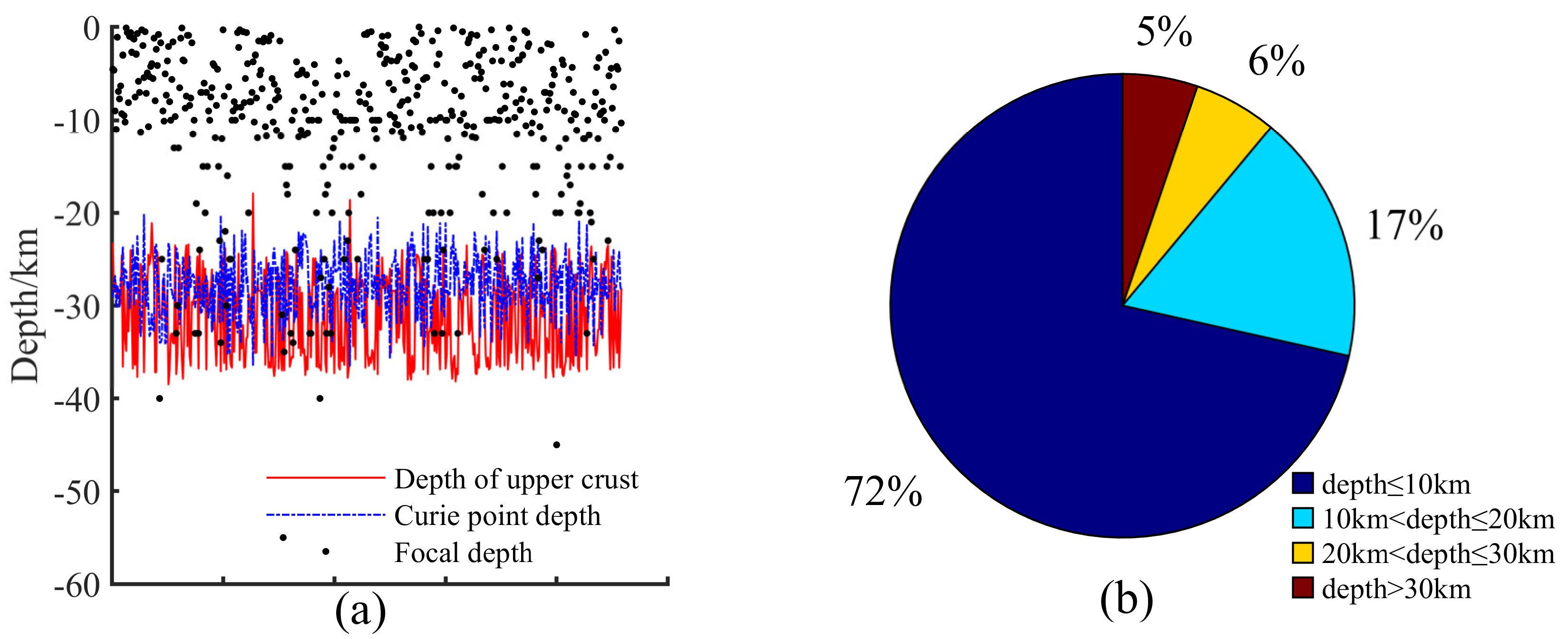
7.3. Evaluation of Errors in the Curie Point Depth
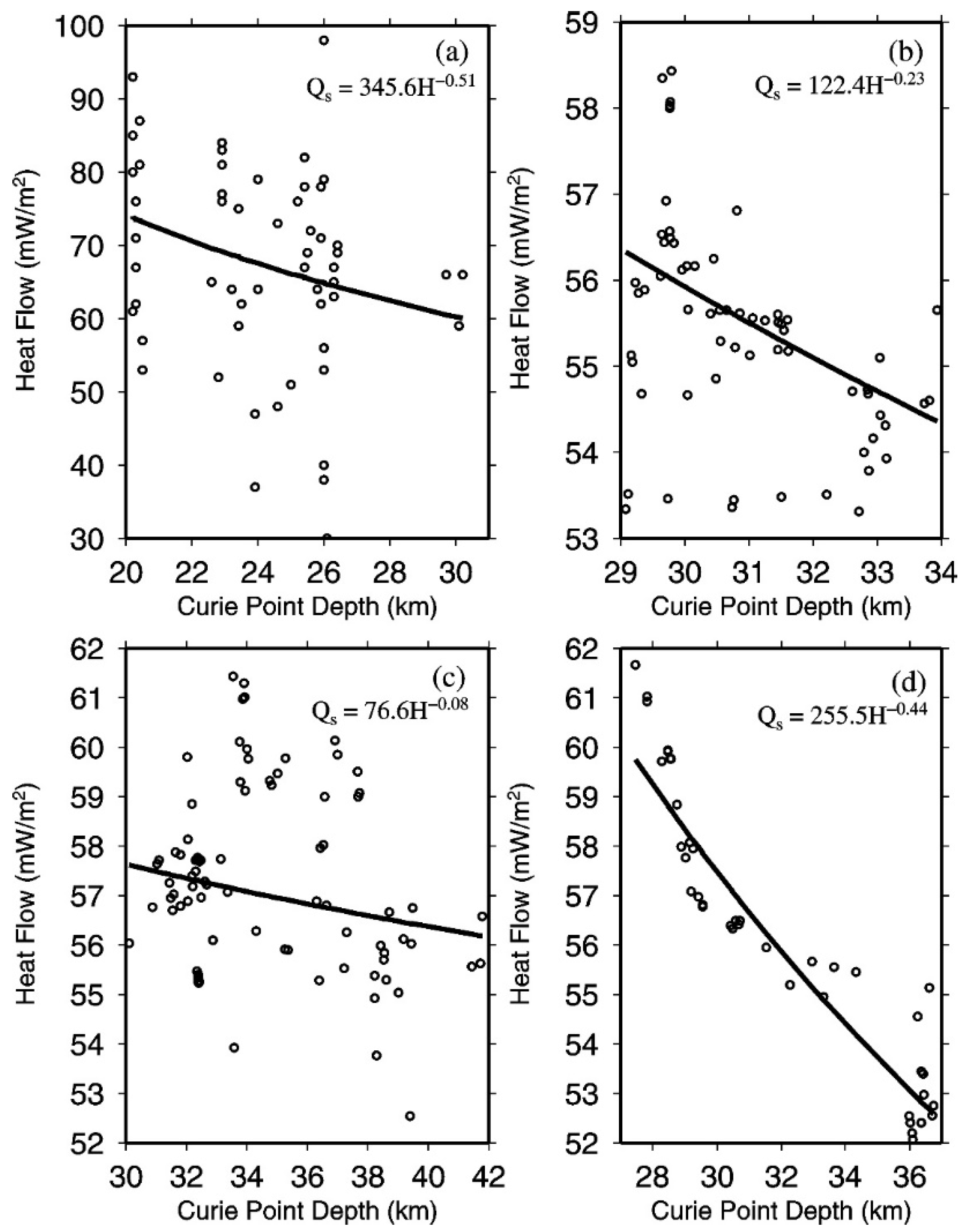
7.4. Relationship Between the Curie Point Depth and Heat Flow
7.5. Correlation Between the Curie Point Depth and Seismicity
8. Discussion
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mavroulis, S.; Mavrouli, M.; Vassilakis, E.; Argyropoulos, I.; Carydis, P.; Lekkas, E. Debris Management in Turkey Provinces Affected by the 6 February 2023 Earthquakes: Challenges during Recovery and Potential Health and Environmental Risks. Appl. Sci. 2023, 13, 8823. [Google Scholar] [CrossRef]
- Işık, E. Structural Failures of Adobe Buildings during the February 2023 Kahramanmaraş (Türkiye) Earthquakes. Appl. Sci. 2023, 13, 8937. [Google Scholar] [CrossRef]
- Liu, Y.B.; Pei, S.P. Lower crustal attenuation in northeastern Tibetan Plateau from ML amplitude. Earthq. Sci. 2021, 34, 378–386. [Google Scholar] [CrossRef]
- Gao, G.M.; Lu, Q.M.; Wang, J.; Kang, G.F. Constraining crustal thickness and lithospheric thermal state beneath the northeastern Tibetan Plateau and adjacent regions from gravity, aeromagnetic, and heat flow data. J. Asian Earth Sci. 2021, 212, 104743. [Google Scholar] [CrossRef]
- Wang, X.C.; Li, Y.H.; Ding, Z.F.; Zhu, L.P.; Wang, C.Y.; Bao, X.W.; Wu, Y. Three-dimensional lithospheric S wave velocity model of the NE Tibetan Plateau and western North China Craton. J. Geophys. Res. Solid Earth 2017, 122, 6703–6720. [Google Scholar] [CrossRef]
- Li, Z.; Guo, B.; Liu, Q.Y.; Chen, J.H.; Li, S.C.; Qi, S.H. P-wave structure of upper mantle beneath the Northeastern Tibetan Plateau from multiscale seismic tomography. Chin. J. Geophys. 2019, 62, 1244–1255, (In Chinese with English abstract). [Google Scholar]
- Xu, W.Y. Physics of Electromagnetic Phenomena of the Earth; University of Science and Technology of China Press: Hefei, China, 2009. [Google Scholar]
- Gailler, L.S.; Lénat, J.F.; Blakely, R.J. Depth to Curie temperature or bottom of the magnetic sources in the volcanic zone of la Réunion hot spot. J. Volcanol. Geoth. Res. 2016, 324, 169–178. [Google Scholar] [CrossRef]
- Zu, Q.; Chen, C.H.; Chen, C.R.; Liu, S.; Yen, H.Y. The relationship among earthquake location, magnetization, and subsurface temperature beneath the Taiwan areas. Phys. Earth Planet. Inter. 2021, 320, 106800. [Google Scholar] [CrossRef]
- Gao, G.M.; Shi, L.; Kang, G.F.; Wu, Y.Y.; Bai, C.H.; Wen, L.W.; Hou, J. Analysis of the lithospheric magnetic anomalies and tectonics in continental China and the adjacent regions using CHAMP satellite data. Stud. Geophys. Geod. 2018, 62, 408–426. [Google Scholar] [CrossRef]
- Prasad, K.N.D.; Bansal, A.R.; Prakash, O.; Singh, A.P. Magneto-thermometric modeling of Central India: Implications for the thermal lithosphere. J. Appl. Geophys. 2022, 196, 104508. [Google Scholar] [CrossRef]
- Santos, D.F.; Silva, J.B.C.; Lopes, J.F. In-depth 3D magnetic inversion of basement relief. Geophysics 2022, 87, 45–56. [Google Scholar] [CrossRef]
- Gao, G.M.; Kang, G.K.; Bai, C.H.; Wen, L.W.; Wang, Z.J.; Li, Y.C. Gravity anomalies and deep structure of the northeastern Tibetan Plateau and adjacent areas. J. Asian Earth Sci. 2025, 278, 106430. [Google Scholar] [CrossRef]
- Okubo, Y.; Yamano, S.; Takanashi, K.; Akazawa, S.; Osato, K.; Terai, A. Constraining the geotherm beneath the Japanese islands from Curie point depth analysis and comparison with seismicity and drillhole data in the Kakkonda geothermal field. Geothermics 2023, 111, 102706. [Google Scholar] [CrossRef]
- Wei, R.Q.; Yu, L. Constraints from satellite crustal magnetic field on the distribution of the epicenters for earthquakes in the continental crust of China. Chin. J. Geophys. 2012, 55, 2643–2650, (In Chinese with English abstract). [Google Scholar]
- Yan, Y.F.; Teng, J.W.; Ruan, X.M.; Hu, G.Z. Aeromagnetic field characteristics and the Wenchuan earthquakes in the Longmenshan mountains and adjacent areas. Chin. J. Geophys. 2016, 59, 197–214, (In Chinese with English abstract). [Google Scholar]
- Wen, L.M.; Kang, G.F.; Bai, C.H.; Gao, G.M. Relationship between crustal magnetic anomalies and strong earthquake activity in the south segment of the China North-South Seismic Belt. Appl. Geophys. 2021, 18, 408–419. [Google Scholar] [CrossRef]
- Gao, G.M.; Kang, G.F.; Li, G.Q.; Bai, C.H. Crustal magnetic anomaly in the Ordos region and its tectonic implications. J. Asian Earth Sci. 2015, 109, 63–73. [Google Scholar] [CrossRef]
- Hamed, S.; Nabi, A.E. Curie point depth beneath the Barramiya-Red Sea coast area estimated from spectral analysis of aeromagnetic data. J. Asian Earth Sci. 2012, 43, 254–266. [Google Scholar]
- Saada, A.S. Curie point depth and heat flow from spectral analysis of aeromagnetic data over the northern part of Western Desert, Egypt. J. Appl. Geophys. 2016, 134, 100–111. [Google Scholar] [CrossRef]
- Trifonova, P.; Zhelev, Z.; Petrova, T.; Bojadgieva, K. Curie point depths of Bulgarian territory inferred from geomagnetic observations and its correlation with regional thermal structure and seismicity. Tectonophysics 2009, 473, 362–374. [Google Scholar] [CrossRef]
- Maus, S. An ellipsoidal harmonic representation of Earth’s lithospheric magnetic field to degree and order 720. Geochem. Geophys. Geosyst. 2010, 11, 1–12. [Google Scholar] [CrossRef]
- Maus, S.; Rother, M.; Stolle, C.; Mai, W.; Choi, S.; Lühr, H.; Cooke, D.; Roth, C. Third generation of the Potsdam magnetic model of the Earth (POMME). Geochem. Geophys. Geosyst. 2006, 7, Q07008. [Google Scholar] [CrossRef]
- Olsen, N.; Davat, D.; Finlay, C.C. LCS-1: A high-resolution global model of the lithospheric magnetic field derived from CHAMP and Swarm satellite observations. Geophys. J. Int. 2017, 211, 1461–1477. [Google Scholar] [CrossRef]
- Meyer, B.; Chulliat, A.; Saltus, R. Derivation and error analysis of the earth magnetic anomaly grid at 2 arc min resolution version 3 (EMAG2v3). Geochem. Geophys. Geosyst. 2017, 18, 4522–4537. [Google Scholar] [CrossRef]
- Yin, A.; Harrison, T.M. Geologic evolution of the Himalayan-Tibetan orogen. Annu. Rev. Earth planet. Sci. 2000, 28, 211–280. [Google Scholar] [CrossRef]
- Zhang, P.; Shen, Z.; Wang, M. Continuous deformation of the Tibetan plateau from global positioning system data. Geology 2004, 32, 809–812. [Google Scholar] [CrossRef]
- Tanaka, A.; Okubo, Y.; Matsubayashi, O. Curie point depth based on spectrum analysis of the magnetic anomalies data in East and Southeast Asia. Tectonophysics 1999, 306, 461–470. [Google Scholar] [CrossRef]
- Xiong, S.Q.; Yang, H.; Ding, Y.Y.; Li, Z.K. Characteristics of Chinese continent Curie point isotherm. Chin. J. Geophys. 2016, 59, 3604–3617, (In Chinese with English abstract). [Google Scholar]
- Shive, P.N.; Blakely, R.J.; Fountain, D.M. Magnetic Properties of the lower continental crust. In Continental Lower Crust, Development in Geotectonics; Fountain, D.M., Arculis, R., Kay, R.W., Eds.; Elsevier: Amsterdam, The Netherlands, 1992; Volume 23, pp. 145–199. [Google Scholar]
- Arnaiz-Rodríguez, M.S.; Orihuela, N. Curie point depth in Venezuela and the Eastern Caribbean. Tectonophysics 2013, 590, 38–51. [Google Scholar] [CrossRef]
- Kang, G.F.; Gao, G.M.; Bai, C.H.; Shao, D.; Feng, L.L. Characteristics of the crustal magnetic anomaly and regional tectonics in the Qinghai-Tibet Plateau and the adjacent areas. Sci. China Earth Sci. 2011, 41, 1577–1585. [Google Scholar]
- Cooper, G.R.J.; Cowan, D.R. Differential reduction to the pole. Comput. Geosci. 2005, 31, 989–999. [Google Scholar] [CrossRef]
- Bonvalot, S.; Balmino, G.; Briais, A.; Kuhn, M.; Peyrefitte, A.; Vales, N.; Biancale, R.; Gabalda, G.; Reinquin, F.; Sarrailh, M. (Eds.) World Gravity Map; Commission for the Geological Map of the World: Paris, France, 2012. [Google Scholar]
- Thébault, E.; Purucker, M.; Whaler, K.A.; Langlais, B.; Sabaka, T.J. The magnetic field of the earth’s lithosphere. Space Sci. Rev. 2010, 155, 95–127. [Google Scholar] [CrossRef]
- Guo, L.H.; Meng, X.H. Preferential filtering for gravity anomaly separation. Comput. Geosci. 2013, 51, 247–254. [Google Scholar] [CrossRef]
- Xia, S.R.; Shi, L.; Li, Y.H. Velocity structures of the crust and uppermost mantal beneath the northeastern margin of Tibetan plateau revealed by double-difference tomography. Chin. J Geophys. 2021, 64, 3194–3206, (In Chinese with English abstract). [Google Scholar]
- Lysak, S.V. Thermal history, geodynamics, and current thermal activity of lithosphere in China. Russ. Geol. Geophys. 2009, 50, 815–825. [Google Scholar] [CrossRef]
- Fu, Y.Y.; Xiao, Z. Ambient nois tomography of Rayleigh and Love wave in North Tibetan and adjacent regions. Chin. J. Geophys. 2020, 63, 860–870, (In Chinese with English abstract). [Google Scholar]
- Hu, S.B.; He, L.; Wang, J. Compilation of heat flow data in the China continental area (3rd ed.). Chin. J. Geophys. 2001, 44, 611–626, (In Chinese with English abstract). [Google Scholar]
- Wang, C.Y.; Li, Y.H.; Lou, H. Issues on crustal and upper-mantle structures associated with geodynamics in the northeastern Tibetan Plateau. Chin. Sci. Bull. 2016, 61, 2239–2263. [Google Scholar]
- Ding, W.X.; Fu, Y.Y.; Gao, Y.; Liao, W.L.; He, Y.J.; Cai, Y.J.; Shen, X.L. Phase velocity tomography of Rayleigh in Qinling-Dabie and adjacent areas using ambient seismic noise. Chin. J. Geophys. 2017, 60, 2959–2968, (In Chinese with English abstract). [Google Scholar]
- Kelemework, Y.; Fedi, M.; Milano, M. A review of spectral analysis of magnetic data for depth estimation. Geophysics 2021, 86, J33. [Google Scholar] [CrossRef]
- Martos, Y.M.; Catalán, M.; Galindo-Zaldivar, J. Curie depth, heat flux, and thermal subsidence reveal the Pacific mantle outflow through the Scotia Sea. J. Geophys. Res. Solid Earth 2019, 124, 10735–10751. [Google Scholar] [CrossRef]
- Didas, M.; Armadillo, E.; Hersir, G.; Cumming, W.; Rizzello, D. Regional thermal anomalies derived from magnetic spectral analysis and 3d gravity inversion: Implications for potential geothermal sites in Tanzania. Geothermics 2022, 103, 102431. [Google Scholar] [CrossRef]
- Carrillo-de la Cruz, J.L.; Prol-Ledesma, R.M.; Gomez-Rodríguez, D.; Rodríguez-Díaz, A. Analysis of the relation between bottom hole temperature data and Curie temperature depth to calculate geothermal gradient and heat flow in Coahuila. Mexico. Tectonophysics 2020, 780, 228397. [Google Scholar] [CrossRef]
- Saibi, H.; Aboud, E.; Gottsmann, J. Curie point depth from spectral analysis of aeromagnetic data for geothermal reconnaissance in Afghanistan. J. Afr. Earth Sci. 2015, 111, 92–99. [Google Scholar] [CrossRef]
- Jiang, G.Z.; Gao, P.; Rao, S.; Zhang, L.Y.; Tang, R.Y.; Huang, F.; Zhao, P.; Pang, Z.H.; He, L.J.; Hu, S.B.; et al. Compilation of heat flow data in the continental area of China (4th ed.). Chinese J. Geophys. 2016, 59, 2892–2910, (In Chinese with English Abstract). [Google Scholar]
- Laske, G.; Masters, G.; Ma, Z.; Pasyanos, M. Update on CRUST1.0-A 1-degree global model of earth’s crust. Geophys. Res. Abstr. 2013, 15, 2658. [Google Scholar]
- Xiang, C.Y.; Zhou, Z.H. Relationship between seismicity and geothermal structure of the lithosphere in Yunnan Provence, China. Earthq. Res. China 2000, 3, 263–272, (In Chinese with English abstract). [Google Scholar]
- McNamara, D.E.; Owens, T.J.; Walter, W.R. Observations of regional phase propagation across the Tibetan Plateau. J. Geophys. Res. 1995, 100, 22215–22229. [Google Scholar] [CrossRef]
- Owens, T.J.; Zandt, G. Implications of crustal property variations for models of Tibetan Plateau evolution. Nature 1997, 387, 37–43. [Google Scholar] [CrossRef]
- Lachenbruch, A.H. Heat flow in the Basin and Range province and thermal effects of tectonic extension. Pure Appl. Geophys. 1978, 117, 34–50. [Google Scholar] [CrossRef]
- Gehrels, G.E.; Yin, A.; Wang, X.F. Magmatic history of the northeastern Tibetan Plateau. J. Geophys. Res. Solid Earth 2003, 108, 2423. [Google Scholar] [CrossRef]
- Liang, H.; Gao, R.; Xue, S.; Han, J. Electrical structure of the middle Qilian Shan revealed by 3-D inversion of magnetotelluric data: New insights into the growth and deformation in the Northeastern Tibetan Plateau. Tectonophysics 2020, 789, 228523. [Google Scholar] [CrossRef]
- Li, H.L.; Fang, J.; Wang, X.S.; Liu, J.; Cui, R.H.; Chen, M. Lithospheric 3-D density structure beneath the Tibetan plateau and adjacent areas derived from joint inversion of satellite gravity and gravity-gradient data. Chin. J. Geophys. 2017, 60, 2469–2479, (In Chinese with English abstract). [Google Scholar]
- Clark, M.K.; Royden, L.H. Topographic ooze: Building the eastern margin of Tibet by lower crustal flow. Geology 2000, 28, 703–706. [Google Scholar] [CrossRef]
- Yang, W.C.; Chen, Z.X.; Hou, Z.Z.; Meng, X.H. Crustal density structures around Chinese continent by inversion of satellite gravity data. Acta. Geol. Sin. 2016, 90, 2167–2175. [Google Scholar]
| NO. | Date | Lon./(°) | Lat./(°) | Ms | Depth/(km) | NO. | Date | Lon./(°) | Lat./(°) | Ms | Depth/(km) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 16 December 1920 | 36.89 | 105.61 | 8.5 | 15 | 191 | 12 September 2000 | 35.33 | 99.3 | 5.1 | 10 |
| 2 | 25 December 1920 | 37.24 | 105.48 | 6.8 | 15 | 192 | 12 September 2000 | 35.39 | 99.34 | 6.1 | 10 |
| 3 | 24 March 1923 | 31.3 | 100.75 | 7 | 15 | 193 | 13 September 2000 | 34.14 | 95.12 | 5 | 33 |
| 4 | 22 May 1927 | 37.65 | 102.49 | 8.0 | 15 | 194 | 20 September 2000 | 35.42 | 99.55 | 5.1 | 33 |
| 5 | 7 March 1928 | 37.67 | 102.13 | 6.2 | 15 | 195 | 28 October 2000 | 32.67 | 92.23 | 5.1 | 33 |
| 6 | 13 July 1930 | 37.97 | 98.26 | 6.5 | 10 | 196 | 30 October 2000 | 32.74 | 92.24 | 5.2 | 33 |
| 7 | 25 December 1932 | 39.5 | 96.62 | 7.9 | 15 | 197 | 26 November 2000 | 35.87 | 90.55 | 5.4 | 33 |
| 8 | 25 August 1933 | 32.01 | 103.68 | 7.3 | 15 | 198 | 10 July 2001 | 39.02 | 97.99 | 5 | 33 |
| 9 | 20 January 1934 | 41.14 | 108.62 | 6.3 | 15 | 199 | 25 July 2001 | 33.17 | 95.6 | 5.5 | 33 |
| 10 | 26 July 1935 | 33.17 | 100.94 | 6.2 | 15 | 200 | 14 November 2001 | 35.65 | 93.96 | 5 | 10 |
| 11 | 7 February 1936 | 35.44 | 103.19 | 6.8 | 15 | 201 | 14 November 2001 | 35.75 | 94.02 | 5.1 | 10 |
| 12 | 7 January 1937 | 35.43 | 97.76 | 7.8 | 15 | 202 | 14 November 2001 | 35.61 | 93.98 | 5.2 | 10 |
| 13 | 17 March 1947 | 33.48 | 99.53 | 7.3 | 15 | 203 | 14 November 2001 | 35.6 | 94.49 | 5.3 | 10 |
| 14 | 18 June 1950 | 34.95 | 99.77 | 5.8 | 30 | 204 | 14 November 2001 | 35.65 | 93.88 | 5.4 | 10 |
| 15 | 21 August 1950 | 33.04 | 91.48 | 6 | 15 | 205 | 14 November 2001 | 35.73 | 93.38 | 5.6 | 10 |
| 16 | 17 September 1950 | 32.44 | 93.96 | 5.6 | 15 | 206 | 14 November 2001 | 35.95 | 90.54 | 8.1 | 10 |
| 17 | 30 October 1950 | 33.17 | 95.85 | 5.7 | 15 | 207 | 18 November 2001 | 35.71 | 93.69 | 5.4 | 10 |
| 18 | 1 August 1951 | 31.54 | 95.31 | 5.5 | 15 | 208 | 18 November 2001 | 35.73 | 93.69 | 5.6 | 10 |
| 19 | 18 November 1951 | 31.06 | 91.26 | 7.7 | 30 | 209 | 19 November 2001 | 35.76 | 93.67 | 5.4 | 10 |
| 20 | 26 December 1951 | 39.49 | 95.53 | 6.2 | 15 | 210 | 30 November 2001 | 36.07 | 91.12 | 5.2 | 10 |
| 21 | 26 December 1951 | 31.24 | 90.78 | 6.3 | 15 | 211 | 1 December 2001 | 35.58 | 93.93 | 5.1 | 10 |
| 22 | 23 January 1952 | 39.73 | 95.44 | 6 | 35 | 212 | 8 December 2001 | 35.73 | 92.77 | 5.3 | 10 |
| 23 | 3 February 1952 | 33.98 | 93.8 | 5.5 | 15 | 213 | 7 February 2002 | 37.93 | 92.15 | 5 | 18 |
| 24 | 6 February 1952 | 39.59 | 98.66 | 5.8 | 15 | 214 | 22 May 2002 | 36.99 | 95.34 | 5 | 10 |
| 25 | 15 June 1952 | 31.37 | 90.92 | 5.9 | 15 | 215 | 29 June 2002 | 34.13 | 94.5 | 5.6 | 33 |
| 26 | 14 September 1952 | 34.35 | 91.86 | 6 | 15 | 216 | 27 September 2002 | 33.36 | 93.57 | 5.1 | 33 |
| 27 | 1 October 1952 | 36.52 | 92.1 | 5.7 | 15 | 217 | 19 October 2002 | 35.65 | 93.13 | 5.1 | 33 |
| 28 | 5 October 1952 | 37.01 | 93.2 | 6.1 | 15 | 218 | 26 October 2002 | 35.14 | 96.1 | 5.4 | 33 |
| 29 | 31 October 1952 | 33.22 | 101.16 | 6.2 | 15 | 219 | 14 December 2002 | 39.74 | 97.44 | 5.6 | 22 |
| 30 | 23 April 1953 | 31.05 | 96.87 | 6 | 10 | 220 | 11 February 2003 | 32.51 | 93.79 | 5.1 | 33 |
| 31 | 11 February 1954 | 38.96 | 101.22 | 7 | 25 | 221 | 17 April 20038 | 37.53 | 96.48 | 6.4 | 14 |
| 32 | 31 July 1954 | 38.62 | 104.15 | 6.9 | 25 | 222 | 3 May 2003 | 37.48 | 96.54 | 5.1 | 10 |
| 33 | 7 February 1958 | 31.46 | 104.01 | 6 | 25 | 223 | 20 May 2003 | 32.68 | 93.09 | 5.2 | 33 |
| 34 | 30 April 1958 | 38.37 | 103.97 | 5.5 | 30 | 224 | 24 May 2003 | 32.61 | 92.34 | 5.1 | 49 |
| 35 | 27 April 1959 | 33.22 | 92.72 | 5.9 | 15 | 225 | 24 May 2003 | 32.59 | 92.43 | 5.1 | 33 |
| 36 | 21 August 1959 | 39.22 | 104.28 | 5.4 | 15 | 226 | 3 July 2003 | 35.71 | 93.71 | 5 | 10 |
| 37 | 28 September 1960 | 32.44 | 95.86 | 5.6 | 15 | 227 | 18 July 2003 | 38.91 | 98.57 | 5 | 10 |
| 38 | 9 November 1960 | 32.71 | 103.63 | 6.3 | 25 | 228 | 6 October 2003 | 38.86 | 100.01 | 5 | 10 |
| 39 | 4 December 1961 | 33.34 | 95.25 | 6.1 | 16 | 229 | 10 October 2003 | 39.58 | 98.22 | 5.1 | 10 |
| 40 | 21 May 1962 | 36.93 | 95.93 | 6.6 | 17 | 230 | 25 October 2003 | 38.35 | 101.04 | 5.2 | 10 |
| 41 | 17 December 1962 | 37.95 | 106.19 | 5.7 | 20 | 231 | 25 October 2003 | 38.4 | 100.95 | 5.8 | 10 |
| 42 | 19 April 1963 | 35.61 | 96.99 | 6.7 | 20 | 232 | 25 October 2003 | 38.38 | 100.98 | 5.8 | 10 |
| 43 | 15 August 1967 | 31.08 | 93.64 | 5.7 | 20 | 233 | 13 November 2003 | 34.71 | 103.83 | 5.1 | 10 |
| 44 | 30 August 1967 | 31.59 | 100.26 | 5.8 | 10 | 234 | 12 December 2003 | 37.63 | 94.59 | 5.1 | 10 |
| 45 | 30 August 1967 | 31.63 | 100.26 | 6.4 | 10 | 235 | 24 February 2004 | 37.49 | 96.83 | 5.1 | 41 |
| 46 | 22 December 1968 | 36.31 | 101.77 | 5.6 | 25 | 236 | 6 March 2004 | 33.29 | 91.95 | 5 | 38 |
| 47 | 24 March 1971 | 35.45 | 98.14 | 6 | 10 | 237 | 7 March 2004 | 31.64 | 91.24 | 5.6 | 11 |
| 48 | 3 April 1971 | 32.16 | 95.04 | 5.8 | 15 | 238 | 16 March 2004 | 37.56 | 96.67 | 5.2 | 14 |
| 49 | 22 May 1971 | 32.3 | 92.1 | 5.6 | 10 | 239 | 4 May 2004 | 37.47 | 96.91 | 5.2 | 10 |
| 50 | 22 July 1972 | 31.36 | 91.44 | 5.9 | 10 | 240 | 4 May 2004 | 37.51 | 96.76 | 5.5 | 14 |
| 51 | 30 August 1972 | 36.62 | 96.56 | 5.5 | 18 | 241 | 10 May 2004 | 37.49 | 96.6 | 5.6 | 10 |
| 52 | 15 January 1973 | 40.43 | 91.07 | 5.1 | 13 | 242 | 24 August 2004 | 32.54 | 92.19 | 5.5 | 10 |
| 53 | 6 February 1973 | 31.7 | 100.02 | 5.1 | 33 | 243 | 7 September 2004 | 34.68 | 103.78 | 5.2 | 10 |
| 54 | 6 February 1973 | 31.4 | 100.58 | 7.4 | 33 | 244 | 10 December 2004 | 35.68 | 93.18 | 5 | 10 |
| 55 | 7 February 1973 | 31.46 | 100.29 | 5.8 | 33 | 245 | 3 March 2009 | 31.8 | 104.79 | 5.1 | 10 |
| 56 | 23 March 1973 | 31.88 | 100.06 | 5.4 | 33 | 246 | 12 March 2009 | 32.39 | 105.1 | 5.3 | 10 |
| 57 | 9 June 1973 | 39.42 | 95.41 | 5 | 33 | 247 | 29 June 2009 | 31.43 | 104.01 | 5.3 | 10 |
| 58 | 16 June 1973 | 37.71 | 95.64 | 5.4 | 33 | 248 | 16 July 2009 | 38.87 | 101.31 | 5.1 | 15 |
| 59 | 21 July 1973 | 35.55 | 96.06 | 5.2 | 33 | 249 | 28 August 2009 | 37.69 | 95.78 | 5 | 10 |
| 60 | 11 August 1973 | 33 | 104.02 | 6.1 | 33 | 250 | 28 August 2009 | 37.65 | 95.71 | 5.6 | 4 |
| 61 | 9 September 1973 | 31.48 | 100 | 5.2 | 33 | 251 | 28 August 2009 | 37.68 | 95.77 | 5.6 | 16 |
| 62 | 9 September 1973 | 31.65 | 100.01 | 5.5 | 33 | 252 | 28 August 2009 | 37.7 | 95.72 | 6.3 | 13 |
| 63 | 9 October 1973 | 31.69 | 99.76 | 5 | 33 | 253 | 29 August 2009 | 37.64 | 95.72 | 5.2 | 10 |
| 64 | 15 January 1974 | 32.91 | 104.2 | 5.7 | 33 | 254 | 30 August 2009 | 37.67 | 95.65 | 5.4 | 10 |
| 65 | 22 September 1974 | 33.58 | 102.45 | 5.1 | 33 | 255 | 31 August 2009 | 37.64 | 95.89 | 5.3 | 10 |
| 66 | 16 November 1974 | 33.05 | 103.98 | 5.2 | 33 | 256 | 28 August 2009 | 37.61 | 95.83 | 5.8 | 6 |
| 67 | 4 January 1975 | 38.53 | 97.51 | 5.4 | 33 | 257 | 1 September 2009 | 37.68 | 95.88 | 5 | 10 |
| 68 | 14 March 1975 | 34.01 | 95.48 | 5.1 | 33 | 258 | 17 September 2009 | 37.64 | 95.94 | 5.1 | 10 |
| 69 | 5 May 1975 | 33.09 | 92.92 | 6.1 | 33 | 259 | 18 September 2009 | 37.65 | 95.59 | 5 | 5 |
| 70 | 7 November 1975 | 33.29 | 95.33 | 5.2 | 33 | 260 | 18 September 2009 | 37.65 | 95.6 | 5.1 | 7 |
| 71 | 16 August 1976 | 32.93 | 104.26 | 5 | 33 | 261 | 2 October 2009 | 39.49 | 96.07 | 5 | 10 |
| 72 | 16 August 1976 | 32.75 | 104.16 | 6.9 | 16 | 262 | 19 October 2009 | 31.97 | 104.61 | 5.1 | 38 |
| 73 | 19 August 1976 | 32.89 | 104.19 | 5.4 | 33 | 263 | 23 October 2009 | 34.9 | 99.46 | 5.1 | 39 |
| 74 | 21 August 1976 | 32.57 | 104.25 | 6.4 | 33 | 264 | 29 October 2009 | 32.52 | 105.24 | 5.2 | 14 |
| 75 | 23 August 1976 | 32.49 | 104.18 | 6.7 | 33 | 265 | 4 November 2009 | 37.65 | 95.76 | 5.1 | 3 |
| 76 | 1 September 1976 | 32.46 | 104.15 | 5.1 | 18 | 266 | 13 December 2009 | 41.72 | 94.32 | 5.4 | 10 |
| 77 | 20 September 1976 | 32.77 | 104.12 | 5 | 42 | 267 | 21 December 2009 | 37.53 | 96.64 | 5 | 10 |
| 78 | 22 September 1976 | 40.03 | 106.33 | 5.7 | 29 | 268 | 1 March 2010 | 32.3 | 105.17 | 5 | 38 |
| 79 | 17 December 1967 | 33.34 | 93.91 | 5.1 | 33 | 269 | 24 March 2010 | 32.52 | 92.83 | 5.4 | 20 |
| 80 | 1 January 1977 | 38.15 | 91.01 | 6.3 | 27 | 270 | 24 March 2010 | 32.51 | 92.71 | 5.7 | 7 |
| 81 | 19 January 1977 | 37.02 | 95.7 | 5.9 | 33 | 271 | 13 April 2010 | 33.17 | 96.55 | 6.9 | 17 |
| 82 | 19 October 1977 | 39.16 | 91.04 | 5.1 | 33 | 272 | 14 April 2010 | 33.07 | 96.62 | 5 | 10 |
| 83 | 7 December 1977 | 35.6 | 94.52 | 5 | 33 | 273 | 14 April 2010 | 33.13 | 96.55 | 5.2 | 10 |
| 84 | 12 July 1978 | 31.91 | 103.04 | 5.3 | 33 | 274 | 14 April 2010 | 32.93 | 96.86 | 5.4 | 23 |
| 85 | 16 August 1978 | 38.38 | 101.36 | 5 | 33 | 275 | 14 April 2010 | 33.2 | 96.45 | 6.1 | 8 |
| 86 | 17 November 1978 | 37.29 | 97.09 | 5 | 33 | 276 | 17 April 2010 | 32.51 | 92.83 | 5.3 | 35 |
| 87 | 2 February 1979 | 39.72 | 90.75 | 5 | 33 | 277 | 25 May 2010 | 31.15 | 103.55 | 5 | 10 |
| 88 | 29 March 1979 | 32.15 | 96.96 | 5.8 | 33 | 278 | 29 May 2010 | 33.17 | 96.07 | 5.8 | 7 |
| 89 | 24 August 1979 | 41.15 | 108.13 | 5.9 | 33 | 279 | 3 June 2010 | 33.3 | 96.09 | 5.1 | 10 |
| 90 | 28 September 1979 | 38.21 | 90.46 | 5 | 22 | 280 | 3 June 2010 | 33.34 | 96.15 | 5.5 | 24 |
| 91 | 2 December 1979 | 38.49 | 90.15 | 5.2 | 33 | 281 | 7 September 2010 | 33.28 | 96.31 | 5.1 | 2 |
| 92 | 6 March 1980 | 35.99 | 91.84 | 5 | 33 | 282 | 10 April 2011 | 31.37 | 100.76 | 5.4 | 43 |
| 93 | 1 June 1980 | 38.9 | 95.64 | 5.2 | 33 | 283 | 15 May 2011 | 32.5 | 105.42 | 5 | 10 |
| 94 | 12 July 1980 | 36.83 | 93.78 | 5.4 | 24 | 284 | 26 June 2011 | 32.45 | 95.95 | 5.3 | 29 |
| 95 | 9 June 1981 | 34.5 | 91.44 | 6 | 10 | 285 | 11 August 2011 | 37.66 | 95.69 | 5 | 10 |
| 96 | 7 November 1981 | 31.33 | 103.97 | 5.1 | 33 | 286 | 31 October 2011 | 32.53 | 105.32 | 5 | 40 |
| 97 | 15 June 1982 | 31.91 | 99.93 | 5.6 | 10 | 287 | 1 November 2011 | 34.54 | 104.17 | 5 | 32 |
| 98 | 27 March 1983 | 34.24 | 92.6 | 5 | 33 | 288 | 3 May 2012 | 40.51 | 98.53 | 5.2 | 10 |
| 99 | 15 June 1983 | 34.23 | 92.94 | 5.2 | 33 | 289 | 11 May 2012 | 37.74 | 102.05 | 5 | 10 |
| 100 | 25 December 1983 | 37.94 | 91.12 | 5 | 31 | 290 | 26 November 2012 | 40.41 | 90.36 | 5 | 10 |
| 101 | 5 January 1984 | 37.97 | 102.19 | 5.5 | 12 | 291 | 18 January 2013 | 31.06 | 99.55 | 5.4 | 8 |
| 102 | 17 February 1984 | 37.69 | 100.8 | 5.3 | 10 | 292 | 30 January 2013 | 32.92 | 94.68 | 5.2 | 22 |
| 103 | 14 June 1984 | 36.92 | 96.48 | 5 | 33 | 293 | 11 February 2013 | 38.48 | 92.37 | 5.3 | 17 |
| 104 | 28 July 1984 | 34.19 | 92.97 | 5.3 | 33 | 294 | 5 June 2013 | 37.6 | 95.93 | 5.1 | 9 |
| 105 | 23 November 1984 | 37.99 | 106.36 | 5.2 | 33 | 295 | 21 July 2013 | 34.51 | 104.26 | 5.9 | 8 |
| 106 | 16 January 1985 | 32.88 | 95.36 | 5 | 33 | 296 | 22 July 2013 | 34.53 | 104.18 | 5.4 | 10 |
| 107 | 24 June 1985 | 33.91 | 104.38 | 5 | 33 | 297 | 19 September 2013 | 37.75 | 101.51 | 5 | 21 |
| 108 | 11 August 1985 | 36.13 | 95.63 | 5.2 | 33 | 298 | 4 October 2013 | 32.01 | 104.48 | 5 | 10 |
| 109 | 20 August 1985 | 41.66 | 90.35 | 5.4 | 33 | 299 | 27 April 2014 | 38.41 | 93.04 | 5.1 | 17 |
| 110 | 20 August 1986 | 34.57 | 91.63 | 6.4 | 33 | 300 | 9 June 2014 | 32.5 | 105.18 | 5 | 17 |
| 111 | 26 August 1986 | 37.69 | 101.72 | 8.1 | 23 | 301 | 2 October 2014 | 36.37 | 97.77 | 5.1 | 12 |
| 112 | 26 August 1986 | 37.68 | 101.59 | 5.4 | 10 | 302 | 15 April 2015 | 39.75 | 106.4 | 5.4 | 10 |
| 113 | 26 August 1986 | 37.72 | 101.5 | 6 | 8 | 303 | 12 October 2015 | 34.3 | 98.23 | 5.1 | 11 |
| 114 | 16 August 1986 | 37.75 | 101.64 | 5.3 | 18 | 304 | 22 November 2015 | 37.99 | 100.35 | 5.1 | 13 |
| 115 | 16 September 1986 | 37.76 | 101.73 | 5.3 | 19 | 305 | 13 January 2016 | 32.65 | 91.63 | 5.2 | 10 |
| 116 | 9 November 1986 | 33.99 | 96.32 | 5 | 10 | 306 | 20 January 2016 | 37.64 | 101.59 | 5 | 10 |
| 117 | 20 November 1986 | 32.58 | 93.01 | 5 | 33 | 307 | 20 January 2016 | 37.67 | 101.64 | 5.9 | 9 |
| 118 | 20 November 1986 | 32.65 | 93.12 | 5.1 | 33 | 308 | 23 February 2016 | 32.06 | 95.04 | 5.1 | 10 |
| 119 | 22 November 1986 | 32.19 | 94.59 | 5 | 33 | 309 | 11 May 2016 | 32.02 | 95.03 | 5.2 | 8 |
| 120 | 20 December 1986 | 36.75 | 93.66 | 5.3 | 33 | 310 | 13 August 2016 | 37.71 | 101.55 | 5.2 | 21 |
| 121 | 7 January 1987 | 34.26 | 103.41 | 5.4 | 33 | 311 | 17 October 2016 | 32.9 | 94.88 | 5.9 | 35 |
| 122 | 25 February 1987 | 38.14 | 91.22 | 5 | 33 | 312 | 17 November 2016 | 32.69 | 96.15 | 5 | 10 |
| 123 | 25 February 1987 | 38.1 | 91.18 | 5.8 | 26 | 313 | 4 December 2016 | 32.42 | 92.12 | 5.2 | 10 |
| 124 | 10 August 1987 | 38.12 | 106.36 | 5.3 | 10 | 314 | 14 December 2016 | 38.58 | 90.05 | 5.1 | 10 |
| 125 | 3 January 1988 | 38.11 | 106.34 | 5.2 | 14 | 315 | 8 August 2017 | 33.19 | 103.86 | 6.5 | 9 |
| 126 | 10 January 1988 | 38.17 | 106.36 | 5.1 | 10 | 316 | 30 September 2017 | 32.28 | 105.04 | 5.1 | 10 |
| 127 | 5 November 1988 | 34.35 | 91.88 | 6.2 | 8 | 317 | 12 October 2017 | 32.07 | 95.05 | 5.1 | 10 |
| 128 | 25 November 1988 | 34.33 | 91.93 | 5.6 | 25 | 318 | 31 October 2017 | 34.91 | 103.29 | 5 | 10 |
| 129 | 26 December 1988 | 39.01 | 99.94 | 5.1 | 10 | 319 | 14 December 2017 | 35.15 | 101.88 | 5 | 9 |
| 130 | 1 March 1989 | 31.49 | 102.46 | 5 | 33 | 320 | 6 April 2018 | 34.56 | 96.52 | 5 | 18 |
| 131 | 13 May 1989 | 35.22 | 91.58 | 5.3 | 33 | 321 | 17 June 2018 | 38.86 | 94.92 | 5 | 10 |
| 132 | 22 September 1989 | 31.58 | 102.43 | 6.1 | 15 | 322 | 3 August 2018 | 34.94 | 92.16 | 5.2 | 19 |
| 133 | 2 November 1989 | 36.04 | 106.23 | 5 | 10 | 323 | 12 September 2018 | 32.72 | 105.66 | 5 | 10 |
| 134 | 14 January 1990 | 37.82 | 91.97 | 6 | 12 | 324 | 20 February 2019 | 38.47 | 97.21 | 5 | 10 |
| 135 | 5 February 1990 | 32.08 | 98.32 | 5 | 10 | 325 | 27 April 2019 | 39.14 | 97.4 | 5 | 20 |
| 136 | 26 April 1990 | 36.05 | 100.33 | 6.2 | 10 | 326 | 16 September 2019 | 38.57 | 100.25 | 5.1 | 17 |
| 137 | 26 April 1990 | 36.24 | 100.25 | 6.3 | 10 | 327 | 27 October 2019 | 35.07 | 102.68 | 5.3 | 10 |
| 138 | 26 April 1990 | 36.04 | 100.27 | 6.3 | 10 | 328 | 9 December 2019 | 31.72 | 104.32 | 5 | 10 |
| 139 | 26 April 1990 | 35.99 | 100.25 | 6.5 | 8 | 329 | 24 January 2020 | 32 | 95.06 | 5.2 | 10 |
| 140 | 7 May 1990 | 36.03 | 100.34 | 5.3 | 33 | 330 | 1 April 2020 | 33.13 | 98.91 | 5.4 | 10 |
| 141 | 15 May 1990 | 36.11 | 100.12 | 5.3 | 14 | 331 | 21 October 2020 | 31.92 | 104.23 | 5.2 | 10 |
| 142 | 2 June 1990 | 32.43 | 92.8 | 5.2 | 13 | 332 | 22 October 2020 | 31.95 | 104.24 | 5.3 | 10 |
| 143 | 2 October 1990 | 32.53 | 94.03 | 5 | 32 | 333 | 19 March 2021 | 31.92 | 92.92 | 5.7 | 8 |
| 144 | 20 October 1990 | 37.09 | 103.78 | 5.7 | 12 | 334 | 22 March 2021 | 31.97 | 92.91 | 5 | 10 |
| 145 | 2 January 1991 | 38.15 | 99.96 | 5.1 | 13 | 335 | 6 April 2021 | 31.87 | 92.91 | 5 | 10 |
| 146 | 13 January 1991 | 40.56 | 105.79 | 5.6 | 16 | 336 | 21 May 2021 | 34.58 | 98.3 | 5.2 | 10 |
| 147 | 15 June 1991 | 38.93 | 105.6 | 5.1 | 28 | 337 | 21 May 2021 | 34.62 | 98.47 | 5.5 | 10 |
| 148 | 2 September 1991 | 37.44 | 95.4 | 5.5 | 10 | 338 | 21 May 2021 | 34.48 | 99.08 | 5.5 | 10 |
| 149 | 14 September 1991 | 40.17 | 105.05 | 5.1 | 25 | 339 | 21 May 2021 | 34.6 | 98.25 | 7.3 | 10 |
| 150 | 20 September 1991 | 36.19 | 100.06 | 5.5 | 13 | 340 | 22 May 2021 | 34.95 | 97.47 | 5.1 | 10 |
| 151 | 30 September 1991 | 37.77 | 101.32 | 5.3 | 20 | 341 | 22 May 2021 | 34.55 | 98.94 | 5.1 | 10 |
| 152 | 12 January 1992 | 39.67 | 98.3 | 5.2 | 22 | 342 | 22 May 2021 | 34.75 | 98.09 | 5.2 | 10 |
| 153 | 23 January 1992 | 34.57 | 93.16 | 5.2 | 33 | 343 | 27 May 2021 | 34.47 | 99.11 | 5.1 | 10 |
| 154 | 16 May 1992 | 36.08 | 99.87 | 5 | 17 | 344 | 30 May 2021 | 34.59 | 98.33 | 5 | 10 |
| 155 | 21 June 1992 | 38.31 | 99.42 | 5 | 20 | 345 | 30 May 2021 | 34.62 | 98.2 | 5.1 | 10 |
| 156 | 20 December 1992 | 37.06 | 96.48 | 5 | 20 | 346 | 3 June 2021 | 34.69 | 97.8 | 5 | 10 |
| 157 | 27 April 1993 | 32.98 | 96.05 | 5 | 33 | 347 | 16 June 2021 | 38.21 | 93.72 | 5.5 | 10 |
| 158 | 4 September 1993 | 37.21 | 94.53 | 5 | 17 | 348 | 8 July 2021 | 34.68 | 97.92 | 5.1 | 10 |
| 159 | 4 September 1993 | 37.19 | 94.61 | 5.1 | 18 | 349 | 13 August 2021 | 34.59 | 97.42 | 5.4 | 14 |
| 160 | 5 September 1993 | 37.19 | 94.64 | 5.1 | 17 | 350 | 13 August 2021 | 34.58 | 97.54 | 5.8 | 8 |
| 161 | 26 October 1993 | 38.48 | 98.66 | 5.9 | 8 | 351 | 25 August 2021 | 38.91 | 95.53 | 5.3 | 10 |
| 162 | 3 January 1994 | 36.03 | 100.1 | 5.7 | 8 | 352 | 26 August 2021 | 38.88 | 95.5 | 5.5 | 15 |
| 163 | 15 February 1994 | 36.1 | 100.16 | 5.6 | 20 | 353 | 18 December 2021 | 38.93 | 92.61 | 5.5 | 10 |
| 164 | 29 June 1994 | 32.57 | 93.67 | 5.9 | 10 | 354 | 19 December 2021 | 38.95 | 92.73 | 5.3 | 10 |
| 165 | 30 June 1994 | 32.54 | 93.68 | 5.1 | 33 | 355 | 29 December 2021 | 37.01 | 94.67 | 5 | 10 |
| 166 | 24 August 1994 | 34.25 | 91.81 | 5.5 | 33 | 356 | 7 January 2022 | 37.73 | 101.13 | 5.1 | 10 |
| 167 | 4 September 1994 | 35.94 | 100.08 | 5.2 | 10 | 357 | 7 January 2022 | 37.82 | 101.28 | 6.6 | 13 |
| 168 | 7 September 1994 | 38.49 | 90.35 | 5.2 | 33 | 358 | 8 January 2022 | 37.78 | 101.24 | 5.1 | 12 |
| 169 | 23 September 1994 | 36.05 | 100.15 | 5.3 | 33 | 359 | 8 January 2022 | 37.77 | 101.26 | 6.9 | 10 |
| 170 | 10 October 1994 | 36.06 | 100.16 | 5.1 | 33 | 360 | 12 January 2022 | 37.72 | 101.51 | 5 | 10 |
| 171 | 28 December 1994 | 35.83 | 90.74 | 5.2 | 33 | 361 | 12 January 2022 | 37.7 | 101.41 | 5.3 | 10 |
| 172 | 12 June 1995 | 39.22 | 95.29 | 5.1 | 24 | 362 | 12 January 2022 | 37.69 | 101.49 | 5.2 | 10 |
| 173 | 9 July 1995 | 35.98 | 100.07 | 5.1 | 33 | 363 | 23 January 2022 | 38.44 | 97.37 | 5.8 | 8 |
| 174 | 21 July 1995 | 36.43 | 103.12 | 5.6 | 13 | 364 | 17 March 2022 | 39.02 | 97.66 | 5.1 | 9 |
| 175 | 5 November 1995 | 32.9 | 92.2 | 5.1 | 24 | 365 | 26 March 2022 | 38.5 | 97.33 | 6 | 10 |
| 176 | 18 December 1995 | 34.51 | 97.35 | 5.7 | 33 | 366 | 15 April 2022 | 38.52 | 97.33 | 5.4 | 10 |
| 177 | 20 December 1995 | 34.49 | 97.47 | 5 | 33 | 367 | 10 June 2022 | 32.24 | 101.85 | 5.2 | 15 |
| 178 | 3 May 1996 | 40.77 | 109.66 | 6 | 26 | 368 | 10 June 2022 | 32.25 | 101.82 | 6 | 13 |
| 179 | 1 June 1996 | 37.36 | 102.8 | 5.2 | 10 | 369 | 10 June 2022 | 32.27 | 101.82 | 5.8 | 10 |
| 180 | 20 November 1996 | 39.6 | 96.68 | 5.8 | 33 | 370 | 24 June 2022 | 41.73 | 90.67 | 5.1 | 25 |
| 181 | 6 January 1997 | 37.04 | 97.84 | 5 | 33 | 371 | 14 August 2022 | 33.14 | 92.85 | 5.9 | 10 |
| 182 | 9 February 1997 | 35.69 | 95.82 | 5.5 | 10 | 372 | 19 October 2022 | 37.69 | 92.3 | 5.5 | 11 |
| 183 | 29 May 1999 | 32.89 | 93.77 | 5.4 | 33 | 373 | 22 December 2022 | 35.56 | 99.14 | 5 | 9 |
| 184 | 27 September 1999 | 34.62 | 101.44 | 5 | 33 | 374 | 24 October 202 | 39.43 | 97.28 | 5.5 | 10 |
| 185 | 5 January 2000 | 32.22 | 92.7 | 5.5 | 33 | 375 | 1 December 2023 | 39.3 | 97.27 | 5 | 9 |
| 186 | 12 February 2000 | 34 | 90.85 | 5.1 | 33 | 376 | 18 December 2023 | 35.7 | 102.79 | 6.2 | 10 |
| 187 | 15 April 2000 | 32.96 | 95.48 | 5.2 | 33 | 377 | 5 March 2024 | 33.52 | 93.01 | 5.3 | 10 |
| 188 | 6 June 2000 | 37.01 | 103.79 | 5.6 | 10 | 378 | 7 March 2024 | 33.58 | 93.01 | 5.5 | 10 |
| 189 | 10 July 2000 | 32.8 | 92.2 | 5.4 | 33 | 379 | 4 April 2024 | 38.39 | 90.93 | 5.5 | 10 |
| 190 | 12 September 2000 | 35.36 | 99.38 | 5 | 10 |
| NO. | Date | Lat./(°) | Lon./(°) | Ms | Depth/(km) | ΔF/(nT) | ΔH/(nT) | ΔX/(nT) | ΔY/(nT) | ΔZ/(nT) | ΔD/(°) | ΔI/(°) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bayan Har Block | ||||||||||||
| 1 | 26 July 1935 | 33.17 | 100.94 | 6.2 | 15 | 9.3 | −1.2 | −2.1 | −21.7 | 13.3 | −2.4 | 0.6 |
| 2 | 7 February 1936 | 35.44 | 103.19 | 6.8 | 15 | 12.5 | 6 | 6.1 | 45.4 | 12 | 5 | 0.1 |
| 3 | 7 January 1937 | 35.43 | 97.76 | 7.8 | 15 | 61.1 | 11.1 | 10.4 | −34.2 | 67.7 | −3.8 | 2 |
| 4 | 17 March 1947 | 33.48 | 99.53 | 7.3 | 15 | −3.4 | 5.3 | 5.4 | 16.1 | −8.5 | 1.7 | −0.6 |
| 5 | 5 October 1952 | 37.01 | 93.2 | 6.1 | 15 | −63.8 | −15.7 | −17.2 | 7.8 | −65.3 | 0.9 | −1.3 |
| 6 | 21 June 1962 | 36.93 | 95.93 | 6.6 | 17 | −23.9 | 11.4 | 11.7 | 0.4 | −36.7 | −0.2 | −1.8 |
| 7 | 19 April 1963 | 35.61 | 96.99 | 6.7 | 20 | 3.1 | −2.2 | −2.8 | 17.5 | 5.9 | 1.9 | 0.4 |
| 8 | 24 March 1971 | 35.45 | 98.14 | 6 | 10 | 10.7 | −7.6 | −7.7 | −15 | 18.6 | −1.7 | 1.1 |
| 9 | 12 September 2000 | 35.39 | 99.34 | 6.1 | 10 | 26.7 | 13.2 | 13.2 | −25 | 23.2 | −2.8 | 0.2 |
| 10 | 14 November 2001 | 35.95 | 90.54 | 8.1 | 10 | 2.1 | 13.1 | 12.2 | −17.4 | −5.8 | −1.9 | −0.9 |
| 11 | 17 April 2003 | 37.53 | 96.48 | 6.4 | 14 | −77.8 | −56.4 | −54.6 | −4.4 | −57.3 | −0.9 | 1.1 |
| 12 | 28 August 2009 | 37.7 | 95.72 | 6.3 | 13 | −45.5 | −42.3 | −41.3 | −41.8 | −27.4 | −5.3 | 1.5 |
| 13 | 21 May 2021 | 34.6 | 98.25 | 7.3 | 10 | 14.2 | 14.6 | 13.7 | −24.5 | 7.2 | −2.6 | −0.4 |
| 14 | 28 December 2023 | 35.7 | 102.79 | 6.2 | 10 | 24.3 | −34.8 | −37.1 | −31.5 | 55.7 | −3.7 | 3.9 |
| Qilian Orogen | ||||||||||||
| 15 | 25 December 1920 | 37.24 | 105.48 | 6.8 | 15 | −14.4 | −1.2 | −2.6 | −9.8 | −15.9 | −1.1 | −0.4 |
| 16 | 22 May 1927 | 37.65 | 102.49 | 8 | 15 | −54.6 | −16.6 | −16.4 | −0.9 | −54.5 | 0 | −0.9 |
| 17 | 7 March 1928 | 37.67 | 102.13 | 6.2 | 15 | −20.5 | −18.6 | −18 | −1.3 | −12.8 | 0 | 0.6 |
| 18 | 13 July 1930 | 37.97 | 98.26 | 6.5 | 10 | 1.5 | 8.4 | 11.5 | −11.5 | −5.6 | −1.5 | −0.7 |
| 19 | 25 December 1932 | 39.5 | 96.62 | 7.9 | 15 | −7.1 | −22.7 | −20 | 14.5 | 3.7 | 1.3 | 1.2 |
| 20 | 26 December 1951 | 39.49 | 95.53 | 6.2 | 15 | 86.7 | 51.8 | 51.8 | 20.4 | 69.9 | 2 | 0.7 |
| 21 | 23 January 1952 | 39.73 | 95.44 | 6 | 35 | 18.3 | −5.7 | −3 | −15.8 | 23 | −2.5 | 1 |
| 22 | 11 February 1954 | 38.96 | 101.22 | 7 | 25 | −2 | 33.6 | 34.8 | 9.9 | −23.3 | 1.7 | −2.6 |
| 23 | 31 July 1954 | 38.62 | 104.15 | 6.9 | 25 | 79.9 | −12.8 | −15 | −53.1 | 102.1 | −6.3 | 4.1 |
| 24 | 26 August 1986 | 37.72 | 101.5 | 8.1 | 8 | −29.5 | −19.4 | −18.6 | −22 | −23.4 | −2.4 | 0.2 |
| 25 | 14 January 1990 | 37.82 | 91.97 | 6 | 12 | 8.2 | 15 | 14.5 | 16.1 | 0.3 | 2.1 | −0.7 |
| 26 | 26 April 1990 | 36.05 | 100.33 | 6.2 | 10 | −15.1 | 9.3 | 10 | −11.9 | −25.7 | −1.3 | −1.4 |
| 27 | 26 April 1990 | 36.24 | 100.25 | 6.3 | 10 | −13 | 9.4 | 10 | −10 | −23.1 | −1.1 | −1.3 |
| 28 | 26 April 1990 | 36.04 | 100.27 | 6.3 | 10 | −3.1 | 18.2 | 19 | −12.3 | −17.2 | −1.3 | −1.5 |
| 29 | 26 April 1990 | 35.99 | 100.25 | 6.5 | 8 | 6.7 | 18.1 | 18.9 | −15 | −5.2 | −1.6 | −1.1 |
| 30 | 7 January 2022 | 37.82 | 101.28 | 6.6 | 13 | −20.8 | −1.5 | −0.2 | −0.5 | −24.6 | 0.2 | −0.8 |
| 31 | 8 January 2022 | 37.77 | 101.26 | 6.9 | 10 | −30 | −14.1 | −12.9 | −12.4 | −27.5 | −1.3 | −0.2 |
| 32 | 26 March 2022 | 38.5 | 97.33 | 6 | 10 | −0.2 | −31.9 | −28.8 | −20.6 | 17.6 | −2.8 | 2.2 |
| 33 | 16 December 1920 | 36.89 | 105.61 | 8.5 | 15 | −31 | −9.2 | −10.7 | −6.3 | −30.4 | −0.7 | −0.5 |
| Qiangtang Block | ||||||||||||
| 34 | 24 March 1923 | 31.3 | 100.75 | 7 | 15 | −0.2 | 9.3 | 8.2 | −38.5 | −8.2 | −4.1 | −0.8 |
| 35 | 25 August 1933 | 32.01 | 103.68 | 7.3 | 15 | −41.7 | −20.5 | −19.8 | 19.6 | −37.5 | 1.9 | −0.7 |
| 36 | 21 August 1950 | 33.04 | 91.48 | 6 | 15 | 13 | 10.1 | 11.3 | −12.6 | 7.7 | −1.4 | −0.2 |
| 37 | 28 December 1951 | 31.06 | 91.26 | 7.7 | 30 | 40.1 | 22.8 | 22.4 | 7.3 | 33.7 | 0.6 | 0.5 |
| 38 | 26 December 1951 | 31.24 | 90.78 | 6.3 | 15 | 22.7 | 39.4 | 42.1 | −13.8 | 1.4 | −2.2 | −2.1 |
| 39 | 14 October 1952 | 34.35 | 91.86 | 6 | 15 | −11.1 | 10 | 9.7 | −9.6 | −21.3 | −1.1 | −1.4 |
| 40 | 31 October 1952 | 33.22 | 101.16 | 6.2 | 15 | 1.8 | 5.2 | 3.9 | −33.9 | −1.5 | −3.7 | −0.3 |
| 41 | 23 April 1953 | 31.05 | 96.87 | 6 | 10 | −13.5 | 19.8 | 21.1 | 18.9 | −37.2 | 2.2 | −2.7 |
| 42 | 4 December 1961 | 33.34 | 95.25 | 6.1 | 16 | −48.9 | −58 | −59.2 | −49.3 | −15.2 | −5.3 | 2.3 |
| 43 | 30 August 1967 | 31.63 | 100.26 | 6.4 | 10 | 15.1 | 10.1 | 9.9 | −13.2 | 11.3 | −1.5 | 0 |
| 44 | 6 February 1973 | 31.4 | 100.58 | 7.4 | 33 | 6.7 | 1.5 | 1.8 | 3.3 | 7.4 | 0.2 | 0.3 |
| 45 | 5 May 1975 | 33.09 | 92.92 | 6.1 | 33 | −5.7 | 17.9 | 18.1 | 22.2 | −22.1 | 2.2 | −1.8 |
| 46 | 1 January 1977 | 38.15 | 91.01 | 6.3 | 27 | −26.8 | 12.9 | 13.4 | −2.7 | −40.1 | −0.1 | −2 |
| 47 | 9 June 1981 | 34.5 | 91.44 | 6 | 10 | −7.4 | 1.7 | 1.6 | −5.8 | −10.5 | −0.6 | −0.5 |
| 48 | 20 August 1986 | 34.57 | 91.63 | 6.4 | 33 | −4.9 | 9.3 | 8.8 | −0.2 | −12.8 | 0 | −1 |
| 49 | 5 November 1988 | 34.35 | 91.88 | 6.2 | 8 | −10.8 | 5 | 4.8 | −8.7 | −17.2 | −1 | −0.9 |
| 50 | 13 April 2010 | 33.17 | 96.55 | 6.9 | 17 | −44.6 | −34.3 | −35 | −11.5 | −29.2 | −1.1 | 0.5 |
| 51 | 14 April 2010 | 33.2 | 96.45 | 6.1 | 8 | −38.5 | −38.5 | −39.3 | −17 | −17.8 | −1.7 | 1.2 |
| Songpan−Ganzi Plateau | ||||||||||||
| 52 | 7 February 1958 | 31.46 | 104.01 | 6 | 25 | −203.5 | −148.6 | −146.6 | 66 | −140.5 | 6.3 | 1.2 |
| 53 | 9 November 1960 | 32.71 | 103.63 | 6.3 | 25 | −43.4 | −7.3 | −6.5 | 28.5 | −50.3 | 2.9 | −1.8 |
| 54 | 11 August 1973 | 33 | 104.02 | 6.1 | 33 | −9.7 | 3.3 | 4.2 | 32.4 | −15.1 | 3.4 | −0.9 |
| 55 | 16 August 1976 | 32.75 | 104.16 | 6.9 | 16 | 7.1 | 12.5 | 12.5 | 4.5 | −1 | 0.5 | −0.8 |
| 56 | 21 August 1976 | 32.57 | 104.25 | 6.4 | 33 | −22 | 30.9 | 30.4 | −13 | −54.5 | −1.2 | −4 |
| 57 | 23 August 1976 | 32.49 | 104.18 | 6.7 | 33 | −37.3 | 11.5 | 11 | −14.1 | −58.4 | −1.4 | −3.2 |
| 58 | 22 September 1989 | 31.58 | 102.43 | 6.1 | 15 | −63.9 | −30.8 | −31.4 | −6.4 | −57.6 | −0.9 | −1 |
| 59 | 8 August 2017 | 33.19 | 103.86 | 6.5 | 9 | −15 | 7.5 | 8.3 | 34.8 | −25.1 | 3.7 | −1.5 |
| 60 | 10 June 2022 | 32.25 | 101.82 | 6 | 13 | −21.8 | 8.6 | 7.3 | −39.3 | −35.5 | −4.3 | −2 |
| Ordos Block | ||||||||||||
| 61 | 20 January 1934 | 41.14 | 108.62 | 6.3 | 15 | 12.8 | 41.8 | 44.4 | 12.8 | −9.5 | 2.2 | −2.6 |
| 62 | 3 May 1996 | 40.77 | 109.66 | 6 | 26 | −149.9 | −50.1 | −46.4 | 36.8 | −144.6 | 4.5 | −1.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, G.; Li, Y.; Kang, G.; Bai, C.; Wen, L. Regional Seismicity of the Northeastern Tibetan Plateau Revealed by Crustal Magnetic Anomalies. Appl. Sci. 2025, 15, 4331. https://doi.org/10.3390/app15084331
Gao G, Li Y, Kang G, Bai C, Wen L. Regional Seismicity of the Northeastern Tibetan Plateau Revealed by Crustal Magnetic Anomalies. Applied Sciences. 2025; 15(8):4331. https://doi.org/10.3390/app15084331
Chicago/Turabian StyleGao, Guoming, Yecheng Li, Guofa Kang, Chunhua Bai, and Limin Wen. 2025. "Regional Seismicity of the Northeastern Tibetan Plateau Revealed by Crustal Magnetic Anomalies" Applied Sciences 15, no. 8: 4331. https://doi.org/10.3390/app15084331
APA StyleGao, G., Li, Y., Kang, G., Bai, C., & Wen, L. (2025). Regional Seismicity of the Northeastern Tibetan Plateau Revealed by Crustal Magnetic Anomalies. Applied Sciences, 15(8), 4331. https://doi.org/10.3390/app15084331





