Spectrum Allocation and Power Control Based on Newton’s Method for Weighted Sum Power Minimization in Overlay Spectrum Sharing
Abstract
1. Introduction
1.1. Background
1.2. Related Work
1.3. Motivation, Contribution, and Organization
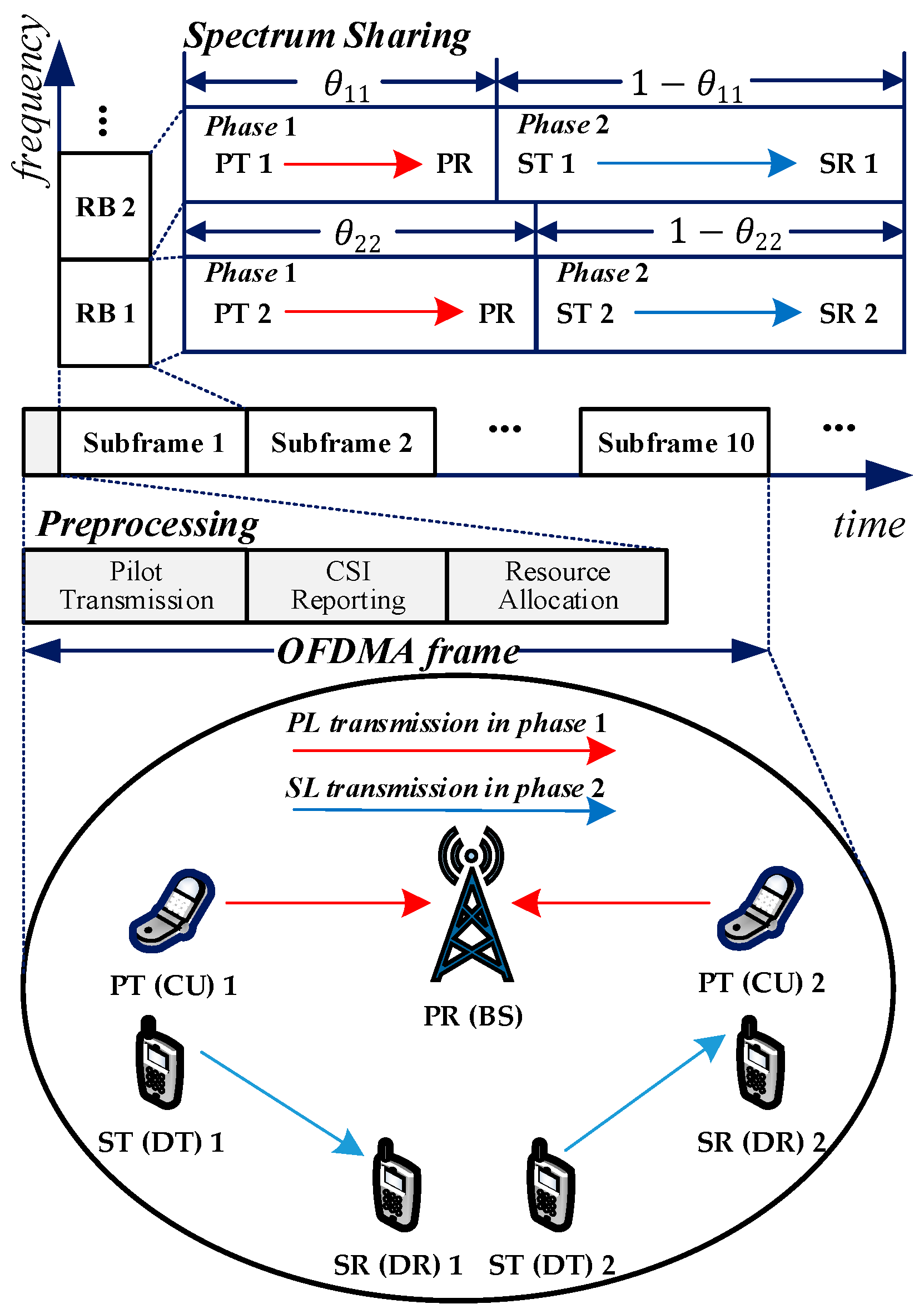
2. System Model and Problem Formulation
3. The Proposed Scheme for WSP Minimization
3.1. Spectrum and Power Allocation Based on Newton’s Method for a Matched PL-SL PAIR
- Case 1
- Case 2
- Case 3
- Case 4
3.2. Link Matching for Multiple PLs and SLs
3.3. Discussion of the Initial Value Selection of Newton’s Method and Weight Adjustment
3.4. Practical Deployment Limitations
4. Simulation and Discussion
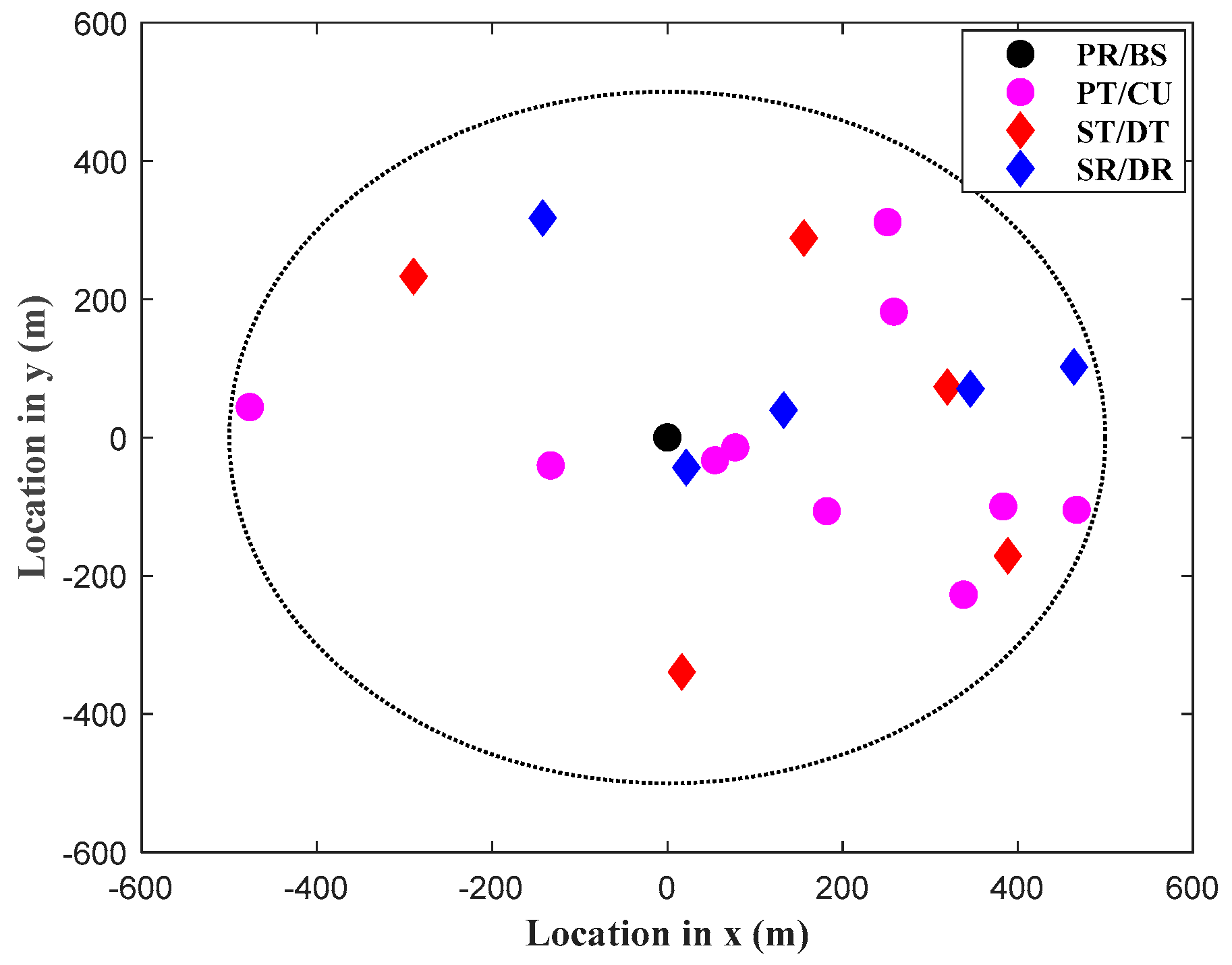
4.1. Simulation Setup and Baseline Schemes
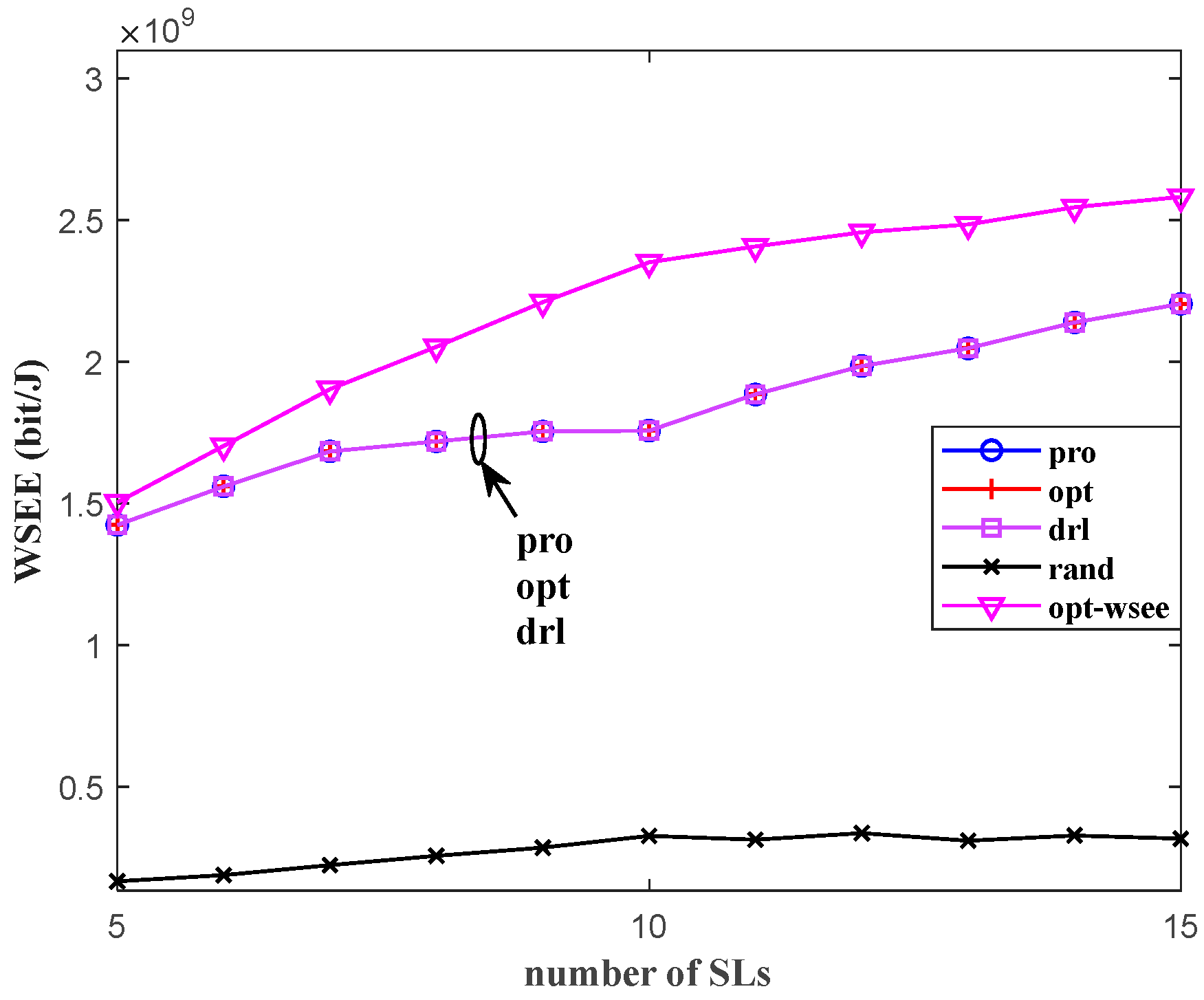
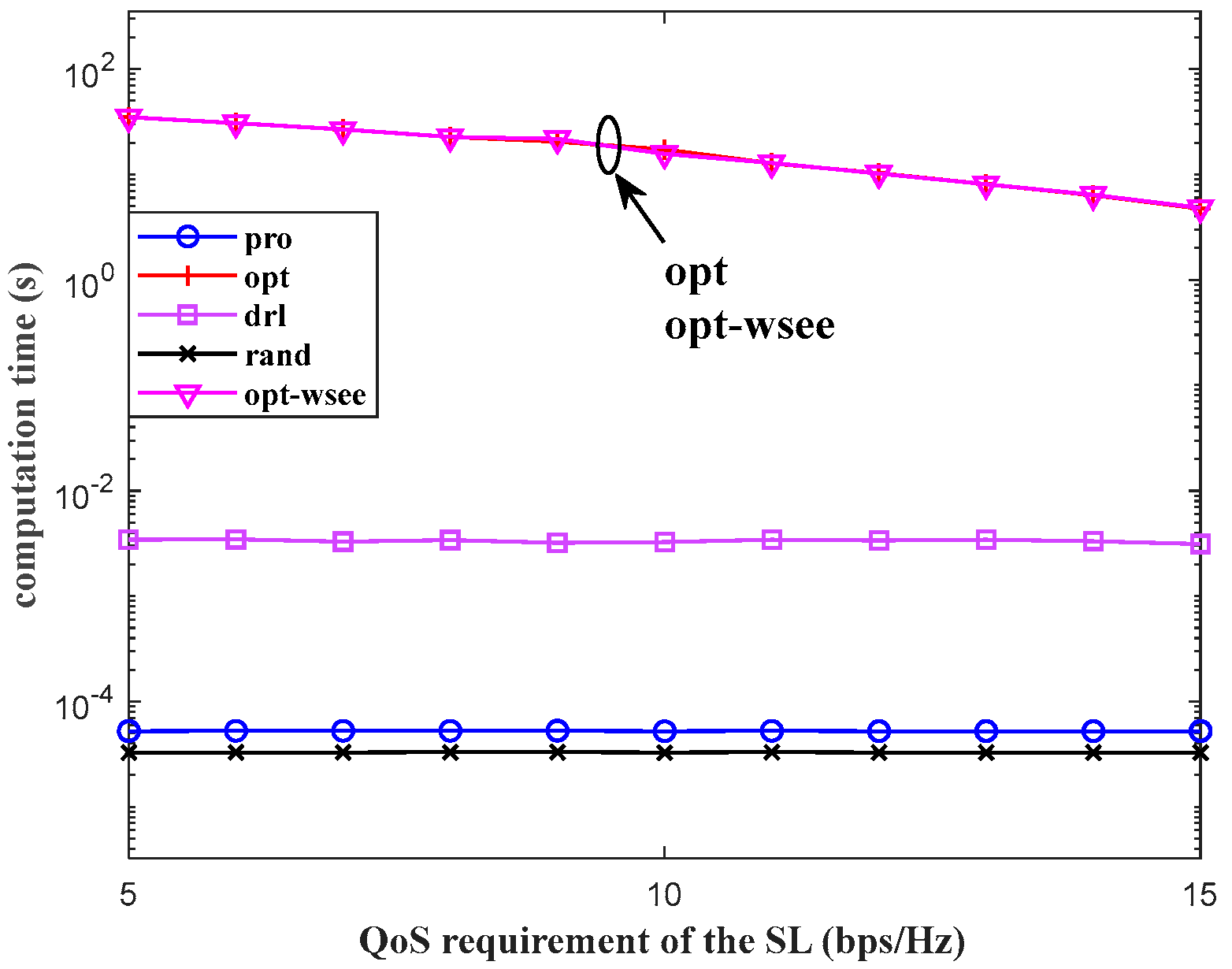
4.2. Performance Analysis for Multiple Links
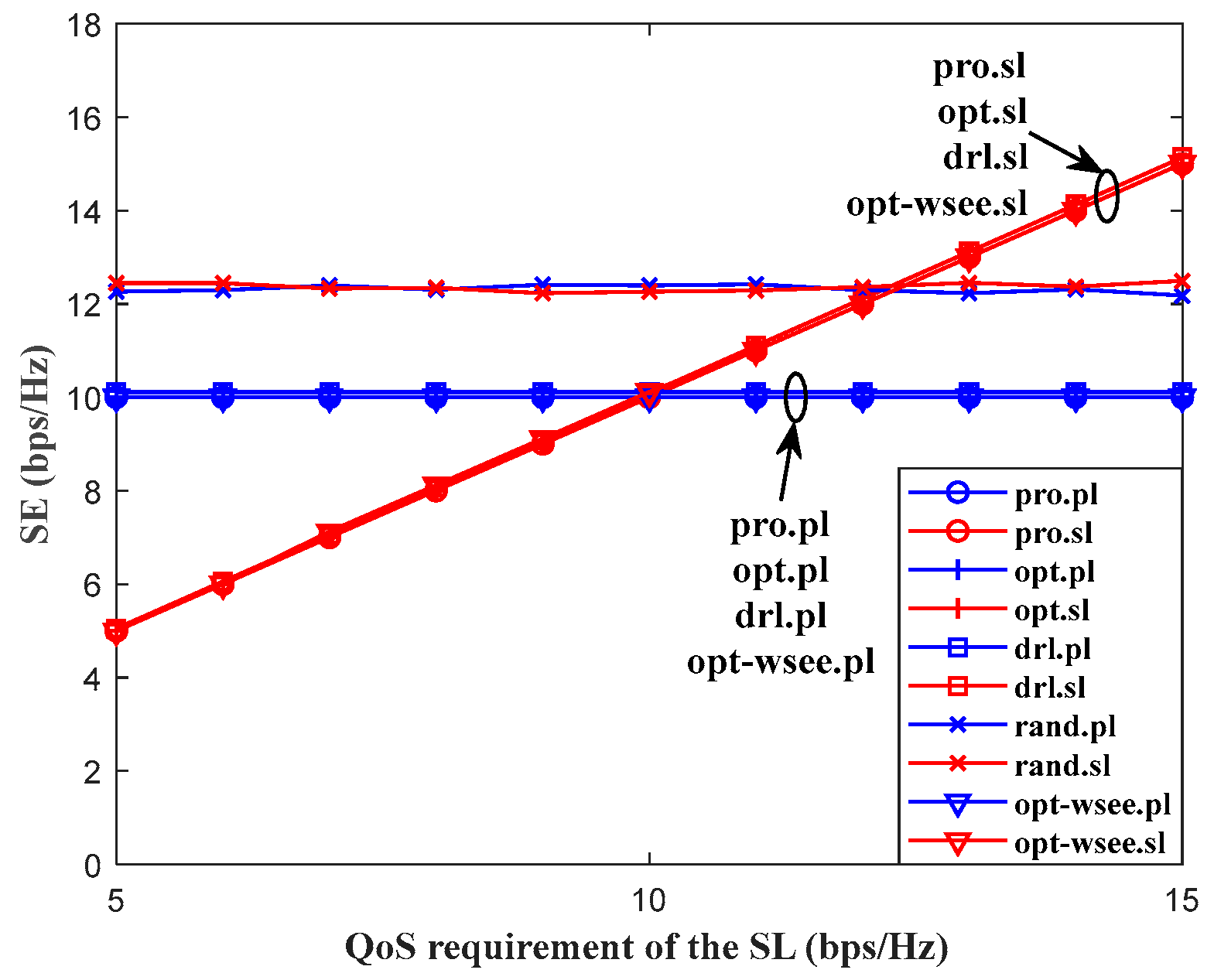
4.3. Performance Analysis for a Single Link Pair
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chowdhury, M.Z.; Shahjalal, M.; Ahmed, S.; Jang, Y.M. 6G Wireless Communication Systems: Applications, Requirements, Technologies, Challenges, and Research Directions. IEEE Open J. Commun. Soc. 2020, 1, 957–975. [Google Scholar] [CrossRef]
- Tehrani, R.H.; Vahid, S.; Triantafyllopoulou, D.; Lee, H.; Moessner, K. Licensed Spectrum Sharing Schemes for Mobile Operators: A Survey and Outlook. IEEE Commun. Surveys Tuts. 2016, 18, 2591–2623. [Google Scholar] [CrossRef]
- Womersley, R. The Future Outlook for Spectrum Sharing. In Spectrum Sharing: The Next Frontier in Wireless Networks; Wiley-IEEE Press: Hoboken/Piscataway, NJ, USA, 2019; pp. 389–404. [Google Scholar] [CrossRef]
- Haykin, S. Cognitive radio: Brain-empowered wireless communications. IEEE J. Sel. Areas Commun. 2005, 23, 201–220. [Google Scholar] [CrossRef]
- Tsiropoulos, G.I.; Dobre, O.A.; Ahmed, M.H.; Baddour, K.E. Radio Resource Allocation Techniques for Efficient Spectrum Access in Cognitive Radio Networks. IEEE Commun. Surv. Tuts. 2016, 18, 824–847. [Google Scholar] [CrossRef]
- Laneman, J.N.; Tse, D.N.C.; Wornell, G.W. Cooperative diversity in wireless networks: Efficient protocols and outage behavior. IEEE Trans. Inform. Theory 2004, 50, 3062–3080. [Google Scholar] [CrossRef]
- Zhang, Q.; Jia, J.; Zhang, J. Cooperative relay to improve diversity in cognitive radio networks. IEEE Commun. Mag. 2009, 47, 111–117. [Google Scholar] [CrossRef]
- Leaves, P.; Moessner, K.; Tafazolli, R.; Grandblaise, D.; Bourse, D.; Tonjes, R.; Breveglieri, M. Dynamic spectrum allocation in composite reconfigurable wireless networks. IEEE Commun. Mag. 2004, 42, 72–81. [Google Scholar] [CrossRef]
- Abode, D.; Adeogun, R.; Berardinelli, G. Power Control for 6G In-Factory Subnetworks with Partial Channel Information Using Graph Neural Networks. IEEE Open J. Commun. Soc. 2024, 5, 3120–3135. [Google Scholar] [CrossRef]
- Mao, B.; Tang, F.; Kawamoto, Y.; Kato, N. AI Models for Green Communications Towards 6G. IEEE Commun. Surv. Tutor. 2022, 24, 210–247. [Google Scholar] [CrossRef]
- Zappone, A.; Sanguinetti, L.; Bacci, G.; Jorswieck, E.; Debbah, M. Energy-Efficient Power Control: A Look at 5G Wireless Technologies. IEEE Trans. Signal Process. 2016, 64, 1668–1683. [Google Scholar] [CrossRef]
- Cao, Y.; Jiang, T.; Wang, C. Cooperative device-to-device communications in cellular networks. IEEE Wireless Commun. 2015, 22, 124–129. [Google Scholar] [CrossRef]
- Le, Q.N.; Yadav, A.; Nguyen, N.-P.; Dobre, O.A.; Zhao, R. Full-Duplex Non-Orthogonal Multiple Access Cooperative Overlay Spectrum-Sharing Networks With SWIPT. IEEE Trans. Green Commun. 2021, 5, 322–334. [Google Scholar] [CrossRef]
- Zappone, A.; Matthiesen, B.; Jorswieck, E.A. Energy Efficiency in MIMO Underlay and Overlay Device-to-Device Communications and Cognitive Radio Systems. IEEE Trans. Signal Process. 2017, 65, 1026–1041. [Google Scholar] [CrossRef]
- Xiao, H.; Jiang, H.; Shi, F.; Luo, Y.; Deng, L.; Mukherjee, M.; Piran, M.J. Energy-Efficient Resource Allocation in Radio-Frequency-Powered Cognitive Radio Network for Connected Vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 22, 5426–5436. [Google Scholar] [CrossRef]
- Wu, Q.; Li, G.Y.; Chen, W.; Ng, D.W.K. Energy-Efficient D2D Overlaying Communications with Spectrum-Power Trading. IEEE Trans. Wireless Commun. 2017, 16, 4404–4419. [Google Scholar] [CrossRef]
- Duan, L.; Gao, L.; Huang, J. Cooperative Spectrum Sharing: A Contract-Based Approach. IEEE Trans. Mob. Comput. 2014, 13, 174–187. [Google Scholar] [CrossRef]
- Lu, W.; Hu, S.; Liu, X.; He, C.; Gong, Y. Incentive Mechanism Based Cooperative Spectrum Sharing for OFDM Cognitive IoT Network. IEEE Trans. Netw. Sci. Eng. 2020, 7, 662–672. [Google Scholar] [CrossRef]
- Yuan, Y.; Yang, T.; Hu, Y.; Feng, H.; Hu, B. Two-Timescale Resource Allocation for Cooperative D2D Communication: A Matching Game Approach. IEEE Trans. Veh. Technol. 2021, 70, 543–557. [Google Scholar] [CrossRef]
- Lyu, J.; Chew, Y.H.; Wong, W.-C. A Stackelberg Game Model for Overlay D2D Transmission with Heterogeneous Rate Requirements. IEEE Trans. Vehi. Technol. 2016, 65, 8461–8475. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, C.-Y.; Wei, H.-Y. Incentive Compatible Overlay D2D System: A Group-Based Framework without CQI Feedback. IEEE Trans. Mob. Comput. 2018, 17, 2069–2086. [Google Scholar] [CrossRef]
- Zhong, Y.; Ge, X. Toward 6G Carbon-Neutral Cellular Networks. IEEE Netw. 2024, 38, 174–181. [Google Scholar] [CrossRef]
- Stancu-Minasian, I.M. Fractional Programming: Theory Methods and Applications; Kluwer: Norwell, MA, USA, 1992. [Google Scholar]
- Shen, K.; Yu, W. Fractional Programming for Communication Systems—Part I: Power Control and Beamforming. IEEE Trans. Signal Process. 2018, 66, 2616–2630. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, J.; Guo, H.; Qi, M.; Kato, N. Envisioning Device-to-Device Communications in 6G. IEEE Netw. 2020, 34, 86–91. [Google Scholar] [CrossRef]
- Hossain, M.A.; Hossain, A.R.; Ansari, N. AI in 6G: Energy-Efficient Distributed Machine Learning for Multilayer Heterogeneous Networks. IEEE Netw. 2022, 36, 84–91. [Google Scholar] [CrossRef]
- Lee, W.; Lee, K. Deep Learning-Based Energy Efficient Resource Allocation for Underlay Cognitive MISO Interference Channels. IEEE Trans. Cogn. Commun. Netw. 2023, 9, 695–707. [Google Scholar] [CrossRef]
- Ji, Z.; Kiani, A.K.; Qin, Z.; Ahmad, R. Power Optimization in Device-to-Device Communications: A Deep Reinforcement Learning Approach with Dynamic Reward. IEEE Wirel. Commun. Lett. 2021, 10, 508–511. [Google Scholar] [CrossRef]
- Wang, C.-X.; You, X.; Gao, X.; Zhu, X.; Li, Z.; Zhang, C.; Wang, H.; Huang, Y.; Chen, Y.; Haas, H.; et al. On the Road to 6G: Visions, Requirements, Key Technologies, and Testbeds. IEEE Commun. Surv. Tuts. 2023, 25, 905–974. [Google Scholar] [CrossRef]
- Yu, Y.; Tang, X. Weighted Sum Power Minimization for Cooperative Spectrum Sharing in Cognitive Radio Networks. IEEE Commun. Lett. 2025, 29, 160–164. [Google Scholar] [CrossRef]
- 3rd Generation Partnership Project (3GPP). NR; Physical Channels and Modulation (Release 18); Document 3GPP TS 38.211, V18.3.0; 3GPP: Valbonne, France, 2024. [Google Scholar]
- 3rd Generation Partnership Project (3GPP). NR; User Equipment (UE) Radio Transmission and Reception; Part 1: Range 1 Standalone (Release 18); Document 3GPP TS 38.101-1, V18.7.0; 3GPP: Valbonne, France, 2024. [Google Scholar]
- Kota, N.R.; Naidu, K. Minimizing Energy Consumption in H-NOMA Based UAV-Assisted MEC Network. IEEE Commun. Lett. 2023, 27, 2536–2540. [Google Scholar] [CrossRef]
- Rockafellar, R.T. Convex Analysis; Princeton University Press: Princeton, NJ, USA, 1997. [Google Scholar]
- Kincaid, D.; Cheney, W. Numerical Analysis: Mathematics of Scientific Computing, 3rd ed.; Brooks Cole: Pacific Grove, CA, USA, 2002. [Google Scholar]
- Munkres, J. Algorithms for the Assignment and Transportation Problems. J. Soc. Ind. Appl. Math. 1957, 5, 32–38. [Google Scholar] [CrossRef]
- Yu, Y.; Tang, X. Hybrid Centralized-Distributed Resource Allocation Based on Deep Reinforcement Learning for Cooperative D2D Communications. IEEE Access 2024, 12, 196609–196623. [Google Scholar] [CrossRef]
- Arbelaez, A.; Mehta, D.; O’Sullivan, B.; Quesada, L. A constraint-based parallel local search for the edge-disjoint rooted distance-constrained minimum spanning tree problem. J. Heuristics 2018, 24, 359–394. [Google Scholar] [CrossRef]
- Nelson, W.A.; Yeduri, S.R.; Jha, A.; Kumar, A.; Cenkeramaddi, L.R. RL-Based Energy-Efficient Data Transmission Over Hybrid BLE/LTE/Wi-Fi/LoRa UAV-Assisted Wireless Network. IEEE/ACM Trans. Netw. 2024, 32, 1951–1966. [Google Scholar] [CrossRef]


| Comparison Dimension | Prior Work [30] | Current Work |
|---|---|---|
| Scenario | Cooperative spectrum sharing | Overlay spectrum sharing |
| Methodology | Newton’s method + graphical method | Newton’s method + KM algorithm |
| Optimization goal | WSP minimization | WSP minimization |
| Solution type | Low-complexity, suboptimal | Optimal |
| Symbol | Definition |
|---|---|
| PL set | |
| SL set | |
| Number of PLs | |
| Number of SLs | |
| PL | |
| SL | |
| Granularity of power levels | |
| Granularity of spectrum-sharing factor levels | |
| Additive white Gaussian noise power density | |
| Channel gain between PT and PR (the BS) | |
| Channel gain between ST and SR | |
| Transmit power of PT (when matches with ) | |
| Transmit power of ST | |
| Spectrum-sharing factor for and | |
| Achievable SE of within one subframe | |
| Achievable SE of within one subframe | |
| Power consumption of within one subframe | |
| Power consumption of within one subframe | |
| Matching indicator for and | |
| Weight of | |
| Weight of | |
| QoS requirement of | |
| QoS requirement of | |
| Minimum transmit power | |
| Maximum transmit power | |
| WSP of link pair and |
| Begin |
| for |
| for |
| select to fulfill , . |
| repeat |
| calculate using (18) |
| until |
| set , obtain |
| end for |
| end for |
| obtain through the KM algorithm with matrix |
| End |
| Symbol | Value |
|---|---|
| Cell radius, | 500 m |
| Number of PLs, | 10 |
| Number of SLs, | 5~15 |
| Granularity of power levels, | 1 dB |
| Granularity of spectrum-sharing factor levels, | 0.01 |
| Gaussian noise spectral density, | −174 dBm/Hz |
| Weight of , | 1 |
| Weight of , | 1 |
| QoS requirement of , | 10 bps/Hz |
| QoS requirement of , | 5 bps/Hz |
| Minimum transmit power, | −40 dBm |
| Maximum transmit power, | 23 dBm |
| Step tolerance | 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Tang, X.; Xie, G. Spectrum Allocation and Power Control Based on Newton’s Method for Weighted Sum Power Minimization in Overlay Spectrum Sharing. Appl. Sci. 2025, 15, 4290. https://doi.org/10.3390/app15084290
Yu Y, Tang X, Xie G. Spectrum Allocation and Power Control Based on Newton’s Method for Weighted Sum Power Minimization in Overlay Spectrum Sharing. Applied Sciences. 2025; 15(8):4290. https://doi.org/10.3390/app15084290
Chicago/Turabian StyleYu, Yang, Xiaoqing Tang, and Guihui Xie. 2025. "Spectrum Allocation and Power Control Based on Newton’s Method for Weighted Sum Power Minimization in Overlay Spectrum Sharing" Applied Sciences 15, no. 8: 4290. https://doi.org/10.3390/app15084290
APA StyleYu, Y., Tang, X., & Xie, G. (2025). Spectrum Allocation and Power Control Based on Newton’s Method for Weighted Sum Power Minimization in Overlay Spectrum Sharing. Applied Sciences, 15(8), 4290. https://doi.org/10.3390/app15084290






