Experimental Investigation into the Number of Phases in Debris Flows
Abstract
1. Introduction
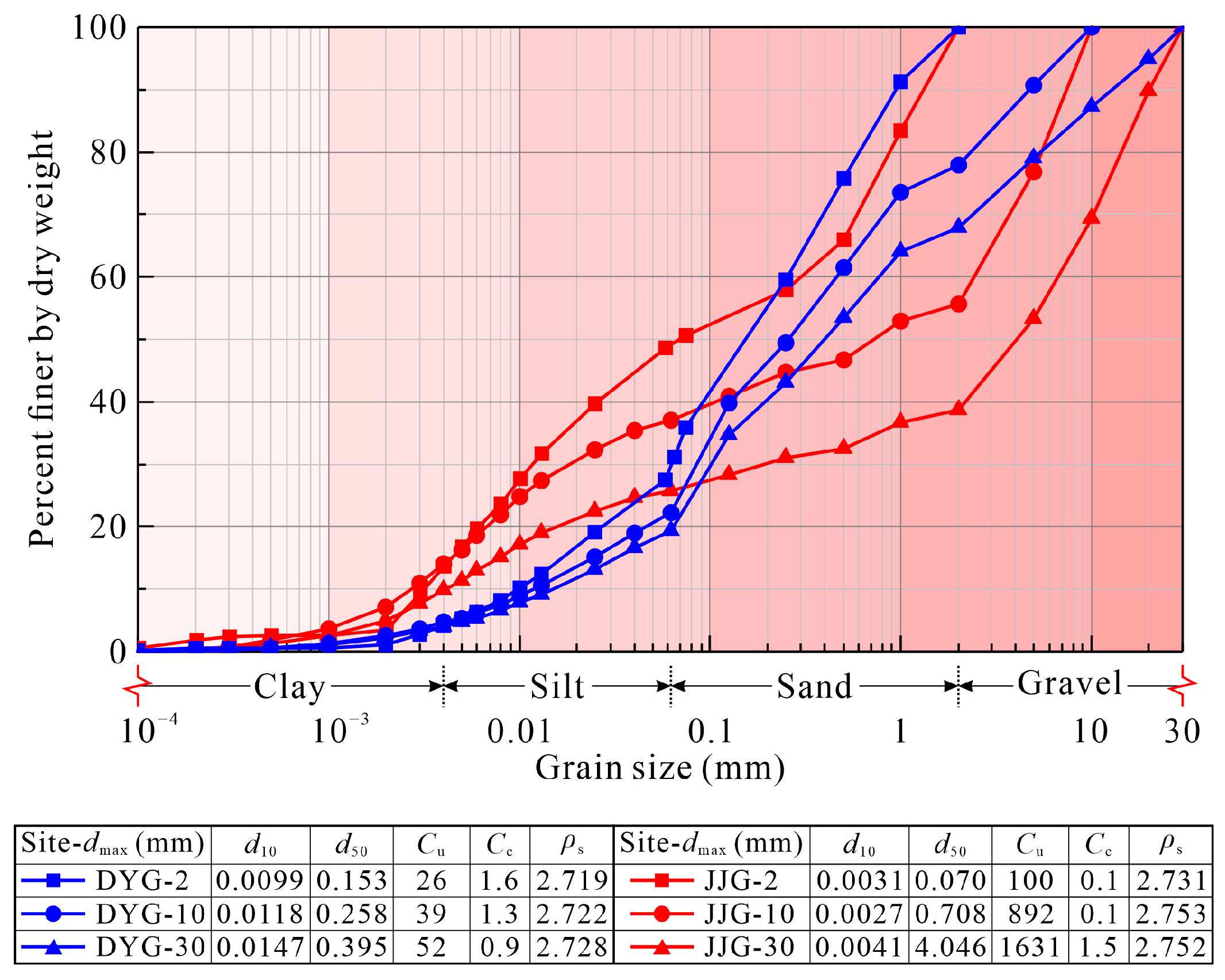
2. Sampling Sites
3. Tested Clastic Materials

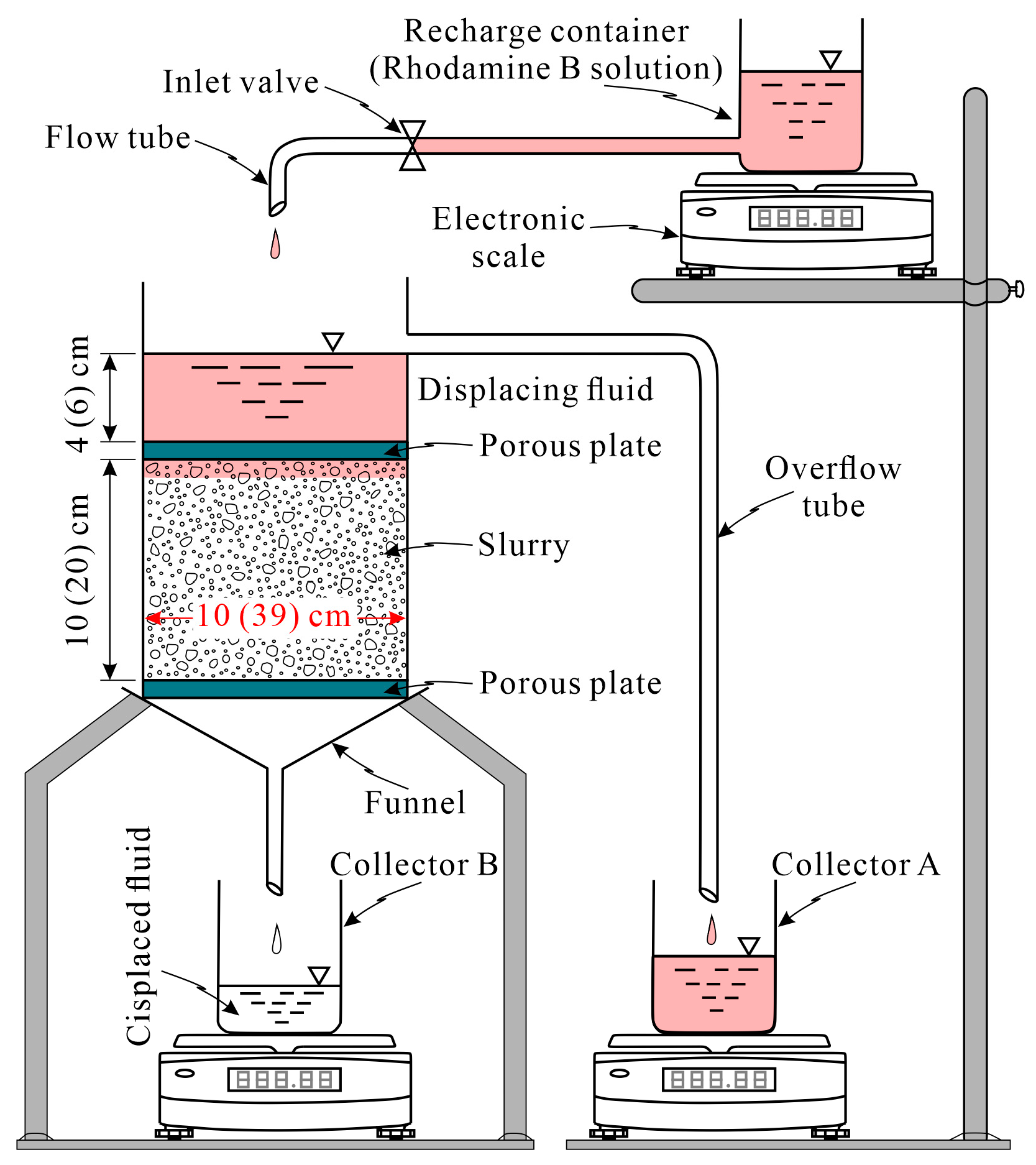
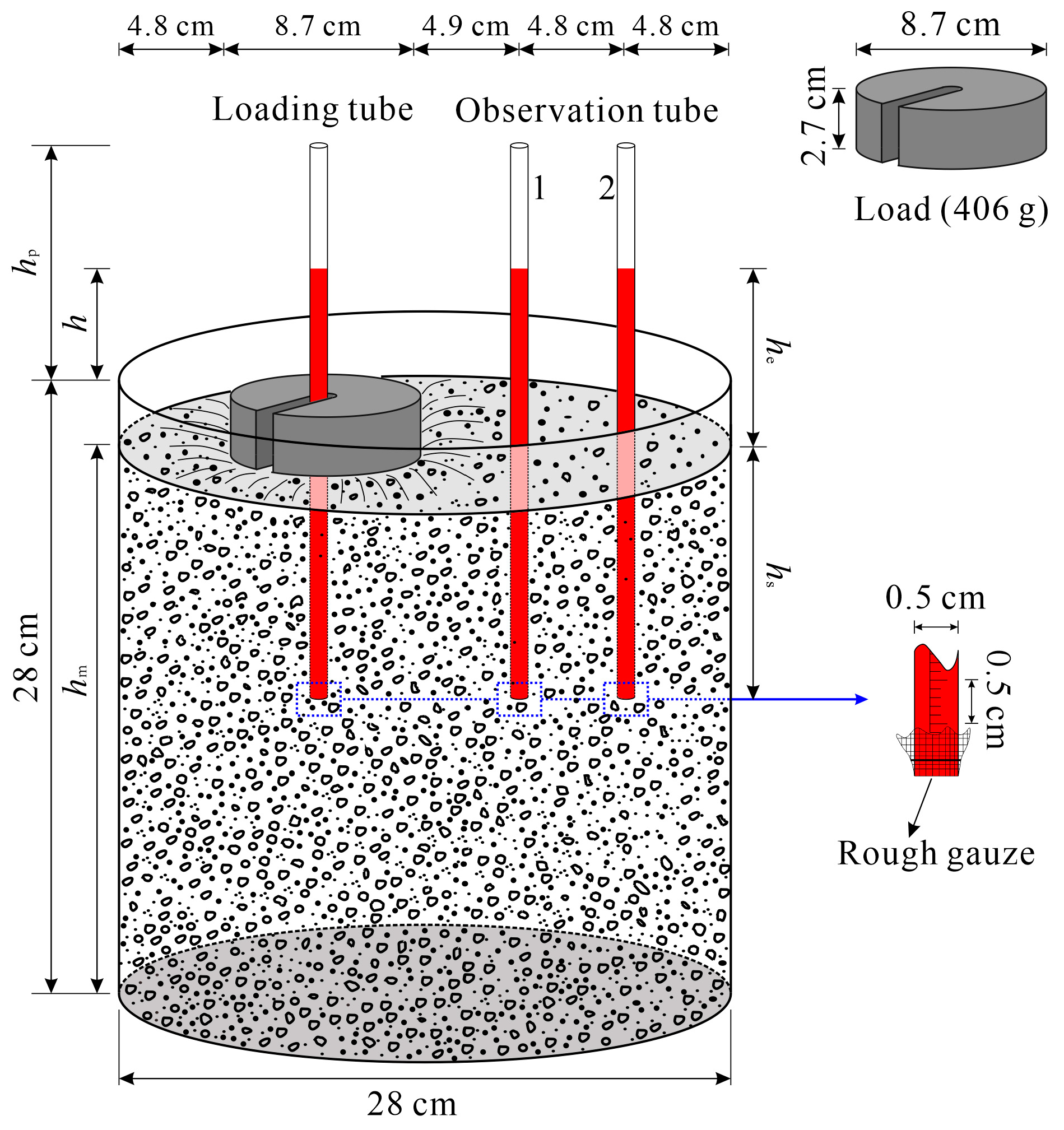
4. Laboratory Experiments
4.1. Escape Test of Fluid
4.2. Displacement Experiment of Fluid (Water) Under Constant-Head Condition
4.3. Relative Motion Experiment of Fluid (Water) and Solids Under Load
4.4. Rheometrical Test of Bulk Behavior of Experimental Debris Flow
5. Results
5.1. Escape of Fluid from Experimental Debris-Flow Deposits
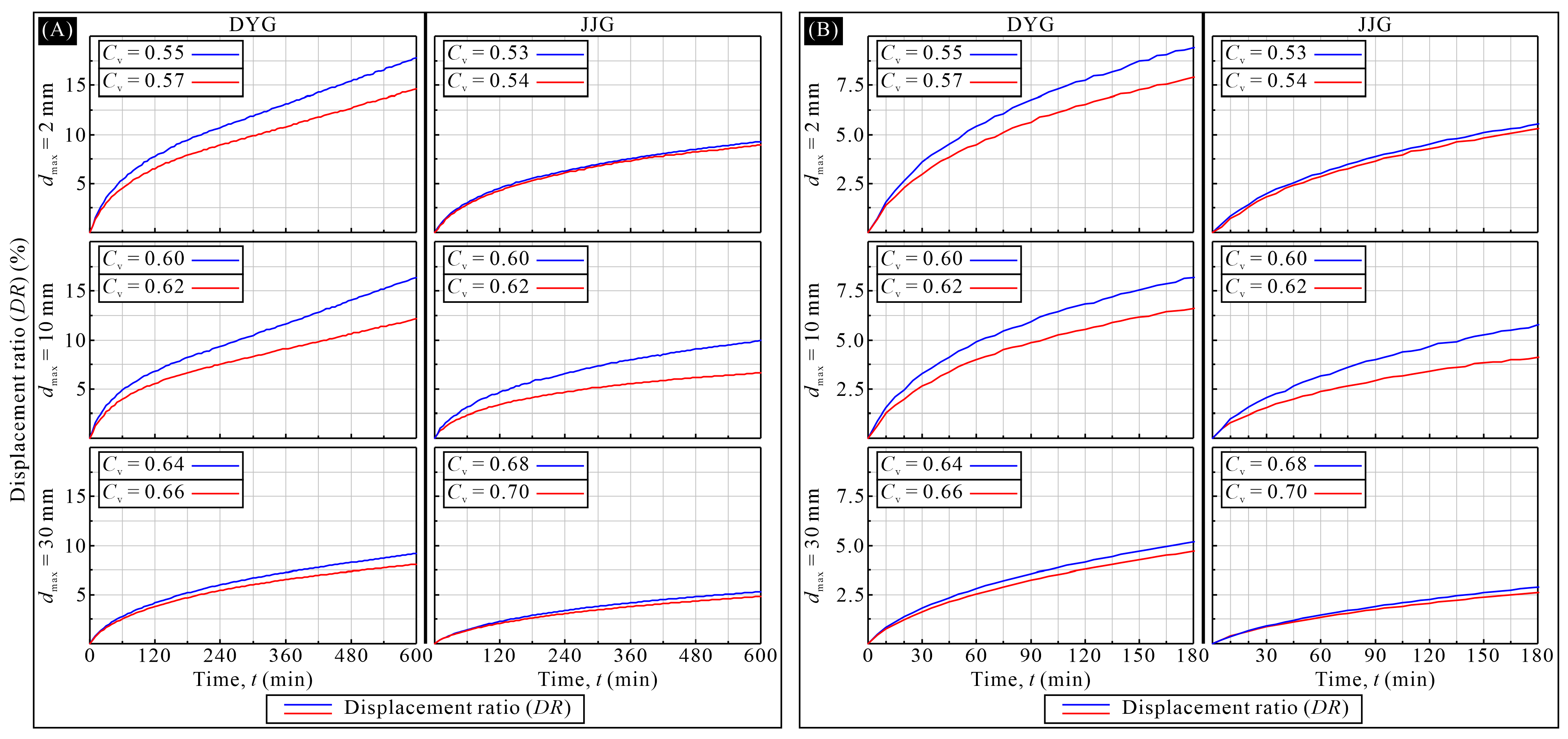
5.2. Response of the Water in Experimental Slurries to Hydraulic Forcing
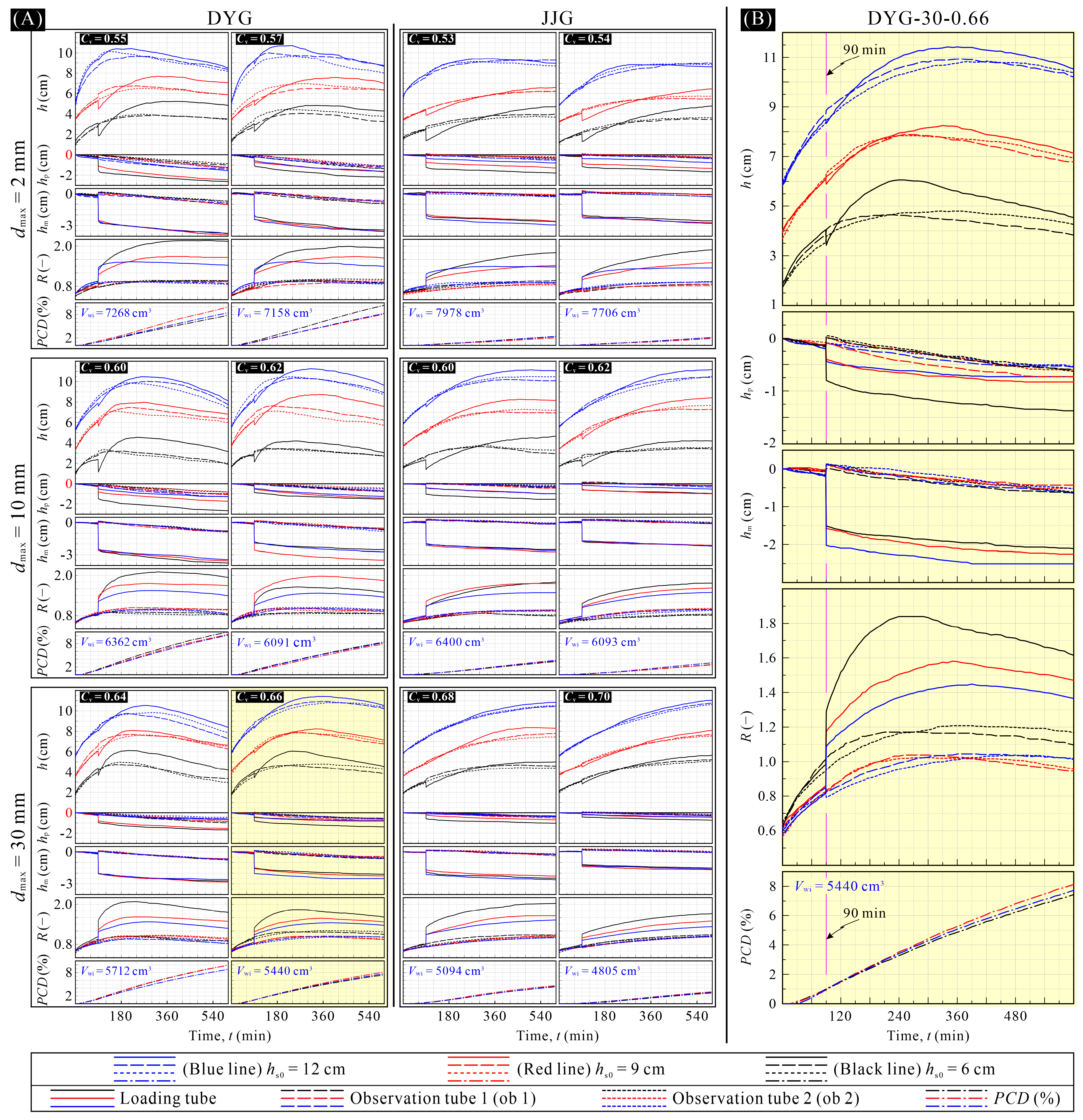
5.3. Response of the Water in Experimental Slurries to Mechanical Forcing
5.3.1. Initial Stage Before Loading (0–90 min)
5.3.2. The Moment When Load Is Applied (90 min)
5.3.3. The Stage in Which the h of the Loading Tube Is Lower than That of the Observational Piezometers
5.3.4. The Stage in Which the h for the Loading Tube Is Higher than That for the Observational Piezometers
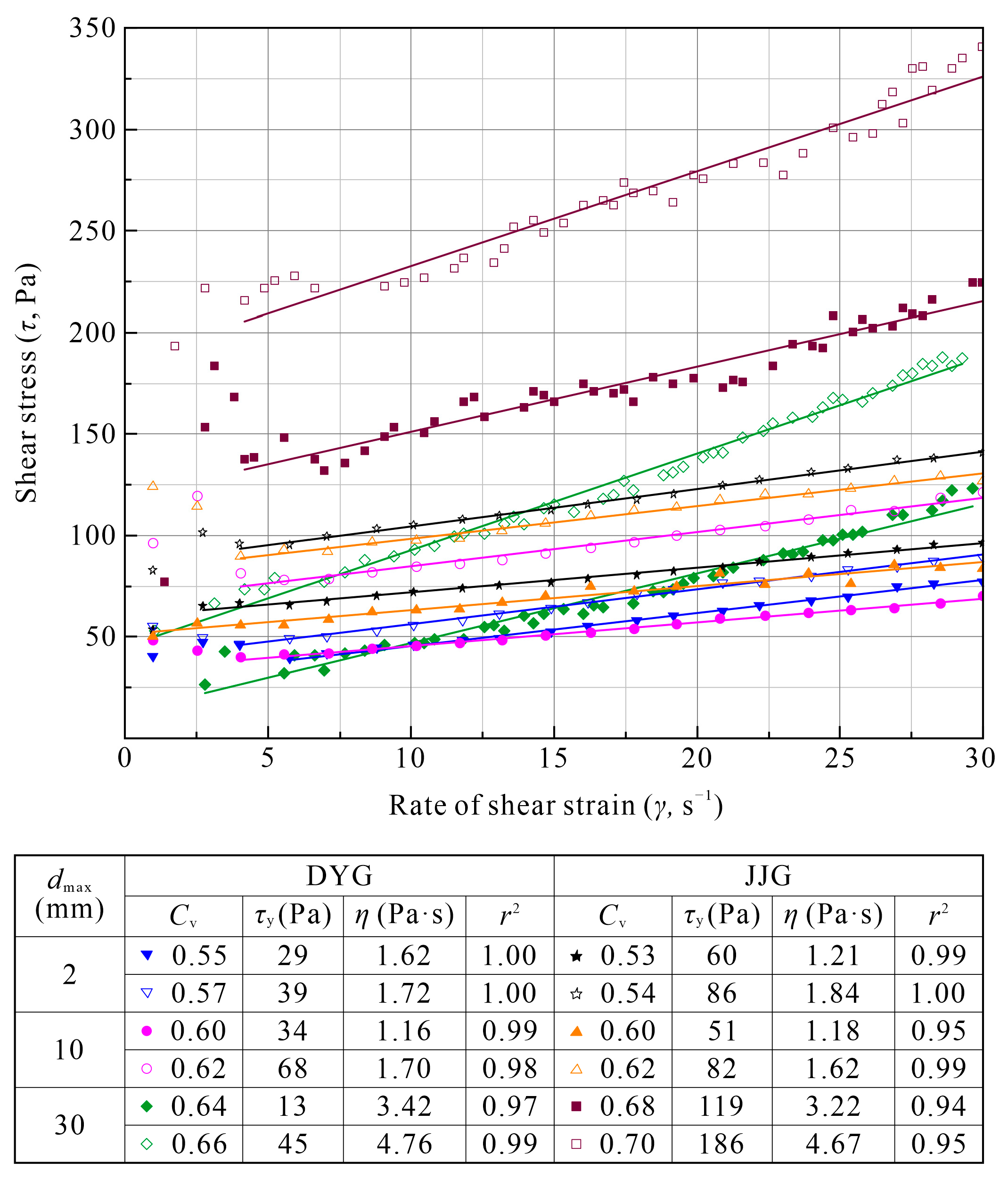
5.4. Rheology of Experimental Debris Flows
6. Discussion
6.1. Relative Motion of Fluid (Water) and Solids in Debris-Flow Bodies
6.2. Bulk Behavior of Debris Flows
6.3. Transported Objects by Debris Flows
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notations
| Ai | Inundated area (cm2) |
| As | Surface area including convex sides of experimental deposits (cm2) |
| Cc | Coefficient of curvature (–) |
| Cr | Coefficient of runout (–) |
| Cu | Coefficient of uniformity (–) |
| Cv | Solid volume concentration (–) |
| dmax | Maximum grain diameter (mm) of tested debris-flow sediment |
| Dmax | Maximum grain diameter of natural debris-flow sediment |
| DR | Displacement ratio (–) |
| h | Piezometric (hydraulic) head (cm) |
| he | Excess water pressure head (cm) |
| hm | Elevation of slurry surface (cm) |
| hp | Elevation of piezometer (cm) |
| hs | Hydrostatic pressure head (cm) |
| hs0 | Initial value of hydrostatic pressure head (cm) |
| J | Hydraulic gradient (–) |
| PCD | Percentage of cumulative discharge (%) |
| Pd | Cumulative percentages of displacing fluid (%) |
| Pe | Cumulative percentages of displaced fluid (%) |
| R | Relative excess water pressure (R = he/hs) (–) |
| r2 | Coefficient of determination |
| S | Solidity (–) |
| t | Time (min) |
| V | Volume of tested slurries (cm3) |
| Vwd | Cumulative volume of displacing fluid (cm3) |
| Vwe | Cumulative volume of effluent (displaced fluid) (cm3) |
| Vwi | Initial volume of water in tested slurries (cm3) |
| w | Water content (wt.%) |
| η | Viscosity of sediment-water mixtures (Pa·s) |
| ρb | Bulk density (g/cm3) |
| ρs | Solid density (grain density) (g/cm3) |
| τy | Yield stress of sediment-water mixtures (Pa) |
References
- Pierson, T.C.; Costa, J.E. A rheologic classification of subaerial sediment-water flows. In Debris Flows/Avalanches: Process, Recognition and Mitigation; Costa, J.E., Wieczorek, G.F., Eds.; Geological Society of America Reviews in Engineering Geology: Boulder, CO, USA, 1987; pp. 1–12. [Google Scholar] [CrossRef]
- Costa, J.E. Rheologic, geomorphic, and sedimentologic differentiation of water floods, hyperconcentrated flows, and debris flow. In Flood Geomorphology; Baker, V.R., Kochel, R.C., Patton, P.C., Eds.; John Wiley & Sons: New York, NY, USA, 1988; pp. 113–122. [Google Scholar]
- Scott, K.M.; Wang, Y.Y. Debris Flows-Geologic Process and Hazard, Illustrated by a Surge Sequence at Jiangjia Ravine, Yunnan, China; Professional Paper 1671; U.S. Geological Survey: Reston, VA, USA, 2004. Available online: https://pubs.usgs.gov/pp/1671/ (accessed on 1 January 2024).
- Coussot, P.; Meunier, M. Recognition, classification and mechanical description of debris flows. Earth-Sci. Rev. 1996, 40, 209–227. [Google Scholar] [CrossRef]
- Coussot, P.; Ancey, C. Rheophysical classification of concentrated suspensions and granular pastes. Phys. Rev. E 1999, 59, 4445–4457. [Google Scholar] [CrossRef]
- Davies, T.R.H. Debris-flow surges—Experimental simulation. J. Hydrol. 1990, 29, 18–46. Available online: https://www.jstor.org/stable/43944650 (accessed on 1 January 2024).
- Sosio, R.; Crosta, G.B.; Frattini, P. Field observations, rheological testing and numerical modelling of a debris-flow event. Earth Surf. Process. Landf. 2007, 32, 290–306. [Google Scholar] [CrossRef]
- D’Agostino, V.; Bettella, F.; Cesca, M. Basal shear stress of debris flow in the runout phase. Geomorphology 2013, 201, 272–280. [Google Scholar] [CrossRef]
- Pierson, T.C. Hyperconcentrated flow-transitional process between water flow and debris flow. In Debris-Flow Hazards and Related Phenomena; Jakob, M., Hungr, O., Eds.; Praxis; Springer: Berlin/Heidelberg, Germany, 2005; pp. 159–202. [Google Scholar] [CrossRef]
- Kaitna, R.; Rickenmann, D.; Schatzmann, M. Experimental study on the rheologic behaviour of debris flow material. Acta Geotech. 2007, 2, 71–85. [Google Scholar] [CrossRef]
- Castelli, F.; Freni, G.; Lentini, V.; Fichera, A. Modelling of a debris flow event in the Enna area for hazard assessment. Procedia Eng. 2017, 175, 287–292. [Google Scholar] [CrossRef]
- Hungr, O.; Morgan, G.C.; Kellerhals, R. Quantitative analysis of debris torrent hazards for design of remedial measures. Can. Geotech. J. 1984, 21, 663–677. [Google Scholar] [CrossRef]
- Iverson, R.M. The physics of debris flows. Rev. Geophys. 1997, 35, 245–296. [Google Scholar] [CrossRef]
- Iverson, R.M.; Logan, M.; Lahusen, R.G.; Berti, M. The perfect debris flow? Aggregated results from 28 large-scale experiments. J. Geophys. Res. Earth Surf. 2010, 115, 1–29. [Google Scholar] [CrossRef]
- Kattel, P.; Kafle, J.; Fischer, J.T.; Mergili, M.; Tuladhar, B.M.; Pudasaini, S.P. Interaction of two-phase debris flow with obstacles. Eng. Geol. 2018, 242, 197–217. [Google Scholar] [CrossRef]
- Brufau, P.; Garcia-Navarro, P.; Ghilardi, P.; Natale, L.; Savi, F. 1D mathematical modelling of debris flow. J. Hydraul. Res. 2000, 38, 435–446. [Google Scholar] [CrossRef]
- Armanini, A.; Fraccarollo, L.; Rosatti, G. Two-dimensional simulation of debris flows in erodible channels. Comput. Geosci. 2009, 35, 993–1006. [Google Scholar] [CrossRef]
- Rosatti, G.; Begnudelli, L. Two-dimensional simulation of debris flows over mobile bed: Enhancing the TRENT2D model by using a well-balanced Generalized Roe-type solver. Comput. Fluids 2013, 71, 179–195. [Google Scholar] [CrossRef]
- Kowalski, J.; Mcelwaine, J.N. Shallow two-component gravity-driven flows with vertical variation. J. Fluid Mech. 2013, 714, 434–462. [Google Scholar] [CrossRef]
- Johnson, A.M.; Rodine, J.R. Debris flow. In Slope Stability; Brunsden, D., Prior, D.B., Eds.; John Wiley & Sons: New York, NY, USA, 1984; pp. 257–361. [Google Scholar]
- U.S. Department of Agriculture (USDA)-Natural Resources Conservation Service (NRCS), National Engineering Handbook, Chapter 3-Engineering Classification of Earth Materials; United States Department of Agriculture: Washington, DC, USA, 2012.
- Major, J.J.; Pierson, T.C. Debris flow rheology: Experimental analysis of fine-grained slurries. Water Resour. Res. 1992, 28, 841–857. [Google Scholar] [CrossRef]
- Pudasaini, S.P. A general two-phase debris flow model. J. Geophys. Res. Earth Surf. 2012, 117, F03010. [Google Scholar] [CrossRef]
- Kaitna, R.; Palucis, M.C.; Yohannes, B.; Hill, K.M.; Dietrich, W.E. Effects of coarse grain size distribution and fine particle content on pore fluid pressure and shear behavior in experimental debris flows. J. Geophys. Res. Earth Surf. 2016, 121, 415–441. [Google Scholar] [CrossRef]
- Kaitna, R.; Rickenmann, D. Flow of different material mixtures in a rotating drum. In Proceedings of the 4th International Conference on Debris-flow Hazard Mitigation: Mechanics, Prediction, and Assessment, Chengdu, China, 10–13 September 2007; Chen, C.L., Major, J.J., Eds.; Millpress: Rotterdam, The Netherlands, 2007; pp. 269–279. [Google Scholar]
- Malet, J.-P.; Remaître, A.; Maquaire, O.; Ancey, C.; Locat, J. Flow susceptibility of heterogeneous marly formations. Implications for torrent hazard control in the Barcelonnette basin (Alpes-de-Haute-Provence, France). In Proceedings of the 3rd International Conference on Debris-Flow Hazard Mitigation: Mechanics, Prediction, and Assessment, Davos, Switzerland, 10–12 September 2003; Rickenmann, D., Chen, C.L., Eds.; Millpress: Rotterdam, The Netherlands, 2003; pp. 351–362. [Google Scholar]
- Pierson, T.C. Dominant particle support mechanisms in debris flows at Mt Thomas, New Zealand, and implications for flow mobility. Sedimentology 1981, 28, 49–60. [Google Scholar] [CrossRef]
- Phillips, C.J.; Davies, T.R.H. Determining rheological parameters of debris flow material. Geomorphology 1991, 4, 101–110. [Google Scholar] [CrossRef]
- Marchi, L.; Arattano, M.; Deganutti, A.M. Ten years of debris-flow monitoring in the Moscardo Torrent (Italian Alps). Geomorphology 2002, 46, 1–17. [Google Scholar] [CrossRef]
- Bardou, E.; Boivin, P.; Pfeifer, H.R. Properties of debris flow deposits and source materials compared: Implications for debris flow characterization. Sedimentology 2007, 54, 469–480. [Google Scholar] [CrossRef]
- Sharp, R.P.; Nobles, L.H. Mudflow of 1941 at Wrightwood, southern California. Bull. Geol. Soc. Am. 1953, 64, 547–560. [Google Scholar] [CrossRef]
- Costa, J.E.; Jarrett, R.D. Debris flows in small mountain stream channels of Colorado and their hydrologic implications. Environ. Eng. Geosci. 1981, 18, 309–322. [Google Scholar] [CrossRef]
- Moscariello, A.; Marchi, L.; Maraga, F.; Mortara, G. Alluvial Fans in the Italian Alps: Sedimentary Facies and Processes. In Flood and Megaflood Processes and Deposits; Martini, I.P., Baker, V.R., Garzón, G., Eds.; Blackwell Publishing Ltd.: Oxford, UK, 2002; pp. 141–166. [Google Scholar] [CrossRef]
- Berti, M.; Simoni, A. Prediction of debris flow inundation areas using empirical mobility relationships. Geomorphology 2007, 90, 144–161. [Google Scholar] [CrossRef]
- Jakob, M. A size classification for debris flows. Eng. Geol. 2005, 79, 151–161. [Google Scholar] [CrossRef]
- Eger, P.M.; Cagliari, J.; Aquino, C.D.; Coelho, O.G.W. Rheologic survey of mass transport events from the geologic record of an Andean Precordilleran slope. Geomorphology 2018, 315, 57–67. [Google Scholar] [CrossRef]
- Hürlimann, M.; Coviello, V.; Bel, C.; Guo, X.; Berti, M.; Graf, C.; Hübl, J.; Miyata, S.; Smith, J.B.; Yin, H.Y. Debris-flow monitoring and warning: Review and examples. Earth-Sci. Rev. 2019, 199, 102981. [Google Scholar] [CrossRef]
- Mckay, L.D.; Driese, S.G.; Smith, K.H.; Vepraskas, M.J. Hydrogeology and pedology of saprolite formed from sedimentary rock, eastern Tennessee, USA. Geoderma 2005, 126, 27–45. [Google Scholar] [CrossRef]
- D’Agostino, V.; Cesca, M.; Marchi, L. Field and laboratory investigations of runout distances of debris flows in the Dolomites (Eastern Italian Alps). Geomorphology 2010, 115, 294–304. [Google Scholar] [CrossRef]
- Remaître, A.; Malet, J.-P.; Maquaire, O. Geomorphology and kinematics of debris flows with high entrainment rates: A case study in the South French Alps. Comptes Rendus Geosci. 2011, 343, 777–794. [Google Scholar] [CrossRef]
- Ilinca, V. Using morphometrics to distinguish between debris flow, debris flood and flood (Southern Carpathians, Romania). Catena 2021, 197, 104982. [Google Scholar] [CrossRef]
- Carter, R.M. A discussion and classification of subaqueous mass-transport with particular application to grain-flow, slurry-flow, and fluxoturbidites. Earth-Sci. Rev. 1975, 11, 145–177. [Google Scholar] [CrossRef]
- Pierson, T.C. Flow behavior of channelized debris flows, Mount St. Helens, Washington. In Hillslope Processes; Abrahms, A.D., Ed.; Routledge: London, UK, 1986; pp. 269–296. [Google Scholar]
- Pérez, F.L. Matrix granulometry of catastrophic debris flows (December 1999) in central coastal Venezuela. Catena 2001, 45, 163–183. [Google Scholar] [CrossRef]
- Ye, Z.M.; Xu, Z.M.; Li, B.; Su, X.; Shi, G.E.; Meng, J.K.; Tian, L. Generation and origin of persistent high excess pore water pressure in debris flows. Geomorphology 2024, 444, 108954. [Google Scholar] [CrossRef]
- Li, J.C. Neotectonic feature of the Nujiang fault zone in western Yunnan. Seismol. Geol. 1998, 20, 312–320. (In Chinese) [Google Scholar]
- Chang, C.W.; Lin, P.S.; Tsai, C.L. Estimation of sediment volume of debris flow caused by extreme rainfall in Taiwan. Eng. Geol. 2011, 123, 83–90. [Google Scholar] [CrossRef]
- Klubertanz, G.; Laloui, L.; Vulliet, L. Identification of mechanisms for landslide type initiation of debris flows. Eng. Geol. 2009, 109, 114–123. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Ren, Z.; Wang, K.; Yang, K.; Tang, Y.J.; Tian, L.; Xu, Z.M. Effect of excess pore pressure on the long runout of debris flows over low gradient channels: A case study of the Dongyuege debris flow in Nu River, China. Geomorphology 2018, 308, 40–53. [Google Scholar] [CrossRef]
- Tang, Y.J.; Xu, Z.M.; Shao, Z.C.; Ren, Z.; Wang, K.; Yang, K.; Tian, L. Laboratory investigations of the role of biofilms on stream-bed surfaces in debris-flow runout. Earth Surf. Process. Landf. 2020, 45, 999–1012. [Google Scholar] [CrossRef]
- Tang, Y.J.; Xu, Z.M.; Yang, T.Q.; Zhou, Z.H.; Wang, K.; Ren, Z.; Yang, K.; Tian, L. Impacts of small woody debris on slurrying, persistence, and propagation in a low-gradient channel of the Dongyuege debris flow in Nu River, Southwest China. Landslides 2018, 15, 2279–2293. [Google Scholar] [CrossRef]
- Yang, K.; Xu, Z.M.; Ren, Z.; Wang, K.; Tang, Y.J.; Tian, L.; Luo, J.Y.; Gao, H.Y. Physico-mechanical performance of debris-flow deposits with particular reference to characterization and recognition of debris flow-related sediments. J. Cent. South Univ. 2020, 27, 2726–2744. [Google Scholar] [CrossRef]
- Yang, K.; Xu, Z.M.; Tian, L.; Wang, K.; Ren, Z.; Tang, Y.J.; Luo, J.Y.; Gao, H.Y. Significance of coarse clasts in viscous debris flows. Eng. Geol. 2020, 272, 105665. [Google Scholar] [CrossRef]
- Hürlimann, M.; Mcardell, B.W.; Rickli, C. Field and laboratory analysis of the runout characteristics of hillslope debris flows in Switzerland. Geomorphology 2015, 232, 20–32. [Google Scholar] [CrossRef]
- Das, B.M. Advanced Soil Mechanics, 3rd ed.; Taylor & Frances: New York, NY, USA, 2008. [Google Scholar]
- Crosta, G.B.; Cucchiaro, S.; Frattini, P. Validation of semi-empirical relationships for the definition of debris-flow behavior in granular materials. In Proceedings of the 3rd International Conference on Debris-Flow Hazard Mitigation: Mechanics, Prediction, and Assessment, Davos, Switzerland, 10–12 September 2003; Rickenmann, D., Chen, C.L., Eds.; Millpress: Rotterdam, The Netherlands, 2003; pp. 821–831. [Google Scholar]
- Godt, J.W.; Coe, J.A. Alpine debris flows triggered by a 28 July 1999 thunderstorm in the central Front Range, Colorado. Geomorphology 2007, 84, 80–97. [Google Scholar] [CrossRef]
- Kim, Y.; Nakagawa, H.; Kawaike, K.; Zhang, H. Study on hydraulic characteristics of sabo dam with a flap structure for debris flow. Int. J. Sediment Res. 2017, 32, 452–464. [Google Scholar] [CrossRef]
- Li, J.; Yuan, J.M.; Bi, C.; Luo, D.F. The main features of the mudflow in Jiangjia Ravine. Z. Für Geomorphol. 1983, 27, 325–341. [Google Scholar] [CrossRef]
- Zhang, S.C. A comprehensive approach to the observation and prevention of debris flows in China. Nat. Hazards 1993, 7, 1–23. [Google Scholar] [CrossRef]
- Chen, J.; He, Y.P.; Wei, F.Q. Debris flow erosion and deposition in Jiangjia Gully, Yunnan, China. Environ. Geol. 2005, 48, 771–777. [Google Scholar] [CrossRef]
- Kang, Z.C.; Cui, P.; Wei, F.Q.; He, S.F. Data Collection of Dongchuan Debris Flow Observation and Research Station Chinese Academy of Sciences (1961–1984); Science Press: Beijing, China, 2006. (In Chinese) [Google Scholar]
- Kang, Z.C.; Cui, P.; Wei, F.Q.; He, S.F. Data Collection of Dongchuan Debris Flow Observation and Research Station Chinese Academy of Sciences (1995–2000); Science Press: Beijing, China, 2007. (In Chinese) [Google Scholar]
- Yang, H.J.; Wei, F.Q.; Hu, K.H.; Wang, C.C. Determination of the suspension competence of debris flows based on particle size analysis. Int. J. Sediment Res. 2014, 29, 73–81. [Google Scholar] [CrossRef]
- Yu, B.; Zhu, Y.; Wang, T.; Zhu, Y.B. A 10-min rainfall prediction model for debris flows triggered by a runoff induced mechanism. Environ. Earth Sci. 2016, 75, 216. [Google Scholar] [CrossRef]
- Guo, X.J.; Li, Y.; Cui, P.; Yan, H.; Zhuang, J.Q. Intermittent viscous debris flow formation in Jiangjia Gully from the perspectives of hydrological processes and material supply. J. Hydrol. 2020, 589, 125184. [Google Scholar] [CrossRef]
- Yang, H.J.; Zhang, S.J.; Hu, K.H.; Wei, F.Q.; Wang, K.; Liu, S. Field observation of debris-flow activities in the initiation area of the Jiangjia Gully, Yunnan Province, China. J. Mt. Sci. 2022, 19, 1602–1617. [Google Scholar] [CrossRef]
- Zhao, T.; Zhou, G.G.D.; Sun, Q.C.; Crosta, G.B.; Song, D.R. Slope erosion induced by surges of debris flow: Insights from field experiments. Landslides 2022, 19, 2367–2377. [Google Scholar] [CrossRef]
- Wagreich, M.; Strauss, P.E. Source area and tectonic control on alluvial-fan development in the Miocene Fohnsdorf intramontane basin, Austria. In Alluvial Fans: Geomorphology, Sedimentology, Dynamics; Harvey, A.M., Mather, A.E., Stokes, M., Eds.; Geological Society, London, Special Publications: London, UK, 2005; Volume 251, pp. 207–216. [Google Scholar] [CrossRef]
- Legg, N.T.; Meigs, A.J.; Grant, G.E.; Kennard, P. Debris flow initiation in proglacial gullies on Mount Rainier, Washington. Geomorphology 2014, 226, 249–260. [Google Scholar] [CrossRef]
- Martin, Y.E.; Johnson, E.A.; Chaikina, O. Gully recharge rates and debris flows: A combined numerical modeling and field-based investigation, Haida Gwaii, British Columbia. Geomorphology 2017, 278, 252–268. [Google Scholar] [CrossRef]
- GB/T 50123–2019; Standard for Geotechnical Testing Method. Ministry of Housing and Urban-Rural Development of the P.R. China & State Administration for Market Regulation: Beijing, China, 2019. (In Chinese)
- Scotto Di Santolo, A.; Pellegrino, A.M.; Evangelista, A.; Coussot, P. Rheological behaviour of reconstituted pyroclastic debris flow. Géotechnique 2012, 62, 19–27. [Google Scholar] [CrossRef]
- Tattersall, G.H. The rationale of a two-point workability test. Mag. Concr. Res. 1973, 25, 169–172. [Google Scholar] [CrossRef]
- Schatzmann, M.; Bezzola, G.R.; Minor, H.-E.; Windhab, E.J.; Fischer, P. Rheometry for large-particulated fluids: Analysis of the ball measuring system and comparison to debris flow rheometry. Rheol. Acta 2009, 48, 715–733. [Google Scholar] [CrossRef]
- De Haas, T.; Braat, L.; Leuven, J.R.F.W.; Lokhorst, I.R.; Kleinhans, M.G. Effects of debris flow composition on runout, depositional mechanisms, and deposit morphology in laboratory experiments. J. Geophys. Res. Earth Surf. 2015, 120, 1949–1972. [Google Scholar] [CrossRef]
- Rodine, J.D.; Johnson, A.M. The ability of debris, heavily freighted with coarse clastic materials, to flow on gentle slopes. Sedimentology 1976, 23, 213–234. [Google Scholar] [CrossRef]
- Simoni, A.; Mammoliti, M.; Berti, M. Uncertainty of debris flow mobility relationships and its influence on the prediction of inundated areas. Geomorphology 2011, 132, 249–259. [Google Scholar] [CrossRef]
- Stancanelli, L.M.; Rosatti, G.; Begnudelli, L.; Armanini, A.; Foti, E. Single or Two-Phase Modelling of Debris-Flow? A Systematic Comparison of the Two Approaches Applied to a Real Debris Flow in Giampilieri Village (Italy). In Landslide Science and Practice; Margottini, C., Canuti, P., Sassa, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 277–283. [Google Scholar] [CrossRef]
- Baselt, I.; De Oliveira, G.Q.; Fischer, J.-T.; Pudasaini, S.P. Deposition morphology in large-scale laboratory stony debris flows. Geomorphology 2022, 396, 107992. [Google Scholar] [CrossRef]
- Willhite, G.P. Waterflooding; Society of Petroleum Engineers: Richardson, TX, USA, 1986. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; Dover: New York, NY, USA, 1988. [Google Scholar]
- ASTM D 2434–68; Standard Test Method for Permeability of Granular Soils (Constant Head). ASTM International: West Conshohocken, PA, USA, 2006.
- Eckersley, J.D. Instrumented laboratory flowslides. Géotechnique 1990, 40, 489–502. [Google Scholar] [CrossRef]
- Fanchi, J.R. Chapter 6-Fluid Properties. Shared Earth Modeling; Butterworth-Heinemann: Amsterdam, The Netherlands, 2002; pp. 87–107. [Google Scholar] [CrossRef]
- Coussot, P.; Piau, J.M. On the behavior of fine mud suspensions. Rheol. Acta 1994, 33, 175–184. [Google Scholar] [CrossRef]
- Coussot, P.; Nguyen, Q.D.; Huynh, H.T.; Bonn, D. Avalanche Behavior in Yield Stress Fluids. Phys. Rev. Lett. 2002, 88, 175501. [Google Scholar] [CrossRef]
- Kameda, J.; Morisaki, T. Sensitivity of clay suspension rheological properties to pH, temperature, salinity, and smectite-quartz ratio. Geophys. Res. Lett. 2017, 44, 9615–9621. [Google Scholar] [CrossRef]
- O’brien, J.S.; Julien, P.Y. Laboratory analysis of mudflow properties. J. Hydraul. Eng. 1988, 114, 877–887. [Google Scholar] [CrossRef]
- Tattersall, G.H.; Bloomer, S.J. Further development of the two-point test for workability and extension of its range. Mag. Concr. Res. 1979, 31, 202–210. [Google Scholar] [CrossRef]
- Major, J.J. Gravity-driven consolidation of granular slurries: Implications for debris-flow deposition and deposit characteristics. J. Sediment. Res. 2000, 70, 64–83. [Google Scholar] [CrossRef]
- Chiarle, M.; Iannotti, S.; Mortara, G.; Deline, P. Recent debris flow occurrences associated with glaciers in the Alps. Glob. Planet. Change 2007, 56, 123–136. [Google Scholar] [CrossRef]
- Collins, B.D.; Stock, G.M. Rockfall triggering by cyclic thermal stressing of exfoliation fractures. Nat. Geosci. 2016, 9, 395–400. [Google Scholar] [CrossRef]
- D’Arcy, M.; Roda-Boluda, D.C.; Whittaker, A.C. Glacial-interglacial climate changes recorded by debris flow fan deposits, Owens Valley, California. Quat. Sci. Rev. 2017, 169, 288–311. [Google Scholar] [CrossRef]
- Hampton, M.A. Competence of fine-grained debris flows. J. Sediment. Petrol. 1975, 45, 834–844. [Google Scholar] [CrossRef]
- Pierson, T.C. Erosion and deposition by debris flows at Mt Thomas, North Canterbury, New Zealand. Earth Surf. Process. Landf. 1980, 5, 227–247. [Google Scholar] [CrossRef]
- Innes, J.L. Debris flows. Prog. Phys. Geogr. 1983, 7, 469–501. [Google Scholar] [CrossRef]
- Cruden, D.M.; Varnes, D.J. Landslide types and processes. In Landslides: Investigation and Mitigation; Turner, A.K., Schuster, R.L., Eds.; Transportation Research Board Spec. Rep.: Washington, DC, USA, 1996; Volume 247, pp. 36–75. [Google Scholar]
- Palucis, M.C.; Ulizio, T.P.; Fuller, B.; Lamb, M.P. Flow resistance, sediment transport, and bedform development in a steep gravel-bedded river flume. Geomorphology 2018, 320, 111–126. [Google Scholar] [CrossRef]
- Remaître, A.; Malet, J.-P.; Maquaire, O.; Ancey, C. Study of a debris-flow Study of a debris-flow event by coupling a geomorphological and a rheological investigation, example of the Faucon stream (Alpes-de-Haute-Provence, France). In Proceedings of the 3rd International Conference on Debris-Flow Hazard Mitigation: Mechanics, Prediction, and Assessment, Davos, Switzerland, 10–12 September 2003; Rickenmann, D., Chen, C.L., Eds.; Millpress: Rotterdam, The Netherlands, 2003; pp. 375–385. [Google Scholar]
- Quan Luan, B.; Remaitre, A.; Van Asch, T.W.J.; Malet, J.-P.; Van Westen, C.J. Analysis of debris flow behavior with a one dimensional run-out model incorporating entrainment. Eng. Geol. 2012, 128, 63–75. [Google Scholar] [CrossRef]
- Pollet, N.; Schneider, J.L.M. Dynamic disintegration processes accompanying transport of the Holocene Flims sturzstrom (Swiss Alps). Earth Planet. Sci. Lett. 2004, 221, 433–448. [Google Scholar] [CrossRef]
- Crosta, G.B.; Frattini, P. Controls on modern alluvial fan processes in the central Alps, northern Italy. Earth Surf. Process. Landf. 2004, 29, 267–293. [Google Scholar] [CrossRef]
- Jakob, M.; Friele, P. Frequency and magnitude of debris flows on Cheekye River, British Columbia. Geomorphology 2010, 114, 382–395. [Google Scholar] [CrossRef]
- Mcardell, B.W.; Bartelt, P.; Kowalski, J. Field observations of basal forces and fluid pore pressure in a debris flow. Geophys. Res. Lett. 2007, 34, L07406. [Google Scholar] [CrossRef]
- Jakob, M.; Anderson, D.; Fuller, T.; Hungr, O.; Ayotte, D. An unusually large debris flow at Hummingbird Creek, Mara Lake, British Columbia. Can. Geotech. J. 2000, 37, 1109–1125. [Google Scholar] [CrossRef]
- Schramm, J.-M.; Weidinger, J.T.; Ibetsberger, H.J. Petrologic and structural controls on geomorphology of prehistoric Tsergo Ri slope failure, Langtang Himal, Nepal. Geomorphology 1998, 16, 107–121. [Google Scholar] [CrossRef]
- Davies, T.R.H.; Mcsaveney, M.J.; Boulton, C.J. Elastic strain energy release from fragmenting grains: Effects on fault rupture. J. Struct. Geol. 2012, 38, 265–277. [Google Scholar] [CrossRef]
- Brideau, M.A.; Yan, M.; Stead, D. The role of tectonic damage and brittle rock fracture in the development of large rock slope failures. Geomorphology 2009, 103, 30–49. [Google Scholar] [CrossRef]
- Harrison, J.P.; Hudson, J.A. Engineering Rock Mechanics: Part 2 Illustrative Worked Examples; Pergamon: Rotterdam, The Netherlands, 2000. [Google Scholar]
- Jing, L. A review of techniques, advances and outstanding issues in numerical modelling for rock mechanics and rock engineering. Int. J. Rock Mech. Min. Sci. 2003, 40, 283–353. [Google Scholar] [CrossRef]
- Hampton, M.A. Buoyancy in debris flows. J. Sediment. Res. 1979, 49, 753–758. [Google Scholar] [CrossRef]
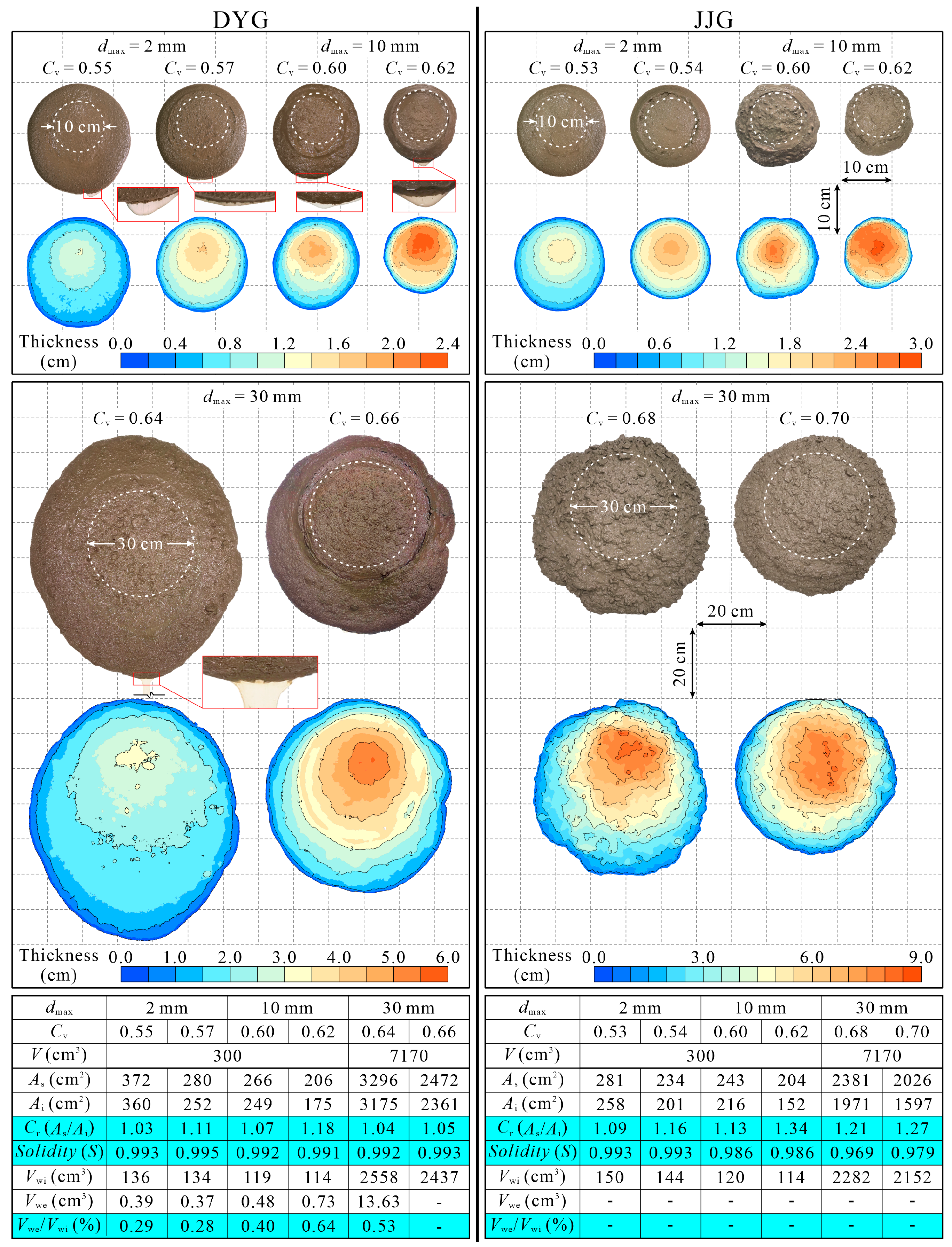



| Slurry Number | Debris Source | dmax (mm) | Cv | ρb (g/cm3) | w (wt.%) |
|---|---|---|---|---|---|
| DYG-2-0.55 | DYG | 2 | 0.55 | 1.95 | 23.2 |
| DYG-2-0.57 | 0.57 | 1.98 | 22.2 | ||
| DYG-10-0.60 | 10 | 0.60 | 2.04 | 19.5 | |
| DYG-10-0.62 | 0.62 | 2.07 | 18.4 | ||
| DYG-30-0.64 | 30 | 0.64 | 2.11 | 16.9 | |
| DYG-30-0.66 | 0.66 | 2.14 | 15.9 | ||
| JJG-2-0.53 | JJG | 2 | 0.53 | 1.91 | 25.4 |
| JJG-2-0.54 | 0.54 | 1.94 | 24.2 | ||
| JJG-10-0.60 | 10 | 0.60 | 2.05 | 19.5 | |
| JJG-10-0.62 | 0.62 | 2.09 | 18.2 | ||
| JJG-30-0.68 | 30 | 0.68 | 2.19 | 14.5 | |
| JJG-30-0.70 | 0.70 | 2.23 | 13.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Xu, Z.-M. Experimental Investigation into the Number of Phases in Debris Flows. Appl. Sci. 2025, 15, 4282. https://doi.org/10.3390/app15084282
Li B, Xu Z-M. Experimental Investigation into the Number of Phases in Debris Flows. Applied Sciences. 2025; 15(8):4282. https://doi.org/10.3390/app15084282
Chicago/Turabian StyleLi, Bin, and Ze-Min Xu. 2025. "Experimental Investigation into the Number of Phases in Debris Flows" Applied Sciences 15, no. 8: 4282. https://doi.org/10.3390/app15084282
APA StyleLi, B., & Xu, Z.-M. (2025). Experimental Investigation into the Number of Phases in Debris Flows. Applied Sciences, 15(8), 4282. https://doi.org/10.3390/app15084282






