Abstract
This paper proposes an adaptive pre-distortion method for mitigating LED nonlinear distortion in Visible Light Communication (VLC)-OFDM systems. The inherent nonlinear characteristics of LEDs disrupt the orthogonality among OFDM subcarriers, causing signal distortion and performance degradation. To overcome this issue while minimizing computational complexity at the transmitter, we introduce a feedback-based nonlinear parameter estimation approach using the Least Squares Method (LSM) and Median Based Method (MBM). These estimated parameters are then fed back to the transmitter, enabling efficient adaptive pre-distortion based on the inverse function of the estimated nonlinear characteristics. This approach reduces computational costs at the transmitter compared to conventional methods requiring high-performance processing. Additionally, we incorporate Frequency Symbol Spreading (FSS) to further enhance robustness against channel impairments such as Rician fading by equalizing the Signal-to-Noise Ratio (SNR) across subcarriers. Simulation results under various channel conditions, including AWGN, Rician fading, and realistic multi-LED lighting scenarios, demonstrate a significant improvement in Bit Error Rate (BER) performance, validating both the effectiveness and practical advantages of the proposed approach.
1. Introduction
In recent years, advancements in multimedia technologies, such as smartphones and televisions, have made high-capacity, high-speed communication a standard expectation. However, these advancements rely on the use of frequency bands, and the available spectrum for Radio Frequency (RF) communication is limited. Consequently, issues such as network congestion and connectivity difficulties have become increasingly common [1,2,3]. To address this challenge, there is growing demand for access to broader frequency resources. In this context, VLC, which utilizes visible light as a transmission medium, has garnered increasing attention. VLC offers significant advantages by exploiting the wide bandwidth of visible light (430 THz to 790 THz), which is substantially larger than the bandwidth of RF communication (3 kHz to 300 GHz).
Furthermore, VLC does not overlap with existing RF frequency bands, making it a promising solution for mitigating spectrum scarcity [4]. Moreover, VLC commonly employs the Intensity Modulation/Direct Detection (IM/DD) scheme, where information is transmitted through variations in light intensity achieved by the high-speed switching of LEDs. This approach enables the construction of communication systems using existing LED lighting and cost-effective photodiodes, making VLC a promising candidate for rapid adoption in the near future [5,6,7]. Recently, VLC systems integrated with OFDM, referred to as VLC-OFDM systems, have gained significant attention for their efficient utilization of frequency resources [8,9]. However, the LEDs used in VLC exhibit nonlinear characteristics between the driving current and emitted optical power, which introduces signal distortion during transmission [10,11,12]. In VLC-OFDM systems, such nonlinearities compromise the orthogonality between subcarriers, leading to substantial degradation of the communication system’s performance [11]. Moreover, the nonlinear characteristics vary significantly not only between different LED types but also among individual LEDs within the same type [10]. This variability becomes even more pronounced in modern LED lighting systems that incorporate multiple LED chips, resulting in increasingly complex nonlinear behaviors. As a result, recent research has focused on developing compensation techniques to mitigate these nonlinear effects and improve the performance and reliability of VLC systems [13,14,15,16,17].
In conventional compensation methods for LED nonlinear characteristics, the transmitter receives the transmitted signal and estimates the nonlinear parameters, which necessitates sophisticated signal processing [14,15]. Consequently, high-performance computational resources must be incorporated into the transmitter. This approach results in prohibitively high costs for individual LED luminaires, rendering it impractical. Moreover, while machine learning-based nonlinear compensation techniques are available, those methods that require offline training at both the transmitter and receiver incur an enormous computational burden [16,17]. Therefore, for adaptive pre-distortion compensation designed to reduce the computational resources required at the transmitter, we propose a feedback-based adaptive pre-distortion method that employs a nonlinear parameter estimator at the receiver. This proposed method estimates the nonlinear characteristics of the transmitting LED using a parameter estimator at the receiver. The estimated parameters are then sent back to the transmitter using FeedBack Information (FBI), generally called Channel State Information (CSI), enabling the transmitter to perform adaptive pre-distortion based on this information. Furthermore, this study demonstrates that channel distortion effects can be mitigated by applying frequency symbol spreading (FSS) [18] to our proposed method, which equalizes the SNR of received signals through symbol spreading. Simulation results demonstrate that the proposed method improves BER performance even for LED lighting systems composed of multiple LED chips, confirming its practicality and potential for real-world applications.
This paper is structured as follows. Section 2 defines the VLC-OFDM system model under IM/DD and the nonlinear distortion caused by LEDs. Section 3 presents the proposed method. Section 4 discusses the results obtained through computer simulations and provides an analysis. Section 5 concludes the study. Finally, future research directions are outlined.
2. System Model
This section first provides an overview of the principles behind VLC-OFDM technology. Additionally, the nonlinear characteristics of LEDs that act as degradation factors in this communication system are explained.
2.1. VLC-OFDM
In VLC-OFDM, the IM-DD scheme has been predominantly considered due to its system simplicity. A block diagram of the IM/DD-based VLC-OFDM communication system is illustrated in Figure 1 [19]. In Figure 1, GI stands for Guard Interval, which refers to the insertion of a portion of the latter part of each OFDM symbol at the beginning of the symbol to mitigate inter-symbol interference caused by multipath delay. A/D denotes Analog-to-Digital Conversion, and P/S represents Parallel-to-Serial Conversion.
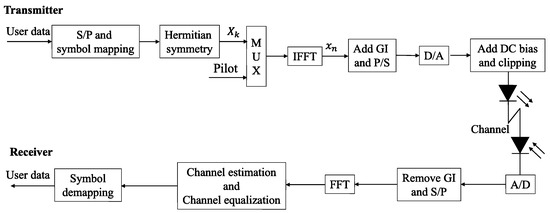
Figure 1.
VLC-OFDM in IM/DD systems.
Unlike conventional RF-OFDM systems, IM/DD systems are unable to transmit complex-valued signals [8], and consequently, they cannot convey phase information. To address this limitation, the frequency-domain signal before IFFT is constrained to satisfy Hermitian symmetry. This is because when Hermitian conjugation is applied to the signal, the IFFT output consists exclusively of real-valued components.
Let … denote the complex-valued symbols to be transmitted. The Hermitian symmetry condition can be expressed as follows:
where represents the complex conjugate of and is the total number of functionally active subcarriers. Under this constraint, the IFFT output yields a real-valued time-domain signal, which is expressed by the following equation.
Furthermore, owing to LEDs, which cannot emit negative optical power, a DC bias component is introduced to ensure non-negative transmitted signals. In this work, the DC bias is superimposed onto the time-domain OFDM signal, as defined by the following equation:
where, represents the current amplitude of the k-th subcarrier (the frequency component), is the frequency of the k-th subcarrier, and denotes the initial phase of the k-th subcarrier.
2.2. LED Characteristic
We consider using the driving circuit for the LED as shown in Figure 2 [10]. Consequently, the static nonlinear relationship between the normalized driving current and the normalized output optical power of the LED can be expressed as a polynomial using a Taylor series expansion as follows:
where is output power, t is the time, and is the coefficient of the l-th-order power of the transfer function. Since the majority of the nonlinear components are concentrated in terms up to the second order [10], we modeled the nonlinearity using the following quadratic equation:
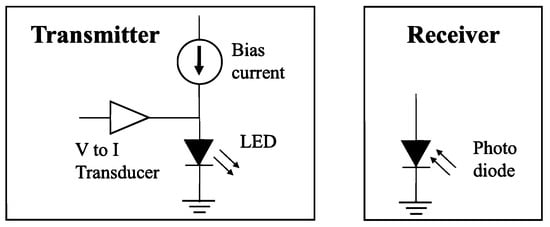
Figure 2.
LED driver circuit.
Here, , , , and represent the nonlinear coefficients and parameter. In addition, exhibits distinct values corresponding to different LED types.
- White LED: = 0.582.
- IR LED: = 0.541.
- Red LED: = 0.732.
The red LED has the most pronounced distortion, with its normalized output power deviating to approximately 1.2–1.3 times the white and IR LED values near a normalized driving current I of 0.5. Due to the significant differences in nonlinear distortion depending on the type of LED, the BER performance varies considerably, especially in higher-order modulation schemes [10]. Additionally, we set the normalized DC current for simulations in this work.
3. Proposed Methods
In this section, we first introduce the proposed method for compensating for the nonlinear distortion of LEDs using adaptive pre-distortion. Next, we present the nonlinear distortion estimation method applied to the proposed approach. Furthermore, to ensure adaptability in real-world environments, we integrate FSS into the proposed method to mitigate the impact of channel distortion.
3.1. Adaptive Pre-Distortion System
In this paper, as shown in Figure 3, we aim to enable optimal pre-distortion compensation for all LEDs at the time of transmission by estimating the nonlinear characteristics of LEDs at the receiver and feeding back the nonlinear coefficients representing these characteristics to the transmitter as FBI. After channel equalization, we estimate nonlinear coefficients obtained by IFFT on the received signal , and obtained by IFFT on the signal after detection . From now on in this work, and used in coefficient estimation will be referred to as reference signals, and N is the number of reference signals used.
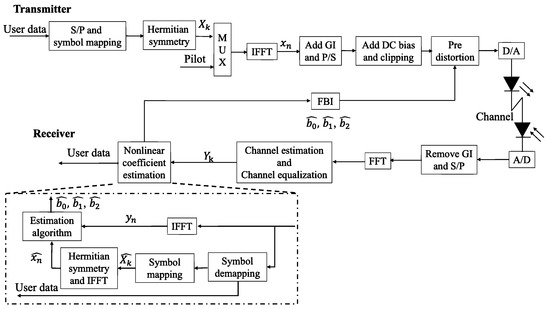
Figure 3.
Proposed adaptive compensation system.
In this work, we use the least squares method (LSM) and median-based method (MBM) as nonlinear coefficients estimation techniques. Specifically, the implementation of pre-distortion using the inverse function of the nonlinear characteristics with the nonlinear coefficients fed back by the FBI enables optimal compensation for all LEDs in the system.
3.1.1. Least Squares Method (LSM)
LSM estimates nonlinear coefficients by minimizing the squared error between reference signals and . LSM for the signal after channel equalization is described in Figure 4. In this case, vector can be determined as follows:
where , , and are represented as
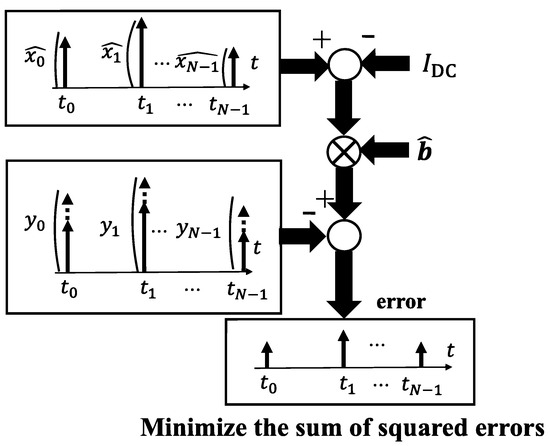
Figure 4.
Principle of LSM.
By determining in this manner, the influence of noise is effectively mitigated.
Denoting the number of reference signals used as N, this algorithm has a computational complexity of .
3.1.2. Median Based Method (MBM)
The overall workflow is schematically illustrated in Figure 5. For the channel-equalized signals, it can be shown that the nonlinear coefficients can be estimated by solving the following equation using x and y:
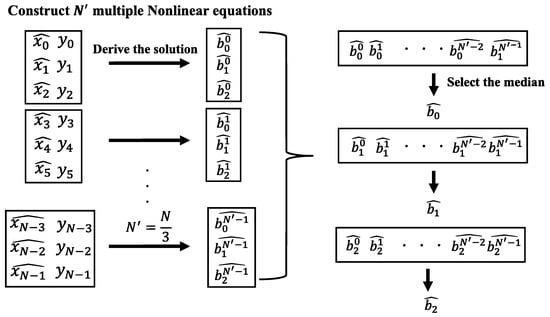
Figure 5.
Principle of MBM.
However, relying on a single equation set results in strong susceptibility to noise, leading to significant estimation errors. To mitigate this issue, we propose MBM. Specifically, multiple sets of independent equations are solved to generate a sequence of coefficient candidates. The final estimate coefficient is then obtained by selecting the median of these candidates.
where . This approach effectively reduces the impact of noise by leveraging the statistical robustness of the median operator, which inherently suppresses outliers caused by impulsive noise or transient distortions. However, this algorithm has a computational complexity of , and therefore higher than that of LSM.
3.2. Adaptive Pre-Distortion System Using FSS
In practical VLC environments, Rician fading is expected to occur. However, this effect can be mitigated using FSS [18]. The FSS process follows the structure illustrated in Figure 6. FSS is a technique in which each subcarrier is randomly spread, as illustrated in Figure 6, and then restored at the receiver, thereby equalizing the SNR across all subcarriers of the received signal. The integrated communication system is depicted in Figure 7. At the transmitter, the modulated signal with for each subcarrier is spread using a pseudonoise (PN) sequence and then summed. In this case, the m-th subcarrier of the n-th OFDM symbol, denoted as , can be expressed as follows:
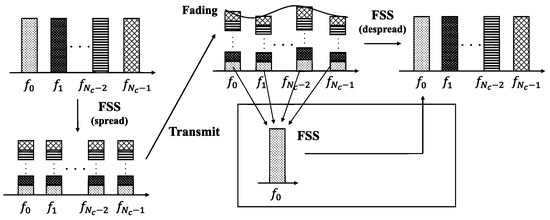
Figure 6.
Concept of FSS.
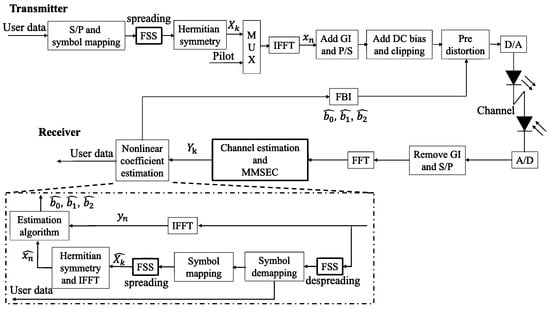
Figure 7.
Proposed adaptive compensation system using FSS.
Through the spreading process of FSS, the impact of frequency-selective fading such as Rician fading is mitigated by equalizing the SNR per subcarrier for .
At the receiver, after channel estimation, Minimum Mean Square Error Combining (MMSEC) is performed using the following equation to preserve the orthogonality of the PN sequence applied during transmission:
Here, r is the received signal and the MMSEC weighting is expressed using the estimated channel and the estimated noise power per subcarrier in the following equation:
Here, S is the average transmitted power. In FSS, despreading is performed, and the detected signal is expressed in the following equation:
Furthermore, by demapping the detected signal and reconstructing the transmitted signal , the nonlinear coefficient b can be estimated by inputting both and the distorted signal into the nonlinear coefficient estimator.
4. Computer Simulation
This section first evaluates and compares the proposed nonlinear coefficient estimation methods to select the most effective approach. Next, the selected method is assessed for its effectiveness in addressing channel distortions under conditions close to real-world environments using FSS. Finally, the feasibility of the proposed method is evaluated by simulating it under realistic lighting conditions with variations in nonlinear parameters .
4.1. Comparison of the Proposed Methods
To facilitate a clear understanding of the performance differences between the two proposed methods, this simulation considers a single-LED illumination system with no variation in nonlinear parameters. The simulation parameters are summarized in Table 1. For the nonlinear parameter characterization, white LEDs were assumed, and the channel model assumes Additive White Gaussian Noise (AWGN). The reason for selecting 16QAM and 64QAM modulation schemes in this study is that these schemes, compared to QPSK or BPSK, carry a greater amount of information and require the consideration of amplitude. Consequently, they are more susceptible to nonlinear effects, thereby facilitating the verification of the effectiveness of the proposed method.

Table 1.
Simulation parameters.
Figure 8 presents the BER performance. The number of reference signals used was 50 for LSM and 600 for MBM in 16QAM, and both methods employed 750 reference signals for 64QAM. At a target BER of , LSM demonstrated an improvement of 2.0 dB compared to the nonlinear LED model for 16QAM and 0.7 dB over MBM. At a target BER of , for 64QAM, a 0.3 dB enhancement was achieved.
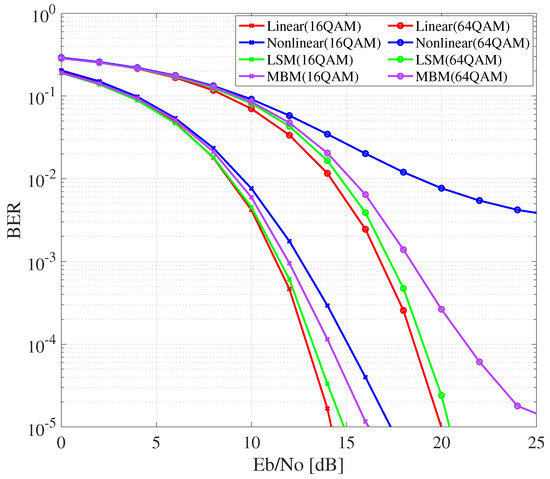
Figure 8.
BER performance with various methods.
Figure 9 illustrates the parameter estimation accuracy under 64QAM modulation with a fixed = 21 dB. The results validate the robustness of the proposed estimation framework, particularly under high-order modulation schemes. Since is the coefficient of the squared term, we focus on this parameter. When using 15 reference signals, the mean absolute error (MAE) of with LSM falls to compared to the MBM. Additionally, for the LSM, it can be observed that the MAE saturates with fewer symbols. For example, in Figure 9, for , the MAE saturates at a reference signal count of six for LSM and at nine for MBM. Therefore, with a simple calculation, the computational complexity at saturation is reduced to 1/13 in LSM.
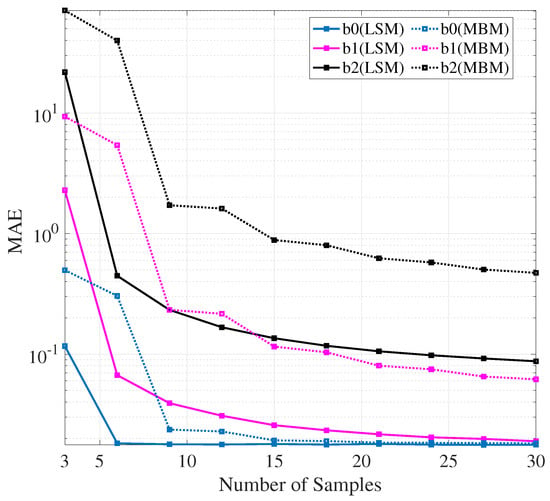
Figure 9.
Parameter estimation accuracy of various methods.
4.2. Evaluation of Rician Fading Impact on and Effectiveness of Proposed Method Using FSS
In the previous section, evaluations were conducted in an AWGN environment. To address conditions closer to real-world scenarios, specifically Rician fading environments, the proposed method integrated with FSS was evaluated. Since the previous section demonstrated that the nonlinear coefficient estimation using LSM achieved favorable estimation accuracy, the focus of this evaluation was on LSM. The simulation parameters were modified from those listed in Table 1, specifically altering the channel model and the number of reference signals. The channel model was configured to represent a three-path Rician fading environment, and the number of reference signals was set to 300.
To evaluate the BER performance under Rician fading, we introduce a parameter known as the K-factor. The K-factor in Rician fading is defined as follows:
where is the power of the Line-of-Sight (LOS) component, while is the total power of the Non-Line-of-Sight (NLOS) components. The K-factor typically ranges from 5 to 25 dB in office environments [20]. In this section, to verify the effectiveness of the method under more challenging conditions, K-factors of 0, 5, and 10 dB were set. Additionally, the lighting conditions remained consistent with those in the previous section.
The BER performance of the proposed method with and without FSS is illustrated in Figure 10, Figure 11 and Figure 12. The proposed method utilizing FSS demonstrated an improvement in by approximately 4.0 dB at K = 0 dB and 1.5 dB at K = 5 dB for a BER of . However, almost no improvement was observed at K = 10 dB. This is attributed to the increasing dominance of the LOS component as K increases, which diminishes the effectiveness of SNR equalization by FSS. Interestingly, for all K-factors, the uncompensated LED exhibited slightly worse BER performance when FSS was used. This degradation is likely due to the nonlinear distortion of the LED, which disrupts the orthogonality of the multiplied during transmission, leading to signal deterioration during despreading at the receiver. Supporting this observation, the BER performance of the linear LED and the proposed compensation method showed better results when FSS was employed. This improvement is attributed to the preservation of orthogonality through distortion compensation.
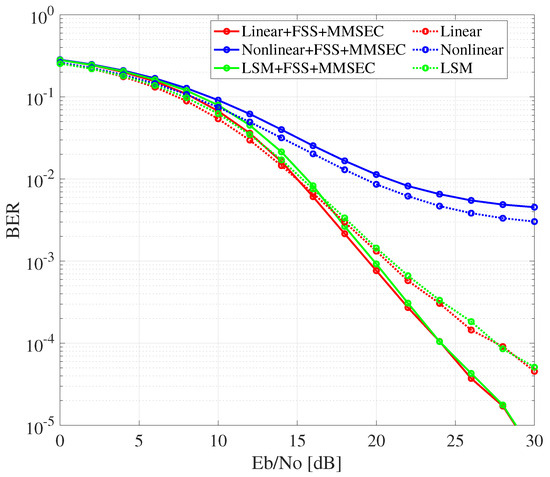
Figure 10.
BER performance of proposed method in Rician fading environment (K = 0 dB).
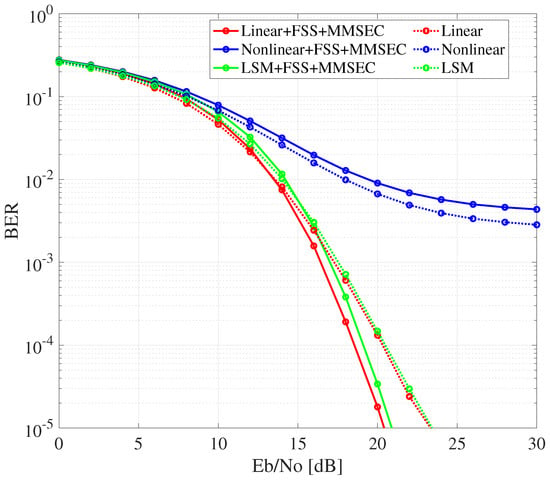
Figure 11.
BER Performance of proposed method in Rician fading environment (K = 5 dB).
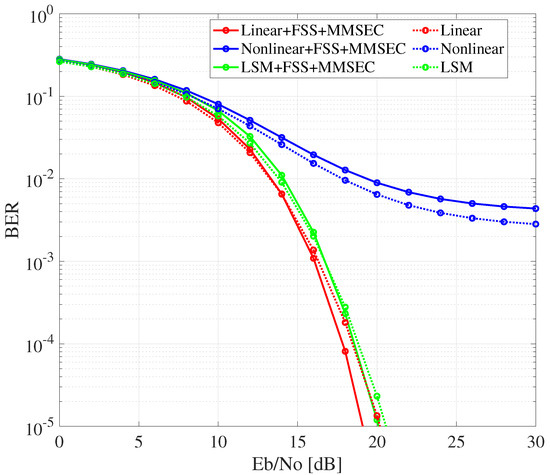
Figure 12.
BER performance of proposed method in Rician fading environment (K = 10 dB).
The estimation accuracy of nonlinear coefficients using the proposed method, with and without FSS, in a Rician fading environment is shown in Figure 13. As in the previous section, each simulation was conducted with a fixed = 21 dB.
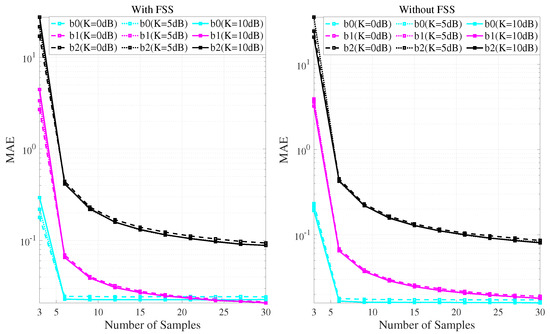
Figure 13.
Estimation accuracy of proposed methods in Rician fading environment.
When the proposed method employs FSS, as well as when it does not, the estimation performance remains almost unchanged regardless of the increase or decrease in the K-factor. This can be attributed to the fact that the BER performance of the uncompensated nonlinear LED is unaffected by variations in the K-factor, implying that the quality of the regenerated signal before distortion , which is used for nonlinear coefficient estimation, is not significantly influenced by the K-factor. Therefore, the proposed nonlinear estimation method demonstrates robustness against variations in the K-factor. Furthermore, in the proposed method utilizing FSS, the coefficient exhibits approximately a 10% degradation compared to the proposed method without FSS. This degradation is likely due to the fact that the uncompensated LED signal, which is used for nonlinear coefficient estimation in the proposed method, experiences a decline in BER performance when FSS is applied. However, when considering the overall system BER performance, the impact of this degradation in estimation accuracy is minimal.
However, when considering the overall BER performance of the system, the impact of the degradation in estimation accuracy is minor. Since the benefits of employing FSS outweigh this slight degradation, the system performance improves as previously described.
4.3. Feasibility of Applying the Proposed Method to Realistic Illumination Models
In the previous sections, the evaluation was conducted using a lighting setup consisting of a single LED without variations in nonlinear coefficients. However, in real-world applications, LED chips exhibit variations in nonlinear coefficients, and a single LED chip has a low luminous flux [21]. Consequently, LED lightings are typically composed of multiple chips, leading to a more complex nonlinear distortion. In this section, we evaluate the effectiveness of the proposed method under such realistic lighting conditions to verify its practical applicability. The simulation parameters are mostly inherited from the previous section, only with changes to and the nonlinear parameters. Specifically, is fixed at 20 dB, while the nonlinear parameters are randomly varied according to a normal distribution with a standard deviation of 0.04. The reason for setting the standard deviation to 0.04 is to assess the practicality of the proposed method under a relatively large variation. The deviation of 0.04 from the nonlinear parameter of white LEDs, = 0.582, nearly matches that of infrared (IR) LEDs, suggesting that such a large variation in standard deviation is unlikely in practical scenarios. Additionally, the simulations assume a three-path Rician fading environment with K = 5 dB. The BER characteristics of the two proposed methods under an increasing number of LEDs per lighting setup are shown in Figure 14.
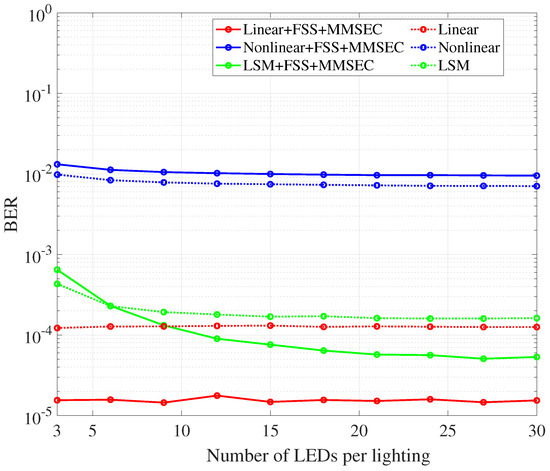
Figure 14.
BER performance of the proposed method in realistic lighting conditions.
As shown in the simulation results, both proposed methods demonstrate a consistent reduction in BER as the number of LEDs increases. This improvement can be attributed to the statistical averaging effect inherent to the normal distribution. Even if a subset of LEDs exhibits significant nonlinear distortion, the collective contribution of multiple LEDs mitigates the impact of outliers through mutual compensation between highly nonlinear and nearly linear parameter sets. For nonlinear LEDs without compensation, the BER reduction for both proposed approaches saturated at approximately . However, after applying pre-distortion compensation using LSM, the BER was reduced to around for both methods, demonstrating the practical feasibility of the proposed approach. Moreover, the current results indicate that the proposed method incorporating FSS achieves better BER performance than the method without FSS when the number of LEDs is six or more, with the improvement saturating at 24 LEDs. Although the necessary number of LEDs may vary depending on the K and , in practical applications, the communication system can be designed by pre-assessing the method both used with and without FSS configurations to maximize the benefits of FSS.
5. Conclusions
We propose an adaptive pre-distortion scheme for VLC OFDM that takes into account the nonlinear characteristics of LEDs. In the proposed scheme, to reduce the computational resources required at the transmitter in conventional nonlinear compensation methods, the nonlinear characteristics of the LED are estimated at the receiver, and the resulting information is fed back via FBI. Compensation is achieved at the transmitter by multiplying the transmitted signal by the inverse function of the estimated information. Two estimation methods are introduced, namely LSM and MBM. In addition, a method that incorporates FSS is integrated into the proposed scheme to address channel distortion in real-world environments. Simulation results under AWGN conditions confirm that both proposed estimation methods improve the bit error rate performance. Moreover, LSM offers lower computational complexity and attains high estimation performance even with a reduced number of reference signals when compared with MBM. Simulations in a Rician fading environment indicate that LSM maintains robust nonlinear estimation performance despite variations in the K-factor and that the incorporation of FSS further enhances BER performance. Finally, simulations conducted under realistic lighting conditions demonstrate favorable BER performance, thereby confirming the practical viability of the proposed scheme.
6. Future Research and Work
This section identifies potential research directions and applicable fields from the following three perspectives.
6.1. Adaptation to VLC-OFDM-Based Indoor Positioning Techniques
Advancements in IoT and factory automation (FA) have created a growing demand for high-precision indoor positioning technologies [22,23]. VLC is particularly promising due to its sharp directionality and reduced multipath attenuation compared to RF-based systems [24]. Among VLC approaches, integration with VLC-OFDM systems has been actively studied to achieve scalability and multi-user compatibility, enabling dual-purpose utilization of VLC for both data communication and positioning [25,26]. Concretely, this technology estimates channel responses from pilot signals transmitted by multiple LEDs and calculates the time difference of arrival (TDOA) to determine user positions. However, nonlinear distortions in LED transmitters critically degrade the accuracy of channel estimation and TDOA measurements. To address this challenge, our study aims to implement a positioning system with enhanced accuracy by applying the proposed nonlinear compensation method, thereby mitigating distortion-induced errors in VLC-based positioning.
6.2. Reduction in Required Number of Reference Signals N
The computational time of the proposed nonlinear compensation method increases in proportion to the required number of reference signals, N. The optimal value of N varies depending on nonlinear parameter and SNR. Therefore, if the SNR and the degree of distortion are known in advance, the required N can be estimated. By estimating the SNR and equipping the receiver with color filters corresponding to the transmitter LEDs to pre-limit the received color components, the necessary number of reference signals can be reduced, thereby decreasing the computational time.
6.3. Application to Adaptive Modulation Techniques
In VLC-OFDM, adaptive modulation techniques that dynamically adjust modulation schemes based on channel state information have been actively researched [27,28]. Through this study, improvements in BER performance have been achieved, enabling the use of higher-order modulation schemes under identical channel conditions. Consequently, adaptive modulation transmission with enhanced throughput is now feasible. Further analysis and the development of optimal adaptive modulation algorithms will be addressed in subsequent research.
Author Contributions
K.S. is the main author. R.O. and G.K. assisted with the methodology and software and provided constructive feedback on every part of the manuscript. C.-J.A. acted as supervisor. All authors have read and agreed to the published version of the manuscript.
Funding
Grant of Science Research from the Japan Society for the Promotion of Science (JSPS) 22K04085.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Dogra, A.; Jha, R.K.; Jain, S. A Survey on Beyond 5G Network with the Advent of 6G: Architecture and Emerging Technologies. IEEE Access 2021, 9, 67512–67547. [Google Scholar] [CrossRef]
- Eryilmaz, A.; Srikant, R. Fair Resource Allocation in Wireless Networks Using Queue-Length-Based Scheduling and Congestion Control. IEEE/ACM Trans. Netw. 2007, 15, 1333–1344. [Google Scholar] [CrossRef]
- Andras, C.M.; Barb, G.; Alexa, F.; Balint, C. Congestion Analysis of Transport Layer in a Multicell 5G DL Communication System. Sensors 2023, 23, 6111. [Google Scholar] [CrossRef] [PubMed]
- Al Hasnawi, R.; Marghescu, I. A Survey of Vehicular VLC Methodologies. Sensors 2024, 24, 598. [Google Scholar] [CrossRef] [PubMed]
- Rehman, S.U.; Ullah, S.; Chong, P.H.J.; Yongchareon, S.; Komosny, D. Visible Light Communication: A System Perspective—Overview and Challenges. Sensors 2019, 19, 1153. [Google Scholar] [CrossRef] [PubMed]
- Geng, Z.; Khan, F.N.; Guan, X.; Dong, Y. Advances in Visible Light Communication Technologies and Applications. Photonics 2022, 9, 893. [Google Scholar] [CrossRef]
- Matus, V.; Maturana, N.; Azurdia-Meza, C.A.; Montejo-Sánchez, S.; Rojas, J. Hardware design of a prototyping platform for vehicular VLC using SDR and exploiting vehicles CAN bus. In Proceedings of the 2017 First South American Colloquium on Visible Light Communications (SACVLC), Santiago, Chile, 13 November 2017; pp. 1–4. [Google Scholar]
- Marshoud, H.; Sofotasios, P.C.; Muhaidat, S.; Karagiannidis, G.K. Multi-user techniques in visible light communications: A survey. In Proceedings of the 2016 International Conference on Advanced Communication Systems and Information Security (ACOSIS), Marrakesh, Morocco, 17–19 October 2016; pp. 1–6. [Google Scholar]
- Loureiro, P.A.; Guiomar, F.P.; Monteiro, P.P. Visible Light Communications: A Survey on Recent High-Capacity Demonstrations and Digital Modulation Techniques. Photonics 2023, 10, 993. [Google Scholar] [CrossRef]
- Inan, B.; Jeffrey Lee, S.C.; Randel, S.; Neokosmidis, I.; Koonen, A.M.J.; Walewski, J.W. Impact of LED Nonlinearity on Discrete Multitone Modulation. J. Opt. Commun. Netw. 2013, 1, 439–451. [Google Scholar] [CrossRef]
- Laakso, M.; Dowhuszko, A.A.; Wichman, R. Empirical evaluation of OFDM waveforms for VLC in the presence of LED nonlinearities. In Proceedings of the 2021 IEEE 32nd Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Helsinki, Finland, 13–16 September 2021; pp. 465–470. [Google Scholar]
- Elgala, H.; Mesleh, R.; Haas, H. A study of LED nonlinearity effects on optical wireless transmission using OFDM. In Proceedings of the 2009 IFIP International Conference on Wireless and Optical Communications Networks, Cairo, Egypt, 28–30 April 2009; pp. 1–5. [Google Scholar]
- Zhang, X.; Liu, P.; Liu, J.; Liu, S. An advanced A-law companding algorithm in VLC-OFDM. In Proceedings of the 2014 IEEE 3rd Global Conference on Consumer Electronics (GCCE), Tokyo, Japan, 7–10 October 2014; pp. 721–722. [Google Scholar]
- Mathias, L.C.; Marinello Filho, J.C.; Abrao, T. Predistortion and Pre-equalization for Nonlinearities and Low-pass Effect Mitigation in OFDM-VLC Systems. Appl. Opt. 2019, 58, 5328–5338. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Jin, J.; Wang, J. Alleviation of LED Nonlinearity Impact in Visible Light Communication Using Companding and Predistortion. IET Commun. 2019, 13, 818–821. [Google Scholar] [CrossRef]
- Wu, X.; Hu, F.; Zou, P.; Chi, N. Application of Gaussian Mixture Model to Solve Inter-Symbol Interference in PAM8 Underwater Visible Light System Communication. IEEE Photonics J. 2019, 11, 1–10. [Google Scholar] [CrossRef]
- Wu, X.; Hu, F.; Zou, P.; Lu, X.; Chi, N. The Performance Improvement of Visible Light Communication Systems Under Strong Nonlinearities Based on Gaussian Mixture Model. Microw. Opt. Technol. Lett. 2020, 62, 547–554. [Google Scholar] [CrossRef]
- Ahn, C.-J.; Harada, H. Superimposed Frequency Symbol Based Adaptive Downlink OFDM with Frequency Spreading and Equalization. In Proceedings of the 2005 Asia-Pacific Conference on Communications, Perth, WA, Australia, 5 October 2005; pp. 1068–1072. [Google Scholar]
- Dissanayake, S.D.; Armstrong, J. Comparison of ACO-OFDM, DCO-OFDM and ADO-OFDM in IM/DD Systems. J. Lightw. Technol. 2013, 31, 1063–1072. [Google Scholar] [CrossRef]
- Liu, S.; Tang, P.; Zhang, J.; Yin, Y.; Tong, Y.; Liu, B.; Liu, G.; Xia, L. Statistical channel modeling for indoor VLC communications based on channel measurements. China Commun. 2024, 21, 131–147. [Google Scholar] [CrossRef]
- Skarżyński, K.; Żagan, W.; Krajewski, K. LED Luminaires: Many Chips—Many Photometric and Lighting Simulation Issues to Solve. Energies 2021, 14, 4646. [Google Scholar] [CrossRef]
- Terças, L.; Alves, H.; de Lima, C.H.M.; Juntti, M. Bayesian-Based Indoor Factory Positioning Using AOA, TDOA, and Hybrid Measurements. IEEE Internet Things J. 2024, 11, 21620–21631. [Google Scholar] [CrossRef]
- Nikonowicz, J.; Mahmood, A.; Ashraf, M.I.; Björnson, E.; Gidlund, M. Indoor Positioning in 5G-Advanced: Challenges and Solution Toward Centimeter-Level Accuracy with Carrier Phase Enhancements. IEEE Wirel. Commun. 2024, 31, 268–275. [Google Scholar] [CrossRef]
- Bastiaens, S.; Alijani, M.; Joseph, W.; Plets, D. Visible Light Positioning as a Next-Generation Indoor Positioning Technology: A Tutorial. IEEE Commun. Surv. Tutor. 2024, 26, 2867–2913. [Google Scholar] [CrossRef]
- Ghimire, B.; Seitz, J.; Mutschler, C. Indoor Positioning Using OFDM-Based Visible Light Communication System. In Proceedings of the 2018 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Nantes, France, 24–27 September 2018; pp. 1–8. [Google Scholar]
- Aminikashani, M.; Gu, W.; Kavehrad, M. Indoor positioning with OFDM Visible Light Communications. In Proceedings of the 2016 13th IEEE Annual Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 9–12 January 2016; pp. 505–510. [Google Scholar]
- Tettey, D.K.; Elamassie, M.; Uysal, M. Implementation of Software-Defined Adaptive DCO-OFDM for Vehicular Visible Light Communication. In Proceedings of the 2023 2nd International Conference on 6G Networking (6GNet), Paris, France, 18–20 October 2023; pp. 1–3. [Google Scholar]
- Wu, L.; Zhang, Z.; Dang, J.; Liu, H. Adaptive Modulation Schemes for Visible Light Communications. J. Lightw. Technol. 2015, 33, 117–125. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).