Damage Behaviour of Quasi-Brittle Composites: Mathematical and Computational Aspects
Abstract
1. Introduction
2. Physical Background and Engineering Simplifications
3. A Model Problem
3.1. Mathematical Preliminaries
3.2. The First Step: A Viscoelastic Model
3.3. The Second Step: Incorporation of Damage
- (i)
- For any fixed , compute three scalar principal values , , corresponding to , the computations being made on . Denoting by I the unit matrix in , it is necessary to find three eigenvalues satisfying
- (ii)
- (iii)
- Introduce the nonlocal form of from (21), motivated by [64], asfor all , with a fixed . A regularising kernel , as suggested by [65], is required in (22) as well.The following approach avoids the problems connected with the non-existence of the solution in the sense of examples from [66,67]. Using the Dirac measure , the seemingly simple choice , followed by , is not allowed, in contrast to the Gaussian kernel from [68] or to the various classes of radial basis function approximations from [69,70].
- (iv)
- Applying the result of (22), evaluate a trial value of damageusing a non-decreasing real continuous function .
- (v)
- Force the irreversibility of damage by (23), i.e., the non-decreasing damage factor in time, using the formula
4. Possible Generalizations
4.1. From Quasi-Static to Dynamic Models
4.2. Macroscopic Cracks and Cohesive Interfaces
4.3. Proper Thermodynamic Formulations
4.4. Structured Deformation
4.5. Contribution of Differential Geometry
5. Computational Approaches
5.1. Finite-Dimensional Schemes
5.2. Illustrative Example
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Section | Item(s) | Topics |
|---|---|---|
| 1 | [1,2,3,4,5,6,7,8] | damage classification: ductile vs. brittle vs. quasi-brittle damage |
| 1 | [9] | review of models for composite structures |
| 1 | [10,11,12,13,14] | multiscale approaches: from electronics up to macroscopic scale |
| 1 | [15,16] | monographs of classical thermomechanics |
| 1 | [17,18] | example of scale bridging for concrete |
| 1 | [19,20,21] | probabilistic computational techniques |
| 1 | [22,23,24,25,26,27] | Mazars model for concrete |
| 1 | [28,29,30,31,32,33,34,35,36] | alternatives and reformulations of Mazars model |
| 1 | [37,38,39,40,41,42,43,44,45,46,47,48] | useful recent results of authors and their collaborators at BUT |
| 2 | [49] | approaches to damage modelling |
| 2 | [50,51,52] | models containing generalized viscoelastic Kelvin chains |
| 3 | [53,54,55,56] | functional analysis: traditional results |
| 3 | [57,58] | functional analysis: modern results |
| 3 | [59] | line geometry |
| 3 | [60] | method od lines for partial differential equations |
| 3 | [61,62] | functional analysis: auxiliary lemmas |
| 3 | [63,64,65,66,67,68,69,70] | nonlocal stresses and damage factor(s) |
| 3 | [71] | functional analysis: an auxiliary result |
| 4 | [72,73] | fundamentals of finite element method(s) |
| 4 | [74,75,76,77] | generalized/extended finite element methods |
| 4 | [78,79] | functional analysis: non-Lipchitzian domains |
| 4 | [80,81] | coupled failure engineering models |
| 4 | [82,83,84] | thermodynamic formulations based on Gibbs energy |
| 4 | [85] | theory of subdifferentials |
| 4 | [86] | thermodynamics of selected materials and processes |
| 4 | [87,88,89] | from small strains/stresses to finite geometry formulations |
| 4 | [90,91,92,93,94,95,96,97] | structured deformation: fundamentals of geometry and physics |
| 4 | [98,99,100,101] | structured deformation: auxiliary lemmas |
| 4 | [102,103,104,105,106] | from Boltzmann to Cosserat continuum |
| 4 | [107,108,109,110,111,112,113] | fundamentals of differential geometry |
| 4 | [114,115] | Weil bundles, Stiefel and Grassmann manifolds |
| 5 | [116,117,118] | numerical solution of nonlinear algebraic systems of equations |
| 5 | [119,120] | adaptive strategies with enrichment functions |
References
- Sumi, I. Mathematical and Computational Analyses of Cracking Formation; Springer: Tokyo, Japan, 2014. [Google Scholar]
- Wisnom, M.R.; Pimenta, S.; Shaffer, M.S.P.; Robinson, P.; Potter, K.D.; Hamerton, I.; Czél, G.; Jalalvand, M.; Fotouhi, M.; Anthony, D.B.; et al. High performance ductile and pseudo-ductile polymer matrix composites: A review. Compos. Part A 2024, 181, 108029. [Google Scholar]
- Cai, W.; Sun, C.; Wang, C.; Qian, L.; Fu, M.F. In-situ experiment and numerical modelling of the intragranular and intergranular damage and fracture in plastic deformation of ductile alloys. Int. J. Plast. 2025, 185, 104217. [Google Scholar]
- Lacondemine, T.; Moriceau, J.; To, T.; Houizot, P.; Célarié, P.; Galusek, D.; Kraxner, J.; Vandenhende, M.; Delaizir, G.; Langlois, R.; et al. Fracture behavior of brittle particulate composites consisting of a glass matrix and glass or ceramic particles with elastic property mismatch. Materialia 2024, 38, 102278. [Google Scholar]
- Papanikolaou, S.; Shanthraj, P.; Thibault, J.; Woodward, C.; Roters, F. Brittle to quasi-brittle transition and crack initiation precursors in crystals with structural inhomogeneities. J. Mater. Sci. Mater. Theory 2019, 3, 5. [Google Scholar]
- Zhu, L.; Hao, L.; Shen, W.; Zhu, C. Quasi-brittle fracture performance of glass fiber composites based on boundary effect model. Eng. Fract. Mech. 2023, 287, 109305. [Google Scholar]
- Luo, P.; Shen, W.; Chen, L.; Yao, Z.; Li, Q.; Zhu, L. Fracture properties of carbon/glass fiber composite laminates with surface scratch damage. Compos. Struct. 2025, 352, 118673. [Google Scholar]
- Islam, S.U.; Waseem, S.A. An experimental study on mechanical and fracture characteristics of hybrid fibre reinforced concrete. Structures 2024, 68, 107053. [Google Scholar]
- Yu, W. A review of modeling of composite structures. Materials 2024, 17, 446. [Google Scholar] [CrossRef]
- Steinhauser, M.O. Computational Multiscale Modelling of Fluids and Solids; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Su, Z.; Oskay, C. Modeling arbitrarily oriented and reorienting multiscale cracks in composite materials with adaptive multiscale discrete damage theory. Comput. Mech. 2022, 70, 1041–1058. [Google Scholar]
- Xian, F.; Zhou, J.; Lian, X.; Shen, J.; Chen, Y. Molecular dynamics simulation of crack propagation in very small grain size nanocopper with different grain size gradients. R. Soc. Chem. Adv. 2024, 14, 616–625. [Google Scholar]
- Du, C.; Huang, W.; Ghaemian, M.; Jiang, S.; Zhao, Z. New nonlocal multiscale damage model for modelling damage and cracking in quasi-brittle materials. Eng. Fract. Mech. 2023, 277, 108927. [Google Scholar] [CrossRef]
- de Borst, R. Fracture and damage in quasi-brittle materials: A comparison of approaches. Theor. Appl. Fract. Mech. 2022, 122, 103652. [Google Scholar] [CrossRef]
- de Castro, A.B. Continuum Thermomechanics; Birkhäuser: Basel, Switzerland, 2005. [Google Scholar]
- Papenfuß, C. Continuum Thermodynamics and Constitutive Theory; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Dutta, S.; Kishen, J.M.C. Micromechanical damage model for plain concrete considering propagation of matrix microcracks. Phys. Mesomech. 2019, 22, 96–106. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. A 1957, 241, 376–396. [Google Scholar]
- Bažant, Z.P.; Le, J.-L. Probabilistic Mechanics of Quasibrittle Structures; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Qi, C.; Lu, C.; Chanyshev, A.I.; Li, X.; Qu, X. Preliminary study on the determination of the Weibull modulus of strength distribution in quasi-brittle materials. Geohazard Mech. 2023, 1, 103–109. [Google Scholar] [CrossRef]
- Wu, J.-Y.; Yao, J.-R.; Le, J.-L. Phase-field modeling of stochastic fracture in heterogeneous quasi-brittle solids. Comput. Methods Appl. Mech. Eng. 2023, 416, 116332. [Google Scholar] [CrossRef]
- Mazars, J. A description of micro- and macroscale damage of concrete structures. Eng. Fract. Mech. 1986, 25, 729–737. [Google Scholar] [CrossRef]
- Jirásek, M. Damage and smeared crack models. In Numerical Modelling of Concrete Cracking; Hofstetter, G., Meschke, G., Eds.; Springer: Vienna, Austria, 2011; pp. 1–49. [Google Scholar]
- Mazars, J.; Hamon, F.; Grang, S. A new 3D damage model for concrete under monotonic, cyclic and dynamic loadings. Mater. Struct. 2015, 48, 3779–3793. [Google Scholar] [CrossRef]
- Havlásek, P.; Grassl, P.; Jirásek, M. Analysis of size effect on strength of quasi-brittle materials using integral-type nonlocal models. Eng. Fract. Mech. 2016, 157, 72–85. [Google Scholar] [CrossRef]
- Bui, T.Q.; Tran, H.T.; Hu, X.; Wu, C.-T. Simulation of dynamic brittle and quasi-brittle fracture: A revisited local damage approach. Int. J. Fract. 2022, 236, 59–85. [Google Scholar] [CrossRef]
- dos Santos, E.J., Jr.; Krahl, P.A.; Monteiro, F.A.C.; Cordeiro, S.G.F. New damage evolution law in plastic damage models for fiber-reinforced cementitious composites. Struct. Concr. 2024, 25, 440–455. [Google Scholar]
- Pereira, L.; Weerheijm, J.; Sluys, L. A numerical study on crack branching in quasi-brittle materials with a new effective rate-dependent nonlocal damage model. Eng. Fract. Mech. 2017, 182, 689–707. [Google Scholar] [CrossRef]
- Lipton, R.P.; Bhattacharya, D. Energy balance and damage for dynamic fast crack growth from a nonlocal formulation. J. Elast. 2025, 157, 5. [Google Scholar] [CrossRef]
- Sun, B.; Guo, T. Multiple factors-based damage level assessment method of concrete structures based on evidential reasoning and particle swarm optimization. Eng. Struct. 2024, 316, 118626. [Google Scholar] [CrossRef]
- Zhang, T.; Li, X.; Hou, Z.; Chen, F.; Fang, Y.; Sun, W. An improved damage plastic model for RC structure FE modelling under cyclic loading conditions. Eng. Struct. 2025, 322, 119135. [Google Scholar] [CrossRef]
- Vodička, R. A computational approach for phase-field model of quasi-brittle fracture under dynamic loading. Int. J. Fract. 2024, 248, 127–152. [Google Scholar] [CrossRef]
- Ulloa, J.; Rodríguez, P.; Samaniego, C.; Samaniego, E. Phase-field modeling of fracture for quasi-brittle materials. Undergr. Space 2019, 4, 10–21. [Google Scholar] [CrossRef]
- Arruda, M.R.T.; Pacheco, J.; Castro, L.M.S.; Julio, E. A modified Mazars damage model with energy regularization. Theor. Appl. Fract. Mech. 2023, 124, 108129. [Google Scholar] [CrossRef]
- Bobiński, J.; Chodkowski, P.; Schönnagel, J. Examination of advanced isotropic constitutive laws under complex stress states in plain and reinforced concrete specimens. In Computational Modelling of Concrete and Concrete Structures; Meschke, G., Pichler, B., Rots, J.G., Eds.; Vienna University of Technology: Vienna, Austria, 2022; pp. 486–495. [Google Scholar]
- Bonhomme, É. Perfect plasticity versus damage: An unstable interaction between irreversibility and Γ-convergence through variational evolutions. ESAIM Control Optim. Calc. Var. 2024, 30, 34. [Google Scholar] [CrossRef]
- Kozák, V.; Chlup, Z.; Padělek, P.; Dlouhý, I. Prediction of traction separation law of ceramics using iterative finite element method. Solid State Phenom. 2017, 258, 186–189. [Google Scholar] [CrossRef]
- Vala, J.; Kozák, V. Computational analysis of quasi-brittle fracture in fibre reinforced cementitious composites. Theor. Appl. Fract. Mech. 2020, 107, 102486. [Google Scholar] [CrossRef]
- Vala, J.; Kozák, V. Non-local damage modelling of quasi-brittle composites. Appl. Math. 2021, 66, 815–836. [Google Scholar] [CrossRef]
- Němec, I.; Vala, J.; Štekbauer, H.; Jedlička, M.; Burkart, D. New Methods in Collision of Bodies Analysis. Available online: https://dml.cz//handle/10338.dmlcz/703195 (accessed on 1 April 2025).
- Vala, J.; Rek, V. On a computational approach to multiple contacts/impacts of elastic bodies. In Proceedings of the 21st PANM Programs and Algorithms of Numerical Mathematics, Hejnice, Czech Republic, 21–26 June 2021; pp. 269–280. [Google Scholar]
- Vala, J. Numerical approaches to the modelling of quasi-brittle crack propagation. Arch. Math. 2023, 59, 295–303. [Google Scholar] [CrossRef]
- Tomáš, J. A higher-order and Weil generalization of Grassmannian. Proc. Struct. Integr. 2023, 43, 67–70. [Google Scholar] [CrossRef]
- Tomáš, J.; Petrák, F. Higher-order and Weil Grassmannian as a space of subalgebras of a Weil algebra. Filomat 2024, 38, 7755–7773. [Google Scholar]
- Trcala, M.; Suchomelová, P.; Bošanský, M.; Hokeš, F.; Němec, I. The generalized Kelvin chain-based model for an orthotropic viscoelastic material. Mech. Time-Depend. Mater. 2024, 28, 1639–1659. [Google Scholar] [CrossRef]
- Trcala, M.; Suchomelová, P.; Bošanský, M.; Němec, I. A constitutive model considering creep damage of wood. Mech. Time-Depend. Mater. 2024, 28, 163–183. [Google Scholar] [CrossRef]
- Kozák, V.; Vala, J. Use of cohesive approaches for modelling critical states in fibre-reinforced structural materials. Materials 2024, 17, 3177. [Google Scholar] [CrossRef] [PubMed]
- Vala, J. Computational smeared damage in the macroscopic analysis of quasi-brittle materials and structures. In Proceedings of the 22nd Algoritmy, Podbanské, Slovakia, 15–20 March 2024; pp. 46–55. [Google Scholar]
- Ren, H.; Rabczuk, T.; Zhuang, X. Variational damage model: A new paradigm for fractures. Front. Struct. Civ. Eng. 2025, 19, 1–21. [Google Scholar] [CrossRef]
- Serra-Aguila, A.; Puigoriol-Forcada, J.M.; Reyes, G.; Menacho, J. Viscoelastic models revisited: Characteristics and interconversion formulas for generalized Kelvin–Voigt and Maxwell models. Acta Mech. Sin. 2019, 35, 1191–1209. [Google Scholar] [CrossRef]
- Gai, P.; Xu, Z.; Spencer, B.F., Jr.; Dai, J.; Li, H. A generalized mechanical model with high-flexibility of viscoelastic damping materials and devices considering frequency and amplitude dependence effects. Eng. Struct. 2023, 288, 116131. [Google Scholar] [CrossRef]
- Al Janaideh, M.; Krejčí, P.; Monteiro, G.A. Memory reduction of rate-dependent Prandtl–Ishlinskiǐ compensators in applications on high-precision motion systems. Phys. B 2024, 677, 415595. [Google Scholar] [CrossRef]
- Kolář, V.; Kratochvíl, J.; Leitner, F.; Ženíšek, A. Berechnung von Flächen- und Raumtragwerken nach der Methode der Finiten Elemente; Springer: Vienna, Austria, 1975. [Google Scholar]
- Rektorys, K. Variational Methods in Mathematics, Science and Engineering; D. Reidel: Dordrecht, The Netherlands, 1977. [Google Scholar]
- Rektorys, K. The Method of Discretization in Time and Partial Differential Equations; D. Reidel: Dordrecht, The Netherlands, 1982. [Google Scholar]
- Kačur, J. Method of Rothe in Evolution Equations; Teubner: Leipzig, Germany, 1985. [Google Scholar]
- Roubíček, T. Nonlinear Partial Differential Equations with Applications; Birkhäuser: Basel, Switzerland, 2005. [Google Scholar]
- Drábek, P.; Milota, I. Methods of Nonlinear Analysis; Birkhäuser: Basel, Switzerland, 2013. [Google Scholar]
- Selig, J.M.; Martins, D. On the line geometry of rigid-body inertia. Acta Mech. 2014, 225, 3073–3101. [Google Scholar] [CrossRef][Green Version]
- Guzmán-Cajica, F.; Guzmán, F.S. Variational quantum Crank-Nicolson and method-of-lines schemes for the solution of initial value problems. Phys. Rev. A 2024, 110, 042415. [Google Scholar] [CrossRef]
- Ciarlet, P.G. On Korn’s Inequality. Chn. Ann. Math. 2010, 31B, 607–618. [Google Scholar] [CrossRef]
- Bühler, I.; Salomon, D.A. Functional Analysis; ETH: Zürich, Switzerland, 2017. [Google Scholar]
- de Vree, J.H.P.; Brekelmans, W.A.M.; van Gils, M.A.J. Comparison of nonlocal approaches in continuum damage mechanics. Comput. Struct. 1995, 55, 581–588. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal Continuum Field Theories; Springer: New York, NY, USA, 2002. [Google Scholar]
- Fasshauer, G.E.; Ye, Q. Reproducing kernels of generalized Sobolev spaces via a Green function approach with distributional operators. Num. Math. 2011, 119, 585–611. [Google Scholar] [CrossRef]
- Evgrafov, A.; Bellido, J.-C. From nonlocal Eringen’s model to fractional elasticity. Math. Mech. Solids 2019, 24, 1935–1953. [Google Scholar] [CrossRef]
- Ceballes, S.; Larkin, K.; Rojas, E.; Ghaffari, S.S.; Abdelkefi, A. Nonlocal elasticity and boundary condition paradoxes: A review. J. Nanopart. Res. 2021, 23, 66. [Google Scholar] [CrossRef]
- Giry, C.; Dufour, F.; Mazars, J. Stress-based nonlocal damage model. Int. J. Solids Struct. 2011, 48, 3431–3443. [Google Scholar] [CrossRef]
- Skala, V. A practical use of radial basis functions interpolation and approximation. Investig. Oper. 2016, 37, 137–145. [Google Scholar]
- Chang, G.; Zhang, X.; Yu, H. Spherical radial basis functions model: Approximating an integral functional of an isotropic Gaussian random field. J. Geod. 2024, 98, 105. [Google Scholar] [CrossRef]
- Brézis, H. Équations et inéquations non-linéaires dans les espaces vectoriel en dualité. Ann. Inst. Fourier 1968, 18, 115–176. [Google Scholar] [CrossRef]
- Belytschko, T.; Gracie, R.; Ventura, G. A review of extended/generalized finite element methods for material modeling. Modell. Simul. Mater. Sci. Eng. 2009, 17, 043001. [Google Scholar] [CrossRef]
- Reddy, J.N. An Introduction to the Finite Element Method; McGraw-Hill: New York, NY, USA, 1984. [Google Scholar]
- Li, H.; Li, J.; Yuan, H. A review of the extended finite element method on macrocrack and microcrack growth simulations. Theor. Appl. Fract. Mech. 2018, 97, 236–249. [Google Scholar] [CrossRef]
- Bento, M.H.C.; Proença, S.P.B.; Duarte, C.A. Well-conditioned and optimally convergent second-order Generalized/eXtended FEM formulations for linear elastic fracture mechanics. Comput. Methods Appl. Mech. Eng. 2022, 394, 114917. [Google Scholar] [CrossRef]
- Iarve, E.V.; Zhou, E.; Ballard, M.K.; Gao, Z.; Adluru, H.K.; Mollenhauer, D. Regularized X-FEM modeling of arbitrary 3D interacting crack networks. Int. J. Numer. Methods Eng. 2025, 126, e7653-18. [Google Scholar] [CrossRef]
- Pike, M.G.; Oskay, C. XFEM modelling of short microfibre reinforced composites with cohesive interfaces. Finite Elem. Anal. Des. 2005, 106, 16–31. [Google Scholar] [CrossRef]
- Burenkov, V.I. Sobolev Spaces on Domains; Teubner: Leipzig, Germany, 1998. [Google Scholar]
- Cianchi, A.; Maz’ya, V.G. Sobolev inequalities in arbitrary domains. Adv. Math. 2016, 293, 644–696. [Google Scholar] [CrossRef]
- Lu, X.; Guo, X.M.; Tan, V.B.C.; Tay, T.E. From diffuse damage to discrete crack: A coupled failure model for multi-stage progressive damage of composites. Comput. Methods Appl. Mech. Eng. 2021, 379, 113760. [Google Scholar] [CrossRef]
- Chafia, Z.; Yvonnet, J.; Bleyer, J.; Vincent, S.; El Ouafa, S. Massively parallel phase field fracture simulations on supercomputers: Towards multi-billion degree-of-freedom computations. Adv. Model. Simul. Eng. Sci. 2024, 11, 25. [Google Scholar] [CrossRef]
- Vilppo, J.; Kouhia, R.; Hartikainen, J.; Kolari, K.; Fedoroff, A.; Calonius, K. Anisotropic damage model for concrete and other quasi-brittle materials. Int. J. Solids Struct. 2021, 225, 111048. [Google Scholar] [CrossRef]
- Kamińska, I.; Szwed, A. A thermodynamically consistent model of quasibrittle elastic damaged materials based on a novel Helmholtz potential and dissipation function. Materials 2021, 14, 6323. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhou, Z.; Wu, M.; Zhen, Z. A thermodynamic based constitutive model considering the mutual influence of multiple physical fields. Nat. Sci. Rep. 2024, 14, 26417. [Google Scholar] [CrossRef]
- van Ackooij, W.; Atenas, F.; Sagastizába, C. Weak convexity and approximate subdifferentials. J. Optim. Theory Appl. 2024, 203, 1686–1709. [Google Scholar] [CrossRef]
- Kružík, M.; Roubíček, T. Mathematical Methods in Continuum Mechanics of Solids; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Branco, R.; Antunes, F.V.; Costa, J.D. A review on 3D-FE adaptive remeshing techniques for crack growth modelling. Eng. Fract. Mech. 2015, 141, 170–195. [Google Scholar] [CrossRef]
- Léger, S.; Pepin, A. An updated Lagrangian method with error estimation and adaptive remeshing for very large deformation elasticity problems: The three-dimensional case. Comput. Methods Appl. Mech. Eng. 2016, 309, 1–18. [Google Scholar] [CrossRef]
- Anantheswar, A.; Wollny, I.; Kaliske, M. Treatment of inelastic material models within a dynamic ALE formulation for structures subjected to moving loads. Int. J. Numer. Methods Eng. 2025, 126, e7599. [Google Scholar] [CrossRef]
- Del Piero, G.; Owen, D.R. Structured deformation of continua. Arch. Ration. Mech. Anal. 1993, 124, 99–155. [Google Scholar] [CrossRef]
- François, M.L.; Royer-Carfagni, G. Structured deformation of damaged continua with cohesive-frictional sliding rough fractures. Eur. J. Mech. A Solids 2005, 24, 644–660. [Google Scholar] [CrossRef]
- Baía, M.; Matias, J.; Santos, P.M. A relaxation result in the framework of structured deformations in a bounded variation setting. Proc. R. Soc. Edinb. Sect. A 2012, 142, 239–271. [Google Scholar] [CrossRef]
- Morandotti, M. Structured deformations and applications. Proc. Appl. Math. Mech. 2017, 17, 711–712. [Google Scholar] [CrossRef]
- Šilhavý, M. The general form of the relaxation of a purely interfacial energy for structured deformations. Math. Mech. Complex Syst. 2017, 5, 191–215. [Google Scholar] [CrossRef]
- Matias, J.; Morandotti, M.; Owen, D.R. Energetic Relaxation to Structured Deformations: A Multiscale Geometrical Basis for Variational Problems in Continuum Mechanics; Springer: Singapore, 2023. [Google Scholar]
- Ren, Y.; Chen, J.; Lu, G. A structured deformation driven nonlocal macro-meso-scale consistent damage model for the compression/shear dominate failure simulation of quasi-brittle materials. Comput. Methods Appl. Mech. Eng. 2023, 410, 115945. [Google Scholar] [CrossRef]
- Krömer, S.; Kružík, M.; Morandotti, M.; Zappale, E. Measure-valued structured deformations. J. Nonlinear Sci. 2024, 34, 100. [Google Scholar] [CrossRef]
- Ambrosio, L.; Fusco, N.; Pallara, D. Functions of Bounded Variations and Free Discontinuity Problems; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Choksi, R.; Fonseca, I. Bulk and interfacial energy densities for structured deformations of continua. Arch. Ration. Mech. Anal. 1997, 138, 37–103. [Google Scholar] [CrossRef]
- Alberti, G. A Lusin type theorem for gradients. J. Funct. Anal. 1991, 100, 110–118. [Google Scholar] [CrossRef]
- Fonseca, I.; Müller, S. Relaxation of quasiconvex functionals in BV(Ω,) for integrands f(x,u,∇u). Arch. Rat. Mech. Anal. 1993, 123, 1–49. [Google Scholar] [CrossRef]
- Cosserat, E.; Cosserat, F. Théories des Corps Déformables; A. Hermann et Fils: Paris, France, 1909. [Google Scholar]
- Hrytsyna, O.R. Nonclassical linear theories of continuum mechanics. J. Math. Sci. 2023, 273, 101–123. [Google Scholar] [CrossRef]
- Hageman, T.; Sabet, S.A.; Borst, R. Convergence in non-associated plasticity and fracture propagation for standard, rate-dependent, and Cosserat continua. Int. J. Numer. Methods Eng. 2021, 122, 777–795. [Google Scholar] [CrossRef]
- Guo, L.; Li, X.; Song, D.; Chen, J.; Liu, X.; Liu, Y. Cosserat constitutive theory and one of its higher-order forms: A rediscussion on the mesh dependence problem. Finite Elem. Anal. Des. 2024, 241, 104224. [Google Scholar] [CrossRef]
- Gillepsie, M.; Springborn, B.; Crane, K. Discrete conformal equivalence of polyhedral surfaces. ACM Trans. Graph. 2021, 40, 103. [Google Scholar]
- Jiménez, V.M.; de León, M. New notions of uniformity and homogeneity of Cosserat media. J. Math. Phys. 2023, 64, 092901. [Google Scholar] [CrossRef]
- Epstein, M.; de León, M. Geometrical theory of uniform Cosserat media. J. Geom. Phys. 1998, 26, 127–170. [Google Scholar] [CrossRef]
- Epstein, M.; Elźanowski, M. Material Inhomogenities and Their Evolution: A Geometric Approach; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Ehresmann, C. Extension du calcules jets aux jets non-holonomes. C. R. Acad. Sci. Paris 1954, 239, 1762–1764. [Google Scholar]
- Grigore, D.R.; Krupka, D. Invariants of velocities and higher-order Grassmann bundles. J. Math. Phys. 1998, 24, 244–264. [Google Scholar] [CrossRef]
- Krupka, D.; Saunders, D. Handbook of Global Analysis; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Kolář, I.; Michor, W.; Slovák, J. Natural Operations in Differential Geometry; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Kolář, I. On the geometry of Weil bundles. Differ. Geom. Appl. 2014, 35, 136–142. [Google Scholar] [CrossRef]
- Park, I.Y. Foliation, jet bundle and quantization of Einstein gravity. Front. Phys. 2016, 4, 25. [Google Scholar] [CrossRef]
- Izmailov, A.F.; Solodov, M.V. Newton-Type Methods for Optimization and Variational Problems; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Neculai, A. Nonlinear Conjugate Gradient Method for Unconstrained Optimization; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Sabah, A.; Al-jilavi, A. Modern free-derivative numerical optimization of approximate algorithms convergence and neutrosophic convergence. Int. J. Neutrosophic Sci. 2025, 25, 115–122. [Google Scholar]
- Mohmadsalehia, M.; Soghrati, S. An automated mesh generation algorithm for simulating complex crack growth problems. Comput. Methods Appl. Mech. Eng. 2022, 398, 115015. [Google Scholar] [CrossRef]
- Ammendolea, D.; Fabbrocino, F.; Leonetti, L.; Lonetti, P.; Pascuzzo, A. An efficient moving-mesh strategy for predicting crack propagation in unidirectional composites: Application to materials reinforced with aligned CNTs. Compos. Struct. 2025, 352, 118652. [Google Scholar] [CrossRef]
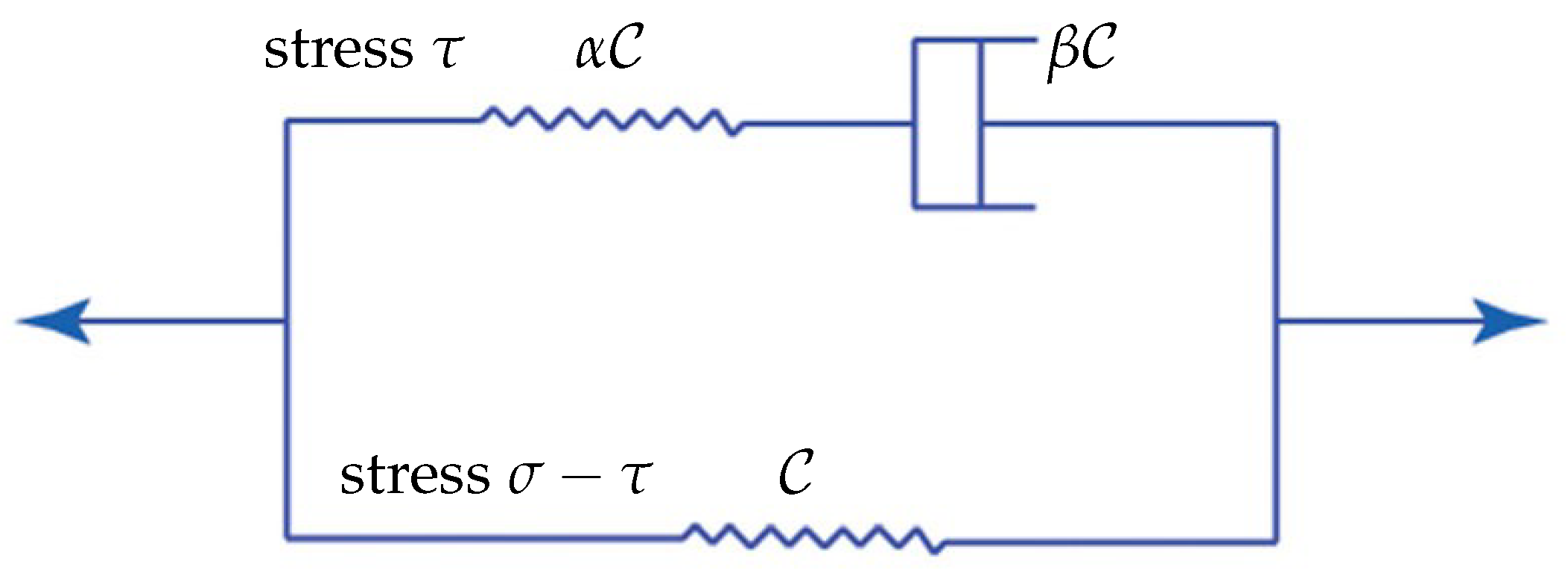
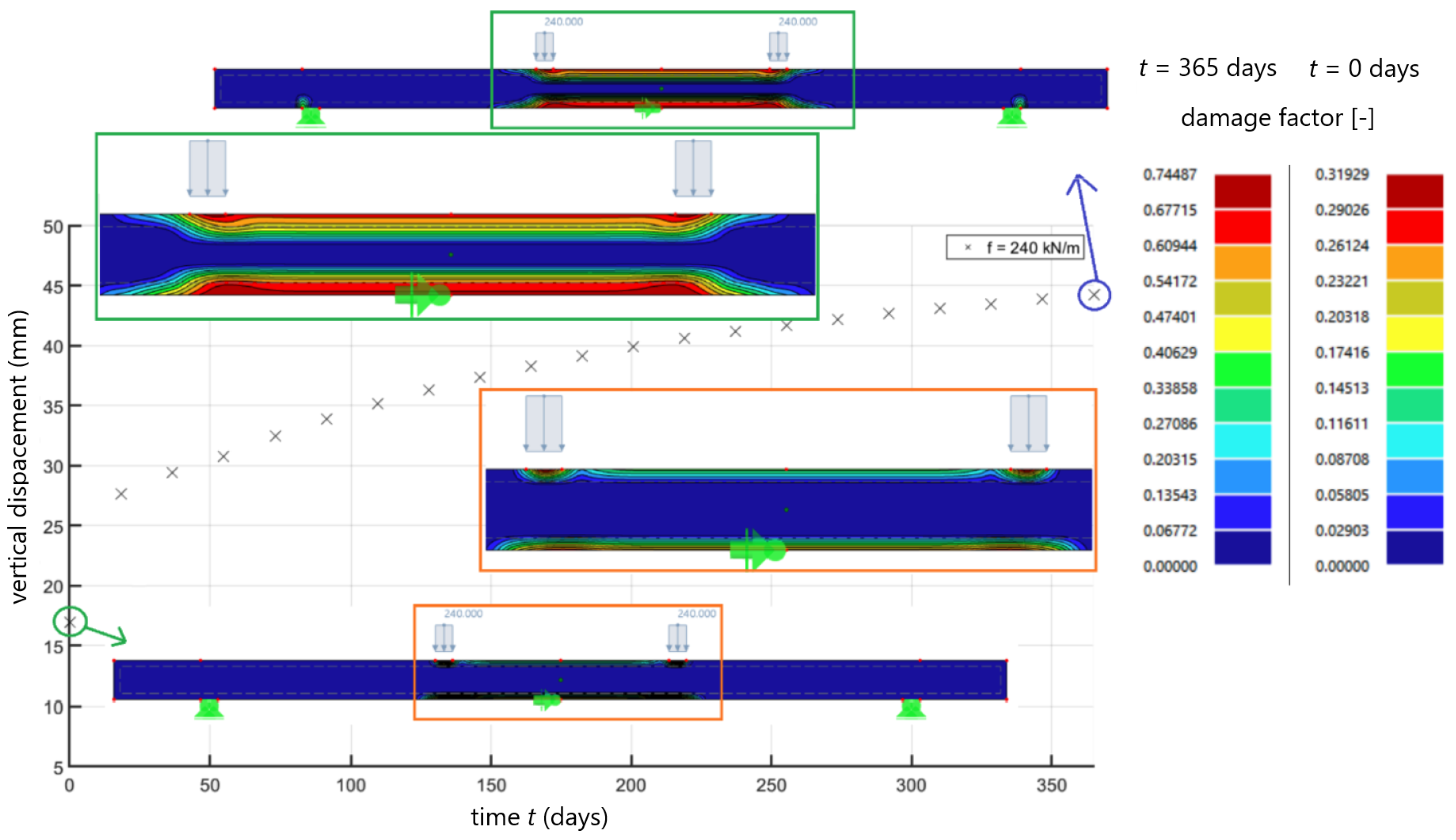
| Step | Topics |
|---|---|
| 1 | weak formulation of a model problem in appropriate Bochner–Sobolev spaces |
| 2 | time-discretised formulation of 1 with a finite number of m steps |
| 3 | step-by-step verification of solvability of 2 |
| 4 | a priori bounds for sequences of approximate solutions, independent of m |
| 5 | weak and strong convergence properties of sequences by 4, |
| 6 | identification of limits by 5 with solution of 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vala, J.; Tomáš, J. Damage Behaviour of Quasi-Brittle Composites: Mathematical and Computational Aspects. Appl. Sci. 2025, 15, 4214. https://doi.org/10.3390/app15084214
Vala J, Tomáš J. Damage Behaviour of Quasi-Brittle Composites: Mathematical and Computational Aspects. Applied Sciences. 2025; 15(8):4214. https://doi.org/10.3390/app15084214
Chicago/Turabian StyleVala, Jiří, and Jiří Tomáš. 2025. "Damage Behaviour of Quasi-Brittle Composites: Mathematical and Computational Aspects" Applied Sciences 15, no. 8: 4214. https://doi.org/10.3390/app15084214
APA StyleVala, J., & Tomáš, J. (2025). Damage Behaviour of Quasi-Brittle Composites: Mathematical and Computational Aspects. Applied Sciences, 15(8), 4214. https://doi.org/10.3390/app15084214






