Construction of Simulation System for USV Motion Control and Design of Multi-Mode Controllers Based on VRX and Simulink
Abstract
1. Introduction
- A high-fidelity and plugin-extensible USV motion control simulation system is developed by integrating Simulink with the VRX environment via ROS2, providing a platform for rapid verification of USV motion control algorithms.
- The feasibility of the proposed simulation system for USV rapid development is validated through path-following water tank experiments, offering an efficient solution to bridge the gap between simulation-based verification and real-world vessel testing of motion control algorithms.
2. USV Dynamic Models
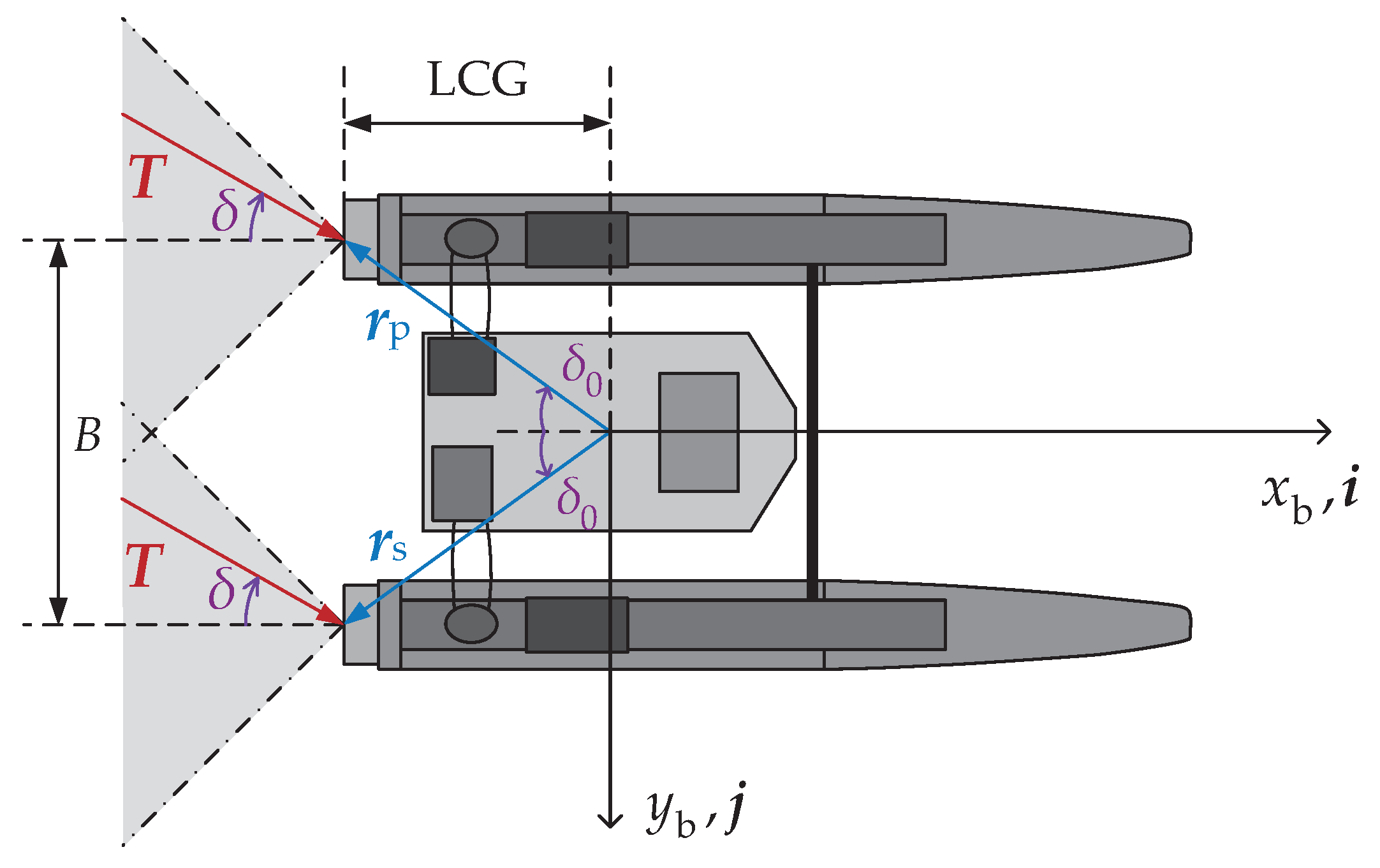
2.1. Reference Frames and Motion Equations
2.2. Thrust
2.3. Wind Force
2.4. Wave Model
3. Controller Design
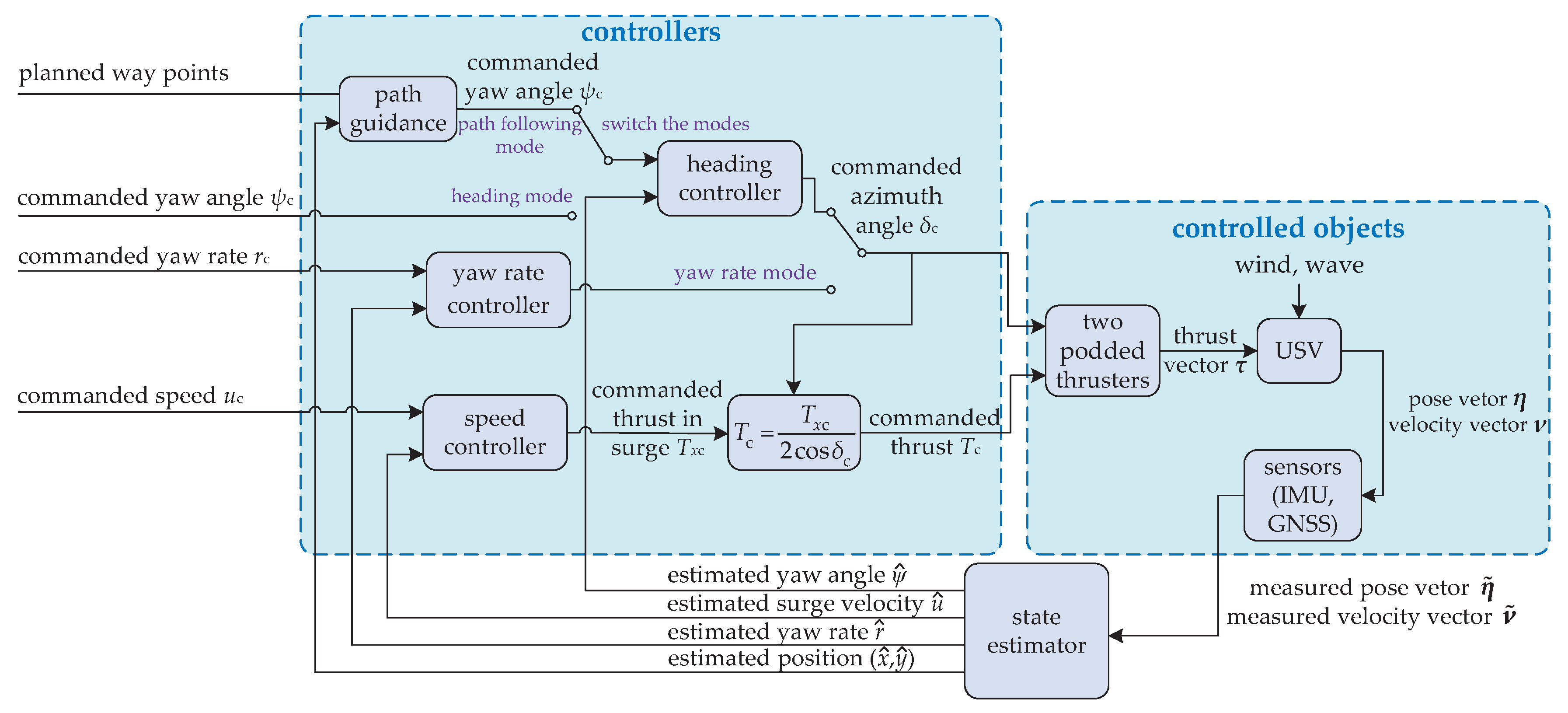
3.1. Control System Architecture
3.2. Speed Control
3.3. Yaw Rate Control
3.4. Heading Control
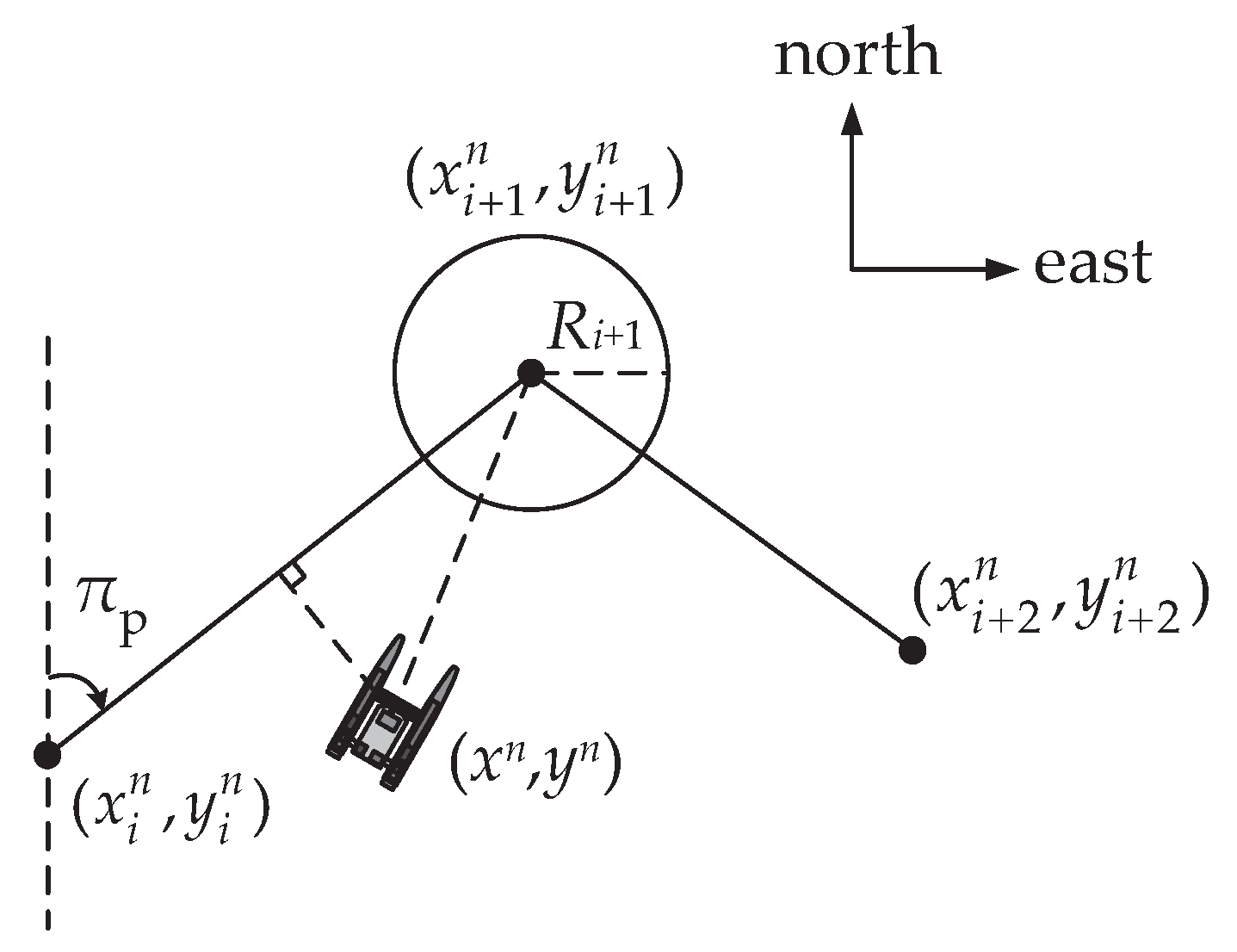
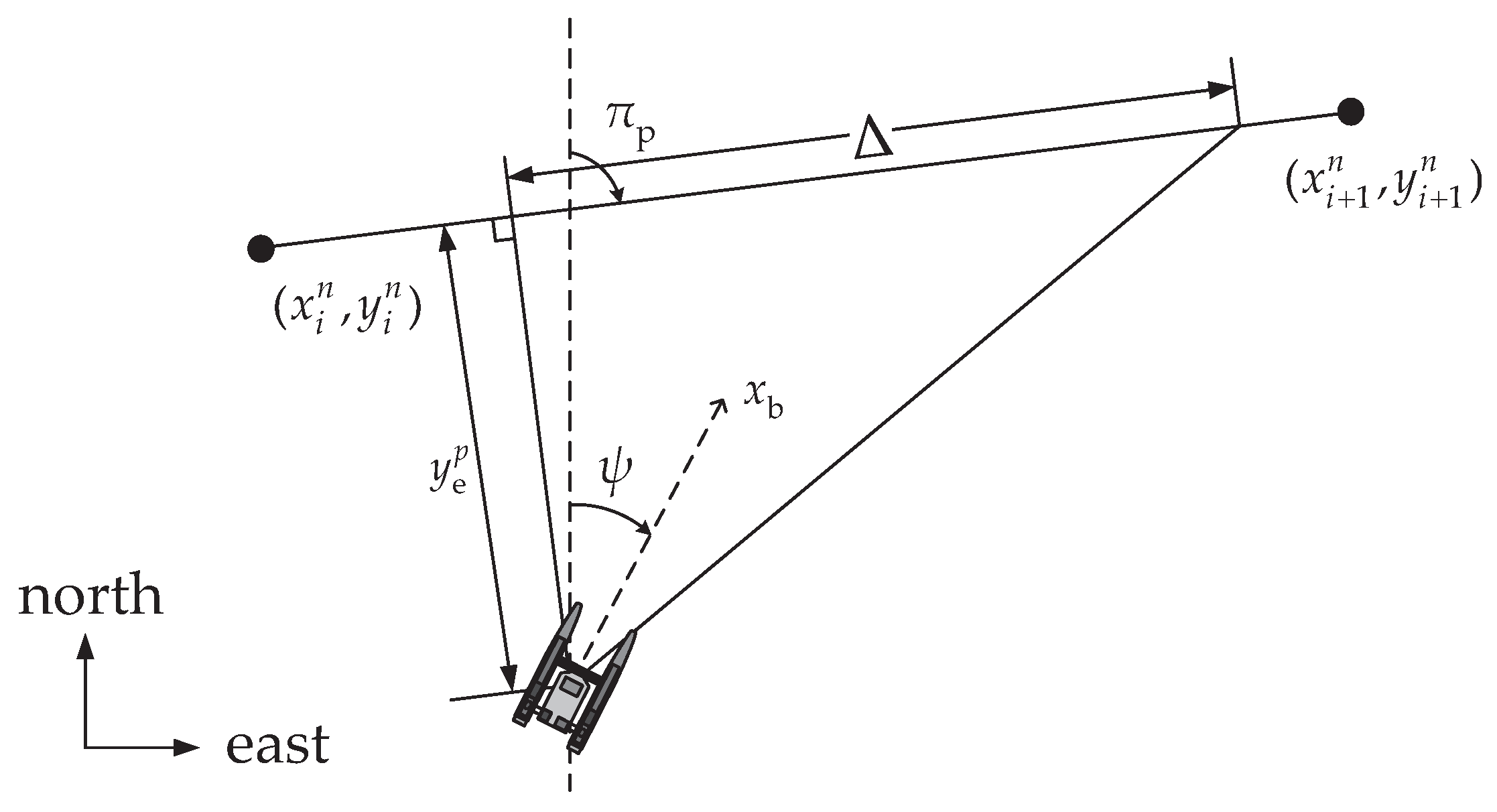
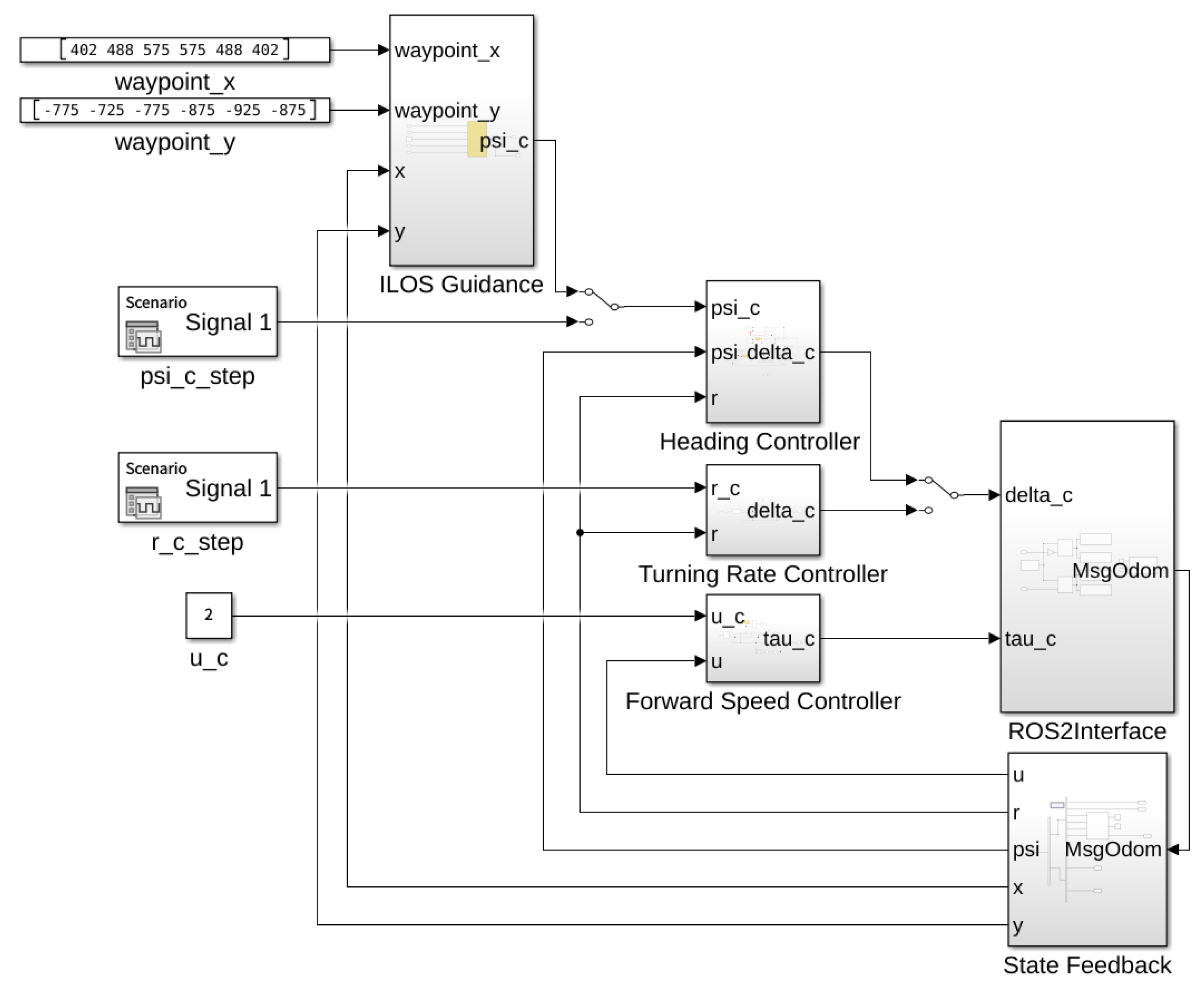
3.5. Path Guidance
4. Simulation System Design
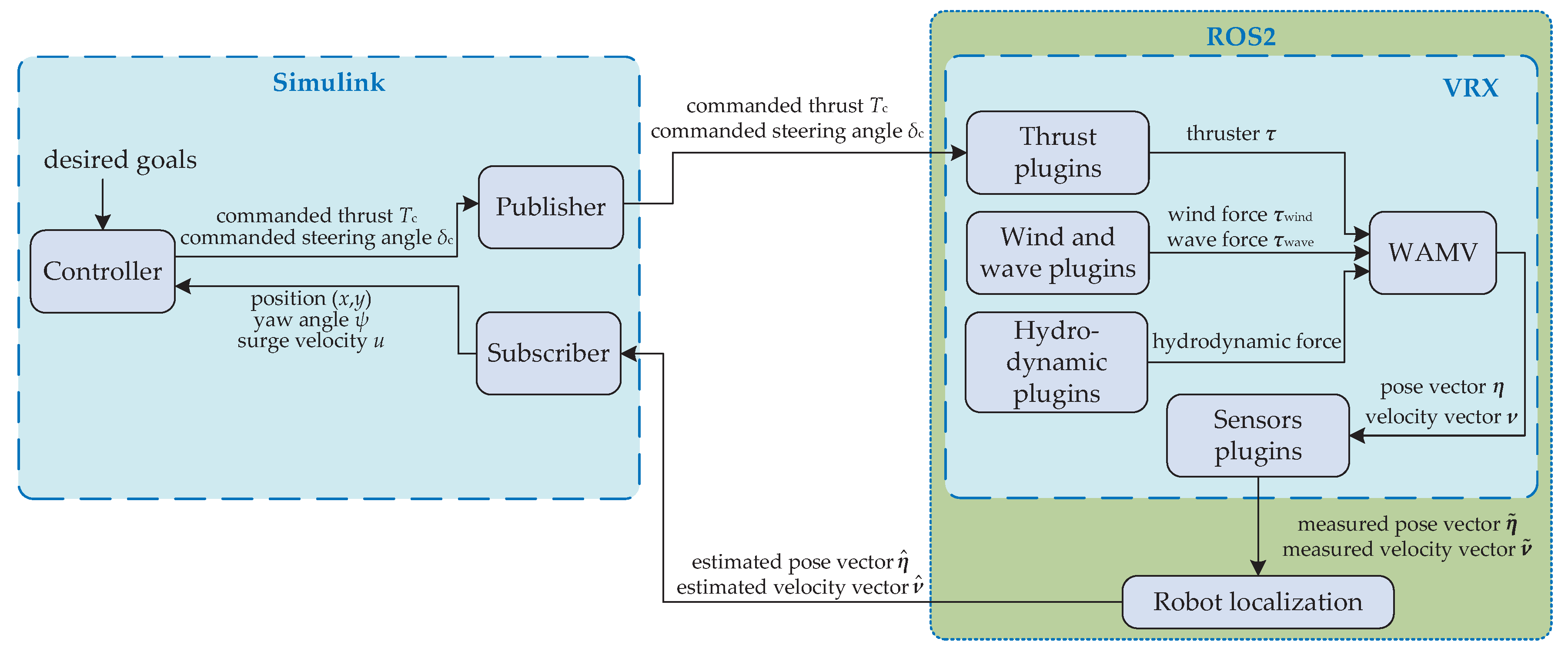
4.1. Design Scheme
4.2. Controller and ROS2 Interface Modules in Simulink
4.3. VRX Configuration
4.4. State Estimator Design
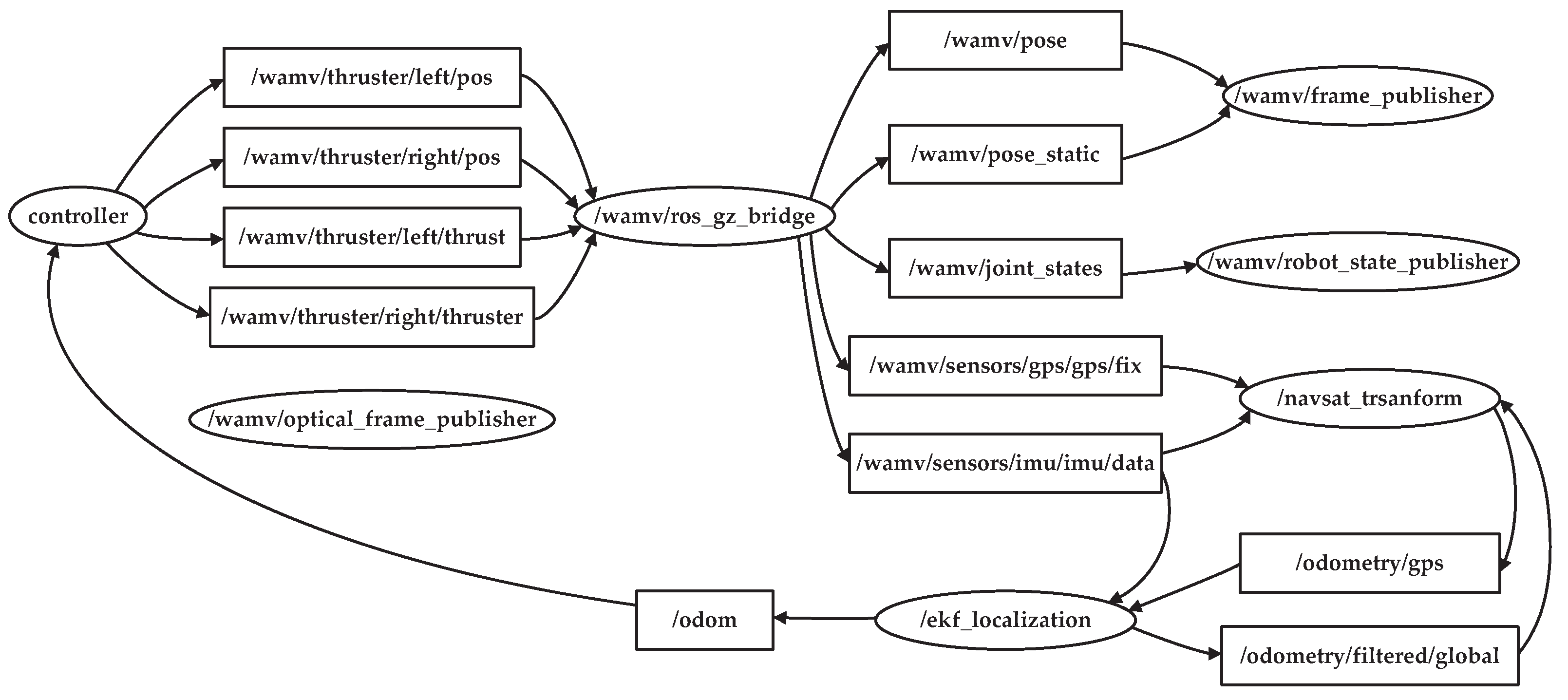
4.5. ROS2 Node and Topic Design
5. Simulation Results and Water Tank Experiments
5.1. Simulation Results
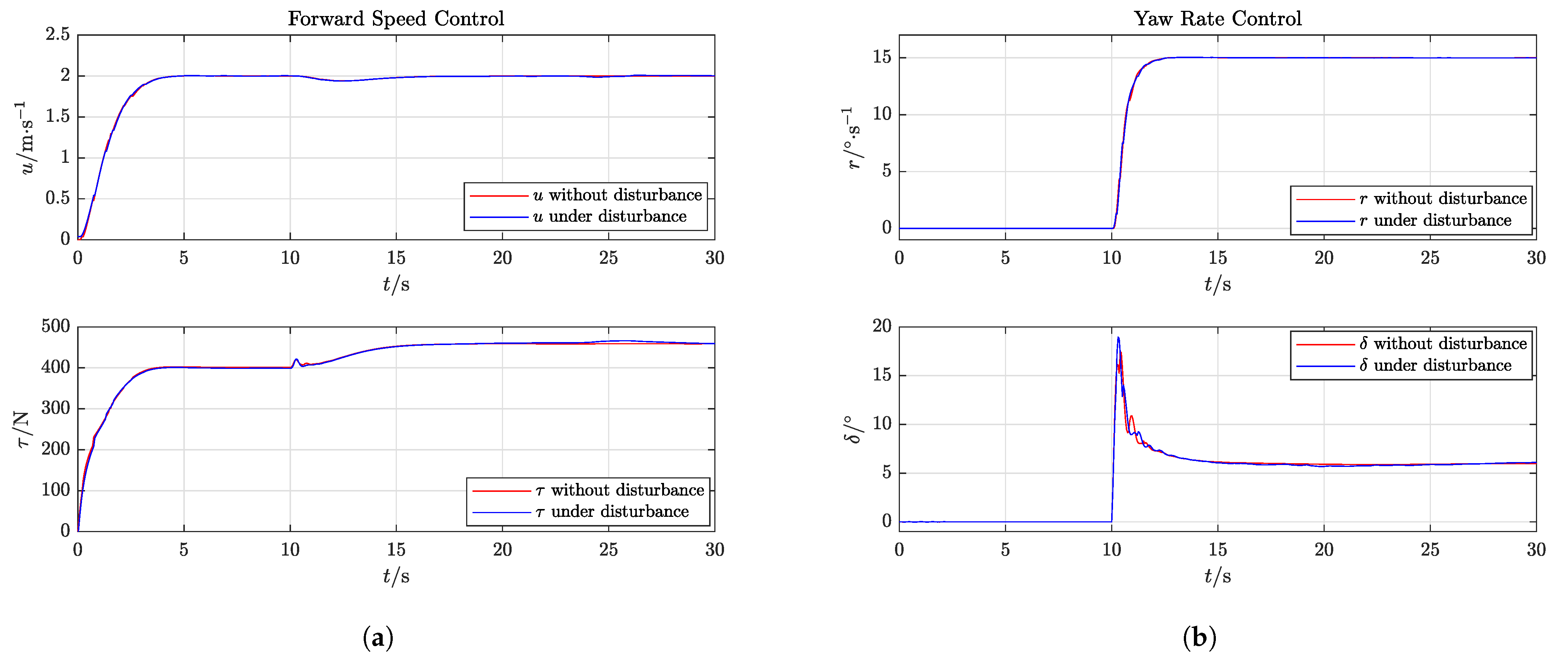
5.1.1. Simulation of Joint Control of Yaw Rate and Surge Velocity
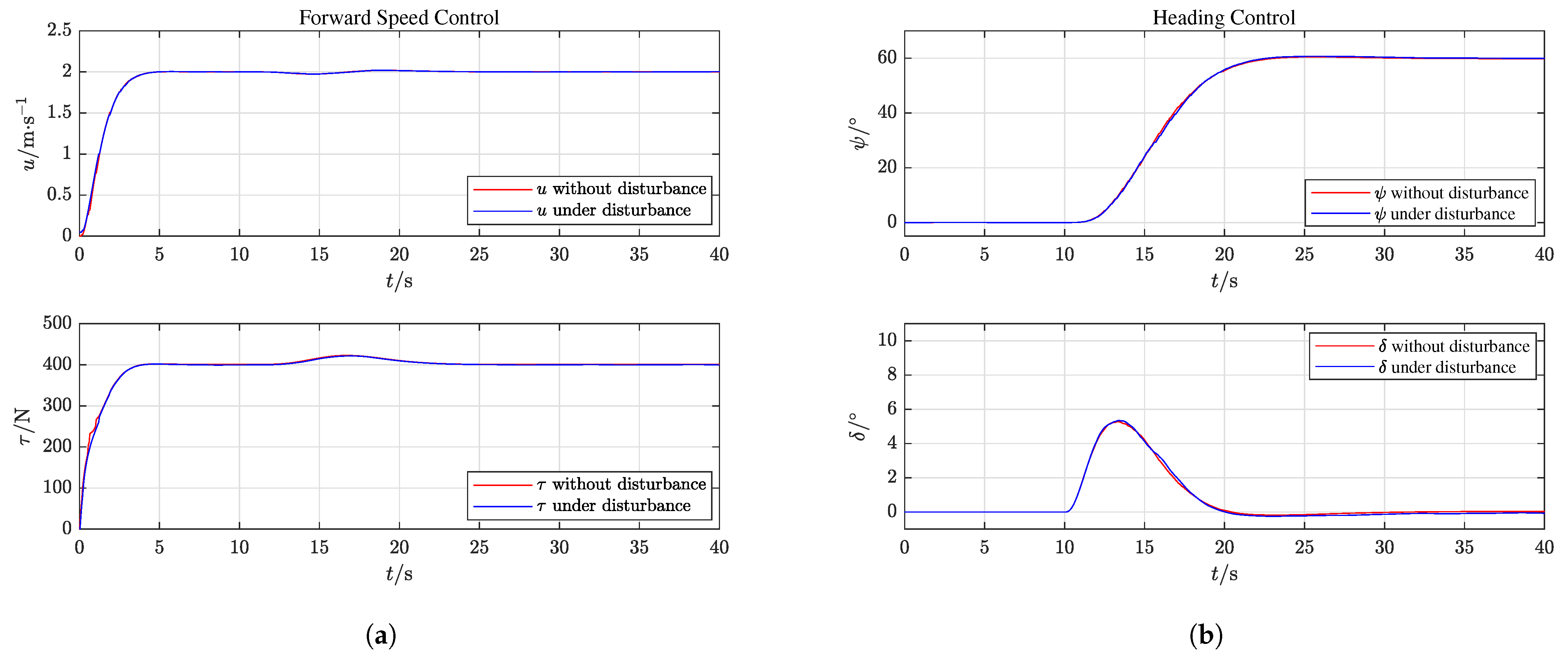
5.1.2. Simulation of Joint Control of Heading and Surge Velocity
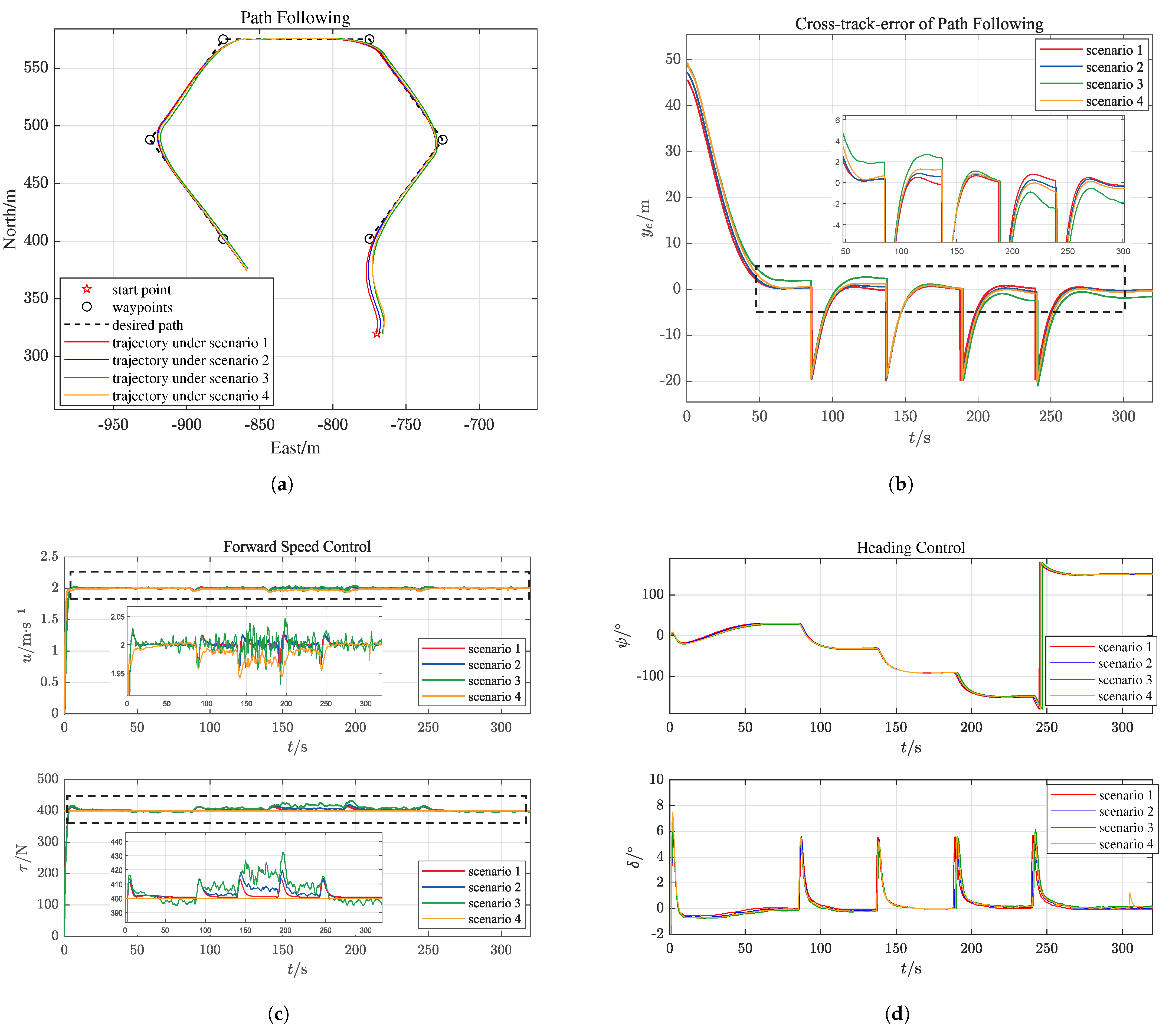
5.1.3. Path-Following Control Simulation
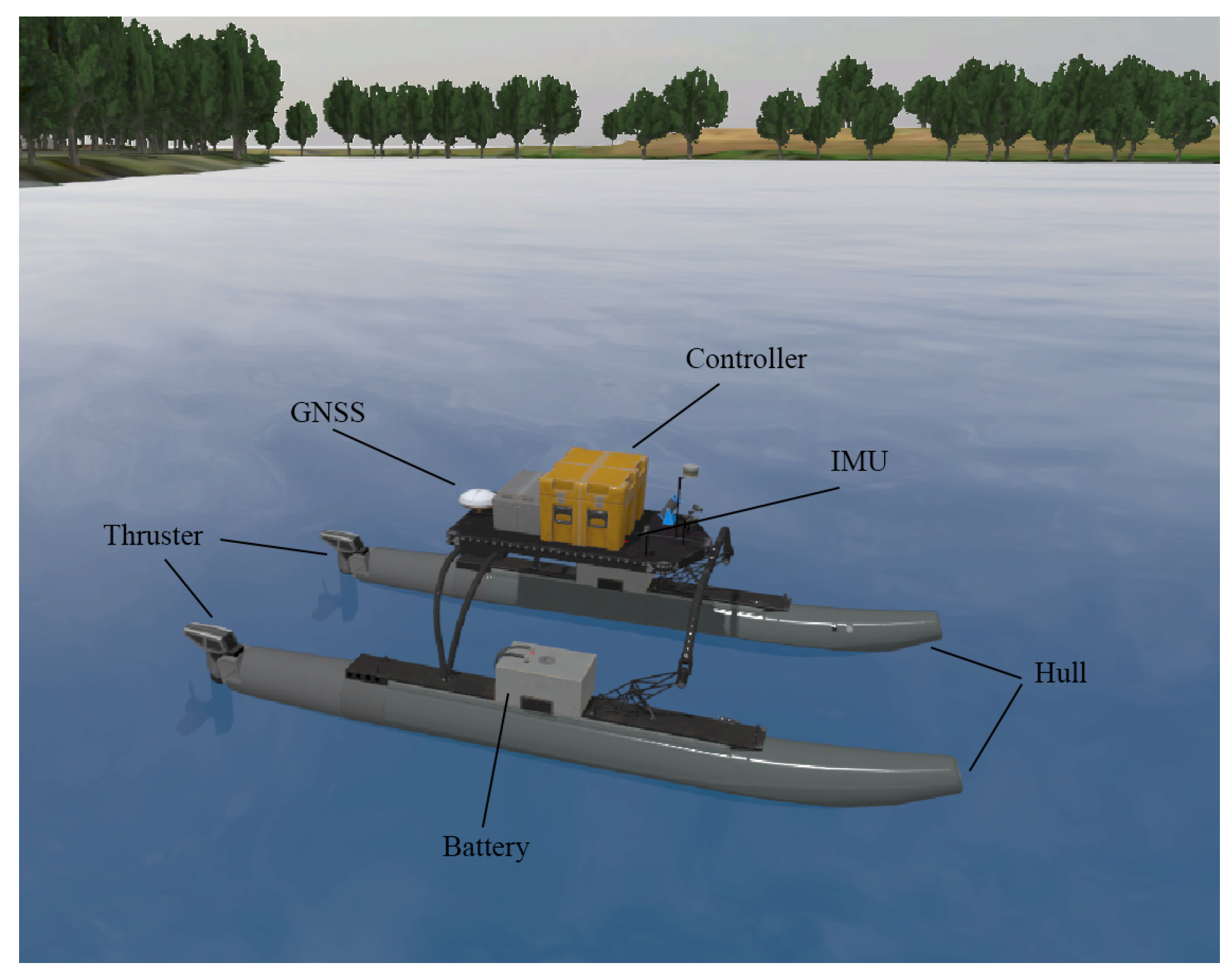
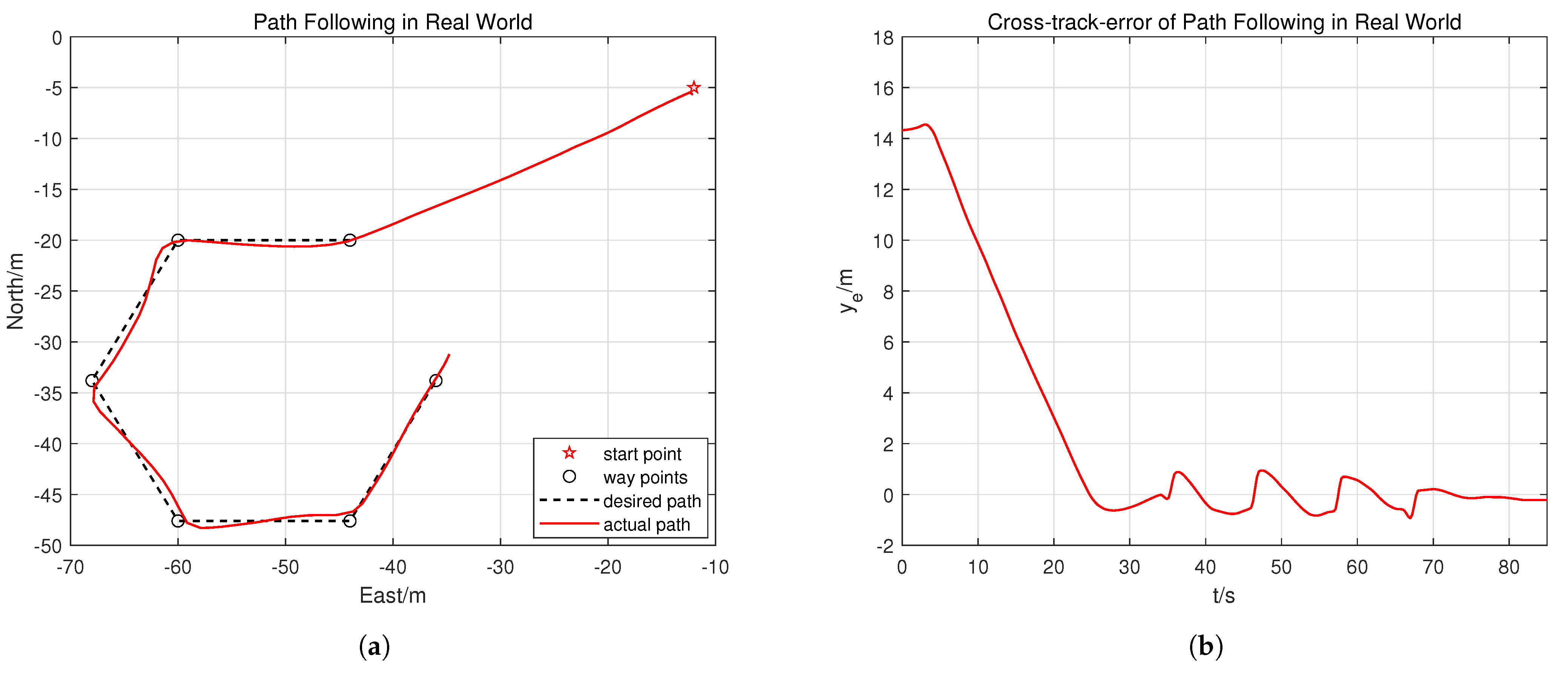
5.2. Water Tank Experiment
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| USV | Unmanned Surface Vehicle |
| VRX | Virtual RobotX |
| ROS | Robot Operating System |
| GNSS | Global Navigation Satellite System |
| IMU | Inertial Measurement Unit |
| OSRF | Open Source Robotics Foundation |
| DDS | Data Distribution Service |
| QoS | Quality of Service |
| WAMV | Wave-Adaptive Modular Vehicle |
| PID | Proportion–Integration–Differentiation |
| EKF | Extended Kalman Filter |
| UKF | Unscented Kalman Filter |
References
- Zhang, J.; Li, X.; Zhou, H.; Wu, X. Analysis and Research on Operational Application of Unmanned Surface Vehicles in Russia-Ukraine Conflict. Digit. Ocean. Underw. Warf. 2024, 7, 616–622. [Google Scholar] [CrossRef]
- Fan, Y.; Yang, S.; Huang, J.; Xiang, X. Design and verification of unmanned surface vehicle integrated simulation platform based on USVSim. J. Ordnance Equip. Eng. 2022, 43, 21–27. [Google Scholar] [CrossRef]
- Xiao, G.; Zheng, G.; Tong, C.; Hong, X. A Virtual System and Method for Autonomous Navigation Performance Testing of Unmanned Surface Vehicles. J. Mar. Sci. Eng. 2023, 11, 2058. [Google Scholar] [CrossRef]
- Paravisi, M.; Santos, D.H.; Jorge, V.; Heck, G.; Gonçalves, L.M.; Amory, A. Unmanned Surface Vehicle Simulator with Realistic Environmental Disturbances. Sensors 2019, 19, 1068. [Google Scholar] [CrossRef] [PubMed]
- Woo, J.; Lee, J.; Kim, N. Obstacle avoidance and target search of an Autonomous Surface Vehicle for 2016 Maritime RobotX challenge. In Proceedings of the 2017 IEEE Underwater Technology (UT), Busan, Republic of Korea, 21–24 February 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Smith, P.; Dunbabin, M. High-Fidelity Autonomous Surface Vehicle Simulator for the Maritime RobotX Challenge. IEEE J. Ocean. Eng. 2019, 44, 310–319. [Google Scholar] [CrossRef]
- Jung, W.; Woo, J.; Kim, N. Recognition of the light buoy for scan the code mission in 2016 Maritime RobotX Challenge. In Proceedings of the 2017 IEEE Underwater Technology (UT), Busan, Republic of Korea, 21–24 February 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Sang, X. Hands-On ROS2 for Robotics Programming: From Introduction to Practice; Machine Press: Beijing, China, 2024. [Google Scholar]
- Chu, Y.; Wu, Z.; Zhu, X.; Yue, Y.; Lim, E.G.; Paoletti, P.; Ma, J. Riverbank Following Planner (RBFP) for USVs Based on Point Cloud Data. Appl. Sci. 2023, 13, 11319. [Google Scholar] [CrossRef]
- Lu, G. Research on Path Planning and Control Method of Unmanned Vessel Based on ROS. Master’s Thesis, Hangzhou Dianzi University, Hangzhou, China, 2023. [Google Scholar]
- Zhang, Y.; Li, H.; Wang, Z. Design of a virtual simulation experimental platform for intelligent control of unmanned surface vehicles based on VRX. Exp. Technol. Manag. 2024, 41, 121–128. [Google Scholar] [CrossRef]
- Bayrak, M.; Bayram, H. COLREG-Compliant Simulation Environment for Verifying USV Motion Planning Algorithms. In Proceedings of the OCEANS 2023–Limerick, Limerick, Ireland, 5–8 June 2023; pp. 1–10. [Google Scholar] [CrossRef]
- Meng, J.; Humne, A.; Bucknall, R.; Englot, B.; Liu, Y. A Fully-Autonomous Framework of Unmanned Surface Vehicles in Maritime Environments Using Gaussian Process Motion Planning. IEEE J. Ocean. Eng. 2023, 48, 59–79. [Google Scholar] [CrossRef]
- ROS Toolbox Getting Started Guide. Available online: https://ww2.mathworks.cn/help/ros/getting-started-with-ros-toolbox.html (accessed on 17 December 2024).
- Fossen, T. Handbook of Marine Craft Hydrodynamics and Motion Control, 2nd ed.; Wiley: Hoboken, NJ, USA, 2021. [Google Scholar]
- Sarda, I.; Qu, H.; Bertaska, I.; Ellenrieder, K. Station-keeping control of an unmanned surface vehicle exposed to current and wind disturbances. Ocean. Eng. 2016, 127, 305–324. [Google Scholar] [CrossRef]
- Bingham, B.; Agüero, C.; McCarrin, M.; Klamo, J.; Malia, J.; Allen, K.; Lum, T.; Rawson, M.; Waqar, R. Toward Maritime Robotic Simulation in Gazebo. In Proceedings of the OCEANS 2019 MTS/IEEE SEATTLE, Seattle, WA, USA, 27–31 October 2019; pp. 1–10. [Google Scholar] [CrossRef]
- Moore, T.; Stouch, D. A Generalized Extended Kalman Filter Implementation for the Robot Operating System. Intell. Auton. Syst. 2016, 302, 335–348. [Google Scholar] [CrossRef]
- Shi, S. Submarine Maneuverability; National Defense Industry Press: Beijing, China, 1995. [Google Scholar]
- Tutorial for the Use of Unmanned Boats. Available online: https://amovlab.com/service (accessed on 30 March 2025).




| Name | Physical Quantity [Unit] | Value |
|---|---|---|
| Vessel Length | L [m] | 4.9 |
| Vessel Width | B [m] | 2.06 |
| Longitudinal Center of Gravity | LCG [m] | 1.4 |
| Economic Speed | [] | 2 |
| Maximum Thrust | [N] | 1000 |
| No Load Draft | D [m] | 0.2 |
| Mass | m [kg] | 180 |
| Moment of Inertia around the Z-axis | [] | 466 |
| Added Mass | [kg] | −9 |
| [kg] | −167 | |
| [] | −335 | |
| Hydrodynamic Coefficients | [] | −100 |
| [] | −150 | |
| [] | −100 | |
| [] | −100 | |
| [] | −800 | |
| [] | −800 | |
| Nomoto Model Parameters | K [] | 2.308 |
| T [s] | 1.724 |
| Name | Physical Quantity [Unit] | Value |
|---|---|---|
| Gyroscope Dynamic Bias Stability | 4.1 | |
| Accelerometer Dynamic Bias Stability | 38.3 | |
| GNSS Horizontal Position Standard Deviation | 1.0 | |
| GNSS Velocity Standard Deviation | 0.1 |
| Parameter [Unit] | Value | Parameter [Unit] | Value |
|---|---|---|---|
| [] | 1.4 | [] | 0.7 |
| [1] | 1 | [1] | 1 |
| [] | 1.3 | [] | 0.6 |
| [] | 3.5 | [m] | 25 |
| [1] | 1 | [1] | 30 |
| [] | 3 | [1] | 0.001 |
| [1] | 1 |
| Scenario | (1) | (2) | (3) | (4) |
|---|---|---|---|---|
| Wind speed | 0 | 3 m/s | 6 m/s | 3 m/s |
| Wind direction | - | 90° | 90° | 90° |
| Wave gain | 0 | 0.5 | 1 | 0.5 |
| Wave period | - | 5 s | 5 s | 5 s |
| Average wave direction | - | 90° | 90° | 90° |
| Surge velocity | 2 m/s | 2 m/s | 2 m/s | open-loop with = 200 N |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, P.; Li, W.; Yang, Y.; Shan, C.; Zhang, Y. Construction of Simulation System for USV Motion Control and Design of Multi-Mode Controllers Based on VRX and Simulink. Appl. Sci. 2025, 15, 4213. https://doi.org/10.3390/app15084213
Jin P, Li W, Yang Y, Shan C, Zhang Y. Construction of Simulation System for USV Motion Control and Design of Multi-Mode Controllers Based on VRX and Simulink. Applied Sciences. 2025; 15(8):4213. https://doi.org/10.3390/app15084213
Chicago/Turabian StyleJin, Peisen, Wenkui Li, Yuhao Yang, Chenyang Shan, and Yawen Zhang. 2025. "Construction of Simulation System for USV Motion Control and Design of Multi-Mode Controllers Based on VRX and Simulink" Applied Sciences 15, no. 8: 4213. https://doi.org/10.3390/app15084213
APA StyleJin, P., Li, W., Yang, Y., Shan, C., & Zhang, Y. (2025). Construction of Simulation System for USV Motion Control and Design of Multi-Mode Controllers Based on VRX and Simulink. Applied Sciences, 15(8), 4213. https://doi.org/10.3390/app15084213





