Prediction Model for the Environmental Noise Distribution of High-Speed Maglev Trains Using a Segmented Line Source Approach
Abstract
Featured Application
Abstract
1. Introduction
2. Analysis of High-Speed Maglev Noise Source Distribution
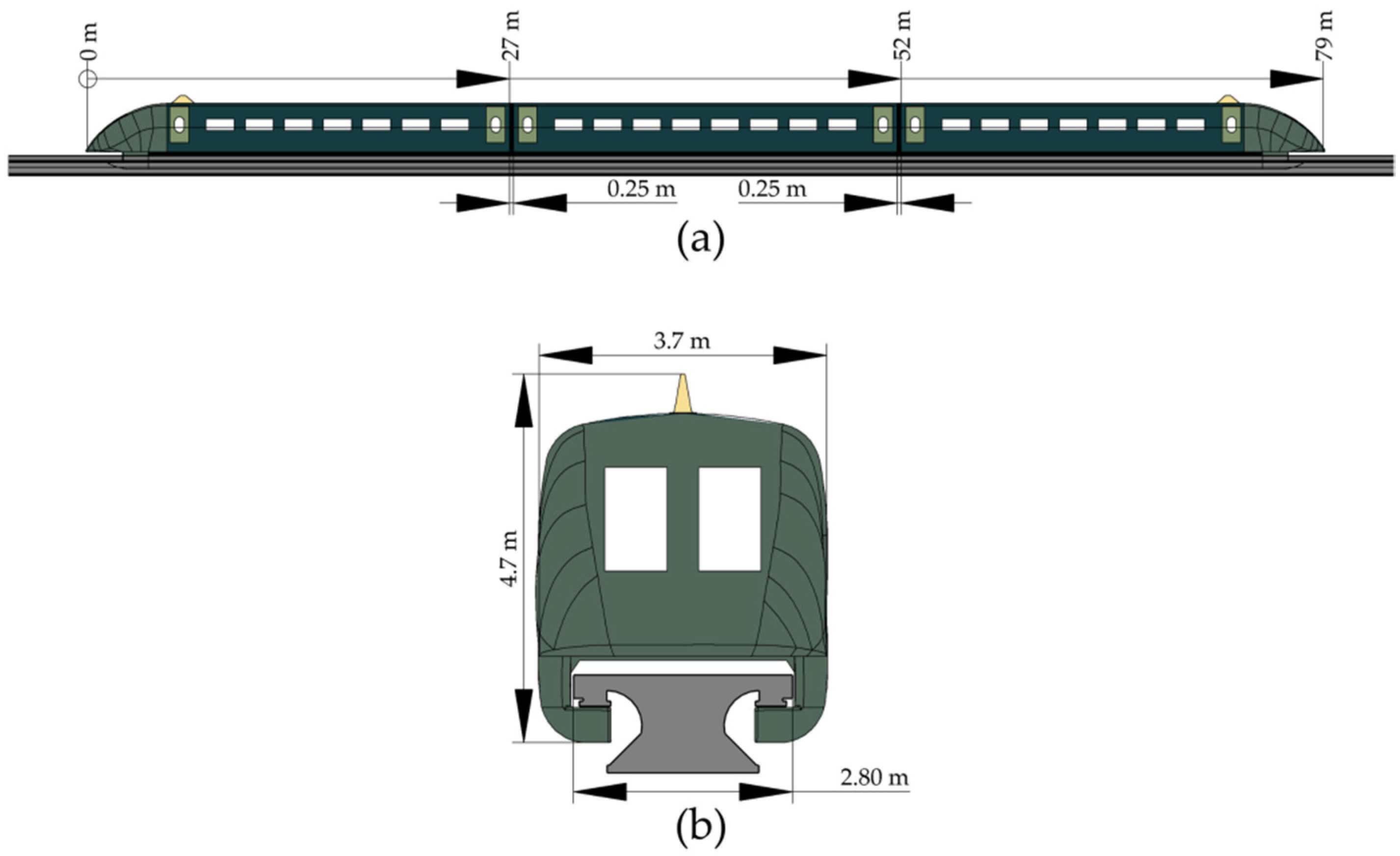
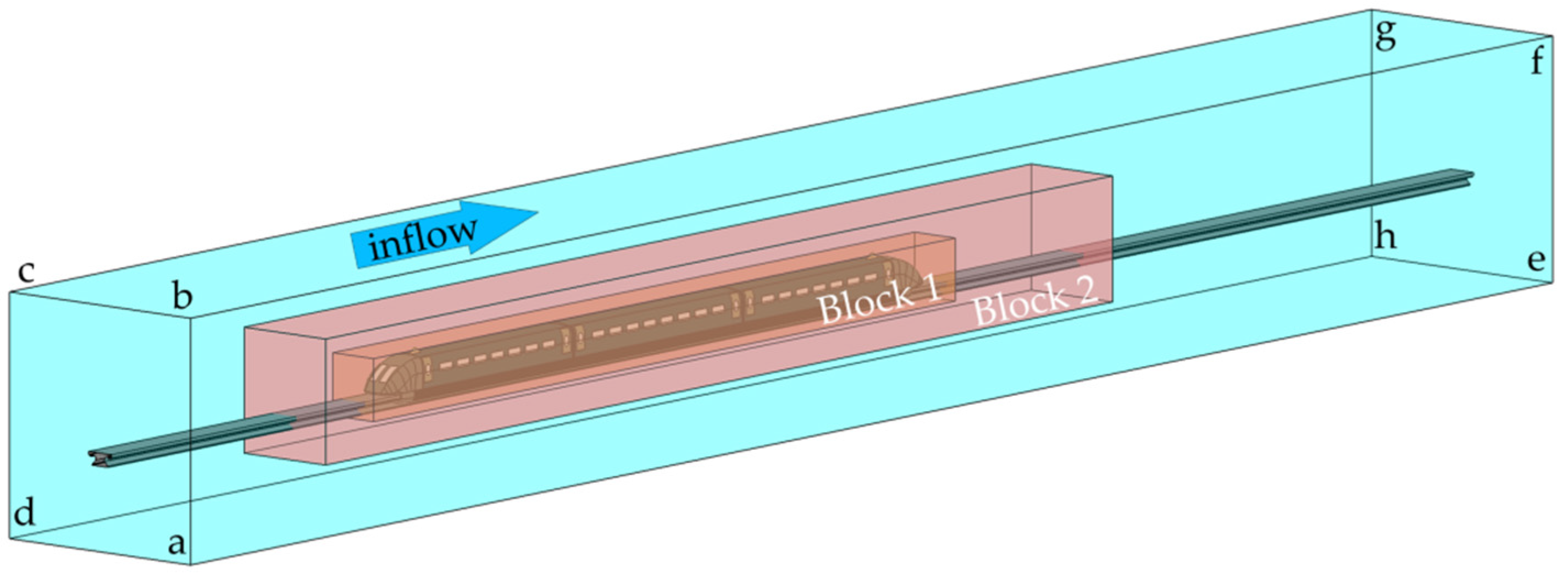
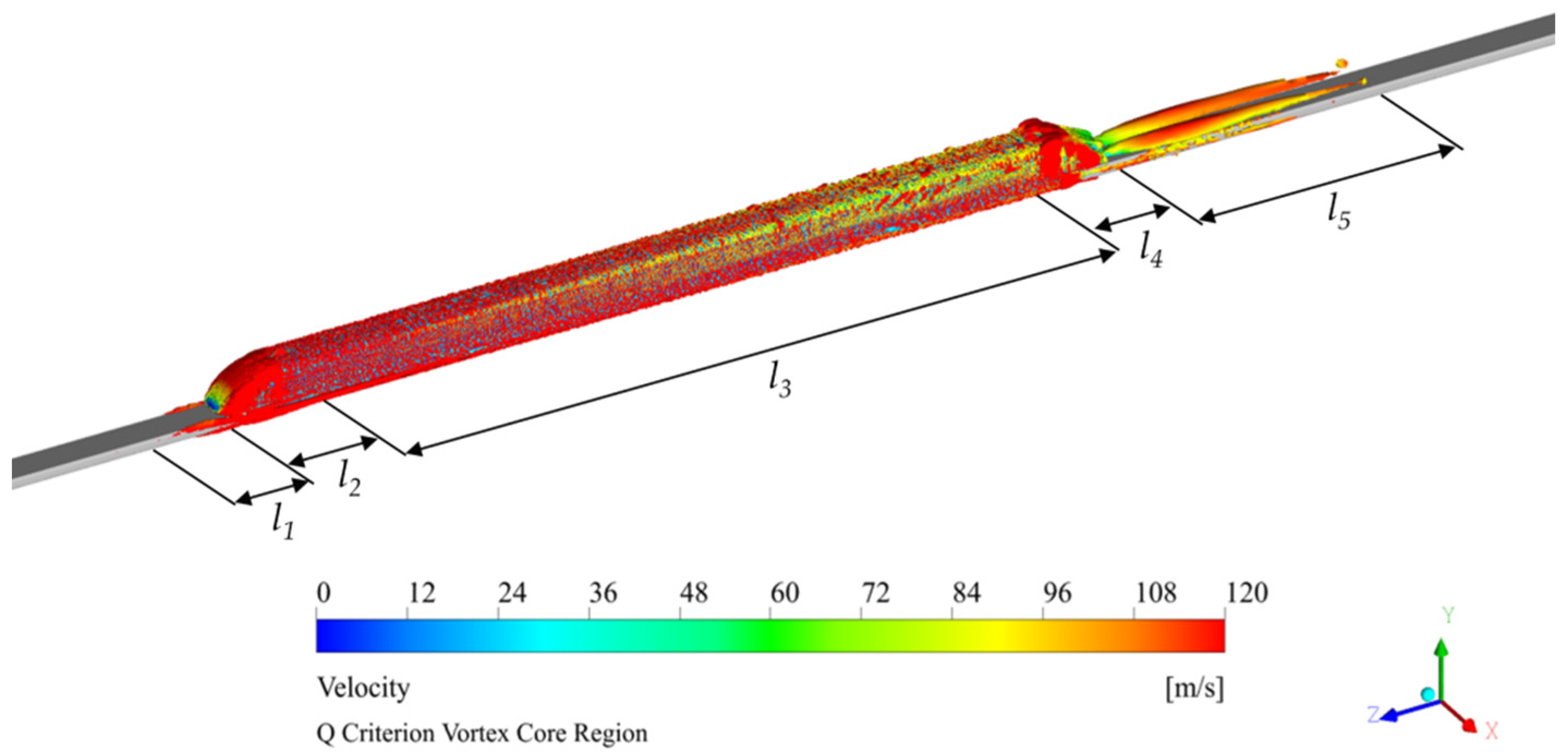
2.1. Numerical Simulation Model of the Flow Field
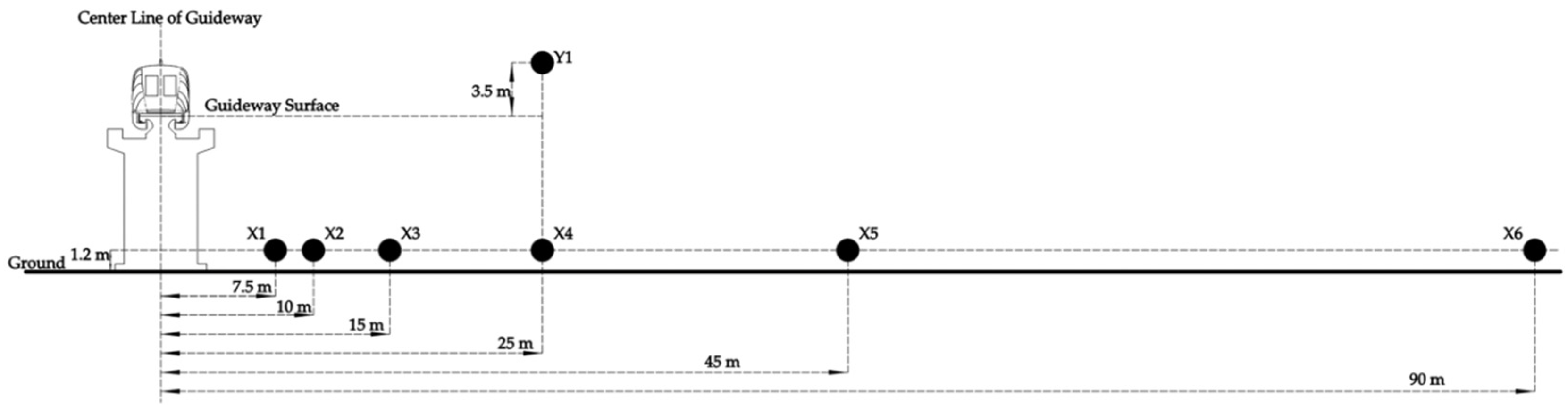
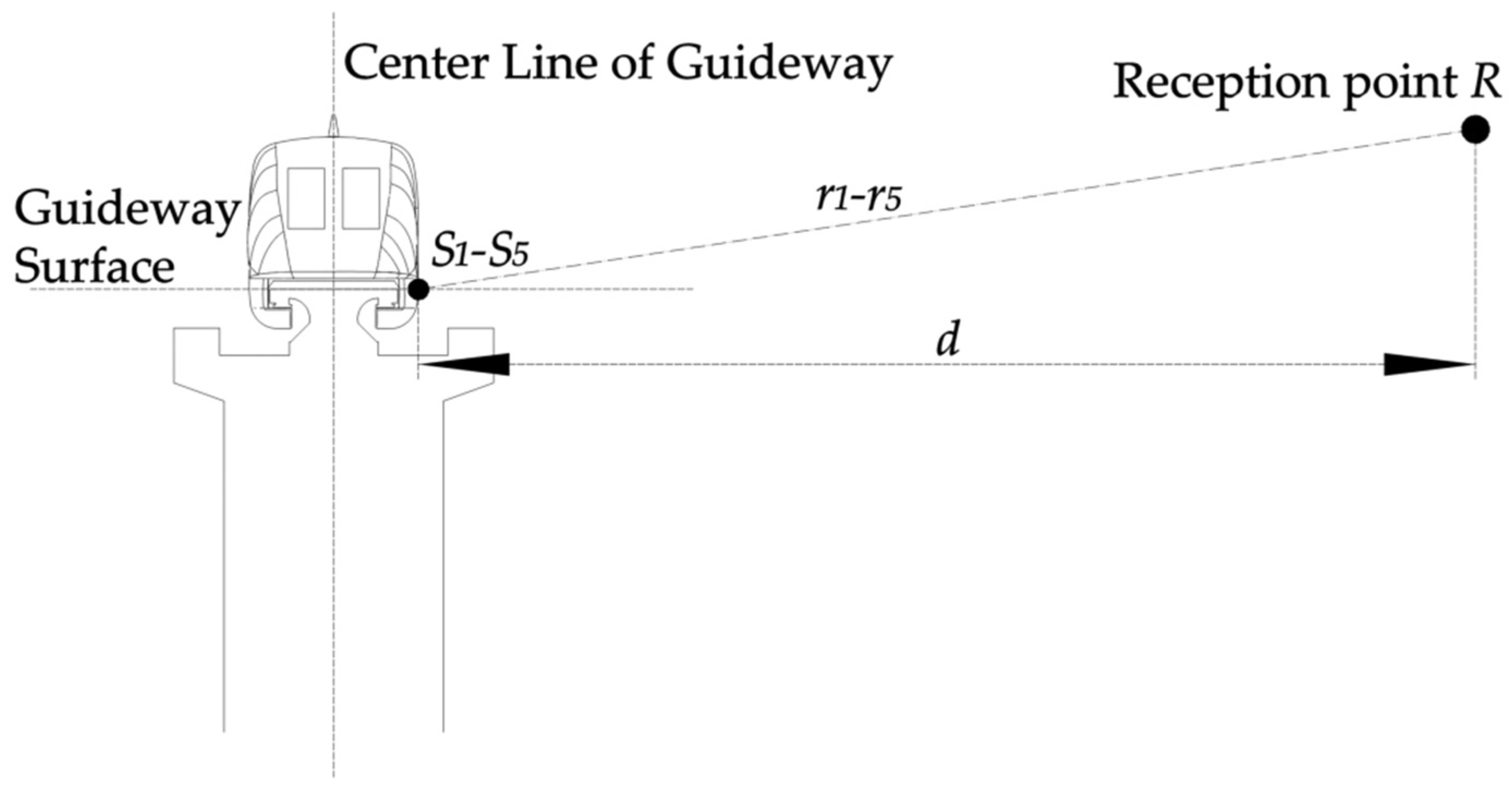
2.2. On-Track Experiment
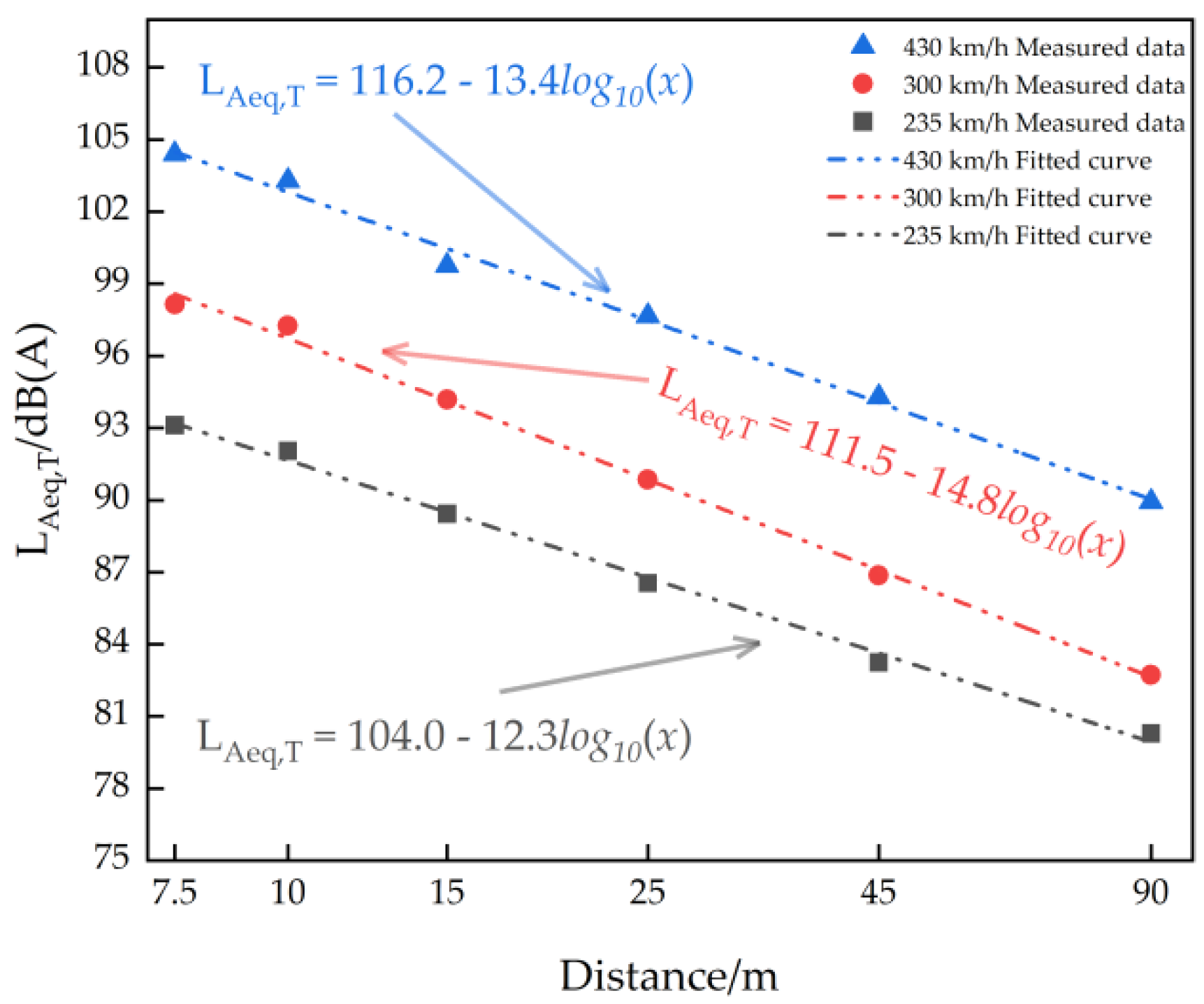
2.3. Analysis of Simulation and Experimental Results
3. Construction of the Noise Prediction Model
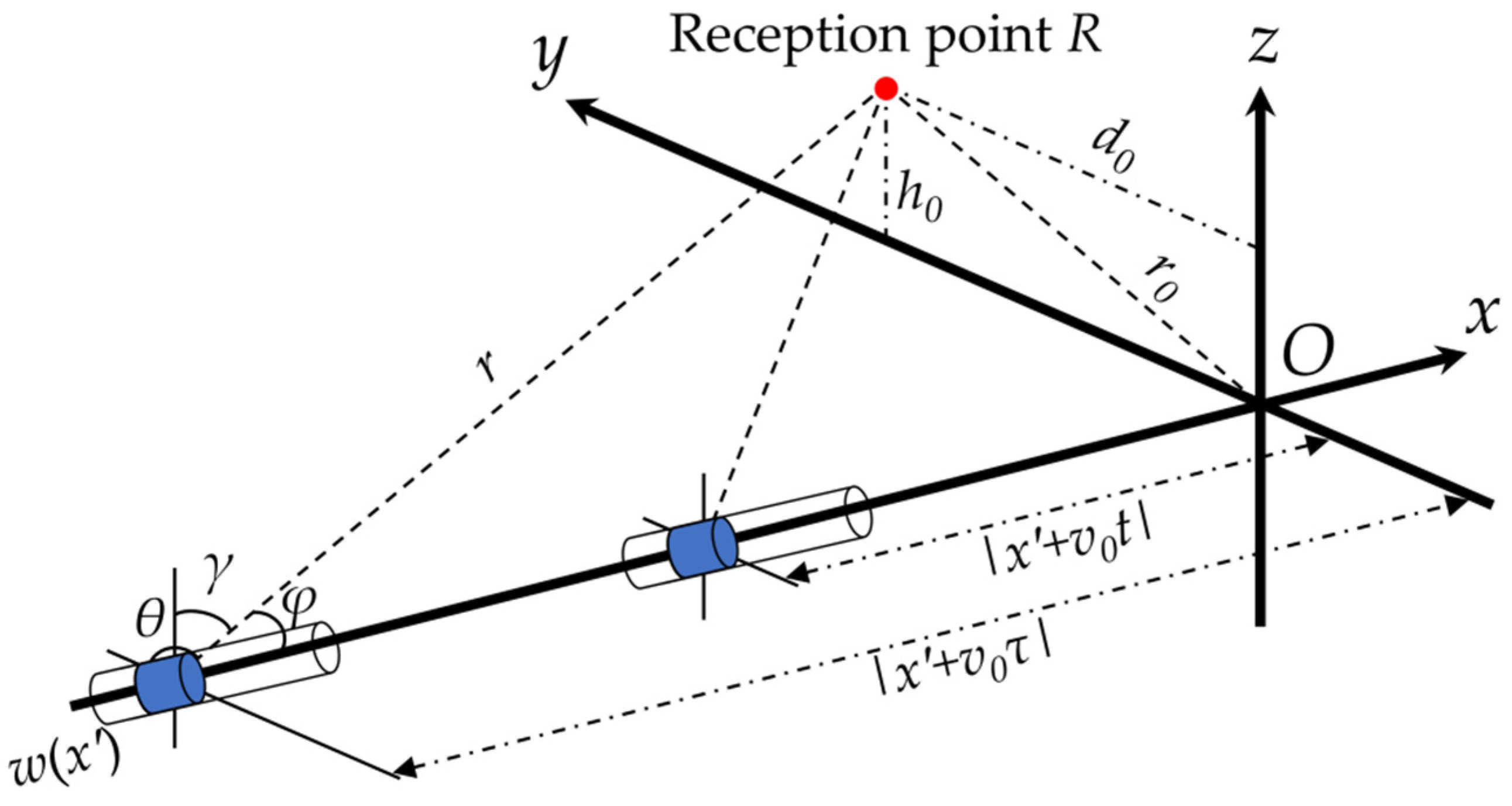
3.1. Finite-Length Incoherent Moving Line Source Model
3.2. Equivalent Source Strength
3.3. Prediction Model and Parameters
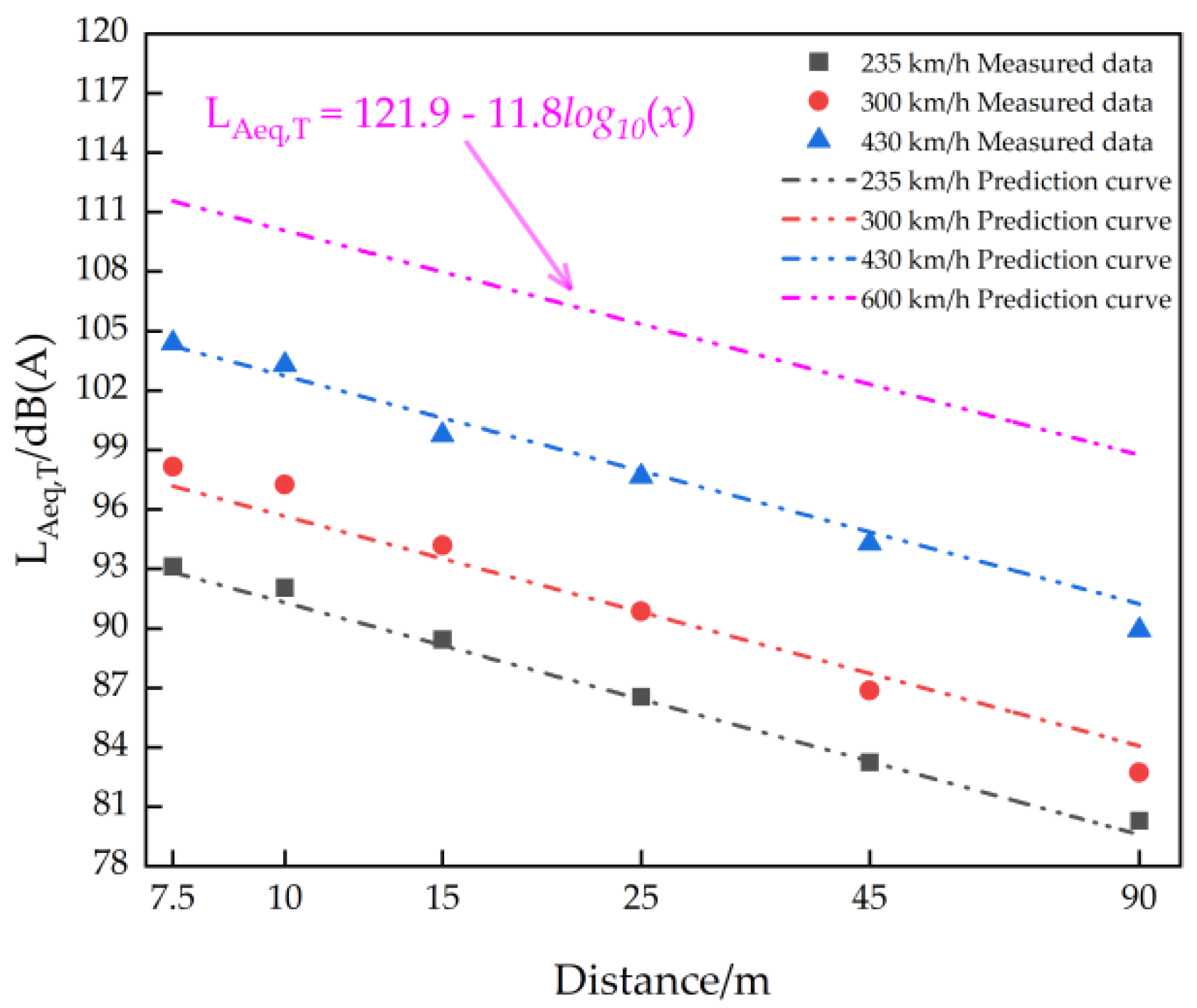
4. Model Verification and Noise Prediction
5. Conclusions
- (1)
- Flow Field Analysis: Incorporating air compressibility effects, the LES method was employed to conduct numerical simulations of the external flow field surrounding a Shanghai Maglev train. The analysis revealed distinct three-dimensional vortical structure distributions with regions of elevated vorticity magnitude concentrated at the vehicle surface and wake zone. Flow separation was observed at the streamlined shoulder of the trailing car, whereas the wake region exhibited a complex array of multiscale vortices with varying intensities, dominated by a pair of counter-rotating ribbon-like trailing vortices. The vortex was the main sound source of fluid flow, and the noise energy was mainly concentrated in the turbulent movement area, such as near the surface of the vehicle body and the wake area. Therefore, the five parts of the turbulent movement around the train were taken as the five-segment line sources.
- (2)
- Model Validation: The results of a five-segment UFL-IMLS equivalent model derived from the flow simulation data demonstrated strong agreement with the on-site measurements. The maximum absolute deviations in the equivalent sound levels across the monitoring points were constrained to 1.3 dB(A), satisfying the requirements of engineering predictions.
- (3)
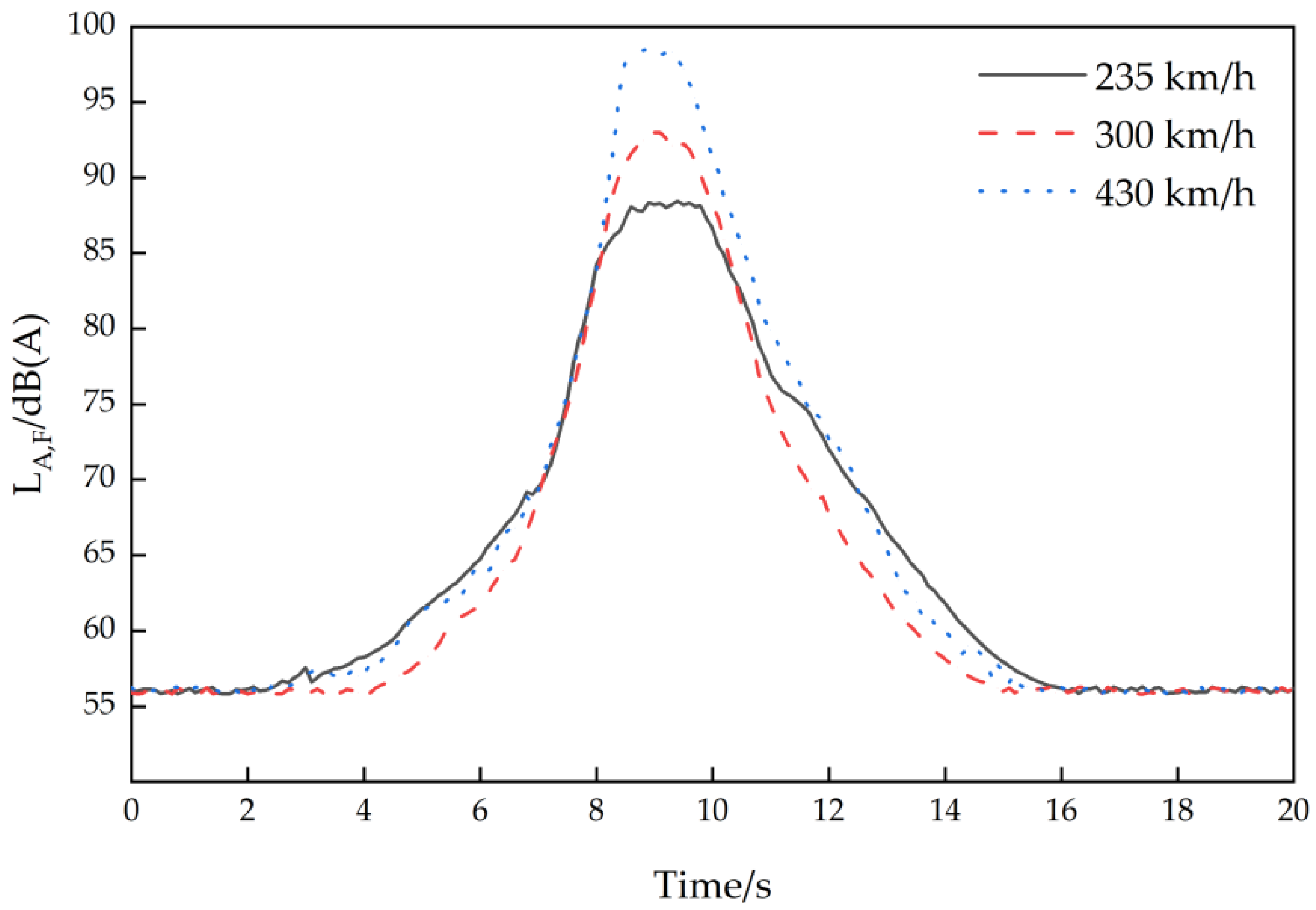
- High-Speed Extrapolation: The validated predictions were extended to 600 km/h operation, generating lateral attenuation curves of equivalent continuous A-weighted SPLs and time-domain profiles and providing critical reference information for ultra-high-speed Maglev noise assessment. The time-domain curves of each velocity had similar trends, and the time-domain curve peaks became sharper with an increase in velocity. The curve trends of equivalent continuous A-weighted SPLs with the lateral distance were the same at each speed, and at 600 km/h, the equivalent continuous A-weighted SPLs decreased by 11.8 dB as the logarithm of the lateral distance doubles.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LES | Large eddy simulation |
| SEL | Sound exposure level |
| SPL | Sound pressure level |
| UFL-IMLS | Uniform finite-length incoherent moving line source |
| SST | Shear stress transport |
| SIMPLE | Semi-implicit pressure-linked equations |
| WALE | Wall-adapting local eddy |
| FFT | Fast Fourier transform |
| CPB | Constant percentage bandwidth |
References
- Prascevic, M.; Gajicki, A.; Mihajlov, D.; Zivkovic, N.; Zivkovic, L. Application of the prediction model “SCHALL 03” for railway noise calculation in Serbia. In Proceedings of the 12th International Symposium Acoustics and Vibration of Mechanical Structures, 23–24 May 2013, Timişoara, Romania; AVMS: Timişoara, Romania, 2013; p. 237. [Google Scholar]
- Bundesbahn, D. Richtlinie zur Berechnung der Schallimmissionen von Schienewegen, Schall03/Akustik03; Bundesbahn Zentralamt: München, Germany, 1990.
- Moehler, U.; Liepert, M.; Kurze, U.J.; Onnich, H. The New German Prediction Model for Railway Noise “Schall 03 2006”—Potentials of the New Calculation Method for Noise Mitigation of Planned Rail Traffic. In Noise and Vibration Mitigation for Rail Transportation Systems; Notes on Numerical Fluid Mechanics and Multidisciplinary Design; Schulte-Werning, B., Thompson, D., Gautier, P.-E., Hanson, C., Hemsworth, B., Nelson, J., Maeda, T., Vos, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 99, pp. 186–192. [Google Scholar]
- Kumar, K.; Bhartia, A.; Mishra, R.K. Monitoring, modeling, and mapping of rail-induced noise at selected stations in megacity Delhi. Int. J. Environ. Sci. Technol. 2023, 20, 10243–10252. [Google Scholar] [CrossRef]
- Tsukernikov, I.E.; Tikhomirov, L.A.; Nevenchannaya, T.O. Projected multifunctional hotel complex noise level prediction from railway trains passing (JSC ‘Russian Railways’ connecting branch section) with sound insulation measures development. In IOP Conference Series: Materials Science and Engineering; IOP Publishing Ltd.: Bristol, UK, 2020; Volume 753, p. 022078. [Google Scholar] [CrossRef]
- Ivanov, N.I.; Boiko, I.S.; Shashurin, A.E. The problem of high-speed railway noise prediction and reduction. Procedia Eng. 2017, 189, 539–546. [Google Scholar] [CrossRef]
- Okada, T. A study on predicting shinkansen noise levels using the sound intensity method. JSME Int. J. Ser. C 2004, 47, 508–511. [Google Scholar] [CrossRef]
- Kawahara, M.; Hotta, H.; Hiroe, M.; Kaku, J. Source Identification and Prediction of Shinkansen Noise by Sound Intensity. In Proceedings of the 1997 International Congress on Noise Control Engineering, InterNoise97, Budapest, Hungary, 25–27 August 1997; Institute of Noise Control Engineering: Wakefield, MA, USA, 1997; pp. 151–154. [Google Scholar]
- Kanda, H.; Tsuda, H.; Ichikawa, K.; Yoshida, S. Environmental noise reduction of Tokaido Shinkansen and future prospect. In Noise and Vibration Mitigation for Rail Transportation Systems; Schulte-Werning, B., Thompson, D., Gautier, P.E., Hanson, C., Hemsworth, B., Nelson, J., Maeda, T., Vos, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–8. [Google Scholar] [CrossRef]
- Hanson, C.E.; Ross, J.C.; Towers, D.A. High-Speed Ground Transportation Noise and Vibration Impact Assessment; U.S. Department of Transportation, Federal Railroad Administration, Office of Railroad Development: Washington, DC, USA, 2012.
- HJ 453-2018; Technical Guidelines for Environmental Impact Assessment of Urban Rail Transit. Ministry of Ecology and Environment, The People’s Republic of China: Beijing, China, 2018.
- Ju, L.; Ge, J.; Guo, Y. Model of high-speed railway noise prediction based on multi-source mode. J. Tongji Univ. (Nat. Sci.) 2017, 45, 58–63. [Google Scholar] [CrossRef]
- Brecher, A.; Disk, D.R.; Fugate, D.; Jacobs, W.; Joshi, A.; Kupferman, A.; Mauri, R.; Valihur, P. Noise Characteristics of the Transrapid TR08 Maglev System. 2002. Available online: https://rosap.ntl.bts.gov/view/dot/8507 (accessed on 1 April 2025).
- Wang, Z.-S.; Wang, F.-Q.; Gao, S.-Y. Research on Prediction of Noises of High Speed Railway Bridge. J. Southwest Jiaotong Univ. 2001, 14, 166–168. [Google Scholar]
- Givargis, S.; Karimi, H. Mathematical, statistical and neural models capable of predicting LA,max for the Tehran–Karaj express train. Appl. Acoust. 2009, 70, 1015–1020. [Google Scholar] [CrossRef]
- Cheng, S.; Ge, J.; Zhang, G.; Liu, S. Separation of turbulent pressure and acoustic pressure on a maglev train window and the contribution of interior noise at high speeds. Appl. Acoust. 2025, 231, 110465. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- ISO 3095:2013; Acoustics-Railway Applications—Measurement of Noise Emitted by Railbound Vehicles. International Organization for Standardization: Geneva, Switzerland, 2013.
- Ffowcs Williams, J.E.; Hawkings, D.L. Sound generation by turbulence and surfaces in arbitrary motion. Philos. Trans. A Math. Phys. Eng. Sci. 1969, 264, 321–342. [Google Scholar]
- Ewert, R.; Schröder, W. Acoustic perturbation equations based on flow decomposition via source filtering. J. Comp. Phys. 2003, 188, 365–398. [Google Scholar] [CrossRef]
- ISO 3745:2012; Acoustics—Determination of Sound Power Levels and Sound Energy Levels of Noise Sources Using Sound Pressure—Precision Methods for Anechoic Rooms and Hemi-anechoic Room. International Organization for Standardization: Geneva, Switzerland, 2012.
- ISO 9613-1:1993; Acoustics, Outdoor Sound Propagation Attenuation Part I: Atmosphere Sound Absorption Calculation. International Organization for Standardization: Geneva, Switzerland, 1993.
- Mao, D.; Hong, Z. Environmental Noise Control Engineering; Higher Education Press: Beijing, China, 2010; p. 308. [Google Scholar]



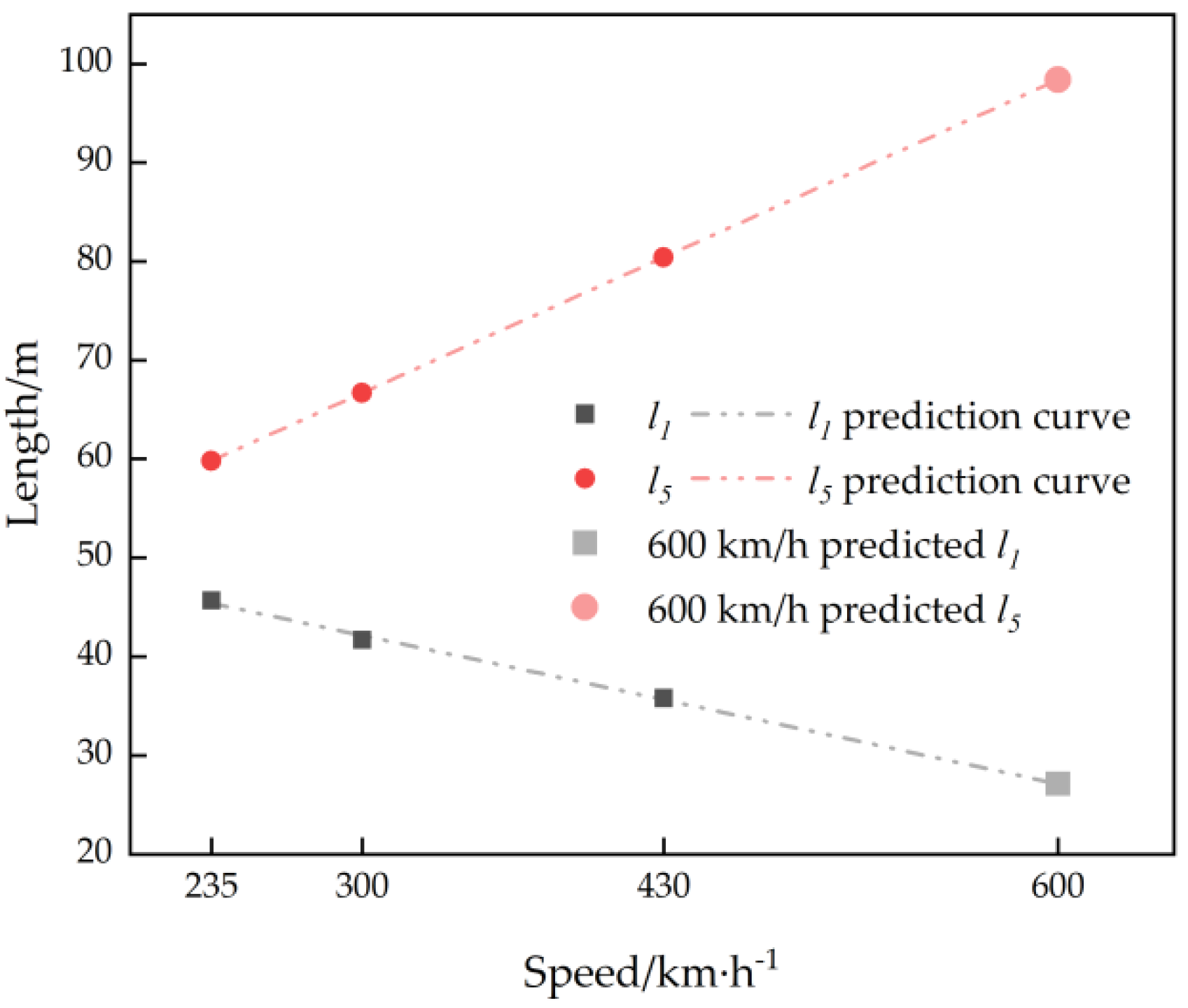
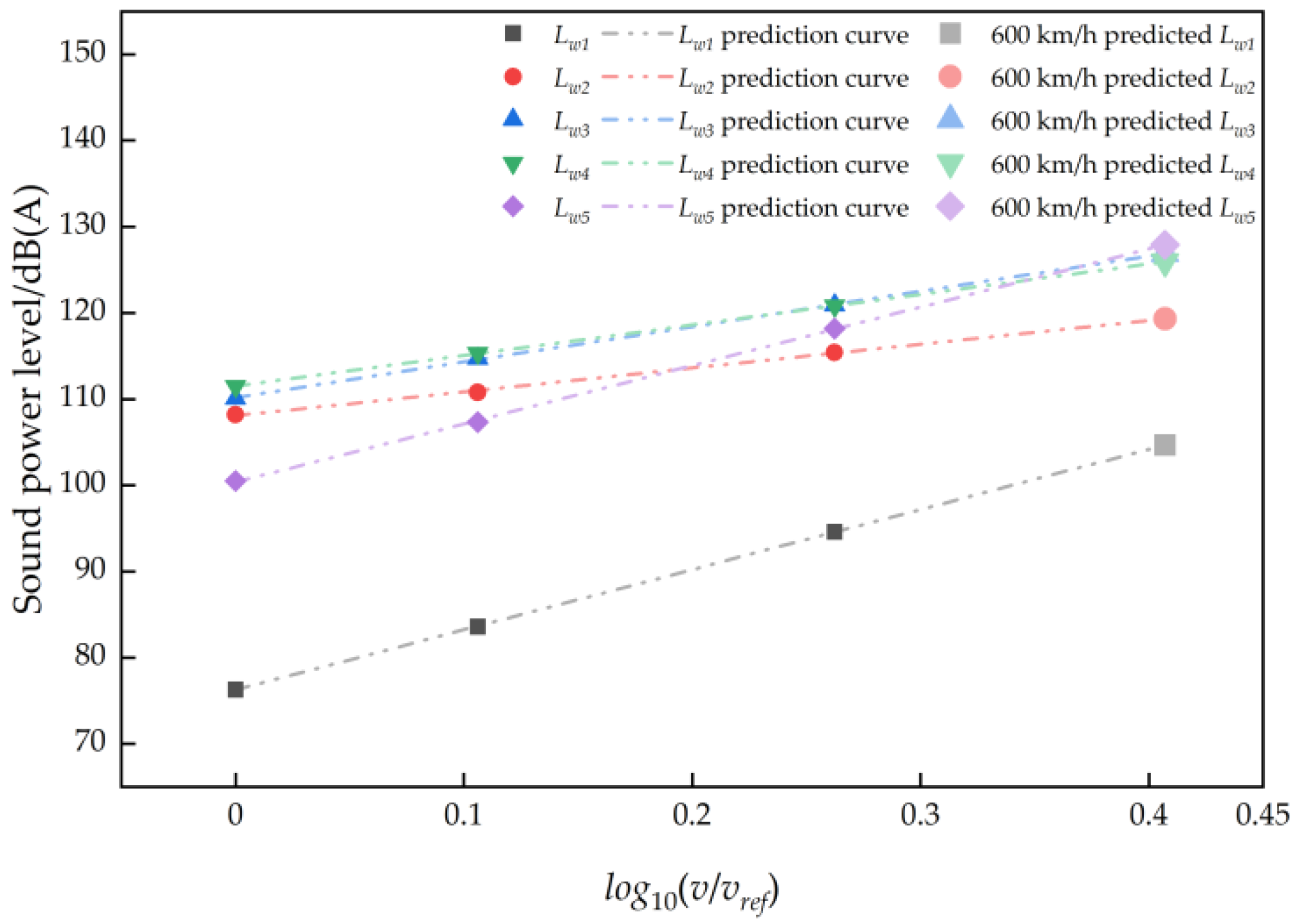
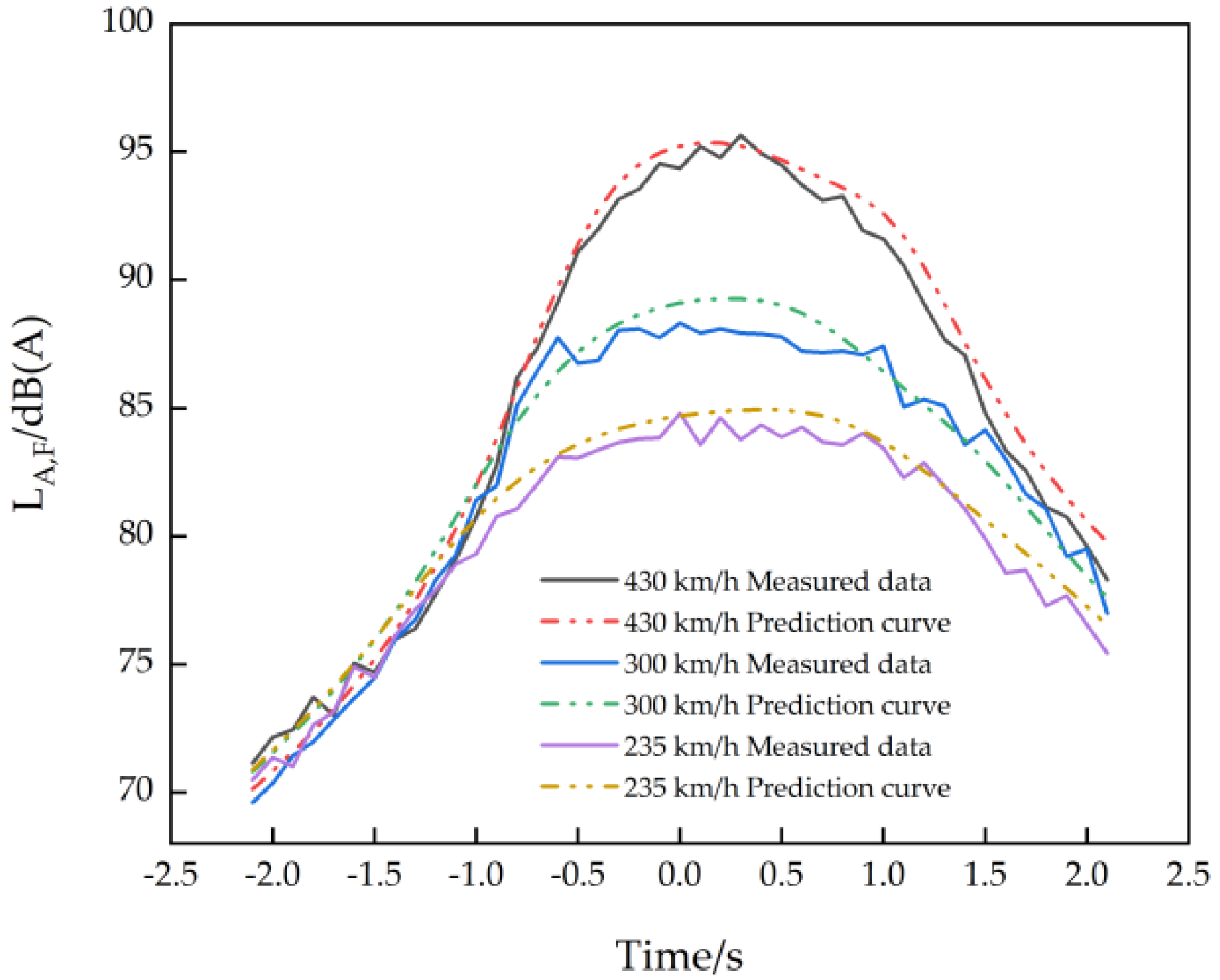
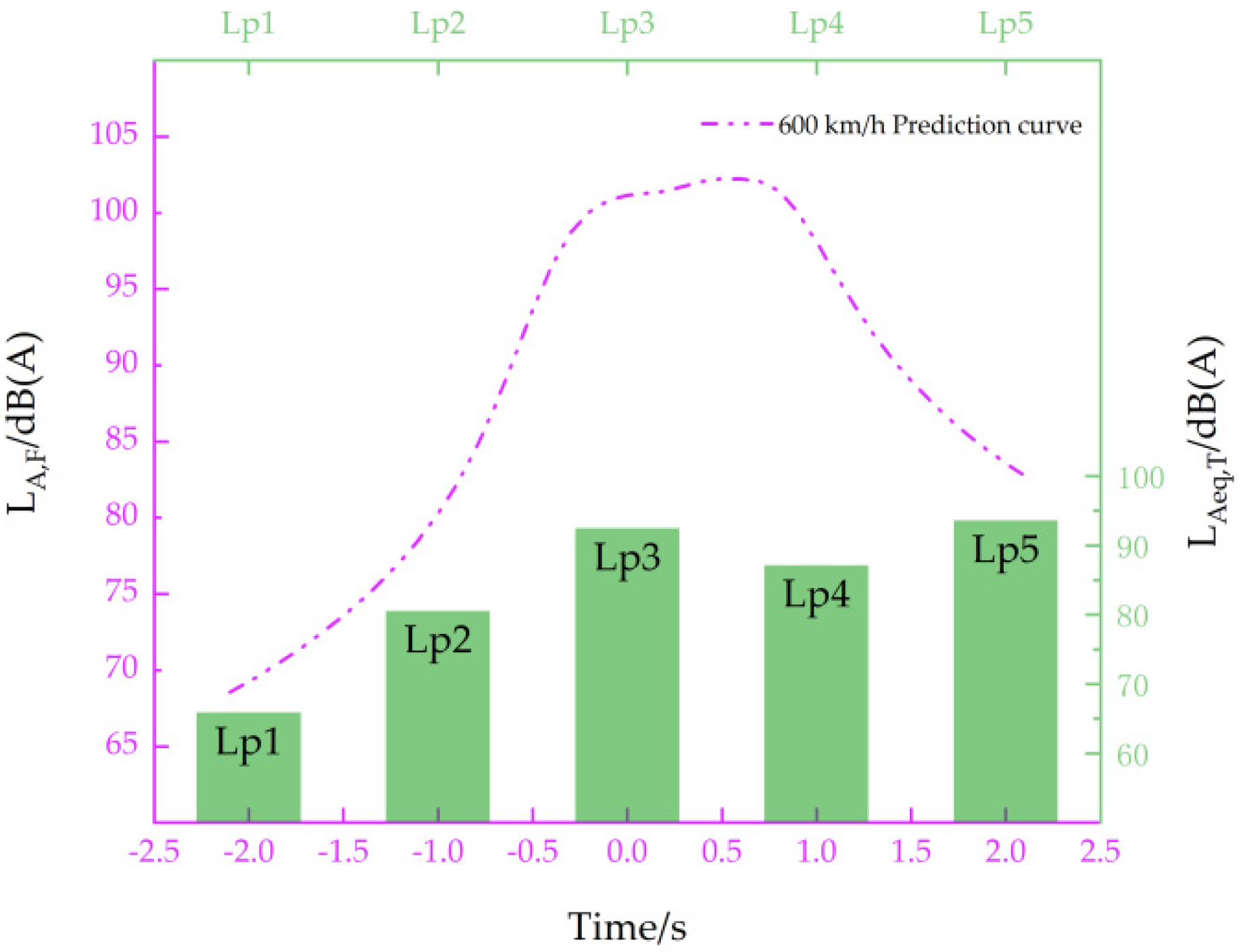
| Train Operating Speed (km/h) | Lw1 | Lw2 | Lw3 | Lw4 | Lw5 |
|---|---|---|---|---|---|
| 235 | 76.3 | 108.2 | 110.1 | 111.5 | 100.5 |
| 300 | 83.6 | 110.8 | 114.7 | 115.3 | 107.3 |
| 430 | 94.6 | 115.4 | 120.9 | 120.8 | 118.2 |
| Train Operating Speed (km/h) | Measured LAeq,E | Predicted LAeq,P | LAeq Error |Δ| |
| 235 | 87.6 | 87.9 | 0.2 |
| 300 | 91.8 | 92.2 | 0.4 |
| 430 | 98.1 | 98.6 | 0.5 |
| Temperature (°C) | Relative Humidity (%) | Octave-Band Center Frequency (Hz) | |||||
|---|---|---|---|---|---|---|---|
| 125 | 250 | 500 | 1000 | 2000 | 4000 | ||
| 25 | 50 | 3.99 × 10−4 | 1.32 × 10−3 | 3.23 × 10−3 | 5.68 × 10−3 | 1.02 × 10−2 | 2.57 × 10−2 |
| 25 | 60 | 3.40 × 10−4 | 1.18 × 10−3 | 3.18 × 10−3 | 5.96 × 10−3 | 1.02 × 10−2 | 2.32 × 10−2 |
| 25 | 70 | 2.96 × 10−4 | 1.06 × 10−3 | 3.08 × 10−3 | 6.19 × 10−3 | 1.04 × 10−2 | 2.19 × 10−2 |
| 35 | 60 | 2.57 × 10−4 | 9.77 × 10−4 | 3.32 × 10−3 | 8.45 × 10−3 | 1.51 × 10−2 | 2.58 × 10−2 |
| 15 | 60 | 4.26 × 10−4 | 1.18 × 10−3 | 2.31 × 10−3 | 4.06 × 10−3 | 9.5 × 10−3 | 3.03 × 10−2 |
| 0 | 60 | 4.01 × 10−4 | 7.79 × 10−4 | 1.78 × 10−3 | 5.50 × 10−3 | 1.93 × 10−2 | 6.33 × 10−2 |
| –10 | 60 | 3.60 × 10−4 | 9.69 × 10−4 | 3.23 × 10−3 | 1.09 × 10−2 | 2.96 × 10−2 | 5.35 × 10−2 |
| rr/rd | ≈1 | ≈1.4 | ≈2 | >2.5 |
| Cg,r,i | 3 | 2 | 1 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, S.; Ge, J.; Ju, L.; Chen, Y. Prediction Model for the Environmental Noise Distribution of High-Speed Maglev Trains Using a Segmented Line Source Approach. Appl. Sci. 2025, 15, 4184. https://doi.org/10.3390/app15084184
Cheng S, Ge J, Ju L, Chen Y. Prediction Model for the Environmental Noise Distribution of High-Speed Maglev Trains Using a Segmented Line Source Approach. Applied Sciences. 2025; 15(8):4184. https://doi.org/10.3390/app15084184
Chicago/Turabian StyleCheng, Shiquan, Jianmin Ge, Longhua Ju, and Yuhao Chen. 2025. "Prediction Model for the Environmental Noise Distribution of High-Speed Maglev Trains Using a Segmented Line Source Approach" Applied Sciences 15, no. 8: 4184. https://doi.org/10.3390/app15084184
APA StyleCheng, S., Ge, J., Ju, L., & Chen, Y. (2025). Prediction Model for the Environmental Noise Distribution of High-Speed Maglev Trains Using a Segmented Line Source Approach. Applied Sciences, 15(8), 4184. https://doi.org/10.3390/app15084184






