A New Signal Processing Method for Time-of-Flight and Center Frequency Estimation
Abstract
1. Introduction
2. Methodology for Estimation of Time-of-Flight and Center Frequency of Signals
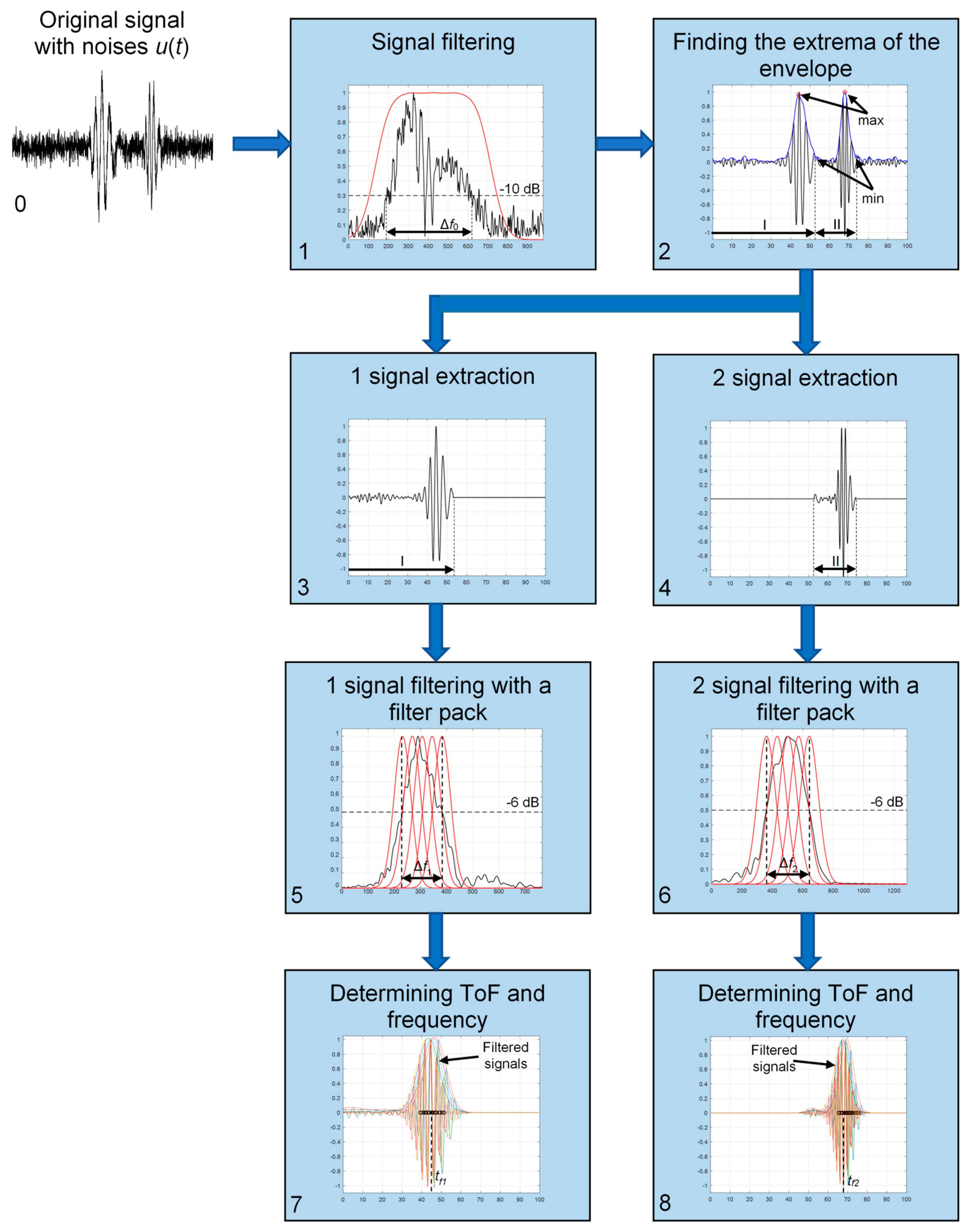
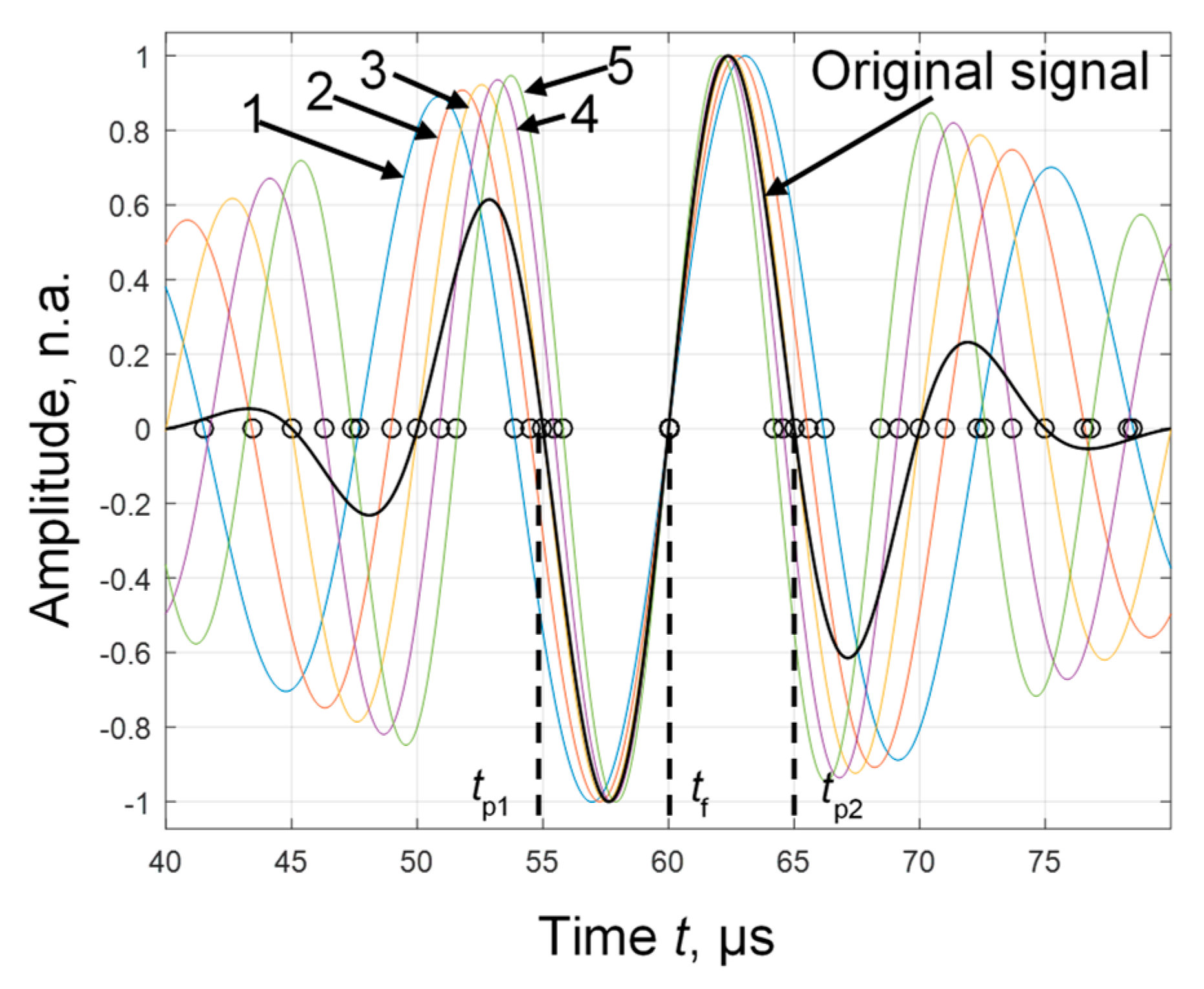
2.1. Signal Processing of Ultrasound Signals with Noises
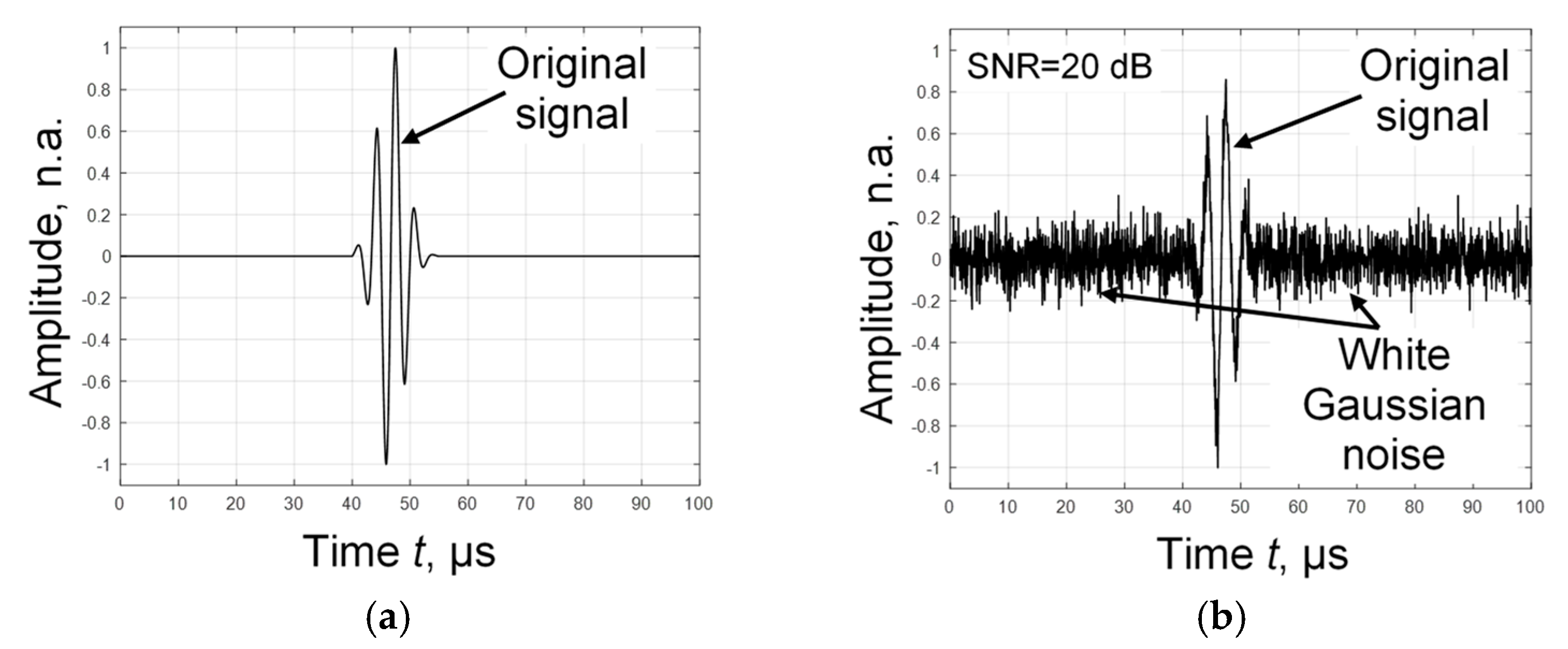
2.2. The Influence of Noise on the Accuracy of the Measured Parameters
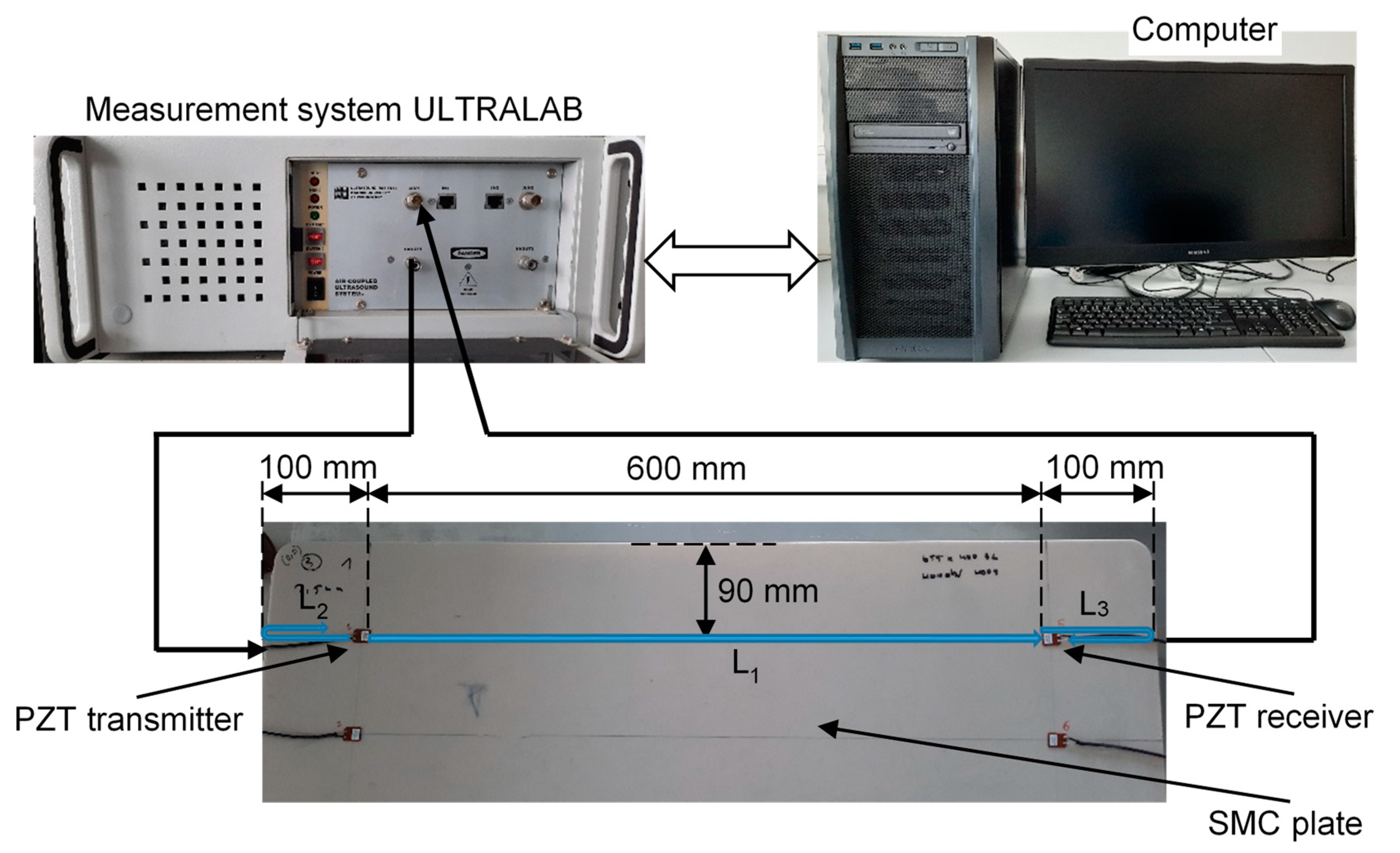
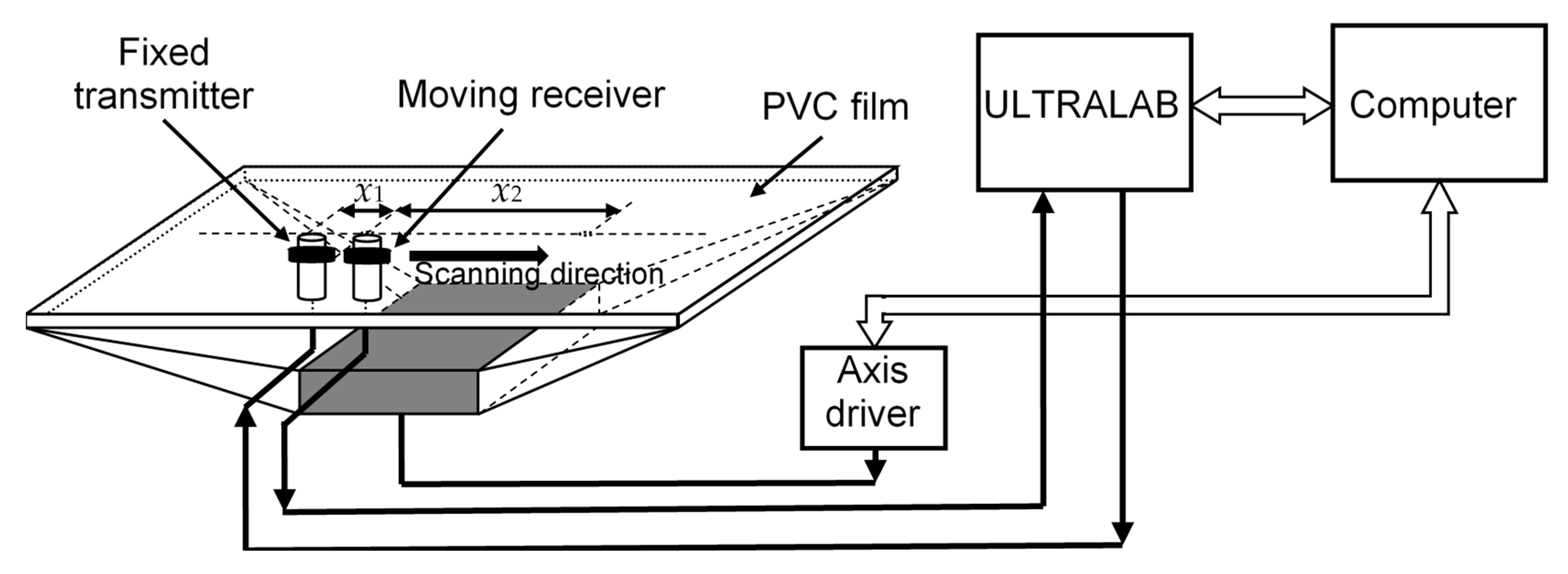
3. Experimental Signal Processing by the Proposed Method
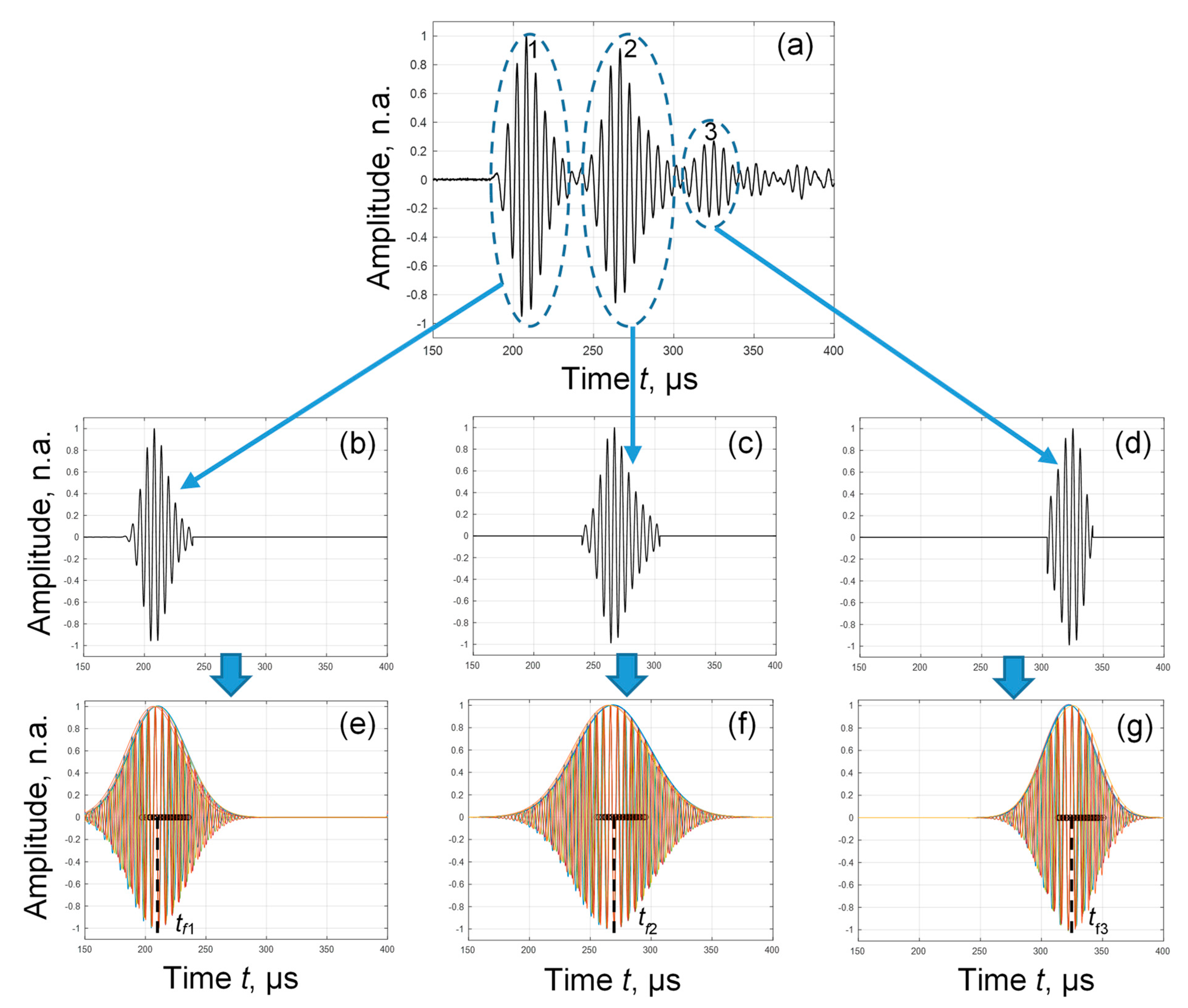
3.1. Estimating the Parameters of the Reflected Signals
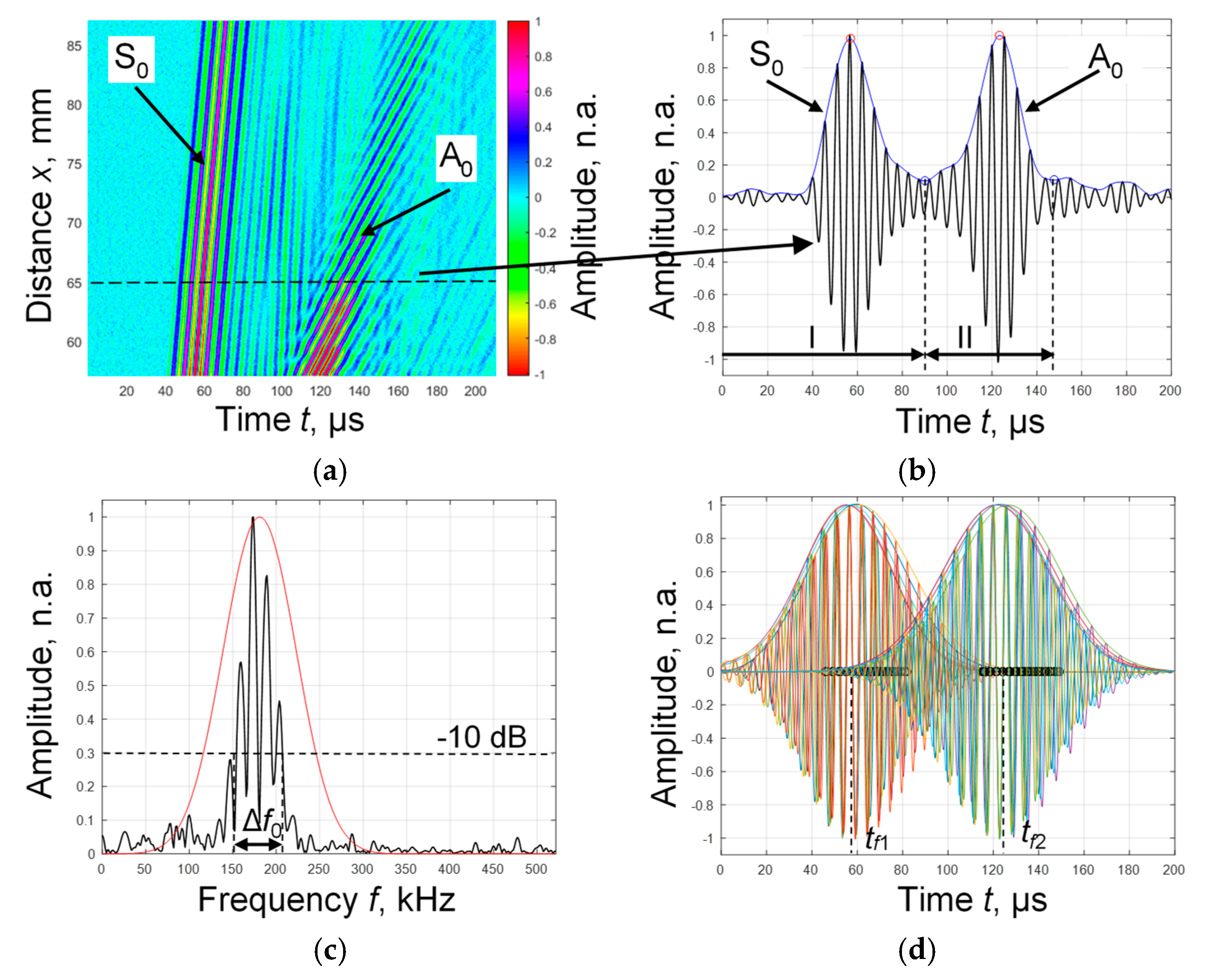
3.2. Separation of the Fundamental Modes
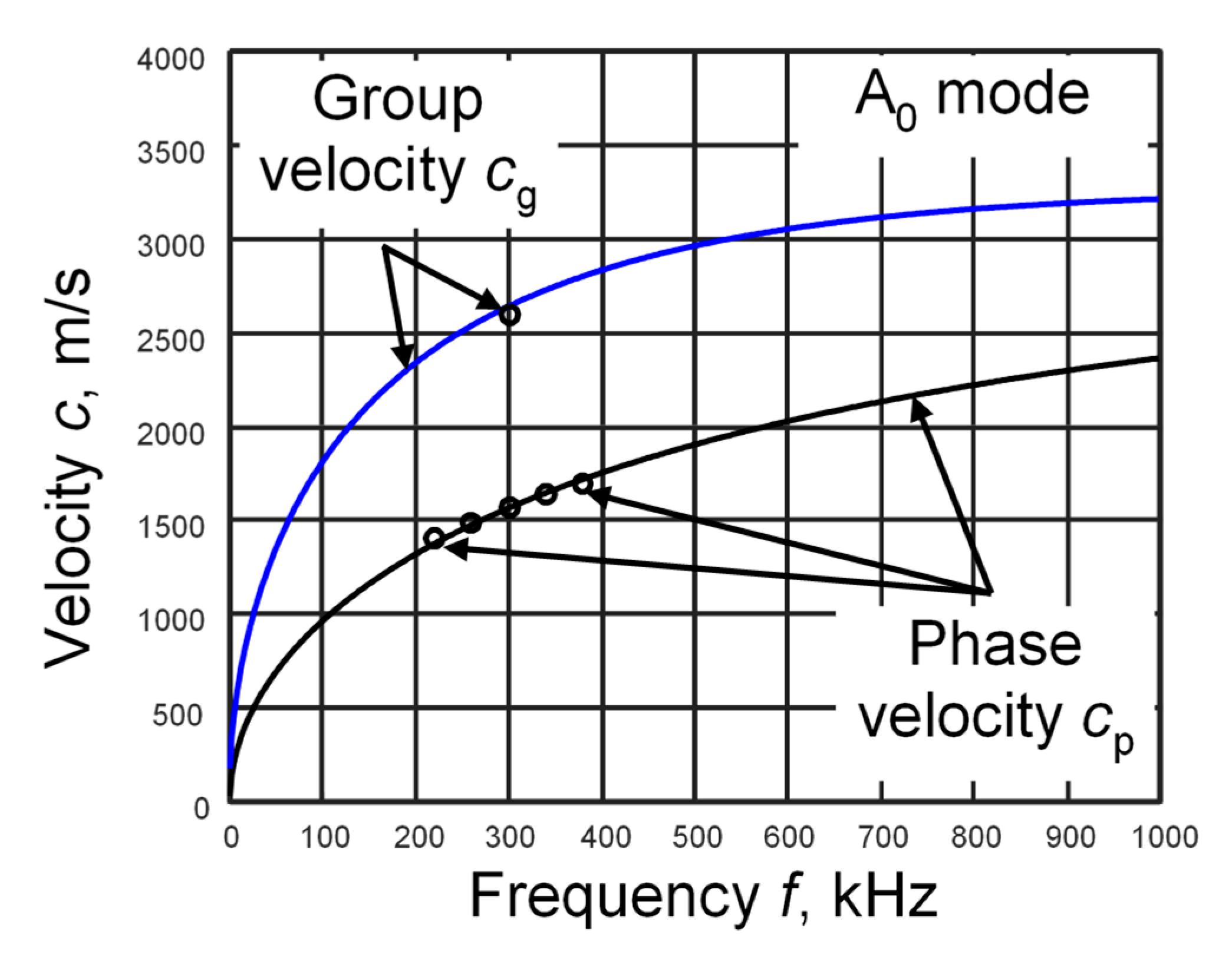
3.3. Phase and Group Velocities Determination
4. Discussion and Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ToF | Time-of-Flight |
| SNR | Signal-to-Noise Ratio |
| STFT | Short-Time Fourier Transform |
| CWT | Continuous Wavelet Transform |
| DWT | Discrete Wavelet Transform |
| FT | Fourier Transform |
| HT | Hilbert Transform |
| LW | Lamb Wave |
| SMC | Sheet Molding Compound |
| PVC | Polyvinyl Chloride |
References
- Xu, B.; Yu, L.; Giurgiutiu, V. Advanced methods for time-of-flight estimation with application to lamb wave structural health monitoring. In Proceedings of the 7th International Workshop on Structural Health Monitoring, Stanford, CA, USA, 9–11 September 2009. [Google Scholar]
- Raya, R.; Frizera, A.; Ceres, R.; Calderón, L.; Rocon, E. Design and evaluation of a fast model-based algorithm for ultrasonic range measurements. Sens. Actuators A Phys. 2008, 148, 335–341. [Google Scholar] [CrossRef]
- Chen, Q.; Li, W.; Wu, J. Realization of a multipath ultrasonic gas flowmeter based on transit-time technique. Ultrasonics 2014, 54, 285–290. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.H.; Song, S.J.; Lee, J.K. Technique for measurements of elastic wave velocities and thickness of solid plate from access on only one side. Jpn. J. Appl. Phys. 2005, 44, 5240–5243. [Google Scholar] [CrossRef]
- Jenot, F.; Ouaftouh, M.; Duquennoy, M. Corrosion thickness gauging in plates using Lamb wave group velocity measurements. Meas. Sci. Technol. 2001, 12, 1287–1293. [Google Scholar] [CrossRef]
- Hoseini, M.R.; Wang, X.; Zuo, M.J. Estimating ultrasonic time of flight using envelope and quasi maximum likelihood method for damage detection and assessment. Measurement 2012, 45, 2072–2080. [Google Scholar] [CrossRef]
- Hull, D.R.; Kautz, H.E.; Vary, A. Measurement of ultrasonic velocity using phase-slope and cross-correlation method. Mater. Eval. 1985, 43, 1455–1460. [Google Scholar]
- Svilainis, L. Review of high resolution time of flight estimation techniques for ultrasonic signals. In Proceedings of the 52nd Annual Conference of the British Institute of Non-Destructive Testing, Telford, UK, 10–12 September 2013. [Google Scholar]
- Khyam, M.O.; Ge, S.S.; Li, X.D.; Pickering, M.R. Highly Accurate Time-of-Flight Measurement Technique Based on Phase-Correlation for Ultrasonic Ranging. IEEE Sens. J. 2017, 17, 434–443. [Google Scholar] [CrossRef]
- Jia, L.; Xue, B.; Chen, S.; Wu, H.; Yang, X.; Zhai, J.; Zeng, Z. A High-Resolution Ultrasonic Ranging System Using Laser Sensing and a Cross-Correlation Method. Appl. Sci. 2019, 9, 1483. [Google Scholar] [CrossRef]
- Hirata, S.; Kurosawa, M.K.; Katagiri, T. Real-time ultrasonic distance measurements for autonomous mobile robots using cross correlation by single-bit signal processing. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3601–3606. [Google Scholar] [CrossRef]
- Cai, C.; Regtien, P.P.L. Accurate digital time-of-flight measurement using self-interference. IEEE Trans. Instrum. Meas. 1993, 42, 990–994. [Google Scholar] [CrossRef]
- Wang, X.F.; Tang, Z.A. A novel method for digital ultrasonic time-of-flight measurement. Rev. Sci. Instrum. 2010, 81, 105112. [Google Scholar] [CrossRef] [PubMed]
- Jackson, J.C.; Summan, R.; Dobie, G.I.; Whiteley, S.M.; Pierce, S.G.; Hayward, G. Time-of-flight measurement techniques for airborne ultrasonic ranging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 343–355. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Li, D.; Xie, W. A novel time-of-flight difference determination method for ultrasonic thickness measurement with ultrasonic echo onset point detection. Appl. Acoust. 2025, 233, 110605. [Google Scholar] [CrossRef]
- Lu, Z.; Ma, F.; Yang, C.; Chang, M. A novel method for Estimating Time of Flight of ultrasonic echoes through short-time Fourier transforms. Ultrasonics 2020, 103, 106104. [Google Scholar] [CrossRef] [PubMed]
- Pomponi, E.; Vinogradov, A.; Danyuk, A. Wavelet based approach to signal activity detection and phase picking: Application to acoustic emission. Signal Process. 2015, 115, 110–119. [Google Scholar] [CrossRef]
- Zhou, H.; Li, P.; Wu, L.; Gao, Q. A wavelet analysis-based matching pursuit algorithm for an accurate ultrasonic TOFD measurement. Insight 2020, 62, 662–668. [Google Scholar] [CrossRef]
- Laddada, S.; Lemlikchi, S.; Guendouzi, F.; Si-Chaib, M.O.; Djelouah, H. Ultrasonic time of flight estimation using Wavelet transforms. In Proceedings of the 7th African Conference on Non Destructive Testing (ACNDT) & the 5th International Conference on NDT and Materials Industry and Alloys (IC-WNDT-MI), Oran, Algeria, 26–28 November 2016. [Google Scholar]
- Sturtevant, B.; Velisavljevic, N.; Sinha, D.; Kono, Y.; Pantea, C. A broadband wavelet implementation for rapid ultrasound pulse-echo time-of-flight measurements. Rev. Sci. Instrum. 2020, 91, 075115. [Google Scholar] [CrossRef] [PubMed]
- da Silva, J.H.B.; de Oliveira, L.D.; Villanueva, J.M.M. Application of Wavelet Transform for Ultrasonic Time of Flight Estimation. In Proceedings of the 6th International Symposium on Instrumentation Systems, Circuits and Transducers (INSCIT), Porto Alegre, Brazil, 22–26 August 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Cheeke, J.D.N. Fundamentals and Applications of Ultrasonic Waves; CRC Press: Boca Raton, FL, USA, 2012; pp. 1–504. [Google Scholar] [CrossRef]
- Tumšys, O. Experimental method for simultaneous determination of the Lamb wave A0 modes group and phase velocities. Materials 2022, 15, 2976. [Google Scholar] [CrossRef] [PubMed]
- MATLAB. User’s Manual. Available online: https://www.mathworks.com/help/matlab/index.html (accessed on 20 September 2024).
- Kažys, R.; Tumšys, O. Simultaneous measurement of thickness and elastic properties of thin plastic films by means of ultrasonic guided waves. Sensors 2021, 21, 6779. [Google Scholar] [CrossRef] [PubMed]
- Mažeika, L.; Draudvilienė, L.; Žukauskas, E. Influence of the dispersion on measurement of phase and group velocities of Lamb waves. Ultragarsas (Ultrasound) 2009, 64, 18–21. Available online: https://www.ultragarsas.ktu.lt/index.php/USnd/article/view/17122 (accessed on 20 September 2024).
- Tumšys, O.; Mažeika, L. Determining the Elastic Constants of Isotropic Materials by Measuring the Phase Velocities of the A0 and S0 Modes of Lamb Waves. Sensors 2023, 23, 6678. [Google Scholar] [CrossRef] [PubMed]

| SNR | 0 dB | 50 dB | 45 dB | 40 dB | 35 dB | 30 dB | 25 dB | 20 dB | 15 dB | 10 dB | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Frequency | |||||||||||
| 100 kHz | 0.002 | 0.005 | 0.009 | 0.017 | 0.050 | 0.052 | 0.054 | 0.159 | 0.580 | 1.460 | |
| 300 kHz | 0.003 | 0.005 | 0.013 | 0.015 | 0.030 | 0.083 | 0.259 | 0.850 | - | - | |
| 500 kHz | 0.004 | 0.006 | 0.027 | 0.091 | 0.134 | 0.296 | 0.419 | - | - | - | |
| 1000 kHz | 0.006 | 0.007 | 0.052 | 0.225 | 0.238 | 0.417 | - | - | - | - | |
| SNR | 0 dB | 50 dB | 45 dB | 40 dB | 35 dB | 30 dB | 25 dB | 20 dB | 15 dB | 10 dB | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ToF | |||||||||||
| 60 μs (100 kHz) | 0 | 0.0007 | 0.0015 | 0.0029 | 0.0061 | 0.0069 | 0.0071 | 0.0161 | 0.0382 | 0.0532 | |
| 46.7 μs (300 kHz) | 0 | 0.0008 | 0.0011 | 0.0033 | 0.0033 | 0.0066 | 0.0093 | 0.0150 | - | - | |
| 44 μs (500 kHz) | 0 | 0.0013 | 0.0014 | 0.0012 | 0.0015 | 0.0027 | 0.0035 | - | - | - | |
| 42 μs (1000 kHz) | 0 | 0.0072 | 0.0065 | 0.0068 | 0.0090 | 0.0150 | - | - | - | - | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tumšys, O. A New Signal Processing Method for Time-of-Flight and Center Frequency Estimation. Appl. Sci. 2025, 15, 5721. https://doi.org/10.3390/app15105721
Tumšys O. A New Signal Processing Method for Time-of-Flight and Center Frequency Estimation. Applied Sciences. 2025; 15(10):5721. https://doi.org/10.3390/app15105721
Chicago/Turabian StyleTumšys, Olgirdas. 2025. "A New Signal Processing Method for Time-of-Flight and Center Frequency Estimation" Applied Sciences 15, no. 10: 5721. https://doi.org/10.3390/app15105721
APA StyleTumšys, O. (2025). A New Signal Processing Method for Time-of-Flight and Center Frequency Estimation. Applied Sciences, 15(10), 5721. https://doi.org/10.3390/app15105721






