Wear Prediction and Mechanism Study of Tunnel Boring Machine Disc Cutter Breaking in Hard–Soft Rock Considering Thermal Effect
Abstract
1. Introduction
2. Rock Composition and Wear Characteristics of Composite Strata
2.1. Composition of Hard and Soft Strata
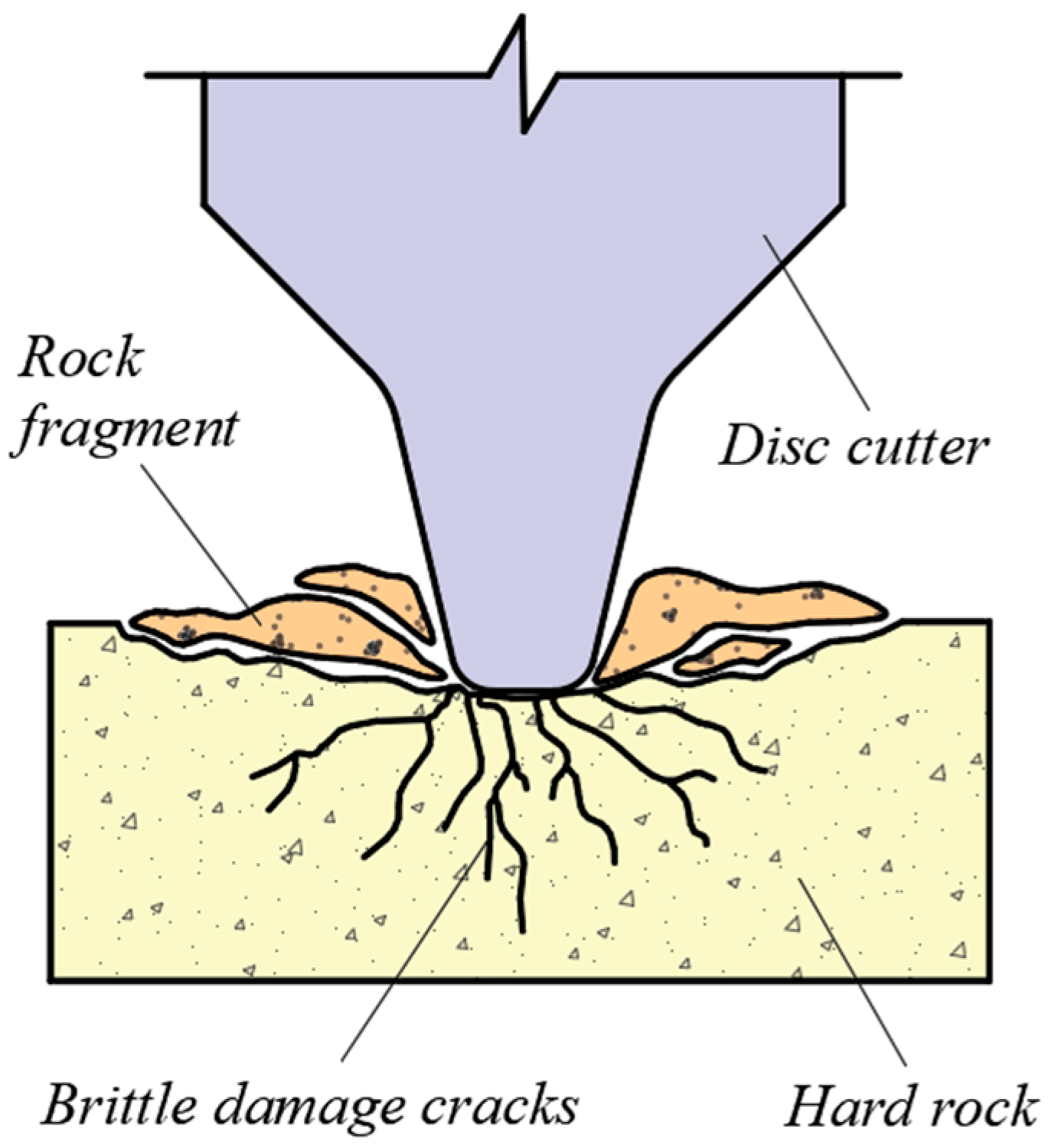
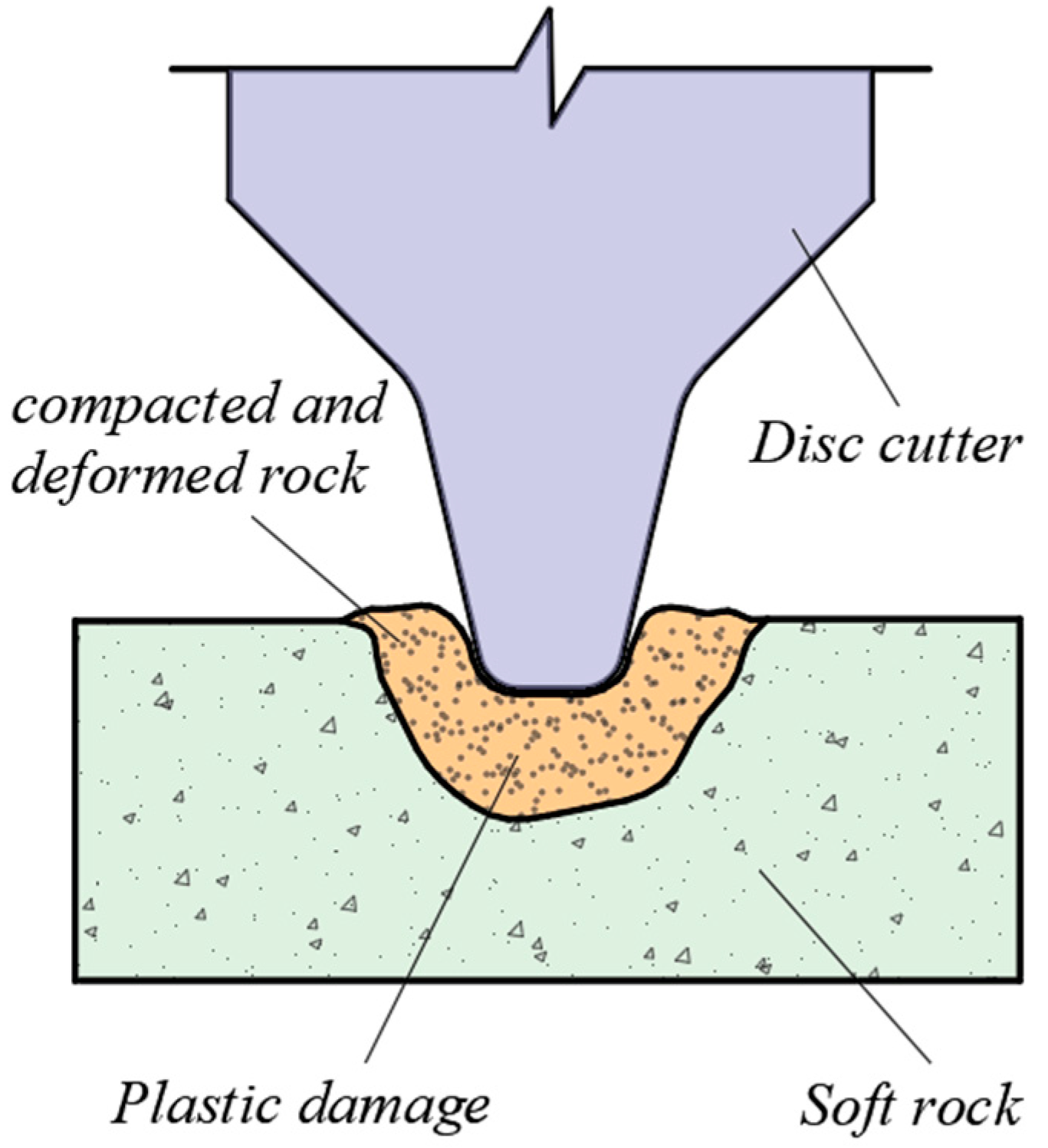
2.2. Wear Types and Wear Phenomena of Disc Cutter
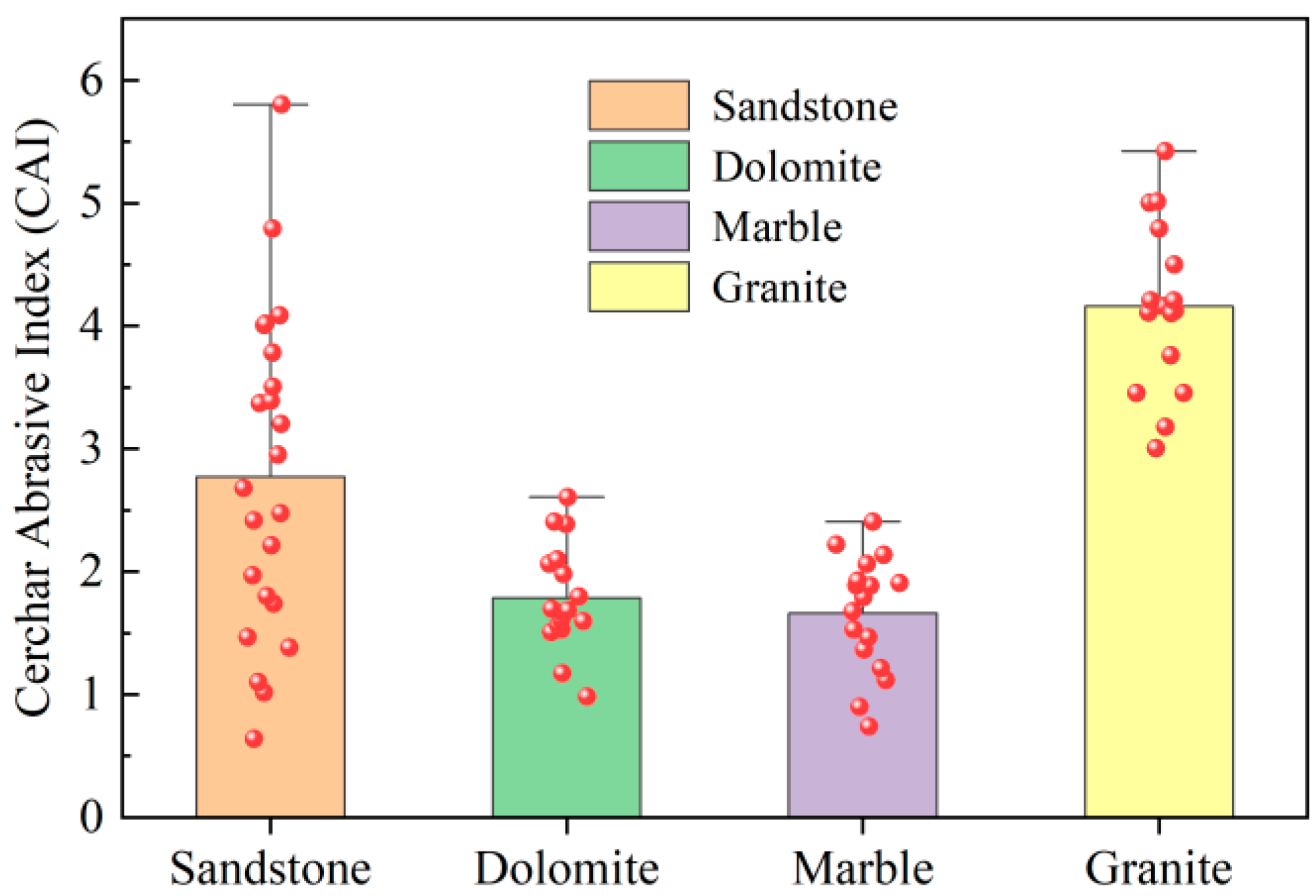
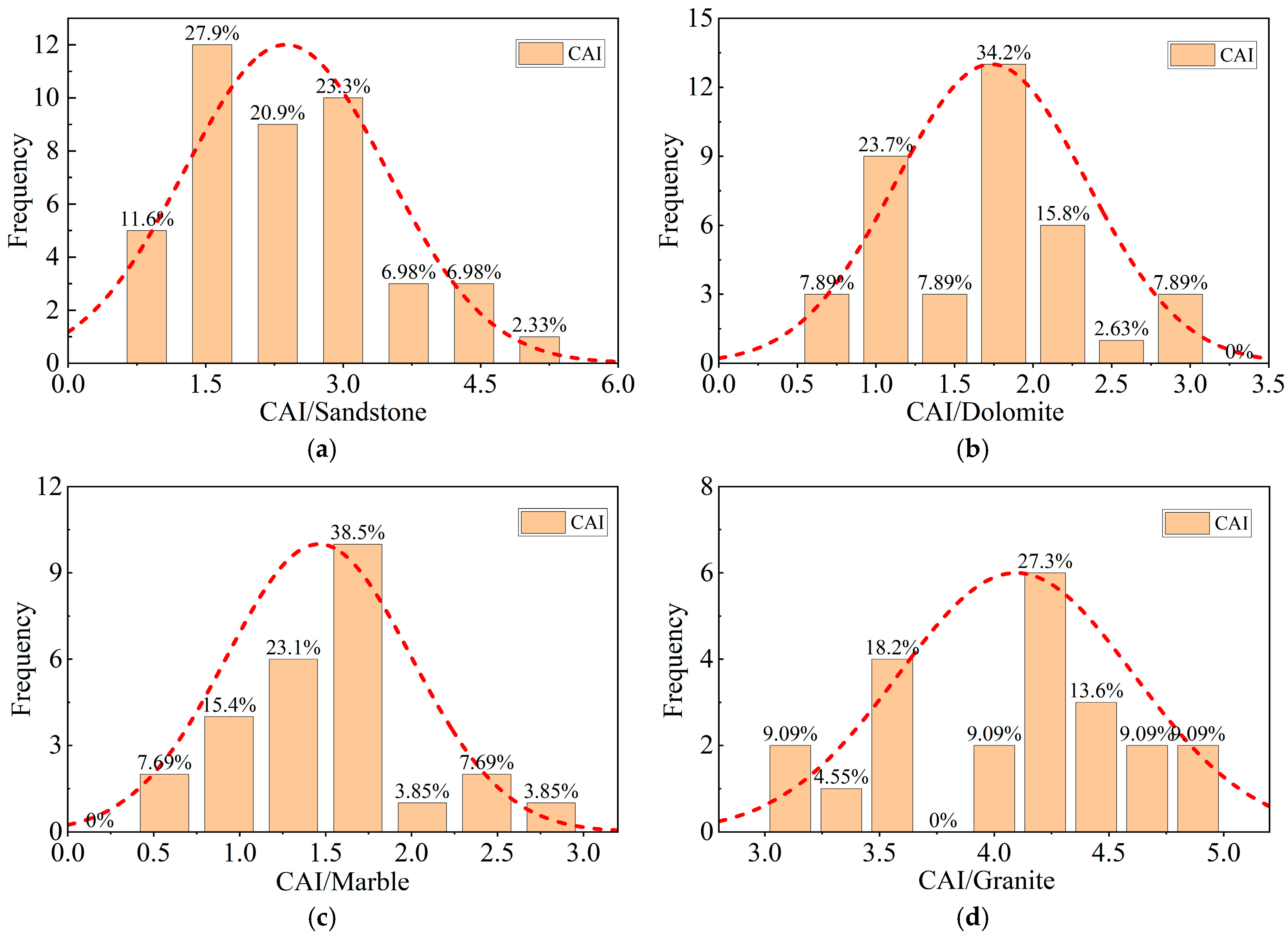
2.3. Rock Abrasion Resistance and Rock Property Variability
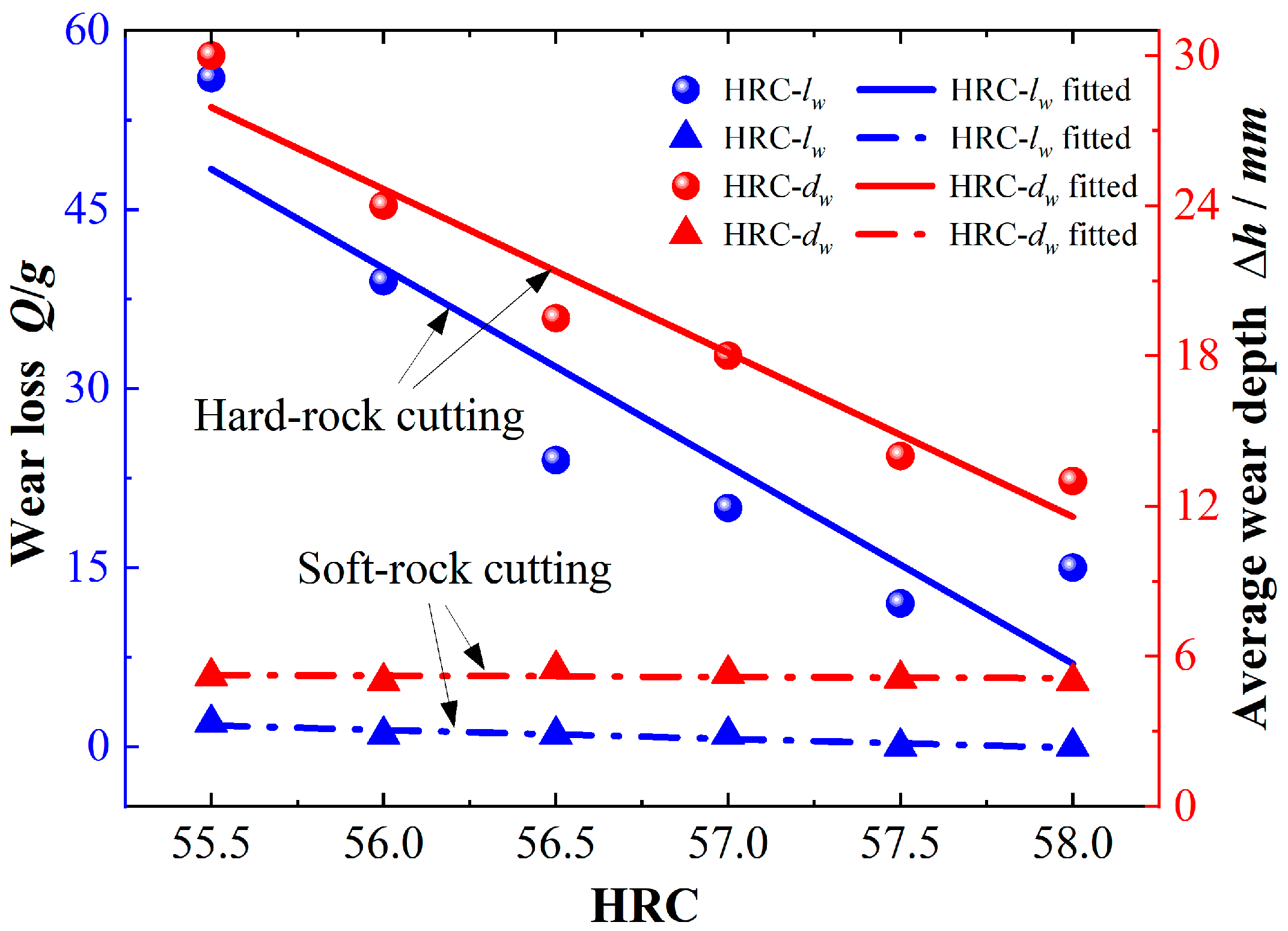
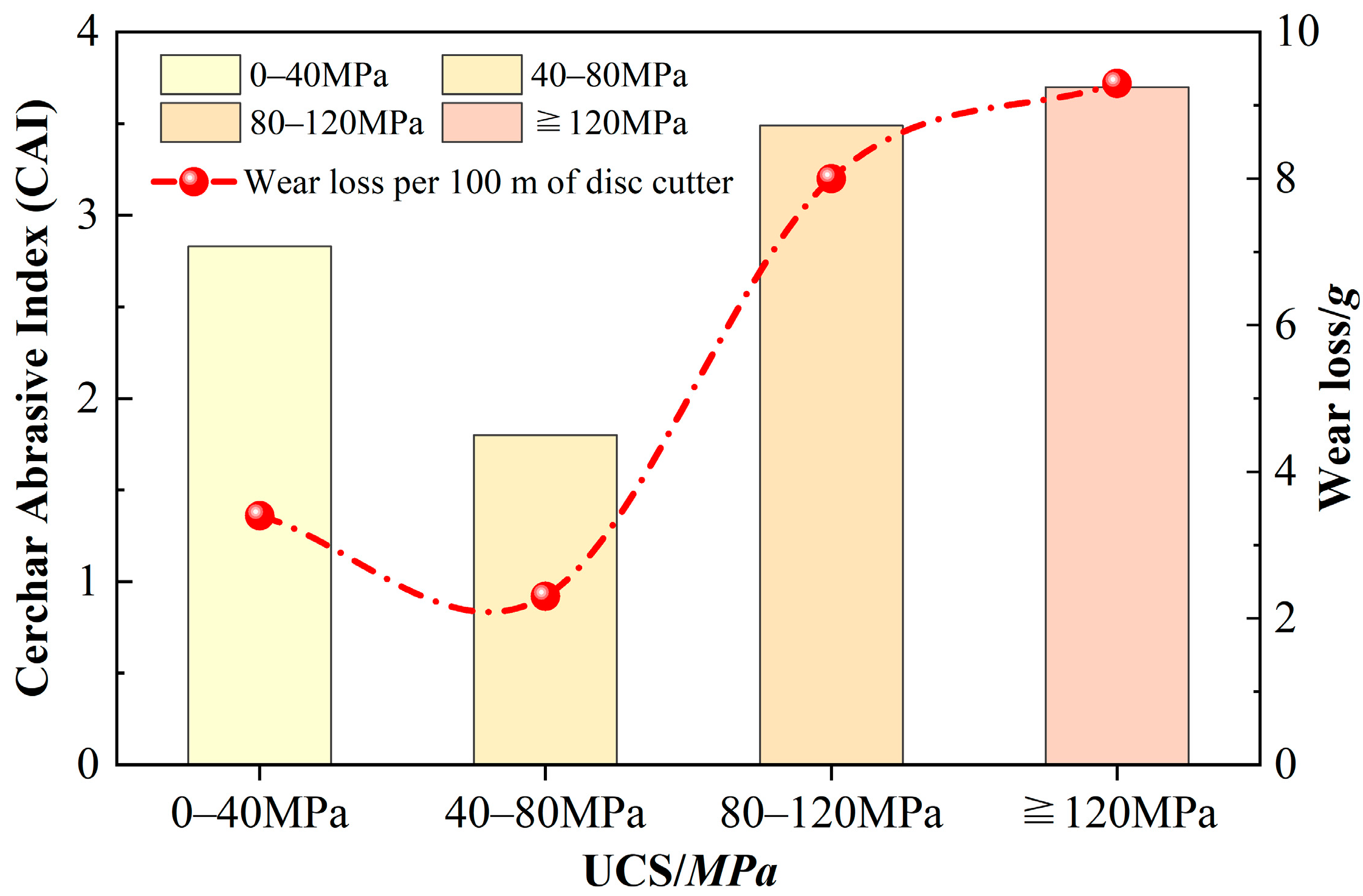
2.4. Relationship Between Rock Strength and Wear
3. Force Model and Relative Motion Analysis of Cutter
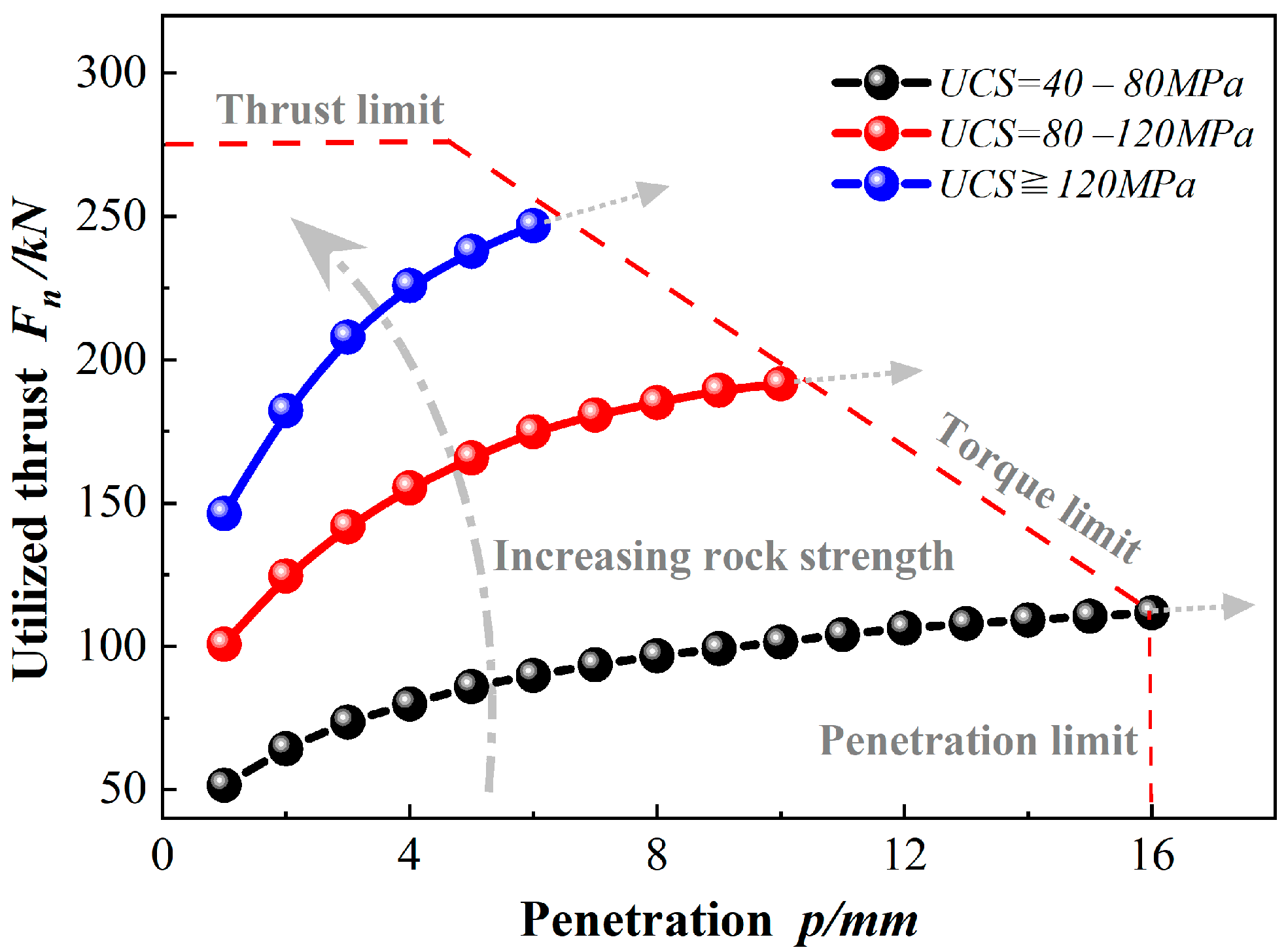
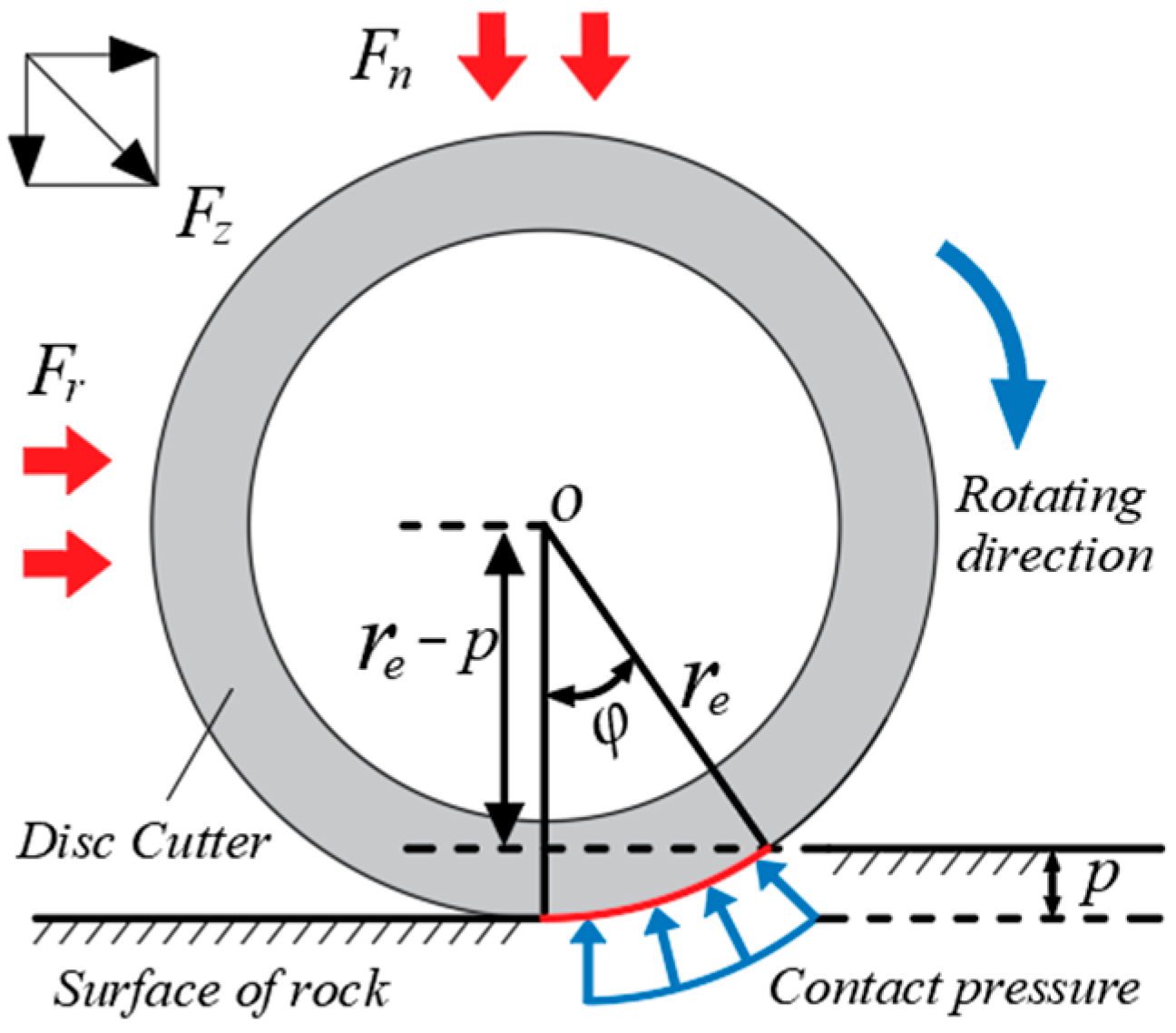
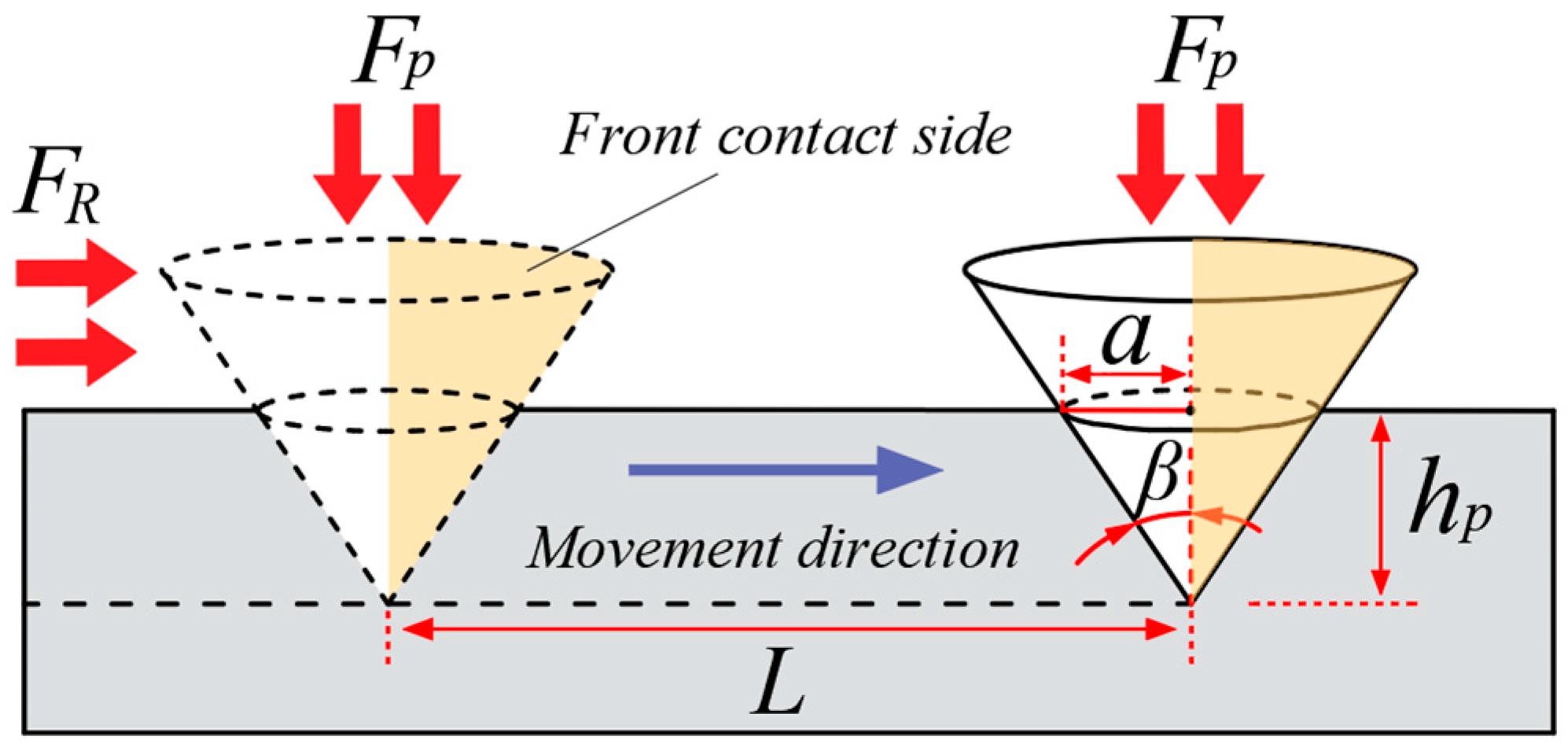
3.1. Rock-Breaking Force Pattern of the Cutter
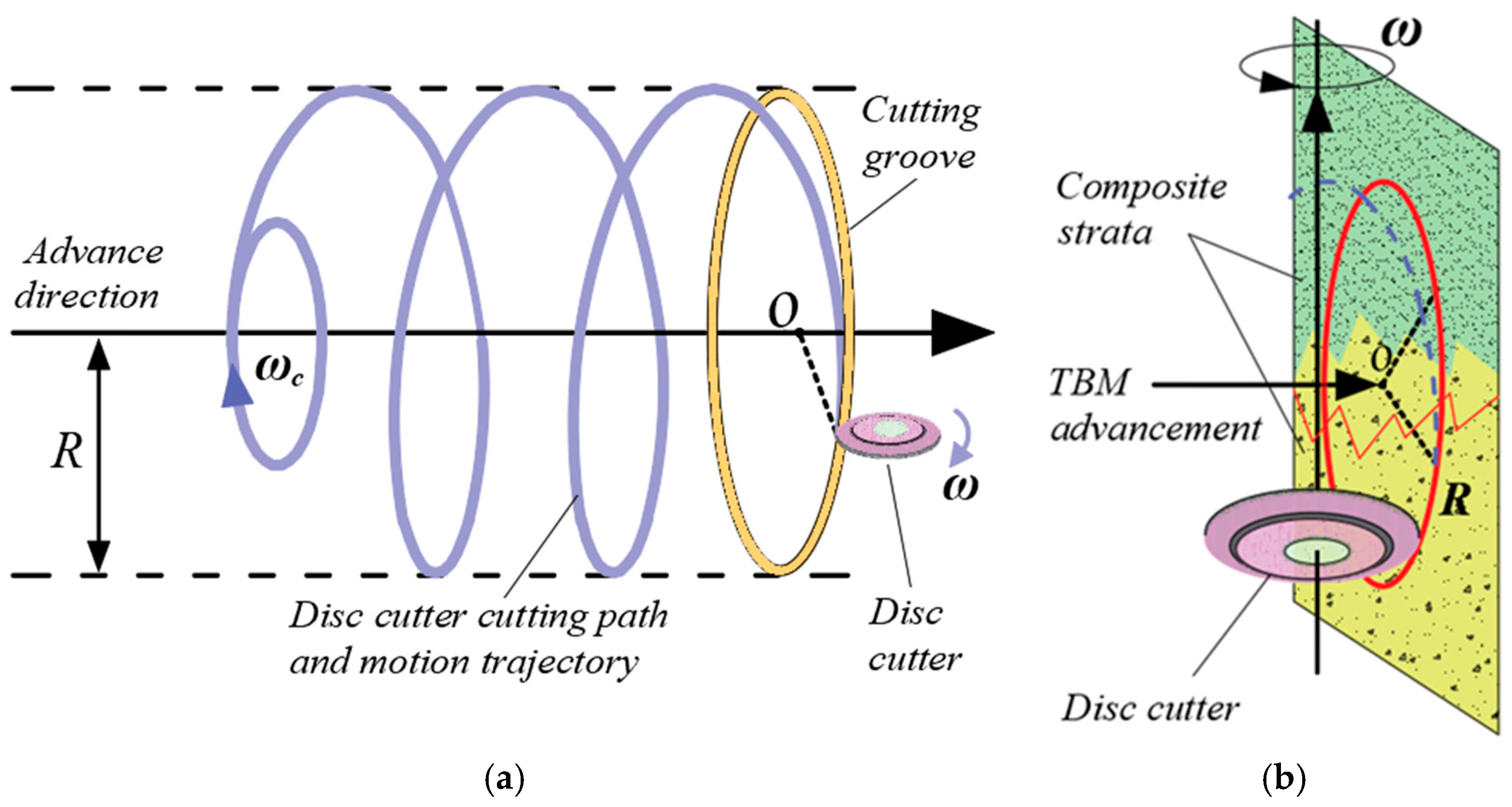
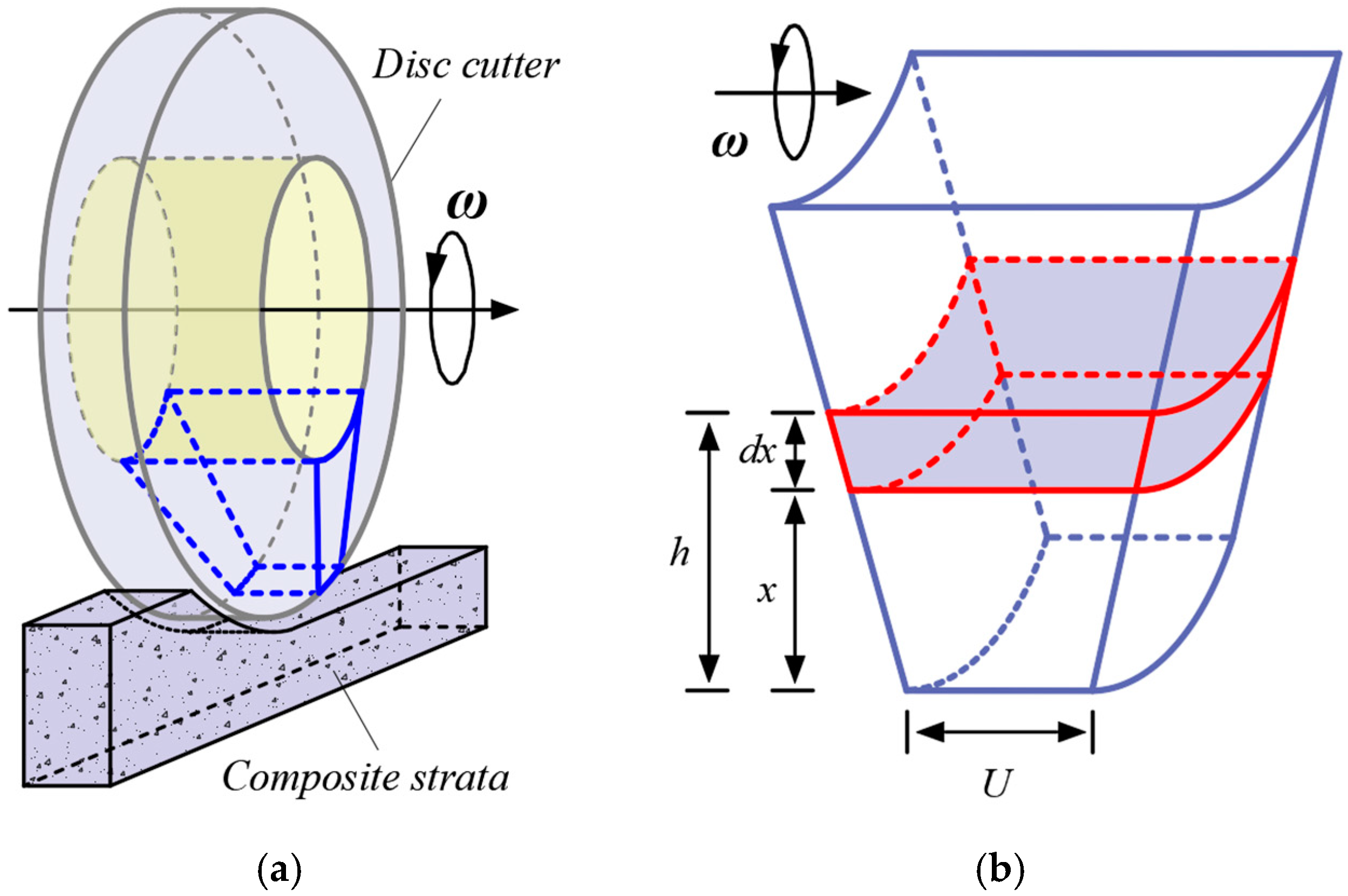
3.2. Analysis of Relative Motion
4. Cutter Wear Mechanism and Calculation Model Considering Thermal Effect
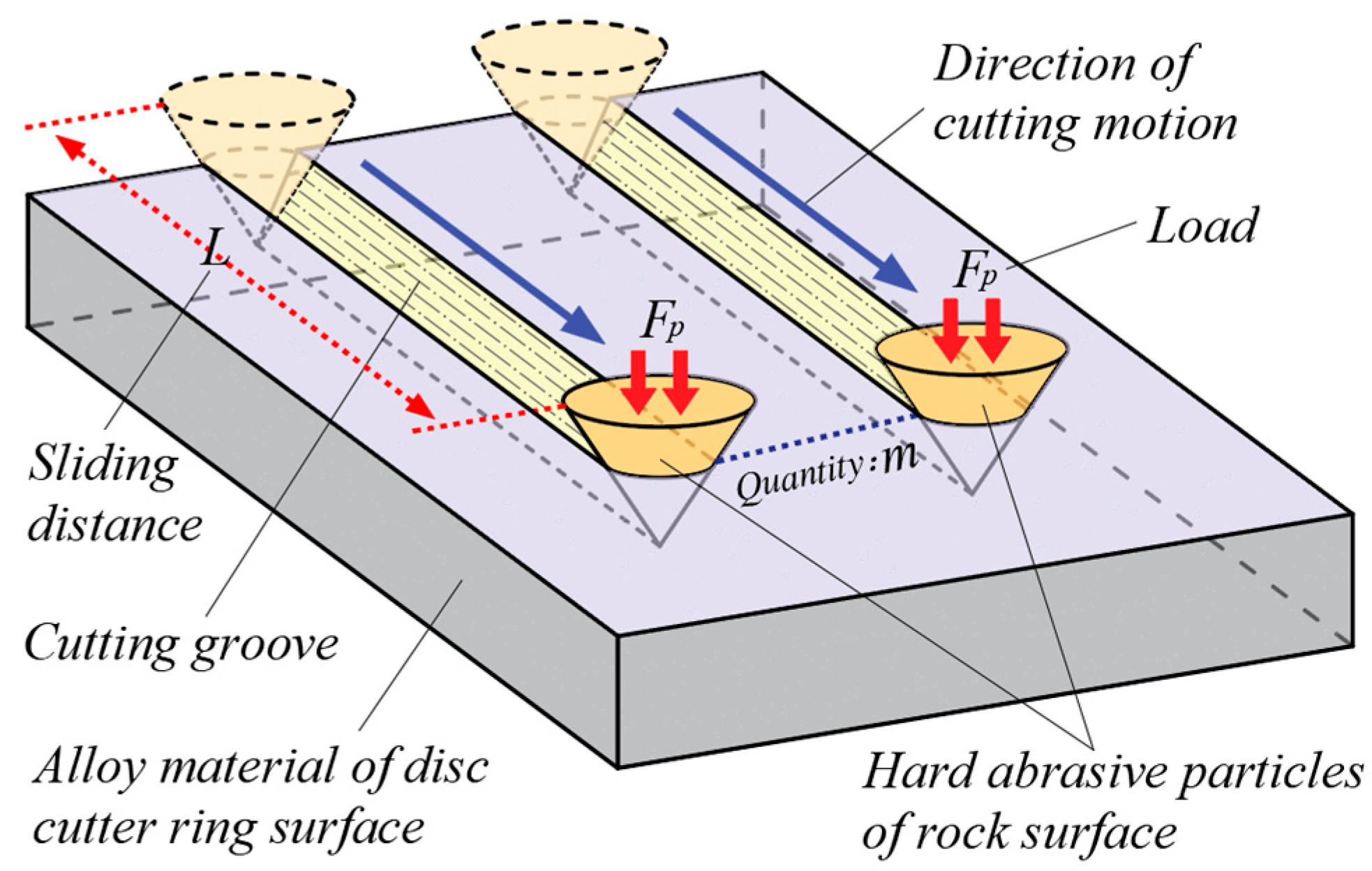
4.1. Abrasive Wear Mechanism and Archard’s Wear Law
4.2. Calculation of Radial Thermal Stresses on the Cutter Ring
4.3. Wear Calculation for Cutting Hard Rock
4.4. Wear Calculation for Cutting Soft Rock
5. Engineering Cases and Comparative Analyses
5.1. Hard-Rock Cutting Cases and Analyses
5.2. Soft-Rock Cutting Cases and Analyses
5.3. Outlook and Further Research
6. Conclusions
- The study shows that the type of cutter ring wear is dominated by abrasive wear, with even wear having the highest probability of occurrence, followed by bias wear and ring chipping. There is a negative correlation between the amount of cutter wear and the hardness of the material, and high hardness can prolong the service life. The penetration of the cutter ring in rocks of different strengths reflects different wear levels.
- High-strength granite has the highest abrasiveness to the steel material of the cutter ring, and the cutter cutting medium-strength rock has less wear, and the full contact friction between the soft rock and the cutter increases the abrasion area and the abrasion amount, which leads to increased wear. An increase in the rock strength makes the rock CAI characteristics and cutter ring wear increase, and this index can reflect the degree of cutter ring wear.
- In the shield tunnelling process, the wear degree of cutting hard rock is higher, and the proportion of wear types is 71% for abrasive wear and 18% for cutting ring breakage, of which uniform wear occupies 54% of the total wear. When cutting soft and hard composite strata, the proportion of abrasive wear decreases to only about 49%, and the proportion of cutter ring breakage is 41%, indicating that cutting soft rock reduces the condition of abrasive wear.
- Comparative analyses show that the damage patterns of hard–soft rock cutting are different. In the cutting process of high-strength rock, the cutter ring wear is mainly at the bottom of the radial outer edge, with uniform wear. The area of cutter wear in cutting soft rock is mainly distributed in the area on both sides of the cutter head, which can easily produce the phenomenon of a cutter rim grinding tip.
- With the same rock strength and considering the temperature effect, the wear depth of cutting hard rock has a power function relationship with the installation radius and is proportional to the shield distance. The predicted value is lower than the actual measured value.
- The wear prediction model considering the thermal effect is closer to the actual value. Cutting medium-hard rock and hard rock, the maximum radius wear depth reaches 25.8 mm and 34.1 mm, respectively, and the prediction error is 3.7% and 5.1%. The errors remain within reasonable limits.
- The predicted wear for cutting soft rock increases gradually with the radius, and the loss of wear mass shows a positive correlation with the cutting distance, with a minimum prediction error of 8.4%. It is generally lower than the actual value.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jin, D.; Yuan, D.; Li, X.; Su, W. Probabilistic analysis of the disc cutter failure during TBM tunneling in hard rock. Tunn. Undergr. Space Technol. 2021, 109, 103744. [Google Scholar] [CrossRef]
- Macias, F.J. Hard Rock Tunnel Boring: Performance Predictions and Cutter Life Assessments. 2016. Available online: https://ntnuopen.ntnu.no/ntnu-xmlui/handle/11250/2429327 (accessed on 7 April 2025).
- Macias, F.J.; Dahl, F.; Bruland, A. New rock abrasivity test method for tool life assessments on hard rock tunnel boring: The rolling indentation abrasion test (RIAT). Rock Mech. Rock Eng. 2016, 49, 1679–1693. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, L.; Xia, Y.; Tan, Q.; Zhu, Z.; Mao, Q.; Zhou, M. Experimental study on wear of TBM disc cutter rings with different kinds of hardness. Tunn. Undergr. Space Technol. 2018, 82, 346–357. [Google Scholar] [CrossRef]
- Plinninger, R.J.; Alber, M.; Düllmann, J. Rock mass-scale factors with an influence on tool wear in the mechanised tunnelling process in hard rock: Gebirgsmaßstäbliche Einflussfaktoren auf den Werkzeugverschleiß bei maschinellen Tunnelvortriebsverfahren im Hartgestein. Geomech. Tunn. 2018, 11, 157–168. [Google Scholar] [CrossRef]
- Deliormanlı, A.H. Cerchar abrasivity index (CAI) and its relation to strength and abrasion test methods for marble stones. Constr. Build. Mater. 2012, 30, 16–21. [Google Scholar] [CrossRef]
- Elbaz, K.; Shen, S.L.; Cheng, W.C.; Arulrajah, A. Cutter-disc consumption during earth pressure balance tunnelling in mixed strata. Proc. Inst. Civ. Eng.-Geotech. Eng. 2018, 171, 363–376. [Google Scholar] [CrossRef]
- Elbaz, K.; Shen, S.L.; Zhou, A.; Yin, Z.Y.; Lyu, H.M. Prediction of disc cutter life during shield tunneling with AI via the incorporation of a genetic algorithm into a GMDH-type neural network. Engineering 2021, 7, 238–251. [Google Scholar] [CrossRef]
- Sun, Z.; Zhao, H.; Hong, K.; Chen, K.; Zhou, J.; Li, F.; Zhang, B.; Song, F.; Yang, Y.; He, R. A practical TBM cutter wear prediction model for disc cutter life and rock wear ability. Tunn. Undergr. Space Technol. 2019, 85, 92–99. [Google Scholar] [CrossRef]
- Balci, C.; Tumaç, D. Investigation into the effects of different rocks on rock cuttability by a V-type disc cutter. Tunn. Undergr. Space Technol. 2012, 30, 183–193. [Google Scholar] [CrossRef]
- Karami, M.; Zare, S.; Rostami, J. Study of common wear prediction models for hard rock TBM disc cutters and comparison with field observation in Kerman water conveyance tunnel. Bull. Eng. Geol. Environ. 2021, 80, 1467–1476. [Google Scholar] [CrossRef]
- Frenzel, C.; Käsling, H.; Thuro, K. Factors influencing disc cutter wear. Geomech. Und Tunnelbau Geomech. Und Tunnelbau 2008, 1, 55–60. [Google Scholar] [CrossRef]
- Lin, L.; Xia, Y.; Zhang, X. Wear characteristics of TBM disc cutter ring sliding against different types of rock. KSCE J. Civ. Eng. 2020, 24, 3145–3155. [Google Scholar] [CrossRef]
- Ren, D.J.; Shen, S.L.; Arulrajah, A.; Cheng, W.C. Prediction model of TBM disc cutter wear during tunnelling in heterogeneous ground. Rock Mech. Rock Eng. 2018, 51, 3599–3611. [Google Scholar] [CrossRef]
- Yu, H.; Tao, J.; Huang, S.; Qin, C.; Xiao, D.; Liu, C. A field parameters-based method for real-time wear estimation of disc cutter on TBM cutterhead. Autom. Constr. 2021, 124, 103603. [Google Scholar] [CrossRef]
- Ren, D.J.; Shen, S.L.; Zhou, A.; Chai, J.C. Prediction of lateral continuous wear of cutter ring in soft ground with quartz sand. Comput. Geotech. 2018, 103, 86–92. [Google Scholar] [CrossRef]
- Wang, L.; Li, H.; Zhao, X.; Zhang, Q. Development of a prediction model for the wear evolution of disc cutters on rock TBM cutterhead. Tunn. Undergr. Space Technol. 2017, 67, 147–157. [Google Scholar] [CrossRef]
- Geng, Q.; Wei, Z.; Ren, J. New rock material definition strategy for FEM simulation of the rock cutting process by TBM disc cutters. Tunn. Undergr. Space Technol. 2017, 65, 179–186. [Google Scholar] [CrossRef]
- Karami, M.; Zare, S.; Rostami, J. Tracking of disc cutter wear in TBM tunneling: A case study of Kerman water conveyance tunnel. Bull. Eng. Geol. Environ. 2021, 80, 201–219. [Google Scholar] [CrossRef]
- Tan, Q.; Zhang, G.J.; Xia, Y.M.; Li, J.F. Differentiation and analysis on rock breaking characteristics of TBM disc cutter at different rock temperatures. J. Cent. South Univ. 2015, 22, 4807–4818. [Google Scholar] [CrossRef]
- Munoz, H.; Taheri, A.; Chanda, E. Rock cutting characteristics on soft-to-hard rocks under different cutter inclinations. Int. J. Rock Mech. Min. Sci. 2016, 87, 85–89. [Google Scholar] [CrossRef]
- Hutchings, I.; Shipway, P. Tribology: Friction and Wear of Engineering Materials; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- Sapigni, M.; Berti, M.; Bethaz, E.; Busillo, A.; Cardone, G. TBM performance estimation using rock mass classifications. Int. J. Rock Mech. Min. Sci. 2002, 39, 771–788. [Google Scholar] [CrossRef]
- Lan, H.; Xia, Y.; Ji, Z.; Fu, J.; Miao, B. Online monitoring device of disc cutter wear–Design and field test. Tunn. Undergr. Space Technol. 2019, 89, 284–294. [Google Scholar] [CrossRef]
- Gong, Q.; Zhao, J. Development of a rock mass characteristics model for TBM penetration rate prediction. Int. J. Rock Mech. Min. Sci. 2009, 46, 8–18. [Google Scholar] [CrossRef]
- Acaroglu, O. Prediction of thrust and torque requirements of TBMs with fuzzy logic models. Tunn. Undergr. Space Technol. 2011, 26, 267–275. [Google Scholar] [CrossRef]
- Ching, J.; Phoon, K.K. Value of geotechnical site investigation in reliability-based design. Adv. Struct. Eng. 2012, 15, 1935–1945. [Google Scholar] [CrossRef]
- Al-Ameen, S.I.; Waller, M.D. The influence of rock strength and abrasive mineral content on the Cerchar Abrasive Index. Eng. Geol. 1994, 36, 293–301. [Google Scholar] [CrossRef]
- Pan, Y.C.; Liu, Q.S.; Liu, J.P.; Kong, X.X.; Peng, X.X.; Liu, Q. Investigation on disc cutter behaviors in cutting rocks of different strengths and reverse estimation of rock strengths from experimental cutting forces. Eur. J. Environ. Civ. Eng. 2021, 25, 1–27. [Google Scholar] [CrossRef]
- Pan, Y.; Liu, Q.; Peng, X.; Liu, Q.; Liu, J.; Huang, X.; Cui, X.; Cai, T. Full-scale linear cutting tests to propose some empirical formulas for TBM disc cutter performance prediction. Rock Mech. Rock Eng. 2019, 52, 4763–4783. [Google Scholar] [CrossRef]
- Xia, Y.; Guo, B.; Tan, Q.; Zhang, X.; Lan, H.; Ji, Z. Comparisons between experimental and semi-theoretical cutting forces of CCS disc cutters. Rock Mech. Rock Eng. 2018, 51, 1583–1597. [Google Scholar] [CrossRef]
- Lan, H.; Xia, Y.; Miao, B.; Fu, J.; Ji, Z. Prediction model of wear rate of inner disc cutter of engineering in Yinsong, Jilin. Tunn. Undergr. Space Technol. 2020, 99, 103338. [Google Scholar] [CrossRef]
- Sun, Z.; Yang, Y.; Chen, K.; Li, F.; Zhou, J.; Zhang, B.; Chen, Q. Disc cutter’s rock breaking ability and wear resistance in extremely hard rock: A case study in Qinling tunnel of Han River to Wei River Water Diversion Project. Geotech. Geol. Eng. 2019, 37, 4901–4910. [Google Scholar] [CrossRef]
- Yagiz, S. Utilizing rock mass properties for predicting TBM performance in hard rock condition. Tunn. Undergr. Space Technol. 2008, 23, 326–339. [Google Scholar] [CrossRef]
- Li, Y.; Di, H.; Yao, Q.; Fu, L.; Zhou, S. Prediction model for disc cutter wear of tunnel boring machines in sandy cobble strata. KSCE J. Civ. Eng. 2020, 24, 1010–1019. [Google Scholar] [CrossRef]
- Tang, S.; Zhang, X.; Liu, Q.; Zhang, Q.; Li, X.; Wang, H. Experimental study on the influences of cutter geometry and material on scraper wear during shield TBM tunnelling in abrasive sandy ground. J. Rock Mech. Geotech. Eng. 2024, 16, 410–425. [Google Scholar] [CrossRef]
- Gharsallaoui, H.; Jafari, M.; Holeyman, A. Cavity expansion in rock masses obeying the “hoek–brown” failure criterion. Rock Mech. Rock Eng. 2020, 53, 927–941. [Google Scholar] [CrossRef]
- Wang, Z.F.; Shen, S.L.; Ho, C.E.; Kim, Y.H. Investigation of field-installation effects of horizontal twin-jet grouting in Shanghai soft soil deposits. Can. Geotech. J. 2013, 50, 288–297. [Google Scholar] [CrossRef]
- Kalayci Sahinoglu, U.; Ozer, U. The prediction of cutter wear from temperature measurements on TBM discs and cutting face. Arab. J. Geosci. 2020, 13, 207. [Google Scholar] [CrossRef]
- Tian, J.; Hu, Y.; Liu, X.; Yang, Z. Wear performance and mechanisms of H13 steels sliding against different Rock types. Surf. Topogr. Metrol. Prop. 2020, 8, 025003. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, K.; Dong, W.; Zhang, B. Study of rock-cutting process by disc cutters in mixed ground based on three-dimensional particle flow model. Rock Mech. Rock Eng. 2020, 53, 3485–3506. [Google Scholar] [CrossRef]
- Wang, L.; Kang, Y.; Zhao, X.; Zhang, Q. Disc cutter wear prediction for a hard rock TBM cutterhead based on energy analysis. Tunn. Undergr. Space Technol. 2015, 50, 324–333. [Google Scholar] [CrossRef]
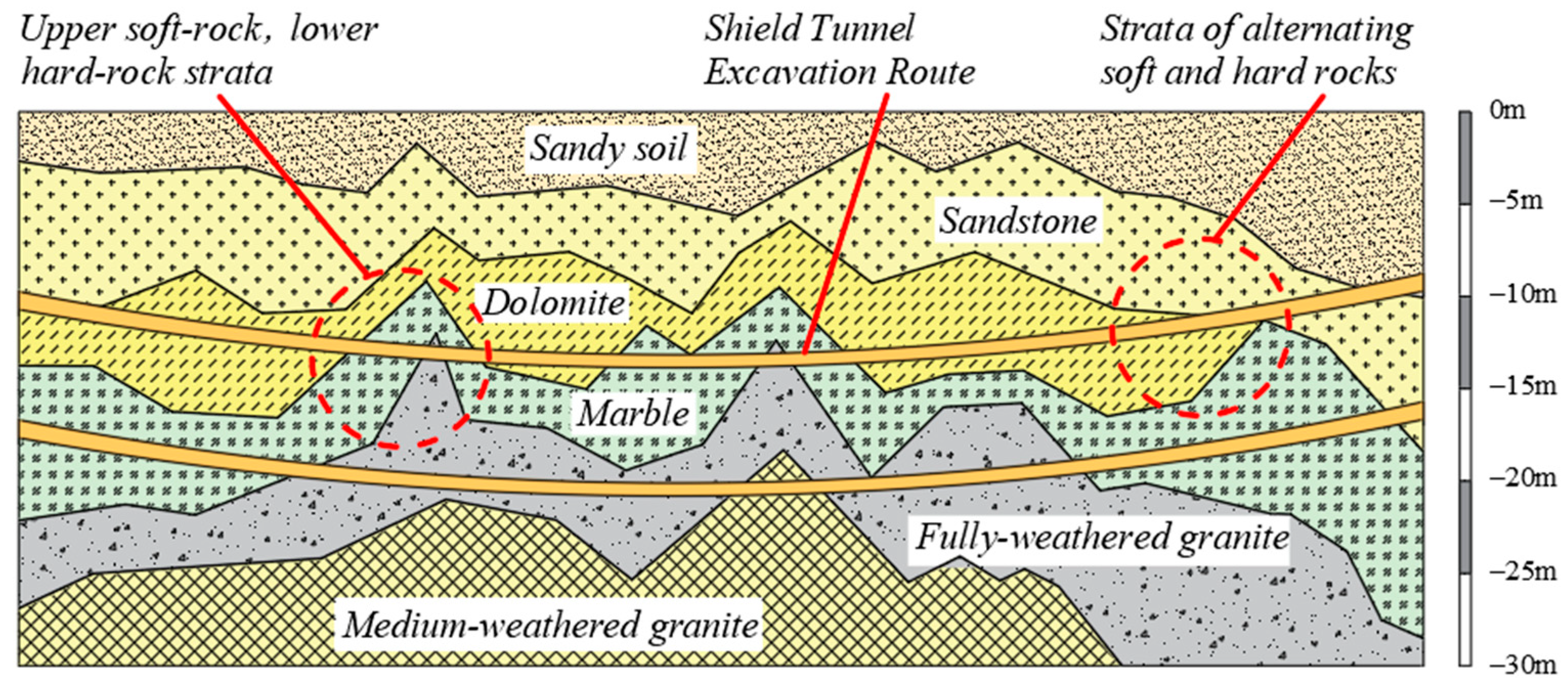
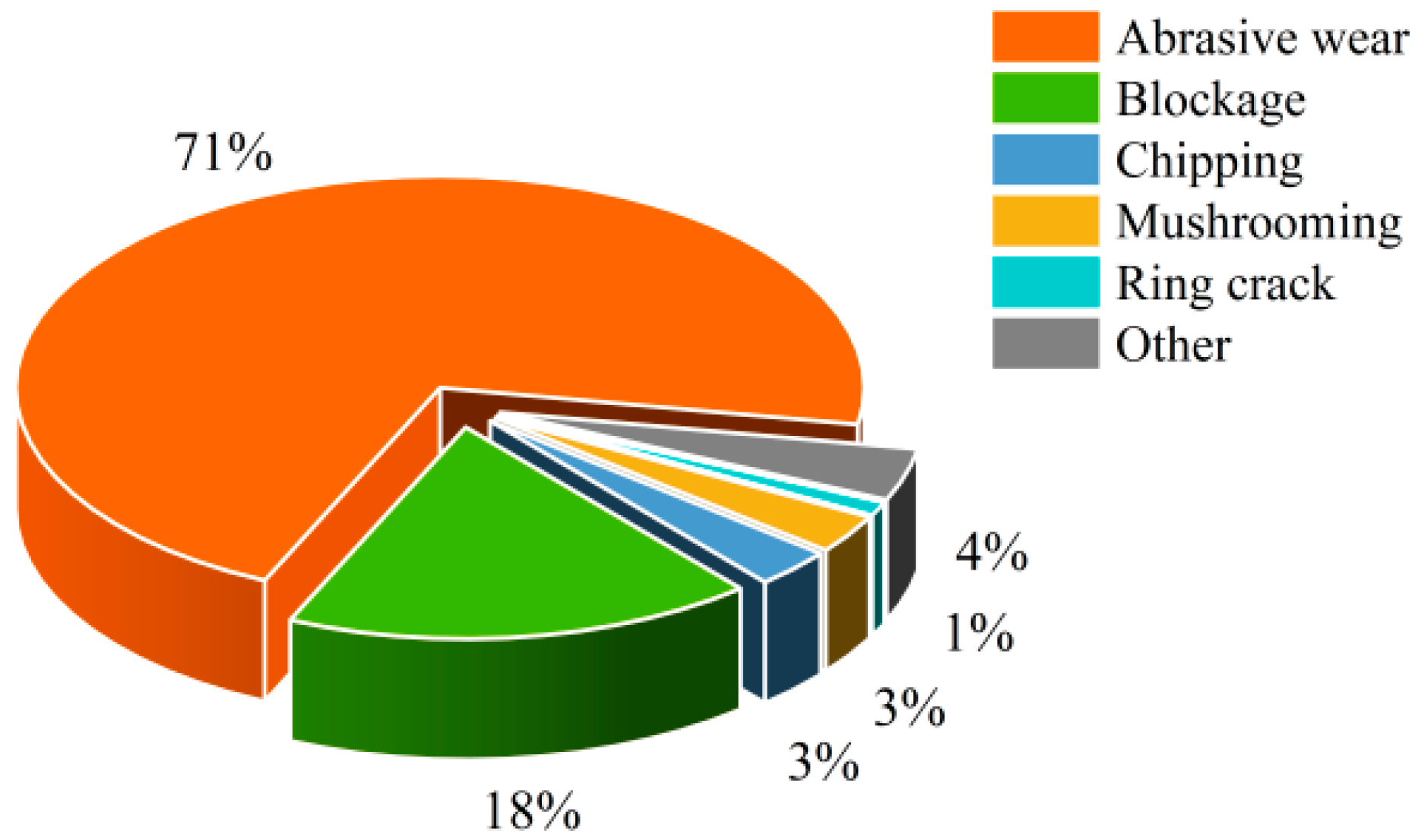
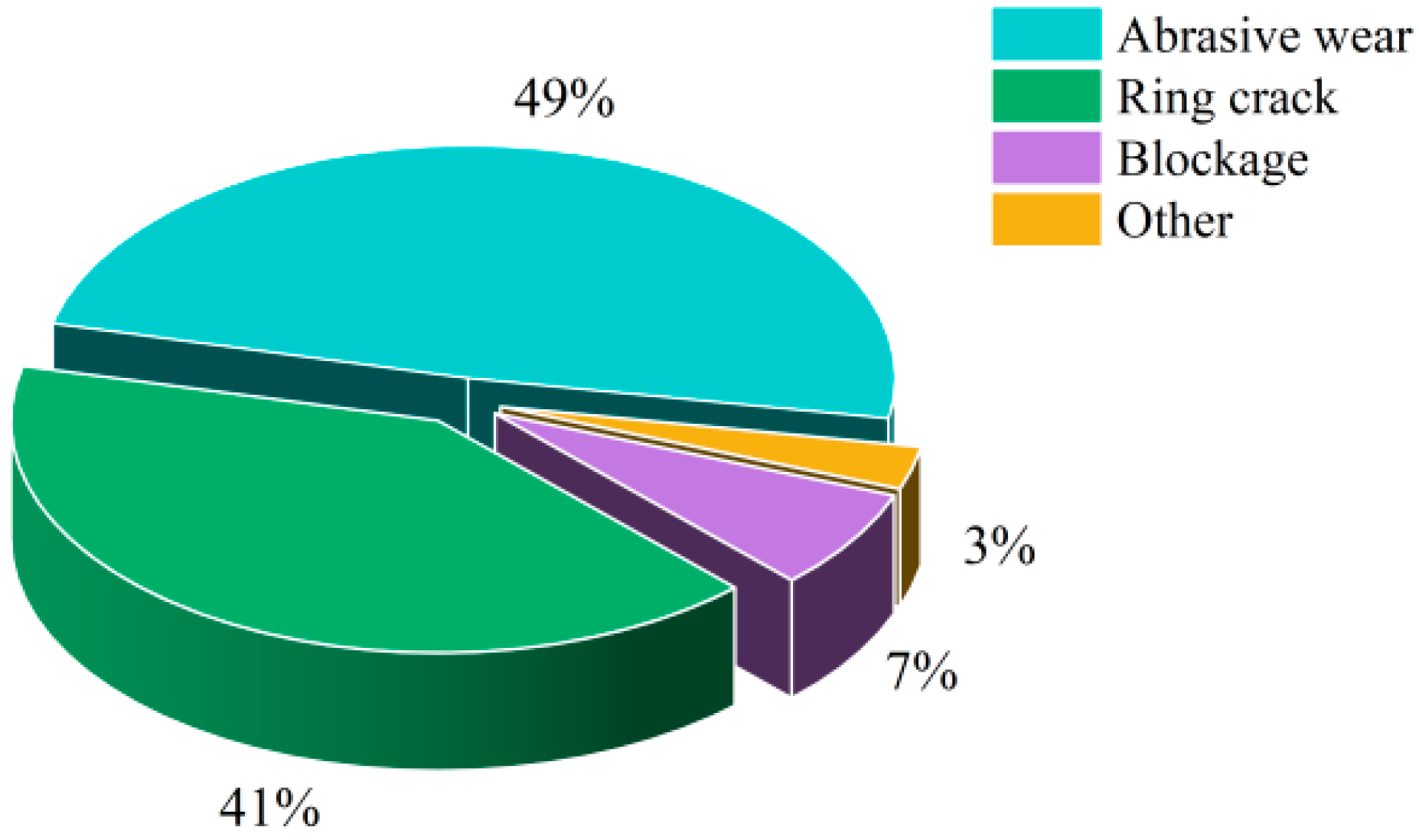
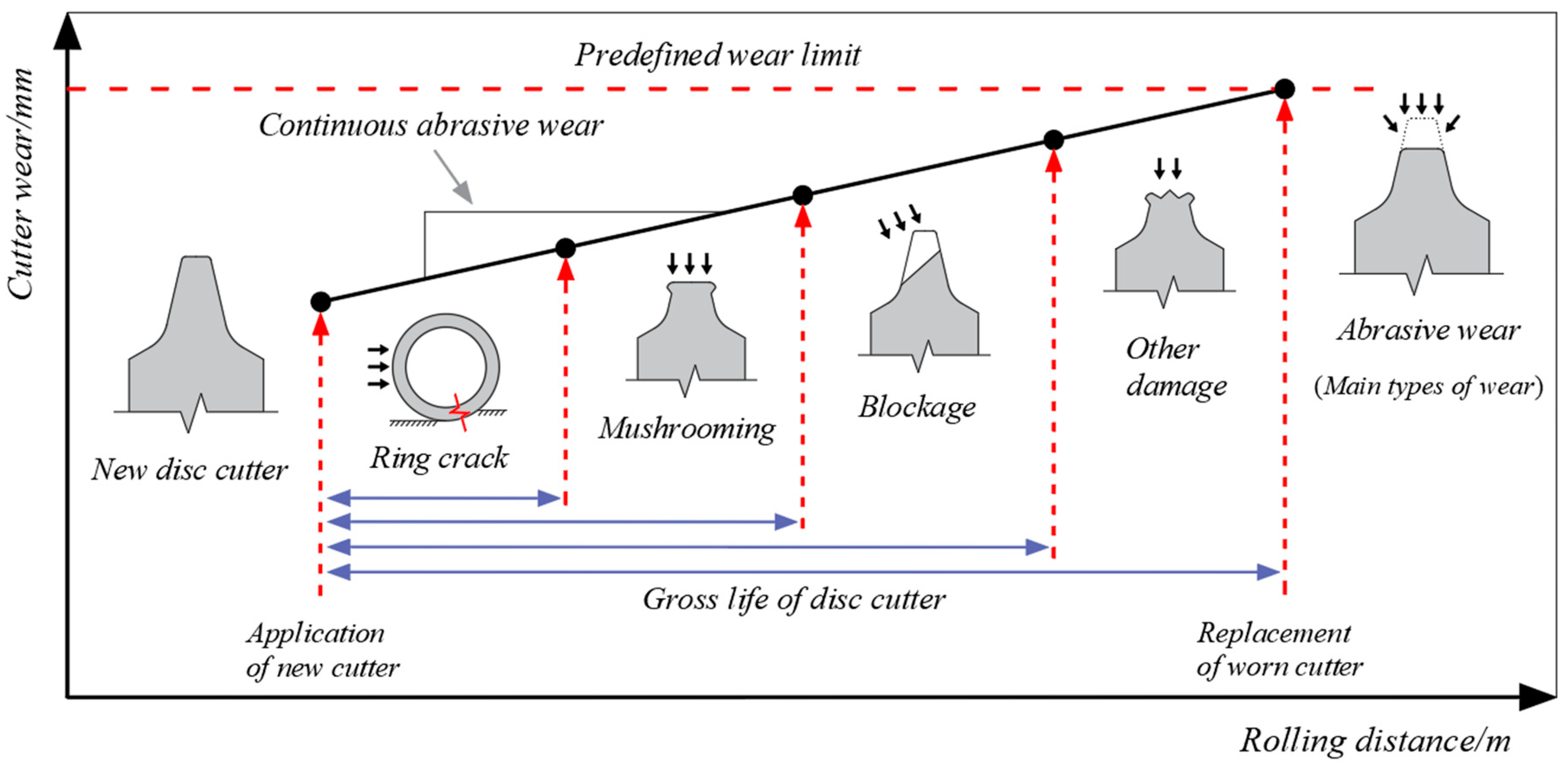

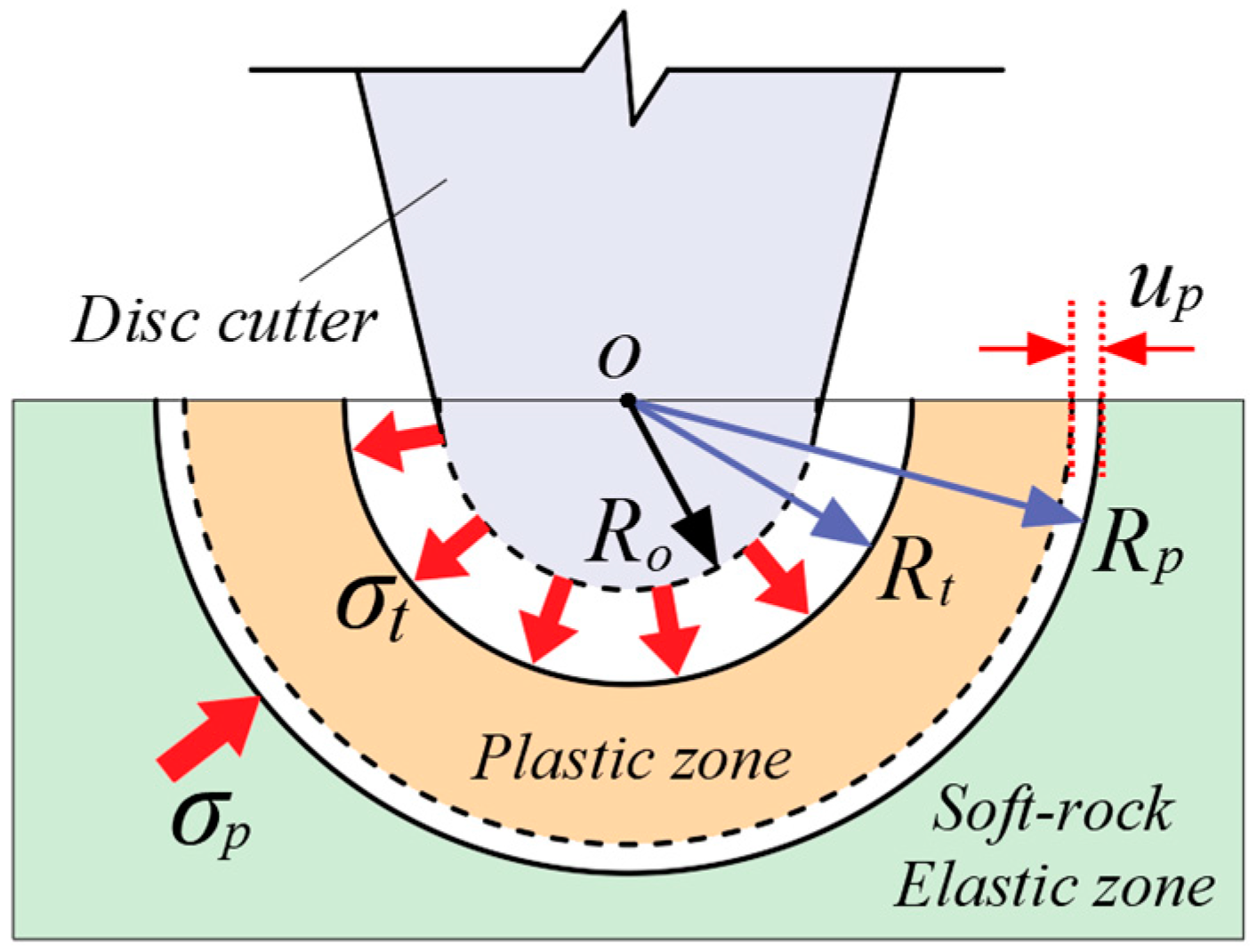
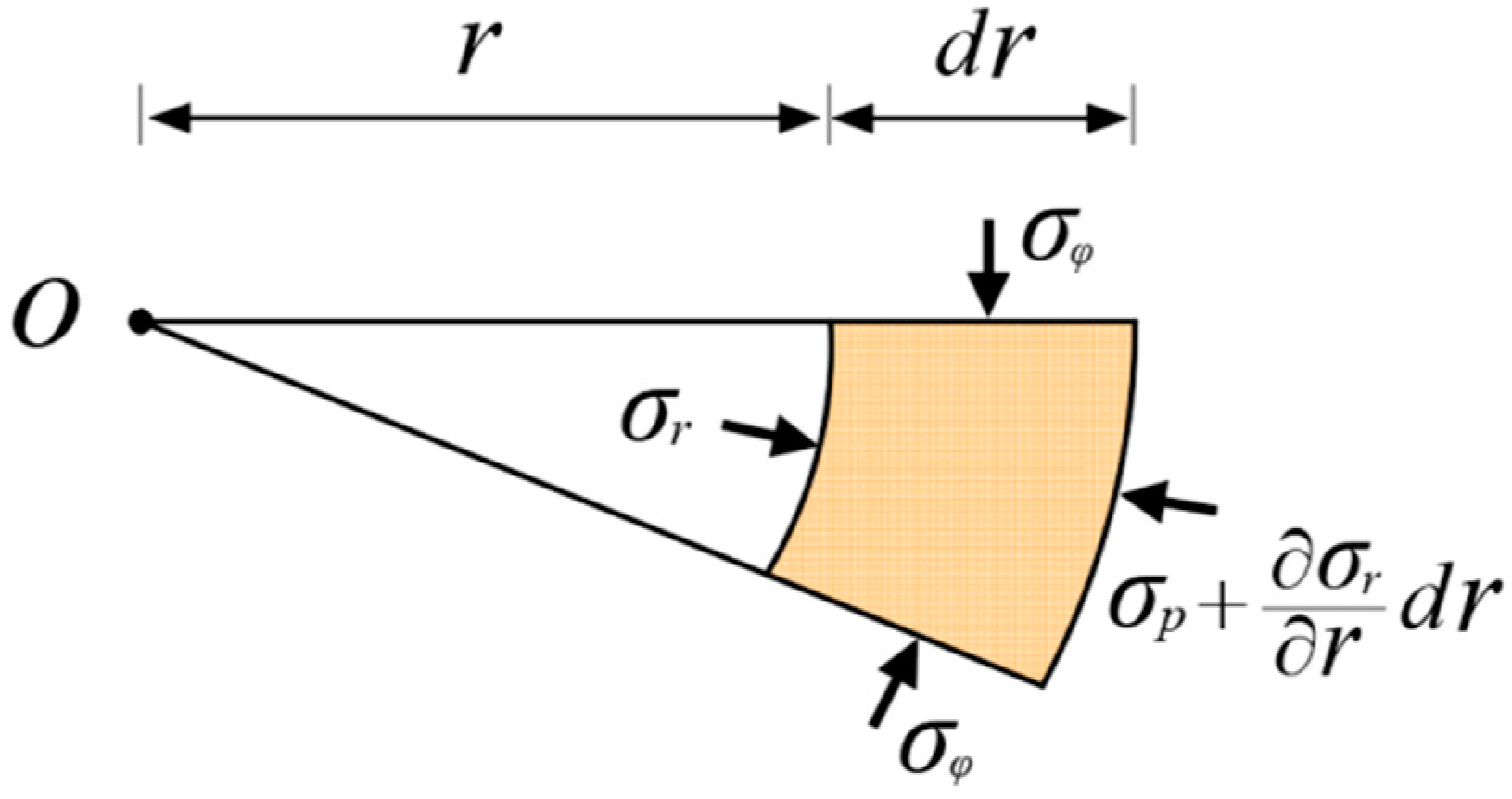


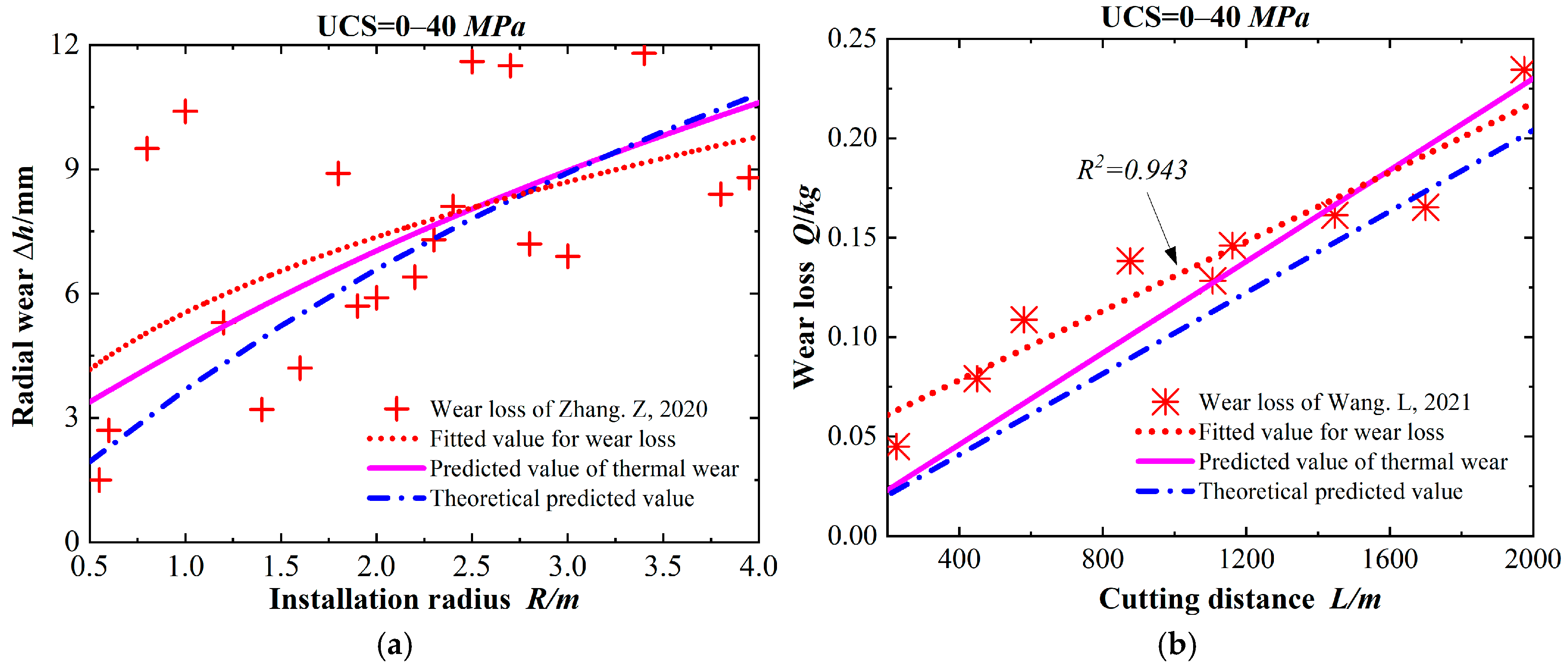
| Parameters | Project Cases | ||
|---|---|---|---|
| NTNU Case | SJTU Case | TUM and BJU Cases | |
| Project location | North-central Europe | South Asia | Central Europe and East Asia |
| Approximate tunnel length (km) | 7.0 | 4.3 | 2.4 |
| Rock samples | Granite | Basalt and breccia | Marble and granite |
| Rock strength range | High–extremely high | Medium–very high | Medium |
| UCS (MPa) | ≥120 | 80–120 | 40–80 |
| Rock density (g/m3) | 2.6~2.7 | 2.8~3.0 | 2.6~3.3 |
| Tunnel diameter (m) | 7.2 | 6.6 | 6.5 |
| Disc cutter diameter (mm) | 483 | 483 | 483 |
| Cutter head rotation speed (rpm) | 0–8.7 | 0–7.0 | 5.5–8.0 |
| Cutter thrust (kN) | 1400 | 1070 | 214 |
| Disc Cutter Ring Material Properties | Value |
|---|---|
| Density (kg/m3) | 7850 |
| Young’s modulus (GPa) | 210 |
| Poisson’s ratio | 0.3 |
| Hardness HRC | 57 |
| Uniaxial compressive (MPa) | 2560 |
| Angle of the disc cutter ring (°) | 26 |
| Ultimate load (MPa) | 250 |
| Parameters | Project Cases | |
|---|---|---|
| Shenzhen Case | Gansu Case | |
| Project location | East Asia | East Asia |
| Approximate tunnel length (km) | 2.7 | 18.2 |
| Rock samples | Highly/moderately weathered granite | Mudstone and gneiss |
| Rock strength range | Low–medium | Low–medium |
| UCS (MPa) | 5–18/15.7–56.8 | 5–68 |
| Rock density (g/m3) | 2.3 | 2.6 |
| Tunnel diameter (m) | 8.5 | 5.75 |
| Disc cutter diameter (mm) | 432 | 432 |
| Cutter head rotation speed (rpm) | 1.8–2.0 | 0–8.1 |
| Cutter thrust (kN) | 500–600 | 21,420 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyu, X.; Chen, Y.; Liao, S.; Fernandez-Steeger, T.M. Wear Prediction and Mechanism Study of Tunnel Boring Machine Disc Cutter Breaking in Hard–Soft Rock Considering Thermal Effect. Appl. Sci. 2025, 15, 4183. https://doi.org/10.3390/app15084183
Lyu X, Chen Y, Liao S, Fernandez-Steeger TM. Wear Prediction and Mechanism Study of Tunnel Boring Machine Disc Cutter Breaking in Hard–Soft Rock Considering Thermal Effect. Applied Sciences. 2025; 15(8):4183. https://doi.org/10.3390/app15084183
Chicago/Turabian StyleLyu, Xiongfei, Youliang Chen, Shaoming Liao, and Tomas Manuel Fernandez-Steeger. 2025. "Wear Prediction and Mechanism Study of Tunnel Boring Machine Disc Cutter Breaking in Hard–Soft Rock Considering Thermal Effect" Applied Sciences 15, no. 8: 4183. https://doi.org/10.3390/app15084183
APA StyleLyu, X., Chen, Y., Liao, S., & Fernandez-Steeger, T. M. (2025). Wear Prediction and Mechanism Study of Tunnel Boring Machine Disc Cutter Breaking in Hard–Soft Rock Considering Thermal Effect. Applied Sciences, 15(8), 4183. https://doi.org/10.3390/app15084183






