A Method for Determining the Displacement Monitoring Index for Rockfill Dams Considering Material Uncertainty
Abstract
1. Introduction
2. Methodology
2.1. SFEM-Based Simulation Method for Parametric Uncertainty
2.1.1. Standard Gaussian Random Fields
2.1.2. Correlated Log-Normal Random Fields for Geotechnical Materials
2.2. Determination of Displacement Monitoring Index for Rockfill Dams
2.2.1. Hybrid Monitoring Model
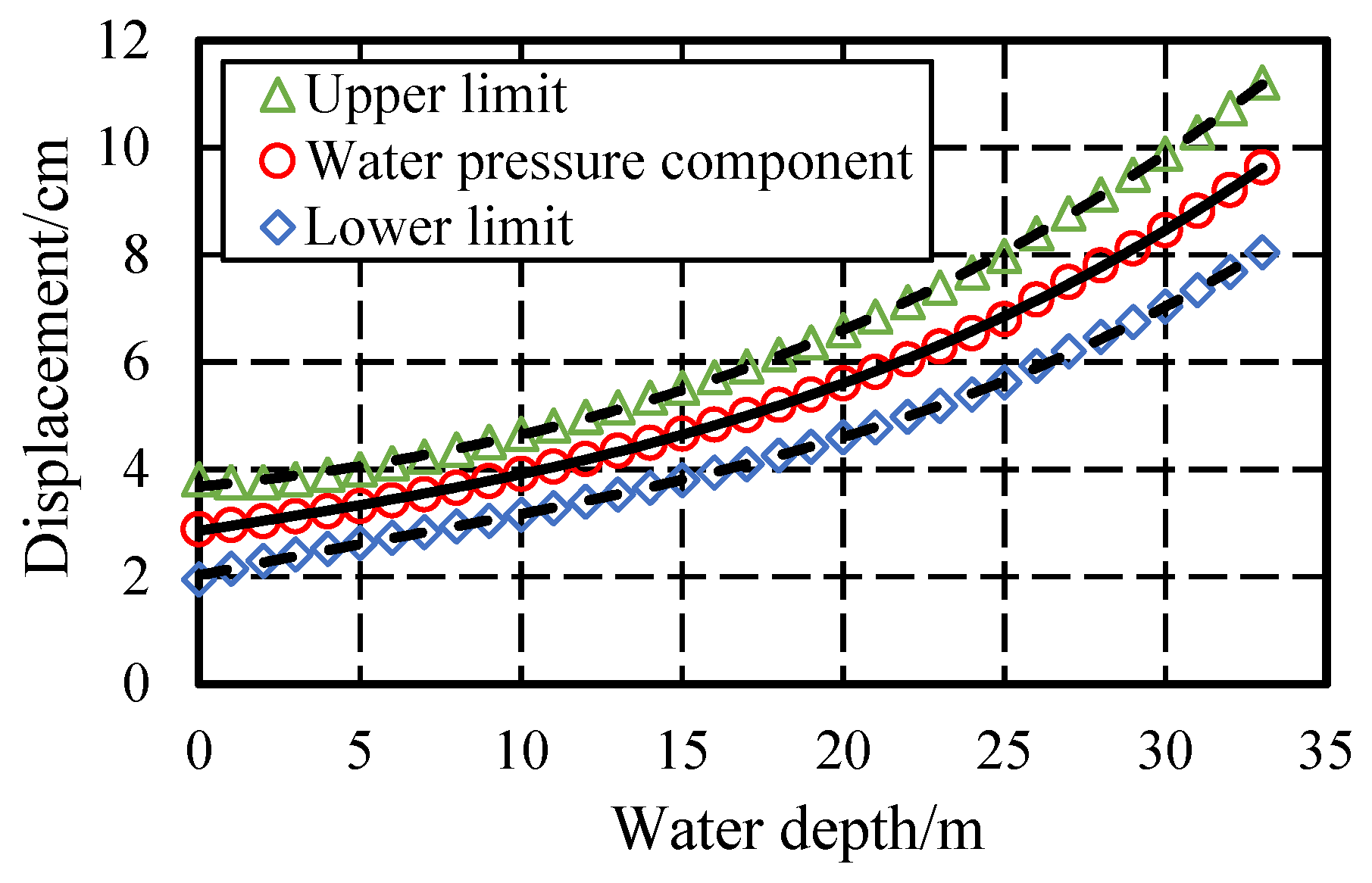
2.2.2. Displacement Monitoring Index
3. Case Study
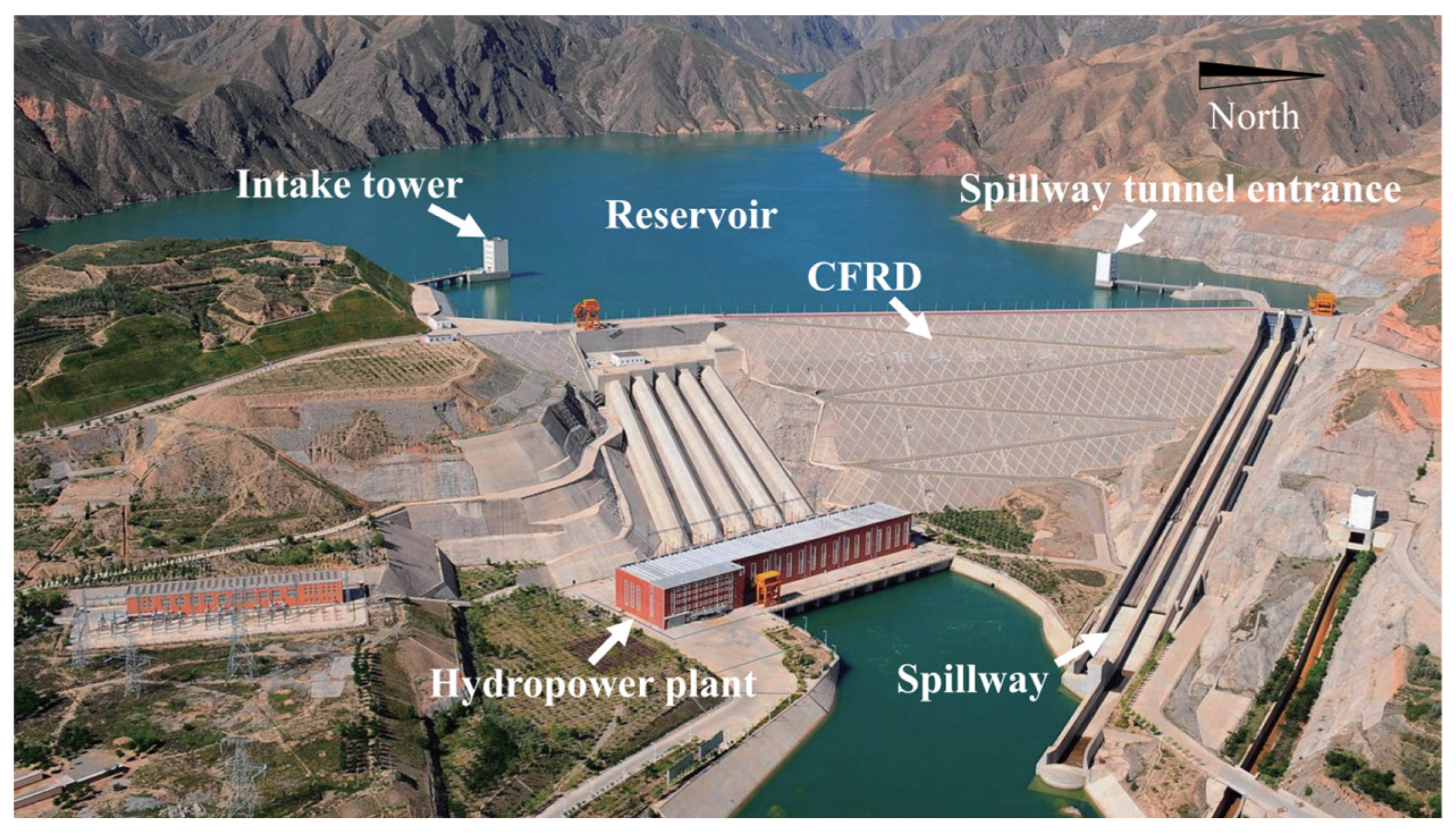
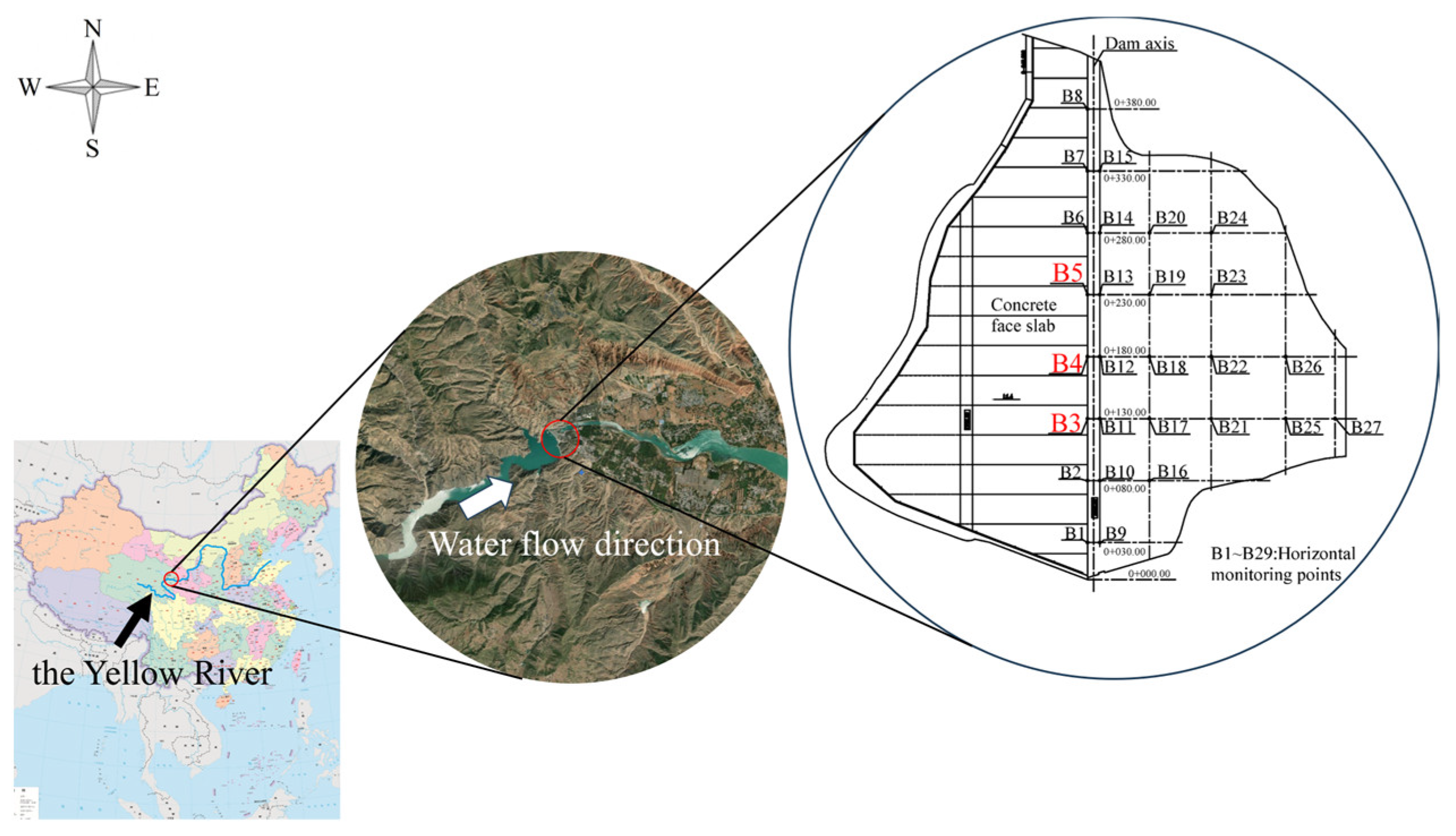
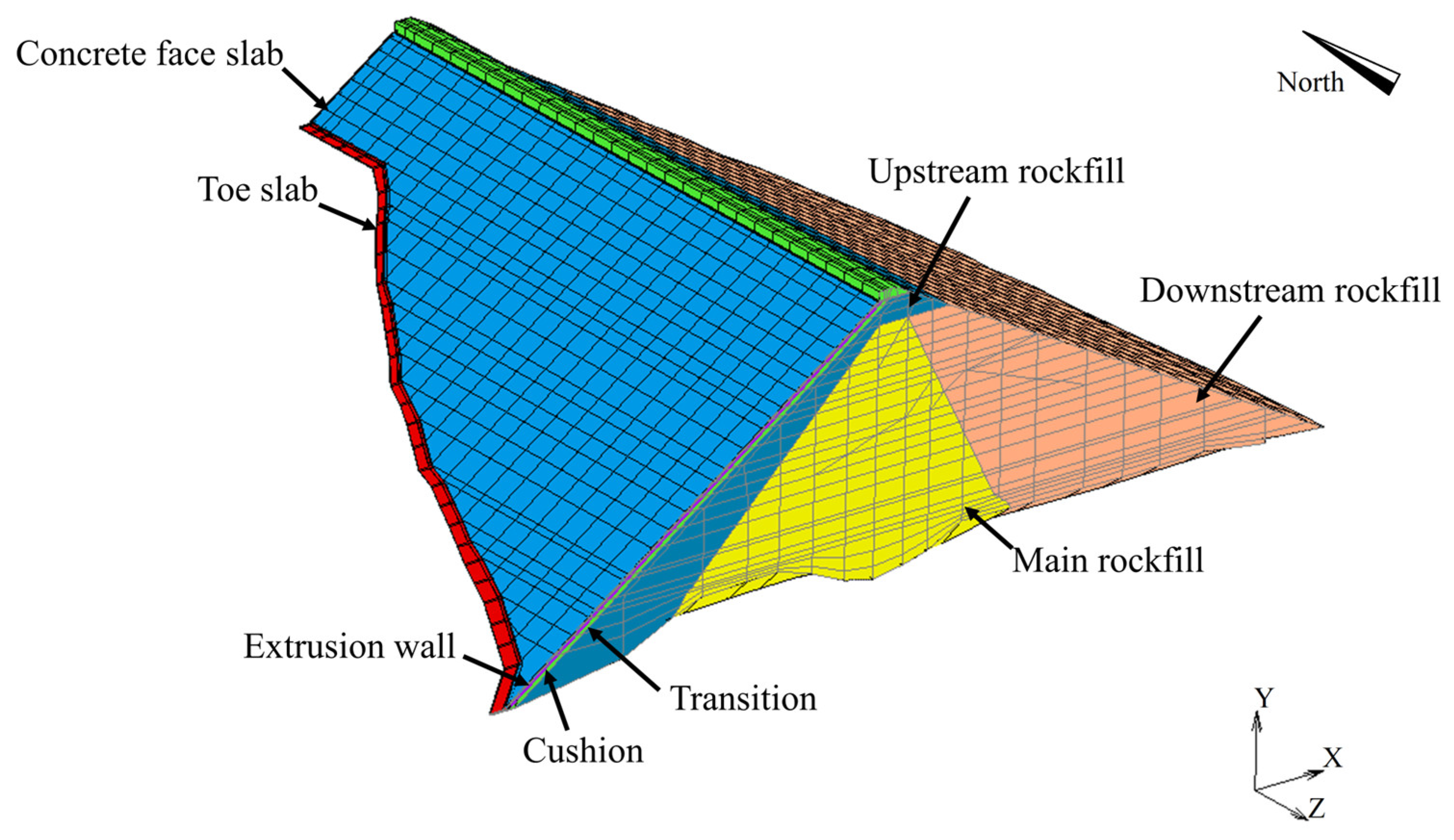
3.1. General Description of the Project
3.2. The Methodological Description of the Analyzed Dam
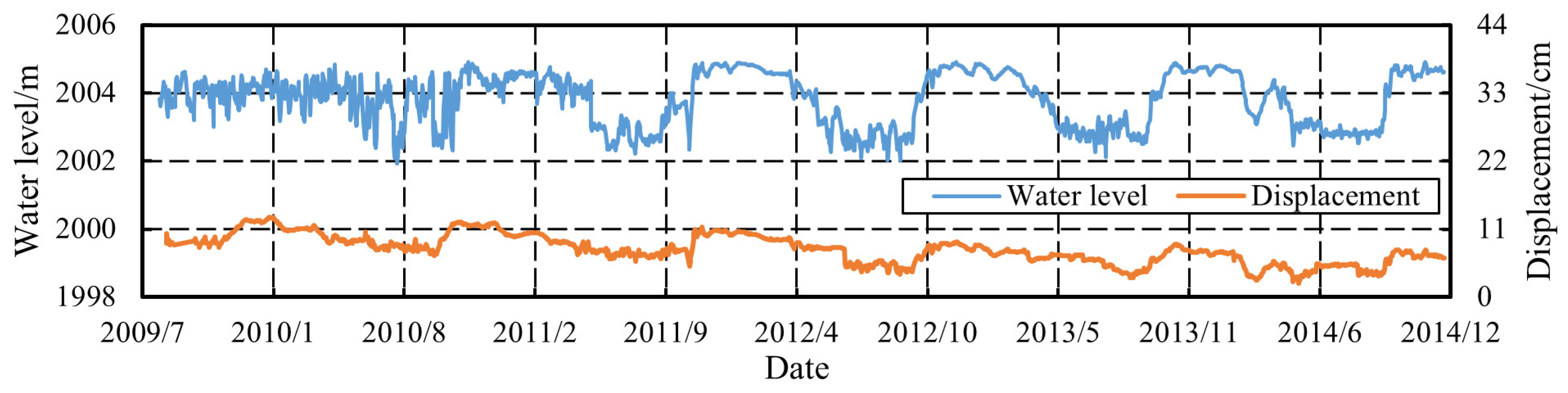
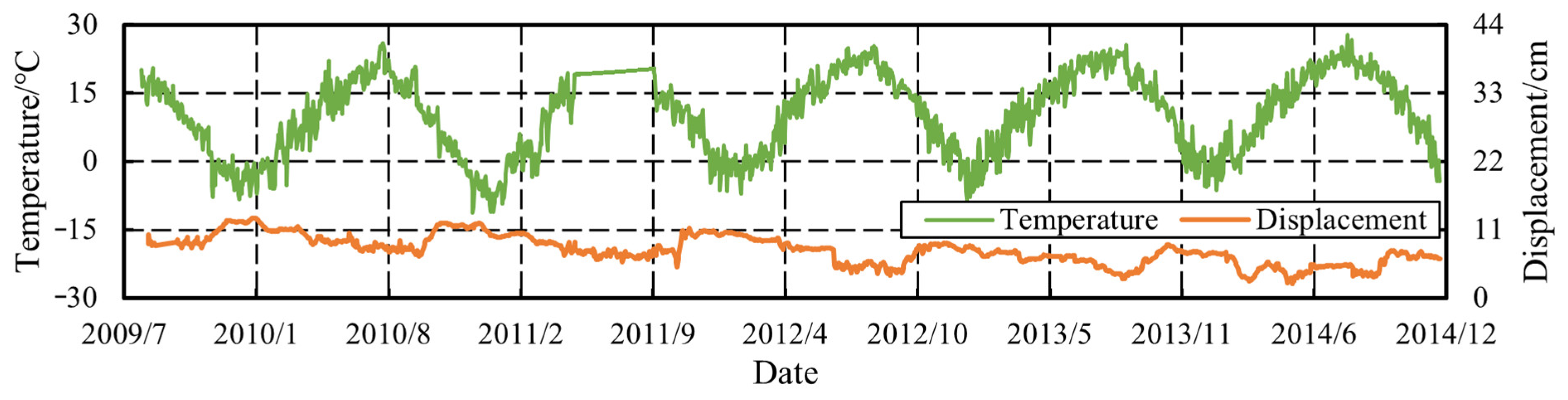
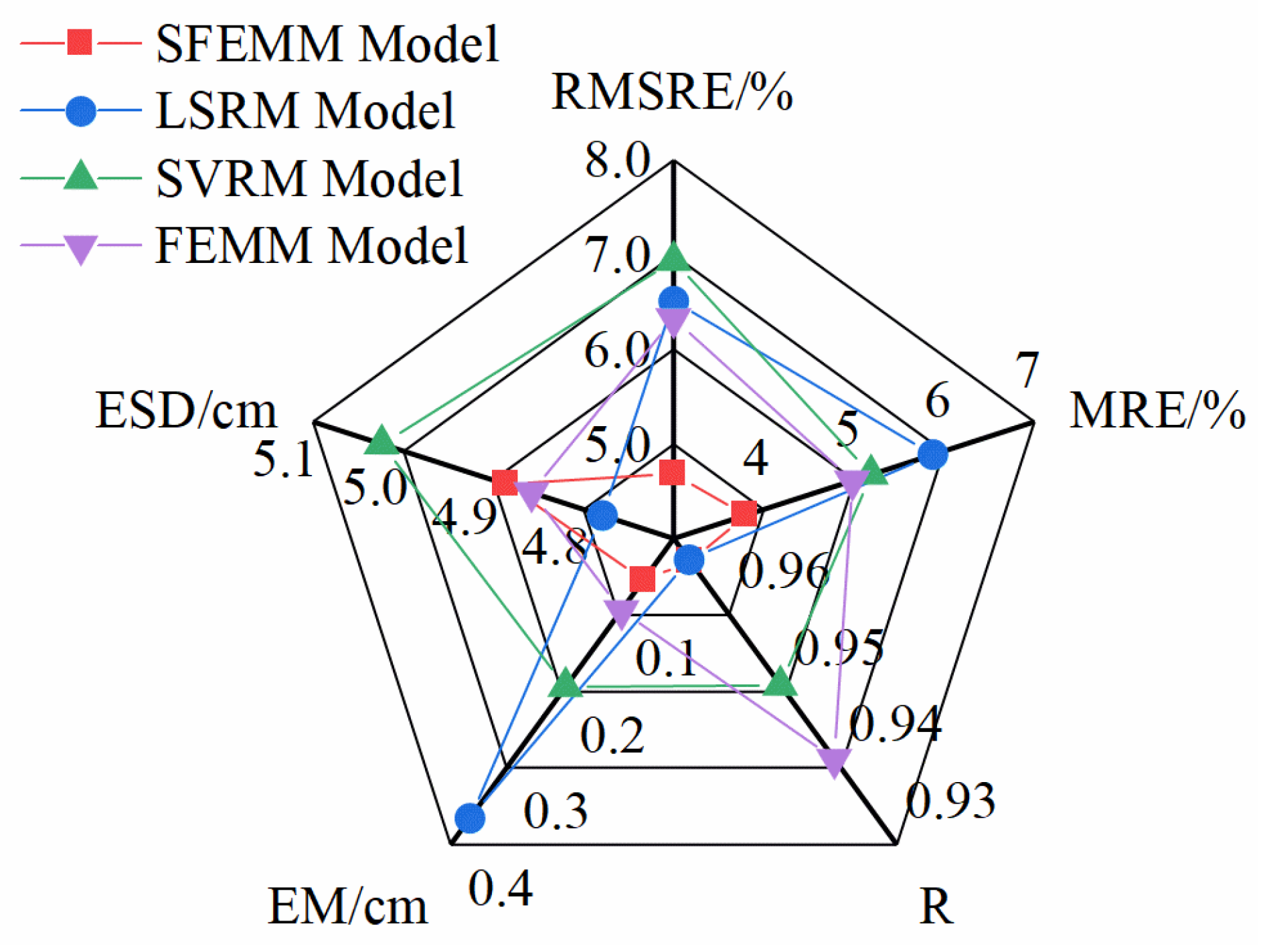
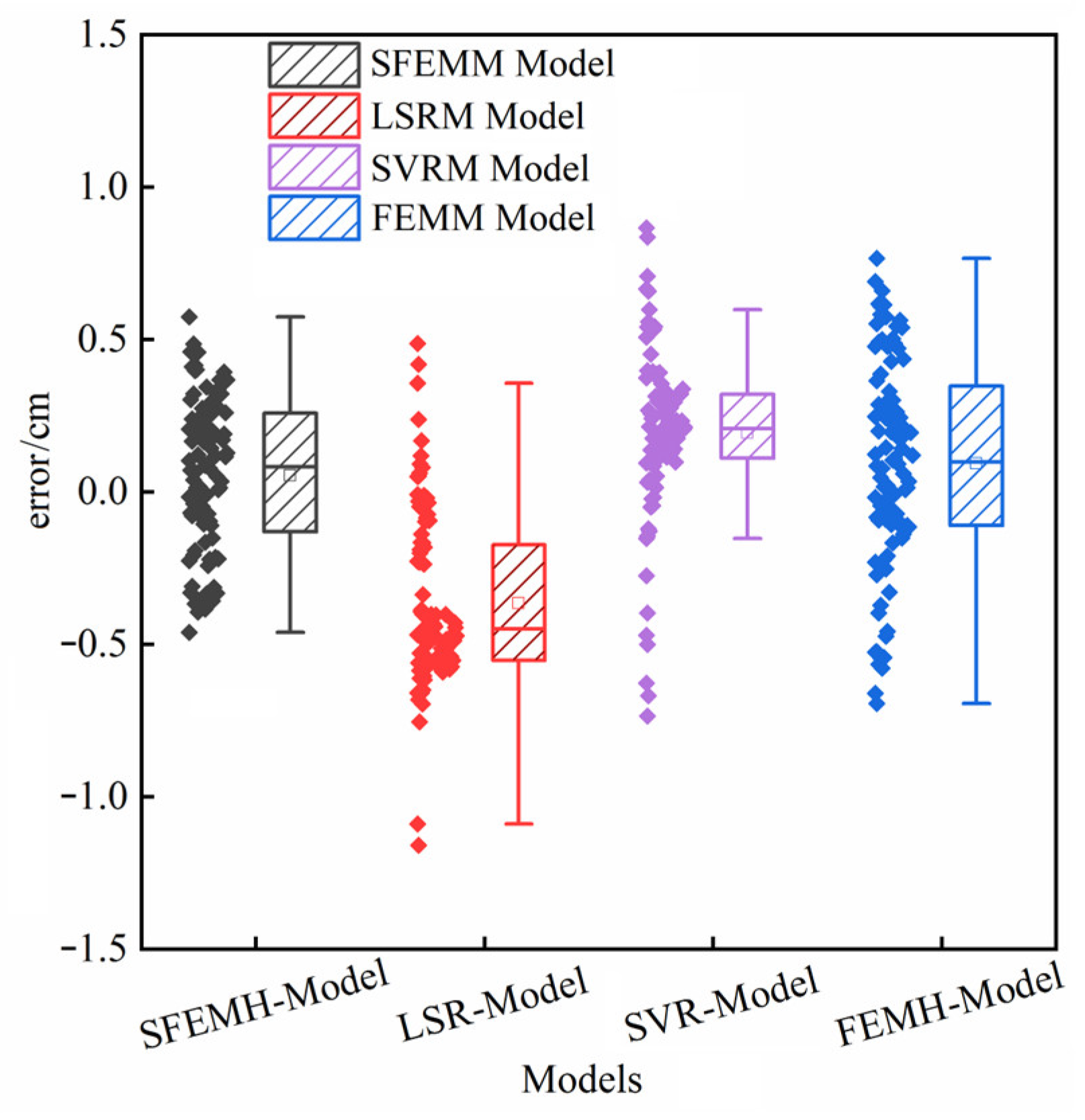
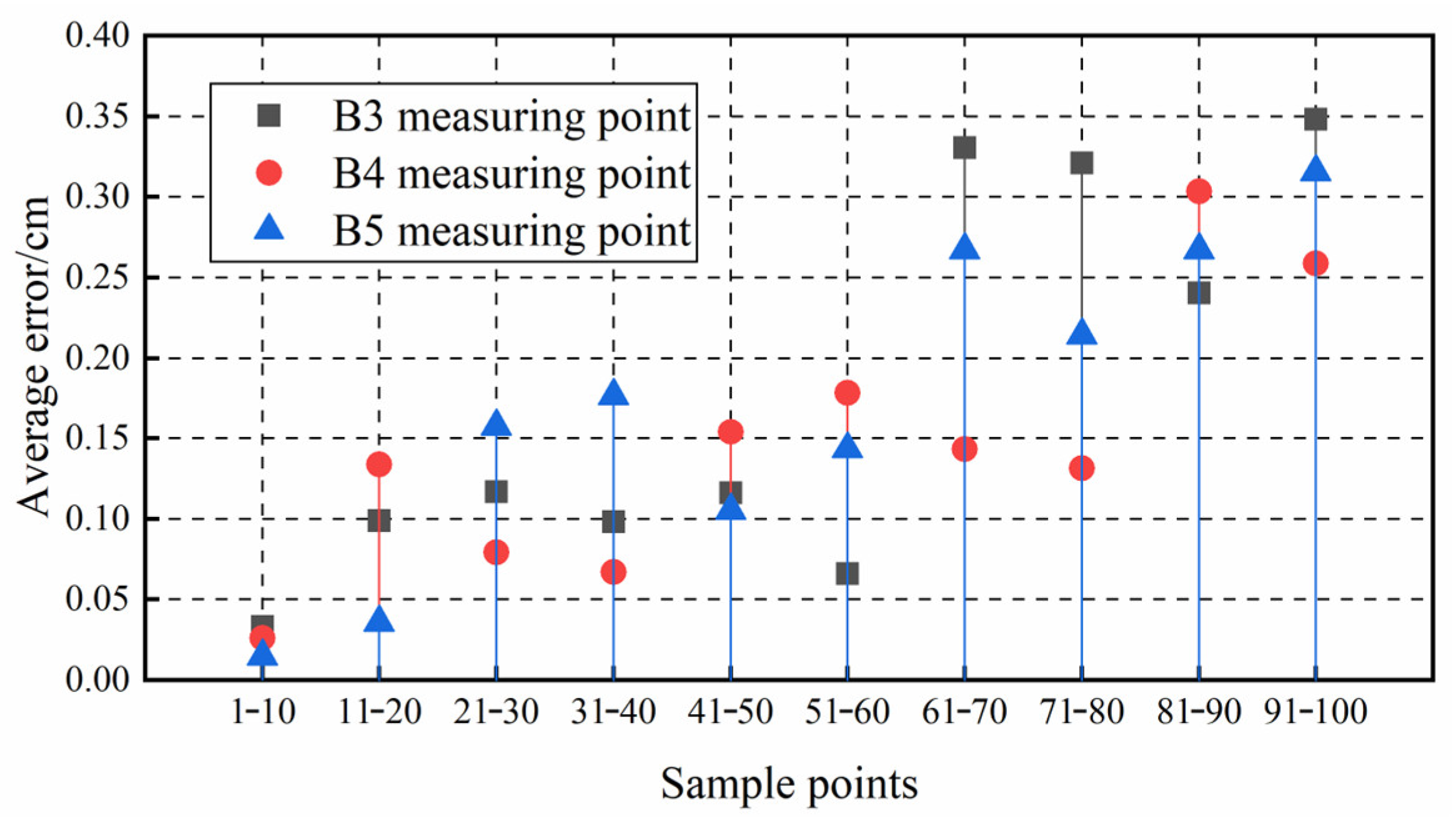
3.3. Analysis Results
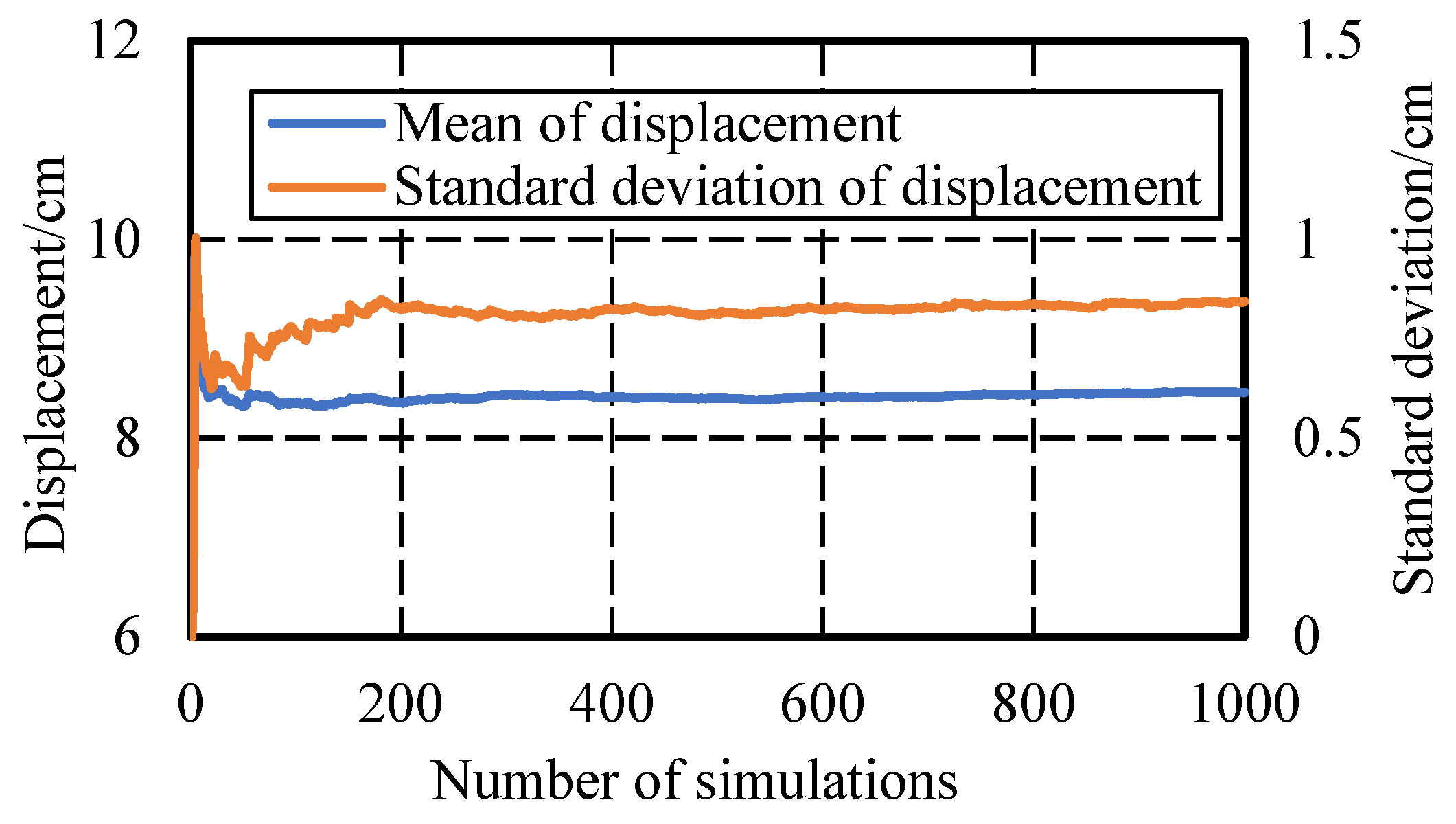
3.3.1. Construction of SFEMM Model
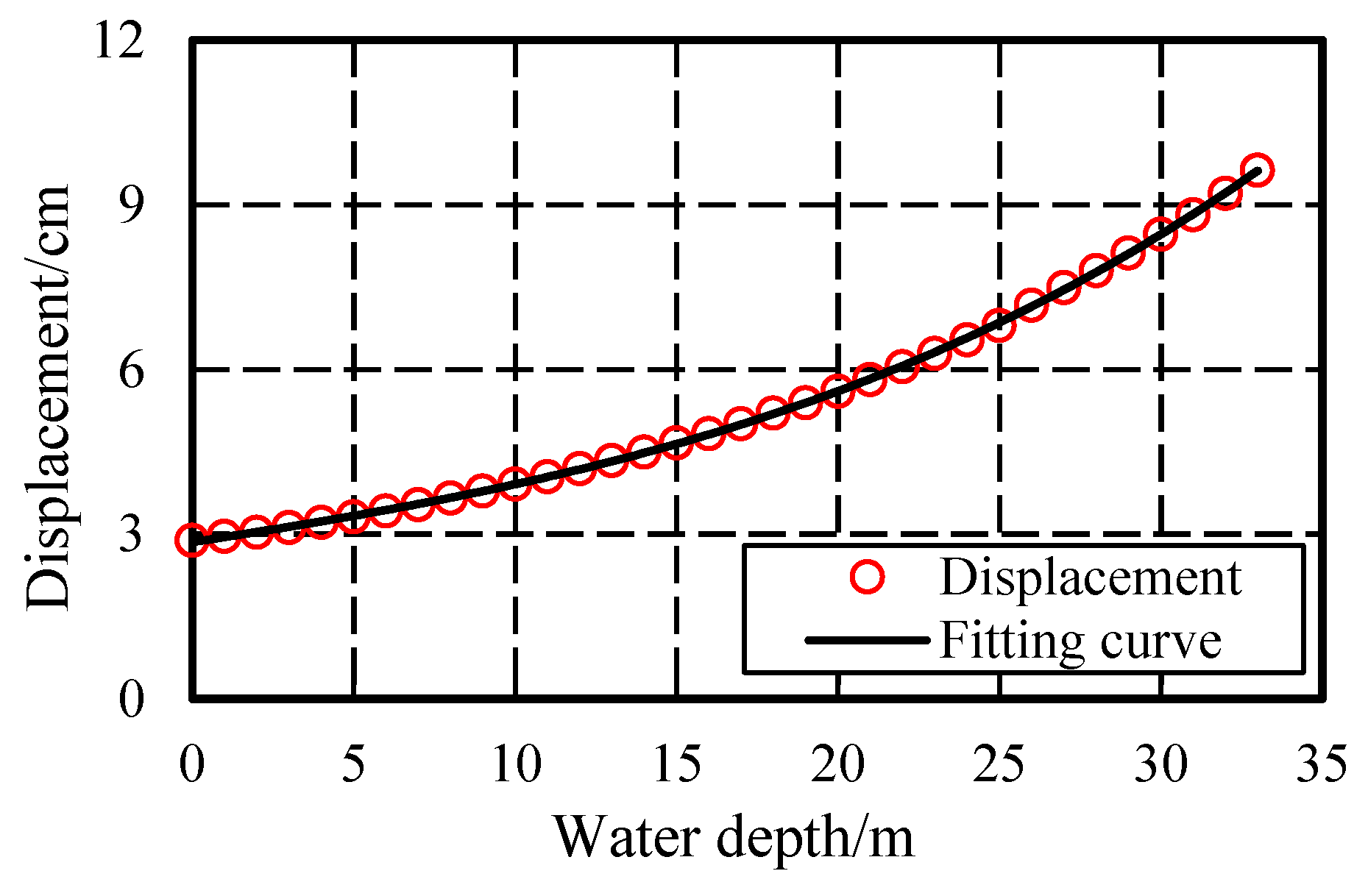
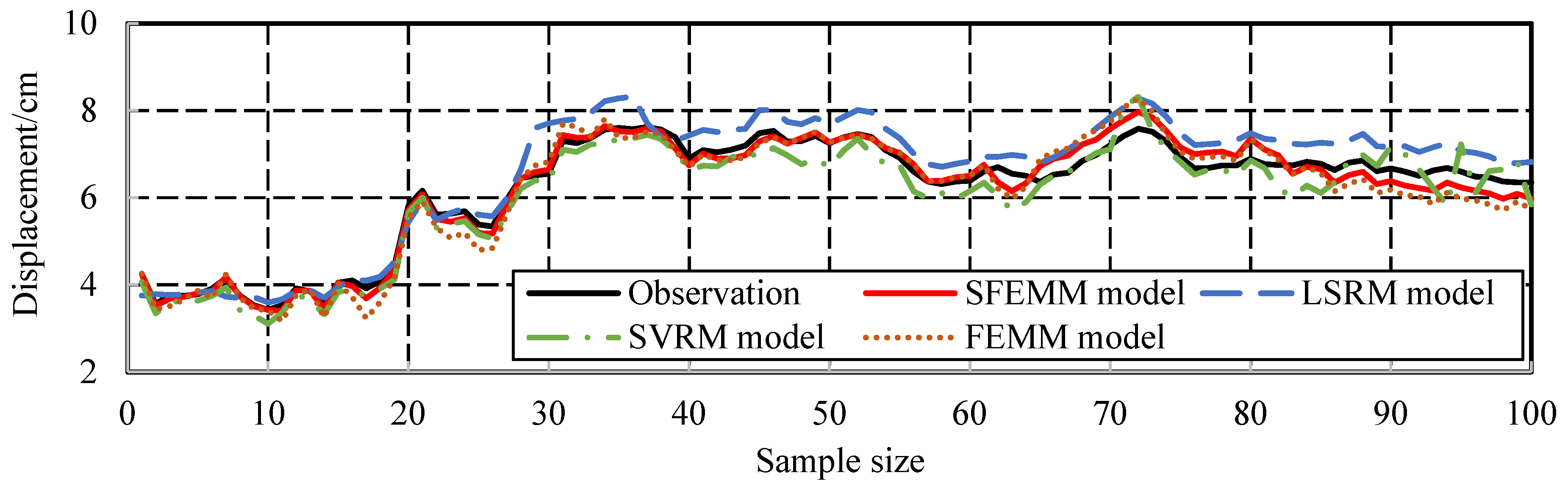
3.3.2. Determination of Monitoring Index
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yao, Y.; Wang, F.; Yang, Z. New development of dam construction technology with complex material for high earth-rock dam. Water Power 2023, 49, 65–71. [Google Scholar]
- Wang, S.; Xu, C.; Gu, C.; Su, H.; Hu, K.; Xia, Q. Displacement monitoring model of concrete dams using the shape feature clustering-based temperature principal component factor. Struct. Control Health Monit. 2020, 27, e2603. [Google Scholar] [CrossRef]
- Li, Z.; Hou, H. Theory and Methods on Dam Safety Monitoring Indexes. Water Power 2010, 36, 64–67. [Google Scholar]
- Li, B.; Yang, J.; Hu, D. Dam monitoring data analysis methods: A literature review. Struct. Control Health Monit. 2020, 27, e2501. [Google Scholar] [CrossRef]
- Ran, L.; Yang, J.; Zhang, P.; Wang, J.; Ma, C.; Cui, C.; Cheng, L.; Wang, J.e.; Zhou, M. A hybrid monitoring model of rockfill dams considering the spatial variability of rockfill materials and a method for determining the monitoring indexes. J. Civ. Struct. Health Monit. 2022, 12, 817–832. [Google Scholar] [CrossRef]
- Huang, Y.; Wan, Z. Study on Viscoelastic Deformation Monitoring Index of an RCC Gravity Dam in an Alpine Region Using Orthogonal Test Design. Math. Probl. Eng. 2018, 2018, 8743505. [Google Scholar] [CrossRef]
- Deng, Z.; Gao, Q.; Huang, M.; Wan, N.; Zhang, J.; He, Z. From data processing to behavior monitoring: A comprehensive overview of dam health monitoring technology. Structures 2025, 71, 108094. [Google Scholar] [CrossRef]
- Zhang, W.; Li, H.; Shi, D.; Shen, Z.; Zhao, S.; Guo, C. Determination of Safety Monitoring Indices for Roller-Compacted Concrete Dams Considering Seepage–Stress Coupling Effects. Mathematics 2023, 11, 3224. [Google Scholar] [CrossRef]
- Li, B. Research on Intelligent Analysis Method for Deformation Monitoring of Gravity Dam. Doctoral Thesis, Xi’an University of Technology, Xi’an, China, 2021. [Google Scholar]
- Wu, Z. Theory and Application of Safety Monitoring for Hydraulic Structures; Higher Education Press: Beijing, China, 2003. [Google Scholar]
- Thomas, F.; Marwan, E.M.; Ghilman, D.; Wolfgang, G.P.; Rene, B. Method for indirect determination of soil parameters for numerical simulation of dikes and earth dams. Appl. Water Sci. 2022, 12, 245. [Google Scholar] [CrossRef]
- Yu, X.; Li, Z.; Wang, Y.; Pang, R.; Lv, X.; Fu, M. Stress–deformation analysis of concrete anti-seepage structure in earth-rock dam on overburden considering spatial variability of geomechanical parameter. Probabilistic Eng. Mech. 2025, 79, 103725. [Google Scholar] [CrossRef]
- Chi, S.; Feng, W.; Jia, Y.; Zhang, Z. Application of the soil parameter random field in the 3D random finite element analysis of Guanyinyan composite dam. Case Stud. Constr. Mater. 2022, 17, e01329. [Google Scholar] [CrossRef]
- Sun, Y.; Huang, J.; Jin, W.; Sloan, S.W.; Jiang, Q. Bayesian updating for progressive excavation of high rock slopes using multi-type monitoring data. Eng. Geol. 2019, 252, 1–13. [Google Scholar] [CrossRef]
- Pang, R.; Yang, Y.; Zhou, Y.; Jing, M.; Xu, B. Seismic reliability analysis of high earth-rockfill dams subjected to mainshock-aftershock sequences using a novel noninvasive stochastic finite element method. Soil Dyn. Earthq. Eng. 2024, 183, 108817. [Google Scholar] [CrossRef]
- Chi, S.; Feng, W.; Jia, Y.; Zhang, Z. Stochastic Finite-Element Analysis of Earth–Rockfill Dams Considering the Spatial Variability of Soil Parameters. Int. J. Geomech. 2022, 22, 04022224. [Google Scholar] [CrossRef]
- Song, Z.; Han, P.; Ma, C.; Zhang, H. Inversion Analysis of Dynamic Parameters of High Panel Rockfill Dams Considering Concept of Uncertaint. Water Resour. Power 2023, 41, 118–122. [Google Scholar] [CrossRef]
- Wang, B.W.; Li, D.Q.; Tang, X.S. Impact of statistical uncertainty in soil parameters on slopestability reliability of rockfill dams. Eng. J. Wuhan Univ. 2019, 52, 758–766. [Google Scholar] [CrossRef]
- Lu, X.; Zhu, S. Stochastic Finite Element Analysis of Rockfill Dam Considering Spatial Variability of Gradation Parameters. Water Power 2022, 48, 81–89. [Google Scholar]
- Wang, J.; Yang, J.; Cheng, L.; Ma, C.; Ran, L. Study on the noninvasive stochastic finite element method of rockfill damconsidering spatial variability of material parameters. J. Water Resour. Water Eng. 2019, 30, 200–207. [Google Scholar] [CrossRef]
- Lumb, P. The variability of natural soils. Can. Geotech. J. 1966, 3, 74–97. [Google Scholar] [CrossRef]
- Stefanou, G. The stochastic finite element method: Past, present and future. Comput. Methods Appl. Mech. Eng. 2008, 198, 1031–1051. [Google Scholar] [CrossRef]
- Tanapalungkorn, W.; Yodsomjai, W.; Keawsawasvong, S.; Nguyen, T.S.; Oye, W.C.; Likitlersuang, S. Stability analysis of tunnel heading in clay with nonstationary random fields of undrained shear strength. Probabilistic Eng. Mech. 2024, 78, 103692. [Google Scholar] [CrossRef]
- Wu, C.; Wang, Z.; Goh, S.H.; Zhang, W. Comparing 2D and 3D slope stability in spatially variable soils using random finite-element method. Comput. Geotech. 2024, 170, 106324. [Google Scholar] [CrossRef]
- Liao, K.; Wu, Y.; Miao, F.; Pan, Y.; Beer, M. Probabilistic risk assessment of earth dams with spatially variable soil properties using random adaptive finite element limit analysis. Eng. Comput. 2022, 39, 3313–3326. [Google Scholar] [CrossRef]
- Shiau, J.; Nguyen, T.; Hung, T.P.T.; Sugawara, J. Probabilistic assessment of passive earth pressures considering spatial variability of soil parameters and design factors. Sci. Rep. 2025, 15, 4752. [Google Scholar] [CrossRef]
- Keshmiri, E.; Ahmadi, M.M. Reliability Analysis of Circular Foundations on Unsaturated Soils Using Monte Carlo Simulation. Geotech. Geol. Eng. 2025, 43, 111. [Google Scholar] [CrossRef]
- Deng, Z.P.; Zhong, M.; Pan, M.; Jiang, S.H.; Niu, J.T.; Zheng, K.H. Reliability Evaluation of Slopes Considering Spatial Variability of Soil Parameters Based on Efficient Surrogate Model. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2024, 10, 04023057. [Google Scholar] [CrossRef]
- Guo, X.; Sun, Q.; Dias, D.; Antoinet, E. Probabilistic assessment of an earth dam stability design using the adaptive polynomial chaos expansion. Bull. Eng. Geol. Environ. 2020, 79, 4639–4655. [Google Scholar] [CrossRef]
- Chen, D.; Xu, D.; Ren, G.; Jiang, Q.; Liu, G.; Wan, L.; Li, N. Simulation of cross-correlated non-Gaussian random fields for layered rock mass mechanical parameters. Comput. Geotech. 2019, 112, 104–119. [Google Scholar] [CrossRef]
- Jiang, S.; Li, D.; Zhou, C.; Fang, G. Slope reliability analysis considering effect of autocorrelation functions. Chin. J. Geotech. Eng. 2014, 36, 508–518. [Google Scholar]
- Jiang, S.; Li, D.; Zhang, L.; Zhou, C. Slope reliability analysis considering spatially variable shear strength parameters using a non-intrusive stochastic finite element method. Eng. Geol. 2014, 168, 120–128. [Google Scholar] [CrossRef]
- Luo, N.; Agarwal, E. Seismic stability and failure mechanisms of gentle and steep slopes considering soil rotated anisotropy and spatial variability. Soil Dyn. Earthq. Eng. 2024, 183, 108821. [Google Scholar] [CrossRef]
- Jiang, S.; Li, J.; Huang, J.; Zhou, C. Spatial variability characterization of the mechanical parameters of structural planes and reliability analysis of rock slopes. Chin. J. Rock Mech. Eng. 2022, 41, 2834–2845. [Google Scholar] [CrossRef]
- Tian, J.; Luo, Y.; Lu, X.; Li, Y.; Chen, J. Physical data-driven modeling of deformation mechanism constraints on earth-rock dams based on deep feature knowledge distillation and finite element method. Eng. Struct. 2024, 307, 117899. [Google Scholar] [CrossRef]
- Liu, X.; Li, Z.; Sun, L.; Yahya, K.E.; Wang, J.; Lu, W. A critical review of statistical model of dam monitoring data. J. Build. Eng. 2023, 80, 108106. [Google Scholar] [CrossRef]
- Gu, C.; Wu, Z. Theory and Methods of Dam and Foundation Safety Monitoring and Their Applications; Hohai University Press: Nanjing, China, 2006. [Google Scholar]
- Zhu, B.; Pei, H.; Yang, Q. Reliability analysis of submarine slope considering the spatial variability of the sediment strength using random fields. Appl. Ocean Res. 2019, 86, 340–350. [Google Scholar] [CrossRef]
- Ran, L.; Yang, J.; Ma, C.; Cheng, L.; Zhou, M. Global sensitivity analysis of parameters based on sPCE: The case study of a concrete face rockfill dam in northwest China. PLoS ONE 2023, 18, e0290665. [Google Scholar] [CrossRef]
- Wu, C.B.; Yan, Q. Sensitivity Analysis of Duncan E-B Model Parameters for Rockfill. Water Resour. Power 2010, 28, 94–96. [Google Scholar]
- Yang, Y.S.; Liu, X.S.; Zhao, J.M.; Wang, X.-G. Parameter sensitivity analysis of Duncan E-B model. J. China Inst. Water Resour. Hydrpower Res. 2013, 11, 81–86. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Lu, X.; Wang, Y.; Zhang, H.; Zhang, P. An online anomaly recognition and early warning model for dam safety monitoring data. Struct. Health Monit. 2019, 19, 796–809. [Google Scholar] [CrossRef]
- Hui, C. Refined Numerical Simulation of Structural Behaviors for High Earth-Rockfill Dam with Considering Real Construction Quality. Doctoral Thesis, Tianjin University, Tianjin, China, 2018. [Google Scholar]
- Zhang, F.; Zhou, Q.; Du, P. Seismic Response Analysis of Cut-Off Wall of Dam Foundation Under Spatial Variability of Parameters. J. Shanghai Jiao Tong Univ. 2022, 56, 684–692. [Google Scholar] [CrossRef]
- Wen, D. The Study on Characteristics of Stress and Deformation of Separated Face Slabs of CFRD. Master’s Thesis, Xinjiang Agricultural University, Urumqi, China, 2015. [Google Scholar]
- Dong, J. Study on Mechanical Properties of Interface Between Soil and Structure. Master’s Thesis, Dalian University of Technology, Dalian, China, 2011. [Google Scholar]
- Feng, W.; Chi, S.; Jia, Y. Random finite element analysis of a clay-core-wall rockfill dam considering three-dimensional conditional random fields of soil parameters. Comput. Geotech. 2023, 159, 105437. [Google Scholar] [CrossRef]
- Chen, H.; Liu, D. Stochastic finite element analysis of rockfill dam considering spatial variability of dam material porosity. Eng. Comput. 2019, 36, 2929–2959. [Google Scholar] [CrossRef]
- Tan, X.; Wang, X.; Khoshnevisan, S.; Hou, X.; Zha, F. Seepage analysis of earth dams considering spatial variability of hydraulic parameters. Eng. Geol. 2017, 228, 260–269. [Google Scholar] [CrossRef]
- Sadeghian, N.; Estalaki, A.M.; Calamak, M. Probabilistic internal erosion analysis in stratified and unstratified foundations of embankment dams using copulas. Nat. Hazards 2024, 120, 12989–13007. [Google Scholar] [CrossRef]
- Ma, C. Intelligent Inversion Analysis of Macro- and Micro-Parameters of Rockfill Based on Discrete Element Method and It’s Engineering Application. Doctoral Thesis, Xi’an University of Technology, Xi’an, China, 2020. [Google Scholar]
- Zewdu, B.A.; Kegne, B.S.; Dessie, W.M.; Asrat, A.N. A Comparative Evaluation of Seepage and Stability of Embankment Dams Using GeoStudio and Plaxis Models: The Case of Gomit Dam in Amhara Region, Ethiopia. Water Conserv. Sci. Eng. 2022, 7, 429–441. [Google Scholar] [CrossRef]
- Mehdi, R.M.; Hossien, R. Uncertainty analysis in probabilistic design of detention rockfill dams using Monte-Carlo simulation model and probabilistic frequency analysis of stability factors. Environ. Sci. Pollut. Res. Int. 2022, 30, 28035–28052. [Google Scholar] [CrossRef]
- Gullnaz, S.; Azzeddine, S. Deep Neural Network and Polynomial Chaos Expansion-Based Surrogate Models for Sensitivity and Uncertainty Propagation: An Application to a Rockfill Dam. Water 2021, 13, 1830. [Google Scholar] [CrossRef]


| Project Name | Type | Height | Impact |
|---|---|---|---|
| A certain rockfill dam | Asphalt concrete-core-wall rockfill dam | 150 m | The calculation results significantly underestimate the stress and deformation of the anti-seepage structure [12]. |
| Liang Hekou | Gravel soil-core-wall rockfill dam | 300 m | Under the influence of aftershocks, there is a significant gap between the analysis results of dam deformation, stability, and seepage and the actual situation [15]. |
| Zi Pingpu | Concrete-face rockfill dam | 156 m | The peak acceleration error of the measuring point increased from 8.16% to 25.17% [17]. |
| Guan Yinyan | Clay-core rockfill dam | 71 m | The maximum vertical displacement value differs from the value calculated using the inversion parameters by more than 8.3% [16]. |
| A certain rockfill dam | Rockfill dam | 150 m | The displacement and stress of the dam are 7% smaller than the actual value [18]. |
| Nuo Zhadu | Core rockfill dam | 216.5 m | The probability of stable failure of the dam slope is significantly lower than the actual value, which underestimates the risk of accidents [19]. |
| Gong Boxia | Concrete-face rockfill dam | 132 m | The vertical displacement value of the dam is 10–26.7% smaller than the measured value [20]. |
| Sress Conditions | Element Stiffness | Parameters |
|---|---|---|
| Pull up | a = 175, b = 47.6 | |
| Pressed | a = 650, b = 41 | |
| Vertical shear | a = 225, b = 40 | |
| Transverse shear | a = 608, b = 560 |
| Type of Interface | (°) | C (kPa) | K1 | n | Kyy (kN/m3) | |
|---|---|---|---|---|---|---|
| Between extrusion wall and cushion | 32 | 2 | 0.8 | 4800 | 1.25 | 108 (pressure) |
| Between toe slab and cushion | 32 | 2 | 0.8 | 4800 | 1.25 | 102 (tension) |
| Zones | ρ (kg/m3) | c (kPa) | φ0 (°) | K | Rf | Kb | n | Kur | ∆φ (°) | m |
|---|---|---|---|---|---|---|---|---|---|---|
| Cushion | 2150 | 0 | 49.4 | 950 | 0.921 | 510 | 0.63 | 1425 | 8.7 | 0.41 |
| Transition | 2130 | 0 | 50.4 | 1180 | 0.911 | 630 | 0.53 | 1770 | 9.3 | 0.3 |
| Upstream rockfill | 2087 | 0 | 50.3 | 710 | 0.61 | 383 | 0.91 | 1065 | 9.3 | 0.19 |
| Main rockfill | 2195 | 0 | 50.5 | 845 | 0.4 | 455 | 0.853 | 1267 | 8.5 | 0.185 |
| Downstream rockfill | 2058 | 0 | 47.5 | 725 | 0.4 | 225 | 0.92 | 1087 | 8 | 0.13 |
| Extrusion wall | 2400 | E = 2.17 × 1010 Pa, ν = 0.167 | ||||||||
| Face slab | 2400 | E = 2.17 × 1010 Pa, ν = 0.167 | ||||||||
| Toe slab | 2400 | E = 2.17 × 1010 Pa, ν = 0.167 | ||||||||
| Zones | (°) | n | Kb | ||||||
|---|---|---|---|---|---|---|---|---|---|
| μ | σ | C.V | μ | σ | C.V | μ | σ | C.V | |
| Upstream rockfill | 50.3 | 5.03 | 0.1 | 0.91 | 0.091 | 0.1 | 383 | 38.3 | 0.1 |
| Main rockfill | 50.5 | 5.05 | 0.1 | 0.853 | 0.0853 | 0.1 | 455 | 45.5 | 0.1 |
| Downstream rockfill | 47.5 | 9.5 | 0.2 | 0.92 | 0.184 | 0.2 | 225 | 45 | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ran, L.; Li, M.; Sun, Y.; Ding, S.; Yang, J.; Ma, C. A Method for Determining the Displacement Monitoring Index for Rockfill Dams Considering Material Uncertainty. Appl. Sci. 2025, 15, 4164. https://doi.org/10.3390/app15084164
Ran L, Li M, Sun Y, Ding S, Yang J, Ma C. A Method for Determining the Displacement Monitoring Index for Rockfill Dams Considering Material Uncertainty. Applied Sciences. 2025; 15(8):4164. https://doi.org/10.3390/app15084164
Chicago/Turabian StyleRan, Li, Meng Li, Yang Sun, Shuo Ding, Jie Yang, and Chunhui Ma. 2025. "A Method for Determining the Displacement Monitoring Index for Rockfill Dams Considering Material Uncertainty" Applied Sciences 15, no. 8: 4164. https://doi.org/10.3390/app15084164
APA StyleRan, L., Li, M., Sun, Y., Ding, S., Yang, J., & Ma, C. (2025). A Method for Determining the Displacement Monitoring Index for Rockfill Dams Considering Material Uncertainty. Applied Sciences, 15(8), 4164. https://doi.org/10.3390/app15084164





