Investigating Load-Bearing Capabilities and Failure Mechanisms of Inflatable Air Ribs
Abstract
1. Introduction
2. The Load-Bearing Performance of Air Ribs with Different Rise–Span Ratios
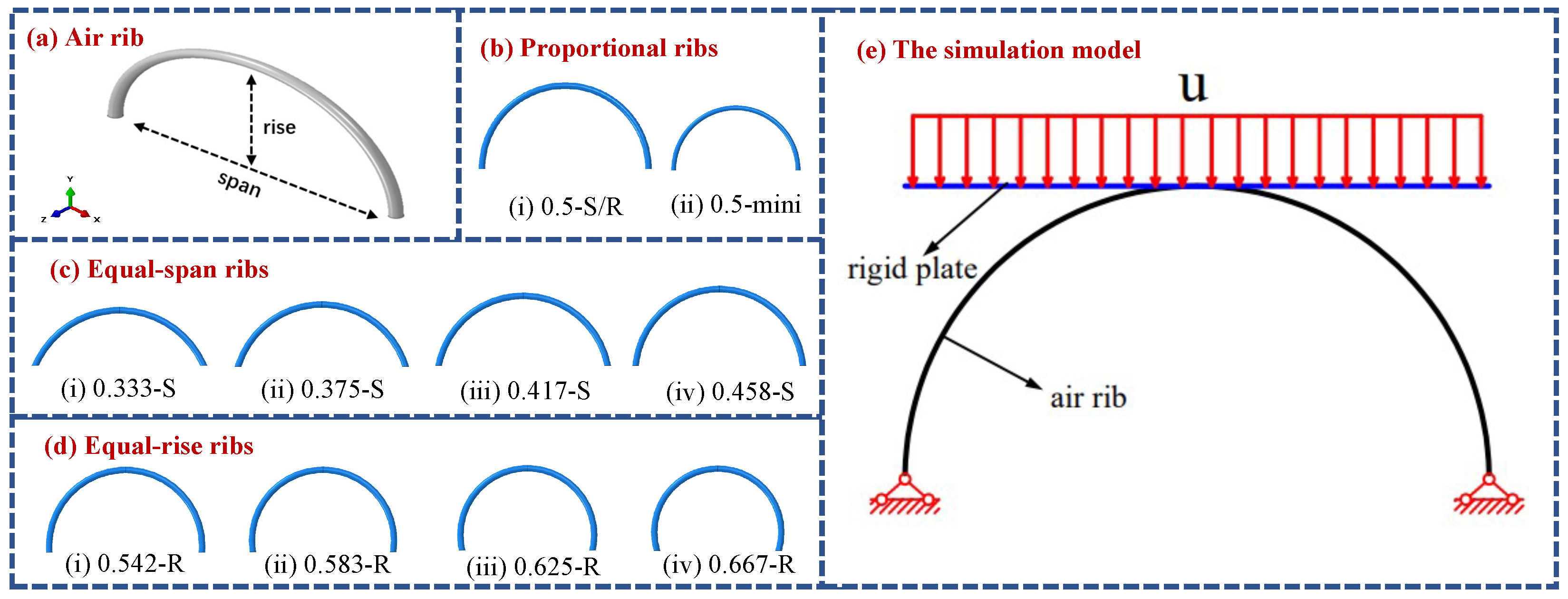
2.1. The Simulation Model of Air Ribs Under Load
- (1)
- Proportional ribs: These ribs maintain a consistent rise–span ratio, with both rise and span scaling proportionally. The rise–span ratio of the air ribs is 0.5, as shown in Figure 1b, and they are named 0.5-S/R and 0.5-mini.
- (2)
- Equal-span ribs: These ribs have a fixed span of 8 m, while the rise varies proportionally. The air ribs are classified based on their rise–span ratios, such as 0.333-S, 0.375-S, 0.417-S, and 0.458-S, as shown in Figure 1c.
- (3)
- Equal-rise ribs: These ribs have a fixed rise of 4 m, while the span varies proportionally. The air ribs are named according to their rise–span ratios, such as 0.532-R, 0.583-R, 0.625-R, and 0.666-R, as shown in Figure 1d.
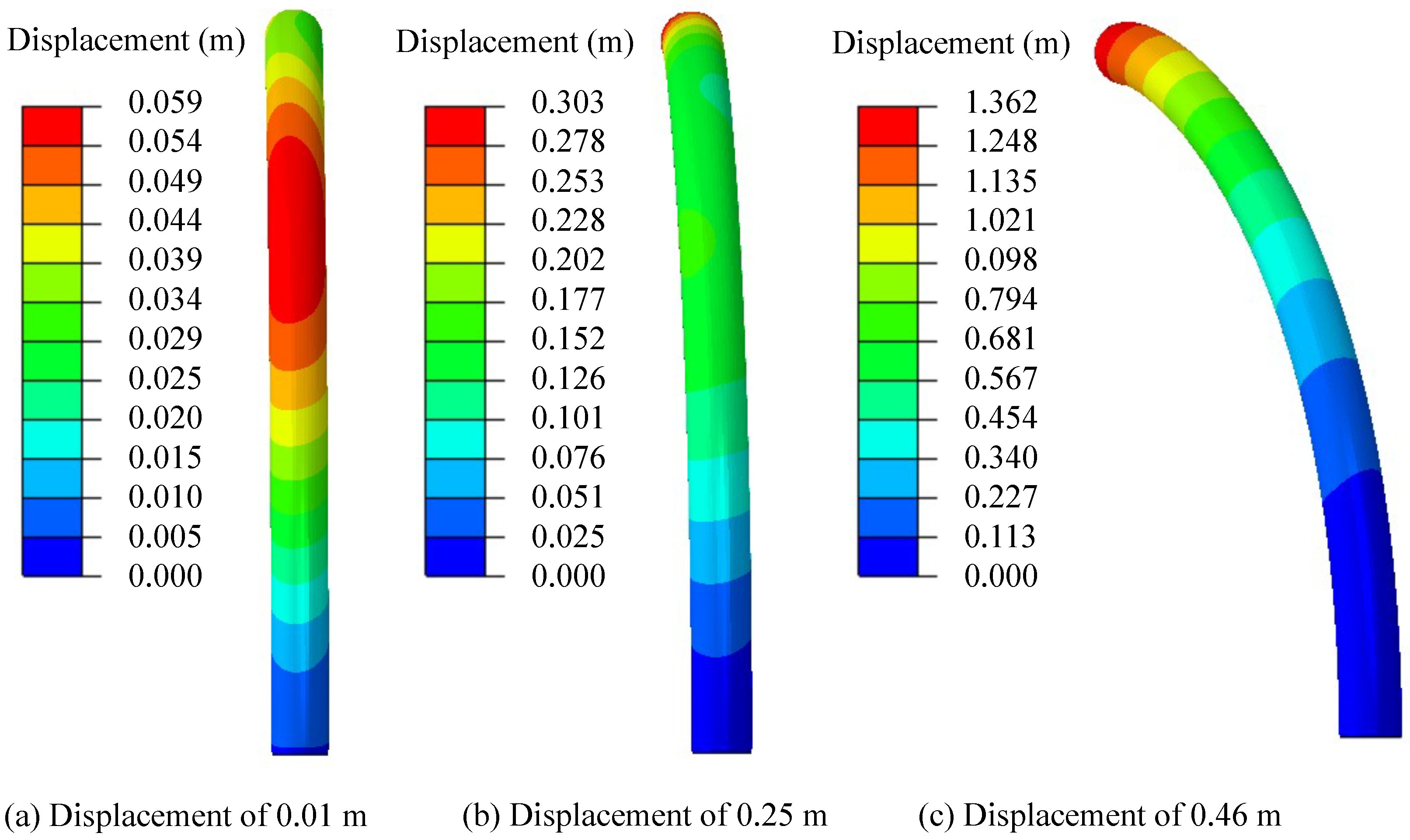
2.2. The Deformation Performance of Air Ribs
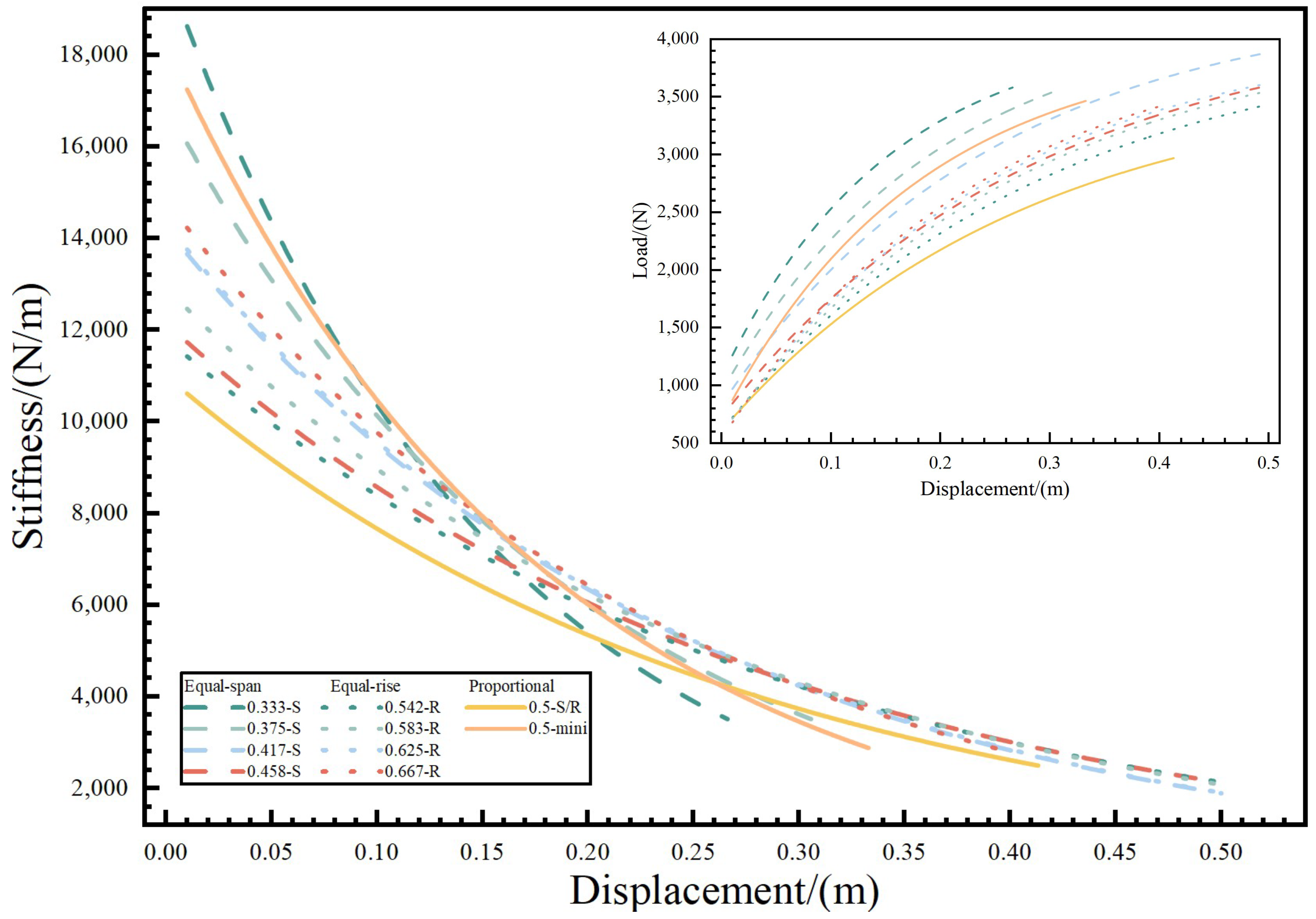
2.3. The Analysis of the Stiffness with Different Rise–Span Ratios
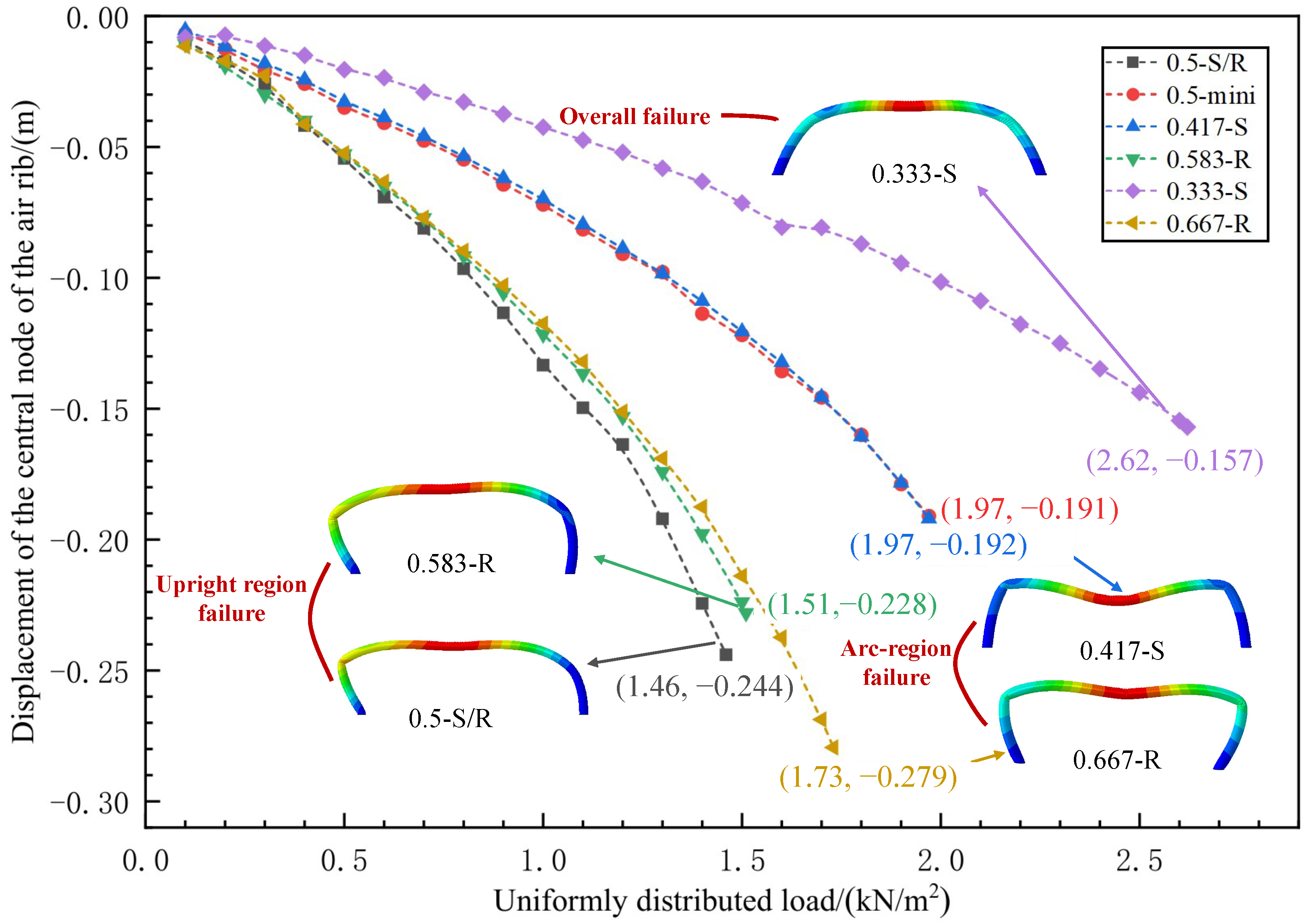
2.4. The Failure Mechanism Analysis of Air Ribs Under Vertical Loading
3. The Load-Bearing Performance of Tents with Different Rise–Span Ratios
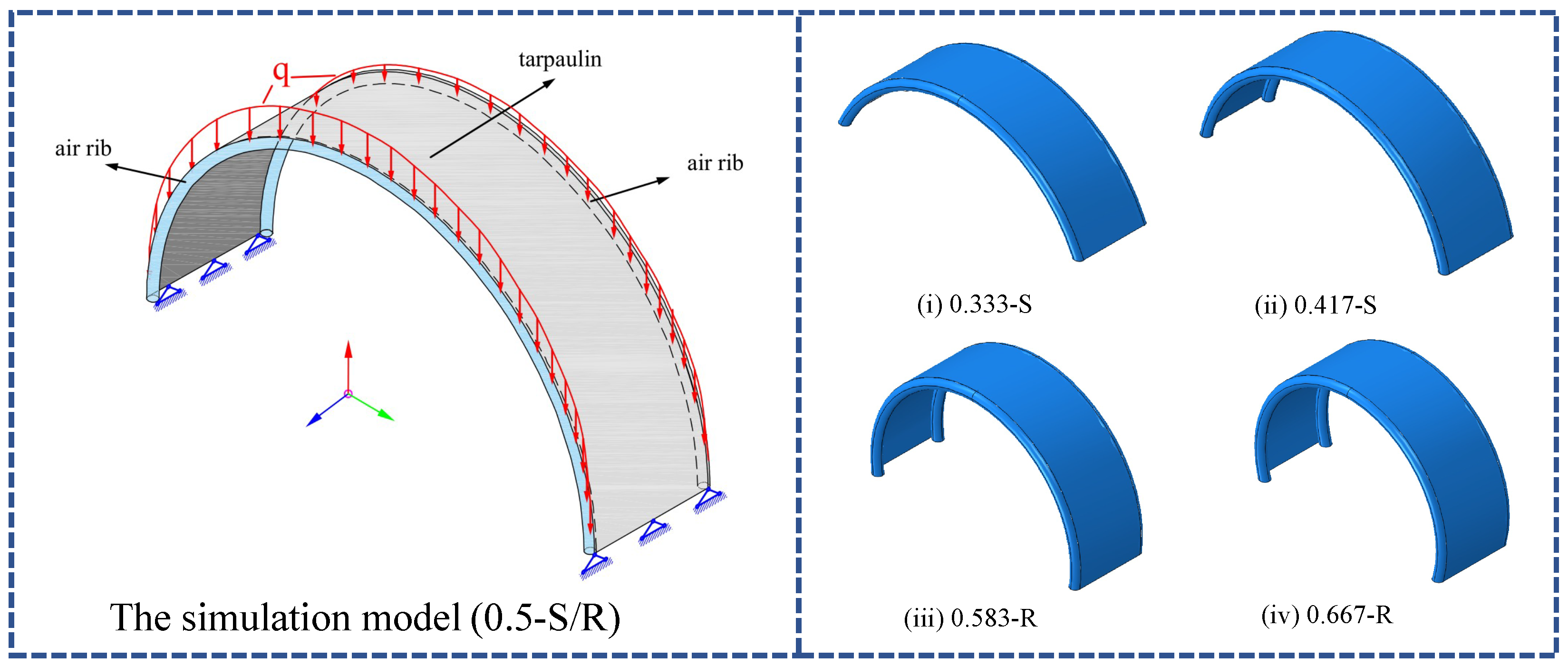
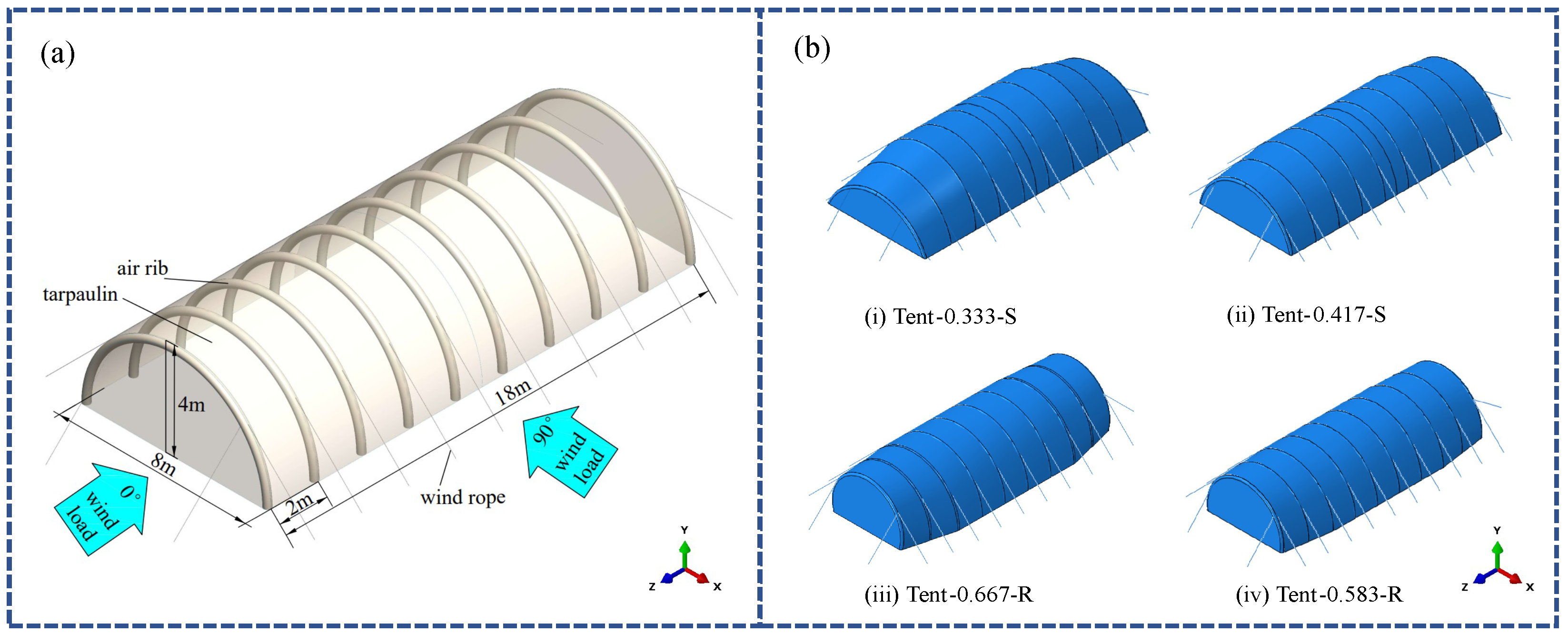
3.1. The Simulation Model of the Tent Under Load
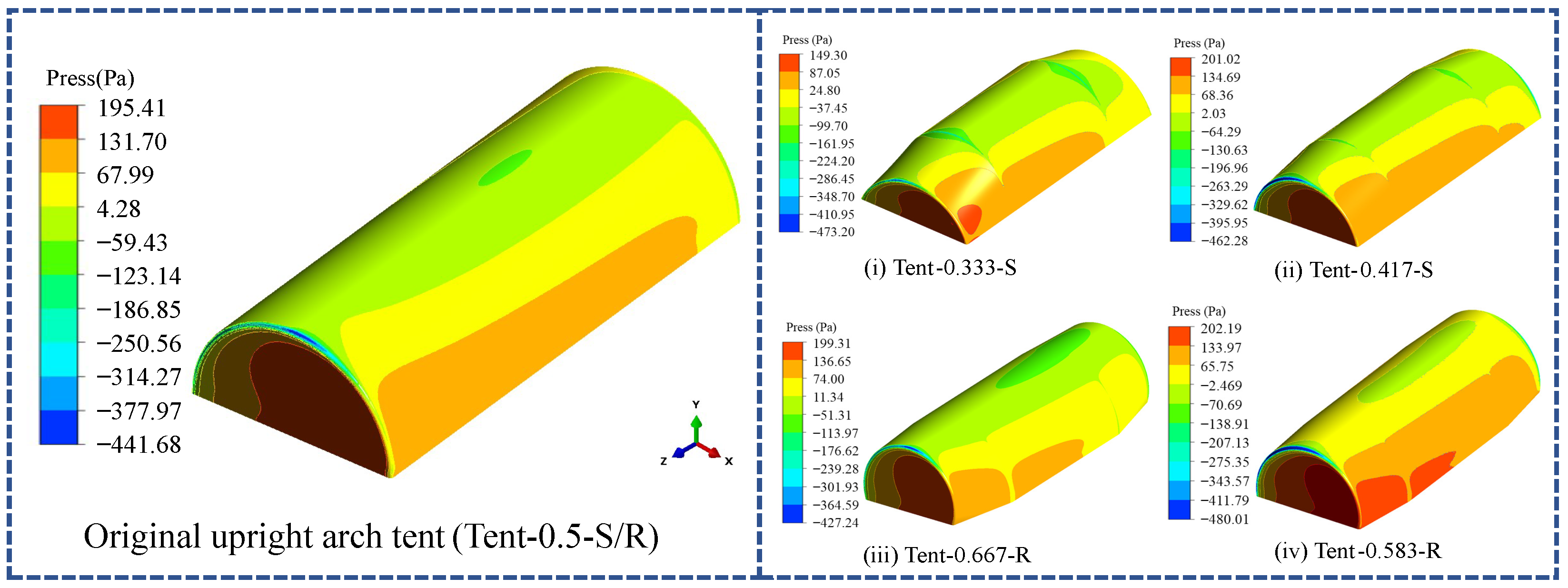
3.2. The Analysis of the Distribution of Wind Pressure
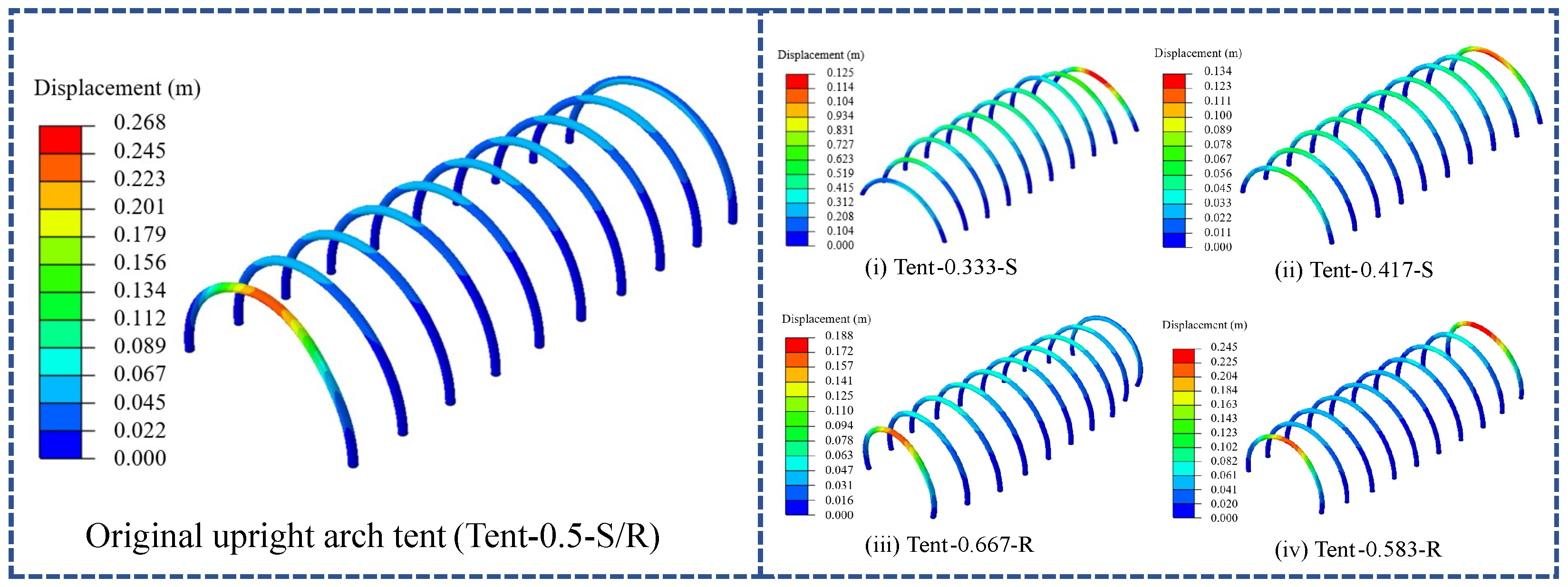
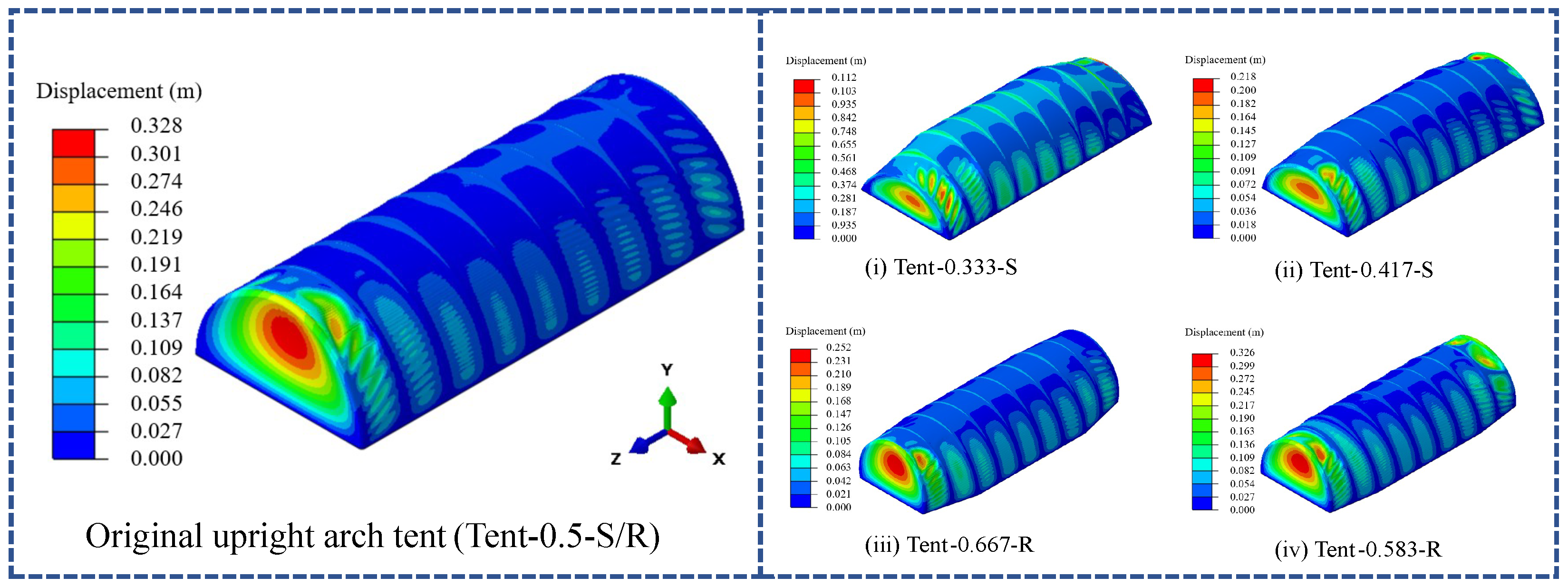
3.3. The Analysis of the Deformation of the Tent
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Motevalli, M.; Uhlemann, J.; Stranghöner, N.; Balzani, D. Geometrically nonlinear simulation of textile membrane structures based on orthotropic hyperelastic energy functions. Compos. Struct. 2019, 223, 110908. [Google Scholar] [CrossRef]
- Kamaliya, P.K.; Upadhyay, S.H. Inflatable antenna structures: Deployment analysis of torus bounded Z-fold scalable planar membrane reflector. Thin-Walled Struct. 2023, 191, 111061. [Google Scholar] [CrossRef]
- López, I.; Piquee, J.; Bucher, P.; Bletzinger, K.-U.; Breitsamter, C.; Wüchner, R. Numerical analysis of an elasto- flexible membrane blade using steady-state fluid–structure interaction simulations. J. Fluids Struct. 2021, 106, 103355. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, Y.; Yu, Q.; Zhang, L. Analysis and design of fabric membrane structures: A systematic review on material and structural performance. Thin-Walled Struct. 2022, 170, 108619. [Google Scholar] [CrossRef]
- Takadate, Y.; Uematsu, Y. Steady and unsteady aerodynamic forces on a long-span membrane structure. J. Wind Eng. Ind. Aerodyn. 2019, 193, 103946. [Google Scholar] [CrossRef]
- Yang, T.; Luo, M.; Zou, Z.; Ma, P. Mechanical properties of the surface membrane of lattice spacer-fabric flexible inflatable composites. Text. Res. J. 2022, 92, 1088–1097. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, Y.; Yoshida, A. Effect of added mass on wind-induced vibration of a circular flat membrane by wind tunnel tests. Int. J. Struct. Stab. Dyn. 2018, 18, 1850156. [Google Scholar] [CrossRef]
- Liu, C.; Pan, R.; Deng, X.; Xie, H.; Liu, J.; Wang, X. Random vibration and structural reliability of composite hyperbolic–parabolic membrane structures under wind load. Thin-Walled Struct. 2022, 180, 109878. [Google Scholar] [CrossRef]
- Sun, X.; Kandel, A.; Wu, Y. Investigation on wind tunnel experiment of oval-shaped arch-supported membrane structures. J. Wind Eng. Ind. Aerodyn. 2020, 206, 104371. [Google Scholar] [CrossRef]
- Kandel, A.; Sun, X.; Wu, Y. Wind-induced responses and equivalent static design method of oval-shaped arch-supported membrane structure. J. Wind Eng. Ind. Aerodyn. 2021, 213, 104620. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, C.; Li, D.; Liu, J.; Deng, X.; Luo, C.; Zhou, G. Study on Wind-Induced Dynamic Response and Statistical Parameters of Skeleton Supported Saddle Membrane Structure in Arching and Vertical Direction. Buildings 2024, 14, 1339. [Google Scholar] [CrossRef]
- Liu, C.; Deng, X.; Zheng, Z. Nonlinear wind-induced aerodynamic stability of orthotropic saddle membrane structures. J. Wind Eng. Ind. Aerodyn. 2017, 164, 119–127. [Google Scholar] [CrossRef]
- Chen, Z.; Wei, C.; Li, Z.; Zeng, C.; Zhao, J.; Hong, N.; Su, N. Wind-induced response characteristics and equivalent static wind-resistant design method of spherical inflatable membrane structures. Buildings 2022, 12, 1611. [Google Scholar] [CrossRef]
- Shi, J.-X.; Wu, Z.; Tsukimoto, S.; Shimoda, M. Design optimization of cable–membrane structures for form-finding and stiffness maximization. Compos. Struct. 2018, 192, 528–536. [Google Scholar] [CrossRef]
- Xue, S.; Li, X.; Li, X.; Dezhkam, M. Automated design of cable-net structures with multi-objective state. Autom. Constr. 2024, 160, 105288. [Google Scholar] [CrossRef]
- Marbaniang, A.L.; Kabasi, S.; Ghosh, S. Interactive exploration of tensile membrane structures for conceptual and optimal design. Structures 2024, 60, 105983. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Dang, L.M.; Lee, J.; Nguyen, P.V. Load-carrying capacity of ultra-thin shells with and without CNTs reinforcement. Mathematics 2022, 10, 1481. [Google Scholar] [CrossRef]
- Zheng, L.; Xu, J.; Li, F.; Zhang, J.; Su, R.; Wang, J.; Liu, Y.; Ru, Y. Analysis of Mechanical Properties of Air-Ribbed Skeleton Membrane Structure. Appl. Sci. 2023, 13, 9545. [Google Scholar] [CrossRef]
- Fan, B.-L.; Shi, M.-Y.; Pang, J.-C.; Wang, J.-Q.; Wang, J.-W. Research on solar power generation disaster relief tent based on inflatable structure. In Proceedings of the International Conference on Energy, Environmental and Civil Engineering (EECE 2019), Wuhan, China, 23–24 June 2019; Volume 5. [Google Scholar]
- Wang, C.G.; Xie, J.; Tan, H.F. Vibration simulations of a wrinkled membrane-inflated arch. J. Aerosp. Eng. 2014, 27, 414–422. [Google Scholar] [CrossRef]
- Liu, Y.; Ru, Y.; Li, F.; Zheng, L.; Zhang, J.; Chen, X.; Liang, S. Structural design and optimization of separated air-rib tents based on response surface methodology. Appl. Sci. 2022, 13, 55. [Google Scholar] [CrossRef]
- Guo, X.; Li, Q.; Zhang, D.; Gong, J. Structural behavior of an air-inflated fabric arch frame. J. Struct. Eng. 2016, 142, 04015108. [Google Scholar] [CrossRef]
- Malm, C.G.; Davids, W.G.; Peterson, M.L.; Turner, A.W. Experimental characterization and finite element analysis of inflated fabric beams. Constr. Build. Mater. 2009, 23, 2027–2034. [Google Scholar] [CrossRef]
- Xue, Z.M.; Wang, C.G.; Kang, J.T.; Tan, H.F. Buckling analysis of an inflated arch including wrinkling based on Pseudo Curved Beam model. Thin-Walled Struct. 2018, 131, 336–346. [Google Scholar] [CrossRef]
- Clapp, J.D.; Young, A.C.; Davids, W.G.; Goupee, A.J. Bending response of reinforced, inflated, tubular braided fabric structural members. Thin-Walled Struct. 2016, 107, 415–426. [Google Scholar] [CrossRef]
- Roekens, J.; De Laet, L.; Mollaert, M.; Luchsinger, R. Experimental and numerical investigation of a tensairity arch. Thin-Walled Struct. 2016, 105, 112–120. [Google Scholar] [CrossRef]
- Zhao, R.; Li, X.; Wang, W.; Xue, S.; Dou, F. Bending performance of highly pressured inflatable membrane arches. Eng. Struct. 2025, 328, 119716. [Google Scholar] [CrossRef]
- CECS 158-2015; China Association for Engineering Construction Standardization. Chinese Technical Specification for Membrane Structures: Beijing, China, 2015.
- Pi, Y.L.; Bradford, M.A.; Tin-Loi, F. Flexural-torsional buckling of shallow arches with open thin-walled section under uniform radial loads. Thin-Walled Struct. 2007, 45, 352–362. [Google Scholar] [CrossRef]
- Yao, N.; Wang, C.; Lu, X.; Du, J. A Method for Calculating the Critical Buckling Load of a Thin-Walled Cylindrical Shell. CN112,364,461B, 19 August 2022. [Google Scholar]
- Wijesooriya, K.; Mohotti, D.; Lee, C.-K.; Mendis, P. A technical review of computational fluid dynamics (CFD) applications on wind design of tall buildings and structures: Past, present and future. J. Build. Eng. 2023, 74, 106828. [Google Scholar] [CrossRef]
- Fu, W.; Yang, H.; Jia, J. Fluid vibration analysis of large-span skeletal membrane structures under pulsating winds. Adv. Civ. Eng. 2023, 2023, 6251962. [Google Scholar] [CrossRef]
- He, Y.; Zhao, Y.; Li, J. Wind vibration response analysis of air rib inflatable tent. Spat. Struct. 2021, 27, 56–61+70. [Google Scholar]
- GB 50009-2012; Code for Building Structure Loads. National Standards of the People’s Republic of China: Beijing, China, 2012.
- Gosling, P.D.; Bridgens, B.N.; Zhang, L. Adoption of a reliability approach for membrane structure analysis. Struct. Saf. 2013, 40, 39–50. [Google Scholar] [CrossRef]
- Wang, X.; Chu, H.; Yang, Q. Numerical analysis of wind-induced response of a wrinkled membrane. Int. J. Struct. Stab. Dyn. 2020, 20, 2050056. [Google Scholar] [CrossRef]

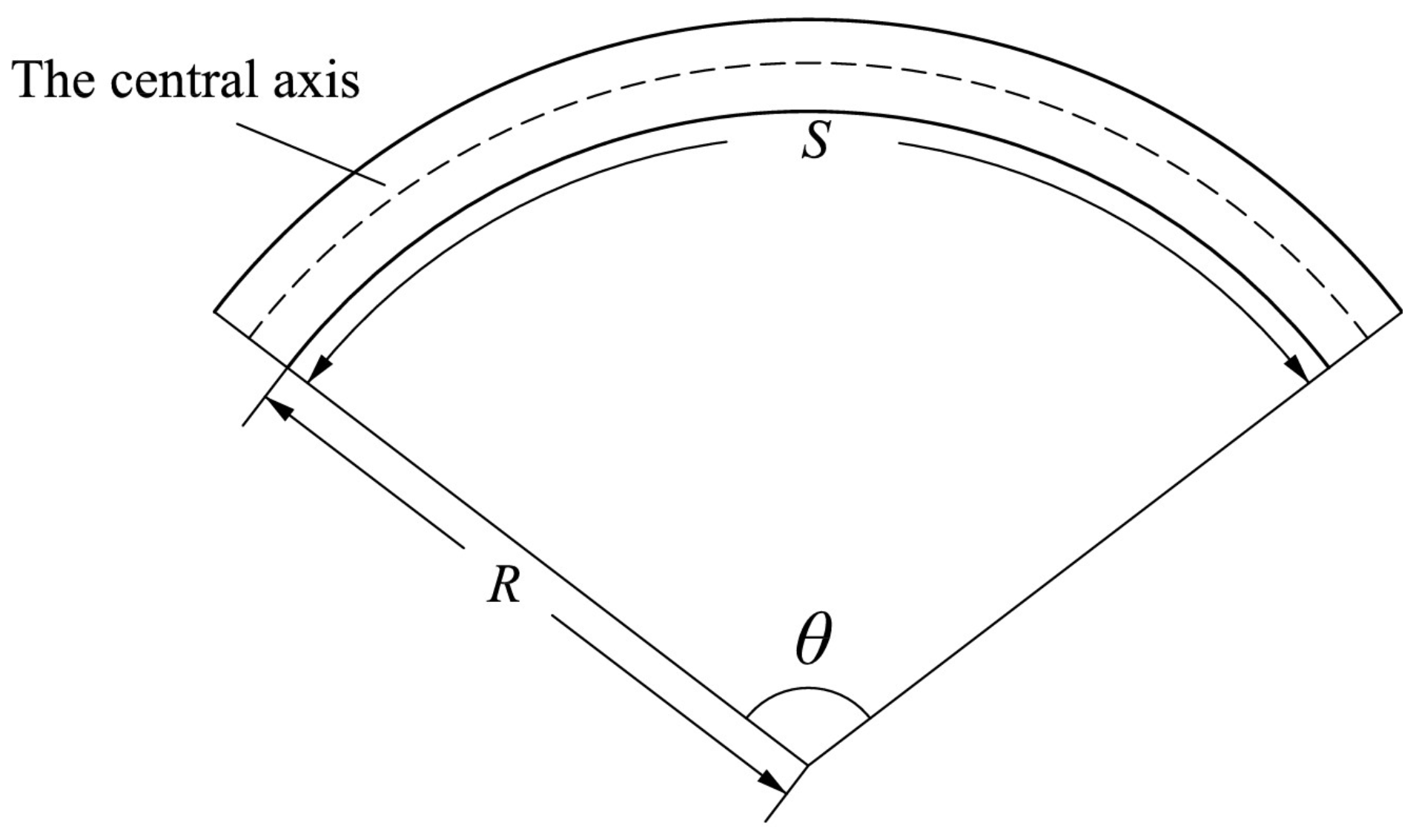
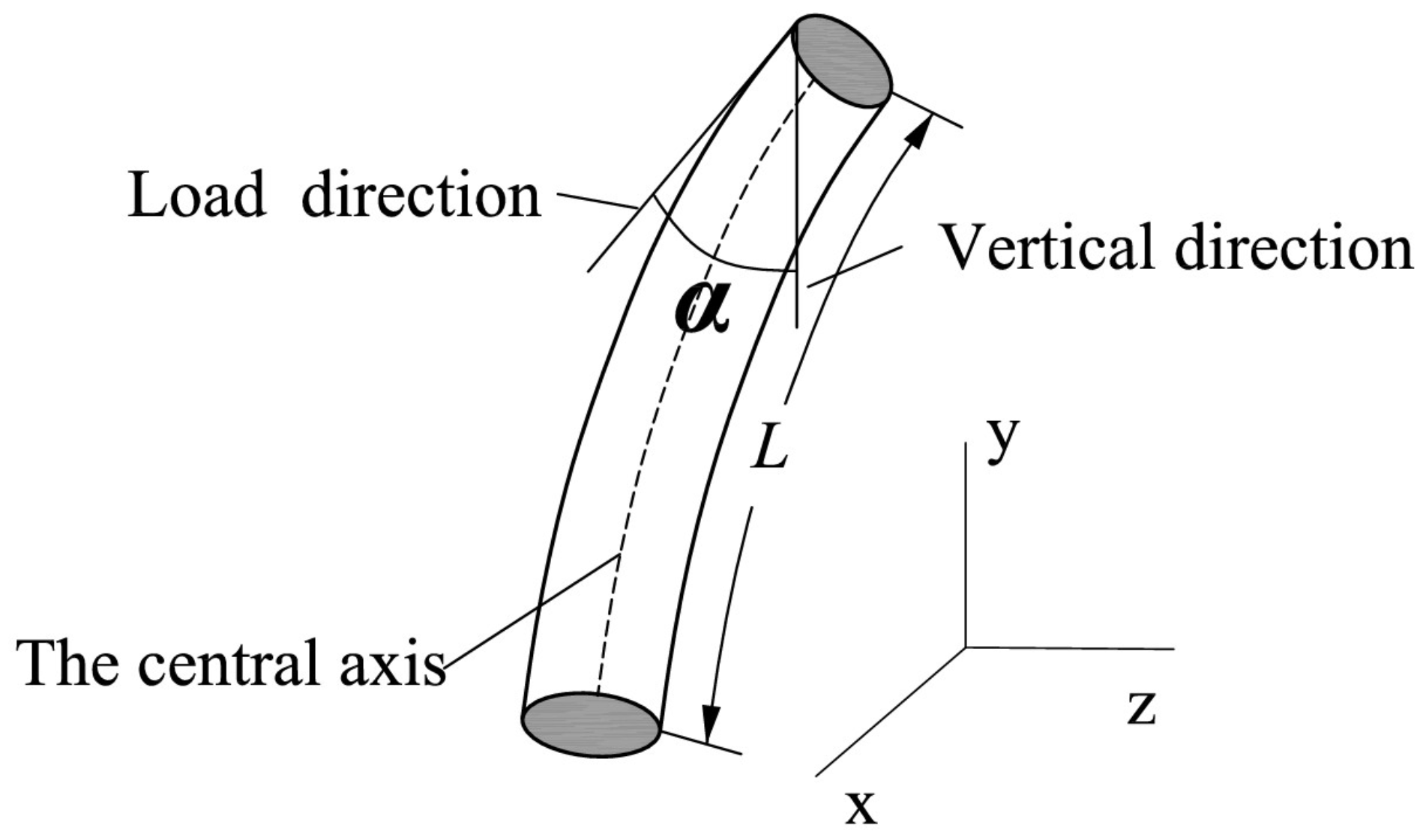

| Air Rib | Rise/(m) | Span/(m) | Thickness /(m) | Density /(Kg/m3) | Elastic Modulus/(MPa) | Poisson’s Ratio | Breaking Strength/(MPa) |
|---|---|---|---|---|---|---|---|
| 0.333-S | 2.67 | 8 | 1010 | 440 | 0.32 | 120.39 | |
| 0.375-S | 3 | 8 | |||||
| 0.417-S | 3.33 | 8 | |||||
| 0.458-S | 3.67 | 8 | |||||
| 0.5-S/R | 4 | 8 | |||||
| 0.542-R | 4 | 7.83 | |||||
| 0.583-R | 4 | 6.86 | |||||
| 0.625-R | 4 | 6.4 | |||||
| 0.667-R | 4 | 6 | |||||
| 0.5-mini | 3.5 | 7 |
| Air Rib | S/(m) | r/(m) | N | |
|---|---|---|---|---|
| 0.417-S | 6.64 | 5.82 | 2.48% | 63.8° |
| 0.667-R | 6.32 | 4.96 | 3.10% | 70.8° |
| 0.583-R | 7.13 | 4.55 | 4.24% | 86.2° |
| 0.5-S/R | 8.15 | 5.90 | 3.74% | 69.6° |
| Air Rib | L/(m) | e/(m) | k | M | |
|---|---|---|---|---|---|
| 0.417-S | 1.81 | 0.07 | 0.73 | 48.2° | 0.61 |
| 0.667-R | 2.09 | 0.05 | 0.83 | 46.9° | 0.56 |
| 0.583-R | 1.84 | 0.11 | 0.63 | 27.3° | 0.38 |
| 0.5-S/R | 2.04 | 0.12 | 0.6 | 32° | 0.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Liang, S.; Li, Y.; Zhang, J. Investigating Load-Bearing Capabilities and Failure Mechanisms of Inflatable Air Ribs. Appl. Sci. 2025, 15, 4154. https://doi.org/10.3390/app15084154
Liu Y, Liang S, Li Y, Zhang J. Investigating Load-Bearing Capabilities and Failure Mechanisms of Inflatable Air Ribs. Applied Sciences. 2025; 15(8):4154. https://doi.org/10.3390/app15084154
Chicago/Turabian StyleLiu, Ying, Shengchao Liang, Yanru Li, and Jun Zhang. 2025. "Investigating Load-Bearing Capabilities and Failure Mechanisms of Inflatable Air Ribs" Applied Sciences 15, no. 8: 4154. https://doi.org/10.3390/app15084154
APA StyleLiu, Y., Liang, S., Li, Y., & Zhang, J. (2025). Investigating Load-Bearing Capabilities and Failure Mechanisms of Inflatable Air Ribs. Applied Sciences, 15(8), 4154. https://doi.org/10.3390/app15084154






