Influence of Structural Parameters on Deformation Behavior of Metal Rhombic Chain Mesh
Abstract
:1. Introduction
2. Materials and Methods
2.1. Numerical Model of Metal Netting
2.2. Analytical Method Validation
2.3. Model Test Validation
3. Results
3.1. Effects of Solidity on Metal Netting Force and Deformation
3.2. Effects of Initial Tension on Metal Netting Deformation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chu, Y.I.; Wang, C.M.; Park, J.C.; Lader, P.F. Review of cage and containment tank designs for offshore fish farming. Aquaculture 2020, 519, 734928. [Google Scholar] [CrossRef]
- Xu, Z.; Qin, H. Fluid-structure interactions of cage based aquaculture: From structures to organisms. Ocean Eng. 2020, 217, 107961. [Google Scholar] [CrossRef]
- Liao, J. Deep-water wind and wave-resistant net-pen aquaculture technology: Extending the ‘blue granary’ to the deep sea. Ocean. Fish. 2019, 9, 64–66. [Google Scholar]
- Nie, Z.W.; Wang, L.; Liu, Y.L.; Shi, J.G.; Min, M.H.; Yu, W.W.; Chen, X.X.; Wang, L.M. Development and application of fishery copper alloy netting. Mar. Fish. 2016, 38, 329–336, (In Chinese with English abstract). [Google Scholar]
- Song, W.; Liang, Z.; Chi, H.; Huang, L.; Zhao, F.; Zhu, L.; Chen, B. Experimental study on the effect of horizontal waves on netting panels. Fish. Sci. 2006, 72, 967–976. [Google Scholar] [CrossRef]
- Swift, M.R.; Fredriksson, D.W.; Unrein, A.; Fullerton, B.; Patursson, O.; Baldwin, K. Drag force acting on biofouled net panels. Trans. Chin. Soc. Agric. Eng. 2006, 35, 292–299. [Google Scholar] [CrossRef]
- Zhan, J.; Jia, X.; Li, Y.; Sun, M.; Guo, G.; Hu, Y. Analytical and experimental investigation of drag on nets of fish cages. Aquac. Eng. 2006, 35, 292–299. [Google Scholar] [CrossRef]
- Li, Y.; Gui, F. Study on the drag coefficient of nodeless plane fishing net. Acta Oceanol. Sin. 2006, 28, 145–151, (In Chinese with English abstract). [Google Scholar]
- Zhan, J.; Su, W.; Li, Y.; Jia, X.; Huang, W. Comparison of Drags on Fish Cages of Different Shapes. China Ocean. Eng. 2006, 20, 457–471. [Google Scholar]
- Fredriksson, D.W. Open Ocean Fish Cage and Mooring System Dynamics; University of New Hampshire: Durham, NH, USA, 2001. [Google Scholar]
- Lader, P.; Fredheim, A.; Lien, E. Dynamic behavior of 3D nets exposed to waves and current. In Proceedings of the 20th International Conference on Offshore Mechanics and Arctic Engineering, Rio de Janeiro, Brazil, 3–8 June 2001. [Google Scholar]
- Gui, F.K.; Li, Y.C.; Zhang, H.H. The Proportional Criteria for Model Testing of Force Acting on Fishing Cage Net. China Offshore Platf. 2002, 17, 22–25, (In Chinese with English abstract). [Google Scholar]
- Li, Y.C.; Gui, F.K.; Zhang, H.H.; Guan, C.T. Simulation criteria of fishing nets in aquiculture sea cage experiments. J. Fish. Sci. China 2005, 12, 179–187, (In Chinese with English abstract). [Google Scholar]
- Lader, P.F.; Fredheim, A. Dynamic properties of a flexible net sheet in waves and current—A numerical approach. Aquac. Eng. 2006, 35, 228–238. [Google Scholar] [CrossRef]
- Chen, T.H.; Meng, A.; Gui, F.K. Effect of wave height and direction on hydraulic characteristics of net of pile-column type net enclosure aquaculture system. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2017, 33, 245–251. [Google Scholar]
- Wang, S.; Feng, D.J.; Gui, F.K. Hydrodynamic characteristics of the net of seam-edge type net enclosure under thecombined wave-current loads. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2022, 38, 60–68. [Google Scholar]
- Tsukrov, I.; Eroshkin, O.; Fredriksson, D.; Swift, M.; Celikkol, B. Finite element modeling of net panels using a consistent net element. Ocean. Eng. 2003, 30, 251–270. [Google Scholar] [CrossRef]
- Zhao, Y.P.; Li, Y.C.; Dong, G.H. Hydrofynamics of fishing net cages in the open sea. Fish. Mod. 2011, 38, 10–16, (In Chinese with English abstract). [Google Scholar]
- Drach, A.; Tsukrov, I.; Decew, J.; Robinson Swift, M.; Celikkol, B.; Hurtado, C.F. Design and modeling of submersible fish cages with copper netting for open ocean aquaculture. In Proceedings of the MARINE V: Proceedings of the V International Conference on Computational Methods in Marine Engineering, Hamburg, Germany, 29–31 May 2013; CIMNE: Barcelona, Spain, 2013. [Google Scholar]
- Cha, B.J.; Kim, H.Y.; Bae, J.H.; Yang, Y.S.; Kim, D.H. Analysis of the hydrodynamic characteristics of chain-link woven copper alloy nets for fish cages. Aquac. Eng. 2013, 56, 79–85. [Google Scholar] [CrossRef]
- Tsukrov, I.; Eroshkin, O.; Paul, W.; Celikkol, B. Numerical modeling of nonlinear elastic components of mooring system. IEEE J. Ocean. Eng. 2005, 30, 37–46. [Google Scholar] [CrossRef]
- Yuan, G.; Gao, F.; Lou, J.; LI, J.; Wang, X. Experimental study on mechanical properties and force transfer mechanism of bolt supported metal mesh. J. China Coal Soc. 2022, 47, 1512–1522, (In Chinese with English abstract). [Google Scholar]
- Liu, H.F.; Chen, C.P.; Zheng, Y.N.; Liang, X.Y. Study of the numerical simulation of characteristics of different flow resistances on a metal chain–link net for aquaculture under currents. Fish. Mod. 2017, 44, 73–79, (In Chinese with English abstract). [Google Scholar]
- Chen, C.P.; Wang, W.; Zheng, J.C.; Shi, X.Y.; Liu, C.F. Numerical simulation on hydrodynamic characteristics of the plane metal net under current. J. Dalian Ocean Univ. 2017, 32, 363–368, (In Chinese with English abstract). [Google Scholar]
- Wu, Q.; You, X.; Huang, L.; Bi, C.; He, S.; Yang, Y.; Wang, G. Hydrodynamic characteristics of rigid net panels for mariculture facilities as determined in flume-tank experiment. Appl. Ocean Res. 2024, 147, 103969. [Google Scholar] [CrossRef]
- Ling, A.J.; Liang, Y.H.; Zhao, D.H.; Fan, Z.Q.; Zhao, Y.P. Progress in hydrodynamic characterization of flexible mesh coat structures for marine aquaculture. Adv. Fish. Sci. 2024, 45, 223–236, (In Chinese with English abstract). [Google Scholar]
- Yu, S.; Qin, H.; Li, P.; Gong, F.; Tian, Y. Experimental study on drag characteristics of the practical rigid net under different current conditions. Front. Mar. Sci. 2023, 10, 1134278. [Google Scholar] [CrossRef]
- Decew, J.C.; Osienski, M.; Drach, A.; Celikkol, B.; Tsukrov, I. Effect of the bending stiffness on the volumetric stability of fish cages with copper alloy netting. In Proceedings of the MARINE V: Proceedings of the V International Conference on Computational Methods in Marine Engineering, Hamburg, Germany, 29–31 June 2013; CIMNE: Barcelona, Spain, 2013. [Google Scholar]
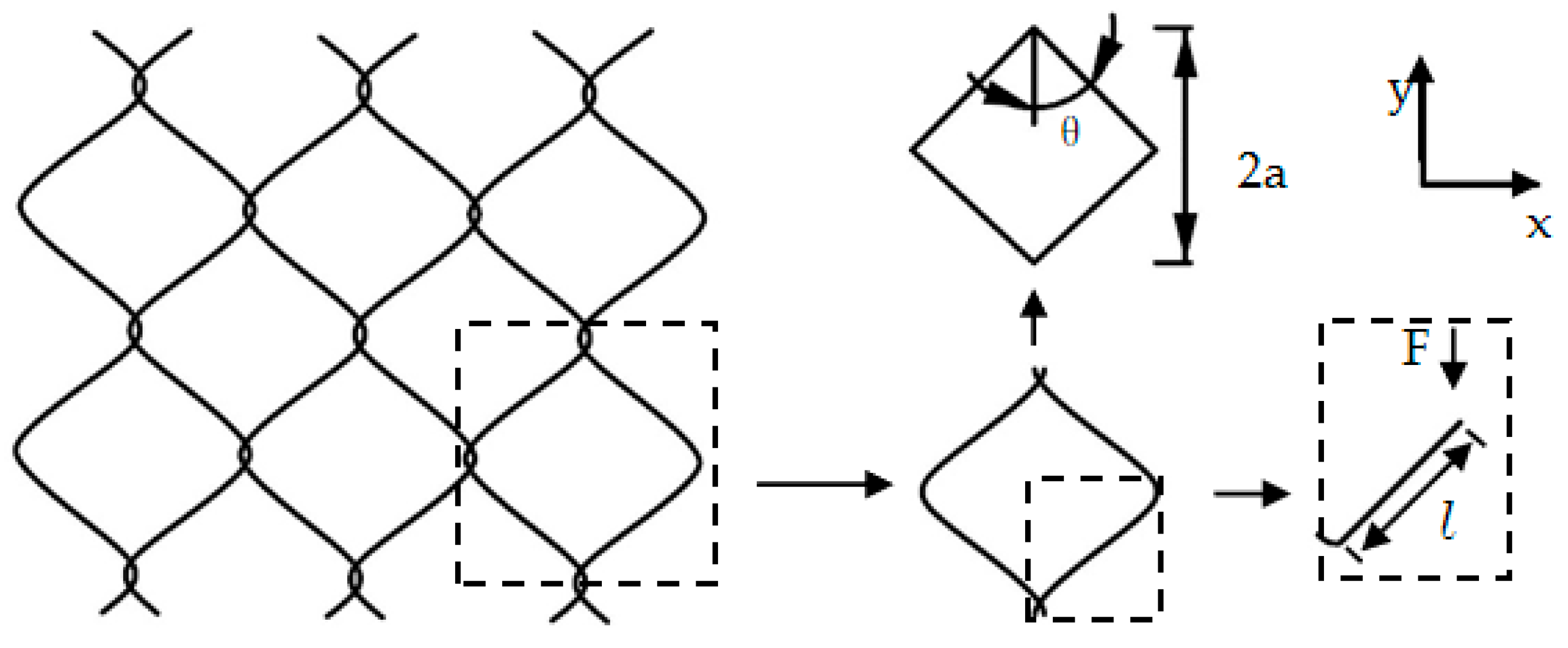
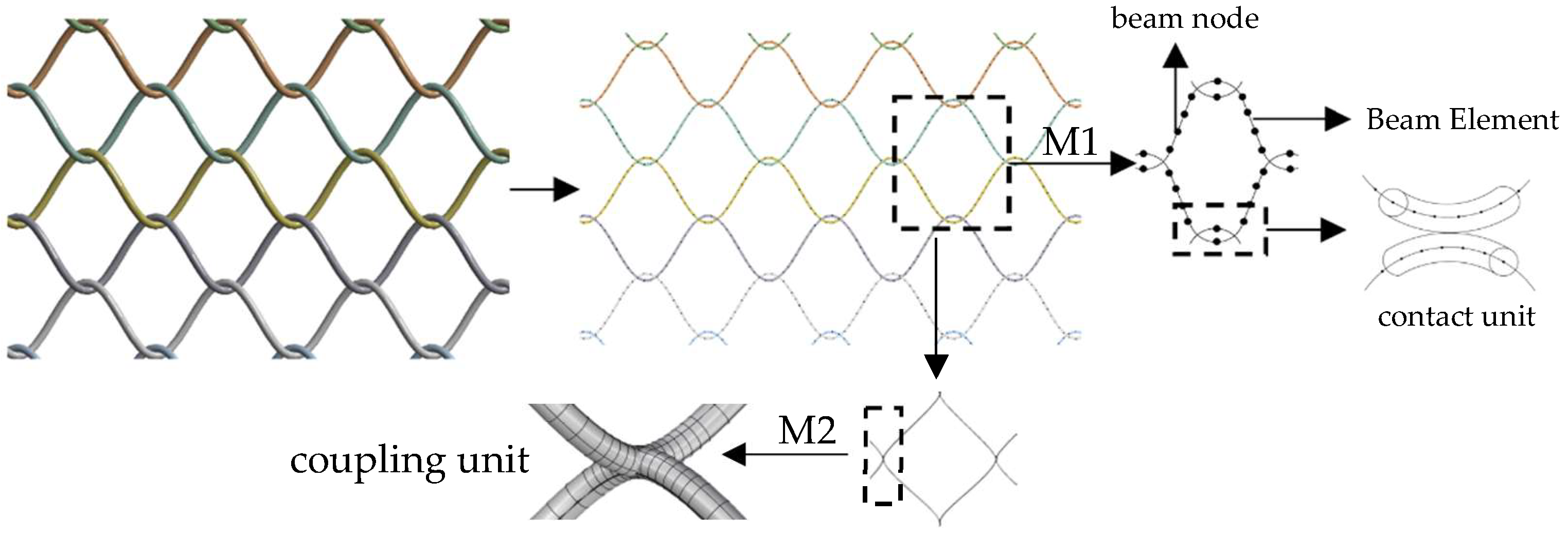
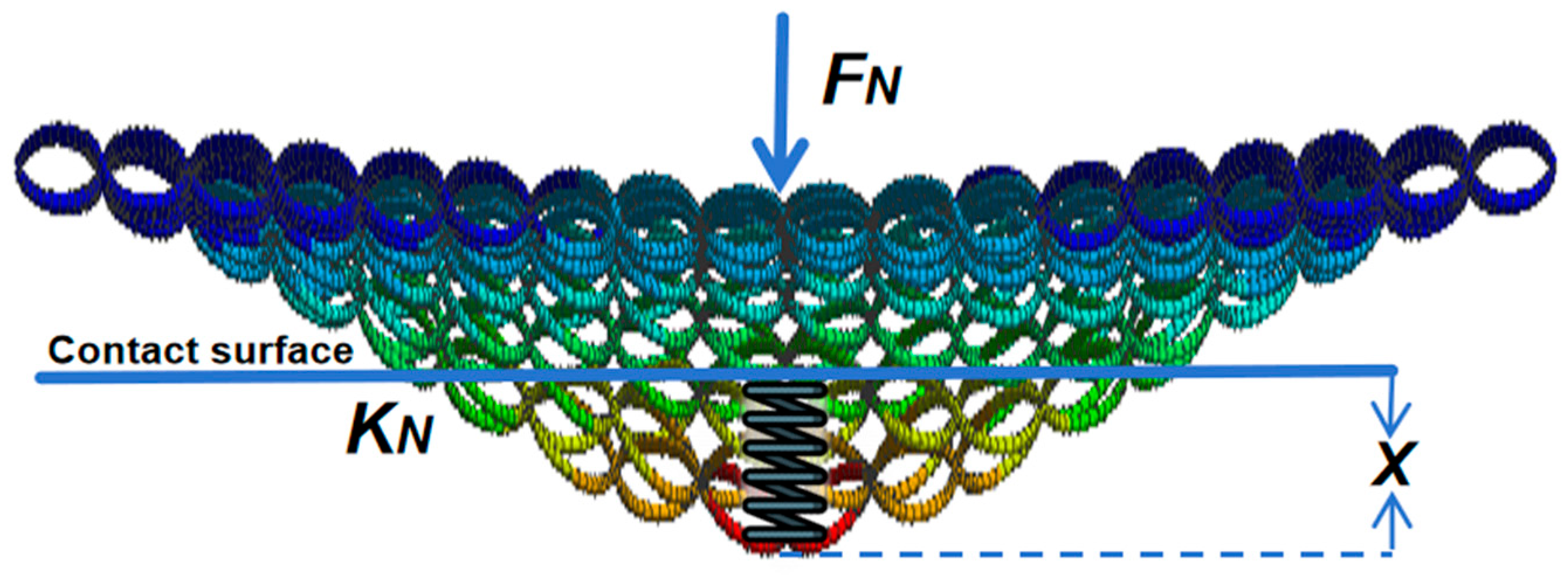


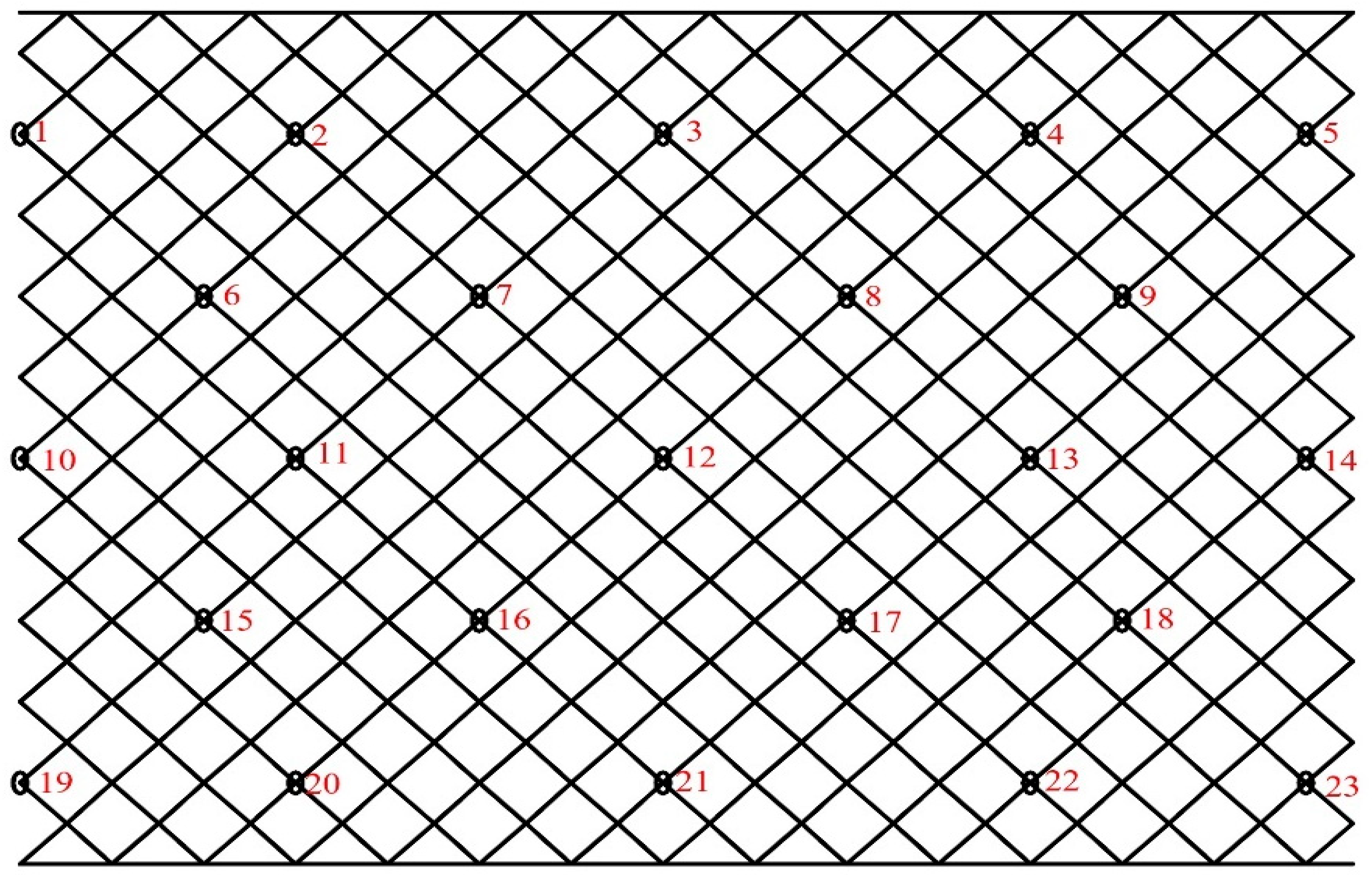
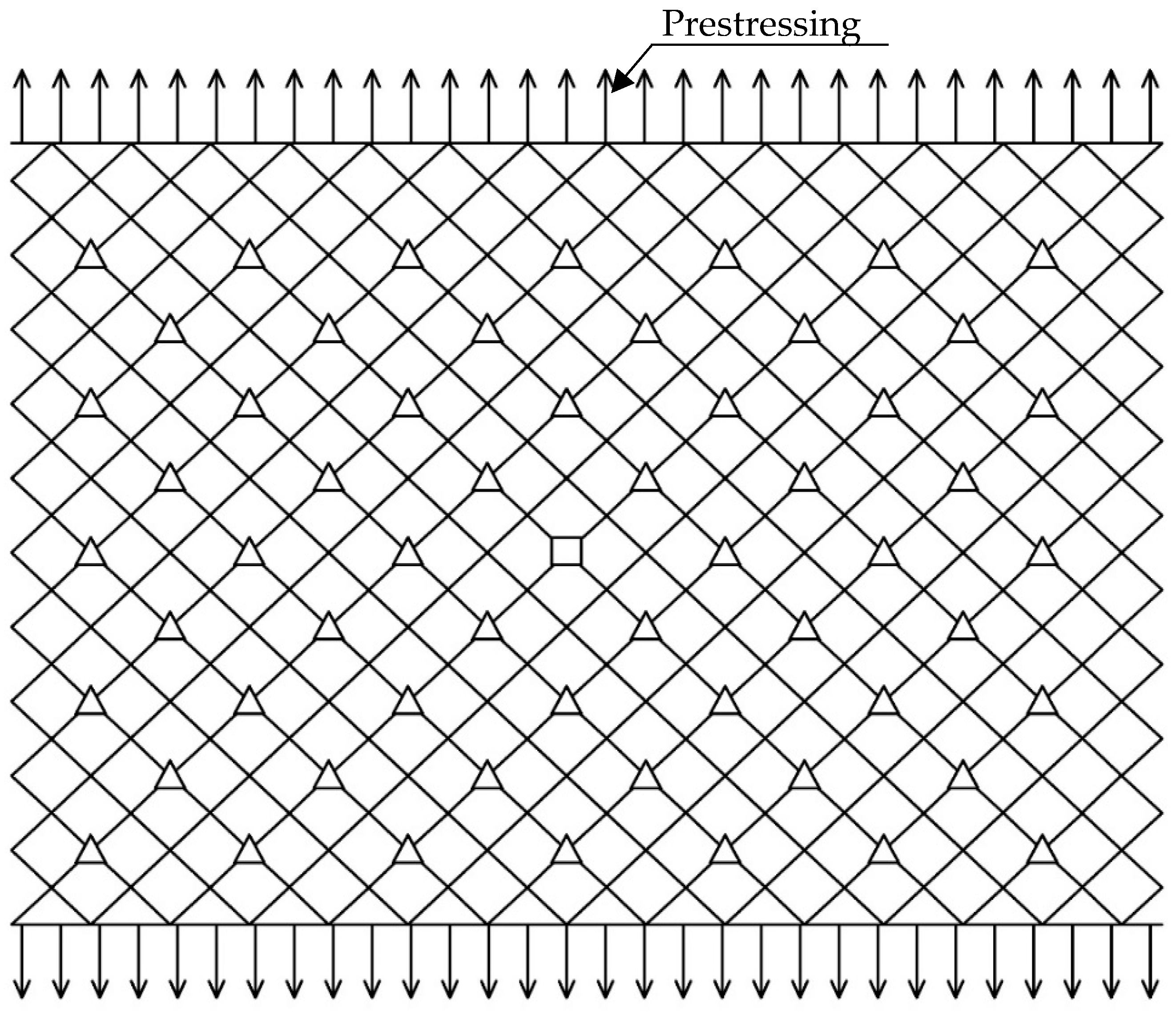

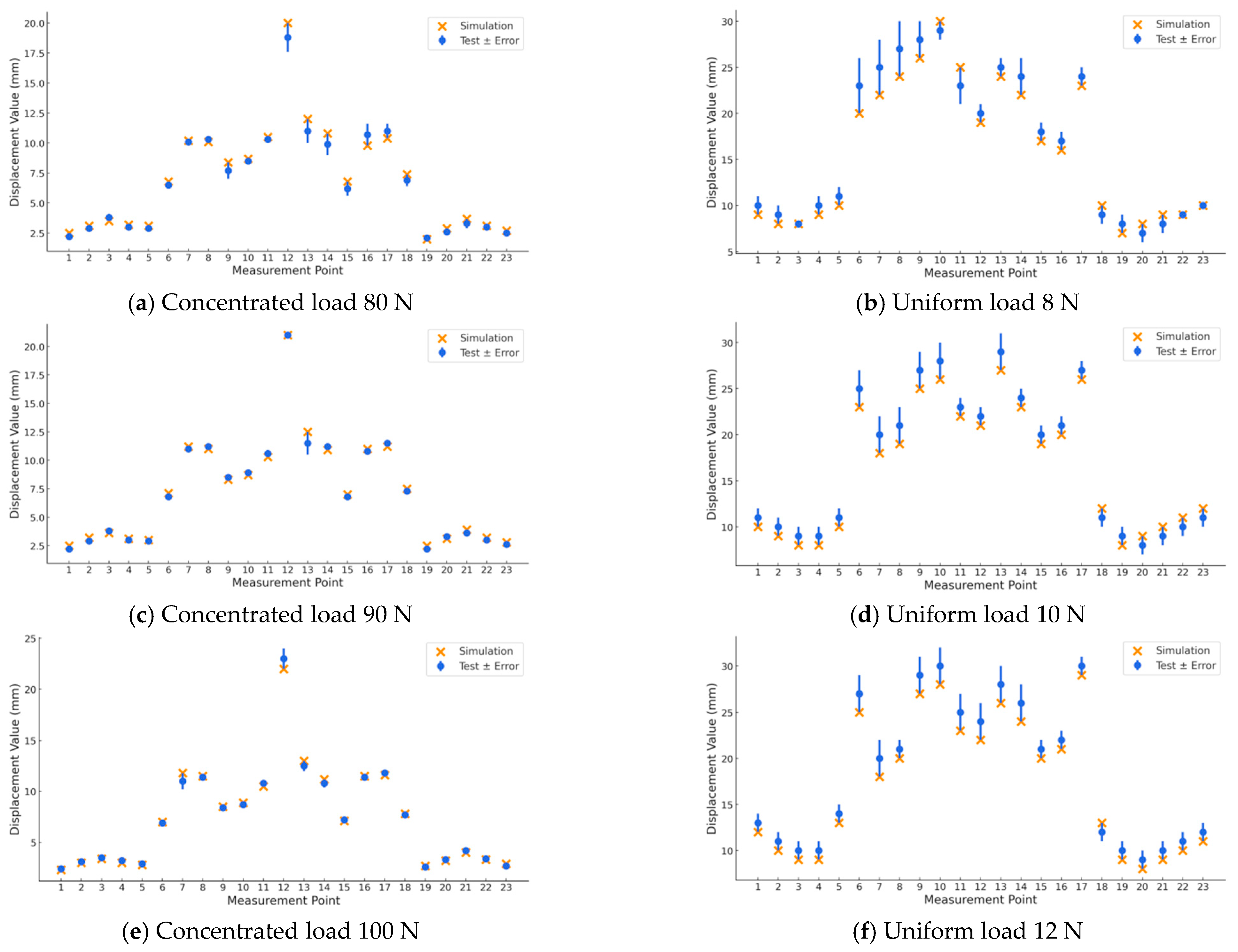

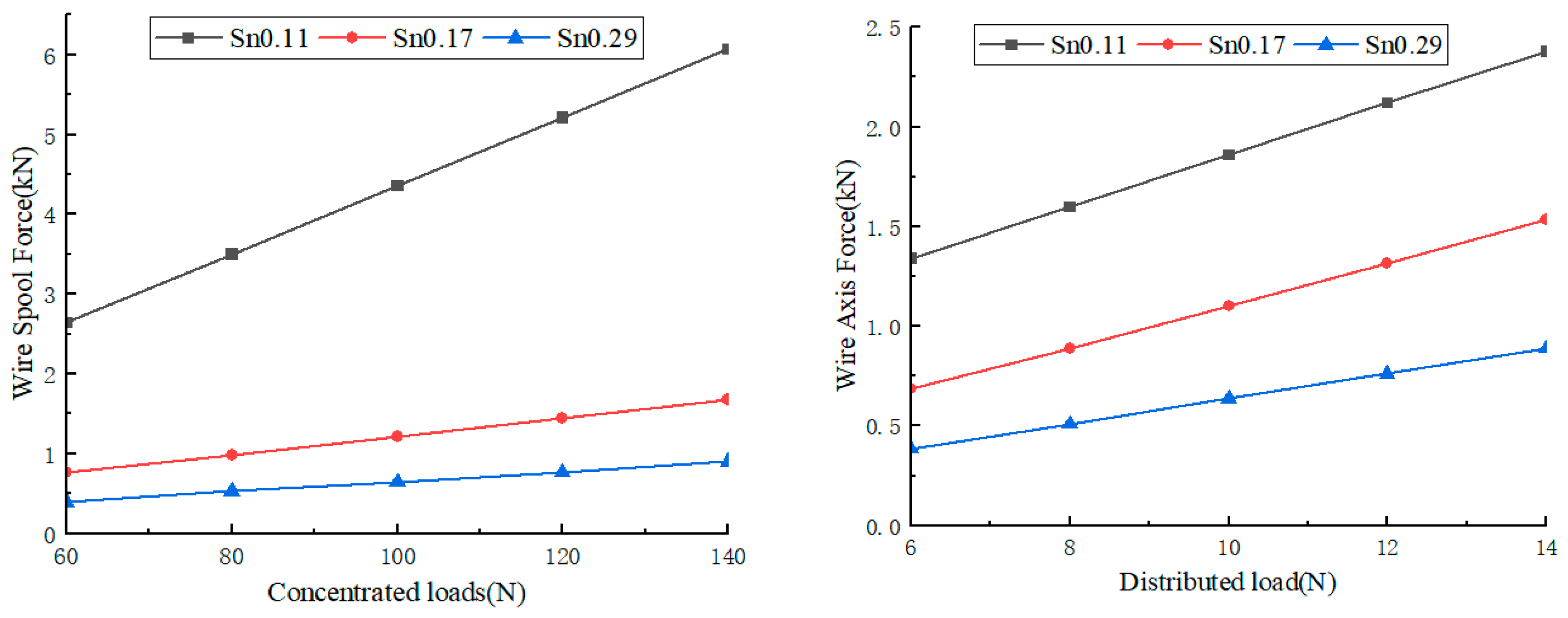


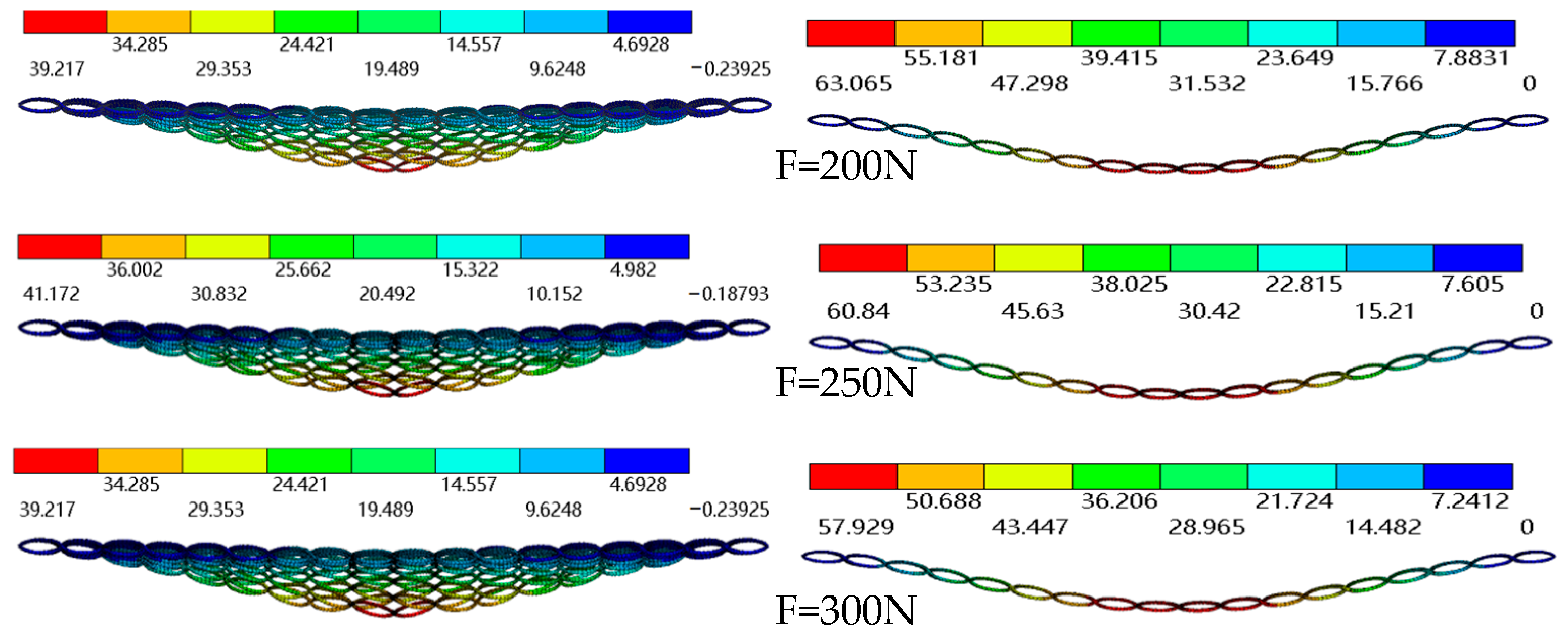
| Mesh Coat Parameters | Mesh Coat Model | ||
|---|---|---|---|
| M2.5-25 | M2.5-30 | M3.5-50 | |
| Mesh size (mm) | 25 | 30 | 50 |
| Wire diameter (mm) | 2.5 | 2.5 | 3.5 |
| Modulus of elasticity E (GPa) | 102 | 109 | 119 |
| Poisson’s ratio | 0.35 | 0.32 | 0.36 |
| Densities ρ (kg/m3) | 8300 | 8400 | 8400 |
| Operating Condition | Resolved Value (mm) | M1 (mm) | Errors (%) | M2 (mm) | Errors (%) |
|---|---|---|---|---|---|
| M2.5-25 | 37.8 | 36.82 | −2.59 | 37.49 | −1.66 |
| M2.5-30 | 35.37 | 33.6 | −5 | 34.8 | −1.61 |
| M3.5-50 | 8.66 | 9.24 | 6.7 | 9.13 | 5.43 |
| Sn | d/mm Net Diameter | l/mm Mesh Size |
|---|---|---|
| 0.11 | 2.5 | 45 |
| 0.17 | 3.2 | 35 |
| 0.29 | 4.0 | 25 |
| Magnitude of Change | |||
|---|---|---|---|
| Concentrated Loads | Distributed Load | ||
| Initial pretension 200 N | 53.07% | 68.68% | |
| 86.38% | 74.72% | ||
| Compactness Sn = 0.11 | 3.48% | 3.52% | |
| 8.07% | 8.14% | ||
| Average Magnitude of Change | Average Magnitude of Change | ||||
|---|---|---|---|---|---|
| Concentrated loads | 60 N | 71.20% | 71.89% | 84.98% | 85.03% |
| 80 N | 71.70% | 84.75% | |||
| 100 N | 72.00% | 85.11% | |||
| 120 N | 72.20% | 85.14% | |||
| 140 N | 72.35% | 85.17% | |||
| Distributed load | 6 N | 48.94% | 41.55% | 71.22% | 66.34% |
| 8 N | 44.59% | 68.04% | |||
| 10 N | 40.76% | 65.75% | |||
| 12 N | 37.86% | 64.02% | |||
| 14 N | 35.60% | 62.67% | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Xu, W.; Chen, C.; Wang, D.; Wang, L. Influence of Structural Parameters on Deformation Behavior of Metal Rhombic Chain Mesh. Appl. Sci. 2025, 15, 4144. https://doi.org/10.3390/app15084144
Yang J, Xu W, Chen C, Wang D, Wang L. Influence of Structural Parameters on Deformation Behavior of Metal Rhombic Chain Mesh. Applied Sciences. 2025; 15(8):4144. https://doi.org/10.3390/app15084144
Chicago/Turabian StyleYang, Jie, Weidong Xu, Changping Chen, Dongya Wang, and Litong Wang. 2025. "Influence of Structural Parameters on Deformation Behavior of Metal Rhombic Chain Mesh" Applied Sciences 15, no. 8: 4144. https://doi.org/10.3390/app15084144
APA StyleYang, J., Xu, W., Chen, C., Wang, D., & Wang, L. (2025). Influence of Structural Parameters on Deformation Behavior of Metal Rhombic Chain Mesh. Applied Sciences, 15(8), 4144. https://doi.org/10.3390/app15084144





