Enhanced Conditional Ground Motion Selection Model Considering Spectral Compatibility and Variability of Three Components for Multi-Directional Analysis
Abstract
1. Introduction
Research Significance
2. Ground Motion Record Selection
2.1. Spectral Matching-Based Record Selection
2.2. Code-Based Record Selection
2.3. Record Selection Based on Scenario-Based Spectrum
2.4. Two- and Three-Directional Ground Motion Selection Considering the Vertical Component
3. Problem Definition and Solution Model
3.1. Definition of the Problem
3.2. Stochastic Solution Model
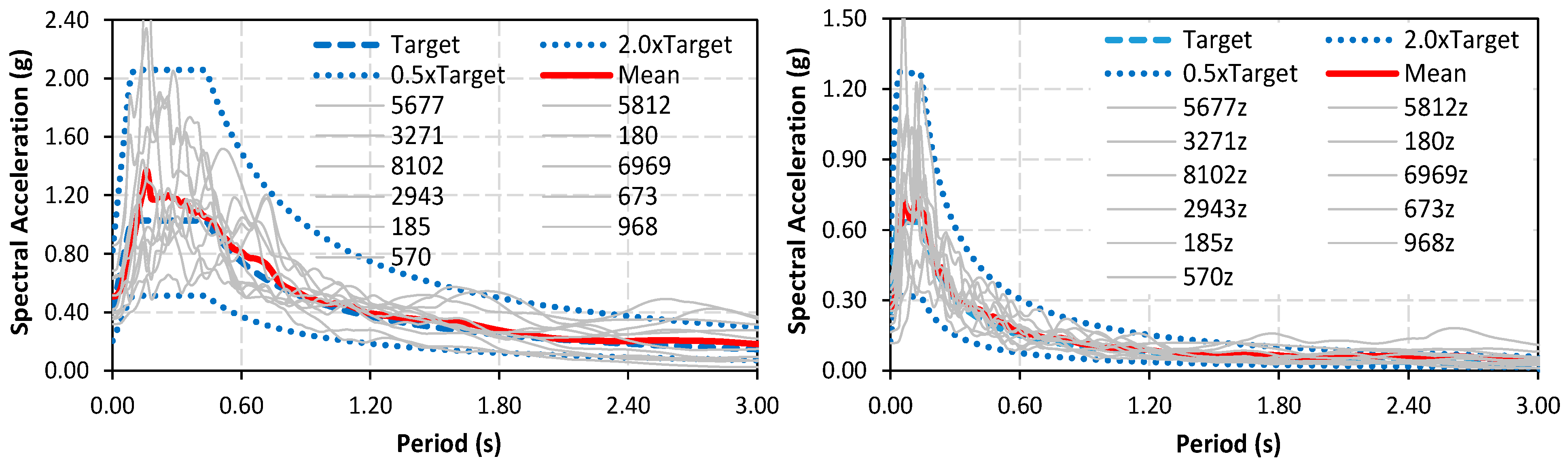
4. Application of Record Selection Model
- A single-scale value was used for all components of GMs.
- Vertical components were selected with horizontal counterparts of the same GM record simultaneously.
- The lower bound for the ratio of the mean spectrum to target spectrum was defined as 1.00, 0.90, and 0.8 for the TBEC, EC8, and scenario-based selections, respectively. The upper bound of this ratio was taken as equal to 1.25. These constraints were applied to both vertical and horizontal GM components.
- Different period ranges for the fitness of horizontal spectral shapes were set: they were set as between 0.1 s and 1.5 s, and 0.2 s and 2.0 s, for T = 1.0 s, and 0.05 s and 0.75 s, and 0.1 s and 1.0 s, for T = 0.5 s for the TBEC and EC8, respectively. For scenario-based selection, the period range was taken as between 0.2 s and 2.0 s. The period range between the mean spectrum and target spectrum for the vertical direction was between 0.1 s and 1.5 s for both seismic code- and scenario-based selections [31,65].
- GMs were selected separately for two- and three-dimensional analysis. Only one orientation of the same GM record (X or Y) in the horizontal direction was enforced in sets for two-dimensional analysis.
- The number of GMs was taken as equal to 7, 11, and 11 for EC8, TBEC, and scenario-based selections.
- Optimization algorithm parameters such as HMS, HMCR, PAR, and bw were taken as equal to 30, 0.9, 0.3, and 0.01, respectively. The maximum iteration was set to 100,000 [23].
5. Summary and Conclusions
- Practitioners can develop customized catalogues by considering the regional seismic characteristics of their site of interest to obtain tailored ground motion records for their analysis.
- The MSE parameter is used to assess the quality of matching between the selected GMs and target spectra. If the MSE values are higher, the compatibility between the selected GMs and target spectra decreases. The scatter in the spectra will generally produce more scatter in the responses, making it difficult to obtain reliable response statistics. The results demonstrated that it is possible to obtain quite low MSE values with the proposed model.
- If desired, the model can incorporate period-dependent spectral variability in both horizontal and vertical components of the selected GM records, irrespective of the target spectral shapes.
- The proposed model is capable of defining limits for record-to-record spectral variability in code-based selection, which may be advantageous for practicing engineers seeking a more comprehensive understanding of structural behavior.
- A single-scale value was used for horizontal and vertical components of a selected GM record to maintain the relative amplitude and phasing of the real GM components.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sextos, A.G. Selection of Ground Motions for Response History Analysis. In Encyclopedia of Earthquake Engineering; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–10. [Google Scholar]
- Han, S.W.; Seok, S.W. Efficient Procedure for Selecting and Scaling Ground Motions for Response History Analysis. J. Struct. Eng. 2014, 140, 06013004. [Google Scholar] [CrossRef]
- Strukar, K.; Sipos, T.K.; Jelec, M.; Hadzima-Nyarko, M. Efficient Damage Assessment for Selected Earthquake Records Based on Spectral Matching. Earthq. Struct. 2019, 17, 271–282. [Google Scholar] [CrossRef]
- Iervolino, I.; Galasso, C.; Cosenza, E. REXEL: Computer Aided Record Selection for Code-Based Seismic Structural Analysis. Bull. Earthq. Eng. 2010, 8, 339–362. [Google Scholar] [CrossRef]
- Palanci, M.; Demir, A.; Kayhan, A.H. The Investigation of Displacement Demands of Single Degree of Freedom Models Using Real Earthquake Records Compatible with TBEC-2018. Pamukkale Univ. J. Eng. Sci. 2021, 27, 251–263. [Google Scholar] [CrossRef]
- Demir, A.; Palanci, M.; Kayhan, A.H. Evaluation of Supplementary Constraints on Dispersion of EDPs Using Real Ground Motion Record Sets. Arab. J. Sci. Eng. 2020, 45, 8379–8401. [Google Scholar] [CrossRef]
- Xu, G.; Guo, T.; Li, A.; Zhou, T.; Shuang, C. Seismic Performance of Steel Frame Structures with Novel Self-Centering Beams: Shaking-Table Tests and Numerical Analysis. J. Struct. Eng. 2025, 151, 04025002. [Google Scholar] [CrossRef]
- Baker, J.W. Conditional Mean Spectrum: Tool for Ground-Motion Selection. J. Struct. Eng. 2011, 137, 322–331. [Google Scholar] [CrossRef]
- Datta, T.K. Seismic Analysis of Structures; Wiley: Hoboken, NJ, USA, 2010; ISBN 9780470824610. [Google Scholar]
- Akkar, S.; Sandıkkaya, M.A.; Bommer, J.J. Empirical Ground-Motion Models for Point- and Extended-Source Crustal Earthquake Scenarios in Europe and the Middle East. Bull. Earthq. Eng. 2014, 12, 359–387. [Google Scholar] [CrossRef]
- Katsanos, E.I.; Sextos, A.G.; Manolis, G.D. Selection of Earthquake Ground Motion Records: A State-of-the-Art Review from a Structural Engineering Perspective. Soil Dyn. Earthq. Eng. 2010, 30, 157–169. [Google Scholar] [CrossRef]
- Caicedo, D.; Karimzadeh, S.; Bernardo, V.; Lourenço, P.B. Selection and Scaling Approaches of Earthquake Time-Series for Structural Engineering Applications: A State-of-the-Art Review. Arch. Comput. Methods Eng. 2024, 31, 1475–1505. [Google Scholar] [CrossRef]
- EN 1998-1:2004; Eurocode-8 Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 2004; ISBN 0580458725.
- TBEC; Turkish Building Earthquake Code. Disaster and Emergency Management Presidency: Ankara, Turkiye, 2018.
- ASCE/SEI 7–16; Minimum Design Loads and Associated Criteria for Buildings and Other Structures. American Society of Civil Engineers (ASCE): Reston, VA, USA, 2017; ISBN 9780784479964.
- Huang, Y.-N.; Whittaker, A.S.; Luco, N.; Hamburger, R.O. Scaling Earthquake Ground Motions for Performance-Based Assessment of Buildings. J. Struct. Eng. 2011, 137, 311–321. [Google Scholar] [CrossRef]
- Shakeri, K.; Khansoltani, E.; Pessiki, S. Ground Motion Scaling for Seismic Response Analysis by Considering Inelastic Response and Contribution of the Higher Modes. Soil Dyn. Earthq. Eng. 2018, 110, 70–85. [Google Scholar] [CrossRef]
- Palanci, M.; Demir, A.; Kayhan, A.H. Quantifying the Effect of Amplitude Scaling of Real Ground Motions Based on Structural Responses of Vertically Irregular and Regular RC Frames. Structures 2023, 51, 105–123. [Google Scholar] [CrossRef]
- Demir, A.; Palanci, M.; Kayhan, A.H. Evaluation the Effect of Amplitude Scaling of Real Ground Motions on Seismic Demands Accounting Different Structural Characteristics and Soil Classes. Bull. Earthq. Eng. 2024, 22, 365–393. [Google Scholar] [CrossRef]
- Demir, A.; Kayhan, A.H.; Palanci, M. Response- and Probability-Based Evaluation of Spectrally Matched Ground Motion Selection Strategies for Bi-Directional Dynamic Analysis of Low- to Mid-Rise RC Buildings. Structures 2023, 58, 105533. [Google Scholar] [CrossRef]
- Sextos, A.G.; Katsanos, E.I.; Manolis, G.D. EC8-Based Earthquake Record Selection Procedure Evaluation: Validation Study Based on Observed Damage of an Irregular R/C Building. Soil Dyn. Earthq. Eng. 2011, 31, 583–597. [Google Scholar] [CrossRef]
- Kohrangi, M.; Bazzurro, P.; Vamvatsikos, D. Conditional Spectrum Bidirectional Record Selection for Risk Assessment of 3D Structures Using Scalar and Vector IMs. Earthq. Eng. Struct. Dyn. 2019, 48, 1066–1082. [Google Scholar] [CrossRef]
- Kayhan, A.H.; Demir, A.; Palanci, M. Multi-Functional Solution Model for Spectrum Compatible Ground Motion Record Selection Using Stochastic Harmony Search Algorithm. Bull. Earthq. Eng. 2022, 20, 6407–6440. [Google Scholar] [CrossRef]
- Kayhan, A.H. Scaled and Unscaled Ground Motion Sets for Uni-Directional and Bi-Directional Dynamic Analysis. Earthq. Struct. 2016, 10, 563–588. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, W. Influence of Structural Parameters on the Vertical Pounding between Girder and Pier in Unequal-Span Girder Bridges under near-Fault Vertical Ground Motions. Sci. Rep. 2025, 15, 9740. [Google Scholar] [CrossRef]
- Yang, H.; Yin, X.; Hao, H.; Bi, K. Theoretical Investigation of Bridge Seismic Responses with Pounding under Near-Fault Vertical Ground Motions. Adv. Struct. Eng. 2015, 18, 453–468. [Google Scholar] [CrossRef]
- Ryan, K.L.; Dao, N.D. Influence of Vertical Ground Shaking on Horizontal Response of Seismically Isolated Buildings with Friction Bearings. J. Struct. Eng. 2016, 142, 04015089. [Google Scholar] [CrossRef]
- Manoukas, G.E. Structural Modelling of Reinforced Concrete Planar Frames under Vertical Ground Motion. Asian J. Civ. Eng. 2021, 22, 1563–1580. [Google Scholar] [CrossRef]
- Manoukas, G.; Tsiggelis, V. The Influence of Vertical Ground Motion on the Design of Common R/C Frames. Appl. Sci. 2025, 15, 1711. [Google Scholar] [CrossRef]
- Gremer, N.; Adam, C.; Medina, R.A.; Moschen, L. Vertical Peak Floor Accelerations of Elastic Moment-Resisting Steel Frames. Bull. Earthq. Eng. 2019, 17, 3233–3254. [Google Scholar] [CrossRef]
- ALMahdi, F.; Fahjan, Y.; Doğangün, A. Scaling of Vertical Component of Seismic Ground Motion. Alex. Eng. J. 2020, 59, 3827–3845. [Google Scholar] [CrossRef]
- Tsalouchidis, K.T.; Moschen, L.; Adam, C. Efficient Selection of up to Three-Component Ground Excitation Sets for Earthquake Engineering Applications. Soil Dyn. Earthq. Eng. 2021, 148, 106734. [Google Scholar] [CrossRef]
- Kumar, A.; Choudhury, D.; Katzenbach, R. Effect of Earthquake on Combined Pile–Raft Foundation. Int. J. Geomech. 2016, 16, 04016013. [Google Scholar] [CrossRef]
- Løkke, A.; Chopra, A.K. Direct Finite Element Method for Nonlinear Analysis of Semi-unbounded Dam–Water–Foundation Rock Systems. Earthq. Eng. Struct. Dyn. 2017, 46, 1267–1285. [Google Scholar] [CrossRef]
- Ruggieri, S.; Uva, G. Extending the Concepts of Response Spectrum Analysis to Nonlinear Static Analysis: Does It Make Sense? Innov. Infrastruct. Solut. 2024, 9, 235. [Google Scholar] [CrossRef]
- Ruggieri, S.; Vukobratović, V. The Influence of Torsion on Acceleration Demands in Low-Rise RC Buildings. Bull. Earthq. Eng. 2024, 22, 2433–2468. [Google Scholar] [CrossRef]
- Araújo, M.; Macedo, L.; Marques, M.; Castro, J.M. Code-Based Record Selection Methods for Seismic Performance Assessment of Buildings. Earthq. Eng. Struct. Dyn. 2016, 45, 129–148. [Google Scholar] [CrossRef]
- Kohrangi, M.; Bazzurro, P.; Vamvatsikos, D.; Spillatura, A. Conditional Spectrum-Based Ground Motion Record Selection Using Average Spectral Acceleration. Earthq. Eng. Struct. Dyn. 2017, 46, 1667–1685. [Google Scholar] [CrossRef]
- Katsanos, E.I.; Sextos, A.G. Structure-Specific Selection of Earthquake Ground Motions for the Reliable Design and Assessment of Structures. Bull. Earthq. Eng. 2018, 16, 583–611. [Google Scholar] [CrossRef]
- Iervolino, I. Assessing Uncertainty in Estimation of Seismic Response for PBEE. Earthq. Eng. Struct. Dyn. 2017, 46, 1711–1723. [Google Scholar] [CrossRef]
- Baltzopoulos, G.; Baraschino, R.; Giorgio, M.; Iervolino, I. Why Determining the Number of Code Spectrum-Matched Records Based on Usual Statistics Is an Ill-Posed Problem. In Proceedings of the 17th World Conference on Earthquake Engineering, Sendai, Japan, 13–18 September 2020. [Google Scholar]
- Demir, A.; Palanci, M.; Kayhan, A.H. Probabilistic Assessment for Spectrally Matched Real Ground Motion Records on Distinct Soil Profiles by Simulation of SDOF Systems. Earthq. Struct. 2021, 21, 395–411. [Google Scholar] [CrossRef]
- Hancock, J.; Bommer, J.J.; Stafford, P.J. Numbers of Scaled and Matched Accelerograms Required for Inelastic Dynamic Analyses. Earthq. Eng. Struct. Dyn. 2008, 37, 1585–1607. [Google Scholar] [CrossRef]
- Kayhan, A.H.; Demir, A. Statistical Evaluation of Drift Demands of Rc Frames Using Code-Compatible Real Ground Motion Record Sets. Struct. Eng. Mech. 2016, 60, 953–977. [Google Scholar] [CrossRef]
- Jayaram, N.; Lin, T.; Baker, J.W. A Computationally Efficient Ground-Motion Selection Algorithm for Matching a Target Response Spectrum Mean and Variance. Earthq. Spectra 2011, 27, 797–815. [Google Scholar] [CrossRef]
- Baker, J.W.; Lee, C. An Improved Algorithm for Selecting Ground Motions to Match a Conditional Spectrum. J. Earthq. Eng. 2018, 22, 708–723. [Google Scholar] [CrossRef]
- Ha, S.J.; Han, S.W. An Efficient Method for Selecting and Scaling Ground Motions Matching Target Response Spectrum Mean and Variance. Earthq. Eng. Struct. Dyn. 2016, 45, 1381–1387. [Google Scholar] [CrossRef]
- Kwong, N.S.; Chopra, A.K. Selecting, Scaling, and Orienting Three Components of Ground Motions for Intensity-Based Assessments at Far-Field Sites. Earthq. Spectra 2020, 36, 1013–1037. [Google Scholar] [CrossRef]
- Akhani, M.; Alidadi, N.; Pezeshk, S. Application of Metaheuristic Algorithms in Ground Motion Selection and Scaling for Time History Analysis of Structures. J. Struct. Eng. 2024, 150, 04024094. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A New Heuristic Optimization Algorithm: Harmony Search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Ye, K.; Chen, Z.; Zhu, H. Proposed Strategy for the Application of the Modified Harmony Search Algorithm to Code-Based Selection and Scaling of Ground Motions. J. Comput. Civ. Eng. 2014, 28, 04014019. [Google Scholar] [CrossRef]
- Macedo, L.; Castro, J.M. SelEQ: An Advanced Ground Motion Record Selection and Scaling Framework. Adv. Eng. Softw. 2017, 114, 32–47. [Google Scholar] [CrossRef]
- Moschen, L.; Medina, R.A.; Adam, C. A Ground Motion Record Selection Approach Based on Multiobjective Optimization. J. Earthq. Eng. 2019, 23, 669–687. [Google Scholar] [CrossRef]
- Kaveh, A.; Mahdipou Moghanni, R.; Javadi, S.M. Ground Motion Record Selection Using Multi-Objective Optimization Algorithms: A Comparative Study. Period. Polytech. Civ. Eng. 2019, 63, 812–822. [Google Scholar] [CrossRef]
- Georgioudakis, M.; Fragiadakis, M. Selection and Scaling of Ground Motions Using Multicriteria Optimization. J. Struct. Eng. 2020, 146, 04020241. [Google Scholar] [CrossRef]
- Carballo, J.E.; Cornell, C.A. Probabilistic Seismic Demand Analysis: Spectrum Matching and Design; Reliability of Marine Structures Program, Department of Civil Engineering, Stanford University: Stanford, CA, USA, 2000. [Google Scholar]
- Abrahamson, N.A. Non-Stationary Spectral Matching. Seismol. Res. Lett. 1992, 63, 30. [Google Scholar]
- Naeim, F.; Alimoradi, A.; Pezeshk, S. Selection and Scaling of Ground Motion Time Histories for Structural Design Using Genetic Algorithms. Earthq. Spectra 2004, 20, 413–426. [Google Scholar] [CrossRef]
- Iervolino, I.; Maddaloni, G.; Cosenza, E. Eurocode 8 Compliant Real Record Sets for Seismic Analysis of Structures. J. Earthq. Eng. 2008, 12, 54–90. [Google Scholar] [CrossRef]
- Ancheta, T.D.; Darragh, R.B.; Stewart, J.P.; Seyhan, E.; Silva, W.J.; Chiou, B.S.-J.; Wooddell, K.E.; Graves, R.W.; Kottke, A.R.; Boore, D.M.; et al. NGA-West2 Database. Earthq. Spectra 2014, 30, 989–1005. [Google Scholar] [CrossRef]
- Das, R.; Sharma, M.; Choudhury, D.; Gonzalez, G. A Seismic Moment Magnitude Scale. Bull. Seismol. Soc. Am. 2019, 109, 1542–1555. [Google Scholar] [CrossRef]
- Campbell, K.W.; Bozorgnia, Y. NGA-West2 Ground Motion Model for the Average Horizontal Components of PGA, PGV, and 5% Damped Linear Acceleration Response Spectra. Earthq. Spectra 2014, 30, 1087–1115. [Google Scholar] [CrossRef]
- Bozorgnia, Y.; Campbell, K.W. Vertical Ground Motion Model for PGA, PGV, and Linear Response Spectra Using the NGA-West2 Database. Earthq. Spectra 2016, 32, 979–1004. [Google Scholar] [CrossRef]
- Coello Coello, C.A. Theoretical and Numerical Constraint-Handling Techniques Used with Evolutionary Algorithms: A Survey of the State of the Art. Comput. Methods Appl. Mech. Eng. 2002, 191, 1245–1287. [Google Scholar] [CrossRef]
- Sriwastav, R.K.; Basu, D. Selection and Scaling of 3-Component Ground Motion Suite for Scenario- and Intensity-Based Assessment of Buildings and Structures. Bull. Earthq. Eng. 2023, 21, 2533–2568. [Google Scholar] [CrossRef]
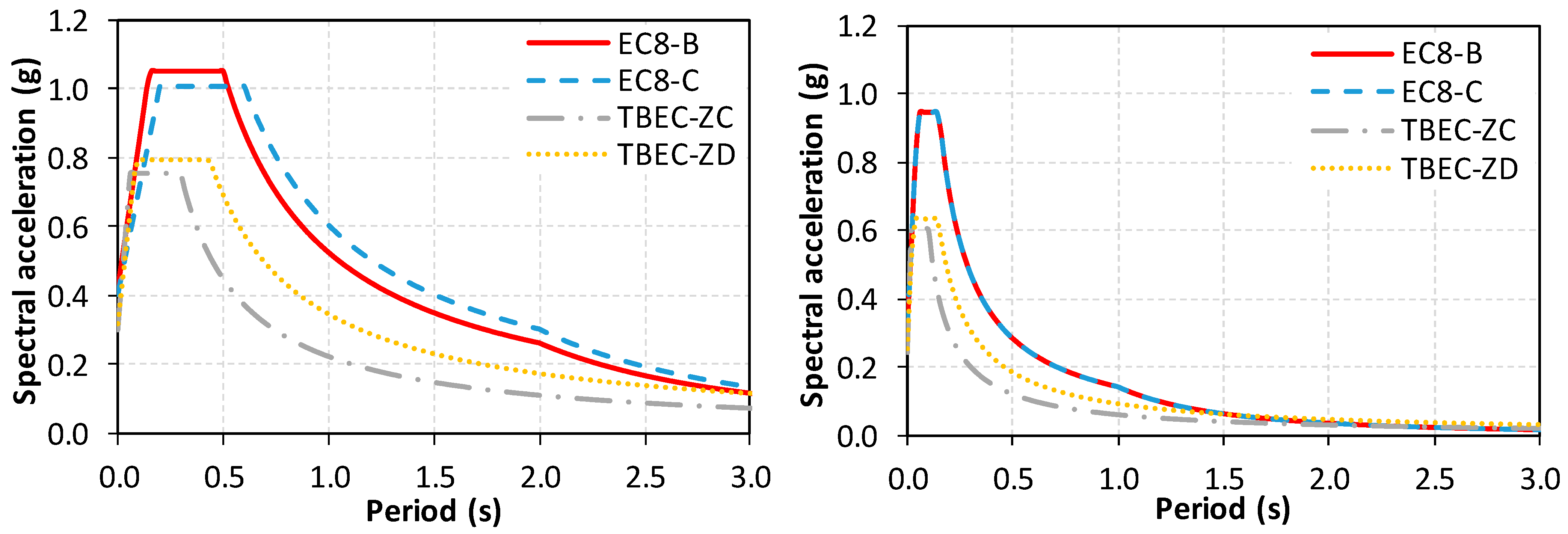
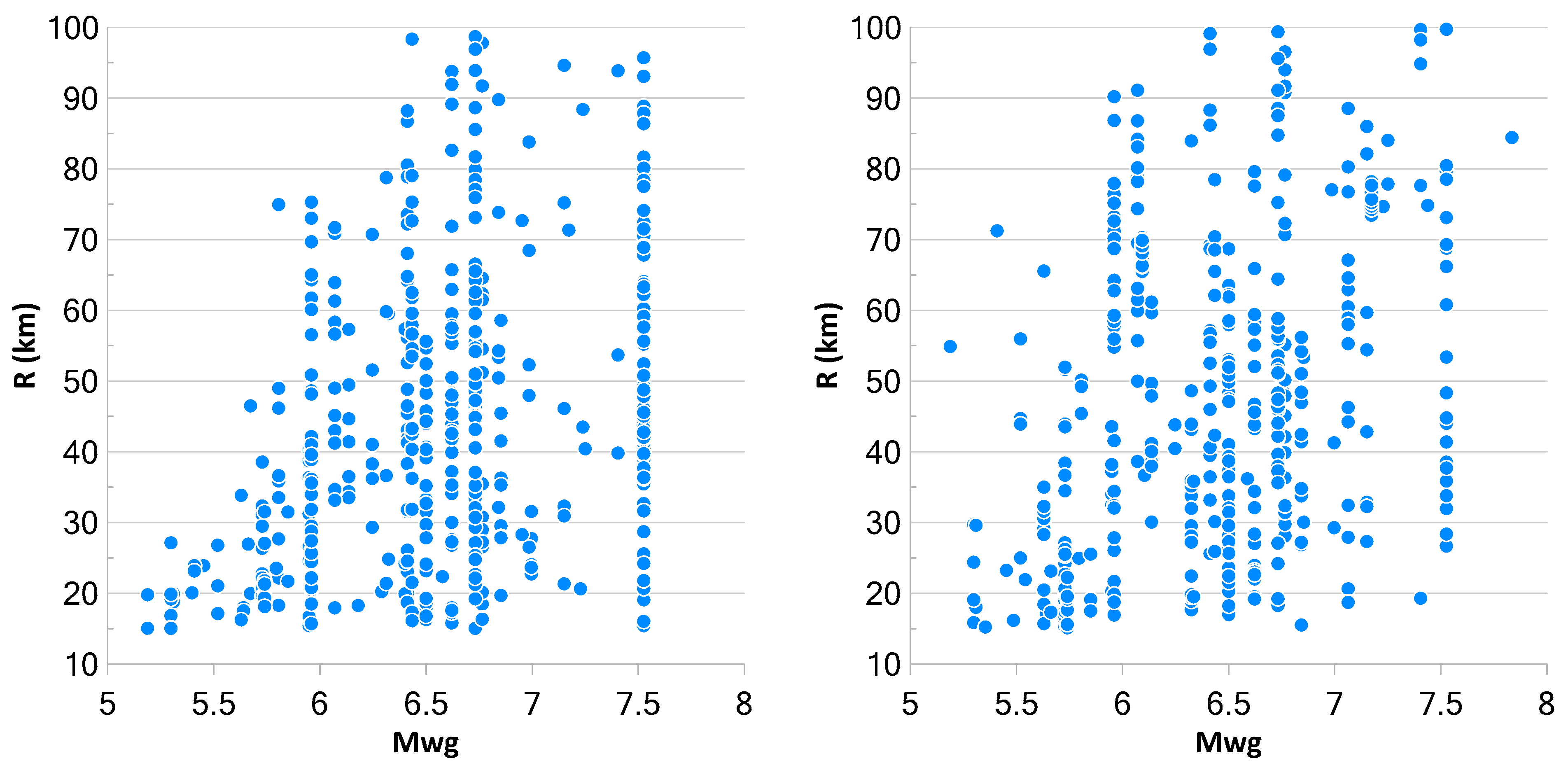
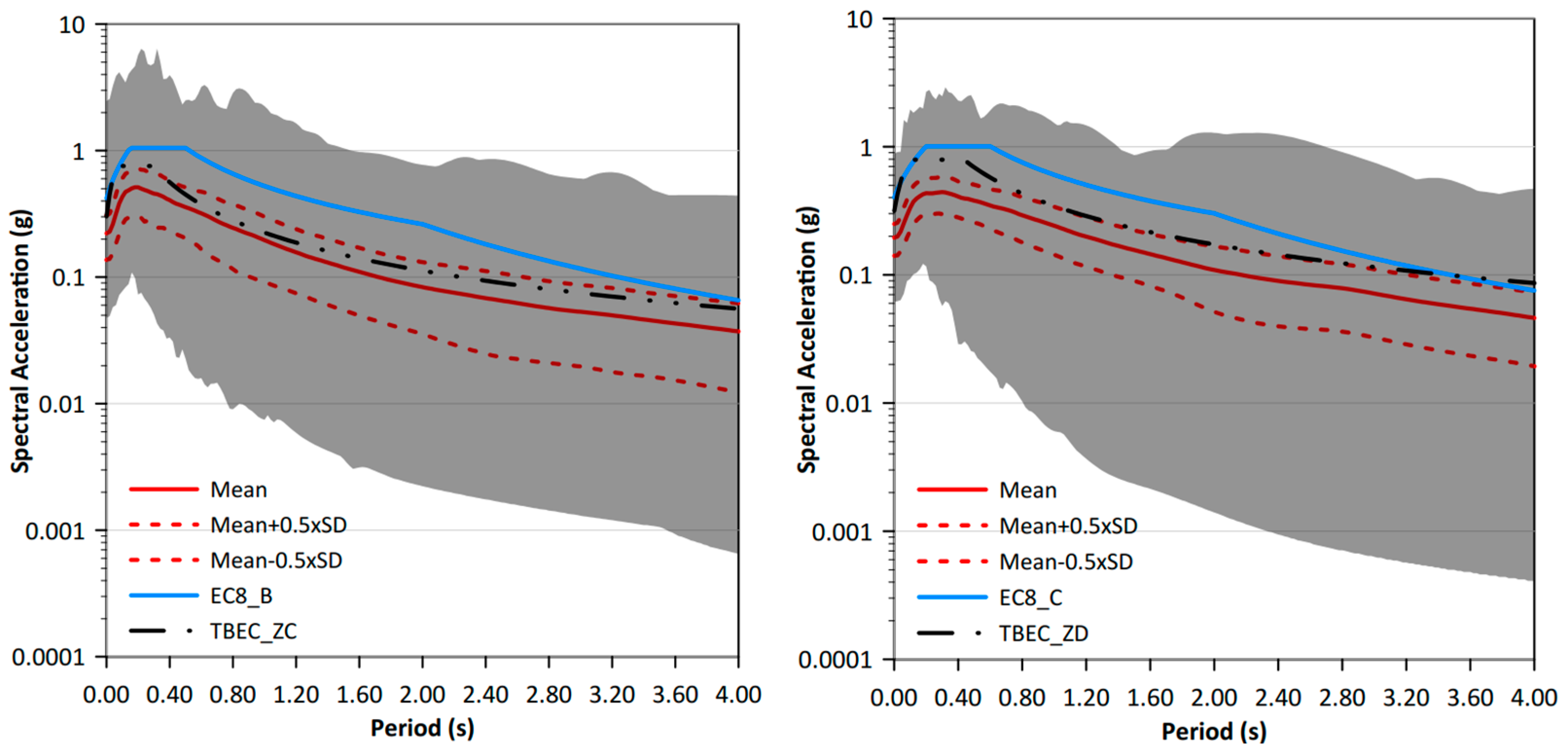

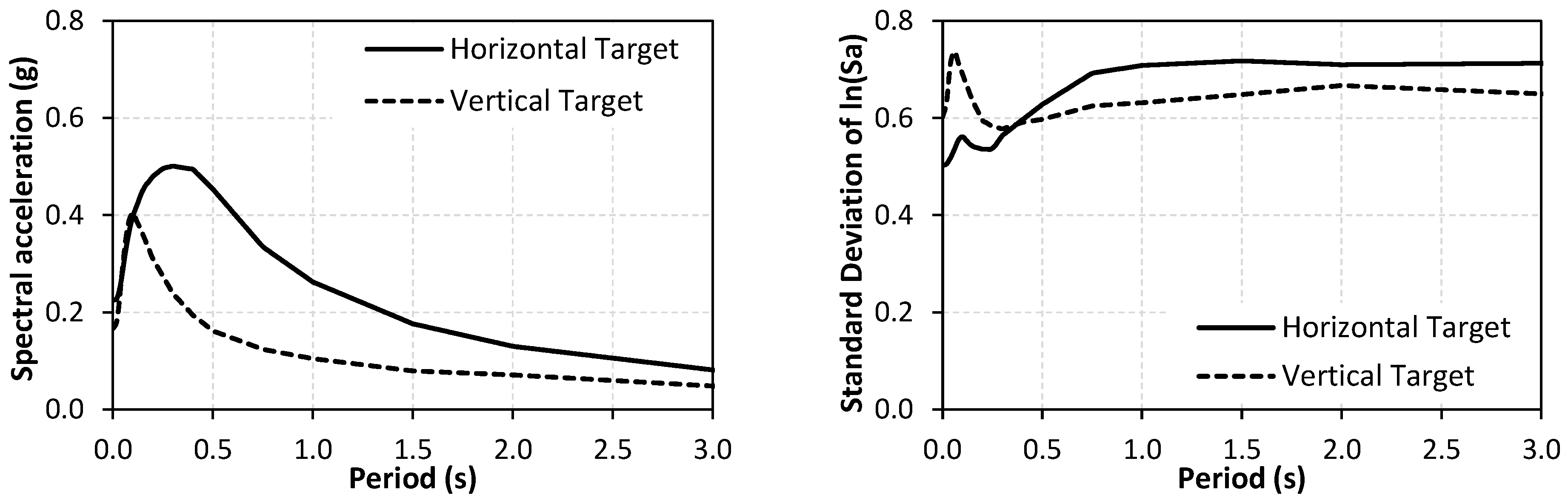



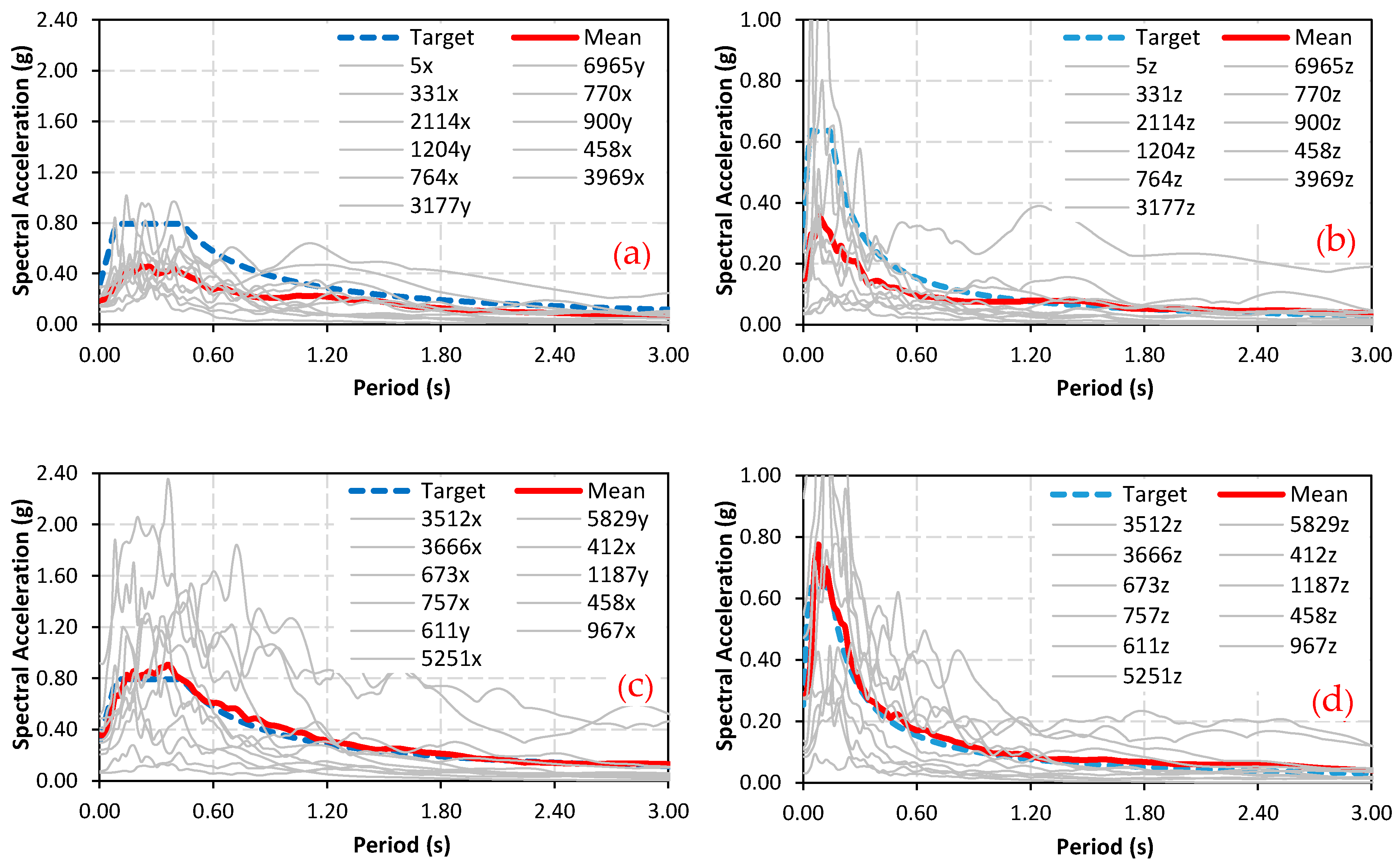
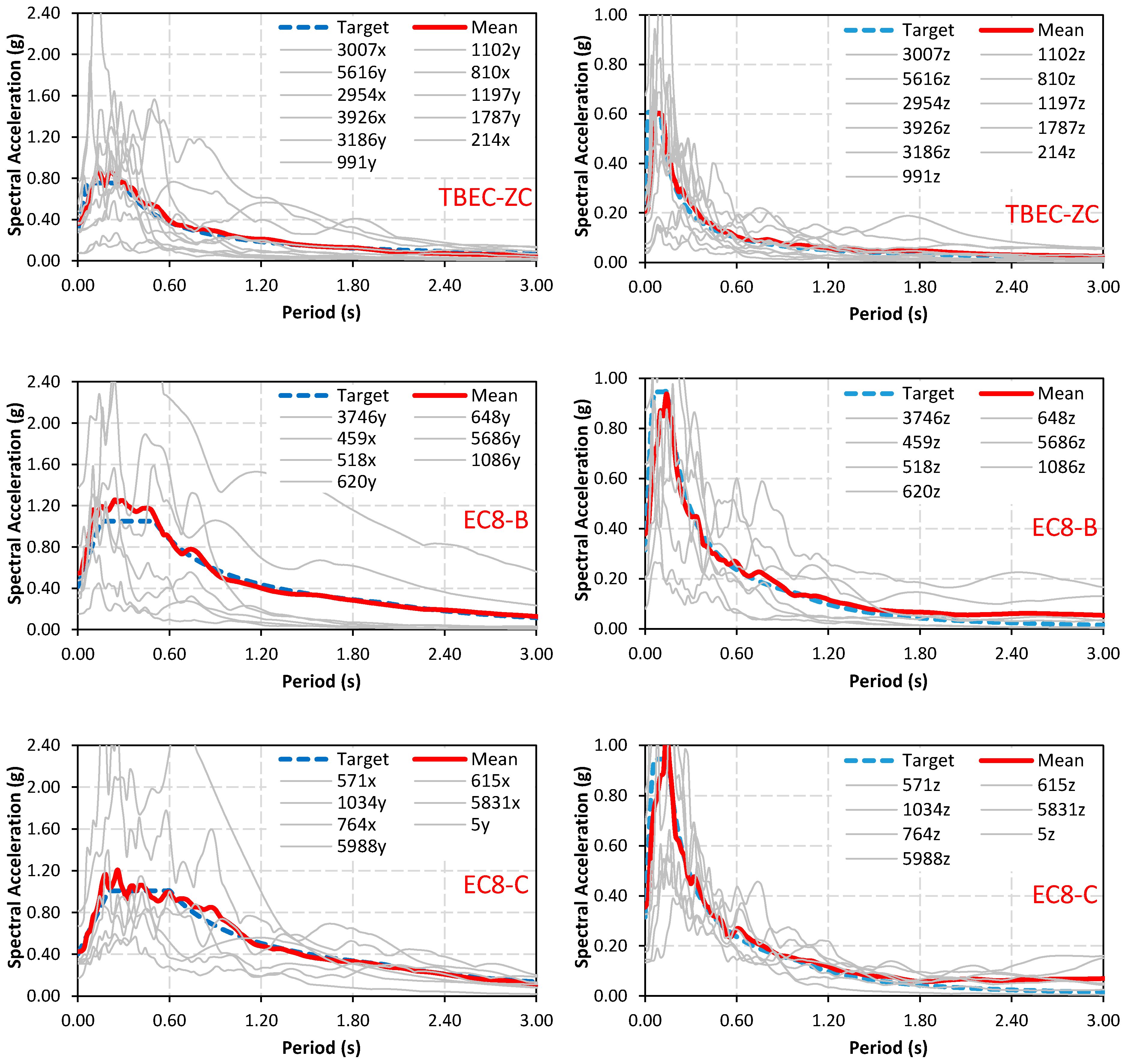
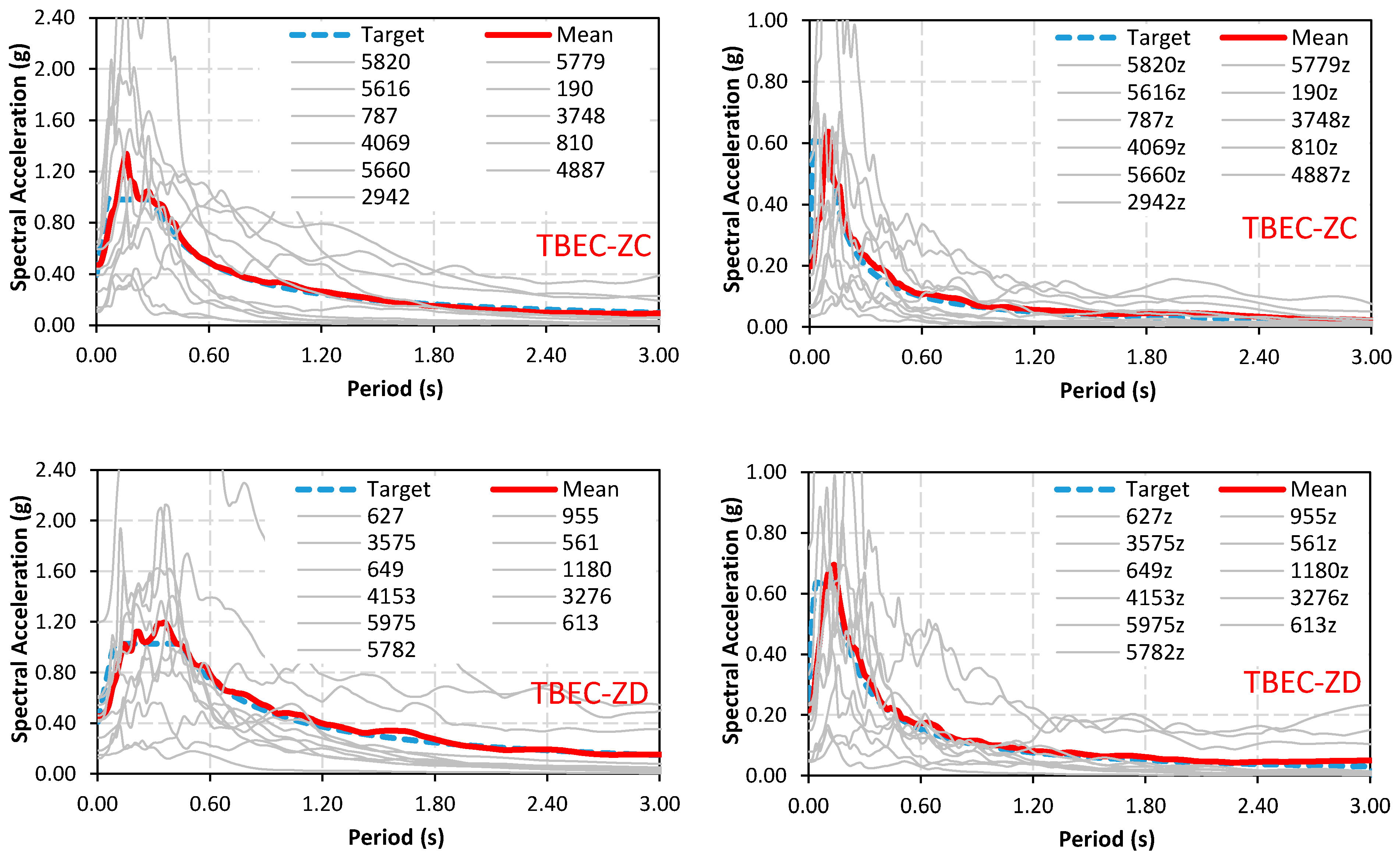

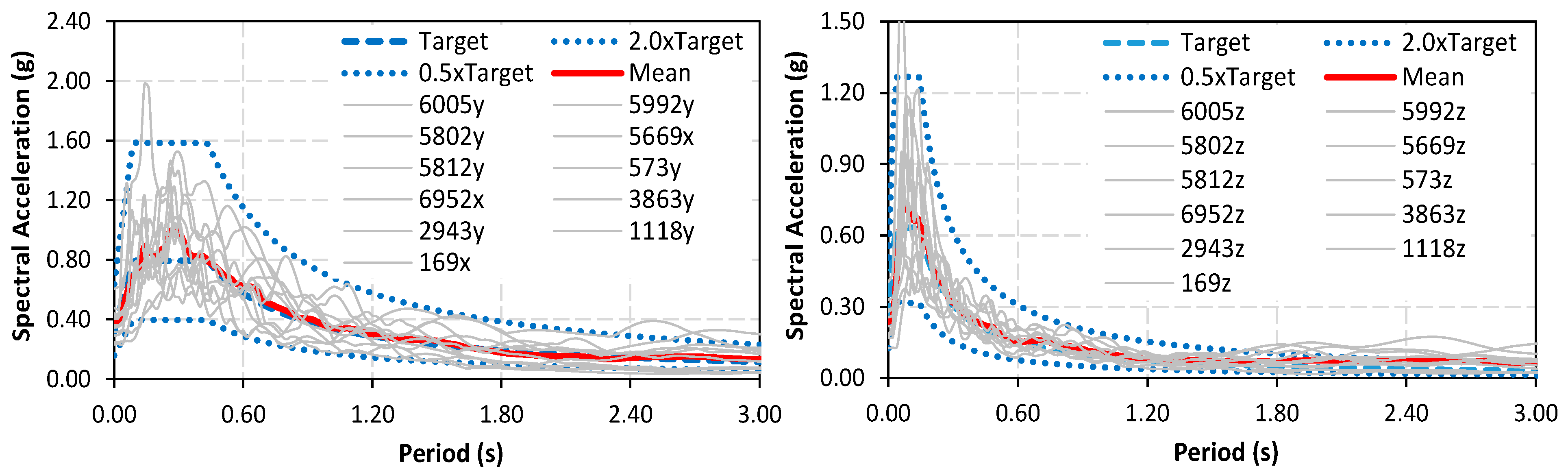

| Parameter | EC8 Horizontal | EC8 Vertical | Parameter | TBEC Horizontal | TBEC Vertical | ||||
|---|---|---|---|---|---|---|---|---|---|
| Soil B | Soil C | Soil B | Soil C | Soil ZC | Soil ZD | Soil ZC | Soil ZD | ||
| Ag | 0.35 | 0.35 | 0.35 | 0.35 | SS | 0.60 | 0.60 | 0.60 | 0.60 |
| ƞ | 1.00 | 1.00 | 1.00 | 1.00 | S1 | 0.15 | 0.15 | 0.15 | 0.15 |
| S | 1.20 | 1.15 | 0.32 | 0.32 | SDS | 0.76 | 0.79 | 0.76 | 0.79 |
| TB (s) | 0.15 | 0.20 | 0.05 | 0.05 | SD1 | 0.23 | 0.35 | 0.23 | 0.35 |
| TC (s) | 0.50 | 0.60 | 0.15 | 0.15 | TA (s) | 0.06 | 0.09 | 0.02 | 0.03 |
| TD (s) | 2.00 | 2.00 | 1.00 | 1.00 | TB (s) | 0.30 | 0.44 | 0.10 | 0.15 |
| TL (s) | 6.00 | 6.00 | 3.00 | 3.00 | |||||
| Vs,30 (m/s) | 360–760 | 180–360 | 360–760 | 180–360 | Vs,30 (m/s) | 360–760 | 180–360 | 360–760 | 180–360 |
| Seismic Codes | 1. Set | 2. Set | 3. Set | 4. Set | Mean | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Hor. | Ver. | Hor. | Ver. | Hor. | Ver. | Hor. | Ver. | Hor. | Ver. | |
| TBDY_2D_ZC | 0.143 | 0.036 | 0.162 | 0.033 | 0.054 | 0.034 | 0.178 | 0.052 | 0.134 | 0.039 |
| TBDY_3D_ZC | 0.126 | 0.036 | 0.232 | 0.033 | 0.177 | 0.048 | 0.131 | 0.069 | 0.166 | 0.046 |
| EC8_2D_ZC | 0.607 | 0.068 | 0.279 | 0.045 | 0.860 | 0.083 | 0.310 | 0.063 | 0.514 | 0.065 |
| EC8_3D_ZC | 1.566 | 0.070 | 1.417 | 0.060 | 0.843 | 0.069 | 1.113 | 0.050 | 1.235 | 0.062 |
| TBDY_2D_ZD | 0.226 | 0.053 | 0.117 | 0.018 | 0.148 | 0.013 | 0.166 | 0.020 | 0.164 | 0.026 |
| TBDY_3D_ZD | 0.262 | 0.039 | 0.062 | 0.014 | 0.193 | 0.037 | 0.298 | 0.028 | 0.204 | 0.029 |
| EC8_2D_ZD | 0.454 | 0.071 | 0.231 | 0.078 | 0.310 | 0.130 | 0.123 | 0.088 | 0.280 | 0.091 |
| EC8_3D_ZD | 0.990 | 0.047 | 0.614 | 0.059 | 1.251 | 0.127 | 1.488 | 0.069 | 1.086 | 0.076 |
| Seismic Codes | 1. Set | 2. Set | 3. Set | 4. Set | Mean | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Hor. | Ver. | Hor. | Ver. | Hor. | Ver. | Hor. | Ver. | Hor. | Ver. | |
| TBDY_2D_ZC | 0.171 | 0.057 | 0.129 | 0.042 | 0.191 | 0.077 | 0.162 | 0.058 | 0.163 | 0.059 |
| TBDY_3D_ZC | 0.364 | 0.076 | 0.245 | 0.014 | 0.257 | 0.064 | 0.197 | 0.063 | 0.266 | 0.054 |
| EC8_2D_ZC | 0.093 | 0.100 | 0.116 | 0.037 | 0.099 | 0.109 | 0.049 | 0.020 | 0.089 | 0.067 |
| EC8_3D_ZC | 1.321 | 0.163 | 1.120 | 0.160 | 0.428 | 0.109 | 1.083 | 0.138 | 0.988 | 0.142 |
| TBDY_2D_ZD | 0.183 | 0.068 | 0.142 | 0.058 | 0.127 | 0.049 | 0.188 | 0.073 | 0.160 | 0.062 |
| TBDY_3D_ZD | 0.276 | 0.138 | 0.623 | 0.106 | 0.295 | 0.072 | 0.438 | 0.069 | 0.408 | 0.096 |
| EC8_2D_ZD | 0.265 | 0.134 | 0.136 | 0.109 | 0.193 | 0.102 | 0.057 | 0.045 | 0.163 | 0.098 |
| EC8_3D_ZD | 0.718 | 0.108 | 0.796 | 0.182 | 0.727 | 0.349 | 0.772 | 0.184 | 0.753 | 0.206 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demir, A.; Palanci, M.; Kayhan, A.H. Enhanced Conditional Ground Motion Selection Model Considering Spectral Compatibility and Variability of Three Components for Multi-Directional Analysis. Appl. Sci. 2025, 15, 4135. https://doi.org/10.3390/app15084135
Demir A, Palanci M, Kayhan AH. Enhanced Conditional Ground Motion Selection Model Considering Spectral Compatibility and Variability of Three Components for Multi-Directional Analysis. Applied Sciences. 2025; 15(8):4135. https://doi.org/10.3390/app15084135
Chicago/Turabian StyleDemir, Ahmet, Mehmet Palanci, and Ali Haydar Kayhan. 2025. "Enhanced Conditional Ground Motion Selection Model Considering Spectral Compatibility and Variability of Three Components for Multi-Directional Analysis" Applied Sciences 15, no. 8: 4135. https://doi.org/10.3390/app15084135
APA StyleDemir, A., Palanci, M., & Kayhan, A. H. (2025). Enhanced Conditional Ground Motion Selection Model Considering Spectral Compatibility and Variability of Three Components for Multi-Directional Analysis. Applied Sciences, 15(8), 4135. https://doi.org/10.3390/app15084135






