Abstract
To address the challenges posed by the interdependence between subway vehicle scheduling and maintenance planning, which complicates joint optimization modeling and solution processes, this study proposes a spatiotemporal network-based joint optimization method for subway vehicle preventive maintenance and scheduling. First, based on spatiotemporal network theory, the transition process between train operation scheduling and preventive maintenance states is analyzed, and a spatiotemporal state network graph is constructed to represent the temporal and spatial transitions of subway vehicles throughout the planning period. The vehicle’s operational workflow is represented as a path within this network. Next, leveraging the generated spatiotemporal network path set, a joint optimization model for preventive maintenance and scheduling is formulated, integrating optimization objectives and constraints to achieve coordinated optimization. Finally, an improved genetic algorithm is employed to solve the model and determine the optimal scheduling and maintenance strategy. The experimental results demonstrate that the proposed method effectively addresses the challenges in modeling and solving the joint optimization problem, enabling efficient coordination between maintenance and scheduling while enhancing the overall operational efficiency in subway vehicle management.
1. Introduction
The maintenance and scheduling of subway vehicles are fundamental to ensuring the orderly, safe, and efficient operation of urban rail transit systems. In daily subway operations, maintenance planning and scheduling are often developed independently, lacking coordination and unified planning. This results in conflicts between maintenance activities and scheduling, leading to reduced operational efficiency and potential safety hazards [1,2]. Therefore, the joint optimization of preventive maintenance and scheduling for subway vehicles is crucial for ensuring operational safety, reducing costs, and improving efficiency.
With the rapid expansion of urban rail transit networks, increasing attention has been given to preventive maintenance and scheduling issues. Traditional fixed-cycle maintenance strategies, which disregard equipment reliability factors, have been found to reduce the maintenance efficiency. Consequently, optimizing subway equipment maintenance has become a key research focus [3,4]. Moreover, maintenance optimization and scheduling optimization are typically addressed as separate research domains, with most studies treating them independently.
Regarding preventive maintenance, Erguido et al. [5] proposed a multi-objective maintenance strategy based on reliability, aiming to enhance key performance indicators of conventional maintenance and organizations, employing simulation-based optimization techniques for solution derivation. Gupta et al. [6] highlighted that identifying critical components is essential in reliability-based maintenance and introduced a hierarchical network approach for ranking such components. Fouladirad et al. [7] analyzed historical data to identify failure patterns and formulated short-term maintenance strategies based on real-time monitoring data. Kamel et al. [8] developed a preventive maintenance scheduling model to optimize costs in complex repairable systems, utilizing intelligent algorithms for problem-solving. Pale et al. [9] proposed a cluster-based preventive maintenance strategy for dragline excavators in open-pit mining, integrating reliability-centered maintenance and operational data analysis to assess failure pattern impacts. Qin et al. [10] modeled a multi-state system incorporating preventive maintenance based on a Markov random process, considering both regular degradation and stochastic failures to meet specific operational demands. Cheng et al. [11] employed the Weibull distribution to model the reliability of key catenary components, extending the maintenance intervals to minimize costs. Doostparast et al. [12] emphasized the necessity of determining failure distribution functions in reliability modeling, noting the widespread application of Weibull distributions in mechanical and electronic component failure analysis.
For train scheduling, Christos et al. [13] developed a rapid genetic algorithm to optimize driver assignments with the objective of minimizing travel costs. White et al. [14] pioneered the application of spatiotemporal network theory to vehicle flow allocation and established a linear programming model for multi-vehicle empty train coordination. An et al. [15] examined optimal turnaround strategies to ensure train schedule execution, considering specific transport demands and capacity constraints. Fioole et al. [16] introduced a multi-train assignment optimization model incorporating operational costs, service quality, and equipment reliability. Canca et al. [17] formulated a mixed-integer programming model for railway vehicle turnaround optimization, aiming to minimize empty train mileage while considering periodic maintenance plans. Lusby et al. [18] proposed a train operation optimization model under multiple constraints, utilizing an improved branch-and-price algorithm for solution derivation. Steinzen et al. [19] developed an integrated multi-train scheduling and crew dispatching model based on spatiotemporal networks, transforming column generation subproblems into resource-constrained shortest path problems for effective problem-solving. Luan et al. [20] applied spatiotemporal network graphs to construct a minimum-cost maximum-flow optimization model, simplifying train operation problems into linear formulations for improved computational efficiency.
Vehicle maintenance and scheduling are interdependent components of urban rail transit operations. Maintenance plans impose scheduling constraints, as vehicles require periodic servicing to restore operational status, while scheduling decisions dictate maintenance timing, subsequently affecting the overall schedule. To enhance operational efficiency and reduce costs, a scientifically integrated optimization approach is necessary. Coordinating preventive maintenance and train scheduling can mitigate disruptions caused by unexpected failures, reduce frequent rescheduling and resource inefficiencies, and prevent issues such as service delays, overcrowding, and diminished passenger satisfaction. Increasingly, researchers have begun exploring joint optimization methodologies. Niu et al. [21] investigated multi-vehicle scheduling in spatiotemporally discrete network scenarios, formulating a linear integer programming model to minimize operational costs, solved via Lagrangian relaxation. Budai et al. [22] optimized maintenance scheduling by minimizing maintenance downtime, constraining the operational time between consecutive maintenance actions. Zhong et al. [23] analyzed subway and railway vehicle cases, demonstrating that integrating maintenance considerations into scheduling reduces overall maintenance expenses. Tian et al. [24] developed a scheduling model constrained by daily operational demands and maintenance plans, optimizing train frequencies and ensuring timely maintenance to prevent over- or under-maintenance. Nishi et al. [25] established a short-term scheduling model incorporating maintenance constraints, solved using column generation.
In summary, while existing research has developed relatively comprehensive joint optimization models for urban rail maintenance and scheduling using spatiotemporal network methods, several issues remain unaddressed: (1) Most optimization models structure maintenance planning based on traditional periodic inspections (e.g., bi-weekly or quarterly), failing to refine maintenance intervals based on actual task durations and lacking precision in defining preventive maintenance cycle constraints. (2) Although spatiotemporal network theory has been integrated into optimization models, current constructions predominantly employ one-dimensional, single-layer network representations that focus solely on train scheduling states, neglecting the intricate spatiotemporal interdependencies between maintenance and scheduling plans. The objectives and limitations of existing studies are shown in Table 1. To address these gaps, this study proposes a joint optimization approach for preventive maintenance and train scheduling based on spatiotemporal network graphs. A multi-layer spatiotemporal network is constructed to represent subway vehicle scheduling and maintenance interactions, and a corresponding optimization model is formulated. An improved genetic algorithm is employed for model solution derivation. Ultimately, the proposed method aims to achieve the integrated optimization of subway vehicle preventive maintenance and scheduling.

Table 1.
The key variable description.
The remainder of this paper is structured as follows. Section 2 describes the construction of the spatiotemporal network for subway vehicle maintenance and scheduling. Section 3 details the joint optimization model based on spatiotemporal network graphs. Section 4 presents the improved genetic algorithm for model solution derivation. Section 5 conducts case studies, and Section 6 concludes the paper.
2. Construction of the Spatiotemporal Network for Subway Vehicle Maintenance and Scheduling
2.1. Fundamental Elements
The spatiotemporal network for subway vehicle maintenance and scheduling proposed in this study consists of two hierarchical layers: the maintenance layer and the scheduling layer. Within this network, the maintenance layer encompasses the vehicle maintenance process, including both preventive and routine maintenance activities, while the scheduling layer pertains to the operational scheduling of subway vehicles, such as trip timing and route adjustments. Each layer comprises fundamental elements, including operation start nodes, operation end nodes, and various operational tasks performed by subway vehicles. These elements form the foundational framework of the spatiotemporal network, where a sequence of operations from the start node to the end node defines the paths within the network. The final spatiotemporal network structure is established based on the aforementioned elements, paths, and hierarchical layers. This network provides a clearer understanding of subway vehicle operations and maintenance processes, serving as a crucial reference for optimizing subway operations. By leveraging this framework, subway vehicle operation plans can be optimized, the overall operational efficiency can be enhanced, and maintenance quality can be improved, thereby offering essential decision-making support for subway system management.
The proposed spatiotemporal network for subway vehicle maintenance and scheduling is represented as a set W = {D, L}, where D denotes the set of nodes within the network, and L represents the set of arcs. The fundamental elements of the network are explained as follows:
- (1)
- Spatiotemporal network nodes: In this network, the set of operational nodes is defined as , where denotes vehicle scheduling operations, represents vehicle maintenance operations, corresponds to the operation start node, and indicates the operation end node, marking the conclusion of the planned operational cycle.
- (2)
- Spatiotemporal network arcs: Within the spatiotemporal network, subway vehicle maintenance, scheduling, and task transitions are represented by maintenance operation arcs, scheduling operation arcs, and state transition arcs, respectively. The horizontal axis denotes time, capturing the start and end times of each operational process, while the vertical axis represents space, indicating the corresponding operational locations. The set of arcs is given as , where denotes scheduling operation arcs, represents maintenance operation arcs, corresponds to task transition arcs, signifies state transition arcs, and marks operation termination arcs. Illustrations of the maintenance, scheduling, and state transition arcs are provided in Figure 1, Figure 2 and Figure 3.
 Figure 1. Maintenance operation arc diagram.
Figure 1. Maintenance operation arc diagram. Figure 2. Scheduling operation arc diagram.
Figure 2. Scheduling operation arc diagram. Figure 3. State transition arc diagram.
Figure 3. State transition arc diagram. - (3)
- Spatiotemporal network paths: Within the subway vehicle maintenance and scheduling spatiotemporal network, the operational paths of subway vehicles are formed by sequentially connecting operation start nodes to operation end nodes, incorporating all necessary operational steps. Given that multiple operational sequences may be available following the completion of each task, each subway vehicle can follow multiple possible paths within the network. By linking the operational sequences chronologically, the operational paths of subway vehicles can be visualized (Figure 4). This representation enables a clearer depiction of subway vehicle operations within the spatiotemporal network, elucidating the interconnections and sequential relationships among different operational phases. Such insights contribute to optimizing subway vehicle scheduling plans and improving operational efficiency.
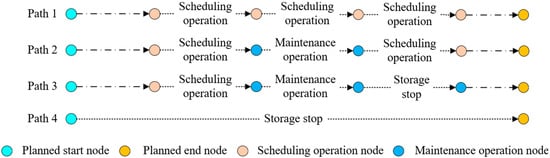 Figure 4. Space–time network path diagram.
Figure 4. Space–time network path diagram.
Path 1 represents a scenario where the train starts from the initial node, undergoes scheduling operations, and continues executing intermediate connection tasks cyclically until the planned period ends, ensuring continuous operation. Path 2 describes a case where the train initially performs scheduling tasks, transitions into maintenance operations upon reaching the maintenance cycle, and resumes scheduling until the end of the planned period. Path 3 illustrates a situation where the train begins with scheduling operations, undergoes maintenance at a later stage, and subsequently enters a storage track in standby mode until the plan concludes. Path 4 depicts a scenario where the train remains inactive throughout the planned period, with a direct connection from the initial to the final node, indicating that no operations are executed. The selection of different paths in the spatiotemporal network reflects various scheduling strategies under different conditions, facilitating more effective planning and coordination of subway train operations.
2.2. Establishment of the Subway Vehicle Maintenance and Scheduling Spatiotemporal Network
To visually represent subway vehicle scheduling and maintenance operations, a multi-level spatiotemporal network diagram is constructed, incorporating three stations: Stations A–C. Station B is directly connected to the subway depot, indicating that trains undergo scheduling and maintenance tasks at this location, while Stations A and C serve as turnaround points. With the fundamental elements and operational paths of the spatiotemporal network established, a multi-level subway vehicle maintenance and scheduling spatiotemporal state network diagram, as illustrated in Figure 5, is developed to describe train scheduling and maintenance processes. This diagram consists of two layers: the scheduling layer and the maintenance layer. By leveraging the spatiotemporal state network diagram, subway vehicle scheduling and maintenance can be optimized. Specifically, station locations and quantities can be adjusted, maintenance sites can be determined, and appropriate scheduling cycles can be formulated to generate a spatiotemporal network diagram that aligns with real-world operational needs.

Figure 5.
Subway vehicle maintenance and scheduling spatiotemporal state network diagram.
In the constructed spatiotemporal state network for subway vehicle maintenance and scheduling, “minutes” are used as the smallest time unit for scheduling. The scheduling cycle begins at 00:00 on the first day and spans 14 days, with the final time point set at 14 × 1440 min. In this diagram, train state transition moments are represented as nodes, while various operational states are depicted as arcs. These include scheduling operation arcs, which indicate scheduling states, and maintenance operation arcs, which represent maintenance states. By integrating these elements, a comprehensive and structured spatiotemporal network for preventive maintenance and train scheduling is formed. This network encapsulates essential operational stages and time intervals, serving as a theoretical foundation for analyzing and optimizing subway vehicle maintenance and scheduling. Moreover, it provides a basis for developing an integrated optimization model for preventive maintenance and scheduling, facilitating more effective management and planning of subway vehicle operations and maintenance.
3. Integrated Optimization Model for Preventive Maintenance and Train Scheduling Based on the Spatiotemporal Network
Through an in-depth analysis of the spatiotemporal network, the integrated optimization of preventive maintenance and train scheduling can be divided into two key steps. First, based on the transition process between train scheduling and preventive maintenance states, a spatiotemporal network diagram for subway vehicle maintenance and scheduling is constructed. This diagram represents the complete execution process of all operational stages from the start to the end of the planning period using paths within the spatiotemporal network. Second, an integrated optimization model for preventive maintenance and train scheduling is formulated. This model is built upon the set of feasible spatiotemporal network paths generated in the first step and is developed based on optimization objectives and constraints. The optimal scheduling plan is then obtained using path search algorithms.
3.1. Problem Description and Assumptions
The integrated optimization of preventive maintenance and train scheduling for subway vehicles must address two core challenges. First, appropriate train assignments must be made for each operational route. Second, trains approaching their maintenance cycle must be scheduled to return to the depot or maintenance base in time for necessary servicing. This ensures that all operational routes have adequately maintained trains and that these trains complete their required maintenance within the designated cycle [26]. From the perspective of train states, this process corresponds to paths within the spatiotemporal network. In the constructed spatiotemporal network, time represents the planning period, while space denotes the actual train locations, such as departure stations, terminal stations, and subway depots. The above analysis confirms that the preventive maintenance and scheduling plan for subway vehicles aligns with the fundamental properties of spatiotemporal networks, providing a solid theoretical foundation for the integrated optimization modeling of subway train scheduling and maintenance based on the spatiotemporal network diagram.
Building upon the spatiotemporal network theory, a detailed analysis of train operations is conducted to clarify temporal and spatial operational processes. An integrated optimization model for preventive maintenance and scheduling is then established under the following assumptions to simplify the problem: (1) The daily train schedule is predetermined throughout the entire planning period, and existing operational routes remain fixed and unmodifiable. (2) The locations of subway depots, turnaround stations, turnaround times, and route structures are known. (3) The depot has a sufficient number of trains, and only a single type of train is considered in the model. Operations such as train coupling or decoupling are not included. (4) Trains in a depot that have completed maintenance are classified as being in a maintained state.
3.2. The Details of the Designed Network
3.2.1. Variable Definition
The key variables of the integrated optimization model for preventive maintenance and train scheduling based on the spatiotemporal network diagram are presented in Table 2.

Table 2.
The key variable description.
3.2.2. Constraints
Each train is allowed to follow only one path at a given time, ensuring that every scheduled operation in the timetable is assigned to a corresponding train. This requirement is expressed as the timetable coverage constraint:
where represents the relationship between the vehicle’s path r and scheduling operations i and j, and represents that the vehicle can only continue scheduling operation j after completing scheduling operation i.
Considering that the turnout state matching requirements need to be met during the train entry and exit process, it is necessary to ensure that there is a minimum time interval between the trains that switch the turnout. The constraint condition is
where represents the time interval between two trains, and represents the train number that needs to switch the turnout.
In the vehicle depot, the number of hot standby vehicles in the depot is limited. The constraint condition of the number of hot standby vehicles in the depot is expressed as
The vehicle cannot be overdue for maintenance, and the advance maintenance should be less than 10% of the maintenance cycle. The constraints are expressed as
3.2.3. Objective Function
In the spatiotemporal network, minimizing the transition time between consecutive scheduling operations enhances vehicle utilization efficiency. The objective function for minimizing total transition time is given as
where represents the traversal of all trains; represents the traversal of all tasks/maintenance operations; i and j represent the traversal of tasks i and j (with i < j, ensuring only adjacent tasks are considered); represents the time interval between the end of task i and the start of task j; and is a binary variable that indicates whether tasks i and j are executed consecutively.
Assume that a train has two maintenance tasks. Task 1: arrival time = 8:00 a.m., completion time = 10:00 a.m.; task 2: arrival time = 11:00 a.m., completion time = 1:00 p.m. The connection time is given by − = 11:00 − 10:00 = 1 h. If the train has multiple maintenance tasks, the time interval for all tasks needs to be calculated similarly and summed.
To optimize maintenance scheduling, unnecessary maintenance within the allowable mileage range should be minimized. The cost-minimization objective over the evaluation period is defined as
where represents the unit cost of maintenance mode m, and represents whether maintenance task r has chosen maintenance mode m. For example, if a train requires maintenance after 5000 km of operation, the following maintenance options are available: (1) minor repair (cost CNY 2000, task number 1); (2) major repair (cost CNY 5000, task number 2). If, within the statistical period, three minor repairs and one major repair are performed, the total maintenance cost is as follows: total cost = 3 × 2000 + 1 × 5000 = 6000 + 5000 = CNY 11,000.
A weighted coefficient approach is adopted to transform the bi-objective function into a single-objective function. The transformed function is formulated as Equation (8). By introducing proportional coefficients and , the balance between the two objectives and is controlled. When is small and is large, the optimization emphasizes maintenance cost reduction, potentially at the expense of scheduling efficiency. Conversely, when is large and is small, the optimization prioritizes minimizing the total transition time, possibly increasing maintenance costs. Given this trade-off, minimizing the total transition time is set as the primary objective.
Penalty factors and are incorporated to ensure feasible solutions by accounting for constraints related to vehicle transport capacity and maintenance feasibility. The final optimization objective is expressed as
3.2.4. Integrated Optimization Model for Preventive Maintenance and Scheduling
Based on the constraints outlined above, an integrated optimization model for preventive maintenance and scheduling is formulated within the spatiotemporal network framework. The connection map of the communication grid to a metro vehicle is presented in Figure 6.

Figure 6.
The connection map of the communication grid to metro vehicle.
S.T.
4. Model Solution Based on Improved Genetic Algorithm
4.1. Algorithm Design
The process of solving the joint optimization problem for preventive maintenance and train scheduling of subway vehicles can be viewed as employing a search algorithm over an existing network to find a set of paths that satisfy the constraints and optimize the objective function. Given the characteristics of the path search problem, genetic algorithms have shown good performance in solving such issues. However, there are limitations when applying this method. For example, the local search capability is restricted: while genetic algorithms perform well in global search, their ability to find local optima in complex problems is limited, requiring more computational resources. Additionally, the convergence speed is slow: traditional genetic algorithms typically require many iterations to find an optimal solution. To address these issues, this paper proposes an improved genetic algorithm, which incorporates tent chaos initialization, tournament selection, and a local search strategy to enhance certain aspects of the algorithm, in line with the characteristics of the subway vehicle preventive maintenance and scheduling optimization problem. The specific improvements are outlined as follows:
- (1)
- Tent chaos initialization
Tent chaos initialization, also known as tent mapping, is a piecewise linear function with uniform probability density, power spectrum density, and ideal correlation properties. Its mathematical expression is given by
Its Lyapunov exponent is
When u > 0.5, λ > 0, Equation (11) is chaotic and can be written as
Then, we can obtain
- (2)
- Tournament selection strategy
The tournament selection strategy simulates a competitive process to select individuals, as follows:
- (1)
- Determine tournament size: Initially, the tournament size, i.e., the number of individuals competing in each round, is chosen. Typically, this value is an integer, denoted as T. In our experiments, we set T = 6.
- (2)
- Randomly select competitors: In each tournament, T individuals are randomly selected from the current population to participate.
- (3)
- Evaluate fitness: The fitness values of the selected individuals are calculated using the problem’s fitness function. Let the fitness values of the T individuals be .
- (4)
- Select winner: The individual with the highest fitness value is chosen as the winner and is copied to the next generation.
- (5)
- Repeat process: The process is repeated until a sufficient number of individuals (typically equal to the population size) are selected to form the next generation.
- (3)
- Population local search strategy
The basic principle of the population local search strategy is to perform k local searches near the best individual after each generation’s genetic evolution. These k individuals are identified, and the one with the highest fitness value, denoted as , is selected. If the fitness of is better than that of X, the fitness of is replaced by that of , and replaces the worst individual in the population; otherwise, the process returns to the previous step.
4.2. Algorithm Process
The proposed improved genetic algorithm (IGA) utilizes real-number encoding. A 10-digit decimal number represents the daily plan set for subway vehicles (), vehicle set (), maintenance tasks (), and scheduling tasks (). The chromosome is encoded as a decimal number. The fitness is calculated by extracting the decimal values from the chromosomes and substituting them into the objective function. The encoding method is illustrated in Figure 7. The upward arrows in each row represent the randomly selected sample points used for subsequent processing.

Figure 7.
Encoding diagram.
The basic concept of IGA is as follows: Tent initialization of the population, selection, crossover, mutation, elite retention strategy, and local search strategy are sequentially applied to maximize the chromosome’s fitness, ultimately obtaining the optimal solution during the iterative process. The pseudocode and solution steps of the algorithm are shown in Figure 8.

Figure 8.
Algorithm flow chart.
- (1)
- Tent chaos initialization of population
The tent map is used to generate a chaotic sequence for initializing the population, ensuring that the initial solutions are uniformly distributed in the solution space, as described by Equation (15), where a = 0.5. After chaos initialization, the population is mapped into the actual solution space.
- (2)
- Selection operator
Tournament selection is employed to choose the genetic candidates. Specifically, k individuals are randomly selected from the entire population with equal probability. The individual with the highest fitness among them is chosen as the parent for the next generation. This process is repeated until the new population reaches the size of the original population.
- (3)
- Crossover operator
A two-point crossover method is applied to the individuals selected by tournament selection. The crossover rate, denoted as , typically ranges from 0.7 to 0.9 [26]. Two paired chromosomes and of length l are selected, and two crossover points, and , are randomly chosen, where . The crossover operation follows these formulae:
- (4)
- Mutation operator
Mutation occurs in biological evolution when certain genes of the parent population are altered with a mutation probability , generating new individuals. In practice, mutation is rare, and is typically set within the range [0.01, 0.20]. Mutation points are selected based on a probability . For an individual , the mutation operation is defined as follows:
Then, the new individual generated after mutation is .
- (5)
- Elite retention strategy
The most optimal individual, with the highest fitness value, found during each generation’s evolution is saved as an elite individual. The remaining N − 1 individuals undergo genetic operations to prevent the loss or degradation of the best genes. The specific steps for the elite retention strategy are shown in Figure 9.

Figure 9.
Elite retention policy flowchart.
- (6)
- Population local search strategy
- ➢
- Initialization: The global variables, input parameters, and constraints are initialized at the start of the algorithm.
- ➢
- Determine maintenance need: Maintenance constraints are used to determine whether minor repairs or secondary repairs are necessary.
- ➢
- Roulette wheel selection for shifts: A roulette wheel selection method is used to search for the most suitable tasks in the feasible solution space of the spatiotemporal network.
- ➢
- Calculate maintenance package number: The number of maintenance packages included in the operation plan is counted to evaluate repair costs.
- ➢
- Evaluate constraints: Distance and time constraints for each vehicle in the spatiotemporal network are calculated to ensure the vehicle’s travel distance and time are within the prescribed limits.
- ➢
- Objective function calculation: The objective function is computed, yielding a comprehensive fitness value representing the current solution’s quality. The algorithm aims to minimize the fitness to find the optimal solution.
- ➢
- Output results: Finally, the fitness values and operation plans are outputted.
5. Case Analysis
To verify the feasibility of the proposed model, it was applied to the operational status of a subway line (Line 1) in a certain city. The relevant data required for the model are summarized as follows. Currently, the first train on Line 1 departs at 5:30 a.m. and the last train returns to the depot at 10:57 p.m. The line spans a total of 27.144 km with 22 stations, each associated with a parking lot and a vehicle depot. The line operates with double-track, one-way traffic on the right side, with trains traveling upward from Station A to Station B and downward from Station B to Station A. There are 36 train sets with 198 vehicles in total. Additionally, there is a return track that operates with a nested large and small route structure. The large route operates 104 trips, and the small route operates 94 trips, with single-trip operating times of 47 min and 39 min, respectively, and a maximum operating speed of 80 km/h. The operational timetable, route table, and maintenance standards are provided in Table 3, Table 4 and Table 5.

Table 3.
Runtime schedule (excerpt).

Table 4.
Operational route table.

Table 5.
Maintenance operation standards table at various levels.
5.1. Algorithm Effectiveness Analysis
The solution results are presented in Table 6. Upon analyzing the results, it is observed that when r = 1 or r = 0, the bi-objective model reduces to a single-objective model where either maintenance cost or connection time is the optimization target. The balance between the maintenance cost and connection time can be adjusted by the weight coefficients and . When is small and is large, the objective function is significantly influenced by the train maintenance schedule, resulting in the lowest train cost but suboptimal train scheduling. Conversely, when is large and is small, the combined optimization model’s total objective is dominated by the total connection time, which minimizes the total connection time but leads to less satisfactory maintenance outcomes. The preventive maintenance and train scheduling plans can be developed by the operations planners based on the actual maintenance requirements and the weight of each objective.

Table 6.
Solution results.
The optimization calculation was performed using MATLAB R2021b on a PC with 8 GB of RAM, an AMD Ryzen7 5800H processor with Radeon Graphics, and Windows 11. The improved genetic algorithm (described in Section 4.2) was used to solve the model. During the computation, the data from Table 1, Table 2 and Table 3 were incorporated into the model. The crossover probability was set to 0.9, mutation probability to 0.09, population size p to 120, and iteration count N to 600. Additionally, the improved genetic algorithm (IIGA) was compared with the traditional genetic algorithm (GA), differential-based optimization (DBO) algorithm, and chaotic genetic algorithm (IGA). The DBO algorithm is an optimization algorithm that explores the solution space through differential operations and effectively guides the search process to avoid falling into local optimality. The IGA is an optimization method that combines chaotic mapping with the GA. The IGA improves the initialization, selection, crossover, and mutation operations in the genetic algorithm by introducing a chaotic sequence, aiming to improve the global search ability of the algorithm and avoid falling into the local optimal solution, thereby improving the efficiency and accuracy of the optimization process.
The objective value iteration curves at = 0.1 and = 0.9 are shown in Figure 10.
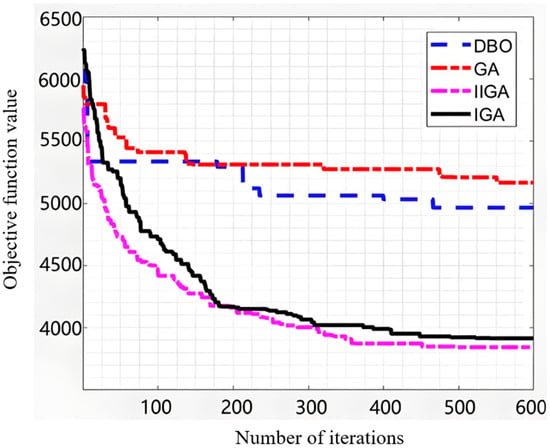
Figure 10.
Target value iteration curve.
As shown in Figure 10, the improved genetic algorithm converges faster than the traditional genetic algorithm, chaotic genetic algorithm, and DBO algorithm, reaching a satisfactory solution set by the 458th generation. In contrast, the DBO algorithm, chaotic genetic algorithm, and traditional genetic algorithm converged at the 479th, 546th, and 554th generations, respectively. The improved genetic algorithm utilizes a tent chaotic mapping strategy for population initialization, which enhances both the convergence speed and solution efficiency due to its randomness, ergodicity, and initial value sensitivity. Moreover, the algorithm employs an elitist retention strategy, preserving the individual with the best fitness value from each generation to avoid the loss of the best genes, thereby accelerating the search process and improving the global convergence. Furthermore, a local search strategy was introduced to find the most suitable tasks within the feasible solution space of the spatiotemporal network after the genetic algorithm iterations, further enhancing the algorithm’s search capability and convergence speed.
5.2. Optimization Result Analysis
In this study, an improved genetic algorithm was employed to solve the subway vehicle maintenance and scheduling problem. As the improved genetic algorithm is a heuristic algorithm with inherent randomness, 10 trials were conducted, and the best results were selected as the final optimization plan. After about 210 s of computation, the optimized preventive maintenance and train scheduling plan was obtained. The maintenance and scheduling plan for subway vehicles within a 14-day period was determined, and the results are summarized in Figure 11. Red means the vehicle needs maintenance, white means the vehicle is in the maintenance window period, and green means the vehicle is operating normally.
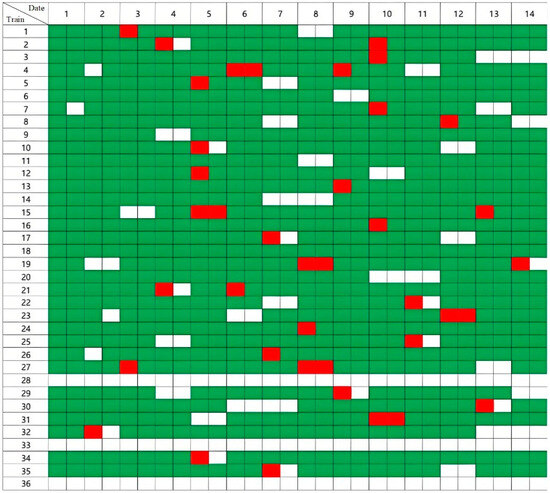
Figure 11.
Metro vehicle maintenance and scheduling plan.
Based on the model’s results, the statistics of the metro train maintenance and scheduling plan for the 14-day period are shown in Table 7. In the table, the “downtime” for each train scheduling task is calculated as 8 h. m1, m2, and m3 correspond to opportunistic group maintenance, secondary repair B, and secondary repair C, respectively.

Table 7.
Metro train maintenance and scheduling plan data statistics table.
Based on the results obtained from the joint optimization model for metro vehicle maintenance and scheduling, as shown in Figure 10, a detailed analysis of the data statistics for the 14-day period was conducted. The analysis reveals that, during the entire plan cycle, a total of 33 trains were required to complete all transportation tasks, which represents a reduction of 3 trains compared to the actual operational plan. Additionally, the maintenance and scheduling activities for all trains included 16 opportunity-based group maintenance operations, 11 secondary maintenance tasks (B package), and 6 secondary maintenance tasks (C package). This study also indicates that, for each maintenance operation, the accumulated mileage since the last maintenance of the trains almost reached the maximum mileage limit specified by the maintenance cycle.
Further analysis of the results from both the train operation and maintenance perspectives was performed. Compared to the pre-optimization scenario, the number of trains was further reduced by 3, resulting in more compact and efficient train operation. The optimization results indicate that the average operating days for each train were 11.25 days. The effective utilization rate of each train during the planning cycle was calculated using the following formula:
where is the number of days that train k is online in the operation cycle T, and is the number of trains used in the operation cycle T. The effective utilization rate of each train before and after optimization in actual operation is calculated according to Equation (19), as shown in Figure 12.
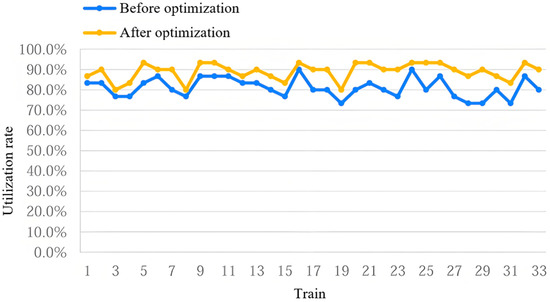
Figure 12.
Comparison of the effective utilization rate of each train before and after optimization.
As shown in Figure 11, the average effective utilization rate of the trains before optimization was 81.01%, which increased significantly to 88.98% after optimization. This indicates a substantial improvement in the train utilization efficiency.
Regarding train maintenance, the optimization results reveal that, within the 14-day period, the vast majority of the trains completed a full maintenance cycle, as scheduled. Most maintenance operations were strategically scheduled during the trains’ idle periods—after returning to the depot at the end of daily operations and before their next deployment. This approach maximized the use of non-operational time for maintenance, thereby reducing the overall maintenance costs. A comparison of the maintenance frequencies before and after optimization is illustrated in Figure 12.
Based on the analysis of Figure 13 and Table 7, it can be observed that during the 14-day operational period, a total of 16 opportunity-based group maintenance operations, 11 secondary maintenance tasks (B package), and 6 secondary maintenance tasks (C package) were performed. The pre-optimization maintenance days amounted to 34.5 days, while post-optimization maintenance days totaled 21.5 days, resulting in a reduction of 13 days of downtime for maintenance, significantly improving compared to the pre-optimization scenario.

Figure 13.
Comparison diagram of maintenance times before and after optimization.
In order to further evaluate the robustness of the improved genetic algorithm, we conducted a statistical analysis of the results of 10 operations and calculated the best value, worst value, average value, and standard deviation of the number of maintenance days. The results are shown in Table 8.

Table 8.
Comparison of the results of the number of maintenance days in ten operations.
The analysis results show that the improved genetic algorithm shows high stability in multiple operations, and the standard deviation of the objective function value is small, indicating that the solution of the algorithm has small fluctuations between different operations and has good robustness. In addition, from the results of different tests, the final optimization scheme shows good optimization effects in reducing the total number of trains and allocating maintenance tasks.
6. Conclusions
This study addresses the challenges in joint optimization modeling and solving caused by the interdependence between subway vehicle scheduling and maintenance planning. A joint optimization method for preventive maintenance and train scheduling based on spatiotemporal network graphs is proposed. First, a multi-level spatiotemporal state network graph is constructed for subway vehicle maintenance and scheduling using spatiotemporal network theory, where paths represent the temporal and spatial transitions of various operations throughout the planning period. Second, a joint optimization model is established, comprehensively considering the constraints of preventive maintenance and scheduling requirements for subway vehicles to achieve coordinated optimization of the maintenance and scheduling plans. Finally, an improved genetic algorithm is employed to solve the model and obtain the optimal scheduling and maintenance plan. The experimental results show that the proposed method can effectively address the difficulties in modeling and solving the joint optimization of subway vehicle maintenance and scheduling, enabling efficient coordinated optimization of both. Specifically, compared to traditional methods, this approach improves vehicle utilization by 7.97% and reduces the number of maintenance shutdowns by 14, simultaneously lowering maintenance costs and improving the scheduling efficiency, fully meeting the actual operational needs.
However, there are still some limitations in this study. First, the subway operation environment is complex and contains uncertain factors, such as unexpected failures and temporary scheduling adjustments, which are not sufficiently considered in the current model. Second, the optimization algorithm’s solving efficiency could be improved, especially in large-scale spatiotemporal networks with numerous constraints. Future research will focus on improvements in the following areas: (1) developing efficient optimization algorithms capable of handling large-scale spatiotemporal networks and complex constraints to enhance computational efficiency; (2) combining deep reinforcement learning techniques to achieve intelligent subway vehicle status assessment and scheduling decisions, improving the model’s adaptability and autonomous optimization ability; and (3) exploring methods that combine graph neural networks with reinforcement learning to improve the solving speed in large-scale networks and enhance the model’s adaptability to complex scheduling environments.
Author Contributions
Conceptualization, C.L.; methodology, Z.X.; software, M.M.; validation, W.L.; writing—original draft preparation, C.L.; writing—review and editing, Z.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
Author Chuanzhen Liu was employed by the company Shanghai Hengjun Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Zhao, S.; Shan, X.; Wu, J.; Zhang, L.; Li, Z.; Liu, X. A Capacity-Utilization-Oriented Stop Planning Approach for High-Speed Railway Network with Stop Distribution Balance. Appl. Sci. 2025, 15, 399. [Google Scholar] [CrossRef]
- Gong, Q.; Yang, L.; Li, Y.; Xue, B. Dynamic Preventive Maintenance Optimization of Subway Vehicle Traction System Considering Stages. Appl. Sci. 2022, 12, 8617. [Google Scholar] [CrossRef]
- Gkonou, N.; Nisyrios, E.; Gkiotsalitis, K. Combined optimization of maintenance works and crews in railway networks. Appl. Sci. 2023, 13, 10503. [Google Scholar] [CrossRef]
- Zhao, K.; Jiang, H.; Li, X.; Wang, R. Ensemble adaptive convolutional neural networks with parameter transfer for rotating machinery fault diagnosis. Int. J. Mach. Learn. Cybern. 2021, 12, 1483–1499. [Google Scholar] [CrossRef]
- Erguido, A.; Crespo, A.; Márquez, E. Reliability-based advanced maintenance modelling to enhance rolling stock manufacturers’ objectives. Comput. Ind. Eng. 2022, 96, 144–146. [Google Scholar] [CrossRef]
- Gupta, G.; Mishra, R.P. Identification of critical components using ANP for implementation of reliability Centered Maintenance. Procedia CIRP 2018, 69, 905–909. [Google Scholar] [CrossRef]
- Fouladirad, M. Dynamic opportunistic maintenance planning for multi-component redundant systems with various types of opportunities. Reliab. Eng. Syst. Saf. 2022, 198, 413–421. [Google Scholar]
- Kamel, G.; Aly, M.F.; Mohib, A.; Afefy, I.H. Optimization of a multilevel integrated preventive maintenance scheduling mathematical model using genetic algorithm. Comput. Ind. Eng. 2022, 15, 247–257. [Google Scholar] [CrossRef]
- Palei, S.K.; Das, S.; Chatterjee, S. Reliability-Centered maintenance of rapier dagline for optimizing replacement interval of dragline components. Min. Metall. Explor. 2022, 37, 1121–1136. [Google Scholar]
- Qin, J.; Li, Z.; Elsadany, A. Reliability modeling for multistate system with preventive maintenance under customer demand. Complexity 2022, 202, 15–19. [Google Scholar] [CrossRef]
- Cheng, H.; Cao, Y.F.; Wang, J.X.; Zhang, W.; Zeng, H. A preventive opportunistic maintenance strategy for the catenary system of high-speed railways based on reliability. Proc. Inst. Mech. Eng. 2022, 234, 1149–1155. [Google Scholar] [CrossRef]
- Doostparast, M.; Kolahan, F.; Dotparast, M. A reliability-based approach to optimize preventive maintenance scheduling for coherent systems. Reliab. Eng. Syst. Saf. 2014, 126, 98–106. [Google Scholar] [CrossRef]
- Christos, V.; Efthimios, H. Combined bus and driver scheduling. Comput. Oper. Res. 2022, 14, 243–259. [Google Scholar]
- White, W.W.; Bomerault, A.M. A network algorithm for empty freight car allocation. IBM. Syst. J. 1969, 8, 147–169. [Google Scholar] [CrossRef]
- An, Y.; Gao, Y.; Wu, N.; Zhu, J.; Li, H.; Yang, J. Optimal scheduling of electric vehicle charging operations considering real-time traffic condition and travel distance. Expert Syst. Appl. 2023, 213, 118941. [Google Scholar] [CrossRef]
- Fioole, P.J.; Kroon, L.; Maroti, G.; Schrijver, A. A rolling stock circulation model for combining and splitting of passenger trains. Eur. J. Oper. Res. 2006, 174, 1281–1297. [Google Scholar] [CrossRef]
- Canca, D.; Sabido, M.; Barrena, E. A Rolling Stock Circulation Model for Railway Rapid Transit Systems. Transp. Res. Procedia 2014, 51, 680–689. [Google Scholar] [CrossRef]
- Lusby, R.M.; Haahr, J.T.; Larsen, J.; Pisinger, D. A branch-and-price algorithm for railway rolling stock rescheduling. Transp. Res. Part B Methodol. 2017, 99, 228–250. [Google Scholar] [CrossRef]
- Steinzen, I.; Gintner, V.; Suhl, L.; Kliewer, N. A time-space network approach for the integrated vehicle and crew scheduling problem with multiple depots. Transp. Sci. 2010, 44, 367–382. [Google Scholar] [CrossRef]
- Luan, X.; Miao, J.; Meng, L.; Corman, F.; Lodewijks, G. Integrated optimization on train scheduling and preventive maintenance time slots planning. Transp. Res. Part C Emerg. Technol. 2017, 80, 329–359. [Google Scholar] [CrossRef]
- Niu, H.; Zhou, X.; Tian, X. Coordinating assignment and routing decisions in transit vehicle schedules: Avariable splitting Lagrangian decomposition approach for solution symmetry breaking. Transp. Res. Part B Methodol. 2018, 107, 70–101. [Google Scholar] [CrossRef]
- Budai, G.; Dekker, R. Adynamic approach for planning preventive railway maintenance activitices. Econom. Institide Res. Pap. 2004, 5, 4171–4176. [Google Scholar]
- Zhong, Q.W.; Zhang, Y.X.; Zhang, Y.; Peng, Q. Rolling stock scheduling with maintenance requirements at the Chinese high speed railway. Transp. Res. 2019, 126, 24–44. [Google Scholar] [CrossRef]
- Tian, H.X.; Shuaim, W. Optimization study of line planning for high speed railway based on an improved multi-objective differential evolution algorithm. IEEE Access 2019, 7, 137731–137743. [Google Scholar] [CrossRef]
- Nishi, T.; Ohno, A.; Inuiguchi, M.; Takahashi, S.; Ueda, K. A combined column generation and heuristics for railway short-term rolling stock planning with regular inspection constraints. Comput. Oper. Res. 2017, 81, 14–25. [Google Scholar] [CrossRef]
- Knypiński, Ł.; Nowak, L. The algorithm of multi-objective optimization of PM synchronous motors. Przegląd Elektrotechniczny 2019, 95, 242–245. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).