A Methodology for Situation Assessing of Space-Based Information Networks
Abstract
Featured Application
Abstract
1. Introduction
2. Related Work
3. Architecture Design
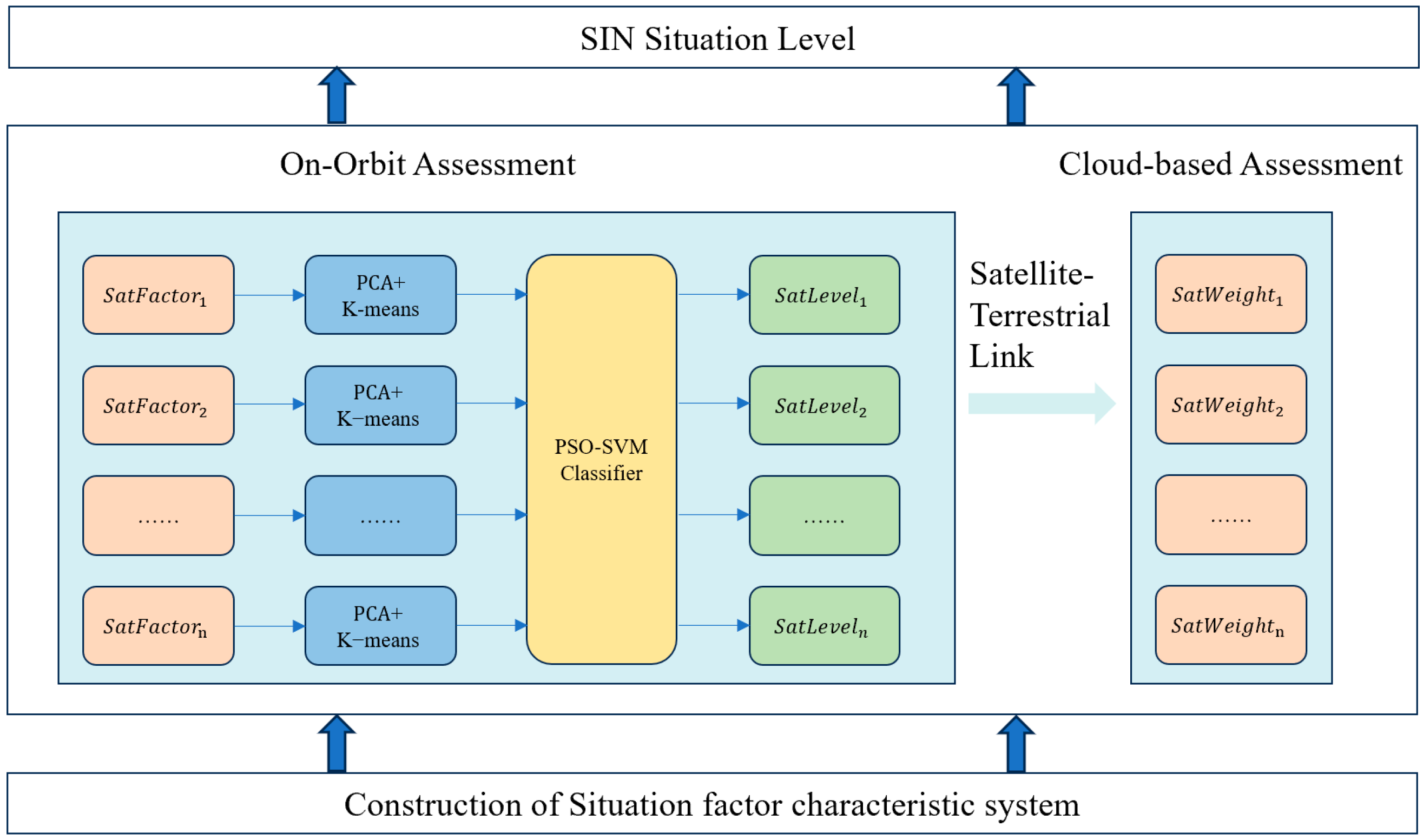
3.1. System Architecture
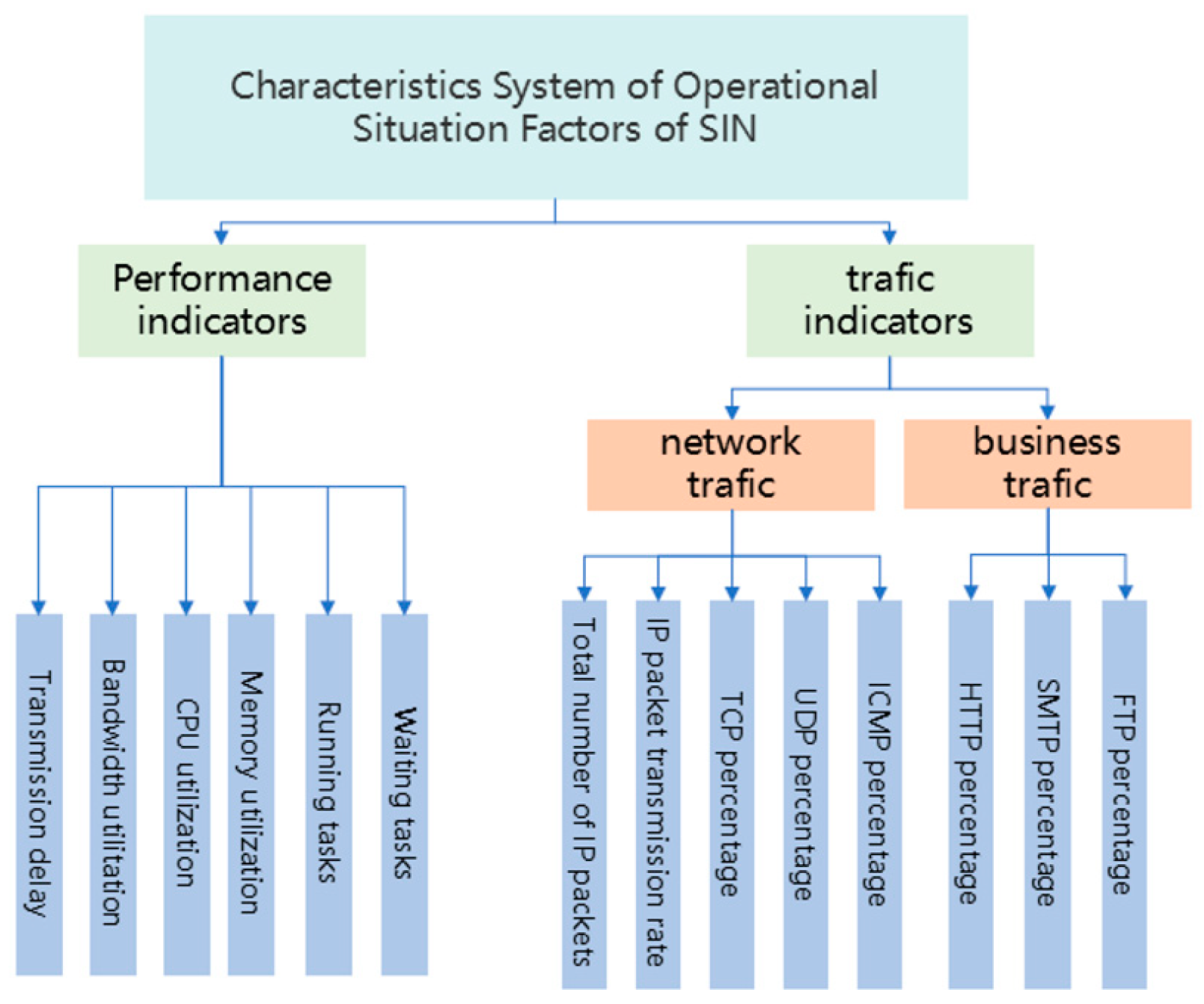
3.2. Assessment Factors
4. Proposed Methodology
4.1. Improved K-Mean Pre-Labeling Algorithm Based on PCA Dimensionality Reduction
4.2. PSO-SVM Model
4.3. CECSA
5. Experiment and Analysis
5.1. Metrics
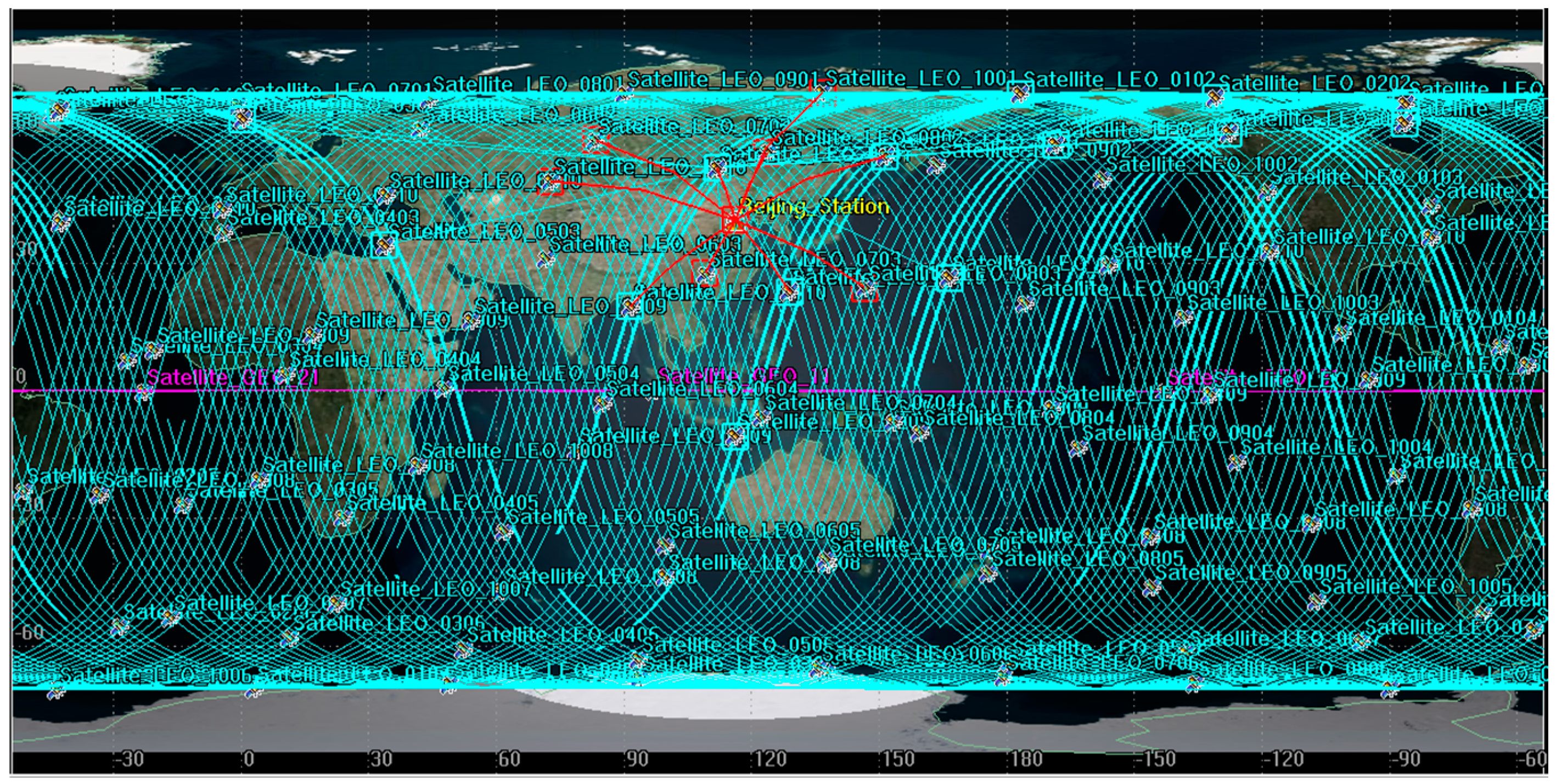
5.2. Experimental Settings
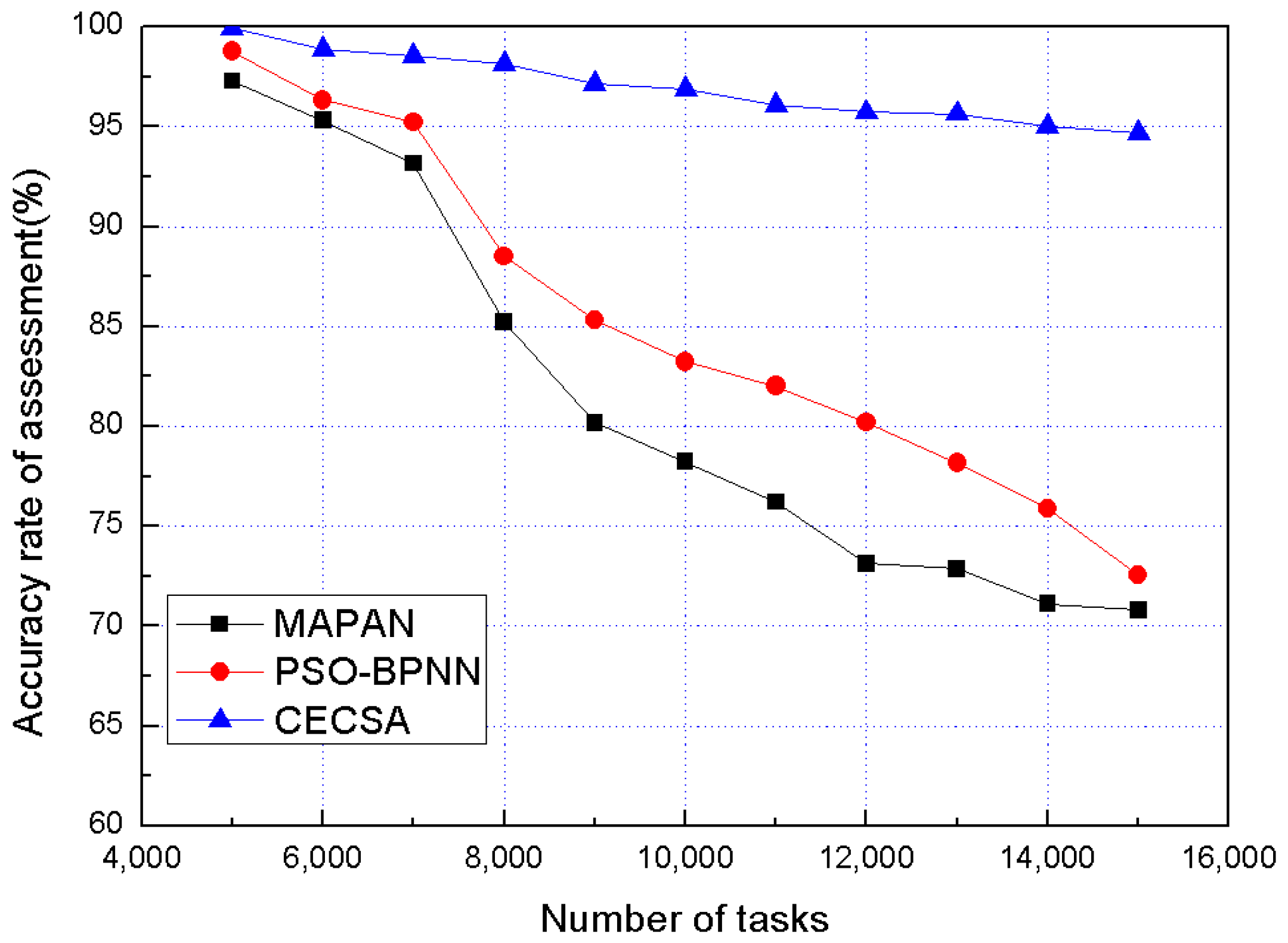
5.3. Result Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, H.; Liu, W.; Li, J.; Quek, T.Q.S. Space Information Network With Joint Virtual Network Function Deployment and Flow Routing Strategy with QoS Constraints. IEEE J. Sel. Areas Commun. 2023, 41, 1737–1756. [Google Scholar] [CrossRef]
- Sun, Y.; Peng, M.; Zhang, S.; Lin, G.; Zhang, P. Integrated Satellite-Terrestrial Networks: Architectures, Key Techniques, and Experimental Progress. IEEE Netw. 2022, 36, 191–198. [Google Scholar] [CrossRef]
- Pan, H.J.; Yao, H.P.; Mai, T.L.; Zhang, N.; Liu, Y. Scalable traffic control using programmable data planes in a space information network. IEEE Netw. 2021, 35, 35–41. [Google Scholar] [CrossRef]
- Chen, S.-J.; Wang, T.-Y.; Fang, C.-S.; Chiang, I.-W. Security Assessment of Low Earth Orbit (LEO) with Software-Defined Networking (SDN) Structure. In Proceedings of the 2023 IEEE 6th International Conference on Knowledge Innovation and Invention (ICKII), Sapporo, Japan, 11–13 August 2023; pp. 620–624. [Google Scholar] [CrossRef]
- Kassas, Z.M.; Kozhaya, S.; Kanj, H.; Saroufim, J.; Hayek, S.W.; Neinavaie, M.; Khairallah, N.; Khalife, J. Navigation with multiconstellation leo satellite signals of opportunity: Starlink, oneweb, orbcomm, and iridium. In Proceedings of the 2023 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 24–27 April 2023; IEEE: New York, NY, USA; pp. 338–343. [Google Scholar]
- Li, D.R.; Shen, X. Research on the Development Strategy of Real-Time and Intelligent Space-Based Information Service System in China. Strateg. Study CAE 2020, 22, 138–143. [Google Scholar] [CrossRef]
- Mi, X.; Song, Y.; Yang, C.; Han, Z.; Yuen, C. MAGIC: Matching Game-Based Resource Allocation With Incomplete Information in Space Communication Network. IEEE Trans. Commun. 2024, 72, 3481–3494. [Google Scholar] [CrossRef]
- Seo, J.; Kim, Y.; Kim, D.; Jung, H. A Survey on Machine Learning for Space-Air-Ground Integrated Network: Key Technologies and Challenges. In Proceedings of the 2024 International Conference on Electronics, Information, and Communication (ICEIC), Taipei, Taiwan, 28–31 January 2024; pp. 1–3. [Google Scholar]
- Dong, Y. Research on Key Technology of Satellite Communication System Operation Control; Institute of Electronic Science and Technology, China Electronics Technology Group Corporation: Beijing, China, 2018. [Google Scholar]
- Lei, S.; Quanjun, L.; Hao, W.; Keqiang, X. Research on Collocation Situation Analysis and Control Optimization of the BeiDou GEO Satellites. In Proceedings of the 2023 IEEE 6th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 24–26 February 2023; pp. 631–637. [Google Scholar]
- Gong, Z.; Zhuo, H. Research on cyberspace situational awareness. J. Softw. 2010, 21, 1605–1619. [Google Scholar]
- Han, C.; Xiong, W.; Jian, P. Data-driven Operational Effectiveness Evaluation of Space-based Information System. In Proceedings of the 2021 IEEE 5th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Xi’an, China, 15–17 October 2021; pp. 1687–1692. [Google Scholar]
- Jiang, S.; Jiang, Y.; Zhou, Y.; Bi, R.; Zeng, J.; Luo, D.; Li, J. Enhancing Satellite Intelligent Prediction with Parameter Correlation and LSTM Multidimensional Forecasting. In Proceedings of the 2023 International Conference on Future Communications and Networks (FCN), Queenstown, New Zealand, 17–20 December 2023; pp. 1–6. [Google Scholar]
- Jou, B.T.; Haug, T.; Holmes, J.; Berthou, P.; Gautier, R. Performance assessment framework and concept of operations in live satellite communication systems. In Proceedings of the 40th International Communications Satellite Systems Conference (ICSSC 2023), Bradford, UK, 24–26 October 2023; pp. 188–194. [Google Scholar]
- Wang, Y.; Kong, C.; Meng, X.; Luo, H.; Li, K.-X.; Wang, J. Systematic Performance Evaluation Framework for LEO Mega-Constellation Satellite Networks. In Proceedings of the ICC 2024—IEEE International Conference on Communications, Denver, CO, USA, 9–13 June 2024; pp. 5616–5621. [Google Scholar] [CrossRef]
- Chan, C.C.; Al Homssi, B.; Al-Hourani, A. Performance Evaluation of Random Access Methods for IoT-over-Satellite. Remote Sens. 2022, 14, 4232. [Google Scholar] [CrossRef]
- Guo, Y.; Skouroumounis, C.; Chatzinotas, S.; Krikidis, I. On User Association in Large-Scale Heterogeneous LEO Satellite Network. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 5994–6010. [Google Scholar] [CrossRef]
- Wang, H.; Guo, L.; Lu, H.; Gao, J. Network Security Situation Assessment Based on PCA-IFOA-PNN. In Proceedings of the 2023 3rd International Conference on Electronic Information Engineering and Computer Communication (EIECC), Wuhan, China, 22–24 December 2023; pp. 423–429. [Google Scholar] [CrossRef]
- Han, J.; Kamber, M.; Pei, J. Data Mining: Concepts and Techniques, 3rd ed.; Morgan Kaufmann: Boston, MA, USA, 2011. [Google Scholar]
- Shin, H.; Lee, K.Y. Deep K-means Clustering Based on Graph Neural Networks: Leveraging Cohesion and Separation in Graph Nodes. In Proceedings of the 2024 IEEE International Conference on Big Data and Smart Computing (BigComp), Bangkok, Thailand, 18–21 February 2024; pp. 190–193. [Google Scholar]
- Zhou, J.; Yang, P.; Peng, P.; Khandelwal, M.; Qiu, Y. Performance evaluation of rockburst prediction based on PSO-SVM, HHO-SVM, and MFO-SVM hybrid models. Min. Metall. Explor. 2023, 40, 617–635. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Juneja, M.; Nagar, S.K. Particle swarm optimization algorithm and its parameters: A review. In Proceedings of the 2016 International Conference on Control, Computing, Communication and Materials (ICCCCM), Allahbad, India, 21–22 October 2016; IEEE: New York, NY, USA; pp. 1–5. [Google Scholar]
- Ding, C.; Zhou, A.; Liu, Y.; Chang, R.N.; Hsu, C.H.; Wang, S. A cloud-edge collaboration framework for cognitive service. IEEE Trans. Cloud Comput. 2020, 10, 1489–1499. [Google Scholar] [CrossRef]
- Sun, T.; Wang, Y.; Yang, G.; Xiong, R.; Yang, K.; Zhang, W. An Industrial Internet Cloud-Edge Collaborative Scheme and Evaluation System. In Proceedings of the 2024 3rd International Conference on Cloud Computing, Big Data Application and Software Engineering (CBASE), Hangzhou, China, 11–13 October 2024; pp. 691–697. [Google Scholar] [CrossRef]
- Liao, Y.; Gou, Y.; Liu, Z.; Zhang, J. Analysis and Design of Financial Wealth Management Platform Based on Cloud Edge Collaboration. In Proceedings of the 2024 3rd International Conference on Artificial Intelligence, Internet of Things and Cloud Computing Technology (AIoTC), Wuhan, China, 13–15 September 2024; pp. 165–168. [Google Scholar] [CrossRef]
- Hurbungs, V.; Bassoo, V.; Fowdur, T.P. A novel One-vs-Next approach for multiclass classification. In Proceedings of the 2024 IEEE Symposium on Computers and Communications (ISCC), Paris, France, 26–29 June 2024. [Google Scholar]
- Huang, J.; Xing, R.; Ma, X.; Zhou, A.; Wang, S. Profit-Aware Task Allocation in Satellite Computing. In Proceedings of the 2024 IEEE International Conference on Web Services (ICWS), Shenzhen, China, 7–13 July 2024; pp. 696–706. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, H.; Liu, R.; Kaushik, A.; Gao, X.; Xu, S. Collaborative Task Offloading Optimization for Satellite Mobile Edge Computing Using Multi-Agent Deep Reinforcement Learning. IEEE Trans. Veh. Technol. 2024, 73, 15483–15498. [Google Scholar] [CrossRef]

| Level | Situation Value | Description |
|---|---|---|
| Level 1 | 0.75~1.0 | The system is in good condition and has sufficient resources |
| Level 2 | 0.5~0.75 | System load is too high |
| Level 3 | 0.25~0.5 | The system is malfunctioning |
| Level 4 | 0~0.25 | The system is down |
| Parameters | Value (Range) |
|---|---|
| Number of tasks | [5000, 15,000] |
| (MB) | [1, 10] |
| (Kcycles/bit) | [1, 1.5] |
| time slot (s) | 5 |
| Number of LEOs | 1280 |
| Number of GEOs | 6 |
| Number of ground stations | 5 |
| Satellite computational capability (Gcycles/s) | 2 |
| Satellite communication capability (Mbps) | [3, 5] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.; Liu, J.; Tang, J.; Liu, X.; Li, Z. A Methodology for Situation Assessing of Space-Based Information Networks. Appl. Sci. 2025, 15, 4127. https://doi.org/10.3390/app15084127
Xu S, Liu J, Tang J, Liu X, Li Z. A Methodology for Situation Assessing of Space-Based Information Networks. Applied Sciences. 2025; 15(8):4127. https://doi.org/10.3390/app15084127
Chicago/Turabian StyleXu, Sai, Jun Liu, Jiawei Tang, Xiangjun Liu, and Zhi Li. 2025. "A Methodology for Situation Assessing of Space-Based Information Networks" Applied Sciences 15, no. 8: 4127. https://doi.org/10.3390/app15084127
APA StyleXu, S., Liu, J., Tang, J., Liu, X., & Li, Z. (2025). A Methodology for Situation Assessing of Space-Based Information Networks. Applied Sciences, 15(8), 4127. https://doi.org/10.3390/app15084127






