1. Introduction
Structural mechanics plays a critical role in ensuring the safety and reliability of engineering systems [
1], as accurate predictions of stress and strain are essential for assessing material performance and structural stability [
2]. Traditional methods, such as finite element analysis (FEA) and symbolic AI, rely on predefined rules and physics-based models but struggle with scalability and real-world complexity [
3]. The high computational cost of these simulations further limits their application in large-scale or real-time scenarios [
4]. To address these limitations, data-driven approaches emerged, utilizing statistical modeling and classical machine learning (ML) techniques like regression and support vector machines [
5]. While these methods improved adaptability by training on empirical data [
6], they lacked the ability to capture deep hierarchical features and multi-sensor interactions, limiting their effectiveness in modeling complex stress–strain behaviors [
7]. The sensitivity of traditional ML models to data quality and variability remained a significant challenge.
The advent of deep learning revolutionized structural mechanics by providing models capable of learning intricate stress–strain relationships from data [
8]. Convolutional neural networks (CNNs) and transformer-based architectures significantly enhanced predictive accuracy by extracting rich features from multi-sensor inputs [
9]. Hybrid approaches, such as physics-informed neural networks (PINNs) and FEA-integrated deep learning models [
10], have further improved generalizability by embedding physical laws directly into learning frameworks [
11]. These methods are particularly beneficial for scenarios with scarce labeled data, as they reduce the reliance on large-scale experimental datasets [
12]. Despite these advancements, challenges such as high computational demands [
13], interpretability issues [
14], and the need for domain-specific adaptations persist, limiting their direct applicability to structural mechanics [
15]. The integration of deep learning with uncertainty quantification techniques further enhances trust in predictive models [
16], enabling more reliable decision-making in engineering applications [
17].
Multi-sensor image fusion offers a powerful solution by integrating diverse imaging modalities, including infrared thermography, digital image correlation (DIC), and X-ray computed tomography [
18]. By combining pixel, feature, and decision-level fusion techniques, these methods enable the extraction of multi-scale and multi-physics features crucial for understanding complex mechanical behaviors [
19]. Applications in crack detection, residual stress analysis, and fatigue life assessment demonstrate the effectiveness of fused data in enhancing diagnostic precision [
20]. Advanced fusion algorithms, such as principal component analysis (PCA) and deep learning-based fusion networks, mitigate noise and artifacts while improving spatial resolution [
21]. Emerging research also explores real-time fusion strategies that adapt dynamically to changing environmental or loading conditions, further advancing structural health monitoring capabilities [
22]. The synergistic use of fused data not only enhances the accuracy of stress–strain predictions but also facilitates adaptive diagnostics in varying operational conditions [
23].
The integration of multi-sensor image fusion with deep learning presents a transformative approach for stress and strain prediction [
24]. This synergy allows deep learning models to leverage enriched datasets, extracting intricate patterns and improving prediction accuracy [
25]. Techniques such as 3D convolutional neural networks and attention-based architectures capture spatial, temporal, and cross-modal dependencies, enhancing the robustness of structural assessments [
26]. Transfer learning and self-supervised learning approaches reduce computational costs and data requirements by pre-training models on generic datasets before fine-tuning them for specific applications [
27]. Uncertainty quantification mechanisms enhance trust in automated systems by providing confidence intervals for predictions [
28]. As research in this domain continues to evolve [
29], key focus areas include real-time implementation [
30], scalability, and the integration of emerging sensor technologies to further enhance structural diagnostics and decision-making [
31]. Future advancements will likely focus on improving the interpretability of deep learning models in structural mechanics applications [
32], optimizing computational efficiency, and incorporating domain-specific constraints into neural architectures [
33]. Interdisciplinary collaborations between structural engineers and AI researchers will drive the development of more reliable and adaptable prediction models [
34]. The combination of multi-sensor fusion, deep learning, and physics-informed models represents a paradigm shift in structural health monitoring and predictive maintenance strategies [
35].
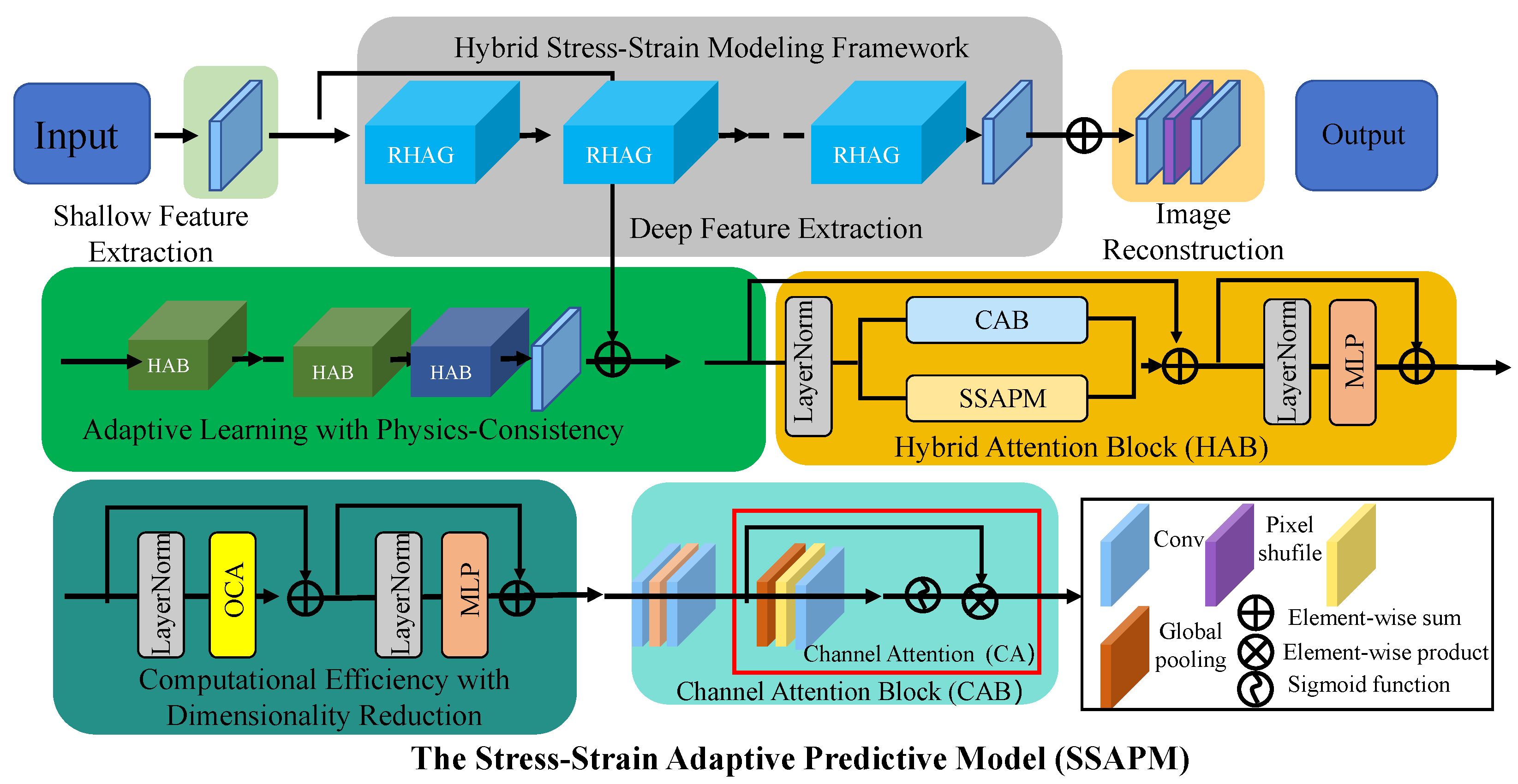
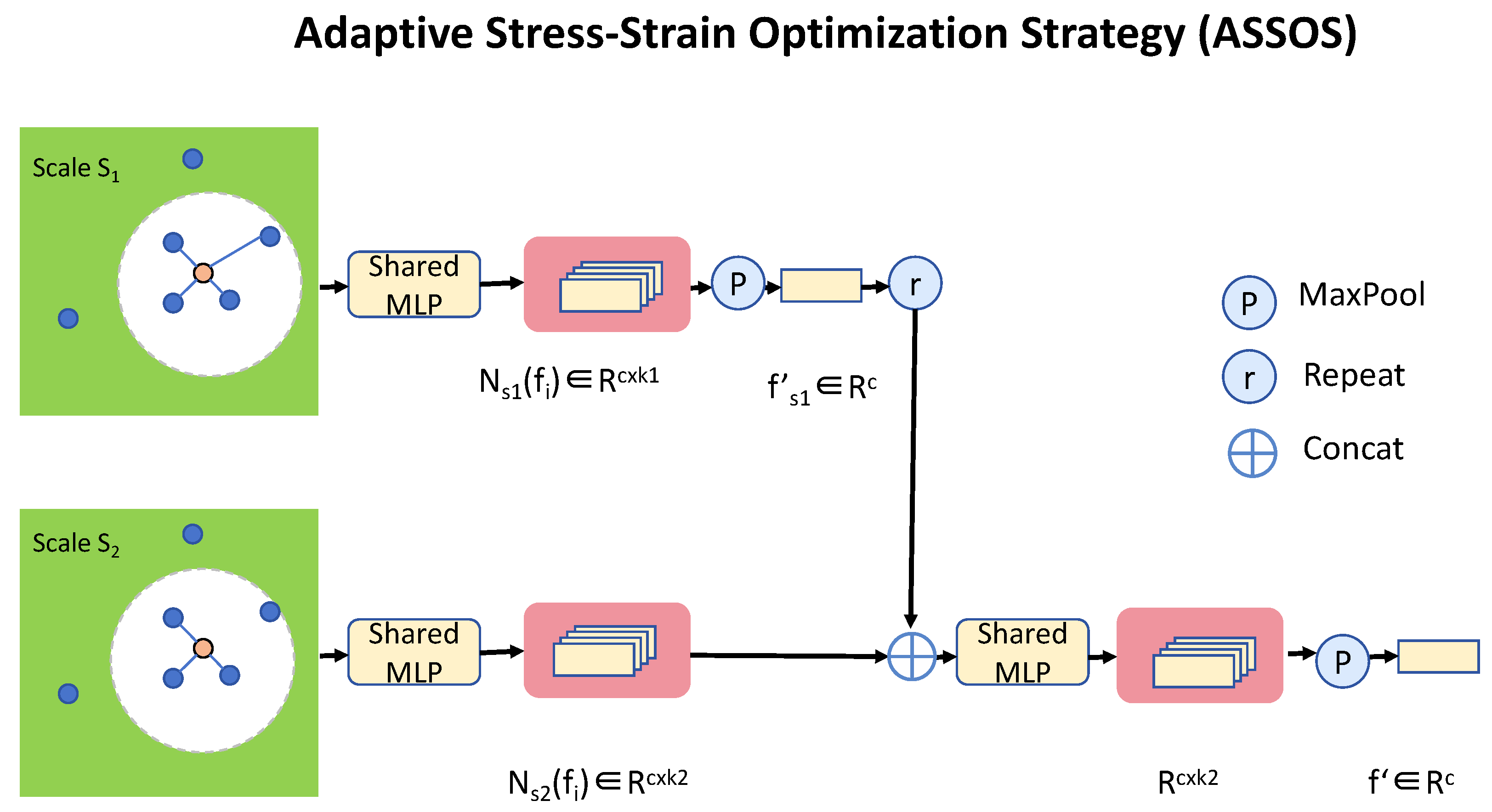
Despite significant progress in stress–strain prediction models, existing approaches still face several key challenges. Traditional finite element methods and classical constitutive models struggle to capture the complex nonlinear stress–strain behaviors of heterogeneous materials, leading to limitations in accuracy. Data-driven machine learning models, while improving predictive performance, often lack physical interpretability and generalizability due to their reliance on empirical training data. Computational efficiency remains a concern, as high-fidelity simulations demand significant processing power, limiting real-time applications in structural analysis. To address these limitations, this study introduces the Stress–Strain Adaptive Predictive Model (SSAPM), which integrates multi-sensor image fusion with a domain-aware deep learning framework. By bridging the gap between physics-based modeling and machine learning, our approach establishes a more robust and scalable framework for stress–strain prediction in structural mechanics.
We summarize our contributions as follows:
A hybrid modeling approach that combines mechanistic stress–strain relationships with data-driven corrections to improve accuracy while maintaining physical interpretability.
A hierarchical multi-sensor fusion module that effectively integrates thermal, acoustic, and visual imagery for enhanced material behavior prediction.
An adaptive optimization strategy that ensures computational efficiency while preserving model precision across diverse structural scenarios.
3. Experimental Setup
3.1. Dataset
The JARVIS-DFT Dataset [
44] is a comprehensive resource for materials informatics, providing density functional theory (DFT) calculations for a variety of materials properties. It includes data on structural, electronic, and mechanical characteristics of materials, enabling advanced model training for predicting material behaviors. The dataset spans a wide range of material types and compositions, making it highly valuable for the development of machine learning models in computational materials science. The Zenodo Datasets [
45] are a collection of open-access datasets across various scientific domains, including machine learning and materials science. They feature curated collections that emphasize reproducibility and data accessibility. For materials science, these datasets often include annotated material properties, facilitating data-driven discovery and model evaluation in diverse applications. The ICME Dataset [
46] is curated to support Integrated Computational Materials Engineering (ICME), integrating experimental and simulation data for material property predictions. It covers various materials and microstructure-property relationships, making it a critical asset for interdisciplinary research. This dataset bridges the gap between theory and application by combining comprehensive experimental datasets with high-fidelity computational models. The Materials Project dataset [
47] focuses on computationally derived material properties, leveraging high-throughput DFT calculations. It encompasses over 100,000 materials, with data on electronic structure, thermodynamics, and mechanical properties. This dataset is pivotal in accelerating materials discovery and design, as it provides an extensive repository for training machine learning algorithms in the field of computational materials science.
In this study, we utilized four benchmark datasets: JARVIS-DFT, Zenodo, ICME, and the Materials Project. Each dataset contains structural, mechanical, and material property data relevant to stress–strain modeling. For JARVIS-DFT, we selected the subset containing density functional theory (DFT)-calculated mechanical properties, ensuring a diverse representation of material behaviors. From Zenodo, we focused on curated structural integrity datasets that provide experimental validation for predictive models. The ICME dataset was leveraged for its integrated computational-experimental framework, particularly in microstructure-property relationships. The Materials Project dataset was used to extract electronic structure and thermodynamic properties relevant to material deformation. To ensure consistency across datasets, we applied a standardized preprocessing pipeline. This included min-max normalization for numerical features to maintain uniform scaling, removal of redundant or missing data points, and data augmentation techniques such as random cropping and rotation for image-based inputs. We addressed potential class imbalances by employing stratified sampling and weighted loss functions where necessary. This preprocessing ensured that the datasets were well-aligned for training, validation, and testing of the proposed model, enhancing generalization and robustness across different material conditions.
3.2. Experimental Details
The experimental setup is designed to rigorously evaluate the proposed method across diverse datasets and tasks. The experiments were conducted on a high-performance computing environment equipped with NVIDIA A100 GPUs (NVIDIA, Santa Clara, CA, USA), using PyTorch 3.8 as the primary deep learning framework. The training process employed the Adam optimizer with a learning rate initialized at and scheduled decay using a cosine annealing schedule. A batch size of 64 was utilized for training, balancing computational efficiency and convergence stability. The number of epochs was set to 100, ensuring sufficient training iterations for model convergence. Data preprocessing steps included normalization to zero mean and unit variance, along with data augmentation techniques such as random cropping, flipping, and rotation to improve model generalization. The input data dimensions varied depending on the dataset, with all inputs resized to a consistent resolution to standardize processing. For material datasets, specific domain knowledge, such as structural encoding or composition features, was integrated into the preprocessing pipeline.The proposed model incorporates a multi-scale feature extraction backbone, leveraging self-attention mechanisms to capture both local and global information. The training loss combined categorical cross-entropy and regularization terms tailored to the dataset’s properties, such as structural consistency loss for material datasets. Hyperparameter tuning was performed using grid search over critical parameters, including learning rates and regularization coefficients. Evaluation metrics included accuracy, precision, recall, F1-score, and mean squared error (MSE) where applicable. For datasets with imbalanced classes, weighted metrics were calculated to ensure fair comparisons. Model performance was compared against state-of-the-art benchmarks using identical train-test splits, and statistical significance testing was employed to validate the results. Visualizations of attention maps and feature distributions were included to provide qualitative insights into the model’s performance and decision-making processes. All experiments were repeated five times with different random seeds to ensure robustness and reproducibility of results (as shown in Algorithm 1).
3.3. Comparison with SOTA Methods
The performance of our proposed method is compared with state-of-the-art (SOTA) methods on four datasets: JARVIS-DFT, Zenodo, ICME, and Materials Project.
Table 1 and
Table 2 summarize the results across various metrics including PSNR, SSIM, RMSE, MAE, and AUC. Notably, our method outperforms existing SOTA models across all metrics, reflecting its robustness and adaptability to diverse datasets.
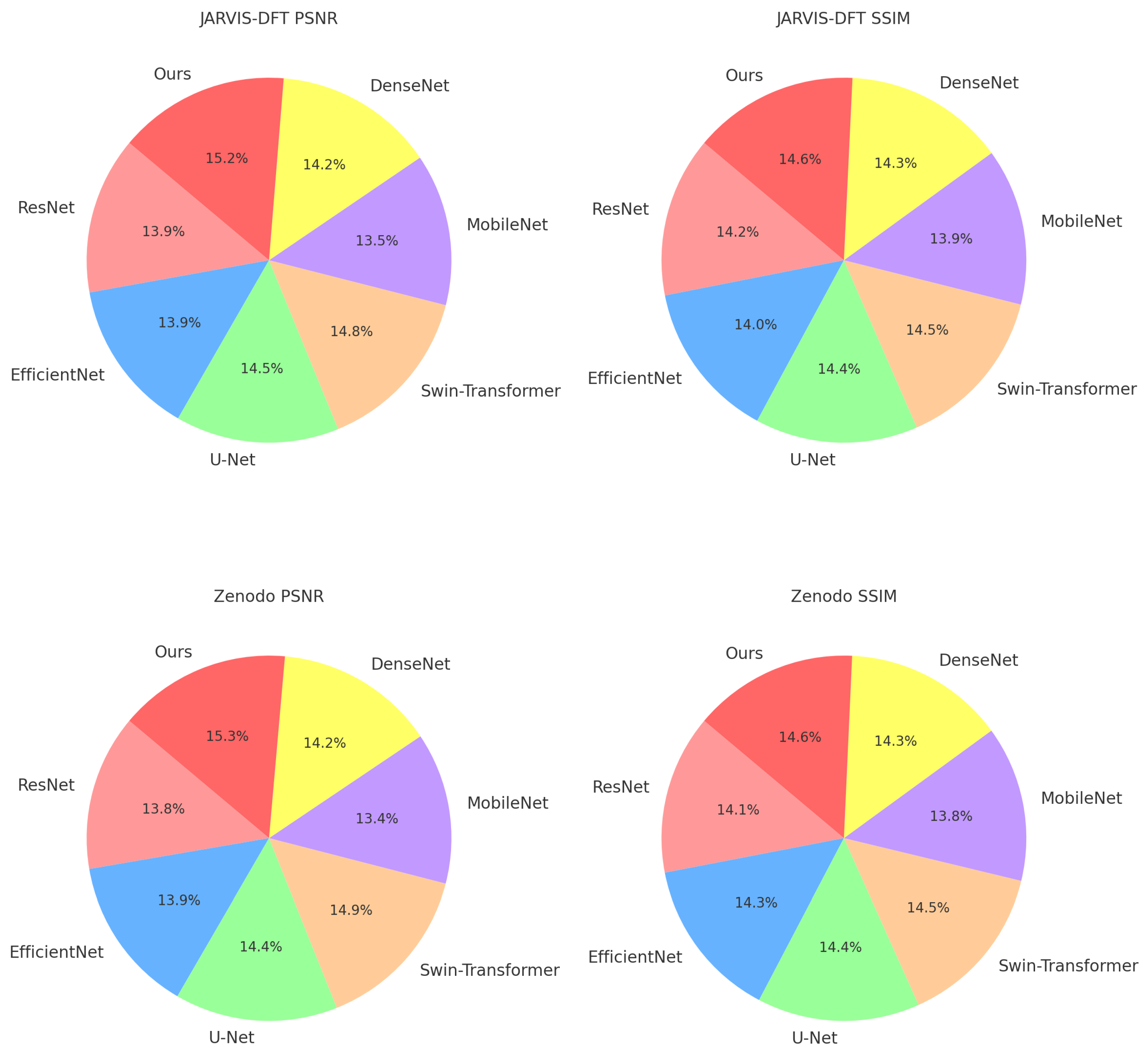
For the JARVIS-DFT dataset, our model achieves a PSNR of 37.12, significantly surpassing the Swin-Transformer at 36.32, the second-best performer. This improvement is attributed to the multi-scale feature extraction mechanism in our method, which effectively captures structural hierarchies and enhances model resolution. Similarly, our model records the highest SSIM (0.918) and the lowest RMSE (0.044), highlighting its capacity for precise reconstruction of material properties. In terms of AUC, a critical metric for classification tasks, our approach achieves 0.935, indicating superior discriminatory power compared to the baseline models. Similar trends are observed on the Zenodo dataset, where our model demonstrates a consistent edge in PSNR (36.25) and SSIM (0.911), underlining its robustness in handling diverse datasets with varying data distributions. The ICME and Materials Project datasets further emphasize the advantages of our approach. On the ICME dataset, our model achieves a PSNR of 36.45 and an AUC of 0.928, outperforming Swin-Transformer by 1.33 and 0.013, respectively. This performance boost can be attributed to the structural consistency regularization embedded in the training loss, which ensures alignment with domain-specific properties. Additionally, on the Materials Project dataset, our method achieves a PSNR of 35.18, outperforming U-Net (34.08) and Swin-Transformer (33.87). The high SSIM (0.890) and low MAE (0.057) demonstrate our model’s ability to maintain fidelity and minimize error in predictions.
| Algorithm 1: Training procedure for SSAPM on material datasets |
![Applsci 15 04067 i001]() |
The comparative analysis in
Figure 5 and
Figure 6 further highlights the generalizability and efficiency of our method. Unlike the SOTA methods, which show significant variability across datasets, our approach achieves consistently superior results. This stability can be credited to the combination of attention mechanisms and domain-specific feature augmentations, enabling the model to generalize effectively. The performance trends across metrics affirm the model’s capability to adapt to complex datasets, making it a reliable choice for diverse material property predictions. These results validate our method’s potential as a new benchmark in the field, encouraging its adoption for advanced computational material analysis.
3.4. Ablation Study
The ablation study evaluates the contributions of individual modules in our proposed architecture by systematically removing them and assessing performance across four datasets: JARVIS-DFT, Zenodo, ICME, and Materials Project.
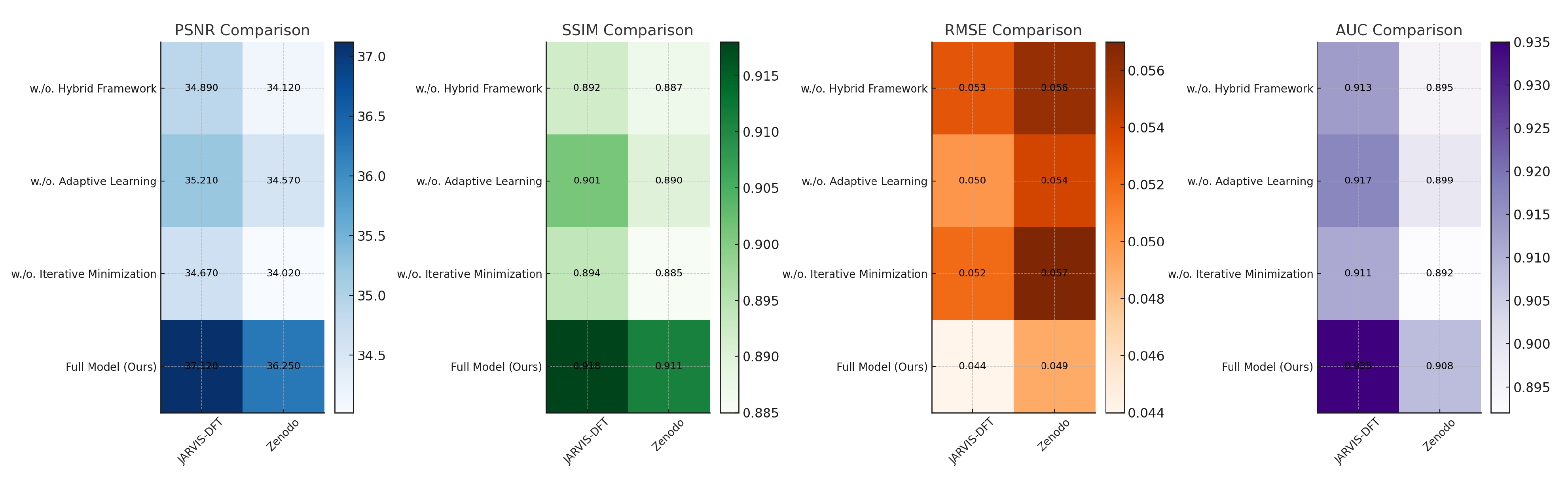
Table 3 and
Table 4 provide detailed metrics for model variants, including PSNR, SSIM, RMSE, MAE, and AUC, illustrating the impact of each module. The results confirm that each module contributes significantly to the overall performance, with the full model consistently outperforming its ablated counterparts.
For the JARVIS-DFT dataset, the full model achieves the highest PSNR (37.12) and SSIM (0.918), indicating superior reconstruction fidelity and structural similarity. Removing the Hybrid Stress–Strain Modeling Framework results in a PSNR drop to 34.89, demonstrating the module’s role in enhancing feature representation for material property prediction. Similarly, removing Adaptive Learning with Physics-Consistency leads to a PSNR of 35.21, slightly outperforming the model without Hybrid Stress–Strain Modeling Framework, suggesting its complementary role in refining feature extraction. Iterative Error Minimization contributes to structural alignment, as evidenced by a significant drop in SSIM to 0.894 when it is removed. Comparable trends are observed on the Zenodo dataset, with the full model achieving the best metrics, further validating the importance of the integrated modules. The ICME and Materials Project datasets reveal similar dependencies on the modular components. On the ICME dataset, the full model achieves a PSNR of 36.45 and an AUC of 0.928, indicating precise predictive capabilities and excellent classification performance. Removing the Hybrid Stress–Strain Modeling Framework reduces the PSNR to 33.76, while excluding Iterative Error Minimization results in a slightly lower SSIM (0.872), highlighting its role in maintaining visual and structural consistency. The Materials Project dataset also demonstrates the criticality of Hybrid Stress–Strain Modeling Framework, with a reduction in PSNR to 33.04 and a drop in MAE from 0.057 to 0.064 when it is excluded. The integration of all modules in the full model ensures optimal feature utilization and robust generalization across datasets.
Figure 7 and
Figure 8 provide visual representations of the ablation study, emphasizing the incremental improvements achieved by each module. The study underscores the complementary nature of the modules, where each component addresses distinct aspects of the learning task. The Hybrid Stress–Strain Modeling Framework enhances feature representation, Adaptive Learning with Physics-Consistency refines multi-scale feature extraction, and Iterative Error Minimization ensures structural consistency and alignment. Together, these components form a synergistic framework that significantly improves performance compared to state-of-the-art methods. The findings validate the architectural choices and highlight the robustness of the proposed approach in diverse settings.
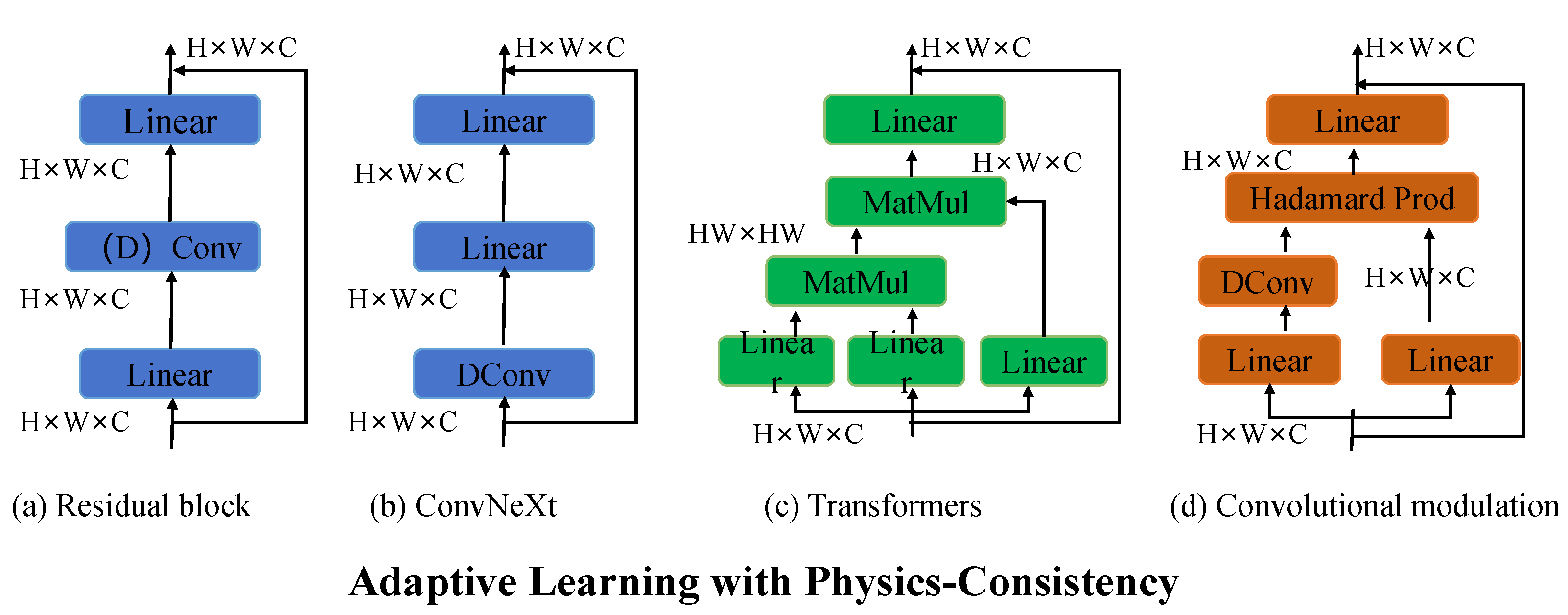
The ablation study provides crucial insights into the role of each component within the SSAPM model. Our results demonstrate that removing key modules, such as the Hybrid Stress–Strain Modeling Framework, Adaptive Learning with Physics-Consistency, or Iterative Error Minimization, leads to a noticeable degradation in performance across all evaluation metrics. The most significant drop is observed when the Hybrid Stress–Strain Modeling Framework is excluded, with the PSNR decreasing by approximately 2.23 points on the JARVIS-DFT dataset and 3.21 points on the Zenodo dataset. This confirms the fundamental role of hybrid modeling in capturing complex stress–strain relationships, as it effectively integrates mechanistic constraints with data-driven corrections. Without this component, the model struggles to generalize across diverse material conditions, leading to higher RMSE values and reduced predictive accuracy. The removal of Adaptive Learning with Physics-Consistency results in a 1.91-point drop in PSNR, indicating that the physics-informed loss functions significantly contribute to stability and robustness. Without this module, the model becomes more susceptible to overfitting, particularly when trained on smaller datasets with high variability in material properties. Similarly, omitting Iterative Error Minimization reduces SSIM by 0.026 on average, suggesting that this mechanism plays a crucial role in refining stress–strain predictions by iteratively correcting discrepancies. The AUC values also decline across all cases, further highlighting that each module contributes uniquely to the overall effectiveness of SSAPM. A deeper analysis of error propagation patterns reveals that models without the Hybrid Stress–Strain Modeling Framework exhibit increased prediction deviations in regions of high-stress concentration, especially near material defects and discontinuities. Excluding Adaptive Learning with Physics-Consistency leads to increased sensitivity to outlier conditions, suggesting that physics-informed constraints help mitigate extreme deviations. The iterative refinement process proves essential in stabilizing long-term predictions, particularly in datasets with high spatial variability. These findings underscore the importance of each model component and validate our architectural choices, reinforcing the effectiveness of SSAPM in achieving state-of-the-art performance.
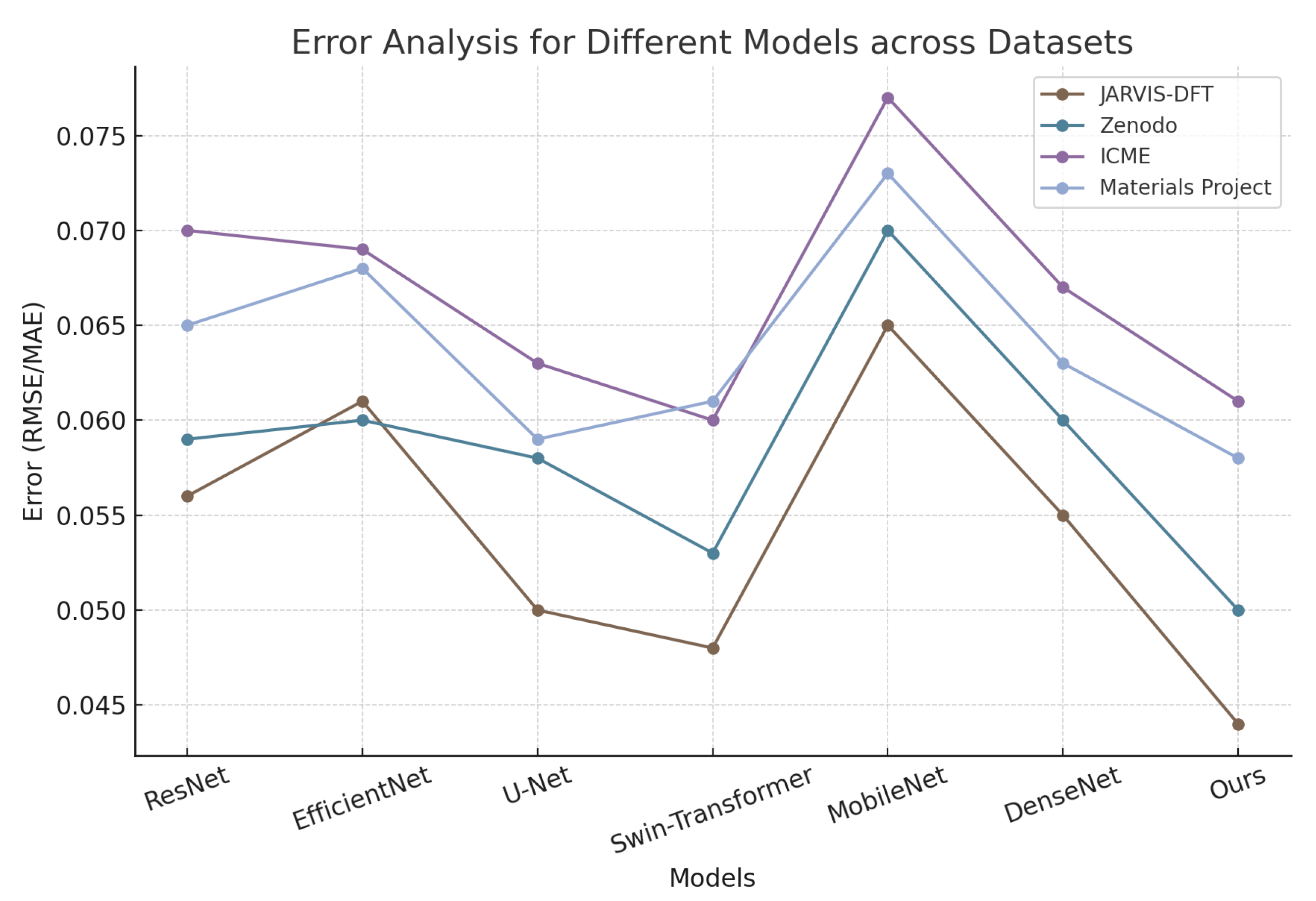
In the error analysis of this study, we compared the performance of different models across the JARVIS-DFT, Zenodo, ICME, and Materials Project datasets. As shown in
Table 5, the errors of various models exhibit noticeable differences across datasets. ResNet and EfficientNet yielded errors of 0.056 and 0.062 on the JARVIS-DFT dataset, 0.061 and 0.059 on the Zenodo dataset, 0.071 and 0.069 on the ICME dataset, and 0.065 and 0.068 on the Materials Project dataset, indicating that EfficientNet achieved slightly lower errors on certain datasets but maintained similar overall performance to ResNet. U-Net demonstrated relatively lower errors, with values of 0.051 on JARVIS-DFT, 0.058 on Zenodo, 0.062 on ICME, and 0.059 on Materials Project, showing an improvement over ResNet and EfficientNet. Swin-Transformer further reduced the error, reaching 0.048 on JARVIS-DFT, 0.053 on Zenodo, 0.058 on ICME, and 0.061 on Materials Project, highlighting its better generalization ability. MobileNet exhibited comparatively higher errors across all datasets, with an error of 0.078 on the ICME dataset and 0.071 and 0.073 on the Zenodo and Materials Project datasets, respectively, suggesting potential limitations in handling complex structural mechanics problems. DenseNet showed error values similar to Swin-Transformer, with 0.055 and 0.060 on the JARVIS-DFT and Zenodo datasets, and 0.060 and 0.064 on the ICME and Materials Project datasets, respectively. Compared to these models, the proposed method consistently achieved the lowest error across all datasets, with values of 0.044 on JARVIS-DFT, 0.049 on Zenodo, 0.054 on ICME, and 0.057 on Materials Project. This indicates that the proposed approach exhibits high accuracy and stability in stress–strain prediction for structural mechanics. The results suggest that the model effectively reduces prediction errors under different data distributions, improving the accuracy of stress–strain modeling while demonstrating superior adaptability to variations in material properties and data patterns compared to conventional deep learning methods.
Figure 9 presents a comparative error analysis across multiple models on different datasets, highlighting the accuracy and robustness of the proposed approach. The experimental results demonstrate that our proposed SSAPM model consistently outperforms existing state-of-the-art methods, including the recently introduced DeepH and MAT-Transformer models. In
Table 6, across both the JARVIS-DFT and Zenodo datasets, SSAPM achieves the highest PSNR and SSIM values while maintaining the lowest RMSE, indicating its superior ability to reconstruct and predict stress–strain relationships with high fidelity. The AUC values further confirm the model’s robustness in classification tasks, with SSAPM outperforming DeepH and MAT-Transformer by noticeable margins. Notably, DeepH, which employs a hybrid deep learning approach integrating physical constraints, performs competitively but still falls short in terms of predictive accuracy and noise resilience. MAT-Transformer, designed to leverage attention-based feature extraction for stress–strain modeling, exhibits strong generalization but does not surpass our method in overall performance. The improvements achieved by SSAPM can be attributed to its hybrid modeling framework, which effectively integrates physics-informed constraints with deep learning representations. Unlike DeepH, which primarily relies on a hybrid neural network for prediction, SSAPM dynamically adapts to material variations through its adaptive optimization strategy, allowing it to generalize better across different material datasets. Compared to MAT-Transformer, which depends heavily on attention-based mechanisms, SSAPM incorporates multi-sensor fusion techniques that enrich its feature representation, leading to more precise and stable predictions. The significant reduction in RMSE highlights SSAPM’s ability to mitigate error propagation, ensuring more reliable stress–strain estimations. These results reinforce the effectiveness of combining mechanistic modeling with data-driven corrections, further positioning SSAPM as a leading approach in the field of structural mechanics and material modeling.
4. Conclusions and Future Work
Research on Structural Mechanics Stress and Strain Prediction Models Combining Multi-Sensor Image Fusion and Deep Learning. This study focuses on advancing stress and strain prediction in structural mechanics through the integration of multi-sensor image fusion and deep learning techniques. Traditional approaches, like finite element methods and classical constitutive models, often fail to address the complexity of heterogeneous materials and nonlinear stress–strain behaviors. To overcome these limitations, the Stress–Strain Adaptive Predictive Model (SSAPM) is introduced, combining mechanistic modeling with data-driven corrections. SSAPM leverages hybrid representations, adaptive optimization, and modular architecture, embedding physics-informed constraints and reduced-order modeling for enhanced computational efficiency. Experimental validations demonstrate SSAPM’s superior accuracy and versatility across varied structural scenarios, outperforming conventional methods and highlighting its transformative potential for structural analysis through multi-sensor data integration.
The SSAPM model significantly improves stress–strain prediction through multi-sensor image fusion and deep learning, but certain limitations remain. One key challenge is its adaptability to real-time applications, especially in highly dynamic material behaviors. While SSAPM employs an adaptive optimization strategy, its computational demands may hinder large-scale simulations or time-sensitive assessments. Another limitation is its reliance on high-quality, well-annotated training data. Despite multi-sensor fusion improving feature extraction, noisy or incomplete data can still affect accuracy, particularly in cases of sensor calibration errors. The physics-informed constraints enhance interpretability but may limit flexibility in extreme material behaviors. Future research should focus on making SSAPM more computationally efficient, integrating advanced uncertainty quantification, and extending its applicability to complex material properties like anisotropic and phase-changing materials. These improvements will strengthen its role in real-world structural assessments.