In this section, we establish the common theoretical foundation of the DG and TDG approaches, setting the stage for the optimized approach introduced in this study. While our primary interest lies in two-dimensional Euler equations, this section begins by considering the one-dimensional conservation law system to establish the core concepts. This approach follows a common practice in computational fluid dynamics, where one-dimensional analyses help verify fundamental properties before extending to higher dimensions.
2.1. Common Approach of TDG Methods
Consider a one-dimensional conservation law, defined on a domain Ω, with solution
and flux
:
Nodal discontinuous Galerkin (nodal DG) schemes typically approximate the solution
by using its nodal values through a discretization process. However, DG methods offer a more flexible alternative, enabling the approximation of the solution
without discretization strictly based on nodal values. Specifically, in the
K-th element, where
lies in the interval
, the
-th component of the solution
can be approximated by a dot product of the expansion coefficient vector
and a basis function vector
. In this study, the basis functions
are chosen as Legendre polynomials [
16], which provide orthogonality and optimal convergence properties for polynomial-based approximations. Given that the basis function vector φ has N components, the approximation achieves a polynomial order of (
. Thus, the approximate solution
within the
K-th element is expressed as:
where
is the basis function matrix:
The numerical solution and basis functions may have different numbers of components for each element and should therefore be distinguished element-wise. However, for better readability of the equations, the superscript is omitted. Specifically, the -th component of the vector, , should be expressed as for K-th element (interval ). For simplicity, it is instead represented as .
To ensure that the approximation
satisfies the governing equation in a weak form, DG methods impose the following integral condition in each element [
1]:
Within this framework, introducing Taylor series expansions for the temporal derivative
enables the construction of TDG methods. By applying high-order Taylor expansions in time, TDG schemes can achieve superior temporal accuracy compared to standard time-stepping methods. This section focuses on a conventional third-order TDG approach [
12], which relies on Lax–Wendroff-type time integration to represent the inertia term
at
, in
K-th element as:
Therefore, the weak formulation of the Euler equations is:
To handle the high-order temporal derivatives,
and
, appearing in Equation (5), the flux Jacobian matrix
is defined as:
From Equation (8), the time-derivative terms and can be transformed into spatial derivatives by and its associated operators. The benefit of this approach is that all the temporal derivative terms in Equation (6) are converted into spatial derivatives, making it possible to obtain a higher-order estimate of the solution by one-step spatial integration. However, it can also be observed that increasing the order of the time Taylor expansion (using the Lax–Wendroff-type formulation) makes the operators related to more complex and consequently increases the number of numerical flux computations. To address this issue, the following sections will demonstrate a detailed explanation of how the optimized TDG method differs from the conventional TDG method, along with an outline of its computational procedure.
2.1.1. Differences Between the Conventional TDG and the Optimized TDG
In conventional TDG method, with Equations (7) and (8), the high-order temporal derivatives can be expressed as [
12]:
Similarly, for the third temporal derivative:
At the time =
n, the estimated value of the second temporal derivatives can be defined as:
Similarly, for the third temporal derivative:
Then, Equations (11) and (12) are substituted into Equation (6), and the spatial integration to obtain the solution at the next time is performed. This conventional TDG procedure elegantly combines spatial discretization (via DG) and temporal discretization (via Taylor expansions) to achieve high-order accuracy. However, a major limitation arises from the complexity of computing . Even for relatively simple conservation laws, such as the Euler equations, forms a third-order tensor that significantly increases computational overhead and complexity.
To avoid the usage of
, in this work, the high-order temporal derivatives are expressed as:
According to Equations (13) and (14), at the time = n, the estimated value of the high-order temporal derivatives can be defined as:
In this work, these new formulations with Equations (15) and (16) utilize
instead of
, effectively avoiding the computational cost associated with high-order tensor operations while maintaining high temporal accuracy.
Figure 1 illustrates difference between
,
, and tensor
at time
n. This figure highlights how the proposed method simplifies tensor operations, reducing computational overhead.
Obviously, to complete the calculations for Equations (15) and (16), we first need to determine the values of
and
. Based on Equation (4), the value of
can be obtained as follows:
Since the two-dimensional matrix
can be expressed in terms of
u and
, the next equation is written as follows:
From this discussion, it is evident that the computational procedure for the optimized TDG method proposed in this work differs from that of the conventional TDG method, which typically begins with a Lax–Wendroff-type time integration scheme and concludes with spatial integration (via the weak formulation of the DG method). In contrast, the optimized TDG method first employs the DG method to perform spatial integration and thus obtain
and
. It then substitutes the time derivative terms into the time Taylor expansion as:
2.1.2. The Calculation of High-Order Temporal Derivatives by the Finite Difference Method Outside the Element
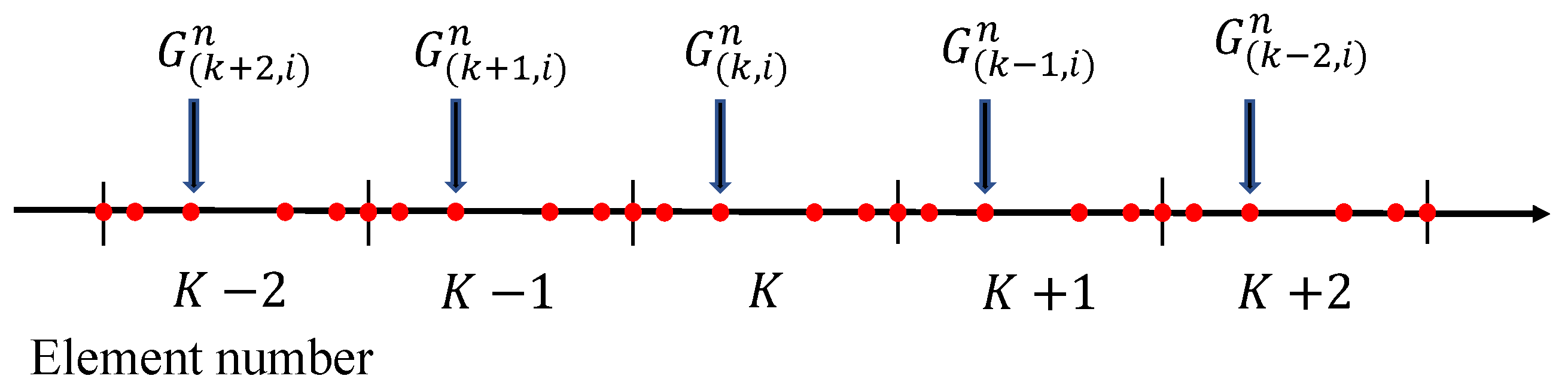
Although the computational cost of the optimized TDG method is lower than that of the conventional TDG method, the computational complexity of the high-order temporal derivatives’ estimation process remains significant. In Equations (33) and (34), the computation of spatial differentiation is necessary to estimate high-order temporal derivative terms
and
. To this end, this study uses the computational strategy optimized in [
8], which applies the FDM to simplify the spatial differentiation calculation procedure. Although the nodal DG method is employed for spatial discretization in this study, the FDM is applied to the discrete nodes. The discrete nodes and elements constructed by the nodal DG method are illustrated in
Figure 2.
When the nodal DG method is used, an estimated solution and an inertia term for a discrete point i in an element K at a time n can be obtained directly by calculating the spatial integral. Consequently, the value of matrix at a point i can be obtained.
According to Equations (15) and (16), functions
and
are derived as follows:
where
,
, and
denote the time, element number, and position number of a point in an element, respectively.
In this study, the fourth-order central difference approximation is used to calculate the high-order temporal derivatives by outside element information. As illustrated in
Figure 3, to calculate the high-order temporal derivatives at a target point i in an element K, the values of functions
and
at point i in four elements surrounding the target point must be obtained.
The difference form of the second-order temporal derivative term is calculated by:
In the same scheme, the different form of the third-order temporal derivative term is obtained by:
These operations are used when the optimized method is applied to the test cases presented in this study, which is called the optimized TDG outside element method.
2.1.3. The Calculation of High-Order Temporal Derivatives by the Finite Difference Method Inside the Element
There will be a distinct disadvantage in the above approach, which is that at the boundaries, it is not possible to construct the center difference format directly. At the edges of the computational domain, it is necessary to use one-side difference form. This problem is relatively easy to solve in one-dimensional problems, but for two-dimensional problems it requires a lot of effort to construct the difference form at the boundary. Especially in terms of computational accuracy, to maintain the computational accuracy of the center difference, then at the boundary, it is necessary to construct a difference form that covers the information of multiple cells.
In the optimized TDG method, the nodal DG approach is utilized to discretize elements into a set of discrete points. Based on this discretization, the information at these points can be leveraged to construct new differential forms. These differential forms are primarily required for estimating first-order spatial derivatives. Compared to the modal DG method, the nodal DG approach provides more detailed information within each element, eliminating the need to rely on data from neighboring elements.
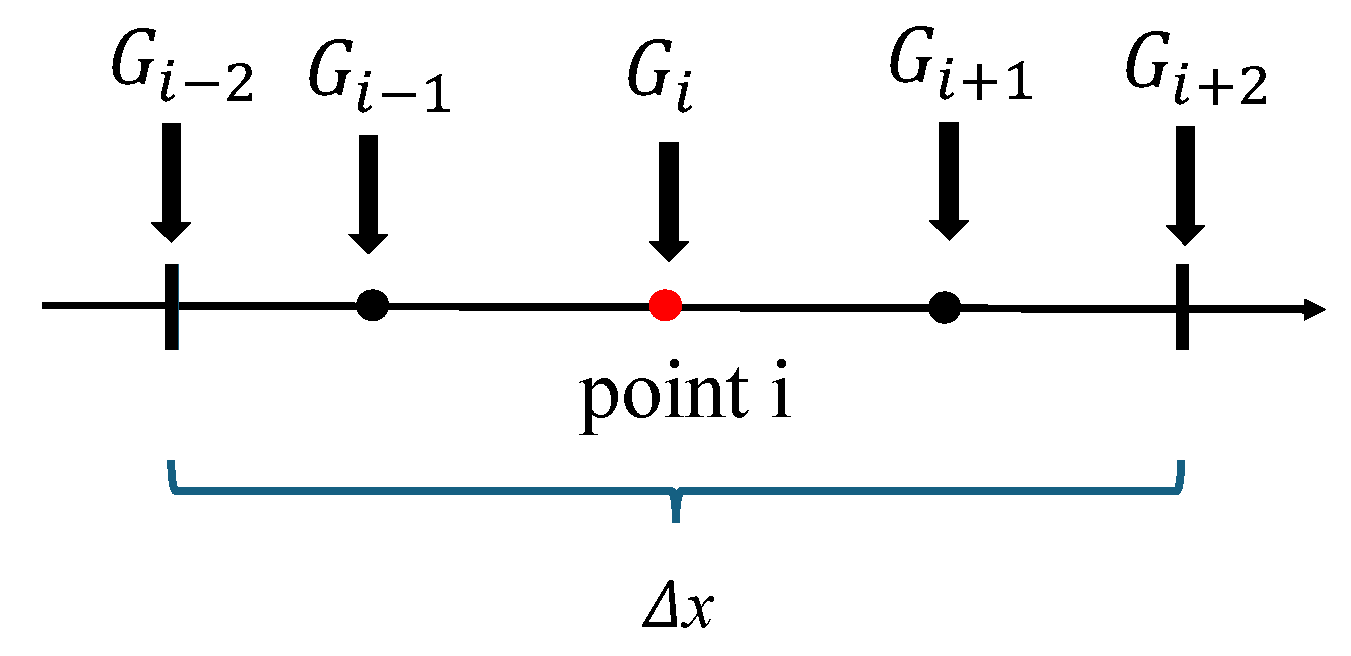
If the central difference method is used, the difference formulation within an element is influenced by the positions of the discrete points. This necessitates special handling for the discrete points located at the edges of the element. To address this, the present study employs a higher-order Taylor expansion to construct a differential structure that effectively utilizes the available information at these points. This approach ensures an organized computational framework, where the coefficients of the differential formulation can be precomputed based on the positions of the discrete points. This precomputation is performed while the mesh remains constant, prior to starting the time iteration process.
This Taylor difference method estimates the first-order spatial derivatives of unknowns at discrete points by employing the estimated values of all discrete points in one element, as in
Figure 3. The process in the one-dimensional format is as follows:
Discretization: A one-dimensional segment is treated as a computational element, which is discretized into N points. The estimated values of the governing equations at these points are known;
Taylor expansion: For each point
in the element, the function values at all other points
are expressed using a Taylor series expansion around
:
where
and higher-order derivatives are unknown;
Equation system: Using the known function values at the discrete points, the Taylor expansions for all N points are combined to form a system of N equations;
Solution: By solving this system of equations, the first-order spatial derivative is computed for each point . Higher-order derivatives may also be obtained if needed, but only the first-order derivative is typically retained in this algorithm;
Output: The algorithm produces the first-order spatial derivative
for each point
in the element and the coefficients
of the N equations system. The finite difference function
is:
The above computations correspond to the process of determining finite difference coefficients based on the positions of discrete points. Consequently, this process can be completed before initiating any temporal iterations, and in each subsequent time step, one may directly use the precomputed coefficient matrices. Next, we will illustrate how to compute higher-order temporal derivatives within a one-dimensional element containing five discrete points, once the finite difference coefficients have been obtained using the approach.
According to Equations (15) and (16), functions
and
in k-th element are derived as follows:
where
n,
k, and
i denote the time, element number, and position number of a point in an element, respectively.
As described in
Section 2.1.2, in element
K, at the time
n, with the functions
(24) and
(25), when the
N order of polynomials is 4, the difference form of the second-order temporal derivative term is calculated by:
Since the same finite difference method is employed to compute the first-order spatial derivatives, the coefficients can likewise be used to calculate the third-order temporal-derivative terms by:
The coefficients vector
and the functions
,
vectors in
K-th element can be defined as:
Since Equations (28)–(30) can be substituted into Equations (26) and (27), the high-order temporal derivatives terms can be calculated as:
Based on the foregoing discussion, the optimized TDG method can be characterized as a hybrid method. Specifically, the first-order temporal derivative at each discrete point is estimated by the DG method from the weak formulation. Subsequently, higher-order temporal derivatives , —commonly employed in the conventional TDG (Lax–Wendroff temporal discretization) framework—are determined by following the approaches outlined in Equations (11) and (12). In this step, the estimated first-order temporal derivative, along with the temporal derivative of matrix A and its higher-order temporal-derivative , are leveraged to infer the and . Thereafter, employing the Taylor series expansion in time allows one to estimate the solution at the next time. Notably, because the higher-order temporal derivatives of matrix A like can be systematically obtained, while maintaining the matrix operators in the two-dimensional matrix form, the usage of the is rendered unnecessary. Therefore, this approach can accommodate higher-order Taylor expansions in time, such as fourth-order or fifth-order expansions, while keeping the temporal derivatives of matrix A in a two-dimensional matrix form, thus avoiding the need for three-dimensional (tensor) or higher-dimensional matrices.
2.2. The Comparison of the Conventional TDG and Optimized TDG
In this section, a comparison is made between the conventional TDG and the optimized TDG (outside form and inside form) by expressing their solutions in an explicit form.
For the conventional TDG method, substituting Equations (11) and (12) into Equation (6), the solutions can be expressed as:
The above results clearly represent a complete integral form, obtained through spatial integration using the weak formulation. To achieve high-accuracy solutions, ∂A⁄∂U and repeated flux calculations were employed.
For optimized TDG with outside finite difference method, substituting Equations (17), (22), and (23) into Equation (19), the solutions can be expressed as:
For optimized TDG with the inside finite difference method, substituting Equations (17) and (31) into Equation (19), the solutions can be expressed as:
Compared to Equation (32), Equations (33) and (34) do not utilize
but instead employ the simpler operator
, as explained in
Section 2.1.2. Furthermore, from Equation (33), it can be observed that the optimized TDG method is a hybrid method combining the DG method and the FDM method. During the application of the FDM method, Equation (33) uses information from elements surrounding the target element for the finite difference calculations. In contrast, Equation (34) demonstrates a way of performing differential calculations using information inside the target element. Clearly, the approach of estimating high-order time derivative terms using internal element information provides better compactness.