Abstract
The Michaelis constant (Km) is defined as the substrate concentration at which an enzymatic reaction reaches half of its maximum reaction velocity. The determination of Km can be applied to the construction and optimization of metabolic networks. Conventional determinations of Km values based on in vitro experiments are time-consuming and expensive. Although there are a series of computational approaches of determining Km values based on deep learning, the complex biological information in enzymatic reactions still makes it challenging to achieve accurate predictions. In this study, we develop a novel deep learning approach called DLERKm for predicting Km by combining the features of enzymatic reactions including products. We constructed a new enzymatic reaction dataset from the Sabio-RK and UniProt databases for the training and testing of DLERKm, which include the information on substrates, products, enzyme sequences, and Km values. DLERKm utilizes pre-trained language models (ESM-2 and RXNFP), molecular fingerprints, and attention mechanisms to extract enzymatic reaction features for the prediction of Km values. To evaluate the performance of DLERKm, we compared it with a state-of-the-art model (UniKP) on the constructed enzymatic reaction datasets. The model prediction results demonstrate that DLERKm achieved superior prediction performances in terms of the evaluated metrics on the benchmark datasets, where the relative improvements of four metrics (RMSE, MAE, PCC, and R2) were 16.3%, 16.5%, 27.7%, and 14.9%, respectively. Ablation experiments and interpretability analysis demonstrate the importance of considering product information when predicting Km values. In addition, DLERKm exhibits reliable predictive performances for different types of enzymatic reactions.
1. Introduction
The enzyme-catalyzed system serves as an essential tool in green chemistry due to its high conversion efficiency, substrate specificity, and mild reaction conditions [1,2,3]. For instance, in the field of carbon neutrality technologies, enzymatic catalysis significantly reduces energy consumption compared to traditional thermocatalytic pathways [4]. In synthetic biology, studies indicate that constructing heterologous biosynthetic pathways essentially involves rationally redesigning enzymatic reaction networks [5,6]. In this process, the Michaelis constant (Km) is defined as the substrate concentration at which an enzymatic reaction reaches half of its maximum reaction velocity [7,8]. The variation in Km provides fundamental information for understanding cellular metabolic regulation, bioinformatics, and microbial resource allocation optimization. For example, decreasing the Michaelis constant (Km) of a key enzyme by an order of magnitude can significantly enhance the efficiency of target product biosynthesis [9,10,11]. Moreover, the Km parameter can be regarded as a performance metric of the “bioengineering chip” and systematically optimizes enzyme-substrate bioinformatics through directed evolution [12,13] and computational modeling [14,15]. As a key constant in enzymatic reaction systems, Km plays a crucial role in the quantitative analysis of bioengineering and biosciences processes.
In conventional enzyme kinetics studies, experimental determinations of Km involve steady-state kinetic analysis [16], nonlinear fitting using the Michaelis–Menten equation [17], and cross-validation with the Lineweaver–Burk double-reciprocal plot method [18]. However, these approaches are typically time-consuming, which significantly increases experimental complexity [19], and impose strict requirements on substrate solubility and enzyme stability [20]. In recent years, the successful applications of deep learning to various fields of bioinformatics have provided new directions for predicting enzyme kinetic parameters [21]. Li et al. [22] constructed a dataset containing 16,838 enzyme-substrate pairs and developed DLKcat employing convolutional neural networks (CNNs), graph neural networks (GNNs), and attention mechanisms to predict turnover number (Kcat) values. Furthermore, Kroll et al. [23] provided a dataset containing 4281 samples of substrate, enzyme sequence, product, and Kcat values and designed a Kcat prediction model named TurNuP. By incorporating ESM-1b [24] and numerical reaction fingerprints to represent enzymatic reactions, TurNuP enhances the generalization ability of enzyme kinetic parameter predictions. Moreover, Kroll et al. [25] proposed a Km prediction model by using molecular fingerprints and graph representations as input features.
In this study, we propose a novel deep learning approach called DLERKm for predicting Km values, which incorporates substrates, products, and enzyme sequences as inputs. The model aims to extract features using deep learning methods from enzymatic reactions to predict Km values (DLERKm). By collecting samples from Sabio-RK [26] and UniProt [27] databases and proper data processing, we constructed a new enzymatic reaction dataset including the information of substrates, products, and enzyme sequences. DLERKm uses a reaction pre-trained language model called RXNFP [28] to extract the features of enzymatic reactions described by SMILES strings, and uses a protein pre-trained language model called ESM-2 [29] to extract the features of enzymes described by amino acid sequences. To capture the molecular chemical property changes in the enzymatic reactions, DLERKm represents the molecular sets of substrates and products in the dataset with 1024-dimensional molecular fingerprints. Furthermore, the extracted features are refined by using channel attention mechanisms [30], which are then fed into fully connected layers to output Km prediction values. We demonstrated the superior prediction performances of DLERKm by visualizing its prediction results and comparing with a benchmark model. Additionally, the ablation experiments and interpretability analysis highlight the significance of incorporating products information when predicting Km values. Moreover, DLERKm demonstrates reliable predictive performances across various types of enzymatic reactions.
Our main contributions are as follows: (i) we incorporate product information into the Km prediction task for the first time and construct a related dataset; (ii) we employ RXNFP to extract enzymatic reaction features for Km prediction for the first time; and (iii) we develop a novel Km prediction model (DLERKm) by integrating multi-modal information from enzymatic reactions. The rest of this paper is organized as follows: Section 2 reviews some related works that are relevant to this article. Section 3 introduces the processing pipeline of the benchmark datasets to be used in this paper and the details of the proposed DLERKm model. Section 4 discusses the prediction performances and results analysis of DLERKm, along with its limitations and potential future research directions.
2. Related Work
In this section, we review a series of related works for predicting Km by using machine learning and deep learning approaches, which are summarized in Table 1.
Borger et al. [31] used EC numbers and biological types as inputs for a linear regression model to predict Km values and tested the model prediction performances through cross-validation. Yan et al. [32] predicted Km values using a multilayer perceptron and optimized cellobiose production. Dai et al. [33] utilized a multilayer perceptron and the physicochemical properties of substrate molecules to improve the accuracy of Km prediction in CYP450-mediated reactions. Maeda et al. [34] proposed the Machine Learning-Aided Global Optimization (MLAGO) algorithm, which predicts Km values by incorporating EC number, compound ID, and organism ID as inputs. The above methods based on traditional machine learning manually designed input features, which limits the prediction performances and practical applications.
In recent years, some deep learning-based methods have been proposed for predicting Km values, due to their powerful nonlinear fitting capabilities and feature extraction abilities. Wang et al. [35] proposed MPEK, which utilizes a protein pre-trained language model called ProtT5 [36] and a molecule pre-trained model called Mole-BERT [37] to extract features from enzyme and molecular sequences, respectively. Shen et al. [38] developed EITLEM, which employs a protein pre-trained language model called ESM-1v to extract the features of enzyme sequences and incorporates substrate molecule information and attention mechanisms. The UniKP model developed by Yu et al. [39] uses a protein pre-trained model called ProtT5-XL-UniRef50 and the SMILES Transformer model as upstream feature extractors and adopts an ensemble model generated by random forest and extreme trees algorithms as the downstream prediction module.
However, as shown in Table 1, existing Km prediction approaches based on deep learning only use enzyme–substrate pairs as inputs, which limits the feature extractions of entire enzymatic reactions for Km predictions. To address this issue, this study constructed a new enzymatic reaction dataset including product information and developed a DLERKm model utilizing the information of substrates, products, and enzymes in enzymatic reactions as inputs to predict Km values.

Table 1.
List of related works on Km predictions.
Table 1.
List of related works on Km predictions.
| Related Work | Architecture | Input | Other Inputs |
|---|---|---|---|
| Borger et al. [31] | Linear regression model | enzyme-substrate | Organism |
| Yan et al. [32] | Multilayer perceptron | enzyme-substrate | / |
| Dai et al. [33] | Multilayer perceptron | enzyme-substrate | Physicochemical properties |
| MLAGO [34] | Random forest model | / | EC, Compound, Organism |
| MPEK [35] | ProtT5, Mole-BERT, Gating network | enzyme-substrate | pH, Temp, Organism |
| EITLEM [38] | ESM-1v, Fingerprints, ProMolAtt | enzyme-substrate | / |
| UniKP [39] | ProtT5, SMILES Transformer, Ensemble module | enzyme-substrate | pH, Temp |
| DLERKm (This study) | ESM-2, RXNFP, Fingerprints, Channel attention | enzyme-substrate-product | / |
3. Materials and Methods
3.1. Benchmark Dataset
Sabio-RK [26] and UniProt [27] are essential databases for metabolic model constructions, which provide critical data support for deep learning-based predictions modeling. Sabio-RK is a database for enzymatic reaction kinetics that integrates kinetic parameters detemrined by experiments (such as Km, Kcat, and Ki), enzymatic reaction (SabioReactionID), and enzyme sequence IDs (UniProtKB AC). UniProt is a widely recognized protein database that offers comprehensive enzyme information, including protein sequences and functional annotations.
As shown in Figure 1A, to construct a ternary dataset of substrates, products, and enzyme sequences for model training and Km prediction, we first collected Sabio-RK for enzymatic reaction entries that include Km values. Then, we collected enzymatic reaction samples from two species with the highest data available on the platform: Homo sapiens (H. sapiens) and Escherichia coli (E. coli). This resulted in a total of 16,322 samples, and more details can be found in Figures S1–S4 of the Supplementary Materials. Furthermore, we removed samples without Km values or corresponding UniProt IDs for enzyme sequences, resulting in 4146 enzyme reaction samples from E. coli and 8672 enzyme reaction samples from H. sapiens. Using the SabioReactionID and UniProtKB AC from these samples, we retrieved substrate SMILES, product SMILES, and enzyme amino acid sequences from Sabio-RK and UniProt databases, where samples that could not be retrieved from the databases or lacks mutation site information were excluded. As a consequence, we obtained yielded a total of 10,122 enzymatic reaction samples.

Figure 1.
The framework of DLERKm. (A) The E. coli and H. sapiens data used in this study were obtained from the SABIO-RK database in which samples include the information of enzymatic reaction IDs, UniProtKB AC numbers, and Km values. After processing, we obtained 2962 enzyme reaction samples from E. coli and 7160 enzyme reaction samples from H. sapiens, respectively, containing the information of substrates, products, enzyme sequences, and Km values. (B) The pre-trained model ESM-2 is employed to extract features from enzyme sequences. (C) The pre-trained model RXNFP is used to extract meaningful features from the enzymatic reaction SMILES strings. (D) Molecular set features are extracted using molecular fingerprints and logical operations. (E) The extracted features are refined using a channel attention mechanism and fed into a feedforward neural network to predict Km values.
Furthermore, we split the datasets of two species into training and test subsets according to the ratio of 8:2. As shown in Figure 2, the benchmark dataset from E. coli include 1932 samples of wild-type enzymes and 1030 samples of mutant enzymes. To maintain the ratio of wild-type and mutant enzymes, we randomly selected 386 wild-type and 207 mutant enzyme reaction samples to form the test set, and the remaining 2369 samples were assigned to the training set. Similarly, the benchmark dataset from H. sapiens include 5823 samples of wild-type enzymes and 1337 samples of mutant enzymes. Following the same procedure, we randomly selected 1164 wild-type and 268 mutant enzyme reaction samples to form the test set, and the remaining 5728 samples were assigned to the training set. Finally, by merging the training sets (resp. test sets) of E. coli and H. sapiens, we obtained a total of 8097 training samples and 2025 test samples, which can be referred to in Table 2.
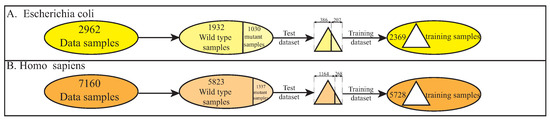
Figure 2.
Data processing steps for E. coli and H. sapiens.

Table 2.
Number of data samples.
3.2. Overall Framework
The overall architecture of the Km prediction model, DLERKm, is shown in Figure 1, which aims to predict Michaelis constant (Km) values by simultaneously using substrate, product, and enzyme information from enzymatic reactions. This model consists of four main components: the enzyme sequence feature extraction module and the enzymatic reaction feature extraction module, the molecular set feature extraction module, and the downstream prediction module.
3.3. Enzyme Sequence and Enzyme Reaction Feature Extraction Modules
In biological reactions, enzyme sequences and enzymatic reactions contain complex, long-distance dependencies and contextual patterns between amino acids and atoms. This complexity makes it difficult for traditional methods to capture all the relevant information. Pre-trained large language models were trained on large-scale biological sequences through self-supervised learning, which possess strong feature representation abilities. These models can efficiently identify key information and improve the accuracy of feature expression to provide biologically meaningful representations for downstream prediction tasks. Among these, the pre-trained model BERT uses the Transformer encoder architecture and is pre-trained on a vast amount of unsupervised prior data [40]. This enhances its ability to represent enzyme sequences and enzymatic reactions, which provides strong support for the prediction of enzyme kinetic parameters. As shown in Figure 3A, the main structure of BERT consists of N encoder layers, each of which is composed of a multi-head attention mechanism, a normalization layer, and a feed-forward layer.

Figure 3.
(A) The structure of BERT-based pre-trained language model, which consists of multi-head attention layers, normalization layers, and feed-forward layers. (B) The structure of the multi-head attention layer, where the input matrix is linearly transformed to obtain query, key, and value, and attention scores are then computed using dot-product attention to update the feature matrix. (C) The feed-forward layer, which is composed of linear layers and activation functions. (D) The channel attention mechanism, which calculates attention scores along the channel dimension of the input tensor and refines the features using broadcasting and residual connections.
For any input matrix , as shown in Figure 3B, the multi-head attention mechanism in the m-th encoder captures the contextual relationships of the sequence based on , , of each input token. The feature matrices obtained from multiple heads are concatenated and processed through residual connections to obtain . Furthermore, the normalized feature matrix is fed into the feed forward neural (FFL) network. After residual connection and normalization, the output matrix is obtained. As shown in Figure 3C, FFL represents the feed-forward neural network. This operation consists of Linear, ReLU, and Linear layers. The details of the encoder layer are provided in Supplementary Note S1. The FFL operator is defined as follows:
To build the ESM-2 model, the Meta-AI research team [29] used a 33-layer transformer encoder structure and treated the output matrix of the final layer as the representation of the protein. The model consists of approximately 650 million parameters and is trained in an unsupervised manner using around 50 million protein amino acid sequences from the UR50D database. This allows the ESM-2 model to effectively learn the internal relationships of amino acid sequences. The training method involves randomly masking a portion of the amino acid sites in the input protein sequence and using the built ESM-2 model to predict the unknown amino acids. In this paper, as shown in Figure 1B, we use the model (ESM2_t33_650M_UR50D) as the enzyme sequence feature extractor for enzyme-catalyzed reactions to obtain high-quality feature representations of the first 400 amino acids in the enzyme sequence. Similarly, the RXNFP [28] pre-trained model consists of multiple transformer encoders and uses the vector of the first token from the model output as the representation of the enzyme-catalyzed reaction SMILES string. RXNFP is trained on the 2.6 M chemical reaction dataset (Pistachio database) and fine-tuned on the USPTO database to result in a feature vector to represent enzyme-catalyzed reaction strings. Here, as shown in Figure 1C, we use the fine-tuned RXNFP to extract the specific representation of enzyme-catalyzed reaction strings.
3.4. Molecular Set Feature Extraction Module
The molecular set feature extraction module is shown in Figure 1D. To represent the chemical property changes in enzymatic reactions, we obtained 1024-dimensional binary molecular fingerprint vectors for the molecules involve in the reactions using the RDKit package [41], where each bit represents a unique chemical property of the molecule. Then, we perform a bitwise OR operation on the molecular fingerprints of the molecules in both the substrate and product sets to obtain molecular fingerprints and , representing the substrate and product sets, respectively. The process is expressed as follows:
where represents the molecular fingerprint of the r-th molecule in the substrate set, and represents the molecular fingerprint of the t-th molecule in the product set.
Furthermore, to describe the changes in the chemical properties of the molecular sets in the enzymatic reaction, we perform bitwise AND and bitwise OR operations on the molecular fingerprints of these two different sets. The results are used as inputs to the linear layer to obtain the feature vectors and for the two molecular sets, respectively. The above operation can be expressed as follows:
Finally, the sum enzymatic reaction fingerprints (SERF) vectors and the difference enzymatic reaction fingerprints (DERF) vectors are fed into inputs to the normalization layer. These final vectors represent the molecular fingerprints of the enzymatic reaction and serve as one of the inputs to the downstream prediction module. The above process is expressed as follows:
3.5. Downstream Prediction Module
The downstream prediction module is shown in Figure 1E. By feeding the concatenated features into the channel attention mechanism, the refined feature matrix is obtained. This process can be represented as follows:
where ChaAtt is defined as the channel attention mechanism, as shown in Figure 3D, and the input matrix is processed by max pooling and average pooling to obtain two one-dimensional vectors. These vectors are then fed into the shared parameter cascaded convolution layer to obtain the input vector and . The process is represented as follows:
the above vectors are added together and passed through a Sigmoid activation function to obtain the channel attention ; the process is expressed as
furthermore, the channel attention is element-wise multiplied with the input matrix using broadcasting and combined with the residual connection to obtain ; the above process is represented as
Finally, the output to predict the Km value is obtained by using an FFL (feed-forward layer) network, which is expressed as
In the training phase of the model, we use the MSE function as the loss function, which is defined as follows:
where b represents the batch size during training, and represents the true Km value for the i-th sample after applying the transformation. Additionally, to prevent certain Km values from being non-computable, we add a bias coefficient of to the original true value, and denotes the i-th sample predicted Km value predicted by DLERKm (Equations (2)–(9)). The Adam optimizer was employed to iteratively adjust the parameters based on the gradient descent method. All experiments were performed on a machine with an Intel(R) Xeon(R) Gold 6226R CPU, 256 GB of RAM (Intel, Santa Clara, CA, USA), and three NVIDIA GTX 4090 GPUs (Nvidia, Santa Clara, CA, USA).
3.6. Evaluation Metrics
In this study, to systematically assess the reliability of the enzyme kinetic parameter DLERKm prediction model, we employ four statistical evaluation metrics: the root mean square error (RMSE) to reflect the overall deviation level between predicted and experimentally measured values, the mean absolute error (MAE) to demonstrate prediction accuracy from the perspective of absolute deviation, the coefficient of determination (R2) to evaluate model fitting performance by quantifying the proportion of explained variance in dependent variables, and the Pearson correlation coefficient (PCC) to specifically assess the strength of linear correlation between predicted and truth values. The mathematical formulations of these metrics are defined as follows:
where n is the number of samples in the test dataset, is the true Km value in the test dataset, is the predicted Km value, is the mean of the true Km values in the test dataset, and is the mean of the predicted Km values.
4. Results
4.1. Ablation Experiment
To evaluate the effectiveness of different input features in the model, we performed ablation studies on DLERKm and its variants to assess prediction performances. By removing the molecular set fingerprint features extracted by molecular set feature extraction module, we obtained a variant of DLERKm, denoted as DLERKm-v1. Additionally, by removing the enzymatic reaction features extracted by RXNFP, we obtained another variant of DLERKm, called DLERKm-v2. The architectures of these two variants are shown in Supplementary Figure S5. Specifically, we used the same hyperparameters to train these models and compared the prediction performances of DLERKm, DLERKm-v1, and DLERKm-v2 on the same test set.
To evaluate the importance of different input features, we compared the prediction performances of DLERKm with its variants. The values of RMSE, MAE, R2, PCC metrics for all these models on the test set are shown in Figure 4. The results show that DLERKm, which incorporates enzyme sequence features, enzyme reaction features, and molecular set features as input, outperforms the other two variant models (DLERKm-v1 and DLERKm-v2) in terms of evaluation metrics. As shown in the Table 3, the relative improvements of DLERKm over DLERKm-v2 in terms of RMSE, R2 and PCC are 0.2%, 0.7%, and 0.3%, respectively. Furthermore, DLERKm-v2 shows improvements over DLERKm-v1 by 4.2%, 8.9%, 6.7%, and 3.3% in terms of RMSE, MAE, R2, and PCC. Moreover, we compared the computation scales of DLERKm and its variants in terms of the training time and GPU memory usage, where more details can be found in Supplementary Table S1. The results illustrate that the computation cost of DLERKm and its variants are almost the same, which means that introducing molecular set fingerprint features and enzymatic reaction features can improve the model prediction performances without consuming additional computation resources.
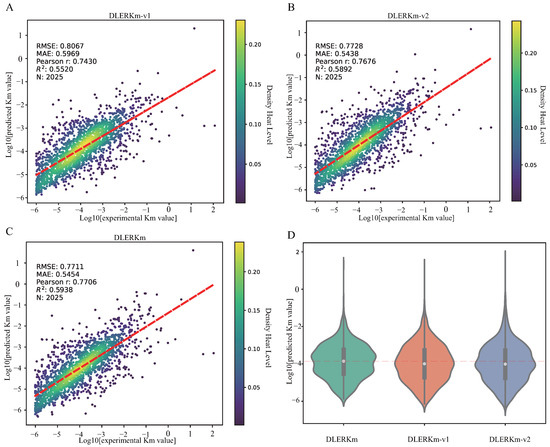
Figure 4.
Prediction results and performances of DLERKm and two variants. (A) Scatter plots of prediction results for DLERKm-v1. (B) Scatter plots of prediction results for DLERKm-v1. (C) Scatter plots of prediction results for DLERKm-v2. (D) Violin plot of prediction results for DLERKm and two variants.

Table 3.
Metric values of prediction results for DLERKm, DLERKm-v1, and DLERKm-v2.
Moreover, to show the interpretability of DLERKm, we investigate the importance of these input features, where the visualization results are shown in Figure 5. The results indicate that products and reaction features are equally important as enzyme sequence and substrate features for Km prediction task, thereby explaining the effectiveness of these features.

Figure 5.
(A) Visualization of channel attention scores for input features for all the test samples. (B) Visualization of mean channel attention scores of various types of input features.
In summary, the above results show that extracting enzymatic reaction features (including product information) is crucial for predicting Km values. Specifically, the interpretability analysis further demonstrates that considering changes in molecular fingerprints (DERF) in enzymatic reactions is the main reason for improving the model prediction performances.
4.2. Comparison with Other Models
To evaluate the prediction performances of DLERKm, we trained and tested DLERKm and UniKP [39] on the same dataset and compared their prediction results by using four evaluation metrics: RMSE, MAE, R2, and PCC. As stated above, UniKP utilizes the pre-trained models ProtT5-XL-U50 and Smiles Transformer to extract enzyme sequence and substrate features, which are then combined with the extra tree algorithm to predict enzymatic kinetic parameters. Compared with other similar models, UniKP has been validated in terms of its reliability in real-world bioengineering tasks [42,43,44]. Therefore, it is meaningful to use UniKP as a benchmark model for comparison.
Figure 6 presents all evaluation metric values of both DLERKm and UniKP. As shown in Table 4, compared with UniKP, DLERKm achieves the improvements of approximately 16.3% and 16.5% in RMSE and MAE on the same test samples. Additionally, the relative improvements of DLERKm over UniKP in terms of R2 and PCC are 27.7% and 14.9%, respectively. Moreover, as illustrated in Figure 6A,B, the correlation between the predicted Km values of DLERKm and the true values is more significant.

Figure 6.
Km value prediction results of DLERKm and UniKP. (A,B) Scatter plots and prediction value distributions of DLERKm and UniKP. (C–F) Distributions of performance metric values for DLERKm and UniKP on different test subsets. (G–J) Comparison of DLERKm and UniKP prediction metric values across different ranges of actual values.

Table 4.
DLERKm and UniKP prediction metric values for RMSE, MAE, R2, and PCC.
Furthermore, we randomly split the test set into ten subsets and recorded the prediction metric values for both models on these ten subsets. As shown in Figure 6C–F, the predictions of DLERKm exhibit better data stability and superior evaluation performance compared with UniKP. Additionally, we also analyzed the distribution of true values in the test set and divided them into four intervals to compare the prediction performances of DLERKm and UniKP at different value scales. As shown in Figure 6G–J, the results show that the evaluation metric values of DLERKm outperform UniKP across all intervals. Specifically, in the four intervals, as shown in Tables S2–S4 of the Supplementary Materials, RMSE, MAE, R2, and PCC achieve improvements of at least approximately 9.32%, 10.55%, 37.58%, and 17.29%, respectively.
Moreover, to compare the prediction performances of DLERKm and UniKP across different types of enzymatic reaction, we divided the test samples into two subsets based on wild-type (1550 samples) and mutant enzymatic reactions (475 samples), respectively. As shown in Figure 7, UniKP performs worse than DLERKm in both wild-type and mutant enzymatic reaction test sets. As shown in Table 5, the relative improvements of DLERKm are 16% and 17% for wild-type and mutant enzymatic reactions in terms of RMSE, respectively. Compared with UniKP, DLERKm shows improvements of 16.3%, 37.7%, and 41.2% across the three metrics (MAE, R2, PCC) for wild-type enzymatic reactions. Moreover, the values of above three metrics increase by approximately 16.8%, 41.2%, and 18.8% for mutant enzymatic reactions, respectively.

Figure 7.
Evaluation metric values of DLERKm and UniKP on different types of enzymatic reaction. DLERKm and UniKP metric values visualization for wild-type enzyme. DLERKm and UniKP metric values visualization for mutant enzyme.

Table 5.
DLERKm evaluation metric values on different types of enzymes.
In summary, we demonstrated that DLERKm has exhibited better goodness of fit and shown improvements in all four evaluation metrics (RMSE, MAE, PCC, R2) when trained and tested on the same dataset as UniKP. The results demonstrate that DLERKm is a more reliable method for high-throughput enzyme screening. Moreover, the model prediction results on wild-type and mutant enzymatic reaction samples illustrate that DLERKm not only excels at extracting features from the wild-type enzyme sequences but also captures the impact of amino acid mutations at specific sites on the Km values.
4.3. The Impact of Enzyme Sequence Similarity on DLERKm Prediction Performance
To validate the generalization ability of DLERKm in predicting other enzymes, we constructed different training subsets by removing training samples that were most similar to the top-K (K = 5, 10, 15, 20) entries in the test set. As shown in Table 6, increasing the number of removed samples from the training set can decrease the similarity between the training and test samples.

Table 6.
The distribution of test set samples after removing the top-K most similar enzyme sequences from the training set, where top-K is determined by selecting the K most similar training samples for each test sequence. The column names in the table (e.g., “0.40–0.80”) represent the similarity range between test samples and training samples, while the values in the table indicate the number of test samples falling within the corresponding similarity range.
Moreover, we trained DLERKm on four different training subsets and tested it on the test set. As shown in Table 7, the results illustrate that the prediction performances of DLERKm decreases as the difference between the training and test set samples increases. This trend is similar to the results of other prediction models [22,23,25]. However, it is worth noting that the PCC metric values remain stable above 0.5, which means that even with a large difference in sequence similarity, DLERKm is still able to provide valuable insights for enzyme screening.

Table 7.
Evaluation metric values (RMSE, MAE, R2, PCC) of DLERKm on the test set trained with different training subsets.
Furthermore, Figure 8 shows the prediction results of the trained DLERKm models according to four training subsets on three sequence similarity ranges. For a given training subset, the model evaluation metric values generally increase as the similarity between enzyme sequences increases. By observing the changes in DLERKm performance metric values across different training subsets, we find that as more samples are removed, the model prediction performance deteriorates. However, in the training subsets corresponding to the Top-5 and Top-10, DLERKm achieves better performances despite having fewer training samples when the training similarity range is 0.80–0.95. We suppose that some redundant samples are removed, which instead helps the model learn the characteristics of enzymatic reactions more effectively.

Figure 8.
Prediction metric values (PCC, R2) of DLERKm under different similarity (enzyme sequence) ranges.
Overall, although changes in sequence similarity generally affect the model results of DLERKm, it still provides relatively reliable predictions even in extreme cases (Top-20). Additionally, through multiple comparisons of DLERKm model prediction performance at different sequence similarities, we find that as sequence similarity increases, the model prediction performance gradually improves. Interestingly, in the test samples under Top-5 and Top-10 with a similarity range of 0.80–0.95, the latter shows better performance. This suggests that constructing a high-quality enzyme catalysis reaction dataset is one of the key directions for improving the model prediction performance.
4.4. Prediction Performance of DLERKm on Different Types of Enzymes
To verify the prediction reliability of DLERKm for different types of enzymes, we divided the test set samples into wild-type and mutant-type based on the presence of mutation sites in the enzymatic reaction samples. Meanwhile, we divided the test samples into two datasets based on species (E. coli and H. sapiens). The trained DLERKm was used to predict the samples in these four sets, and we compared the performances using the RMSE, MAE, R2, and PCC metrics.
As shown in Figure 9, the prediction results illustrate that DLERKm can provide better linear characteristics (Pearson correlation) on wild-type enzyme samples compared to mutant enzymes. As shown in Figure 10, the results demonstrate that DLERKm prediction performance on H. sapiens outperforms the other three types of enzymes. Additionally, the violin plot indicates that the prediction results generally have a smoother distribution on the dataset. Specifically, as shown in Table 8, the model prediction results on wild-type enzymes show improvements of approximately 7.2%, 4.1%, 5.3%, and 2.6% in terms of RMSE, MAE, and R2 compared with mutant enzymes, respectively. Moreover, for two species types in the test samples, DLERKm performs better on Homo sapiens samples. In the first two evaluation metrics (RMSE and MAE), the predictions for H. sapiens show improvements of about 9.8% and 7.5% compared to E. coli, while the latter two metrics (R2 and PCC) show an increase of 15.4% and 7.4%, respectively.

Figure 9.
DLERKm prediction results visualization for different types of enzymes. (A) DLERKm prediction results visualization for wild-type enzymes. (B) DLERKm prediction results visualization for mutant-type enzymes. (C) DLERKm prediction results visualization for E. coli type enzymes. (D) DLERKm prediction results visualization for H. sapiens type enzymes.

Figure 10.
DLERKm prediction results visualization for different types of enzymatic reactions. The bar chart on the left describes the four prediction metrics (RMSE, MAE, R2, PCC) of DLERKm on different types of datasets. Specifically, for each metric, the bar charts from left to right represent the predicted values of DLERKm for wild-type enzymatic reactions, mutant enzymatic reactions, E. coli-type enzymatic reactions, and H. sapiens-type enzymatic reactions. The violin plot on the right shows the distribution of predicted values of DLERKm across four types of enzyme datasets. In each violin plot, the dashed line represents the range of the predicted values interquartile range. The top and bottom of the violin plot represent the maximum and minimum predicted values, respectively.

Table 8.
DLERKm evaluation metric values (RMSE, MAE, R2, PCC) on enzymes (wild-type and mutant) and species (H. sapiens and E. coli).
Overall, DLERKm achieved good prediction performances across the four test subsets (wild-type, mutant, E. coli, and H. sapiens). For the wild-type enzymatic reaction and mutant-type enzymatic reaction test subsets, DLERKm performed better on the former than on the latter, which means that the model has a better feature extraction ability for the native enzyme sequences in organisms. Moreover, the differences in data distribution within the training samples or the feature variations among different species may have led to DLERKm achieving better prediction performances on H. sapiens enzymatic samples compared to E. coli enzymatic samples.
Furthermore, we divided the corresponding test samples of H. sapiens and E. coli into wild-type enzymatic reactions and mutant enzymatic reactions. As shown in Figure 11, the DLERKm prediction results show considerable goodness of fit in predicting Km across all datasets. Moreover, Figure 12 shows that DLERKm prediction performance on H. sapiens wild-type enzymatic reactions is better than on other enzymatic reactions. Additionally, the violin plot indicated that the prediction results have a smoother distribution on the dataset. Specifically, as shown in Table 9, for wild-type and mutant enzymatic reaction samples in H. sapiens, the prediction results of DLERKm on the H. sapiens wild-type enzyme samples demonstrate better accuracy for the four evaluation metrics, where the relative improvements of the four evaluation metric values are 9.8%, 5.9%, 17.6%, and 6.18%, respectively. In addition, for enzymatic reaction samples in E. coli, DLERKm demonstrates better prediction results on the mutant enzyme samples. Although RMSE slightly increases, MAE achieves an improvement of approximately 4.3%, and R2 and PCC increase by approximately 19.8% and 9.4%, respectively.
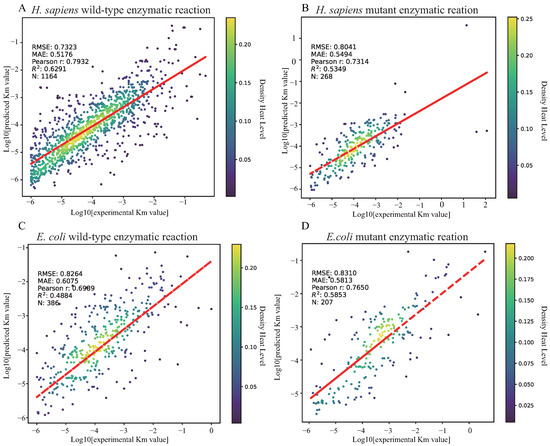
Figure 11.
DLERKm prediction results visualization for different types of enzymes. (A) DLERKm prediction results visualization for wild-type enzymes of H. sapiens. (B) DLERKm prediction results visualization for mutant-type enzymes of H. sapiens. (C) DLERKm prediction results visualization for wild-type enzymes of E. coli. (D) DLERKm prediction results visualization for mutant-type enzymes of E. coli.
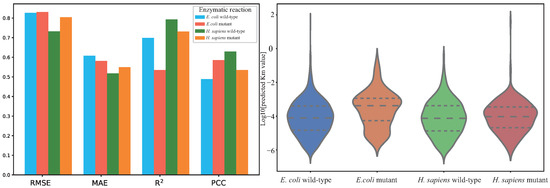
Figure 12.
DLERKm prediction results visualization for different types of enzymatic reaction (wild-type and mutant) of E. coli and H. sapiens. For each metric, the bar charts sequentially represent DLERKm predicted values for E. coli (wild-type and mutant) and H. sapiens (wild-type and mutant). The violin plot on the right shows the distribution of predicted values of DLERKm across four types of enzyme datasets. The right violin plot illustrates the distribution of DLERKm predicted values across four datasets. For each plot, the dashed line denotes the interquartile range and the vertical extremities (top and bottom of the violin shape) correspond to the maximum and minimum predicted values, respectively.

Table 9.
DLERKm evaluation metric values (RMSE, MAE, R2, PCC) for species (H. sapiens and E. coli) of different enzymatic reactions (wild-type and mutant).
In summary, regardless of whether the species type is H. sapiens or E. coli, DLERKm can effectively extract the enzymatic reaction features catalyzed by wild-type enzymes. Additionally, since H. sapiens wild-type enzyme samples account for the largest proportion in the training set, DLERKm achieves the best performance on the corresponding test subset. Moreover, given that the number of training enzymatic reaction samples for H. sapiens mutant and E. coli mutant is approximately the same, DLERKm performs better in predicting the former. This is because the abundant H. sapiens wild-type enzyme samples provide useful information, which highlights the importance of transfer learning in predicting Km values.
4.5. Discussion
DLERKm can effectively extract features of enzymatic reactions (including the products) by using EMS-2, RXNFP, and molecular fingerprints. The ablation experiment results show that DLERKm can adaptively learn the importance of these features based on various enzymatic reaction samples. Difference enzymatic reaction fingerprints (DERF) are the most important input features as they reflect changes in the chemical properties of enzymatic reactions, which directly determine the energy barrier height and the stability of the transition state. Furthermore, we conducted different experiments to analyze the prediction results of DLERKm from multiple dimensions. The experimental results illustrate that DLERKm can provide superior prediction performances regardless of whether the samples have low similarity or involve different types of enzymatic reactions. Specifically, for samples of wild-type and H. sapiens enzymatic reactions, DLERKm demonstrates reliable prediction performances. Therefore, DLERKm is expected to provide valuable insights into metabolic pathway optimization, targeted drug molecule screening, and directed evolution of protein sequences.
Although DLERKm has made significant improvements in accurately predicting Km values, the differences in its prediction results across different samples highlight an important limitation. As a supervised learning model, DLERKm prediction performances are inevitably influenced by the true Km labels. Furthermore, due to the limited feature set of samples in the benchmark dataset, DLERKm may overlook other potential feature factors that affect DLERKm prediction performances.
In future research, to improve the prediction performances of enzymatic kinetic parameters across diverse enzyme classes, we aim to construct a high-quality benchmark dataset and refine a mixture-of-experts (MoE) framework by incorporating multi-modal feature information. In addition, the prediction and generalization ability of DLERKm can be further validated through biological experiments.
5. Conclusions
The Michaelis constant (Km) is an essential parameter of enzymatic reactions, which plays a critical role in the quantitative analysis of bioengineering. The determination of Km values through biological experiments is time-consuming and resource-intensive, and such experiments are also greatly influenced by external environmental factors. Although deep learning-based Km prediction models have addressed the above issues to some extent, the accuracy of these methods in predicting Km values for complex enzymatic reactions is limited due to the lack of product information features.
In this paper, we proposed a new deep learning model named DLERKm to predict the Michaelis constant (Km) values based on enzymatic reactions. To construct a dataset of enzymatic reactions including product information for predicting Km, we collected enzymatic reaction samples and enzyme sequence samples from Sabio-RK and UniProt databases. Through data processing, we obtained a benchmark dataset consisting of 10,122 samples, which was further divided into training and test subsets based on the ratio of 8:2. Specifically, the ratio of wild-type enzymatic reactions to mutant enzymatic reactions in the test set is consistent with the ratio in the benchmark dataset. DLERKm consists of enzyme sequence feature extraction module, enzymatic reaction feature extraction module, molecular set feature extraction module, and downstream prediction module. The enzyme sequence feature and enzymatic reaction feature extraction modules leverage ESM-2 and RXNFP to extract enzyme sequence and enzymatic reaction features, respectively. The molecular set feature extraction module uses the molecular fingerprints of products and substrates to extract the features of enzymatic reaction fingerprints. The downstream prediction module further refines the above features by using a channel attention mechanism and concatenates them with an FFL to predict Km values.
By conducting ablation experiments and interpretability analysis, we validated the contributions of different input features of DLERKm. The results of the ablation experiments and interpretability analysis also indicated the importance of considering the information of products in enzymatic reactions. Compared with UniKP, DLERKm achieved superior prediction performances, where the relative improvements across the four metrics (RMSE, MAE, PCC, and R2) are 16.3%, 16.5%, 27.7%, and 14.9%, respectively. We further validated the predictive performances of DLERKm on samples with different sequence similarities. The results illustrated that DLERKm maintained reliable prediction performances on samples with lower similarity. Moreover, by comparing the evaluation metric values on samples from different types of enzymatic reactions, the experimental results showed that DLERKm exhibited better prediction performances on wild-type and H. sapiens enzymatic reaction samples.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/app15074017/s1, Figures S1–S4: The detailed information of the downloaded datasets; Figure S5: The architecture of DLERKm-v1 and DLERKm-v2; Table S1: The average training time and GPU memory usage of DLERKm and its variants across datasets; Tables S2–S4: The prediction metric values across different ranges of true values [26,45]; Note S1: The details of the encoder layer.
Author Contributions
Conceptualization, Y.L. and K.W.; methodology, Y.L. and K.W.; investigation, Y.L. and K.W.; data curation, Y.L.; software, Y.L.; supervision, K.W.; validation, Y.L. and K.W.; writing—original draft preparation, Y.L.; writing—review and editing, K.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (62373166), and the China Postdoctoral Science Foundation (2022M711362).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data and code presented in this study are openly available at https://github.com/kaiwang-group/DLERKm (accessed on 22 March 2025).
Acknowledgments
The authors thank the reviewers and editors for their work.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Herrlé, C.; Fadlallah, S.; Toumieux, S.; Wadouachi, A.; Allais, F. Sustainable mechanosynthesis of diamide tetraols monomers and their enzymatic polymerization. Green Chem. 2024, 26, 1462–1470. [Google Scholar]
- Kua, G.K.B.; Nguyen, G.K.T.; Li, Z. Enzymatic strategies for the biosynthesis of N-acyl amino acid amides. ChemBioChem 2024, 25, e202300672. [Google Scholar]
- Kajal, K.; Shakya, R.; Rashid, M.; Nigam, V.; Kurmi, B.D.; Gupta, G.D.; Patel, P. Recent green chemistry approaches for pyrimidine derivatives as a potential anti-cancer agent: An overview (2013–2023). Sustain. Chem. Pharm. 2024, 37, 101374. [Google Scholar]
- Ebikade, E.O.; Sadula, S.; Gupta, Y.; Vlachos, D.G. A review of thermal and thermocatalytic valorization of food waste. Green Chem. 2021, 23, 2806–2833. [Google Scholar]
- Lin, J.; Yin, X.; Zeng, Y.; Hong, X.; Zhang, S.; Cui, B.; Yang, D. Progress and prospect: Biosynthesis of plant natural products based on plant chassis. Biotechnol. Adv. 2023, 69, 108266. [Google Scholar]
- Liu, J.; Wang, X.; Dai, G.; Zhang, Y.; Bian, X. Microbial chassis engineering drives heterologous production of complex secondary metabolites. Biotechnol. Adv. 2022, 59, 107966. [Google Scholar]
- Rai, R.; Samanta, D.; Goh, K.M.; Chadha, B.S.; Sani, R.K. Biochemical unravelling of the endoxylanase activity in a bifunctional GH39 enzyme cloned and expressed from thermophilic Geobacillus sp. WSUCF1. Int. J. Biol. Macromol. 2024, 257, 128679. [Google Scholar]
- De Bruijn, V.M.; Te Kronnie, W.; Rietjens, I.M.; Bouwmeester, H. Intestinal in vitro transport assay combined with physiologically based kinetic modeling as a tool to predict bile acid levels in vivo. ALTEX-Altern. Anim. Exp. 2024, 41, 20–36. [Google Scholar]
- Yang, B.; Wu, C.; Teng, Y.; Chou, K.J.; Guarnieri, M.T.; Xiong, W. Tailoring microbial fitness through computational steering and CRISPRi-driven robustness regulation. Cell Syst. 2024, 15, 1133–1147. [Google Scholar]
- Batianis, C.; van Rosmalen, R.P.; Major, M.; van Ee, C.; Kasiotakis, A.; Weusthuis, R.A.; Dos Santos, V.A.M. A tunable metabolic valve for precise growth control and increased product formation in Pseudomonas putida. Metab. Eng. 2023, 75, 47–57. [Google Scholar]
- Wirth, N.T.; Gurdo, N.; Krink, N.; Vidal-Verdú, À.; Donati, S.; Férnandez-Cabezón, L.; Nikel, P.I. A synthetic C2 auxotroph of Pseudomonas putida for evolutionary engineering of alternative sugar catabolic routes. Metab. Eng. 2022, 74, 83–97. [Google Scholar] [PubMed]
- Zheng, W.; Yu, H.; Fang, S.; Chen, K.; Wang, Z.; Cheng, X.; Wu, J. Directed evolution of L-threonine aldolase for the diastereoselective synthesis of β-hydroxy-α-amino acids. ACS Catal. 2021, 11, 3198–3205. [Google Scholar]
- Dinmukhamed, T.; Huang, Z.; Liu, Y.; Lv, X.; Li, J.; Du, G.; Liu, L. Current advances in design and engineering strategies of industrial enzymes. Syst. Microbiol. Biomanuf. 2021, 1, 15–23. [Google Scholar]
- Cournia, Z.; Chipot, C. Applications of free-energy calculations to biomolecular processes. A collection. J. Chem. Inf. Model. 2024, 64, 2129–2131. [Google Scholar]
- Åqvist, J.; Brandsdal, B.O. Computer simulations of the temperature dependence of enzyme reactions. J. Chem. Theory Comput. 2025, 21, 1017–1028. [Google Scholar]
- Northrop, D.B. Steady-state analysis of kinetic isotope effects in enzymic reactions. Biochemistry 1975, 14, 2644–2651. [Google Scholar]
- Ritchie, R.J.; Prvan, T. Current statistical methods for estimating the Km and Vmax of Michaelis-Menten kinetics. Biochem. Educ. 1996, 24, 196–206. [Google Scholar]
- Khyadea, V.B.; Hershko, A. Attempt on magnification of the mechanism of enzyme catalyzed reaction through bio-geometric model for the five points circle in the triangular form of Lineweaver-Burk plot. Int. J. Emerg. Sci. Res. 2020, 1, 1–19. [Google Scholar]
- Nilsson, A.; Nielsen, J.; Palsson, B.O. Metabolic models of protein allocation call for the kinetome. Cell Syst. 2017, 5, 538–541. [Google Scholar]
- Kudalkar, G.P.; Tiwari, V.K.; Berkowitz, D.B. Exploiting Archaeal/Thermostable enzymes in synthetic chemistry: Back to the future? ChemCatChem 2024, 16, e202400835. [Google Scholar]
- Wang, F.; Dai, X.; Shen, L.; Chang, S. GraphEPN: A Deep Learning Framework for B-Cell Epitope Prediction Leveraging Graph Neural Networks. Appl. Sci. 2025, 15, 2159. [Google Scholar] [CrossRef]
- Li, F.; Yuan, L.; Lu, H.; Li, G.; Chen, Y.; Engqvist, M.K.; Nielsen, J. Deep learning-based k cat prediction enables improved enzyme-constrained model reconstruction. Nat. Catal. 2022, 5, 662–672. [Google Scholar] [CrossRef]
- Kroll, A.; Rousset, Y.; Hu, X.P.; Liebrand, N.A.; Lercher, M. Turnover number predictions for kinetically uncharacterized enzymes using machine and deep learning. Nat. Commun. 2023, 14, 4139. [Google Scholar] [CrossRef] [PubMed]
- Rives, A.; Meier, J.; Sercu, T.; Goyal, S.; Lin, Z.; Liu, J.; Fergus, R. Biological structure and function emerge from scaling unsupervised learning to 250 million protein sequences. Proc. Natl. Acad. Sci. USA 2021, 118, e2016239118. [Google Scholar] [CrossRef]
- Kroll, A.; Engqvist, M.K.; Heckmann, D.; Lercher, M.J. Deep learning allows genome-scale prediction of Michaelis constants from structural features. PLoS Biol. 2021, 19, e3001402. [Google Scholar] [CrossRef]
- Wittig, U.; Rey, M.; Weidemann, A.; Kania, R.; Müller, W. SABIO-RK: An updated resource for manually curated biochemical reaction kinetics. Nucleic Acids Res. 2018, 46, D656–D660. [Google Scholar] [CrossRef]
- UniProt Consortium. UniProt: A worldwide hub of protein knowledge. Nucleic Acids Res. 2019, 47, D506–D515. [Google Scholar] [CrossRef]
- Schwaller, P.; Probst, D.; Vaucher, A.C.; Nair, V.H.; Kreutter, D.; Laino, T.; Reymond, J.L. Mapping the space of chemical reactions using attention-based neural networks. Nat. Mach. Intell. 2021, 3, 144–152. [Google Scholar] [CrossRef]
- Cordoves-Delgado, G.; García-Jacas, C.R. Predicting antimicrobial peptides using ESMFold-predicted structures and ESM-2-based amino acid features with graph deep learning. J. Chem. Inf. Model. 2024, 64, 4310–4321. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Borger, S.; Liebermeister, W.; Klipp, E. Prediction of enzyme kinetic parameters based on statistical learning. Genome Inform. 2006, 17, 80–87. [Google Scholar]
- Yan, S.M.; Shi, D.Q.; Nong, H.; Wu, G. Predicting Km values of beta-glucosidases using cellobiose as substrate. Interdiscip. Sci. Comput. Life Sci. 2012, 4, 46–53. [Google Scholar] [CrossRef] [PubMed]
- Dai, H.; Xu, Q.; Xiong, Y.; Liu, W.L.; Wei, D.Q. Improved prediction of michaelis constants in CYP450-mediated reactions by resilient back propagation algorithm. Curr. Drug Metab. 2016, 17, 673–680. [Google Scholar] [CrossRef] [PubMed]
- Maeda, K.; Hatae, A.; Sakai, Y.; Boogerd, F.C.; Kurata, H. MLAGO: Machine learning-aided global optimization for Michaelis constant estimation of kinetic modeling. BMC Bioinform. 2022, 23, 455. [Google Scholar]
- Wang, J.; Yang, Z.; Chen, C.; Yao, G.; Wan, X.; Bao, S.; Jiang, H. MPEK: A multitask deep learning framework based on pre-trained language models for enzymatic reaction kinetic parameters prediction. Brief. Bioinform. 2024, 25, bbae387. [Google Scholar] [CrossRef]
- Elnaggar, A.; Heinzinger, M.; Dallago, C.; Rehawi, G.; Wang, Y.; Jones, L.; Rost, B. Prottrans: Toward understanding the language of life through self-supervised learning. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 7112–7127. [Google Scholar]
- Xia, J.; Zhao, C.; Hu, B.; Gao, Z.; Tan, C.; Liu, Y.; Li, S.Z. Mole-BERT: Rethinking pre-training graph neural networks for molecules. ChemRxiv 2023. [Google Scholar]
- Shen, X.; Cui, Z.; Long, J.; Zhang, S.; Chen, B.; Tan, T. EITLEM-Kinetics: A deep-learning framework for kinetic parameter prediction of mutant enzymes. Chem Catal. 2024, 4, 9. [Google Scholar] [CrossRef]
- Yu, H.; Deng, H.; He, J.; Keasling, J.D.; Luo, X. UniKP: A unified framework for the prediction of enzyme kinetic parameters. Nat. Commun. 2023, 14, 8211. [Google Scholar] [CrossRef]
- Wang, K.; Zeng, X.; Zhou, J.; Liu, F.; Luan, X.; Wang, X. BERT-TFBS: A novel BERT-based model for predicting transcription factor binding sites by transfer learning. Brief. Bioinform. 2024, 25, bbae195. [Google Scholar] [CrossRef]
- Aires-de-Sousa, J. GUIDEMOL: A Python graphical user interface for molecular descriptors based on RDKit. Mol. Inform. 2021, 43, e202300190. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, T.; Miao, M. Semi-rational design in simultaneous improvement of thermostability and activity of β-1, 3-glucanase from Alkalihalobacillus clausii KSMK16. Int. J. Biol. Macromol. 2024, 283, 137779. [Google Scholar]
- Ding, N.; Yuan, Z.; Ma, Z.; Wu, Y.; Yin, L. AI-Assisted Rational Design and Activity Prediction of Biological Elements for Optimizing Transcription-Factor-Based Biosensors. Molecules 2024, 29, 3512. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Liu, H.; Wang, X.; Li, Q.; Xu, S.; Sun, C.; Suo, H. Encapsulation of Immobilized β-Glucosidase with Calcium Metal–Organic Frameworks for Enhanced Stability in Hydrolysis of Cellobiose. Langmuir Eng. 2024, 40, 18727–18735. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).