A Method of Estimating an Object’s Parameters Based on Simplication with Momentum for a Manipulator
Abstract
1. Introduction
2. System Modeling
3. Estimation Algorithms
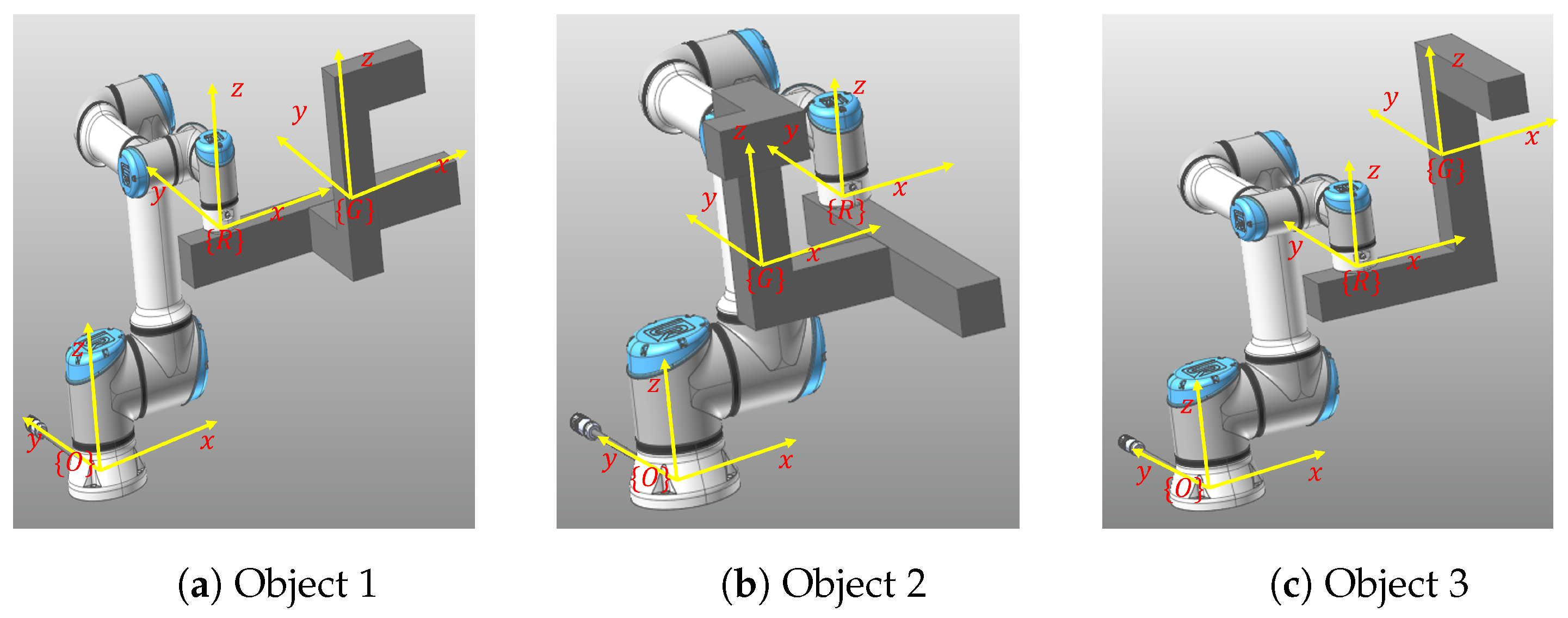
4. Parameter Estimation Simulation
4.1. Simulation Setup
4.2. Simulation Result and Analysis
4.3. Comparison with Previous Studies
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Khalil, W.; Dombre, E. Modeling, Identification and Control of Robots, 3rd ed.; Taylor and Francis: London, UK, 2002. [Google Scholar]
- Mavrakis, N.; Stolkin, R. Estimation and exploitation of objects’ inertial parameters in robotic grasping and manipulation: A survey. Robot. Auton. Syst. 2020, 124, 103374. [Google Scholar]
- Chien, C.H.; Aggarwal, J.K. Identification of 30 objects from multiple slihouettes using quadtrees/octrees. Comput. Vision Graph. Image Process. 1986, 36, 256–272. [Google Scholar] [CrossRef]
- Mirtich, B. Fast and accurate computation of polyhedral mass properties. J. Graph. Tools 1996, 1, 31–50. [Google Scholar]
- Lines, J.A.; Tillett, R.D.; Ross, L.G.; Chan, D.; Hockaday, S.; McFarlane, N.J.B. An automatic image-based system for estimating the mass of free-swimming fish. Comput. Electron. Agric. 2001, 31, 151–168. [Google Scholar]
- Omid, M.; Khojastehnazhand, M.; Tabatabaeefar, A. Estimating volume and mass of citrus fruits by image processing technique. J. Food Eng. 2010, 100, 315–321. [Google Scholar]
- Yu, Y.; Arima, T.; Tsujio, S. Estimation of object inertia parameters on robot pushing operation. In Proceedings of the International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 1657–1662. [Google Scholar]
- Methil, N.S.; Mukherjee, R. Pushing and steering wheelchairs using a holonomic mobile robot with a single arm. In Proceedings of the International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 5781–5785. [Google Scholar]
- Artashes, M.; Burschka, D. Visual estimation of object density distribution through observation of its impulse response. In Proceedings of the International Conference on Computer Vision Theory and Applications, Barcelona, Spain, 21–24 February 2013; pp. 586–595. [Google Scholar]
- Franchi, A.; Petitti, A.; Rizzo, A. Distributed estimation of the inertial parameters of an unknown load via multi-robot manipulation. In Proceedings of the Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014; pp. 6111–6116. [Google Scholar]
- Wu, J.; Wang, J.; You, Z. An overviel of dynamic parameter identification of robots. Robot. -Comput.-Integr. Manuf. 2010, 26, 414–419. [Google Scholar] [CrossRef]
- Ljung, L. System Identification: Theory for the User, 2nd ed; Prentice-Hall: Hoboken, NJ, USA, 1999. [Google Scholar]
- Atkeson, C.G.; An, C.H.; Hollerbach, J.M. Estimation of inertial parameters of manipulator loads and links. Int. J. Robot. Res. 1986, 5, 101–119. [Google Scholar] [CrossRef]
- Radkhah, K.; Kulic, D.; Croft, E. Dynamic Parameter Identification for the CRS A460 Robot. In Proceedings of the International conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 3842–3847. [Google Scholar]
- Choi, J.S.; Yoon, J.H.; Park, J.H.; Kim, P.J. A numerical algorithm to identify independent grouped parameters of robot manipulator for control. In Proceedings of the Advanced Intelligent Mechatronics, Budapest, Hungary, 4–6 July 2011; pp. 373–378. [Google Scholar]
- Swevers, J.; Verdonck, W.; Schutter, J.D. Dynamic Model Identification for Industrial Robots. IEEE Control Syst. Mag. 2007, 27, 58–71. [Google Scholar]
- Bahloul, A.; Tliba, S.; Chitour, Y. Dynamic Parameters Identification of an Industrial Robot with and Without Payload. IFAC-Pap. 2018, 51, 443–448. [Google Scholar]
- Dutkiewicz, P.; Kozlowski, K.R.; Wroblewski, W.S. Experimental identification of robot and load dynamic parameters. In Proceedings of the Conference on Control Applications, Vancouver, BC, Canada, 13–16 September 1993; pp. 767–776. [Google Scholar]
- Traversaro, S.; Brossette, S.; Escande, A.; Nori, F. Identification of fully physical consistent inertial parameters using optimization on manifolds. In Proceedings of the International Conference on Intelligent Robots and Systems, Daejeon, Republic of Korea; 2016; pp. 5446–5451. [Google Scholar]
- Wensing, P.M.; Kim, S.; Slotine, J.J.E. Linear matrix inequalities for physically consistent inertial parameter identification: A statistical perspective on the mass distribution. IEEE Robot. Autom. Lett. 2018, 3, 60–67. [Google Scholar] [CrossRef]
- Cehajic, D.; Dohmann, P.B.; Hirche, S. Estimating unknown object dynamics in human-robot manipulation tasks. In Proceedings of the International Conference on Robotics and Automation, Singapore, 29 May–3 June 2017; pp. 1730–1737. [Google Scholar]
- Jang, J.; Park, J.H. Parameter identification of an unknown object in human-robot collaborative manipulation. In Proceedings of the International Conference on Control, Automation and Systems, Busan, Republic of Korea, 13–16 October 2020; pp. 1086–1091. [Google Scholar]
- Park, J.; Shin, Y.S.; Kim, S. Object-Aware Impedance Control for Human–Robot Collaborative Task With Online Object Parameter Estimation. IEEE Trans. Autom. Sci. Eng. 2024, 22, 8081–8094. [Google Scholar] [CrossRef]
- Nadeau, P.; Giamou, M.; Kelly, J. Fast Object Inertial Parameter Identification for Collaborative Robots. In Proceedings of the International Conference on Robotics and Automation, Philadelphia, PA, USA, 23–27 May 2022; pp. 3560–3566. [Google Scholar]
- Kurdas, A.; Hamad, M.; Vorndamme, J.; Mansfeld, N.; Abdolshah, S.; Haddadin, S. Online Payload Identification for Tactile Robots Using the Momentum Observer. In Proceedings of the International Conference on Robotics and Automation, Philadelphia, PA, USA, 23–27 May 2022; pp. 5953–5959. [Google Scholar]
- Pavlic, M.; Markert, T.; Matich, S.; Burschka, D. RobotScale: A Framework for Adaptable Estimation of Static and Dynamic Object Properties with Object-dependent Sensitivity Tuning. In Proceedings of the International Conference on Robot and Human Interactive Communication, Busan, Republic of Korea, 28–31 August 2023; pp. 668–674. [Google Scholar]
- Taie, W.; ElGeneidy, K.; L-Yacoub, A.A.; Ronglei, S. Online Identification of Payload Inertial Parameters Using Ensemble Learning for Collaborative Robots. IEEE Robot. Autom. Lett. 2024, 9, 1350–1356. [Google Scholar] [CrossRef]
- Baek, D.; Peng, B.; Gupta, S.; Ramos, J. Online Learning-Based Inertial Parameter Identification of Unknown Object for Model-Based Control of Wheeled Humanoids. IEEE Robot. Autom. Lett. 2024, 9, 11154–11161. [Google Scholar] [CrossRef]
- Shan, S.; Pham, Q.C. Fast Payload Calibration for Sensorless Contact Estimation Using Model Pre-Training. IEEE Robot. Autom. Lett. 2024, 9, 9007–9014. [Google Scholar] [CrossRef]
- Wenzel, T.A.; Burnham, K.J.; Blundell, M.V.; Williams, R.A. Dual extended Kalman filter for vehicle state and parameter estimation. Veh. Syst. Dyn. 2006, 44, 151–171. [Google Scholar] [CrossRef]
- Best, M.C.; Newton, A.P.; Tuplin, S. The identifying extended Kalman filter: Parameteric system identification of a vehicle handling model. Proc. Inst. Mech. Eng. Part J. -Multi-Body Dyn. 2007, 221, 87–98. [Google Scholar] [CrossRef]
- Hong, S.; Lee, C.; Borrelli, F.; Hendrick, K. A novel approach for vehicle inertial parameter identification using a dual Kalman filter. Intell. Transp. Syst. IEEE Trans. 2015, 16, 151–160. [Google Scholar] [CrossRef]
- Yang, B.; Fu, R.; Sun, Q.; Jiang, S.; Wang, C. State estimation of buses: A hybrid algorithm of deep neural network and unscented Kalman filter considering mass identification. Mech. Syst. Signal Process. 2024, 213, 111368. [Google Scholar] [CrossRef]
- Universal Robots e-Series User Manual UR16e Original instructions (en); Universal Robots: Odense, Denmark, 2021.
- Flash, T.; Hogan, N. The Coordination of Arm Movements: An Experimentally Confirmed Mathematical Model. J. Neurosci. 1985, 5, 1688–1703. [Google Scholar] [CrossRef]
- Bazerghi, A.; Goldenberg, A.A.; Apkarian, J. An Exact Kinematic Model of PUMA 600 Manipulator. IEEE Trans. Syst. Man, Cybern. 1984, SMC-14, 483–487. [Google Scholar] [CrossRef]
- Szkodny, T. Modelling of Kinematics of the IRb-6 Manipulator. Comput. Math. Appl. 1995, 29, 77–94. [Google Scholar] [CrossRef]
- Shen, Y.; Jia, Q.; Wang, R.; Huang, Z.; Chen, G. Learning-Based Visual Servoing for High-Precision Peg-in-Hole Assembly. Actuators 2023, 12, 144. [Google Scholar] [CrossRef]

| Angular Velocity (mrad/s) | Force (mN) | Torque (mNm) | |
|---|---|---|---|
| Low Noise | 0.25 | 50 | 2.50 |
| Moderate (Mode) Noise | 0.50 | 100 | 5 |
| High Noise | 1.00 | 330 | 6.70 |
| Parameter | Object 1 | Object 2 | Object 3 |
|---|---|---|---|
| m (kg) | 8.12 | 9.06 | 1.02 |
| (m) | 2.62 | −1.26 | 1.88 |
| (m) | −1.14 | −2.70 | −5.20 |
| (m) | 3.20 | 4.50 | 1.70 |
| (kg·m2) | 2.39 | 3.42 | 4.43 |
| (kg·m2) | 1.40 | −3.00 | 2.70 |
| (kg·m2) | −2.30 | 1.15 | −1.11 |
| (kg·m2) | 2.93 | 3.00 | 4.43 |
| (kg·m2) | 8.60 | 3.80 | 1.11 |
| (kg·m2) | 3.03 | 3.52 | 1.96 |
| Estimation Errors (%) | Motion Range | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.05 | 0.025 | |||||||
| Noise Level | Noise Level | Noise Level | |||||||
| Low | Mode | High | Low | Mode | High | Low | Mode | High | |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | |
| 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.3 | |
| 6.2 | 6.2 | 4.8 | 7.0 | 6.6 | 1.7 | 5.7 | 5.1 | 5.3 | |
| 3.3 | 3.0 | 1.9 | 3.4 | 3.7 | 0.6 | 3.0 | 1.8 | 9.0 | |
| 1.1 | 1.7 | 9.0 | 4.2 | 0.4 | 16.3 | 6.3 | 6.4 | 42.1 | |
| 0.2 | 1.2 | 11.5 | 1.9 | 7.6 | 13.0 | 3.3 | 3.2 | 14.5 | |
| 3.6 | 3.6 | 1.3 | 4.8 | 4.3 | 0.3 | 3.5 | 4.7 | 5.2 | |
| 1.2 | 0.9 | 4.8 | 1.4 | 1.6 | 9.3 | 1.0 | 3.6 | 14.8 | |
| 0.1 | 0.0 | 2.0 | 0.1 | 0.2 | 2.0 | 0.5 | 0.2 | 3.0 | |
| Estimation Errors (%) | Motion Range | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.05 | 0.025 | |||||||
| Noise Level | Noise Level | Noise Level | |||||||
| Low | Mode | High | Low | Mode | High | Low | Mode | High | |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.3 | |
| 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | |
| 0.3 | 0.1 | 2.6 | 0.1 | 0.5 | 3.8 | 0.7 | 1.8 | 9.8 | |
| 0.2 | 0.9 | 5.6 | 0.6 | 0.8 | 7.8 | 1.2 | 2.0 | 7.3 | |
| 0.2 | 3.0 | 4.5 | 2.8 | 1.2 | 23.5 | 8.2 | 5.6 | 75.5 | |
| 2.3 | 1.9 | 6.4 | 2.6 | 2.0 | 6.1 | 2.0 | 6.4 | 18.8 | |
| 0.0 | 0.2 | 4.0 | 0.7 | 0.3 | 8.2 | 0.8 | 1.6 | 22.5 | |
| 0.3 | 1.4 | 15.9 | 2.1 | 9.4 | 26.9 | 1.1 | 0.9 | 41.0 | |
| 0.1 | 0.6 | 2.5 | 0.4 | 1.0 | 0.1 | 1.3 | 3.0 | 4.7 | |
| Estimation Errors (%) | Motion Range | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.05 | 0.025 | |||||||
| Noise Level | Noise Level | Noise Level | |||||||
| Low | Mode | High | Low | Mode | High | Low | Mode | High | |
| 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | |
| 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | |
| 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | |
| 1.0 | 1.0 | 0.4 | 1.0 | 1.0 | 1.8 | 0.9 | 0.0 | 7.6 | |
| 3.0 | 3.3 | 0.6 | 3.3 | 3.2 | 9.8 | 3.6 | 1.1 | 35.8 | |
| 0.7 | 4.9 | 8.3 | 0.1 | 3.4 | 22.1 | 4.4 | 8.8 | 18.8 | |
| 0.0 | 0.3 | 1.0 | 0.9 | 0.4 | 9.6 | 2.4 | 0.8 | 20.9 | |
| 4.5 | 4.6 | 1.6 | 4.3 | 5.1 | 10.4 | 4.5 | 0.0 | 33.5 | |
| 3.2 | 2.5 | 1.9 | 2.9 | 0.4 | 0.2 | 0.1 | 2.8 | 9.2 | |
| 0.6 | 0.2 | 1.1 | 0.6 | 1.8 | 3.7 | 1.4 | 0.4 | 7.3 | |
| Joints | 0.1 | 0.05 | 0.025 | ||||
|---|---|---|---|---|---|---|---|
| Linear | Angular | Linear | Angular | Linear | Angular | ||
| Range of joint motion (rad) | 2.44 | 2.41 | 1.13 | 1.21 | 5.43 | 6.10 | |
| 6.51 | 2.61 | 5.03 | 1.26 | 2.94 | 6.20 | ||
| 2.20 | 5.80 | 9.08 | 2.89 | 4.07 | 1.44 | ||
| 2.84 | 1.31 | 1.41 | 6.64 | 7.01 | 3.33 | ||
| 6.60 | 9.99 | 3.37 | 5.00 | 1.62 | 2.50 | ||
| 2.44 | 1.24 | 1.13 | 6.22 | 5.43 | 3.11 | ||
| Maximum joint velocity (rad/s) | |||||||
| 9.08 | |||||||
| Maximum joint acceleration (rad/s2) | |||||||
| Items | Directions | Method in [13] | Method in [18] | Method in [26] | Proposed Method | |
|---|---|---|---|---|---|---|
| Displacement range | x | 107 | 121 | 99.5 | 10 | |
| Linear (cm) | y | 59.3 | 42.3 | 89.1 | 10 | |
| z | 12.2 | 22.8 | 54.7 | 10 | ||
| x | 2610 | 124 | 4530 | 100 | ||
| Angular (mrad) | y | 1660 | 388 | 3100 | 100 | |
| z | 914 | 1200 | 3710 | 100 | ||
| Maximum speed | x | 126 | 139 | 239 | 18.8 | |
| Linear (cm/s) | y | 89.6 | 71.5 | 186 | 18.8 | |
| z | 15.0 | 23.9 | 131 | 18.8 | ||
| x | 3670 | 199 | 3640 | 188 | ||
| Angular (mrad/s) | y | 2350 | 424 | 5630 | 188 | |
| z | 1500 | 1210 | 4570 | 188 | ||
| Maximum acceleration | x | 226 | 242 | 1230 | 57.7 | |
| Linear (cm/s2) | y | 253 | 225 | 905 | 57.7 | |
| z | 31.5 | 25.6 | 934 | 57.7 | ||
| x | 9520 | 548 | 20,900 | 577 | ||
| Angular (mrad/s2) | y | 5640 | 831 | 24,400 | 577 | |
| z | 4770 | 2490 | 21,800 | 577 | ||
| Motion | Joint | Method in [13] | Method in [18] | Method in [26] |
|---|---|---|---|---|
| 1.57 | 1.22 | 2.59 | ||
| 1.05 | 0.52 | 1.44 | ||
| 1.57 | 1.22 | 1.14 | ||
| Range of joint angles (rad) | 3.14 | 0.70 | 1.17 | |
| 1.57 | 2.44 | 3.24 | ||
| 1.57 | 1.84 | |||
| 0.84 | ||||
| 2.94 | 2.29 | 2.21 | ||
| 1.96 | 0.98 | 2.21 | ||
| 2.94 | 2.29 | 1.20 | ||
| Maximum joint velocity (rad/s) | 5.89 | 1.31 | 2.10 | |
| 2.94 | 4.58 | 2.30 | ||
| 2.94 | 2.10 | |||
| 2.50 | ||||
| 4.53 | 3.85 | 3.77 | ||
| 3.03 | 1.65 | 6.81 | ||
| 4.53 | 3.85 | 2.53 | ||
| Maximum joint acceleration (rad/s2) | 9.06 | 2.20 | 7.54 | |
| 4.53 | 7.70 | 3.26 | ||
| 4.53 | 4.80 | |||
| 14.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, J.; Park, J.H. A Method of Estimating an Object’s Parameters Based on Simplication with Momentum for a Manipulator. Appl. Sci. 2025, 15, 3989. https://doi.org/10.3390/app15073989
Jang J, Park JH. A Method of Estimating an Object’s Parameters Based on Simplication with Momentum for a Manipulator. Applied Sciences. 2025; 15(7):3989. https://doi.org/10.3390/app15073989
Chicago/Turabian StyleJang, Jaeyoung, and Jong Hyeon Park. 2025. "A Method of Estimating an Object’s Parameters Based on Simplication with Momentum for a Manipulator" Applied Sciences 15, no. 7: 3989. https://doi.org/10.3390/app15073989
APA StyleJang, J., & Park, J. H. (2025). A Method of Estimating an Object’s Parameters Based on Simplication with Momentum for a Manipulator. Applied Sciences, 15(7), 3989. https://doi.org/10.3390/app15073989





