Temporal Enhancement of Top-N Recommendation on Heterogeneous Graphs

Abstract

Heterogeneous information networks (HINs) have seen rapid development and have attracted extensive attention because of their effectiveness in recommender systems. Although many existing models based on HINs for recommender systems have obtained good recommendation performance on account of their superior ability to process heterogeneous data and capture rich semantic information, there are still several problems. Firstly, the temporal relations among different nodes in meta-paths, which include users and items, are rarely considered in HINs. Secondly, the interactions among meta-paths, users, and items are similarly often overlooked. Thirdly, their ability to learn the heterogeneous information of users and items is limited. In view of the above problems, we propose a system for the temporal enhancement of top-N recommendations on HINs called TMRec. Specifically, we first adopted long short-term memory (LSTM) and residual self-attention (RSA) to process users and items and enhance the network’s ability to both learn the heterogeneous information in them and capture the temporal relations among them. Second, we designed a novel method for processing meta-paths, including deep perception self-attention (DPSA), max pooling, and L₂-normalization, that can effectively obtain the temporal relations among different nodes in meta-paths. Third, we used collaborative attention to process meta-paths, users, and items to obtain their interactions. Finally, extensive experiments were conducted on four public datasets of recommender systems to verify the superiority of our method compared with state-of-the-art top-N recommendation models.

1. Introduction

Recommender systems, especially top-N recommender systems, play a key role in our daily life [1]. Traditional models of recommender systems recommend interest items to different users based on historical feedback information [2,3] based on methods such as collaborative filtering [2]. Recently, more and more auxiliary data have also been applied in recommender systems for improving their performance [4,5]. However, the complexity and heterogeneity of auxiliary data pose a big challenge for their use in recommender systems.

Today, graph neural network (GNN)-based models [6,7,8,9,10] have achieved significant success in recommender systems. Specifically, in a GNN, first, the interactions of users, items, and auxiliary information are considered to be a graph structure. Then, the information representation of users and items is obtained with an information propagation mechanism. For example, SVD++ [6] enriches the representation of users by incorporating implicit feedback on items, in addition to explicit interactions. ItemRank [7] constructs an item-to-item graph based on the interaction history, where the edges in the graph represent the similarity among items. It then uses a random walk algorithm to obtain the probability of a user visiting each item, which is used to rank the items. However, these networks cannot effectively capture complex heterogeneous information. Consequently, heterogeneous information networks (HINs) [11,12], which include nodes and links, have been proposed for recommender systems due to their effective ability to acquire the semantic and representation information of nodes. The nodes in HINs include users and items, while links are meta-paths representing the relations among nodes. Many HIN-based methods [13,14,15] have been proposed, such as hierarchical attention network (HAN) [13] and meta-path-based context for top-N recommendation (MCRec) [16].

Although many existing models based on HINs for recommender systems have shown better performance due to their superior ability to process heterogeneous data and capture rich semantic information, they still face several problems. Firstly, although some researchers have focused on the explicit information of meta-paths, the proposed methods do not consider the temporal relations among different nodes in meta-paths [17]; this is mainly due to the fact that the static embedding methods used in such studies are subject to limitations and time dependency is often not taken into account. For example, users’ browsing and purchasing behaviors on e-commerce platforms exhibit a certain order over time. The temporal relations among different nodes can help capture the sequence of these behaviors, thereby allowing for a better prediction of what content users may be interested in next. Secondly, although in HINs the relations between nodes are considered, the interactions between nodes and meta-paths are not accounted for [18]. Thirdly, HINs cannot effectively learn the heterogeneous information of nodes [16]. For example, a movie recommender system includes various entity types, such as users, movies, directors, and actors, and the relationships among them exhibit high heterogeneity.

In view of these problems, a system for the temporal enhancement of top-N recommendations on HINs called TMRec is proposed in this study. It is mainly based on two architectures: long short-term memory (LSTM) [19], which can remember important information and forget irrelevant details by controlling the flow of information, and residual self-attention (RSA) [20], which can dynamically focus on the most important parts of information, rather than processing all input information uniformly. Therefore, we adopt these two methods for learning heterogeneous information among users or items, as well as effectively capturing the temporal relations among users or items. Specifically, LSTM focuses on the temporal relations between nodes of the same type, such as users or items, and RSA combines multiple sandwich networks and gated self-attention networks, where each sandwich network includes convolutional neural networks (CNNs) [21] and linear rectification functions. Further, RSA can effectively reduce the problems of information loss and overfitting to enhance the ability to learn relationships among nodes of the same type. In addition, we introduce a deep perception self-attention (DPSA) model with max pooling and L₂-normalization to process meta-paths. Compared with the previous methods, it can effectively capture the temporal relations among different nodes in meta-paths. DPSA is a novel self-attention network. Unlike traditional self-attention models, it adopts deep convolutional neural networks (DCNNs) with different convolutional kernels and a residual network (ResNet) to obtain the query, key, and value. In DPSA, the DCNNs with different convolutional kernels can learn from multiple perspectives, thereby improving the performance of the model. ResNet can effectively address the problems of vanishing and exploding gradients, thereby enhancing the model’s learning capability. Their combination can enhance the perceptual ability for different nodes in meta-paths [22]. Finally, we adopt the collaborative attention model to connect the learning results of meta-paths, users, and items to obtain the interactions between nodes and meta-paths. The contributions of our work are summarized as follows:

(1)

We propose a system for the temporal enhancement of top-N recommendations on HINs called TMRec. It can improve the performance of recommender systems by learning the temporal relations of nodes and meta-paths.

(2)

We adopt the architectures of LSTM and RSA for embedding the learning of users and items, which can highlight the temporal relations and interactions among users or items. This can also enhance the ability to learn heterogeneous information from these nodes.

(3)

We use DPSA with max pooling and L₂-normalization to learn the interactions among users and items in meta-paths. Additionally, collaborative attention is introduced to obtain the interactions of meta-paths, users, and items.

(4)

Extensive experiments are conducted on four public datasets of recommender systems. The results demonstrate that the performance of the proposed TMRec model is largely improved compared with other SOTA models.

The structure of this paper is organized as follows: In Section 2, we introduce related work on recommender systems, heterogeneous information networks, and network embedding. In Section 3, we introduce the definition of a heterogeneous information network and the main notations used. In Section 4, we explain the framework of the proposed TMRec in detail. In Section 5, we present the experiments conducted and analyze their results, which demonstrate the effectiveness of our model. Section 6 includes the conclusion of our study.

2. Related Work

In this section, related studies associated with our work are presented, with the topics including recommender systems, heterogeneous information networks, and network embedding.

2.1. Recommender Systems

Recommender systems are critical to preventing an information explosion by choosing suitable items for one specific user according to their interaction history and preferences. The two scenarios of recommender systems are rating prediction and top-N recommendation. The latter involves presenting information to users in the form of a recommendation list; for example, the paper recommendations in Academic Toutiao, the music recommendations in Xiami, and the course recommendations in NetEase Cloud Classroom are all top-N recommendations. In early studies, recommendations were always conducted with collaborative filtering (CF) methods, which utilize historical interactions [23]. CF-based models for recommender systems include item-based k-nearest neighbor (ItemKNN) [2], Bayesian personalized ranking (BPR) [3], matrix factorization (MF) [24], and neural collaborative filtering (NCF) [25]. Additional information, including social information [26], location information [27], and heterogeneous information [12], is leveraged in many works to solve the cold-start problems of CF-based methods. Moreover, some universal frameworks, which are intended to combine context information, have been proposed [25]. Recently, owing to the success of deep learning (DL) architectures, researchers have employed deep models such as convolutional neural networks [28], autoencoders [29], and multi-layer perceptrons (MLPs) to obtain latent features from data. Further, meta-paths have been widely employed in recommendation models because of their rich semantic information. Shi et al. [22] proposed a heterogeneous information network for recommendations that constructs homogeneous sequences with a type constraint and filtering in meta-paths. Moreover, Hu et al. [16] proposed MCRec for recommendations, a model which explicitly combines meta-path-based context and designs a three-way neural interaction. Finally, the efficient neighborhood-based interaction model, NIRec, can capture and aggregate rich interaction patterns at the node and path levels through convolution operations for recommendation [30].

2.2. Heterogeneous Information Networks and Network Embedding

Heterogeneous information networks (HINs), also known as heterogeneous graphs, which are made up of different types of nodes and edges, have attracted extensive attention and developed rapidly since they are ubiquitous in the real world. Research studies on learning representations in heterogeneous networks are emerging in classification [31], clustering [32], link prediction [33], and recommendation [34]. Although HIN-based recommender systems have achieved good performance, the embedding representation is always high-dimensional and sparse. Instead, we need a low-dimensional and dense representation for downstream tasks [35]. Network embedding allows one to obtain low-dimensional and dense vector representations for users and items for the understanding of the semantic meaning among nodes. DeepWalk is a classical network embedding method proposed for the learning of representations with the strategy of combining random walk and skip-gram [36]. Likewise, Node2vec, an improvement on DeepWalk, adopts a biased random walk method to replace the previous random walk generation method to more flexibly learn information [37]. However, these models are only applied in homogeneous networks. At present, several works have been conducted to explore representations in heterogeneous networks. For instance, HIN2vec learns the embedding representations of various nodes and meta-paths in a heterogeneous graph with diverse methods of prediction training [38]. Xu et al. [39] first proposed a representative model which encodes the edges of HINs, achieving good results. Heterogeneous graph neural network (HetGNN) encodes the heterogeneous contents of various kinds of nodes and aggregates them by category [40].

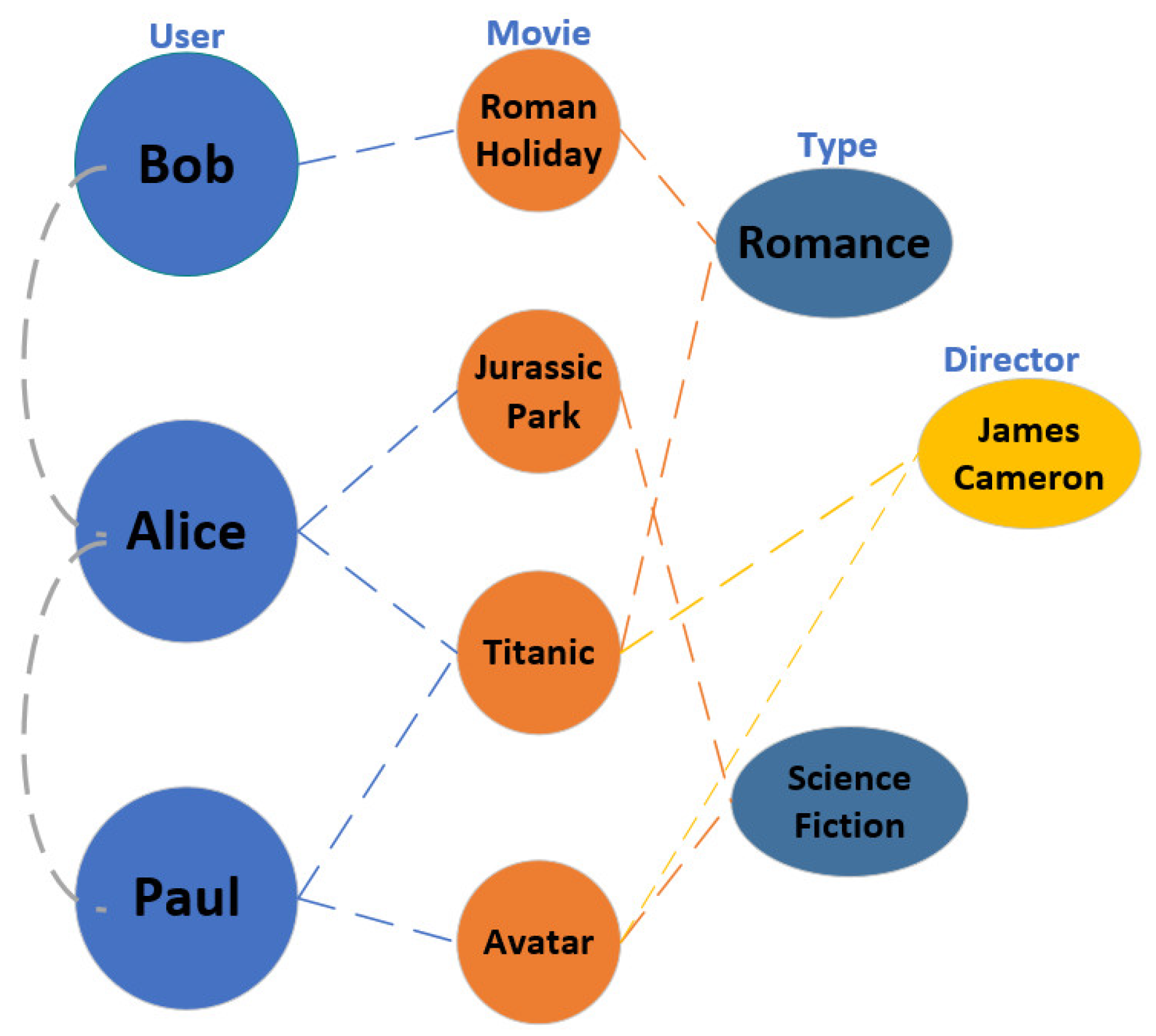
3. Preliminaries

In this section, we introduce the definition of a heterogeneous information network and the main notations used.

Recently, more and more attention has been paid to heterogeneous graphs of the type $G=(V,E)$, where V and E represent node sets and edge sets, respectively. The node mapping function $\alpha :V\to A$ denotes the sets of node types; likewise, the edge mapping function $\beta :E\to B$ denotes the sets of edge types, with $\left|A\right|+\left|B\right|>2$. As a promising network, it can model complex objects and links, which correspond to different types of nodes and edges in the graph, respectively.

HINs can expose underlying connections by establishing a logical network, which allows one node on a heterogeneous graph to transfer feedback information to another connection node. We present an example of an HIN for recommendation in Figure 1. Bob interacts with Titanic through the path $user\to movie\to type\to movie$, which is called a meta-path in the HIN. Here, it is the relationship of specific users, films, genres, and directors, and it is mainly used to combine the features of nodes and the relations among them.

Next, the main notations used in this study and their descriptions are summarized in

Table 1. Notations and their descriptions.

Notation	Description
${\mathbf{m}}_u$	User’s embedding after lookup layer
${\mathbf{n}}_i$	Item’s embedding after lookup layer
${\mathbf{x}}_u$	Low-dimensional representations of users
${\mathbf{y}}_i$	Low-dimensional representations of items
${{\mathbf{x}}_u}^{\prime }$	Improved user’s embedding after LSTM module
${\tilde{\mathbf{x}}}_u$	Final user’s embedding after self-attention mechanism
${\tilde{\mathbf{y}}}_i$	Final item’s embedding after self-attention mechanism
${\mathbf{h}}_p$	Embedding of path instance p
${\mathbf{c}}_p$	Initial embedding of meta-path
${{\mathbf{c}}_p}^{\prime }$	Embedding of meta-path after L2-normalization
${\mathbf{c}}_{u,i}$	Final embedding of meta-path after co-attention mechanism module
${\mathbf{r}}_{u,i}$	Embedding of final fusion

.

4. The Proposed Model

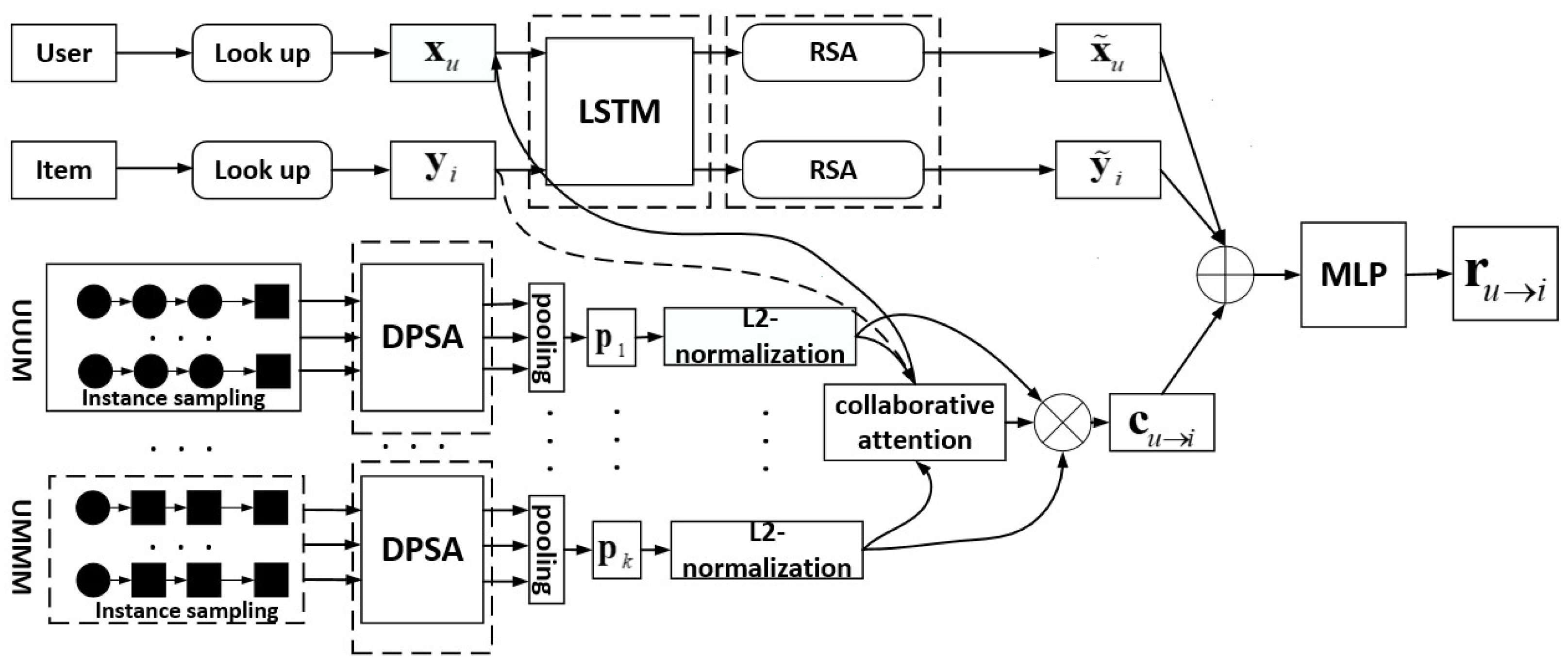
4.1. Overall Framework

In this study, we propose a recommender system called TMRec for the determination of the temporal relation of each sequence to enhance the embeddings. The proposed model can be divided into three parts: user embedding representation learning, item embedding representation learning, and meta-path embedding learning. Firstly, LSTM can remember important information and forget irrelevant details by controlling the flow of information. Moreover, RSA, which includes multiple sandwich networks and gated self-attention networks, can dynamically focus on the most important parts of information. Therefore, we adopt LSTM and RSA to process users and items, respectively, as they can effectively capture the heterogeneous and temporal relations among users and items. Secondly, DPSA has better learning ability for different nodes in meta-paths on account of its deep convolutional neural networks with different convolutional kernels and a residual network within the self-attention mechanism; therefore, we use it with max pooling and L2-normalization to process the meta-paths for determining the heterogeneous and temporal relations among nodes of different types in the data to improve the representations. Thirdly, collaborative attention is used for enhancing the ability to obtain the interactions of users, items, and meta-paths. The overall framework of the proposed TMRec is described in Figure 2.

Specifically, we acquire the embeddings of users, items, and meta-paths and combine them as the final embedding to perform a recommendation task. It is worth mentioning that the embeddings of the users and items are generated in the same way, and we take user embeddings as an example to describe the framework. After a lookup layer is employed to obtain low-dimensional and dense vectors, we utilize the LSTM module to process the data and the RSA module to determine the importance of each node and learn more meaningful embeddings. As for the meta-path embeddings, we use priority scores to generate high-quality path instances and aggregate them into a meta-path embedding with the DPSA module to improve the representation. In addition, we use L2-normalization to process the embedding of a single meta-path to avoid overfitting. Then, the final meta-path embedding is obtained with a co-attention mechanism in the case where user and item embeddings are used as input. Finally, we concatenate the above three embeddings into a representation for top-N recommendations.

4.2. User and Item Embeddings

First, we utilize a lookup layer to transform the representations of users and items into low-dimensional and dense vectors. Here, we define a user’s representation and an item’s representation as ${\mathbf{m}}_u\in {\mathbf{R}}^{\left|U\right|\times 1}$ and ${\mathbf{n}}_i\in {\mathbf{R}}^{\left|I\right|\times 1}$, respectively. In the lookup layer, there are two transformation matrices specific for users and items, namely, $\mathbf{M}\in {\mathbf{R}}^{\left|U\right|\times d}$ and $\mathbf{N}\in {\mathbf{R}}^{\left|I\right|\times d}$, respectively, where the numbers of users and items are denoted by $\left|U\right|$ and $\left|I\right|$, respectively, and d is the dimension of each embedding. The low-dimensional representations of users and items are given as follows:

$${\mathbf{x}}_u={\mathbf{M}}^T{\mathbf{m}}_u$$

(1)

$${\mathbf{y}}_i={\mathbf{N}}^T{\mathbf{n}}_i$$

(2)

The LSTM architecture and the self-attention mechanism are utilized for user and item embedding learning to account for the importance of inner interactions and mutual influence, which are often not considered. LSTM is employed for solving the problem of gradient disappearance and gradient explosion in long-sequence training. There are three gates in LSTM: the input gate, the forget gate, and the output gate. Moreover, there is a “processor”, called a cell, in every gate. When a message enters the LSTM network, it must be judged as useful or not according to the rules. Only the information that meets the criteria is retained, while inconsistent information is forgotten with the forget gate. Taking user embeddings as an example, LSTM can be formulated as follows:

$${{\mathbf{x}}_u}^{\prime }=LSTM({\mathbf{x}}_u,\theta )$$

(3)

where all the related parameters are expressed as $\theta$ in LSTM. The specific representations of LSTM are shown in the formulas below.

(a) The input state vector of the t-th user in the user sequence is shown as follows:

$${\widehat{\mathbf{C}}}_t=tanh({\mathbf{W}}_c\odot [{\mathbf{h}}_{t-1},{\mathbf{x}}_t]+{\mathbf{b}}_c)$$

(4)

where tanh is the hyperbolic tangent activation function, ⊙ denotes the Hadamard product, ${\mathbf{h}}_{t-1}$ denotes the hidden layer output vector of the $(t-1)$-th user in the user sequence, ${\mathbf{x}}_t$ is the low-dimensional embedding representation of the t-th user in the sequence, and ${\mathbf{W}}_c$ and ${\mathbf{b}}_c$ denote the learnable parameter and the bias vector of the input state, respectively.

(b) The input vector of the t-th user in the user sequence is as follows:

$${\mathbf{i}}_t=\sigma ({\mathbf{W}}_i\odot [{\mathbf{h}}_{t-1},{\mathbf{x}}_t]+{\mathbf{b}}_i)$$

(5)

where $\sigma$ is the activation function, and ${\mathbf{W}}_i$ and ${\mathbf{b}}_i$ denote the learnable parameter and the bias vector of the input gate, respectively.

(c) The forget gate vector of the t-th user in the user sequence is as follows:

$${\mathbf{f}}_t=\sigma ({\mathbf{W}}_f\odot [{\mathbf{h}}_{t-1},{\mathbf{x}}_t]+{\mathbf{b}}_f)$$

(6)

where ${\mathbf{W}}_f$ and ${\mathbf{b}}_f$ denote the learnable parameter and the bias vector of the forget gate, respectively.

(d) The overall state vector of the t-th user in the user sequence is as follows:

$${\mathbf{C}}_t={\mathbf{f}}_t·{\mathbf{C}}_{t-1}+{\mathbf{i}}_t·{\widehat{\mathbf{C}}}_t$$

(7)

where ${\mathbf{C}}_{t-1}$ denotes the overall state vector of the $(t-1)$-th user in the user sequence and · denotes the pointwise multiplication operator.

(e) The output vector of the t-th user in the user sequence is as follows:

$${\mathbf{o}}_t=\sigma ({\mathbf{W}}_0\odot [{\mathbf{h}}_{t-1},{\mathbf{x}}_t]+{\mathbf{b}}_0)$$

(8)

where ${\mathbf{W}}_0$ and ${\mathbf{b}}_0$ denote the learnable parameter and the bias vector of the output gate, respectively.

(f) The hidden layer output vector of the t-th user in the user sequence is as follows:

$${\mathbf{h}}_t={\mathbf{o}}_t·tanh\left({\mathbf{C}}_t\right)$$

(9)

Researchers have introduced self-attention into recommender systems in some HIN-based methods based on the attention mechanism of the natural language neighborhood. However, traditional self-attention has some limitations, such as information loss and overfitting. Therefore, we adopt RSA for processing users and items. Specifically, RSA includes two sandwich networks and gated self-attention (GSA) networks for solving the problem of information loss. At the same time, we use residual connections to solve the problem of overfitting. The process of RSA is shown as follows:

(a) We use the first sandwich network to process ${{\mathbf{x}}_u}^{\prime }$ and obtain the result, which is shown as follows:

$${\widehat{\mathbf{x}}}_u=CNN\left(ReLU\left(CNN\left({{\mathbf{x}}_u}^{\prime }\right)\right)\right)$$

(10)

where $CNN(·)$ is the convolutional neural network and $ReLU(·)$ is the rectified linear unit.

(b) We use a residual connection to combine ${\widehat{\mathbf{x}}}_u$ and ${{\mathbf{x}}_u}^{\prime }$ and feed them into the second sandwich network. The result can be obtained with the following formula:

$${\check{\mathbf{x}}}_u={\widehat{\mathbf{x}}}_u+{{\mathbf{x}}_u}^{\prime }+CNN\left(ReLU\left(CNN({\widehat{\mathbf{x}}}_u+{{\mathbf{x}}_u}^{\prime })\right)\right)$$

(11)

(c) We use a residual connection to combine ${{\mathbf{x}}_u}^{\prime }$ and ${\check{\mathbf{x}}}_u$ and feed them into the GSA module. The result can be obtained with the following formula:

$${\tilde{\mathbf{x}}}_u={\check{\mathbf{x}}}_u+{{\mathbf{x}}_u}^{\prime }+GSA\left({\check{\mathbf{x}}}_u\right)$$

(12)

where $GSA(·)$ is the gated self-attention network, whose formula is shown as follows:

$$\begin{array}{c}GSA\left({\check{\mathbf{x}}}_u\right)=Sigmoid\left(FC\left({\check{\mathbf{x}}}_u\right)\right)+tanh(FC({\displaystyle \frac{CNN\left({\check{\mathbf{x}}}_u\right)CNN{\left({\check{\mathbf{x}}}_u\right)}^T}{\sqrt{d}}}FC({\check{\mathbf{x}}}_u)))\hfill \end{array}$$

(13)

where $Sigmoid(·)$ and $tanh(·)$ are nonlinear activation functions and $FC(·)$ is a fully connected layer.

Because the process for items is the same as that for users, we can obtain ${\tilde{\mathbf{y}}}_i$ as follows:

$${\tilde{\mathbf{y}}}_i={\check{\mathbf{y}}}_u+{{\mathbf{y}}_u}^{\prime }+GSA\left({\check{\mathbf{y}}}_u\right)$$

(14)

4.3. Meta-Path Embedding

Meta-path embedding learning aims at learning the explicit representation of meta-paths to improve mutual interactions. The key point of this representation is to generate path instances according to their importance. In this part, a temporal convolutional network module is introduced to capture the temporal relations and reliance of the nodes in each meta-path instance sequence.

4.3.1. Sampling of High-Quality Path Instances

Different meta-paths mean different semantic and interactive relationships between different types of nodes. There are several meta-paths in Figure 1. For instance, meta-path UMTM is a sequence of a user node, a movie node, a type node, and a movie node, which indicates that people fall in love with movies of the same type. Path-based similarity measures are used in HINs to enhance the representations of nodes and links [41]. Moreover, nodes can be reached with different meanings through meta-paths. Given a meta-path UMTM in a heterogeneous information network, a new term, meta-path instance $u_1{m}_1{t}_1{m}_2$, is defined as a sequence consisting of various nodes following the architecture of meta-path UMTM. Specifically, Bob likes watching Roman Holiday, which is a romance, and he is very likely interested in Titanic, which is of the same type; then, $Bob\to RomanHoliday\to Romance\to Titanic$ is a meta-path instance. Multiple meta-path instances of this form can make up a meta-path.

The embedding of meta-path P is obtained from the embedding aggregation of path instances; thus, their high-quality sampling is necessary. However, path instance sampling approaches, such as meta-path-based random walk, are inefficient, as they affect meta-path embedding generation. In a path, a source node should be linked to a node of higher priority in each step. Traditional paths obtained with the random walk method are usually composed of nodes that may not be highly related, so they may not have rich semantic information. Therefore, in order to distinguish the different priorities of different nodes, a priority score based on node similarity is presented. In such a case, nodes are more closely related if their priority score is high. Specifically, we first utilize the singular value decomposition (SVD) feature to learn the latent vector representation of each node [42,43]. Secondly, we calculate the priority score between connected nodes for each path instance. Then, we perform uniform averaging or summation operations. Next, we compare and sort the final priority scores of all path instances. Finally, we choose the path instances with the top-M scores to generate meta-path embeddings.

4.3.2. Single Meta-Path Embedding

After obtaining high-quality meta-path instances, we learn path instance embeddings and aggregate them to generate a meta-path embedding. Considering the sequence characteristics of meta-paths, especially the temporal logic, DPSA, which is an improved self-attention model, is utilized. It is a powerful tool that can be run in parallel on multiple paths and process sequence-type data. Compared with traditional self-attention, DPSA has the following improvements: (1) it uses a deep CNN (DCNN) to obtain the values of query and key, which further includes several CNNs with different kernels, and (2) it uses ResNet to obtain the value of self-attention. These improvements can help to enhance the perceptual ability for meta-paths and obtain the temporal relations among different nodes in a meta-path. The formula of DPSA is shown as follows:

$$\begin{array}{c}{\mathbf{h}}_p=Softmax\left(DCNN\left({\mathbf{E}}_p\right)DCNN{\left({\mathbf{E}}_p\right)}^T\right)ResNet\left({\mathbf{E}}_p\right)\hfill \end{array}$$

(15)

where ${\mathbf{E}}_p$ is the matrix of meta-path instance p and $DCNN(·)$ is the deep CNN, whose formula is shown as follows:

$$\begin{array}{c}DCNN\left({\mathbf{E}}_p\right)=CN{N}_1\left({\mathbf{E}}_p\right)+CN{N}_3\left({\mathbf{E}}_p\right)+CN{N}_5\left({\mathbf{E}}_p\right)+CN{N}_7\left({\mathbf{E}}_p\right)\hfill \end{array}$$

(16)

where $CN{N}_1(·)$, $CN{N}_3(·)$, $CN{N}_5(·)$ and $CN{N}_7(·)$ are CNNs with different kernel sizes.

Moreover, $ResNet(·)$ is the residual network, whose formula is shown as follows:

$$\begin{array}{c}ResNet\left({\mathbf{E}}_p\right)={\mathbf{E}}_p+BN\left(ReLU\left(FC\left(BN\left(ReLU\left(FC\left({\mathbf{E}}_p\right)\right)\right)\right)\right)\right)\hfill \end{array}$$

(17)

where $BN(·)$ denotes batch normalization.

In addition, because a meta-path is composed of path instances, the max-pooling operation needs to be applied to such instances as follows:

$${\mathbf{c}}_p=\text{max-pooling}{\left({\mathbf{h}}_p\right)}_{p=1}^M$$

(18)

where M is the number of path instances, and max-pooling is the operation performed on M meta-path instances to obtain the most important embedding features among them.

After obtaining the embedding of a single meta-path, we introduce L2-normalization to process it and, importantly, prevent overfitting:

$${{\mathbf{c}}_p}^{\prime }={\mathrm{L}}_2\left({\mathbf{c}}_p\right)$$

(19)

where L₂ denotes the normalization operation, which is a common method for training deep learning models and solving overfitting problems.

4.3.3. Meta-Path Aggregation

Different meta-paths may have different importance because every user may have their own preferences. An individual user is also likely to make different choices and have different interactions with other entities. A good meta-path embedding includes the semantics of each meta-path and accurately distinguishes them. Therefore, the introduction of an attention mechanism is critical. Considering the impact of users and items on the importance of different meta-paths, we consider enhancing the representation of meta-path embeddings by inputting user and item embeddings into the attention mechanism. This structure is called a collaborative attention mechanism. It differs from self-attention precisely in that it considers not only the interaction and influence within each meta-path but also the influence of users and items on the meta-path. Since different meta-paths have different semantics and importance, we introduce a two-layer neural network for the calculation of the attention scores, which are given as follows:

$${\lambda }_{u,i,p}^{\left(1\right)}=ReLU({\mathbf{w}}_u^{\left(1\right)}{\mathbf{x}}_u+{\mathbf{w}}_i^{\left(1\right)}{\mathbf{y}}_i+{\mathbf{a}}^{\left(1\right)})$$

(20)

$${\lambda }_{u,i,p}^{\left(2\right)}=ReLU({\mathbf{w}}^{\left(2\right)}{\lambda }_{u,i,p}^{\left(1\right)}+{\mathbf{a}}^{\left(2\right)})$$

(21)

where ${\mathbf{w}}_u^{\left(1\right)}$ and ${\mathbf{w}}_i^{\left(1\right)}$ are the weight matrices for users and items, respectively; ${\mathbf{a}}^{\left(1\right)}$ is the bias vector in the first layer; ${\mathbf{w}}^{\left(2\right)}$ and ${\mathbf{a}}^{\left(2\right)}$ are the weight vector and the bias vector, respectively, in the second layer; and ReLU is the activation function.

The final attention weights can be acquired by normalizing the attention scores as follows:

$${\lambda }_{u,i,p}={\displaystyle \frac{{\lambda }_{u,i,p}^{\left(2\right)}}{{\displaystyle \sum _{a\in {\mathbf{M}}_{u,i}}}{\lambda }_{u,i,a}^{\left(2\right)}}}$$

(22)

Finally, we obtain the meta-path embedding with the co-attention mechanism as follows:

$${\mathbf{c}}_{u,i}=\sum _{p\in M_{u,i}}{{\lambda }_{u,i,p}·{\mathbf{c}}_p}^{\prime }$$

(23)

4.4. Embedding Fusion

After having obtained improved user, item, and meta-path embeddings, we combine the three embeddings to obtain the final vector representation of the overall interaction, as shown in the following formula:

$${\mathbf{r}}_{u,i}=MLP({\tilde{\mathbf{x}}}_u\oplus {\tilde{\mathbf{y}}}_i\oplus {\mathbf{c}}_{u,i})$$

(24)

where ⊕ denotes the concatenation operation, and the MLP component is implemented in two hidden layers with ReLU as the activation function and in the output layer of the model with the Sigmoid function. Training an efficient model requires the establishment of a suitable optimization objective function. The objective function of traditional system models for top-N recommendation is the square error loss function. Based on our model, the objective function can be formulated as follows:

$${\mathbf{\sigma }}_{u,i}=-\log {\mathbf{r}}_{u,i}-E_{n\sim p_{neg}}[log(1-log{\mathbf{r}}_{u,n})]$$

(25)

Here, the first term of expression (24) is the modeled interaction, and the second term denotes the negative feedback generated by noise distribution $p_{neg}$, which denotes a uniform distribution of noise in the model.

5. Experiments

The experimental settings, indicators, and results of the proposed TMRec model for top-N recommendations are introduced in detail in this section.

5.1. Datasets and Metrics

We adopted three datasets widely used for recommender systems in different areas: the Movielens dataset for movies, the LastFM dataset for music, and the Yelp dataset for business. The Movielens dataset contains movie rating data, which include movie ratings, movie metadata (genre and era), and demographic data about the user (age, zip code, gender, occupation, etc.); in this dataset, there are 943 users, 1682 movies, and 18 genres. As for the LastFM dataset, it includes a list of users’ most popular artists and the number of times the latter have been played; specifically, there are 1892 users, 17,632 artists, and 11,945 tags. Finally, in the Yelp dataset, there are 16,239 users, 14,267 businesses, and 47 cities. In addition, we also used DUNN to further demonstrate the effectiveness of the proposed TMRec. DUNN [18] is a real-world dataset comprising offline transactions spanning a two-year period from around 2000 households. It has 2500 users, 16,780 items, and 269,974 transactions.

We adopted the widely used metrics of recall at rank-10 ($Recall@10$), normalized discounted cumulative gain at rank-10 ($NDCG@10$), precision at rank-10 ($Prec@10$), and F-score to quantitatively evaluate the proposed TMRec model. It is worth noting that the higher the metrics, the better the model performance. We averaged the results of 10 experiments to obtain more accurate experimental results.

5.2. Implementation Details

We performed the experiments on the proposed TMRec model with the Python libraries Keras and Tensorflow. The implementation details of our experiments are shown as follows: Before training a neural network, its full value and bias must be initialized. For our experiments, the Gaussian distribution and adaptive moment estimation (Adam) were used. The former was used to initialize model parameters randomly, and the latter, which distributes the same learning rate to each parameter and adapts independently as learning progresses, was utilized to optimize the model. Additionally, we selected appropriate meta-path instances in our datasets: $UMUM$, $UMGM$, $UUUM$ and $UMMM$ in Movielens and $UATA$, $UAUA$, $UUUA$ and $UUA$ in LastFM; the number of path instances was 5. In addition, we determined a basis for selecting appropriate hyperparameter values for the TMRec model with extensive experiments. Specifically, when training the network, the batch size, the regularization parameter, and the learning rate were set to 256, 0.001, and 0.001, respectively. In addition, we set the layers of LSTM to 2. We selected a $1\times 1$ CNN, a $3\times 3$ CNN, a $5\times 5$ CNN, and a $7\times 7$ CNN as the main components of the DCNN. Lastly, the activation function of the hidden layer was the ReLU function, the number of layers (k) was 5, and the corresponding dimensions of each layer were 512, 256, 128, 64 and 32. For all experiments, we divided the dataset into 80% for training and the remaining 20% for testing with the cross-validation method. In addition, we performed experiments on comparison models from previous studies; their hyperparameter values were set as indicated in the respective publications. Moreover, the split into 80% and 20% of the dataset for training and testing was also applied for these comparison models. All the experimental results, conducted in the same machine under the same conditions, are the averages of 10 experiments.

5.3. Experimental Results Analysis

In this subsection, we compare the proposed TMRec model with several other methods for top-N recommendation. The comparison models can be divided into two categories: CF-based models, including ItemKNN, BPR, MF, and NCF, and HIN-based models, including the meta-paths HAN, MCRec, AMERec, and MEGNN.

(1)

ItemKNN [2]: It is a classical method of collaborative filtering using previous items as the reference. For example, if one wants to predict $u_1$’s rating on movie $m_1$, one first needs to keep a list of k movies that $u_1$ has watched and evaluated and then give a prediction of the rating of $m_1$ by $u_1$ according to the historical ratings.

(2)

BPR [3]: It is a commonly used recommendation model in current recommender systems. Unlike other methods based on a user scoring matrix, it mainly adopts the users’ implicit feedback (such as clicks and favorites) to sort items through the maximum posterior probability obtained by the Bayesian analysis of problems and then generates recommendations.

(3)

MF [24]: It is proposed to solve the shortcomings of CF, which has a weak ability to process sparse matrices. It optimizes the MF model with the cross-entropy loss.

(4)

NCF [25]: It is a variant of the traditional collaborative filtering model. Since the previous inner product of collaborative filtering is too simple to perform well, it utilizes an MLP to replace this operation, combining neural networks and collaborative filtering.

(5)

HAN [13]: It adopts a hierarchical structure of the attention mechanism, including node-level and semantic-level attention. The former is used to distinguish the importance of nodes in a meta-path, while the latter is utilized to learn how much each meta-path contributes to the generation of the final embedding.

(6)

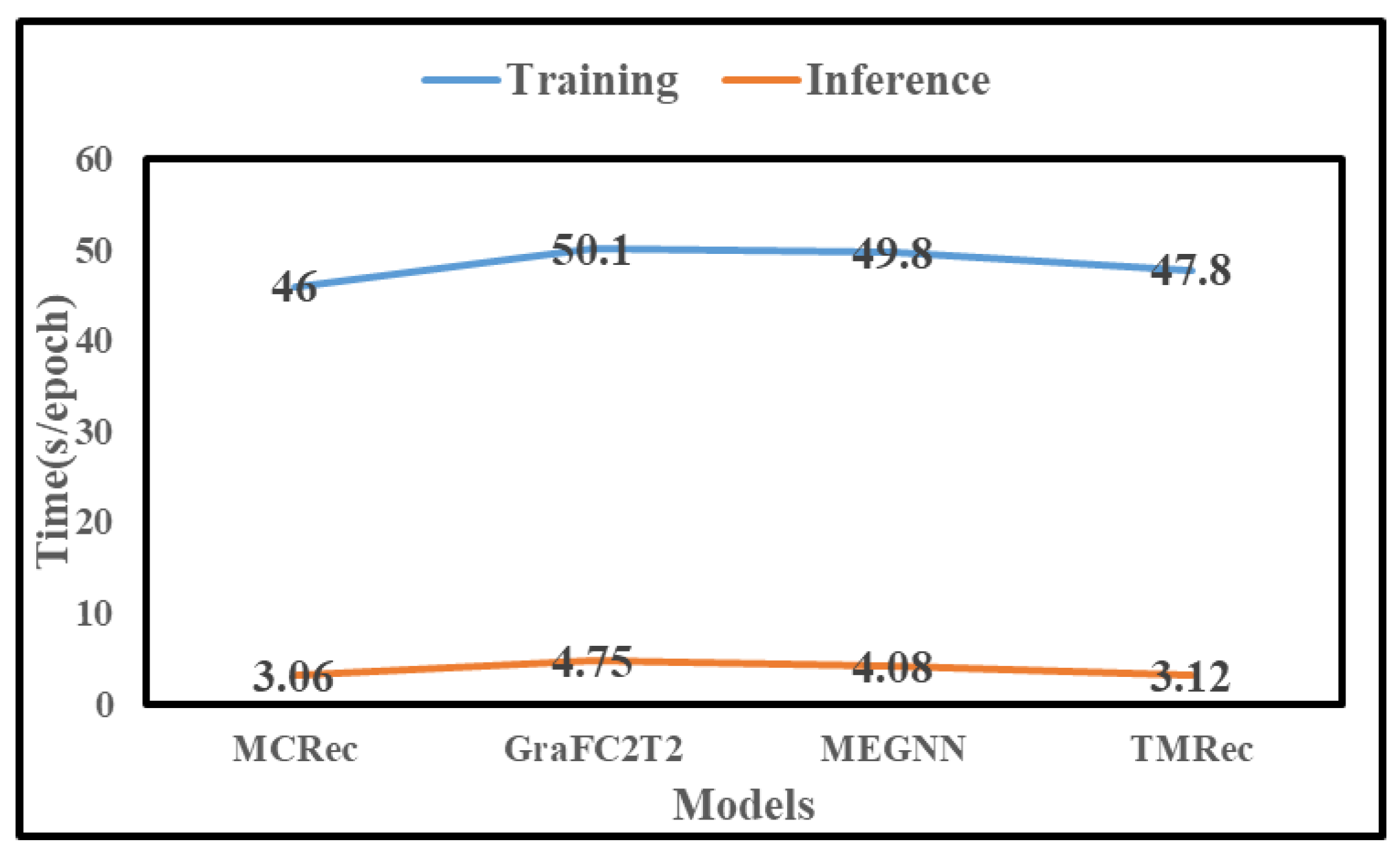
MCRec [16]: It is the first method to explicitly express meta-paths, which are combined with the user and item embeddings for recommendation. It also introduces the co-attention mechanism to mutually enhance the representations of meta-paths, users, and items.

(7)

GraFC2T2 [17]: It is a general graph-based framework that combines some side information for top-N recommendation. It encodes content-based features, and temporal and trust information into a complex graph and uses personalized PageRank on this graph to provide recommendations.

(8)

MEGNN [44]: It is capable of discovering and extracting the most expressive meta-paths and avoids manually defining multiple meta-paths. It also uses a heterogeneous convolution module to generate trainable heterogeneous graph structures.

The results of the proposed model and baselines on three datasets are shown in

Table 2. Comparison with state-of-the-art models.

Model	Movielens			LastFM			Yelp
	Prec@10	Recall@10	NDCG@10	Prec@10	Recall@10	NDCG@10	Prec@10	Recall@10	NDCG@10
ItemKNN	0.2578	0.1536	0.5692	0.4160	0.4513	0.7981	0.1386	0.5421	0.5378
BPR	0.3011	0.1946	0.6459	0.4129	0.4492	0.8099	0.1403	0.5651	0.5531
MF	0.3247	0.2053	0.6511	0.4364	0.4634	0.7921	0.1481	0.5991	0.6011
NCF	0.3256	0.2165	0.6682	0.454	0.4678	0.8104	0.1490	0.6001	0.6007
HAN	0.3356	0.2155	0.6845	0.4720	0.4978	0.8421	0.1602	0.6123	0.6134
MCRec	0.3415	0.2213	0.6876	0.4770	0.5028	0.8491	0.1674	0.6312	0.6300
GraFC2T2	0.3400	0.2181	0.6866	0.4764	0.4991	0.8433	0.1652	0.6212	0.6274
MEGNN	0.3410	0.2214	0.6861	0.4773	0.5018	0.8490	0.1670	0.6305	0.6305
TMRec	0.3568	0.2381	0.7011	0.4933	0.5186	0.8691	0.1851	0.6497	0.6485

.

The major findings from Table 2 are reported below.

(1)

The proposed TMRec consistently outperforms all baselines on the three datasets. The results show the effectiveness of TMRec in top-N recommendation tasks; the model considers the temporal relations of nodes of different kinds and the mutual influence of nodes of the same type in user and item embedding learning.

(2)

It can be clearly seen that when comparing the two different types of methods, HIN-based methods perform better than CF-based methods in general. As HIN-based methods can catch richer semantic information, they are particularly useful in addressing cold-start problems in recommendation. Therefore, they have been more widely used in recommendation tasks, especially when there are many different types of nodes and links in a dataset.

(3)

TMRec outperforms HAN, MCRec, and MEGNN among the HIN-based methods. HAN utilizes a hierarchical attention mechanism at the node and semantic levels, while MCRec employs a co-attention mechanism for the user, item, and meta-path embeddings. In addition, MEGNN considers the selection of meta-paths without considering the explicit expression of the meta-paths. In contrast, the proposed TMRec model uses co-attention in meta-path embedding learning and self-attention in user and item embedding learning. From the above results, we can find that the co-attention mechanism is more suitable for paths composed of different types of nodes, while the self-attention mechanism is more useful for paths composed of nodes of the same type. In addition, although GraFC2T2 considers the temporal information among different entities, its ability to capture heterogeneous information is limited. Therefore, the proposed TMRec achieves better performance than GraFC2T2 because of important components such as LSTM, RSA, and DPSA.

(4)

We can see from Table 2 that Prec@10, Recall@10, and NDCG@10 are increased by 0.0406, 0.0395, and 0.0448, respectively, compared with the average values of the comparison models on the LastFM dataset and by 0.0359, 0.0323, and 0.0412, respectively, on the Movielens dataset. These experimental results demonstrate that the proposed TMRec has better performance in these scenarios. In contrast to these two datasets, Prec@10, Recall@10 and NDCG@10 are increased by 0.0359, 0.0323, and 0.0412, respectively, compared with the average values of the comparison models on the Yelp dataset. Although TMRec’s advantage over the other models is relatively lower on the Yelp dataset, it still exhibits better recommendation performance.

In order to further demonstrate the effectiveness of the proposed TMRec, we also carried out some experiments on the DUNN dataset on TOP-10 by using the comparison models. Additionally, we used the F-score to evaluate their performance on TOP-10. The experimental results are shown in Figure 3.

We can see from Figure 3 that the F-score of the proposed TMRec model is 0.8097. It achieves the highest F-score, indicating that it has the best performance among the comparison models. In addition, it is evident that the reduction in the standard deviation from ItemKNN to TMRec reflects an improvement in the stability of the proposed model. This is particularly important in real-world applications where consistent performance is crucial.

In order to show the advantage in time complexity of the proposed TMRec, we investigated the training and inference time of MCRec, GraFC2T2, MEGNN, and TMRec, as shown in Figure 4.

We can see from Figure 4 that the proposed TMRec has a lower time cost than GraFC2T2 and MEGNN, which demonstrates its advantage in time complexity. In addition, although TMRec has a higher time cost than MCRec, it shows better performance. In summary, the experimental results indicate that TMRec has better time complexity and superior performance.

5.4. Ablation Study

Ablation studies were conducted to evaluate the performance and systematically analyze the effectiveness of the TCN, LSTM, and self-attention modules and included (1) TMRec-DPSA: a variant of TMRec without the DPSA module; (2) TMRec-LSTM: a variant of TMRec without the long short-term memory module; and (3) TMRec-RSA: a variant of TMRec without RSA in the user and item embeddings. The results of the ablation studies are presented in

Table 3. The results of the ablation studies.

Model		TMRec	TMRec-DPSA	TMRec-LSTM	TMRec-RSA
Movielens	Prec@10	0.3568	0.3527	0.3561	0.3564
	Recall@10	0.2381	0.2338	0.2354	0.2355
	NDCG@10	0.7011	0.6995	0.7002	0.7007
LastFM	Prec@10	0.4933	0.4869	0.4912	0.4917
	Recall@10	0.5186	0.5149	0.5173	0.5177
	NDCG@10	0.8681	0.8642	0.8630	0.8639
Yelp	Prec@10	0.1851	0.1805	0.1823	0.1827
	Recall@10	0.6497	0.6436	0.6471	0.6475
	NDCG@10	0.6485	0.6442	0.6453	0.6458

.

We can find from Table 3 that the three improvements clearly have positive effects on recommendation performance. Further, LSTM and RSA in user and item embedding learning play a more important role in TMRec than DPSA. They enhance meta-path embeddings by capturing the temporal relations of internal nodes. In addition, DPSA in meta-path embedding learning is helpful in determining the mutual influence and dependence in a path consisting of nodes of the same type, which also enhances user and item embeddings. In summary, all the modules we introduced in TMRec are important for recommendation performance.

6. Conclusions

In this study, we propose a model for temporally enhanced top-N recommendation on HINs called TMRec for effectively capturing the temporal relations and heterogeneous information of users, items, and meta-paths. Firstly, we adopted long short-term memory (LSTM) and residual self-attention (RSN) to process users and items and enhance the system’s ability to both learn the heterogeneous information in them and capture the temporal relations among them. Secondly, we designed a novel method for processing meta-paths, which includes deep perception self-attention (DPSA), max-pooling, and L₂-normalization. It can effectively obtain the temporal relations among different nodes in meta-paths. Thirdly, we use collaborative attention to process meta-paths, users, and items to obtain their interactions. Finally, extensive experiments were conducted on three public datasets of recommender systems to prove the superiority of our method compared with state-of-the-art top-N recommendation models. Although TMRec can improve the performance of recommender systems, most meta-paths are manually selected, which may hinder the application of the model on different tasks and datasets. In the future, we will conduct research on how to automatically generate meta-paths and introduce this strategy into the recommendation task to further improve performance. For example, we could automatically capture path instances between entities that have different semantics. In addition, we have not considered some important auxiliary information for recommendation, so we will develop a method to obtain much more auxiliary information to boost performance.