Valve Internal Leakage Signal Enhancement Method Based on the Search and Rescue Team–Coupled Multi-Stable Stochastic Resonance Algorithm

Abstract

The leakage signal of the hydraulic valve is a weak, nonlinear, and non-periodic signal that is easily overpowered by background noise from the surroundings. To address this issue, the Search and Rescue Team (SaRT) algorithm was introduced to adaptive coupled stochastic resonance, and a new signal-enhancement method based on SaRT for coupled multi-stable stochastic resonance (CMSR) was proposed for enhancing valve-leakage vibration signals. Initially, the method employs the rescaling technique to preprocess the signal, thereby transforming the fault signal into a small-parameter signal. Subsequently, the mutual correlation gain is utilized as an adaptive measure function of the SaRT algorithm to optimize the parameters of the coupled multi-stable stochastic resonance system. Ultimately, the output signal is solved by the fourth-order Runge–Kutta method. This study validated the method using sinusoidal signals and leakage signals of the check valve. The results demonstrate that all CMSR parameters require optimization. Furthermore, the noise reduction was effective for three different leakage signals of faulty check valves, in which the highest in the number of interrelationships increased by 6.9569 times and the highest amplitude ratio of the peak frequency increased by 11.7004 times. The data quality was significantly improved.

1. Introduction

The hydraulic valve is the “control center” of a hydraulic system, controlling and adjusting the whole system. Its performance and stability directly affect the overall performance and operation efficiency of the hydraulic system. Leakage is a common fault of hydraulic valves. Utilizing vibration monitoring facilitates the discernment of the low-to-mid-frequency characteristics inherent in leakage signals. The vibration signal associated with valve leakage typically manifests as a weak, nonlinear, and non-periodic signal, which is particularly susceptible to being obscured by environmental background noise, thereby complicating the extraction of fault-characteristic information. Consequently, it is imperative to implement noise-suppression techniques and enhance the vibration signal characteristics associated with hydraulic valve leakage, as this ensures the acquisition of reliable data for precise pattern identification and quantitative diagnostic evaluation of leakage conditions in hydraulic systems.

In the processing of hydraulic valve-leakage signals, advanced signal processing techniques, particularly wavelet transform-based denoising, empirical mode decomposition (EMD), and variational mode decomposition (VMD), are widely employed for effective noise suppression. Hou et al. [1] proposed an enhanced wavelet threshold function denoising algorithm, which effectively reduced the interference of environmental noise on the leakage signal of the safety valve. Shen et al. [2] successfully applied the Empirical Mode Decomposition (EMD) method to analyze fault signals in aircraft hydraulic systems, demonstrating its capability for effective fault-characteristic extraction in noisy environments. Similarly, Jegadeeshwaran et al. [3] implemented Variational Mode Decomposition (VMD) for processing hydraulic brake vibration signals, significantly enhancing fault classification accuracy. While these conventional signal-processing methods demonstrate certain noise-filtering capabilities, they exhibit inherent limitations: (1) incomplete noise suppression, (2) potential loss of critical fault-related information during the denoising process, and (3) an inability to effectively enhance fault characteristics. These limitations necessitate the development of more sophisticated signal-processing techniques for hydraulic system fault diagnosis.

Stochastic resonance (SR), a nonlinear phenomenon first proposed by Benzi et al. [4] during their investigation of paleoclimate transitions between glacial and interglacial periods, describes a unique mechanism where the combined effects of weak periodic signals, noise, and nonlinear systems produce an enhanced system output when the optimal noise intensity or system parameters are achieved [5]. This counterintuitive phenomenon, where noise can paradoxically enhance signal detection rather than degrade it, has gained significant attention across multiple disciplines. Recent applications have demonstrated its effectiveness in diverse fields, including mechanical fault diagnosis [6,7], image processing and enhancement [8,9], magnetic anomaly detection [10,11], and biomedical signal analysis [12,13]. The ongoing development of SR technology has witnessed significant advancements in two key aspects: novel parameter-optimization algorithms and enhanced nonlinear system models. Regarding parameter optimization, Liang et al. [14] developed an innovative stochastic resonance detection method incorporating a fast artificial fish swarm algorithm, effectively addressing the challenge of slow convergence rates in adaptive parameter-induced stochastic resonance for weak-signal detection. Hao et al. [15] proposed an adaptive stochastic resonance detection method based on an improved artificial fish swarm algorithm to solve the following problems: the adaptive stochastic resonance system easily falls into local optima and the convergence speed in the process of parameter optimization is slow. Cong et al. [16] proposed a combination strategy using the adaptive weighted particle swarm optimization algorithm and general scale transformation stochastic resonance to achieve effective diagnosis of friction faults between the rotor and stator. Huang et al. [17] used four strategies: Sobol sequence initialization, exponential convergence factor, adaptive position update, and Cauchy–Gaussian mixed variation to improve the basic gray wolf optimization algorithm. The structural parameters of multi-stable stochastic resonance are optimized by improving the gray wolf algorithm, and the effective detection of bearing fault signals is realized. Regarding advancements in nonlinear system models, significant progress has been made in developing sophisticated SR systems. Zhang et al. [18] proposed a new model of a tristable stochastic resonance system. Zhang et al. [19] innovated an adaptive two-dimensional piecewise tristable stochastic resonance method. Suo et al. [20] contributed a mutual information-assisted feedforward cascaded SR approach, demonstrating enhanced signal-processing capabilities. In parallel developments, Zhang et al. [21] successfully implemented a coupled bistable system for weak-signal feature extraction, with the experimental results confirming its superior detection performance compared to conventional single bistable systems. Li et al. [22] proposed a high-dimensional spatial model based on a coupled bistable stochastic resonance system and analyzed the output signal-to-noise ratio of the high-dimensional spatially coupled bistable stochastic resonance system in different dimensions. The results showed that the output signals of these coupled ends with the same system parameters were the same. He et al. [23] proposed a novel and complex unsaturated piecewise linear four steady-state stochastic resonance system, which was applied to the early fault diagnosis of various bearing models under Gaussian white noise and demonstrated excellent fault detection capabilities. Further extending this concept, Cui et al. [24] developed an advanced coupled multi-stable SR method. Notably, Xia et al. [25] introduced a groundbreaking three-dimensional coupled multi-stable periodic potential-induced SR framework for rolling bearing diagnosis. Meng et al. [26] proposed a novel stochastic resonance method for multi-stable coupled arrays driven by asymmetric tripartite noise. In addition, Ai et al. [27] proposed a stochastic resonance model based on color noise and time delay, and transformed the classical bistable symmetric potential into a double-well variable potential well, which can directly control the barrier height through adjusting the parameters.

SR and its improved methods have made significant progress in the field of weak signal detection. However, there is still a clear research gap in its application in reducing noise and enhancing weak feature extraction of leakage signals in hydraulic valves. The existing literature indicates that although the stochastic resonance method theoretically has the potential to enhance weak signals, its practical application in complex mechanical system fault diagnosis, especially in the processing of hydraulic valve-leakage fault signals, has not been fully explored. The innovation of this article lies in combining a new search and rescue team optimization algorithm with coupled multi-stable stochastic resonance, and applying it to the field of hydraulic valve-leakage signal enhancement. This method achieved effective noise reduction and enhancement of hydraulic valve-leakage fault signals by optimizing the system parameters and inputting them into a coupled multi-stable model. In addition, this method uses the Fourier transform to perform frequency domain analysis on the processed signal, further verifying the superiority of the proposed method in weak feature extraction. This study fills the application gap of stochastic resonance theory in hydraulic valve fault diagnosis.

The remainder of this article is organized as follows. Section 2 presents the theoretical foundations, including the SaRT algorithm framework, performance evaluation metrics, and fundamental principles of coupled multi-stable systems. Section 3 details the comprehensive implementation process of the proposed SaRT-CMSR algorithm. Section 4 details the systematic parameter analysis using synthetic sinusoidal signals to investigate the influence of key system parameters on the output characteristics of coupled multi-stable systems. Section 5 presents the validation of the proposed method through experimental case studies, applying the SaRT-CMSR system for noise suppression and feature enhancement of leakage-induced vibration signals in three types of faulty check valves. The enhanced signals were subsequently analyzed through the Fourier transform to extract their frequency domain characteristics, demonstrating the method’s effectiveness. Finally, Section 6 summarizes the main conclusions and discusses potential applications and future research directions.

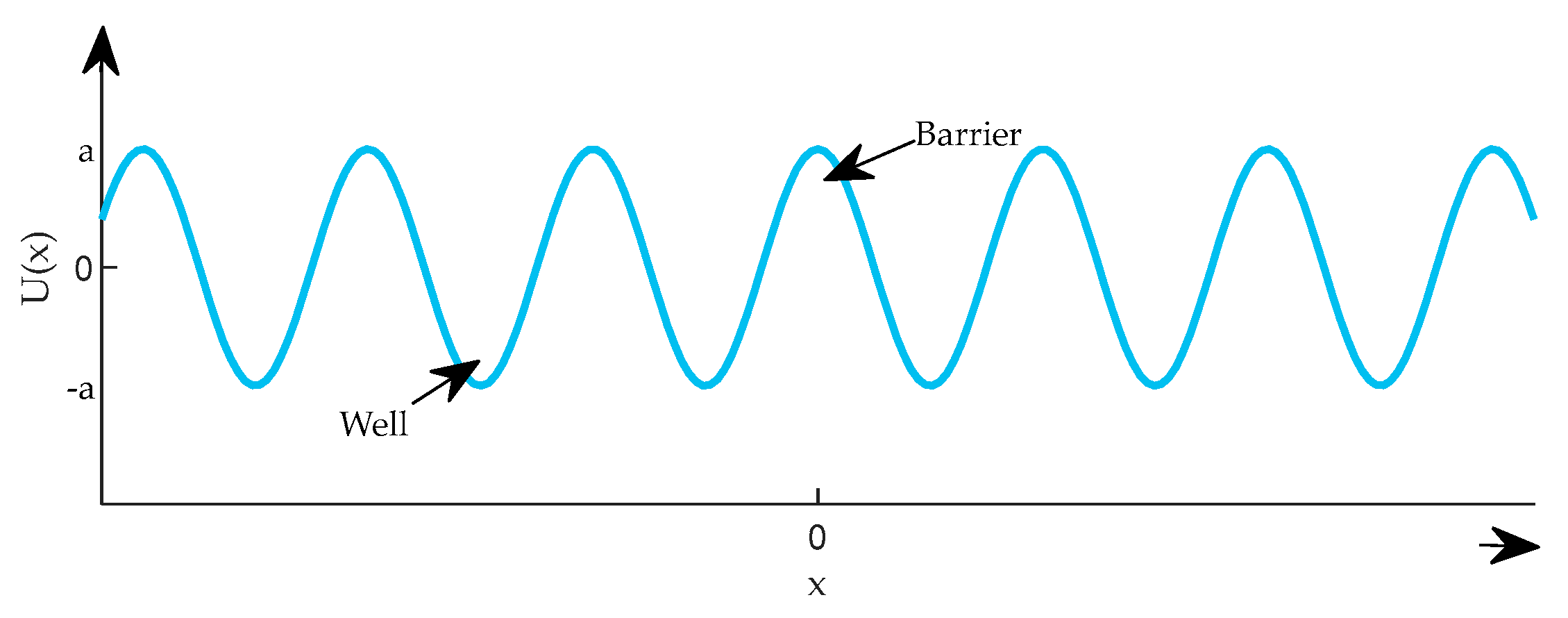
2. Theoretical Model

2.1. Coupled Multi-Stable System Model

At present, there are many system models with different steady-state numbers for stochastic resonance, such as the monostable model, bistable model, tristable model, and periodic multi-stable model. Among these, the periodic multi-stable model exhibits unique advantages due to its multiple potential barriers and wells, enabling complex particle transitions across different energy states. This dynamic behavior can be mathematically described by the Langevin equation:

$${\displaystyle \frac{dx}{dt}}=-U^{\prime }\left(x\right)+s(t)+n(t),$$

(1)

where U(x) represents the multi-stable potential function model, s(t) denotes the target signal to be detected, and n(t) represents Gaussian white noise with a zero mean and noise intensity D. The multi-stable potential function U(x) can be mathematically expressed as

$$U(x)=-a\cos (bx),$$

(2)

where a and b are the system parameters. The potential function model is shown in Figure 1, which contains multiple potential wells and barriers.

The coupled model enhances SR performance through strategic modification of the nonlinear system architecture. This innovative approach incorporates inter-system interactions between individual SR models, utilizing coupling coefficients as weighting parameters to optimize system performance. Specifically, the coupled SR model demonstrates superior capability in generating more reliable output signals and effectively extracting weak signal characteristics, particularly under conditions of intense noise interference. The mathematical representation of the coupled multi-stable system model is expressed as follows:

$$\left\{\begin{array}{l}{\displaystyle \frac{dx}{dt}}=-U^{\prime }(x)+\gamma (y-x)+s(t)\hfill \\ {\displaystyle \frac{dy}{dt}}=-V^{\prime }(x)+\gamma (y-x)\hfill \end{array}\right.,$$

(3)

where γ is the coupling coefficient; s(t) is the collected noisy input signal; x(t) is the final output signal of the system; and U(x) and V(y) are both periodic multi-stable models, which can be expressed as

$$\left\{\begin{array}{c}U(x)=-a\cos (bx)\\ V(x)=-c\cos (dx)\end{array}\right.,$$

(4)

where a and b represent the controlled system parameters, while c and d denote the control system parameters. Through the substitution of Equation (4) into Equation (3), the system output described by Equation (3) is numerically solved using the fourth-order Runge–Kutta method, as mathematically represented in Equation (5).

$$\left\{\begin{array}{l}{k}_1=h[-ab\sin (b{x}_n)+\gamma (y_n-x_n)+s_n]\hfill \\ j_1=h[-cd\sin (d{y}_n)+\gamma (y_n-x_n)]\hfill \\ k_2=h[-ab\sin (b(x_n+0.5k_1))+\gamma (y_n-(x_n+0.5k_1))+s_n]\hfill \\ j_2=h[-cd\sin (d(y_n+0.5j_1))+\gamma ((y_n+0.5j_1)-x_n)]\hfill \\ k_3=h[-ab\sin (b(x_n+0.5k_2))+\gamma (y_n-(x_n+0.5k_2))+s_n]\hfill \\ j_3=h[-cd\sin (d(y_n+0.5j_2))+\gamma ((y_n+0.5j_2)-x_n)]\hfill \\ k_4=h[-ab\sin (b(x_n+k_3))+\gamma (y_n-(x_n+k_3))+s_n]\hfill \\ j_4=h[-cd\sin (d(y_n+j_3))+\gamma ((y_n+j_3)-x_n)]\hfill \\ x_{n+1}=x_n+{\displaystyle \frac{1}{6}}(k_1+2k_2+3k_3+k_4)\hfill \\ y_{n+1}=y_n+{\displaystyle \frac{1}{6}}(j_1+2j_2+3j_3+j_4)\hfill \end{array}\right.,$$

(5)

2.2. System Optimization Evaluation Indicators

Stochastic resonance triggers resonance synchronization between nonlinear systems and input signals, transforming noise energy to low-frequency signals and amplifying weak-signal features. Stochastic resonance shifts noise energy to low-frequency signals and amplifies the weak signal characteristics by triggering resonance synchronization between the nonlinear system and the input signal. The signal-to-noise ratio (SNR) and the correlation number are widely used as evaluation indicators of the output effect of the system. Fauve et al. [28] pioneered the formal definition of the SNR in the context of SR, establishing it as the ratio of the power spectral density at the output signal frequency to the background noise power spectral density at the corresponding frequency within a bistable system. Mathematically, this relationship is expressed as

$$SNR={\displaystyle \frac{1}{S_N(\Omega )}}\underset{\Delta \Omega \to 0}{\lim }{\displaystyle {\int }_{\Omega -\Delta \Omega }^{\Omega +\Delta \Omega }S(\Omega )}d\Omega ,$$

(6)

where S(Ω) is the spectral density of the periodic signal and S_N(Ω) is the spectral density of the background noise. However, this SNR calculation method is inherently limited to periodic input signals, providing only local signal-to-noise ratio measurements.

Certain scholars have adopted the residence time distribution ratio [29] and the bit error rate as metrics for assessing the quality of output signals in systems. The residence time distribution ratio is particularly apt for appraising periodic responses within the realm of coupled stochastic resonance. The bit error rate serves as a criterion for evaluating binary digital signals that have undergone processing via stochastic resonance. Given that valve-leakage signals typically exhibit non-periodic characteristics, this conventional approach is inadequate for evaluating random resonance output signals. To address this limitation, this study employed correlation coefficient gain as the optimization metric for the CMSR system. The correlation coefficient, which quantifies the linear relationship between two variables, ranges from −1 to 1. When the absolute value approaches unity, it indicates a stronger correlation and consequently better system output performance. Mathematically, the correlation coefficient is expressed as

$$r(X,Y)={\displaystyle \frac{Cov(X,Y)}{\sqrt{Var\left[X\right]Var\left[Y\right]}}},$$

(7)

where Cov(X, Y) is the covariance between X and Y, Var[X] is the variance of X, and Var[Y] is the variance of Y. The cross-correlation gain is quantitatively determined by comparing two key metrics: (1) the cross-correlation between the original signal and the input signal, and (2) the cross-correlation between the original signal and the output signal. This comparative analysis can be mathematically expressed as

$$CcG={\displaystyle \frac{r(X,Z)}{r(X,Y)}},$$

(8)

where X is the original signal, Y is the system noise input signal, and Z is the system noise reduction output signal.

2.3. SaRT Optimization Algorithm

The SaRT algorithm, a new meta-heuristic optimization algorithm, was proposed by Tong et al. [30]. It can achieve a more stable solution of high-dimensional problems and has been verified by multiple verification cases and engineering problems. It solves the NP-hard problem with very good convergence accuracy and has good accuracy, robustness, and parameter insensitivity. The SaRT algorithm is biologically inspired by the collaborative behavior of search and rescue teams, where each team member conducts multi-directional exploration with one direction consistently oriented toward a dynamically updated central point. This central point is continuously refined based on the current global best solution, facilitating effective information exchange and cooperation among team members to achieve optimal global search performance. The fundamental principles of the SaRT algorithm are summarized below.

Initialize the team:

$$X^{c-1}={[x_1^{c-1},x_2^{c-1},\mathrm{\dots }{x}_i^{c-1}\mathrm{\dots }{x}_n^{c-1}]}^T,$$

(9)

where c is the number of iterations; X^c−1 is a team; x_i^c−1 (i = 1, 2…) is a row vector with dimension w; and w is the dimension of the problem. Using the following equation to construct the search space Xs^c for x_i^c,

$$X{s}_i^c=X{s}_i^{c-1}+b_i^c\times D_i^c,(i=1,2,\mathrm{\dots },n),$$

(10)

where D_i^c is the direction matrix, and its magnitude is (w + 1) × w; b_i^c is the step size; Xs_i^c−1 is formed by copying x_i^c−1. X^c−1 is updated to X^c according to Xs_i^c. The search and rescue teams receive updates.

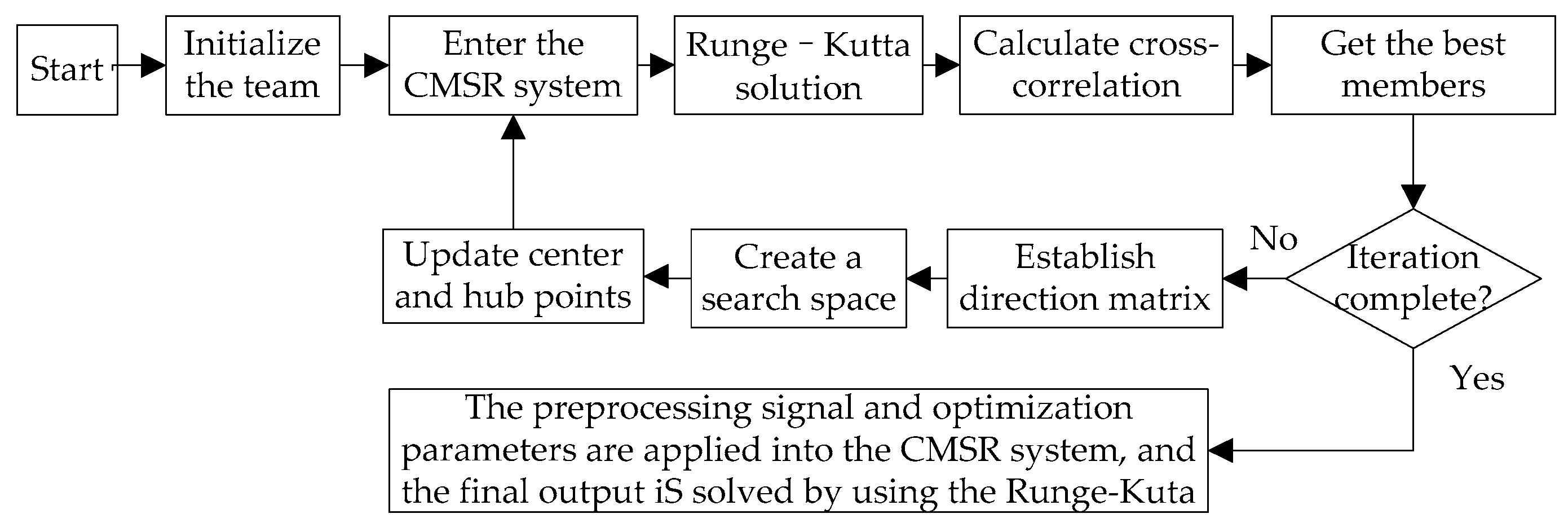
3. SaRT-CMSR-Based Signal Enhancement Method

The detection of leakage-induced vibration signals in hydraulic valves presents significant challenges due to their susceptibility to environmental noise interference, resulting in obscured fault characteristics. To address this critical issue, this study proposes an innovative adaptive CMSR method integrated with the SaRT optimization algorithm. The implementation framework comprises the following systematic steps:

• Spectral Analysis: The Fourier transform is performed on the leakage vibration signal inside the valve to observe the frequency domain characteristics of the original signal;
• Signal Preprocessing: Signal conditioning is implemented through a rescaling transformation, converting the leakage fault signals into small-parameter signals via secondary sampling to facilitate the subsequent processing;
• SaRT Algorithm Initialization: The optimization team parameters are configured, where each member’s parameters are evaluated through the CMSR system. The system output is computed using the fourth-order Runge–Kutta method, with correlation coefficients calculated to identify optimal team members;
• Iterative Optimization: Direction matrices are constructed and search spaces are defined for systematic optimization, providing continuous updates to team members and updating the center points through iterative refinement;
• Final Signal Processing: The optimization parameters obtained in step (4) and the pre-processing signal in step (2) are input into the CMSR system. The fourth-order Runge–Kutta method is used to solve the final output signal, and the noise reduction and feature enhancement of the noisy signal are realized.

The algorithm flow chart is shown in Figure 2 below.

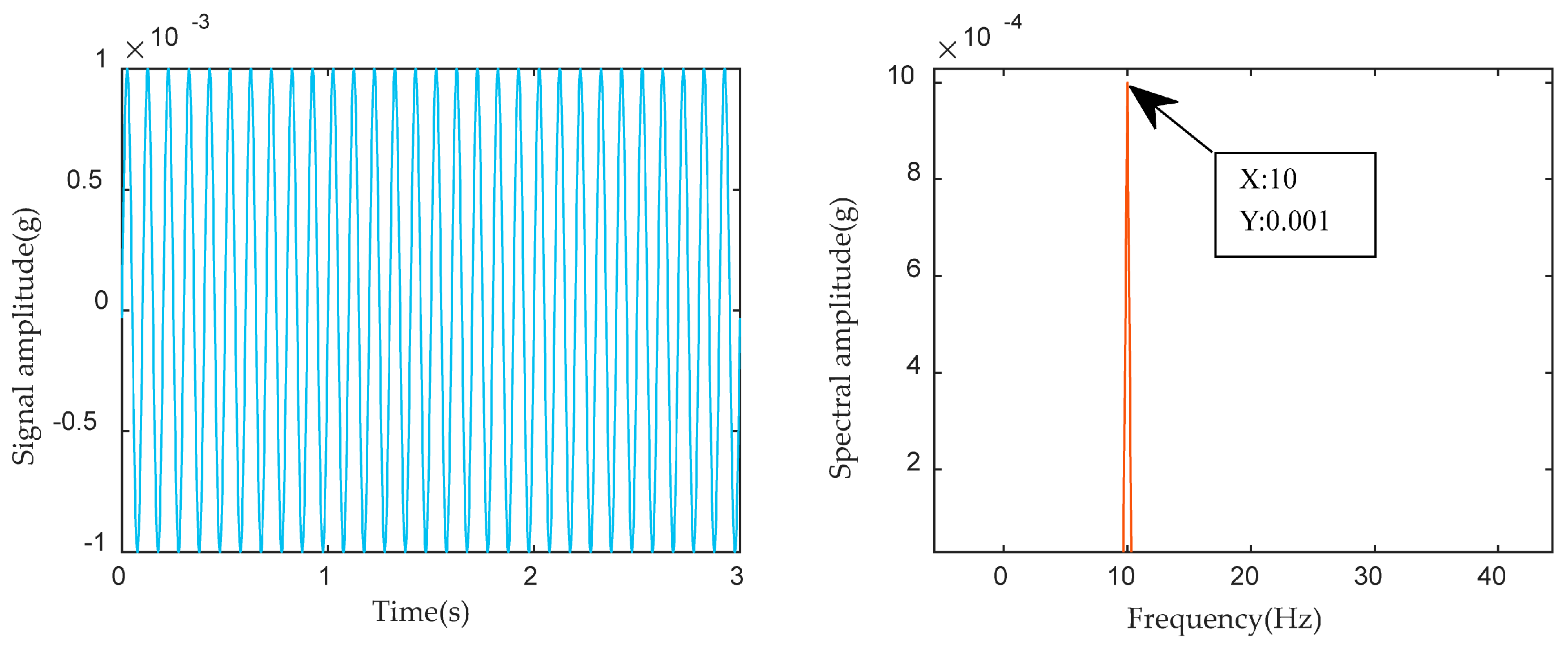
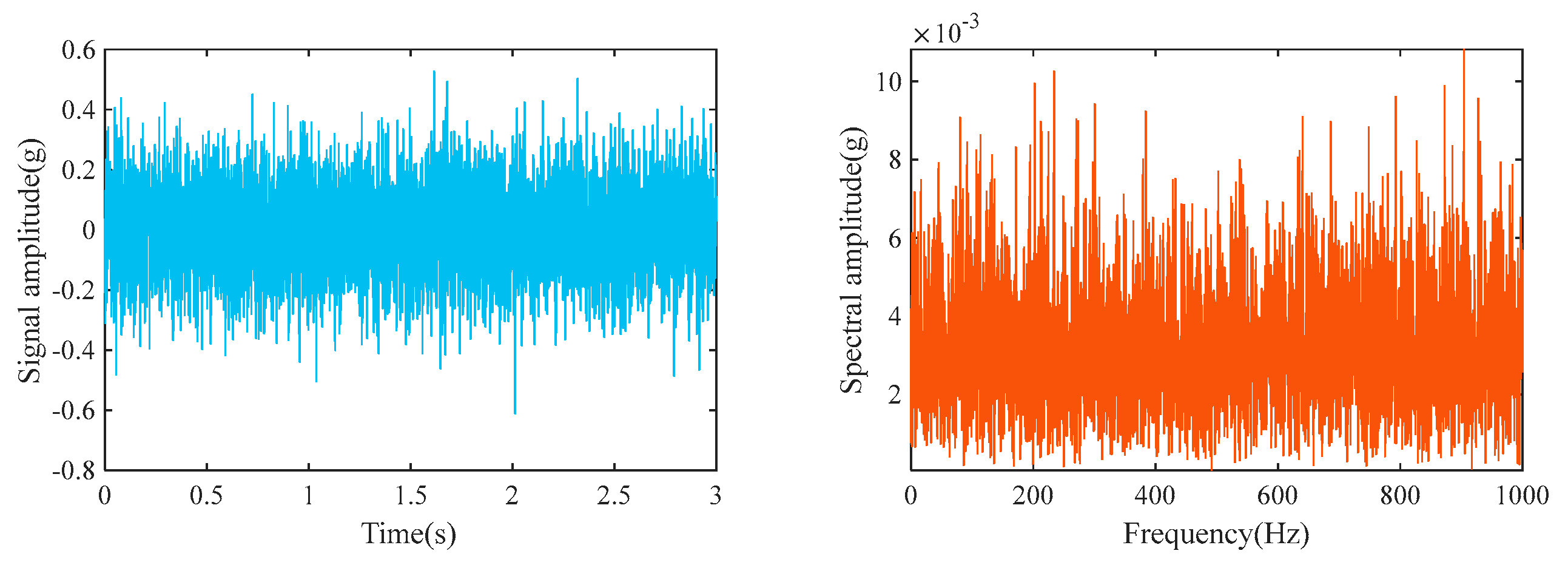
4. System Parameter Analysis

Due to the inherent limitations of adiabatic approximation theory and linear response theory, the SR input signal must satisfy strict amplitude and frequency constraints, specifically requiring both parameters to be less than 1. To address this requirement, this study employed a rescaling transformation for signal preprocessing. Given that the amplitude of valve-leakage signals naturally satisfies the amplitude constraint (being significantly less than 1), only frequency scaling is necessary. For systematic parameter analysis, we constructed a synthetic sinusoidal signal with additive noise, characterized by an amplitude A < 1 and frequency f > 1 Hz. The mathematical representation of the input signal is given by

$$S(t)=A\sin (2\pi ft)+noise(t),$$

(11)

where noise(t) is Gaussian white noise, the noise intensity is 0.01, the signal sampling frequency is f_s = 2000 Hz, and the sampling time is t = 3 s. In the formula, the signal strength is A = 0.001 and the signal frequency is f = 10 Hz. Initially, the controlled system parameters were fixed at a = b = 1. The SaRT-CMSR algorithm was employed to optimize the multi-objective parameters, including the control system parameters c and d, coupling coefficient, and rescaling factor, using the cross-correlation gain as the objective function. The optimized system output was subsequently obtained. Figure 3 illustrates the time and frequency domain characteristics of the pure sinusoidal signal. Figure 4 depicts the time and frequency domain representations of the noisy signal, where the signal is entirely obscured by noise. Figure 5 presents the time and frequency domain diagrams of the output signal from the SaRT-CMSR system.

From Figure 5, it can be easily concluded that although the noise was suppressed and the spectral amplitude value was enhanced, the peak frequency of the output signal was not equal to the original frequency. Then, without fixing the parameters a and b, all the parameters were optimized together, and this system output is shown in Figure 6. In this case, the noise was greatly suppressed, and the peak frequency of the output spectrum was equal to the original frequency. The correlation between the output noise reduction signal and the original signal was 0.8553, and the cross-correlation gain was 75.58. At this time, the system parameters were a = 0.3, b = 2.5967, c = 0.1648, d = 8.4951, and the rescaling multiple R_m = 201, and the signal amplitude increased by 2390 times. In similar studies, the coupling SR method fixes the parameters of the controlled system and only optimizes the parameters of the control system. Comparing the two output results, it can be seen that the parameters of the controlled system also have an important impact on the output results. Because parameter a controls the barrier height of the controlled system, when the signal amplitude is very small relative to the barrier height, the Brownian particles cannot over-migrate between potential wells. When the signal amplitude is too large relative to the barrier height, the Brownian particles will jump irregularly between the potential wells, which cannot achieve the effect of noise reduction enhancement. At the same time, parameter b controls the barrier width, which has an important impact on the synergistic resonance between the signal and the system. Therefore, in this study, the parameters a and b of the controlled system were also used as the parameters to be optimized.

5. Verification Based on Leakage Signal in Check Valve

In the initial stages of hydraulic valve leakage, the hydraulic circuit pressure remains relatively stable, making detection challenging when using conventional pressure sensors due to their installation and removal complexities. While acoustic emission sensors offer an alternative, their deployment requires precise coupling with the measurement surface to ensure optimal acoustic transmission, which presents operational difficulties. Additionally, acoustic emission signals, characterized by their ultra-high frequency nature, demand high sampling rates and generate large data volumes, consequently reducing the data-processing efficiency. Magnetic vibration sensors are easy to install and can capture low-frequency features in leakage signals. Therefore, this experiment collected the leakage vibration signals inside the valve as the research object.

The check valve is an important hydraulic component that controls the flow direction of the fluid medium, and its wear has a great impact on the performance and efficiency of the hydraulic system. In this study, the SV10PB1-30B hydraulic check valve produced by Huade Company was used as the experimental object. Based on three common types of valve leakage, namely permeation leakage, gap leakage, and jet leakage, this experiment configured three distinct fault conditions in the check valve: entire seal surface defect, local seal surface defect, and eccentric spool defect. These configurations were designed to simulate the actual leakage scenarios of check valves in engineering applications. The fault check valve element is shown in Figure 7. From left to right, this included an entire seal surface defect check valve, local seal surface defect check valve, and eccentric spool defect check valve. The experiment was carried out using an RCYCS-G hydraulic system failure test bench. The test bench is shown in Figure 8. The test bench consists of a load-lifting module, a control module, and a hydraulic circuit module where the tested check valve is located. Through the data acquisition system, the leakage vibration signals in the check valve of entire seal surface defect, local seal surface defect, and eccentric spool defect are collected. The data acquisition box model was NI PX1e-1062Q, the data acquisition card model was NI PXI 4492, and the vibration accelerometer model was 1A111E. The sensor installation position is shown in Figure 9.

The experimental procedure was systematically conducted in three distinct phases: lifting, pressure holding, and falling. Prior to experimentation, calibrated weights were applied to the test bench to ensure that the check valve could sustain a predetermined load pressure during the pressure-holding phase. During the pressure-holding stage, the leakage signals in the check valve of three different fault types were collected at a sampling rate of 2000 Hz for a duration of 3 s. There were no other disturbances such as motor vibrations when the test bench was turned on during the pressure-holding phase, so the ambient background noise was low. To enhance the practical relevance of the experimental conditions, Gaussian white noise with an intensity of 0.0008 was introduced to the internal leakage signal, effectively obscuring the original signal and generating a noisy signal. Subsequently, these three preprocessed fault signals were processed through the SaRT-CMSR system for parameter optimization, yielding the corresponding system output signals. The spectral characteristics of each signal were then extracted through Fourier transform analysis. Figure 10, Figure 11, and Figure 12 present the signal processing results for three distinct fault conditions: (1) entire seal surface defect, (2) local seal surface defect, and (3) eccentric spool defect, respectively. Each figure is organized in a three-column format: the first column displays the original signal, the second column shows the noise-corrupted input signal, and the third column presents the enhanced output signal from the SaRT-CMSR system.

Table 1. Comparison of cross-correlation between input and output signals of check valve leakage experiment.

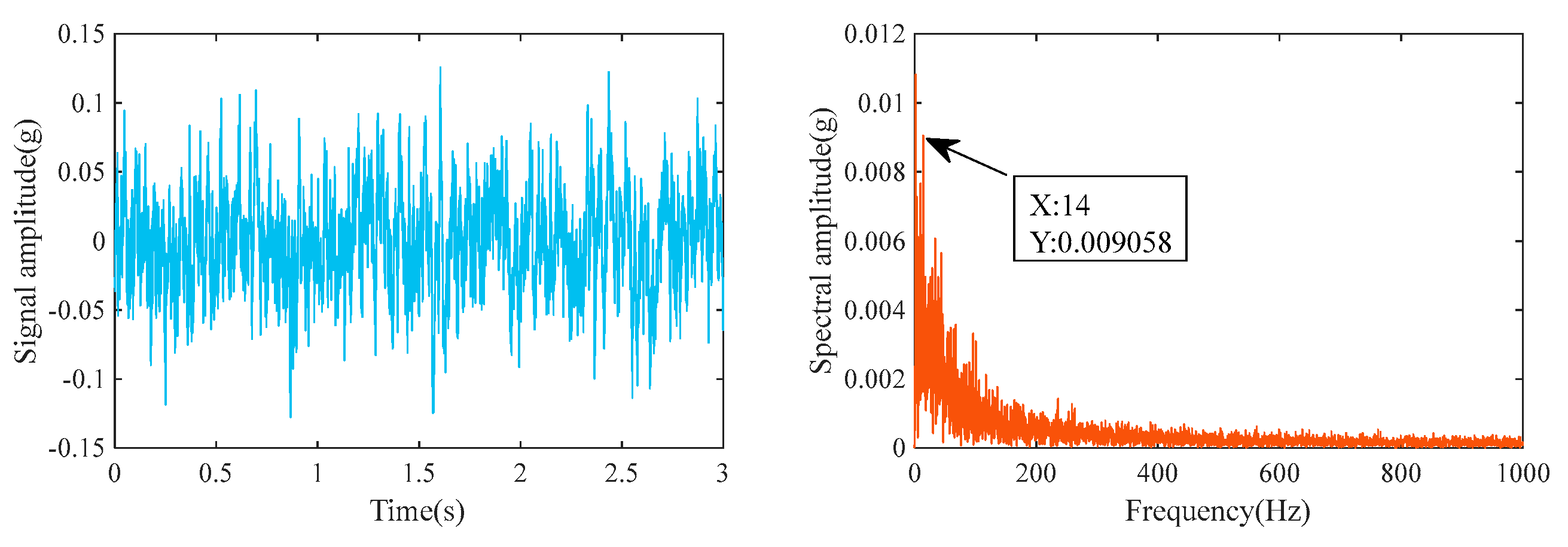
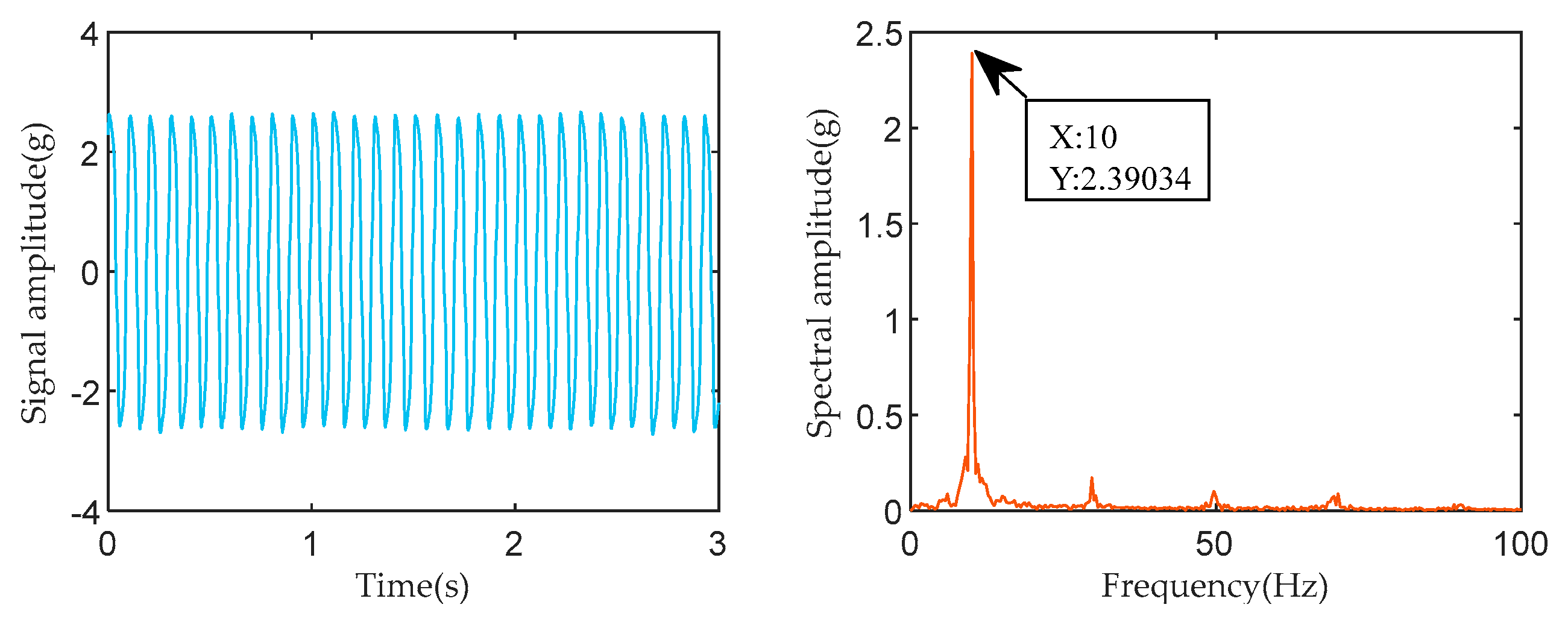
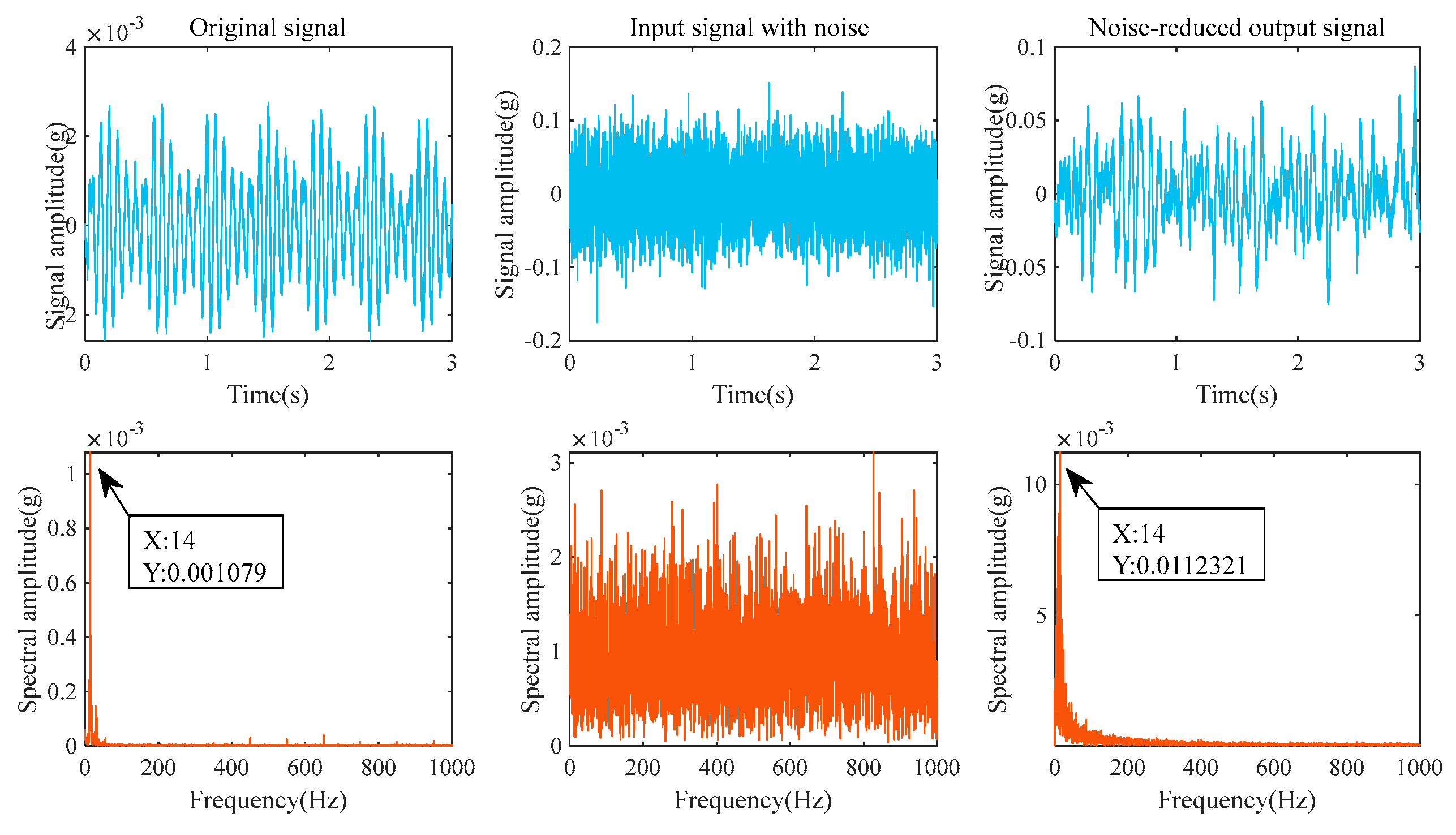
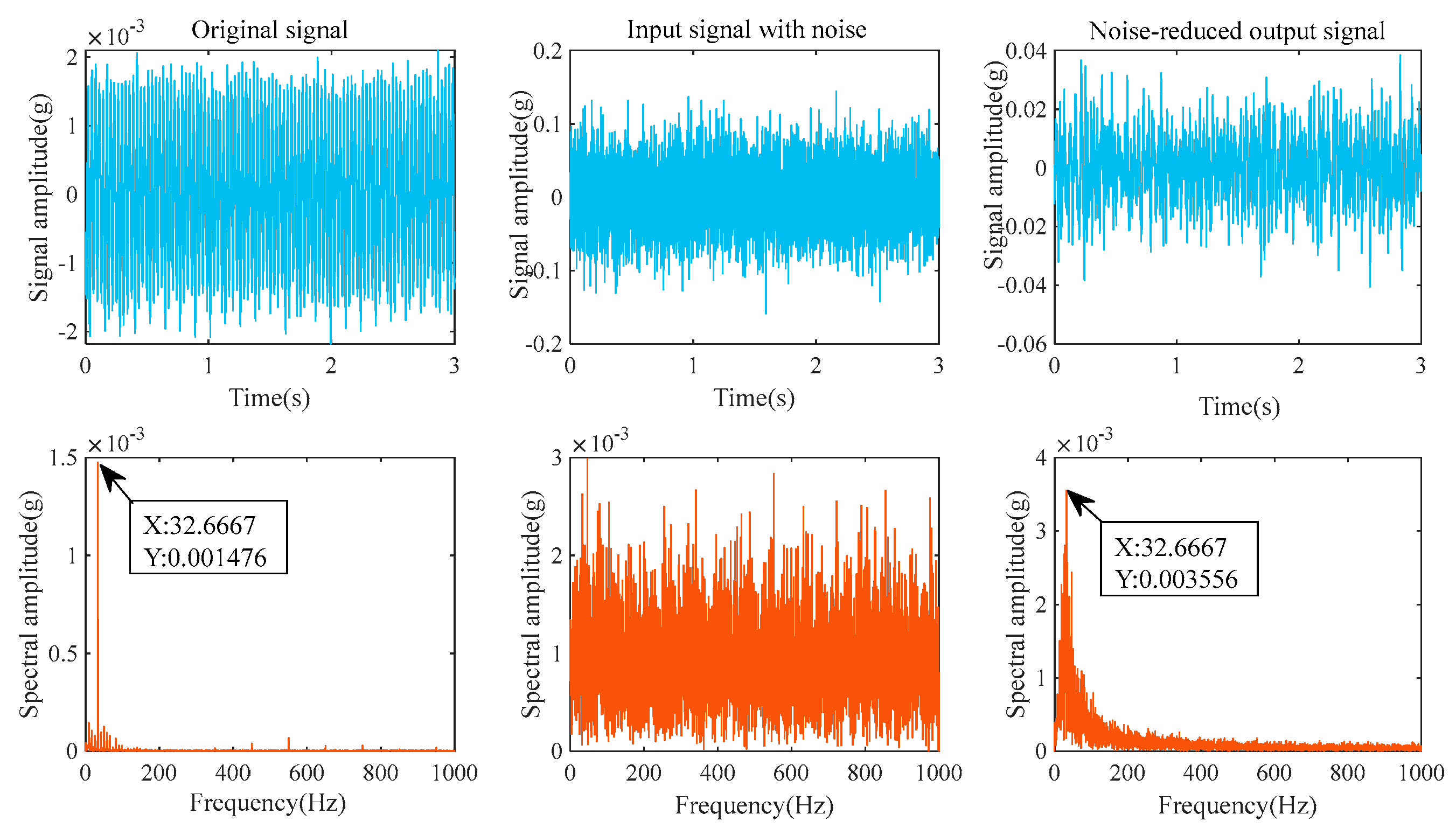
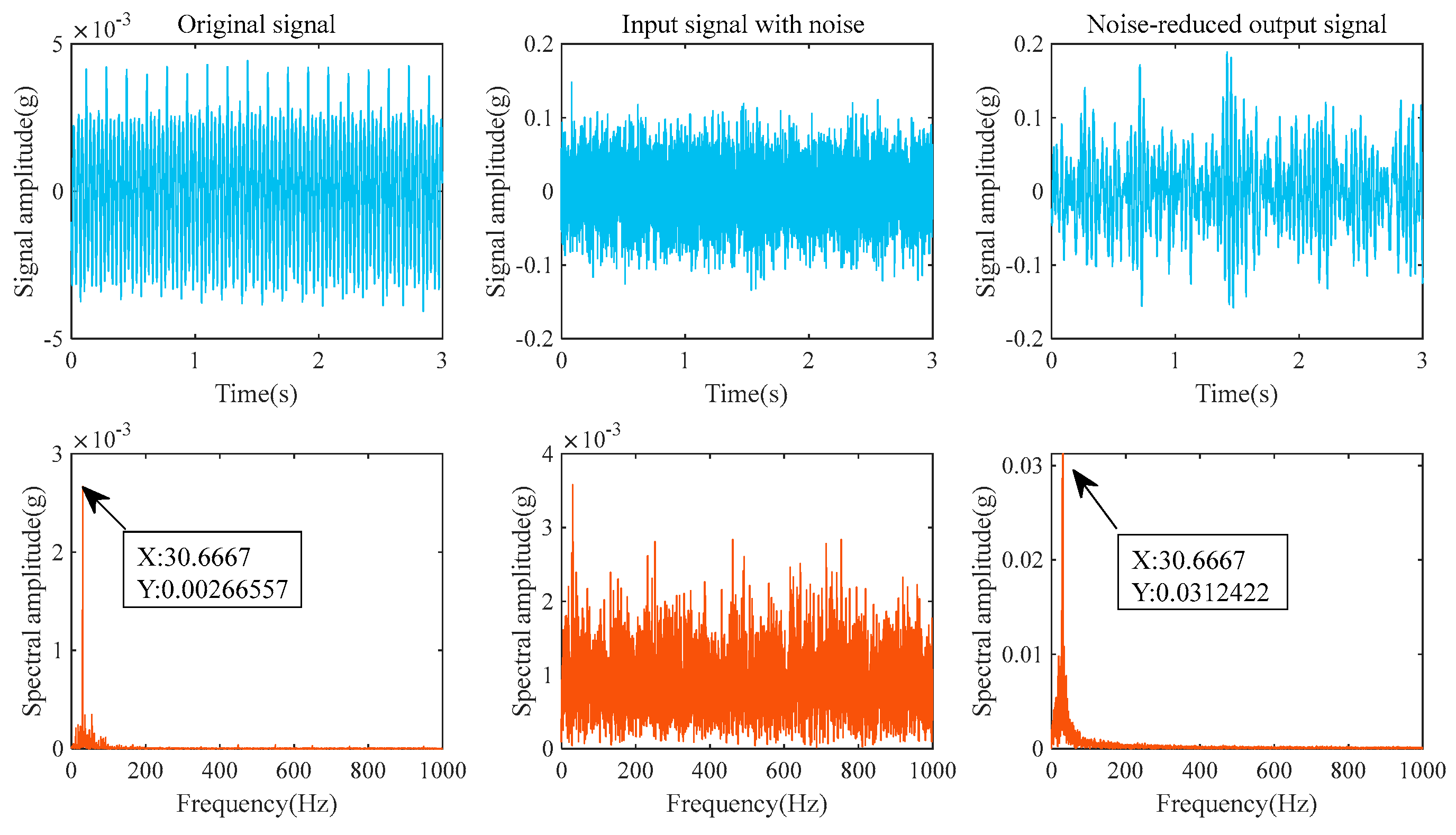
Valve Core	The Number of Relationships Between the Noisy Input Signal and the Original Signal	The Number of Relationships Between the Noise-Canceled Output Signal and the Original Signal	Cross-Correlation Gain
Entire seal surface defect	0.0453	0.3151	6.9569
Local seal surface defect	0.0436	0.1924	4.4128
Eccentric spool defect	0.0691	0.3977	5.7554

shows the number of pairs used in calculating the correlation between the input and output signals in the check valve leakage experiment. The amplitudes of the original signal and the output signal in the frequency domain are shown in

Table 2. Frequency domain amplitude ratio of original and output signals of check valve leakage experiment.

Valve Core	Original Signal Spectral Amplitude	Output Signal Spectral Amplitude	Is the Peak Frequency Equal	Amplitude Ratio
Entire seal surface defect	0.00108	0.01123	Yes	10.3981
Local seal surface defect	0.00148	0.00356	Yes	2.4054
Eccentric spool defect	0.00267	0.03124	Yes	11.7004

. The experimental results demonstrated significant cross-correlation gains: 6.9569 for the globally damaged spool, 4.4128 for the locally damaged spool, and 5.7554 for the eccentric fault spool. Notably, the proposed SaRT-CMSR method successfully enhanced all three types of fault signals that were initially completely obscured by white noise, achieving both effective noise reduction and accurate fault frequency identification. Specifically, the method preserved the original signal’s peak frequency while significantly amplifying its amplitude. These findings, derived from a comprehensive analysis of the leakage signals across the three distinct fault conditions, conclusively validate the feasibility and effectiveness of the SaRT-CMSR method for enhancing valve-leakage signals in practical applications.

To further investigate the influence of the controlled system parameters, the leakage signal from an eccentric spool defect check valve was employed as a case study. The controlled system parameters were set to a = b = 1. The noise reduction output signal processed by the SaRT-CMSR method is shown in Figure 13. After fixing the parameters of the controlled system, the output cross-correlation gain of the system was 3.3204. The spectral analysis indicated that while the processed signal maintained the same peak frequency as the original signal, its amplitude was significantly attenuated, failing to achieve the desired enhancement effect. A comparative analysis between Figure 12 and Figure 13 showed a suboptimal performance for the output in Figure 13. These experimental findings provide empirical validation of the parametric analysis results presented in Section 4, confirming the critical role of parameter optimization in system performance.

6. Conclusions

This study presents a novel approach that integrates a search and rescue team optimization algorithm into adaptive CMSR systems, extending its application to the field of valve-leakage signal enhancement. The cross-correlation gain is used as the adaptive optimization index, and the preprocessed signal is input into the system after optimization to obtain the system output. Experimental validation using check valve-leakage signals demonstrated the efficacy of the proposed method in achieving simultaneous noise reduction and signal enhancement. The results indicate significant improvement in fault frequency peak detection, with enhanced capability for leakage-signal characterization in noisy operational environments. This advancement establishes a robust foundation for subsequent leakage pattern recognition and quantitative diagnostic analyses in hydraulic valve systems, potentially contributing to more accurate and reliable condition monitoring in industrial applications.

Through comprehensive analysis of simulation signal parameters, this study concluded that effective optimization of the CMSR system requires not only the adjustment of control system parameters but also the optimization of controlled system parameters. This dual-parameter optimization strategy was empirically validated through measured signal processing, demonstrating its critical role in enhancing system performance. The experimental results confirmed that the simultaneous optimization of both parameter sets significantly improves the system’s processing capabilities.

This study successfully accomplished noise suppression and signal enhancement in the detection of one-way valve leakage. Considering the universal characteristics of hydraulic valve-leakage mechanisms, the proposed algorithm has the potential for generalization to internal leakage signal enhancement across different valve types. Future research directions could involve integrating this methodology with deep learning techniques to advance valve-leakage fault diagnosis capabilities.